Open Access Article
Open Access ArticleComplex three-dimensional graphene structures driven by surface functionalization†
Duc Tam
Ho
 a,
Viet Hung
Ho
b,
Vasudeo
Babar
a,
Sung Youb
Kim
a,
Viet Hung
Ho
b,
Vasudeo
Babar
a,
Sung Youb
Kim
 *b and
Udo
Schwingenschlögl
*b and
Udo
Schwingenschlögl
 *a
*a
aPhysical Science and Engineering Division (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia. E-mail: udo.schwingenschlogl@kaust.edu.sa
bDepartment of Mechanical Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Republic of Korea. E-mail: sykim@unist.ac.kr
First published on 30th April 2020
Abstract
The origami technique can provide inspiration for fabrication of novel three-dimensional (3D) structures with unique material properties from two-dimensional sheets. In particular, transformation of graphene sheets into complex 3D graphene structures is promising for functional nano-devices. However, practical realization of such structures is a great challenge. Here, we introduce a self-folding approach inspired by the origami technique to form complex 3D structures from graphene sheets using surface functionalization. A broad set of examples (Miura-ori, water-bomb, helix, flapping bird, dachshund dog, and saddle structure) is achieved via molecular dynamics simulations and density functional theory calculations. To illustrate the potential of the origami approach, we show that the graphene Miura-ori structure combines super-compliance, super-flexibility (both in tension and compression), and negative Poisson's ratio behavior.
Materials with complex 3D structures can exhibit extraordinary properties such as critical transition to bistability in a square twist origami,1 high mechanical strength close to the theoretical limit in lightweight classy carbon lattices,2 switchable radio-frequency capacity in morphable mesostructures,3 negative refraction in metamaterials formed by split-ring resonators and wires,4 and negative thermal expansion in origami metamaterials.5 As a result, complex 3D structures are important in various fields such as micro-electromechanical systems,6 biomedical devices,7 robotics,8 and solar cells.9 Among the fabrication techniques, self-folding origami is powerful to create 3D structures from 2D sheets.10,11 In the traditional origami technique 3D objects are created by folding paper sheets by hand, whereas in self-folding origami other driving forces at pre-defined areas of the 2D sheets activate folding. For example, stresses can be introduced in thin films via capillary forces,12,13 pre-stretching (in active multilayers),14,15 or responsive materials such as shape memory polymers16,17 and hydrogels.18,19 The introduced stresses act as driving forces to cause out-of-plane bending of the 2D sheets.
Graphene, a 2D material with many excellent properties,20 can serve as prototypical constituent for forming complex 3D structures that have new functionalities not seen in graphene or macroscale counterparts. From the mechanical point of view, the high flexibility of the 2D material enables formation of 3D structures without damages. However, so far only simple 3D graphene structures have been addressed, such as nanotubes,21 nanoscrolls,22 and basic polyhedra,23,24 using single-side hydrogenation21–24 or nanodroplets that generate capillary forces25 to drive the 3D transformation. The reason is that the control over the folding angle, which is essential for the construction of complex 3D structures, is still challenging even for macroscale objects.10 Therefore, new approaches, which can control the folding angle, must be developed to achieve highly complex 3D graphene structures with novel material properties.
In this study, we combine molecular dynamics (MD) simulations, density functional theory (DFT) calculations, and an analytical model to demonstrate that surface functionalization of graphene can be exploited to construct complex 3D structures from 2D material sheets. The approach requires preparation of a 2D folding pattern (locations, directions, and widths of the folds) at which the functionalization is conducted, see Fig. 1a. The pseudo surface stresses induced by the surface functionalization cause out-of-plane bending of the 2D material sheet at the functionalized areas. Our analytical model suggests that the folding angle can be controlled readily by three parameters: adatom type, width of the folds, and density of the adatoms. Consequently, many 3D graphene structures can be obtained from graphene sheets with properly designed 2D folding patterns. Demonstrations are presented for three adatom types (hydrogen, nitrogen, and fluorine) to construct complex structures (Miura-ori, water-bomb, helix, flapping bird, dachshund dog, and saddle). Novel mechanical properties not seen in any previous graphene structure are found, including super-compliance, super-flexibility (both in tension and compression), and negative Poisson's ratio behavior. The introduced approach provides a promising route to 3D functional nano-devices with unique material properties based on 2D materials.
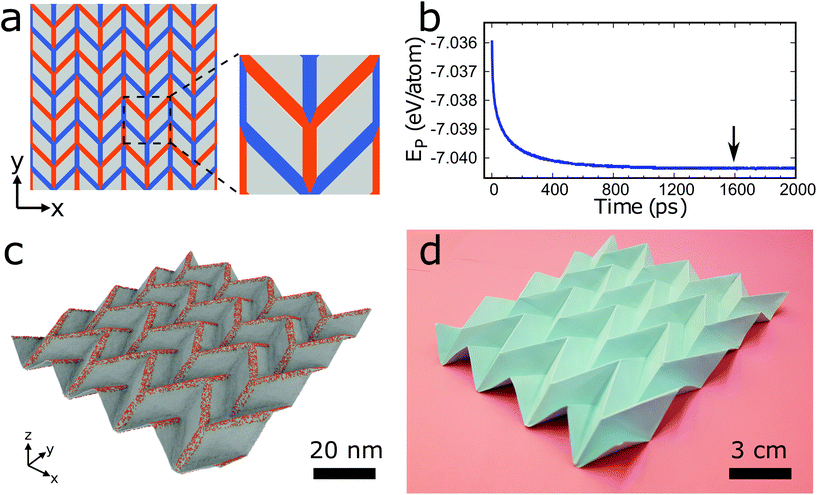
Fig. 1a–d displays an example of the surface functionalization approach to transform a graphene sheet into a 3D structure. We first focus on obtaining a well-known origami tessellation, the Miura-ori structure, using hydrogenation and MD simulations. We begin with a pre-defined 2D folding pattern, which is a set of intersecting lines that become future folds (see Fig. 1a). We note that these lines have finite width in contrast to zero width in the traditional origami technique. Hydrogen atoms are placed onto the lines colored in red in Fig. 1a on the front side of the graphene sheet with a certain density (ratio of the number of hydrogen atoms and the number of carbon atoms) to generate future mountain folds and onto the lines colored in blue on the back side of the graphene sheet with the same density to generate future valley folds. We choose a width of the patterning lines of w = 2.5 nm, density of the hydrogen atoms of ρ = 15%, and initial size of the unitcell of 24.3 nm × 24.3 nm. The model of Fig. 1a (4 × 4 supercell) consists of about 385![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, which are modeled using the second generation REBO (REBO-II) potential.26 To eliminate edge effects, we apply periodic boundary conditions in the in-plane directions. Initially, a molecular statics simulation is carried out using the conjugate gradient method. Then, the system is equilibrated at 300 K using an isothermal-isobaric ensemble (for details see Simulation methods section). Fig. 1b shows that the potential energy as a function of the MD simulation time decreases and begins to saturate after about 1200 ps. The structure at 1600 ps (which is marked by an arrow in Fig. 1b) is presented in Fig. 1c. Fig. 1d shows a photograph of a paper Miura-ori structure folded by hand, which is 1.5 × 106 times larger than the graphene Miura-ori structure (same 2D folding pattern except for the fact that the width of the patterning lines is negligible for the paper structure). Our approach of surface functionalization is able to deliver a pre-defined 3D graphene structure. We also employ DFT calculations to study the formation of graphene Miura-ori structures using hydrogen, nitrogen, and fluorine adatoms to ensure generality of our findings. Due to the high computational cost, we consider small systems with 144 atoms (see Fig. S1a in ESI†). Our results confirm that Miura-ori graphene structures can be obtained by hydrogenation, nitrogenation, or fluorination of graphene sheets (see Fig. S1b in ESI†). Molecular statics simulations with the REBO-II potential for the graphene Miura-ori structure using hydrogenation as an example show excellent agreement with the DFT results (Fig. S1b in ESI†). Both the DFT and molecular statics results clearly demonstrate that surface functionalization with different adatom types can be employed to construct origami structures from graphene sheets. We will explain the mechanism of the folding in the following.
000 atoms, which are modeled using the second generation REBO (REBO-II) potential.26 To eliminate edge effects, we apply periodic boundary conditions in the in-plane directions. Initially, a molecular statics simulation is carried out using the conjugate gradient method. Then, the system is equilibrated at 300 K using an isothermal-isobaric ensemble (for details see Simulation methods section). Fig. 1b shows that the potential energy as a function of the MD simulation time decreases and begins to saturate after about 1200 ps. The structure at 1600 ps (which is marked by an arrow in Fig. 1b) is presented in Fig. 1c. Fig. 1d shows a photograph of a paper Miura-ori structure folded by hand, which is 1.5 × 106 times larger than the graphene Miura-ori structure (same 2D folding pattern except for the fact that the width of the patterning lines is negligible for the paper structure). Our approach of surface functionalization is able to deliver a pre-defined 3D graphene structure. We also employ DFT calculations to study the formation of graphene Miura-ori structures using hydrogen, nitrogen, and fluorine adatoms to ensure generality of our findings. Due to the high computational cost, we consider small systems with 144 atoms (see Fig. S1a in ESI†). Our results confirm that Miura-ori graphene structures can be obtained by hydrogenation, nitrogenation, or fluorination of graphene sheets (see Fig. S1b in ESI†). Molecular statics simulations with the REBO-II potential for the graphene Miura-ori structure using hydrogenation as an example show excellent agreement with the DFT results (Fig. S1b in ESI†). Both the DFT and molecular statics results clearly demonstrate that surface functionalization with different adatom types can be employed to construct origami structures from graphene sheets. We will explain the mechanism of the folding in the following.
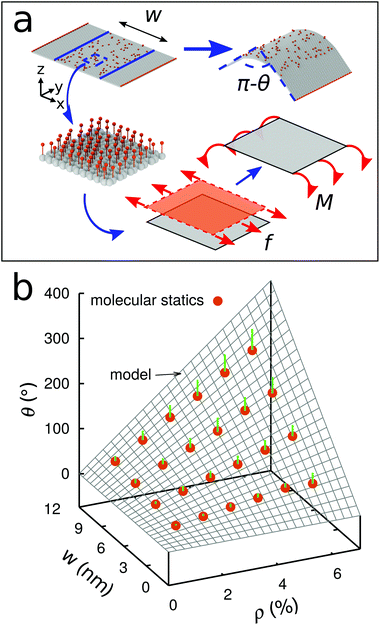
We next develop an analytical model to understand the mechanism of the folding using the classical plate theory (Kirchhoff–Love plate theory) with some modifications. For simplicity of the analysis, we consider the case that the 2D folding pattern consists solely of one line with width w and infinite length Ly due to the periodic boundary condition in this direction, see Fig. 2a. Hydrogenation causes cylindrical folding of the graphene sheet as demonstrated in Fig. 2a. We suppose that surface functionalization generates isotropic pseudo surface stresses serving as driving forces that fold locally the 2D material sheet. The 2D material sheet is assumed to be only subject to pure bending due to the pseudo surface stresses. We predict that the folding angle θ (Fig. 2a) is given by (see ESI†)
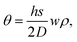 | (1) |
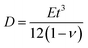 , as in the classical plate theory, because the definition of the thickness t is ambiguous in the bending.27 Rather, D can be calculated by obtaining the strain energy of the corresponding nanotube as a function of the nanotube radius.28 To validate the prediction of the analytical expression of eqn (1), we conduct various molecular statics simulations (with REBO-II potential) for the 2D folding pattern in Fig. 2a with different values of w (ranging from 2.7 nm to 10.8 nm) and ρ (ranging from 1% to 6%). For the case of hydrogenation of graphene, we obtain s = 9.7 N m−1 and D = 0.225 nN nm (see ESI†), in good agreement with the experimental value of 0.192 nN nm.29 We present in Fig. 2b a comparison between the folding angle predicted by the analytical model and the results of the molecular statics simulations, showing good agreement especially at smaller folding angles. When the deformation becomes very large the mechanical response becomes non-linear, i.e., the linear assumption of our theory breaks down. Both the analytical model and simulation demonstrate that the folding angle of a graphene sheet induced by surface functionalization with a given adatom type is directly proportional to both w and ρ.
, as in the classical plate theory, because the definition of the thickness t is ambiguous in the bending.27 Rather, D can be calculated by obtaining the strain energy of the corresponding nanotube as a function of the nanotube radius.28 To validate the prediction of the analytical expression of eqn (1), we conduct various molecular statics simulations (with REBO-II potential) for the 2D folding pattern in Fig. 2a with different values of w (ranging from 2.7 nm to 10.8 nm) and ρ (ranging from 1% to 6%). For the case of hydrogenation of graphene, we obtain s = 9.7 N m−1 and D = 0.225 nN nm (see ESI†), in good agreement with the experimental value of 0.192 nN nm.29 We present in Fig. 2b a comparison between the folding angle predicted by the analytical model and the results of the molecular statics simulations, showing good agreement especially at smaller folding angles. When the deformation becomes very large the mechanical response becomes non-linear, i.e., the linear assumption of our theory breaks down. Both the analytical model and simulation demonstrate that the folding angle of a graphene sheet induced by surface functionalization with a given adatom type is directly proportional to both w and ρ.
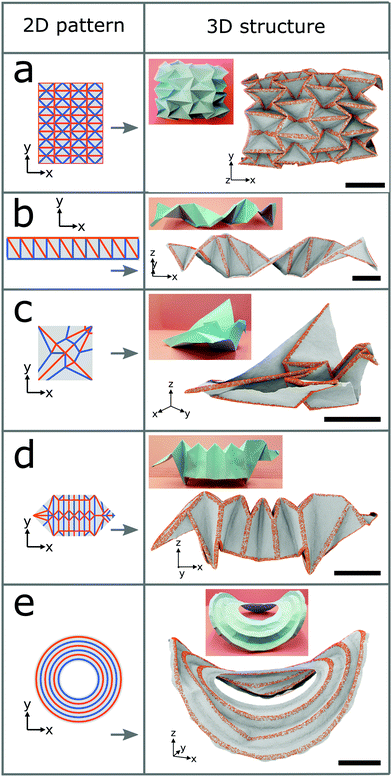
We now employ the surface functionalization to form diverse complex structures as shown in Fig. 3. A schematic of the 2D folding pattern for the 3D transformation is provided in each case. Hydrogen is chosen as the adatom and the folds have widths of 2.5 nm. The densities of the hydrogen atoms are 20%, 30%, 30%, and 15% for the water-bomb, helix, flapping bird, and saddle structures, respectively, and for the dachshund dog structure they range from 10% to 30%. Fig. 3a shows the water-bomb structure, as an example of a complex tessellation origami, representative of dome-like structures with positive average Gaussian curvature (while that of the Miura-ori structure is zero). Macroscale water-bomb structures are used for many applications such as medical stents,30 animal robots,31 and deformable wheels.32 The helix structure of Fig. 3b may be used as nanometer-sized molecular spring or as inductor. More complex flapping bird and dachshund dog structures are shown in Fig. 3c and d, respectively. To obtain the dachshund dog structure different densities of the hydrogen atoms must be used for different line segments. Finally, we show in Fig. 3e the saddle structure (with negative average Gaussian curvature) with curved instead of straight folds as in the other cases. The pseudo surface stresses induced by the surface functionalization in this case not only generate the folding but also trigger global buckling due to the geometrical constraint.33 As a result, the obtained structure is characterized by both the folding and global buckling behaviors. Demonstrations of the self-folding origami approach so far are restricted to structures with simple folding patterns even on the macroscale. The ability of producing complex 3D structures proves the robustness of our self-folding approach by controlling the folding angle via the adatom type, width of the folds, and density of the adatoms. The transformations from graphene sheets to complex 3D structures by hydrogenation are illustrated in Fig. S4 in the ESI† for all the cases of Fig. 1c and 3.
We have confirmed that our conclusions do not depend critically on the ambient conditions (see a comparison of results at 1 atm pressure in Fig. S5 in ESI†) and that folds with larger widths can be used without further complications (see Fig. S6 in ESI† for a case with w = 17.2 nm). Our MD simulations also show that the 2D folding pattern is not compromised by diffusion of the hydrogen atoms. In addition, defects in the graphene sheet do not pose a limitation to the effectiveness of our approach (see Fig. S7 in ESI† for a case with double vacancies). Importantly, existing fabrication techniques indicate that practical realization of the proposed scheme is likely to be possible. In particular, surface functionalization of graphene with highly tunable density of adatoms has been realized by routes such as plasma functionalization,34,35 thermal cracking,36 and Birch-type hydrogenation.37 Patterning of functionalized graphene has been demonstrated with 18 nm resolution for hydrogenation using electron beam irradiation38,39 and with 40 nm resolution for fluorination using thermochemical nanolithography.40
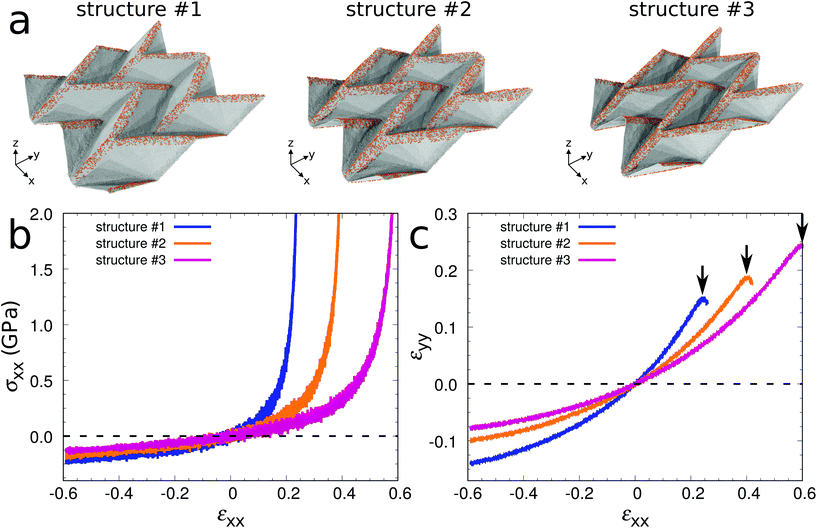
To illustrate that extraordinary 3D graphene structures can be obtained by surface functionalization, we demonstrate in the following a unique combination of mechanical properties for graphene Miura-ori structures. Fig. 4a shows three equilibrated structures obtained by MD simulations at 300 K (#1: w = 2.5 nm and ρ = 15%; #2: w = 3.7 nm and ρ = 15%; #3: w = 2.5 nm and ρ = 20%). To save computational time, we use a 2 × 2 supercell after confirming that the difference between the equilibrated structures of the 2 × 2 and 4 × 4 supercell models is negligible. The geometrical parameters of the three structures are different due to different folding angles (see Table 1). Fig. 4b shows stress–strain curves under uniaxial stress in the x-direction. After equilibration at 300 K, tensile or compressive strain is applied in the x-direction with a strain rate of 108 s−1. During the loading process, the stress component in the y-direction is kept at zero to model uniaxial stress. We first consider structure #2. At small strain (both in tension and compression) the stress linearly increases as the applied strain increases. The Young's modulus Exx is defined to be the average slope of the stress–strain curve in the small strain interval from −0.05 to 0.05. It turns out to be 0.60 GPa, about three orders of magnitude smaller than that of graphene (750 GPa, obtained by our MD simulation using the same procedure as for the graphene Miura-ori structure), indicating super-compliance of the structure. Super-compliance is required in applications such as epidermal electronics to avoid mechanical mismatch to soft substrates.41 Under tension the stress increases significantly as the applied strain reaches a critical value of εc = 0.40, when the structure is almost flattened. Under compression the magnitude of the stress increases gradually without structure failure even at a very large strain of −0.60, whereas it is known that a graphene sheet is subject to buckling already at small strain. These results demonstrate super-flexibility of the structure both in tension and compression. Furthermore, the structure shows expansion/contraction in the y-direction when stretched/compressed in the x-direction, see Fig. 4c. In other words, it exhibits negative Poisson's ratio behavior (auxeticity). This auxeticity is observed in an extremely wide range of applied strain. We note that the Young's modulus, flexibility, and Poisson's ratio of the Miura-ori structures depend on the geometry, which can be controlled by changing the folding angle in eqn (1) (see Fig. 4 and Table 1). We therefore have shown that graphene sheets can be transformed into graphene Miura-ori structures to exhibit simultaneously super-compliance, super-flexibility (both in tension and compression), and negative Poisson's ratio behavior.
| L x | L y | t | E xx (GPa) | ν xy | ε c | |
|---|---|---|---|---|---|---|
| Structure #1 | 39.6 | 42.1 | 6.0 | 1.00 | −0.44 | 0.25 |
| Structure #2 | 34.7 | 40.6 | 6.6 | 0.60 | −0.30 | 0.40 |
| Structure #3 | 30.4 | 38.7 | 7.3 | 0.38 | −0.22 | 0.60 |
The mechanical properties of our graphene Miura-ori structures cannot be attained from any known graphene structure. Techniques such as kirigami and scroll42–44 can provide super-compliance and/or super-stretchability for electrodes,44 strain sensors,45 and epidermal electronics.41 However, in these cases super-flexibility applies to the tension case only, whereas Miura-ori structures show super-flexibility both in tension and compression. In addition, although materials and metamaterials with negative Poisson's ratio behavior have been investigated widely46,47 because of their counter-intuitive behavior, only few studies have described auxeticity in graphene.48–51 Even in these cases auxeticity appears only under extreme circumstances, such as high temperature in graphene with thermally induced ripples (above 1500 K)51 and very small applied strain (less than 0.005) in graphene ribbons.50 Exceptional work showing auxeticity at room temperature has dealt with rippled graphene,48 but the auxeticity is observed within a relatively small range of applied tensile strain (0.0 to 0.15). On the other hand, in graphene Miura-ori structures tunable auxeticity appears at room temperature and in an extremely wide range of tensile and compressive strain (−0.6 to 0.6). The modifications of the mechanical properties of the graphene Miura-ori structures highlight the great potential of the surface functionalization approach to design graphene metamaterials. It is noted that the combination of such excellent mechanical properties is solely due to the 3D geometry. Furthermore, material properties of 3D graphene structures can be tailored by chemical modification and surface corrugation. For example, hydrogenated/chlorinated graphene even with low coverage density of adatoms has much lower electrical conductivity than pristine graphene,52,53 and surface corrugation opens a band gap in graphene.54 Hydrogenation of graphene strongly affects the photoluminescence.55
In summary, we propose a design approach to form complex 3D structures by locally folding graphene sheets through surface functionalization. The underlying mechanism of the folding, which is associated with the pseudo surface stress induced by the surface functionalization, is studied systematically. The design approach is based on folds at specific locations with mountain/valley assignments. The folding angle is controlled by the adatom type, widths of the folds, and density of the adatoms. MD simulations and DFT calculations show that various complex 3D graphene structures can be created. The obtained graphene Miura-ori structures show a unique combination of mechanical properties (super-compliance, super-flexibility both in tension and compression, and auxeticity). The possibilities offered by the proposed design approach are not restricted to the cases presented here. Further 3D graphene structures with desirable properties may be tailored via combinations of 3D geometry, chemical modification, and surface corrugation.
Simulation methods
Molecular statics and MD simulations
We employ the LAMMPS code56 for performing the simulations and the open tool OVITO for visualizations.57 The interaction between the atoms is modeled by the REBO-II potential.26 The zigzag and armchair directions of graphene correspond to the x- and y-directions, respectively. Initially, hydrogen atoms are randomly attached to the carbon atoms in the designated areas with given densities. In the case of the Miura-ori structures periodic boundary conditions are applied in the x- and y-directions. The system is initially relaxed by a molecular statics simulation with the conjugate gradient method and then dynamically equilibrated at 300 K using an MD simulation. The conjugate gradient minimization is deemed to be convergent when the total energy change between successive iterations divided by the total energy is less than 10−16. The MD simulations of the Miura-ori structures are executed in the isothermal-isobaric ensemble to ensure that the stress components are zero in the in-plane directions. The convergence of the potential energy is demonstrated in Fig. 1b. For the other structures the MD simulations are carried out in the canonical ensemble. A timestep of 1 fs is chosen in all MD simulations.DFT calculations
Three graphene Miura-ori structures with hydrogen, nitrogen, or fluorine surface functionalization are studied by Kohn–Sham self-consistent density functional theory, as implemented in the SIESTA code,58 using a double zeta plus polarization basis set. The core electrons are described by norm-conserving Troullier–Martins pseudopotentials and the exchange–correlation interaction is treated in the generalized gradient approximation (Perdew–Burke–Ernzerhof flavor). We consider the 1 × 1 supercell (16.85 Å × 15.81 Å) shown in Fig. S1a† with 3D periodic boundary conditions and a 20 Å thick vacuum layer along the z-direction. The reciprocal space is sampled on a Monkhorst Pack 3 × 3 × 1 k-mesh and an energy cutoff of 300 Ry is used. The atomic force criterion of the structure relaxation is set to 5 meV Å−1.Author contribution
Duc Tam Ho, Viet Hung Ho, and Vasudeo Babar carried out the simulations. Sung Youb Kim and Udo Schwingenschlögl supervised the project.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
The research reported in this publication was supported by funding from King Abdullah University of Science and Technology. Computational resources were provided by the UNIST Supercomputing Center. S. Y. K. acknowledges support from the Mid-Career Researcher Support Program (No. 2019R1A2C2011312) of the National Research Foundation of Korea.References
- J. L. Silverberg, J.-H. Na, A. A. Evans, B. Liu, T. C. Hull, C. D. Santangelo, R. J. Lang, R. C. Hayward and I. Cohen, Nat. Mater., 2015, 14, 389–393 CrossRef CAS PubMed.
- J. Bauer, A. Schroer, R. Schwaiger and O. Kraft, Nat. Mater., 2016, 15, 438–443 CrossRef CAS PubMed.
- H. Fu, K. Nan, W. Bai, W. Huang, K. Bai, L. Lu, C. Zhou, Y. Liu, F. Liu, J. Wang, M. Han, Z. Yan, H. Luan, Y. Zhang, Y. Zhang, J. Zhao, X. Cheng, M. Li, J. W. Lee, Y. Liu, D. Fang, X. Li, Y. Huang, Y. Zhang and J. A. Rogers, Nat. Mater., 2018, 17, 268–276 CrossRef CAS PubMed.
- D. R. Smith, J. B. Pendry and M. C. K. Wiltshire, Science, 2004, 305, 788–792 CrossRef CAS PubMed.
- E. Boatti, N. Vasios and K. Bertoldi, Adv. Mater., 2017, 29, 1700360 CrossRef PubMed.
- J. Rogers, Y. Huang, O. G. Schmidt and D. H. Gracias, MRS Bull., 2016, 41, 123–129 CrossRef.
- C. L. Randall, E. Gultepe and D. H. Gracias, Trends Biotechnol., 2012, 30, 138–146 CrossRef CAS PubMed.
- S. Felton, M. Tolley, E. Demaine, D. Rus and R. Wood, Science, 2014, 345, 644–646 CrossRef CAS PubMed.
- X. Guo, H. Li, B. Y. Ahn, E. B. Duoss, K. J. Hsia, J. A. Lewis and R. G. Nuzzo, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20149–20154 CrossRef CAS PubMed.
- S. J. P. Callens and A. A. Zadpoor, Mater. Today, 2018, 21, 241–264 CrossRef.
- X. Ning, X. Wang, Y. Zhang, X. Yu, D. Choi, N. Zheng, D. S. Kim, Y. Huang, Y. Zhang and J. A. Rogers, Adv. Mater. Interfaces, 2018, 5, 1800284 CrossRef.
- R. R. A. Syms and E. M. Yeatman, Electron. Lett., 1993, 29, 662–664 CrossRef.
- D. H. Gracias, V. Kavthekar, J. C. Love, K. E. Paul and G. M. Whitesides, Adv. Mater., 2002, 14, 235–238 CrossRef CAS.
- J.-H. Cho, T. James and D. H. Gracias, Adv. Mater., 2010, 22, 2320–2324 CrossRef CAS PubMed.
- V. B. Shenoy and D. H. Gracias, MRS Bull., 2012, 37, 847–854 CrossRef CAS.
- Y. Liu, J. K. Boyles, J. Genzer and M. D. Dickey, Soft Matter, 2012, 8, 1764–1769 RSC.
- J. Cui, S. Yao, Q. Huang, J. G. M. Adams and Y. Zhu, Soft Matter, 2017, 13, 3863–3870 RSC.
- Z. L. Wu, M. Moshe, J. Greener, H. Therien-Aubin, Z. Nie, E. Sharon and E. Kumacheva, Nat. Commun., 2013, 4, 1586 CrossRef PubMed.
- J.-H. Na, A. A. Evans, J. Bae, M. C. Chiappelli, C. D. Santangelo, R. J. Lang, T. C. Hull and R. C. Hayward, Adv. Mater., 2014, 27, 79 CrossRef PubMed.
- Y. Zhu, S. Murali, W. Cai, X. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924 CrossRef CAS PubMed.
- D. Yu and F. Liu, Nano Lett., 2007, 7, 3046–3050 CrossRef CAS PubMed.
- S. Zhu and T. Li, J. Phys. D: Appl. Phys., 2013, 46, 075301 CrossRef.
- L. Zhang, X. Zeng and X. Wang, Sci. Rep., 2013, 3, 03162 CrossRef PubMed.
- S. Zhu and T. Li, ACS Nano, 2014, 8, 2864–2872 CrossRef CAS PubMed.
- N. Patra, B. Wang and P. Král, Nano Lett., 2009, 9, 3766–3771 CrossRef CAS PubMed.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef CAS.
- Y. Huang, J. Wu and K. C. Hwang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245413 CrossRef.
- Q. Lu, M. Arroyo and R. Huang, J. Phys. D: Appl. Phys., 2009, 42, 102002 CrossRef.
- R. Nicklow, N. Wakabayashi and H. G. Smith, Phys. Rev. B: Solid State, 1972, 5, 4951–4962 CrossRef.
- K. Kuribayashi, K. Tsuchiya, Z. You, D. Tomus, M. Umemoto, T. Ito and M. Sasaki, Mater. Sci. Eng., A, 2006, 419, 131–137 CrossRef.
- C. D. Onal, R. J. Wood and D. Rus, IEEE/ASME Trans. Mechatronics, 2013, 18, 430–438 Search PubMed.
- B. P. Rhoads and H.-J. Su, Proceedings of the ASME, 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2016, V05BT07A021.
- M. A. Dias, L. H. Dudte, L. Mahadevan and C. D. Santangelo, Phys. Rev. Lett., 2012, 109, 114301 CrossRef PubMed.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- M. Baraket, S. G. Walton, E. H. Lock, J. T. Robinson and F. K. Perkins, Appl. Phys. Lett., 2010, 96, 231501 CrossRef.
- R. Balog, B. Jørgensen, J. Wells, E. Lægsgaard, P. Hofmann, F. Besenbacher and L. Hornekær, J. Am. Chem. Soc., 2009, 131, 8744–8745 CrossRef CAS PubMed.
- X. Zhang, Y. Huang, S. Chen, N. Y. Kim, W. Kim, D. Schilter, M. Biswal, B. Li, Z. Lee, S. Ryu, C. W. Bielawski, W. S. Bacsa and R. S. Ruoff, J. Am. Chem. Soc., 2016, 138, 14980–14986 CrossRef CAS PubMed.
- S. Ryu, M. Y. Han, J. Maultzsch, T. F. Heinz, P. Kim, M. L. Steigerwald and L. E. Brus, Nano Lett., 2008, 8, 4597–4602 CrossRef CAS PubMed.
- J. Liu, S. Chen, R. Papadakis and H. Li, Nanotechnology, 2018, 29, 415304 CrossRef PubMed.
- W.-K. Lee, M. Haydell, J. T. Robinson, A. R. Laracuente, E. Cimpoiasu, W. P. King and P. E. Sheehan, ACS Nano, 2013, 7, 6219–6224 CrossRef CAS PubMed.
- S. Zhu, Y. Huang and T. Li, Appl. Phys. Lett., 2014, 104, 173103 CrossRef.
- Z. Qi, D. K. Campbell and H. S. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245437 CrossRef CAS.
- M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill, P. Y. Huang, A. R. Ruyack, J. W. Kevek, B. Kobrin, D. A. Muller and P. L. McEuen, Nature, 2015, 524, 204–207 CrossRef CAS PubMed.
- N. Liu, A. Chortos, T. Lei, L. Jin, T. R. Kim, W.-G. Bae, C. Zhu, S. Wang, R. Pfattner, X. Chen, R. Sinclair and Z. Bao, Sci. Adv., 2017, 3, e1700159 CrossRef PubMed.
- Y. Wang, R. Yang, Z. Shi, L. Zhang, D. Shi, E. Wang and G. Zhang, ACS Nano, 2011, 5, 3645–3650 CrossRef CAS PubMed.
- C. Huang and L. Chen, Adv. Mater., 2016, 28, 8079–8096 CrossRef CAS PubMed.
- J.-W. Jiang, S. Y. Kim and H. S. Park, Appl. Phys. Rev., 2016, 3, 041101 Search PubMed.
- J. N. Grima, S. Winczewski, L. Mizzi, M. C. Grech, R. Cauchi, R. Gatt, D. Attard, K. W. Wojciechowski and J. Rybicki, Adv. Mater., 2014, 27, 1455–1459 CrossRef PubMed.
- V. H. Ho, D. T. Ho, S.-Y. Kwon and S. Y. Kim, Phys. Status Solidi B, 2016, 253, 1303–1309 CrossRef CAS.
- J.-W. Jiang and H. S. Park, Nano Lett., 2016, 16, 2657–2662 CrossRef CAS PubMed.
- J.-W. Jiang, T. Chang and X. Guo, Nanoscale, 2016, 8, 15948–15953 RSC.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- B. Li, L. Zhou, D. Wu, H. Peng, K. Yan, Y. Zhou and Z. Liu, ACS Nano, 2011, 5, 5957–5961 CrossRef CAS PubMed.
- K.-K. Bai, Y. Zhou, H. Zheng, L. Meng, H. Peng, Z. Liu, J.-C. Nie and L. He, Phys. Rev. Lett., 2014, 113, 086102 CrossRef PubMed.
- K. E. Whitener, J. Vac. Sci. Technol., A, 2018, 36, 05G401 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Stukowski, Model. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr01733g |
| This journal is © The Royal Society of Chemistry 2020 |