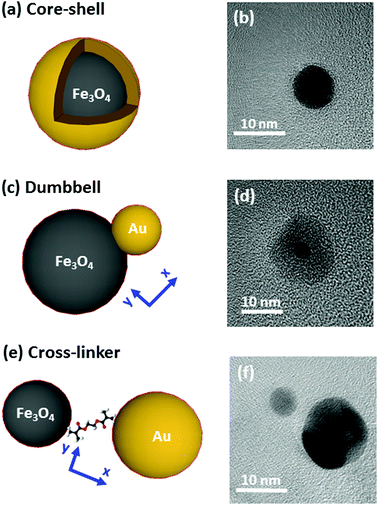
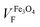Hybrid magnetite–gold nanoparticles as bifunctional magnetic–plasmonic systems: three representative cases†
J.
Canet-Ferrer
 *ab,
P.
Albella
*ab,
P.
Albella
 bc,
A.
Ribera
a,
J. V.
Usagre
a and
S. A.
Maier
a
bc,
A.
Ribera
a,
J. V.
Usagre
a and
S. A.
Maier
a
aInstituto de ciencia molecular (ICMol) de la Universidad de Valencia, c/ Catedrático José Beltrán Martínez num. 2, E46980 Paterna, Spain. E-mail: jose.canet-ferrer@uv.es
bEXSS Group, Physics Department, Imperial College London, London, SW7 2AZ, UK
cUniversity Institute for Intelligent Systems and Numerical Applications in Engineering (SIANI), University of Las Palmas de Gran Canaria, Las Palmas de Gran Canaria, 35017, Spain
First published on 12th April 2017
Abstract
Hybrid systems based on magnetite and gold nanoparticles have been extensively used as bifunctional materials for bio- and nano-technology. The properties of these composites are assumed to be closely related to the magnetite to gold mass ratio and to the geometry of the resulting hetero-structures. To illustrate this, we compare and analyze the optical and magnetic properties of core–shell, dumbbell-like dimers and chemical cross-linked pairs of magnetite and gold nanoparticles in detail. We explore how the combination of gold with magnetite can lead to an improvement of the optical properties of these systems, such as tunability, light scattering enhancement or an increase of the local electric field at the interface between magnetic and plasmonic constituents. We also show that although the presence of gold might affect the magnetic response of these hybrid systems, they still show good performance for magnetic applications; indeed the resulting magnetic properties are more dependent on the NP size dispersion. Finally, we identify technological constraints and discuss prospective routes for the development of further magnetic–plasmonic materials.
Conceptual insightsHuge efforts are being made not only to find novel hybrid magnetic–plasmonic structures and to optimize the procedures, but also to improve their efficiency and reproducibility. However, the wide range of different applications that rely on hybrid magnetic–plasmonic materials, make it very difficult to find a unique system fulfilling all the requirements. This makes it hard to choose the best option for each case. The main difference here with respect to previous works, is that we opted for presenting a detailed comparison between the magnetic and optical properties in three representative cases, instead of only paying attention to the design of hetero-structures. Our aim is to illustrate the capabilities of magnetic–plasmonic systems in all possible scenarios. We believe that the main novelty is that we distinguish the role played by both the magnetic and the plasmonic clusters in the resulting material properties. Moreover, the results are presented in a way that they can be easily extrapolated to other composites. Consequently, with this comparison we offer a tool to qualitatively foresee the properties of different kinds of hetero-structures. Based on the systems here described, the reader is invited to evaluate the most relevant parameters for the pursued technological application. |
Introducction
Emerging nanotechnologies are continuously demanding the development of hybrid materials able to provide multiple functionalities on the same technological platform. For this reason, in the last few years the synthesis of magnetic–plasmonic noble metal nanoparticles (NPs) has received a lot of attention.1–3 In these systems, the magnetism and the optical properties arising from localized surface plasmon resonances (LSPRs) co-exist at the metal–dielectric interfaces.4,5 Among the different options, magnetite–gold systems are being extensively developed, mainly because they have successfully shown the above mentioned capabilities together with high chemical stability both in aqueous media6,7 (as required for biological applications) and in organic solvents (compatible with organic electronics and lithography resists).8,9 Gold NPs support plasmon resonances in ultra-violet, visible and near infrared and can be combined with colloidal quantum dots, dyes and other functional molecules.10,11 Magnetite NPs support electron paramagnetic resonances at microwave frequencies and allow selective filtering, ordering and positioning on a surface in the presence of an external magnetic field.12,13 In addition, the assembling of the resulting materials on a surface enables additional applications.7,14,15However, synthesis is still one of the main difficulties during the development of manifold composites. A wide range of procedures for the fabrication of multi-functional hetero-structures based on NPs can be found in the literature.16 Depending on the application, the options vary from the most compact core–shell NPs to more complex composites with multiple nano- or micro-clusters of different compositions.4,17–19 Since several step reactions are usually required, these approaches are still challenging; and the fabrication techniques show important issues that need to be solved, such as the efficiency, reproducibility, or filtering of undesired products. Huge efforts are being made to find novel structures, to optimize the syntheses and to prove the applications mentioned above. In most works, the bi-functionality of these hybrid structures is demonstrated, but without paying enough attention to the physics leading to those properties. In fact, very few works have studied in detail the coupling between magnetic and plasmonic clusters.20,21
In this work, we compare the electric and magnetic properties of: core–shell NPs, dumbbell-like dimers and chemical cross-linked pairs of magnetite and gold NPs; Fe@Au, Fe(Au) and Fe–Au, respectively. We focus on these because they are representative cases with strong, moderate and low electromagnetic interaction between their constituents, respectively. The highest interaction is found in the Fe@Au configuration, where the LSPR can be tuned with the core size, and the magnetic core is completely covered by the plasmonic shell. An alternative to reduce the gold content in the hybrid system is found on the Fe(Au), by growing small gold clusters on large magnetite NPs. It is also worthy to note that Fe(Au) has been mainly developed for applications in catalysis, but rarely employed in plasmonics.22,23 Consequently, there is a clear lack of reports on the optical properties of this system. Since very recently some authors proposed the use of Fe(Au) for surface enhanced Raman spectroscopy (SERS), fluorescence or optical labelling,24–26 here we aim to provide the theoretical background required for the application of Fe(Au) in these and further developments. The lowest electromagnetic interaction is observed at the Fe–Au because of the inter-particle distance due the linker molecule length. As an advantage, the energy of LSPR is not affected by the presence of the magnetic NP after cross-linking. Based on a comparison of these systems, a complete overview of the hybrid NP composites is offered here. Our results can be used as a reference for a qualitative forecast of magnetic and plasmonic properties of more complex systems.
Experimental section
The systems under study are depicted in Fig. 1 and accompanied by their corresponding representative TEM images. The complete structural characterization is presented in the ESI.†Synthesis
Synthesis of the nanostructures has been carried out by thermal decomposition of gold and iron oxide precursors under argon environment in organic solution at a controlled temperature. More details about the procedures are offered in the ESI.† In Fig. 1, we show on the left an illustration, and on the right a TEM image of the systems under study (core–shell, dumbbell and cross-linker configurations). Firstly, in Fig. 1(a) and (b) we show the Fe@Au as obtained by growing a gold shell by injection of gold precursor in a solution of previously synthesized Fe3O4 NPs (which are used as nucleation centers).27 In particular we present the case of magnetite NPs with an average core diameter of DC = 5.1 ± 0.7 nm. The diameter of the NP increases up to DC–S = 7.2 ± 1.2 nm after the shell growth (see ESI†). Small variations of the core diameter can be achieved by the accurate control of the synthesis parameters during thermal decomposition of the iron precursor (temperature, solvent, concentration, time, etc.), while maintaining an average shell thickness of about 1 nm. Also note, that for larger tuning capabilities, NPs with cores ranging between DC = 4–100 nm and shells up to 40 nm can also be prepared.27–31For the case of the dumbbell, Fe(Au) composites have been synthesised with minor modifications on the procedures of ref. 32. The synthesis begins with the growth of Fe3O4 NPs but in this case, the gold precursor is injected before all the iron oxide precursor in the solution runs out. Under these conditions, the iron oxide NPs act as seeds (i.e. nucleation centers) for the gold clusters [see Fig. 1(c)]. A TEM micrograph corresponding to the case of DAu = 2.9 ± 0.8 nm gold NPs grown on iron oxide seeds is shown as an example in Fig. 1(d). The average diameter of the iron oxide is DFe = 11 ± 3 nm with a certain size and shape distribution. Even though this method allows the fabrication of sizes from DAu = 2 to 8 nm for gold and from DFe = 4 to 20 nm for iron oxide,33,34 in this work we focus on small gold NPs to demonstrate that in this situation we found a minor influence of gold on the magnetic properties.
Finally, Fe–Au is obtained from the chemical cross-linking of magnetic and plasmonic NPs [see Fig. 1(e)]. The strategy is based on previous studies demonstrating that the –NH2 groups of the capping can be readily substituted by stronger ligands (such as –HS or –COOH).35 In Fig. 1(f) we show a TEM micrograph corresponding to the cross-linking of magnetite and gold NPs with diameters of DFe = 7 ± 3 and DAu = 12 ± 3 nm respectively. This procedure allows the combination of previously synthetized gold and iron oxide NPs and it offers multiple combination possibilities.36–38 The procedure includes two dialysis steps to remove extra surfactants and remaining reagents to prevent the formation of large aggregates, as confirmed by dynamic light scattering measurements (DLS), see the ESI.†
Optical properties
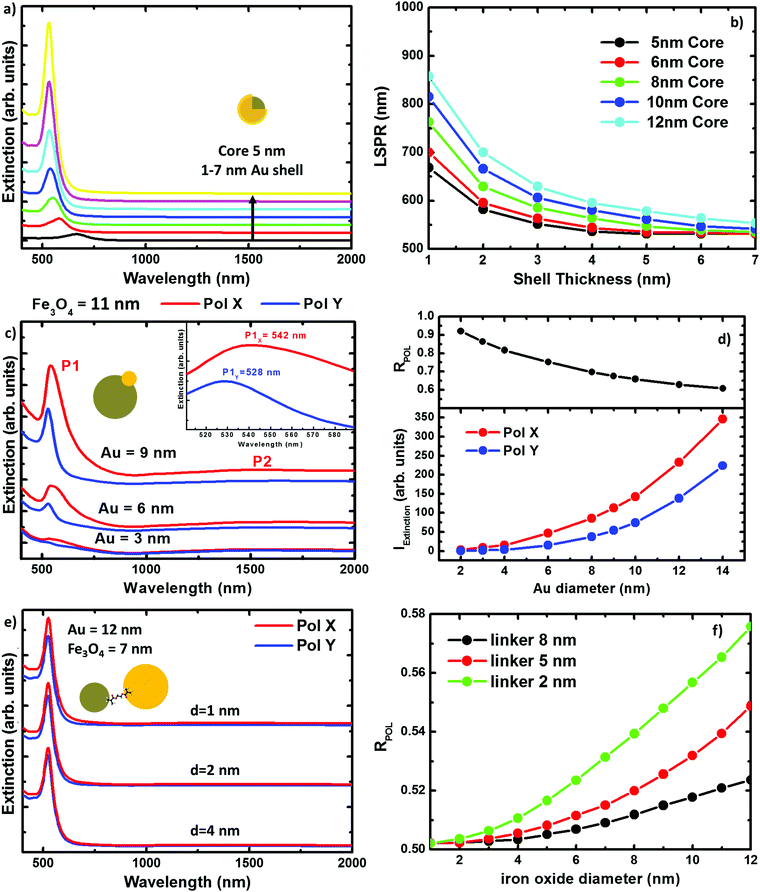
The extinction spectra of the samples in organic solution are plotted in Fig. 2 (red lines) together with its corresponding numerical simulation (in black), and with the spectra from solutions containing the same concentration of magnetite NPs (in dark yellow), i.e. 0.1 mg ml−1. The Fe@Au NPs with DC = 5.1 ± 0.7 nm core diameter (CC–S = 7.2 ± 1.2 nm after shell growth) present a red tone in chloroform, attributed to the LSPR of the gold. In agreement with numerical simulations, the spectrum is dominated by a broad peak centered at λ = 535 nm, see Fig. 2(a). As a reference, we plot the intensity spectrum of bare iron oxide NPs; this consists of a background starting at the near-infrared and increasing its intensity as we move to higher energies. This spectrum explains the pale tone usually found in magnetite NP solutions.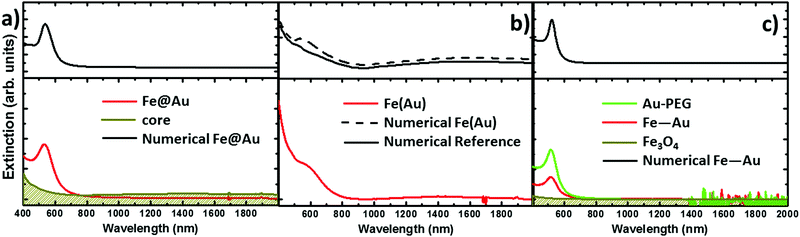 | ||
| Fig. 2 Experimental extinction cross section from NPs in solution (concentration 0.1 mg ml−1). (a) Fe@Au in red and reference Fe3O4 NPs in dark yellow. In this plot the numerical simulation (dashed in black) corresponds to the average extinction spectrum weighted according to the shell size distribution (as described in ESI†). (b) Fe(Au) in red and numerical simulation dashed in black; for this sample we could not got the proper reference since the iron oxide growth is strongly affected by the introduction of the gold precursor. Instead, the dumbbell structure and bare Fe3O4 NPs are compared in the numerical spectra, in black. (c) Fe–Au in red, Au–PEG in green, reference Fe3O4 NPs in dark yellow and numerical simulation dashed in black. Notice in (b and c) the numerical simulation corresponds to a single NP since the relative size variation does not affect the spectral location of the extinction peaks. | ||
In Fig. 2(b) we show Fe(Au) nanostructures with DAu = 2.9 ± 0.8 nm gold NPs grown on DFe = 11 ± 3 nm iron oxide NPs, in organic solution. Now, the extinction spectrum is dominated by magnetite because of the lower gold content in the system. However, the position of the LSPR of gold NPs can be observed around λ = 540 ± 20 nm, as expected from the numerical simulations. This uncertainty is found because the LSPR barely protrudes from the iron oxide background, making the accurate deconvolution of the peak position or broadening estimation difficult. Another important signature of the iron oxide is found at near-infrared wavelengths, with the presence of a broad band centred at λ = 1400–1500 nm, see Fig. 2(b). The intensity of this peak could be explained by the larger amount of iron oxide in this hetero-structure. Also, in the numerical simulations shown in the next section we can expect a certain influence of the gold NPs on the extinction enhancement.
In Fig. 2(c) we show the extinction spectrum measured before and after the cross-linking process of magnetite and gold NPs with diameter sizes of DFe = 7 ± 3 and DAu = 12 ± 3 nm respectively. The extinction spectrum of the gold NP in water after functionalization with PEG is plotted in green showing the LSPR around λ = 520 nm. The spectrum of the magnetite NPs in toluene is depicted in dark yellow. The red plot corresponds to the previous Au–PEG solution after magnetite incorporation. The Fe–Au system is proposed as an example of a low electromagnetic interaction between the magnetic and plasmonic NPs. Indeed the difference between both Au–PEG and Fe–Au solutions consists of a decrease of the peak intensity, but notice that this reduction might be negligible if the spectra were normalized to the number of Au NPs. On the other hand, the near infrared band of the iron oxide cannot be characterized in this sample due to the water absorption bands in that spectral range. Moreover, theoretical simulations in the following section do not indicate relevant optical activity at these frequencies in the case of magnetite NPs of 7 nm diameter.
Numerical study
Numerical simulations of the three hybrid systems have been carried out to explain the experimental extinction spectra. The calculations have been performed by means of the boundary element method (BEM).39,40 Details about the method and its reliability for describing the scattering and absorption response of NPs can be found in the literature.41–44In Fig. 3 we plot the extinction spectra for the three systems under study considering different NP sizes. This illustrates the impact of the NP size on the optical properties for every geometry. In Fig. 3(a), we plot the extinction spectra corresponding to the DC = 5 nm core Fe@Au covered by different thick shells. It can be seen, that the LSPR is found around 700 nm in the case of thinner shells, e.g. 1 nm, and it is blue shifted as the shell thickness is increased. In the case of the 7 nm shell, the LSPR is found at 528 nm very close to the value expected for solid gold NPs. Also worth mentioning is that there is no sign of iron oxide around λ = 1500 nm. This is in good agreement with the experimental results and means that the NIR absorption of the core is negligible in comparison with the shell contribuiton. In Fig. 3(b), we show how the tuning range can be extended up to 900 nm wavelength by varying the core radius from DC = 5 to 12 nm. This means a 400 nm range for tuning, which is a good figure if compared with the size variations required. Both, the blue-shift with the shell thickness and the red-shift due to the core size increase, can be explained in terms of the hybridation model,20,45,46 as will be discussed later.
In Fig. 3(c) we show the extinction peak P1 associated to the LSPR in the Fe(Au) hetero-structure for a fixed magnetite diameter of DFe = 11 nm. It can be seen how, in the case of gold NPs with diameters smaller than DAu = 3 nm, the LSPR of the gold NP does not stand out much from the background. Also in good agreement with our experimental measurements, the LSPR signature in structures with DAu = 3 nm can be identified as a low intensity peak, which starts to dominate the extinction spectra as the dumbbell holds larger gold NPs. On the other hand, a dependence of these spectra on the incident light polarization can be observed, see Fig. 3(d). These polarization effects can be explained in terms of the system symmetry and in particular they are associated to the different strength of dipolar moments induced in any particle. Hence, the electromagnetic interaction between both constituents can be revealed by the evaluation of the polarization anisotropy. To do that, the polarization ratio is defined as RPOL = IEXTX/(IEXTX + IEXTY), where IEXTX and IEXTY are the integrated intensity of the extinction peak at the corresponding polarization direction [see axes at Fig. 1(b)]. The difference between the IEXTX and IEXTY becomes more important in the case of larger gold NPs, see red and blue lines in the Fig. 3(d). However, higher RPOL values are found for the dumbbells hosting the smallest gold NPs, in black. This can be attributed to the interaction between the plasmonic and magnetic NPs, and is more important when the diameter of the iron oxide cluster widely exceeds the gold one. For example, in the case of small gold clusters IEXTY takes the values expected for isolated gold NPs; in contrast IEXTX gets enhanced about 10 times. However, the enhancement starts to be compensated as the size of the gold NPs approaches the iron oxide diameter, reducing the polarization anisotropy. Importantly, the near-infrared absorption peak associated to the iron oxide (P2) also shows polarization dependence. As a result we can conclude that the gold cluster not only contributes with its own optical properties but it also increases the optical activity of the iron oxide. Notice that the polarization anisotropy cannot be measured due to the Brownian motion and random orientation of the NPs in solution, but it could be relevant if this system were employed on functionalized surfaces.
Finally when working with Fe–Au, the linker length represents an important parameter, in some cases as significant as the NP size. Conductive linkers would enable additional resonances arising from monopolar modes due to charge transfer through the molecular bonds.47,48 However, in this research, the only role of the linker is keeping a gap between the gold and the iron oxide NPs. This is because of the linker in use [thyol carboxilyc polyethylene glycol (PEG Mw = 3400)], which is essentially formed by a large (and high resistivity) carbon chain. In Fig. 3(e) we show the extinction spectra calculated for Fe–Au hetero-structures considering magnetite and gold NPs of DFe = 7 and DAu = 12 nm in diameter, respectively; and separated by gaps of d = 1, 2 and 4 nm. Even for such small distances, numerical simulations do not reveal any frequency shift of the LSPRs. This is an expected result if we take into account the low shift observed in the Fe(Au), where the NPs are in close contact. However, as shown in Fig. 3(f) the maximum of the extinction spectra decreases with the linker length showing certain polarization dependence for shorter inter-particle distances. Both, the extinction enhancement and the polarization anisotropy depend on the size of the NPs forming the hetero-structure. In the following, we will show how this can be attributed to the presence of a hot spot between both NPs.
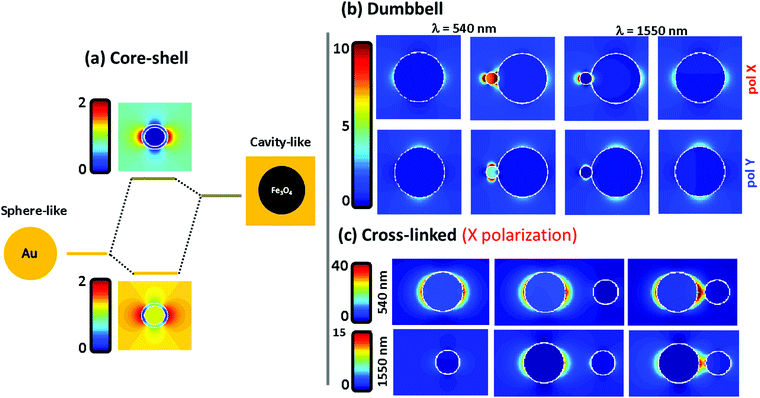
To understand the far field spectral response, shown in the previous figure, we plot in Fig. 4 the electromagnetic near field distribution of the three hetero-structures. It is well known that the optical resonances shown by the Fe@Au come from the coupling between the external and internal resonances at the shell. In Fig. 4(a) the sphere-like mode corresponds to the LSPR on the air–gold interface while the cavity mode corresponds to the resonance occurring at the gold–magnetite interface. In the case of a magnetite core (with ε ≤ 5 at the spectral range of interest49) the cavity mode is expected to appear at higher energies than that of the sphere mode.21 Due to the interaction between such resonances, bonding and antibonding modes are split. The bonding mode correlates with the peak shown in Fig. 3(a), at smaller energies than that of the sphere mode. However, the splitting of the bonding and anti-bonding modes will depend on the strength of the coupling between the outer and the inner LSPRs. Hence, the blue-shift of the absorption peak can be understood by a reduction of the coupling degree as the shell radius is increased.
Fig. 4(b) shows the electric near-field distribution calculated for the dumbbell configuration at the wavelengths of interest for both polarizations. In our simulations we have considered that the NPs are connected so that 10% of the gold NP radius is covered by iron oxide. Notice that the gold cluster is formed before the iron oxide precursor fully runs out. Then, iron oxide still grows in the presence of the gold NPs, leaving the latter partially embedded. In terms of calculus, this approach avoids singularities in the geometry, and allows us to define the gold NPs as a closed surface improving the accuracy of the BEM algorithm.50 This is possible in our system because of the dielectric character of the iron oxide which will allow certain shape modifications with minor consequences on the numerical results51,52 (see the ESI†). At λ = 540 nm the LSPR of the gold is affected by the presence of the iron oxide when the system is excited with X-polarized light. This results in an enhancement of the field distribution close to the interface and explains the higher extinction calculated in this direction. The reason is that the dipoles induced in both constituents are spatially overlapped when impinging with X-polarized light, driving to a dipole–dipole interaction responsible for the red-shift50 [from λ = 520 nm for single Au NPs to λ = 540 nm for the Fe(Au)]. In contrast, under Y-polarization there is a negligible dipolar interaction explaining the polarization anisotropy. At λ = 1550 nm an analogous situation is found, responsible for the moderate increase of P2 for X-polarization. It is worth noting that at this wavelength the field enhancement is small in dumbbells with a DAu = 3 nm Au NP, but it rises up dramatically with the diameter of the gold NP (an example is shown in the ESI†). As a result, we can expect both: a polarization dependent enhancement of LSPR from the gold NP due an asymmetric dipole–dipole interaction in the presence of the iron oxide; and an improvement of the optical activity of the iron oxide at the NIR due to the increase of the electric field distribution surrounding the gold NPs.
In Fig. 4(c) the near-field distribution of the magnetic and plasmonic constituents of the Fe–Au is represented in different situations: as isolated NPs (left) and as Fe–Au with inter-particle distances of d = 8 and d = 2 nm (middle and right respectively). The hot spot suggested by the results in Fig. 3 can be observed in the case of short inter-particle distances. But notice that the intensity of this hot spot does not differ too much with respect to the case of isolated gold NPs. The low electromagnetic interaction between both NPs can be attributed to gap size but also to the dielectric character of the magnetite. For example, in ref. 50 it is predicted that gaps below 0.1 times the NP radius are required to observe coupling between gold disk dimers, and gaps of about half the radius are required to observe a clear red shift of the LSPR. On the one hand, we cannot expect an important resonance shift in the Fe–Au when the linker length is larger than the magnetite NP. But on the other hand, the dielectric constant of the iron oxide prevents a high field increase at the hot spots. Then, TEM imaging is performed to estimate the effective linker length. A wide range of gaps is observed in the TEM images (see the ESI†), but notice that the inter-particle distances are strongly influenced by electrostatic and adhesion forces, that the linker suffers during the solvent evaporation. As a result, the effective linker length is randomly modified when the Fe–Au is deposited on a surface, and the inter-particle distances found in the TEM images are not representative of the linker length in solution. For this reason, the Fe–Au gap is estimated to be in the order of d = 10 nm, according to the hydrodynamic size of gold NPs after functionalization with PEG. Under these conditions we can be sure that the Fe–Au system is representative of a low electromagnetic interaction between constituents. We have indeed, not observed any insights into the presence of NP aggregates in solution. These results should be taken into account for the design of manifold composites, since only in the case of large clusters in close contact will the electromagnetic interaction between constituents be relevant.
Magnetic properties
The applications of hybrid systems are mainly determined by their magnetic properties, so it is essential to describe the magnetism of these systems. Magnetite is a ferrimagnet; an ordered material where the spins are antiparallel aligned forming magnetic domains. In contrast to antiferromagnets, ferrimagnets show a non-zero spontaneous magnetization because their individual moments are not completely cancelled in these domains.53 The bulk magnetite is found forming multi-domain structures since the magnetostatic energy is increased with the domain size.54,55 However, the energy required to maintain a domain wall into a NP is not compensated by the corresponding magnetostatic potential decrease, and hence, single superparamagnetic domains are observed at the nanometer scale.56 In Fig. 5 we show magnetic measurements carried out on our three representative cases. The magnetization curves are measured at different temperatures by sweeping the external magnetic field from 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to −50
000 to −50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe. However, we plot the range between 10
000 Oe. However, we plot the range between 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and −5000 for a better view of the hysteresis loops. The results are summarized in Table 1.
000 and −5000 for a better view of the hysteresis loops. The results are summarized in Table 1.
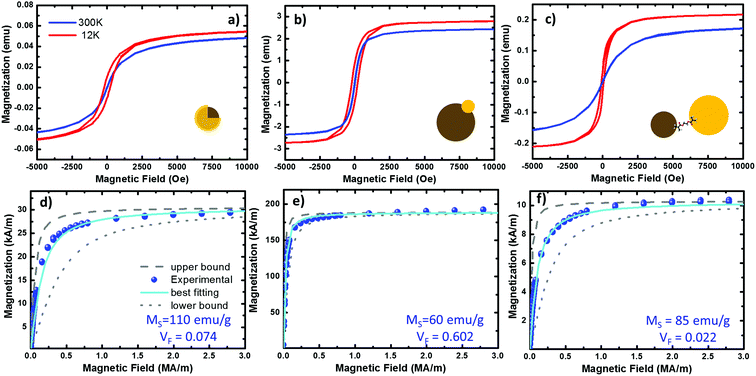 | ||
| Fig. 5 Magnetization curves from the three systems under study. (a–c) Hysteresis plots of the Fe@Au, Fe(Au) and Fe–Au respectively, measured at 300 (in blue) and 12 K (in red) on NP powder samples of 32.92, 42.41 and 40.4 mg respectively. (d–f) fitting of the room temperature hysteresis loops from the Fe@Au, Fe(Au) and Fe–Au respectively. The scatters represent the experimental data while the best fit to eqn (1) is plotted in cyan. The upper (dashed in grey) and lower (doted in grey) bound curves illustrate the size distribution effects on the magnetization. For the fitting we have considered the NP diameter distribution obtained from counting statistics. For the bound curves we considered a fixed NP size corresponding to the larger and smaller NP diameter observed on the distribution. | ||
| Magnitude | Fe@Au | Fe(Au) | Fe–Au |
|---|---|---|---|
| M S (300 K) (emu) | 5.1 | 2.57 | 0.051 |
| M R (300 K) (emu) | ∼0.04 | 0.087 | ∼5 × 104 |
| M R/MS (300 K) | ∼0.01 | 0.03 | ∼0.01 |
| H C (300 K) (Oe) | 12 | 15 | 14 |
| M S (12 K) (emu) | 6.7 | 2.89 | 0.058 |
| M R (12 K) (emu) | 1.2 | 0.87 | 0.01 |
| M R/MS (12 K) | 0.18 | 0.30 | 0.17 |
| H C (12 K) (Oe) | 74 | 210 | 203 |
At room temperature, the magnetization curves present very low coercitive fields (in the order of HC ∼ 10 Oe) in the three systems under study, blue lines in Fig. 5(a)–(c). As expected from superparamagnetic NPs, the temperature must be reduced to find a clear increase of HC, curves in red. Superparamagnetic magnetite NPs always present MR/MS < 0.1.15,57 In Fe@Au the ratio between the remanent and the saturation magnetization is MR/MS ∼ 0.01 at room temperature, well below superparamagnetic values. However, at very low temperatures the HC is increased; for example, at 12 K we found HC = 74 Oe and MR/MS = 0.18. In a similar way, Fe(Au) also presents low hysteresis at room temperature. In this case MR/MS = 0.03 is a bit larger, but still in the range of superparamagnetism. As a difference, the coervitivity is considerably larger than that of Fe@Au (e.g. at 12 K HC = 210 Oe with MR/MS = 0.30), and an increase in the coercive field is observed below 100 K. This means that in Fe(Au), superparamagnetism is inhibited at higher temperatures. The same behaviour is observed for Fe–Au, superparamagnetism at room temperature with negligible hysteresis (with MR/MS < 0.01), and superparamagnetism inhibition as the temperature is reduced (e.g. MR/MS = 0.17 at 12 K).
Because of the behaviour observed we can conclude that our NPs are single domain and superparamagnetic, even though AC measurements are usually required for distinguishing superparamagnetism from ensemble spin states (such as spin glasses). Under these conditions, the experimental magnetization curves can be fitted to a superparamagnetic model using the Langevin approach:58
| MEXP = VFMS[coth(α) − 1/α] | (1) |
From the best fitting (χ2 = 1 × 10−2) on the Fe@Au we found high magnetization values of MS = 572 kA m−1 (i.e. 110 emu g−1) and volume fractions of VF = 0.053 (i.e. 5.3% in volume). Notice the volume fraction only accounts for the volume of magnetite in the sample, and according to geometrical considerations, the volume of gold should be about 3.56 times larger (see the ESI†). Then, the volume of Fe@Au in the powder would be in the order of 19% and the rest must be surfactant or other organic residuals. Given the high relative density of gold ρAu = 19.3 and the low relative density of the surfactant (usually in the order of ρ = 1.2 for organic molecules), the volume fraction drives to a concentration of MFe@AuF = 82% in mass for the whole core–shell system.
In the case of Fe(Au), the experimental magnetization also fits the Langevin approach (χ2 = 2 × 10−3), giving values of MS = 312 kA m−1 (60 emu g−1) and VF = 0.602. The higher volume fraction points out that this system is clearly designed to give more importance to the magnetic constituent, reducing the volume of gold up to 5% (according to geometrical considerations). This way we can estimate a composition of about MFe(Au)F = 74% in mass of Fe(Au) with 26% of organic residual. In the case of Fe–Au we found MS = 442 kA m−1 (85 emu g−1) and VF = 0.0022 with χ2 = 1.5 × 10−2. In contrast to the Fe(Au), in this case we show a reduction in the volume fraction of iron oxide due to the larger size of the gold cluster, which can be estimated to be about 6.4 times the volume of iron oxide one. This would drive to a mass content of about MFe–AuF = 73%.
The saturation values obtained are a good reference for checking the quality of our magnetic clusters. MS is considerably reduced in the presence of crystal defects or impurities, or because of the co-existence of additional iron oxide phases: such as maghemite or hematite. At room temperature, saturation values of 475 kA m−1 (90 emu g−1) are expected for high quality crystalline magnetite,59,60 considerably higher than other iron oxides. As a result, we can assume magnetite is the dominant phase in the magnetic cluster of Fe–Au, because we have obtained values very close to those expected for magnetite. In contrast, in the case of Fe(Au) a reduction of MS is observed. This can be related to the synthesis procedure. As described above, the iron oxide cluster continues growing after gold injection, but when hosting the gold, the charges of the magnetite surface are not well-balanced. This drives the non-isotropic growth responsible for the broad shape and size distribution observed. TEM images together with the values obtained from the fitting suggest that the crystallinity and stoichiometry of the resulting iron oxide might be altered under these conditions. The opposite case is found for the Fe@Au where the observed saturation values are larger than expected, i.e. about 20% higher than crystalline magnetite. This can be understood as an overestimation of MS in the Langevin approach. In the next section, we discuss the origin of such overestimation.
For a better discussion first we study the dependence of the coercivity on the temperature; with this we are going to estimate the anisotropy constant (K). Considering randomly oriented non-interacting NPs, HC is described by this simple expression:61
| HC(T) = H0[1 − (T/TB)] (for T < TB) | (2) |
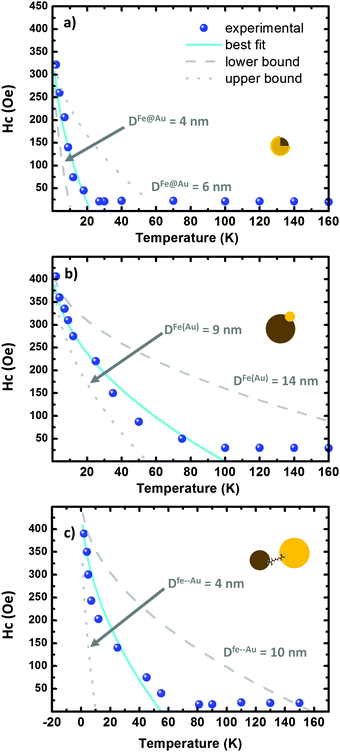 | ||
| Fig. 6 (a–c) Hysteresis plots as a function of the temperature on the Fe@Au, Fe(Au) and Fe–Au respectively. The scatters correspond to the experimental data while the fitting to eqn (2) is depicted in cyan. The lower and upper bound are dotted and dashed in grey, respectively. The grey curves are generated by using the fitting parameters in Table 3. | ||
| System | H 0 (Oe) | H 0 (kA m−1) | T B (K) | K (kJ m−3) | LN |
|---|---|---|---|---|---|
| Fe@Au | 390 | 31.0 | 22 | 11.1 | 1.4 |
| Fe(Au) | 431 | 34.2 | 100 | 6.7 | 1.9 |
| Fe–Au | 472 | 37.5 | 55 | 10.4 | 1.4 |
Similar values of H0 are found in the three systems under study. In Fe@Au we found a slightly lower value, H0 = 31.0 kA m−1 (390 Oe), consistent with the smaller NPs and with the low coercivity. However, we found the highest anisotropy constant, KFe@Au = 11.1 kJ m−3. In Fe–Au, we find an anisotropy constant close to the core–shell values, just a bit lower (i.e. KFe–Au = 10.4 kJ m−3). These values are on the order of those for bare magnetite NPs. In the case of Fe(Au) we obtain KFe(Au) = 6.7 kJ m−3. Consistent with the saturation values, the reduction on KFe(Au) can be explained by variations in stoichiometry or crystallinity. For instance, the anisotropy constant of maghemite is about three times lower than that of magnetite. On the other hand, the differences in TB are clearly related with the different NP size dispersion. Fe@Au shows lower values, TB = 22 K, coinciding with the smaller diameter of the core NPs. Consistently TB is increased to 100 and 55 K for Fe(Au) and Fe–Au, respectively. Within the non-interacting approach, TB can be related with the anisotropy constant as follows:64
TB = KV/[kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(τm/τ0)] ln(τm/τ0)] | (3) |
Comparison of results and impact on potential applications
With the help of optical and magnetic characterization, the advantages and disadvantages of the three systems are compared to discuss in detail their potential technological interests. Due to the wide range of applications that may rely on such hybrid magnetic–plasmonic materials, it is hard to find the best option to be employed in each case. To throw light on this, the capabilities of our magnetic–plasmonic systems have been described in different scenarios: a range of NP sizes, gold to iron oxide ratios, inter-particle distances, etc. With this is mind, the results discussed in the previous sections have been presented in such a way that they can be extrapolated to more complex hetero-structures. For example, Fe@Au would represent the particular case where magnetic NPs are embedded. The behaviour observed in the Fe(Au) system also gives insights into the properties we should expect from decorated NPs.4,19 On the other hand, some composites contain magnetic and plasmonic NPs close to each other, but not in contact with each other. Sometimes they are separated by polymers, functional molecules or silica microspheres.38,66 The response of these composites could be discussed based on our studies of the Fe–Au heterostructures.Particular cases are discussed below, but as general remarks, we can mention that the effects of gold on the magnetic properties are mainly related to the reduction of the volume fraction of iron oxide in the system. However, the effect of size dispersion would be more determinant, hindering possible diamagnetic effects. It is also worthy to mention that we did not observe hard restrictions on the potential applications, in the sense that superparamagnetism is preserved at room temperature in any case.
Core–shell: embedded magnetic NPs
From Fig. 3 we can expect a broad tuning range for the optical response of plasmonic systems with embedded dielectric NPs. However, the tuning capabilities seem to be considerably reduced in practice. A properly weighted average shows that this reduction is due to the higher contribution of the thicker shell NPs. This fact must be taken into account in optical applications. For example, Fe@Au could be employed for sensing functional molecules by carrying out SERS measurements at the LSPR wavelength. However, bio-sensing often demands the use of longer wavelengths to avoid fluorescence from functional molecules, and typically 785 nm laser diodes are employed for that purpose. In principle, LSPRs at this wavelength can be supported by Fe@Au structures with cores ranging from 8 to 12 nm and shells thinner than 2 nm. However, due to the higher contribution of the thicker shell NPs the ensemble spectra will be blue-shifted from the average. Filtering of these undesired thick shell NPs is technically hard, and a more reliable strategy to overcome this issue would consist in the synthesis of large core NPs. Considering the shell dispersion estimated in our core–shell NPs (e.g. DFe@Au = DCORE + 2.1 ± 1.2 nm), cores of about DCORE = 20 nm would be required to fit the resonance of the NP distribution to 785 nm.Regarding magnetism, we got figures really close to the ones expected for magnetite NPs. Only in the case of the saturation in magnetization we found overestimated values. In samples with a significant content of gold, diamagnetic effects might cause deviation from the Langevin approach even to magnetization curves without evident saturation.33,67 In our Fe@Au we observe that MS overestimation is about 20% (from 90 emu g−1 expected for bare magnetite NPs to 110 emu g−1). Quantifying the diamagnetic effects arising from the presence of gold, would require a study out of the scope of this work. On the one hand, AC measurements would be required in order find the proper relaxation times in the presence and in the absence of the gold shell. On the other hand, a range of narrow shell thickness distributions would be desirable. These developments would be more related for the case of optimization of the synthetic routes. Moreover, a deeper study would apply only to the particular system under investigation. Here we prefer to tackle the problem from a more general point of view, and discuss about the nature of such overestimation. According to the definition α = πμ0MSd3H/(6kBT); MS will increase its value during the fitting to compensate the reduction on the fixed parameters: d, H or T. The most reasonable error source is the NP size dispersion; firstly, because it is estimated from the counting statistics, and secondly, because α depends on d3. As far as the other parameters are concerned, the temperature error can be neglected while 20% damping of H is exaggerated for a few nm shell. In the end, the important conclusion is that Fe@Au NPs exhibit good performance for magnetic applications and magnetic capabilities similar to the bare magnetite NPs, but taking advantage of the bio-compatibility of the gold shell.
Dumbbell: decorated NPs
Results from dumbbell hetero-structures show the possibilities of large magnetic NPs decorated with small gold clusters for photomagnetism. Particularly relevant is the absorption of the iron oxide at the near-infrared, as observed in the Fe(Au) system. There is a clear trend in photomagnetism to move to near-infrared wavelengths. For example, to date light-induced excited spin-state trapping (LIESST) measurements have been mostly carried out with visible lasers. However recent studies have found that LIESST active materials can be more efficient by exciting the molecular ligands using larger wavelengths.68,69 Combination of LIESST active NPs with gold clusters would be an interesting strategy to manage magnetic states via light absorption enhancement. In the case of iron oxide, dumbbell structures favour the absorption peak at telecom wavelengths [P2 in Fig. 3(c)], which is another interesting scenario to explore further applications of iron oxide in photomagnetism.In our numerical simulations, an important absorption can be observed by increasing the size of the gold cluster. But notice that, the main advantage of the Fe(Au) is the reduction of gold content. Importantly, the stoichiometry of the iron oxide could be affected when the magnetic cluster is grown in the presence of gold, as concluded from magnetic measurements. This could be a point to improve in further developments.
Cross-linked NPs: many cluster composites and aggregates
In the linker hetero-structure, we found a weak hot-spot between the magnetic and plasmonic NPs. As a difference with respect to metal–metal cross-linked systems, the Fe–Au case showed no energy shift when changing the inter-particle distance, even in the case of very small gaps. Certainly relevant for further developments is to know that small clusters of iron oxide do not affect the LSPR of the gold NP. This means that the optical properties of the original plasmonic constituent are preserved after cross-linking.The linker system also helps to retain the properties of the magnetic NPs. The magnetization measurements fit very well the Langevin approach and the saturation and anisotropy constant values are really close to crystalline magnetite values. The result is that the magnetic and plasmonic constituents can be synthesized, besides tailoring their respective properties. This is an advantage with respect to other procedures where the growth of one constituent depends on the other one. Customizing the optical response while keeping superparamagnetism will improve the already demonstrated capabilities of the magnetite–gold hybrids.
Conclusions
Fe@Au, Fe(Au) and Fe–Au hetero-structures have been studied as representative cases of different coupling degrees between magnetic and plasmonic NPs. The three hybrid systems are compared to illustrate the contribution of both the gold and the iron oxide NPs to the magnetic- and plasmonic-properties respectively. The iron oxide NPs provide magnetic activity, and most of the time, they also contribute to improve the optical response, e.g. increasing the tuning range or the light scattering when forming the hetero-structures. In certain circumstances, an excessive presence of gold may affect the magnetic capabilities of the resulting materials, mainly due to the reduction of the iron oxide volume fraction, but in a good balance, the plasmonic constituent should not affect the potential applications as concluded from magnetic characterization. Indeed, magnetic properties seem to be more dependent on the NP diameter and NP size dispersion hindering possible effects related to the gold. With these results, we have discussed the technological limits of the systems and we have given some tips to improve the new generation of magnetite–gold based functional materials. Moreover, the comparison among the three hetero-structures can be extrapolated to more complex composites since the systems under study are representative of NPs enclosed, in contact or separated from each other. This offers a qualitative prediction about the capabilities of novel systems, opening the possibility to predict the interaction between different constituents and the consequences on the performance of the resulting materials.Acknowledgements
Financial support from the EU (ERC Advanced Grant SPINMOL), the Spanish MINECO (MAT2011-22785, co-financed by FEDER) and the Generalidad Valenciana (Programs Prometeo) is gratefully acknowledged. The corresponding author J. C.-F. thanks the Generalitat Valenciana for his research grant for the development of magneto–plasmonic materials funded by means of the Vali+d program (APOSTD/2013/076). “P. A. acknowledges Programa “Viera y Clavijo” de la Agencia Canaria de Investigacioń, Innovacion y Sociedad de la Informacion (ACIISI) y la Universidad de las Palmas de Gran Canaria (ULPGC)”. The authors have been carried out numerical simulations employing MATLAB software (The MNMBEM package published by A. Trügler and U. Hohenester). The authors are also grateful to Prof. E. Coronado for his support and valuable discussions at the beginning of project; A. López help with the DLSs in the ESI;† M. J. Recio-Carretero for her collaboration on the structural characterization, J. M. Martínez and Dra G. Agustí-Lopez for the assistance during the magnetic measurements; and Dra A. Forment and V. Mkhitaryan for proof reading the manuscript.References
- F. Caruso, M. Spasova, A. Susha, M. Giersig and R. A. Caruso, Chem. Mater., 2001, 13, 109–116 CrossRef CAS.
- A. L. Morel, S. I. Nikitenko, K. Gionnet, A. Wattiaux, J. Lai-Kee-Him, C. Labrugere, B. Chevalier, G. Deleris, C. Petibois, A. Brisson and M. Simonoff, ACS Nano, 2008, 2, 847–856 CrossRef CAS PubMed.
- G. K. Larsen, W. Farr and S. E. Hunyadi Murph, J. Phys. Chem. C, 2016, 120, 15162–15172 CAS.
- C. J. Meledandri, J. K. Stolarczyk and D. F. Brougham, ACS Nano, 2011, 5, 1747–1755 CrossRef CAS PubMed.
- T. Murakami, H. Nakatsuji, N. Morone, J. E. Heuser, F. Ishidate, M. Hashida and H. Imahori, ACS Nano, 2014, 8, 7370–7376 CrossRef CAS PubMed.
- H. Wang, Y. Ding, S. Su, D. Meng, A. Mujeeb, Y. Wu and G. Nie, Nanoscale Horiz., 2016, 1, 394–398 RSC.
- Y. Shen, X. Cheng, G. Li, Q. Zhu, Z. Chi, J. Wang and C. Jin, Nanoscale Horiz., 2016, 1, 290–297 RSC.
- M. Caminale, L. Anghinolfi, E. Magnano, F. Bondino, M. Canepa, L. Mattera and F. Bisio, ACS Appl. Mater. Interfaces, 2013, 5, 1955–1960 CAS.
- J. Goebl, Y. Liu, S. Wong, S. Zorba and Y. Yin, Nanoscale Horiz., 2016, 1, 64–68 RSC.
- A. Rakovich, P. Albella and S. A. Maier, ACS Nano, 2015, 9, 2648–2658 CrossRef CAS PubMed.
- X. Zhang, P. Li, Á. Barreda, Y. Gutiérrez, F. González, F. Moreno, H. O. Everitt and J. Liu, Nanoscale Horiz., 2016, 75–80 RSC.
- M. Dabiri, M. Shariatipour, S. K. Movahed and S. Bashiribod, RSC Adv., 2014, 4, 39428–39434 RSC.
- L. G. Abraçado, D. M. S. Esquivel, O. C. Alves and E. Wajnberg, J. Magn. Reson., 2005, 175, 309–316 CrossRef PubMed.
- H. Wang, Y. Zhang, H. Xia, Q. Chen, K.-S. Lee and H. Sun, Nanoscale Horiz., 2016, 1, 201–211 RSC.
- T. Yang, C. Shen, Z. Li, H. Zhang, C. Xiao, S. Chen, Z. Xu, D. Shi, J. Li and H. Gao, J. Phys. Chem. B, 2005, 109, 23233–23236 CrossRef CAS PubMed.
- J. Lim and S. A. Majetich, Nano Today, 2013, 8, 98–113 CrossRef CAS.
- P. J. Chen, Y. Da Kang, C. H. Lin, S. Y. Chen, C. H. Hsieh, Y. Y. Chen, C. W. Chiang, W. Lee, C. Y. Hsu, L. De Liao, C. T. Fan, M. L. Li and W. C. Shyu, Adv. Mater., 2015, 27, 6488–6495 CrossRef CAS PubMed.
- J. Reguera, D. Jiménez de Aberasturi, N. Winckelmans, J. Langer, S. Bals and L. M. Liz-Marzán, Faraday Discuss., 2016, 191, 47–59 RSC.
- J. A. Hachtel, S. Yu, A. R. Lupini, S. T. Pantelides, M. Gich, A. Laromaine and A. Roig, Faraday Discuss., 2016, 215–227 RSC.
- C. Radloff and N. J. Halas, Nano Lett., 2004, 4, 1323–1327 CrossRef CAS.
- C. S. Levin, C. Hofmann, T. A. Ali, A. T. Kelly, E. Morosan, P. Nordlander, K. H. Whitmire and N. J. Halas, ACS Nano, 2009, 3, 1379–1388 CrossRef CAS PubMed.
- B. Wu, H. Zhang, C. Chen, S. Lin and N. Zheng, Nano Res., 2009, 2, 975–983 CrossRef CAS.
- F. H. Lin and R. A. Doong, J. Phys. Chem. C, 2011, 115, 6591–6598 CAS.
- J. Huang, Y. Sun, S. Huang, K. Yu, Q. Zhao, F. Peng, H. Yu, H. Wang and J. Yang, J. Mater. Chem., 2011, 21, 17930 RSC.
- C. Kaewsaneha, P. Tangboriboonrat, D. Polpanich, M. Eissa and A. Elaissari, ACS Appl. Mater. Interfaces, 2013, 5, 1857–1869 CAS.
- Z.-C. Zhang, B. Xu and X. Wang, Chem. Soc. Rev., 2014, 43, 7870–7886 RSC.
- I. Y. Goon, L. M. H. Lai, M. Lim, P. Munroe, J. J. Gooding and R. Amal, Chem. Mater., 2009, 21, 673–681 CrossRef CAS.
- M. Spasova, V. Salgueiriño-Maceira, A. Schlachter, M. Hilgendorff, M. Giersig, L. M. Liz-Marzán and M. Farle, J. Mater. Chem., 2005, 15, 2095 RSC.
- X. Xue, V. Sukhotskiy and E. P. Furlani, Sci. Rep., 2016, 6, 35911 CrossRef CAS PubMed.
- Z. Xu, Y. Hou and S. Sun, J. Am. Chem. Soc., 2007, 129, 8698–8699 CrossRef CAS PubMed.
- E. A. Chaffin, S. Bhana, R. T. O’Connor, X. Huang and Y. Wang, J. Phys. Chem. B, 2014, 118, 14076–14084 CrossRef CAS PubMed.
- H. Yu, M. Chen, P. M. Rice, S. X. Wang, R. L. White and S. Sun, Nano Lett., 2005, 5, 379–382 CrossRef CAS PubMed.
- G. Jiang, Y. Huang, S. Zhang, H. Zhu, Z. Wu and S. Sun, Nanoscale, 2016, 8, 17947–17952 RSC.
- C. Xu, B. Wang and S. Sun, J. Am. Chem. Soc., 2009, 131, 4216–4217 CrossRef CAS PubMed.
- Z. Xu, C. Shen, Y. Hou, H. Gao and S. Sun, Chem. Mater., 2009, 21, 1778–1780 CrossRef CAS.
- M. Wang, C. Wang, K. L. Young, L. Hao, M. Medved, T. Rajh, H. C. Fry, L. Zhu, G. S. Karczmar, C. Watson, J. S. Jiang, N. M. Markovic and V. R. Stamenkovic, Chem. Mater., 2012, 24, 2423–2425 CrossRef CAS.
- R. L. Truby, S. Y. Emelianov and K. A. Homan, Langmuir, 2013, 29, 2465–2470 CrossRef CAS PubMed.
- E. Peng, E. S. G. Choo, C. S. H. Tan, X. Tang, Y. Sheng and J. Xue, Nanoscale, 2013, 5, 5994–6005 RSC.
- U. Hohenester and A. Trügler, Comput. Phys. Commun., 2012, 183, 370–381 CrossRef CAS.
- E. J. R. Vesseur, F. J. G. De Abajo and A. Polman, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–6 CrossRef.
- G. Baffou, P. Berto, E. Bermúdez Ureña, R. Quidant, S. Monneret, J. Polleux and H. Rigneault, ACS Nano, 2013, 7, 6478–6488 CrossRef CAS PubMed.
- A. Jakab, C. Rosman, Y. Khalavka, J. Becker, A. Trügler, U. Hohenester and C. Sönnichsen, ACS Nano, 2011, 5, 6880–6885 CrossRef CAS PubMed.
- J. Becker, A. Trügler, A. Jakab, U. Hohenester and C. Sönnichsen, Plasmonics, 2010, 5, 161–167 CrossRef CAS.
- A. Trügler, J. C. Tinguely, G. Jakopic, U. Hohenester, J. R. Krenn and A. Hohenau, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–6 CrossRef.
- E. Prodan, C. J. Radloff, N. J. Halas and P. Norlander, Science, 2003, 302, 419–422 CrossRef CAS PubMed.
- P. Nordlander, C. Oubre, E. Prodan, K. Li and M. I. Stockman, Nano Lett., 2004, 4, 899–903 CrossRef CAS.
- O. Pérez-González, N. Zabala, A. G. Borisov, N. J. Halas, P. Nordlander and J. Aizpurua, Nano Lett., 2010, 10, 3090–3095 CrossRef PubMed.
- O. P. González, N. Zabala and J. A. Leioa, UPV/EHU, 2011 Search PubMed.
- W. F. J. Fontijn, P. J. van der Zaag, M. A. C. Devillers, V. A. M. Brabers and R. Metselaar, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5432–5442 CrossRef CAS.
- I. Romero, J. Aizpurua, G. W. Bryant and F. J. García De Abajo, Opt. Express, 2006, 14, 9988–9999 CrossRef PubMed.
- V. Häfele, A. Trügler, U. Hohenester, A. Hohenau, A. Leitner and J. R. Krenn, Opt. Express, 2015, 23, 10293 CrossRef PubMed.
- F. J. G. De Abajo, J. Phys. Chem. C, 2008, 112, 17983–17987 Search PubMed.
- D. Faivre and R. B. Frankel, Iron Oxides: From Nature to Applications, Wiley, New York, 2016 Search PubMed.
- S. Upadhyay, K. Parekh and B. Pandey, J. Alloys Compd., 2016, 678, 478–485 CrossRef CAS.
- K. Woo, J. Hong, S. Choi, H. Lee, J. Ahn, C. S. Kim and S. W. Lee, Chem. Mater., 2004, 16, 2814–2818 CrossRef CAS.
- D. L. Leslie-Pelecky and R. D. Rieke, Chem. Mater., 1996, 8, 1770–1783 CrossRef CAS.
- G. F. Goya, T. S. Berquó, F. C. Fonseca and M. P. Morales, J. Appl. Phys., 2003, 94, 3520–3528 CrossRef CAS.
- V. B. Barbeta, R. F. Jardim, P. K. Kiyohara, F. B. Effenberger and L. M. Rossi, J. Appl. Phys., 2010, 107, 73913 CrossRef.
- R. E. Rosensweig, Ferrohydrodynamics, Dover Publications, 1997 Search PubMed.
- N. T. K. Thanh, Magnetic Nanoparticles: From Fabrication to Clinical Applications, CRC Press, 2012 Search PubMed.
- S. P. Gubin, Y. A. Koksharov, G. B. Khomutov and G. Y. Yurkov, Russ. Chem. Rev., 2005, 74, 489–520 CrossRef CAS.
- E. C. Stoner and E. P. Wohlfarth, Philos. Trans. R. Soc., A, 1948, 240, 599–642 CrossRef.
- F. T. Parker, M. W. Foster, D. T. Margulies and A. E. Berkowitz, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 7885–7891 CrossRef CAS.
- O. Petracic, Superlattices Microstruct., 2010, 47, 569–578 CrossRef CAS.
- H. T. Yang, H. L. Liu, N. N. Song, H. F. Du, X. Q. Zhang, Z. H. Cheng, J. Shen and L. F. Li, Appl. Phys. Lett., 2011, 98, 2012–2015 Search PubMed.
- X. Meng and Z. Zhang, J. Colloid Interface Sci., 2017, 485, 296–307 CrossRef CAS PubMed.
- H. Zeng and S. Sun, Adv. Funct. Mater., 2008, 18, 391–400 CrossRef CAS.
- F. Pointillart, X. Liu, M. Kepenekian, B. Le Guennic, S. Golhen, V. Dorcet, T. Roisnel, O. Cador, Z. You, J. Hauser, S. Decurtins, L. Ouahab and S.-X. Liu, Dalton Trans., 2016, 45, 11267–11271 RSC.
- O. Iasco, E. Rivire, R. Guillot, M. Buron-Le Cointe, J. F. Meunier, A. Bousseksou and M. L. Boillot, Inorg. Chem., 2015, 54, 1791–1799 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Summary of magnetic properties of different kinds of magnetite nanoparticles to be compared with the different systems under study. TEM images, counting statistics and DLS measurements of the hybrid systems and corresponding reference samples. See DOI: 10.1039/c6nh00225k |
| This journal is © The Royal Society of Chemistry 2017 |