Aqueous alteration of potassium-bearing aluminosilicate minerals: from mechanism to processing

Abstract

The anticipated increase in demand for potassium fertilizers and alumina from developing nations experiencing a high-rate of population growth brings a global sustainability concern. Most of these countries do not have economically viable resources for both commodities; and the environmental footprint of existing technologies may compromise local ecosystems. Alternatives, both in terms of resources and extraction technologies, are therefore needed. Aqueous alteration of potassium-bearing aluminosilicate minerals has been proposed as an alternative to both traditional K-fertilization and alumina production. This work discusses the mechanism of aqueous alteration of aluminosilicate minerals, and the chemical processes that have been proposed to date. Although extensive studies are found in the fields of geochemistry and materials chemistry, their results have rarely been analysed and engineered to allow a proper control and design of chemical processing. The review suggests that such a multi-disciplinary approach is required to enable new technologies that both comply with green chemistry principles and are economically viable.

---

Taisiya Skorina

Taisiya (Taya) Skorina is a Sr. materials chemist at 3M corporate research materials laboratory (3M CRML). Dr Skorina received her M.Sc and PhD in materials chemistry from the D. Mendeleev University of Chemical Technology of Russia. Prior to starting her career in industry, Dr Skorina was a visiting scientist at the Department of Chemistry & Biochemistry at Arizona State University and a postdoctoral associate in Dr Allanore's research group at MIT. Taya's research focuses on the physical chemistry of silicates, in particular, on the development of resource-efficient synthetic technologies to obtain silicate-based functional inorganic and hybrid materials.

Antoine Allanore

Antoine Allanore received his higher education in Nancy (France) where he earned a diploma in chemical process engineering from Ecole Nationale Supérieure des Industries Chimiques and an M.Sc and PhD from Lorraine University. Dr Allanore joined the Massachusetts Institute of Technology (USA) in 2010, after several years of service as a research engineer for ArcelorMittal R&D, working on the development of alternative iron production methods with low emissions. In 2012, he was appointed the T.B. King Assistant Professor of Metallurgy in the Department of Materials Science & Engineering at MIT, where his research group aims at transposing green chemistry principles to materials extraction and manufacturing processes.

---

1. Introduction

Inorganic fertilizers are essential for crop production, in particular to supply nutrients such as nitrogen, phosphorus, and potassium. For the latter, 95% of the global production is dedicated to agriculture in the form of water-soluble salts (e.g., KCl), commonly named “potash”. The potassium content in potash varies from 50 to 60 wt% in equivalent K₂O. The global demand of potash recently exceeded 32 million metric tons of K₂O, and a significant increase is foreseen in the coming decade.^1,2 The main ore for the production of potash is sylvinite – a physical mixture of minerals sylvite (KCl) and halite (NaCl), typically with 20–30 wt% K₂O. A few countries of the northern hemisphere (Canada, Russia, Belarus, and Germany) exploit the major rock-salt deposits and control more than 70% of the existing potash market. As far as the global availability of KCl for agriculture is concerned, the United Nations Food and Agriculture Organization (FAO) has emphasized a risk of a temporary shortage in the near future.³ The reported data, presented in Fig. 1 for each geographical location reveal an actual imbalance in potassium nutrients for Africa and Asia, where the difference between demand and supply is negative. A nutrient audit conducted by Sheldrick⁴ pointed out that the factual demand for potash in these regions is underestimated by the FAO, and that the search for local alternative sources of potassium is already crucial for a sustainable development of these regions. In fact, the FAO's survey takes into account only the demand from customers currently represented in the global market i.e., customers with the ability to purchase potassium fertilizer at the current price. This clearly does not include the whole agricultural community. In other words, nutrients currently removed from the soils by crops in Africa, Asia, Latin America, Central Europe, Caribbean, and Oceania are not compensated; and hence these lands are already experiencing a shortage of potassium. Their rapid population growth suggests that the situation may worsen.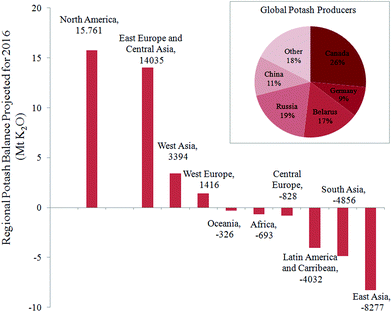

Fig. 1 Projection of the regional potash balance of import vs. export according to the FAO for 2016 (ref. 3) in million metric tonnes of K₂O equivalent. Inset shows the current national distribution of potash producers.

Besides the limited geographical availability, traditional potash fertilizers comprise highly soluble salts, which are not necessarily the most efficient and sustainable nutrient source for all types of soils. Tropical soils, for example, typically have low cation exchange capacity and call for fertilizers with a controlled and gradual rate of nutrient release. Moreover, substantial leaching of salts from agricultural fields can lead to the accumulation of chlorides and nitrates in ground water causing long-term environmental issues related to the sink capacity of the earth.^1,5–8 Therefore, a green alternative source of potassium needs to be earth-abundant and must allow controlled availability of K with a minimal co-release of environmentally harmful elements. In this context, earth-abundant potassium-bearing rocks may offer a suitable alternative.

Potassium-bearing framework (tecto-) aluminosilicate minerals† may contain up to 30 wt% K₂O (e.g., for kalsilite), and have been proposed as a substitute source of potassium.^1,9–11 In addition, their high alumina content (up to 32 wt% Al₂O₃) might offer a local alternative to bauxites – the ore used for alumina production worldwide. Al₂O₃ content in bauxites varies from 30 to 60 wt% and more than 85% of its global production (89 million tons in 2010) is consumed to produce aluminium, a commodity market in constant growth.¹² The current production of alumina from bauxite is through the Bayer process, which exhibits notoriously high energy and chemical consumption, along with the generation of a large amount of waste of ecological concern (e.g., “red mud”).¹³

However, for products such as potash and alumina the transition from a conventional to a new mineral source, in particular of lower grades, is rarely economically and ecologically acceptable using traditional extraction technologies. In other words, novel mineral sources call for novel processing approaches designed in accordance with the green chemistry paradigm.^14–17

Ground K-bearing silicates (“stone-meal”) were suggested as an alternative source of potassium for agriculture in the beginning of the twentieth century.¹⁸ This approach does not involve any chemical process, and implies only crushing and grinding with a minimal amount of energy (around 20 kWh t⁻¹ when modern grinding techniques are used). Despite its simplicity, this approach has not yet been successfully implemented in mainstream agriculture, possibly due to the slow rate of potassium release from the majority of tested minerals.^1,9–11,19

The design of chemical processing to extract potassium and aluminium from earth-abundant K-bearing silicates is also a multi-century endeavour, traced back to 1856 and still pursued.^20,21 Two main approaches have been proposed: high-temperature (pyrometallurgy) and hydrothermal treatment. For the former, the process temperature ranges between 600 °C and 1400 °C. These methods require additives that form eutectics or exhibit a miscibility gap with the silicate of interest. The need for these additives (fluxes, typically salts of alkaline and/or alkaline earth metal) is a challenge for green chemistry. First, the compatibility of the additive with the downstream application (e.g., fertilizer) has to be thoroughly evaluated, and second, such an approach leads to a large volume of by-products, which have to be disposed or recycled. Finally, the quenching step, typical for such processing, requires water regeneration facilities.

Hydrothermal methods typically operate at lower temperatures (150 °C–300 °C) and elevated pressure, and utilize water as the reagent. Hydrothermal methods aim to accelerate the natural decomposition of K-bearing silicates by aqueous fluids, a reaction that is responsible for soil formation on the geological timescale. It therefore appears particularly appropriate to discuss what knowledge has been gained from nature to design hydrothermal methods according to green chemistry principles.

Despite substantial prior research, the industrial production of alumina from non-bauxite ores is implemented only in a few countries of the former USSR,²² but none of these methods is currently used for potassium extraction. Earlier reviews^23,24 are focussed on the technical developments related to the transformation of K-bearing silicates into various products from 1856 to 1995. The present work is dedicated to the fundamental chemical mechanisms for the aqueous alteration of K-bearing silicates, with the objective of linking the knowledge available from geochemistry and materials chemistry studies. The primary objective of this paper is to demonstrate that linking these fields is needed to identify green chemistry strategies, suitable for the specific usage of earth-abundant K-bearing tectosilicates as a source of potassium and, potentially, aluminium.

The first section is a brief description of the occurrence and properties of K-bearing tectosilicates. Section 3 is an analysis of the recent geochemical studies related to the aqueous alteration of K-bearing tectosilicates with the primary focus on the dissolution mechanism. This section discusses the rate-controlling parameters for the dissolution and identifies the challenges related to the direct use of K-bearing tectosilicates as sustainable substitutes for potash in agriculture. Section 4 describes the hydrothermal alteration processes proposed for such minerals, focusing on the underlying chemical mechanism and the corresponding green chemistry challenges and benefits.

2. K-bearing tectosilicates as earth-abundant raw materials

In 1917, the 27^th session of the British Institute of Mining and Metallurgy was devoted to “A Neglected Chemical Reaction and an Available Source of Potash”,²⁵ where E. Ashcroft introduced the research related to potassium extraction from K-feldspars processed at 1000 °C in the presence of NaCl, moisture and air. Arguing the practical significance of the method, he said:

“It is, perhaps, not always appreciated that feldspar is the most abundant mineral in the earth's known crust. Hatch gives us, in a striking little table in his text-book on mineralogy, an estimate of 1% for metal ores and 1% for salts, lime, magnesia, etc., and 48% for feldspars. Potash feldspar, though, representing only one species of the feldspars, constitutes, nevertheless, a large proportion, probably, the predominant proportion, and very little consideration enables us to realize that potash, so far from being a scarce substance in nature, is really most abundant”.²⁶

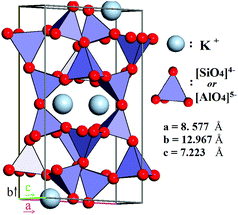
According to contemporary views, feldspars comprise a group of minerals that constitute 60% of both the continental and the oceanic crusts of our planet. In particular, they are common in igneous rocks such as granites, gneisses and schists, and also occur in metamorphic, and some sedimentary rocks,²⁷ thereby, being almost evenly distributed across liveable continents. Feldspars are crystalline aluminosilicates with the general formula M¹⁺/M²⁺(Al,Si)₄O₈, often written as MT₄O₈, where T stands for an element in tetrahedral coordination with oxygen. M¹⁺ and M²⁺ represent an alkaline or alkaline-earth metal, acting as a charge-compensating cation. The feldspars crystal lattice is composed of corner-sharing AlO₄⁵⁻ and SiO₄⁴⁻ tetrahedra linked in an infinite 3D framework. This defines feldspars as “framework silicates” or tectosilicates (see Fig. 2). The composition of pure K-feldspar (KAlSi₃O₈) is 18 wt% Al₂O₃ and 16.9 wt% K₂O, though most feldspar minerals²⁸ have the general formula

K_xNa_yCa_1−(x+y)Al_2−(x+y)Si_2+(x+y)O₈.

Fig. 2 Idealized crystalline structure of microcline: the red spheres represent oxygen atoms; silicon and aluminum atoms are within the [SiO₄]⁴⁻ and [AlO₄]⁵⁻ tetrahedra, and the potassium charge-balancing cations are the blue spheres.

The degree of ordering of Al and Si among the T-sites leads to a structural transition between monoclinic and triclinic symmetries. Three polymorphs of K-feldspar have been identified by X-ray diffraction, ranked by the degree of ordering: microcline, orthoclase, and sanidine. The phases observed in natural rocks are inherited from the temperature of magma solidification, its cooling rate, and their subsequent geological history.^29,30 Besides these polymorphs, a variety of terminology exists for K-feldspar-bearing minerals depending on their geological origin (e.g., “Adularia” from the Adula Mountains, St. Gotthard, Switzerland a low-temperature form of potassium feldspars, whose structural state is nearly equally represented by microcline and orthoclase).

Feldspathoids represent another group of tectosilicate minerals with a higher potassium and aluminium content, because of their under-saturation in silica with respect to feldspars. They are more rare minerals than feldspars, though attractive in terms of potassium and aluminium extraction. Minerals nepheline (Na₃KAl₄Si₄O₁₆), kalsilite (KAlSiO₄), and leucite (KAlSi₂O₆) are members of this group.

K-Feldspars and feldspathoids typically constitute up to 90% of common rocks such as granites or syenites, and can form deposits of a relatively high grade, making them an abundant and locally available reserve of potassium and aluminium. Moreover, it is possible to find deposits that can be mined by open quarry, and not by deep-mining typical for such salts as sylvinite. The conversion of these reserves into sustainable resources however requires the development of adequate extraction technologies suitable for the foreseen materials product. From a green chemistry perspective, a promising way to achieve potassium availability from K-feldspars and feldspathoids is to expose them to an aqueous solution by analogy with geochemical weathering. Therefore, the following section reviews the most recent geochemical studies related to the mechanism of aqueous dissolution of these minerals, using K-feldspars (later named KFS) as the paragon of K-bearing tectosilicates.

3. Dissolution mechanism of K-bearing silicates, as derived from geochemical studies

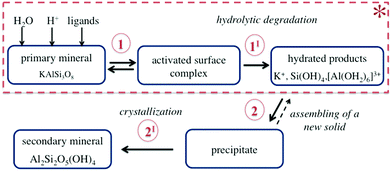
Chemical weathering is the natural process of mineral alteration mediated by fluid, which results in the replacement of primary rock-forming minerals by secondary minerals, more stable under the given conditions.^31,32 During weathering, several reactions occur simultaneously at the mineral–fluid interface as schematically shown in Fig. 3.

Fig. 3 Schematic of the aqueous alteration of K-bearing framework aluminosilicates and the scope of the present review (*). During dissolution (marked by the dotted line), the reactants form a metastable activated complex on the mineral surface (step 1). The chemical nature and composition of the species contained in the fluid determine both the complex and hydrated products to be formed after the irreversible decomposition of the mineral (step 1^I). For instance, silica and alumina hydrates shown in this schematic exist at pH ≤ 3. The formation of a new solid may involve precipitation of a metastable intermediate (step 2) followed by structural and compositional changes (step 2^I), which lead to the formation of secondary crystalline phases.

The dissolution of K-bearing silicates involves the release of charge-balancing cations (e.g., K⁺) via ion exchange, adsorption/desorption of the dissolved species at the mineral surface exposed to the fluid (step 1 in Fig. 3), and hydrolytic degradation of the T–O–T linkages (step 1^I in Fig. 3). The ultimate step is the removal of hydrated alumina and silica species from the crystal lattice (see Fig. 4). A new solid phase is formed along the dissolution profile due to the assembly of metastable precipitates, followed by nucleation, growth, and recrystallization of a secondary mineral (steps 2 and 2^I in Fig. 3).

Fig. 4 Schematic of the proton-promoted dissolution of K-bearing tecto-aluminosilicates, illustrating the dissolution of one cluster. The tetrahedra can contain Si or Al.

In geological systems, molecular flow in the vicinity of a mineral surface is often space-constrained, which causes local oversaturation of aqueous silica, alumina, and other ions. The surface of a primary mineral offers a lower energy barrier for nucleation, thereby serving as a substrate for the precipitates. New phases therefore appear preferentially at the fluid–mineral interface, starting the propagation of the weathering profile at the macro-scale.^33–35

At a low fluid saturation, the dissolution rates obtained for K-feldspars at room temperature in acidic solutions (pH range 1–5) in the laboratory vary from 10⁻¹³ to 10⁻¹⁰ mol_KFS m⁻² s⁻¹.³⁶ The rates observed on geological sites are typically 10–3000 times slower.³⁷ This inhibition of mineral dissolution in natural fluids is attributed to high saturation states of these fluids, the formation of a secondary phase at the fluid–mineral interface, seasonal temperature fluctuations, and partial wetting of the mineral surface.³⁸

The focus of the present work is mineral alteration aimed at increasing the availability of potassium and aluminium. Therefore, only the highest dissolution rate, i.e., corresponding to the dissolution under low fluid saturation states, also named “far from equilibrium dissolution” is discussed below (see the dotted area in Fig. 3). The precipitation of a secondary phase from oversaturated solutions is therefore not addressed.

Many studies prior to the 1980s referred to solid-state diffusion through a partially altered surface layer as the rate-determining step in the dissolution of rock forming silicate minerals.^39–41 Later, this diffusion-controlled model was reconsidered, and surface reactions at the fluid–mineral interface (namely, the detachment of a surface complex illustrated by step 1^I in Fig. 3), were proposed as the rate-limiting step.^42,43 Recently, high-resolution transmission electron microscopy has been extensively used to examine the surface of Ca-feldspars during acidic dissolution.⁴⁴ A step-like change in Ca, Al and Si concentrations in the pre-surface layer has been reported at the nanometer scale. Such an abrupt concentration profile is considered incompatible with the diffusion-controlled dissolution model, but rather suggests an interfacial dissolution–re-precipitation mechanism: “Non-stoichiometric dissolution is limited to a layer of few unit cells, and may result in re-polymerization of silica fragments when dissolution rate of amorphous silica is slower than net mineral dissolution rate”.³⁵

Based on considerable experimental and theoretical work, the net dissolution process has been expressed as the following series of elemental chemical steps (see also Fig. 3 and 4):

1. Ion-exchange (proton ↔ charge balancing cation), fast and reversible;

2. Surface + water molecule ↔ surface species, fast and reversible;

3. Surface species → dissolved species, slow and irreversible.

However, this scheme does not distinguish the role of the network-forming elements (Al and Si) in the formation of a surface complex. A series of studies over a broad range of pH showed distinct reaction mechanisms for different surface entities (e.g., Al–O–Si and Si–O–Si).^45–47 For instance, the ab initio molecular orbital (MO) modelling of Al transition from 4- to 6-fold coordination state at the feldspar–water interface in acidic pH has been proposed. This model combined with cross-polarization magic angle spinning ²⁷Al solid-state nuclear magnetic resonance (CPMAS-NMR) demonstrates the formation of a 6-fold coordinated aluminium ion “on the feldspar surface prior to the ion release in the aqueous phase”.⁴⁸ This feature distinguishes the dissolution behaviour of aluminium in aqueous fluids from the other ions that constitute K-bearing aluminosilicates.

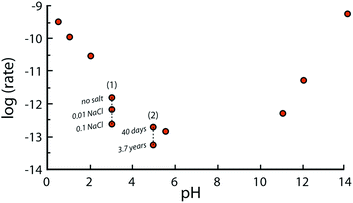
It should also be emphasized that far from equilibrium dissolution rates measured in laboratories are typically referred to as “steady-state” dissolution, though the rates often do not reach constant values.⁴⁹ In other words, no plateau is reached for potassium, aluminium, and silicon concentration as functions of time in most of the flow experiments with fine-ground minerals.⁵⁰ For example, the rate of Si-release from plagioclase feldspar observed after 200 days was between 1.5 and 4.10⁻¹² mol m⁻² s⁻¹ at pH = 5 and 25 °C, but decreased to 2 × 10⁻¹⁴ mol m⁻² s⁻¹ after 3.7 years⁵¹ (see Fig. 5). This phenomenon can be explained by variations in the surface area and roughness during long-term leaching experiments. Another explanation may be the reduced driving force for the release of Si and other elements once the fluid is approaching saturation with respect to the corresponding ions.⁵² The longest experiment reported to date (>6 years) reveals that freshly crushed plagioclase had not reached steady-state dissolution within such a timeframe. In contrast, the laboratory dissolution of naturally pre-weathered granite exhibited relatively constant rates after only several months. Nevertheless, the term “steady-state dissolution” is used to describe the period when the rate of mineral dissolution stabilizes at a quasi-constant value.

Fig. 5 Effect of pH on far-from equilibrium dissolution rates of K-feldspars under ambient conditions; (1) effect of ionic strength at constant pH of the fluid; (2) effect of leaching time at constant pH of the fluid.

Whilst the details of the dissolution mechanism remain a subject of research, the experimental dissolution rates measured in the laboratory for K-bearing silicates, and particularly K-feldspars, are fairly well established. On a geological time scale, these rates are affected by large-scale dissolution/re-precipitation events, which ultimately drive the genesis of sediments, soils and landscapes, determining soil fertility and the composition of ground water.^53,54 On the industrial and agricultural time scales, however, the low-temperature dissolution of K-feldspars and feldspathoids in non-aggressive aqueous fluids is prohibitively slow: the mean lifetimes of a 1 mm crystal of K-feldspar and nepheline in an exogenic cycle are 520 000 and 211 000 years, respectively.⁵⁵

This reality points out to the need to design a chemical medium more efficient than weathering fluids in order to accelerate the release of the ions of interest from K-bearing aluminosilicate minerals. High acidity (resp. basicity), organic and inorganic ligands, and the presence of various defects in mineral lattice can accelerate the dissolution rate in aqueous fluids. These and other factors, crucial for the design of a green chemistry process and the effective use of K-bearing silicates, are reviewed in the forthcoming sections.

3.1. Far-from-equilibrium dissolution in aqueous fluids

3.1.1. Effect of pH. It has been proposed that the dissolution rate of feldspars and feldspathoids is a function of protonation of alumina. The surface charge of alumina groups, predominantly positive (≡Al–OH₂⁺) in proton-promoted dissolution and negative (≡Al–O⁻) in hydroxyl-promoted dissolution, varies in acidic and basic fluids respectively. The influence of protonation of ≡Si–OH and bridging ≡Si–O–Si≡ surface sites is not to be discounted as well.^56–59

Fig. 5 depicts the net dissolution rate of K-feldspars and feldspathoids with respect to pH. The rate is reported to increase with a decrease in pH lower than 4; it is almost pH independent near the neutral region; and increases with an increase in basicity for pH greater than 8.

For pH lower than 4, the rate law can be written as follows:

R_H = k_H⁺aⁿ (1)

where, k_H⁺ is the proton-promoted dissolution rate constant that ranges from 10⁻¹⁰ to 10⁻⁸ mol_KFS m⁻² s⁻¹, and a is the activity of H⁺, raised to the power n.

Likewise, for pH greater than 8:

R_OH = k_OH⁻b^m (2)

where, b is the activity of [OH⁻], and k_OH⁻ varies from 10^−10.43 to 10^−7.33 mol_KFS m⁻² s⁻¹.

Estimates of n and m vary from 0.4 to 1 and 0.3 to 0.7, respectively.³⁴ In eqn (1) and (2), n and m encompass the influence of intrinsic properties of the minerals such as crystal imperfections that accumulate an excess of free energy. More generally, the dissolution rate as a function of pH is expressed using a pseudo first-order approximation, as follows:

R_pH = kS_c (3)

where, S_c is the surface charge (mol m⁻²) that can be estimated by surface titration,^41,59 and k is the apparent rate constant (s⁻¹). The surface charge value obtained for albite varies from 10^−4.25 to 10⁻⁶ mol m⁻² in the pH range 2–11, with a minimum in the vicinity of neutral pH; whereas k is typically 10^−6.5 and 10^−6.1 s⁻¹ for acidic and basic solutions, respectively.⁵⁸

However, the usage of large amounts of strong acids/bases for extraction is a serious environmental challenge, because such reagents have to be synthesized, and possibly regenerated. They also require reactor materials that are compatible with such corrosive media, most which have a significant environmental impact during their extraction (e.g. titanium).

3.1.2. Effect of powder preparation. Since the surface concentration of specific active sites (S_c in eqn (3)) can be directly measured in a broad pH range, the rates derived from a surface speciation model usually match laboratory data obtained for an identical sample. However, besides pH, inhomogeneity of mineral surface also leads to variations in S_c. This effect might be caused by the bulk intrinsic inhomogeneity of a mineral or sample preparation such as surface roughness and lattice distortions induced by grinding. Analogous to the modification of the isoelectric point of silica induced by mechanical treatment – up to 0.4 units and higher⁶⁰ – the S_c measured for K-bearing silicates also varies depending on the powder preparation method. The role of surface charge seems to be even more critical when one considers water molecule dynamics in the vicinity of an oxide surface: the ability of water to dissociate and subsequent proton transfer are highly affected by the surface properties of the solid phase.^61,62 Dove and co-workers demonstrated the surface-control of solvent reactivity for SiO₂ polymorphs,^63,64 but this information is not available for most of the K-bearing silicates. Moreover, it is still unclear, which functional groups form at the fluid–mineral interface at different stages of the dissolution process and how their interactions with water molecules modify the surface chemistry in various pH ranges. This information might be crucial, however, to design novel green extraction schemes. A mechanical pre-treatment of the minerals is indeed an appealing method from a green chemistry perspective, e.g. mechanoactivation^65,66 or ultra-sound treatments.⁶⁷

3.1.3. Effect of inorganic ions. Besides pH, mineral dissolution rate is also sensitive to the competitive absorption of dissolved species other than H⁺/OH⁻. Natural fluids often contain inorganic ions such as Na⁺, K⁺, Ca²⁺, Mg²⁺, Al³⁺, and more complex polynuclear ions of alumina and silica as well as anionic species that play a role in the dissolution of silicate minerals.^68–71 In contrast to the hydrolysis of silica, where alkali cations can weaken the Si–O bonds, and, thereby, promote hydrolysis^62,72–74 the rate of dissolution of feldspars in acidic to near-neutral pH decreases with increase in the ionic strength of the fluid. For instance, K-feldspar dissolution rates (T = 25 °C, pH = 3) measured in flow reactors with an influent containing 0.01 and 0.1 mol l⁻¹ NaCl were 7.15 × 10⁻¹³ and 2.59 × 10⁻¹³ mol_KFS m⁻² s⁻¹, respectively. Interestingly, the rate observed in the same reactor but in the absence of foreign ions, was as high as 1.63 × 10⁻¹² mol_KFS m⁻² s⁻¹ (Fig. 5). A competition of foreign ions with H⁺ in acidic fluids for the exchange sites on mineral surfaces is put forward to explain this observation.⁶⁶ The fact that cations with a relatively large hydrated size (e.g., (CH₃)₄N⁺) exert a lower inhibition on the dissolution rate is in good agreement with this hypothesis. However, it has been demonstrated⁷⁵ that the hydrated size of a cation is not the only parameter determining the cation-exchange selectivity of the aluminosilicate surface, and that the stability of ≡T–O–M and ≡T–OH surface complexes should also be taken into consideration.⁷⁶

Aqueous silica and alumina speciation have been extensively studied in the field of sol–gel chemistry,^62,77,78 and the role of framework-forming elements at concentrations below solubility line deserves attention for mineral dissolution studies as well. The oligomerization of silica in undersaturated solutions (4, 12, and 21 mmol_SiO2 l⁻¹) was studied as a function of ionic strength (0.01–0.24 M_NaCl), and pH 3–11, at 25 °C using a colorimetric silicomolybdate method.⁷⁹ This study supports the hypothesis that natural fluids undersaturated with respect to SiO₂ may slowly approach steady-state equilibrium with respect to amorphous silica, and thereby, inhibit mineral dissolution. From a green chemistry standpoint, not much flexibility is offered on the choice of the inorganic ions for K-feldspar processing, in particular for fertilizers, as the use of alkali (Na⁺) has to be strictly controlled for agronomic applications. Some micronutrient elements could be considered as acceptable (e.g., Fe, Mn, Mo, or Zn) though the concentration/cost/benefits still remain to be quantified.

3.1.4. Ligand-promoted dissolution. In addition to the critical role of pH, the dissolution of aluminosilicate minerals can be modified by a variety of organic ligands. The dependence of the dissolution rate on the nature and the concentration of ligands has been extensively studied.^80–86 Organic acids with anionic groups capable of complexing aluminium provide both ligands and protons that participate in mineral degradation. The rate law for the acidic dissolution of feldspars in the presence of a ligand is proposed to be the sum of proton- and ligand-promoted rates:

R_t = R_H + R_L (4)

where R_t is the overall dissolution rate, R_H and R_L are the proton-promoted and ligand-promoted rates, respectively. By analogy with R_H, R_L is expressed as k_La^m_L where k_L refers to the ligand-promoted rate constant, and a_L is the activity of the ligand (L).⁸⁷ Dissolution rates for feldspars have been evaluated at 25 °C with pH 3–7 in oxalic acid with concentrations ranging from 0 to 8 millimoles per liter.⁸⁸ It has been suggested that the pure ligand-promoted rate is a function of the activities of HC₂O₄⁻ (bioxalate) and C₂O₄²⁻ (oxalate), and may be expressed as:

R_t = 10^−12.8(a_HOX⁻ + a_OX²⁻)^0.75 (5)

where, a_HOX⁻ and a_OX²⁻ are the activities of HC₂O₄⁻ and C₂O₄²⁻, respectively.

Organic ligands can therefore enhance the dissolution rate of feldspar under acidic conditions up to 15 times. The increase of surface area of the feldspar powder during dissolution in oxalic acid, determined to be of one to two orders of magnitude, has however not been taken into account in this evaluation. Aside from this surface area increase, it has been observed that ligand-promoted dissolution is also dependent upon the degree of Al–Si ordering in K-feldspars.⁸⁹ A 5-fold increase in the cumulative Si concentration was observed after 75 h with respect to dissolution in the absence of organic ligands for highly disordered sanidine; whereas 90% increase was reported for highly ordered albite. It should be emphasized that this study was designed to replicate the conditions of geological carbon sequestration (P_CO2 = 100 atm, T = 90 °C, 0.1 M_NaCl, initial pH = 3.1, oxalate/acetate concentrations 0, 0.01 and 1 M). Under these conditions, both ligands enhanced the net rate of dissolution, though oxalate showed a more prominent effect than acetate.

The corresponding rate is also influenced by the aluminum/iron content of the mineral. In pure synthetic aluminosilicates, aluminum is the only element prone to complexation, whilst feldspar-bearing rocks always contain other complex-forming elements, e.g. iron. Aluminum and iron form stable coordination complexes with hard Lewis bases such as OH⁻, F⁻, PO₄³⁻ SO₄²⁻, C₂O₂²⁻, CH₃COO⁻, ROH, RO⁻ or RNH₂. The most stable complexes are obtained with multidentate ligands with negative oxygen electron-pair donors.⁹⁰ This organo-mineral interaction mediated by fluids constitutes the chemical basis of bio-weathering, where both proton-promoted and ligand promoted mechanisms might be involved. Other parameters being equal, the efficiency of carboxylic anions of a low molecular weight for the dissolution of silicate minerals has been ranked as: citrate ≥ oxalate > maleate.

In the context of agricultural applications of K-bearing silicates, the effect of organic ligands might be considered as a soft processing approach. The usage of organic acids available in nature (e.g., substances produced by plants, fungi, and bacteria) is one possible approach that may alleviate the reliance on inorganic acids.⁹¹ In particular, organic acids can modify their binding properties with a minor pH shift, which on a large scale implies a lower consumption of inorganic acids or bases. Such a soft chemistry approach could ultimately help to reduce waste production during the downstream recovery of K or Al. Clearly, a better understanding of organic acids might pave the way for the design of green chemistry methods for potassium extraction, in particular for agricultural needs, as discussed in section 3.2.

3.1.5. Effect of temperature. For feldspars, the net dissolution rate typically increases by about two orders of magnitude with an increase in temperature of 100 °C in the range 25–300 °C at constant pH. For albite, an increase from 10⁻¹² (25 °C, pH = 3) to 10⁻⁶ mol_KFS m² s⁻¹ at (300 °C, pH = 3) has been reported.⁹² Generally, the temperature dependence of a reaction constant (k) is expressed by an Arrhenius equation:

k = A exp(−E_a/RT) (6)

where, A is the pre-exponential factor, and E_a the activation energy; R the gas constant; and T the temperature in degree Kelvin. But, the difficulty in applying eqn (6) to feldspar dissolution is that the dependence of the dissolution rate on temperature is affected by the pH of the dissolving fluid and vice-versa. For instance, an increase in the temperature at constant pH leads to an enhanced cation/decreased anion adsorption on oxides (Al₂O₃, Fe₂O₃, TiO₂, and feldspars). This reality exacerbates the effect of acidity on the dissolution rate.^62,93 Therefore, an Arrhenius expression for the dissolution of aluminosilicate minerals is valid only within a given pH range and, more generally, for a constant composition of the fluid.^94,95 The temperature and pH dependences for albite dissolution in acidic fluids have been derived from experimental data using an Arrhenius-like model⁹⁶:

log R = −2.71 − 3410/T − 0.5pH (7)

This equation is valid in the 5–300 °C temperature and 1–5 pH ranges. The net activation energy is proposed to be equal to 65 kJ mol_KFS⁻¹ and independent of pH. According to this model, the maximum dissolution rate for albite at pH = 1 and T = 363 K (90 °C) is 2.34 × 10⁻⁰⁹ mol_KFS m² s⁻¹. Generally, for feldspars and feldspathoids, the variation of the logarithm of the rate with pH at elevated temperatures displays a U-shape^89,97 similar to that for ambient temperature represented in Fig. 5.

The operational standard molar activation enthalpies (ΔH_app = E_a − RT) for K-feldspar are typically obtained in experiments where temperature is changed and all other parameters are kept constant; significant amounts of such data are gathered in Arnorsson and Stefansson's paper.⁹⁸ In earlier literature, ΔH_app varies to a high extent: from 19 to 200 kJ mol_KFS^−1.34. Such a broad range is caused by differences in experimental conditions or approaches of kinetic modelling. For instance, a study⁹⁹ performed for albite and adularia at 25–200 °C reported apparent activation enthalpies of 80 and 37 kJ mol_KFS⁻¹ for low and neutral pH respectively. Another study for albite performed at 25 and 70 °C reported values of 119, 54, and 32 kJ mol_KFS⁻¹ for acidic, neutral and basic pH, respectively.¹⁰⁰

In spite of such discrepancies, ΔH_app proposed for feldspar dissolution in acidic fluids is reproducibly higher than that for neutral pH. In contrast, activation energies calculated from the slope of Arrhenius plot shall exhibit the highest value for the slowest reaction (here, the neutral dissolution), if the reaction mechanism does not differ. Surprisingly, such deviation has not been particularly addressed, and might be an indication of a greater temperature dependence of the rate-limiting reaction under acidic conditions, meaning that the reaction mechanisms in acidic and neutral pH are different. In this context, the higher empirical ΔH_app values calculated for a strongly acidic pH are compensated by a higher pre-exponential factor (A). The variation of A with pH, in turn, can be discussed in the context of pH dependence of the surface concentration of sites potentially available for complex formation. As mentioned in section 3.1.1, feldspar surface charge has the lowest values at neutral pH and increases linearly with a decrease in pH.⁵⁹ Such an increase in surface charge promotes hydrolysis by reducing the energy barrier for proton transfer to the transition state,¹⁰¹ and might be driven by the protonation of oxygen atoms located in the bridging hydroxo groups on the surface. Therefore, one can speculate that the pre-exponential factor A for data obtained at a given pH and fitted to an Arrhenius model reflects the surface concentration of sites potentially available for complex formation, which, in turn, varies with fluid acidity.

The temperature leverage to accelerate the rate of leaching remains extremely powerful at the process level, and may be compatible with the green-chemistry approach. For instance, the targeted range of temperature for the hydrothermal treatment of K-bearing silicates remains relatively low – 100 to 300 °C (see section 4) opening the possibility of using waste heat from other high-temperature process.

3.1.6. Crystallographic control and future directions for dissolution studies. As mentioned in 3.1.2, various crystal defects, both intrinsic and those introduced by sample preparation affect mineral dissolution kinetics. Surface inhomogeneity at the sub-micron to atomic scale might be caused by bulk inhomogeneity of a geological origin (e.g., textural imperfections, recrystallized areas, rock microstructure, etc.) or by sample preparation (e.g., surface roughness and lattice distortions induced by grinding). Surface inhomogeneities affect the mineral surface charge and, hence, the pH dependence of the dissolution rate (see section 3.1.2). In addition to defects, preferential dissolution along particular crystal planes has also been reported for many minerals, including feldspars.^102–104 Despite experimental evidence of the crystallographic control of mineral dissolution, none of the models reviewed in section 3.1 quantify this effect.

It should be noted that there is also a lack of methods to predict the extent of lattice distortion (sometimes called amorphization) of a mineral surface caused by different grinding techniques. Laser and gas adsorption analyses provide important information about particle size distribution and specific surface area of a mineral powder – parameters that are typically taken into account in dissolution studies. However, the influence of the duration and method of grinding on the dissolution cannot be quantified by only these two parameters. Factors such as Fe-poisoning introduced by steel-containing milling media, non-cumulative particle size effect (e.g., particles of sub-micron size dissolve relatively faster than those of micron size, regardless of cumulative surface area), mechanically-induced lattice distortions, etc. can have a key influence on the dissolution kinetics, especially in short-term dissolution experiments.

The role of structural defects in mineral dissolution kinetics, often covered under the term microstrain, has been integrated in a stepwave model (DSM).^105,106 This model takes into account surface topography and attempts to link far-from-equilibrium dissolution rates with those derived from near-equilibrium studies. In other words, DSM is aimed at integrating the atomic scale mineral–fluid interaction with bulk dissolution experiments and macro-scale geochemical observations. One experimental method to observe reacting surfaces with atomic resolution for the validation of the DSM model is vertical scanning interferometry (VSI). It provides nanometer vertical resolution, and 0.5 microns lateral resolution.¹⁰⁷

Most of the mechanisms reviewed in this section have been derived from bulk dissolution experimental data combined with post-immersion solid phase characterization or ab initio modeling.⁷⁴ However, a gap exists between the rate law derived from dissolution experiments and molecular simulation. A better understanding of far from equilibrium dissolution kinetics could be obtained by quantifying the effect of surface defects and nanometer-sized aqueous intermediates formed on the mineral surface. Combining modern spectroscopic methods^108,109 with computational simulations is a critical endeavour. Such investigations can help to identify elementary reactions that take place on the mineral surface, and ultimately describe pH-sensitive competitive ion adsorption, the role of crystallographic orientation of dissolving planes and the inhibiting/promoting effect of organic ligands. Such a level of understanding of mineral dissolution mechanisms, in turn, will be highly beneficial for designing selective, cost- and energy effective extraction schemes for minerals.

3.2. Mineral alteration in soil environment for agricultural application

The above sections demonstrate that a significant body of knowledge about the far from equilibrium dissolution of K-bearing silicates is available. However, the mechanism of mineral dissolution under natural conditions is complex, one of the outstanding factors being the soil environment itself. It is generally proposed that the rates measured in the field are significantly slower than those obtained in the laboratory, though hardly predictable.^110,111,113 Modern geochemical kinetic modelling allows the prediction of weathering rates in different soils and climates, but requires input parameters such as pH and bulk density of soil, contact surface area, average rate of nutrient uptake by plants, and fluctuations of the moisture content.^112,113 Moreover, laboratory experiments typically do not reproduce the actual fluid paths in the soil as well as the soil chemistry. Taking into account the biota dynamics and symbiosis effect makes the situation even more complicated. Though plants, microbes, fungi and bacteria are known to be involved in the natural alteration of minerals,¹¹⁴ limited data are available on the actual mechanisms of K-bearing silicate mineral dissolution coupled with plant growth and harvesting.^115–117

Kinetic models that integrate the variability of temperature and fluid composition, changes in the textural and chemical properties of the mineral surface, partial surface wetting, and the role of biota are still missing. Such modelling calls for further multidisciplinary studies, which will allow the prediction of the rates of natural mineral alteration with a better accuracy. From the perspective of green fertilization, a detailed understanding of the inorganic and organic (bio) chemistry involved in mineral dissolution is needed to evaluate the chances of success of the as-ground K-bearing silicates for fertilizing applications (“stone-meal” approach). This knowledge will help identify mineral candidates with the most appropriate geological histories that perform most efficiently for a given soil composition and crop culture, allowing their direct use in agricultural application. The use of as-ground materials offers the most sustainable alternative to existing inorganic fertilizers, since it requires only a minimal amount of chemical processing and mechanical energy. However, as discussed above, the dissolution rate and the availability of K from such minerals may not suffice for all soils and agronomical practices. Also, this approach is not possible for Al extraction, suggesting that chemical processing is critical to transform K-feldspar reserves into resources.

4. Hydrothermal processing of K-bearing silicates

From the perspective of chemical processing of K-bearing silicates, for fertilizers or alumina production, the processes proposed to date favour the use of strong aqueous solutions of acids or bases and temperature, i.e. hydrothermal processes. The environmental impact of these reagents has been established,^118,119 and their by-product status makes them affordable. Though alternative reagents may become available, as suggested in section 3, it is within this paradigm that most processes have been developed as reviewed below.

4.1 Classification and scope of processing schemes

The most recent review of hydrothermal methods was published in 1998,²⁴ adopting an approach similar to the one published 86 years before.²³ Both are comprehensive in terms of factual chemical engineering procedures, but do not highlight the chemical mechanism and the structure–property relationships that constitute their basis. As mentioned in section 3, the covalent nature of aluminosilicate anions constituting the framework of K-bearing tectosilicates ultimately implies that their water-mediated reactions at ambient temperature and pressure are often kinetically controlled, i.e. the intrinsic reaction rates are slower than the transport of the reactants/products. Most of the hydrothermal techniques have therefore been designed to accelerate the rate of hydrolytic degradation of the aluminosilicate anionic framework.

The proposed hydrothermal processes can be separated in the following categories: (i) techniques aiming at complete mineral decomposition i.e. dissolution followed by the recovery of aluminium and potassium as salts from aqueous solutions^24,120–123 and (ii) mineral alteration by aqueous solutions of extreme pH, where the products (typically, a mixture of the parent mineral and newly formed phases) are subjected to the subsequent extraction of potassium by leaching or ion-exchange.^124–126

The processes in category (i) aim to fully dissolve the mineral in strong inorganic acids or bases, and seek the separation of silica ions with the subsequent recovery of aluminium and potassium in the form of crystalline chlorides,¹¹⁸ nitrates,¹²⁷ and sulfates.¹²⁰ In order to reach completion and achieve an acceptable rate for industrialization, elevated temperature and pressure are chosen to accelerate the reaction kinetics, along with an intensive agitation and large amount of mineral acids or alkaline/alkaline earth hydroxides (typically, Ca(OH)₂), as well as around 10-times the amount of water needed for stoichiometric extraction.

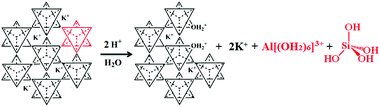
The complete extraction of crystalline salts of K and Al from K-bearing aluminosilicates requires a separation step, an energy intensive process seeking to isolate silica from the reacting system. The most common method is a drastic change of the pH implying a large consumption of acids and bases. The next step is a physical separation of colloidal silica from the solution, again an energy and capital-intensive unit operation. This separation leaves behind highly alkaline or acidic residues, which have to be handled as liquid chemical waste. If crystallization of KCl, KNO₃, K₂SO₄, etc. is involved, water has to be evaporated requiring a significant energy input. From a sustainability standpoint, this complete extraction process has very similar features to the Bayer process used for aluminium extraction from bauxite. Such an extraction concept unavoidably causes a large amount of liquid and solid waste if aluminosilicate minerals are used as raw materials, which contradicts with a key principle of green chemistry and engineering, which aims to “maximize the incorporation of all materials used in the process into the products, and prevent creation of wastes rather than treat or clean up waste after it has been created”.¹²⁸ In addition, complete disintegration is very capital, energy and chemical intensive in order to be conducted in an environmentally acceptable manner.¹²⁹ The only, somewhat unique, example of the industrial application of a full extraction process for feldspathoids is with nepheline, to produce alumina for aluminium production. It is currently in operation in a small number of countries from the former Soviet Union.^130,131 Historically, the lack of suitable bauxite in Russia and the occurrence of high grade nepheline ores along with the request of Soviet authorities for the domestic production of this metal help to contextualize the origin of such a complex hydrothermal extraction scheme. The issue of siliceous wastes from such processes is unavoidable, and was partially solved by the obligation of the cement industry to utilize them for the manufacturing of “nepheline cement”. The wastes of nepheline refining are indeed enriched in dicalcium silicate (Ca₂SiO₄, belite) – an industrial mineral contained in Portland cement and responsible for the development of the late strength of concrete. Being capable of hydrolytic hardening, such belite-rich waste was successfully applied in construction. Another potential solution to the problem of waste handling during alumina recovery from nepheline is the combined processing of nepheline to produce soda, potash, Portland cement and alumina.^132,133 Complete recovery of a minor component from a mineral is challenging due to the need for excessive amounts of synthetic chemicals, water, along with the inherent amount of waste generated by the separation steps. Although it is possible to envision a completely “environmentally neutral” process for the separation of KAlSi₃O₈ into alumina, silica and a salt of K, the encumbered capital, operating and energy costs have to date prevented its industrial-scale development.

The processes of category (ii) rely on dissolution/re-precipitation promoted by relatively low amounts of alkaline/alkaline- earth hydroxides. These processing schemes typically do not allow the transport of the dissolved products and lead to in situ re-precipitation – conditions commonly achieved in batch, semi-batch, and sometimes, continuous reactors without agitation.^121,134 For such high over-saturation conditions, the space constraint leads to the precipitation of poorly crystallized products, or a mixture of crystalline and semi-crystalline precipitates. The discrimination between the steps of hydrothermal dissolution and ion precipitation is however very challenging conceptually and experimentally.¹³⁵ As a practical example, another commercially important group of materials produced using a similar process are synthetic zeolites. For this group of materials, the fundamental understanding of hydrothermal crystallization/condensation is still in its developing stage, despite being industrially conducted since 1950. Altogether, there is still a lack of information about the intermediate phases formed in solution and in the vicinity of the surface.¹³⁶ The interest in these processes lies in their ability to generate only solid products and by-products, which are easier to handle, transform or stockpile than liquids. The chemical identity and physical state of by-products are in part linked to the degree of conversion of the original mineral, dictated by the technology suggested by the inventors. A shorter processing time, less aggressive conditions and lower temperature and pressure clearly favour the economics and enhance the sustainability of the process, but also tend to lower the degree of conversion.

None of the processes from category (ii) has yet been successfully applied for large-scale potassium extraction from K-bearing tectosilicates. To evaluate the viability of such processes, and understand their relevance at a large-scale, the performances of the precipitated products for a given application must be optimized. From that standpoint, the proposed processes have rarely been designed and conducted with a thorough characterization of the intermediate products formed at each step, so that it is currently not possible to predict their performance, for example from the perspective of their agricultural application. From the green chemistry standpoint, processes from category (ii) may be more suitable, because they do not require separation, liquid waste handling, and significant water recovery. In other words, hydrothermally driven mineral alteration aimed at increasing the availability of ions of interest (e.g., potassium) meets the “atom economy principle”, which declares that “synthetic methods should be designed to maximize the incorporation of all materials used in the process into the final product”.¹²⁴ The limitations in our knowledge described in section 3 for the fundamental chemical mechanisms, as well as the difficulty of in situ monitoring for hydrothermal reactions, call for more thorough and multi-disciplinary research. The next section represents a brief summary of fundamentals relevant to the hydrothermal alteration of aluminosilicate minerals.

4.2. Hydrothermal dissolution – re-precipitation of K-bearing silicates in aqueous fluids

The hydrothermal dissolution of aluminosilicate minerals and glasses involves the same chemical events as the ones described for dissolution under ambient conditions, discussed in section 3.^137–139 The water-mediation model offers an acceptable framework for discussion, whether or not a visible liquid phase has been isolated in the proposed hydrothermal methods.¹³¹ Accordingly, the key chemical steps are the breaking of T–O–T bonds (hydrolysis) and the formation of new bonds (condensation), both mediated by water and promoted by H⁺ or strong nucleophiles (e.g. OH⁻ or F⁻). Temperature and pressure are typically higher than 100 °C and 1 bar, respectively, so that the dielectric constant of water and viscosity decrease, improving the solvation power and mobility of the water molecules⁶² (section 3.1).

For a fixed pH, the chemistry of the anionic species resulting from mineral dissolution is determined by their electronegativity, charge and the coordination number of the oxide-forming element.^63,76 At high saturation states and pH above 7 – conditions commonly proposed for the processing methods of category (ii)^{23,24,121–123} – metastable precipitates form and re-dissolve slowly. The speciation of silica and alumina under such conditions is very sensitive to the time–temperature history, fluid composition or the presence of a mineral surface.⁷⁶ Solutions oversaturated with respect to silica at high pH, for example, contain monomeric silica anions SiO_x(OH)^x−_4−x coexisting with molecular Si(OH)₄ and polynuclear (polymeric) species. The increase in pH promotes deprotonation and depolymerization of aqueous silica, while increasing ionic strength may cause loss of stability and ultimate precipitation in the amorphous state.⁷⁶ The structure of such a precipitate is determined by the initial size distribution of the silica anions, with more compact silica gel inherited from a larger amount of monomers in solutions obtained at high pH.⁶²

The chemistry of oxides of the IIIB group such as aluminium (ionic radius 0.5 Å) differs from that of silicon (ionic radius 0.42 Å) due to the lower electronegativity of the former and its ability to form complexes of coordination number greater than 4. As far as Al³⁺ aqueous speciation is concerned, its coordination number with water is commonly 6, and the unhydrolyzed cation [Al(OH₂)₆]³⁺ exists below pH = 3. With increasing pH, Al³⁺ forms polynuclear ions, e.g., [Al₃(OH)₄(OH₂)₉]⁵⁺ and the Al¹³-ion.⁷⁶ Aluminium ions, in turn, can pre-combine and co-polymerize with siliceous anions, with a high sensitivity on variations in temperature, composition/pH, or rates of precipitation. Aside from these factors, the catalytic role of F⁻ deserves special attention. In aqueous solutions, the fluoride ion is a nucleophilic agent as strong as OH⁻ and tends to coordinate directly with Al and Si, weakening the Si–O–Al bridges, and leading to the formation of hydrophobic Si–O–Si bridges. The presence of even minor F⁻ impurities can therefore increase both dissolution and precipitation rates in a hydrothermal reactor, and influence the final state of the dissolution products.^75,140 Besides amorphous products, the crystallization of silicate phases can also be observed in hydrothermal reactors. For example, the hydrothermal treatment of feldspars with lime (Ca(OH)₂) typically results in the formation of tobermorites^141,142 calcium silicate hydrates with the chemical formula Ca₅Si₆O₁₇(OH)₂·5H₂O or Ca₄Si₆O₁₅(OH)₂·5H₂O. Tobermorites are characterized by their different basal spacings and can adopt various structures depending on the process conditions.¹⁴³ Although crystallization of the new phases occurs in the direct vicinity of the mineral, epitaxial growth is not guaranteed.¹⁴⁴

5. Perspectives

Despite a substantial scientific background, many technological attempts, and geopolitical motivation, the industrial usage of primary K-bearing rock forming minerals in global material extraction is scarce. Dissolution kinetics makes the low-temperature natural extraction from these minerals unlikely to provide access to K and Al at a rate of industrial relevance, as depicted in section 3. Therefore chemical processes have to be envisioned, if possible adopting green chemistry principles. As far as traditional extraction techniques based on full extraction (category (i)) are concerned, their considerable energy cost and the need for handling the corresponding by-products have prevented their industrialization in the free global market, and are challenged by green chemistry concepts. With such realities in mind, only synergetic approaches seem viable, i.e., processes from category (ii), where “synergy” implies avoiding waste generation by incorporating a maximum of beneficial components and using local energy sources. Building up on the remarkable advances of the zeolite industry, a precise control in the hydrothermal dissolution–precipitation treatment of K-bearing feldspars and feldspathoids may provide the desired structural arrangement of the precipitated products with a microstructure and phase composition suitable to obtain a controlled rate of potassium release and/or enhanced weathering rate during agricultural application.

Notes and references

1. D. A. Manning, Agron. Sustainable Dev., 2010, 30, 281–294.
2. 81st IFA Annual Conference, Chicago (USA), 20–22 May 2013, http://www.fertilizer.org/imis20/images/Library_Downloads/2013_chicago_ifa_summary.pdf?WebsiteKey=411e9724-4bda-422f-abfc-8152ed74f306&=404%3bhttp%3a%2f%2fwww.fertilizer.org%3a80%2fen%2fimages%2fLibrary_Downloads%2f2013_chicago_ifa_summary.pdf, (accessed October 2014).
3. Current world fertilizer trends and outlook to 2016, ftp://ftp.fao.org/ag/agp/docs/cwfto16.pdf, (accessed October 2014).
4. W. F. Sheldrick, J. K. Syers and J. Lingard, Nutr. Cycling Agroecosyst., 2002, 62, 61–72.
5. D. Keeney and R. A. Olson, Crit. Rev. Environ. Sci. Technol., 1986, 16, 257–304.
6. J.-K. Böhlke, Hydrogeol. J., 2002, 10, 153–179.
7. O. H. Leonardos, W. S. Fyfe and B. I. Kronberg, Chem. Geol., 1987, 60, 361–370.
8. O. H. Leonardos, S. H. Theodoro and M. L. Assad, Nutr. Cycling Agroecosyst., 2000, 56, 3–9.
9. S. Scovino and D. L. Rowell, Fert. Res., 1988, 17, 71–83.
10. Y. Tokunaga, Fert. Res., 1991, 30, 55–59.
11. A. K. Bakken, H. Gautneb and K. Myhr, Acta Agric. Scand., Sect. B, 1997, 47, 129–134.
12. P. N. Martens, M. Mistry and M. Ruhrberg, in Sustainable Metals Management, ed. A. V. Gleich, R. U. Ayres and S. Gößling-Reisemann, Springer, Netherland, 2006, pp. 97–111.
13. E. Balomenos, D. Panias and I. Paspaliaris, Miner. Process. Extr. Metall. Rev., 2011, 32, 69–89.
14. R. Herrington, Nat. Geosci., 2013, 6, 892–894.
15. Expanding boundaries of exploration (Editorial), Nature Geoscience, 2013, 6, 891.
16. O. Vidal, B. Goffé and N. Arndt, Nat. Geosci., 2013, 6, 894–896.
17. U. B. Pal, J. Metals, 2008, 60, 43–47.
18. E. E. De Turk, Ph.D. Thesis, University of Illinois, 1919.
19. O. H. Leonardos, W. S. Fyfe and B. I. Kronberg, Chem. Geol., 1987, 60, 361–370.
20. China Pat. CN 103193253 A, 2013.
21. L. M. Zhang, J. J. Liu and H. Y. Hu, Adv. Mater. Res., 2014, 838, 2552–2555.
22. A. G. Suss, A. A. Damaskin, A. S. Senyuta, A. V. Panov and A. A. Smirnov, Light Met., 2014, 105–109.
23. A. S. Cushman and G. W. Coggeshall, J. Franklin Inst., 1912, 663–678.
24. R. J. Rajagopala, R. Nayak and A. Suryanarayana, Asian J. Chem., 1998, 10, 690–706.
25. E. A. Ashcroft, Inst. Min. Metall. Bull., 1917, 159, 1–20.
26. E. A. Ashcroft, Inst. Min. Metall. Bull., 1918, 160.
27. Framework Silicates: Feldspars, ed. W. A. Deer, J. Zussman and R. A. Howie, Geological Society, 2001, vol. 4.
28. Feldspars and Their Reactions, Proceedings of the NATO Advanced Study Institute on Feldspars and Their Reactions, ed. I. Parsons, Edinburgh, United Kingdom, June 29–July 10, 1993,Springer, Berlin, 1994, vol. 421.
29. A. Putnis, An introduction to mineral sciences, Cambridge University Press, 1992.
30. A. Navrotsky, Physics and chemistry of earth materials, Cambridge University Press, 1994, vol. 6.
31. G. M. Gadd, Mycol. Res., 2007, 111, 3–49.
32. A. Putnis, Mineral. Mag., 2002, 66, 689–708.
33. E. H. Oelkers, Geochim. Cosmochim. Acta, 2001, 65, 3703–3719.
34. A. E. Blum and L. L. Stillings, Rev. Mineral. Geochem., 1995, 31, 291–351.
35. R. Hellmann, R. Wirth, D. Daval, J. P. Barnes, J. M. Penisson, D. Tisserand and R. L. Hervig, Chem. Geol., 2012, 294, 203–216.
36. L. L. Stillings and S. L. Brantley, Geochim. Cosmochim. Acta, 1995, 59, 1483–1496.
37. A. F. White and S. L. Brantley, Chem. Geol., 2003, 202, 479–506.
38. P. Warfvinge and H. Sverdrup, Water, Air, Soil Pollut., 1992, 63, 119–143.
39. R. Wollast, Geochim. Cosmochim. Acta, 1967, 31, 635–648.
40. H. C. Helgeson, Geochim. Cosmochim. Acta, 1971, 35, 421–469.
41. T. Paces, Geochim. Cosmochim. Acta, 1973, 37, 2641–2663.
42. A. Blum, Nature, 1988, 331, 431–433.
43. W. Stumm, Chemistry of the solid-water interface: Processes at the mineral-water and particle-water interface in natural systems, John Wiley & Son Inc., 1992.
44. R. Hellmann, J. M. Penisson, R. L. Hervig, J. H. Thomassin and M. F. Abrioux, Phys. Chem. Miner., 2003, 30, 192–197.
45. S. Nangia and B. J. Garrison, Theor. Chem. Acc., 2003, 127, 271–284.
46. C. P. Morrow, S. Nangia and B. J. Garrison, J. Phys. Chem. A, 2009, 113, 1343–1352.
47. Y. Yang, Y. Min and Y. S. Jun, Phys. Chem. Chem. Phys., 2013, 15, 18491–18501.
48. L. J. Criscenti, S. L. Brantley, K. T. Mueller, N. Tsomaia and J. D. Kubicki, Geochim. Cosmochim. Acta, 2005, 69, 2205–2220.
49. R. S. Arvidson and A. Luttge, Chem. Geol., 2010, 269, 79–88.
50. A. C. Lasaga, Rev. Mineral. Geochem., 1995, 31, 23–86.
51. D. L. Suarez and J. D. Wood, Chem. Geol., 1996, 132, 143–150.
52. M. S. Beig and A. Lüttge, Geochim. Cosmochim. Acta, 2006, 70, 1402–1420.
53. S. Uroz, C. Calvaruso, M. P. Turpaul and P. Frey-Klett, Trends Microbiol., 2009, 17, 378–387.
54. Y. Goddéris, J. Z. Williams, J. Schott, D. Pollard and S. L. Brantley, Geochim. Cosmochim. Acta, 2010, 74, 6357–6374.
55. A. C. Lasaga, J. Geophys. Res., 1984, 89, 4009–4025.
56. Aquatic surface chemistry: Chemical processes at the particle-water interface, ed. W. Stumm, Wiley, 1987, vol. 87.
57. C. Amrhein and D. L. Suarez, Geochim. Cosmochim. Acta, 1988, 52, 2785–2793.
58. P. V. Brady and J. V. Walther, Geochim. Cosmochim. Acta, 1989, 53, 2823–2830.
59. A. E. Blum and A. C. Lasaga, Geochim. Cosmochim. Acta, 1991, 55, 2193–2201.
60. X. Y. Lin, F. Creuzet and H. Arribart, J. Phys. Chem., 1993, 97, 7272–7276.
61. P. Fletcher and G. Sposito, Clay Miner., 1989, 24, 375–391.
62. J. Jean-Pierre, M. Henry and J. Livage, Metal oxide chemistry and synthesis: from solution to solid state, Wiley-Blackwell, 2000.
63. A. F. Wallace, G. V. Gibbs and P. M. Dove, J. Phys. Chem. A, 2010, 114, 2534–2542.
64. P. M. Dove, Rev. Mineral. Geochem., 1995, 31, 235–290.
65. S. James, C. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić and D. Waddell, et al. , Chem. Soc. Rev., 2012, 41, 413–447.
66. D. Tromans and J. Meech, Miner. Eng., 2001, 14, 1359–1377.
67. K. Swamy, K. Narayana and V. Misra, Ultrason. Sonochem., 2005, 12, 301–306.
68. L. L. Stillings and S. L. Brantley, Geochim. Cosmochim. Acta, 1995, 59, 1483–1496.
69. I. J. Muir and H. W. Nesbitt, Geochim. Cosmochim. Acta, 1991, 55, 3181–3189.
70. E. H. Oelkers and J. Schott, Geochim. Cosmochim. Acta, 1995, 59, 5039–5053.
71. H. Strandh, L. G. Pettersson, L. Sjöberg and U. Wahlgren, Geochim. Cosmochim. Acta, 1997, 61, 2577–2587.
72. J. P. Icenhower and P. M. Dove, Geochim. Cosmochim. Acta, 2000, 64, 4193–4203.
73. P. M. Dove, Geochim. Cosmochim. Acta, 1999, 63, 3715–3727.
74. G. Berger, E. Cadore, J. Schott and P. M. Dove, Geochim. Cosmochim. Acta, 1994, 58, 541–551.
75. S. M. Auerbach, K. A. Carrado and P. K. Dutta, Handbook of zeolite science and technology, CRC Press, 2003.
76. C. A. Ohlin, E. M. Villa, J. R. Rustad and W. H. Casey, Nat. Mater., 2010, 9, 11–19.
77. R. K. Iler, The chemistry of silica: solubility, polymerization, colloid and surface properties, and biochemistry, Wiley-Interscience, 1979.
78. Sol–gel science: the physics and chemistry of sol–gel processing, ed. C. J. Brinker and G. W. Scherer, Elsevier, 1990.
79. G. A. Icopini, S. L. Brantley and P. J. Heaney, Geochim. Cosmochim. Acta, 2005, 69, 293–3003.
80. G. Furrer and W. Stumm, Geochim. Cosmochim. Acta, 1986, 50, 1847–1860.
81. E. P. Manley and L. J. Evans, Soil Sci., 1986, 141, 106–112.
82. M. Alisa Mast and J. I. Drever, Geochim. Cosmochim. Acta, 1987, 51, 2559–2568.
83. E. Wieland and W. Stumm, Geochim. Cosmochim. Acta, 1992, 56, 3339–3355.
84. S. A. Welch and W. J. Ullman, Geochim. Cosmochim. Acta, 1993, 57, 2725–2736.
85. A. C. Lasaga, J. M. Soler, J. Ganor, T. E. Burch and K. L. Nagy, Geochim. Cosmochim. Acta, 1994, 58, 2361–2386.
86. S. A. Welch and W. J. Ullman, Geochim. Cosmochim. Acta, 1996, 60, 2939–2948.
87. J. I. Drever and L. L. Stillings, Colloids Surf., A, 1997, 120, 167–181.
88. L. L. Stillings, J. I. Drever, S. L. Brantley, Y. Sun and R. Oxburgh, Chem. Geol., 1996, 132, 79–89.
89. Y. Yang, Y. Min and Y. S. Jun, Environ. Sci. Technol., 2012, 47, 150–158.
90. A. E. Martell, R. D. Hancock, R. M. Smit and R. J. Motekaitis, Coord. Chem. Rev., 1996, 149, 311–328.
91. K. Bosecker, FEMS Microbiol. Rev., 1997, 20, 591–604.
92. R. Hellmann, Geochim. Cosmochim. Acta, 1994, 58, 595–611.
93. M. L. Machesky, B. L. Bischoff and M. A. Anderson, Environ. Sci. Technol., 1989, 23, 580–587.
94. W. M. Murphy and H. C. Helgeson, Geochim. Cosmochim. Acta, 1987, 51, 3137–3153.
95. M. Murphy and H. C. Helgeson, Am. J. Sci., 1989, 289, 17–10.
96. Y. Chen and S. L. Brantley, Chem. Geol., 1997, 135, 275–290.
97. R. Hellmann, Geochim. Cosmochim. Acta, 1995, 59, 1669–1697.
98. S. Arnorsson and A. Stefansson, Am. J. Sci., 1999, 299, 173–209.
99. H. C. Helgeson, W. M. Murphy and P. Aagaard, Geochim. Cosmochim. Acta, 1984, 48, 2405–2432.
100. K. G. Knauss and T. J. Wolery, Geochim. Cosmochim. Acta, 1986, 50, 2481–2497.
101. J. D. Kubicki, J. O. Sofo, A. A. Skelton and A. V. Bandura, J. Phys. Chem. C, 2012, 116, 17479–17491.
102. P. Fenter, C. Park, L. Cheng, Z. Zhang, M. P. S. Krekeler and N. C. Sturchio, Geochim. Cosmochim. Acta, 2003, 67, 197–211.
103. D. Daval, R. Hellmann, G. D. Saldi, R. Wirth and K. G. Knauss, Geochim. Cosmochim. Acta, 2013, 107, 121–134.
104. Y. Yang, Y. Min, J. Lococo and Y.-S. Jun, Geochim. Cosmochim. Acta, 2014, 126, 574–594.
105. A. C. Lasaga and A. Luttge, Science, 2001, 291, 2400–2404.
106. A. Lttge, U. Winkler and A. C. Lasaga, Geochim. Cosmochim. Acta, 2003, 67, 1099–1116.
107. A. Luettge, E. W. Bolton and A. C. Lasaga, Am. J. Sci., 1999, 299, 652–678.
108. Z. Zhang, P. Fenter, N. C. Sturchio, M. J. Bedzyk, M. L. Machesky and D. J. Wesolowski, Surf. Sci., 2007, 601, 1129–1143.
109. Applications of Synchrotron Radiation in Low-Temperature Geochemistry and Environmental Sciences, ed. P. A. Fenter, M. L. Rivers, N. C. Sturchio and S. R. Sutton, Mineralogical, Society of America, 2002, vol. 49.
110. M. Land, J. Ingri and B. Öhlander, Appl. Geochem., 1999, 14, 761–774.
111. Y. Goddéris, C. Roelandt, J. Schott, M.-C. Pierret and L. M. François, Rev. Mineral. Geochem., 2009, 70, 411–434.
112. J. L. Palandri and Y. K. Kharaka, A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling, No. OPEN-FILE-2004-1068. GEOLOGICAL SURVEY MENLO PARK CA, 2004.
113. J. D. Rimstidt, Geochemical Rate Models: An Introduction to Geochemical Kinetics, Cambridge University Press, 2013.
114. D. B. Gleeson, N. Clipson, K. Melville, G. M. Gadd and F. P. McDermott, Microb. Ecol., 2005, 50, 360–368.
115. H. Sverdrup and P. Warfvinge, Rev. Mineral. Geochem., 1995, 31, 485–541.
116. A. F. White, A. E. Blum, M. S. Schulz, T. D. Bullen, J. W. Harden and M. L. Peterson, Geochim. Cosmochim. Acta, 1996, 60, 2533–2550.
117. R. A. Lybrand and C. Rasmussen, Chem. Geol., 2014, 381, 26–39.
118. H. Brunn, R. Bretz, P. Fankhauser, T. Spengler and O. Rentz, Int. J. Life Cycle Assess., 1996, 1(4), 221–225.
119. L. Thannimalay, S. Yusoff, S. Zawawi and N. Zin, Australian Journal of Basic and Applied Sciences, 2013, 7(2), 421–431.
120. A. Cushman, US Pat, US851922 A, 1907.
121. A potash solution for Brazil's growing potash problem, http://www.verdepotash.com/English/Projects/cerrado-verde-potash/phase-ii-conventional-potash/default.aspx (accessed October 2014).
122. China Pat, CN 103172074, 2013.
123. C. Wang, H. Yue, C. Li, B. Liang, J. Zhu and H. Xie, Ind. Eng. Chem. Res., 2014, 53, 7971–7978.
124. Y. Q. Liu, H. T. Xia and H. W. Ma, Adv. Mater. Res., 2012, 549, 65–69.
125. J. Q. Zhang, J. L. Cao, X. W. Liu and H. F. Guo, J. Synth. Cryst., 2013, 5, 041.
126. J. Wang, B. Zhao, L. LI and J. Cao, J. Chin. Ceram. Soc., 2014, 42, 340–348.
127. W. Xu and W. Jian, Geology of Chemical Minerals, 2000-2; online abstract, http://en.cnki.com.cn/Article_en/CJFDTOTAL-HGKC200002005.htm (accessed October 2014).
128. T. E. Norgate, S. Jahanshahi and W. J. Rankin, J. Cleaner Prod., 2007, 15, 838–848.
129. P. Anastas and J. Warner, Green chemistry: theory and practice, Oxford University Press, 2000.
130. A. Sverdlin, in Handbook of Aluminum, ed. G. E. Totten and D. S. MacKenzie, Marcel Dekker, Inc., New York, 2003, ch. 1, vol. 1, pp. 1–31.
131. V. Smirnov, J. Miner., 1996, 48, 24–26.
132. I. P. Narkevitch and V. V. Pechkovsk, Recycling and waste disposal technology of inorganic substances, Khimiya, Moscow, 1984 (in Russian).
133. M. L. Varlamov, S. V. Benkovsky, E. L. Krichevskaya and A. S. Romanets, Production of soda ash and potash at complex processing of nepheline raw materials, Khimiya, Moscow, 1977 (in Russian).
134. S. J. T. Hangx and C. J. Spiers, Chem. Geol., 2009, 265, 88–98.
135. C. S. Cundy and P. A. Cox, Chem. Rev., 2003, 103, 663–702.
136. K. Byrappa and T. Adschiri, Prog. Cryst. Growth Charact. Mater., 2007, 53, 117–166.
137. R. Hellmann, Geochim. Cosmochim. Acta, 1994, 58, 595–611.
138. J. M. Gautier, E. H. Oelkers and J. Schott, Geochim. Cosmochim. Acta, 1994, 58, 4549–4560.
139. E. H. Oelkers, Geochim. Cosmochim. Acta, 2001, 65, 3703–3719.
140. T. Skorina and I. Tikhomirova, J. Mater. Sci., 2012, 47, 5050–5059.
141. G. O. Assarsson, J. Phys. Chem., 1960, 64, 626–632.
142. J. H. v. Aardt and S. Visser, Cem. Concr. Res., 1977, 7, 39–44.
143. E. Bonaccorsi, S. Merlino and A. R. Kampf, J. Am. Ceram. Soc., 2005, 88, 505–512.
144. K. G. Dunkel and A. Putnis, Eur. J. Mineral., 2014, 26, 61–69.

---

Footnote

† Feldspars and feldspathoids later in this review are named “K-bearing silicates”.

---