Simultaneous determination of multiple components in explosives using ultraviolet spectrophotometry and a partial least squares method†
Tao Lua,
Yuan Yuanc,
Xuan Heb,
Menglong Lia,
Xuemei Pu*a,
Tao Xu*b and
Zhining Wen*a
aCollege of Chemistry, Sichuan University, Chengdu 610064, People’s Republic of China. E-mail: xmpuscu@scu.edu.cn; Fax: +86-028-85412290; Tel: +86-028-85412290
bInstitute of Chemical Materials, Chinese Academy of Engineering Physics, Mianyang 621900, People’s Republic of China
cCollege of Management, Southwest University for Nationalities, Chengdu 610041, People’s Republic of China
First published on 13th January 2015
Abstract
The quantitative analysis of explosives is very important for national defence and security inspection. However, conventional analytical methods are complicated and time-consuming because of the complexity of the explosive samples. Herein, we proposed a new quantitative method, which combined ultraviolet (UV) spectrophotometry with partial least squares regression (PLS-1 and PLS-2), to quickly determine the content of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclo-octane (HMX), hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX) and 2,4,6-trinitrotoluene (TNT) simultaneously from mixed explosive samples. The calibration models were constructed by using 49 reference samples in the calibration set and optimized by full cross-validation. The predictive performance of the optimized models was validated by 21 explosive samples in an independent test set. The standard errors of prediction (SEP) were lower than 1.4 μg mL−1 for HMX, 2.2 μg mL−1 for RDX, and 0.8 μg mL−1 for TNT in both PLS models. Finally, the optimized PLS-1 and PLS-2 models were successfully applied to simultaneously determine the three explosive ingredients in eight polymer bonded explosives (PBXs). The average recovery was close to 100% for each of the three components. Thus, UV spectrophotometry combined with PLS regression can be considered as a promising strategy to conduct the determination of HMX, RDX and TNT in practice.
1. Introduction
2,4,6-Trinitrotoluene (TNT), hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX) and 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclo-octane (HMX) are polynitro-explosives. Also, they are three of the most widely used secondary explosive ingredients in ammunition formulation and plastic explosives.1–3 The majority of military explosives and commercial ones contain large amounts of composite materials, which mainly contain one to three energetic compounds (e.g., HMX, RDX, TNT) as the main components, and a small quantity of organic compounds (e.g., waxes, stabilizers, plasticizers, oils) as fillers.4 In recent years, a surge in explosive-based terrorist activity has led to enormous damage to society.5–8 Therefore, it is important for national defence and security inspection to identify the types of explosives rapidly and determine their content accurately.In the past decades, a great number of analytical methods have been developed in the field. The most common methods involve ion mobility spectrometry (IMS),9–12 mass spectrometry (MS),13–15 Raman spectroscopy,5,16,17 THz spectroscopy,18–20 laser induced breakdown spectroscopy (LIBS),21–24 gas chromatography (GC),25–27 high performance liquid chromatography (HPLC)28–31 and some combined methods (viz. HPLC-MS29 and GC-MS32). Although these instrumental techniques are highly selective and sensitive, most of the devices are rather bulky, expensive, and time-consuming,33 impeding quick and on-line determination. Thus, it is quite necessary to develop new methods or improve the existing analytical techniques to enable faster, more sensitive, less expensive and simpler determinations to facilitate the determination of explosives.
It is known that ultraviolet (UV) spectrophotometry can easily and quickly be used for the quantitative analysis of a specific compound with a high degree of accuracy. However, they cannot be directly applied in the analysis of military and commercial explosives because multiple components are involved in these explosives and some components have very similar physicochemical properties, leading to highly overlapped absorption bands in UV spectra.34–36 Thus, UV spectrophotometers have commonly been used as detectors in HPLC for the determination of explosives and other complicated samples.
Chemometrics was firstly introduced by Svan Wold37 in 1972, which utilized mathematical and statistical approaches to design optimal steps in experiments and extracted maximal information from the experimental data.38 Multivariate calibration methods in chemometrics play an important role in multicomponent resolution and quantification34,39–43 and have been successfully used to solve problems which exist in the spectral data of complicated mixtures, such those that involve collinearity, band overlaps and interactions.44–49 Partial least squares (PLS) regression initiated by Wold50 has been successfully used in multicomponent quantitative analysis in many complicated cases.39,51–55 The calibration of multiple response data by PLS can be performed via two methods, namely constructing multiple models with one response (viz., PLS-1) and building one model with multiple responses (viz., PLS-2).56 The former executes the decomposition and regression for only a single component at a time, while the latter calculates latent variables based on all of the components and only one calibration matrix is used.
Based on the considerations above, we herein combine UV spectrophotometry with a PLS algorithm to develop a new method to simultaneously determine the content of HMX, RDX and TNT in mixed explosives. We firstly construct the PLS-1 and PLS-2 models by using a well-designed calibration set, which included 49 reference samples with known proportions of HMX, RDX and TNT. Then, the models were validated by an independent test set. Finally, the optimized PLS models were applied to eight polymer bonded explosives. Satisfactory results were obtained from the PLS models, indicating that UV spectrophotometry in combination with PLS has the potential to be realized as a simple, quick and accurate quantitative determination method for either single-component or multicomponent explosives.
2. Experimental
2.1. Chemical reagents and stock solutions
HMX, RDX, TNT and eight polymer bonded explosives (PBXs) based on the three analytes were provided by the Yinguang Chemical Plant, China. Analytical reagent grade acetonitrile was purchased from Chengdu Kelong Chemical Reagent Factory (Chengdu, China) and further purified by means of the following steps. The acetonitrile was refluxed for four hours after the phosphorus pentoxide (P2O5) as desiccant was completely added, then the solution was distillation at 82 °C in dimethyl silicone oil pan. Stock solutions of 1014 μg mL−1 HMX, 1002 μg mL−1 RDX and 1010 μg mL−1 TNT were prepared by dissolving the appropriate amount of the analyte in acetonitrile and diluting to the mark with acetonitrile in 50 mL volumetric flasks.2.2. Standard solutions and sample solutions
Stock solutions of HMX, RDX and TNT were utilized to construct the calibration set. These stock solutions were properly diluted to give work solutions with concentration ranges of 0.81–32.45 μg mL−1 for HMX, 0.80–28.06 μg mL−1 for RDX, and 0.81–26.66 μg mL−1 for TNT. The calibration set consisted of 49 samples, including 15 single-component mixtures, 9 binary-component mixtures and 25 ternary-component mixtures.To validate the calibration models, an independent test set, including 21 samples with one to three components, was randomly prepared using the same stock solutions with concentrations within the limits of the calibration set.
For the purpose of testing the predictive performance of the optimized PLS models in real cases, we validated the models by using eight real PBX samples. The real explosives were weighed and then powdered in a mortar. An appropriate amount of the accurately weighed homogenous powder mixture was dissolved with acetonitrile and then filtered. 1.00 mL of this filtrate was diluted to 50.00 mL with acetonitrile.
2.3. Apparatus and software
Absorption spectra were recorded in a wavelength (λ) range of 190–400 nm at 1 nm intervals with respect to a blank of acetonitrile in a 1 cm quartz cell, using a Hitachi U-1900 UV-Vis spectrophotometer (Tokyo, Japan) with a scan rate of 400 nm min−1 and slit width of 4.0 nm.All data obtained from the experiments were gathered in a data matrix using Microsoft Office Excel (version 2010) and transferred to MATLAB software. All calculations were done using MATLAB (version 2013 a).
2.4. Procedures
| Parameter | HMXa (228 nm) | RDXa (197 nm) | TNTa (228 nm) |
|---|---|---|---|
| a The values in parentheses correspond to the maximum absorption wavelength.b The LOD (limit of detection) was determined by a signal-to-noise ratio (S/N) = 3 for each analyte.c The LOQ (limit of quantitation) was determined by a signal-to-noise ratio (S/N) = 10 for each analyte. | |||
| Linear range (μg mL−1) | 0.41–33.29 | 0.62–29.12 | 0.29–27.13 |
| Intercept | 0.0087 | 0.0479 | 0.0411 |
| Slope | 68.966 | 64.038 | 81.460 |
| Correlation coefficient | 0.9992 | 0.9961 | 0.9992 |
| LODb (μg mL−1) | 0.27 | 0.33 | 0.23 |
| LOQc (μg mL−1) | 0.91 | 1.11 | 0.77 |
3. Results and discussion
Fig. 1 shows the chemical structures of HMX, RDX and TNT, and Fig. 2 exhibits their corresponding absorbance spectra. As can be observed from Fig. 2, the spectra of HMX, RDX and TNT exhibit considerable overlap, which prevents the direct determination by means of a classical univariate calibration method without prior separation. Thus, it is necessary to use multivariate calibration techniques, such as PLS, to realize the simultaneous determination of HMX, RDX and TNT in the mixed explosive samples. | ||
| Fig. 2 Absorption spectra of 8.11 μg mL−1 HMX (black line), 8.02 μg mL−1 RDX (red line) and 7.27 μg mL−1 TNT (blue line). | ||
3.1. The calibration set: construction of PLS models
| Sample no. | HMX | RDX | TNT | Sample no. | HMX | RDX | TNT |
|---|---|---|---|---|---|---|---|
| Ternary mixtures | Binary mixtures | ||||||
| 1 | 0.81 | 0.80 | 0.81 | 26 | — | 0.80 | 7.27 |
| 2 | 0.81 | 8.02 | 7.27 | 27 | — | 8.02 | 13.74 |
| 3 | 0.81 | 15.23 | 13.74 | 28 | — | 15.23 | 20.20 |
| 4 | 0.81 | 22.44 | 20.20 | 29 | — | 22.44 | 26.66 |
| 5 | 0.81 | 28.06 | 26.66 | 30 | 0.81 | 28.06 | — |
| 6 | 8.11 | 0.80 | 7.27 | 31 | 17.04 | 15.23 | — |
| 7 | 8.11 | 8.02 | 13.74 | 32 | 32.45 | 0.80 | — |
| 8 | 8.11 | 15.23 | 20.20 | 33 | 8.11 | — | 0.81 |
| 9 | 8.11 | 22.44 | 26.66 | 34 | 25.15 | — | 13.74 |
| 10 | 8.11 | 28.06 | 0.81 | Single component solutions | |||
| 11 | 17.04 | 0.80 | 13.74 | 35 | 0.81 | — | — |
| 12 | 17.04 | 8.02 | 20.20 | 36 | 8.11 | — | — |
| 13 | 17.04 | 15.23 | 26.66 | 37 | 17.04 | — | — |
| 14 | 17.04 | 22.44 | 0.81 | 38 | 25.15 | — | — |
| 15 | 17.04 | 28.06 | 7.27 | 39 | 32.45 | — | — |
| 16 | 25.15 | 0.80 | 20.20 | 40 | — | 0.80 | — |
| 17 | 25.15 | 8.02 | 26.66 | 41 | — | 8.02 | — |
| 18 | 25.15 | 15.23 | 0.81 | 42 | — | 15.23 | — |
| 19 | 25.15 | 22.44 | 7.27 | 43 | — | 22.44 | — |
| 20 | 25.15 | 28.06 | 13.74 | 44 | — | 28.06 | — |
| 21 | 32.45 | 0.80 | 26.66 | 45 | — | — | 0.81 |
| 22 | 32.45 | 8.02 | 0.81 | 46 | — | — | 7.27 |
| 23 | 32.45 | 15.23 | 7.27 | 47 | — | — | 13.74 |
| 24 | 32.45 | 22.44 | 13.74 | 48 | — | — | 20.20 |
| 25 | 32.45 | 28.06 | 20.20 | 49 | — | — | 26.66 |
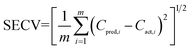 | (1) |
To determine the optimum number of factors, the SECV value was calculated in the same way each time after a new factor was added to the models. The variation of the SECV values with respect to the number of factors was shown in Fig. 3. It was required that the SECV value of the model with the optimum number of factors was not significantly greater than the minimal SECV. The F-statistic was used to make the significance determination by means of a comparison of the calculated F-value with the cutoff value (α = 0.25), which was proposed to be a good criterion by Haaland and Thomas.60 As a result, the optimum number of factors in the PLS-1 and PLS-2 models for HMX and RDX was determined to be 9. For TNT determination, the optimum number of factors were 10 for the PLS-1 model and 14 for the PLS-2 one. Table 3 lists the optimum number of factors selected, the standard error of calibration (SEC), standard error of cross-validation (SECV), standard error of prediction (SEP) and the correlation coefficient of determination (Rcal2) in the calibration set for each analyte. As can be seen from Table 3, satisfactory results are obtained for all the analytes in the PLS-1 and PLS-2 models, confirming the reliability of the two models constructed.
 | ||
Fig. 3 Plot of standard error of cross-validation (SECV) vs. the number of factors in the PLS-1 and PLS-2 calibration models for HMX ( ), RDX ( ), RDX ( ) and TNT ( ) and TNT ( ). ). | ||
| PLS-1 | PLS-2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Factorsa | SECb | SECVc | SEPd | Rcal2 | Factorsa | SEC | SECV | SEP | Rcal2 | |
| a The optimum number of factors.b Standard error of the calibration set.c Standard error of cross-validation.d Standard error of the independent test set. | ||||||||||
| HMX | 9 | 1.2325 | 2.0428 | 1.2579 | 0.9898 | 9 | 1.3191 | 2.1097 | 1.371 | 0.9883 |
| RDX | 9 | 0.8285 | 1.9730 | 1.6706 | 0.9938 | 9 | 0.9488 | 2.0962 | 2.1091 | 0.9919 |
| TNT | 10 | 0.1331 | 0.4498 | 0.6959 | 0.9998 | 14 | 0.2168 | 0.4507 | 0.7787 | 0.9995 |
In addition, the outliers in the regression models were detected by using residual analysis.43,57,58 In general, a residual (εi) is defined as the difference between an experimental observation and a predicted value from a regression model, εi = yact,i − ypred,i where yact,i is the real value and ypred,i is the predicted value by the regression model. Fig. 4 shows the residual values for the three components of the calibration samples in the PLS-1 model. As can be seen from Fig. 4, the residuals are scattered closely around the horizontal line, confirming that there are no outliers in the calibration samples and the regression model constructed is reliable. Similarly, the outliers were not detected by the residual plot in the PLS-2 model (see Fig. S1, ESI†).
3.2. Validation of the PLS models by the independent test set
To validate the predictive performance of the optimized models, an independent test set of 21 samples containing 7 ternary-component samples, 8 binary-component samples and 6 one-component samples was prepared. The reference values of the explosive compositions are listed in the first three columns of Table 4. The constructed PLS-1 and PLS-2 models were used to estimate the content of HMX, RDX and TNT in the independent test set and the results are listed in Table 4. As can be seen from Table 4, the estimated concentrations are close to the reference ones. Also, residual analysis was carried out for the three components of the independent test samples in the PLS regression models (see Fig. 4 and Fig. S1†). Similarly, no outliers were detected in the independent data set.| Reference values | Predicted values | |||||||
|---|---|---|---|---|---|---|---|---|
| HMX | RDX | TNT | PLS-1 | PLS-2 | ||||
| HMX | RDX | TNT | HMX | RDX | TNT | |||
| Ternary mixtures | ||||||||
| 22.50 | 15.00 | 5.00 | 22.27 | 14.23 | 5.37 | 22.68 | 14.80 | 5.67 |
| 12.50 | 20.00 | 12.50 | 13.82 | 19.26 | 12.70 | 14.42 | 20.02 | 12.98 |
| 8.92 | 26.45 | 25.10 | 8.37 | 26.87 | 26.08 | 9.68 | 28.59 | 26.61 |
| 16.22 | 9.62 | 12.14 | 14.58 | 10.80 | 11.71 | 15.14 | 11.45 | 11.98 |
| 31.64 | 23.25 | 19.39 | 29.70 | 26.55 | 19.08 | 30.33 | 27.37 | 18.93 |
| 19.47 | 8.02 | 6.48 | 18.99 | 8.95 | 6.09 | 19.29 | 9.13 | 6.02 |
| 7.30 | 9.62 | 6.48 | 7.91 | 8.49 | 6.48 | 8.03 | 8.49 | 6.43 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Binary mixtures | ||||||||
| 30.01 | — | 12.93 | 28.08 | 1.42 | 12.36 | 28.02 | 1.76 | 12.69 |
| 19.47 | — | 6.48 | 20.10 | −0.04 | 6.16 | 20.48 | 0.28 | 6.04 |
| — | 20.04 | 14.57 | 1.12 | 21.12 | 14.03 | 1.92 | 22.13 | 14.20 |
| — | 18.44 | 8.08 | 0.02 | 19.49 | 7.45 | 0.64 | 20.35 | 7.60 |
| — | 12.83 | 24.24 | 1.96 | 14.46 | 23.02 | 2.61 | 15.45 | 22.91 |
| 8.11 | 6.41 | — | 9.81 | 5.91 | 0.03 | 10.01 | 6.31 | −0.07 |
| 10.00 | 20.00 | — | 10.65 | 20.56 | −0.23 | 11.34 | 21.50 | −0.24 |
| 2.43 | 7.21 | — | 2.14 | 7.55 | −0.07 | 2.27 | 7.77 | −0.09 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Single-component solutions | ||||||||
| 4.87 | — | — | 4.31 | 0.20 | 0.02 | 4.16 | −0.01 | −0.03 |
| 31.64 | — | — | 30.60 | 1.44 | −0.19 | 31.36 | 2.51 | −0.19 |
| — | 4.81 | — | −0.59 | 4.87 | 0.07 | −0.77 | 4.62 | 0.08 |
| — | 27.25 | — | 1.06 | 26.80 | 0.02 | 1.74 | 27.79 | 0.19 |
| — | — | 3.24 | −1.31 | 1.18 | 3.06 | −1.40 | 1.05 | 3.06 |
| — | — | 25.86 | −2.62 | 2.23 | 23.44 | −2.22 | 2.37 | 23.26 |
Table 5 lists the correlation coefficient of determination (Rpred2) and standard error of prediction (SEP) for the independent prediction set. As shown in Table 5, SEP values are lower than 1.4 for HMX, 2.2 for RDX, and 0.8 for TNT. Rpred2 values are higher than 0.98 for the three components. In addition, the recovery rates obtained by PLS-1 were 99.33% for HMX, 102.82% for RDX and 97.21% for TNT. The recovery rates obtained by PLS-2 were 102.63% for HMX, 106.57% for RDX and 98.11% for TNT. These results demonstrated that the constructed PLS-1 and PLS-2 models have high predictive abilities for the simultaneous determination of HMX, RDX and TNT in the mixtures.
| Parameters | HMX | RDX | TNT | |||
|---|---|---|---|---|---|---|
| PLS-1 | PLS-2 | PLS-1 | PLS-2 | PLS-1 | PLS-2 | |
| a The value refers to mean recovery for each component. Recovery (%) = 100 × (Cpred/Cact), Cpred represents the prediction concentration, Cact represents the actual concentration. | ||||||
| SEP | 1.2579 | 1.3710 | 1.6706 | 2.1091 | 0.6959 | 0.7787 |
| Rpred2 | 0.9879 | 0.9852 | 0.9869 | 0.9841 | 0.9953 | 0.9930 |
| Recoverya (%) | 99.33 | 102.63 | 102.82 | 106.57 | 97.21 | 98.11 |
3.3. Application of the optimized models to the real samples
In order to test the applicability of the proposed methods to the real samples, the optimized PLS models were further used to simultaneously determine HMX, RDX and TNT in real explosive samples. Eight real PBX samples (three replicates per sample) were prepared as we describe in the Experimental section above. The results derived from the PLS-1 and PLS-2 models are summarized in Table 6. As can be observed, the obtained results are satisfactory with a good recovery yield in general (average values of 101.19%, 95.27% and 95.42% in the PLS-1 model, and 102.12%, 96.24% and 93.38% in the PLS-2 model for HMX, RDX and TNT, respectively). The results indicate that our proposed methods can be applied to simultaneously determine HMX, RDX and TNT in the real explosives. Thus, this method, based on UV-spectroscopy combined with chemometrics has the potential to be a simple, quick and accurate analysis method for explosive determination.| Reference values | Predicted valuesa | |||||||
|---|---|---|---|---|---|---|---|---|
| HMX | RDX | TNT | PLS-1 | PLS-2 | ||||
| HMX | RDX | TNT | HMX | RDX | TNT | |||
| a The average values of three independent determinations. Comp.A5 (99% RDX and 1% stearic acid), tritonal (80% TNT and 20% aluminium powder), X-2042 (92% HMX and 8% polymer), Comp.B-2 (60% RDX and 40% TNT), cyclotol (70% RDX and 30% TNT), LX-14 (95.9% HMX, 1.9% TNT and 2.2% polymer), PBX-71 (49% HMX, 48% RDX, 1.5% F2311 and 1.5% F2314) and PBX-T-1 (45% HMX, 30%RDX, 20%TNT and 5% ammonium nitrate). | ||||||||
| Comp.A5 | ||||||||
| — | 10.50 | — | −0.99 | 9.86 | 0.21 | −1.25 | 9.40 | 0.28 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Tritonal | ||||||||
| — | — | 12.12 | −1.41 | 1.67 | 10.95 | −1.17 | 1.32 | 10.92 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| X-2042 | ||||||||
| 18.44 | — | — | 20.05 | −0.91 | −0.03 | 20.90 | 0.25 | 0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Comp.B-2 | ||||||||
| — | 7.42 | 4.94 | −0.04 | 6.78 | 4.60 | −0.28 | 6.52 | 4.71 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Cyclotol | ||||||||
| — | 8.56 | 3.76 | −0.21 | 7.75 | 3.75 | −0.57 | 7.29 | 3.83 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| LX-14 | ||||||||
| 19.30 | — | 0.38 | 18.62 | 0.64 | 0.37 | 18.00 | 0.73 | 0.35 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| PBX-71 | ||||||||
| 9.76 | 9.60 | — | 8.85 | 10.00 | −0.08 | 8.91 | 10.07 | −0.06 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| PBX-T-1 | ||||||||
| 13.50 | 9.06 | 6.06 | 14.37 | 8.73 | 5.85 | 14.93 | 9.43 | 5.91 |
4. Conclusions
In this work, we have successfully applied partial least squares (PLS) regression to simultaneously determine the content of HMX, RDX and TNT in single-component, binary-component and ternary-component explosive samples, based on their UV spectra. Multivariate calibration models were built from the raw spectral data matrices of the calibration set using the PLS-1 and PLS-2 methods and further verified through the independent test set of the explosive mixtures. Finally, eight real polymer bonded explosives were used to check the applicability of the models. The results showed that the contents of HMX, RDX and TNT in the mixed explosives can be satisfactorily estimated by our proposed method, indicating that it is feasible for UV spectrophotometry in combination with chemometric techniques to be developed as a simple, quick and reliable analysis method to realize the simultaneous multicomponent determination of explosives.Acknowledgements
This project is supported by the National Science Foundation of China (Grant no. U1230121 and 21273154).References
- S. Babaee and A. Beiraghi, Anal. Chim. Acta, 2010, 662, 9–13 CrossRef CAS PubMed
.
- T. Lo, I. S. Gregory, C. Baker, P. F. Taday, W. R. Tribe and M. C. Kemp, Vib. Spectrosc., 2006, 42, 243–248 CrossRef CAS PubMed
.
- D. J. Funk, F. Calgaro, R. D. Averitt, M. L. T. Asaki and A. J. Taylor, Appl. Spectrosc., 2004, 58, 428–431 CrossRef CAS PubMed
.
- X. Cetó, A. M. O’Mahony, J. Wang and M. Del Valle, Talanta, 2013, 107, 270–276 CrossRef PubMed
.
- M. López-López and C. García-Ruiz, TrAC, Trends Anal. Chem., 2014, 54, 36–44 CrossRef PubMed
.
- R. J. Colton and J. N. Russell, Science, 2003, 299, 1324–1325 CrossRef CAS PubMed
.
- A. Fainberg, Science, 1992, 299, 1531–1537 Search PubMed
.
- S. F. Hallowell, Talanta, 2001, 54, 447–458 CrossRef CAS
.
- C. G. Fraga, D. R. Kerr and D. A. Atkinson, Analyst, 2009, 134, 2329–2337 RSC
.
- D. S. Moore, Sens. Imag. Int. J., 2007, 8, 9–38 CrossRef PubMed
.
- G. A. Buttigieg, A. K. Knight, S. Denson, C. Pommier and M. Bonner Denton, Forensic Sci. Int., 2003, 135, 53–59 CrossRef CAS
.
- T. L. Buxton and P. D. B. Harrington, Anal. Chim. Acta, 2001, 434, 269–282 CrossRef CAS
.
- J. J. Brady, E. J. Judge and R. J. Levis, Rapid Commun. Mass Spectrom., 2010, 24, 1659–1664 CrossRef CAS PubMed
.
- J. F. Garcia-Reyes, J. D. Harper, G. A. Salazar, N. A. Charipar, Z. Ouyang and R. G. Cooks, Anal. Chem., 2011, 83, 1084–1092 CrossRef CAS PubMed
.
- K. Sovová, K. Dryahina, P. Španěl, M. Kyncl and S. Civiš, Analyst, 2010, 135, 1106–1114 RSC
.
- J. C. Carter, S. M. Angel, M. Lawrence-Snyder, J. Scaffidi, R. E. Whipple and J. G. Reynolds, Appl. Spectrosc., 2005, 59, 769–775 CrossRef CAS PubMed
.
- C. Eliasson, N. A. Macleod and P. Matousek, Anal. Chem., 2007, 79, 8185–8189 CrossRef CAS PubMed
.
- H. B. Liu and Y. Q. Chen, Opt. Express, 2006, 14, 415–423 CrossRef CAS
.
- J. Chen, Y. Q. Chen, H. W. Zhao, G. J. Bastiaans and X. C. Zhang, Opt. Express, 2007, 15, 12060–12067 CrossRef CAS
.
- M. R. Leahy-Hoppa, M. J. Fitch and R. Osiander, Anal. Bioanal. Chem., 2009, 395, 247–257 CrossRef CAS PubMed
.
- J. L. Gottfried, F. C. De Lucia Jr, C. A. Munson and A. W. Miziolek, J. Anal. At. Spectrom., 2008, 23, 205–216 RSC
.
- J. L. Gottfried, F. C. De Lucia Jr, C. A. Munson and A. W. Miziolek, Anal. Bioanal. Chem., 2009, 395, 283–300 CrossRef CAS PubMed
.
- J. Moros, J. Serrano, C. Sánchez, J. Macías and J. J. Laserna, J. Anal. At. Spectrom., 2012, 27, 2111–2122 RSC
.
- S. Sunku, M. K. Gundawar, A. K. Myakalwar, P. P. Kiran, S. P. Tewari and S. V. Rao, Spectrochim. Acta, Part B, 2013, 79–80, 31–38 CrossRef CAS PubMed
.
- S. A. Barshick and W. H. Griest, Anal. Chem., 1998, 70, 3015–3020 CrossRef CAS
.
- M. Nambayah and T. I. Quickenden, Talanta, 2004, 63, 461–467 CrossRef CAS PubMed
.
- C. J. Miller, G. Elias, N. C. Schmitt and C. Rae, Sens. Imag. Int. J., 2010, 11, 61–75 CrossRef PubMed
.
- T. F. Jenkins, D. C. Leggett, C. L. Grant and C. F. Bauer, Anal. Chem., 1986, 58, 170–175 CrossRef CAS
.
- D. Gaurav, A. K. Malik and P. K. Rai, Crit. Rev. Anal. Chem., 2007, 37, 227–268 CrossRef CAS
.
- D. Gaurav, A. K. Malik and P. K. Rai, J. Hazard. Mater., 2009, 172, 1652–1658 CrossRef PubMed
.
- P. Bansal, D. Gaurav, N. Nidhi, A. K. Malik and F. M. Matysik, Chromatographia, 2012, 75, 739–745 CAS
.
- J. Yinon and S. Zitrin, Modern Methods and Applications in Analysis of Explosives, John Wily & Sons Ltd, West Sussex, England, 1993 Search PubMed.
- L. Senesac and T. G. Thundat, Mater. Today, 2008, 11, 28–36 CrossRef CAS
.
- T. Azzouz and R. Tauler, Talanta, 2008, 74, 1201–1210 CrossRef CAS PubMed
.
- C. B. Ojeda and F. S. Rojas, Anal. Chim. Acta, 2004, 518, 1–24 CrossRef PubMed
.
- J. Kapinska, Talanta, 2004, 64, 801–822 CrossRef PubMed
.
- B. Lavine and J. Workman, Anal. Chem., 2008, 80, 4519–4531 CrossRef CAS PubMed
.
- J. W. Einax, Anal. Bioanal. Chem., 2008, 390, 1225–1226 CrossRef CAS
.
- E. Dinc, D. Baleanu, G. Ioele, M. De Luca and G. Ragno, J. Pharm. Biomed. Anal., 2008, 48, 1471–1475 CrossRef CAS PubMed
.
- M. De Luca, G. Ioele, A. Risoli and G. Ragno, Microchem. J., 2006, 83, 24–34 CrossRef CAS PubMed
.
- H. D. Li, Y. Z. Liang, Q. S. Xu and D. S. Cao, Anal. Chim. Acta, 2009, 648, 77–84 CrossRef CAS PubMed
.
- Z. C. Liu, W. S. Cai and X. G. Shao, Analyst, 2009, 134, 261–266 RSC
.
- J. C. L. Alves and R. J. Poppi, Analyst, 2013, 138, 6477–6487 RSC
.
- H. Martens and T. Naes, Multivariate Calibration, Wiley, Chichester, 1989, vol. 7 Search PubMed
.
- Y. N. Ni and X. F. Gong, Anal. Chim. Acta, 1997, 354, 163–171 CrossRef CAS
.
- B. Hemmateenejad, R. Ghavami, R. Miri and M. Shamsipur, Talanta, 2006, 68, 1222–1229 CrossRef CAS PubMed
.
- X. G. Shao, X. H. Bian and W. S. Cai, Anal. Chim. Acta, 2010, 666, 32–37 CrossRef CAS PubMed
.
- R. Ergon, Chemom. Intell. Lab. Syst., 2006, 81, 68–73 CrossRef CAS PubMed
.
- J. F. Nie, H. L. Wu, X. M. Wang, Y. Zhang, S. H. Zhu and R. Q. Yu, Anal. Chim. Acta, 2008, 628, 24–32 CrossRef CAS PubMed
.
- H. Wold, in Systems Under Indirect Observation, ed. H. Joreskog and H. Wold, North-Holland, Amsterdam, 1982 Search PubMed
.
- G. Ragno, G. Ioele and A. Risoli, Anal. Chim. Acta, 2004, 512, 173–180 CrossRef CAS PubMed
.
- Y. H. Yuan, Y. Z. Liang, G. X. Xie, H. D. Li, D. S. Cao and Q. S. Xu, Analyst, 2013, 138, 6412–6421 RSC
.
- J. El Haddad, F. de Miollis, J. Bou Sleiman, L. Canioni, P. Mounaix and B. Bousquet, Anal. Chem., 2014, 86, 4927–4933 CrossRef CAS PubMed
.
- D. Chen, W. S. Cai and X. G. Shao, Anal. Chim. Acta, 2007, 598, 19–26 CrossRef CAS PubMed
.
- J. El Haddad, B. Bousquet, L. Canioni and P. Mounaix, TrAC, Trends Anal. Chem., 2013, 44, 98–105 CrossRef CAS PubMed
.
- J. P. Andries, Y. V. Heyden and L. M. Buydens, Anal. Chem., 2013, 85, 5444–5453 CrossRef CAS PubMed
.
- M. del Olmo, C. Díez, A. Molina, I. de Orbe and J. L. Vílchez, Anal. Chim. Acta, 1996, 335, 23–33 CrossRef CAS
.
- R. B. Keithley, M. L. Heien and R. M. Wigheman, TrAC, Trends Anal. Chem., 2009, 28, 1127–1136 CrossRef CAS PubMed
.
- X. L. Cheng, J. Y. Wan, P. Li and L. W. Qi, J. Chromatogr. A, 2011, 1218, 5774–5786 CrossRef CAS PubMed
.
- D. M. Haaland and E. V. Thomas, Anal. Chem., 1988, 60, 1193–1202 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra12647e |
| This journal is © The Royal Society of Chemistry 2015 |




