Open Access Article
Open Access ArticleJahn–Teller effects in initial and final states: high-resolution X-ray absorption, photoelectron and Auger spectroscopy of allene†
Eva
Muchova
 a,
Daniel
Hollas
a,
Daniel
Hollas
 b,
David M. P.
Holland
b,
David M. P.
Holland
 c,
Camila
Bacellar
d,
Ludmila
Leroy
d,
Thomas R.
Barillot
d,
Luca
Longetti
c,
Camila
Bacellar
d,
Ludmila
Leroy
d,
Thomas R.
Barillot
d,
Luca
Longetti
 d,
Marcello
Coreno
e,
Monica
de Simone
d,
Marcello
Coreno
e,
Monica
de Simone
 f,
Cesare
Grazioli
f,
Cesare
Grazioli
 f,
Majed
Chergui
f,
Majed
Chergui
 d and
Rebecca A.
Ingle
d and
Rebecca A.
Ingle
 *g
*g
aDepartment of Physical Chemistry, University of Chemistry and Technology, Technická 5, 166 28 Prague, Czech Republic
bCentre for Computational Chemistry, School of Chemistry, University of Bristol, Bristol, BS8 1TS, UK
cDaresbury Laboratory, Daresbury, Warrington, Cheshire WA4 4AD, UK
dLaboratoire de Spectroscopie Ultrarapide, Ecole Polytechnique Fédérale de Lausanne, ISIC, FSB, CH-1015 Lausanne, Switzerland
eISM-CNR, Istituto di Struttura dei Materiali, LD2 Unit, 34149 Trieste, Italy
fIOM-CNR, Istituto Officina dei Materiali, 34149 Trieste, Italy
gDepartment of Chemistry, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: r.ingle@ucl.ac.uk
First published on 17th February 2023
Abstract
Carbon K-edge resonant Auger spectra of gas-phase allene following excitation of the pre-edge 1s → π* transitions are presented and analysed with the support of EOM-CCSD/cc-pVTZ calculations. X-Ray absorption (XAS), X-ray photoelectron (XPS), valence band and non-resonant Auger spectra are also reanalysed with a series of computational approaches. The results presented demonstrate the importance of including nuclear ensemble effects for simulating X-ray observables and as an effective strategy for capturing Jahn–Teller effects in spectra.
1 Introduction
Molecular spectroscopy concerns the understanding of the light-matter interactions through the interpretation of molecular spectra. Over the years, the wealth of spectroscopic methods available has transformed our understanding of the electronic and nuclear structure of molecules and their associated dynamics. Independent of the experimental technique used to record it, a spectrum consists of features, each with an associated position, lineshape, linewidth and intensity. While the exact physical phenomena that contribute to the observed signal in a spectroscopy experiment are dependent on the experimental method used, the understanding of the way in which these physical processes relate to the observed spectral features is the key to describing the properties and dynamical behaviour of the molecule of interest.Often, establishing the relationship between molecular properties and spectroscopic observables relies on the use of quantum chemical models. The use of core-level spectroscopies and X-ray methods that are ‘element selective’, by probing transitions involving highly localised orbitals, can help circumvent some of the complexities associated with interpreting congested spectra, often encountered with valence shell ionisation, with many contributing transitions. However, the accurate modelling of X-ray observables still poses a unique set of challenges for quantum chemical modelling.1–6 Despite these challenges, core-level spectroscopies have been successfully used to study a number of different reaction types7–10 including electrocyclic ring-opening reactions,11 charge-transfer and charge migration processes,12–14 as well as the interplay between open-shell spin-coupling and Jahn–Teller distortion.15,16
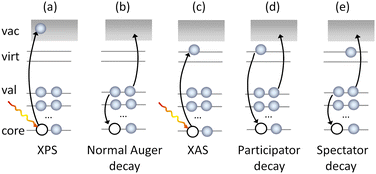
The complementary nature of the experimental observables means that the joint use of core-level techniques such as X-ray absorption (XAS), X-ray photoelectron spectroscopy (XPS) and Auger electron spectroscopy (AES) (Fig. 1) can provide a full characterisation of the core, valence and virtual orbitals of a molecule. Of these techniques, Auger spectroscopy, especially when performed in resonance with an electronic transition (Fig. 1), can recover information on core and valence electronic structure, dissociation dynamics,17–20 the vibrational structure of the neutral or ionised system17,21–23 and contributions of the Renner–Teller effect24 or even interactions in solutions,25 making AES a powerful and flexible tool for molecular spectroscopy.
The Auger process is, however, complex as it involves the contributions of multiple decay mechanisms and associated electronic configurations, including normal (2 hole, 2h), participator (1 hole, 1h) and spectator (2 hole, 1 particle, 2h1p) processes (see Fig. 1. Note, such classification is also not unambiguous because the final states may also have mixed 1h and 2h1p characters).
The first attempts to build the theory of Auger decay by Wentzel26 used a perturbative approach. The Auger decay can be viewed as two individual steps – (i) core ionisation or excitation and (ii) emission of the Auger electron. The initial state with a core hole can then be treated as an electronically metastable state (resonance) which undergoes a spontaneous decay. A more sophisticated alternative uses the X-ray Raman scattering theory, where the Auger electron is considered to be scattered from the photoexcited state.3,27 Extensions of this model include consideration of the resonant intermediate states and the effect of direct excitation channels on the scattering cross-sections (ref. 28 and references therein). Other models have included the effects of the incident X-ray polarisation on the initially populated states.29 Another class of methods is based on the Fano-Feschbach time-independent approach30,31 which views the electronic resonances as discrete states embedded in a continuum of states. The construction of the decay states including the continuum part is challenging in standard electronic structure calculations as the outgoing electron cannot be properly represented with square-integrable functions. Existing approaches either (i) completely neglect the continuum part (for example methods based on electron populations analysis on a core-ionized atom such as in ref. 32) or (ii) describe the outgoing electron implicitly (complex absorbing potential approach,33,34 Stieltjes imaging35) or (iii) describe the outgoing electron with an appropriate continuum orbital.36–40 All mentioned methods also suggest that the outgoing electron is emitted from the atom that was ionized or excited (one-center approximation) which is troublesome for larger molecules and in cases of charge migration. Clearly, even though various methods have been introduced, including highly accurate Fano-ADC approaches,41,42 the practical use and predictive power remains limited especially for larger molecules with complex orbital space.
In this work, we combine experiment and theory to understand the X-ray absorption and Auger-type spectra of the smallest, odd-numbered cumulene, allene. In its ground electronic state, allene belongs to the D2d point group and its symmetry gives two unusual aspects to its electronic structure. First, the molecular orbitals of allene can be represented in terms of canonical molecular orbitals adapted to either the mirror plane elements (D2) or to the two rotation axes (C2v), see Fig. 2.43–46 The choice of the molecular orbitals is completely arbitrary. If we adopt the two rotation axes, we end up with the so called helical molecular orbitals that span the whole length of the molecule43 and are of interest for their role in the reactivity and physical properties of such molecules.43–49 Secondly, after the removal of an electron, allene exhibits a characteristic Jahn–Teller distortion along internal coordinates which can lead to bond-length changes, torsion, or both, with recent work by Garner et al.43 suggesting the torsional motion is energetically stabilising for the allene cation. By combining state-of-the-art quantum chemical approaches with the nuclear ensemble approach (NEA),50,51 that naturally captures accurate peak positions, widths, and intensities as well as non-Condon effects, a new analysis and decomposition of the high-resolution XAS spectra of allene can be performed. From this, it is possible to interpret the spectral features in resonant Auger spectra. Overall, the present work demonstrates that simulations based on the nuclear ensemble approach represent an accurate and efficient tool for interpreting X-ray spectra, especially if characteristic changes in the excited or ionized states, such as Jahn–Teller splitting, are involved and do not require any prior assumptions about the shapes of the potentials involved.
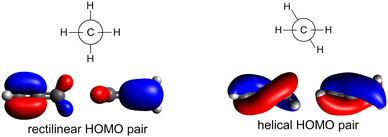 | ||
| Fig. 2 Degenerate HOMO pairs of allene adapted according to mirror plane (left) or to rotation (right). | ||
2 Methods
2.1 Experimental methods
All measurements were performed at the GasPhase endstation at the Elettra Synchrotron radiation facility.52 Allene (>97%, Apollo Scientific) was introduced to the interaction region at a pressure of ∼5 mbar using an effusive gas jet. For the high-resolution XAS measurements, a monochromatised beam of approximately 40 meV of bandwidth was scanned in steps of 10 meV across the feature of interest and absorption spectra were recorded in total ion yield mode using a charged particle detector placed close to the interaction region. Energy calibrations were performed using carbon dioxide as a reference gas.53Photoelectron spectra and normal and resonant Auger spectra were recorded with a Scienta SES-200 hemispherical analyser mounted at the magic angle (57.4°) to the electric vector of the incident light. All core–hole spectra were recorded under experimental conditions so that the dominant contribution to the lineshape would be the core–hole lifetime broadening. For the XPS measurements, a pass energy of 20 eV and a spectrometer entrance slit width of 0.8 mm was used to give a theoretical spectrometer resolution of 40 meV. For the normal and resonant Auger measurements, a 20 eV pass energy and a spectrometer entrance slit width of 2.5 mm were used to give a theoretical spectrometer resolution of 125 meV. Photoelectron spectra of the argon 3s and 3p lines were measured to provide an energy calibration of the valence band PES of allene as well as to check the energy resolution of the spectrometer. As with the XAS measurements, carbon dioxide was used as a reference gas for all energy calibrations.54
2.2 Theoretical methods
We performed the sampling by ab initio molecular dynamics (MD) in the gas phase. The simulations were performed at the B3LYP/6-31+G* level. The temperature was set to 300 K, using the generalized Langevin equation (GLE) thermostat69,70 to account for the nuclear quantum effects. The time step was set to 0.5 fs and the total length of the simulation was set to 20 ps. 400 equally distanced frames from MD were used for further calculations of all types of X-ray spectra. Note, that in NEA the majority of generated structures lack symmetry, e.g. we used symmetry unrestricted solutions in the ab initio calculations, yet we sometimes use the symmetry-related nomenclature to distinguish the molecular orbitals. Some authors claim that relaxing the symmetry restrictions is important for the correct description of ionisation and excitation since it allows the so-called hole localization.71
| Method | Central carbon | Terminal carbons |
|---|---|---|
| Exp. | 290.9 | 290.6 |
| MOM/CCSD(T)/comb DZ | 292.4 | 292.1 |
| MOM/CCSD(T)/comb TZ | 290.7 | 290.8 |
| MOM/LC-ωPBE/comb DZ | 291.1 | 290.8 |
| MOM/LC-ωPBE/comb TZ | 290.0 | 289.7 |
| MOM/LC-ωPBE/comb QZ | 290.0 | 289.6 |
| CVS-EOM-IP-CCSD/cc-pVTZ | 291.7 | 291.4 |
| CVS-EOM-IP-CCSD/aug-cc-pVTZ | 291.7 | 291.3 |
| CVS-EOM-IP-CCSD/u-aug-cc-pVTZ | 291.5 | 291.1 |
| CVS-EOM-IP-CCSD/aug-cc-pVQZ | 291.5 | 291.1 |
| CVS-EOM-IP-CCSD/u-aug-cc-pVQZ | 291.4 | 291.0 |
The resonant Auger measurements were performed for 5 incident photon energies spanning the pre-edge feature. We modelled the corresponding resonant Auger spectra using selected geometries and with excitation energies coincident with the experimental incident photon energy window (±45 meV; the experimental incident photon bandwidth was 90 meV and the theoretical excitation energies were shifted). The calculated stick spectra were Gaussian broadened by 0.1 eV. The continuum orbital was treated as a plane wave, which is computationally more practical compared to a Coulomb wave orbital, even though we may speculate that the Coulomb wave might provide slightly better agreement with the experiment.40
3 Results
Interpretation of the resonant Auger spectra of a molecule requires a proper description of both the core and valence electronic structure of a molecule. In Auger decay, one possible process is the ejection of an electron from the occupied valence orbitals and so valence band photoelectron spectra are a useful tool to help interpret this subset of contributions. The XPS spectra can be used to determine core-level binding energies and are therefore important for determining the energetics of the Auger electrons. The XAS spectrum contains information on the transitions that are excited in the initial step of the resonant Auger process and therefore determine what decay processes will then occur. First, we will present an analysis of the valence band, XPS and XAS spectra to understand the contributions to the final resonant Auger spectra and validate the computational approach chosen.3.1 Valence band photoelectron spectra
The valence band photoelectron spectrum of allene was recorded at an incident photon energy of 65 eV (Fig. 3) and exhibits three prominent features at binding energies below 20 eV that are consistent with those previously reported in photoelectron spectra recorded with He(I), He(II) and synchrotron sources (ref. 93–95 and references therein). The first band, beginning at 9.2 eV, has been assigned to the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state and arises from ionisation from the 2e HOMO orbital. The orbitals are depicted in Fig. S9 in ESI.† The band displays a characteristic splitting due to Jahn–Teller distortion.96–98 The theoretical study by Woywod and Domcke97 showed that this band structure could be understood in terms of the Jahn–Teller coupling involving the ν4 (b1) and the ν6 (b2) antisymmetric C
2E state and arises from ionisation from the 2e HOMO orbital. The orbitals are depicted in Fig. S9 in ESI.† The band displays a characteristic splitting due to Jahn–Teller distortion.96–98 The theoretical study by Woywod and Domcke97 showed that this band structure could be understood in terms of the Jahn–Teller coupling involving the ν4 (b1) and the ν6 (b2) antisymmetric C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching modes.
C stretching modes.
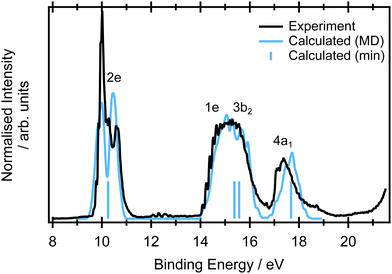 | ||
| Fig. 3 Experimental (black) valence band photoemission spectra. The blue stick spectrum represents the EOM-IP-CCSD/cc-pVTZ calculations for the minimum energy structure. The blue line corresponds to the spectra calculated at the same level for a set of 400 geometries within NEA. Each ionisation energy was phenomenological Gaussian broadened by 0.05 eV to reflect the limited number of calculated points. The calculated spectrum is unshifted in energy and the relative intensities of the measured and NEA calculated spectra was set to yield the best overlap. The respective orbitals are depicted in Fig. S9 in ESI.† The single point calculations are included to show the relative energies of the transitions and do not contain any intensity information so have been arbitrarily set to be equal. | ||
At binding energies between 14 and 17 eV, ionisation from the 1e and 3b2 orbitals results in a complex photoelectron band,93 attributed to the overlapping contributions from the Ã2E and the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 states. Several vibrational progressions associated with the Ã2E are evident in the binding energy range ∼14–15.2 eV. A detailed theoretical analysis, using a model diabatic Hamiltonian within the linear vibronic coupling scheme, showed that the totally symmetric vibrational mode ν2 (a1) and a single Jahn–Teller active mode ν7 (b2) account for the observed progressions.97,98 Similar vibronic structure was observed in the absorption bands associated with Rydberg states belong to series converging onto the à 2E state ionisation threshold.99 The full photoelectron spectrum was later modelled using a second-order vibronic Hamiltonian.100 The final outer valence photoelectron band, centered around 17.6 eV, is attributed to the (4a1)−1
2B2 states. Several vibrational progressions associated with the Ã2E are evident in the binding energy range ∼14–15.2 eV. A detailed theoretical analysis, using a model diabatic Hamiltonian within the linear vibronic coupling scheme, showed that the totally symmetric vibrational mode ν2 (a1) and a single Jahn–Teller active mode ν7 (b2) account for the observed progressions.97,98 Similar vibronic structure was observed in the absorption bands associated with Rydberg states belong to series converging onto the à 2E state ionisation threshold.99 The full photoelectron spectrum was later modelled using a second-order vibronic Hamiltonian.100 The final outer valence photoelectron band, centered around 17.6 eV, is attributed to the (4a1)−1 ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2A1 state.
2A1 state.
Calculated total photoionisation cross sections for the minimum energy structure are included in the Table S2 in ESI.† The intensity can be also estimated based on the norms of Dyson orbitals. The Dyson norms are provided in Table S3 in ESI.† The norms are almost equal for all valence band ionisations. For nuclear ensemble calculations, we assume that the intensity is equal for all ionisations, the spectra are constructed as an energy histogram.
In the NEA approach, it is assumed that the ground state nuclear density determines the spectral shape. If this hypothesis is fulfilled, NEA provides an accurate envelope of the peaks, though features originating from vibronic progressions will be missing. The geometric effects from the Jahn–Teller distortion are well captured, as is demonstrated in Fig. 3. The combination of an accurate electronic structure method (EOM-IP-CCSD with a cc-pVTZ basis set) and NEA provides accurate peak positions for the first feature at 9.7 eV and the weaker shoulder at 10.31 eV, and reproduces the experimentally observed peak widths. Moreover, via sampling of ground state configurational space it naturally captures the double peak character of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E band. The peak position and large width of the Ã2E/
2E band. The peak position and large width of the Ã2E/![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 feature is also in a very good agreement with the experiment. The peak position and the width of the spectral feature corresponding to the ionisation from the 4a1 orbital is in excellent agreement with the experiment.
2B2 feature is also in a very good agreement with the experiment. The peak position and the width of the spectral feature corresponding to the ionisation from the 4a1 orbital is in excellent agreement with the experiment.
For further interpretation of the Auger spectra, it is important to stress that the key spectral features are relatively broad and that ionized allene exhibits Jahn–Teller splitting which is accurately captured within NEA.
3.2 X-Ray photoelectron spectra
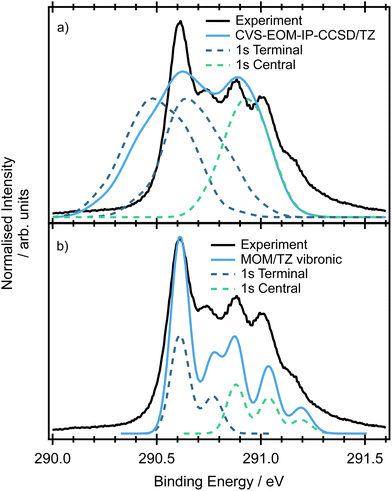
The minimum energy structure for allene has two non-equivalent carbon environments, one on the central carbon and the other on the two terminal carbons. A typical core-shell XPS spectrum has several characteristics: (i) line positions which reflect the chemical environment of the atom that has been ionised, (ii) a line shape which reflects the core–hole relaxation dynamics and (iii) vibronic structure which reflects the change in geometry after ionisation. The experimental XPS spectrum (Fig. 4) of allene shows significantly more structure than expected from two photoelectron peaks associated with the central and terminal carbon environments. This additional complexity indicates the possible presence of vibronic progressions in the spectrum.The CCSD(T), LC-ωPBE or CVS-EOM-IP-CCSD calculated core-binding energies are presented in Table 1 for the minimal geometry and in Table S4 in ESI.† The electronic configurations of the lowest energy 1s orbitals are (1a1)2(1b2)2(2a1)2. The lowest energy orbital (1a1)2 is localized on the central carbon atom, while the two (1b2)2(2a1)2 orbitals are localized on the terminal carbons and are degenerate. The estimated energy difference between the first and second core ionisation energies is 0.3 eV, which is in agreement with the experimental value of 0.3 eV. Note, that the MOM/CCSD(T) with the triple-zeta quality basis set provides remarkably accurate results on the absolute scale, with a difference between the calculated and experimental energies being less than 0.2 eV. Also note, that fully uncontracted basis sets have a very good performance and provide a cost-effective approach to larger basis sets, see Table S4 in ESI.†
The spectra simulated by NEA are shown in Fig. 4(a). The relative positions of the peaks at 290.9 and 290.6 eV obtained at both the fc-CVS-EOM-IP-CCSD and MOM/LC-ωPBE levels are accurate, although the peak widths are slightly broader. The peak attributed to the terminal carbons (maximum at 290.9 eV) is composed of two overlapping peaks that are 0.15 eV apart, e.g. a small splitting is observed. This small splitting is probably a result of lifted symmetry and may be also partially caused by incomplete sampling of the ground state nuclear density. In this case, NEA provides an accurate but incomplete picture due to the absence of vibronic transitions.
The double-harmonic parallel approximation was used to model the vibronic XPS spectrum. The optimized geometries are provided in ESI,† Table S6. While ionisation of the core orbitals of the central carbon atom keeps the molecular symmetry, ionisation of one of the terminal carbons leads to symmetry breaking via C–C bond alternation. The simulated spectrum is provided in Fig. 4(b). As can be inferred from the figure, the peak positions are well reproduced and the vibronic model predicts shoulders at 290.77 eV (in the case of the terminal carbons ionisation) and two shoulders at 291.03 eV and 291.18 eV (in the case of the central carbon ionisation) in agreement with the experiment. The shoulders can be attributed to the ν9 and ν10 modes (see Table S7 in ESI†).
By understanding the contributions to the overall spectral shape and being able to identify the origins of the vibronic progressions, experimental ionisation energies of 290.9 and 290.6 eV can be extracted for the central and terminal carbon environments respectively.
The key observations which are useful for the interpretation of Auger spectra are the peak assignments obtained from our calculations. We have shown that the binding energies of the peaks corresponding to the terminal and core carbon atoms are ∼0.3 eV apart and that the rest of the complex spectral envelope probably corresponds to vibrational excitations.
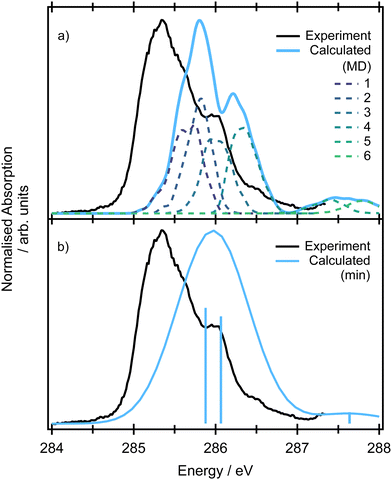
3.3 X-Ray absorption spectra
The pre-edge absorption features of allene show a complex line shape, with the most intense region centred at 285.2 eV and a series of irregularly spaced, weaker features (Fig. 5). Previous electron energy loss measurements101 had attributed the feature to a combination of two overlapping 1s → π* transitions, though from the limitations of the resolution of the electron energy loss spectra and available XPS measurements it was unclear as to whether the energetic separation of the transitions arose from a difference in the energy of the initial core–hole states (0.3 eV based on the XPS measurements) on the central and terminal carbons or the final π* states, as both are expected to be degenerate.102The theoretical spectra modelled for the minimum energy structure are presented in Fig. S11 in ESI† at the CVS-EOM-EE-CCSD and TDDFT levels. If we use the conventional picture (orbitals are depicted in Fig. 2), the two degenerate lowest-energy transitions correspond to the excitations from the degenerate (1b2)2 (2a1)2 core orbitals localized on the terminal carbons to the pair of unoccupied LUMO π* orbitals of 3e symmetry. The two degenerate transitions corresponding to the excitations from the (1a1)2 localized on the central carbon to the pair of LUMO π* orbitals reflect the energy difference between the initial core–hole states (∼0.3 eV, see Table 1). The natural transition orbitals corresponding to the excitations at the CVS-EOM-CCSD/cc-pVTZ level are depicted in Fig. S10 in ESI.† The intensities of transitions in terms of oscillator strengths are approximately the same for all transitions at both the CVS-EOM-EE-CCSD and TDDFT levels. The modelled spectra exhibit only one broad peak arising from convolution of the individual transitions. The transitions at ∼287 eV with significantly less intensity correspond to the transitions from the degenerate (1b2)2(2a1)2 orbitals of the terminal carbons to the perpendicular unoccupied LUMO π* orbitals. We can conclude that the spectral shape is not correctly described using only the minimum energy structure because the spectral feature at 286 eV is not reproduced.
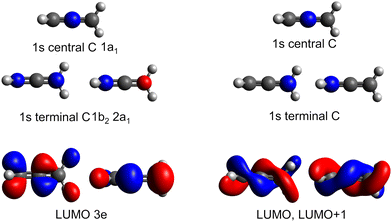
As in the case of valence band photoelectron spectra, using a NEA approach to model the XAS spectrum may be more useful (Fig. 5 at the CVS-EOM-EE-CCSD or Fig. S11 at the TDDFT level in ESI†). With the inclusion of the NEA, the shape of the broad band and a shoulder at 286 eV are in very good agreement with the experiment and can be decomposed into the contributions from individual transitions. The transitions are labelled as (according to the dominant contribution; the transitions are, however, heavily mixed) 1: terminal 1s(1) → LUMO, 2: central 1s → LUMO, 3: terminal 1s(2) → LUMO and LUMO+1, 4: central 1s → LUMO+1 and more diffuse LUMO+2 and LUMO+3, 5: terminal 1s(1) → LUMO and LUMO+1, 6: terminal 1s(2) → LUMO and LUMO+1. For structures generated within NEA, neither the core orbitals of the terminal carbons nor the pair of LUMO orbitals are degenerate (see Fig. 6); we assign (1) to the lowest-energy core orbital and (2) to the second lowest-energy orbital. The typical observed shape of LUMOs is helical (see Fig. 6). As in the case of valence photoelectron spectra, we may assume that reduction of symmetry leads to the Jahn–Teller splitting of the electronic states. As a result, we may observe a convolution of four peaks instead of two peaks (as is calculated for a minimum energy structure, see Fig. 5 which gives rise to the observed spectral shape). Since via NEA it is impossible to assign particular vibrational modes involved in Jahn–Teller splitting, we calculated energy profiles along the normal coordinates; the profiles are provided in Fig. S12 in ESI.† The figure shows that particularly the mode ν7 (b2) is involved. The NEA approach also captures the non-Franck–Condon effects; the magnitude of the effect is shown in Fig. S13 (ESI†). In the case of allene, non-Condon effects are minor and do not affect the overall shape of the spectrum.
The suggested assignment is especially important with respect to the interpretation of the resonant Auger spectra. The overall structure is clearly a superposition of transitions from the core orbitals of the terminal and central carbon atoms and based on the simulations, we assume that the shoulder at 286 eV arises from Jahn–Teller splitting and not from a vibrational progression.
3.4 Non-resonant Auger spectra
The non-resonant Auger spectrum of allene recorded at an incident photon energy of 400 eV is shown in Fig. 7. The spectrum has not been corrected for the electron scattering background. The spectrum has two intense features at high kinetic energies at ∼262 eV and ∼257 eV, together with several overlapping features towards lower kinetic energies. Since, during the Auger decay, one electron fills the core hole and another electron is ejected from a valence orbital, the spectra reflect the energetic separation between the peaks in the valence photoelectron spectra (the separation between the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and à bands (Fig. 3) is ∼4.8 eV and between the Ã/
and à bands (Fig. 3) is ∼4.8 eV and between the Ã/![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) bands is 2.3 eV). The recorded spectral features are relatively broad and do not show any vibrational progressions.
bands is 2.3 eV). The recorded spectral features are relatively broad and do not show any vibrational progressions.
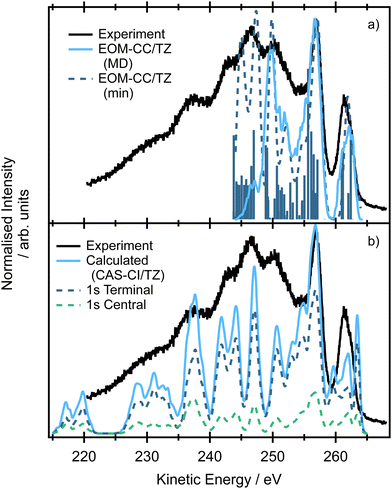
The spectra modelled using the EOM-CC formalism for the minimum energy structure and within the NEA approach are presented in Fig. 7(a). The high-energy peak at ∼261 eV corresponds to the situation where an electron is ejected either from the terminal or central carbon 1s core orbital (e.g. contributions from multiple ionisations are involved as we showed previously) and the final dicationic (2h) states involve the pair of HOMO and HOMO−1 (in the case of NEA, degenerate 2e HOMO for the minimum energy structure). The second peak at ∼257 eV corresponds to the final states in which both HOMO−2 and HOMO−3 (in the case of NEA, 1e and 3b2 for the minimum energy structure) are involved, which may explain both higher intensity and relative broadness of the peak. The calculations suggest that the broad peak centered at ∼251 eV also involves the lower lying valence orbital HOMO−5 (4a1). The broad peaks centered at ∼246 and ∼242 eV correspond to the final states in which the holes are localized in the 3b2, 4a1 or 2b2 orbitals. Due to technical reasons the calculations of final dicationic states involving inner-valence orbitals were not possible. Note that the Auger spectrum of allene is rather congested; the lines are broadened due to the finite core–hole lifetimes, multiple core–hole initial states are prepared by the incident radiation, and a large number of final states contribute to the overall shape of the spectrum. On the other hand, the vibrational progressions are smeared out and in this case NEA can provide a very accurate spectral envelope. As can be inferred from Fig. 7, the theoretical widths are in an excellent agreement with the experiment.
The spectrum simulated by NEA and two-hole population analysis, based on the CAS-CI wavefunction, provides a similar picture (Fig. 7b), yet the agreement with the experiment is less convincing. The first peak in which the final holes are localized in the pair of the HOMO orbitals (2e) shows a complex structure and is shifted towards higher kinetic energies. The complex feature centered at ∼257 eV involves final states with holes localized in HOMO−5 (4a1, for comparison, these dicationic states were predicted by EOM-CCSD calculations to contribute to the peak centered at ∼251 eV). The lower energy peaks are due to the final states with two holes in lower-lying valence orbitals. The energy region between 220 and 235 eV is due to the states with the holes in the more strongly bound inner-valence orbitals. Clearly, the two-hole population analysis may serve as a first estimate of the spectrum, more accurate methods, however, should be used to correctly assign the individual contributions.
3.5 Resonant Auger spectra
With an understanding of the character and nature of the transitions contributing to the pre-edge XAS feature, it is now possible to interpret the resonant Auger spectrum of allene. Resonant Auger spectra have been recorded with an incident photon bandwidth of 90 meV at five photon energies, 285.02, 285.32, 285.56, 285.94, 286.54 eV (Fig. 8). The overall shape of the Auger spectra recorded for photon energies <286 eV are reasonably similar and consistent with those previously recorded over a smaller kinetic energy range.103 The spectrum recorded at hν = 286.54 eV shows the most pronounced differences, particularly on the highest kinetic energy features, and a very different overall intensity profile. The reduced absorption cross-section at 286.54 eV means the signal-to-background levels in the Auger spectrum are significantly lower.At the high-energy tail of the spectra (∼275 eV), there appears a sharp and intense spectral feature. As the photon energy is increased from 285.02 to 285.32 eV the sharp band broadens. On reaching higher excitation energies (285.56 and 286.94 eV) a shoulder, which is approximately a third of the intensity of the sharp feature, appears on the high-kinetic energy side. This spectral feature should correspond to the final states in which the hole is localized in one of the HOMO orbitals although only the spectrum at hν = 286.54 eV shows the distinctive Jahn–Teller splitting seen in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state.
2E state.
In the range of 267–271 eV, there are two distinct spectral features for photon energies of 285.02, 285.32, 285.56 and 285.94 eV. The intensity of the features clearly changes with the excitation energy. While for the lowest excitation energy of 285.02 eV, the lower-energy feature is more intense and the higher-energy peak is a shoulder, for excitation energies of 285.32 and 285.56 eV the intensities level off and for 285.94 eV, the higher-energy peak is more intense. According to the valence band photoemission spectra, the peaks arise from the decay processes leading to ionisation from the valence pair of HOMO−2 and HOMO−3 orbitals (1e), HOMO−4 (3b2) and HOMO−5 (4a1) orbitals.
The decay of core excited states, leading to ions with holes in their valence shells, may occur through participator or spectator Auger processes.104 In a participator Auger decay, which is equivalent to autoionisation, the excited electron takes part in the decay. Either a valence electron fills the inner hole and the excited electron is ejected, or the excited electron fills the hole and an electron is ejected from one of the valence orbitals. The end result is the formation of a one-hole ionic state.
In a spectator Auger decay, the excited electron remains as a spectator during the decay. A valence electron fills the inner hole, and an electron is ejected from one of the valence orbitals. Such processes lead to the formation of two-hole-one-particle-excited (2h1p) satellite states. The binding energies of these satellites are normally higher than those associated with the single hole states. Although 2h1p states may be formed through direct ionisation from the molecular ground state, the cross section for such processes is usually small. Spectator decay may enhance the population of satellite states, as well as affecting the photoionisation dynamics.
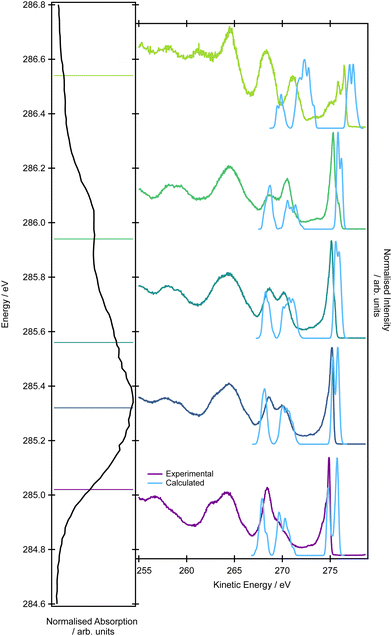
The simulations of the resonant Auger spectra were performed at five photon energies to match the regions of the XAS spectrum covered in the experiment: 285.47, 285.77, 286.01, 286.22 (the peak maximum of the shoulder), 287.47 eV (the peak maximum). The resonance energies in the calculations were shifted compared to the experimental values; the value of 0.45 eV mirrors the difference between the position of the maximum in the XAS experimental spectrum and in the EOM-EE-CCSD/cc-pVTZ theoretical spectrum. It is important to mention that it is not possible to accurately model the resonant Auger spectra using only the minimum energy structure because the individual excitation energies do not necessarily correspond to energy regions covered by the experimental photon bandwidth. In the calculations, we aimed to interpret the high-kinetic energy tail of the resonant spectrum (the energy range between 265–275 eV). We considered only the participator process leading to the final 1h states which should be dominant in this energy region.
The first feature at ∼275 eV exhibits a double peak structure. The calculated intensities and peak spacing, however, vary for the five photon energies. For the photon energies of 285.02 and 285.32 eV (285.47, 285.77 eV in theory), the higher-energy feature is more intense. For the photon energies of 285.56 and 285.94 eV (286.01 and 286.22 eV in theory), the opposite trend is observed. The spacing between the peaks varies, and for the four photon energies it is 0.9, 0.5, 0.3 and 0.3 eV. Simulations confirmed that the peaks arise from the decay leading to states with a hole in the pair of HOMO orbitals (2e). The expected Jahn–Teller splitting is also observed. The interpretation of intensity changes is rather complex because it is affected not only by the overlap of the initial and final states but also changes with geometry. Generally, we observed that the intensity of the higher-energy peak is lower if the initial state involves excitations from the central carbon atom, while if the excitation is from the terminal carbons, the intensity of the higher-energy tail is higher. The calculated lineshapes and their incident photon energy dependence is overall in good agreement with the experimentally observed trends.
For the second and third peaks in the energy range between 265–275 eV, the calculations confirmed the experimental assignment. The final 1h states corresponding to the higher-energy peak have a hole localized in the pair of HOMO−2 and HOMO−3 (1e) and HOMO−4 (3b2), while the states corresponding to the lower-energy peak have the hole in the HOMO−5 (4a1) orbital. As in the valence band photoelectron spectrum, it is not possible to distinguish individual peaks corresponding to the states with a hole in the pair of HOMO−2 and HOMO−3 (1e) and HOMO−4 (3b2). It is also difficult to disentangle the varying intensity of this spectral feature because it is a superposition of three contributions and each contribution has a different dependency on the geometrical parameters.
As already discussed, it seems likely that spectator Auger decay, which is not included in the theoretical simulation, affects the final states formed in this energy region. The resonantly excited Auger spectra recorded at photon energies of 285.02, 285.32, 285.56 and 285.94 eV, all involving the C1s → π* transition, are plotted in Fig. S16 (ESI†). The kinetic energies of the individual spectra have been shifted slightly so that the peak around 274 eV in each spectrum, due to formation of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E state, aligns. The (kinetic energy shifted) valence shell photoelectron spectrum recorded at a photon energy of 65 eV has also been plotted in Fig. S16 (ESI†). These spectra show that participator Auger decay results in the formation of the
2E state, aligns. The (kinetic energy shifted) valence shell photoelectron spectrum recorded at a photon energy of 65 eV has also been plotted in Fig. S16 (ESI†). These spectra show that participator Auger decay results in the formation of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E, Ã2E/
2E, Ã2E/![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2, and possibly the
2B2, and possibly the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2A1 single hole valence states. The additional intensity observed between the peaks associated with the Ã2 E/
2A1 single hole valence states. The additional intensity observed between the peaks associated with the Ã2 E/![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2 and the
2B2 and the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2A1 states is most likely due to a spectator Auger decay, forming a 2h1p satellite state, where the excited electron remains in the π* orbital. Energetic considerations suggest that this 2h1p satellite corresponds to the configuration in which one electron from the 2e orbital has been ejected and another from the same orbital has been excited into the π* orbital. The next peak in the resonantly excited spectra, occurring at an electron kinetic energy around 264 eV, probably corresponds to a 2h1p satellite having a configuration with a hole in the 2e orbital together with another hole in the 1e orbital, with one of these electrons being ejected and the other excited into the π* orbital.
2A1 states is most likely due to a spectator Auger decay, forming a 2h1p satellite state, where the excited electron remains in the π* orbital. Energetic considerations suggest that this 2h1p satellite corresponds to the configuration in which one electron from the 2e orbital has been ejected and another from the same orbital has been excited into the π* orbital. The next peak in the resonantly excited spectra, occurring at an electron kinetic energy around 264 eV, probably corresponds to a 2h1p satellite having a configuration with a hole in the 2e orbital together with another hole in the 1e orbital, with one of these electrons being ejected and the other excited into the π* orbital.
The non-resonantly excited Auger spectrum is plotted in Fig. S17 (ESI†), together with the resonantly excited Auger spectra whose kinetic energies have been shifted to lower energy by ∼7.6 eV so that the peaks at energies below ∼260 eV approximately align. In a non-resonant Auger spectrum, the peaks arise from transitions into two-hole (2h) final states. For resonant excitation with the initially excited electron remaining as a spectator to the subsequent decay, the peaks in the Auger spectrum are due to transitions into 2h1p states. In this case, the resonantly excited Auger spectrum generally resembles the non-resonantly excited spectrum, but the corresponding features are shifted to higher kinetic energy by several eV. This shift is due to the shielding provided by the electron in the excited orbital. For the spectra plotted in Fig. S17 (ESI†), this excited orbital corresponds to the π* orbital. The shift we observe for the resonantly excited (C1s → π*) spectra in allene (∼7.6 eV) is significantly larger than that (∼4 eV) measured for the resonantly excited (C1s → σ*) spectra in CH3I.105
Overall, the general agreement of the calculated resonant Auger spectra with experiment is satisfactory; the peak positions and widths are very well reproduced with a good estimate of the relative peak intensities. For some incident photon energies, such as 285.94 eV (286.22 eV in theory), the relative peak intensities are not so well reproduced, and further work is required to fully understand the factors influencing the intensity distributions. The discrepancy may be due to the fact, that the calculations predict high intensity for the peak corresponding to the initial state involving excitations of the central carbon atom and final states with a hole in the HOMO−5 orbitals (4a1). We may speculate that the observed varying intensities reflect different contributions of the terminal and central carbon atoms to the valence band and LUMO and LUMO+1 orbitals (higher contribution results in higher intensity) or that the sharpness of the peak reflects the shape of the excited-state potential surface.
4 Conclusions
We report a characterisation of the valence and core electronic structure of allene using a number of core-level spectroscopic techniques. The experimental findings were accompanied by theoretical simulations based on nuclear ensemble methods. We demonstrate that NEA represents a useful tool for spectra simulation which allows us to reproduce the spectral shape without any previous assumptions for the excited or ionized potential energy surfaces. We also show the magnitude of non-Condon effects. Our work demonstrates a tractable quantum chemical approach which can be extended to the calculation of features in resonant Auger spectra and can be used for more complex polyatomic systems where many methods struggle due to the number of possible electronic configurations involved or extreme computational demands. This is an incredibly important development for the viability of resonant Auger spectroscopy and its time resolved variant as a tool for chemical dynamics. The good levels of agreement with the valence contributions to the resonant Auger spectra measured in this work show the promise of such an approach and also further demonstrates the limitation of using single-point calculations on minimum energy structures for simulating experimental observables in polyatomic systems. We emphasise as well that, without the correct assignment of the individual transitions in the XAS spectrum within NEA, the interpretation of the signals observed in the resonant Auger experiments would be impossible.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank C. Puglia (Uppsala University, Sweden) and the Carl Tygger Foundation for making available the SES-200 photoelectron analyser at the Gas Phase beamline, Elettra, Italy. The research leading to this result has been supported by the project CALIPSOplus under Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. E. M. thanks the Czech Science Foundation for the support via project number 21-26601X (EXPRO project). D. M. P. H. is grateful to the Science and Technology Facilities Council (United Kingdom) for financial support.Notes and references
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- S. Tsuru, M. L. Vidal, M. Pápai, A. I. Krylov, K. B. Møller and S. Coriani, Struct. Dyn., 2021, 8, 024101 CrossRef CAS PubMed.
- F. Gel'mukhanov, M. Odelius, S. P. Polyutov, A. Föhlisch and V. Kimberg, Rev. Mod. Phys., 2021, 93, 35001 CrossRef.
- N. A. Besley, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, 1–22 Search PubMed.
- T. Northey, J. Duffield and T. J. Penfold, J. Chem. Phys., 2018, 149, 124107 CrossRef CAS PubMed.
- C. J. Milne, T. J. Penfold and M. Chergui, Coord. Chem. Rev., 2014, 277, 44–68 CrossRef.
- P. M. Kraus, M. Zürch, S. K. Cushing, D. M. Neumark and S. R. Leone, Nat. Rev. Chem., 2018, 2, 82–94 CrossRef CAS.
- E. Gagnon, P. Ranitovic, X. M. Tong, C. L. Cocke, M. M. Murnane, H. C. Kapteyn and A. S. Sandhu, Science, 2007, 317, 1374–1378 CrossRef CAS PubMed.
- M. Maiuri, M. Garavelli and G. Cerullo, J. Am. Chem. Soc., 2020, 142, 3–15 CrossRef CAS PubMed.
- H. Fukuzawa, T. Takanashi, E. Kukk, K. Motomura, S. Ichi Wada, K. Nagaya, Y. Ito, T. Nishiyama, C. Nicolas, Y. Kumagai, D. Iablonskyi, S. Mondal, T. Tachibana, D. You, S. Yamada, Y. Sakakibara, K. Asa, Y. Sato, T. Sakai, K. Matsunami, T. Umemoto, K. Kariyazono, S. Kajimoto, H. Sotome, P. Johnsson, M. S. Schöffler, G. Kastirke, K. Kooser, X. J. Liu, T. Asavei, L. Neagu, S. Molodtsov, K. Ochiai, M. Kanno, K. Yamazaki, S. Owada, K. Ogawa, T. Katayama, T. Togashi, K. Tono, M. Yabashi, A. Ghosh, K. Gokhberg, L. S. Cederbaum, A. I. Kuleff, H. Fukumura, N. Kishimoto, A. Rudenko, C. Miron, H. Kono and K. Ueda, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- A. R. Attar, A. Bhattacherjee, C. D. Pemmaraju, K. Schnorr, K. D. Closser, D. Prendergast and S. R. Leone, Science, 2017, 356, 54–59 CrossRef CAS PubMed.
- H. Yong, N. Zotev, J. M. Ruddock, B. Stankus, M. Simmermacher, A. M. Carrascosa, W. Du, N. Goff, Y. Chang, D. Bellshaw, M. Liang, S. Carbajo, J. E. Koglin, J. S. Robinson, S. Boutet, M. P. Minitti, A. Kirrander and P. M. Weber, Nat. Commun., 2020, 11, 1–6 CrossRef PubMed.
- T. Katayama, T. Northey, W. Gawelda, C. J. Milne, G. Vankó, F. A. Lima, R. Bohinc, Z. Németh, S. Nozawa, T. Sato, D. Khakhulin, J. Szlachetko, T. Togashi, S. Owada, S. Ichi Adachi, C. Bressler, M. Yabashi and T. J. Penfold, Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- H. J. Wörner, C. A. Arrell, N. Banerji, A. Cannizzo, M. Chergui, A. K. Das, P. Hamm, U. Keller, P. M. Kraus, E. Liberatore, P. Lopez-Tarifa, M. Lucchini, M. Meuwly, C. Milne, J. E. Moser, U. Rothlisberger, G. Smolentsev, J. Teuscher, J. A. V. Bokhoven and O. Wenger, Struct. Dyn., 2017, 4, 061508 CrossRef PubMed.
- M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, M. L. Vidal, A. I. Krylov, S. Coriani and S. R. Leone, J. Phys. Chem. A, 2020, 124, 9524–9531 CrossRef CAS PubMed.
- M. L. Vidal, M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, S. R. Leone, A. I. Krylov and S. Coriani, J. Phys. Chem. A, 2020, 124, 9532–9541 CrossRef CAS PubMed.
- O. Travnikova, E. Kukk, F. Hosseini, S. Granroth, E. Itälä, T. Marchenko, R. Guillemin, I. Ismail, R. Moussaoui, L. Journel, J. Bozek, R. Püttner, P. Krasnov, V. Kimberg, F. Gel'mukhanov, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2022, 24, 5842–5854 RSC.
- A. C. F. Santos, O. Travnikova, N. Boudjemia, T. Marchenko, R. Guillemin, I. Ismail, D. Koulentianos, D. Céolin, F. Gel'mukhanov, M. Simon, M. N. Piancastelli and R. Püttner, J. Vac. Sci. Technol., A, 2022, 40, 042801 CrossRef CAS.
- O. Travnikova, V. Kimberg, R. Flammini, X.-J. Liu, M. Patanen, C. Nicolas, S. Svensson and C. Miron, J. Phys. Chem. Lett., 2013, 4, 2361–2366 CrossRef CAS.
- T. J. Wolf, F. Holzmeier, I. Wagner, N. Berrah, C. Bostedt, J. Bozek, P. Bucksbaum, R. Coffee, J. Cryan, J. Farrell, R. Feifel, T. Martinez, B. McFarland, M. Mucke, S. Nandi, F. Tarantelli, I. Fischer and M. Gühr, Appl. Sci., 2017, 7, 681 CrossRef.
- E. Kukk, G. Snell, J. D. Bozek, W. T. Cheng and N. Berrah, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 63, 062702 CrossRef.
- J. D. Bozek, S. E. Canton, E. Kukk and N. Berrah, Chem. Phys., 2003, 289, 149–161 CrossRef CAS.
- L. S. Cederbaum, P. Campos, F. Tarantelli and A. Sgamellotti, J. Chem. Phys., 1998, 95, 6634 CrossRef.
- C. Miron, V. Kimberg, P. Morin, C. Nicolas, N. Kosugi, S. Gavrilyuk and F. Gel'mukhanov, Phys. Rev. Lett., 2010, 105, 093002 CrossRef PubMed.
- M. A. Brown, M. Faubel and B. Winter, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2009, 105, 174–212 RSC.
- G. Wentzel, Z. Physik, 1927, 43, 524–530 CrossRef CAS.
- F. Gel'mukhanov and H. Ågren, Phys. Rep., 1991, 312, 87–330 CrossRef.
- M. P. Ljungberg, Phys. Rev. B, 2017, 96, 1–12 CrossRef.
- V. Kimberg, N. Kosugi and F. Gel’mukhanov, J. Chem. Phys., 2009, 130, 114302 CrossRef PubMed.
- U. Fano, Phys. Rev., 1961, 124, 1866 CrossRef CAS.
- H. Feschbach, Rev. Mod. Phys., 1964, 36, 1076–1078 CrossRef.
- M. Mitani, O. Takahashi, K. Saito and S. Iwata, J. Electron Spectrosc. Relat. Phenom., 2003, 128, 103–117 CrossRef CAS.
- F. Matz and T. C. Jagau, J. Chem. Phys., 2022, 156, 114117 CrossRef CAS PubMed.
- A. Ghosh, N. Vaval and S. Pal, Chem. Phys., 2017, 482, 160–164 CrossRef CAS.
- V. Carravetta and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 1022 CrossRef CAS PubMed.
- L. Inhester, C. F. Burmeister, G. Groenhof and H. Grubmüller, J. Chem. Phys., 2012, 136, 144304 CrossRef CAS PubMed.
- G. Grell, O. Kühn and S. I. Bokarev, Phys. Rev. A, 2019, 100, 042512 CrossRef CAS.
- G. Grell and S. I. Bokarev, J. Chem. Phys., 2020, 152, 074108 CrossRef CAS PubMed.
- W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084124 CrossRef CAS PubMed.
- W. Skomorowski and A. I. Krylov, J. Chem. Phys., 2021, 154, 084125 CrossRef CAS PubMed.
- P. Kolorenč and V. Averbukh, J. Chem. Phys., 2011, 135, 134314 CrossRef PubMed.
- P. Kolorenč and V. Averbukh, J. Chem. Phys., 2020, 152, 214107 CrossRef PubMed.
- M. H. Garner, R. Laplaza and C. Corminboeuf, Phys. Chem. Chem. Phys., 2022, 24, 26134–26143 RSC.
- M. H. Garner, R. Hoffmann, S. Rettrup and G. C. Solomon, ACS Cent. Sci., 2018, 4, 688–700 CrossRef CAS PubMed.
- M. H. Garner and C. Corminboeuf, Org. Lett., 2020, 22, 8028–8033 CrossRef CAS PubMed.
- M. H. Garner and C. Corminboeuf, Chem. Commun., 2021, 57, 6408–6411 RSC.
- P. Pinter and D. Munz, J. Phys. Chem. A, 2020, 124, 10100–10110 CrossRef CAS PubMed.
- Y. Orimoto, Y. Aoki and A. Imamura, J. Phys. Chem. C, 2019, 123, 11134–11139 CrossRef CAS.
- W. Bro-Jørgensen, M. H. Garner and G. C. Solomon, J. Phys. Chem. A, 2021, 125, 8107–8115 CrossRef PubMed.
- R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1–14 Search PubMed.
- A. Prlj, E. Marsili, L. Hutton, D. Hollas, D. Shchepanovska, D. R. Glowacki, P. Slavíček and B. F. Curchod, ACS Earth Space Chem., 2022, 6, 207–217 Search PubMed.
- R. R. Blyth, R. Delaunay, M. Zitnik, J. Krempasky, R. Krempaska, J. Slezak, K. C. Prince, R. Richter, M. Vondracek, R. Camilloni, L. Avaldi, M. Coreno, G. Stefani, C. Furlani, M. de Simone, S. Stranges and M. Y. Adam, J. Electron Spectrosc. Relat. Phenom., 1999, 101, 959–964 CrossRef.
- M. Tronc, G. C. King and F. H. Read, J. Phys. B: At. Mol. Phys., 1979, 12, 137–157 CrossRef CAS.
- V. Myrseth, J. D. Bozek, E. Kukk, L. J. Sathre and T. D. Thomas, J. Electron Spectrosc. Relat. Phenom., 2002, 122, 57–63 CrossRef CAS.
- G. Herzberg, Electronic spectra and electronic structure of polyatomic molecules, Van Nostrand, New York, 1966 Search PubMed.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. Janesko, R. Gomperts, B. Mennucci, H. Hratchian, J. Ortiz, A. Izmaylov, J. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. Montgomery, J. Peralta, F. Ogliaro, M. Bearpark, J. Heyd, E. Brothers, K. Kudin, V. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. Burant, S. Iyengar, J. Tomasi, M. Cossi, J. Millam, M. Klene, C. Adamo, R. Cammi, J. Ochterski, R. Martin, K. Morokuma, O. Farkas, J. Foresman and D. Fox, Gaussian 09, Revision A.02, 2016 Search PubMed.
- S. Y. Lee, R. C. Brown and E. J. Heller, J. Phys. Chem., 1983, 87, 2045–2053 CrossRef CAS.
- S. Y. Lee, J. Chem. Phys., 1998, 76, 3064 CrossRef.
- F. D. Sala, R. Rousseau, A. Görling and D. Marx, Phys. Rev. Lett., 2004, 92, 183401 CrossRef PubMed.
- P. C. D. Couto, D. Hollas and P. Slavíček, J. Chem. Theory Comput., 2015, 11, 3234–3244 CrossRef PubMed.
- W. Zeng, S. Gong, C. Zhong and C. Yang, J. Phys. Chem. C, 2019, 123, 10081–10086 CrossRef CAS.
- B. N. Frandsen, S. Farahani, E. Vogt, J. R. Lane and H. G. Kjaergaard, J. Phys. Chem. A, 2020, 124, 7047–7059 CrossRef CAS PubMed.
- C. Wiebeler, F. Plasser, G. J. Hedley, A. Ruseckas, I. D. Samuel and S. Schumacher, J. Phys. Chem. Lett., 2017, 8, 1086–1092 CrossRef CAS PubMed.
- Š. Sršeň, J. Sita, P. Slavíček, V. Ladányi and D. Heger, J. Chem. Theory Comput., 2020, 16, 6428–6438 CrossRef PubMed.
- M. Ončák, L. Šištík and P. Slavíček, J. Chem. Phys., 2010, 133, 174303 CrossRef PubMed.
- Z. Tóth, J. Kubečka, E. Muchová and P. Slavíček, Phys. Chem. Chem. Phys., 2020, 22, 10550–10560 RSC.
- D. Hollas, E. Muchová and P. Slavíček, J. Chem. Theory Comput., 2016, 12, 5009–5017 CrossRef CAS PubMed.
- M. N. Pohl, E. Muchová, R. Seidel, H. Ali, Š. Sršeň, I. Wilkinson, B. Winter and P. Slavíček, Chem. Sci., 2019, 10, 848–865 RSC.
- M. Ceriotti, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2009, 103, 030603 CrossRef PubMed.
- M. Ceriotti, G. Bussi and M. Parrinello, J. Chem. Theory Comput., 2010, 6, 1170–1180 CrossRef CAS.
- R. Broer and W. C. Nieuwpoort, THEOCHEM, 1998, 458, 19–25 CrossRef.
- P. A. Pieniazek, S. E. Bradforth and A. I. Krylov, J. Chem. Phys., 2008, 129, 074104 CrossRef PubMed.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1998, 101, 8938 CrossRef.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- D. S. Ranasinghe, J. T. Margraf, A. Perera and R. J. Bartlett, J. Chem. Phys., 2019, 150, 074108 CrossRef PubMed.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z. Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. D. Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P. T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. Hanson-Heine, P. H. Harbach, A. Hauser, M. F. Herbst, M. H. Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y. P. Li, J. Liang, M. Liebenthal, H. H. Lin, Y. S. Lin, F. Liu, K. Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S. P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. Menger, J. M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y. C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J. D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. Deprince, R. A. Distasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C. P. Hsu, T. C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. Thom, A. Tkatchenko, D. G. Truhlar, T. V. Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206 CrossRef CAS.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- R. Sarangi, M. L. Vidal, S. Coriani and A. I. Krylov, Mol. Phys., 2020, 118, e1769872 CrossRef.
- S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540 CrossRef CAS PubMed.
- S. Gozem and A. I. Krylov, The ezSpectra suite: An easy-to-use toolkit for spectroscopy modeling, 2021, https://iopenshell.usc.edu/downloads.
- M. Stener, G. Fronzoni and M. de Simone, Chem. Phys. Lett., 2003, 373, 115–123 CrossRef CAS.
- S. DeBeer George, T. Petrenko and F. Neese, Inorganica Chim. Acta, 2008, 361, 965–972 CrossRef CAS.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder, C. Song, A. V. Titov, I. S. Ufimtsev, L. P. Wang and T. J. Martínez, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1494 CAS.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef CAS PubMed.
- X. Li, X. Jia, A. S. P. Paz, Y. Cao and W. J. Glover, J. Am. Chem. Soc., 2022, 144, 19668–19672 CrossRef CAS PubMed.
- D. Bokhan, D. N. Trubnikov, A. Perera and R. J. Bartlett, Chem. Phys. Lett., 2018, 692, 191–195 CrossRef CAS.
- T. Kuś and A. I. Krylov, J. Chem. Phys., 2011, 135, 084109 CrossRef PubMed.
- M. Musial, A. Perera and R. J. Bartlett, J. Chem. Phys., 2011, 134, 114108 CrossRef PubMed.
- P. Baltzer, B. Wannberg, M. Lundqvist, L. Karlsson, D. M. P. Holland, M. A. MacDonald and W. von Niessen, Chem. Phys., 1995, 196, 551–567 CrossRef CAS.
- Z. Z. Yang, L. S. Wang, Y. T. Lee, D. A. Shirley, S. Y. Huang and W. A. Lester, Chem. Phys. Lett., 1990, 171, 9–13 CrossRef CAS.
- A. D. Bawagan, T. K. Ghanty, E. R. Davidson and K. H. Tan, Chem. Phys. Lett., 1998, 287, 61–69 CrossRef CAS.
- L. S. Cederbaum, W. Domcke and H. Köppel, Chem. Phys., 1978, 33, 319–326 CrossRef CAS.
- C. Woywod and W. Domcke, Chem. Phys., 1992, 162, 349–358 CrossRef CAS.
- S. Mahapatra, L. S. Cederbaum and H. Köppel, J. Chem. Phys., 1999, 111, 10452–10463 CrossRef CAS.
- D. M. P. Holland and D. A. Shaw, Chem. Phys., 1999, 243, 333–339 CrossRef CAS.
- S. Mahapatra, G. A. Worth, H. D. Meyer, L. S. Cederbaum and H. Köppel, J. Phys. Chem. A, 2001, 105, 5567–5576 CrossRef CAS.
- R. N. Sodhi and C. E. Brion, J. Electron Spectrosc. Relat. Phenom., 1985, 37, 1–21 CrossRef CAS.
- R. A. Ingle, A. Banerjee, C. Bacellar, T. R. Barillot, L. Longetti, M. Coreno, M. D. Simone, F. Zuccaro, L. Poletto, P. Miotti, A. Röder, A. Stolow, M. S. Schuurman, M. Odelius and M. Chergui, J. Phys. B: At., Mol. Opt. Phys., 2022, 55, 044001 CrossRef.
- O. Travnikova, PhD thesis, 2008.
- V. Schmidt, Electron Spectrometry of Atoms using Synchrotron Radiation, Cambridge University Press, 1997 Search PubMed.
- R. Forbes, S. T. Pratt, A. De Fanis, A. R. Milosavljević, C. Nicolas, J. D. Bozek, N. A. Besley and D. M. P. Holland, Phys. Rev. A, 2020, 101, 023408 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05299g |
| This journal is © the Owner Societies 2023 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: