Triel bonds within anion···anion complexes

Abstract

The ability of two anions to interact with one another is tested in the context of pairs of TrX₄⁻ homodimers, where Tr represents any of the triel atoms B, Al, Ga, In, or Tl, and X refers to a halogen substituent F, Cl, or Br. None of these pairs engage in a stable complex in the gas phase, but the situation reverses in water where the two monomers are held together by Tr⋯X triel bonds, complemented by stabilizing interactions between X atoms. Some of these bonds are quite strong, notably those involving TrF₄⁻, with interaction energies surpassing 30 kcal mol⁻¹. Others are very much weaker, with scarcely exothermic binding energies. The highly repulsive electrostatic interactions are counteracted by large polarization energies.

---

Introduction

Interest in noncovalent bonds is exemplified by the longstanding and continuing level of scientific interest in hydrogen bonding.^1,2 But noncovalent interactions are not limited only to this particular type, and the diversity and versatility of interactions other than hydrogen bonds represent an important ingredient in wide ranging and novel chemical phenomena,³ such as crystal engineering, catalysis, and biochemistry, just to name a few.^4–17 The triel bond (TrB) is a new and intriguing member of this group, which has been the subject of ongoing study.^18–23 Because the various Tr atoms are typically the center of a TrR₃ planar trigonal molecule, they frequently have associated with them a positive region of molecular electrostatic potential (MEP) situated directly above the Tr atom. This so-called π-hole, connected with an empty Tr p-orbital, is amplified by electron-withdrawing R substituents^23–31 and is able to attract a Lewis base so as to engage in a stable molecular complex.^21,32–39 The resulting triel bond can be rather strong and has been shown to be important in interaction with N-heterocyclic carbenes,⁴⁰ design of hydrogen storage materials,⁴¹ or play a catalytic role in organic and inorganic chemical reactions.^42–44 Very recently, borane complexes have been screened for possible biomolecular recognition abilities.⁴⁵

Ideas concerning the σ-hole predate the earliest discussions of the π-hole.^46–49 A σ-hole^24,28,29 is generated along the extension of a covalent bond axis. A classic example is the σ-hole that develops on the halogen X atom of a R–X unit, which leads to the formation of a R–X⋯Nuc halogen bond with a nucleophile. The usual trigonal planar arrangement of a TrR₃ molecule prevents the formation of a σ-hole within the molecular plane, which is why discussion of TrBs is usually limited to π-hole bonds. There are a few highly specialized circumstances in which a σ-hole, or something resembling it, can occur on a Tr atom,^50–52 usually in either a highly strained cyclic unit or an aromatic structure where the hole does not lie opposite another atom, so does not fit the usual definition of a σ-hole. The issue of σ-hole triel bonding is thus in its infancy at this point.

The description of the magnitude of σ-hole or π-hole-based interactions are typically derived from calculation of the interaction or bond energies. Alternatively, the strength of such contacts may be estimated by the NBO or QTAIM approach and predicted in some degree by the measuring of molecular electrostatic potential extrema located at the interacting units. However, it was recently demonstrated that the strength of many noncovalent interaction types (as halogen, tetrel or pnictogen bonding) can be also quantitatively measured in terms of vibrational spectroscopy parameters obtained through the local mode analysis^53–56 realized via LMODEA software.⁵⁷

Another forefront area in current research is the idea that a pair of anions might be able to interact with one another in an attractive fashion. Despite the obvious strong Coulombic repulsive forces obstructing such an attraction, there are a growing number of works which document via both experimental and computational evidence that complexes can be formed between anions in certain situations.^37,58–72 In the gas phase, these anion–anion complexes are usually metastable, in that their dissociation to a pair of anions is an exothermic process but one that is impeded by an energy barrier.^{37,58,59,61,66,71} Immersion of the system in a solvent, attenuates the electrostatic repulsions and typically allows a fully exothermic association process^{37,58,59,61,66,68} or a similar effect can occur if counterions are added to the system.⁶⁷ Similar trends have been reported in the case of H-bonded complexes between ions of like charge.^61–64,69 As an illustrative example, our own group recently showed that HgCl₃⁻ anions are stacked directly above one another in a crystal structure.⁶⁷ This anion–anion stabilization is held together by a π-hole spodium bond, and facilitated by crystal packing forces and counterions. The electrostatic repulsions were counteracted by exchange, and dispersion components, and especially by polarization. Similar conclusions pertained to other model anion⋯anion (MX₃⁻)₂ dimers (M = Zn, Cd, Hg; X = Cl, Br, I)⁶⁶ whose formation was exothermic when immersed in water or ethanol solvent. There still remains much to be learned as to the various forces involved in these anion-anion complexes, and what sorts of environments are needed to overcome the Coulombic repulsions.

The present work seeks to better understand this question of stabilizing anion–anion forces. There has as yet been no investigation of the ability of Tr atoms to participate in such anti-electrostatic complexes. In order to extend our understanding to triel bonds, a series of TrX₄⁻ units were examined (see Scheme 1), with regard to their possible interactions with one another within the context of homodimers. The full range of Tr atoms B, Al, Ga, In, and Tl were incorporated into these systems, as well as three different halogen X atoms F, Cl, and Br. As a particularly important aspect of this work, each TrX₄⁻ anion is tetrahedral, so the central Tr atom does not have the usual π-hole. Instead, there are four σ-holes, each along an extension of a Tr–X bond. This work thus encompasses the first study of σ-hole bonding by the triel family of atoms. A survey of the Cambridge Structural Database tells us how common such triel σ-hole anion–anion complexes might be, and provides some experimental contact to the calculations. Questions of particular interest include the sort of environment required for a pair of TrX₄⁻ anions to interact attractively with one another, and how strong might the triel bonds be. Can the interactions in fact be unambiguously attributed to triel bonds, and what might be the ancillary bonds that might emerge. How does the triel bond strength change as the central Tr atom is switched out for another, or as different X substituents are applied.

Scheme 1 Monomers considered in this work.

Computational methods

Full unconstrained optimization of isolated anions and complexes were performed at the MP2/aug-cc-pVDZ level of theory.^73–75 The aug-cc-pVDZ-PP basis set including effective core potentials was used for heavy triel atoms (In and Tl) in order to incorporate relativistic effects.^76,77 The B3LYP-D3/def2TZVPP^78–80 level of theory was used to more fully model the full crystal geometry (two anions and surroundings) of YORZEK⁸¹ as found in the Cambridge Structural Database (CSD, ver. 5.42) archives.⁸² It has been shown in the literature that this functional yield structures and cohesive energies, for a representative set of systems, including those with triel atoms.^83–88 Harmonic vibrational analysis verified true minima on the potential energy surfaces with all positive frequencies. Calculations were carried out in the gas phase and several other solvents including water, 1,2-ethane-diol, acetone, and dichlorethane using the PCM (polarizable continuum model) simulation.⁸⁹ The interaction energy (E_int) of each complex was evaluated as the difference in total electronic energy between the fully optimized complex and its subunits in the geometries adopted within the complex; the binding energy (E_b) takes as its reference fully optimized isomers. The basis set superposition error (BSSE) was removed via the counterpoise procedure introduced by Boys and Bernardi.⁹⁰ All calculations were carried out with the aid of the Gaussian 16, Rev. C.01 code.⁹¹ The MEP (molecular electrostatic potential) was evaluated on the 0.001 a.u. electronic isodensity contour via the MultiWFN program,^92,93 and visualized by VMD software.⁹⁴ The QTAIM (atoms-in-molecules)⁹⁵ and NCI^96,97 (noncovalent index) techniques were applied so as to display and quantify molecular diagrams regarding the topological properties by means of the AIMAll⁹⁸ and MultiWFN programs, respectively. Decomposition of the interaction energies in water solvent was carried out through the LMOEDA protocol⁹⁹ embedded in GAMESS-US (version 2020-R2) software¹⁰⁰ at MP2/aug-cc-pVDZ level. NBO analysis was conducted using the DFT generated wavefunction via the NBO 7.0 program.^101,102

Results

The salient components of the system of interest were extracted from the crystal structure and are displayed in Fig. 1. The two TlCl₄⁻ anions are disposed in such a way that a Cl atom of one anionic unit lies nearly along the extension of a Cl–Tl axis of the other, with a R(Tl⋯Cl) distance of some 3.641 Å. There is a mirror-image second interaction with the same dimensions involving the Tl of the other anion. These arrangements are closely parallel to what would be expected were there a pair of Tl⋯Cl triel bonds present, utilizing the σ-hole on each Tl atom. To probe this situation in a bit more depth, AIM analysis of the TlCl₄⁻ dimer supported the presence of these two triel bonds, with bond critical point densities of 0.007 a.u., adding also three Cl⋯Cl bond paths with a very similar density. NCI analysis buttressed this conclusion, as illustrated in Fig. S1 (ESI†). The CSD⁸² archives contain 6 similar crystal structures (see Fig S2 in ESI†) of TrX₄²⁻ dimer geometries. Among them, four contain an Al⋯Cl linkage, one Ga⋯Cl and one Tl⋯Br interaction. The triel bond distance varies between 3.562 and 3.727 Å.

Fig. 1 The original geometry of YORZEK crystalline solid.⁸¹

This idea that a pair of TrX₄⁻ anions can interact with one another in such a way as to form a pair of triel bonds was examined in a much broader sense, by considering five Tr atoms B, Al, Ga, In, and Tl. As halogen ligands, X = F, Cl, and Br were brought into the mix. The first step in the analysis is an examination of the molecular electrostatic potential (MEP) surrounding each anion monomer. This MEP was computed in both the gas phase and immersed in aqueous solvent. An example is displayed in Fig. 2 for TlCl₄⁻ in water. Since the moiety being probed is an anion, the MEP is of course negative throughout. But it is least negative along the extension of each Tr–X bond axis, as indicated by the red area in Fig. 2. V_s,max is defined as the maximal value of the MEP on the ρ = 0.001 a.u. isodensity surface, and is designated as a σ-hole, despite its negative sign.

Fig. 2 MEP of TlCl₄⁻ in water solvent. Color scale is −0.14 a.u. (blue) to −0.11 a.u. (red).

The maxima on these surfaces are listed in Table 1 for the various anions in both the gas phase and in aqueous solution. There seems to be little influence of solvent on the depth of these σ-holes. There are several principal trends in the data. For the lighter triel atoms, V_s,max becomes less negative as the X ligand changes from F to Cl to Br, but this trend reverses as the heavier Tr atoms display less sensitivity to the nature of X. For any given ligand, the σ-hole becomes less negative as the Tr atom grows in size, especially noticeable for X = F. Overall, the least negative σ-hole is associated with InCl₄⁻, and BF₄⁻ has the most negative.

Table 1 MEP maxima on isolated TrX₄⁻ anions (kcal mol⁻¹)

Anion	Gas	Water
BF4^−	−116.2	−116.3
AlF4^−	−85.4	−85.6
GaF4^−	−78.8	−78.5
InF4^−	−57.9	−55.5
TlF4^−	−62.1	−59.4
BCl4^−	−82.7	−81.7
AlCl4^−	−80.4	−81.0
GaCl4^−	−79.0	−79.8
InCl4^−	−61.6	−62.2
TlCl4^−	−63.2	−63.4
BBr4^−	−73.7	−72.3
AlBr4^−	−73.7	−72.7
GaBr4^−	−72.6	−71.5
InBr4^−	−63.0	−64.7
TlBr4^−	−64.2	−65.7

---

Dimers

In the gas phase, only three of the anions are able to form a homodimer that represents a minimum on the potential energy surface. Three fluorinated systems (TrF₄)⁻₂ where Tr is one of the three heaviest atoms Ga, In, and Tl, are metastable minima with positive interaction energies of 37, 15, and 22 kcal mol⁻¹, respectively. It is only when immersed in water that all of the anions engage in stable homodimers. Most of these structures are symmetric with two equivalent (TrX₄)⁻ units and both intermolecular R(Tr⋯X) distances equal to one another. These bond lengths are contained in Table 2 where they are compared with the sum of their vdW radii in the last column. There is a good deal of variety in this comparison. With the exception of BF₄⁻, the fluorinated dimers have very short distances, just barely longer than 2 Å. This distance is much shorter than the vdW sum, and only slightly longer than the sum of covalent radii. Those systems containing Cl and Br are quite different. Whereas the R(Tr⋯X) distance exceeds the vdW sum for the lighter Tr atoms, it is considerably shorter than this point of comparison for In and Tl.

Table 2 Triel bond distances (Å) in anion⋯anion homodimers in water

Constituents	R(Tr⋯X)	vdW radii sum^136
a Dimers with R(Tr⋯X) longer than sum of corresponding vdW radii.
BF4^−	4.047/4.060^a	3.37
AlF4^−	2.026	3.71 (cov: 1.78)
GaF4^−	2.093	3.78 (cov: 1.79)
InF4^−	2.187	3.89 (cov: 1.99)
TlF4^−	2.259	3.93 (cov: 2.02)
BCl4^−	4.481/4.500^a	3.73
AlCl4^−	4.414/4.421^a	4.07
GaCl4^−	4.350/4.377^a	4.14
InCl4^−	3.033/3.036	4.25
TlCl4^−	3.249/3.234	4.29
BBr4^−	4.274^a	3.77
AlBr4^−	4.355/4.358^a	4.11
GaBr4^−	4.312/4.349^a	4.18
InBr4^−	3.934/3.941	4.29
TlBr4^−	3.722/3.718	4.33

---

The energetics of these complexes reflect many of the trends observed in the distances. As reported in Table 3, the interaction energies of the fluorinated dimers (again with the exception of BF₄) are quite negative, commensurate with their short bond lengths that approach covalent values. This exothermicity is tempered when the monomer deformation energies are factored in, so that the binding energies in the last column are somewhat less negative, some even slightly positive after counterpoise correction. The interaction energies of the chlorinated and brominated dimers are consistent with bond lengths: these quantities are more negative for the heavier Tr atoms. Note however, that negative interaction and binding energies are achieved even for the smaller Tr atoms for which the intermolecular distance exceeded the vdW sum. With respect to comparison between different halogen ligands, the brominated dimers are more stable than X = Cl for the lighter Tr, but this pattern reverses for In and Tl. Of course, correlations between bond length and strength are not perfect¹⁰³ but the former does serve as a useful indicator of the latter in most cases.

Table 3 Interaction and binding energies (kcal mol⁻¹) of anion⋯anion homodimers in water

Constituents	E int	E b
a Energies corrected by BSSE in parentheses.
BF4^−	−0.22 (0.66)^a	−0.23 (0.65)
AlF4^−	−27.66 (−23.22)	−0.64 (3.80)
GaF4^−	−28.79 (−21.20)	−7.24 (0.34)
InF4^−	−39.66 (−33.65)	−22.04 (−16.03)
TlF4^−	−34.68 (−26.57)	−20.48 (−12.37)
BCl4^−	−1.96 (−0.77)	−1.96 (−0.77)
AlCl4^−	−2.58 (−0.83)	−2.55 (−0.80)
GaCl4^−	−2.87 (−0.89)	−2.83 (−0.85)
InCl4^−	−11.31 (−5.28)	−4.41 (1.62)
TlCl4^−	−9.08 (−3.03)	−5.80 (0.25)
BBr4^−	−2.63 (−0.50)	−2.61 (−0.48)
AlBr4^−	−4.43 (−0.89)	−4.34 (−0.80)
GaBr4^−	−4.84 (−1.04)	−4.73 (−0.93)
InBr4^−	−6.06 (−2.52)	−5.37 (−0.64)
TlBr4^−	−7.79 (−1.69)	−6.47 (−0.37)

---

Nature of bonding

AIM analysis of these various dimers leads to some intriguing findings. As may be seen in Fig. S3 (ESI†), the molecular diagrams suggest not only Tr⋯X bond paths, but also X⋯X paths between atoms on different subunits. In fact, in several of these dimers, particularly the weak ones, it is only the latter sort of bond path that appears. More specifically, AIM shows only X⋯X bond paths in the dimers where Tr = B, combinations of Al or Ga with Cl and Br, and In combined with Br. In short, there are triel bond paths only for the more strongly bound dimers, with interaction energy greater than 6 kcal mol⁻¹. Two of these molecular diagrams are presented in Fig. 3 for (GaCl₄⁻)₂ and (InCl₄⁻)₂ as an illustration of the different sorts of noncovalent interactions.

Fig. 3 AIM molecular diagrams of (a) (GaCl₄⁻)₂ and (b) (InCl₄⁻)₂. Numbers on bond paths refer to the density at the bond critical point.

Fig. 4 Three views of NCI diagram of (a) (GaCl₄⁻)₂ and (b) (InCl₄⁻)₂. Colors represent various type of interaction: blue – strong noncovalent interactions, green – interaction of average strength, brown – very weak interactions, red – repulsion. Black arrows point to the green regions corresponding to the attractive interaction between the triel atom and the chlorine from the other subsystem. The interactions between the chlorine atoms correspond to the orange arrows.

The salient characteristics of the bond paths are collected in Table 4, for those complexes in which there is a Tr⋯X bond path present. (Of course, there are actually two of these bonds present due to the molecular symmetry). The other sort of bond path reported in Table 4 is the strongest of the X⋯X bonds, that between the two X atoms that are involved in the triel bond. According to the AIM analysis, the latter X⋯X bond cannot be ignored as some of its properties are comparable to those of the dominant Tr⋯X triel bonds. Focusing on the triel bonds, the density tends to grow as the Tr bond becomes stronger. Its Laplacian is positive, and also shows larger values for the triel bonds than for the X⋯X interactions. Coupled with the very small values of the energy density H, these bonds can be comfortably characterized as noncovalent bonds. The reader should be aware that there are instances in the literature wherein AIM interpretation of noncovalent bonding can be problematic.^104,105

Table 4 AIM properties (a.u.) of homodimers in water for which a triel bond path is present

Bond	ρ	∇^2ρ	H
AlF4^−
Al⋯F	0.033	0.258	0.006
F⋯F	0.039	0.161	−0.005
GaF4^−
Ga⋯F	0.049	0.245	−0.009
F⋯F	0.032	0.132	−0.004
InF4^−
In⋯F	0.056	0.322	−0.001
F⋯F	0.025	0.099	−0.002
TlF4^−
Tl⋯F	0.058	0.308	−0.002
InCl4^−
In⋯Cl	0.017	0.056	0.001
Cl⋯Cl	0.013	0.038	0.001
TlCl4^−
Tl⋯Cl	0.014	0.044	0.001
Cl⋯Cl	0.010	0.029	0.001
TlBr4^−
Tl⋯Br	0.007	0.021	0.001
Br⋯Br	0.007	0.019	0.000

---

NCI represents an alternate pictorial means of analyzing the topology of the electron density. Specific noncovalent interactions between subsystems are indicated by arrows as indicated in Fig. 4. Black arrows point to green regions corresponding to the attractive interaction between the triel atom and the Cl from the partner subsystem. Interactions between Cl atoms are indicated by the orange arrows. There are arrows of both colors present in both (GaCl₄⁻)₂ and (InCl₄⁻)₂, suggesting both systems contain noncovalent bonds of both types. A point of disagreement with AIM arises in that AIM did not suggest a triel bond between the Tr and Cl atoms in the (GaCl₄⁻)₂ complex, NCI does predict such an attraction. As a secondary issue, NCI detects more Cl⋯Cl interactions than does AIM in the case of (InCl₄⁻)₂.

NBO offers a somewhat different perspective on the binding in these complexes. The (GaCl₄⁻)₂ and (InCl₄⁻)₂ dimers again offer an illuminating view of these two viewpoints. According to AIM, the only interactions within the former structure are six bonds between Cl atoms on the two subunits, albeit only weak ones with ρ_BCP equal to 0.003 a.u. or less. (InCl₄⁻)₂, on the other hand, is viewed by AIM as containing a pair of In⋯Cl interactions with density 0.017 a.u., with a supplement arising from one Cl⋯Cl pair of 0.013 a.u. The results of NBO analysis of (GaCl₄⁻)₂ are presented in Fig. 5a and b in the form of the orbitals that interact with one another with appreciable values of second-order perturbation energy E(2). The primary interaction, with E(2) = 0.6 kcal mol⁻¹, involves the lone pair of one Cl atom of the upper molecule and the antibonding σ*(GaCl) of its partner in Fig. 5a. It is the Cl atom that lies directly opposite the donor Cl lone pair which is involved in this transfer. This sort of diagram is typical of triel and related noncovalent bonds so offers evidence of a triel bond in this dimer, contrary to the AIM view. The only other interactions in this complex transfer charge from the same Cl lone pair to each of the three other σ*(GaCl) orbitals, one of which is illustrated in Fig. 5b, but E(2) for these transfers are much smaller, only 0.10–0.13 kcal mol⁻¹. (It should be mentioned here that the symmetry of these complexes leads to a mirror image picture of the interactions where it is the lone pair of the lower molecule transferring charge to the antibonding orbitals of the upper one.).

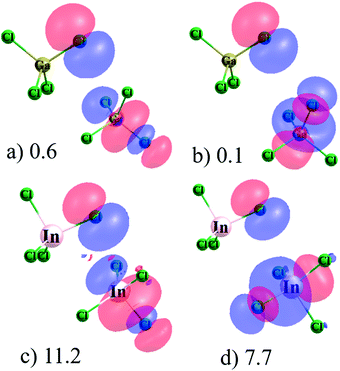Fig. 5 View of interacting NBO localized orbitals in (a) and (b) (GaCl₄⁻)₂ and (c) and (d) (InCl₄⁻)₂.

Turning next to the (InCl₄⁻)₂ complex, there are much stronger inter-orbital interactions as pictured in Fig. 5c and d. As in the (InCl₄⁻)₂ case, the Cl lone pair of the upper molecule is the source of the transfer in all these pairs. The acceptor orbitals are again σ*(InCl), with the highest degree of transfer involving that Cl which lies opposite the Cl donor in Fig. 5c, with E(2) amounting to 11.2 kcal mol⁻¹. E(2) for the other three σ*(InCl) orbitals, one of which is pictured in Fig. 5d, range between 6.5 and 7.7 kcal mol⁻¹. This entire picture of NBO orbitals involved in these transfers in either the Ga or In systems is entirely consistent with a typical triel or other related noncovalent bond, so the NBO interpretation of these complexes, both weak and strong, would be that of a triel bond.

Another window into the nature of the bonding in these dimers is derived from electron density shifts that accompany the complexation. Maps of these shifts in three dimensions are computed by subtracting the sum of the densities of the two unperturbed monomers from that of the full dimer, with all atoms fixed in their dimer positions. The purple regions in Fig. 6 denote increases in density that arise as the two monomers interact with one another, and losses are shown in green. Due to the much closer contact within the (InCl₄⁻)₂ dimer, the shifts are of greater intensity than they are in (GaCl₄⁻)₂. In order then to compare the density shifts on a more equal footing, the contours for (GaCl₄⁻)₂ in Fig. 6a represent a density change of 0.0006 a.u. as compared to the larger 0.0015 a.u. contours in Fig. 6b.

Fig. 6 Electron density difference maps caused by dimerization of (a) (GaCl₄⁻)₂ and (b) (InCl₄⁻)₂. Purple and green regions respectively denote gain and loss of density. Contour shown in (a) is 0.0006 a.u. and that in (b) is 0.0015 a.u.

There are fundamental differences between the patterns for the two dimers. The changes within (GaCl₄⁻)₂ indicate nearly equal polarizations of each of the three Cl atoms on each monomer that are oriented toward the partner. These polarizations from green to purple shift density away from the partner. The fourth Cl atom accrues a bit of additional density, indicated by the surrounding purple regions. There is very little charge motion that involves the Ga atoms, nor the region between them and the Cl atoms on the neighboring subunit. This pattern is consistent with the AIM diagnosis of weak interactions between neighboring Cl atoms, with no Tr atom involvement.

The shifts within (InCl₄⁻)₂ in Fig. 6b are quite different. There are both gains and losses in the intermolecular region. There is a clear loss/gain pattern along the In⋯Cl path which is characteristic of triel and other noncovalent bonds. There is also a sizable green region of density loss at the center of the system, coupled with gains along the Cl⋯Cl axis, which may be symptomatic of the Cl⋯Cl bonding interaction that is flagged by the AIM diagram. All in all, these density shift patterns are consistent with the AIM version of the bonding in these two complexes.

The individual components of decomposition of the total interaction energy of the chloride cases are collected in Table 5. The trends appear to break down into two overarching categories. The first three dimers listed are the weakest of the five. A second distinguishing feature is that there is no AIM Tr⋯Cl triel bond path in these weaker complexes, while such a path is present in the other two. The interaction energy in the three weakly bound dimers are completely dominated by polarization which accounts for 95% of the total attractive energy. While polarization is also important for the two stronger complexes, its contribution drops a bit to 74–78%, as exchange vastly raises its contribution from 4 to 35–50 kcal mol⁻¹. On a percentage basis, this enhancement brings the exchange component up to roughly 20%, and dispersion ramps up to about 5%. It might also be noted that the electrostatic component is highly repulsive in all cases, and must be overcome by the other factors. While factors such as geometry relaxation and electron density reorganization can at times complicate the interpretation of individual components of the total interaction energy,^104–107 they nonetheless offer a valuable window into the sources of stability. Similar caveats apply to the MEP since it is most apt when species are some distance apart, and interactions between potentials do not include the kinetic aspects of the interaction.

Table 5 LMOEDA/MP2/aug-cc-pVDZ decomposition of the interaction energy (E_int) of studied complexes into electrostatic (E_es), exchange (E_ex), repulsion (E_rep), polarization (E_pol) and dispersion (E_disp) components. All quantities in kcal mol⁻¹

	E es	E ex	%	E rep	E pol	%	E disp	%	E int
BCl4^−⋯BCl4^−	157.5	−3.24	2	4.60	−156.6	96	−3.01	2	−0.75
AlCl4^−⋯AlCl4^−	147.2	−3.52	2	5.34	−147.4	95	−4.20	3	−2.58
GaCl4^−⋯GaCl4^−	146.5	−4.31	3	6.29	−146.1	95	−3.45	2	−1.07
InCl4^−⋯InCl4^−	125.6	−49.2	22	86.6	−161.0	74	−8.50	4	−6.5
TlCl4^−⋯TlCl4^−	133.1	−34.6	18	59.3	−153.7	78	−9.40	5	−5.3

---

Environmental effects

The forgoing data were focused on either the in vacuo situation, or when the systems are placed in the very high dielectric solvent water. These two scenarios represent two extremes on a continuum. Many environments in which these systems might find themselves, especially in a crystal, represent some intermediate situation. In order to examine how other environments might affect these systems, (TlCl₄⁻)₂ was taken as a prototype dimer, and its properties calculated in the situations listed in Table 6. When immersed in water, the optimized distance is 3.24 Å, at which point the interaction energy is −3.03 kcal mol⁻¹. When the monomer deformations are added, the binding energy becomes slightly positive. As the solvent becomes less polar, i.e. as ε drops down to 40 and then 20, the interaction energy rises in magnitude to −10 kcal mol⁻¹, although E_b remains slightly endothermic. For less polar solvent, in this case dichloroethane with ε = 10, the dimer is no longer able to form a stable complex. A single point calculation of the dimer in the geometry it adopts within the crystal is highly endothermic, and does not even represent a true minimum. The last row of Table 6 considers the environment not as a surrounding polarizable continuum, but rather as a pair of C₅H₆N⁺ pyridinium cations, positioned just as they are in the crystal. With these two counterions present, the interaction energy between the pair of (TlCl₄⁻)⋯pyr⁺ units becomes negative, albeit only slightly so. This result suggests that the presence of the counterions are a crucial factor in the ability of the two anions to engage with one another.

Table 6 Calculated intermolecular distance and energetics (kcal mol⁻¹) of the (TlCl₄⁻)₂ system in various environments

Environment	ε	R(Tr⋯Cl), Å	E int	E b
a System is not converged. b Not optimized.
Water	78	3.234/3.249	−3.03	0.25
1,2-Ethane-diol	40	3.257/3.230	−10.20	0.92
Acetone	20	3.275/3.263	−9.20	1.97
Dichloroethane	10	—^a	—	—
Gas phase (in geometry of crystal)	1	3.641^b	+48.00	—
Gas phase (in geometry of crystal) with two counterions	1	3.641^b	−0.58	—

---

Summary and discussion

The Coulombic repulsion between the two anions overwhelms any attractive force in the gas phase. However, the attenuation of these repulsions by placement of the system within a dielectric continuum enables the noncovalent bonds to form, leading to stable dimers. The most strongly bound involve TrF₄⁻ dimers where Tr is Al, Ga, In, or Tl, and interaction energies are greater than 20 kcal mol⁻¹. Binding energies which include monomer deformations are less exothermic, some even slightly positive. BF₄⁻ dimer, in contrast, is barely bound at all. Within the group of chlorinated systems InCl₄⁻ and TlCl₄⁻ are more strongly bound 3–5 (kcal mol⁻¹) than are those of the lighter Tr atoms, less than 1 kcal mol⁻¹. With respect to X = Br, the interaction energies of the TrBr₄⁻ dimers, range between 0.5 and 2.5 kcal mol⁻¹.

As for the sorts of noncovalent bonds that are present, there is some disagreement amongst the analyses that rest on electron density topology and the NBO treatment of interorbital transfers. AIM bond paths are not present between the Tr of one monomer and X on its partner in all cases. Triel bond paths are present only for the more strongly bound dimers, with interaction energy greater than 6 kcal mol⁻¹. Other AIM bond paths suggest intermolecular X⋯X bonds, for most but not all of the dimers. NCI analysis indicates both Tr⋯X and X⋯X bonds are present. The NBO interorbital second-order perturbation energies are consistent with the presence of a triel bond in these dimers, whereas maps of electron density shifts are more consistent with the AIM interpretation.

The observed patterns of anion⋯anion interactions observed here are consistent with prior work involving related systems. The overall conclusion from many of these studies is that formation of a complex may be possible in the gas phase, but the dimer is typically only metastable with respect to dissociation to a pair of anions. The situation changes in solution where the dimer represents a thermodynamically stable minimum. H-bonded complexes constitute the largest subset of these sorts of systems^63,108–122 but the categories continue to grow. The number of halogen-bonded dimers between pairs of anions is rising,^72,123–129 augmented recently by pnicogen bonds.¹³⁰ Another category places a metal atom at the center of each anion,^131–133 whether alkaline earth metal or the Zn family. Inert gas atoms too can involve themselves in anion⋯anion interactions as when AeX₅⁻ (Ae = Kr, Xe) binds to a small anion.¹³⁴

In terms of overall stability, some of these complexes are fairly tightly bound. In aqueous solution the binding energy of CN⁻ with the various MCl₃⁻ anions, where M is a group 2A atom ranges up to 20 kcal mol^−1 131 and lies in a similar range for 2B atoms Zn, Cd, or Hg.¹³² Pnicogen bonds between anions are even stronger, more than 20 kcal mol⁻¹ for the ZCl₄⁻ series, with Z = P, As or Sb.¹³⁰ Interaction energies are quite a bit smaller, less than 2 kcal mol⁻¹, when any of several small anions engages in an aerogen bond with AeX₅⁻.¹³⁴ Of particular relevance to the systems examined here, when TrCl₄⁻ interacts with CN⁻ in water, the interaction energy approaches 50 kcal mol⁻¹.¹³⁵

Turning away from highly compact anions like CN⁻ anion, to a pair of MX₃⁻ units where M is a member of the Zn family, interaction energies lie in the 2–8 kcal mol⁻¹ range, again in water.⁶⁶ These quantities are similar to those computed here for the TrX₄⁻ anions, with the exceptions of some of the more strongly bound TrF₄⁻ homodimers. With respect to the electrostatic component of these dimerizations, E_es is large and positive, highly repulsive, much like the aforementioned ZnX₃⁻ spodium-bonded dimers.⁶⁶

Evidence of anion⋯anion interactions based on the σ-hole which is considered in the current work may stimulate further studies of new supramolecular dianionic synthons of similar architecture and stabilization scheme. It is anticipated that these ideas may find application in crystal engineering or materials chemistry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financed in part by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology and by the US National Science Foundation under Grant No. 1954310. A generous allotment of computer time from the Wroclaw Supercomputer and Networking Center is acknowledged.

References

1. S. Scheiner, Struct. Chem., 2019, 30, 1119–1128.
2. S. Scheiner, J. Indian Inst. Sci., 2020, 100, 61–76.
3. I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180.
4. C. Zhou, Y. Tian, M. Wang, A. Rose, T. Besara, N. K. Doyle, Z. Yuan, J. C. Wang, R. Clark, Y. Hu, T. Siegrist, S. Lin and B. Ma, Angew. Chem., Int. Ed., 2017, 56, 9018–9022.
5. M. Brynda, M. Geoffroy and G. Bernardinelli, Chem. Commun., 1999, 961–962,  10.1039/a901083a.
6. P. Vermeeren, T. A. Hamlin, F. M. Bickelhaupt and I. Fernandez, Chem. – Eur. J., 2021, 27, 5180–5190.
7. T. A. Hamlin, F. M. Bickelhaupt and I. Fernandez, Acc. Chem. Res., 2021, 54, 1972–1981.
8. R. M. Gomila and A. Frontera, Front. Chem., 2020, 8, 395.
9. A. Gini, M. Paraja, B. Galmes, C. Besnard, A. I. Poblador-Bahamonde, N. Sakai, A. Frontera and S. Matile, Chem. Sci., 2020, 11, 7086–7091.
10. K. T. Mahmudov, M. N. Kopylovich, M. F. C. Guedes da Silva and A. J. L. Pombeiro, Dalton Trans., 2017, 46, 10121–10138.
11. D. Bulfield and S. M. Huber, Chem. – Eur. J., 2016, 22, 14434–14450.
12. A. Frontera and A. Bauzá, Org. Biomol. Chem., 2021, 19, 6858–6864.
13. J. A. Fernández Riveras, A. Frontera and A. Bauzá, Phys. Chem. Chem. Phys., 2021, 23, 17656–17662.
14. M. D. N. Pina, A. Frontera and A. Bauza, ACS Chem. Biol., 2020, 15, 1942–1948.
15. M. D. Pina, A. Frontera and A. Bauz, J. Phys. Chem. Lett., 2020, 11, 8259–8263.
16. M. K. Bhattacharyya, U. Saha, D. Dutta, A. Frontera, A. K. Verma, P. Sharma and A. Das, New J. Chem., 2020, 44, 4504–4518.
17. P. Scilabra, G. Terraneo and G. Resnati, Acc. Chem. Res., 2019, 52, 1313–1324.
18. S. J. Grabowski, ChemPhysChem, 2014, 15, 2985–2993.
19. S. J. Grabowski, J. Comput. Chem., 2018, 39, 472–480.
20. S. J. Grabowski, Struct. Chem., 2017, 28, 1163–1171.
21. S. J. Grabowski, ChemPhysChem, 2015, 16, 1470–1479.
22. S. J. Grabowski, Molecules, 2015, 20, 11297–11316.
23. S. J. Grabowski, ChemPhysChem, 2015, 16, 1470–1479.
24. P. Politzer and J. S. Murray, J. Comput. Chem., 2018, 39, 464–471.
25. A. Bauza, A. Frontera and T. J. Mooibroek, Cryst. Growth Des., 2016, 16, 5520–5524.
26. A. Bauza and A. Frontera, Phys. Chem. Chem. Phys., 2015, 17, 24748–24753.
27. J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548.
28. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2021, 23, 16458–16468.
29. A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517.
30. A. Bauza, T. J. Mooibroek and A. Frontera, Chem. Commun., 2015, 51, 1491–1493.
31. P. Politzer and J. S. Murray, Theor. Chem. Acc., 2021, 140, 7.
32. W. Zierkiewicz, M. Michalczyk and S. Scheiner, Molecules, 2020, 25, 635.
33. S. J. Grabowski, Coord. Chem. Rev., 2020, 407, 213171.
34. T. A. Ford, J. Mol. Struct., 2020, 1210, 128020.
35. M. D. Esrafili and P. Mousavian, Mol. Phys., 2018, 116, 388–398.
36. Q. Yang, Q. Li and S. Scheiner, ChemPhysChem, 2021, 22, 1461–1469.
37. R. Wysokinski, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 4818–4828.
38. R. Wang, C. Luo, Q. Li and S. Scheiner, Int. J. Quantum Chem., 2021, 121, e26526.
39. A. Bauza and A. Frontera, ChemPhysChem, 2016, 17, 3181–3186.
40. Z. Chi, W. Dong, Q. Li, X. Yang, S. Scheiner and S. Liu, Int. J. Quantum Chem., 2019, 119, e25867.
41. C. W. Hamilton, R. T. Baker, A. Staubitz and I. Manners, Chem. Soc. Rev., 2009, 38, 279–293.
42. S. Bhunya, T. Malakar, G. Ganguly and A. Paul, ACS Catal., 2016, 6, 7907–7934.
43. J. P. Mancinelli and S. M. Wilkerson-Hill, ACS Catal., 2020, 10, 11171–11176.
44. K. T. Mahmudov, A. V. Gurbanov, F. I. Guseinov and M. F. C. G. da Silva, Coord. Chem. Rev., 2019, 387, 32–46.
45. D. B. Diaz and A. K. Yudin, Nat. Chem., 2017, 9, 731–742.
46. P. Politzer, P. Lane, M. C. Concha, Y. G. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311.
47. J. S. Murray, P. Lane and P. Politzer, Int. J. Quantum Chem., 2007, 107, 2286–2292.
48. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
49. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
50. M. D. Esrafili and P. Mousavian, Chem. Phys. Lett., 2017, 678, 275–282.
51. L. Gao, Y. Zeng, X. Zhang and L. Meng, J. Comput. Chem., 2016, 37, 1321–1327.
52. Q. Q. Yang, B. H. Zhou, Q. Z. Li and S. Scheiner, ChemPhysChem, 2021, 22, 481–487.
53. D. Setiawan, E. Kraka and D. Cremer, J. Phys. Chem. A, 2015, 119, 1642–1656.
54. V. Oliveira and E. Kraka, J. Phys. Chem. A, 2017, 121, 9544–9556.
55. V. Oliveira, E. Kraka and D. Cremer, Inorg. Chem., 2017, 56, 488–502.
56. D. Sethio, V. Oliveira and E. Kraka, Molecules, 2018, 23, 2763.
57. E. Kraka, W. Zou and Y. Tao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1480.
58. W. Zierkiewicz, R. Wysokinski, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
59. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
60. O. Mo, M. M. Montero-Campillo, M. Yanez, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2020, 124, 1515–1521.
61. M. O. Miranda, D. J. R. Duarte and I. Alkorta, ChemPhysChem, 2020, 21, 1052–1059.
62. L. M. Azofra, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2020, 124, 2207–2214.
63. L. M. Azofra, J. Elguero and I. Alkorta, Phys. Chem. Chem. Phys., 2020, 22, 11348–11353.
64. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2015, 119, 183–194.
65. G. Blanger-Chabot and H. Braunschweig, Angew. Chem., Int. Ed., 2019, 58, 14270–14274.
66. R. Wysokiński, W. Zierkiewicz, M. Michalczyk and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 13853–13861.
67. R. Wysokinski, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2021, 22, 818–821.
68. A. Grabarz, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Molecules, 2021, 26, 2116.
69. A. S. R. Chesman, J. L. Hodgson, E. I. Izgorodina, A. Urbatsch, D. R. Turner, G. B. Deacon and S. R. Batten, Cryst. Growth Des., 2014, 14, 1922–1932.
70. R. Prohens, A. Portell, M. Font-Bardia, A. Bauza and A. Frontera, Chem. Commun., 2018, 54, 1841–1844.
71. D. Quinonero, I. Alkorta and J. Elguero, ChemPhysChem, 2020, 21, 1597–1607.
72. D. Quinonero, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2016, 18, 27939–27950.
73. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
74. C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 0618–0622.
75. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
76. K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
77. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
78. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
79. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
80. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
81. B. D. James, M. B. Millikan, B. W. Skelton and A. H. White, Main Group Met. Chem., 1993, 16, 335.
82. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
83. A. N. Alexandrova, K. A. Birch and A. I. Boldyrev, J. Am. Chem. Soc., 2003, 125, 10786–10787.
84. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410.
85. T. R. Galeev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2011, 13, 21655–21656.
86. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
87. A. P. Sergeeva, Z. A. Piazza, C. Romanescu, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 18065–18073.
88. D. Y. Zhao, Y. S. Li, M. Y. Xu, Z. M. Li, H. Zhang and L. Yu, J. Mol. Liq., 2021, 343, 117528.
89. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
90. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
91. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016.
92. T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323.
93. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
94. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38.
95. R. Bader, Atoms In Molecules. A Quantum Theory, Clarendon Press, Oxford, 1990.
96. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
97. P. de Silva and C. Corminboeuf, J. Chem. Theory Comput., 2014, 10, 3745–3756.
98. A. T. Keith, AIMAll (Version 14.11.23), TK Gristmill Software, Overland Park KS, USA, 2014.
99. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
100. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102.
101. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
102. F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440.
103. M. Kaupp, B. Metz and H. Stoll, Angew. Chem., Int. Ed., 2000, 39, 4607–4609.
104. M. Jabłoński, J. Comput. Chem., 2018, 39, 2183–2195.
105. C. R. Wick and T. Clark, J. Mol. Model., 2018, 24, 142.
106. C. Dieter and K. Elfi, Curr. Org. Chem., 2010, 14, 1524–1560.
107. J. Andrés, P. W. Ayers, R. A. Boto, R. Carbó-Dorca, H. Chermette, J. Cioslowski, J. Contreras-García, D. L. Cooper, G. Frenking, C. Gatti, F. Heidar-Zadeh, L. Joubert, Á. Martín Pendás, E. Matito, I. Mayer, A. J. Misquitta, Y. Mo, J. Pilmé, P. L. A. Popelier, M. Rahm, E. Ramos-Cordoba, P. Salvador, W. H. E. Schwarz, S. Shahbazian, B. Silvi, M. Solà, K. Szalewicz, V. Tognetti, F. Weinhold and É.-L. Zins, J. Comput. Chem., 2019, 40, 2248–2283.
108. S. R. Kass, J. Am. Chem. Soc., 2005, 127, 13098–13099.
109. I. Mata, I. Alkorta, E. Molins and E. Espinosa, ChemPhysChem, 2012, 13, 1421–1424.
110. I. Mata, I. Alkorta, E. Molins and E. Espinosa, Chem. Phys. Lett., 2013, 555, 106–109.
111. I. Mata, E. Molins, I. Alkorta and E. Espinosa, J. Phys. Chem. A, 2014, 119, 183–194.
112. F. Weinhold and R. A. Klein, Angew. Chem., Int. Ed., 2014, 53, 11214–11217.
113. G. Frenking and G. F. Caramori, Angew. Chem., Int. Ed., 2015, 54, 2596–2599.
114. I. Alkorta, I. Mata, E. Molins and E. Espinosa, Chem. – Eur. J., 2016, 22, 9226–9234.
115. E. M. Fatila, E. B. Twum, A. Sengupta, M. Pink, J. A. Karty, K. Raghavachari and A. H. Flood, Angew. Chem., Int. Ed., 2016, 55, 14057–14062.
116. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
117. F. Weinhold, Inorg. Chem., 2018, 57, 2035–2044.
118. R. Barbas, R. Prohens, A. Bauzá, A. Franconetti and A. Frontera, Chem. Commun., 2019, 55, 115–118.
119. D. A. Cullen, M. G. Gardiner and N. G. White, Chem. Commun., 2019, 55, 12020–12023.
120. N. G. White, CrystEngComm, 2019, 21, 4855–4858.
121. W. Zhao, B. Qiao, J. Tropp, M. Pink, J. D. Azoulay and A. H. Flood, J. Am. Chem. Soc., 2019, 141, 4980–4989.
122. L. M. Azofra, J. Elguero and I. Alkorta, J. Phys. Chem. A, 2020, 124, 2207–2214.
123. G. Wang, Z. Chen, Z. Xu, J. Wang, Y. Yang, T. Cai, J. Shi and W. Zhu, J. Phys. Chem. B, 2016, 120, 610–620.
124. C. Wang, Y. Fu, L. Zhang, D. Danovich, S. Shaik and Y. Mo, J. Comput. Chem., 2018, 39, 481–487.
125. Z. Zhu, G. Wang, Z. Xu, Z. Chen, J. Wang, J. Shi and W. Zhu, Phys. Chem. Chem. Phys., 2019, 21, 15106–15119.
126. J. M. Holthoff, E. Engelage, R. Weiss and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 11150–11157.
127. T. Maxson, A. S. Jalilov, M. Zeller and S. V. Rosokha, Angew. Chem., Int. Ed., 2020, 59, 17197–17201.
128. K. Ghosh, A. Frontera and S. Chattopadhyay, CrystEngComm, 2021, 23, 1429–1438.
129. Y. Li, L. Meng and Y. Zeng, ChemPlusChem, 2021, 86, 232–240.
130. S. Scheiner, R. Wysokiński, M. Michalczyk and W. Zierkiewicz, J. Phys. Chem. A, 2020, 124, 4998–5006.
131. W. Zierkiewicz, R. Wysokiński, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 870–877.
132. R. Wysokiński, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2020, 21, 1119–1125.
133. R. Wysokiński, W. Zierkiewicz, M. Michalczyk and S. Scheiner, ChemPhysChem, 2021, 22, 818–821.
134. A. Grabarz, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Molecules, 2021, 26, 2116.
135. R. Wysokiński, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 4818–4828.
136. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04296c

---