 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Variations in calcite growth kinetics with surface topography: molecular dynamics simulations and process-based growth kinetics modelling†
Mariëtte
Wolthers
*ab,
Devis
Di Tommaso
a,
Zhimei
Du
a and
Nora H.
de Leeuw
ab
aDepartment of Chemistry, University College London, 20 Gordon Street, London WC1 H0AJ, U.K. E-mail: m.wolthers@ucl.ac.uk
bDepartment of Earth Sciences-Geochemistry, Utrecht University, P.O. Box 80021, 3508 TA Utrecht, the Netherlands
First published on 30th May 2013
Abstract
It is generally accepted that cation dehydration is the rate-limiting step to crystal growth from aqueous solution. Here we employ classical molecular dynamics simulations to show that the water exchange frequency at structurally distinct calcium sites in the calcite surface varies by about two orders of magnitude. The decrease in water exchange frequency with progressive embedding of surface calcium ions is thought to be rate limiting to subsequent attachment of carbonate ions during calcite growth. Therefore, a process-based calcite growth kinetics model, reparameterized using the water exchange frequencies computed from molecular dynamics simulations, is used to illustrate the impact of these variations on kink-formation rate, step velocities and bulk growth rate. The calculated frequencies of kink formation show a strong variation with surface structures, which can be amplified depending on the saturation state and calcium to carbonate ratio of the solution. Modelled and measured step velocities and bulk growth rates are generally in agreement, showing that variations in calcite growth rates and step velocities observed experimentally might be at least partially induced by surface topography.
Introduction
Since the discovery of the fundamental control of water exchange kinetics on metal reactivity in chemical and biological systems,1 it has also been shown to govern the kinetics of reactions at mineral–water interfaces such as adsorption,2 crystal growth and dissolution.3–5 Several process-based mineral growth and dissolution kinetics models relate water exchange kinetics to the attachment and detachment frequencies of constituent ions generally,3,6 and in particular in calcite.7–10Calcite is the most stable long-term sink for carbon,11 and as such, precipitation of calcite directly from solution and through mineral carbonation is currently one of the most viable routes for carbon sequestration.12 The key issue in efficient and directed calcite precipitation and in determining the long-term stability of calcite-trapped CO2 is a fundamental understanding of the processes controlling crystal growth13–15 and dissolution.16
When a calcite crystal is cleaved, growing and/or dissolving, the dominant face exposed is the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface,15,16 usually featuring acute and obtuse step edges around growth spirals and etch pits17 (Fig. 1). Direct observations of this surface have demonstrated that these structurally different step edges vary in spreading velocity during dissolution and growth.13,16,18,19 Many simulation studies have focused on the interaction of water with the (10
4) surface,15,16 usually featuring acute and obtuse step edges around growth spirals and etch pits17 (Fig. 1). Direct observations of this surface have demonstrated that these structurally different step edges vary in spreading velocity during dissolution and growth.13,16,18,19 Many simulation studies have focused on the interaction of water with the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface,20–25 but with the notable exception of Cooke and Elliott,24 no water exchange frequencies of surface sites have thus far been reported. Cooke and Elliott reported average residence times for water molecules in the hydration shell of surface calcium in the (10
4) surface,20–25 but with the notable exception of Cooke and Elliott,24 no water exchange frequencies of surface sites have thus far been reported. Cooke and Elliott reported average residence times for water molecules in the hydration shell of surface calcium in the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface, and in the step edges and corners of nano-particles of different sizes. They observed that for all of their calcite nano-particles, except the smallest one, the calculated water residence times varied significantly between corners, edges and faces.
4) surface, and in the step edges and corners of nano-particles of different sizes. They observed that for all of their calcite nano-particles, except the smallest one, the calculated water residence times varied significantly between corners, edges and faces.
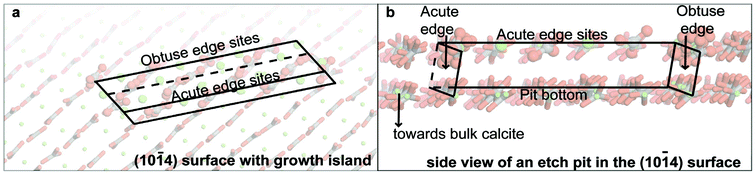 | ||
| Fig. 1 Illustration of the various surface sites (a) top view of a growth island and (b) side view of an etch pit. No water molecules are shown for visibility and one pit edge was cut away as well. | ||
Simulations of the approach and catchment of ions during mineral growth have shown the importance of desolvation of both the surface and the approaching ion.5,22 Furthermore, while desolvation of an approaching calcium ion can be assisted by additives in solution such as small carboxylated molecules26 or phosphonate molecules,27 the structure of water at CaCO3 cluster–water interfaces has been shown to be the key in determining the CaCO3 nucleation pathway.14 However, no study has investigated the kinetics of progressive desolvation of surface calcium ions during calcite growth in relation to the surface structure. In a recent calcite growth kinetics model,7 a different approach to describing the calcite growth mechanism was chosen, partly following the general approach of Zhang and Nancollas6 for ionic crystal growth. It was assumed that the attachment frequency of calcium is controlled by its dehydration or water exchange frequency (∼10+8 s−1).3,22 The attachment frequency of carbonate and bicarbonate to the calcite surface was thought to be limited by the dehydration frequency of surface calcium sites, i.e. the progressive embedding of calcium ions, in agreement with previous experimental considerations.8 The resulting process-based growth rate equation7 agrees with measured calcite growth-step velocities and bulk growth rates over broad ranges of ionic strength, pH, solution stoichiometry and degree of supersaturation, since it takes into account surface speciation as well as solution composition changes. However, in calculating step velocities, it does not discriminate between acute and obtuse steps.
Given the crucial role played by kink sites and step edge structures of spirals and etch pits during calcite growth and dissolution, and the rate limitation imposed by water exchange events between solution and surface calcium, we have determined the water exchange frequency for a range of such sites at the calcite surface, differentiating between structurally distinct sites (face versus acute and obtuse edge and corner sites, Fig. 1). The results were used to refine a process-based calcite growth kinetics model.7 The refined growth model includes distinct step velocities for acute versus obtuse growth steps and is able to reproduce experimentally observed variability in bulk growth rates in relation to topographical variations.
Methods
Computational methods
The interaction of liquid water with the structurally heterogeneous calcite surface was investigated using classical molecular dynamics (MD) simulations with an established forcefield,25 that accurately describes the water–calcite interface, as detailed in Wolthers et al.28 These atomistic simulation methods are based on the Born model of solids29 which assumes that the ions in the crystal interact via long-range electrostatic forces and short-range forces, including both the repulsions and the Van der Waals' attractions between neighbouring electron charge clouds, and, where appropriate, angle-dependent forces to allow for directionality of bonding as, for example, in the covalent carbonate anion.30 The electronic polarizability of the ions is included via the shell model of Dick and Overhauser31 in which each polarizable ion, in the present case the oxygen ion, is represented by a core and a massless shell, connected by a spring. The polarizability of the model ion is then determined by the spring constant and the charges of the core and shell. We assigned the oxygen shell a mass of 0.2 a.u.,32 which is small compared to the mass of the hydrogen atom of 1.0 a.u., thereby ensuring that there would be no exchange of energy between vibrations of oxygen core and shell with those between oxygen and hydrogen.33 However, due to the small shell mass, we had to run the MD simulation with a small timestep of 0.2 fs in order to keep the system stable.The computer code used for the MD simulations was DL_POLY 2.20.34 In the DL_POLY code, the integration algorithms are based around the Verlet leap-frog scheme35 and we have used the Nosé–Hoover algorithm36 for the thermostat. The Nosé–Hoover parameters were set at 0.5 ps for both the thermostat and barostat relaxation times.
We have simulated a repeating calcite slab, containing 840 CaCO3 units, with a growth island of 16 CaCO3 units on one side and an etch pit of the same size in the other side of the slab (Fig. 1). The 22 Å gap between the repeating slabs was filled with 2048 water molecules, resulting in a simulation cell containing 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 species including shells. The simulation cell was equilibrated for 140 ps NPT (constant number of particles, pressure and temperature), at P = 1 atm and 300 K, leading to a water density of ρ = 1.21 g cm−3.22 A similar procedure was carried out at 320 K and 340 K after which the statistics were collected for approximately three nanoseconds at 340 K and one nanosecond at the other temperatures. The simulation cell was tested successfully for absence of gap size effects and strain.
912 species including shells. The simulation cell was equilibrated for 140 ps NPT (constant number of particles, pressure and temperature), at P = 1 atm and 300 K, leading to a water density of ρ = 1.21 g cm−3.22 A similar procedure was carried out at 320 K and 340 K after which the statistics were collected for approximately three nanoseconds at 340 K and one nanosecond at the other temperatures. The simulation cell was tested successfully for absence of gap size effects and strain.
We have used the parameters for the short-range interactions in calcite derived empirically by Pavese et al.,30 who reported very good agreement between their simulated and experimental thermal dependence of structural and elastic properties of calcite. It has been shown in a previous study25 of the surface structures and stabilities of three calcium carbonate polymorphs, namely calcite, aragonite and vaterite, that the potential model derived by Pavese et al.30 for calcite is directly transferable to different calcium carbonate phases, accurately reproducing the experimental morphologies of all three polymorphs.
The potential parameters used for the intra- and inter-molecular water interactions are those initially described in a paper of MD simulations on MgO surfaces.37 For the interactions between water molecules and calcite surfaces, we have used the potential parameters previously fitted to calcite25 and successfully used in MD simulations of water adsorption at point defects and crystal dissolution from calcite steps.38 These potential parameters reproduce the experimental heat of formation of calcite from its aqueous ions to an acceptable degree of accuracy (within 20 kJ mol−1), even though the parameters were not fitted to this process. Moreover, de Leeuw and Parker25 have verified these potential parameters by simulating the structure of ikaite, a calcium carbonate hexahydrate, and found good agreement between calculated and experimental structural data. Calculating the change in enthalpy at 298 K for ikaite, calcite, and water, the change in interaction energy for the dissociation of ikaite per water molecule is 47 kJ mol−1. This compares to experimental values of 47–50 kJ mol−1,39 and suggests that the energies of interactions between calcium, carbonate and water are accurate and realistic. Recent evaluation of the water potential parameters used has shown that previously reported non-physical behaviour22,40 is an artefact of the size of the simulation cell.28 The cell dimensions used here are large enough to prevent such non-physical behaviour. Moreover, assessment of our potential with respect to the calcium–oxygen distances of small calcium ion–water clusters showed excellent agreement with density functional theory calculations.28 For an overview of all potential parameters and detailed re-evaluation of the force field see Wolthers et al.28
Our calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surfaces feature an etch pit and a growth island (Fig. 1), terminated by steps that have either an acute or obtuse angle to the surface. We refer to sites positioned in step edges as either acute or obtuse edge sites. Calcium corners are either acute or obtuse in our cell, while CO3 corner sites terminate one acute and one obtuse edge. Calcium and carbonate ions embedded within the atomically flat faces surrounding these low-coordinated surface features are referred to here as face sites.
4) surfaces feature an etch pit and a growth island (Fig. 1), terminated by steps that have either an acute or obtuse angle to the surface. We refer to sites positioned in step edges as either acute or obtuse edge sites. Calcium corners are either acute or obtuse in our cell, while CO3 corner sites terminate one acute and one obtuse edge. Calcium and carbonate ions embedded within the atomically flat faces surrounding these low-coordinated surface features are referred to here as face sites.
For carbonate oxygen, Oc, an additional label indicates whether the oxygen points out of the surface towards the water molecules (‘type A’), if it is approximately level with carbon in the crystal truncation plane (‘type X’), or pointing in towards the bulk crystal (‘type B’). During equilibration and, to a lesser extent, over the course of the production runs, some carbonate surface groups rotated, for example turning type B oxygen into an A or X position. This rotation was observed to be most significant for growth island corners, and decreases for edge sites and face sites, with face sites showing only minor rotation during equilibration and none during production. This rotation caused counter-intuitive similar average water exchange frequencies observed for the various types of carbonate oxygen atoms.
Characterization of the dynamics of the hydration shell of calcium
The frequency of water exchange in the first hydration shell of the structurally distinct calcium surface sites has been quantified using the “direct” method proposed by Hofer and coworkers.41 This method has been successfully applied previously for, among others, the characterization of the dynamics of the coordination shell of hydrated alkaline earth metal ions and their carbonate and bicarbonate complexes.43 Complete trajectories of molecular dynamics simulations of our calcite surface were analysed for water molecule movement. Whenever a water molecule crossed the boundary of a specified coordination shell, its path was followed, and if its new position outside or inside this shell lasted for more than 0.5 ps, the event was accounted as a real exchange event. The value of 0.5 ps was chosen, since this results in a good measure of ligand exchange processes.41 For calcium, the first shell was defined to fall within the first minimum of the calcium versus water oxygen (Ca–OW) radial distribution function that is within 3.3 Å at the three temperatures tested (Fig. S1a, ESI† for the 340 K example). Similarly for carbonate oxygen, the first shell was defined to fall within the first minimum of the OC–OW in the radial distribution function at 4.0 Å for all three temperatures (Fig. S1b, ESI† for 340 K example). The water exchange frequency for the structurally distinct sites was subsequently calculated from the total number of exchange events in the simulation trajectory.Process-based growth kinetics model
Wolthers et al.7 have derived a process-based calcite growth kinetics model in order to account for the observed dependence of the calcite crystal growth rate on the cation to anion ratio in solution. They have extended the growth model for binary symmetrical electrolyte crystals6 by combining it with the surface complexation model for the chemical structure of the calcite–aqueous solution interface.44 Table S1, ESI† summarizes the model equations, Table S2, ESI† summarizes model parameters and Table S3, ESI† explains the nomenclature. In the current refinement, the frequencies of attachment of carbonate (kB1) and bicarbonate (kB2) to the various (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface features (Fig. 1) are assumed to equal the normalized frequency of water exchange of surface calcium sites as listed in Table 1. Normalization was performed by rescaling all water exchange frequencies such that the frequency for Ca2+ in 2027 water molecules, calculated using the shell model potential, equals the 300 K experimental value.45 From experimental bulk growth rate data46 and surface chemistry information7 it was previously derived that the overall attachment frequency to calcite of the carbonate and bicarbonate, referred to below as (bi-)carbonate, is about twice as fast as attachment by calcium. This constraint is kept in the refined model, and therefore the attachment of aqueous calcium to the calcite surface is also controlled by surface topography. Model detachment frequency, kink formation energy and edge work values were reoptimized using the MS Excel solver tool (Newton's method) by obtaining the lowest residual sum of squares (RSS) for model fits to measured step velocities10,13 and model to measured bulk growth rate data;46 the surface roughness parameter7 was ignored.
4) surface features (Fig. 1) are assumed to equal the normalized frequency of water exchange of surface calcium sites as listed in Table 1. Normalization was performed by rescaling all water exchange frequencies such that the frequency for Ca2+ in 2027 water molecules, calculated using the shell model potential, equals the 300 K experimental value.45 From experimental bulk growth rate data46 and surface chemistry information7 it was previously derived that the overall attachment frequency to calcite of the carbonate and bicarbonate, referred to below as (bi-)carbonate, is about twice as fast as attachment by calcium. This constraint is kept in the refined model, and therefore the attachment of aqueous calcium to the calcite surface is also controlled by surface topography. Model detachment frequency, kink formation energy and edge work values were reoptimized using the MS Excel solver tool (Newton's method) by obtaining the lowest residual sum of squares (RSS) for model fits to measured step velocities10,13 and model to measured bulk growth rate data;46 the surface roughness parameter7 was ignored.
 ) per nanosecond in the first coordination shella of the calcium ions with a duration of more than 0.5 ps41 at 340 K. The numbers of exchange events are averaged over the number of each type of surface
) per nanosecond in the first coordination shella of the calcium ions with a duration of more than 0.5 ps41 at 340 K. The numbers of exchange events are averaged over the number of each type of surface ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Ca site. Also reported is a comparison of the mean residence times (MRT) of water molecules in the first-shell of Ca2+ computed using ab initio and classical MD simulations
Ca site. Also reported is a comparison of the mean residence times (MRT) of water molecules in the first-shell of Ca2+ computed using ab initio and classical MD simulations
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Ca site position Ca site position |
t sim (ps) |
|
logkwb (s−1) | logknormwc (s−1) | MRT (ps) |
|---|---|---|---|---|---|
| a Defined by the first minimum of the Ca–OW radial distribution functions, which lies at 3.5 Å for all calcium sites (Fig. S1a, ESI). b Water exchange frequency, i.e. the number of exchange events per second, average and standard deviation in ∼3 ns production. c Normalized to experimental value for calcium in water.45 d This study, shell model potential. e DFT (Car–Parrinello) MD simulations.43 f Hybrid ab initio (Hartree–Fock) quantum mechanical/molecular mechanical simulations.41 g Classical MD simulation at 300 K conducted in this study using a calcium–oxygen water Lennard-Jones potential parameterized by Dang and Smith42 and the SPC/E water model. h Classical MD simulation at 300 K conducted in this study using a calcium–oxygen water Lennard-Jones potential parameterized by Raiteri et al.21 and the SPC/E water model. i Classical MD at 300 K.24 j Experimental value.45 k Using Impey methods and 2 ps duration minimum for exchange events. | |||||
| Flat face | 3071 | 78 | 10.41 ± 0.08 | 7.06 | 42.3 |
| Pit corner | 3071 | 283 | 10.93 ± 0.16 | 7.43 | 11.0 |
| Obtuse pit edge | 3071 | 942 | 11.48 ± 0.05 | 7.80 | 6.1 |
| Acute pit edge | 3071 | 996 | 11.51 ± 0.06 | 7.82 | 6.2 |
| Obtuse island edge | 3071 | 676 | 11.34 ± 0.07 | 7.70 | 8.5 |
| Acute island edge | 3071 | 1338 | 11.65 ± 0.10 | 7.92 | 4.6 |
| Obtuse island corner | 3071 | 1048 | 11.51 ± 0.15 | 7.82 | 9.0 |
| Acute island corner | 3071 | 1791 | 11.76 ± 0.13 | 7.99 | 5.2 |
| Ca2+ in 2027H2Od | 2988 | 3499 | 12.07 ± 0.02 | 8.20j | 7.0 |
| Ca2+ in 53H2Oe | 19.3 | 5 | 11.41 | 23.3 | |
| Ca2+ in 199H2Of | 21.8 | 4 | 11.26 | 43.2 (22.0k) | |
| Ca2+ in 999H2Og | 1199 | 80 | 217.1 | ||
| Ca2+ in 999H2Oh | 1199 | 44 | 10.5 | ||
| Ca2+ in 255H2Oi | 1000 | 39 | |||
Results and discussion
Water exchange frequencies
Fig. 2 shows the number of exchange events at the structurally different sites as averaged per nanosecond production at 340 K. No systematic trend in water exchange events was observed with time: many sites show a decrease between the first and second nanosecond and then a slight increase while some sites show the opposite trend (Fig. 2). The range in number of exchange events for every ∼80 ps of trajectory (error bars in Fig. 2) narrows between the first and second nanosecond of production time and then remains constant. This suggests that the configuration is at equilibrium. The variation observed in number of water exchange events at the island edges and corners is larger than for pit edges. While this may be a real effect of the geometrically more open structure of the island, it cannot be excluded that it is caused by the small size of the island (Fig. 1) whereby opposite edges can affect each other. | ||
| Fig. 2 Average number of water exchange events at structurally different surface calcium sites at 340 K for three consecutive nanoseconds of production. The error bars indicate the standard deviation of the number of exchange events per ∼80 ps of production within each nanosecond. Note that for face sites, error bars are either equal to or smaller than the squares. | ||
Table 1 shows that for calcium ions at the flat face sites the observed water exchange frequency is nearly two orders of magnitude lower than for the hydrated calcium ion, which has been obtained from the simulation of one calcium ion in 2027 water molecules. The water exchange frequency at the surface significantly increases with decreasing surface coordination, i.e., going from face to edge to corner site, approaching the values for the hydrated calcium ion computed using our shell model potential, first principles Car–Parrinello MD simulations43 and hybrid ab initio (Hartree–Fock) quantum mechanical/molecular mechanical simulations.41 As expected, the water exchange events also increase with increasing temperature (Table S4, ESI†) and water exchange frequencies for carbonate oxygen atoms are several orders of magnitude higher than for surface calcium (Table S5, ESI†), thereby suggesting very strongly that calcium de-hydration is indeed the rate-determining step in the growth and dissolution of calcium carbonate.
At all temperatures studied, calcium water exchange frequencies increase in the same order: face < pit corners < obtuse edges = obtuse corners < acute edges < acute corners (Fig. 2 for 340 K). The same trend in water exchange frequencies was previously observed by Cooke and Elliott for calcite nanoparticles24 and for the stepped versus flat (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface, although their absolute frequencies at 300 K were slightly lower than observed here, which could be due to their different potential parameters to describe water–water interaction (Lennard-Jones22) and method employed to define exchange events (Impey method47). In fact, the value of the mean residence time of water in the first hydration shell of Ca2+ varies by approximately 20 ps if the same MD trajectory is analysed using either the Impey procedure or the “direct” method.41
4) surface, although their absolute frequencies at 300 K were slightly lower than observed here, which could be due to their different potential parameters to describe water–water interaction (Lennard-Jones22) and method employed to define exchange events (Impey method47). In fact, the value of the mean residence time of water in the first hydration shell of Ca2+ varies by approximately 20 ps if the same MD trajectory is analysed using either the Impey procedure or the “direct” method.41
Our results show that, if we were to follow the step-wise desolvation of a single fully hydrated calcium to a bulk lattice calcium during calcite growth, we would see its desolvation slow down: the transition of this calcium from a kink into an edge will be faster than its subsequent transition from an edge to a face position, while the final step from face to bulk calcium will be slower still. Moreover, because the water exchange frequency at the obtuse sites is always lower than the water exchange frequency at the acute sites (see Table 1), calcium desolvation will also be slower when calcium enters calcite via an obtuse step than through an acute step. Furthermore, if carbonate and bicarbonate attachment frequencies are indeed controlled by surface calcium dehydration,7,8 our results suggest that obtuse edge movement might be slowest during dissolution and spiral growth. This observation agrees well with atomic force microscopy (AFM) data under certain growth conditions (e.g. at Ca/CO3 activity ratios <1),13 but not consistently.9,10,13,19,48 To investigate this inconsistent behaviour of step velocities, and translate the MD simulations result to the macroscopic scale, we normalized the water exchange frequencies for different surface calcium sites (Table 1) and used them to refine a process-based calcite growth kinetics model.7
Given the mineralogical and biological significance of calcium, we have also reported in Table 1 the mean residence time (MRT) of water molecules in the first coordination sphere of Ca2+ computed from the potential model used in the present work, as well as the values obtained with other classical and first principles MD simulations. Although it is not the aim of this work to conduct an in-depth assessment of the available potential models for the simulation of the dynamical properties of calcium in water, it is interesting to note that the frequencies of water exchange obtained by the potential model used in this study are in better agreement with ab initio results than those obtained using a Lennard-Jones description for the calcium–oxygen interaction, which give exchange frequencies which are too slow.
Process-based growth model
While the previously published process-based calcite growth kinetics model7 generally agrees well with measured growth-step velocities and bulk growth rates over broad ranges of ionic strength, pH, solution stoichiometry and degree of supersaturation, it does not discriminate between different surface structures such as acute versus obtuse steps and corners. In the refined model (Tables S1–S3, ESI†), the attachment of (bi-)carbonate ions is assumed to be controlled by surface calcium dehydration,7,8 leading to different attachment frequencies depending on surface topography. Since the attachment frequencies of calcium and (bi-)carbonate ions are related through the calcite solubility product (KS, Table S1, ESI†), the refined calcium attachment frequencies also vary depending on surface topography.In Fig. 3, the refined overall attachment frequencies for (bi-)carbonate and calcium ions at the acute and obtuse edges are compared with previously reported attachment frequencies. The previously reported frequencies all resulted from fitting AFM data by kinetic growth models for binary electrolyte crystals6 of varying levels of mechanistic detail. While Stack and Grantham10 applied the binary electrolyte growth model directly, Nielsen et al.48 extended it to include isotopic exchange mechanisms and Wolthers et al.7 extended the binary to ternary model to include bicarbonate into a consequently pH-dependent growth model. It must be noted that all models have a degree of interdependency amongst the parameters: a combination of lower attachment frequencies with lower detachment frequencies may lead to an equally good fit to step velocities as a set of higher frequencies. This explains, for example the large difference in frequencies of Stack and Grantham10 and Wolthers et al.,7 that were partly based on fitting the same data.
![Comparison of carbonate, k[CO32−] (a), and calcium, k[Ca2+] (b), ion attachment frequencies at acute and obtuse edge sites derived from fitting AFM step velocities and constrained by MD simulations. [1] This study, plotting k̄B as k[CO32−] and k̄A as k[Ca2+], calculated according to Tables S2 and S3, ESI at pH 10 and k[CO32−] = kB1 ≈ k[HCO3−] = kB2 ≈ kw of calcium sites within pit edges; [2] as [1] for island edges, this study; [3] derived from fitting7 average AFM step velocities,10,13 making no distinction between acute and obtuse steps; [4] derived from separate fits to acute and obtuse AFM step velocities,10 [5] derived from separate fits48 to acute and obtuse AFM step velocities;49 [6] derived from separate fits48 to acute and obtuse AFM step velocities.9](/image/article/2013/CE/c3ce40249e/c3ce40249e-f3.gif) | ||
Fig. 3 Comparison of carbonate, k[CO32−] (a), and calcium, k[Ca2+] (b), ion attachment frequencies at acute and obtuse edge sites derived from fitting AFM step velocities and constrained by MD simulations. [1] This study, plotting ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) B as k[CO32−] and B as k[CO32−] and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) A as k[Ca2+], calculated according to Tables S2 and S3, ESI† at pH 10 and k[CO32−] = kB1 ≈ k[HCO3−] = kB2 ≈ kw of calcium sites within pit edges; [2] as [1] for island edges, this study; [3] derived from fitting7 average AFM step velocities,10,13 making no distinction between acute and obtuse steps; [4] derived from separate fits to acute and obtuse AFM step velocities,10 [5] derived from separate fits48 to acute and obtuse AFM step velocities;49 [6] derived from separate fits48 to acute and obtuse AFM step velocities.9 A as k[Ca2+], calculated according to Tables S2 and S3, ESI† at pH 10 and k[CO32−] = kB1 ≈ k[HCO3−] = kB2 ≈ kw of calcium sites within pit edges; [2] as [1] for island edges, this study; [3] derived from fitting7 average AFM step velocities,10,13 making no distinction between acute and obtuse steps; [4] derived from separate fits to acute and obtuse AFM step velocities,10 [5] derived from separate fits48 to acute and obtuse AFM step velocities;49 [6] derived from separate fits48 to acute and obtuse AFM step velocities.9 | ||
Because the MD simulation results have been used here to constrain the attachment frequencies, the refined process-based growth model parameters do not show this interdependency. The refined attachment frequencies show a clear but subtle variation with surface topography (in log scale, Fig. 3) and are in general agreement with the previously published values, although the interdependency amongst the latter makes a more detailed comparison ineffective.
We have calculated kink formation frequencies, step velocities and bulk growth rates for the specified sites at the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface using the refined model (Tables S1–S3, ESI†). Fig. 4 shows the new results of kink formation at actual experimental conditions.46 Frequencies of kink formation show a variation with surface structure of up to two orders of magnitude, and this variation depends on solution composition (Fig. 4). The kink formation frequency differences are amplified by solution stoichiometry and degree of supersaturation, Ω, because solution composition strongly affects the kinetic ionic ratio (ri in Table S1, ESI†) and the anion detachment frequency (
4) surface using the refined model (Tables S1–S3, ESI†). Fig. 4 shows the new results of kink formation at actual experimental conditions.46 Frequencies of kink formation show a variation with surface structure of up to two orders of magnitude, and this variation depends on solution composition (Fig. 4). The kink formation frequency differences are amplified by solution stoichiometry and degree of supersaturation, Ω, because solution composition strongly affects the kinetic ionic ratio (ri in Table S1, ESI†) and the anion detachment frequency (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B, Table S2, ESI†) in the model.
B, Table S2, ESI†) in the model.
 | ||
| Fig. 4 Kink formation rate variation calculated by the process-based growth model7 refined by assuming attachment frequencies of carbonate and bicarbonate ions that are identical to normalized water exchange frequencies for the various surface calcium sites (Table 1). Model conditions were identical to experimental conditions of Nehrke et al.46 Kink formation rates were calculated using the equation for ic in Table S1, ESI† and model parameter as listed in Table S2, ESI.† Note the different scales of the y-axes. | ||
Acute and obtuse step velocities, calculated using the refined model, together with measured AFM velocities10,13 are presented in Fig. 5. In the refined model, obtuse-step velocities agree well with measurements, in contrast to acute step velocities. Measured acute step velocities are generally about an order of magnitude lower than model acute step velocities (open squares and diamonds in Fig. 5). Some of the observed discrepancies may be related to small variations in experimental conditions during the experiments. The calcite surface speciation and process-based growth model calculations were performed on measured input solution chemistry data and initial calcite surface area. Small variations in solution chemistry over the course of the measurements, such as changes in solution composition due to gas exchange, will alter solution stoichiometry and Ω, and may lead to orders of magnitude differences in kink formation rate (Fig. 4) and therefore model step velocities. Another possible explanation for the remaining discrepancy between experimental and calculated acute step velocities might be related to the more dynamic environment at the acute edges (see values of log kw at acute sites in Table 1). Additives and electrolyte ions are known to change the solvation environment.43,50,51 The higher water exchange frequencies at acute edges compared to obtuse steps is likely to increase the probability of additive attachment,52 enhancing or inhibiting step propagation, thus narrowing the range of measured step velocities compared to modelled step velocities.
 | ||
| Fig. 5 Absolute, experimentally measured and process-based growth model step velocities, calculated for the experimental conditions during measurements of (■,◆) obtuse and (□,◇) acute step velocities on growing calcite surfaces observed with AFM at {Ca2+}/{CO32−} = raq ≈ 1.0, pH 8.5 at 1 < Ω < 3.6 (squares13) and 7 < pH < 9, 10−3 < raq < 103, in NaCl background electrolyte and 2.2 < Ω < 2.7 (diamonds10). Solid line indicates x = y; RSS = 2.1 × 10−17 m s−1. Step velocities were calculated using the equation Vc= ρc·a·uc, where a is the mean ionic diameter for calcite (Table S3, ESI†) and equations for ρc and uc as listed in Table S1, ESI.† | ||
The variation in bulk growth rate for the various calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface features with solution stoichiometry is illustrated in Fig. 6. Nehrke et al.46 observed an optimum in growth rate at a near one-to-one solution stoichiometry at constant pH of 10.2 and a constant Ω of 5 and 16 (open and closed triangles in Fig. 6, respectively). The different model lines in Fig. 6 represent bulk growth rates calculated using the attachment frequencies for the indicated surface sites and therefore show the observed variation in bulk growth rates that can be caused by variations in surface topography at identical solution composition. The model lines also indicate that, depending on surface topography, the dependency of bulk growth rate on solution stoichiometry (at constant pH and Ω) may vary strongly. As can be seen in Fig. 6, the model lines generally agree with the bulk growth rate data, except at Ω 5 near a 1
4) surface features with solution stoichiometry is illustrated in Fig. 6. Nehrke et al.46 observed an optimum in growth rate at a near one-to-one solution stoichiometry at constant pH of 10.2 and a constant Ω of 5 and 16 (open and closed triangles in Fig. 6, respectively). The different model lines in Fig. 6 represent bulk growth rates calculated using the attachment frequencies for the indicated surface sites and therefore show the observed variation in bulk growth rates that can be caused by variations in surface topography at identical solution composition. The model lines also indicate that, depending on surface topography, the dependency of bulk growth rate on solution stoichiometry (at constant pH and Ω) may vary strongly. As can be seen in Fig. 6, the model lines generally agree with the bulk growth rate data, except at Ω 5 near a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, where even the fastest model growth rates underestimate the observed growth rates. Some of the discrepancy may again originate from small variations between actual experimental solution composition and the input solution composition, which were used for the calcite surface speciation and process-based growth rate modelling, although these experiments were performed in a gas-tight closed system. Another explanation may be related to a change in actual calcite growth mechanism depending on solution stoichiometry.
1 stoichiometry, where even the fastest model growth rates underestimate the observed growth rates. Some of the discrepancy may again originate from small variations between actual experimental solution composition and the input solution composition, which were used for the calcite surface speciation and process-based growth rate modelling, although these experiments were performed in a gas-tight closed system. Another explanation may be related to a change in actual calcite growth mechanism depending on solution stoichiometry.
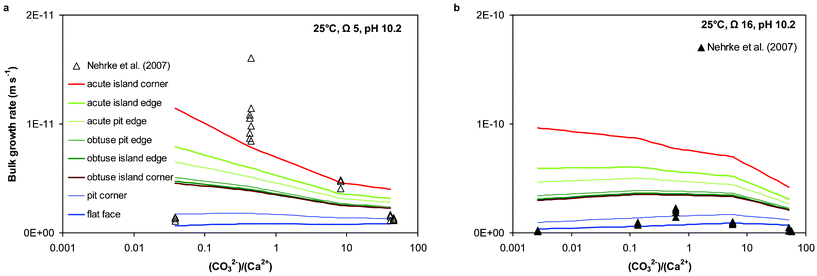 | ||
Fig. 6 Comparison of absolute bulk growth rates between measured in individual experiments46 and modelled data at experimental conditions for the various calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface features. Bulk growth rates were calculated using the equation for Rc in Table S1, ESI† and model parameter as listed in Table S2, ESI.† Note the different scales of the y-axes. 4) surface features. Bulk growth rates were calculated using the equation for Rc in Table S1, ESI† and model parameter as listed in Table S2, ESI.† Note the different scales of the y-axes. | ||
It is generally known that at low to moderate degrees of supersaturation, such as Ω 5 (Fig. 6a), calcite growth is dominated by spiral growth.13 Such a growth spiral consists of four step edge directions, two mirrored acute steps and two mirrored obtuse steps,17 and bulk growth rate at such conditions results from advancement of these steps, as well as kink formation at these steps.52 At higher degrees of supersaturation, such as Ω 16 (Fig. 6b), the formation of new growth islands (two-dimensional surface nucleation) becomes increasingly important.13 More recently, it has also been shown that two-dimensional surface nucleation may occur even at low to moderate degrees of supersaturation, depending on solution stoichiometry.50 Surface nucleation mechanisms are not implemented in the process-based calcite growth kinetics model and may explain some of the discrepancies between calculated and measured bulk growth data in Fig. 6. Nevertheless, the model rates in Fig. 6 generally agree with measured rates, suggesting that some of the variation in bulk growth rates obtained at identical solution conditions might have been caused by variations in seed-surface topography.
Conclusions and implications
Our results quantify the previously observed9,10,13 effect of surface topography differences on surface dynamics. We can conclude that, depending on surface structure and position:1) water exchange frequencies for surface calcium ions vary by up to one order of magnitude,
2) kink formation frequencies vary by up to two orders of magnitude, and
3) bulk growth rates can vary by more than two orders of magnitude at the same solution composition;
4) the dependency on solution stoichiometry of growth rate changes as well.
Our calculated bulk growth rates and obtuse step velocities generally compare favourably with measured obtuse step advancement rates. In the case of acute steps, disparity between process-based model and experiment may be explained by a higher sensitivity of the acute steps to additives or electrolyte ions due to their higher water exchange frequencies.
Since water exchange kinetics are key indicators of chemical reactivity,53 our results imply surface topography-dependent reactivity of calcite towards constituent and contaminant ions, which has important implications in, for example, the fields of biomineralization and mineral engineering. For example, when (nano-)calcite is synthesised with specific morphologies and sizes,54 our results may help aims to produce (nano-)particles with specific kinetic properties. Moreover, the effect of surface topography on the dynamics of interfacial water is likely to affect isotope fractionation48 and adsorption of foreign elements by calcite.52 For example, topography-induced variations in dynamics at the surface may cause discrepancies between experimental trace metal uptake studies if different calcite seed materials or different preparation techniques are used. This could explain, for example, the ongoing debate on Cd uptake by calcite, where Cd uptake mechanisms are related to calcite surface dynamics.55
This study shows that atomic scale information that can be obtained from MD calculations, such as water exchange kinetics at structurally different surface sites, can be “scaled up” to develop predictive models describing the reactivity of minerals from a macroscopic point of view.
Acknowledgements
EPSRC's High End Computing Programme (EP/F067496) and NERC's HPC (NE/J018856/1) funded our use of HECToR, UK's national high-performance computing service, provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc and NAG Ltd. This work was supported by the Netherlands Organisation for Scientific Research [fellowship #863.06.006] and Natural Environment Research Council [fellowship #NE/J018856/1] to MW and Royal Society International Joint Project to MW and NHdL.References
- M. Eigen, Pure Appl. Chem., 1963, 6, 97–115 CrossRef CAS.
- K. Hachiya, M. Sasaki, Y. Saruta, N. Mikami and T. Yasanuga, J. Phys. Chem., 1984, 88, 23–31 CrossRef CAS.
- (a) A. E. Nielsen and J. M. Toft, J. Cryst. Growth, 1984, 67, 278–288 CrossRef CAS; (b) A. E. Nielsen, J. Cryst. Growth, 1984, 67, 289 CrossRef CAS.
- (a) O. S. Pokrovsky and J. Schott, Environ. Sci. Technol., 2002, 36, 426 CrossRef CAS; (b) I. Sethmann, A. Putnis, O. Grassmann and P. Lobmann, Am. Mineral., 2005, 90, 1213 CrossRef CAS.
- S. Piana, F. Jones and J. D. Gale, J. Am. Chem. Soc., 2006, 128, 13568 CrossRef CAS.
- J. Zhang and G. H. Nancollas, J. Colloid Interface Sci., 1998, 200, 131 CrossRef CAS.
- M. Wolthers, G. Nehrke, J.-P. Gustafsson and P. Van Cappellen, Geochim. Cosmochim. Acta, 2012, 77, 121 CrossRef CAS.
- J. Christoffersen and M. R. Christoffersen, J. Cryst. Growth, 1990, 100, 203 CrossRef CAS.
- K. Larsen, K. Bechgaard and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2010, 74, 558 CrossRef CAS.
- A. G. Stack and M. C. Grantham, Cryst. Growth Des., 2010, 10, 1414 Search PubMed.
- D. Archer and E. Maier-Reimer, Nature, 1994, 367, 260–263 CrossRef CAS.
- (a) J. P. Kaszuba, D. R. Janecky and M. G. Snow, Appl. Geochem., 2003, 18, 1065 CrossRef CAS; (b) T. F. Xu, J. A. Apps and K. Pruess, J. Geophys. Res.: Solid Earth, 2003, 108, 2071 CrossRef; (c) G. Montes-Hernandez, F. Renard, N. Geoffroy, L. Charlet and J. Pironon, J. Cryst. Growth, 2007, 308, 228 CrossRef CAS.
- H. H. Teng, P. M. Dove and J. J. DeYoreo, Geochim. Cosmochim. Acta, 2000, 64, 2255 CrossRef CAS.
- P. Raiteri and J. Gale, J. Am. Chem. Soc., 2010, 132, 17623 CrossRef CAS.
- S. Stipp and F. M. Hochella, Geochim. Cosmochim. Acta, 1991, 55, 1723 CrossRef CAS.
- (a) I. N. Macinnis and S. L. Brantley, Geochim. Cosmochim. Acta, 1992, 56, 1113–1126 CrossRef CAS; (b) Y. Liang, A. S. Lea, D. R. Baer and M. H. Engelhard, Surf. Sci., 1996, 351, 172 CrossRef CAS.
- J. Paquette and R. J. Reeder, Geochim. Cosmochim. Acta, 1995, 59, 735–749 CrossRef CAS.
- (a) P. E. Hillner, A. J. Gratz, S. Manne and P. K. Hansma, Geology, 1992, 20, 359 CrossRef CAS; (b) P. M. Dove and M. F. Hochella, Geochim. Cosmochim. Acta, 1993, 57, 705 CrossRef CAS; (c) A. J. Gratz, P. E. Hillner and P. K. Hansma, Geochim. Cosmochim. Acta, 1993, 57, 491 CrossRef CAS.
- S. L. S. Stipp, C. M. Eggleston and B. S. Nielsen, Geochim. Cosmochim. Acta, 1994, 58, 3023 CrossRef.
- (a) N. H. de Leeuw and S. C. Parker, J. Chem. Soc., Faraday Trans., 1997, 3, 467 RSC; (b) A. C. Lasaga and A. Lüttge, Eur. J. Mineral., 2003, 15, 603 CrossRef CAS; (c) R. T. Cygan, K. Wright, D. K. Fisler, J. D. Gale and B. Slater, Mol. Simul., 2002, 28, 475 CrossRef CAS; (d) T. D. Perry IV, R. T. Cygan and R. Mitchell, Geochim. Cosmochim. Acta, 2007, 71, 5876 CrossRef; (e) J. D. Gale, P. Raiteri and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2011, 13, 16666 RSC; (f) C. L. Freeman, J. H. Harding, D. Quigley and P. M. Rodger, J. Phys. Chem. C, 2011, 115, 8175 CrossRef CAS; (g) A. Villegas-Jimenez, A. Mucci and M. A. Whitehead, Langmuir, 2009, 25, 6813 CrossRef CAS; (h) J. S. Lardge, D. M. Duffy, J. M. Gillan and M. Watkins, J. Phys. Chem. C, 2010, 114, 2664 CrossRef CAS.
- P. Raiteri, J. D. Gale, D. Quigley and P. M. Rodger, J. Phys. Chem. C, 2010, 114, 5997 CAS.
- S. Kerisit and S. C. Parker, J. Am. Chem. Soc., 2004, 126, 10152 CrossRef CAS.
- D. Spagnoli, S. Kerisit and S. C. Parker, J. Cryst. Growth, 2006, 294, 103–110 CrossRef CAS.
- D. J. Cooke and J. A. Elliott, J. Phys. Chem., 2007, 127, 104706 CrossRef.
- N. H. de Leeuw and S. C. Parker, J. Phys. Chem. B, 1998, 102, 2914 CrossRef CAS.
- L. M. Hamm, A. F. Wallace and P. M. Dove, J. Phys. Chem. B, 2010, 114, 10488 CrossRef CAS.
- E. Ruiz-Agudo, D. Di Tommaso, C. V. Putnis, N. H. de Leeuw and A. Putnis, Cryst. Growth Des., 2010, 10, 3022 CAS.
- M. Wolthers, D. Di Tommaso, Z. Du and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2012, 14, 15145–15157 RSC.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, Oxford, 1954 Search PubMed.
- A. Pavese, M. Catti, S. C. Parker and A. Wall, Phys. Chem. Miner., 1996, 23, 89 CrossRef CAS.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90 CrossRef.
- (a) P. J. Mitchell and D. Fincham, J. Phys.: Condens. Matter, 1993, 5, 1031 CrossRef CAS; (b) R. Ferneyhough, D. Fincham, G. D. Price and M. J. Gillan, Modell. Simul. Mater. Sci. Eng., 1994, 2, 1101–1110 CrossRef CAS.
- P. M. Oliver, S. C. Parker, R. G. Egdell and F. H. Jones, J. Chem. Soc., Faraday Trans., 1996, 92, 2049 RSC.
- T. R. Forester and W. Smith, DL_POLY User Manual, CCLRC, Daresbury Laboratory, U.K., 1995.
- L. Verlet, Phys. Rev., 1967, 195, 98 CrossRef.
- (a) S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef; (b) W. G. Hoover, Phys. Rev. A, 1985, 31, 1695 CrossRef.
- N. H. de Leeuw and S. C. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 13901–13908 CrossRef CAS.
- (a) N. H. de Leeuw and S. C. Parker, J. Chem. Phys., 2000, 112, 4326–4333 CrossRef CAS; (b) N. H. de Leeuw, S. C. Parker and J. H. Harding, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13792–13799 CrossRef CAS.
- J. L. Bischoff, J. A. Fitzpatrick and R. J. Rosenbauer, J. Geol., 1993, 101, 21 CAS.
- P. J. van Maaren and D. van der Spoel, J. Phys. Chem. B, 2001, 105, 2618–2626 CrossRef CAS.
- T. S. Hofer, H. T. Tran, C. F. Schwenk and B. M. Rode, J. Comput. Chem., 2004, 25, 211 CrossRef CAS.
- L. Dang and D. E. Smith, J. Chem. Phys., 1993, 99, 4229 CrossRef.
- D. Di Tommaso and N. H. de Leeuw, Cryst. Growth Des., 2010, 10, 4292 CAS.
- M. Wolthers, L. Charlet and P. Van Cappellen, Am. J. Sci., 2008, 308, 905–941 CrossRef CAS.
- S. Petrucci, in Ionic Interactions, Vol. 2, Kinetics and Structure, ed. S. Petrucci, Academic Press, New York, 1971 Search PubMed.
- G. Nehrke, G. J. Reichart, P. Van Cappellen, C. Meile and J. Bijma, Geochim. Cosmochim. Acta, 2007, 71, 2240–2249 CrossRef CAS.
- R. Impey, P. Madden and I. McDonald, J. Phys. Chem., 1983, 87, 5071 CrossRef CAS.
- L. C. Nielsen, D. J. DePaolo and J. J. De Yoreo, Geochim. Cosmochim. Acta, 2012, 86, 166 CrossRef CAS.
- K. Davis, PhD thesis, Rice University, 2008.
- M. Kowacz, C. V. Putnis and A. Putnis, Geochim. Cosmochim. Acta, 2007, 71, 5168–5179 CrossRef CAS.
- A. I. Vavouraki, C. V. Putnis, A. Putnis and P. G. Koutsoukos, Chem. Geol., 2008, 253, 243–251 CrossRef CAS.
- J. J. De Yoreo, L. A. Zepeda-Ruiz, R. W. Friddle, S. R. Qiu, L. E. Wasylenki, A. A. Chernov, G. H. Gilmer and P. M. Dove, Cryst. Growth Des., 2009, 9, 5135–5144 CAS.
- L. Helm and A. E. Merbach, Chem. Rev., 2005, 105, 1923 CrossRef CAS.
- Y.-Y. Kim, L. Ribeiro, F. Maillot, O. Ward, S. J. Eichorn and F. C. Meldrum, Adv. Mater., 2010, 22, 2082 CrossRef CAS.
- (a) J. A. Davis, C. C. Fuller and A. D. Cook, Geochim. Cosmochim. Acta, 1987, 51, 1477–1490 CrossRef CAS; (b) S. L. Stipp, M. F. Hochella, G. A. Parks and J. O. Leckie, Geochim. Cosmochim. Acta, 1992, 56, 1941–1954 CrossRef CAS; (c) R. Van der Weijden, J. Meima and R. N. J. Comans, Mar. Chem., 1994, 57, 119–132 CrossRef; (d) A. Martin–Garin, P. Van Cappellen and L. Charlet, Geochim. Cosmochim. Acta, 2003, 67, 2763–2774 CrossRef; (e) Z. Li, A. Hofmann, M. Wolthers and P. Thomas, J. Colloid Interface Sci., 2012, 368, 434–442 CrossRef CAS; (f) E. Tertre, J. Page and C. Beaucaire, Environ. Sci. Technol., 2012, 46, 10055–10062 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables listing key equations, parameters and nomenclature of the process-based calcite growth model. Tables listing water exchange frequencies at 300 and 320 K for surface calcium and 300, 320 and 340 K for surface oxygen in carbonate groups. See DOI: 10.1039/c3ce40249e |
| This journal is © The Royal Society of Chemistry 2013 |

