Beyond inertness: a critical perspective on design strategies for stable thermoelectric interfaces

Abstract

Interfacial stability in thermoelectric devices has evolved from empirical metallization toward a multi-objective engineering paradigm that integrates chemical, mechanical, and electronic considerations under prolonged high-temperature operation. This review critically analyses four dominant strategies, thermodynamic inertness, controlled reactivity, thermomechanical compliance, and kinetic suppression, highlighting their conceptual foundations, practical implementations, and inherent trade-offs. While achieving a sub-5 µΩ cm² contact resistivity is now routine, the primary challenge lies in mitigating complex, multi-modal degradation pathways that dictate device lifetime. We argue for a strategic shift toward architected, functionally graded interfaces incorporating adhesion layers, electronic tuning, kinetic barriers, and mechanical buffers, supported by operando characterisation and predictive lifetime modelling. Furthermore, manufacturability and scalability of advanced designs must be rigorously assessed against industrial processes such as atmospheric plasma spraying and brazing. Mastering interfacial architectures is essential for enabling the production of durable and commercially viable thermoelectric generators.

---

Surafel Shiferaw Legese

Surafel Shiferaw Legese is a PhD scholar in the Department of Materials Engineering at the Indian Institute of Science (IISc), Bangalore. He earned his B. Eng. and M. Eng. degrees in Materials Science and Engineering from the Jimma Institute of Technology, Jimma University, Ethiopia. His research addresses critical contact challenges in thermoelectric devices through interface engineering. Currently, he is focused on the simultaneous development of thermoelectric materials and their corresponding contact layers to optimise interface stability and device reliability. He specialises in advanced electron microscopy and alloy development.

Kamanio Chattopadhyay

Kamanio Chattopadhyay is a distinguished National Science Chair and emeritus Professor at the Department of Materials Engineering, Indian Institute of Science (IISc). He earned his PhD from Banaras Hindu University. A Fellow of all major Indian science and engineering academies and a distinguished honorary member of the Indian and Japan Institute of Metals, he founded the Interdisciplinary Centre for Energy Research at IISc. His research spans quasicrystals, nanomaterials, and metastable materials. Currently, he focuses on high-temperature structural alloys and thermoelectric materials. He has authored over 500 papers and mentored more than 50 doctoral scholars.

---

1. Introduction

The promise of thermoelectric (TE) technology lies in its unique ability to directly convert heat into electricity and vice versa through a solid-state mechanism.^1–4 This dual functionality has attracted significant attention for applications in waste heat recovery, localised cooling, space power systems, and emerging microelectronic energy solutions.^5–7 At the heart of this technology are thermoelectric materials, whose performance is governed by the dimensionless figure of merit (zT).^8–11 For decades, extensive efforts have been invested in optimising zT by engineering carrier concentrations, tuning the band structure, introducing resonant levels, nanostructuring to suppress phonon transport, and leveraging entropy stabilisation or defect chemistry.^12–14 These strategies have delivered remarkable progress, with several systems achieving peak zT > 2, yet these gains often fail to translate to robust, high-efficiency devices in real-world settings.

One critical factor that limits device-level performance and has long been underemphasized in the literature is the stability of the contact metal interfaces with thermoelectric materials.¹⁵ While bulk material optimisation has become increasingly sophisticated, interfacial degradation remains a significant bottleneck in translating high zT values into long-term, operationally stable devices.^16,17 In thermoelectric modules, metal–semiconductor interfaces facilitate low-resistance electrical connections and ensure mechanical integrity and efficient thermal coupling.^18,19 These interfaces are exposed to extreme thermal gradients, high current densities, and thermomechanical cycling, often leading to complex degradation phenomena including chemical interdiffusion, void generation, intermetallic formation, delamination, and mechanical cracking.^20–23 The performance degradation caused by these effects is not merely marginal; it can be catastrophic, leading to total device failure notwithstanding the structural integrity of the thermoelectric legs.

Despite the thermoelectric community's growing awareness of these challenges, interface stability has largely continued to be an afterthought, typically addressed through empirical contact metallisation strategies or borrowed solutions from the broader semiconductor industry. However, thermoelectric materials differ fundamentally from conventional semiconductors: they often possess narrow band gaps, high anisotropies, and polar surfaces and are frequently operated at elevated temperatures, where kinetic processes accelerate degradation.^24,25 Moreover, the operational efficiency of a thermal model assumes ideal contact behaviour, a condition hardly achieved in practice. In fact, even modest increases in interfacial electrical or thermal resistance can severely suppress the net output power and conversion efficiency.²⁶

Given this complexity, a fundamental rethinking of how interfaces are approached in thermoelectric systems is urgently needed. The current literature on contact interfaces in thermoelectrics is fragmented, often focusing on individual material systems or specific contact schemes, and lacks a unified, comparative framework. As a result, researchers and engineers are frequently forced to navigate interfacial issues empirically, without access to a systematic understanding of degradation mechanisms or design principles.

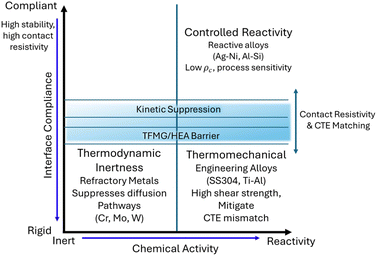
In this perspective, we cut through that fragmentation by constructing a unified analytical framework. While rich in system-specific solutions, the current literature remains fragmented. Our analysis reveals that the field has implicitly converged on four distinct, and often competing, strategies for achieving interfacial stability: thermodynamic inertness, controlled reactivity, thermomechanical compliance, and kinetic suppression. Thermodynamic inertness seeks a chemically inert interface while strategically controlling reactivity through a planned reaction to form a self-limiting barrier. In contrast, thermomechanical compliance prioritises mechanical integrity over chemical purity, and kinetic suppression uses novel material structures to freeze the interface in a metastable state. Finally, thermoelectric module preparations comprise the overarching processes of joining and assembly that integrate these strategies. By critically assessing the fundamental trade-offs inherent to these four philosophies, we provide a clear and cohesive framework for guiding future research and development toward truly reliable thermoelectric devices, while addressing challenges across different classes of thermoelectric materials.

To navigate this complex landscape, we propose a unified conceptual framework that organises these disparate approaches. Fig. 1 maps the four dominant design strategies onto orthogonal axes of chemical activity (from inert to reactive) and interface compliance (from rigid to compliant). This diagram visualises the fundamental trade-offs defining the field, illustrating, for example, how the pursuit of thermodynamic inertness often necessitates mechanical rigidity, while kinetic suppression strategies (central band) attempt to decouple these properties. This framework serves as the structural backbone for the critical analysis that follows.

Fig. 1 Conceptual framework mapping of the four dominant interface design strategies against the fundamental trade-offs of chemical activity and interface compliance. The diagram illustrates the design conflicts inherent in current methodologies: (1) thermodynamic inertness (bottom-left) prioritises chemical stability using refractory metals (e.g., W and Mo) but often suffers from mechanical rigidity and CTE mismatch; (2) controlled reactivity (top-right) achieves low contact resistivity via engineered reactions but risks process-induced instability; (3) thermomechanical compliance (bottom-right) sacrifices chemical simplicity to ensure structural integrity using CTE-matched alloys (e.g., SS304). The central band, kinetic suppression, represents a distinct materials-science strategy (utilising TFMGs or HEAs) that effectively decouples these trade-offs, allowing for the independent tuning of barrier properties to balance chemical inertness with mechanical compliance.

2. Strategy 1: the pursuit of thermodynamic inertness

The most intuitive and seemingly ideal approach for designing a stable metal-thermoelectric interface is to pursue thermodynamic inertness. This strategy is built on the conceptual gold standard of preventing chemical degradation by selecting a contact material that has a minimal, or ideally zero, chemical potential gradient with the thermoelectric material at operational temperatures. The goal is to create a thermally inert interface with a near-zero interfacial reaction energy, thereby preventing the formation of brittle, high-resistance intermetallic compounds (IMCs) and ensuring the junction's integrity over thousands of hours.

This design philosophy has been pivotal in translating the high material-level zT of some systems into high-performance, durable devices. The most spectacular validation of this approach has been demonstrated in half-Heusler (hH) compounds. Due to their high intrinsic conductivity, hH alloys are extremely sensitive to even minor parasitic resistances, demanding a nearly perfect interface. Initial efforts with common metals and brazes proved inadequate, leading to thick, inhomogeneous reaction layers and high contact resistance.

A pioneering approach, demonstrated by Liu et al., moved the field from empirical trial-and-error to systematic, thermodynamically guided design. This strategy involves using first-principles calculations to screen for elements that are both thermodynamically inert and kinetically stable against hH compounds at high temperatures. The screening criterion aims to identify materials with a near-zero interfacial reaction energy (E_IR) to ensure thermal stability, coupled with a high activation energy for migration (E_Mig) that kinetically hinders atomic diffusion. This thermodynamic screening identified Group VIB elements, particularly chromium (Cr) and molybdenum (Mo), as nearly ideal candidates for both MNiSn and MCoSb thermoelectric systems. Experimental validation confirmed this prediction spectacularly. Cr/hH and Mo/hH joints, even after ageing at 1073 K for 30 days, exhibited clean, atomically sharp interfaces with no detectable reaction layers (Fig. 2a). This thermally inert interface resulted in an ideal ohmic contact with an exceptionally low specific contact resistivity of <1 µΩ cm².²⁷ This breakthrough in interface design, grounded in the pursuit of thermodynamic inertness, has been directly responsible for enabling hH modules to operate stably at temperatures up to 1100 K, unlocking their peak performance and achieving record conversion efficiencies.

Fig. 2 A comparative analysis of the thermodynamic inertness strategy, illustrating the ideal case versus the pragmatic trade-off. (a) A high-resolution TEM micrograph and corresponding EDS maps of a Cr/half-Heusler (ZrNiSn_0.99 Sb_0.01) junction, demonstrating atomic direct bonding with no observable chemical reaction layer. This perfect chemical inertness is combined with elite electrical performance, yielding an ultra-low specific contact resistivity of <1 µΩ cm².²⁷ (b) An SEM micrograph of a Ni/Co–P/PbTe joint. The Co–P solder paste layer functions successfully as an inert barrier, creating a clean interface that efficiently inhibits interdiffusion and prevents the catastrophic reactions observed with Ni. However, this chemical stability comes at a direct, measured cost: a two-fold increase in specific contact resistivity (11.75 µΩ cm² to 21.75 µΩ cm²), which is an engineering compromise to ensure long-term device reliability (adapted from Hsieh et al., with permission from Elsevier).²⁹

A similar success story for this strategy is found in PbTe-based thermoelectric materials, which are notoriously difficult to make contact with due to the extreme chemical reactivity of tellurium. High-throughput screening and previous studies have identified cobalt (Co) as a superior electrode candidate compared to Ni in Ni/PbTe due to its chemical inertness and low diffusion coefficient in PbTe.²⁸ This principle has been demonstrated in practice using an electroless-plated Co–P alloy as an effective diffusion barrier. This Co–P layer, when applied to n-PbTe, was shown to successfully inhibit the severe reactions near the melting point with Cu electrodes and the deep grain-boundary penetration seen with Ni electrodes, resulting in a clean interface (Fig. 2b). While this represented a major improvement in chemical stability, it also introduced a clear performance trade-off. The addition of the Co–P layer, when used with a solder paste, has increased the specific contact resistivity to ∼21.75 µΩ cm².²⁹ Although this value was roughly twofold higher than that of a direct Ni/PbTe joint (11.75 µΩ cm²), it was deemed an acceptable trade-off for a commercial module, successfully prioritising long-term chemical inertness and reliability over the lowest possible initial contact resistance. Furthermore, alloys based on this principle, such as Co₈₀Fe₂₀, have been successfully used as diffusion barriers in high-efficiency nanostructured PbTe modules, enabling stable operation at hot-side temperatures up to 873 K.^30–33

In both the half-Heusler and PbTe examples, selecting an inert material proved to be the key that unlocked stable, low-resistance performance. However, a critical analysis of this strategy reveals that chemical inertness is an insufficient and, at times, misleading metric for success. An exclusive focus on chemical stability can blind researchers to other, more catastrophic, failure modes.

The skutterudite (SKD) system provides the definitive case study for this critical flaw. Systematic investigations into metal/SKD interactions have identified refractory metals, such as tungsten (W) and molybdenum (Mo), as ideal from a chemical perspective; they show almost no interaction with the SKD material and are highly effective at preventing diffusion. By the standard of thermodynamic inertness, they are a perfect choice. However, these metals are entirely unsuitable as standalone contact layers. The failure lies in their thermomechanical properties. Chemically inert W and Mo possess very low coefficients of thermal expansion (CTE), in the range of 4.5–5.4 × 10⁻⁶ K⁻¹. This creates a severe mismatch with both n-type (∼9.5 × 10⁻⁶ K⁻¹) and p-type (∼11.5 × 10⁻⁶ K⁻¹) skutterudites. This mismatch guarantees that upon thermal cycling, the resulting thermomechanical stress will inevitably lead to joint failure, cracking, and delamination. Conversely, a metal like titanium (Ti), which has a much more compatible CTE (∼8.6 × 10⁻⁶ K⁻¹), is so highly reactive with antimony that it, too, is unusable.^34–36

This skutterudite dilemma perfectly illustrates the central trade-off. The pursuit of thermodynamic inertness, when followed in isolation, can lead to a design that trades a slow chemical failure mode for a rapid and catastrophic mechanical one. This critical analysis leads to an unavoidable conclusion: while an inert chemical interface is desirable, it must be viewed as a foundational requirement, not a complete solution. A successful interface must be holistically engineered, and the assumption that chemical safety is the only metric for success is a pitfall that has hindered progress in mechanically mismatched systems.

3. Strategy 2: controlled reactivity as a design tool

In direct contrast to the preventative philosophy of thermodynamic inertness, a more advanced and subtle strategy involves controlled reactivity. This approach represents a paradigm shift, moving from the prevention of all reactions to the intentional design of a specific, beneficial reaction. The goal is to use a barrier material that is deliberately chosen to react with the thermoelectric material in situ during fabrication. This controlled reaction is engineered to form a thin, thermodynamically stable, and highly conductive intermetallic compound (IMC). The newly formed layer acts as a perfect, self-limiting diffusion barrier, halting any further degradation. When successful, this high-risk, high-reward strategy can be a multi-functional solution. It can yield superior mechanical bonding by creating a strong, graded metallurgical interface, and in its most advanced forms, it can even be used to actively tailor the electronic properties of the junction to lower contact resistance. The challenge, however, is having control of the layer.

The GeTe system, which is plagued by both high chemical reactivity and a mechanically stressful rhombohedral-to-cubic phase transition (600–700 K), provides the most compelling examples of this strategy.^37–40 A simple inert barrier is often insufficient to handle the severe thermomechanical challenge. Recognising this, researchers have engineered an Al–Si alloy, specifically Al₆₆Si₃₄, not for its inertness, but for its reactive potential and its coefficient of thermal expansion (CTE) that closely matches GeTe across the operational temperature range. During the bonding process, aluminium was designed to react with GeTe. This reaction formed a zipper-like interface composed of Al₂Te₃ and secondary Ge phases. This metallurgical bond, a direct product of the controlled reaction, provided exceptional mechanical strength. In a remarkable demonstration of the strategy's success, the joint's shear strength was found not to be degraded by thermal ageing, and its strength unexpectedly increased by over 50% to 41.7 MPa after 16 days of ageing at 500 °C.⁴¹ The contact resistivity remained stable and low (26.11 µΩ cm²), demonstrating that a reactive interface, when properly engineered and controlled, can yield highly robust and reliable joints that simultaneously achieve both chemical and mechanical stability.

An even more fascinating case in GeTe involves a cobalt (Co) barrier. While Co was found to effectively suppress detrimental Cu–Te reactions by forming a stable CoTe₂ IMC layer at the interface, it also provided an active, performance-enhancing function. Co atoms were found to diffuse from the barrier, in a controlled manner, into the GeTe lattice and occupy intrinsic Ge vacancy sites.⁴² This process, a direct result of the interfacial design, acted as a donor, optimising the carrier concentration while simultaneously increasing electrical conductivity and reducing thermal conductivity. It led to a 56% increase in the joint's zT value following long-term ageing. This case represents the success of the controlled reactivity philosophy, transforming the diffusion barrier from a passive component into an active, performance-enhancing element of the device itself.

This approach has also been applied with great success to solve specific failure modes in half-Heusler (hH) systems. For p-type FeNb_0.88 Hf_0.12Sb materials, a pure silver (Ag) barrier was found to be unstable. Despite silver's relative nobility, it reacted with the hH material to form a low-melting-point Ag₃Sb phase, which caused catastrophic joint failure during thermal ageing. The solution was not to find a completely different, inert metal, but to control the reaction by alloying silver with a small amount of nickel (Ag_0.9Ni_0.1). Nickel was specifically included to react selectively with niobium (Nb) from the hH matrix. This intentionally driven reaction formed a stable, bilayered IMC structure of Ni₃Nb/Ni₆Nb₇ and Ni₃Ni/Fe₅Nb₃. This ∼20 µm thick layer proved to be an excellent and self-limiting diffusion barrier, preventing any further detrimental reactions.⁴³ The engineered interface not only solved the stability problem but also provided robust mechanical bonding (with a shear strength >40 MPa) and an ultra-low contact resistivity of just 0.4 µΩ cm². This serves as a classic example of using a reactive additive to transform an unstable interface into a high-performance, multifunctional one.

The controlled reactivity principle is also the most effective solution for Mg-based thermoelectric materials. In this material, high reactivity and volatility make stable contact notoriously difficult. While direct Ni contact is unstable, researchers discovered that the in situ-formed reaction product itself could be used as a dedicated barrier. For the Mg₃Sb₂ system, a dedicated barrier made of the Mg_4.3Sb₃Ni phase was used to create a graded interface.⁴⁴ This layer, being chemically similar to both the contact and the TE material, is remarkably stable, maintaining a contact resistivity of ∼10 µΩ cm² and a shear strength of ∼20 MPa even after 20 days of ageing at 673 K. However, the high intrinsic resistivity of this phase limited peak performance. This led to a refinement of the strategy, as further studies identified the Mg_1.2SbNi phase that has significantly lower resistivity. Using this phase as the pre-designed, in situ formed barrier improved the device conversion efficiency by 33% while retaining excellent stability. This represents a highly mature version of the controlled reactivity strategy. It is not just about forming a stable layer, but about iterating the design to form the most conductive stable layer, thereby optimising the entire device.

The strategy extends beyond just forming a physical barrier. It can be used to engineer the electronic properties of the junction. For n-type Mg_3+δBi_1.5Sb_0.5 Zintl phases, an engineered NiFe alloy contact demonstrated exceptional reliability. It forms a stable, metallic NiMgBi buffer layer at the interface. This in situ formed metallic layer acts as a perfect diffusion barrier while simultaneously ensuring a low-resistance ohmic contact, maintaining a low ρ_c of ∼1.3 × 10⁻⁵ Ω cm² after over 2100 hours of ageing.⁴⁵

Another similar but distinct example can be found in Bi₂Te₃ systems. Here, a strategy was developed that moved beyond merely blocking diffusion to actively engineering the reaction for electronic benefit. The introduction of a silver (Ag) interlayer at the Cu/Bi₂Te₃ interface was found to induce the formation of specific, beneficial interfacial compounds, Cu₄Ag₃Te₄ and Ag₂Te.⁴⁶ These intentionally formed phases were shown to lower the potential barrier height at the junction, facilitating charge transport and achieving an exceptionally low contact resistivity. This represents a highly sophisticated application of the strategy, where the reaction is designed not for mechanical stability, but purely for electronic enhancement.

The case studies, drawn from GeTe, half-Heuslers, Mg systems, and Zintl phases, clearly demonstrate the powerful, multifunctional benefits of the controlled reactivity approach. It can solve complex, multifaceted problems that the simple strategy of an inert interface cannot, simultaneously providing mechanical robustness, chemical stability, and even electronic enhancement. However, it is a high-risk, high-reward approach that is exceptionally sensitive to processing conditions.

The concept of controlled reactivity demands a delicate balance. The literature shows that slight, difficult-to-manage deviations can lead to catastrophic failure. A definitive example of this risk is the classic failure mode observed in Bi₂Te₃ modules joined with common tin-based solders. While the tin (Sn) in the solder is intended to form a strong metallurgical bond, its high chemical activity with tellurium (Te) is difficult to control. One study on a Bi_0.5Sb_1.5Te₃/Cu joint found that this uncontrolled reaction had caused the solder to be exhausted quickly during ageing at 150 °C. This led to the formation of a thick, brittle Sn–Te intermetallic layer that grew from 50 µm to 90 µm, and a continuous crack was observed at the interface. The result was a catastrophic failure of the joint's mechanical integrity, with the bonding strength drastically decreasing from 8.6 MPa to just 1.5 MPa. This illustrates how a failure to manage the reaction pathway can lead to a new, fatal failure mode.⁴⁷ This requirement for extreme, lab-grade process control is a formidable barrier to cost-effective, commercial-scale manufacturing. In real-world applications, where operational fluctuations, thermal cycling, and slight manufacturing variances are inevitable, a strategy that relies on such a precise kinetic balance is inherently fragile. The controlled reaction can easily become uncontrolled, resulting in a premature end to the device's lifespan. Therefore, while this strategy is perhaps the most elegant and powerful from a materials design perspective, its practical implementation remains a significant challenge.

4. Strategy 3: thermomechanical compliance as a primary driver

Beyond the intricate chemical negotiations of inertness and reactivity, a third, more pragmatic strategy exists: thermomechanical compliance. This engineering-first approach is founded on the reality that a perfectly inert or functionally reactive interface is untenable if the device fails catastrophically due to mechanical stress. The primary goal of this strategy is to prevent mechanical failure, such as cracking, delamination, and leg fracture, by prioritising the matching of the coefficient of thermal expansion (CTE) between the thermoelectric material and the contact layer above all other considerations.

This approach is non-negotiable for thermoelectric systems that are either exceptionally brittle (like skutterudites) or possess an intrinsically high CTE (like Mg-based Zintl phases). In these materials, the significant thermal gradients and repeated thermal cycling inherent to device operation induce severe internal stresses, which are governed by the CTE mismatch (Δα) between the bonded layers.^48–50 Even a small mismatch can lead to microcrack formation, which rapidly propagates and leads to a catastrophic increase in internal resistance or complete mechanical failure of the joint. Therefore, this strategy deliberately selects contact materials not for their chemical purity or simplicity, but for their specific mechanical properties that ensure the joint's physical integrity.

The Mg-based Zintl phases, Mg₃Sb₂ and Mg₂Si, serve as the strongest and clearest examples of this philosophy in practice. These materials are promising due to their low cost and strong performance, but their high intrinsic CTEs make them exceptionally difficult to bond to. Initial attempts to bring these materials into contact with common metals, such as pure iron (Fe) or nickel (Ni), were unsuccessful. While Fe is a common contact, it has a significant CTE mismatch with Mg₃Sb₂ (Fe: ∼14.9 × 10⁻⁶ K⁻¹ vs. Mg₃Sb₂: ∼23.8 × 10⁻⁶ K⁻¹).⁵¹ This mismatch causes the joint's shear strength to degrade rapidly upon thermal ageing. Similarly, direct Ni contacts on Mg₂Si-based compounds (Ni: ∼13 × 10⁻⁶ K⁻¹ vs. Mg₂Si: ∼17–18 × 10⁻⁶ K⁻¹) were shown to induce significant thermal stress, resulting in extensive cracking within the brittle thermoelectric leg itself, as shown in Fig. 3a. These failures were not primarily chemical; they were mechanical in nature.^52,53

Fig. 3 Impact of CTE matching on thermomechanical stability. (a) Failure from CTE mismatch: SEM image of a Ni/Mg₂Si_1−xSn_x joint after high-temperature operation. A large CTE mismatch between Ni and the brittle TE leg induces thermal stress, leading to severe cracking and catastrophic failure. (Adapted from Pham et al., with permission from Elsevier).⁵² (b) Solution via CTE matching: SEM image of a 304SS/Mg₂Si joint. Using 304SS with a closer CTE match mitigates thermal stress, preventing failure and yielding a chemically complex yet mechanically robust interface.⁴² (Adapted from Jayachandran et al., with permission from Elsevier).⁵³

In the thermomechanical compliance strategy, instead of searching for another pure, inert material to replace pure Fe, 304 Stainless Steel (304SS) was used. From a purely chemical or electrical perspective, 304SS is a complex and dirty material, an alloy of Fe, Cr, and Ni. However, its selection was a deliberate engineering choice. The austenitic (FCC) crystal structure of 304SS enables a much higher CTE (∼18.9 × 10⁻⁶ K⁻¹), which offers a significantly better mechanical match to Mg₃Sb₂.⁵¹ This choice, which prioritised CTE matching over everything else, solved the problem of primary failure mode. The 304SS interface resulted in a vastly superior performance, characterised by low initial contact resistivity (∼5.1 µΩ cm²), excellent stability after 400 hours of ageing, and a robust shear strength of over 31 MPa.⁵¹ This success was replicated in the Mg₂Si system, where 304SS foil was also found to be a highly effective interlayer, as shown in Fig. 3b. This philosophy has been extended to other engineered alloys, including cupronickel (Cu₇₀Ni₃₀) and high-entropy alloys like FeCrTiMnMg, all of which were specifically designed to match the TE material's CTE and thus ensure mechanical reliability.^54,55

The same logic applies to the brittle, ceramic-like skutterudite (SKD). For these materials, the pursuit of thermodynamic inertness (strategy 1) often leads directly to mechanical failure. Refractory metals like tungsten (W) and molybdenum (Mo) are almost perfectly chemically inert toward skutterudites.³⁵ However, they are completely unsuitable as standalone contacts because their very low CTEs (4.5–5.4 × 10⁻⁶ K⁻¹) create a severe thermomechanical mismatch with the SKD legs (CTEs of ∼9.5–11.5 × 10⁻⁶ K⁻¹).^34,36 The resulting thermal stress inevitably leads to joint fracture. The solution, once again, was to design for compliance. Researchers developed complex alloys, such as Ti–Al alloys, specifically because their CTE could be tuned to more closely match that of the skutterudite. For instance, Ti_83.7Al_10.7Si_5.6 was shown to form a stable interface with high shear strength (>30 MPa) after 16 days of ageing, a success attributed directly to its stable network structure and its matched CTE.⁵⁶ This demonstrates a clear, conscious trade-off: the relative chemical simplicity of W or Mo was sacrificed for the complex, multi-element (and more reactive) Ti–Al alloy, all to satisfy the non-negotiable demand for thermomechanical compliance.

A critical analysis of this strategy reveals it to be a pragmatic, engineering-first approach. It correctly identifies that catastrophic mechanical failure during thermal cycling is the most immediate and definitive failure mode for many systems. It is a philosophy of mitigation that solves the most pressing problem, ensuring that the device can be fabricated and can survive its initial operational cycles without fracturing. However, this pragmatism comes at a significant cost, which is the core trade-off of this strategy. By prioritising CTE matching, the design almost always accepts a compromised chemical or electrical interface. A material like 304SS or a complex Ti–Al alloy is, by its very nature, a cocktail of elements. It is not thermodynamically inert. While it may not react catastrophically, it creates a complex chemical potential gradient at the interface. This strategy effectively guarantees a certain level of mechanical reliability but, in doing so, may condemn the device to a faster rate of slow, diffusion-based degradation that a more inert (but mechanically mismatched) barrier would have prevented.

5. Strategy 4: kinetic suppression via novel structures

The final strategy is a purely materials-science-driven approach, distinct from the previous three. Instead of managing chemical thermodynamics (strategies 1 & 2) or macroscopic mechanical stress (strategy 3), this philosophy seeks to kinetically suppress degradation. The approach implicitly accepts that a reaction is thermodynamically favourable (unlike strategy 1) but aims to make the reaction rate so infinitesimally slow that it becomes irrelevant over the device's operational lifetime.

The goal is to design an interfacial material that, at the atomic level, physically hinders or blocks the diffusion pathways that allow elements to migrate. All solid-state diffusion is governed by kinetic factors, primarily the diffusion coefficient (D) and the activation energy (Q), as described by an Arrhenius relationship, where diffusion is exponentially dependent on temperature.⁵⁷ In standard polycrystalline metals, atomic transport is dominated by grain boundary diffusion, where the loosely packed atoms at grain boundaries create high-speed highways for diffusion. The diffusion coefficient along these boundaries can be many orders of magnitude higher than that through the bulk crystal lattice.⁵⁸ The strategy of kinetic suppression, therefore, is an engineering effort to eliminate or block these fast diffusion pathways, forcing any atomic migration to occur via the much slower, high-activation-energy process of bulk diffusion. This is achieved by creating materials in a non-equilibrium or highly complex state, such as amorphous metals or intricate, high-entropy crystalline alloys, which effectively freeze the interface.

The most intuitive and effective example of this approach is the use of amorphous materials, or metallic glasses, as diffusion barriers. An amorphous material, by its very nature, is grain-boundary-free. It is a disordered, liquid-like structure that has been frozen in a solid state. This lack of any organised crystal lattice or grain boundary network inherently blocks the rapid diffusion pathways. This was demonstrated spectacularly in the PbTe system, a material notoriously difficult to create stable contacts for. A sputter-deposited Ti-based thin-film metallic glass (TFMG), with a complex composition of Ti_45.8Zr_9.5Cu_29.5Nb_8.6Co_6.6, was used as a diffusion barrier between a Cu electrode and the PbTe leg.⁵⁹ As Fig. 4a shows, the results were a remarkable success. The amorphous TFMG layer was shown to completely inhibit interdiffusion and remained fully amorphous even after annealing at 673 K for up to 48 hours. Its performance was starkly contrasted with that of a standard, polycrystalline Ti film under the exact same conditions. The crystalline Ti barrier failed catastrophically in just 8 hours, as shown in Fig. 4b, reacting completely to form thick, detrimental Ti–Te intermetallic compounds and Pb precipitates that destroyed the interface. The amorphous structure of the TFMG, by eliminating grain boundary pathways, provided a near-perfect kinetic barrier, achieving a low specific contact resistivity in the range of 25–33 µΩ cm² and solving a degradation problem that its crystalline equivalent could not.

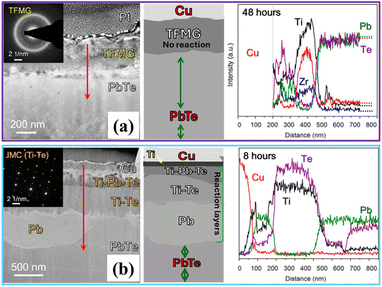Fig. 4 A multi-layered demonstration of the kinetic suppression strategy. (a) A TEM micrograph, SAED pattern (inset), and EDS line scan of the Cu/TFMG/PbTe interface after 48 hours of high-temperature annealing. The SAED pattern's diffuse halo confirms that the barrier is amorphous. This grain-boundary-free structure provides a nearly perfect kinetic barrier, suppressing diffusion and resulting in a clean, stable interface, as confirmed by the sharp EDS profile. (b) A TEM micrograph, SAED pattern (inset), and EDS line scan of a conventional Cu/Ti/PbTe barrier after only 8 hours of annealing. The SAED pattern's sharp spots confirm that it is crystalline. These crystal grain boundaries acted as diffusion pathways, enabling rapid, catastrophic interdiffusion and the formation of a thick Ti–Te/Ti–Pb–Te intermetallic compound (IMC) layer, as indicated by the wide, overlapping EDS profile.⁵⁹

Where a fully amorphous structure is not feasible or desired (for instance, at higher operating temperatures where it would crystallise), a parallel approach is to create kinetic suppression at the microstructural level. If grain boundaries cannot be eliminated, they can be engineered to reduce their impact. This was ingeniously demonstrated in the skutterudite system using a Ni–Cr barrier with a narrow-channel structure. This barrier was fabricated with chromium (Cr) particles embedded within a nickel (Ni) matrix. This design does not stop diffusion, but it controls it. Any antimony (Sb) atoms diffusing from the skutterudite are forced to navigate a long, tortuous path around the Cr particles within the Ni matrix channels.⁶⁰ This clever microstructural engineering dramatically lengthens the effective diffusion distance. Since diffusion-limited growth follows parabolic kinetics (where thickness x scales with the square root of time t, or x x² = k_t), doubling the required diffusion path quadruples the time it takes for a reaction layer to reach a critical thickness.^61,62 This narrow-channel design successfully prevented the formation of CTE-mismatched NiSb, kept the contact resistivity below 12 µΩ cm², and most critically, maintained high bonding strength after an extensive 70 days of ageing at 823 K.

The third and perhaps most advanced application of this philosophy is the design of complex crystalline alloys. This strategy makes the bulk lattice itself a poor medium for diffusion. If an amorphous structure is a frozen liquid with no pathways, a complex crystalline alloy is a blocked and disordered solid. By introducing atoms of significantly different sizes or chemical properties into a crystal lattice, severe lattice distortion is created. This distortion increases the activation energy (Q) required for an atom to jump from one lattice site to the next, effectively creating sluggish diffusion kinetics. An initial example of this was observed in skutterudite systems, where an Fe₈₀Cr_17.5Mo_2.5 alloy demonstrated superior stability compared to a Mo-free alloy.⁶³ The severe lattice distortion induced by the large molybdenum (Mo) atoms, which act as anchors in the lattice, was credited with slowing the degradation process.

High-Entropy Alloys (HEAs) leverage this principle to its theoretical extreme. By combining five or more elements in near-equimolar ratios, HEAs create a state of maximum crystalline disorder and lattice strain. This complex, distorted lattice inherently exhibits sluggish diffusion. This was successfully applied to p-type skutterudites, where an FeCoNiCrMo HEA barrier was shown to form stable Mo₃Sb₇ phases at the interface that effectively hindered diffusion and maintained a low contact resistivity of ∼4.2 µΩ cm² after 640 hours of high-temperature ageing.⁶⁴ This same HEA-driven sluggish diffusion principle was also used to design a multicomponent FeCrTiMnMg alloy for Mg₃Sb₂ systems. This alloy was specifically engineered to achieve slow diffusion kinetics, resulting in both low contact resistance (∼4.0 µΩ cm²) and high shear strength (36.7 MPa), with excellent thermal stability.⁵⁴ In these cases, the material is not thermodynamically inert (it does react to form stable phases), but its degradation is kinetically blocked by the engineered sluggishness of its own lattice.

Despite the impressive and highly sophisticated performance of these advanced materials, this materials-science-driven strategy contains a critical, latent uncertainty: the long-term stability of the metastable state itself. The core issue is that these materials, both amorphous glasses and complex HEAs, are not in their thermodynamic ground state. They are kinetically trapped in a non-equilibrium state, and it is this very trapped nature that provides the barrier function. While this state provides an exceptional barrier, the thermodynamic driving force for them to relax into a more stable, lower-energy state (e.g., to crystallise or phase-separate) is ever-present. The critical, and largely unaddressed, uncertainty is how long this metastable state will last under the thousands of hours of constant thermal load experienced during real-world device operation.

There is a significant and very real risk that after 1000 to 5000 hours, the amorphous TFMG layer could suddenly reach its crystallisation temperature and nucleate new, stable crystalline phases. This event would abruptly and catastrophically eliminate the barrier's effectiveness by creating a new network of grain boundaries, reopening pathways for diffusion and leading to rapid failure. Similarly, a high-entropy alloy could, over long-term annealing, begin to phase-separate into the simpler, more thermodynamically stable binary or ternary compounds that it was formed from. This would also create new phase boundaries and destroy the homogeneous lattice distortion responsible for its sluggish diffusion.

This strategy, therefore, essentially pauses degradation, but the thermodynamic driving force for failure remains a constant threat. It makes predicting the device's true operational lifetime exceptionally challenging. A simple Arrhenius plot based on initial, slow degradation cannot account for a sudden, non-linear failure event, such as crystallisation. This metastability is the fundamental trade-off of this brilliant but uncertain strategy, highlighting a critical area for future research: understanding not only the initial performance of these barriers but also their long-term structural evolution under operational stress.

The necessity of kinetic suppression is even more pronounced in the case of superionic conductors, such as copper and silver chalcogenides (e.g., Cu_2−xSe and Ag₂Te), which exhibit exceptional thermoelectric performance but suffer from catastrophic failure driven by electromigration.^65,66 Unlike conventional alloys, where degradation is dominated by chemical interdiffusion, these “liquid-like” materials undergo rapid cation migration under an electric current, resulting in Cu⁺/Ag⁺ depletion at the cathode and the precipitation of metallic material at the anode. Consequently, thermodynamic inertness alone is insufficient to guarantee stability for these systems. For these material classes, interface design must prioritise kinetic suppression, utilising strictly ion-blocking but electronically conducting interlayers, such as graphitic carbon barriers or dense refractory diffusion inhibitors, to physically arrest the ionic flux. Without such kinetically engineered barriers, even chemically compatible interfaces remain vulnerable to void formation and device disintegration during long-term operation.^67,68 In this sense, practical deployment of Cu/Ag chalcogenide superionic thermoelectrics will likely rely on architected, ion-confining interfaces rather than direct metallization.

While the four strategies above provide a qualitative framework, interface design in practice requires approximate numerical targets. Drawing on reported data for stable modules and joints, we therefore propose working ‘target design windows’ for the key metrics that control interface reliability: specific contact resistivity, shear strength, CTE mismatch, long-term degradation rate, and reaction layer thickness. These literature-derived benchmarks are summarised in Table 1 and are intended as practical design guidelines rather than strict universal limits.

Table 1 Summary of the proposed target design windows and performance thresholds for reliable thermoelectric interfaces

Key parameter	Target/threshold	Scientific rationale	Ref.
Contact resistivity (ρc)	≤10^−4 Ω cm^2	Essential to limit parasitic Joule heating and voltage drops; values in the 10^−4–10^−3 Ω cm^2 range significantly degrade effective zT (zTeff) and power output, particularly in high-current generators	69–75
Shear strength (τ)	>20 MPa	Essential to withstand mechanical shock during module assembly (dicing) and accumulated shear stress from thermal cycling. A strength exceeding 20 MPa ensures that the interface is not the structural weak point relative to the bulk thermoelectric material	76–79
CTE mismatch (Δα)	<10–20%	Crucial to minimise residual stress and cycling fatigue during thermal operations. Mismatches exceeding 20% typically generate shear stresses at the interface that surpass the bond strength, leading to microcracking and eventual delamination	80–83
Degradation rate	< 10% over ≥1000 h (at Top)	Limits performance drift to acceptable bounds. A resistance increase exceeding 10% typically signals the transition to non-linear degradation modes (e.g., void coalescence or runaway Joule heating), marking the device's functional end-of-life	84–88
Reaction layer thickness	≤20 µm (self-limiting)	Context-dependent: while inert barriers require minimal thickness (<1 µm), engineered reactive layers (strategy 2) are mechanically stable up to ∼20 µm. The critical failure mode is not thickness itself, but uncontrolled growth (>50 µm), which triggers cracking	88–92

---

Fig. 5 maps how different thermoelectric contact designs populate the joint “property space” when both electrical and mechanical requirements are considered. Along the x-axis, each symbol represents a distinct thermoelectric material/contact material architecture, while the y-axis reports its aged specific contact resistivity and shear strength, with simple thresholds drawn at ρ_c ≤ 100 µΩ cm² and τ ≥ 20 MPa to indicate a practical design window for device operation. Systems that fall below the resistivity threshold and above the strength threshold demonstrate that carefully engineered interfaces, utilising concepts such as tailored reactivity, graded or alloyed barriers, and CTE-matched electrodes, can simultaneously satisfy both transport and reliability constraints. Conversely, points lying outside this window, particularly those with high ρ_c and modest τ, exemplify failure modes associated with thin or overly reactive barriers, highlighting the risks of relying on nominally “standard” contact schemes. Taken together, the plot emphasises the central perspective that future progress will come from consciously positioning contact designs within this confined, jointly optimised region of the property space, rather than pursuing electrical or mechanical performance in isolation.

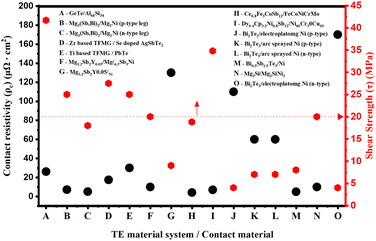Fig. 5 Multi-objective assessment of interfacial reliability. A mapping of the joint property space for various distinct thermoelectric material/contact architectures (A–O), plotting aged specific contact resistivity (ρ_c, left axis) against shear strength (τ, right axis). The dotted lines delineate a proposed “target design window” (by ρ_c ≤ 100 µΩ cm² and τ ≥ 20 MPa), representing the threshold for reliable device operation. Data points falling within this quadrant indicate architectures where advanced design strategies (e.g., graded interlayers or CTE-matched alloys) have successfully reconciled transport efficiency with mechanical robustness, while outliers highlight the limitations of standard metallization schemes. (See the inset for material system codes).^93–101

6. The decisive role of thermoelectric module preparation

The four strategies discussed thus far, thermodynamic inertness, controlled reactivity, thermomechanical compliance, and kinetic suppression, represent the design philosophies for an ideal interface. However, these philosophies are not independent choices; their success or failure is inextricably linked to the fabrication method used to create the junction. The specific preparation method is arguably the single most decisive factor, as it acts as the real-world filter that determines whether a theoretical design can be practically realised. The choice of the process, with its unique parameters of temperature, pressure, and time, can just as easily enable a sophisticated strategy as it can catastrophically undermine it. This final pillar, therefore, analyses the most common preparation methods as strategies in themselves, each with a unique profile of advantages and critical trade-offs.

High-temperature, high-pressure methods, such as Spark Plasma Sintering (SPS) and hot-pressing, are the established workhorses of the field, particularly for high-performance, high-temperature materials. The combination of high temperature and mechanical pressure is exceptionally effective at creating dense, robust metallurgical bonds and ensuring intimate physical contact, which is critical for minimising both electrical and thermal contact resistance.^102,103 This approach is particularly successful for joining dissimilar and brittle materials that are otherwise difficult to bond. For instance, in the fabrication of segmented legs, a highly stable junction between a high-temperature half-Heusler alloy and a p-type Ca₃Co₄O₉ oxide was achieved using an Ag foil brazing process within an SPS system. This technique yielded an exceptionally low contact resistance of ∼100 µΩ cm² and demonstrated excellent durability, with analysis confirming clean, reaction-free interfaces.^104,105 In this context, the SPS process was the key enabler, providing the necessary energy and pressure to form a perfect bond without shattering the brittle oxide. However, this high-energy approach is a double-edged sword. The high temperatures (often > 800 °C) and pressures can be a critical flaw. They provide an enormous amount of thermal energy that can easily overwhelm a kinetic barrier (strategy 4), causing an amorphous layer to crystallise or an HEA to phase-separate before the device is ever even used. Furthermore, this method is completely unsuitable for materials with volatile components, such as Zintl phases (Mg and Zn) or chalcogenides (Te and Se), which would sublimate and decompose under these conditions.

Brazing and soldering represent a more traditional, liquid-phase approach to joining. These methods are often preferred for their scalability and compatibility with complex, multi-leg module assemblies. The primary advantage is the ability to form strong joints at temperatures significantly lower than the melting point of the thermoelectric material itself. The selection of the braze or solder alloy is a critical design choice.^106–108 For example, in BiCuSeO devices, soldering with a BiCu₈₀AgP alloy via a low-temperature (600 °C) hot pressing process proved vastly superior to high-temperature soldering. The controlled, low-temperature process was key to success, as it prevented the segregation of interfacial phases and the formation of resistive compounds, such as Bi₂O₃ and Cu₂Se, leading to a uniform, robust joint and a 6.6-fold increase in operational lifetime.¹⁰⁹ The con of this strategy, however, is its inherent complexity. The introduction of a braze or solder adds a new, multi-component layer to the interface, creating two new junctions that must be managed (e.g., TE-to-braze and braze-to-electrode). This new layer can be a source of thermomechanical stress from its own CTE, or worse, an active source of diffusion, as is famously the case with Sn-based solders in Bi₂Te₃ modules, where Sn diffusion leads to the formation of brittle, high-resistance SnTe intermetallics.^110–112

To overcome the challenges of both high-temperature pressing and traditional brazing, a new class of advanced, low-temperature joining techniques has emerged, often enabling the most sophisticated interfacial designs. These methods are specifically designed to create a mechanically strong, thermally stable joint at a low processing temperature, making them the only viable option for highly volatile materials. For Zintl phases, which cannot survive high-temperature processing, the low-temperature sintering of silver nanoparticles (Ag NPs) has been a breakthrough. This technique enables bonding at temperatures as low as 573 K (300 °C) by harnessing the nanoscale properties of the particles. The resulting joint, composed of sintered, porous silver, is mechanically robust and, critically, remains stable at much higher operating temperatures, enabling the fabrication of full-Zintl devices with exceptional conversion efficiencies.⁴⁸ A parallel set of techniques is Transient Liquid Phase (TLP) and Solid-Liquid Interdiffusion (SLID) bonding.^36,113 These methods use a low-melting-point interlayer (e.g., Sn or Al) that is designed to react completely with the bonding surfaces (e.g., Co or Ni) during a controlled thermal process. This reaction consumes the low-temperature liquid and forms new, high-melting-point intermetallic compounds, creating a joint that remains stable far above its own fabrication temperature. This controlled reactive process, successfully employed in skutterudite and Zintl systems, produces contacts with exceptionally low resistivity. The trade-off for these advanced methods is their complexity, cost, and sensitivity. They often require pristine, vacuum-prepared surfaces and are far less tolerant of process variations than a simple hot-press.

Finally, it is crucial to distinguish module-level fabrication techniques (such as SPS) from the fundamental research techniques used to study them. Our perspective is that an overemphasis on manufacturing-oriented methods, which are inherently complex, has created a knowledge gap. The Diffusion Couple Technique (DCT) is a central concept in this fundamental science. While not a fabrication method, its primary advantage is its ability to isolate pure thermal-kinetic effects from the mixed variables of pressure and thermomechanical stress. This provides a clean environment for fundamental analysis, which is often obscured in a multi-variable manufacturing process. This is a critical advantage, because while complex phases (such as Ni_3−xTe and Ni₅Pb₂Te₃) that we identified in the PbTe/Ni system may also form during a rapid fabrication process, the convoluted nature of those methods makes it nearly impossible to study their fundamental mechanisms of formation and transformation. The DCT, by isolating the variables, is the most fundamental method that provides the clean, time-dependent data needed to map this complex phase evolution, validate thermodynamic (CALPHAD) models, and identify novel, metastable phases. It is the ideal platform for studying and systematically comparing the role of alloying additions (such as Fe and Co) in Ni contact metal for PbTe, allowing the quantification, at an atomic level, of how these elements (e.g., Ni–Fe and Ni–Co) fundamentally alter the reaction pathways.^114–116

However, this specialised focus is also the DCT's primary drawback, and our own comparative analysis from this perspective highlights the gap. As a pure research tool, its results do not capture the multi-physics reality of a real-world device for three critical reasons. First, it neglects the influence of fabrication-induced variables. Therefore, while our DCT study (Fig. 6b and c) shows the formation of the brittle Ni₃Te₂ and Ni₅Pb₂Te₃ phases, we cannot predict from this experiment alone whether the high pressure of SPS fabrication would have altered or even suppressed their formation entirely. Second, it fails to account for thermomechanical stress. A diffusion couple is annealed isothermally, whereas a real module operates under a steep thermal gradient. This means our DCT results, which show chemically stable Ni–Fe and Ni–Co layers (Fig. 6b and c), tell us nothing about their mechanical integrity. We cannot know if that same layer would crack and fail under the thermal gradient's shear stress, much like the catastrophic failure we highlighted in the Ni/Mg₂Si joint mentioned in strategy 3 (Fig. 3a). Third, the technique imposes stringent experimental constraints even to achieve this idealised state. From our experience, maintaining the chemical integrity of these highly reactive metal/semiconductor interfaces is a significant challenge. It requires meticulously sealing the couples in quartz ampoules under a high vacuum, typically on the order of 10⁻⁵ Torr, to prevent oxidative interference during high-temperature annealing, a step that adds significant complexity and time to the analysis. This highlights the critical gap that future research must bridge, connecting the fundamental, thermo-chemical data from laboratory couples with the complex, thermo-mechanical reality of a fully assembled and operational thermoelectric module.

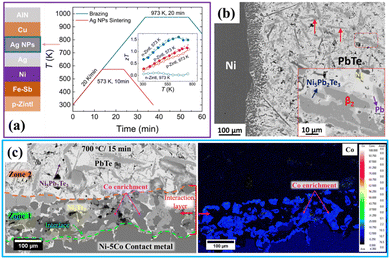Fig. 6 Comparative analysis of module-level fabrication and interface design strategies. (a) Conventional high-temperature brazing (973 K) vs. breakthrough low-temperature Ag nanoparticle sintering (573 K), enabling stable assembly of volatile materials like Zintl phases.⁴⁸ (b) Baseline Diffusion Couple Technique (DCT) study of a Ni/PbTe interface showing uncontrolled reactions and thick brittle intermetallics (Ni₅Pb₂Te₃ and β₂-Ni₃Te₂).¹¹⁴ (Adapted from Kumar et al., with permission from Elsevier).¹¹⁴ (c) Engineered solution using strategy 2 (controlled reactivity): 5 at% Co in Ni suppresses vigorous reactions, forming a stable Ni₃Te₂ layer and a Co-enriched zone. This (b) and (c) comparison illustrates how DCT informs alloying strategies for chemically robust interfaces. (unpublished work from Surafel Shiferaw Legese and Kamanio Chattopadhyay).

7. Conclusion and outlook

The development of robust interfaces remains the critical bottleneck in transitioning thermoelectric generators from laboratory prototypes to reliable power sources. This review has critically examined the transition from empirical metallization to a rigorous, multi-objective design paradigm. Fundamentally, we argue that interface design is not merely about selecting materials, but about navigating two intrinsic physical conflicts.

7.1. Electronic transparency vs. chemical inertness

High electrical conductivity requires strong orbital overlap (metallic bonding), which inherently drives chemical reactivity. Conversely, thermodynamic stability implies closed-shell interactions or strong ionic bonds that often impede the electron flow.

7.2. Mechanical strength vs. thermomechanical compliance

Strong, rigid interfaces resist shear forces but accumulate catastrophic stress during thermal cycling, whereas compliant interfaces relieve stress but often lack the mechanical integrity required for module assembly.

The four strategies discussed represent distinct approaches for resolving these dilemmas. Thermodynamic inertness and controlled reactivity operate within the bounds of these intrinsic material constraints, optimising either stability or conductivity at the expense of the other. In contrast, thermomechanical compliance and kinetic suppression represent “architectural decoupling” strategies. By introducing diffusion barriers (kinetic) or stress-absorbing interlayers (compliance), these strategies physically separate the conflicting requirements, allowing the interface to be both chemically inert yet electronically conductive, or mechanically strong yet structurally compliant.

7.3. Outlook and future directions

To translate these conceptual strategies into practical realities, the community must move beyond ad hoc experimentation toward a more standardised and data-driven approach. We propose the following roadmap.

7.3.1. Standardisation of reliability benchmarks and reporting protocols. The field currently suffers from fragmented data, where stability is often defined arbitrarily. We propose that the community adopts the “target design windows” defined in this review, ρ_c ≤ 10⁻⁴ Ω cm², τ ≥ 20 MPa, and CTE mismatch <20%, as standard pass/fail reporting criteria. Furthermore, reporting standards must evolve: future publications on TE contacts should mandatorily include not just initial resistivity, but also time-dependent evolution data (Δρ_c(t)) and post-ageing mechanical strength to allow for cross-study comparisons.

7.3.2. From static to operando characterisation. Reliance on isothermal diffusion couples (DCT) leads to blind spots regarding failure mechanisms driven by gradients and fields. Future research must prioritise operando characterisation techniques. Specifically, the integration of in situ TEM to observe phase nucleation in real-time and high-temperature micro-mechanical testing to measure strength evolution under service conditions is essential. Understanding how electric currents drive electromigration in superionic conductors (e.g., Cu_2−xSe) or how thermal cycling induces crack propagation in brittle silicides will require testing protocols that mimic the dynamic module environment.

7.3.3. Data-driven discovery and high-throughput screening. The search for stable diffusion barriers and interlayers is currently a slow and iterative process. There is a significant opportunity to leverage materials genome approaches and Machine Learning (ML) to accelerate this process. By compiling databases of interface reaction energies, diffusion coefficients, and phase diagram data, ML models could predict the stability of thousands of potential barrier materials against common TE matrices. High-throughput experimental validation using diffusion multiples could then rapidly verify these predictions, moving the field from trial-and-error to rational design.

7.3.4. Bridging the gap to manufacturing and scalability. A scientifically perfect interface is useless if it cannot be manufactured at scale. Research must expand to assess the compatibility of advanced interface designs with industrial processes such as Atmospheric Plasma Spraying (APS), Spark Plasma Sintering (SPS), and automated brazing. We must rigorously evaluate how processing variables, such as sintering pressure, plasma velocity, and surface roughness, impact the integrity of the contact. Strategies that rely on fragile nanostructures or expensive vacuum deposition may need to be adapted for robust, low-cost manufacturing.

7.3.5. Towards functionally graded architectures. Ultimately, the ideal thermoelectric interface is unlikely to be a single material layer. The future lies in Functionally Graded Materials (FGMs) and architected multi-layers that spatially resolve the intrinsic tensions discussed above. By designing continuous gradients in composition and porosity, we can smooth out CTE mismatches, suppress atomistic diffusion, and maintain low electrical resistance simultaneously. The realisation of such complex architectures will require advances in additive manufacturing and multi-material sintering techniques.

Mastering these interfaces is the final frontier in enabling durable, commercially viable thermoelectric generators that can operate reliably for decades.

Author contributions

Surafel Shiferaw Legese: conceptualisation, methodology, formal analysis, investigation, writing – original draft. Kamanio Chattopadhyay: resources, supervision, funding acquisition, writing – review & editing, project administration. Both authors have read and agreed to the published version of the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

This article is a perspective review of previously published studies, and all data supporting the findings are available in the cited references.

Acknowledgements

The authors acknowledge support from the Department of Materials Engineering, Indian Institute of Science. We are also grateful to Professor Alok Paul and Dr Dipanjan Kumar for their insightful discussions. One of the authors (Kamanio Chattopadhyay) acknowledges support from the Anusandan National Research Foundation through the award of a National Science Chair. The authors acknowledge the use of Google's Gemini Pro 2.5 for assistance in rephrasing and rewriting sections of the manuscript to improve clarity and readability. The authors reviewed, edited, and verified all AI-generated content and are fully responsible for the final manuscript.

References

1. J. He and T. M. Tritt, Science, 2017, 357(1979), eaak9997.
2. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
3. T. Cole, Science, 1983, 221(1979), 915–920.
4. S. S. Legese and F. E. Olu, J. Indian Inst. Sci., 2022, 102, 237–279.
5. P. Baskaran and M. Rajasekar, RSC Adv., 2024, 14, 21706–21744.
6. R. Singh, S. Dogra, S. Dixit, N. I. Vatin, R. Bhardwaj, A. K. Sundramoorthy, H. C. S. Perera, S. P. Patole, R. K. Mishra and S. Arya, Hybrid Adv., 2024, 5, 100176.
7. H. Jouhara, N. Khordehgah, S. Almahmoud, B. Delpech, A. Chauhan and S. A. Tassou, Therm. Sci. Eng. Prog., 2018, 6, 268–289.
8. D. D. Sarma, ACS Energy Lett., 2021, 6, 3715–3718.
9. S. S. Legese, D. Chandravanshi, S. S. S. Gadhavajhala, V. Pal, A. T. Serbesa, B. Srinivasan, F. E. Olu and C. S. Tiwary, J. Mater. Sci., 2025, 60, 1313–1327.
10. G. Tan, F. Shi, S. Hao, L.-D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2016, 7, 12167.
11. H. S. Kim, W. Liu, G. Chen, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci., 2015, 112, 8205–8210.
12. S. Sulaiman, I. Sudin, U. M. B. Al-Naib and M. F. Omar, Cryst., 2022, 12(8), 1076.
13. Q. Zhu, S. Wang, X. Wang, A. Suwardi, M. H. Chua, X. Y. D. Soo and J. Xu, Nanomicro Lett., 2021, 13, 119.
14. S. Wang, C. Chang, S. Bai, B. Qin, Y. Zhu, S. Zhan, J. Zheng, S. Tang and L.-D. Zhao, Chem. Mater., 2023, 35, 755–763.
15. W. Zuo, H. Chen, Z. Yu, Y. Fu, X. Ai, Y. Cheng, M. Jiang, S. Wan, Z. Fu, R. Liu, G. Cheng, R. Xu, L. Wang, F. Xu, Q. Zhang, D. Makarov and W. Jiang, Nat. Mater., 2025, 24, 735–742.
16. Y. Fu, X. Ai, Z. Hu, S. Zhao, X. Lu, J. Huang, A. Huang, L. Wang, Q. Zhang and W. Jiang, Nat. Commun., 2024, 15, 9355.
17. J. Chu, J. Huang, R. Liu, J. Liao, X. Xia, Q. Zhang, C. Wang, M. Gu, S. Bai, X. Shi and L. Chen, Nat. Commun., 2020, 11, 2723.
18. K. Yue, W. Zhu, Q. He, X. Nie, X. Qi, C. Sun, W. Zhao and Q. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 39053–39061.
19. S. Ayachi, S. Park, B. Ryu, S. Park, E. Mueller and J. de Boor, Adv. Phys. Res., 2024, 3, 2300077.
20. Y. Zhang, H. He, C. Niu, Y. Wu, M. Liu, S. Liu, Y. Liu, C. Wu and M. Rong, ACS Appl. Mater. Interfaces, 2024, 16, 1137–1147.
21. M. T. Barako, W. Park, A. M. Marconnet, M. Asheghi and K. E. Goodson, J. Electron. Mater., 2013, 42, 372–381.
22. H. Wu, A. T. Wu, P. Wei and S. Chen, Mater. Res. Lett., 2018, 6, 244–248.
23. M. M. Al Malki, G. Jeffrey Snyder and D. C. Dunand, Int. Mater. Rev., 2023, 68, 1050–1074.
24. J. He and T. M. Tritt, Science, 2017, 357(1979), eaak9997.
25. S. Puthran, G. S. Hegde and A. N. Prabhu, J. Electron. Mater., 2024, 53, 5739–5768.
26. R. Bjørk, J. Electron. Mater., 2015, 44, 2869–2876.
27. R. Liu, Y. Xing, J. Liao, X. Xia, C. Wang, C. Zhu, F. Xu, Z.-G. Chen, L. Chen, J. Huang and S. Bai, Nat. Commun., 2022, 13, 7738.
28. M. Liu, X. Zhang, Y. Wu, Z. Bu, Z. Chen, W. Li and Y. Pei, ACS Appl. Mater. Interfaces, 2023, 15, 6169–6176.
29. H.-C. Hsieh, C.-H. Wang, W.-C. Lin, S. Chakroborty, T.-H. Lee, H.-S. Chu and A. T. Wu, J. Alloys Compd., 2017, 728, 1023–1029.
30. A. Singh, S. Bhattacharya, C. Thinaharan, D. K. Aswal, S. K. Gupta, J. V Yakhmi and K. Bhanumurthy, J. Phys. D Appl. Phys., 2009, 42, 015502.
31. P. Jood, M. Ohta, A. Yamamoto and M. G. Kanatzidis, Joule, 2018, 2, 1339–1355.
32. B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, Science, 2021, 371(1979), 830–834.
33. X. Hu, P. Jood, M. Ohta, M. Kunii, K. Nagase, H. Nishiate, M. G. Kanatzidis and A. Yamamoto, Energy Environ. Sci., 2016, 9, 517–529.
34. A. Grytsiv, G. Rogl, E. Bauer and P. Rogl, J. Phase Equilib. Diffus., 2020, 41, 365–377.
35. M. Gu, S. Bai, J. Wu, J. Liao, X. Xia, R. Liu and L. Chen, J. Mater. Res., 2019, 34, 1179–1187.
36. C. Stiewe and E. Müller, Solid State Sci., 2024, 148, 107423.
37. T. Xing, Q. Song, P. Qiu, Q. Zhang, M. Gu, X. Xia, J. Liao, X. Shi and L. Chen, Energy Environ. Sci., 2021, 14, 995–1003.
38. M. Hong, M. Li, Y. Wang, X.-L. Shi and Z.-G. Chen, Adv. Mater., 2023, 35, 2208272.
39. G.-K. Ren, L. Song, R. Liu, L. Ma, Y. Tian, Z. Wei, Y. Shi, Z. Zheng, Y. Zhao and Y.-H. Lin, Appl. Phys. Rev., 2025, 12, 021303.
40. M. Furci, G. Marini and M. Calandra, Phys. Rev. Lett., 2024, 132, 236101.
41. J. Li, S. Zhao, J. Chen, C. Han, L. Hu, F. Liu, W. Ao, Y. Li, H. Xie and C. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 18562–18569.
42. C.-H. Kung, J.-Y. Huang, K.-W. Cheng, C.-H. Ku, Q.-M. Huang, V. K. Ranganayakulu, Y.-Y. Chen, Y.-G. Lin, S.-J. Chiu and A. T. Wu, Mater. Chem. Phys., 2024, 323, 129649.
43. J. Zhu, F. Liu, B. Gong, X. Wang, W. Ao, C. Zhang, Y. Li, L. Hu, H. Xie, K. Gu and J. Li, J. Electron. Mater., 2019, 48, 6815–6822.
44. Y. Wang, J. Chen, Y. Jiang, M. Ferhat, S. Ohno, Z. A. Munir, W. Fan and S. Chen, ACS Appl. Mater. Interfaces, 2022, 14, 33419–33428.
45. S. Song, Z. Liang, C. Xu, Y. Wang, X. Shi, W. Ren and Z. Ren, Soft Sci., 2022, 2(3), 13.
46. Z. Liu, L. Shen, J. Yan, Z. Liu and Z. Liu, J. Alloys Compd., 2024, 1001, 175101.
47. T.-H. Chuang, S.-W. Hsu, Y.-C. Lin, W.-T. Yeh, C.-H. Chen, P.-I. Lee, P.-C. Wu and H.-P. Cheng, J. Electron. Mater., 2020, 49, 3391–3399.
48. L. Yin, X. Li, X. Bao, J. Cheng, C. Chen, Z. Zhang, X. Liu, F. Cao, J. Mao and Q. Zhang, Nat. Commun., 2024, 15, 1468.
49. X. Shao, R.-H. Liu, L. Wang, J. Chu, G.-H. Bai, S.-Q. Bai, M. Gu, L.-N. Zhang, W. Ma and L.-D. Chen, J. Inorg. Mater., 2020, 35, 224–230.
50. Z. Zhang, M. Gurtaran and H. Dong, ACS Appl. Energy Mater., 2024, 7, 5629–5646.
51. L. Yin, C. Chen, F. Zhang, X. Li, F. Bai, Z. Zhang, X. Wang, J. Mao, F. Cao, X. Chen, J. Sui, X. Liu and Q. Zhang, Acta Mater., 2020, 198, 25–34.
52. N. H. Pham, N. Farahi, H. Kamila, A. Sankhla, S. Ayachi, E. Müller and J. de Boor, Mater. Today Energy, 2019, 11, 97–105.
53. B. Jayachandran, B. Prasanth, R. Gopalan, T. Dasgupta and D. Sivaprahasam, Mater. Res. Bull., 2021, 136, 111147.
54. X. Wu, Y. Lin, Z. Han, H. Li, C. Liu, Y. Wang, P. Zhang, K. Zhu, F. Jiang, J. Huang, H. Fan, F. Cheng, B. Ge and W. Liu, Adv. Energy Mater., 2022, 12, 2203039.
55. R. Chetty, J. Babu and T. Mori, ACS Appl. Energy Mater., 2024, 7, 12112–12118.
56. J. Li, S. Zhao, J. Chen, G. Bai, L. Hu, F. Liu, W. Ao, Y. Li, H. Xie and C. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 44858–44865.
57. B. I. Boltaks, J. I. Carasso and H. J. Goldsmid, Defect Diffus. Forum, 1970, 4, 360–369.
58. J. Jaseliunaite and A. Galdikas, Materials, 2020, 13(5), 1051.
59. C.-C. Yu, H. Wu, M. T. Agne, I. T. Witting, P.-Y. Deng, G. J. Snyder and J. P. Chu, APL Mater., 2019, 7, 013001.
60. F. Guo, W. Shi, Y. Sun, H. Tong, H. Wu, Z. Liu, W. Cai and J. Sui, Acta Mater., 2025, 284, 120591.
61. H. Wang, F. Liu, T. Zhang, G. Yang and Y. Zhou, Acta Mater., 2009, 57, 3072–3083.
62. Z. Cui, F. Gao and J. Qu, J. Mech. Phys. Solids, 2013, 61, 293–310.
63. H. Pan, Z. Sun, H. Geng, Q. Chang, B. Zhang and L. Zhang, J Materiomics, 2025, 11, 100859.
64. Z. Sun, X. Chen, J. Zhang, H. Geng and L. X. Zhang, J Materiomics, 2022, 8, 882–892.
65. P. Qiu, M. T. Agne, Y. Liu, Y. Zhu, H. Chen, T. Mao, J. Yang, W. Zhang, S. M. Haile, W. G. Zeier, J. Janek, C. Uher, X. Shi, L. Chen and G. J. Snyder, Nat. Commun., 2018, 9, 2910.
66. L. Staab, T. Kötzsch, T. J. Noack and O. Oeckler, Appl. Phys. Lett., 2023, 122, 083901.
67. D. Yang, H. Bai, X. Su, Z. Li, T. Luo, J. Li, H. Tang, H. Luo, Q. Zhang, C. Uher, J. Wu and X. Tang, Cell Rep. Phys. Sci., 2021, 2, 100345.
68. P. Ying, Q. Jian, Y. Gong, T. Song, Y. Yang, Y. Geng, J. Huang, R. Sun, C. Chen, T. Shen, Y. Li, W. Dou, C. Liang, Y. Liu, D. Xiang, T. Feng, X. Fei, Y. Zhang, K. Song, Y. Zhang, H. Wu and G. Tang, Nat. Commun., 2025, 16, 3305.
69. A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466–479.
70. G. J. Snyder and T. S. Ursell, Phys. Rev. Lett., 2003, 91, 148301.
71. J. Mao, J. Shuai, S. Song, Y. Wu, R. Dally, J. Zhou, Z. Liu, J. Sun, Q. Zhang, C. dela Cruz, S. Wilson, Y. Pei, D. J. Singh, G. Chen, C.-W. Chu and Z. Ren, Proc. Natl. Acad. Sci., 2017, 114, 10548–10553.
72. M. S. El-Genk and H. H. Saber, Energy Convers. Manage., 2003, 44, 1069–1088.
73. V. Trivedi, M. Battabyal, B. S. Murty and R. Gopalan, Ceram. Int., 2022, 48, 29175–29182.
74. Z. Sun, X. Chen, J. Zhang, H. Geng and L. X. Zhang, J Materiomics, 2022, 8, 882–892.
75. T. Caillat, A. Zoltan, L. Zoltan and G. J. Snyder, US Pat., US6673996B2, 2004.
76. D. Zhao, X. Li, L. He, W. Jiang and L. Chen, Intermetallics, 2009, 17, 136–141.
77. H. Xia, F. Drymiotis, C.-L. Chen, A. Wu, Y.-Y. Chen and G. Jeffrey Snyder, J. Mater. Sci., 2015, 50, 2700–2708.
78. B. S. Yilbas, S. S. Akhtar and A. Z. Sahin, Energy, 2016, 114, 52–63.
79. Z. Sun, X. Chen, J. Zhang, H. Geng and L. X. Zhang, J Materiomics, 2022, 8, 882–892.
80. A. Wieder, J. Camut, A. Duparchy, R. Deshpande, A. Cowley, E. Müller and J. de Boor, Mater. Today Energy, 2023, 38, 101420.
81. S. He, S. Lehmann, A. Bahrami and K. Nielsch, Adv. Energy Mater., 2021, 11, 2101877.
82. W. Li, S. Ghosh, N. Liu and B. Poudel, Joule, 2024, 8, 1274–1311.
83. A. d P. Shyikira, G. Skomedal and P. Hugh Middleton, Mater. Today: Proc., 2021, 44, 3467–3474.
84. Z. Bu, X. Zhang, Y. Hu, Z. Chen, S. Lin, W. Li, C. Xiao and Y. Pei, Nat. Commun., 2022, 13, 237.
85. J. Bu, Z. Sun, H. Pan, Z. Chen, J. Li, H. Geng, R. Liu and L. Zhang, J. Mater. Sci. Technol., 2026, 259, 36–43.
86. P. Amirkhizi, M. Hedayati, M. A. Madre, O. J. Dura, M. A. Torres, A. Sotelo, A. V Kovalevsky and Sh. Rasekh, J. Alloys Compd., 2025, 1013, 178628.
87. P. Ying, H. Reith, K. Nielsch and R. He, Small, 2022, 18, 2201183.
88. P. Ziolkowski, P. Blaschkewitz and E. Müller, Measurement, 2021, 177, 109247.
89. Y. Fu, Q. Zhang, Z. Hu, M. Jiang, A. Huang, X. Ai, S. Wan, H. Reith, L. Wang, K. Nielsch and W. Jiang, Energy Environ. Sci., 2022, 15, 3265–3274.
90. H. Xia, F. Drymiotis, C.-L. Chen, A. Wu and G. J. Snyder, J. Mater. Sci., 2014, 49, 1716–1723.
91. Y. Fu, X. Ai, Z. Hu, S. Zhao, X. Lu, J. Huang, A. Huang, L. Wang, Q. Zhang and W. Jiang, Nat. Commun., 2024, 15, 9355.
92. A. d P. Shyikira, G. Skomedal and P. Hugh Middleton, Mater. Today: Proc., 2021, 44, 3467–3474.
93. S. Chen, T. Zhang, J. Cheng, B. Ma, X. Ma, X. Li, L. Yin, L. Wen, J. Mao, F. Cao and Q. Zhang, Natl. Sci. Rev., 2025, 12, nwaf227.
94. V. Trivedi, M. Battabyal, B. S. Murty and R. Gopalan, Ceram. Int., 2022, 48, 29175–29182.
95. W. Liu and S. Bai, J Materiomics, 2019, 5, 321–336.
96. G. Joshi, D. Mitchell, J. Ruedin, K. Hoover, R. Guzman, M. McAleer, L. Wood and S. Savoy, J. Mater. Chem. C, 2019, 7, 479–483.
97. S. Chen, Y. Chen, S. Ohno, L. Xu, W. Fan, L. Xue, M. Ferhat and Y. Wu, Phys. Status Solidi A, 2020, 217, 1901035.
98. Y. Wang, J. Chen, Y. Jiang, M. Ferhat, S. Ohno, Z. A. Munir, W. Fan and S. Chen, ACS Appl. Mater. Interfaces, 2022, 14, 33419–33428.
99. X. Wu, Z. Han, Y. Zhu, B. Deng, K. Zhu, C. Liu, F. Jiang and W. Liu, Acta Mater., 2022, 226, 117616.
100. J. Zhang, P. Wei, H. Zhang, L. Li, W. Zhu, X. Nie, W. Zhao and Q. Zhang, ACS Appl. Mater. Interfaces, 2023, 15, 22705–22713.
101. Z. Sun, X. Chen, J. Zhang, H. Geng and L. X. Zhang, J Materiomics, 2022, 8, 882–892.
102. Y. Le Godec and S. Le Floch, Materials, 2023, 16(3), 997.
103. W.-T. Chiu, C.-L. Chen and Y.-Y. Chen, Sci. Rep., 2016, 6, 23143.
104. W. Li, A. Nozariasbmarz, R. A. Kishore, H. B. Kang, C. Dettor, H. Zhu, B. Poudel and S. Priya, ACS Appl. Mater. Interfaces, 2021, 13, 53935–53944.
105. L. T. Hung, N. Van Nong, L. Han, R. Bjørk, P. H. Ngan, T. C. Holgate, B. Balke, G. J. Snyder, S. Linderoth and N. Pryds, Energy Technol., 2015, 3, 1143–1151.
106. J. H. Grebenkemper, Y. Hu, D. Barrett, P. Gogna, C.-K. Huang, S. K. Bux and S. M. Kauzlarich, Chem. Mater., 2015, 27, 5791–5798.
107. J. Zhang, Q. Liu, K.-F. Liu, W.-J. Tan, X.-C. Liu and S.-Q. Xia, Inorg. Chem., 2021, 60, 4026–4033.
108. K. guo, Q. cao and J. zhao, J. Rare Earths, 2013, 31, 1029–1038.
109. J. Yi, X. Zhang, S. Chen, T. Sun, Q. Jiang and Y. Liu, Ceram. Int., 2025, 51, 10774–10782.
110. C. Jiang, X. Fan, Z. Rong, C. Zhang, G. Li, B. Feng, J. Hu and Q. Xiang, J. Electron. Mater., 2017, 46, 1363–1370.
111. S.-W. Pak, H. Tatsumi, J. Wang, A. T. Wu and H. Nishikawa, Intermetallics, 2025, 179, 108686.
112. C.-H. Wang, H.-C. Hsieh, Z.-W. Sun, V. K. Ranganayakulu, T.-W. Lan, Y.-Y. Chen, Y.-Y. Chang and A. T. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 27001–27009.
113. K. Placha, R. S. Tuley, M. Salvo, V. Casalegno and K. Simpson, Materials, 2018, 11(12), 2483.
114. D. Kumar, M. P. Singh, N. Ravishankar and K. Chattopadhyay, Acta Mater., 2022, 241, 118385.
115. D. Kumar, C. A. Muse, O. E. Femi, N. Ravishankar and K. Chattopadhyay, Acta Mater., 2023, 261, 119410.
116. D. Kumar, M. P. Singh, N. Ravishankar and K. Chattopadhyay, Acta Mater., 2024, 263, 119535.

---