Microstructure engineered multiphase tellurides with enhanced thermoelectric efficiency
Varinder
Pal
a,
Duraisamy
Sivaprahasam
b,
Chandra Sekhar
Tiwary
 *a and
Manas
Paliwal
*a
*a and
Manas
Paliwal
*a
aDepartment of Metallurgical and Materials Engineering, Indian Institute of Technology, Kharagpur, West Bengal 721302, India. E-mail: manas.paliwal@metal.iitkgp.ac.in; chandra.tiwary@metal.iitkgp.ac.in
bCenter for Automotive Energy Materials (CAEM), International Advanced Research Centre for Powder Metallurgy & New Materials (ARCI), IIT Madras, Chennai, Tamil Nadu 600113, India
First published on 26th November 2025
Abstract
Thermoelectricity is one of the most important and extensively researched ways to recycle waste heat and enable efficient energy conversion without involving any movable parts. Multiphase thermoelectrics (TEs) are found to be better contenders than single-phase TEs, owing to their freedom to tune the interface, phase assemblage, defects, etc. Multiphase TEs provide the advantage of energy filtering, modulation doping, enhanced phonon scattering, higher structural integrity, and magnetic effects over single-phase materials. These engineered microstructural features and atomic arrangements result in a significant effect on the electronic and thermal transport in these materials. Moreover, tellurides among the chalcogenides have gained a lot of attention for their applicability as room-to-medium temperature range TE materials. In the present work, recent advancements in multiphase TEs based on tellurium are reviewed. Thus, this review focuses on some interesting ternary systems (Ag–Bi–Te, Bi–Cu–Te, Bi–Ga–Te, Bi–In–Te, Ga–In–Te, and Sn–Ga–Te) of the Ag–Bi–In–Ga–Sn–Te multicomponent system. Recent advancements in phase diagram engineering, microstructure evolution, processing conditions, and the role of these techniques in optimising the TE performance of multiphase materials belonging to the above-mentioned ternary systems have been discussed.
1 Introduction
Thermoelectricity, a solid-state mechanism, has shown its impactful influence on waste heat recovery by providing a direct conversion between thermal and electrical energy. The energy conversion efficiency of thermoelectric (TE) devices is directly dependent on the material properties and the thermal gradient across the two ends of the device. A material's ability is defined using a TE figure of merit (zT), which dictates the thermal and electronic transport in the material. Electronic and thermal transport is determined by the material properties like electrical conductivity (σ), Seebeck coefficient (S), and thermal conductivity (κ) of the material. These properties define the zT of a material, as given in eqn (1):1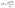 | (1) |
As evident in eqn (1), to achieve high zT, high σ and S with low κ are required. Thus, the material must conduct electrons/holes like that in crystalline materials, while heat must be conducted like that in amorphous materials to achieve the Phonon-Glass Electron-Crystal (PGEC) concept.2 There are various classes of materials being explored for TE applications, such as clathrates,3,4 chalcogenides,5–8 skutterudites,9,10 Half-Heusler,11,12 Zintl phases,13,14 oxide-based,15 organic,16,17 nanostructured TEs,18–21etc. Moreover, these materials can also be classified based on their operational temperature as low temperature (<573 K), room to medium temperature (573–873 K), and high temperature (>873 K) TE materials.2 Among the chalcogenides, tellurides are emerging TE materials with a wide application range in the room to medium temperature range.22–27 These materials offer applications in the fields of automobiles, power plants, medical science, electronics, aerospace, space exploration, solar TE hybrid systems, defence and military, biotechnology, etc.28,29 There are various telluride phases such as Bi2Te3, SnTe, In2Te3, In2Te5, InTe, GaTe, Ga2Te3, GaInTe2, AgBiTe2, Ag2Te, Cu3Te2, Cu2Te, etc.,30–40 which have shown significant improvement in their TE performance over time. Moreover, depending on the number of phases in a TE material, it can be classified as single-phase or multiphase. Single-phase materials comprise a characteristic crystal structure under specific composition, temperature, and pressure conditions. In the case of single-phase materials, doping, alloying, solid solutioning, changing processing conditions, etc., are usually used to tune charge and phonon transport.41 In addition, for a single-phase material, electronic band structure and phonon dispersion relationships can be easily generated using computational tools,42,43 which can aid in understanding the electron and phonon transport. On the other hand, in the case of multiphase materials, consisting of more than one phase (of the same or a different crystal structure), these calculations become computationally expensive and time-consuming due to structural complexity, an increased number of atoms, interfaces, defects, disorder, etc.44–46 Meanwhile, multiphase systems can aid in achieving selective conduction of high-energy charge carriers along with strong scattering of phonons.47 Although incorporating more than one phase in a material can open the freedom to tune the electronic and thermal transport, it also comes with computational and characterisation challenges. The coexistence of two or more phases with different concentrations, types of defects, and interfaces can alter the electronic and thermal transport significantly. Defects in these phases (vacancies, antisites, dislocations, stacking faults, etc.) can enhance or hinder electronic and thermal transport.48,49 In addition, depending on the type of phase (metallic, semiconductor, or insulator) present in the material, the transport behaviour differs.50 Therefore, phase diagrams, defects, and interface engineering are crucial in determining the material's overall TE response while developing multiphase TEs.
This review discusses recent advancements in some of the Telluride-based systems of the Ag–Bi–In–Ga–Sn–Te multicomponent system. In addition, various processing techniques like solid solutioning, directional solidification, heat treatments, etc., which are employed to prepare and tune the TE properties of these multiphase TEs, will be discussed. The review covers various aspects of multiphase TEs in six sections. We will start with a brief introduction to the fundamentals of TEs in Section 2. Section 3 will discuss the importance and the key strategies to develop multiphase TEs. In Section 4, the phase diagram engineering of six interesting ternary systems of the Ag–Bi–In–Ga–Sn–Te multicomponent system will be discussed. Section 5 shows microstructure engineering and its impact on the TE properties of these systems using different phase diagrams, processing conditions, composition control, and types of primary/secondary phases. Section 6 will discuss some of the theoretical models available, which are/can be used to strengthen the understanding of transport phenomena in multiphase TEs. At last, a summary with key achievements and challenges in multiphase TEs will be provided.
2 Fundamentals of thermoelectric properties
As mentioned in eqn (1), zT defines a material's ability to efficiently convert thermal to electrical energy or vice versa. Moreover, it requires a material to have high σ and S with low κ to achieve high zT. Electrical conductivity dictates the ability of a material to conduct electrons/holes under specific conditions (external potential, temperature, photons, etc.). Furthermore, the σ of a material depends on the concentration (n) and the mobility (µ) of charge carriers as described below:51| σ = nee|µe| + npe|µp| | (2) |
Similarly, ‘S’, a material property, defines the ability of a material to generate a voltage (ΔV) under an applied temperature difference (ΔT) across the material, which can be given by eqn (3):2
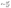 | (3) |
In addition to this, S can be related to n and the density of states effective mass (m*) through a simplified relationship for metals or degenerate semiconductors using the Mott relationship55 provided in eqn (4):
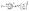 | (4) |
Thus, it is evident from eqn (2) and (4) that n shows direct dependence on σ, and an inverse dependence on S. In addition, the S shows a direct relationship with m*. Thus, optimum n and m* values are desired to have balanced S and σ. It has been observed that the n range lying between 1019 and 1021 cm−1 (semiconductor range) generally leads to optimised S and σ, resulting in the maximum zT. Thus, instead of higher doping levels, it is always an optimum doping level that should provide higher σ without significantly reducing S. In addition to this, S can be related to the density of states and the Fermi distribution function through the Mott relationship:55
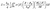 | (5) |
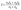 | (6) |
Other than σ and S, κ also plays a significant role in deciding the zT of a material. It usually comprises two contributions: lattice (κl) and electronic (κe), as shown in eqn (7). In the case of semiconductors and insulators, a large amount of heat is usually carried by the lattice, while for metals and degenerate semiconductors, the electronic contribution is also significant.
| κtot = κe + κl | (7) |
Using the Wiedemann–Franz Law,62κe is usually computed using the relationship given in eqn (8), where L is the Lorenz number, which is considered to be 2.44 × 10−8 WΩK−2 for metals and degenerate semiconductors.
| κe = σLT | (8) |
In addition, Kim et al.63 observed that L and the experimentally determined S can be related using a simple relationship eqn (9)
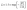 | (9) |
This relationship holds good for |S| >10 µV K−1.
In the case of narrow bandgap materials, there are enough electron–hole pairs created at high temperatures, which carry heat toward the cold end and recombine to liberate that heat, thus aiding in heat transfer.61 Therefore, the total electronic contribution to the thermal conductivity can be expressed as in eqn (10):
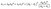 | (10) |
On the other hand, κl dictates how efficiently heat is carried by phonons in a material. Using classical kinetic theory, κl can be related to the heat capacity at constant volume (Cv), phonon group velocity (v), and mean free path (l) of the phonon by the following relationship:64
 | (11) |
Meanwhile, l can be related to relaxation time (τ) by eqn (12)
| l = τv | (12) |
The several scattering mechanisms responsible for limiting the mean-free path can be related to τ by eqn (13)
 | (13) |
In addition to the longitudinal zT of a TE (discussed above), transverse zT (shown in eqn (14)) for transverse thermoelectric materials also gained attention in recent years.74,75 Transverse thermoelectricity is based on the Nernst/Ettingshausen effect, wherein an electric field develops perpendicular to both the applied temperature gradient and the magnetic field.74 This is different from traditional longitudinal thermoelectricity, where the temperature gradient and electrical current flow in the same direction. Recently, a detailed review has been published by Adachi et al.76 which summaries the fundamentals, progress and challenges experienced over the years in the field of transverse thermoelectric conversion.
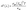 | (14) |
3 Why multiphase thermoelectrics
Multiphase materials contain two or more phases simultaneously contributing to thermal and electronic transport. Although the idea of multiphase materials for advancing TEs seems to be intuitive, several challenges have been raised in the community against its implementation. On introducing a second phase, possible scattering of charge carriers at the interface and poor energy band alignment can lead to a reduction in σ and S. Moreover, the phases will have different phase stability, crystal structures, and microstructures, which can significantly deteriorate the TE and mechanical stability. Tuning the volume fraction, grain morphology, atomic defects, and interface to maximise σ and S are some of the key challenges in these materials. Moreover, it was believed that the zT of a multiphase TE can never be beyond the highest value of one of the constituent phases,77 till a two-phase composite based on SiGe-Si was reported with enhanced zT compared to that of the individual phases.78,79 The high zT was attributed to inhomogeneous selective doping of Si via B and P instead of the SiGe phase, resulting in enhanced µ.78 Thus suggesting the role of band engineering at the interface, which favoured the easy transfer of charge from one phase to the other, resulting in enhanced zT.79 After the success story of achieving enhanced zT in SiGe-Ge multiphase materials, significant interest has emerged among researchers to understand and explore different multiphase TEs.Although the transport of charge carriers and phonons can be explained by the calculated electronic bands and phonon spectrum in the case of single-phase materials, the presence of secondary phases requires further attention. Understanding individual phases and the interfaces between them is essential to determine the overall behavior of the material. Over the years, it has been observed that multiphase TEs are preferable to single-phase materials as they offer more freedom to tune the transport properties.50 The development of multiphase alloys involves phase diagram engineering, band structure engineering and interface engineering, as shown in Fig. 1. Moreover, introducing two or more phases into the systems impacts the band structure of the constituent phases due to possible doping and changes in the solubility of the impurities in the constituent phases. The improvement in the TE behaviour in multiphase TE materials primarily relies on energy filtering, enhanced phonon scattering, modulation doping, and magnetic effects (illustrated in Fig. 1).47,50,80 As illustrated in Fig. 1, the charge carriers with low energy are filtered out by potential barriers created by the secondary phases, which leads to a high S without much loss of σ.50 On the other hand, modulation doping reduces the charge carrier scattering due to the presence of ionized impurities.50 These impurities spatially separate the conduction carriers from the host atoms and thus lead to an increase in σ of the material. In addition, for highly anisotropic alloys, crystallite alignments along a preferential orientation can lead to easy charge transport, thus increasing the µ of charge carriers. Moreover, in multiphase TEs, high frequency phonons are scattered at the point defects due to atomic mismatch and the presence of vacancies, and low-frequency phonons are usually scattered by the interface, grain boundaries, etc., which leads to further reduction in κl. On the other hand, introducing secondary magnetic phases introduces magnetic ions. Thus, from the hot to cold end of the TE leg, there will be varying magnon density. These magnons can drag the charge carriers along with them, resulting in a significant increase in σ.81 In addition, more detailed explanations and effects of different magnetic phases on the TE properties are discussed by Fortulan and Yamini.50 Fortulan and Yamini50 reviewed various success stories and advancements using the above-mentioned effects in multiphase TEs. In addition, the effect of different types of the secondary phase on the electronic band structure is usually understood by heterojunctions between the phases involved. For that, information on the electron affinity, bandgap, and/or work function of the involved phases is usually required.82 Thus, it can be inferred that multiphase TEs make it possible to strongly scatter phonons and low charge carriers resulting in enhanced S and σ.
 | ||
| Fig. 1 Schematic illustration of various engineering strategies and effects of secondary phases and interfaces in multiphase TEs. | ||
Moreover, the use of anisotropic or layered multiphase structures can be promising to enhance transverse zT compared to single-phase materials. Ando et al.83 designed a multilayer composite of tilted SmCo5 (magnetic phase) and Bi0.2Sb1.8Te3 (TE phase) at a particular angle. Thus, an increased transverse voltage, owing to the internal magnetization and strong coupling between Seebeck and anomalous Nernst effects, was observed without the need for a large external magnetic field. Hirai et al.84 investigated the tilted multilayers of a magnetic topological phase with non-conductive top layers. They observed a hybrid effect which leads to enhanced Sxy, combining the Berry curvature driven anomalous Nernst voltage with anisotropic transport attributed to the tilt geometry. There are some other interesting studies wherein multiphase materials in transverse TEs have been explored.85,86 Thus, multiphase TEs provide freedom to change the phase fractions, which can control the anisotropy, carrier concentration and magnetic field response. As summarised from recent studies, TE materials with combined magnetic and semiconductor phases can provide strong magneto–thermoelectric coupling. In addition, other than the properties of the individual phases, the type of interface between these phases can play a vital role in further enhancing the transverse thermopower.
4 Application of thermodynamic databases in thermoelectrics
In recent years, a lot of new and interesting ternary systems have been explored for TE applications. The design and optimisation of new TE materials rely on phase diagrams to determine composition, phase fraction, solidification pathways, and appropriate heat treatment cycles. The CALPHAD (CALculation of PHAse Diagrams) approach87 integrates crystallographic data, thermodynamic, and thermochemical information, and physical properties, including the magnetic characteristics of all relevant phases, obtained from both experimental measurements and theoretical calculations, to construct a self-consistent thermodynamic database. The basic principle to determine the phase equilibria involves Gibbs free energy (G) minimization, using a developed database which contains optimised G of all the phases with changing composition, temperature, and pressure of a thermodynamic system. The CALPHAD method depends on experimentally assessed thermodynamic data and parameter optimization, making it highly reliable for multicomponent and industrially relevant systems where accurate phase equilibria are required. In contrast, first-principles or Open Quantum Materials Database (OQMD) derive thermodynamic properties from electronic structure computations, allowing the exploration of new or experimentally inaccessible systems and the prediction of metastable phases. In addition, the formation energies predicted at 0 K determined using OQMD can be used for defining the unknown compounds and the end members of a solution phase and thus, aid in precise modeling of the phases using compound energy formalism (CEF) or other models wherein the Gibbs free energy of the pseudo-compounds or end members is usually not known. Moreover, the 0 K energetics can be extended to the finite temperature using the quasi-harmonic phonon models and entropy corrections, which thus can be directly used as the Gibbs free energy of the phase in CALPHAD. However, OQMD is often computationally intensive and less effective for high-entropy or multi-component systems due to combinatorial complexity. Moreover, these two approaches (CALPHAD and OQMD) are mutually reinforcing within a prediction–validation loop: first-principles calculations provide initial thermodynamic insights and phase stability trends, which can guide CALPHAD assessments; conversely, CALPHAD modeling and experimental data can validate and refine first-principles predictions. This integrated strategy enhances both the predictive accuracy and reliability of computational phase diagram design. Various thermodynamic models are used to fit the available data to optimize the G of all the phases, including pure elements, stoichiometric/non-stoichiometric compounds, solid/liquid solutions, and the gases as a function of temperature, pressure, and composition.87–89 Moreover, using the CALPHAD approach, solutions in the subsystems are extended to a multicomponent system by appropriate extrapolation techniques.90 The developed phase diagrams provide a road map for a variety of material processing operations, including crystal growth, joining, melting, and casting. To improve control over material properties and performance, they will also be essential in understanding phase changes, optimising heat treatments, and directing solid-state reactions. Recently, the addition of the Debye–Einstein model in the Cp (used in determining the κ) estimation widened the applicability of CALPHAD at low temperatures.91,92 In addition, it also provides information about the crystal structure, homogeneity ranges, site occupancies, first and second order transitions, thermal expansion coefficients (a parameter to decide the compatibility of a TE device), and other physical properties of the different phases in various temperature and pressure ranges.Moreover, the CALPHAD-based relationship93 with the solubility limit was used to determine the carrier concentration in PbSe, which gives a good fit with the experimentally observed carrier concentration compared to that determined using DFT. In addition, a new CALPHAD method was developed, which uses the heat capacity, thermal expansion, and adiabatic bulk modulus information to determine the κl of insulators and semiconductors.94 Later, κ of the solid solutions and two-phase materials was modelled using Redlich–Kister (RK) polynomials95 by Huang et al.96 In addition, they also incorporated the interface scattering parameter with linear temperature dependence for the multiphase materials. Apart from this, various aspects of CALPHAD in the TE field were reviewed by Li et al.97 There are various success stories wherein CALPHAD played an important role in discovering new TE materials such as the new filling fraction limit (FFL) of CexCo4Sb12 from 0.09 to 0.2 at 1123 K, which result in the discovery of a new alloy Ce0.14Co4Sb12 with a zT of 1.3 at 850 K,98,99 similar for FFL of In, Ga, and Yb in CoSb3.100–102 Similarly, AgCuX (X = S, Se, Te),103,104 PbTe–Sb2Te3,105 and Bi0.5Sb1.5Te3–Te106 are some of the systems, where CALPHAD played a significant role. Thus, phase diagrams dictate the experimental conditions and the composition limits to target a specific phase assemblage and type of reaction by elucidating the presence of miscibility gaps, phase separations, and the presence and stability ranges of intermetallic compounds. Moreover, nanoprecipitate formation in a solution with a miscibility gap can be estimated by selecting the compositions lying in the metastable regions between the binodal and spinodal lines, which are predicted by CALPHAD. These precipitates act as energy filters and phonon scatterers to enhance the S and reduce κl.60 Even as summarised by Femi et al.,107 eutectic microstructures can also play a vital role in selectively scattering long-wavelength phonons and maintaining structural integrity. These precipitation and eutectic morphologies can be predicted and understood using phase diagrams.
Considering the importance of the phase diagrams, a review focusing on the impact of phase diagram engineering in the Ag–Bi–Se, Pb–Te–Ga, Zn–Sb–In, Ga–Sb–Te, Bi–Ga–Te, Bi–Ge–Te, Bi–Cu–Te, and Cu–Ga–Te ternary systems was reported by Deng et al.108 They reviewed some of the interesting studies, wherein phase diagrams helped to choose compositions, understand the obtained phase assemblage, and correlate them to changes in TE properties. The present work reviews some of the recently explored tellurium-based ternary systems: Ag–Bi–Te, Bi–Cu–Te, Bi–Ga–Te, Bi–In–Te, Ga–In–Te, and Sn–Ga–Te, which have a detailed and almost complete thermodynamic description based on CALPHAD. Moreover, using these developed thermodynamic databases, researchers calculated the specific pseudo-binary phase diagrams of known interesting TE phases to design new multiphase TEs. In the following subsections, we will discuss the latest thermodynamics/phase equilibria advancements in these ternary systems. Fig. 2 shows the liquidus projections of these ternary systems using the developed thermodynamic databases (except in the case of Bi–In–Te, it is experimentally determined).
 | ||
| Fig. 2 Liquidus projections of (a) Ag–Bi–Te,114 Copyright 2024, Elsevier Ltd., (b) Bi–Cu–Te,39 Copyright 2023, Springer Nature (c) Bi–Ga–Te,181 Copyright 2023, Elsevier B.V., (d) Bi–In–Te,186 Copyright 2017, Elsevier B.V., (e) In–Ga–Te,192 Copyright 2022, Springer Nature, and (f) Sn–Ga–Te,204 Copyright 2023, ASM International, ternary systems. Symbols marked show the compositions of the investigated alloys and arrows represent the solidification pathways. | ||
4.1 Advancements in phase equilibria of silver–bismuth–tellurium (Ag–Bi–Te)
The Ag–Bi–Te ternary system consists of phases such as Bi2Te3, β, Ag2Te, Ag5Te3, AgBiTe2, etc., which have been reported as potential TE materials.35,38,70,109–113 Recently, a complete thermodynamic description of the Ag–Bi–Te ternary system was attempted by Serbesa et al.114 using the CALPHAD approach. They first optimized the binaries (Ag–Te, Bi–Te, and Ag–Bi) and then the corresponding ternary using a Toop-like asymmetric approximation with Te as an asymmetric component.115 They used the G of pure elements from the Scientific Group Thermodata Europe (SGTE) database,116 and the G of pure compounds was fitted using heat capacity, standard enthalpy, and entropy at 298.15 K available in the literature. To explain the diverse nature of the liquid solution (positive change in mixing enthalpy (ΔHmix) in Bi–Ag and negative ΔHmix in Bi–Te and Ag–Te) in the binaries and the ternary liquid, the Modified Quasichemical Model (MQM)117 was used. Moreover, the Ag–Te binary system shows a miscibility gap in the liquid phase, which was precisely captured using the MQM. In addition, compound energy formalism (CEF)89 was used to model Bi2Te3 and BiTe solid solutions. The experimentally observed allotropic forms of the binary compounds were considered while developing the thermodynamic database. They observed a reasonable agreement with the experimental studies on the Ag–Bi–Te ternary by Babanly et al.118 and Stegherr et al.119 Babanly et al.118 developed various alloys in the Ag5Te3–Bi2Te3, AgBiTe2–Te, AgBiTe2–Bi, and Ag–Bi2Te vertical sections. Moreover, they also constructed an isothermal section based on their experimental results at 400 K. On the other hand, Stegherr et al.119 explored the phase equilibria in the Ag2Te–Bi2Te3 pseudo-binary phase diagram, which showed the formation of a high-temperature phase, AgBiTe2, at 828 K. The calculated liquidus projections with the primary crystallizing phases from the ternary liquid are shown in Fig. 2(a). Using the developed thermodynamic database, various compositions in the Ag2Te–Bi2Te3 sections were selected, and their TE behavior was explored by Serbesa et al.114 In addition, these compositions were cast, which shows the formation of the AgBiTe2 phase as predicted by Scheil cooling calculations.There are various experimental studies on the Ag–Bi, Ag–Te, and Bi–Te binary systems to find stable and reliable phase equilibria. They used a variety of experimental and thermodynamic methods. The Ag–Bi system shows a simple eutectic phase diagram. Early studies by Heycook and Neville,120 Petrenko,121 and Nathans and Leider122 showed a eutectic reaction (L → fcc_Ag + rhombo_Bi) at about 535 K and 4.7 at% Ag. They also showed that fcc_Ag has limited Bi solubility.121,123–128 Thermochemical data from calorimetry129,130 and activity measurements126,131–140 corroborated these findings, while thermodynamic modelling progressed from the Redlich–Kister approach141 to the MQM.142,143 The Ag–Te system has been investigated using thermal, X-ray, DTA, and calorimetric methods,144–153 uncovering various polymorphs (Ag2Te and Ag5Te3) and significant short-range ordering in the liquid phase (minimum at XTe = 0.33).150–152 Predel and Piehl's154 activity measurements and Karakaya and Thompson's155 and Gierlotka's156,157 CALPHAD optimisation matched with each other. Mao et al.,158 Gierlotka et al.,159 and Kumar et al.160 have also optimised the Bi–Te system thermodynamically using regular solution, associate, and MQM models, respectively. The parameters based on the MQM model gave the best agreement. Drezewowska and Onderka's161 reassessment suggested more low-temperature phases (Bi7Te3 and Bi2Te), but these were not included by Kumar et al.160 Together, these studies create a consistent thermodynamic framework for all three binary systems, which is a strong base for modelling the ternary Ag–Bi–Te system.
Similar to the Ag–Bi–Te system, the Ag–Sb–Te system is also an important ternary system for TE applications. There is an interesting phase, AgSbTe2, which shows a very high TE performance (zT > 1.6). Although there is no complete thermodynamic description available for the system, there are various thermodynamic studies that investigate the Ag2Te–AgSbTe2,162 Ag2Te–Sb2Te3,163 and isothermal sections at 523 and 673 K.164 Thus, a complete thermodynamic description of this system by utilizing the available thermodynamic information can help design multiphase alloys based on Ag–Sb–Te.
4.2 Advancements in phase equilibria of bismuth–copper–tellurium (Bi–Cu–Te)
Another interesting ternary system, Bi–Cu–Te in the field of TEs, has been thermodynamically optimized by Serbesa et al.39 They used the thermodynamic modelling parameters of the Bi–Te binary system from Kumar et al.165 The Cu–Te binary system was reassessed using the MQM, as earlier studies used associate models, which lag in describing the entropy accurately.166,167 After a detailed literature survey, they considered four intermetallic compounds: Cu2Te, Cu63Te37, CuTe, Cu3Te2, and Cu4Te3 with six, one, two, three, and two polymorphic forms, respectively, in the Cu–Te binary system. They incorporated the Cu3Te2 intermetallic for the first time while considering the experimental observations by Yahyaoglu et al.168 Mao et al.,158 Gierlotka et al.,159 and Kumar et al.160 worked on optimising the Bi–Te system using different models as mentioned in Section 4.1. The developed database by Kumar et al.160 was the most consistent with experimental data of the Bi–Te system. The Cu–Te system, first modelled by Huang et al.166 and then improved by Yu et al.,167 showed that there are many intermetallics (CuTe, Cu2Te, Cu4Te3, and Cu3−xTe2) and a lot of polymorphisms, which were observed by both experimental and DFT data.127,168–173 Serbesa et al.39 utilised the MQM model to characterise the Cu–Te liquid phase and introduced Cu3Te2 for the first time in thermodynamic optimisation based on the experimental observations using microstructural analysis and XRD. On the other hand, Chakrabarti and Laughlin174 reviewed the Bi–Cu system, while Wang et al.143 provide thermodynamic optimisation. The system is a eutectic one with limited solubility between Bi and Cu. Their MQM- and CEF-based model parameters were used without any changes by Serbesa et al.39 In general, these consistent thermodynamic datasets provide a strong basis for accurately predicting and modelling the phase diagram of the Bi–Cu–Te system. In addition, short-range ordering (SRO) in the Cu-rich region of the liquid was precisely captured by the MQM. On the other hand, the Cu–Bi binary system is a simple eutectic with negligible solubility of Cu in Bi or vice versa.174 Serbesa et al.39 used the thermodynamically optimised parameters developed by Wang et al.143 for the Cu–Bi binary system, wherein they used the MQM for the description of the liquid phase. The negative ΔHmix in Bi–Te and Cu–Te liquids and the positive ΔHmix in Bi–Cu were captured precisely by the MQM. To explain the experimentally constructed Cu2Te–Bi2Te3 pseudo-binary phase diagram, Serbesa et al.39 used Te as an asymmetric component along with ternary interaction parameters in the liquid phase. Finally, using the developed database, liquidus projections were calculated, and it was observed that the miscibility gap in the Cu–Te binary system was extended to the ternary space (as shown in Fig. 1(b)). The developed database was used to design various alloys for the TE application by Serbesa et al.,39 which will be explained in Section 5.2.4.3 Advancements in phase equilibria of bismuth–gallium–tellurium (Bi–Ga–Te)
The Bi–Ga–Te ternary system with Bi2Te3, Bi4Te3, Bi2Te, Ga2Te3, GaTe, Ga3Te4, and Ga2Te5 attracted a lot of attention in TE applications.35,175–177 Lin et al.178 reported an experimentally constructed isothermal section of Bi–Ga–Te at 523 K using the alloys prepared in an ampoule at 1223 K for 12 hours and post-annealed at 523 K for at least 6 months, followed by water quenching. Later, thermodynamic modelling of the Bi–Ga–Te system was performed by Kumar et al.,165 affording a thermodynamic description throughout the whole composition range. While developing the database, a thorough literature survey of the system was performed. They used the MQM117 to precisely capture the diverse changes in the liquid behaviour (negative change in mixing enthalpy in Ga–Te and Bi–Te and positive mixing enthalpy in Bi–Ga liquid) along with SRO. The Gibbs free energy of the ternary liquid solution in the Bi–Ga–Te system was approximated using the Toop-like asymmetric approximation, where Te was an asymmetric component.115 They did not use any ternary parameter in liquid solution to describe the phase equilibria in the ternary system. They reported a reasonable agreement with the experimentally observed vertical sections such as GaTe–Bi, Ga2Te3–Bi2Te3, GaTe–Bi2Te3, and Ga2Te3–Bi sections.179,180 Moreover, two ternary eutectics were observed in the system: one between L, β, Bi, and Ga3Te4, and the other between L, Bi2Te3, Ga2Te3, and Te phases. They also observed a miscibility gap extended from the Ga–Te binary, as evident in Fig. 2(c). Moreover, the calculated liquidus projection was used by Pal et al.181 with some compositions marked in Fig. 1(c) to design multiphase alloys for TE applications. Using the developed thermodynamic database, the solidification path and the phase fraction evolution of the as-cast microstructures were explained via Scheil cooling calculations.4.4 Advancements in phase equilibria of bismuth–indium–tellurium (Bi–In–Te)
The Bi–In–Te system constitutes InBi, In5Bi3, In2Bi, Bi2Te3, In2Te3, InTe, In4Te3, In2Te5, (Bi2)m(Bi2Te3)n, etc. phases which are important from the TE perspective.182–185 No complete thermodynamic modelling is available for this ternary. However, experimentally, there is a detailed investigation by Chen et al.186 to construct the phase diagram of the system. They reported a ternary compound BiIn2Te4 for the first time in some of the alloys annealed at 423 K. To construct the liquidus projections, they prepared 88 alloys and tried to understand the liquid to solid transformations (the constructed liquidus projections are shown in Fig. 2(d)). In addition, Bi2Te3 also shows a solubility of about 8.7 at% In in some of the investigated alloys, which can be incorporated using CEF. As evident, there is a miscibility gap in the In–Te binary system, which was extended to the ternary system. Thus, using the experimentally observed phase transformation and the liquidus projections, a self-consistent thermodynamic database can be developed. There are studies in the Bi2Te3–In2Te3 pseudo-binary phase diagram that show a eutectic at 844 K and 66 ± 0.5 at% Bi2Te3.187,188 A maximum solubility of 20 at% In2Te3 in Bi2Te3 was observed at the eutectic temperature. Moreover, they performed thermal analysis, microstructural examination, and XRD to construct pseudo-binary phase diagrams. Apart from these studies, there are some experimental investigations on InTe–Bi and InTe–InBi isopleths, which can be considered while developing a thermodynamic model for the system.189,1904.5 Advancements in phase equilibria of indium–gallium–tellurium (In–Ga–Te)
The In–Ga–Te ternary system has interesting phases, which have been explored for TE applications, such as In2Te3, Ga2Te3, InTe, In3Te4, In2Te5, etc.7,31,40,182,191 A complete thermodynamic description of the system was provided by Pal et al.,192 in which they have used the CALPHAD approach to develop a thermodynamic database. In–Te and In–Ga binaries were first modelled by Pal et al.192 with the liquid phase being modelled by the MQM117 while CEF89 used for the solid solutions. The optimized parameters for the Ga–Te binary developed by Kumar et al.165 were used to develop the complete thermodynamic description of the ternary. The experimentally investigated vertical sections of GaTe–InTe by Kuliev et al.193 show the limited solubility due to the difference in crystal structures. On the other hand, Ga2Te3–In2Te3 by Wooley et al.194 and by Yamanaka et al.195 shows a complete solid solubility of both the phases throughout the temperature range owing to their same crystal structure (defect zinc blende cubic). In addition, R. Blachnik and E. Klose196 reported ΔHmix of the different alloy compositions at 973, 1073, and 1173 K, which were also considered by Pal et al.192 In addition, a ternary line compound GaInTe2 was also incorporated in the database after its observation in an alloy. They incorporated the (Ga,In)2(Te)3 and (In,Ga)(Te) solid solutions to explain the solubilities in Ga2Te3 and In2Te3, and in InTe and GaTe. Ternary liquid phase was extrapolated using ‘Toop-like’ asymmetric approximation115 considering Te as an asymmetric component. No ternary interaction parameter was required in the liquid phase to fit the available experimental data. As seen in Fig. 2(e), there is a miscibility gap in the liquidus projection extending from both In–Te and Ga–Te binaries. In addition, the symbols marked are the compositions investigated using the developed thermodynamic database, while the arrows show the solidification path.4.6 Advancements in phase equilibria of Tin–gallium–tellurium (Sn–Ga–Te)
Another interesting ternary system, comprising SnTe, is a promising candidate for replacing PbTe in the thermoelectric field.197 In addition to SnTe, the other phases, such as Ga2Te3 and GaTe, with narrow to wide bandgaps.185,198 Kumar et al.199 provided a complete thermodynamic database for the ternary system by considering almost all the available experimental and theoretical examinations. They also used the MQM to describe Sn–Te, Ga–Sn, and Ga–Te liquid solutions, while SnTe and BCT solid solutions were modelled using CEF. The description of Ga–Te was included from their previous work.165 Moreover, a similar Toop-like interpolation method with Te as an asymmetric component was able to describe the ternary liquid phase. In addition, there are various vertical sections such as Ga2Te3–SnTe200,201 and GaTe–SnTe,200,202 which have been experimentally explored in the system. A ternary compound, Ga6SnTe10, which has been reported experimentally by different researchers,201,203 has been incorporated by Kumar et al.199 in the thermodynamically optimised database. There are ternary eutectics, one at the Te-rich side, between SnTe, Te, and Ga2SnTe10 phases, and another at the Sn-rich side (between SnTe, BCT, and GaTe phases), which were further observed experimentally by Pal et al.,204 as evident in Fig. 2(e). In addition, the arrows marked show the direction of the solidification pathways or the change in liquidus with decreasing temperature.As observed in all the reviewed developed thermodynamic databases based on tellurides, a Toop-like symmetric approximation with Te as an asymmetric component can explain the behaviour of the ternary liquid. Thus, the ternary system Bi–In–Te can be optimised using a similar approach. At last, all these developed thermodynamic databases, along with other ternaries and the quaternary systems, can be combined and incorporated into the Ag–Bi–In–Ga–Sn–Te multicomponent system.
5 Microstructure-processing conditions and TE properties
Most of the above-mentioned phase diagrams are explored around a limited pseudo-binary phase diagram that comprises phases with already known TE properties. In the subsequent sections, we will review some of the interesting studies that investigate the electronic and thermal transport in these ternary systems over recent years.5.1 Silver–bismuth–tellurium (Ag–Bi–Te) thermoelectrics
Ag–Bi–Te, as seen in the previous section, consists of some of the interesting phases such as AgBiTe2, Ag2Te, and Bi2Te3. Takigawa et al.112 reported (AgBiTe2)1−x(Ag2Te)x based composites for TE applications. They developed these alloys using a vertical furnace wherein they held the liquid at a higher temperature to allow Ag2Te crystallisation with the high-temperature AgBiTe2 phase also. Fig. 3(a) shows the microstructure with Ag2Te along with the AgBiTe2 phase in the (AgBiTe2)0.25(Ag2Te)0.75 alloy. They observed a significant change in the grain size from 200 microns to 10 microns by changing the Ag2Te proportion from 0.75 to 0.5. They observed the highest σ and S of single-phase Ag2Te at room temperature compared to that of the composite, while the presence of 0.75 Ag2Te along with Bi2Te3 leads to the lowest κl due to scattering of long-wavelength phonons at the grain boundaries. The highest zT of 8 × 10−4 was observed for the Ag2Te alloy, but the alloy with 0.5 Ag2Te was found to have about three times higher zT than that of AgBiTe2. Later, they tried to understand µH in these composites, wherein they observed the highest µH at 243 K for the alloy with 0.875 Ag2Te, which was higher compared to that of the constituent phases, suggesting electron transfer from AgBiTe2 to the Ag2Te phase in the alloy.205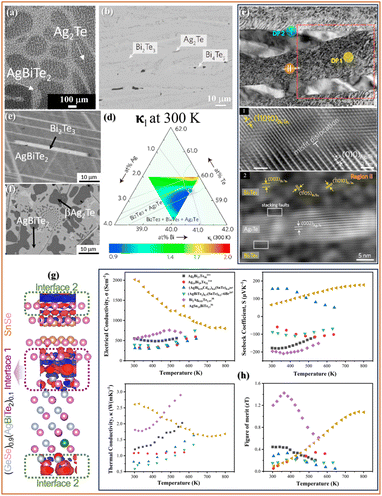 | ||
| Fig. 3 SEM-BSE micrograph of (a) (AgBiTe2)0.25(Ag2Te)0.75,112 Copyright 2011, The Materials Research Society, (b) BSE micrograph of Ag-37.5Bi-55Te (at%), (c) TEM analysis of Bi2Ag0.03Te2.97, (d) lattice thermal conductivity(κl) mapping at 300 K superimposed on the isothermal section,38 Copyright 2021, Elsevier Ltd., SEM micrograph of (e) Ag19.3Bi28.6Te52 and (f) Ag39Bi16.5Te44.5,114 Copyright 2024, Elsevier Ltd., (g) differential charge density of the (GeSe)0.09(AgBiTe2)/SnSe composite,208 and (h) TE properties of different multiphase TEs as a function of temperature.36,38,114,207,211 | ||
To understand the effect of Ag2Te in the Bi2Te3 matrix, Drzewowska et al.161 prepared alloys with varying Ag2Te compositions from 0 to 0.648 using a pseudo-binary section of Bi2Te3–Ag2Te.206 They used spark plasma sintering (SPS) to develop these alloys from the powders of Bi2Te3 and Ag2Te. They observed an interesting jump in the σ vs. T curve for the alloys with higher Ag2Te content between 413 and 423 K due to the monoclinic to cubic phase transformation of Ag2Te. Moreover, they observed an n-type conduction for all the alloys, with the highest zT of 0.43 at 373 K for Ag5Bi37Te58 at room temperature in the presence of Bi2Te3 and Ag2Te phases (shown in Fig. 3(h)).
Yen et al.38 reported an extensive study of the Ag–Bi–Te ternary system using phase diagram engineering and carrier optimisation. They used 35 alloys, annealed at 523 K for six months, to construct an isothermal section. As shown in Fig. 3(b), the microstructure shows the formation of elongated Bi2Te3, Ag2Te (dark), and Bi4Te5 phases in the Ag-37.5 at.%Bi-55 at.%Te alloy. Instead of the secondary phases, they reported that the presence of Ag in the Bi2Te3 can produce Agi defects in the van der Waals gaps, which generate an extra electron, while the AgBi defects introduce 2 holes. To further understand the defect formations, higher resolution transmission electron microscopy (TEM) showed the formation of Ag2Te nanoprecipitates for the Bi2Ag0.03Te2.97 alloy (shown in Fig. 3(c)). Moreover, they observed the presence of misfit dislocations between Bi2Te3 and Ag2Te in region I (shown in Fig. 3(c)1) and piled-up stacking faults at the Bi2Te3/Ag2Te interfaces in region II (shown in Fig. 3(c)2). Thus, the presence of nanoprecipitates of Ag2Te and defects between these phases resulted in a significant decrease in κl. Fig. 3(d) shows the change in κl with the change in the phase assemblage at 300 K; the lowest κl was obtained for alloys with Bi2Te3–Ag2Te and Bi2Te3–Bi4Te3–Ag2Te phase combinations. As evident, the regions at the centre of the phase diagram with varying phase fractions of Ag2Te, Bi2Te3, and Bi4Te5 show a κl lower than 1. In addition, the variation in the TE properties with temperature is shown in Fig. 3(h), and Bi2Ag0.03Te2.97 shows the highest zT of 1.4 at 363 K, with an average zT of 1.
In a recent study by Serbesa et al.,114 different alloy compositions were selected using the thermodynamically optimised phase diagram of Ag–Bi–Te. They were successful in attaining the AgBiTe2 phase in the as-cast alloys with low Ag content. In addition, they attained the high-temperature cubic phase of Ag2Te in these alloys. As evident in Fig. 4(e) and (f), the long needle-like morphology of Bi2Te3 along with AgBiTe2 and AgBiTe2/Ag2Te phases, was obtained, respectively. These microstructural features resulted in a significant decrease in κ (<1 W m−1 K−1), resulting in a zT of about 0.42 at 550 K (shown in Fig. 3(h)). On the other hand, the alloy with Ag2Te and AgBiTe2 shows comparatively higher σ but very low S, resulting in the highest zT of 0.15 at 375 K, but still higher than reported by Takigawa et al.112 for composites based on these phases. Other than the Ag–Bi–Te ternary, there are various reports with AgBiTe2 being used along with other phases, such as SnTe, to enhance the TE performance. A similar attempt was made by Zhao et al.,207 wherein they successfully attained the high-temperature cubic AgBiTe2 phase at room temperature by SnTe alloying. By adding SnTe, they observed an increased configurational entropy in the system, which increased the thermodynamic stability of the AgBiTe2 phase. Moreover, they also added Cd and Br to further enhance the TE performance of the alloys. Variations in the TE properties with temperature for the same are shown in Fig. 3(h). The highest zT of 0.21 at 423 K and 0.33 at 381 K was achieved for (AgBiTe2)0.7(SnTe)0.3-Br 6% and (AgBi0.99Cd0.01Te2)0.6(SnTe)0.4 alloys.
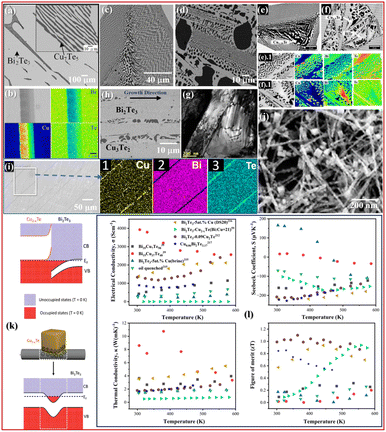 | ||
| Fig. 4 SEM-BSE micrograph of the as-grown (a) (Bi2Te3)0.91(Cu2Te)0.09 and (b) EDS mapping at the grain boundary in the (Bi2Te3)0.95(Cu2Te)0.05 alloy,212 Copyright 2018, Elsevier Ltd., and BSE micrograph of (c) Cu10.7Bi32.4Te56.9 and (d) Cu37Bi15Te48,39 Copyright 2023, Springer Nature, BSE micrograph of Bi2Te3-5at%Cu-(e) brine quenched and (f) oil quenched, along with EDS mapping, (g) bright field image showing high defect density under the zone-axis conditions of brine-quenched Bi2Te3-5at%Cu,215 Copyright 2024, Springer Nature, (h) SEM-BSE micrograph of Bi2Te3-5at%Cu directionally solidified at 20 µm s−1 parallel to growth direction,216 Copyright 2024, Elsevier Ltd., (i) SEM micrograph of Cu0.06Bi2Te3.17 along with EDS mapping,217 Copyright 2019, American Chemical Society, (j) SEM image of a Bi2Te3 nanowire with Cu2−xTe cubic particles, (k) energy band diagram at a heterojunction between Cu2−xTe and Bi2Te3, charge distribution, and energy band diagram of a Bi2Te3 nanowire in contact with a Cu2−xTe nanoparticle,59 Copyright 2021, Elsevier B.V., and (l) variation of TE properties with temperature.39,59,212,215–217 | ||
Moreover, the addition of AgBiTe2 in SnTe has been reported to be a significant improvement when compared to AgSbTe2 due to relatively effective hole neutralisation by Bi.36 Although there was no secondary phase observable using XRD and SEM techniques, TEM analysis revealed nano-precipitate in the AgSn15BiTe17 alloy. Thus, a solid solution and the secondary Ag-rich nanoprecipitate in the alloy lead to a significant reduction in κl. Moreover, AgBiTe2 addition increases the number of charge carriers in the alloy with deteriorating mobility, leading to a significant decrease in the overall σ of these alloys. Thus, a potential lead-free AgSn15BiTe17 alloy with the highest zT of 1.1 at 775 K was developed. A recent study also shows the impact of interfaces between AgBiTe2 and GeSe to achieve high TE performance.208Fig. 3(g) shows differential charge density analyses that show 2 different types of interfaces, one with covalent bonding (interface 1) and the other with ionic bonding (interface 2), with red regions showing charge accumulation, while blue regions show the depletion of charge.
Thus, thermoelectric performance in multiphase Ag–Bi–Te alloys arises from a combination of microstructural, defect, and interfacial mechanisms that collectively tune electrical and thermal transport. Takigawa et al.112 demonstrated that varying Ag2Te content in (AgBiTe2)1−x(Ag2Te)x composites controls grain size and interfacial density, where fine-grained microstructures (10 µm) enhance phonon scattering and reduce lattice thermal conductivity (κl), while charge transfer from AgBiTe2 to Ag2Te owing to the difference in the chemical potentials. Similarly, Drzewowska et al.161 showed that in the Bi2Te3–Ag2Te pseudo-binary system, the monoclinic–cubic transition of Ag2Te near 413–423 K modulates σ(T), and the two-phase nanostructure suppresses κl through boundary scattering. Yen et al.38 further revealed that Ag-induced point defects (Agi, AgBi) in Bi2Te3 tailor carrier polarity, while nanoscale Ag2Te precipitates and misfit dislocations at Bi2Te3/Ag2Te interfaces effectively scatter phonons, achieving κl < 1 W m−1 K−1 and zT = 1. Serbesa et al.114 obtained similar κl suppression (<1 W m−1 K−1) in AgBiTe2–Ag2Te multiphase alloys due to needle-like Bi2Te3 morphologies and coherent interfaces. Alloying-based phase stabilization and defect control were emphasized by Zhao et al.,207 where SnTe addition increased configurational entropy and stabilized cubic AgBiTe2 at room temperature, while Cd and Br doping tuned carrier concentration and reduced κl, yielding zT ∼0.3–0.4. In the AgSn15BiTe17 alloy, Bi effectively neutralized holes and introduced Ag-rich nano-precipitates that reduced κl, enabling zT = 1.1 at 775 K.36 Furthermore, first-principles analysis of AgBiTe2/GeSe interfaces208 revealed that covalent versus ionic bonding at phase boundaries governs charge accumulation and phonon scattering. Thus, it can be inferred that the understanding of interfaces and phase engineering plays a vital role in understanding the transport behaviour in the multiphase TEs.
Similar to AgBiTe2, AgSbTe2 is also an interesting ternary compound that has been explored extensively. In a recent review by Li et al.,209 it has been summarised that pristine AgSbTe2 can provide a zT of around 1.7 owing to the PGEC transport mechanism. Moreover, the work done by Wang et al.210 explores the role of the presence of different phases along with AgSbTe2, which results in a significant change in the TE performance of the multiphase alloys. They reported the presence of the secondary phases along with AgSbTe2 such as Sb7Te and Ag5Te3, which play a significant role in determining the TE properties. Further increments in the alloys can be made by understanding and optimising the secondary phases.
5.2 Bismuth–copper–tellurium (Bi–Cu–Te) thermoelectrics
In the Bi–Cu–Te ternary systems, there are various phases such as Bi2Te3, CuTe, Cu7Te5, Cu3Te2, Cu2Te, etc., which are of interest for TE applications. Among the various sections, the pseudo-binary phase diagram of Bi2Te3–Cu2Te has been extensively explored. Wu and Yen212 prepared two series of alloys (Bi2Te3)1−x(Cu2Te)x (where x = 0.01 to 0.09) and CuyBi2−yTe3 using the Bridgman method. They maintained the growth rate of 4.2 K h−1 from 903 K to a temperature of 803 K, where alloys were solidified. In addition, they also constructed an isothermal section at 523 K using various alloys annealed at 523 K for six months. Fig. 4(a) and (b) show the microstructure of the as-grown Cu0.09Bi1.91Te3 alloy, which revealed a eutectic lamellar of Bi2Te3/Cu7Te5 along with primary Bi2Te3. They observed the maximum solubility of Cu in Bi2Te3 to be 3 at%, which can be accommodated in the van der Waals gaps of Bi2Te3. In the Bi2Te3 phases, it has been observed that Cu, when intercalated at the van der Waals gap between two Bi2Te3 layers, acts as a donor while its presence at the Bi site makes it an acceptor.213 In addition, the presence of a small fraction of Cu2−xTe phase (having a low work function) is found to inject charge carriers into the Bi2Te3 matrix.214 Wu and Yen212 observed with increasing Cu2Te content (from 0 to 0.09), there is precipitation of Cu7Te5 phase along with Bi2Te3, resulting into a complete p to n transition. Moreover, due to lamellar arrangements of the phases, the interface-enhanced phonon scattering leads to a significant reduction in κ, resulting in a high zT of 1.07 at 360 K. In addition, due to the increase in the fraction of Cu7Te5, the overall PF was observed to be constant with temperature, resulting in an interesting average zT of around 1 for the whole investigated temperature range (shown in TE properties in Fig. 4(l)).Serbesa et al.39 reported a complete thermodynamic description of the Bi–Cu–Te ternary system, which helped them to choose specific compositions. They prepared the as-cast alloys with varying Cu fractions from 0 to 37 at% in Bi2Te3. As seen in the microstructure in Fig. 4(c), there is a eutectic growth between the Cu3Te2 (dark phase) and Bi2Te3 (grey colored) phases along with primary Bi2Te3 grains in Cu10.7Bi32.4Te56.9 and the formation of dendritic Cu3Te2, Bi2Te3, and the eutectic mixture of Bi2Te3 and Cu3Te2 in Cu37Bi15Te48 (shown in Fig. 4(d)). The variation of the volume fraction of phases and the change in the interlamellar spacing resulted in decreased κ for the alloys. Recently, Legese et al.215 further investigated the effect of the cooling rate on the microstructure and TE properties of Bi2Te3-5at%Cu, wherein they used brine-ice and food-grade oil as quenching media. They observed a change in stoichiometry from Cu1.25Te (brine, shown in Fig. 4(e) and (e).1) to Cu1.5Te in the oil-quenched alloy, as shown in Fig. 4(f). In addition, there was precipitation of Bi and BiTe phases along with Bi2Te3 and Cu1.5Te in the oil-quenched sample due to a slower cooling rate (as shown in Fig. 4(f)1). Fig. 4(g) shows the presence of a large number of dislocations in the quenched alloy, which reduced κl for the alloy. In addition, they also observed a p–n transition for the alloy, while the oil-quenched alloy showed n-type conduction throughout the investigated temperature range (shown in Fig. 4(l)).
On the other hand, a study investigated the role of solidification velocity (V) in the Bi2Te3-5at%Cu alloy using the Bridgman technique.216 They used three V: 50, 20, and 10 µm s−1 to change the grain morphology and the elemental distribution. In all the alloys, they observed the formation of Bi2Te3 and Cu3Te2 phases as shown in Fig. 4(h). They reported that the increase in V led to finer grains, which led to reduced κ due to pronounced scattering of high-wavelength phonons. In addition, the highest zT of 0.93 at 442 K was observed for the alloy solidified at 20 µm s−1; changes in the TE properties with temperature are provided in Fig. 4(l).
The work reported by Cha et al.217 shows the influence of the excess Te condition in Bi2Te3 along with the presence of Cu. In addition, they observed the formation of elongated rod-shaped regions (Cu rich) in Cu0.06Bi2Te3.17 alloys prepared using SPS, as shown in Fig. 4(i). The presence of the secondary phase led to an enhancement of S and σ due to the energy filtering effect. In addition, the κ at room temperature for this alloy was also low compared to other Te-excess alloys with low Cu concentration. The highest zT of 0.85 was observed for the alloy at RT. Other than multiphase approaches, an interesting study to create nanodomains of Cu2Te in n-type Bi2Te3 was carried out by Zhang et al.,59 wherein they used nanoparticles of Cu2Te on Bi2Te3 as shown in Fig. 4(j). They observed very low κ < 0.9 W m−1 K−1 for all the investigated samples. The energy filtering effect due to the nanodomains of Cu2−xTe resulted in selective charge carrier filtering, thus enhancing the overall zT. Moreover, the heterojunction between Cu2−xTe and Bi2Te3 shows the formation of an accumulation layer, as shown in Fig. 4(k), due to band bending at the interface. The presence of Cu2−xTe cubic particles over the Bi2Te3 nanowire shows electron movement from Cu2−xTe to the Bi2Te3 nanowire, which can be viewed as the Fermi level (EF) lying in the conduction band at the interface. In addition, using ultraviolet photoelectron spectroscopy (UPS), Cu2−xTe is found to possess a lower work function compared to Bi2Te3, and thus the movement of electrons from Cu2−xTe to Bi2Te3 will be favoured. Similar effects of the Cu2−xTe phases in the above-discussed Bi–Cu–Te-based multiphase TE reports can be linked. Thus, from bulk to nano-dimensions, multiphase TEs in the Bi–Cu–Te ternary have shown significant improvement in terms of heat and charge carrier transport.
Wu and Yen212 observed that Cu incorporation in Bi2Te3 up to 3 at% occurs via intercalation in the van der Waals gaps, where Cu acts as a donor, whereas substitutional Cu on Bi sites behaves as an acceptor. The coexistence of Bi2Te3 and Cu7Te5 lamellae led to p–n conduction switching and strong interface-induced phonon scattering, yielding a high zT of 1.07 at 360 K. Serbesa et al.39 showed eutectic coupling between Bi2Te3 and Cu3Te2 and variation in interlamellar spacing, effectively suppressed κl. Legese et al.215 revealed that faster quenching (brine) produced Cu1.25Te with high dislocation density and lower κl, while slower cooling (oil) resulted in Cu1.5Te with additional Bi and BiTe precipitates, causing a conduction-type reversal and enhanced carrier scattering. In a related study, varying solidification velocity during Bridgman growth216 refined grain size and improved phonon scattering, where an optimal velocity (20 µm s−1) balanced electrical and thermal transport, achieving zT = 0.93 at 442 K. Cha et al.217 demonstrated that Cu addition under Te-rich conditions produced Cu-rich rod-like secondary phases, which promoted energy filtering of charge carriers and lowered κ, enhancing zT to 0.85 at room temperature. At the nanoscale, Zhang et al.59 embedded Cu2−xTe nanodomains into Bi2Te3, forming heterojunctions with band bending and electron accumulation at the interface, which induced energy-dependent carrier filtering and drastically reduced κ (<0.9 W m−1 K−1). Overall, these studies show that in Bi–Cu–Te multiphase systems, thermoelectric enhancement comes from a combination of Cu-induced carrier modulation, interfacial phonon scattering, and energy-filtering mechanisms that work from bulk to nanoscale architectures.
5.3 Bismuth–indium–tellurium (Bi–In–Te) thermoelectrics
In this particular system, Bi2Te3, In2Te3, In2Te5, and other phases are available, which in combination, have shown significant enhancement in the TE properties. Among the various possible combinations, Bi2Te3–In2Te3 has been explored extensively due to its interesting crystal structure. Nagao and Ferhat218 reported the TE properties of Bi2(1−x)In2xTe3 alloys. They observed the highest zT of 0.6 at 300 K with x = 0.2, attributed to high S and reduced κ due to the presence of In2Te3 along with Bi2Te3.Liu et al.183 investigated the effect of growth and kinetics in Bi-7.5In-60Te (at%) of the Bi2Te3-In2Te3 pseudo-binary phase diagram (shown in Fig. 5(a)). Alloys were prepared using the seeding zone melting technique.188 This alloy was annealed at different temperatures (773 K and 573 K) for 72 h, and step annealing was first performed at 573 K and then at 773 K. The step annealing was to modify the nucleus density of In2Te3 and the lamellar structure and chemical composition uniformity. The microstructure shows longer lamellar structures of In2Te3 and Bi2Te3 by step annealing, as shown in Fig. 5(b). Although there is not much change in κl for the two-step annealed alloy and the alloy with annealing at 573 K, as κ was limited by bipolar conduction, the two-step annealing shows a significant decrease in S (shown in Fig. 5(m)). They observed a zT of 0.045 at 773 K for the two-step annealed alloy. On the other hand, the alloy annealed at 573 K shows a zT of 0.065 at the same temperature. Later, Liu et al.219 investigated the effect of varying annealing temperature (773 and 723 K for 3 days, while at 673 K for 7 days) in the Bi1.625In0.375Te3 alloy to understand the change in the microstructure and corresponding change in TE properties. The initial alloy was prepared using seeding zone melting. The microstructures revealed the change in the phase fractions due to the change in In solubility from 6.2 to 3 at% as the temperature of annealing was lowered from 773 to 673 K (Fig. 5(c) to (e)). In addition, they observed a coherent interface between these phases with crystallographic orientation of <−211>In2Te3//<1–100>Bi2Te3, {111}In2Te3//{0001}Bi2Te3 as evident in Fig. 5(f) and (g). Thus, using proper heat treatment, a higher interface density was achieved, which increases zT from 0.065 to 0.26.183
 | ||
| Fig. 5 (a) Pseudo-binary phase diagram of Bi2Te3–In2Te3, (b) BSE micrograph of Bi1.625In0.375Te3 annealed at 673 K,183 Copyright 2015, The Minerals, Metals and Materials Society, BSE micrograph of Bi1.625In0.375Te3 annealed at (c) 773 K, (d) 723 K, and (e) 673 K, (f) TEM image and (g) selected area diffraction pattern (SADP) in Bi1.625In0.375Te3 annealed at 673 K,219 Copyright 2016, American Chemical Society, BSE micrographs of (Bi,In)2Te3(∼3 at% In); (h) 4 at% In, and (i) 6 at% In, (j) HRTEM image of the Bi2Te3/In2Te3 interface suggesting a sharp interface, and (k) schematic illustrating the band bending at the Bi2Te3/In2Te3 interface. Eg: band gap; EC: conduction band; EV: valence band; EF: Fermi level; ΔEC: offset of the conduction band; ΔEV: offset of the valence band,220 (l) schematic illustrating the crystallographic orientation relationship (001)Bi2Te3//(031)In2Te3, [010]Bi2Te3//[100]In2Te3,221 Copyright 2018, Elsevier B.V., and (m) variation of TE properties with temperature.183,219,221 | ||
In all the studies reported by Liu and co-researchers (discussed above), the initial alloys do not exhibit grains oriented in a single preferred direction after solidification.183,219 In a later report,220 they annealed (Bi1−x,Inx)2Te3 solid solution (grown parallel to {001} plane) at 673 K for 6 days. To understand the effect of interface density, samples with 3, 4, 6, and 7.5 at% In were prepared using the seeding zone melting technique (as shown in Fig. 5(h) and (i)). They observed a slightly higher Te content (>60 at%) in Bi2Te3 and a lower Te content in In2Te3 (<60 at%). In addition, the TEM image shown in Fig. 5(j) shows a sharp and coherent interface between Bi2Te3 and In2Te3, which leads to an electron accumulation layer. On increasing the In fraction, the alloys show a significant decrease in S with increasing σ. The alloy with the highest interface density, i.e., eutectic composition, resulted in a significant decrease in κl, which leads to the maximum zT of 0.29 at 348 K along the growth direction. Compared to the single-phase solid solution, the Bi2Te3–In2Te3 multiphase shows enhanced zT. There was a drastic decrease in the zT along the direction perpendicular to growth due to a drastic decrease in σ. In addition, the variation of the TE properties with temperature for the same alloy is shown in Fig. 5(m). The heterojunction of Bi2Te3–In2Te3 was supplemented to understand the possible band bending (Fig. 5(k)). The flow of electrons from In2Te3 to (Bi,In)2Te3 leads to balancing EF, which in turn yields band bending. In addition, the metal-like behaviour surface state of Bi2Te3 is one of the reasons for the increase in σ with increasing interface density.
In their later work,221 they prepared Bi-13.5In-60Te and Bi-16.5In-60Te using induction melting followed by a Bridgman-type furnace. The growth was performed at 20 K min−1 and 10 µm s−1 velocities. To understand the interface, an alloy with maximum In solubility, i.e., 8.5 at%, was prepared using seeding zone melting. They observed a superstructure In2Te3 phase with an orthorhombic crystal structure, which was not observed in other solid-state transformations. The corresponding change in the crystallographic relationship between the two phases as observed by TEM analysis ((003)Bi2Te3//(031)In2Te3 and [010]Bi2Te3//[100]In2Te3) is illustrated using a schematic in Fig. 5(l). This change in the crystallographic orientation and the interface density observed a significant improvement in TE performance with the highest S, lowest σ and κ (<0.6 W m−1 K−1) for the eutectic composition, resulting in the highest zT of 0.12. The change in the TE properties of the various alloys investigated with temperature is shown in Fig. 5(m).
5.4 Bismuth–gallium–tellurium (Bi–Ga–Te) thermoelectrics
The Bi–Ga–Te ternary system, as discussed in the phase diagram section, comprises interesting semiconductor phases such as Bi2Te3, Ga2Te3, GaTe, Bi2Te, etc. Hazama et al.222 tried to understand the possible energy filtering/tunneling effect by introducing the nanosized Ga2Te3 phase in the Bi2Te3/Ga2Te3 composite. They prepared Bi2−xGaxTe3 (0 ≤ x ≤ 0.25) alloys using SPS. Fig. 6(a) shows the Bi2Te3 grains along with the Ga2Te3 phase for the Bi1.85Ga0.15Te alloy prepared using SPS. On annealing this alloy at 773 K, the precipitation of Te was observed, as shown in Fig. 6(b). In addition, they performed the DFT simulation using PBE-GGA to determine the energy vs. momentum diagram for the Ga2Te3 and Bi2Te3 phases. Using the band structure information of both the phases, a possible Bi2Te3/Ga2Te3 heterojunction was designed (shown in Fig. 6(c)), wherein the (0001) direction of Bi2Te3 aligned with the (111) direction of the Ga2Te3. They considered the experimentally observed band gaps of 0.2 and 1.2 eV for the Bi2Te3 and Ga2Te3 phases, respectively. In addition, the Ga2Te3 phase produces halo rings indicating non-crystallinity; the effect of this non-crystallinity on electronic transport was not discussed by the authors (shown in Fig. 6(d)). As per Hazama et al.222 taking into account the asymmetry of the density of states concerning EF, a reduction in the Ga2Te3 content can result in a further increase in the PF because the number of electron carriers passing through the Ga2Te3 potential height increases when the potential width is decreased due to the tunnelling effect. Variation in TE properties for the alloy with the highest zT is shown in TE properties Fig. 6(k). The highest zT of 0.38 was obtained for the Bi1.88Ga0.12Te3 alloy annealed at 673 K. | ||
| Fig. 6 BSE micrograph of Bi1.85Ga0.15Te3 prepared using (a) SPS and (b) SPS and annealing at 773 K, (c) band offset between Ga2Te3 and Bi2Te3, (d) TEM image and the selected area electron diffraction (SAED) patterns of the Bi1.9Ga0.1Te3 alloy,222 Copyright 2017, Elsevier B.V., (e) BSE micrograph of the directionally grown Bi1.91Ga0.09Te3 alloy, (f) BSE micrographs of thermally equilibrated Bi-20Ga-60Te, Bi-15Ga-57.5Te, Bi-10Ga-45Te, Bi-20Ga-45Te, Bi-30Ga-50Te, and Bi-20Ga-30Te (at%) alloys, (g) magnified isothermal section with Seebeck coefficient mapping at 300 K,178 Copyright 2020, American Chemical Society, BSE micrograph of the Bi2Te3–25Ga2Te3 alloy directionally solidified at 10 µm s−1 (h) parallel to the growth direction with EDS mapping, (i) perpendicular to the growth direction,223 Copyright 2024, IOP Publishing Ltd., and (j) SAED pattern of the ternary Bi2Te3–In2Te3–Ga2Te3 material,224 Copyright 2017, Elsevier Ltd., and (k) variation of TE properties with temperature.178,223,224 | ||
In a recent study by Lin et al.,178 34 alloy compositions of Bi–Ga–Te were investigated to develop an isothermal section at 573 K. The microstructure of Bi1.91Ga0.09Te3 reveals well-defined elongated Bi2Te3 grown parallel to the growth direction with the formation of Bi2Te3/Ga2Te3 eutectic at grain boundaries (shown in Fig. 6(e)). They performed TE measurements of these alloys and reported a significant change in TE transport with changing the phase assemblage. As reported, they observed σ and S decoupling mainly due to the excess Te and the additional impurity levels due to Ga in the Bi2Te3 phase. The alloys were prepared using the Bridgeman technique. In addition, the presence of secondary phase Ga2Te3, Te, and Bi4Te3, along with the Bi2Te3, affects the performance of the multiphase TE. They observed the highest S for the (Bi2Te3)0.93(Ga2Te5)0.07 alloy with Ga2Te3 and Te as the secondary phases along with Bi2Te3 (shown in Fig. 6(k)). In addition, it also shows high σ and low κ, leading to a zT of 1.5 at 300 K. The Ga+ or Ga3+ substitution at Bi3+ can lead to an expanded ab plane of Bi2Te3, which expands the basal plane. As the Ga addition increases up to 0.03 in Bi2−bGabTe3, a p–n transition was observed. Similar transitions were observed for the other three alloy series (Bi2Te3)1−a(Ga2Te5)a, (Bi2Te3)1−c(GaTe)c, and Bi2GadTe3−d. They developed various alloys with three phases: Bi2Te3 + Bi4Te5 + Ga2Te3, Bi2Te + Bi4Te3 + Ga2Te3, and GaTe + Ga2Te3 + Bi4Te3 and two phases: Bi7Te3 + Ga2Te3 and Bi + Bi7Te3 + GaTe (as shown in Fig. 6(f)). A color map in Fig. 6(g) shows the variation of S on the changing phase assemblage at 300 K. Recently, using the thermodynamically optimised Bi–Ga–Te thermodynamic database, the eutectic composition in the Bi2Te3–Ga2Te3 pseudo-binary phase diagram was obtained.223 To understand the effect of the change in the interface between Bi2Te3 and Ga2Te3, the alloy was directionally solidified using the Bridgeman technique to alter the microstructure. As shown in Fig. 6(h), the alloy solidified at 10 µm s−1 revealed a Ga2Te3 needle-like structure aligned parallel to the growth direction. These changes in the lamellar spacing and crystal orientations affected the mobility of the charge carriers. In addition, there is a lateral growth of Ga2Te3 in the eutectic colonies observed along the transverse direction (shown in Fig. 6(i)). The TE properties measured along the growth direction show a significant change in σ and S, resulting in a maximum zT of 0.38 for the alloy solidified at 20 µm s−1 solidification velocity. In addition, a significant drop in κl was observed for the alloy with finely distributed eutectic lamellae. Moreover, Kim et al.224 reported an interesting study on Bi2Te3–In2Te3–Ga2Te3 thin films on a PET substrate. As shown in Fig. 6(j), they observed (−11 0), (2 2 1), and (1 3 1) planes for the Bi2Te3 phase suggesting a rhombohedral crystal structure; (5 1 1), (8 2 2), and (9 3 3) planes for In2Te3; and the (2 0 0), (2 2 0), and (3 1 1) planes in Ga2Te3. The variation of the TE properties of some alloys is shown in Fig. 6(k). As evident, the highest zT for n-type conduction was observed for (Bi2Te3)0.93(Ga2Te5)0.07 at 300 K and for p-type Bi1.99Ga0.01Te3.
5.5 Tin–gallium–tellurium (Sn–Ga–Te) and indium–gallium–tellurium (In–Ga–Te) thermoelectrics
In the Sn–Ga–Te ternary system, among all the phases, SnTe is one of the most explored phases as a potential replacement for PbTe.197 However, SnTe exhibits challenges such as a high concentration of Sn vacancies, which reduces S and increases κ.225 Additionally, SnTe's narrow band gap (∼0.18 eV) and the substantial energy disparity (0.3–0.4 eV) between its light and heavy hole bands diminish the contribution of heavy holes to electronic transport, thereby compromising its TE performance relative to PbTe.226 Hong et al.177 investigated Ga1.8SnTe5.2, Ga2SnTe5, and Ga2.2SnTe4.8 alloy compositions. The alloys were prepared by heating the elements in an ampoule at 1273 K, followed by SPS. They observed the formation of Ga2Te5, SnTe, and Te phases using XRD. SEM analysis shows the formation of Ga0.74SnTe2.01Ga and Ga10.91SnTe6.62 regions in the Ga2SnTe5 alloy, as shown in Fig. 7(a). In addition, Ga2SnTe5 showed the highest zT of 0.16 at 549 K, among the other investigated alloys. The other TE properties of the Ga2SnTe5 alloy are shown in Fig. 7(f). Orabi et al.227 investigated the Sn1.03−xGaxTe (x = 0, 0.02, 0.03, 0.05, 0.07, and 0.1) alloy series. They observed an interesting ultra-low κl below the amorphous limit at elevated temperature. They observed a complete solubility of Ga up to 0.05, beyond which GaTe crystallizes as nanoprecipitates (shown in Fig. 7(b)). To further understand the effect of Ga substitution at the Sn site, they performed a density functional theory analysis (DFT). As indicated by first-principles calculation, Ga substitution decreases the number of electrons, leading to a EF close to the valence band, which leads to the activation of several hole pockets in the valence band. Remarkably, S improved significantly by Ga-doping and GaTe precipitation. The presence of GaTe can be seen as an energy filter, which leads to an increase in S at higher temperatures. Moreover, the variation of the TE properties of alloy with a Ga content of 0.07 in Sn1.03−xGaxTe is shown in Fig. 7(f). Other than the crystalline phases, various amorphous TE alloys based on Sn–Ga–Te systems are explored. Zhang et al.228 prepared bulk glass of [(Ga2Te3)34(SnTe)66]100−x-Snx (x = 0 to 10 mol%) using melt spinning followed by SPS, wherein they reported an ultra-low κ of 0.16 W m−1 K−1. Moreover, they observed the formation of Ga6SnTe10 along with SnTe on annealing the as-spun [(Ga2Te3)34(SnTe)66]92-Sn8, as shown in Fig. 7(c). In another report,229 Agx[(Ga2Te3)34(SnTe)66]100−x(x = 0 to 18) based amorphous alloys were fabricated using melt-spinning and the formation of Ga6SnTe10 was reported (shown in Fig. 7(d)). Moreover, the addition of Ag affected the SRO, which resulted in improved S and κ. The highest zT of 0.09 was observed for the addition of Ag at 465 K. In addition to these studies, there are various reports wherein multiphases and doping in SnTe have shown tremendous improvement in TE performance by bandgap and interface engineering, which has been reviewed extensively by Moshwa et al.197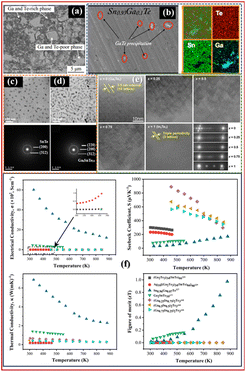 | ||
| Fig. 7 (a) SEM-BSE micrograph of Ga2SnTe5,177 Copyright 2012, Northwest Institute for Nonferrous Metal Research (China) Elsevier Ltd., (b) SEM micrograph of the Sn0.93Ga0.1Te alloy with EDS mapping,227 Copyright 2017, American Chemical Society, TEM image and corresponding SAED pattern of [(Ga2Te3)34(SnTe)66]92-Sn8 annealed at (c)513 K and (d) 533 K,228 (e) TEM images and electron diffraction patterns of Ga1−xInx−2Te3 (x = 0, 0.25, 0.5, 0.75, and 1),195 Copyright 2009, TMS, and (f) TE properties of different alloys with temperature.177,195,227,229 | ||
In the In–Ga–Te ternary system, In2Te3, Ga2Te3, InTe, etc., are some of the interesting phases explored for TE applications. Yamanaka et al.195 investigated the Ga2Te3–In2Te3 binary system. The alloys were prepared by melting the elements in stoichiometry, followed by annealing at 973 K for 2 weeks, followed by hot pressing. They observed interesting two-dimensional vacancy planes with 3.5 nm intervals at the (111) plane in Ga2Te3. On the other hand, they observed the triple periodicity along the [111] direction of In2Te3 as shown in Fig. 7(e). The alloys in between the end members showed a random periodicity of these 2D vacancy planes. Moreover, they observed a complete solubility of phases in the investigated alloys due to the similar crystal structures of both phases. They found the minimum κ of 0.25 W m−1 K−1 to 0.5 W m−1 K−1 for x = 0.25 and 0.5 in (Ga1−xInx)2Te3. Ga2Te3 showed the highest zT of 0.16 when compared to In2Te3 and other solid solutions. Variations of TE properties for solid solutions are shown in the TE Fig. 7(f). In addition, Gojayev et al.191 investigated the InGaTe2 phase using experimentation and DFT calculations to understand the electronic band structure. They prepared the alloy by heating the elements in stoichiometry at 1273 K for 24 h, followed by homogenization at 973 K for 8 h in an ampoule. From the obtained XRD spectrum, there is a clear formation of secondary phases such as GaTe and Te, which can be explained by the developed thermodynamic database.192 In addition, the calculated band structure shows a direct bandgap of 0.56 eV for InGaTe2. Jacobsen et al.185 investigated the effect of high pressure on the transport and structural properties of InTe, GaTe, and GaInTe2 phases. They observed that tetragonal GaInTe2 undergoes a structural transformation at 9.25 GPa, which changes the conduction type. For some of these materials (InTe and InGaTe2), this yields a lower efficiency than ambient conditions. However, for GaTe, an increase in zT of 14 times at 8 GPa was observed when compared to that without applied external pressure.
6 Theoretical models for multiphase TEs
The electronic and thermal transport behaviour of new phases is usually explored theoretically by first-principles calculations. These calculations are used to develop electronic band structure and phonon dispersion relationships to understand the new phases with/without defects. These calculations are usually computationally expensive, while performing these simulations for multiple phases is comparatively more challenging and expensive. Instead of using density functional theory, empirical relationships to understand the TE properties are usually applied. The simplest approach to understanding transport phenomena at high temperature is performed using Single Parabolic Band (SPB) approximation.61 In SPB, a single parabolic band with acoustic phonon scattering as the dominant scattering mechanism is assumed. The model uses experimentally observed temperature-dependent transport properties like S, σ, and RH to determine the band structure information. In addition, for materials with roles of multiple bands in the electronic transport, a Multiband Parabolic Model (MBP) was proposed by Agrawal et al.,230 which provides valuable insights into the band structure. In the case of multiphase TEs, the effective transport property of the multiphase is usually averaged between the constituent phases using their volume fraction and transport property. This is one of the easiest approaches, but it always results in a lower value for the composite compared to individual phases.For understanding the electronic properties in the multiphase TEs, effective medium theory (EMT) was proposed by Bruggeman, wherein the effective electrical and thermal conductivities of the composite comprising isotropic components are related to the phase fraction and the individual component property.231Eqn (15) relating the volume fraction (vi) and individual phase properties (ζi) to that of the effective multiphase TE property (ζ) is one of the most widely used relationships:
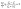 | (15) |
Landauer232 used this equation by replacing ζ with σ to evaluate the effective σ for the composite with metallic phases. In a similar study by Odelevskii,233 the effective κ of the multiphase was evaluated by replacing ζ with κ. Moreover, it was observed that the effective S can be determined by replacing ζ by σ/S.234 Sonntag used the EMT formalism for the heat flow and chemical potential to obtain a relationship for metals or degenerate semiconductors.235,236 EMT works well for phases with similar properties but fails when the fraction approaches the percolation threshold. Thus, McLachlan et al.237provided a generalized effective medium theory (GEMT), which incorporated percolation theory as shown in eqn (16):
 | (16) |
 | (17) |
7 Current application scenario and challenges of multiphase TEs
In the current usage, multiphase TEs are used as TE devices for cooling and power generation applications. Moreover, these can be used in the field of human body energy harvesting using wearable and flexible electronics. The radioisotope TE generators (RTGs) in aerospace, high-temperature energy harvesting, power plants, turbines, and utilizing geothermal energy are some of the applications of multiphase TEs. Other than generators, TE coolers for thermal management in satellites, microelectronics, etc., are some of the other application fields. When compared to the well-known single phases like SnTe, In2Te3, and Bi2Te3, the multiphase materials provide a pathway to attain zT higher than 1.5 with engineered phase fraction, interfaces, and the involved individual phases. Achieving the high conversion efficiency in multiphase TEs comes with some challenges, such as phase segregation. Repetitive use of the devices based on multiphase TEs can result in phase separations and interfacial reactions, which can deteriorate the TE performance of the material. Moreover, the self-doping, impurity levels, and defects in these materials require precise control over the manufacturing process and the post-processing conditions, which is one of the key challenges in these materials. In addition, the two phases might consist of different mechanical strengths, which will challenge the mechanical stability of the material. At last, some of the elements mentioned in the current review are mostly costly due to their limited abundance. In addition, some of these materials are toxic, thus challenging environmental sustainability. Although the review discusses more about Te based TE materials, the research focus should also be centred on TE devices wherein efforts are being made to optimise the TE device for enhanced efficiency.241–243 As mentioned, there are four layers starting with a metallization layer on the top of the TE leg, followed by a solder layer, a conducting strip and a ceramic plate at top.244 One of the challenges is to decide on the conductive strip material for a particular TE material, which should offer higher electrical and thermal conductivity, a minimum coefficient of thermal expansion difference (between the contact material and TE material), and retain higher mechanical stability at the operational temperature.244 Thus, the type of interface between the TE material and the contact also affects the electronic and thermal transport.245 In the case of multiphase TE materials, this can be more challenging owing to the presence of more than one phase. Thus, the selection of the contact material requires greater attention to overcome several engineering challenges including interfacial stability, diffusion control, and long-term reliability under thermal gradients. On the other hand, the phase transitions with temperature are also an important aspect of the TE behaviour as observed for single phase TEs.246 As there will be more than one phase in the multiphase TE material, the effect of phase transitions on each phase will contribute to the overall electronic and thermal transport. Such transitions can be leveraged to modulate carrier concentration and phonon scattering, providing new pathways for improving the efficiency and adaptability of TE materials.8 Summary and future outlook
In the current paper, we have reviewed the phase diagram, microstructure evolution, and interface engineering in six interesting Te-based ternary systems. As observed, these engineering techniques play a crucial role in deciding the transport behaviour of multiphase TEs. Some of the key observations from the present review are summarised below:• The developed thermodynamic databases of the ternary systems can be combined to build a complete thermodynamic database for the Te-based multicomponent system using appropriate extrapolation techniques. This can aid in designing new multicomponent TE materials with the desired phase assemblage.
• The CALPHAD-based model has shown its applicability from phase equilibria to the determination of the carrier concentration and the thermal conductivity. Thus, this method can be further used to design TE materials.
• A more generalised Gibbs Free energy expression with incorporated electrical resistivity and thermal conductivity can help in predicting the phases with desired properties at specific temperatures.
• The microstructure consisting of different phase assemblages, phase fractions, interface densities, defect concentrations, and types of defects is one of the key microstructural features that play an important role in deciding the transport properties.
• In the case of multiphase TEs, the interface between the two phases can be viewed as a heterojunction, which shows the possible alignment of EF.
• The interface tuning thus helped in selectively filtering high-energy charge carriers with limited conduction of heat, leading to a simultaneous increase in S and decrease in κ.
• Better contact materials and robust interfaces are necessary for advancements in TE device engineering, particularly for multiphase Te-based systems where temperature-driven transitions along with various phases are present. There are encouraging opportunities to enhance thermoelectric efficiency, stability, and long-term device reliability by controlling the interfacial and phase-related effects.
• Multiphase TEs, comprising magnetic and semiconducting phases with engineered microstructures, can be used to exploit the electron–phonon–spin interactions to maximise the transverse zT.
Author contributions
Varinder Pal: writing – original draft, review and editing, and conceptualization. Duraisamy Sivaprahasam: writing – review and editing. Manas Paliwal and Chandra Sekhar Tiwary: supervision and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Acknowledgements
The authors are thankful to the Metallurgical and Materials Engineering Department of Indian Institute of Technology Kharagpur for the resources.References
- D. M. Rowe, in Thermoelectrics Handbook, CRC Press, 2018 Search PubMed.
- D. M. Rowe, in Thermoelectrics Handbook: Macro to Nano, CRC Press, 1st edn, 2006 Search PubMed.
- S. Stefanoski, M. Beekman and G. S. Nolas, in The Physics and Chemistry of Inorganic Clathrates SSMATERIALS, Springer, 2014, pp.169–191 Search PubMed.
- J.-A. Dolyniuk, B. Owens-Baird, J. Wang, J. V. Zaikina and K. Kovnir, Mater. Sci. Eng., R, 2016, 108, 1–46 CrossRef.
- O. Meroz and Y. Gelbstein, Phys. Chem. Chem. Phys., 2018, 20, 4092–4099 RSC.
- J. Jiang, L. Chen, S. Bai, Q. Yao and Q. Wang, J. Cryst. Growth, 2005, 277, 258–263 CrossRef CAS.
- M. R. Shankar and A. N. Prabhu, J. Mater. Sci., 2023, 58, 16591–16633 CrossRef CAS.
- S. Slathia, C. Wei, M. Tripathi, R. Tromer, S. D. Negedu, C. S. Boland, S. Sarkar, D. S. Galvao, A. Dalton and C. S. Tiwary, 2D Mater., 2024, 11, 035006 CrossRef CAS.
- B. C. Sales, D. Mandrus, B. C. Chakoumakos, V. Keppens and J. R. Thompson, Phys. Rev. B, 1997, 56, 15081–15089 CrossRef CAS.
- Y. Tian, A. A. Sirusi, S. Ballikaya, N. Ghassemi, C. Uher and J. H. Ross, Phys. Rev. B, 2019, 99, 125109 CrossRef CAS.
- R. J. Quinn and J.-W. G. Bos, Mater. Adv., 2021, 2, 6246–6266 RSC.
- W. G. Zeier, S. Anand, L. Huang, R. He, H. Zhang, Z. Ren, C. Wolverton and G. J. Snyder, Chem. Mater., 2017, 29, 1210–1217 CrossRef CAS.
- M. Wolf, R. Hinterding and A. Feldhoff, Entropy, 2019, 21, 1058 CrossRef CAS.
- W. Tan, Y. Liu, M. Zhu, T. Zhu, X. Zhao, X. Tao and S. Xia, Inorg. Chem., 2017, 56, 1646–1654 CrossRef CAS PubMed.
- A. Shukla, N. Tripathi and D. T. Marx, in Dynamic Processes in Solids, Elsevier, 2023, pp. 137–152 Search PubMed.
- M. S. Abbasi, R. Sultana, I. Ahmed, M. Adnan, U. A. Shah, M. S. Irshad, H. N. Vu, L. T. Do, H. H. Thi Vu, T.-D. Pham, H. X. Nang and V.-D. Dao, Renewable Sustainable Energy Rev., 2024, 200, 114579 CrossRef CAS.
- M. Lindorf, K. A. Mazzio, J. Pflaum, K. Nielsch, W. Brütting and M. Albrecht, J. Mater. Chem. A, 2020, 8, 7495–7507 RSC.
- N. S. Abishek and K. Gopalakrishna Naik, J. Cryst. Growth, 2021, 565, 126141 CrossRef CAS.
- Z. Luo, X. Zhang, X. Hua, G. Tan, T. P. Bailey, J. Xu, C. Uher, C. Wolverton, V. P. Dravid, Q. Yan and M. G. Kanatzidis, Adv. Funct. Mater., 2018, 28, 1801617 CrossRef.
- C. M. Zeuthen, L. R. Jørgensen, L. J. Støckler, M. Roelsgaard, A.-C. Dippel and B. B. Iversen, J. Mater. Chem. A, 2022, 10, 1473–1480 RSC.
- G. Tan, F. Shi, S. Hao, L.-D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2016, 7, 12167 CrossRef CAS PubMed.
- Y. Sun, F. Guo, Y. Feng, C. Li, Y. Zou, J. Cheng, X. Dong, H. Wu, Q. Zhang, W. Liu, Z. Liu, W. Cai, Z. Ren and J. Sui, Nat. Commun., 2023, 14, 8085 CrossRef CAS PubMed.
- I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5(6), 1800904 CrossRef.
- Y. Yu, X. Xu, M. Bosman, K. Nielsch and J. He, Nat. Rev. Electr. Eng., 2024, 1, 109–123 CrossRef.
- M. Karunanithy, G. Prabhavathi, A. H. Beevi, B. H. A. Ibraheem, K. Kaviyarasu, S. Nivetha, N. Punithavelan, A. Ayeshamariam and M. Jayachandran, J. Nanosci. Nanotechnol., 2018, 18, 6680–6707 CrossRef CAS PubMed.
- P. K. Sharma, T. D. Senguttuvan, V. K. Sharma and S. Chaudhary, Mater. Today Energy, 2021, 21, 100713 CrossRef CAS.
- T. Cao, X.-L. Shi, M. Li, B. Hu, W. Chen, W.-D. Liu, W. Lyu, J. MacLeod and Z.-G. Chen, eScience, 2023, 3, 100122 CrossRef.
- M. d'Angelo, C. Galassi and N. Lecis, Energies, 2023, 16, 6409 CrossRef.
- I. Petsagkourakis, K. Tybrandt, X. Crispin, I. Ohkubo, N. Satoh and T. Mori, Sci. Technol. Adv. Mater., 2018, 19, 836–862 CrossRef CAS PubMed.
- S. J. Khengar, P. R. Parmar, N. Modi and P. B. Thakor, J. Phys. Condens. Matter, 2023, 35, 475702 CrossRef CAS PubMed.
- G. Y. Huang, N. M. Abdul-Jabbar and B. D. Wirth, Acta Mater., 2014, 71, 349–369 CrossRef CAS.
- L. Song, J. Zhang, A. Mamakhel and B. B. Iversen, ACS Appl. Electron. Mater., 2024, 6, 2925–2934 CrossRef CAS.
- K. Guo, J. Zhang, Y. Zhang, L. Liu, S. Yuan, Y. Jiang, J. Luo and J. T. Zhao, ACS Appl. Energy Mater., 2021, 4, 5015–5023 CrossRef CAS.
- P. P. Shetty, N. Kondekar, A. C. Thenuwara, M. G. Boebinger, S. C. Wright, M. Tian and M. T. McDowell, Matter, 2020, 3, 1246–1262 Search PubMed.
- N. Zulkepli, J. Yunas, M. A. Mohamed and A. A. Hamzah, Micromachines, 2021, 12(7), 734 CrossRef PubMed.
- G. Tan, F. Shi, H. Sun, L.-D. Zhao, C. Uher, V. P. Dravid and M. G. Kanatzidis, J. Mater. Chem. A, 2014, 2, 20849–20854 RSC.
- Z. Ma, J. Lei, D. Zhang, C. Wang, J. Wang, Z. Cheng and Y. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 33792–33802 Search PubMed.
- W. T. Yen, H. C. Huang, K. K. Wang and H. J. Wu, Mater. Today Phys., 2021, 19, 100416 CrossRef CAS.
- A. T. Serbesa, V. Pal, P. R. Sreeram, S. S. Legese, B. Kumar, C. G. Adamo, S. Mukherjee, M. Paliwal, F. E. Olu, C. S. Tiwary and K. Chattopadhyay, J. Mater. Sci., 2023, 58, 16462–16473 CrossRef CAS.
- A. V. Sanchela, A. D. Thakur and C. V. Tomy, J. Electron. Mater., 2022, 51, 2266–2272 CrossRef CAS.
- J. An, M.-K. K. Han and S.-J. J. Kim, J. Solid State Chem., 2019, 270, 407–412 CrossRef CAS.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 Search PubMed.
- M. T. Yin and M. L. Cohen, Phys. Rev. B, 1982, 25, 4317–4320 Search PubMed.
- L. Sun, M. A. L. Marques and S. Botti, Nat. Commun., 2021, 12, 811 Search PubMed.
- H. Zheng, X.-G. Li, R. Tran, C. Chen, M. Horton, D. Winston, K. A. Persson and S. P. Ong, Acta Mater., 2020, 186, 40–49 Search PubMed.
- C. J. Bartel, J. Mater. Sci., 2022, 57, 10475–10498 CrossRef CAS.
- N. Nandihalli, Crit. Rev. Solid State Mater. Sci., 2023, 48, 361–410 CrossRef CAS.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054 Search PubMed.
- C. Wu, X.-L. Shi, L. Wang, W. Lyu, P. Yuan, L. Cheng, Z.-G. Chen and X. Yao, ACS Nano, 2024, 18, 31660–31712 Search PubMed.
- R. Fortulan and S. Aminorroaya Yamini, Materials, 2021, 14, 6059 CrossRef CAS PubMed.
- N. W. Ashcroft and N. D. Mermin, in Solid State Physics, Harcourt College Publishers, 1976 Search PubMed.
- W. Zhang, L. Huang, X. Mi, H. Xie, X. Feng and J. H. Ahn, cMat, 2024, 1(1), e13 CrossRef.
- R. Saha, K. Gupta and C. J. Gómez García, Cryst. Growth Des., 2024, 24, 2235–2265 Search PubMed.
- S. Abbasi, R. B. Ladani, C. H. Wang and A. P. Mouritz, Mater. Des., 2020, 195, 109014 Search PubMed.
- M. Cutler and N. F. Mott, Phys. Rev., 1969, 181, 1336–1340 CrossRef CAS.
- T. Zhu, L. Hu, X. Zhao and J. He, Adv. Sci. DOI:10.1002/advs.201600004.
- D. L. Medlin and G. J. Snyder, Curr. Opin. Colloid Interface Sci., 2009, 14, 226–235 CrossRef CAS.
- B. S. Subathra, M. Saminathan, P. Wesley, L. Ravi, M. Battabyal, D. Sarkar, S. Perumal and Ravikirana, Intermetallics, 2024, 167, 108233 CrossRef CAS.
- Y. Zhang, C. Xing, Y. Liu, M. Li, K. Xiao, P. Guardia, S. Lee, X. Han, A. Ostovari Moghaddam, J. Josep Roa, J. Arbiol, M. Ibáñez, K. Pan, M. Prato, Y. Xie and A. Cabot, Chem. Eng. J., 2021, 418, 129374 Search PubMed.
- S. N. Girard, K. Schmidt-Rohr, T. C. Chasapis, E. Hatzikraniotis, B. Njegic, E. M. Levin, A. Rawal, K. M. Paraskevopoulos and M. G. Kanatzidis, Adv. Funct. Mater., 2013, 23, 747–757 Search PubMed.
- A. F. May and G. J. J. Snyder, in Thermoelectrics and its Energy Harvesting, CRC Press, 2012, pp. 11–18 Search PubMed.
- C. Kittel, in Introduction to Solid State Physics, 8th edn, 2005, pp. 156–157 Search PubMed.
- H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506 Search PubMed.
- C. Kittel, in Introduction to Solid State Physics, 8th edn, 2005, p. 122 Search PubMed.
- E. Maciá-Barber, Thermoelectric materials: Advances and applications, 2015 Search PubMed.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- Y. Zhang, J. Mater., 2016, 2, 237–247 Search PubMed.
- G. A. Slack, Solid State Phys., 1979, 34, 1–71 CAS.
- D. G. Cahill and R. O. Pohl, Phys. Rev. B, 1987, 35, 4067–4073 CrossRef CAS PubMed.
- D. Wu, J. Guo, Z.-H. H. Ge and J. Feng, Nanomaterials, 2021, 11, 3390 Search PubMed.
- S. Yoon, O.-J. Kwon, S. Ahn, J.-Y. Kim, H. Koo, S.-H. Bae, J.-Y. Cho, J.-S. Kim and C. Park, J. Electron. Mater., 2013, 42, 3390–3396 CrossRef CAS.
- D. Liu, X. Li, P. M. De Castro Borlido, S. Botti, R. Schmechel and M. Rettenmayr, Sci. Rep., 2017, 7, 1–13 Search PubMed.
- A. Zevalkink, D. M. Smiadak, J. L. Blackburn, A. J. Ferguson, M. L. Chabinyc, O. Delaire, J. Wang, K. Kovnir, J. Martin, L. T. Schelhas, T. D. Sparks, S. D. Kang, M. T. Dylla, G. J. Snyder, B. R. Ortiz and E. S. Toberer, Appl. Phys. Rev., 2018, 5, 021303 Search PubMed.
- T. Feng, Z. Zhou, P. Wang, Z. Liao, Y. Wang, H. Zhao, W. Zhang and W. Liu, Next Energy, 2024, 3, 100105 Search PubMed.
- H. Manako, S. Ohsumi, Y. J. Sato, R. Okazaki and D. Aoki, Nat. Commun., 2024, 15, 3907 Search PubMed.
- H. Adachi, F. Ando, T. Hirai, R. Modak, M. A. Grayson and K. Uchida, Appl. Phys. Express, 2025, 18, 090101 Search PubMed.
- D. J. Bergman and L. G. Fel, J. Appl. Phys., 1999, 85, 8205–8216 Search PubMed.
- M. Zebarjadi, G. Joshi, G. Zhu, B. Yu, A. Minnich, Y. Lan, X. Wang, M. Dresselhaus, Z. Ren and G. Chen, Nano Lett., 2011, 11, 2225–2230 CrossRef CAS PubMed.
- B. Yu, M. Zebarjadi, H. Wang, K. Lukas, H. Wang, D. Wang, C. Opeil, M. Dresselhaus, G. Chen and Z. Ren, Nano Lett., 2012, 12, 2077–2082 CrossRef CAS PubMed.
- X. Lu, G. Pan, Z. Shi, B. Xu and Y. Lou, Mater. Chem. Front., 2023, 7, 4707–4722 RSC.
- C.-C. Zhao and C. Xiao, Rare Met., 2021, 40, 752–766 Search PubMed.
- Y. Zhang and G. D. Stucky, Chem. Mater., 2014, 26, 837–848 CrossRef CAS.
- F. Ando, T. Hirai, A. Alasli, H. Sepehri-Amin, Y. Iwasaki, H. Nagano and K. Uchida, Energy Environ. Sci., 2025, 18, 4068–4079 Search PubMed.
- T. Hirai, F. Ando, H. Sepehri-Amin and K. Uchida, Nat. Commun., 2024, 15, 9643 Search PubMed.
- W. Zhou, T. Sasaki, K. Uchida and Y. Sakuraba, Adv. Sci., 2024, 11(18), 2308543 Search PubMed.
- R. Modak, Y. Sakuraba, T. Hirai, T. Yagi, H. Sepehri-Amin, W. Zhou, H. Masuda, T. Seki, K. Takanashi, T. Ohkubo and K. Uchida, Sci. Technol. Adv. Mater., 2022, 23, 767–782 Search PubMed.
- N. Saunders and A. P. Miodownik, in CALPHAD: Calculation of Phase Diagrams A Comprehensive Guide, Elsevier, 1998 Search PubMed.
- A. D. Pelton, in Phase Diagrams and Thermodynamic Modeling of Solutions, Elsevier, 2019, pp. 189–191 Search PubMed.
- M. Hillert, J. Alloys Compd., 2001, 320, 161–176 CrossRef CAS.
- P. Chartrand and A. D. Pelton, J. Phase Equilib., 2000, 21, 141–147 CrossRef CAS.
- Z. Li, S. Bigdeli, H. Mao, Q. Chen and M. Selleby, Phys. Status Solidi, 2017, 254(2), 1600231 CrossRef.
- S. Bigdeli and M. Selleby, Calphad, 2019, 64, 185–195 Search PubMed.
- M. C. Peters, J. W. Doak, J. E. Saal, G. B. Olson and P. W. Voorhees, J. Electron. Mater., 2019, 48, 1031–1043 CrossRef CAS.
- A. E. Gheribi and P. Chartrand, Calphad, 2012, 39, 70–79 Search PubMed.
- O. Redlich and A. T. Kister, Ind. Eng. Chem., 1948, 40, 345–348 Search PubMed.
- L. Huang, S. Liu, Y. Du and C. Zhang, Calphad, 2018, 62, 99–108 Search PubMed.
- X. Li, Z. Li, C. Chen, Z. Ren, C. Wang, X. Liu, Q. Zhang and S. Chen, J. Mater. Chem. A, 2021, 9, 6634–6649 RSC.
- Y. Tang, R. Hanus, S. Chen and G. J. Snyder, Nat. Commun., 2015, 6, 7584 Search PubMed.
- D. T. Morelli, G. P. Meisner, B. Chen, S. Hu and C. Uher, Phys. Rev. B, 1997, 56, 7376–7383 Search PubMed.
- Y. Tang, Y. Qiu, L. Xi, X. Shi, W. Zhang, L. Chen, S.-M. Tseng, S. Chen and G. J. Snyder, Energy Environ. Sci., 2014, 7, 812–819 Search PubMed.
- Y. Tang, S. Chen and G. J. Snyder, J. Mater., 2015, 1, 75–84 Search PubMed.
- W. Gierlotka, S. Chen, W. Chen, J. Chang, G. J. Snyder and Y. Tang, Metall. Mater. Trans. A, 2015, 46, 1488–1499 CrossRef CAS.
- M. Hong, Z. Chen, L. Yang, Y. Zou, M. S. Dargusch, H. Wang and J. Zou, Adv. Mater., 2018, 30(11), 1705942 Search PubMed.
- Y. Niu, S. Li, J. Mao, C. Yang, Q. Zhang, Q. Zhang, J. Jiang, C. Wang and Z. Ren, Nano Energy, 2020, 77, 105297 CrossRef CAS.
- N. A. Heinz, T. Ikeda, Y. Pei and G. J. Snyder, Adv. Funct. Mater., 2014, 24, 2135–2153 Search PubMed.
- S. Il Kim, K. H. Lee, H. A. Mun, H. S. Kim, S. W. Hwang, J. W. Roh, D. J. Yang, W. H. Shin, X. S. Li, Y. H. Lee, G. J. Snyder and S. W. Kim, Science, 2015, 348, 109–114 Search PubMed.
- S. S. Legese and F. E. Olu, J. Indian Inst. Sci., 2022, 102, 237–279 Search PubMed.
- P.-Y. Deng, W.-T. Yen, Y.-F. Tsai, I.-L. Jen, B.-C. Chen and H.-J. Wu, Adv. Energy Sustainability Res., 2021, 2(9), 2100054 CrossRef.
- A. K. Gautam and N. Khare, J. Mater., 2023, 9, 310–317 Search PubMed.
- T. Sakakibara, Y. Takigawa, A. Kameyama and K. Kurosawa, J. Ceram. Soc. Jpn., 2002, 110, 259–263 Search PubMed.
- T. Irie, T. Takahama and T. Ono, Jpn. J. Appl. Phys., 1963, 2, 72 Search PubMed.
- Y. Takigawa, T. Imoto, T. Sakakibara and K. Kurosawa, MRS Proc., 1998, 545, 105 Search PubMed.
- H. Zhu, J.-Y. Zhao and C. Xiao, Rare Met., 2021, 40, 2829–2837 CrossRef CAS.
- A. T. Serbesa, V. Pal, S. S. Legese, S. Mukherjee, S. Das, B. Kumar, C. G. Adamo, P. R. R. Sreeram, M. Paliwal, E. F. Olu, C. S. Tiwary and K. Chattopadhyay, J. Phys. Chem. Solids, 2024, 190, 111995 Search PubMed.
- A. D. Pelton, Calphad, 2001, 25, 319–328 CrossRef CAS.
- A. T. Dinsdale, Calphad, 1991, 15, 317–425 Search PubMed.
- A. D. Pelton, S. A. Degterov, G. Eriksson, C. Robelin and Y. Dessureault, Metall. Mater. Trans. B, 2000, 31, 651–659 CrossRef.
- M. B. Babanly, Y. M. Shykhyev, N. B. Babanly and Y. A. Yusibov, Russ. J. Inorg. Chem., 2007, 52, 434–440 CrossRef.
- A. Stegherr, P. Eckerlin and F. Wald, Int. J. Mater. Res., 1963, 54, 598–600 Search PubMed.
- C. T. Heycock and F. H. Neville, Philos. Trans. R. Soc. Lond. - Ser. A Contain. Pap. a Math. or Phys. Character, 1897, 189, 25–69 Search PubMed.
- G. I. Petrenko, Z. Anorg. Chem., 1906, 50, 133–144 CrossRef CAS.
- M. W. Nathans and M. Leider, J. Phys. Chem., 1962, 66, 2012–2015 CrossRef CAS.
- O. J. Kleppa, J. Phys. Chem., 1956, 60, 446–452 CrossRef CAS.
- T. Sano, M. Miyake and T. Konishi, Technol. Rep. Osaka Univ., 1960, 10, 815 CAS.
- M. Miyake and T. Sano, J. Jpn. Inst. Met., 1962, 26, 386–390 CrossRef.
- D. Schmid, V. Behrens and T. Hehenkamp, Acta Metall., 1988, 36, 621–625 CrossRef CAS.
- M. Hansen, K. Anderko and H. W. Salzberg, J. Electrochem. Soc., 1958, 105, 260C CrossRef.
- H. H. Chiswick and R. Hultgren, Bull. Am. Inst. Min. Metall. Eng., 1940, 137, 442–446 Search PubMed.
- K. Itagaki and A. Yazawa, Trans. Jpn. Inst. Met., 1969, 10, 259–266 CrossRef.
- R. Castanet, Y. Claire, M. Gilbert and M. Laffitte, in Revue Internationale des Hautes Temperatures et des Refractaires, 1970, vol. 7, pp. 51–59 Search PubMed.
- K. Kameda and K. Yamaguchi, J. Jpn. Inst. Met., 1991, 55, 536–544 CrossRef CAS.
- A. Kusoffsky, Acta Mater., 2002, 50, 5139–5145 CrossRef CAS.
- Z. Gregorczyk, Rocz. Chem., 1961, 35, 307–316 Search PubMed.
- A. Vecher and Y. Gerasimov, Dokl. Akad. Nauk SSSR, 1961, 141, 381–383 CAS.
- J. B. Raynor, Ber. Bunsenges. Phys. Chem., 1963, 67, 629–632 CrossRef CAS.
- G. F. Voronin, A. M. Evseev and V. I. Goryacheva, Zh. Fiz. Khim., 1967, 41, 3041–3045 CAS.
- H. N. Prasad, Banaras Metall., 1971, 4, 62–64 CAS.
- B. Predel and A. Emam, Int. J. Mater. Res., 1973, 64, 496–501 CrossRef CAS.
- B. Brunetti, D. Gozzi, M. Iervolino, A. Latini and V. Piacente, J. Chem. Eng. Data, 2007, 52, 1394–1400 Search PubMed.
- A. T. Aldred and J. N. Pratt, Trans. Faraday Soc., 1963, 59, 673 Search PubMed.
- U. r Kattner and W. J. Boettinger, J. Electron. Mater., 1994, 23, 603–610 Search PubMed.
- J. Liu, C. Guo, C. Li and Z. Du, Thermochim. Acta, 2012, 539, 44–50 CrossRef CAS.
- J. Wang, S. Cui and W. Rao, J. Electron. Mater., 2018, 47, 4056–4069 Search PubMed.
- V. Koern, Naturwissenschaften, 1939, 27, 432 CrossRef CAS.
- R. v. Kujawa, Z. Phys. Chem., 1963, 222, 325–329 CrossRef CAS.
- R. V. Kujawa, Phys. Status Solidi, 1965, 12, 169–180 Search PubMed.
- F. C. Kracek and C. J. Ksanda, Trans., Am. Geophys. Union, 1940, 21, 363 CrossRef.
- C. R. Veale, J. Less-Common Met., 1966, 11, 50–63 CrossRef CAS.
- K. P. Mamedov and M. F. Gadzhiev, Solid State Phys., 1977, 19, 2196–2197 CAS.
- R. Castanet, Y. Claire and M. Laffitte, J. Chim. Phys., 1971, 68, 1133–1137 CrossRef CAS.
- R. Castanet and M. Laffitte, Rev. Int. Hautes Temp. Refract., 1974, 11, 103–107 CAS.
- R. Castanet and C. Bergman, J. Chem. Thermodyn., 1979, 11, 83–92 CrossRef CAS.
- T. Maekawa and T. Yokokawa, J. Chem. Thermodyn., 1975, 7, 505–506 Search PubMed.
- B. Predel and J. Piehl, Int. J. Mater. Res., 1975, 66, 33–38 CrossRef CAS.
- I. Karakaya and W. Thompson, J. Phase Equilib., 1991, 12, 56–63 CrossRef CAS.
- W. Gierlotka, J. Alloys Compd., 2009, 485, 231–235 CrossRef CAS.
- W. Gierlotka, J. Łapsa and K. Fitzner, J. Phase Equilib. Diffus., 2010, 31, 509–517 Search PubMed.
- C. Mao, M. Tan, L. Zhang, D. Wu, W. Bai and L. Liu, Calphad, 2018, 60, 81–89 CrossRef CAS.
- W. Gierlotka, Calphad, 2018, 63, 6–11 CrossRef CAS.
- B. Kumar, C. S. Tiwary, M.-K. Paek and M. Paliwal, Calphad, 2021, 74, 102326 CrossRef CAS.
- S. Drzewowska and B. Onderka, J. Phase Equilib. Diffus., 2023, 44, 429–444 CrossRef CAS.
- S. S. Ragimov and A. Aliev, Neorg. Mater., 2007, 43, 1184–1186 CrossRef CAS.
- R. Georg Maier, Meteorol. Z., 54, 311 Search PubMed.
- H.-J. Wu and S.-W. Chen, Acta Mater., 2011, 59, 6463–6472 CrossRef CAS.
- B. Kumar, C. S. S. Tiwary, M.-K. Paek, M. Paliwal, C. S. S. Tiwary, M. Paliwal, M.-K. Paek and M. Paliwal, Calphad, 2021, 74, 102326 CrossRef CAS.
- D. Huang, R. Han, Y. Wang and T. Ye, J. Alloys Compd., 2021, 855, 157373 CrossRef CAS.
- S. Yu, J. Wang, D. Cui, S. Chen, Q. Wu and Y. Du, J. Phase Equilib. Diffus., 2022, 43, 193–213 CrossRef CAS.
- M. Yahyaoglu, M. Ozen, Y. Prots, O. El Hamouli, V. Tshitoyan, H. Ji, U. Burkhardt, B. Lenoir, G. J. Snyder, A. Jain, C. Candolfi and U. Aydemir, Chem. Mater., 2021, 33, 1832–1841 CrossRef CAS.
- R. Blachnik, M. Lasocka and U. Walbrecht, 1983, 431–438.
- A. L. N. Stevels, PhD thesis, University of groningen, 1969.
- T. Mizota, K. Koto and N. Morimoto, Mineral. J., 1973, 7, 252–261 CrossRef CAS.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- D. J. Chakrabarti and D. E. Laughlin, Bull. Alloy Phase Diagrams, 1984, 5, 148–155 CrossRef CAS.
- C. Kim, K. Kurosaki, M. Ishimaru, H. Muta and S. Yamanaka, J. Electron. Mater., 2011, 40, 999–1004 CrossRef CAS.
- T. H. Vu, A. T. Pham, V. Q. Nguyen, J. Park, S. Park and S. Cho, J. Solid State Chem., 2021, 298, 122155 CrossRef CAS.
- H. Fu, P. Ying, J. Cui, X. Zhang and Y. Yan, Rare Met. Mater. Eng., 2012, 41, 767–771 CrossRef CAS.
- C. Lin, W. Yen, Y. Tsai and H. Wu, ACS Appl. Energy Mater., 2020, 3, 1311–1318 CrossRef CAS.
- P. G. Rustamov, N. A. Seidova and M. G. Shakhbazov, Zh. Neorg. Khim., 1976, 21, 860–862 CAS.
- P. G. Rustamov, N. A. Seidova and M. G. Shakhbazov, Zh. Neorg. Khim., 1976, 21, 764–768 CAS.
- V. Pal, B. Kumar, M.-K. Paek, C. S. Tiwary and M. Paliwal, Mater. Chem. Phys., 2023, 297, 127366 CrossRef CAS.
- S. Misra, A. Léon, P. Levinský, J. Hejtmánek, B. Lenoir and C. Candolfi, J. Mater. Chem. C, 2021, 9, 14490–14496 RSC.
- D. Liu, X. Li, R. Schmechel and M. Rettenmayr, J. Electron. Mater., 2016, 45, 1654–1660 CrossRef CAS.
- S. Chen, N. Logothetis, L. Ye and J. Liu, Mater. Today: Proc., 2015, 2, 610–619 Search PubMed.
- M. K. Jacobsen, Y. Meng, R. S. Kumar and A. L. Cornelius, J. Phys. Chem. Solids, 2013, 74, 723–728 CrossRef CAS.
- S. Chen, S. Lu and J. Chang, J. Alloys Compd., 2017, 722, 499–508 CrossRef CAS.
- L. R. Scherpereel, P. L. Palumbo and E. A. Peretti, J. Less-Common Met., 1968, 14, 41–46 CrossRef CAS.
- D. Liu, H. Engelhardt, X. Li, A. Löffler and M. Rettenmayr, CrystEngComm, 2015, 17, 3076–3081 RSC.
- D. J. Bologna and E. A. Peretti, Trans. Am. Soc. Met., 1963, 56, 194 CAS.
- E. J. Ryan and E. A. Peretti, Trans. Metall. Soc. AIME, 1966, 236, 1507 CAS.
- E. M. Gojayev, S. S. Osmanova, S. I. Safarova and D. M. Gafarova, Int. J. Mod. Phys. B, 2021, 35, 2150029 CrossRef CAS.
- V. Pal, B. Kumar, J. Choi, B. Kumar, C. S. Tiwary, M. Paliwal and M.-K. Paek, J. Mater. Sci., 2022, 57, 18178–18194 CrossRef CAS.
- A. A. Kuliev, Z. G. Kagramanyan, D. M. Suleimanov and V. V. Prud’ko, Chem. Informationsdienst, 1974, 5, 1895–1896 Search PubMed.
- J. C. Woolley, D. G. Lees and B. A. Smith, J. Less-Common Met., 1959, 1, 199–201 CrossRef CAS.
- S. Yamanaka, M. Ishimaru, A. Charoenphakdee, H. Matsumoto and K. Kurosaki, J. Electron. Mater., 2009, 38, 1392–1396 CrossRef CAS.
- R. Blachnik and E. Klose, J. Alloys Compd., 2000, 305, 144–152 CrossRef CAS.
- R. Moshwan, L. Yang, J. Zou and Z. Chen, Adv. Funct. Mater. DOI:10.1002/adfm.201703278.
- G.-Y. Huang, N. M. Abdul-Jabbar and B. D. Wirth, Acta Mater., 2014, 71, 349–369 CrossRef CAS.
- B. Kumar, M. Paliwal, C. S. Tiwary and M.-K. Paek, Metals, 2021, 11, 1363 CrossRef CAS.
- B. Gather, E. Irle and R. Blachnik, J. Less-Common Met., 1987, 136, 183–191 CrossRef CAS.
- T. T. Dedegkaev, S. M. Duguzhev, T. B. Zhukova, B. T. Melekh and V. A. Moshnikov, Zh. Tekh. Fiz., 1985, 55, 2408–2410 CAS.
- P. G. Rustamov, B. B. Kuliev, M. A. Aliyanov and E. M. Kuliev, Phys. Status Solidi, 1970, 3, K139–K141 CrossRef CAS.
- M. Guittard, F. Alapini, S. Jaulmes, M. Julien-Pouzol and J. Flahaut, Mater. Res. Bull., 1978, 13, 1157–1161 CrossRef CAS.
- V. Pal, B. Kumar and M. Paliwal, J. Phase Equilib. Diffus., 2023, 44, 642–653 CrossRef CAS.
- T. Sakakibara, Y. Takigawa and K. Kurosawa, Jpn. J. Appl. Phys., Part 1, 2002, 41, 2842–2844 CrossRef CAS.
- A. Stegherr, P. Eckerlin and F. Wald, Int. J. Mater. Res., 1963, 54, 598–600 CrossRef CAS.
- T. Zhao, L. Z. Yang, Y. Zhou, H. J. Liao, Z. Y. Huang, J. Li, X. Lu and X. Y. Zhou, Rare Met., 2022, 41, 4149–4155 CrossRef CAS.
- M. Zhang, X. Shi, S. Liu, R. Moshwan, T. Cao, W. Chen, Y. Chen, M. Li, C. Zhang, N. Li, B. Hu, W. Lyu, W. Liu, G. Tang and Z. Chen, Adv. Funct. Mater., 2025, 35, 2500898 CrossRef CAS.
- L. Li, B. Hu, Q. Liu, X. Shi and Z. Chen, Adv. Mater., 2024, 36, 2409275 CrossRef CAS PubMed.
- H. Wang, J.-F. Li, M. Zou and T. Sui, Appl. Phys. Lett., 2008, 93, 202106 CrossRef.
- S. Drzewowska, T.-W. W. Lan and B. Onderka, Arch. Metall. Mater., 2021, 67, 5–15 Search PubMed.
- H.-J. Wu and W.-T. Yen, Acta Mater., 2018, 157, 33–41 CrossRef CAS.
- K. H. Seo, B. G. Kim, C.-H. Lim, S.-H. Kim, K.-M. Lee, J.-Y. Kim and S.-M. Choi, CrystEngComm, 2017, 19, 2750–2757 RSC.
- Y. Zhang, Y. Liu, M. Calcabrini, C. Xing, X. Han, J. Arbiol, D. Cadavid, M. Ibáñez and A. Cabot, J. Mater. Chem. C, 2020, 8, 14092–14099 Search PubMed.
- S. S. Legese, D. Chandravanshi, S. S. S. Gadhavajhala, V. Pal, A. T. Serbesa, B. Srinivasan, F. E. Olu and C. S. Tiwary, J. Mater. Sci., 2025, 60, 1313–1327 CrossRef CAS.
- G. M. Jigi, V. Pal, B. S. Haile, P. R. Sreeram, D. Pati, S. D. Negedu, M. Paliwal, F. E. Olu and C. S. Tiwary, J. Alloys Compd., 2025, 1010, 177935 CrossRef CAS.
- J. Cha, C. Zhou, S. P. Cho, S. H. Park and I. Chung, ACS Appl. Mater. Interfaces, 2019, 11, 30999–31008 CrossRef CAS PubMed.
- J. Nagao and M. Ferhat, AIP Conf. Proc., 2000, 504, 1494–1499 CrossRef CAS.
- D. Liu, J. Stötzel, M. Seyring, M. Drüe, X. Li, R. Schmechel and M. Rettenmayr, Cryst. Growth Des., 2016, 16, 617–624 CrossRef CAS.
- D. Liu, X. Li, P. M. de C. Borlido, S. Botti, R. Schmechel and M. Rettenmayr, Sci. Rep., 2017, 7, 43611 CrossRef PubMed.
- D. Liu, C. Dreβler, M. Seyring, S. Teichert and M. Rettenmayr, J. Alloys Compd., 2018, 748, 730–736 CrossRef CAS.
- H. Hazama, Y. Masuoka, H. Yamamoto, H. Suto, Y. Kinoshita, M. Ishikiriyama and R. Asahi, J. Alloys Compd., 2017, 726, 578–586 CrossRef CAS.
- V. Pal, S. S. Legese, P. R. Sreeram, K. Chattopadhyay, M. Paliwal and C. S. Tiwary, J. Phys. D Appl. Phys., 2025, 58, 095502 CrossRef CAS.
- S. H. Kim, T. Min, J. W. Choi, S. H. Baek, J.-P. Choi and C. Aranas, Energy, 2018, 144, 607–618 CrossRef CAS.
- J. A. Kafalas, R. F. Brebrick and A. J. Strauss, Appl. Phys. Lett., 1964, 4, 93–94 CrossRef CAS.
- X. Zhang, D. Wang, H. Wu, M. Yin, Y. Pei, S. Gong, L. Huang, S. J. Pennycook, J. He and L.-D. Zhao, Energy Environ. Sci., 2017, 10, 2420–2431 RSC.
- R. Al Rahal Al Orabi, J. Hwang, C.-C. Lin, R. Gautier, B. Fontaine, W. Kim, J.-S. Rhyee, D. Wee and M. Fornari, Chem. Mater., 2017, 29, 612–620 CrossRef CAS.
- H. Zhang, Y. Zhang and G. Li, Metals, 2023, 13, 532 CrossRef CAS.
- H. Zhang, Y. Zhang, C. Chen, P. Yu, L.-M. Wang and G. Li, ACS Appl. Mater. Interfaces, 2023, 15, 19170–19177 CrossRef CAS PubMed.
- B. Agrawal, J. de Boor and T. Dasgupta, Cell Rep. Phys. Sci., 2024, 5, 101781 CrossRef CAS.
- D. A. G. Bruggeman, Ann. Phys., 1937, 421, 160–178 CrossRef.
- R. Landauer, J. Appl. Phys., 1952, 23, 779–784 CrossRef CAS.
- G. N. Dul’nev, Y. P. Zarichnyak and V. V. Novikov, J. Eng. Phys., 1976, 31, 856–869 CrossRef.
- I. Webman, J. Jortner and M. H. Cohen, Phys. Rev. B, 1977, 16, 2959–2964 CrossRef CAS.
- J. Sonntag, Phys. Rev. B, 2005, 71, 115114 CrossRef.
- J. Sonntag, Phys. Rev. B, 2006, 73, 045126 CrossRef.
- D. S. McLachlan, M. Blaszkiewicz and R. E. Newnham, J. Am. Ceram. Soc., 1990, 73, 2187–2203 CrossRef CAS.
- J. Sonntag, J. Phys. Condens. Matter, 2009, 21, 175703 CrossRef PubMed.
- J.-B. Vaney, A. Piarristeguy, V. Ohorodniichuck, O. Ferry, A. Pradel, E. Alleno, J. Monnier, E. B. Lopes, A. P. Gonçalves, G. Delaizir, C. Candolfi, A. Dauscher and B. Lenoir, J. Mater. Chem. C, 2015, 3, 11090–11098 RSC.
- A. G. Rösch, F. Giunta, M. M. Mallick, L. Franke, A. Gall, J. Aghassi-Hagmann, J. Schmalian and U. Lemmer, Adv. Theory Simul., 2021, 6, DOI:10.1002/adts.202000284.
- P. Baskaran and M. Rajasekar, Chem. Eng. J., 2025, 506, 159929 CrossRef CAS.
- R. He, G. Schierning and K. Nielsch, Adv. Mater. Technol., 2018, 3, 1700256 CrossRef.
- X.-L. Shi, N.-H. Li, M. Li and Z.-G. Chen, Chem. Rev., 2025, 125, 7525–7724 CrossRef CAS PubMed.
- W. Liu, Q. Jie, H. S. Kim and Z. Ren, Acta Mater., 2015, 87, 357–376 CrossRef CAS.
- X. Wu and W. Liu, J. Mater., 2024, 10, 748–750 Search PubMed.
- A. Li, L. Wang, X. Wu, J. Li, X. Wang, G. Wu, Z. Hu and T. Mori, Sci. Adv., 2025, 11, eadx7115 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |
