Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Challenges with relativistic GW calculations in solids and molecules
Gaurav
Harsha
 a,
Vibin
Abraham
a,
Vibin
Abraham
 a and
Dominika
Zgid
a and
Dominika
Zgid
 *ab
*ab
aDepartment of Chemistry, University of Michigan, Ann Arbor, Michigan 48109, USA. E-mail: zgid@umich.edu
bDepartment of Physics, University of Michigan, Ann Arbor, Michigan 48109, USA
First published on 20th March 2024
Abstract
For molecules and solids containing heavy elements, accurate electronic-structure calculations require accounting not only for electronic correlations but also for relativistic effects. In molecules, relativity can lead to severe changes in the ground-state description. In solids, the interplay between both correlation and relativity can change the stability of phases or it can lead to an emergence of completely new phases. Traditionally, the simplest illustration of relativistic effects can be done either by including pseudopotentials in non-relativistic calculations or alternatively by employing large all-electron basis sets in relativistic methods. By analyzing different electronic properties (band structure, equilibrium lattice constant and bulk modulus) in semiconductors and insulators, we show that capturing the interplay of relativity and electron correlation can be rather challenging in Green's function methods. For molecular problems with heavy elements, we also observe that similar problems persist. We trace these challenges to three major problems: deficiencies in pseudopotential treatment as applied to Green's function methods, the scarcity of accurate and compact all-electron basis sets that can be converged with respect to the basis-set size, and linear dependencies arising in all-electron basis sets, particularly when employing Gaussian orbitals. Our analysis provides detailed insight into these problems and opens a discussion about potential approaches to mitigate them.
I. Introduction
Computational methods in ab initio electronic structure theory have become indispensable tools in the design and study of new functional materials and molecules. For many years, mean-field methods such as density functional theory1,2 (DFT) and Hartree–Fock (HF) were the commonly employed simulation tools mostly due to their low computational cost and reasonable accuracy. However, recently, due to advances in computational resources as well as algorithms, sophisticated methods capturing electronic correlation beyond the mean-field approximation have gathered much more attention. Examples include coupled cluster,3,4 perturbation theories for wave functions and Green's functions,5–9 and embedding methods,10–19 among others.The development of new electronic structure methods is primarily driven by one or both of the following objectives: (i) accurate description of electron correlation, and (ii) applicability to realistic systems with a large number of electrons. Addressing both of these challenges satisfactorily is usually very difficult. For instance, low-scaling mean-field methods such as DFT and HF (with 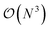 and
and 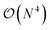 computational costs, respectively, N being a measure of system size) can be applied to very large systems. However, they often lack quantitative accuracy. On the other hand, coupled cluster with single, double and perturbative triple excitation, i.e., CCSD(T), is considered as the gold standard for description of dynamical correlation, but has limited applicability due to its high
computational costs, respectively, N being a measure of system size) can be applied to very large systems. However, they often lack quantitative accuracy. On the other hand, coupled cluster with single, double and perturbative triple excitation, i.e., CCSD(T), is considered as the gold standard for description of dynamical correlation, but has limited applicability due to its high 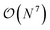 scaling. Consequently, greater recovery of correlation effects usually comes hand-in-hand with an increased computational cost.
scaling. Consequently, greater recovery of correlation effects usually comes hand-in-hand with an increased computational cost.
The GW method,5,20–22 derived from Hedin's perturbation theory for the single-particle Green's function, offers a reasonable balance between accuracy and cost. In comparison to DFT or HF, it provides a high-level description of correlation effects at a formal scaling of 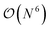 , which is usually brought down to
, which is usually brought down to 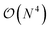 by using approximations such as the density-fitting procedure.23–25 The good accuracy of GW can be explained by its diagrammatic similarities with theories like coupled cluster and random phase approximation.26–29 Additionally, GW has shown versatility in its application to both finite30–39 and extended systems.40–45
by using approximations such as the density-fitting procedure.23–25 The good accuracy of GW can be explained by its diagrammatic similarities with theories like coupled cluster and random phase approximation.26–29 Additionally, GW has shown versatility in its application to both finite30–39 and extended systems.40–45
As the applications of computational methods are expanded to systems with heavy elements, another challenge arises: the problem of accurate inclusion of relativity. Even for elements in the third and fourth rows of the periodic table, relativistic effects are important.46 While for a full relativistic description, the 4-component Dirac equation, instead of the regular non-relativistic Schrödinger equation, should be solved, solving the 4-component equation is a formidable task and not strictly necessary for most systems if only the electronic structure properties are of interest. Several approximations have been proposed to introduce the full relativistic physics into an effective Hamiltonian that describes only the electronic degrees of freedom. The most widely used approximation follows the work of Breit,47 where the Dirac equation is reduced to a Schrödinger-like equation with an effective Dirac–Coulomb–Breit Hamiltonian that contains the relativistic terms. Theories such as the Douglas–Kroll–Hess48–52 approach and the exact two-component53–57 (X2C) theory introduce further approximations to make relativistic calculations achievable. Several ab initio implementations for realistic systems of the relativistic GW theory have emerged in the condensed matter community,58–61 and in the quantum chemistry community,37,62,63 where the latter are based on the X2C Hamiltonian.
Calculations in the X2C approach are generally performed using all-electron basis sets since current pseudopotentials (PPs) or effective core potentials (ECPs) do not recover relativistic effects, such as spin–orbit coupling (SOC). Most modern implementations or ab initio relativistic codes are capable of handling relativistic elements, at least up to the 5th or 6th row, including the Lanthanides, in the periodic table. Yet, performing reliable GW calculations for accurate electronic structure properties still remains an arduous task. Considering that the GW approximation is the simplest in the hierarchy of Hedin's perturbation theory, it offers an understandably limited accuracy in describing electron correlation. However, factors other than the accuracy of the GW method, e.g., poor quality and availability of basis sets, lack of effective PPs, etc., can have a larger impact on the quality of results, particularly in heavy elements.
In this discussion article, we analyze the factors that hinder the applicability of the sophisticated machinery of GW to both solids and molecules containing heavy elements. In particular, we first highlight the need for all-electron relativistic calculations due to the inability of PPs to account for many important relativistic effects. We then investigate problems with achieving the basis set convergence in GW calculations. This is followed by results that highlight linear dependencies arising in larger basis sets. Such problems often aggravate the issue of slow convergence with respect to basis set size. Finally, we also comment on possible improvements of experimental results that are ultimately necessary for benchmarking and validating new theoretical methods. By investigating multiple properties of solids and molecules, we perform a comprehensive analysis of how several external factors, other than the accuracy of the method itself, influence the results in self-consistent GW (scGW).
This article is organized as follows: in Section II, we recap some of the theoretical concepts on which the majority of this paper is based. This is followed by computational and implementation details in Section III. In Section IV, we analyze various hurdles, one by one, for the application of scGW to relativistic systems. A general discussion and conclusions on possible factors behind these challenges, along with the current and future developments that can address these problems, is presented in Section V.
II. Methods
In this work, we employ mean-field methods and self-consistent GW (scGW) theory within the X2C relativistic formalism.53–57 While most of the theoretical and implementation details can be found in ref. 39, 63 and 64, here we provide a brief overview of important concepts, namely the relativistic Hamiltonian, scGW theory, and Birch–Murnaghan65,66 equation of state that we use to study bulk properties in materials. Note that while GW by itself21,40,64,67–73 provide excellent results for weakly correlated compunds, it is also important for embedding approaches74–80 where it is usually employed as a low-level method for treating the environment.A. Relativistic Hamiltonian: exact two-component formalism
The X2C formalism is widely used among electronic structure relativistic methods.55–57,81 In this formalism, the four-component one-body Dirac–Coulomb Hamiltonian H4C1e is used as a starting point on which a unitary transformation is performed that decouples the eigenvectors with large and small eigenvalues, generally labeled as large and small components,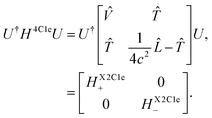 | (1) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the local Coulomb potential,
is the local Coulomb potential, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the kinetic energy matrix, and the
is the kinetic energy matrix, and the ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) operator is defined as
operator is defined as![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) = ( = (![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) · ·![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ) )![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ( (![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) · ·![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ). ). | (2) |
The assumption invoked in the X2C formalism is that after the unitary transformation, the large component can be effectively considered as an electron, even though in principle, it mixes the electronic and positronic components. Therefore, the large-component Hamiltonian HX2C1e+ is used as the one-body Hamiltonian in electronic structure calculations, along with the usual two-electron integrals. We should note that no relativistic correction is used for the latter.
The formalism described so far is called the X2C1e approximation. By definition, this approximation breaks the Sz spin-symmetry and necessitates the use of generalized spin-orbitals in subsequent calculations. Another approximation, known as the spin-free X2C1e (sfX2C1e) approximation, is also popular. In sfX2C1e, only the spin-independent contribution arising from the ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) -operator in eqn (2) is considered. Given that sfX2C1e leads to a symmetry-adapted Hamiltonian, for several systems, where negligible or no SOC is present, using sfX2C1e greatly reduces the computational cost and memory requirements in a calculation, without any accuracy loss. Even when SOC cannot be neglected, total energy trends in sfX2C1e do not differ significantly from X2C1e.39
-operator in eqn (2) is considered. Given that sfX2C1e leads to a symmetry-adapted Hamiltonian, for several systems, where negligible or no SOC is present, using sfX2C1e greatly reduces the computational cost and memory requirements in a calculation, without any accuracy loss. Even when SOC cannot be neglected, total energy trends in sfX2C1e do not differ significantly from X2C1e.39
B. Self-consistent GW
Hedin's equations5 define a perturbation theory where the one-particle Green's function G, the vertex function Γ, the irreducible polarizability Π0, the screened Coulomb interaction W, and the self-energy Σ are related through a set of integro-differential equations. This is traditionally represented as Hedin's pentagram diagram. In the GW approximation, higher-order corrections to the vertex arising from G are ignored and the vertex Γ is approximated as a Dirac delta function in space-time. As a result, the self-energy is expressed as a product of the interacting Green's function G and the screened Coulomb potential W.Hedin's equations or the GW approximation can be evaluated either on the real or imaginary axis. Here, we work with the finite-temperature (or Matsubara imaginary axis) formalism described in ref. 63 and 64. The one-particle imaginary-time Green's function is defined as
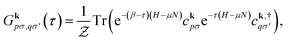 | (3) |
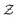 is the partition function, defined as
is the partition function, defined as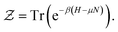 | (4) |
In the GW approximation, the self-energy on the imaginary time/frequency axis is approximated as
| Σk[G](iωn) = Σk∞[G] + Σkc[G](iωn), | (5) |
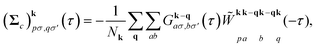 | (6) |
![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) is the effective screened Coulomb interaction, and Nk is the number of k-points sampled in the Brillouin zone (BZ). The summations are performed over momentum vectors q in the BZ, as well as the atomic orbitals a and b in the unit cell. The new Green's function is then defined by the Dyson equation,
is the effective screened Coulomb interaction, and Nk is the number of k-points sampled in the Brillouin zone (BZ). The summations are performed over momentum vectors q in the BZ, as well as the atomic orbitals a and b in the unit cell. The new Green's function is then defined by the Dyson equation,| [Gk(iωn)]−1 = (iωn + μ)Sk − Hk0 − Σk(iωn), | (7) |
![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) . The total electronic energy is calculated using the Galitskii–Migdal formula,
. The total electronic energy is calculated using the Galitskii–Migdal formula,| E = E1b + E2b, | (8a) |
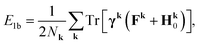 | (8b) |
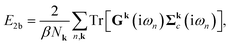 | (8c) |
| Fk = H0 + Σk∞, | (9) |
C. Equation of state for solids
For periodic solids, the relationship between energy and volume in a unit cell is called the equation of state. Several different parametrizations of this equation are available. Fitting the energy-volume data to these forms allows us to estimate the equilibrium volume (and in turn, the lattice constant), the bulk modulus, and other related quantities. One of the most commonly used parametrizations, the Birch–Murnaghan66 equation of state is defined as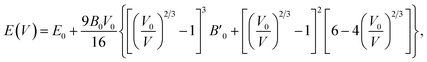 | (10) |
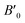 denotes the derivative of the bulk modulus with respect to the cell volume V, taken at V0. The Murnaghan65 and Vinet82 equations are other notable parametric forms. For the purpose of this paper, we fit the energy-volume data to eqn (10) using the least-squares optimization.
denotes the derivative of the bulk modulus with respect to the cell volume V, taken at V0. The Murnaghan65 and Vinet82 equations are other notable parametric forms. For the purpose of this paper, we fit the energy-volume data to eqn (10) using the least-squares optimization.
III. Computational details
All of our calculations are performed with Gaussian-type orbitals (GTO) or their periodic generalizations.83,84 For initializing all the calculations, we use PySCF84,85 where we generate the one- and two-electron integrals, and perform mean-field calculations such as Hartree–Fock (HF) or DFT. For the density-fitting in two-electron integrals, we employ even-tempered Gaussian orbitals86 with progression factor 2.0 for both molecules and extended systems. For the relativistic calculations, we use x2c-nZVPall (n = S, T, Q) family of basis sets.87 In contrast to the traditionally used uncontracted bases for the relativistic calculations, the x2c family of basis sets contains contracted bases minimizing the number of basis functions without a significant sacrifice of overall accuracy. To construct the initial Dirac Hamiltonian, the basis set is completely uncontracted (as is also programmed, by default, in PySCF).All the dynamical quantities, i.e., imaginary-time and frequency dependent objects, in scGW are stored using sparse grids.88–93 Sufficiently large grids are used to avoid loss of information in Fourier transforms performed over successive iterations of the GW cycle. To obtain spectral functions, ionization potentials (IPs) and band gaps, the Matsubara Green's function in our calculations is analytically continued to the real-frequency axis. We use the Nevanlinna analytical continuation to accomplish this task.94 To avoid poles on the real axis, a small broadening, a positive imaginary term, is added to the real-frequency grid, i.e.,
 | (11) |
For IP and band-gap calculations, we employ η = 0.01 a.u. and η = 0.001 a.u., respectively. For photoelectron spectra of HgCl2, we have chosen a broadening of η = 0.002 a.u. to match the experimental peak widths, while in Fig. 1, η = 0.005 a.u. is used. All our calculations are converged with rigorous thresholds. In particular, we ensure that the particle number is converged to a relative tolerance of 10−8 and the total energy to an absolute tolerance of 10−5 a.u. The finite-temperature scGW code used here is accessible via GitHub.95
A. Need for relativistic corrections
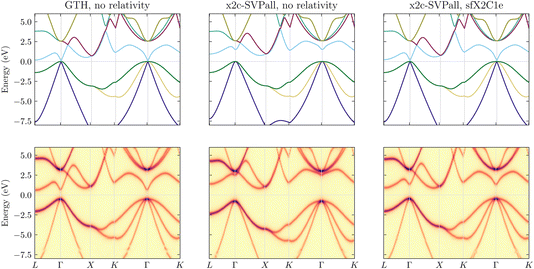
Before we begin discussing the challenges associated with the application of relativistic scGW, it is important to justify the necessity of incorporating relativistic effects into correlated all-electron (AE) calculations. We accomplish this by studying the band structure of germanium. In Fig. 1, we plot three different band structure results evaluated using both PBE and scGW for germanium with a diamond lattice, and lattice constant a = 5.657 Å. For all these calculations, we used a 6 × 6 × 6 k-mesh sampling in the BZ.In the top left panel, we employ the GTH basis set and PPs, where the relativistic effects are built directly into the PPs. Here, we find that PBE predicts a semiconducting phase with 0 eV band gap at the Γ point. The top middle and right panels show PBE calculations with and without the inclusion of scalar relativistic effects, respectively. Both were performed using an AE basis, namely x2c-SVPall. Right away, one finds that non-relativistic AE-PBE yields a qualitatively incorrect result with an indirect and sizeable band gap of 1 eV between the Γ and L high-symmetry points. By including scalar relativistic effects at the sfX2C1e level, the band gap is closed resulting in a correct DFT band structure, similar to the GTH results. For germanium, SOC effects are known to be negligible and therefore not considered here.
While both the top left and top right panels of Fig. 1 display the correct band structure of germanium at the PBE level, the experimental results yield a band structure with an indirect band gap of 0.7 eV between the Γ and L points, and this only fortuitously somewhat resembles the band structure from the middle panel evaluated with an AE basis and non-relativistic PBE. Consequently, to recover the experimental result for the right reason, both the relativistic treatment and inclusion of correlation beyond the DFT level is necessary. This is confirmed by the scGW results, shown in the lower panels of Fig. 1. For the scGW results, the band structure for the AE basis set without any relativistic effects is further distorted such that the conduction band, specially near the Γ-point, is pushed upwards and an indirect band gap larger than 2 eV is predicted between the Γ and L points. With appropriate inclusion of relativity, the AE scGW results provide a better quality band structure, with an indirect band gap of ∼1.3 eV, which agrees far better with the experimental value of 0.7 eV.
IV. Results
We are now well-equipped to explore the challenges with relativistic GW calculations. In each of the subsections, we describe a specific issue with supporting data. Further analysis and discussion on these results is presented in Section V.A. Deficiency of pseudopotentials
Modern PPs are designed to account for relativistic effects and, in doing so, eliminate the need for including relativity in subsequent calculations. The GTH PPs and associated basis sets by Goedecker–Teter–Hutter102,103 constitute one such example. While the use of PPs generally provides a good description of valence-shell band structures, as can be observed from Fig. 1, they are far from adequate for other properties that are generally derivable from total energy. We investigate the performance of AE and PP-based basis sets for three materials with a diamond-lattice: Si, Ge, and αSn. With an increasing atomic number and core size, they serve as excellent representative examples to validate the importance of a proper description of the core orbitals.In Table 1, by comparing PBE and scGW predictions for lattice constants and bulk moduli against their respective experimental values, we demonstrate that as the atomic number of compounds requiring relativistic treatment increases, and consequently the size of their core (approximated using PPs) increases, the accuracy of the PP-based results decreases, necessitating the use of AE basis sets to achieve agreement with experiments.
| Material | Basis set | Lattice constant (Å) | Bulk modulus (GPa) | ||||
|---|---|---|---|---|---|---|---|
| PBE | scGW | Exp. | PBE | scGW | Exp. | ||
| Si | GTH-DZVP-MOLOPT-SR | 5.499 | 5.456 | 5.431 (ref. 96) | 84.8 | 96.6 | 97.9 (ref. 97) |
| x2c-TZVPall (sfX2C1e) | 5.494 | 5.413 | 83.4 | 102.5 | |||
| def2-TZVP (non-relativistic) | 5.491 | 5.411 | 84.0 | 100.9 | |||
| Ge | GTH-DZVP-MOLOPT-SR | 5.812 | 5.733 | 5.657 (ref. 98) | 52.8 | 66.4 | 75.0 (ref. 99) |
| x2c-TZVPall (sfX2C1e) | 5.769 | 5.609 | 56.9 | 83.9 | |||
| αSn | GTH-DZVP-MOLOPT-SR | 6.711 | 6.649 | 6.489 (ref. 100) | 32.6 | 32.6 | 53.1 (ref. 101) |
| x2c-TZVPall (sfX2C1e) | 6.663 | 6.391 | 35.2 | 54.3 | |||
For Si, which does not require relativistic corrections, using AE basis set over PPs has virtually no impact on the quality of the results. On the other hand, for αSn, AE results provide a significant improvement, which is even more pronounced in scGW than in PBE. We use the GTH-DZVP-MOLOPT-SR basis set with a GTH-PBE PP for the PP-based calculations, and the x2c-TZVPall basis set, which is the largest basis where we could reliably perform equation-of-state calculations, for AE calculations.
For Si and other elements where the size of the atomic core is small and the relativistic effects are negligible, PPs are usually capable of yielding very good results. However, as the atomic number increases, the problems with PPs become more noticeable, as illustrated for germanium and subsequently α-Sn. In Fig. 2, we showcase more examples where scGW evaluated in AE basis sets provides highly accurate results for both equilibrium lattice constants and bulk moduli. In contrast, the scGW results evaluated using GTH PPs are significantly worse than those obtained with PBE based on GTH PP. Particularly, in ZnX (X = S, Se, Te), AE relativistic scGW is highly effective in contrast to the GTH results. This poor performance of GTH PPs with scGW can be attributed to missing correlation contribution arising from the overlap of zinc's inner p and d orbitals with the inner p orbitals of the chalcogen.
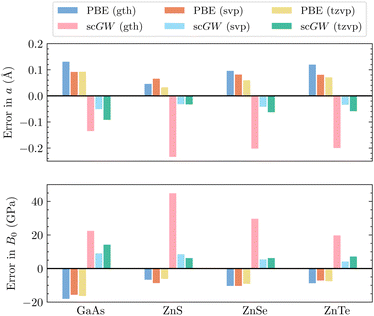 | ||
| Fig. 2 Errors in (top) lattice constants a, and (bottom) bulk moduli B0 for selected materials. All compounds are calculated with GTH-DZVP-MOLOPT-SR, x2c-SVPall and x2c-TZVPall basis sets. Both AE-PBE and AE-scGW results are reported using the sfX2C1e Hamiltonian, with a 4 × 4 × 4 k-mesh sampling. Experimental values for lattice constants and bulk moduli can be found in ref. 104, 105 and 106–108 respectively. | ||
In Green's function calculations such as scGW, when AE basis sets are employed, the core orbitals are described by self-energy matrix elements that have both static and dynamic parts. In contrast, when PPs are used, the dynamic part of the self-energy is entirely missing from the description of the core orbitals. For light elements such as Si, the magnitude of the dynamic self-energy for the core orbitals is small, and in addition, there are also only a few core orbitals. Consequently, the error of neglecting these self-energies is overall insignificant. On the other hand, given the large number of core orbitals in heavy elements, the number of dynamic core–core and core–valence self-energy matrix elements neglected by PPs is significant. Moreover, the mixing between valence and outer-core orbitals becomes important, resulting in sizable values of the outer core and core–valence self-energy matrix elements. Since the calculations involving PPs, by design, cannot include any dynamic self-energy for the core, it is reasonable to expect that for elements where such self-energy contributions are significant, the use of PPs will result in sizeable errors. These errors can be additionally compounded by a lack of good, well-optimized PPs for heavier elements. Therefore, it is worth noting that for Green's function methods, the use of PPs poses a different set of problems than for DFT. The DFT results can only be affected by a lack of well-optimized PPs, while Green's function methods would always be penalized by the absence of dynamic self-energy even for the best optimized PPs. For some lighter elements, one can only hope that these dynamic self-energy matrix elements have insignificant values; however, this assumption cannot be generally fulfilled.
B. Convergence issues in basis sets
For heavy elements, the very large size of the one-electron basis sets effectively hinders the ability to investigate convergence with respect to basis-set size in AE calculations. While for molecules, this formidable challenge can still be overcome, it becomes insurmountable in calculations of solids. The problem is relatively mild, often almost non-existent, at the level of DFT or HF, but quickly becomes aggravated for correlated calculations such as scGW. This can also be understood by the fact that basis sets are usually optimized at the atomic level using SCF calculations. Such behavior has also been observed by Kutepov in ref. 44, where DFT calculations converged far more rapidly than scGW while using linearized augmented-plane-wave (LAPW) basis functions. Here, we examine such convergence issues in detail.First, we look at IPs for AgCl, AgBr and AgI, which are representative examples of closed-shell relativistic molecules with increasing SOC as we go from Cl to I. These systems have been widely used to benchmark recent implementations of relativistic GW methods.37,39,60 For these molecules, in Table 2, we show IPs evaluated in PBE0 and scGW with x2c-TZVPall and x2c-QZVPall basis sets. Using these two IP values, an extrapolated IP value (also reported in Table 2) is calculated assuming an inverse relationship between IP and the number of atomic orbitals (AOs) in the respective basis set. We use the scalar relativistic Hamiltonian in all these calculations. Comparing these trends graphically in Fig. 3, we can clearly observe that for PBE0, the extrapolated IPs are within 0.1 eV of QZ, displaying a fast convergence. However, for scGW, the quadruple-ζ results are far from converged, with extrapolation leading to changes of more than 0.2 eV. It is worth mentioning that an extrapolation based on two calculations, triple- and quadruple-ζ, is already far from ideal, especially when the resultant corrections are so large. Having quintuple-ζ results would greatly enhance the quality of the results. However, even without considering the computational challenge that such a calculation poses, in many relativistic basis sets, including x2c, quintuple-ζ bases are simply not available.
| Basis | AgCl | AgBr | AgI | |||
|---|---|---|---|---|---|---|
| PBE0 | scGW | PBE0 | scGW | PBE0 | scGW | |
| x2c-TZVPall | 7.51 | 9.54 | 7.18 | 9.11 | 6.77 | 8.46 |
| x2c-QZVPall | 7.58 | 9.78 | 7.23 | 9.29 | 6.83 | 8.64 |
| Extrapolated | 7.67 | 10.09 | 7.29 | 9.53 | 6.89 | 8.86 |
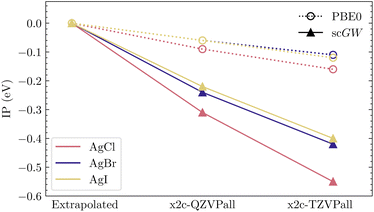 | ||
| Fig. 3 Graphical representation of convergence trends in Table 2. All IPs are reported relative to the respective extrapolated values, which shows that scGW exhibits a much slower convergence than PBE0. | ||
Next, we look at the band structure in relativistic solids, with a focus on AgBr and CdSe. For AgBr, a rock-salt crystal structure with a = 5.774 Å is considered, while the zinc blende phase in CdSe with a = 6.05 Å is used. All calculations were performed using a 4 × 4 × 4 k-mesh sampling, using x2c-SVPall, x2c-TZVPall and x2c-QZVPall basis sets. An inverse temperature of β = 300 a.u.−1 was used. For the QZVPall basis with AgBr, diffuse s and p orbitals with Gaussian exponents smaller than 0.05 were removed to avoid linear dependencies in the basis set. High angular momentum g-orbitals were removed from the QZVPall basis set in both systems.
For AgBr, in ref. 63, Yeh et al. noted poor convergence of band-gap values along the path containing special symmetry points. Here we present further data contrasting scGW convergence trends against PBE.
In Table 3, we present direct and indirect band gaps in AgBr and CdSe, with x2c-SVPall, x2c-TZVPall and x2c-QZVPall basis sets. Already at the triple-ζ level, for both systems, PBE band gaps are well converged to within 0.05 eV when compared with the quadruple-ζ basis. However, scGW once again shows much slower convergence trends, and going from triple- to quadruple-ζ still introduces corrections larger than 0.1 eV for CdSe and 0.2 eV for AgBr.
| Basis | Orbitals | L–L | Γ–Γ | X–X | L–Γ | ||||
|---|---|---|---|---|---|---|---|---|---|
| PBE | scGW | PBE | scGW | PBE | scGW | PBE | scGW | ||
| AgBr | |||||||||
| x2c-SVPall | 85 | 3.887 | 6.73 | 2.536 | 5.38 | 3.926 | 7.68 | 0.699 | 3.71 |
| x2c-TZVPall | 111 | 3.833 | 6.50 | 2.529 | 5.23 | 3.901 | 7.49 | 0.688 | 3.54 |
| x2c-QZVPall | 167 | 3.776 | 6.31 | 2.546 | 5.00 | 3.886 | 7.17 | 0.678 | 3.34 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| CdSe | |||||||||
| x2c-SVPall | 88 | 3.209 | 5.53 | 0.663 | 2.73 | 5.006 | 6.98 | 1.428 | 3.60 |
| x2c-TZVPall | 111 | 3.193 | 5.46 | 0.659 | 2.69 | 5.004 | 6.94 | 1.433 | 3.55 |
| x2c-QZVPall | 192 | 3.179 | 5.30 | 0.633 | 2.56 | 5.003 | 6.87 | 1.406 | 3.40 |
Finally, in Table 4 we show convergence trends for lattice constants of Si, Ge, GaAs, αSn, and InSb. All these systems have a diamond (zinc blende for GaAs and InSb) structure, with an increasing size of atomic core as we go from Si to InSb. Similar to previous observations, the convergence of scGW values is more than 2–3 times slower than for PBE. At the level of DFT, it seems that only for Si does the larger basis set marginally improve the agreement with experiment, while for all the other materials, the results either do not change or become worse. Consequently, one can suspect that DFT optimization of higher level bases is not as effective as lower level bases since the convergence with respect to the basis size is achieved relatively early on. This suspicion is somewhat confirmed when examining the scGW results. Almost all SVPall scGW results are surprisingly close to experiment and do not seem to be improved in a larger basis. For periodic systems, an extrapolation procedure, similar to the one used for molecular IPs, cannot be considered. This is because SVP is not a sufficiently large basis and using it together with only the TZVP basis would lead to largely inaccurate extrapolated data. While for molecular systems, QZ-level calculations remain accessible and make extrapolations possible, for the periodic systems, these calculations are extremely expensive and mostly out of reach.
| System | PBE | scGW | Exp. | ||||
|---|---|---|---|---|---|---|---|
| SVP | TZVP | Diff. | SVP | TZVP | Diff. | ||
| Si | 5.504 | 5.494 | −0.010 | 5.453 | 5.413 | −0.04 | 5.431 (ref. 96) |
| Ge | 5.779 | 5.773 | −0.006 | 5.622 | 5.559 | −0.063 | 5.657 (ref. 98) |
| GaAs | 5.747 | 5.748 | 0.001 | 5.600 | 5.559 | −0.041 | 5.653 (ref. 104) |
| α-Sn | 6.620 | 6.663 | 0.043 | 6.456 | 6.391 | −0.065 | 6.489 (ref. 100) |
| InSb | 6.597 | 6.64 | 0.043 | 6.463 | 6.381 | −0.082 | 6.479 (ref. 109) |
C. Linear dependencies
For correlated calculations, the quest for converging properties to a complete basis-set limit is not only affected by slower convergence and a lack of larger basis sets, but also by linear dependencies arising in the large basis sets. Particularly in solids, due to close packing of atoms, adding more basis functions introduces strong linear dependencies among the atomic orbitals. As a result, the condition number of the overlap matrix becomes too large even for an easy execution of mean-field methods. The problem of linear dependencies is not unique to the GTOs considered here, and has been reported in other kinds of orbital representations, namely Slater-type orbitals (STO), and also in LAPW.36,110–112Even though linear dependencies are more severe in ionic compounds, they also remain problematic in covalent compounds (such as silicon) and arise at small bond distances in all compounds. One way to remedy this problem in GTO basis sets is to simply remove the diffuse functions. These orbitals have long tails because of their small Gaussian exponents, leading to an increased overlap with other atomic orbitals. However, when studying bulk properties, such a procedure generally does more harm than good. When the bonds are stretched, the lack of diffuse orbitals leads to a deficient description of atomic bonds and substantially alters the equation of state, causing significant errors in both the equilibrium lattice constant and bulk modulus. This phenomenon is investigated for silicon in Table 5 and Fig. 4, where we have considered a rather simple case of non-relativistic calculation involving the widely used def2-TZVP basis set. Here, all orbitals with Gaussian exponents smaller than 0.1 were dropped, leading to lattice constants differing by more than 0.1 Å and over 50% error in the bulk modulus. Note that an ad-hoc re-introduction of diffuse functions as we stretch the bonds introduces jumps in the energy–volume curve, precluding a reliable fit to the Birch–Murnaghan equation. Even though the computational cost is still affordable, due to arising linear dependencies, converging DFT and GW calculations for Si with a larger basis set proves extremely challenging and is therefore not pursued here.
| Method | a (Å) | B 0 (GPa) |
|---|---|---|
| PBE | 5.491 | 84.01 |
| PBE w/o diffuse orbs. | 5.378 | 124.04 |
| scGW | 5.411 | 100.93 |
| scGW w/o diffuse orbs. | 5.306 | 146.88 |
| Experiment96,97 | 5.431 | 97.8 |
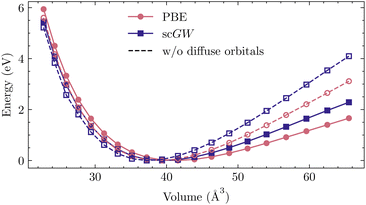 | ||
| Fig. 4 Energy–volume curves corresponding to Table 5. | ||
D. Lack of an accurate experimental reference
To benchmark new theoretical methods that are pushing the limits of accuracy and applicability, reliable experimental references are necessary. Here, we consider the HgCl2 molecule as an example to highlight a potential area where better experimental data can provide feedback to improve theoretical methods. In Fig. 5, we compare scGW results with two different experimental spectra for HgCl2. In one of the experiments by Boggess et al.113 (labeled Exp-1 in the plot), the SOC splitting is unresolved in both the first and second IPs. Results by Eland et al.114 (Exp-2 in Fig. 5) clearly resolve the SOC splitting in the first IP (2Πg state), but report difficulty with the second peak (2Πu state). Among the GW results, scalar relativistic corrections (sfX2C1e) capture the overall peak structure, producing a spectra similar to Exp-1. However, the spin-free theory understandably misses out on the SOC splitting, which, in turn, is captured at the X2C1e level. In fact, for scGW with X2C1e, spin–orbit splitting is visible for both 2Πg and 2Πu states. For the first ionization peak, scGW predicts a 0.16 eV splitting for the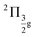 and
and 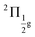 states, which is close to the experimental value of 0.12 eV. Similarly, for the
states, which is close to the experimental value of 0.12 eV. Similarly, for the 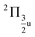 and
and 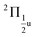 states, a splitting of 0.12 eV is predicted, but the corresponding results are not resolved in the experiments.
states, a splitting of 0.12 eV is predicted, but the corresponding results are not resolved in the experiments.
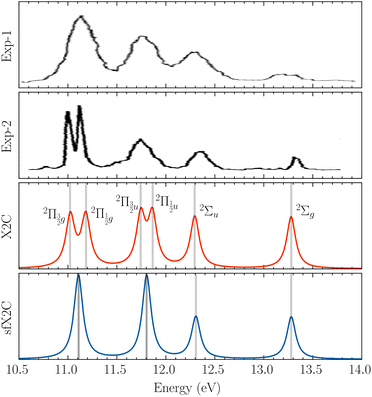 | ||
| Fig. 5 Comparison of experimental spectra with scGW results for HgCl2, obtained with both scalar and two-component relativistic effects. For these calculations, we have used the x2c-QZVPall basis. Both experimental spectra, Exp-1 by Boggess et al.113 and Exp-2 by Eland et al.,114 are shifted by 0.35 eV to match the associated IP peaks. | ||
V. Discussion and conclusions
We have presented ample numerical evidence that when employing Green's function methods, particularly scGW, the current frameworks of PPs and orbital representation encounter challenges in fully realizing the potential of precise quantum chemistry calculations for relativistic systems. One of the challenges is that PPs are not adept in accurately describing properties other than valence-shell electronic structure, such as band gaps and ionization potentials. When a material is pressurized, e.g., while studying the equation of state, the correlation effects arising from the overlap between atomic cores cannot be captured by PPs, and highly expensive AE calculations become unavoidable. Effective cores and PPs where a smaller number of electrons are modelled as part of the core offer one way to overcome this hurdle, and while some candidates are available,115–119 more developments and systematic benchmarks of new ECPs and PPs are desirable.Additionally, it should be noted that when using PPs in Green's function methods, there is an inherent error that comes from the absence of dynamic self-energy matrix elements for core and core–valence sectors, even if the best optimized PPs are employed. Especially for heavier elements, one can surmise that such a PP approximation will lead to significant errors since both the values and the number of outer-core dynamic self-energy matrix elements may be large. Consequently, even with the most optimized PPs, as they are formulated now, we can expect significant errors.
For correlated methods such as scGW, understanding the basis set convergence is a bit difficult. Even when well designed and optimized basis sets are available,120 correlated methods generally exhibit a slower convergence than mean-field ones. Yet, the fact that basis sets are optimized at the level of mean-field cannot be overlooked and, in fact, is potentially one of the reasons behind faster convergence in DFT and HF.121,122 For lighter elements, basis-set convergence is easily achieved and such problems do not require any particular attention. However, the same is not true for heavy elements where relativity is also important. The issues with basis sets for heavy elements is well known and has been a topic of recent research.123,124
Furthermore, most quantum chemistry basis sets have been optimized for molecular applications. When these are applied to solids, not only may the molecular level optimization prove insufficient, additional problems related to linear dependency and unfavorable convergence trends are more prone to arise. Recently, Ye et al.125 also noticed similar problems and proposed correlation-consistent basis sets optimized for solids. Another way to improve the quality of basis sets is to perform a material-specific optimization.126 These developments, including other means to eliminate linear dependencies,127,128 are yet to be applied to relativistic materials and molecules. It is also likely that a better one-particle orbital representation, with strictly orthogonal atomic orbitals, may be required to simultaneously overcome the issues related to convergence and linear-dependencies.129–131 Consequently, one can expect that in the future explicitly orthogonal single-particle orbitals, such as tensor-train numerical STOs,132 or orthogonal gausslets,129–131 will show promise to solve the problem of linear dependency. Constructing PPs and basis functions from correlated calculations may also offer a viable route to improve the reliability of relativistic calculations.
Lastly, we also show that as theoretical methods become more accurate, better and reliable experimental benchmarking data with well-resolved photoelectron spectra are desirable to both validate theoretical results and push for new theoretical developments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research and Office of Basic Energy Sciences, Scientific Discovery through Advanced Computing (SciDAC) program under Award Number DE-SC0022198. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 using NERSC awards BES-ERCAP0029462 and BES-ERCAP0024293.References
- W. Kohn and J. M. Luttinger, Ground-State Energy of a Many-Fermion System, Phys. Rev., 1960, 118, 41 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133 CrossRef.
- T. D. Crawford and H. F. Schaefer, An Introduction to Coupled Cluster Theory for Computational Chemists, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, John Wiley & Sons, Inc., 2000, pp. 33–136 Search PubMed.
- R. J. Bartlett and M. Musiał, Coupled-cluster theory in quantum chemistry, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- L. Hedin, New Method for Calculating the One-Particle Green's Function with Application to the Electron-Gas Problem, Phys. Rev., 1965, 139, A796 CrossRef.
- N. E. Dahlen and R. van Leeuwen, Self-consistent solution of the Dyson equation for atoms and molecules within a conserving approximation, J. Chem. Phys., 2005, 122, 164102 CrossRef PubMed.
- J. J. Phillips and D. Zgid, Communication: the description of strong correlation within self-consistent Green's function second-order perturbation theory, J. Chem. Phys., 2014, 140, 241101 CrossRef PubMed.
- A. A. Rusakov and D. Zgid, Self-consistent second-order Green's function perturbation theory for periodic systems, J. Chem. Phys., 2016, 144, 054106 CrossRef PubMed.
- G. P. Chen, V. K. Voora, M. M. Agee, S. G. Balasubramani and F. Furche, Random-Phase Approximation Methods, Annu. Rev. Phys. Chem., 2017, 68, 421 CrossRef CAS PubMed.
- A. Georges, G. Kotliar, W. Krauth and M. J. Rozenberg, Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions, Rev. Mod. Phys., 1996, 68, 13 CrossRef CAS.
- A. I. Lichtenstein, M. I. Katsnelson and G. Kotliar, Finite-Temperature Magnetism of Transition Metals: An ab initio Dynamical Mean-Field Theory, Phys. Rev. Lett., 2001, 87, 067205 CrossRef CAS PubMed.
- G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet and C. A. Marianetti, Electronic structure calculations with dynamical mean-field theory, Rev. Mod. Phys., 2006, 78, 865 CrossRef CAS.
- G. Knizia and G. K.-L. Chan, Density Matrix Embedding: A Simple Alternative to Dynamical Mean-Field Theory, Phys. Rev. Lett., 2012, 109, 186404 CrossRef PubMed.
- A. A. Kananenka, E. Gull and D. Zgid, Systematically improvable multiscale solver for correlated electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121111 CrossRef.
- T. N. Lan, A. A. Kananenka and D. Zgid, Communication: towards ab initio self-energy embedding theory in quantum chemistry, J. Chem. Phys., 2015, 143, 241102 CrossRef PubMed.
- S. Wouters, C. A. Jiménez-Hoyos, Q. Sun and G. K.-L. Chan, A Practical Guide to Density Matrix Embedding Theory in Quantum Chemistry, J. Chem. Theory Comput., 2016, 12, 2706 CrossRef CAS PubMed.
- D. Zgid and E. Gull, Finite temperature quantum embedding theories for correlated systems, New J. Phys., 2017, 19, 023047 CrossRef.
- A. A. Rusakov, S. Iskakov, L. N. Tran and D. Zgid, Self-Energy Embedding Theory (SEET) for Periodic Systems, J. Chem. Theory Comput., 2019, 15, 229 CrossRef CAS PubMed.
- C. Sun, U. Ray, Z.-H. Cui, M. Stoudenmire, M. Ferrero and G. K.-L. Chan, Finite-temperature density matrix embedding theory, Phys. Rev. B, 2020, 101, 075131 CrossRef CAS.
- F. Aryasetiawan and O. Gunnarsson, TheGW method, Rep. Prog. Phys., 1998, 61, 237 CrossRef CAS.
- D. Golze, M. Dvorak and P. Rinke, The GW Compendium: A Practical Guide to Theoretical Photoemission Spectroscopy, Front. Chem., 2019, 7, 377 CrossRef CAS PubMed.
- L. Reining, The GW approximation: content, successes and limitations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1344 Search PubMed.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Integral approximations for LCAO-SCF calculations, Chem. Phys. Lett., 1993, 213, 514 CrossRef CAS.
- Q. Sun, T. C. Berkelbach, J. D. McClain and G. K.-L. Chan, Gaussian and plane-wave mixed density fitting for periodic systems, J. Chem. Phys., 2017, 147, 164119 CrossRef PubMed.
- H.-Z. Ye and T. C. Berkelbach, Fast periodic Gaussian density fitting by range separation, J. Chem. Phys., 2021, 154, 131104 CrossRef CAS PubMed.
- G. E. Scuseria, T. M. Henderson and I. W. Bulik, Particle-particle and quasiparticle random phase approximations: connections to coupled cluster theory, J. Chem. Phys., 2013, 139, 104113 CrossRef PubMed.
- M. F. Lange and T. C. Berkelbach, On the Relation between Equation-of-Motion Coupled-Cluster Theory and the GW Approximation, J. Chem. Theory Comput., 2018, 14, 4224 CrossRef CAS PubMed.
- R. Quintero-Monsebaiz, E. Monino, A. Marie and P.-F. Loos, Connections between many-body perturbation and coupled-cluster theories, J. Chem. Phys., 2022, 157, 231102 CrossRef CAS PubMed.
- J. Tölle and G. Kin-Lic Chan, Exact relationships between the GW approximation and equation-of-motion coupled-cluster theories through the quasi-boson formalism, J. Chem. Phys., 2023, 158, 124123 CrossRef PubMed.
- A. Stan, N. E. Dahlen and R. v. Leeuwen, Fully self-consistent GW calculations for atoms and molecules, Europhys. Lett., 2006, 76, 298 CrossRef CAS.
- F. Caruso, P. Rinke, X. Ren, M. Scheffler and A. Rubio, Unified description of ground and excited states of finite systems: the self-consistent GW approach, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 081102 CrossRef.
- N. Marom, F. Caruso, X. Ren, O. T. Hofmann, T. Körzdörfer, J. R. Chelikowsky, A. Rubio, M. Scheffler and P. Rinke, Benchmark of GW methods for azabenzenes, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245127 CrossRef.
- M. J. van Setten, F. Weigend and F. Evers, The GW-Method for Quantum Chemistry Applications: Theory and Implementation, J. Chem. Theory Comput., 2013, 9, 232 CrossRef CAS PubMed.
- M. J. van Setten, F. Caruso, S. Sharifzadeh, X. Ren, M. Scheffler, F. Liu, J. Lischner, L. Lin, J. R. Deslippe, S. G. Louie, C. Yang, F. Weigend, J. B. Neaton, F. Evers and P. Rinke, GW100: Benchmarking G0W0 for Molecular Systems, J. Chem. Theory Comput., 2015, 11, 5665 CrossRef CAS PubMed.
- F. Caruso, M. Dauth, M. J. van Setten and P. Rinke, Benchmark of GW Approaches for the GW100 Test Set, J. Chem. Theory Comput., 2016, 12, 5076 CrossRef CAS PubMed.
- A. Förster and L. Visscher, Low-Order Scaling Quasiparticle Self-Consistent GW for Molecules, Front. Chem., 2021, 9, 736591 CrossRef PubMed.
- A. Förster, E. van Lenthe, E. Spadetto and L. Visscher, Two-Component GW Calculations: Cubic Scaling Implementation and Comparison of Vertex-Corrected and Partially Self-Consistent GW Variants, J. Chem. Theory Comput., 2023, 19, 5958 CrossRef PubMed.
- M. Wen, V. Abraham, G. Harsha, A. Shee, B. Whaley and D. Zgid, Comparing self-consistent GW and vertex corrected G0W0 (G0W0Γ) accuracy for molecular ionization potentials, arXiv, 2023, arXiv:2311.12209 [physics:chem-ph], DOI:10.48550/arXiv.2311.12209.
- V. Abraham, G. Harsha and D. Zgid, Relativistic fully self-consistent GW for molecules: total energies and ionization potentials, arXiv, 2024, arXiv:2401.11303 [physics:chem-ph], DOI:10.48550/arXiv.2401.11303.
- S. V. Faleev, M. van Schilfgaarde and T. Kotani, All-Electron Self-Consistent GW Approximation: Application to Si, MnO, and NiO, Phys.Rev. Lett., 2004, 93, 126406 CrossRef PubMed.
- M. Shishkin and G. Kresse, Self-consistent GW calculations for semiconductors and insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235102 CrossRef.
- A. Kutepov, S. Y. Savrasov and G. Kotliar, Ground-state properties of simple elements from GW calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 041103 CrossRef.
- A. L. Kutepov, Self-consistent solution of Hedin's equations: semiconductors and insulators, Phys. Rev. B, 2017, 95, 195120 CrossRef.
- A. L. Kutepov, Ground state properties of 3d metals from self-consistent GW approach, J. Phys.: Condens. Matter, 2017, 29, 465503 CrossRef PubMed.
- M. Grumet, P. Liu, M. Kaltak, J. Klimeš and G. Kresse, Beyond the quasiparticle approximation: fully self-consistent GW calculations, Phys. Rev. B, 2018, 98, 155143 CrossRef CAS.
- P. Pyykkö, Relativistic Effects in Chemistry: More Common Than You Thought, Annu. Rev. Phys. Chem., 2012, 63, 45 CrossRef PubMed.
- G. Breit, Dirac's Equation and the Spin-Spin Interactions of Two Electrons, Phys. Rev., 1932, 39, 616 CrossRef CAS.
- M. Douglas and N. M. Kroll, Quantum electrodynamical corrections to the fine structure of helium, Ann. Phys., 1974, 82, 89 CAS.
- B. A. Hess, Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations, Phys. Rev. A, 1985, 32, 756 CrossRef CAS PubMed.
- B. A. Hess, Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators, Phys. Rev. A, 1986, 33, 3742 CrossRef CAS PubMed.
- T. Nakajima and K. Hirao, The Douglas–Kroll–Hess Approach, Chem. Rev., 2012, 112, 385 CrossRef CAS PubMed.
- M. Reiher and A. Wolf, Douglas–Kroll–Hess Theory, in Relativistic Quantum Chemistry, John Wiley & Sons, Ltd, 2014, pp. 469–501 Search PubMed.
- W. Kutzelnigg and W. Liu, Quasirelativistic theory equivalent to fully relativistic theory, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- W. Liu and W. Kutzelnigg, Quasirelativistic theory. II. Theory at matrix level, J. Chem. Phys., 2007, 126, 114107 CrossRef PubMed.
- W. Liu and D. Peng, Exact two-component Hamiltonians revisited, J. Chem. Phys., 2009, 131, 031104 CrossRef PubMed.
- Q. Sun, W. Liu, Y. Xiao and L. Cheng, Exact two-component relativistic theory for nuclear magnetic resonance parameters, J. Chem. Phys., 2009, 131, 081101 CrossRef PubMed.
- L. Cheng and J. Gauss, Analytic energy gradients for the spin-free exact two-component theory using an exact block diagonalization for the one-electron Dirac Hamiltonian, J. Chem. Phys., 2011, 135, 084114 CrossRef PubMed.
- R. Sakuma, C. Friedrich, T. Miyake, S. Blügel and F. Aryasetiawan, GW calculations including spin-orbit coupling: application to Hg chalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085144 CrossRef.
- A. Kutepov, K. Haule, S. Y. Savrasov and G. Kotliar, Electronic structure of Pu and Am metals by self-consistent relativistic GW method, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155129 CrossRef.
- P. Scherpelz, M. Govoni, I. Hamada and G. Galli, Implementation and Validation of Fully Relativistic GW Calculations: Spin–Orbit Coupling in Molecules, Nanocrystals, and Solids, J. Chem. Theory Comput., 2016, 12, 3523 CrossRef CAS PubMed.
- C. Holzer and W. Klopper, Ionized, electron-attached, and excited states of molecular systems with spin–orbit coupling: two-component GW and Bethe–Salpeter implementations, J. Chem. Phys., 2019, 150, 204116 CrossRef PubMed.
- M. Kühn and F. Weigend, One-Electron Energies from the Two-Component GW Method, J. Chem. Theory Comput., 2015, 11, 969 CrossRef PubMed.
- C.-N. Yeh, A. Shee, Q. Sun, E. Gull and D. Zgid, Relativistic self-consistent GW: exact two-component formalism with one-electron approximation for solids, Phys. Rev. B, 2022, 106, 085121 CrossRef CAS.
- C.-N. Yeh, S. Iskakov, D. Zgid and E. Gull, Fully self-consistent finite-temperature GW in Gaussian Bloch orbitals for solids, Phys. Rev. B, 2022, 106, 235104 CrossRef CAS.
- F. D. Murnaghan, The Compressibility of Media under Extreme Pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244 CrossRef CAS PubMed.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- M. van Schilfgaarde, T. Kotani and S. Faleev, Quasiparticle Self-Consistent GW Theory, Phys. Rev. Lett., 2006, 96, 226402 CrossRef CAS PubMed.
- T. Kotani, M. van Schilfgaarde and S. V. Faleev, Quasiparticle self-consistent GW method: a basis for the independent-particle approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165106 CrossRef.
- H. Cao, Z. Yu, P. Lu and L.-W. Wang, Fully converged plane-wave-based self-consistent GW calculations of periodic solids, Phys. Rev. B, 2017, 95, 035139 CrossRef.
- S. V. Faleev, M. van Schilfgaarde and T. Kotani, All-electron self-consistent GW approximation: application to Si, MnO, and NiO, Phys. Rev. Lett., 2004, 93, 126406 CrossRef PubMed.
- M. van Schilfgaarde, T. Kotani and S. Faleev, Quasiparticle self-consistent GW theory, Phys. Rev. Lett., 2006, 96, 226402 CrossRef CAS PubMed.
- T. A. Pham, H.-V. Nguyen, D. Rocca and G. Galli, GW calculations using the spectral decomposition of the dielectric matrix: verification, validation, and comparison of methods, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155148 CrossRef.
- M. Govoni and G. Galli, Large scale GW calculations, J. Chem. Theory Comput., 2015, 11, 2680 CrossRef CAS PubMed.
- S. Biermann, F. Aryasetiawan and A. Georges, First-principles approach to the electronic structure of strongly correlated systems: combining the GW approximation and dynamical mean-field theory, Phys. Rev. Lett., 2003, 90, 086402 CrossRef CAS PubMed.
- F. Nilsson, L. Boehnke, P. Werner and F. Aryasetiawan, Multitier self-consistent GW + EDMFT, Phys. Rev. Mater., 2017, 1, 043803 CrossRef.
- S. Choi, A. Kutepov, K. Haule, M. van Schilfgaarde and G. Kotliar, First-principles treatment of Mott insulators: linearized QSGW+DMFT approach, npj Quantum Mater., 2016, 1, 16001 CrossRef.
- T. N. Lan, A. Shee, J. Li, E. Gull and D. Zgid, Testing self-energy embedding theory in combination with GW, Phys. Rev. B, 2017, 96, 155106 CrossRef.
- T. Zhu and G. K.-L. Chan, Ab initio full cell GW + DMFT for correlated materials, Phys. Rev. X, 2021, 11, 021006 CAS.
- S. Iskakov, C.-N. Yeh, E. Gull and D. Zgid, Ab initio self-energy embedding for the photoemission spectra of NiO and MnO, Phys. Rev. B, 2020, 102, 085105 CrossRef CAS.
- C.-N. Yeh, S. Iskakov, D. Zgid and E. Gull, Electron correlations in the cubic paramagnetic perovskite Sr(V, Mn)o3: results from fully self-consistent self-energy embedding calculations, Phys. Rev. B, 2021, 103, 195149 CrossRef CAS.
- J. Liu, Y. Shen, A. Asthana and L. Cheng, Two-component relativistic coupled-cluster methods using mean-field spin-orbit integrals, J. Chem. Phys., 2018, 148, 034106 CrossRef PubMed.
- P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, Temperature effects on the universal equation of state of solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1945 CrossRef CAS PubMed.
- R. Dovesi, R. Orlando, C. Roetti, C. Pisani and V. Saunders, The Periodic Hartree-Fock Method and Its Implementation in the Crystal Code, Phys. Status Solidi B, 2000, 217, 63 CrossRef CAS.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, Recent developments in the PySCF program package, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed.
- Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, PySCF: the Python-based simulations of chemistry framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340 Search PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, Automatic Generation of Auxiliary Basis Sets, J. Chem. Theory Comput., 2017, 13, 554 CrossRef CAS PubMed.
- P. Pollak and F. Weigend, Segmented contracted error-consistent basis sets of double- and triple-ζ valence quality for one- and two-component relativistic all-electron calculations, J. Chem. Theory Comput., 2017, 13, 3696 CrossRef CAS PubMed.
- A. A. Kananenka, J. J. Phillips and D. Zgid, Efficient temperature-dependent green's functions methods for realistic systems: compact grids for orthogonal polynomial transforms, J. Chem. Theory Comput., 2016, 12, 564 CrossRef CAS PubMed.
- A. A. Kananenka, A. R. Welden, T. N. Lan, E. Gull and D. Zgid, Efficient temperature-dependent green's function methods for realistic systems: using cubic spline interpolation to approximate Matsubara Green's functions, J. Chem. Theory Comput., 2016, 12, 2250 CrossRef CAS PubMed.
- E. Gull, S. Iskakov, I. Krivenko, A. A. Rusakov and D. Zgid, Chebyshev polynomial representation of imaginary-time response functions, Phys. Rev. B, 2018, 98, 075127 CrossRef CAS.
- X. Dong, D. Zgid, E. Gull and H. U. R. Strand, Legendre-spectral Dyson equation solver with super-exponential convergence, J. Chem. Phys., 2020, 152, 134107 CrossRef CAS PubMed.
- J. Li, M. Wallerberger, N. Chikano, C.-N. Yeh, E. Gull and H. Shinaoka, Sparse sampling approach to efficient ab initio calculations at finite temperature, Phys. Rev. B, 2020, 101, 035144 CrossRef CAS.
- H. Shinaoka, N. Chikano, E. Gull, J. Li, T. Nomoto, J. Otsuki, M. Wallerberger, T. Wang and K. Yoshimi, Efficient ab initio many-body calculations based on sparse modeling of Matsubara Green's function, SciPost Physics Lecture Notes, 2022, 63 DOI:10.21468/SciPostPhysLectNotes.63.
- J. Fei, C.-N. Yeh, D. Zgid and E. Gull, Analytical continuation of matrix-valued functions: Carathéodory formalism, Phys. Rev. B, 2021, 104, 165111 CrossRef CAS.
- S. Iskakov, C.-N. Yeh, P. Pokhilko, Y. Yu, L. Zhang, G. Harsha, V. Abraham, M. Wen, M. Wang, J. Adamski, T. Chen, E. Gull and D. Zgid, Green/WeakCoupling: Implementation of fully self-consistent finite-temperature many-body perturbation theory for molecules and solids, arXiv, 2024, preprint, arXiv:2406.18479 [cond-mat.mtrl-sci], DOI:10.48550/arXiv.2406.18479.
- P. Becker, P. Scyfried and H. Siegert, The lattice parameter of highly pure silicon single crystals, Z. Phys. B: Condens. Matter, 1982, 48, 17 CrossRef CAS.
- H. J. McSkimin and P. Andreatch Jr, Elastic Moduli of Silicon vs. Hydrostatic Pressure at 25.0°C and -195.8°C, J. Appl. Phys., 1964, 35, 2161 CrossRef CAS.
- O. Brümmer, V. Alex and G. Schulze, Anwendung der Elektronenstrahlmikrosonde für das Weitwinkel-Durchstrahlverfahren, Ann. Phys., 1972, 483, 118 CrossRef.
- H. J. McSkimin and P. Andreatch Jr, Elastic Moduli of Germanium versus Hydrostatic Pressure at 25.0°C and -195.8°C, J. Appl. Phys., 1963, 34, 651 CrossRef.
- J. Thewlis and A. R. Davey, Thermal Expansion of Grey Tin, Nature, 1954, 174, 1011 CrossRef CAS.
- C. J. Buchenauer, M. Cardona and F. H. Pollak, Raman Scattering in Gray Tin, Phys. Rev. B: Solid State, 1971, 3, 1243 CrossRef.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- T. Fukumori and K. Futagami, Measurements of Lattice Parameters and Half-Widths of the Rocking Curve on GaAs Crystal by the X-Ray Double-Crystal Method Using a Cu Kα Doublet, Jpn. J. Appl. Phys., 1988, 27, 442 CrossRef CAS.
- R. J. Nelmes and M. I. McMahon, Structural Transitions in the Group IV, III-V, and II-VI Semiconductors under Pressure, in Semiconductors and Semimetals, ed. T. Suski and W. Paul, Elsevier, 1998, ch. 3, vol. 54, pp. 145–246 Search PubMed.
- C. F. Cline and D. R. Stephens, Volume Compressibility of BeO and Other II-VI Compounds, J. Appl. Phys., 1965, 36, 2869 CrossRef CAS.
- J. S. Blakemore, Semiconducting and other major properties of gallium arsenide, J. Appl. Phys., 1982, 53, R123 CrossRef CAS.
- J. Pellicer-Porres, D. Martínez-García, C. Ferrer-Roca, A. Segura, V. Muñoz-Sanjosé, J. P. Itié, A. Polian and P. Munsch, High-pressure phase diagram of ZnSexTe1−x alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035210 CrossRef.
- M. E. Straumanis and C. D. Kim, Lattice Parameters, Thermal Expansion Coefficients, Phase Width, and Perfection of the Structure of GaSb and InSb, J. Appl. Phys., 1965, 36, 3822 CrossRef CAS.
- T. Kotani and M. van Schilfgaarde, Fusion of the LAPW and LMTO methods: the augmented plane wave plus muffin-tin orbital method, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125117 CrossRef.
- L. G. Jiao and Y. K. Ho, Application of Löwdin’s canonical orthogonalization method to the Slater-type orbital configuration-interaction basis set, Int. J. Quantum Chem., 2015, 115, 434 CrossRef CAS.
- F. Karsai, F. Tran and P. Blaha, On the importance of local orbitals using second energy derivatives for d and f electrons, Comput. Phys. Commun., 2017, 220, 230 CrossRef CAS.
- G. W. Boggess, J. D. Allen and G. K. Schweitzer, The photoelectron spectra of gaseous zinc(II) and cadmium(II) chlorides, bromides, and iodides, J. Electron Spectrosc. Relat. Phenom., 1973, 2, 467 CrossRef CAS.
- J. Eland, Photoelectron spectra and chemical bonding of mercury(II) compounds, Int. J. Mass Spectrom. Ion Phys., 1970, 4, 37 CrossRef CAS.
- L. E. Roy, P. J. Hay and R. L. Martin, Revised Basis Sets for the LANL Effective Core Potentials, J. Chem. Theory Comput., 2008, 4, 1029 CrossRef CAS PubMed.
- M. Burkatzki, C. Filippi and M. Dolg, Energy-consistent small-core pseudopotentials for 3d-transition metals adapted to quantum Monte Carlo calculations, J. Chem. Phys., 2008, 129, 164115 CrossRef CAS PubMed.
- A. Weigand, X. Cao, T. Hangele and M. Dolg, Relativistic Small-Core Pseudopotentials for Actinium, Thorium, and Protactinium, J. Phys. Chem. A, 2014, 118, 2519 CrossRef CAS PubMed.
- A. Zaitsevskii, N. S. Mosyagin, A. V. Oleynichenko and E. Eliav, Generalized relativistic small-core pseudopotentials accounting for quantum electrodynamic effects: construction and pilot applications, Int. J. Quantum Chem., 2023, 123, e27077 CrossRef CAS.
- A. N. Hill, A. J. H. M. Meijer and J. G. Hill, Correlation Consistent Basis Sets and Core Polarization Potentials for Al–Ar with ccECP Pseudopotentials, J. Phys. Chem. A, 2022, 126, 5853 CrossRef CAS PubMed.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- J. Lee, X. Feng, L. A. Cunha, J. F. Gonthier, E. Epifanovsky and M. Head-Gordon, Approaching the basis set limit in Gaussian-orbital-based periodic calculations with transferability: performance of pure density functionals for simple semiconductors, J. Chem. Phys., 2021, 155, 164102 CrossRef CAS PubMed.
- K. J. Rueda Espinosa, A. A. Kananenka and A. A. Rusakov, Novel Computational Chemistry Infrastructure for Simulating Astatide in Water: From Basis Sets to Force Fields Using Particle Swarm Optimization, J. Chem. Theory Comput., 2023, 19, 7998 CrossRef CAS PubMed.
- C. Zhang and L. Cheng, Atomic mean-field approach within exact two-component theory based on the Dirac–Coulomb–Breit Hamiltonian, J. Phys. Chem. A, 2022, 126, 4537 CrossRef CAS PubMed , pMID: 35763592..
- H.-Z. Ye and T. C. Berkelbach, Correlation-Consistent Gaussian Basis Sets for Solids Made Simple, J. Chem. Theory Comput., 2022, 18, 1595 CrossRef CAS PubMed.
- Y. Zhou, E. Gull and D. Zgid, Material-Specific Optimization of Gaussian Basis Sets against Plane Wave Data, J. Chem. Theory Comput., 2021, 17, 5611 CrossRef CAS PubMed.
- S. Lehtola, Curing basis set overcompleteness with pivoted Cholesky decompositions, J. Chem. Phys., 2019, 151, 241102 CrossRef PubMed.
- S. Lehtola, Accurate reproduction of strongly repulsive interatomic potentials, Phys. Rev. A, 2020, 101, 032504 CrossRef CAS.
- S. R. White and E. M. Stoudenmire, Multisliced gausslet basis sets for electronic structure, Phys. Rev. B, 2019, 99, 081110 CrossRef CAS.
- Y. Qiu and S. R. White, Hybrid gausslet/Gaussian basis sets, J. Chem. Phys., 2021, 155, 184107 CrossRef CAS PubMed.
- S. R. White and M. J. Lindsey, Nested gausslet basis sets, J. Chem. Phys., 2023, 159, 234112 CrossRef CAS PubMed.
- N. Jolly, Y. N. Fernández and X. Waintal, Tensorized orbitals for computational chemistry, arXiv, 2023, preprint arxiv:2308.03508, 10.48550 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |