Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Including the bioconcentration of pesticide metabolites in plant uptake modeling†
Zijian
Li
 *a and
Peter
Fantke
*a and
Peter
Fantke
 b
b
aSchool of Public Health (Shenzhen), Sun Yat-sen University, Shenzhen, Guangdong 518107, China. E-mail: lizijian3@mail.sysu.edu.cn
bQuantitative Sustainability Assessment, Department of Environmental and Resource Engineering, Technical University of Denmark, Bygningstorvet 115, 2800 Kgs. Lyngby, Denmark
First published on 29th September 2023
Abstract
Although several models of pesticide uptake into plants are available, there are few modeling studies on the bioconcentration of metabolites in plants. Ignoring metabolites in plant uptake models can result in an underestimation of the parent compound's overall impacts on human health associated with pesticide residues in harvested food crops. To address this limitation, we offer a metabolite-based plant uptake model to predict the bioconcentration of the parent compound and its metabolites in plants. We used the uptake of glyphosate and its major metabolite (aminomethylphosphonic acid, AMPA) into potato as an example. The analysis of variability revealed that soil properties (affecting the soil sorption coefficient), dissipation half-life in soil, and metabolic half-life in the potato had a significant impact on the simulated AMPA concentration in the potato, indicating that regional variability could be generated in the plant bioconcentration process of metabolites. The proposed model was further compared using the non-metabolite model. The findings of the comparison suggested that the non-metabolite model, which is integrated with the AMPA bioconcentration process, can predict the AMPA concentration in the potato similarly to the proposed model. In conclusion, we provide insight into the bioconcentration process of metabolites in tuber plants from a modeling viewpoint, with some crucial model inputs, such as biotransformation and metabolic rate constants, requiring confirmation in future studies. The modeling demonstration emphasizes that it is relevant to consider bioaccumulation of metabolites, which can propagate further into increased overall residues of harmful compounds, especially in cases where metabolites have higher toxicity effect potency than their respective parent compounds.
Environmental significanceAlthough plant uptake models for pesticides are well established, there has been relatively limited research concerning the bioconcentration of their metabolites. This gap could potentially result in an underestimation of related health risks posed to consumers. To bridge this gap, we have integrated the uptake kinetics of pesticide metabolites for inclusion in plant uptake models. Our simulation results demonstrate that the bioconcentration process of metabolites should not be disregarded when assessing human health risks. |
1. Introduction
Pesticides have a vital role in enhancing crop yield, guaranteeing food security, and fostering agricultural economic expansion. After pesticide application, pesticide residues may persist in crops and be transferred into other environmental media such as air, soil, and water, posing a threat to human and ecological health.1–4 To assess human and environmental health concerns, experimental and modeling studies have made substantial efforts to explore plant uptake of pesticides, which has generated crucial data (e.g., residue concentrations in crops at harvest).5 Modeling tools (e.g., mechanism-based uptake and data-driven dissipation models) have become promising to aid regulatory experts and risk assessors in high-throughput simulations of residue concentrations in plants as a result of the registration of hundreds of agricultural active ingredients.6Models of plant uptake of pesticides have been actively researched. The simulation results of cutting-edge modeling methodologies were validated by field observations, resulting in precise estimates of pesticide levels in plants. For instance, the foliar vegetation uptake model was developed on the basis of a one-compartment sink model7 and was used for ecological risk assessment and grazing land management.8,9 The fruit tree uptake model was derived from a multiple-compartment transport model,10,11 which was adapted for usage in several tree species.12–14 In addition, a matrix-based modeling module was introduced to simulate pesticide concentrations in harvested crops,15,16 which had been used for human health risk assessment and lifecycle impact analysis.6,17 Other modeling research studies had also contributed to the comprehension of plant uptake of pollutants, which aided risk assessment and phytoremediation tremendously.18–25
Some pesticides can be metabolized into harmful metabolites in environmental media or plant tissues, according to studies. Soil bacteria, for instance, can biotransform glyphosate into aminomethylphosphonic acid (AMPA), which offers an extra threat to human or ecological health.26,27 Consequently, AMPA formation must be accounted for in the fate and transport model of glyphosate in soil; otherwise, the hazards to human health posed by glyphosate in soil may be underestimated. Thus, neglecting metabolites in the plant uptake model could lead to an underestimation of the health risks to consumers posed by the parent compound in crops. In this study, we used glyphosate, one of the most widely applied pesticides on the global market,28 as a modeling example. Glyphosate has a number of metabolites reaching the environment,29 and its primary metabolite AMPA29–34 has been shown to be toxic to humans.35,36 In addition, glyphosate and its metabolites are frequently detected in soil and crops,34 and the active metabolite (i.e., AMPA) is occasionally found at higher levels than glyphosate in plant tissues.37 However, there are few studies on plant uptake models of metabolites; the absence of such models could hinder the regulatory process of the parent compound in crops.
To address this deficiency, we suggested a modeling strategy to simulate the bioconcentration process of the parent compound and its metabolites in plants. The three primary factors are as follows:
(i) Because the tuber uptake model is well-established,38–41 we used the potato uptake of glyphosate as an example to conduct the modeling experiment. A reliable bioconcentration method for the parent compound and its metabolites can be demonstrated using potato as a model plant. In addition, glyphosate and its primary metabolite AMPA pose a global threat to public health, especially in the soil-plant system.42
(ii) We considered biotransformation (through activity of soil microorganisms) and metabolic (through activity of plant enzymes) rate constants of substances as placeholder variables due to data limitations. We performed a variability analysis to determine the effect of several relevant factors on the simulation outcomes. The suggested model allows users to alter these model inputs with flexibility.
(iii) We examined the proposed model using the non-metabolite model despite the lack of field data to support it. The non-metabolite model pertains to the plant uptake model that excludes the transformation of parent compounds into metabolites within the plant. Instead, the non-metabolite model factors in the uptake of metabolites from external environmental sources (such as soil, air, and plant surface). In this context, the non-metabolite model treats metabolites as separately assessed chemicals in terms of the bioconcentration process. The results of the comparison can assist regulatory scientists and risk assessors in refining their regulatory expertise regarding the parent compound. From a modeling perspective, this study could shed light on the bioconcentration of toxic compounds in plants.
2. Materials and methods
2.1 General modeling framework
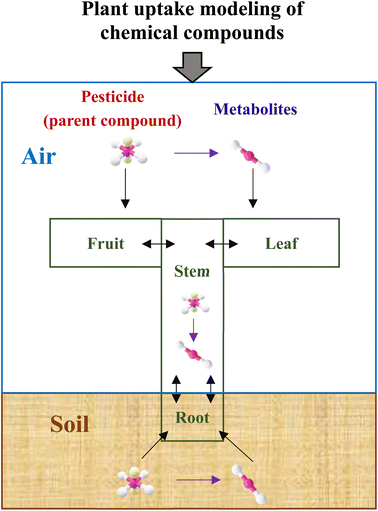
Fig. 1 depicts a general modeling framework for simulating the uptake of pesticide metabolites by plants. The diagram shows where the metabolites are generated, such as in environmental media and plant tissues, and how they end up in certain plant tissues, including the uptake and elimination pathways. When pesticides are applied to croplands, they are distributed in various environmental media, such as soil, air, and plant surfaces.15 Plants can take up these pesticides via different uptake routes.15,43,44 Pesticides can also be degraded and broken down into metabolites, which can be taken up by plants via similar uptake routes as their mother compounds.45 Additionally, metabolites can be generated in plant tissues via the degradation process of their mother compounds. In this study, we use potatoes as a model plant, since pesticide uptake both via leaves from air and via tubers from soil and roots contributes to residual concentrations in the harvested crop components.39,46 The considered pesticide transport, plant uptake and metabolism processes are, however, also applicable to a wider range of food and feed crops.2.2 General model for potato uptake of metabolites
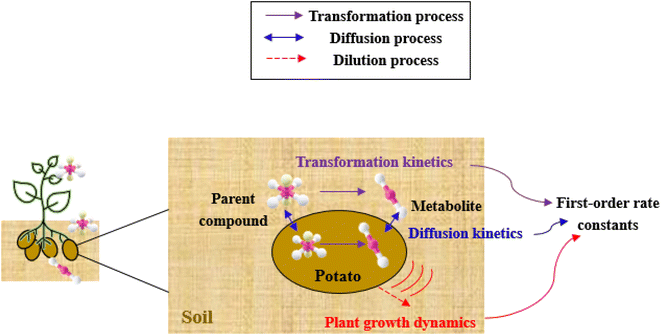
The framework for bioconcentration modeling of pesticide metabolites in potatoes is depicted in Fig. 2. The bioconcentration model was proposed on the basis of current potato uptake models,16,38–40 in which diffusion is the principal uptake or elimination pathway of chemicals between potatoes and soil. These potato uptake models employed in this study conceptually depict the potato as having a spherical shape, utilizing first-order rate constants to characterize the uptake and elimination kinetics of pesticides within the potato. The diffusion-driven kinetic behavior of pesticides captures the exchange of pesticides between the potato and soil. Within the potato structure, these models further incorporate a rate constant to account for the dilution effect on pesticide bioconcentration stemming from potato growth. From a risk and impact assessment perspective and due to data constraints, these models typically omit the biodegradation or biotransformation processes of pesticides within potato tissue.47 However, our study deviates from this approach by incorporating such processes, as our primary focus centers on considering the generation of pesticide metabolites. Both soil and potatoes are involved in the transformation of the parent compound into metabolites. Additionally, the parent compound and metabolites in potatoes undergo dilution due to potato growth. Contrary to root plants, xylem and phloem transport did not significantly contribute to the uptake of pesticide residues by tubers;38,46,48 hence, the bioconcentration of parent compounds and their metabolites in potato leaves was not simulated in this study. After pesticide application, the parent compound (i.e., the active ingredient) will first deposit in the surface soil and then be degraded into metabolites; therefore, the proposed model assumes that the initial concentrations of pesticides in tubers and the initial concentrations of metabolites in the soil and tubers are both zero.To simplify the simulation process, the following assumptions are made. First, the transformation of parent compounds and their metabolites is assumed to be irreversible, especially when enzymes (such as soil microorganisms and plant P450s) serve as catalysts for the chemical reactions. Second, we only consider the parent compound's first-level transformation (i.e., the breakdown of metabolites into higher-order transformation products is not considered). Third, it is assumed that the formation of metabolites conforms to the first-order kinetics corresponding to the degradation of the parent compound.45 Then, the general model for describing the tuber uptake of the parent compound and its metabolites from soil can be expressed using the following equations.
Within the soil compartment:
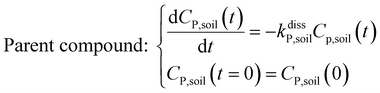 | (1) |
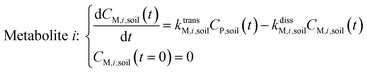 | (2) |
Within the plant compartment (generic crop):
 | (3) |
 | (4) |
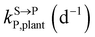 ,
, 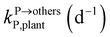 , kMetP,plant (d−1),
, kMetP,plant (d−1), 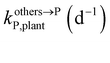 and kgrowplant (d−1) are the soil-to-plant uptake, plant-to-other parts elimination, metabolic, other parts-to-plant uptake, and dilution (due to the plant growth) rate constants of the pesticide parent compound, respectively;
and kgrowplant (d−1) are the soil-to-plant uptake, plant-to-other parts elimination, metabolic, other parts-to-plant uptake, and dilution (due to the plant growth) rate constants of the pesticide parent compound, respectively; 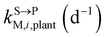 , ktransM,i,plan (d−1),
, ktransM,i,plan (d−1), 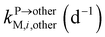 , kMetM,i,plant (d−1), and
, kMetM,i,plant (d−1), and 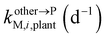 are the soil-to-plant uptake, production, plant-to-other parts elimination, metabolic, and other parts-to-plant uptake rate constants of the metabolite i, respectively.
are the soil-to-plant uptake, production, plant-to-other parts elimination, metabolic, and other parts-to-plant uptake rate constants of the metabolite i, respectively.
Within the tuber compartment as an additional component for potato as an example crop, we have:
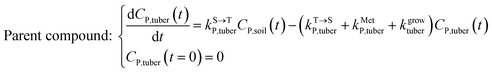 | (5) |
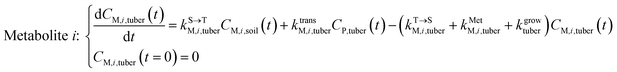 | (6) |
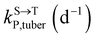 ,
, 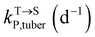 , kMetP,tuber (d−1), and kgrowtuber (d−1) are the soil-to-tuber uptake, tuber-to-soil elimination, metabolic, and dilution rate constants of the parent compound, respectively;
, kMetP,tuber (d−1), and kgrowtuber (d−1) are the soil-to-tuber uptake, tuber-to-soil elimination, metabolic, and dilution rate constants of the parent compound, respectively; 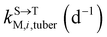 , ktransM,i,tuber (d−1),
, ktransM,i,tuber (d−1), 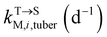 , and kMetM,i,tuber (d−1) are the soil-to-tuber uptake, production (via metabolism of the parent compound), tuber-to-soil elimination, and metabolic rate constants of metabolite i, respectively. The analytical solutions of CP,tuber(t) and CM,i,tuber(t) are provided in the ESI file.†
, and kMetM,i,tuber (d−1) are the soil-to-tuber uptake, production (via metabolism of the parent compound), tuber-to-soil elimination, and metabolic rate constants of metabolite i, respectively. The analytical solutions of CP,tuber(t) and CM,i,tuber(t) are provided in the ESI file.†
2.3 Added toxicity factor
To analyze the toxic effect of the parent compound and its metabolites in potatoes on humans, we applied the added toxicity factor (ATF, dimensionless) of the pesticide (the parent compound), which is defined as the toxicity ratio of metabolite i to the pesticide and can be expressed as follows: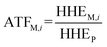 | (7) |
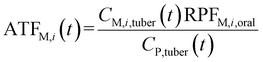 | (8) |
![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0065_20d1.gif) P, dimensionless) as follows:
P, dimensionless) as follows: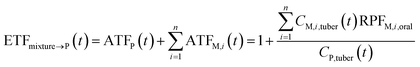 | (9) |
If the parent compound and its metabolites have the same toxicological properties (or they are considered to do so due to information limitations), eqn (8) and (9) can be further expressed as follows:
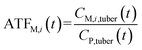 | (10) |
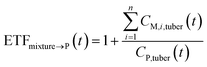 | (11) |
2.4 Model application (glyphosate)
Due to a lack of knowledge on AMPA's toxicity in humans,52–54 AMPA is assigned a RPFM,i,oral value of 1 because its toxicity profile and mechanism of action are thought to be comparable to those of glyphosate. The ESI file† contains the complete equations of CP,tuber(t) and CM,i,tuber(t), as well as the model input data. In addition, Maggi et al. (2020)42 assessed glyphosate and AMPA concentrations in global surface soils. We used the data of Maggi et al. (2020)42 to estimate the potential toxic pressure of the combination of glyphosate and AMPA in potatoes, which can benefit risk and impact assessors in predicting the health risks via crop consumption. The simulation results are provided in Table S1.† The model input variables, which encompass first-order uptake and elimination rate constants for glyphosate and AMPA, growth rate constants, and partition coefficients, were derived using established and validated modeling methodologies.38,39 The calculations for these variables are provided in the ESI file† (Section S2).2.5 Variability analysis
Environmental variables (e.g., soil quality and weather) have been shown to greatly affect plant uptake of soil pollutants, particularly for underground crops (e.g., root and tuber crops). Consequently, it is required to assess the variability in the simulated concentrations of the parent compound and its metabolites, which can give spatiotemporal simulations, in order to extend the suggested model beyond the local level. To do this, we altered the organic carbon–water partition coefficients and dissipation rate constants of compounds in the soil in order to generate the variable intervals of the simulated concentrations of the parent component and its metabolites in the potato. Due to the lack of information on metabolic rate constants of pesticides in plant tissues (including tubers),41,55,56 we also varied the metabolic rate constants of glyphosate and AMPA in tubers to evaluate the effect of metabolic kinetics on the simulation results. The variability intervals of the simulated concentrations of the parent compound and its metabolites in potatoes were subsequently generated. The analysis of variability can aid users in carrying out the modeling exercise in regional settings. The method to perform the variability analysis is provided in the ESI file.†2.6 Model comparison
To test the suggested method for simulating the bioconcentration of metabolites in potatoes, we compared the simulation results (i.e., the residue concentrations in the potato) between the proposed metabolite model and the non-metabolite model. For the non-metabolite model, the metabolites of the parent compound are not taken into account; instead, the metabolic rate of the parent compound in potatoes is set to zero for conservative risk assessment.38–40 Consequently, for the non-metabolite model, an equivalent toxicity factor is calculated based on the concentration of the parent compound in the potato. Hence, the comparison results can be used to examine the conservatism of the suggested metabolite and non-metabolite models in assessing the risk to human health. Furthermore, while the non-metabolite model does not consider biotransformation of the parent compound within the plant tissue, it can consider the bioconcentration of metabolites formed in soil, in air, or on plant surfaces, based on separately modeling metabolite uptake into plants. As a cross-check, we have compared the simulation results between the metabolite and non-metabolite models in terms of metabolite concentrations in potatoes.3. Results and discussion
3.1 Processes of glyphosate and AMPA bioconcentration in potatoes
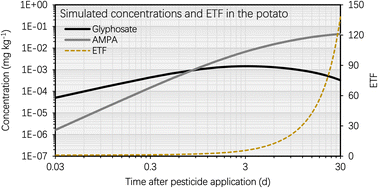
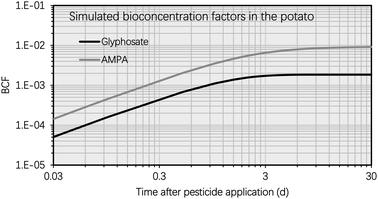
This section entails the simulated concentration of glyphosate and its primary toxic metabolite (i.e., AMPA) in potato as a function of time following glyphosate application (Fig. 3). The simulation was based on an initial glyphosate concentration of 1 mg kg−1 in the soil, which users can set arbitrarily (see eqn [s4a]–[s4b] in Section S1†). This value was chosen as it falls within the range of current, realistic application doses, field observations, or analytical detections.57,58 The simulation results for the BCF remain generally unaffected by variations in pesticide and metabolite concentrations in the soil. This highlights that the BCF could serve as a more stable indicator for assessing the bioconcentration potential in potatoes compared to solely considering the absolute chemical concentration values. Fig. S1† shows the simulated soil concentrations of glyphosate and AMPA. Fig. 3 illustrates that the concentration of glyphosate in the potato increased rapidly following pesticide application, as predicted by the simulation results. For instance, the maximum concentration of glyphosate in the potato was reached approximately 3 d after the application of the pesticide. This phenomenon is the result of a greater elimination rate constant of glyphosate in potatoes compared to the uptake rate constant. The glyphosate elimination from the potato includes tuber-to-soil diffusion, metabolic, and growth dilution processes, for which the elimination rate constants were simulated as 0.69 d−1, 0.15 d−1, and 0.14 d−1, respectively (Section S1†); however, the uptake rate constant of glyphosate in the potato (via the soil-to-tuber diffusion process) was estimated to be 1.7 × 10−3 d−1 (Section S1†). Consequently, the inflection point (i.e., the maximum value) of the dissipation curve of glyphosate in the potato occurred shortly after pesticide application.In contrast, the simulated AMPA concentration in the potato increased over the selected time period (i.e., from 0 d to 30 d). For instance, 5 d after glyphosate application, the simulated AMPA concentration in potato (i.e. 0.012 mg kg−1) was less than 30% of the simulated concentration 30 d after glyphosate application (i.e. 0.2 mg kg−1). This observation is a result of the increased uptake of AMPA by potatoes. The potato uptake of AMPA includes not only the soil-to-tuber diffusion process, but also the parent compound-to-metabolite production process (i.e., the biotransformation of glyphosate into AMPA in the potato); additionally, the elimination route via biotransformation (i.e., the metabolic rate constant) of AMPA was not considered due to a lack of data. Thus, the simulated bioconcentration process of AMPA displayed a different pattern from that of glyphosate. This difference in the simulated concentrations of glyphosate and AMPA in the potato is also evident in Fig. 4, where the bioconcentration factor (BCF, defined as the compound concentration ratio between the potato and soil) for AMPA was significantly greater than that for glyphosate. Fig. 3 further demonstrates that the simulated ETF of glyphosate in the potato increased more rapidly with increasing time following pesticide application. 5 d after pesticide treatment, the simulated ETF of glyphosate in potatoes was 10, and 10 d after pesticide application, this value was roughly 25. This upward trend was a result of the declining glyphosate concentration and the increasing AMPA concentration in the potato. We chose to conclude the simulation at 30 d, considering that the pre-harvest interval (PHI) for glyphosate in many crops typically spans from 7 to 28 d.59 Additionally, we noted a consistent increase in the simulated ETF value and AMPA concentration in potatoes throughout the potato growth period. This increase is attributed to the lack of a degradation rate constant for AMPA in potatoes, stemming from data limitations. As necessary data become accessible, this calculation can be refined by incorporating the degradation rate constant into the model.
3.2 Variability analysis
This section presents the findings of the variability test to assess the effect of dissipation kinetics in the soil, soil sorption partition coefficient (KOC, L kg−1) and metabolic kinetics in the potato on the simulation results. Fig. 5A depicts the variability intervals of the simulated concentrations of glyphosate and AMPA in the potato when the dissipation rate constants of glyphosate and AMPA in the soil were varied. The intervals ‘1’ of glyphosate and AMPA were calculated using the maximum dissipation rate constants of glyphosate and AMPA in the soil, whereas the intervals ‘2’ were calculated using the minimum dissipation rate constants. Using the highest dissipation rate constants of glyphosate and AMPA in the soil, the simulated glyphosate concentration in the potato was significantly lower than that using the minimum dissipation rate constants. This was because there were fewer glyphosate residues in the soil (using the maximum dissipation rate constants), limiting the mass transfer of glyphosate into the potato. In contrast, the simulated AMPA concentration in the potato when using the maximum dissipation rate constants of glyphosate and AMPA in the soil was significantly higher than that when using the minimum rate constants. AMPA in the soil is formed by the biotransformation (part of the overall dissipation process) of glyphosate in the soil; therefore, employing the maximum dissipation rate constant of glyphosate in the soil would boost the mass transfer process of AMPA from the soil to the potato. For example, 5 d after glyphosate application, when using the maximum dissipation rate constants of glyphosate and AMPA in the soil, the simulated AMPA concentration in the potato (i.e., 2.6 × 10−3 mg kg−1) was 12 times higher than that (i.e., 2.1 × 10−4 mg kg−1) when using the minimum dissipation rate constants.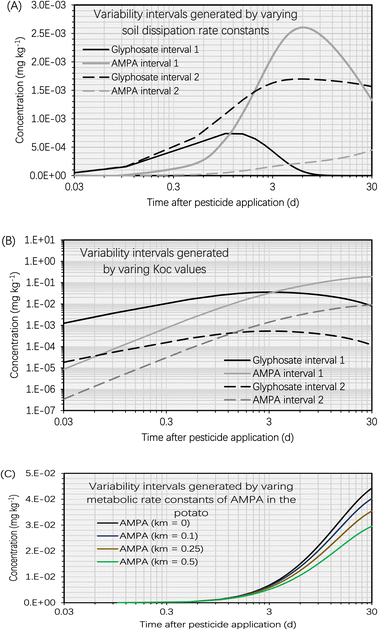 | ||
| Fig. 5 (A) Variability intervals of simulated concentrations of glyphosate and AMPA in the potato plotted against time (t, d) after glyphosate application (t = 0 d). The simulation was based on an initial glyphosate concentration of 1 mg kg−1 in the soil. Variability interval 1 was generated using the maximum dissipation rate constants of glyphosate and AMPA in the soil. Variability interval 2 was generated using the minimum dissipation rate constants of glyphosate and AMPA in the soil. The ranges of dissipation rate constants of glyphosate and AMPA in the soil are provided in S3.1.† (B) Variability intervals of simulated concentrations of glyphosate and AMPA in the potato plotted against time (t, d) after glyphosate application (t = 0 d). The simulation was based on an initial glyphosate concentration of 1 mg kg−1 in the soil. Variability interval 1 was generated using the minimum soil sorption partition coefficients (KOC, L kg−1) of glyphosate and AMPA. Variability interval 2 was generated using the maximum KOC values of glyphosate and AMPA. The ranges of dissipation rate constants of glyphosate and AMPA in the soil are provided in S3.2.† (C) Variability intervals of simulated concentrations of AMPA in the potato plotted against time (t, d) after glyphosate application (t = 0 d). The simulation was based on an initial glyphosate concentration of 1 mg kg−1 in the soil. Variability intervals were generated by setting the metabolic rate constants (km, d−1) of AMPA in the potato to 0 d−1, 0.1 d−1, 0.25 d−1, and 0.5 d−1. Due to little information on the metabolic kinetics of AMPA in plants,41,56 we arbitrarily set the metabolic rate constants to test the variability. | ||
The variability test on KOC had a different effect on the simulation findings than the soil dissipation rate constant. The intervals ‘1’ of glyphosate and AMPA were calculated using the minimum soil sorption partition coefficients of glyphosate and AMPA in the soil, whereas the intervals ‘2’ were calculated using the maximum soil sorption partition coefficients. Fig. 5B demonstrates that the variability intervals of the simulated glyphosate and AMPA concentrations in potatoes followed the same trend. For instance, the simulated concentrations of glyphosate and AMPA in potato using the minimum KOC values (i.e., intervals ‘1’) were greater than those using the maximum KOC values (i.e., intervals ‘2’). This is due to the fact that the KOC value of the chemical determines the associated soil–water partition coefficient (KSW, L kg−1) which in turn influences the soil-to-tuber diffusion rate constant of the compound. Consequently, low KOC values of glyphosate and AMPA led to low simulated KSW values (i.e., more residues will dissolve in the water phase of the soil), which accelerated the soil-to-tuber diffusion process. In addition, we noticed significant fluctuations in the simulated concentrations of glyphosate and AMPA in potatoes. For instance, 5 d after glyphosate application, the simulated AMPA concentration in the potato was 5.6 × 10−2 mg kg−1 using the minimum KOC value of AMPA (i.e., 1160 L kg−1) compared to 2.5 × 10−3 mg kg−1 using the maximum KOC value of AMPA (i.e., 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 L kg−1). The predicted glyphosate concentrations in the potato likewise exhibited a great deal of variance. Glyphosate and AMPA are ionizable chemicals whose KOC values are significantly influenced by the soil type, pH, charge, and organic matter content.60 Consequently, the heterogeneity of soil conditions can result in a wide range of simulated concentrations of glyphosate and AMPA in potatoes.
800 L kg−1). The predicted glyphosate concentrations in the potato likewise exhibited a great deal of variance. Glyphosate and AMPA are ionizable chemicals whose KOC values are significantly influenced by the soil type, pH, charge, and organic matter content.60 Consequently, the heterogeneity of soil conditions can result in a wide range of simulated concentrations of glyphosate and AMPA in potatoes.
As there is limited information on the metabolic kinetics (i.e., metabolic rate constants) of pesticides in plants,41,56 we performed the model exercise with a metabolic rate constant of zero for AMPA (Section S2†). Although this cautious approach may be valid for human health risk assessment,38–40 it may overestimate the concentration of pesticides in harvested crops. In order to investigate the effect of AMPA's metabolic kinetics on the simulation findings, we altered the metabolic rate constant of AMPA in the potato. The variation in the simulated AMPA concentrations in the potato increased with increasing time, as depicted in Fig. 5C of the simulation findings. For instance, 5 d after glyphosate application, the simulated AMPA concentrations in potatoes were 1.2 × 10−2 mg kg−1 and 8.9 × 10−3 mg kg−1 using the metabolic rate constants of AMPA in potatoes of 0 d−1 and 0.5 d−1, respectively, which ranged by nearly 40%. Nevertheless, 30 d after glyphosate application, the predicted AMPA concentrations in potato differed by nearly 50 percent. This was attributed to the increased AMPA concentration in the potato with time, which raised the AMPA mass loss rate according to first-order metabolic kinetics. The metabolic kinetics of AMPA had a lower effect on the bioconcentration of glyphosate and AMPA in potatoes compared to the soil dissipation kinetics and KOC.
3.3 Model comparison and recommendations
In this section, we compare the simulation findings for the suggested metabolite and non-metabolite models, which can assist risk assessors and chemical destiny modelers in improving plant uptake models for human health risk assessment. Due to the omission of the glyphosate metabolic process in the non-metabolite model, the simulated concentration of glyphosate in the potato was greater in the non-metabolite model than in the metabolite model, as shown in Fig. 6. Approximately 6 d after glyphosate application, the variation in the simulated glyphosate concentrations between the metabolite and non-metabolite models reached its maximum value, with the glyphosate concentration simulated using the non-metabolite model being approximately 20% higher than that simulated using the metabolite model. The simulation results suggested that the tuber-to-soil diffusion process dominated the overall elimination kinetics of glyphosate due to the high hydrophilicity of glyphosate (i.e., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW of −3.4), which resulted in a high simulated tuber–water partition coefficient of glyphosate. Moreover, 30 d after glyphosate application, the difference in glyphosate concentrations between the metabolite and non-metabolite models was negligible (i.e., 7 × 10−5 mg kg−1) due to the low simulated glyphosate concentrations in the potato using both models. Thus, the non-metabolite model agreed with the metabolite model in forecasting the glyphosate concentration in the potato at harvest, as demonstrated by recent modeling studies on various pesticides.38–40
KOW of −3.4), which resulted in a high simulated tuber–water partition coefficient of glyphosate. Moreover, 30 d after glyphosate application, the difference in glyphosate concentrations between the metabolite and non-metabolite models was negligible (i.e., 7 × 10−5 mg kg−1) due to the low simulated glyphosate concentrations in the potato using both models. Thus, the non-metabolite model agreed with the metabolite model in forecasting the glyphosate concentration in the potato at harvest, as demonstrated by recent modeling studies on various pesticides.38–40
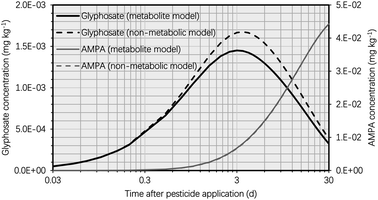 | ||
| Fig. 6 Simulated glyphosate and AMPA concentrations in the potato plotted against time (t, d) after glyphosate application (t = 0 d) using the metabolite model compared to the simulated concentrations using the non-metabolite model. The simulation was based on an initial glyphosate concentration of 1 mg kg−1 in the soil. In keeping with current potato uptake models, the metabolic rate constant of glyphosate in the potato was set to zero for the non-metabolite model.38–40 | ||
As the major metabolite of glyphosate (i.e., AMPA) in the potato could have hazardous effects on human health,52–54 the uptake process of AMPA in the potato must be incorporated into the non-metabolite model. AMPA concentrations in global soil reveal the potential toxicity of AMPA in potatoes,42 The potential risk of AMPA to consumers depends on both its quantity (in terms of the residue bioconcentration potential in plants) and the toxicity (in terms of chemical-intrinsic hazard properties). Therefore, high concentrations of AMPA in soils may result in elevated levels of AMPA in potatoes (Table S1†). As a result, when evaluating the bioconcentration of glyphosate in potatoes, the presence of AMPA cannot be ignored. In order to improve the non-metabolite model, we disregarded the biotransformation of glyphosate into AMPA in potatoes (i.e., the metabolic rate constant of glyphosate in the potato was set to zero to be consistent with the non-metabolite model). Thus, the bioconcentration of AMPA in potatoes, which was solely formed in the soil due to the breakdown of glyphosate, can be recreated using the non-metabolic model via the soil-to-tuber diffusion process. Fig. S2† demonstrates that the simulated AMPA concentrations in the potato did not differ significantly between the two models when t was greater than 5 d. This concordance between the two models was the result of low simulated glyphosate concentrations in the potato, which led to a low rate of AMPA synthesis via biotransformation. Incorporating the uptake of AMPA from the soil into the tuber, the non-metabolite model is therefore able to forecast AMPA concentrations in the potato.
The outcomes and methodology could aid risk assessors in evaluating health risks for consumers and preventing the oversight of potential hazards arising from metabolites. While we focused on potatoes and glyphosate as our demonstration, the modeling approach we propose is versatile and can be applied to various plant species, chemical species, environmental conditions, and regions. Further details are provided in Section 2.6 of the ESI file.†
4. Summary and conclusions
In this study, we developed a metabolite-based modeling strategy to mimic the bioconcentration process of pesticides and their metabolites in plants. Using the tuber plant as an illustration, we demonstrated the bioconcentration process of glyphosate and its most toxic metabolite (i.e., AMPA). The simulation results suggested that the bioconcentration process of AMPA cannot be disregarded, since the simulated concentration of AMPA in potatoes could pose a greater risk to human health than that of glyphosate. The modeling exercise, which employed glyphosate, highlighted the importance of considering the bioaccumulation of metabolites in plants, particularly those with higher toxicity or lower dissipation kinetics than their parent compounds. The results also indicated that soil properties, dissipation kinetics of pesticides in the soil, and metabolic kinetics of pesticides in the potato had a significant impact on the simulated concentrations of glyphosate and AMPA in the potato, which should be taken into account in regional-specific risk assessments. Due to a paucity of information regarding the biotransformation and metabolic rate constants of parent compounds and their metabolites in plant tissues, the bioconcentration model of metabolites in plants (i.e., the model is only applicable when the kinetics of metabolites are known) can be improved by implementing the following suggestions:(i) Advanced techniques, such as mechanism-based models, in silico predictions (e.g., quantitative structure–activity relationship), and in vitro analysis, should be developed to collect information on soil-, plant-, and chemical-specific biotransformation half-lives of parent compounds and their metabolites;
(ii) Multiple compartment plant uptake models, including roots, leaves, fruits, trees, and periderms, should be combined with the metabolite uptake process to thoroughly mimic the bioconcentration process of metabolites in diverse plant components;
(iii) To apply regulatory methods (e.g., environmental standards) for limiting levels of metabolites in crops at harvest before necessary data (e.g., biotransformation kinetics) are available, regulatory approaches such as read-across and expert judgment are required.
(iv) The biotransformation (through the activity of soil microorganisms) and metabolic (through the activity of plant enzymes) kinetics and toxicity of pesticides and their transformation products (e.g., metabolites) should be collected in a database. To establish such a database, it is necessary to undertake a comprehensive literature review of experimental or field studies.61 In addition to experimental data, degradation pathway models (such as EnviPath) can be regarded as a supplemental tool.62
Appendix
ESI file – model input data and analytical solutions.†Author contributions
Zijian Li: conceptualization, methodology, data curation, formal analysis, writing – original draft, writing – review & editing, resources, funding acquisition. Peter Fantke: conceptualization, methodology, discussion, writing – review & editing, funding acquisition.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was financially supported by the National Natural Science Foundation of China (Grant No. 42107495), as well as by the SPRINT project (grant agreement no. 862568) funded under the European Union's Horizon 2020 Research and Innovation program, and by the “Safe and Efficient Chemistry by Design (SafeChem)” project funded by the Swedish Foundation for Strategic Environmental Research (grant no. DIA 2018/11). Certain figures were created with the assistance of Microsoft 3D models and icons.References
- P. Fantke, R. Friedrich and O. Jolliet, Environ. Int., 2012, 49, 9–17 CrossRef CAS PubMed
.
- M. B. Kosnik, M. Z. Hauschild and P. Fantke, Environ. Sci. Technol., 2022, 56, 4776–4787 CrossRef CAS PubMed
.
- J. Wang, R. P. J. Hoondert, N. W. Thunnissen, D. van de Meent and A. J. Hendriks, Sci. Total Environ., 2020, 720, 137579 CrossRef CAS PubMed
.
- A. Mendez, C. A. Ng, J. P. M. Torres, W. Bastos, C. Bogdal, G. A. dos Reis and K. Hungerbuehler, Environ. Sci. Pollut. Res., 2016, 23, 10317–10334 CrossRef CAS PubMed
.
- Q. Liu, Y. Liu, F. Dong, J. B. Sallach, X. Wu, X. Liu, J. Xu, Y. Zheng and Y. Li, Environ. Pollut., 2021, 275, 116637 CrossRef CAS PubMed
.
- N. Pang, X. Fan, P. Fantke, S. Zhao and J. Hu, Environ. Pollut., 2020, 256, 113285 CrossRef CAS PubMed
.
- S. Trapp and M. Matthies, Environ. Sci. Technol., 1995, 29(9), 2333–2338 CrossRef CAS PubMed
.
- Z. Li, ACS Agric. Sci. Technol., 2021, 1(4), 338–346 CrossRef CAS
.
- Z. Li, J. Environ. Manage., 2020, 276, 111334 CrossRef CAS PubMed
.
- S. Trapp, D. Rasmussen and L. Samsøe-Petersen, SAR QSAR Environ. Res., 2003, 14(1), 17–26 CrossRef CAS PubMed
.
- S. Trapp, SAR QSAR Environ. Res., 2007, 18(3–4), 367–387 CrossRef CAS PubMed
.
- L. C. Paraíba, Chemosphere, 2007, 66(8), 1468–1475 CrossRef PubMed
.
- Q. An, Y. Wu, D. Li, X. Hao, C. Pan and A. Rein, Pest Manage. Sci., 2022, 78(6), 2679–2692 CrossRef CAS PubMed
.
- A. Mendez, L. E. Castillo, C. Ruepert, K. Hungerbuehler and C. A. Ng, Sci. Total Environ., 2018, 613, 1250–1262 CrossRef PubMed
.
- P. Fantke, R. Charles, L. F. de Alencastro, R. Friedrich and O. Jolliet, Chemosphere, 2011, 85(10), 1639–1647 CrossRef CAS PubMed
.
- P. Fantke, P. Wieland, C. Wannaz, R. Friedrich and O. Jolliet, Environ Model Softw., 2013, 40, 316–324 CrossRef
.
- P. Fantke and O. Jolliet, Int. J. Life Cycle Assess., 2016, 21, 722–733 CrossRef CAS
.
- S. Trapp, J. Shi and L. Zeng, Environ. Toxicol. Chem., 2023, 42, 793–804 CrossRef CAS PubMed
.
- J. G. Burken and J. L. Schnoor, J. Environ. Eng., 1996, 122(11), 958–963 CrossRef
.
- J. G. Burken and J. L. Schnoor, Environ. Sci. Technol., 1998, 32(21), 3379–3385 CrossRef CAS
.
- M. Bagheri, K. Al-jabery, D. Wunsch and J. G. Burken, Sci. Total Environ., 2020, 698, 133999 CrossRef CAS PubMed
.
- M. Bagheri, K. Al-jabery, D. C. Wunsch and J. G. Burken, Sci. Total Environ., 2019, 651, 561–569 CrossRef CAS PubMed
.
- M. Bagheri, X. He, N. Oustriere, W. Liu, H. Shi, M. A. Limmer and J. G. Burken, Sci. Total Environ., 2021, 751, 141418 CrossRef CAS PubMed
.
- A. Rein, C. N. Legind and S. Trapp, SAR QSAR Environ. Res., 2011, 22(1–2), 191–215 CrossRef CAS PubMed
.
-
A. Rein, P. Bauer-Gottwein and S. Trapp, in Groundwater Quality Management in a Rapidly Changing World : 7th International Groundwater Quality Conference, IAHS Press, Zurich, Switzerland, 2010 Search PubMed
.
- C. P. M. Bento, S. van der Hoeven, X. Yang, M. M. J. P. M. Riksen, H. G. J. Mol, C. J. Ritsema and V. Geissen, Environ. Pollut., 2019, 244, 323–331 CrossRef CAS PubMed
.
-
S. Daouk, Fate of the herbicide glyphosate and its metabolite AMPA in soils and their transfer to surface waters : A multi-scale approach in the Lavaux vineyards, western Switzerland, University of Lausanne Open Archive, 2013 Search PubMed
.
- E. M. Brovini, B. C. T. de Deus, J. A. Vilas-Boas, G. R. Quadra, L. Carvalho, R. F. Mendonça, R. de O. Pereira and S. J. Cardoso, Sci. Total Environ., 2021, 771, 144754 CrossRef CAS PubMed
.
- M. Kwiatkowska, P. Jarosiewicz, J. Michałowicz, M. Koter-Michalak, B. Huras and B. Bukowska, PLoS One, 2016, 11(6), e0156946 CrossRef PubMed
.
- S. Guilherme, M. A. Santos, I. Gaivão and M. Pacheco, Environ. Sci. Pollut. Res., 2014, 21, 8730–8739 CrossRef CAS PubMed
.
- S. O. Duke and S. B. Powles, Pest Manage. Sci., 2008, 64(4), 319–325 CrossRef CAS PubMed
.
- K. N. Reddy, A. M. Rimando, S. O. Duke and V. K. Nandula, J. Agric. Food Chem., 2008, 56(6), 2125–2130 CrossRef CAS PubMed
.
- V. Silva, L. Montanarella, A. Jones, O. Fernández-Ugalde, H. G. J. Mol, C. J. Ritsema and V. Geissen, Sci. Total Environ., 2018, 621, 1352–1359 CrossRef CAS PubMed
.
- M.-X. Chen, Z.-Y. Cao, Y. Jiang and Z.-W. Zhu, J. Chromatogr. A, 2013, 1272, 90–99 CrossRef CAS PubMed
.
- A. Grandcoin, S. Piel and E. Baurès, Water Res., 2017, 117, 187–197 CrossRef CAS PubMed
.
- S. Richard, S. Moslemi, H. Sipahutar, N. Benachour and G. E. Seralini, Environ. Health Perspect., 2005, 113(6), 716–720 CrossRef CAS PubMed
.
- M. Helander, A. Pauna, K. Saikkonen and I. Saloniemi, Sci. Rep., 2019, 9(1), 19653 CrossRef CAS PubMed
.
- S. Trapp, A. Cammarano, E. Capri, F. Reichenberg and P. Mayer, Environ. Sci. Technol., 2007, 41(9), 3103–3108 CrossRef CAS PubMed
.
- R. Juraske, C. S. Mosquera Vivas, A. Erazo Velásquez, G. García Santos, M. B. Berdugo Moreno, J. Diaz Gomez, C. R. Binder, S. Hellweg and J. A. Guerrero Dallos, Environ. Sci. Technol., 2011, 45(2), 651–657 CrossRef CAS PubMed
.
- L. C. Paraíba and K. Kataguiri, Chemosphere, 2008, 73(8), 1247–1252 CrossRef PubMed
.
- S. Xiao, Y. Gong, Z. Li and P. Fantke, J. Agric. Food Chem., 2021, 69(12), 3607–3616 CrossRef CAS PubMed
.
- F. Maggi, D. la Cecilia, F. H. M. Tang and A. McBratney, Sci. Total Environ., 2020, 717, 137167 CrossRef CAS PubMed
.
- P. Fantke, J. A. Arnot and W. J. Doucette, J. Environ. Manage., 2016, 181, 374–384 CrossRef PubMed
.
- W. J. Doucette, C. Shunthirasingham, E. M. Dettenmaier, R. T. Zaleski, P. Fantke and J. A. Arnot, Environ. Toxicol. Chem., 2018, 37(1), 21–33 CrossRef CAS PubMed
.
- Z. Li, Ecotoxicol. Environ. Saf., 2021, 222, 112490 CrossRef CAS PubMed
.
- Z. Li, J. Environ. Manage., 2021, 296, 113180 CrossRef CAS PubMed
.
- Z. Li and P. Fantke, Pest Manage. Sci., 2023, 79, 1154–1163 CrossRef CAS PubMed
.
- Z. Li, J. Hazard. Mater., 2022, 434, 128911 CrossRef CAS PubMed
.
- R. Altenburger, S. Scholz, M. Schmitt-Jansen, W. Busch and B. I. Escher, Environ. Sci. Technol., 2012, 46, 2508–2522 CrossRef CAS PubMed
.
- R. Altenburger, M. Nendza and G. Schüürmann, Environ. Toxicol. Chem., 2003, 22, 1900 CrossRef CAS PubMed
.
- T. Backhaus, Å. Arrhenius and H. Blanck, Environ. Sci. Technol., 2004, 38, 6363–6370 CrossRef CAS PubMed
.
-
FAO, Pesticide Residues in Food, Lyons, France, 1997 Search PubMed
.
- D. Asnicar, C. Cappelli, A. S. Sallehuddin, N. A. Maznan and M. G. Marin, J. Mar. Sci. Eng., 2020, 8(9), 661 CrossRef
.
- A. Connolly, M. A. Coggins and H. M. Koch, Toxics, 2020, 8(3), 60 CrossRef CAS PubMed
.
- S. Xiao, Z. Li and P. Fantke, Pest Manage. Sci., 2021, 77(11), 5096–5108 CrossRef CAS PubMed
.
- R. E. Jacobsen, P. Fantke and S. Trapp, SAR QSAR Environ. Res., 2015, 26(4), 325–342 CrossRef CAS PubMed
.
- L. J. Marek and W. C. Koskinen, Pest Manage. Sci., 2014, 70, 1158–1164 CrossRef CAS PubMed
.
- C. Pelosi, C. Bertrand, V. Bretagnolle, M. Coeurdassier, O. Delhomme, M. Deschamps, S. Gaba, M. Millet, S. Nélieu and C. Fritsch, Chemosphere, 2022, 301, 134672 CrossRef CAS PubMed
.
- European Food Safety Authority, EFSA J., 2013, 11(11), 3456 Search PubMed
.
-
C. Bento, Glyphosate and aminomethylphosphonic acid (AMPA) behavior in loess soils and off-site transport risk assessment, Wageningen University, 2018 Search PubMed
.
- R. van Zelm, M. A. J. Huijbregts and D. van de Meent, Environ. Sci. Technol., 2010, 44, 1004–1009 CrossRef CAS PubMed
.
- J. Wicker, T. Lorsbach, M. Gütlein, E. Schmid, D. Latino, S. Kramer and K. Fenner, Nucleic Acids Res., 2016, 44, D502–D508 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3em00266g |
| This journal is © The Royal Society of Chemistry 2023 |