Reply to the ‘Comment on “Perturbation theory of scattering for grazing-incidence fast-atom diffraction”’ by G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. S. Casagrande, E. A. Sánchez, M. S. Gravielle and H. Khemliche, Phys. Chem. Chem. Phys., 2023, 25, DOI: 10.1039/D3CP02486E

Abstract

In this Reply, we show that criticisms of perturbation theory for grazing-incidence fast-atom diffraction (GIFAD) are ill-founded. We show explicitly that our formulation (W. Allison, S. Miret-Artés and E. Pollak, Phys. Chem. Chem. Phys., 2022, 24, 15851) provides a similar precision in describing the observed phenomena as ab initio potentials. Since that is the main criterion to distinguish between methods, it seems reasonable to conclude that the perturbation approach using a Morse-type potential reproduces the essential aspects of the dynamics correctly. In addition we expand on the historical context and summarize the physical insights provided by our methods.

---

1 Introduction

The Comment¹ allows scope for further discussion of the relationship between grazing-incidence, fast-atom diffraction (GIFAD) and conventional low-energy atom-scattering.^2,3 In particular, it offers a good opportunity to bring these seemingly diverging strands of scientific development together. Also, in the present Reply we clarify the claims of our original paper,⁴ as it has wrongly been taken as an attempt to “debunk or contradict” earlier work.^5,6

We do not criticise the detailed calculation methods in Bocan et al.'s original papers.^5,6 Our aim was, and is, to enhance understanding of the phenomenology and provide insights into the relationship between features in the potential and features in the experimental observations that are not obtained from a purely numerical approach. We summarize the physical insights provided by our perturbation approach at the end of this Reply.

We also respond directly to various issues in the order given in the Comment;¹ specifically:

• We discuss the applicability of perturbation theory, which is well established. Some effects are evident in 1st-order while others appear, especially at low scattering energies, in 2nd-order. One cannot dismiss the huge literature on perturbation-theory because one particular effect may be absent in the first-order.

• We show explicitly that a parameterised Morse potential can describe the He/KCl(100) system to the same degree of accuracy as fully numerical results. If two different potentials can fit the data with the same precision, it is clear that further experimental insight is needed in order to distinguish features that are essential to the dynamics.

• We discuss the question of processing GIFAD patterns and specifically the question of whether lack of collimation and/or monochromaticity play a significant role in the analysis of experiment. We argue that, more importantly, the large separation of diffraction peaks and systematic errors in the approximations used to analyse experiment, lead to difficulties in the interpretation of experiment.

• We give a more detailed explanation of the historical context, and discuss whether the increase in the rainbow angle (or corrugation) “cannot be fully explained in terms of dynamic effects”. Our first order results show that the dominant effect arises from the modulation of the well-depth across the scattering channel. There is also a 2nd-order effect that should be considered, which arises due to the softness of the repulsive wall of the potential and may become evident, especially at low scattering energies. These effects can be described qualitatively as refraction within the well⁷ or by the repulsive wall.⁸

In writing our original paper,⁴ and in responding to the Comment,¹ we are at a disadvantage since we have no access to the original data. Therefore, in this Reply, our analysis is presented in the same context as the Comment.¹

2 The applicability of perturbation theory

Section 2 of the Comment states “low normal-energy GIFAD for He/KCl(001) is not within the range of validity of the FOP approach”. Here, FOP stands for first-order perturbation theory. First-order perturbation theory is not the whole story but it does a remarkable job in encapsulating the essential features of GIFAD scattering, by which we mean the dominance of out-of-plane scattering in a direction that includes the specular peak.³ The detailed argument, which we will provide in a future publication, follows a similar course to that given some years ago by Henkel et al.⁹ in the context of atomic diffraction in thin phase gratings. We note that similar phenomenology also occurs, at large angles of incidence, in surface scattering of molecular hydrogen,^10,11 which emphasises the generality of the phenomena under discussion.

Before discussing the details, we remind the reader of the key results in our original work.⁴

We employ potentials with the well-known Morse form, which has many benefits. It is widely used (see for example ref. 12 and 13) and represents the key elements of the real potential, such as the attractive-well and the soft-wall, using a minimal number of parameters. The variation, perpendicular to the surface has the form

V_M(z) = V₀[exp(−2αz) − 2 exp(−αz)], (1)

where V₀ is the depth of the attractive well and α is the “softness parameter”. Lateral modulation is introduced by a rigid displacement, in z, as a function of the coordinate parallel to the surface.^12,14 We use a displacement function, aligned perpendicular to the scattering plane, having the simplest symmetry needed to describe recent grazing-incidence experiments⁶where the surface has a periodicity of l. A single sinusoidal term provides a good approximation for analysis of the 〈100〉 azimuth, as demonstrated below; however, in other directions further terms in a Fourier series may be needed (see, for example, ref. 15).

We apply different displacement amplitudes to the repulsive and attractive terms in the potential. The effect is to modulate the well depth across the scattering channel, which plays a critical part in describing the observed phenomenology. Thus, the potential becomes

V_M(z,x) =V₀[exp(−2α(z − h_rh(x))) − 2 exp(−α(z − h_ah(x)))], (3)

where h_r and h_a respectively give the amplitude of the displacement in the repulsive and attractive terms. Four parameters define the potential: V₀ gives the overall depth of the attractive well; α is the softness; while h_r and h_a define the displacement amplitudes. The ratio, h_a/h_r, is a dimensionless parameter that modulates the well depth across the scattering channel (Here we use the same definition as in our original paper, for the 〈100〉 azimuth see Fig. 1 in ref. 4. The position of the K and Cl⁻ ions, which we denote as the top-site, corresponds to x = l/4 while the hollow site, midway between the ions, occurs at x = 3l/4).

Contributions to the rainbow angle for classical scattering from this potential, when calculated in first-order and second-order are, respectively (eqn (4.3) and, for h_a/h_r = 1, eqn (4.5) in ref. 4),

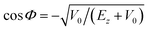andwhere the contribution of the hard wall (hw) is K_hw = 2πh_r/l, and the function G(E_z) is defined in eqn (4.4).⁴ The terms in square brackets show a zero-th order term of magnitude unity, together with the respective first-order correction (eqn (4)) and second-order contribution (eqn (5)).

It is instructive to examine the criticism of perturbation theory in the light of these two equations. Fig. 1, in the Comment,¹ shows a normal energy dependence in the ratio of quantities that, in first-order perturbation theory, have the same normal energy dependence. That approach has factored out the first-order effects, to some extent. It simply gives emphasis to the contribution from higher-order terms in the perturbation series.

In fact Fig. 1¹ shows that, provided E_z/V₀ > 4, the ratio is approximately constant, as predicted by first-order perturbation theory. It follows that the predictions of first-order theory are valid everywhere except at the lowest energies, where it may be necessary to include a second term.

The second-order contribution (eqn (5), and displayed in Fig. 3 of our original paper⁴) is zero near E_z/V₀ ≈ 4 with a sharp increase at lower energies and a more gentle increase at higher energies. The phenomenology is exactly that required.

The perturbation theory that we have developed assumes that the small parameters are h_a and h_r. One may pose the question, small relative to what? A straightforward answer is small relative to the lattice length, and this implies through the relation K_hw = 2πh_r/l that the rainbow angle is small. This is not the case when the energy becomes sufficiently small. The lower the energy the higher one must go in the order of perturbation theory.

In our opinion, first-order theory combined with a sensibly parameterised potential, is able to describe the rainbow scattering of He from the KCl(100) surface at an acceptable level, as we demonstrate below. Higher order terms, in particular, second-order terms in the perturbation series may be required, at very low energies, if a more precise description of the dynamics is warranted.

3 The applicability of a suitable Morse potential

Here we show that our Morse potential and first-order theory describes the scattering as well as some potentials derived from ab initio calculations. All one needs to do is use sensible values for the parameters in eqn (4).

To make our point we use the data in the energy-normalised form of the Comment (Fig. 4¹). The value of V₀ used to normalise the data is not given so we cannot provide a definitive description of the data. All we can do is demonstrate that the Morse potential does, indeed, represent the data, in the form given.

The case of the 〈110〉 azimuth is the most difficult but the Morse potential works well. The Comment acknowledges that “for 〈110〉 (Fig. 4(a)) Morse based calculations give a reasonable accord with DFT-based ones (and hence, with experiments)”. Thus, we make no further comment and proceed to the case of 〈100〉.

For the 〈100〉 azimuth, even better agreement may be obtained, with the right parameters. Fig. 1, here, shows that with a better value for K_hw and a slightly different value for h_a/h_r the result is entirely satisfactory. The results of first-order perturbation theory using the Morse potential form are shown as the solid black line. The predictions of perturbation theory follow the trends displayed by the experimentally derived data at least as well as the DFT potentials. Indeed, if anything, perturbation theory does a significantly better job than the DFT-PBE potential.

Fig. 1 Application of first-order perturbation theory with a corrugated Morse potential to the energy-normalised data in the 〈100〉 azimuth.¹ Experimental data, grey circles, are extracted from Fig. 4(b) of the Comment.¹ The calculated theory is shown as solid lines: red, DFT-PBE potential; blue, DFT-vdW1 potential; green, DFT-vdW2 potential. The first-order perturbation results are shown as a solid black line, where we have used tan(K_hw) = 33°, and h_a/h_r = 0.65. Note, these parameters should not be regarded as a best-fit using the Morse potential (see text).

It is evident that a sensibly parameterised Morse potential can describe the scattering in so far as the experiment illuminates those dynamics. Whether, the potentials “fit” each other is an entirely different question. Note that the parameters we use in Fig. 1 should not be regarded as a best-fit of the Morse potential model because the value of V₀ is unspecified.

4 Experimental processing of GIFAD patterns

There is a clear difference of opinion over the question of terminology. We prefer to frame our discussion in terms of the rainbow angle rather than “corrugation” – it is a matter of taste, since as we have shown, the two quantities are necessarily related. In a semi-classical picture, the SIVR⁶ corrugation samples the potential along straight-line trajectories above the top and hollow sites whereas the classical rainbow trajectory is most sensitive to the slope roughly midway between the SIVR trajectories. The two quantities are related since one cannot increase the slope in a smooth manner without changing the “corrugation” – an effect that, with a sinusoidal modulation and first-order perturbation theory, gives the same energy dependence to both quantities (though not necessarily, as we point out above, in higher order).

Identifying a classical rainbow angle in a diffraction experiment, with widely spaced diffraction peaks, is a tricky proposition. If the angular and energy collimation is very poor, it could be argued, as in the Comment, that “a non-zero rainbow Bragg overlapping may occur”, providing direct evidence in the data. However, the collimation and energy spread in their experiment⁵ is too good for that to be the case. Fig. 2 in Phys. Rev. B, v104⁶ shows well resolved peaks at all energies, especially at low energy, where the present discussion is focused. As a result, and unlike the case for heavier projectiles, for example Ne,⁷ some analysis of the diffraction intensities is required to extract a rainbow angle, or “corrugation” from the experimental data.

In the present case, rainbow angles and “corrugation” have been obtained, for example inref. 5, using an approximate hard-wall model coupled with an analysis that uses the basic Eikonal approximation for the dynamics (see ESI inref. 5, eqn (4)–(6)). There is an intrinsic error in using a hard wall model, and especially the use of Eikonal scattering. The effects are well-documented in the context of helium scattering from stepped copper surfaces,¹⁶ where the errors are shown to be both significant and systematic. It would be helpful for everyone to have a quantitative discussion of such intrinsic uncertainties.

5 Scattering phenomenology with perpendicular energy comparable to the well-depth

Here, we discuss the “unexpectedness” of the observed behaviour and whether or not there is any new qualitative phenomenology in the case of He/KCl(100).^1,5,6 In particular, we discuss the statement that the effects “cannot be fully explained in terms of dynamic effects”.

Evidence from other experiments and earlier work by some of the present authors suggests that the underlying phenomenon is widespread and that the observed behaviour is straightforward to understand. The most significant feature is the change in rainbow angle as the perpendicular energy is reduced. The effect was reported for Ar scattering from adsorbed H on a metal surface (Ar/2H-W(100)), in the work of Schweizer et al.¹⁷ Their Fig. 11 displays the phenomenon explicitly for Ar scattering. They also recognised that the origin lay in the effect of the attractive potential, and showed the effect could be described qualitatively using the simple, square-well model of Klein and Cole.¹⁸ A similar observation was reported for Ar scattering from LiF(001).¹⁹ In the case of GIFAD, a dramatic increase in rainbow angle at low energy is clearly visible, for the He/KCl(001) system, in the calculations reported by Specht et al.¹⁵ All of the above work predates 2011. Our conclusion is that there is nothing “anomalous” about the He/KCl system.

More recently, the effect was demonstrated most elegantly in GIFAD measurements on Ne/LiF(001) scattering,⁷ which were contemporaneous with the present experiments.⁵ In the case of Ne scattering, the greater mass of the projectile and its shorter wavelength give a sufficiently large number of open diffraction channels to reveal the change in rainbow angle directly.

The classical and semi-classical analysis by Pollak and Miret-Artés^14,20,21 offered a more quantitative approach than considered previously. They used a Morse potential where both terms in eqn (1) are modulated, in z, with the same function and reproduced the effects achieved with quantum calculations and an ab initio potential,²² as well as describing the phenomenology observed in low-energy experiments. One benefit of an analytic approach^14,21 is that the generality of phenomena is more readily apparent.

In the case of non-normal incidence the presence of an attractive well will generally result in a rainbow angle that decreases as the incident energy increases.^14,20,23 The effect is evident from, for example, eqn (3.15) and (4.14) of Zhou et al.²⁰Fig. 2(a) shows the effect calculated to first order in perturbation theory. Here, the rainbow angle is plotted as a function of the normal energy for the case of an attractive well without modulation of its depth (h_a/h_r = 1 in eqn (3)) for different values of the incidence angle. The scattering geometry here is that of the conventional low-energy experiment, where the scattering is observed in-plane and the corrugation is also in that direction. The rainbow angle decreases continuously as the energy increases, which can be understood as arising from refraction by the attractive well.^18,23 To second-order one observes asymmetry in the forward and back-scattered rainbow angles.²¹ The greater the incidence angle, the greater the refraction effect. Notice that as one approaches normal incidence the “refraction” effect disappears in the first-order theory. However, it is non-zero away from the specular direction if higher-order terms are included.⁴

Fig. 2 Energy dependence of the rainbow angle in first-order perturbation theory with a corrugated Morse potential. (a) Shows the behaviour as the angle of incidence changes, calculated using eqn (3.15) and (4.14) of Zhou et al.²⁰ Here, θ_i is measured from the surface normal so that GIFAD scattering corresponds to θ_i = 0°. (b) Shows the effect of modulating the well-depth across the GIFAD scattering channel, calculated using eqn (4), h_a/h_r < 1, red line, corresponds to a deeper well in the centre of the scattering channel, as observed on alkali halide (001) surfaces; h_a/h_r > 1, blue line, has the deeper well on the top site.⁴ Other parameters are chosen arbitrarily as the effects we illustrate are generic. For information, the rainbow constant in the hard-wall limit, K_hw = 0.63, while the values of α and l are those for Morse potential and the 〈100〉 azimuth taken directly from the Comment.¹

The absence of a first-order contribution when the well depth has no spatial variation (i.e. h_a/h_r = 1) raises the question of why these effects are observed so clearly in the GIFAD scattering geometry, where the slow degree of freedom in the motion corresponds to normal incidence and the corrugation is normal to the scattering plane. We believe the answer lies in the lateral modulation of the well depth, which is a subtle, but important, feature of potentials calculated ab initio.⁶Fig. 2(b) illustrates the effect using the first-order result given by eqn (4), as h_a/h_r and the depth modulation is varied. The interest in Fig. 2(b) is that it shows the change in rainbow angle can be positive or negative depending on where the deepest well is located. The results for scattering from alkali halides indicate h_a/h_r < 1 showing the well is deeper in the centre of the scattering channel, in what we term the hollow site, exactly as reproduced in the ab initio potentials. The fact that the first-order theory can reproduce these effects, as we have shown above, confirms its utility.

6 Summary

In the present Reply we have addressed arguments given in the Comment¹ directly. Our analysis shows that perturbation theory using a corrugated Morse potential can represent the data at least as well as fully numerical potentials. In addition, our approach illustrates that the physical origin of the observed phenomena lies in the modulation of the well depth across the scattering channel.

It seems to us that similar phenomenology is evident in many examples of surface scattering and that the basic phenomenology has been understood, at least qualitatively, since 1979¹⁸ More recently the perturbation approach has provided a better, and more quantitative, description. In our opinion, the key features in the scattering can be explained rationally and relatively simply.

Fig. 2 provides a pictorial summary of the phenomena. When there is no modulation of the well depth, the first-order effect arises from refraction by the well. Fig. 2(a) shows the generic behaviour. The rainbow angle decreases with energy and is most marked at large angles of incidence. At normal incidence, the GIFAD geometry, the first-order contribution is zero unless there is a modulation in the well-depth (i.e. h_a/h_r ≠ 1). Fig. 2(b) shows the behaviour, to first-order, when the well-depth is modulated. Not only does the modulation manifest itself in first-order, but its phase with respect to the scattering channel, is revealed. In making these observations we should emphasise that there are always second-order contributions, but generally such effects are weaker and will be most prominent at low scattering energy, where the first order perturbation theory may break down and the effect of the well is greater. This phenomenology is in good agreement with all the observations and calculations.

Perturbation theory, whether in first-order or second-order, offers analytic results that allow a degree of analysis that is not available to an approach that is entirely numerical. In that sense, we see our contribution as complementary to the numerical work of Bocan et al., and not directly competitive.

Author contributions

All authors contributed equally to this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Philippe Roncin and Matthew Ord for critical reading of our manuscript and for their helpful suggestions. SMA would like to thank support from Fundación Humanismo y Ciencia. EP thanks the Israel Science Foundation for its generous support. WA acknowledges support from the Cambridge Atom Scattering Facility (https://atomscattering.phy.cam.ac.uk) and EPSRC award EP/T00634X/1.

Notes and references

1. G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. S. Casagrande, E. A. Sánchez, M. S. Gravielle and H. Khemliche, Phys. Chem. Chem. Phys., 2023, 25 10.1039/D3CP02486E.
2. A. Muzas, F. Gatti, F. Martín and C. Díaz, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 382, 49–53.
3. M. Debiossac, P. Pan and P. Roncin, Phys. Chem. Chem. Phys., 2021, 23, 7615.
4. W. Allison, S. Miret-Artés and E. Pollak, Phys. Chem. Chem. Phys., 2022, 24, 15851–15859.
5. G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. Casagrande, M. S. Gravielle, E. A. Sánchez and H. Khemliche, Phys. Rev. Lett., 2020, 125, 096101.
6. G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. S. Casagrande, E. A. Sánchez, M. S. Gravielle and H. Khemliche, Phys. Rev. B, 2021, 104, 235401.
7. M. Debiossac, P. Roncin and A. G. Borisov, J. Phys. Chem. Lett., 2020, 11, 4564–4569.
8. W. F. Avrin and R. P. Merrill, Surf. Sci., 1994, 311, 269–280.
9. C. Henkel, J.-Y. Courtois and A. Aspect, J. Phys. II, 1994, 4, 1955–1974.
10. D. Farías, C. Díaz, P. Rivière, H. F. Busnengo, P. Nieto, M. F. Somers, G. J. Kroes, A. Salin and F. Martín, Phys. Rev. Lett., 2004, 93, 246104.
11. P. Nieto, D. Barredo, D. Farías and R. Miranda, J. Phys. Chem. A, 2011, 115, 7283–7290.
12. A. S. Sanz and S. Miret-Artés, Phys. Rep., 2007, 451, 37–154.
13. P. Pan, M. Debiossac and P. Roncin, Phys. Rev. B, 2021, 104, 165415.
14. S. Miret-Artés and E. Pollak, Surf. Sci. Rep., 2012, 67, 161–200.
15. U. Specht, M. Busch, J. Seifert, H. Winter, K. Gärtner, R. Włodarczyk, M. Sierka and J. Sauer, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 799–803.
16. S. Miret-Artes, J. Toennies and G. Witte, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5881.
17. E. K. Schweizer, C. T. Rettner and S. Holloway, Surf. Sci., 1991, 249, 335–349.
18. J. R. Klein and M. W. Cole, Surf. Sci., 1979, 81, L319–L324.
19. T. Kondo, H. S. Kato, T. Yamada, S. Yamamoto and M. Kawai, Eur. Phys. J. D, 2006, 38, 129–138.
20. Y. Zhou, E. Pollak and S. Miret-Artés, J. Chem. Phys., 2014, 140, 024709.
21. E. Pollak and S. Miret-Artés, J. Phys. Chem. C, 2015, 119, 14532–14541.
22. A. Azuri and E. Pollak, J. Chem. Phys., 2015, 143, 014705.
23. E. Pollak and J. Tatchen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115404.

---