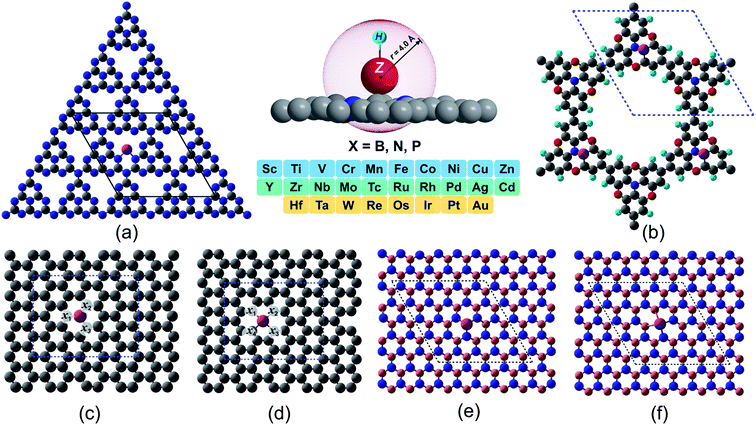
Machine learning assisted high-throughput screening of transition metal single atom based superb hydrogen evolution electrocatalysts†
Muhammad
Umer
a,
Sohaib
Umer
a,
Mohammad
Zafari
a,
Miran
Ha
 a,
Rohit
Anand
a,
Amir
Hajibabaei
a,
Ather
Abbas
b,
Geunsik
Lee
a,
Rohit
Anand
a,
Amir
Hajibabaei
a,
Ather
Abbas
b,
Geunsik
Lee
 *a and
Kwang S.
Kim
*a and
Kwang S.
Kim
 *a
*a
aCenter for Superfunctional Materials, Department of Chemistry, Ulsan National Institute of Science and Technology (UNIST), 50 UNIST-gil, Ulsan 44919, Republic of Korea. E-mail: gslee@unist.ac.kr; kimks@unist.ac.kr
bUrban and Environmental Engineering, Ulsan National Institute of Science and Technology (UNIST), 50 UNIST-gil, Ulsan 44919, Republic of Korea
First published on 2nd February 2022
Abstract
Carbon-based transition metal (TM) single-atom catalysts (SACs) have shown great potential toward electrochemical water splitting and H2 production. Given that two-dimensional (2D) materials are widely exploited for sustainable energy conversion and storage applications, the optimization of SACs with respect to diverse 2D materials is of importance. Herein, using density functional theory (DFT) and machine learning (ML) approaches, we highlight a new perspective for the rational design of TM-SACs. We have tuned the electronic properties of ∼364 rationally designed catalysts by embedding 3d/4d/5d TM single atoms in diverse substrates including g-C3N4, π-conjugated polymer, pyridinic graphene, and hexagonal boron nitride with single and double vacancy defects each with a mono- or dual-type non-metal (B, N, and P) doped configuration. In ML analysis, we use various types of electronic, geometric and thermodynamic descriptors and demonstrate that our model identifies stable and high-performance HER electrocatalysts. From the DFT results, we found 20 highly promising candidates which exhibit excellent HER activities (|ΔGH*| ≤ 0.1 eV). Remarkably, Pd@B4, Ru@N2C2, Pt@B2N2, Fe@N3, Fe@P3, Mn@P4 and Fe@P4 show practically near thermo-neutral binding energies (|ΔGH*| = 0.01–0.02 eV). This work provides a fundamental understanding of the rational design of efficient TM-SACs for H2 production through water-splitting.
1. Introduction
To reduce fossil fuel consumption and mitigate global warming, tremendous attention has been paid to hydrogen as a renewable fuel.1,2 Water electrolysis is regarded as an ideal approach for high-purity hydrogen generation, which is of great significance for global clean energy deployment and ecological environmental protection.3–5 The key aspect to promote this technology is the development of inexpensive, stable and high-performance electrocatalysts.6,7 Platinum (Pt) based catalysts have been most practical and efficient for the hydrogen evolution reaction (HER), however, the practical implementations for electrochemical hydrogen production have been thwarted by high cost and natural scarcity of Pt. Recently, for cost-effective and highly active electrocatalysts it has been suggested to utilize ultra-low loading of precious metals such as Pt, Ru, Rh, Pd and Ir as SACs which show very small overpotentials for the HER.8–13 Meanwhile, considerable efforts are being made to search for new cost-effective, stable and active non-noble metal electrocatalysts to replace these precious noble metals.14–18 Recently, a vast number of different classes of materials have emerged in the field of electrocatalysis, such as metal carbides,19,20 nitrides,21–23 phosphides,24 and two dimensional (2D) material families including metal oxides,25–27 layered double hydroxides (LDHs),28,29 graphene,30,31 MXenes,32–34 phosphorene,35 graphitic carbon nitride (g-C3N4)36,37 and TM dichalcogenides (TMDs).38,39 These diverse types of materials have been widely exploited for various electrocatalytic applications, and indeed have shown impressive electrocatalytic activities towards the HER,40,41 oxygen evolution/reduction reaction (OER/ORR),22,30,42–44 nitrogen reduction reaction (NRR),45–48 carbon dioxide reduction reaction (CO2RR)49 ammonia oxidation reaction (AOR),50etc. Among these heterogeneous material classes, graphene-supported TM-SACs have gained considerable attention due to their well-defined atomically dispersed active sites and tunable electrocatalytic properties. The electronic properties and durability of TM-SACs can be controlled by the modification of the coordination environment and the formation of particular types of vacancies on the surface.51 In principle, by tuning these two parameters, the HER performance of these materials can be substantially improved. Extensive work has been done on series of different non-metal (B, N, P, and S) doped TM-SACs with various metal-nonmetal configurations, which have shown great potential towards multifunctional electrocatalytic applications.52–54 Also, significant efforts have been devoted to identifying 2D materials beyond graphene that offer a greater degree of tunability and excellent conductivity. For example, Galeotti et al. successfully fabricated a two-dimensional π-conjugated polymer (2DCP) with kagome lattices in the mesoscale order.55 The 2DCP exhibited excellent stability with a tunable bandgap and high carrier mobility. Given these advantages, we also sought to consider 2DCP. Theoretical exploration of key insights is advantageous for promoting experimental development of new high-performance HER catalysts.40,56–58 Recently, the ML approach has shown immense potential to accelerate the discovery of energy materials59,60 and electrocatalysts. Various geometric and electronic descriptors have been proposed to guide the design and screening of catalyst properties, such as Coulomb matrix,61 bag of bonds (BOB),62 smooth overlap of atomic positions (SOAP),63 adsorption free energy d-band center,64etc. Recently, Jäger et al. predicted the hydrogen adsorption free energies on various nanoclusters by using SOAP, many-body tensor representation (MBTR), and atom-centered symmetry function (ACSF) descriptors.65 To this end, substantial interest has been devoted to developing such descriptors which can be directly employed to design and screen catalysts without performing extensive DFT calculations.Herein, we adopted a stepwise screening strategy and investigated the stability and activity of several experimentally feasible 2D structures for H2 production. By DFT calculations we screened over 364 catalysts, and out of these we found that 20 catalysts exhibit excellent stabilities and near-zero overpotentials. Based on the thermodynamic stability energy (Estab) and dissolution potential (Udiss), we further classified the catalysts into four different groups and assessed their HER activities. For the ML study, we initially considered basic physicochemical properties as possible features to train various ML models. In order to recognize the intrinsic factors that govern the stability and activities, we further employed the subsequent equation learning method using the sure independence screening and sparsifying operator (SISSO) approach (see ESI Note 2†).66 The top-ranked SISSO generated descriptors were further passed to the feature selection step. By using the step forward feature selection method, we carefully evaluated the feature importance and reserved only the most relevant features in the database for the catalytic performance prediction. Our identified descriptors and systematic screening strategy provide a stepping stone toward designing durable and high-performance electrocatalysts.
2. Computational methods
DFT calculations were carried out by using the Vienna ab initio simulation package (VASP)67 with the projector augmented wave (PAW) method.68 We set a kinetic energy cutoff of 500 eV for plane-wave expansion of the electronic wave function. The exchange–correlation interaction was treated by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).69,70 For geometry optimization we use a 3 × 3 × 1 Monkhorst–Pack k-point grid, however, a denser 7 × 7 × 1 k-point grid was chosen for electronic structure calculations. A vacuum of 15 Å along the z-axis was set throughout all the calculations to avoid interactions between repeated images. The energy and force convergence criteria were set to 10−5 eV and 0.01 eV Å−1, respectively. Given that the HER reaction intermediate adsorption/desorption is a surface phenomenon, the effect of the van der Waals (vdW) interaction was accounted for by applying the Tkatchenko–Sheffler (TS) dispersion correction method.71 The solvation effect was taken into account by using the pure implicit solvent model as implemented in VASPsol.72 In order to evaluate the HER activities we utilized different active sites and calculated the differential hydrogen adsorption Gibbs free energies by using the computational hydrogen electrode (CHE) model developed by Nørskov et al.:73| ΔGH* = ΔEnH* + ΔEnH*(ZPE) − TΔS + eU + pH × kBT × ln(10) | (1) |
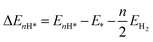 | (2) |
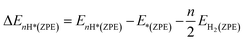 | (3) |
The ΔS is obtained from
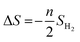 | (4) |
The theoretical overpotential ηHER is given by
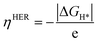 | (5) |
To compare the HER performance of promising candidates, we calculated the exchange current densities (io) by utilizing free energy values at pH = 0.
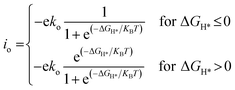 | (6) |
Furthermore, in our ML analysis, we employed various ML classification and regression models to classify the structural stabilities and to predict HER activities. To estimate the model performance, we employed the Monte-Carlo cross-validation method.75 The data samples were randomly split 100 times into different training and test sets with 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 split ratios and the weight-averaged prediction errors were presented for each ML model.
2 split ratios and the weight-averaged prediction errors were presented for each ML model.
3. Results and discussion
3.1 Structural stability
In spite of exhibiting excellent electrocatalytic activities, the practical applications rely strongly on the long-lasting stability/durability of catalysts. Using DFT calculations, we first investigated the thermodynamic and electrochemical stabilities of ∼364 rationally designed catalysts by using a combination of 28 (3d/4d/5d) transition metal (TM) atoms with 13 kinds of experimentally available substrates (C4, N4, B4, N2C2, B2C2, B2N2, 2DCP, g-C3N4, h-B2N2, h-BN, C3, N3 and B3). Fig. 1 and Fig. S3 and S4† present all the geometrical structures we used in this study. In order to obtain the TM binding strength, we calculated the embedding energies (Eemb) by using the following equation:| Eemb = ETM@surf − Esurf − ETM | (7) |
 | (8) |
The  and n represent the standard dissolution potential of the bulk TM and the number of electrons involved in dissolution, respectively. The materials with Udiss > 0 vs. the standard hydrogen electrode (SHE) are regarded to be electrochemically stable. The exact Udiss values are listed in Table S3.† A catalyst with Estab < 0 and Udiss > 0 is considered to be thermodynamically and electrochemically stable. According to our defined stability criteria, we grouped all the catalysts into four classes (G1: unaggregatable and indissoluble, G2: aggregatable and indissoluble, G3: unaggregatable and dissoluble, G4: aggregatable and dissoluble) depicted in Fig. 2 and Table S4.† It is worth noting that most of the experimentally synthesized catalysts are falling into our stability evaluation criteria, which suggests the reliability and feasibility of our approach. The computed Estab and Udiss values reveal that the substrates such as C4, N4, N2C2, 2DCP, h-BN, h-B2N2 and C3 are good supports to form single atom moieties. Generally, the early TM-SACs such as Sc, Ti, Cr, V, Y, Zr, Nb, Hf and Ta are more likely to be stabilized thermodynamically (Eemb < 0), however, their negative Udiss values indicate that these catalysts are electrochemically unstable under acidic conditions. We found that, particularly, the 3d-TMs including Mn, Fe, Co, Ni and Cu in double vacancy sites have planar structures with strong metal-support interactions and exhibit excellent stabilities. Among 4d- and 5d-TMs, the elements of Ru, Rh, Pd, Ir and Pt display superior thermodynamic and electrochemical stabilities on all the surfaces studied here. To further check the dynamic stability of single and double vacancy systems, we performed the DFT-based ab initio molecular dynamics (AIMD) simulations at 500 K by using the Nose–Hoover thermostat method78 and also sparse Gaussian process regression (SGPR)79,80 machine-learning DFT potential/force based AIMD simulations which reproduced the DFT-based AIMD simulation results in a much faster manner which can be readily extended to other metal cases using universal potential generation. Fig. S5† illustrates that during the AIMD simulations the energy and temperature remain within a small range, indicating the stability of these structures. Our identified mono- and dual-type non-metal doped TM-SACs hold outstanding promise for synthesis.
and n represent the standard dissolution potential of the bulk TM and the number of electrons involved in dissolution, respectively. The materials with Udiss > 0 vs. the standard hydrogen electrode (SHE) are regarded to be electrochemically stable. The exact Udiss values are listed in Table S3.† A catalyst with Estab < 0 and Udiss > 0 is considered to be thermodynamically and electrochemically stable. According to our defined stability criteria, we grouped all the catalysts into four classes (G1: unaggregatable and indissoluble, G2: aggregatable and indissoluble, G3: unaggregatable and dissoluble, G4: aggregatable and dissoluble) depicted in Fig. 2 and Table S4.† It is worth noting that most of the experimentally synthesized catalysts are falling into our stability evaluation criteria, which suggests the reliability and feasibility of our approach. The computed Estab and Udiss values reveal that the substrates such as C4, N4, N2C2, 2DCP, h-BN, h-B2N2 and C3 are good supports to form single atom moieties. Generally, the early TM-SACs such as Sc, Ti, Cr, V, Y, Zr, Nb, Hf and Ta are more likely to be stabilized thermodynamically (Eemb < 0), however, their negative Udiss values indicate that these catalysts are electrochemically unstable under acidic conditions. We found that, particularly, the 3d-TMs including Mn, Fe, Co, Ni and Cu in double vacancy sites have planar structures with strong metal-support interactions and exhibit excellent stabilities. Among 4d- and 5d-TMs, the elements of Ru, Rh, Pd, Ir and Pt display superior thermodynamic and electrochemical stabilities on all the surfaces studied here. To further check the dynamic stability of single and double vacancy systems, we performed the DFT-based ab initio molecular dynamics (AIMD) simulations at 500 K by using the Nose–Hoover thermostat method78 and also sparse Gaussian process regression (SGPR)79,80 machine-learning DFT potential/force based AIMD simulations which reproduced the DFT-based AIMD simulation results in a much faster manner which can be readily extended to other metal cases using universal potential generation. Fig. S5† illustrates that during the AIMD simulations the energy and temperature remain within a small range, indicating the stability of these structures. Our identified mono- and dual-type non-metal doped TM-SACs hold outstanding promise for synthesis.
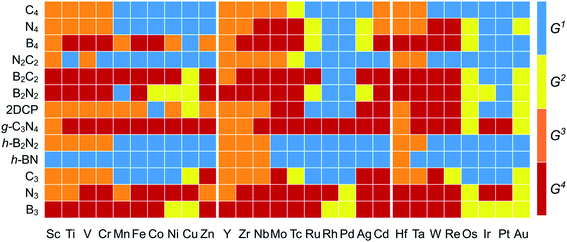 | ||
| Fig. 2 Stability classification of proposed 2D surfaces based on TM embedding over metal bulk cohesive energies (Estab) and electrochemical dissolution potential (Udiss) values (Tables S2 and S3†). Four different classes (G1/G2/G3/G4) of stabilities are represented with (blue/yellow/orange/brown color) [G1: unaggregatable and indissoluble, G2: aggregatable and indissoluble, G3: unaggregatable and dissoluble, G4: aggregatable and dissoluble]. | ||
3.2 HER activity and the reaction mechanism
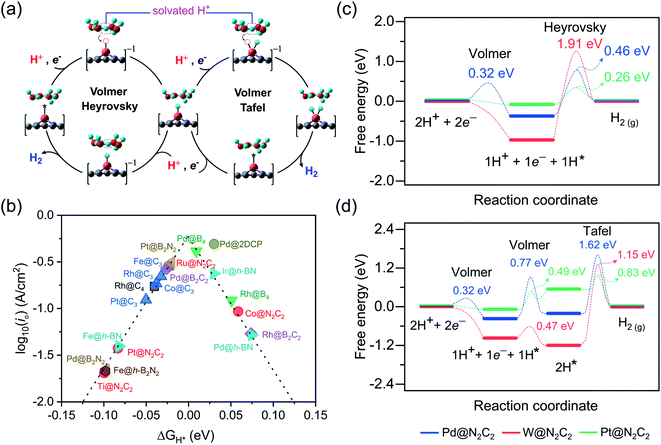
Under standard conditions, the HER may go through two possible mechanistic pathways involving the hydrogen adsorption in the first step through the Volmer reaction (H+ + e− → H* where the asterisk denotes an adsorbed state), and in the second step the H2 desorption takes place through either the Heyrovsky reaction (H* + H+ + e− → H2) or the Tafel reaction pathway (2H* → H2) (Fig. 3a). For an ideal HER electrocatalyst, the Sabatier principle suggests a thermoneutral binding condition i.e. |ΔGH*| = 0 of hydrogen adsorption,81 since too strong or too weak H-adsorption would decrease the overall reaction rate. In order to establish a definite structure–activity relationship, we utilized different active sites and estimated the H-binding strength (ΔEH*) over a wide range of 2D materials (Fig. S3 and S4†). We found that in most of the double vacancy systems H atoms preferentially get adsorbed at the bond edge site (i.e. M–X, X = C, B, N). In the cases of Co/Ni/Cu/Pd/Ag/Pt/Au at C4, Cr/Fe/Co/Ni at B4, Ni/Rh/Pd/Pt at N2C2, Mn/Co/Ni/Cu/Pd/Pt at B2C2, Co/Ni/Cu/Pd/Pt at B2N2 and Mn/Fe/Co/Ni/Cu/Zn/Rh/Pd/Ag/Ir/Pt/Au at h-B2N2 templates, the active site is shared by metal and surface non-metal atoms. In contrast, hydrogen tends to bind at a metal site in all the single vacancy systems. For better understanding of structural properties, we calculated the metal to hydrogen bond distance (dM–H) and the angle (φH–M–Y) between adsorbed hydrogen (H) on a TM atom (M) and H on its first coordinating nearest neighbor non-metal atom (Y) of the 2D support (Tables S6, S7 and Fig. S6, S7†). Compared with the metal top site, we found that H-adsorption at the bond edge site exhibits a shorter bond distance (dM–H) with a smaller bond angle (φH–M–Y), which is also obvious from their optimal ΔEH* values (Table S8†).In order to determine the HER activities, we calculated hydrogen adsorption Gibbs free energies and HER overpotentials (ηHER) for each system and considered the condition of |ΔGH*| ≤ 0.1 eV as a descriptor. Relative to an ideal HER electrocatalyst such as Pt, we compared the HER free energy values of undoped systems with those of their mono- and dual-type non-metal doped templates. The computed ΔGH* values are listed in Table S9† and their relative HER activities are presented in HER free energy diagrams shown in Fig. S8–S12.† To find the high-performance catalysts we plot the volcano curve for the exchange current density (io) as a function of ΔGH* values (Fig. 3b). We have found promising durable catalysts with excellent HER activities (i.e. |ΔGH*| ≤ 0.1 eV) (Table S10†), such as Rh(−0.04) at C4, Rh(0.05)/Pd(0.01) at B4, Ti(−0.10)/Co(0.06)/Ru(−0.02)/Pt(−0.08) at N2C2, Rh(0.07)/Pd(−0.03) at B2C2, Pd(−0.10)/Pt(−0.02) at B2N2, Fe(−0.02)/Co(−0.04)/Rh(−0.03)/Pt(−0.05) at C3, Fe(−0.08)/Pd(0.07)/Ir(0.03) at h-BN and Pd(0.03) at 2DCP. In particular, Pd@B4, Pt@B2N2, Pd@2DCP and Ru@N2C2 have almost thermoneutral H-adsorption Gibbs free energies and are located around the top of the volcano plot.
For getting deep insight into the kinetic aspects of the reaction mechanism, we investigated various TM-SACs and calculated the energy barriers for three elementary reaction steps (Volmer step, Heyrovsky step, and Tafel step) of the HER. By using the climbing-image nudged elastic band (CI-NEB) method, we interpolated seven images between the initial and final states. Herein, we presented the HER mechanism over Pd@N2C2, W@N2C2 and Pt@N2C2 surfaces. Fig. 3a demonstrates the mechanism for each reaction step involved in the HER. Initially, in the Volmer step, we considered a layer of three water molecules over these surfaces along with one hydronium ion (H3O+). The solvated proton82 from the water layer is transferred to the surface and is favorably adsorbed at the Pd–C bond edge site with an activation barrier of 0.32 eV, while W@N2C2 having metal top as the most active site for the HER shows a barrierless first Volmer reaction step. Similarly, Pt@N2C2 having the Pt–C bond edge as the most active site for H adsorption exhibits a barrierless first Volmer reaction step.
In the second step, the hydrogen evolution takes place either by the Heyrovsky or Tafel reaction mechanism. In the Heyrovsky reaction pathway, the solvated proton from the water layer reacts with the adsorbed H atom to form molecular H2, while in the Tafel reaction pathway the two adsorbed H-atoms next to each other react to form a H2 molecule. Fig. 3c and d present the activation barriers and free energy values of Volmer–Heyrovsky and Volmer–Tafel reaction steps for H2 evolution. The calculated energy barriers indicate that after adsorption of the first H-atom, both the second Volmer step and the Heyrovsky reaction step compete with each other to accomplish the HER process. A precise probing of the local atomistic structure revealed that the adsorbed hydrogen may form a Kubas42 type stable dihydrogen complex83 which may change the overall kinetics of the reaction. We found that on Pd@N2C2 and Pt@N2C2 surfaces the second H-atom is adsorbed at the Pd–C and Pt–C bond edge sites in the trans-form. Their first and second adsorbed H-atoms are separated by 3.21 Å and 2.13 Å, which exhibit large activation barriers of 1.62 eV and 0.83 eV, respectively, indicating that the H2 formation through the Tafel reaction pathway is not favorable. In contrast, the W@N2C2 catalyst favors the Volmer–Tafel reaction pathway with an activation barrier of 1.15 eV due to the favored direct migration of adsorbed H-atoms to form molecular H2. These results indicate that the accelerated HER kinetics is tightly associated with the coordination geometry of the active site and the spatial alignment of reaction intermediates, which intimately govern the overall HER performance of catalysts.
3.3 Machine learning modelling
ML is becoming more popular for the semi-automated and quantitative discovery of data correlations in chemistry and materials science.45,61,62,65,84 Although many data-driven strategies are being successfully utilized in heterogeneous catalysis,79,85 ML still remains at an early stage due to numerous underexplored material data for water electrocatalysis. We adopted a stepwise multistage screening strategy for discovering promising electrocatalysts with enhanced HER activities. We employed different ML classification and regression models for the prediction of Estab, Udiss and HER differential Gibbs free energies. Fig. S2† demonstrates our stepwise feature selection strategy and ML protocol for training, testing and validation of different ML models used in this work.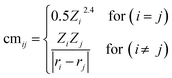 | (9) |
Being a local descriptor, cmij facilitates the comparison of chemical environments around adsorption sites within a certain cutoff radius (rcut). To be constrained specifically on the metal site and its neighboring non-metal active sites we calculated cmij at three cutoff radii (3, 4 and 5 Å). As the Coulomb matrix is symmetric with off-diagonal elements corresponding to the Coulomb repulsion between atoms i and j, while diagonal elements correspond to a polynomial fit of atomic self-energies to nuclear charges, we considered nine Coulomb matrix elements from the upper triangular part of the total-sorted elements within a 4 Å (optimum) rcut. For training our ML models we adopted a stepwise feature selection strategy by taking into account feature–feature correlation and feature importance (Fig. S13†) which are calculated by using the Pearson correlation coefficient and mutual information method, respectively (Fig. 4a and b). Low-ranked features with high feature–feature correlation values (>0.6) are removed from our feature set, and after preprocessing, the final features were imported for training different ML models.
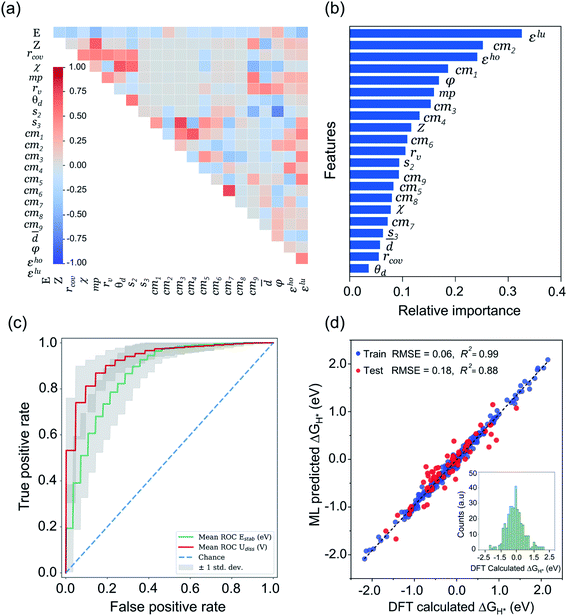 | ||
| Fig. 4 ML analysis for prediction of durable high performing electrocatalysts. (a) The heatmap of Pearson correlation coefficient matrix among the selected 21 features/descriptors (see Tables S11 and S12†). The intensity of colors represents the direct correlation (E: H-adsorption/free energy). (b) The most important features ranking predicted by mutual information (MI) method. (c) Receiver operating characteristic (ROC) curve for ERT-classifier and the corresponding area under the curve (AUC) for classification of Estab and Udiss. The mean ROC is calculated among curves for 100 random splits into the training and validation sets for predicting the thermodynamic and electrochemical stabilities. (d) Comparison of DFT computed ΔGH* values with those of predicted by CatBoost regression model, while the inset of histograms denotes the values calculated by our DFT workflow. | ||
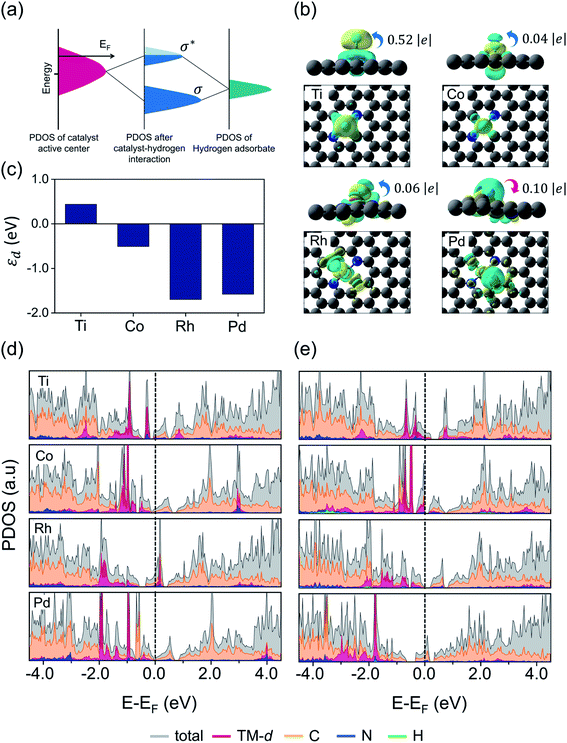
After classifying all the catalysts into stable and unstable classes, in the second step we constructed a ML regression model for the prediction of HER activities. It is worth noting that our input properties for training the ML regression model are ideally available and require only one step calculation of H-adsorbed geometry optimization. For learning the structure–activity relationship we characterized the local atomic and electronic environment of active sites by using various electronic and structural descriptors in combination with the elemental feature set from periodic table properties. Unlike the classification problem, here we used the Coulomb matrix (cmij) descriptor based on DFT-optimized geometries. For training our ML regression model we used a DFT-fitted model with a set of total 21 features, including 6 elemental features (Z: atomic number, rcov: covalent radius, χ: Pauling electronegativity, mp: melting point, rv: radius of the last occupied valence orbital, and θd: unpaired d-electrons), 4 DFT-derived features (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) : average distance from TM to four nearest coordinating atoms, φ: angle between adsorbed hydrogen on TM and the sorted first nearest surface non-metal atom, εho: highest-occupied Kohn–Sham eigenvalue and εlu: lowest-unoccupied Kohn–Sham eigenvalue), 2 SISSO generated features (s2 and & s3) and 9 Coulomb matrix elements (cm1 through cm9). The features presented in Fig. 4a and b are the ones that we finally imported to train different ML regression models. The root-mean-square error (RMSE) and the coefficient of determination values (R2) for each model are demonstrated in Fig. S17.† Among the nine different ML regression models which we tested for prediction of HER activities, the CatBoost regression model exhibited the highest accuracy with 0.18 eV RMSE and 0.88 R2 score. Fig. 4d demonstrates an obvious linear relationship in the whole data set, indicating that the predicted results of the CatBoost regression model are in good agreement with DFT-calculated data. In order to examine the accuracy of our model, we conducted more predictions on 41 stable candidates (see Fig. S15 and S18†). The model predicted that Sc@P3, Fe@P3, Zr@P3, Au@P3, Cr@P4, Mn@P4, Fe@P4, Nb@P4, Mo@P4, Ru@P4 and Ir@P4 are high performance HER electrocatalysts. We further performed DFT calculations for these candidates and compared the results with the ML predicted values (see Table S14†). The small mean square error (0.012 eV) demonstrates the great reliability of our model. To encode the significance of the ML model and interpret the contribution of each feature/descriptor, we adopt the analysis framework of SHAP (Shapley Additive exPlanation).86 The SHAP values provide a deep insight into the prediction results. We computed the SHAP values and mean absolute SHAP values for each feature/descriptor, which are presented in Fig. S19.† It is worth noting that the features εlu, cm2, s2 and φ have the highest mean absolute SHAP values and these features are considered to be more critical in the model and have great impact on the prediction results. The feature values of εlu, cm2 and s2 show a negative correlation with the SHAP values, while φ shows a positive correlation with the SHAP values. The mean absolute SHAP values for cm7, cm8, cm9 and Z demonstrate that these features have the lowest impact on the prediction performance of the model. However, we observed that removal of any single feature from the set of 21 selected features decreases the overall prediction performance. Therefore, it is important to keep all these features for the future prediction analysis of high performance HER catalysts.
: average distance from TM to four nearest coordinating atoms, φ: angle between adsorbed hydrogen on TM and the sorted first nearest surface non-metal atom, εho: highest-occupied Kohn–Sham eigenvalue and εlu: lowest-unoccupied Kohn–Sham eigenvalue), 2 SISSO generated features (s2 and & s3) and 9 Coulomb matrix elements (cm1 through cm9). The features presented in Fig. 4a and b are the ones that we finally imported to train different ML regression models. The root-mean-square error (RMSE) and the coefficient of determination values (R2) for each model are demonstrated in Fig. S17.† Among the nine different ML regression models which we tested for prediction of HER activities, the CatBoost regression model exhibited the highest accuracy with 0.18 eV RMSE and 0.88 R2 score. Fig. 4d demonstrates an obvious linear relationship in the whole data set, indicating that the predicted results of the CatBoost regression model are in good agreement with DFT-calculated data. In order to examine the accuracy of our model, we conducted more predictions on 41 stable candidates (see Fig. S15 and S18†). The model predicted that Sc@P3, Fe@P3, Zr@P3, Au@P3, Cr@P4, Mn@P4, Fe@P4, Nb@P4, Mo@P4, Ru@P4 and Ir@P4 are high performance HER electrocatalysts. We further performed DFT calculations for these candidates and compared the results with the ML predicted values (see Table S14†). The small mean square error (0.012 eV) demonstrates the great reliability of our model. To encode the significance of the ML model and interpret the contribution of each feature/descriptor, we adopt the analysis framework of SHAP (Shapley Additive exPlanation).86 The SHAP values provide a deep insight into the prediction results. We computed the SHAP values and mean absolute SHAP values for each feature/descriptor, which are presented in Fig. S19.† It is worth noting that the features εlu, cm2, s2 and φ have the highest mean absolute SHAP values and these features are considered to be more critical in the model and have great impact on the prediction results. The feature values of εlu, cm2 and s2 show a negative correlation with the SHAP values, while φ shows a positive correlation with the SHAP values. The mean absolute SHAP values for cm7, cm8, cm9 and Z demonstrate that these features have the lowest impact on the prediction performance of the model. However, we observed that removal of any single feature from the set of 21 selected features decreases the overall prediction performance. Therefore, it is important to keep all these features for the future prediction analysis of high performance HER catalysts.
4. Conclusion
In summary, by means of the DFT combined ML framework, we demonstrated that mono- or dual-type non-metal (B, N & P) doping in a proper choice of support (g-C3N4, 2DCP, graphene and hexagonal boron nitride) can substantially enhance the HER activity and stability. In order to unveil the structure–activity relationship, we constructed various kinds of electronic and geometric descriptors which work universally for these systems. Our descriptors for prediction of stabilities are easily accessible and exclusively based on elemental properties, however for the prediction of HER activities we used the H-adsorbed converged geometry for creating Coulomb matrix elements. Besides this we also employed a SISSO method to create more feature space. Based on our ML analysis we found that ERT-Extremely Randomized Trees classifier showed the best ROC-AUC scores of 0.87 and 0.93 for the prediction of Estab, and Udiss, respectively, while the CatBoost regression model predicted the HER activities with a minimum test RMSE of 0.18 eV and 0.88 R2 score. Moreover, through our DFT analysis we elucidated the potential dependence of the coordination environment and charge transfer behavior on activation energy values of different reaction mechanisms of the HER. Out of ∼364 catalysts, we found 20 most promising catalysts which exhibited excellent stabilities and superior activities toward the HER. Particularly, Pd@B4, Ru@N2C2, Pd@B2C2, Pt@B2N2, Ir@h-BN, Fe@C3, Rh@C3, and Pd@2DCP and ML-recommended systems Fe@P3, Mn@P4 and Fe@P4 exhibited an ultra-small magnitude of the HER overpotential (ηHER ≅ −0.01 to −0.03 V), much better than that of commercial Pt based catalysts. We believe that our established DFT based ML framework should be equally applicable to other 2D systems and spur both theoretical and experimental research in a wider effort to explore ideal HER catalysts.Author contributions
M. U. performed the DFT calculations and ML analysis. S. U. helped in ML analysis. M. Z., M. H., A. R. A. H. and A. A. helped in analysis. M. U. drafted the manuscript and K. S. K. revised it. G. L. and K. S. K. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Basic Science Research Program (2021R1I1A1A01050280, 2021R1I1A1A01050085, 2021R1A2C1006039 and 2019R1A4A1029237) through National Research Foundation of Korea (NRF) funded by the Ministry of Education. It was also supported by the A.I. Incubation Project Fund (1.210091.01) of UNIST (Ulsan National Institute of Science & Technology). The supercomputing resources including technical support are from the National Supercomputing Center KISTI (KSC-2021-CRE-0193, and KSC-2020-CRE-0146).References
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- G. Glenk and S. Reichelstein, Nat. Energy, 2019, 4, 216–222 CrossRef CAS.
- Y. Yang, Y. Qian, H. Li, Z. Zhang, Y. Mu, D. Do, B. Zhou, J. Dong, W. Yan and Y. Qin, Sci. Adv., 2020, 6, eaba6586 CrossRef CAS PubMed.
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- J. N. Tiwari, N. K. Dang, S. Sultan, P. Thangavel, H. Y. Jeong and K. S. Kim, Nat. Sustain., 2020, 3, 556–563 CrossRef.
- S. Cobo, J. Heidkamp, P.-A. Jacques, J. Fize, V. Fourmond, L. Guetaz, B. Jousselme, V. Ivanova, H. Dau and S. Palacin, Nat. Mater., 2012, 11, 802–807 CrossRef CAS PubMed.
- A. Le Goff, V. Artero, B. Jousselme, P. D. Tran, N. Guillet, R. Métayé, A. Fihri, S. Palacin and M. Fontecave, Science, 2009, 326, 1384–1387 CrossRef CAS PubMed.
- M. Li, Q. Ma, W. Zi, X. Liu, X. Zhu and S. F. Liu, Sci. Adv., 2015, 1, e1400268 CrossRef PubMed.
- N. K. Dang, M. Umer, P. Thangavel, S. Sultan, J. N. Tiwari, J. H. Lee, M. G. Kim and K. S. Kim, J. Mater. Chem. A, 2021, 9, 16898–16905 RSC.
- A. M. Harzandi, S. Shadman, M. Ha, C. W. Myung, D. Y. Kim, H. J. Park, S. Sultan, W.-S. Noh, W. Lee and P. Thangavel, Appl. Catal., B, 2020, 270, 118896 CrossRef CAS.
- H. Jin, S. Sultan, M. Ha, J. N. Tiwari, M. G. Kim and K. S. Kim, Adv. Funct. Mater., 2020, 30, 2000531 CrossRef CAS.
- S. Sultan, M. H. Diorizky, M. Ha, J. N. Tiwari, H. Choi, N. K. Dang, P. Thangavel, J. H. Lee, H. Y. Jeong and H. S. Shin, J. Mater. Chem. A, 2021, 9, 10326–10334 RSC.
- J. N. Tiwari, N. K. Dang, H. J. Park, S. Sultan, M. G. Kim, J. Haiyan, Z. Lee and K. S. Kim, Nano Energy, 2020, 78, 105166 CrossRef CAS.
- L. A. King, M. A. Hubert, C. Capuano, J. Manco, N. Danilovic, E. Valle, T. R. Hellstern, K. Ayers and T. F. Jaramillo, Nat. Nanotechnol., 2019, 14, 1071–1074 CrossRef CAS PubMed.
- A. Bruix, J. T. Margraf, M. Andersen and K. Reuter, Nat. Catal., 2019, 2, 659–670 CrossRef CAS.
- S. Anantharaj, S. R. Ede, K. Sakthikumar, K. Karthick, S. Mishra and S. Kundu, ACS Catal., 2016, 6, 8069–8097 CrossRef CAS.
- S. Sultan, J. N. Tiwari, A. N. Singh, S. Zhumagali, M. Ha, C. W. Myung, P. Thangavel and K. S. Kim, Adv. Energy Mater., 2019, 9, 1900624 CrossRef.
- J. N. Tiwari, A. N. Singh, S. Sultan and K. S. Kim, Adv. Energy Mater., 2020, 10, 2000280 CrossRef CAS.
- S. Li, B. Chen, Y. Wang, M.-Y. Ye, P. A. van Aken, C. Cheng and A. Thomas, Nat. Mater., 2021, 1–8 Search PubMed.
- C. Eames and M. S. Islam, J. Am. Chem. Soc., 2014, 136, 16270–16276 CrossRef CAS PubMed.
- A. Fischer, J. O. Müller, M. Antonietti and A. Thomas, ACS Nano, 2008, 2, 2489–2496 CrossRef CAS PubMed.
- J. N. Tiwari, A. M. Harzandi, M. Ha, S. Sultan, C. W. Myung, H. J. Park, D. Y. Kim, P. Thangavel, A. N. Singh and P. Sharma, Adv. Energy Mater., 2019, 9, 1900931 CrossRef.
- M. B. Stevens, M. E. Kreider, A. M. Patel, Z. Wang, Y. Liu, B. M. Gibbons, M. J. Statt, A. V. Ievlev, R. Sinclair, A. Mehta, R. C. Davis, J. K. Nørskov, A. Gallo, L. A. King and T. F. Jaramillo, ACS Appl. Energy Mater., 2020, 3, 12433–12446 CrossRef CAS.
- F. Yu, H. Zhou, Y. Huang, J. Sun, F. Qin, J. Bao, W. A. Goddard, S. Chen and Z. Ren, Nat. Commun., 2018, 9, 1–9 CrossRef PubMed.
- W. Cheng, H. Zhang, D. Luan and X. W. D. Lou, Sci. Adv., 2021, 7, eabg2580 CrossRef CAS PubMed.
- C. Wang and L. Qi, Angew. Chem., Int. Ed., 2020, 59, 17219–17224 CrossRef CAS PubMed.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- A. N. Singh, M. H. Kim, A. Meena, T. U. Wi, H. W. Lee and K. S. Kim, Small, 2021, 17, 2005605 CrossRef CAS PubMed.
- P. Zhai, M. Xia, Y. Wu, G. Zhang, J. Gao, B. Zhang, S. Cao, Y. Zhang, Z. Li and Z. Fan, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed.
- H.-Y. Zhuo, X. Zhang, J.-X. Liang, Q. Yu, H. Xiao and J. Li, Chem. Rev., 2020, 120, 12315–12341 CrossRef CAS PubMed.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS.
- S. Bai, M. Yang, J. Jiang, X. He, J. Zou, Z. Xiong, G. Liao and S. Liu, npj 2D Mater. Appl., 2021, 5, 1–15 CrossRef.
- A. Bhat, S. Anwer, K. S. Bhat, M. I. H. Mohideen, K. Liao and A. Qurashi, npj 2D Mater. Appl., 2021, 5, 1–21 CrossRef.
- R. Anand, A. S. Nissimagoudar, M. Umer, M. Ha, M. Zafari, S. Umer, G. Lee and K. S. Kim, Adv. Energy Mater., 2021, 2102388 CrossRef CAS.
- M. Wu and X. C. Zeng, Nano Lett., 2016, 16, 3236–3241 CrossRef CAS PubMed.
- Z. Zhuang, Y. Li, Z. Li, F. Lv, Z. Lang, K. Zhao, L. Zhou, L. Moskaleva, S. Guo and L. Mai, Angew. Chem., 2018, 130, 505–509 CrossRef.
- F. K. Kessler, Y. Zheng, D. Schwarz, C. Merschjann, W. Schnick, X. Wang and M. J. Bojdys, Nat. Rev. Mater., 2017, 2, 1–17 Search PubMed.
- X. Chia and M. Pumera, Nat. Catal., 2018, 1, 909–921 CrossRef CAS.
- D. Y. Kim, M. Ha and K. S. Kim, J. Mater. Chem. A, 2021, 9, 3511–3519 RSC.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- C. Zhou, J. Y. Zhao, P. F. Liu, J. Chen, S. Dai, H. G. Yang, P. Hu and H. Wang, Chem. Sci., 2021, 12, 10634–10642 RSC.
- M. Ha, D. Y. Kim, M. Umer, V. Gladkikh, C. W. Myung and K. S. Kim, Energy Environ. Sci., 2021, 14, 3455–3468 RSC.
- M. D. Hossain, Z. Liu, M. Zhuang, X. Yan, G. L. Xu, C. A. Gadre, A. Tyagi, I. H. Abidi, C. J. Sun and H. Wong, Adv. Energy Mater., 2019, 9, 1803689 CrossRef.
- X. Guo, S. Lin, J. Gu, S. Zhang, Z. Chen and S. Huang, ACS Catal., 2019, 9, 11042–11054 CrossRef CAS.
- M. Zafari, D. Kumar, M. Umer and K. S. Kim, J. Mater. Chem. A, 2020, 8, 5209–5216 RSC.
- C. Liu, Q. Li, C. Wu, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, J. Am. Chem. Soc., 2019, 141, 2884–2888 CrossRef CAS PubMed.
- M. Zafari, A. S. Nissimagoudar, M. Umer, G. Lee and K. S. Kim, J. Mater. Chem. A, 2021, 9, 9203–9213 RSC.
- C. Ling, Y. Zhang, Q. Li, X. Bai, L. Shi and J. Wang, J. Am. Chem. Soc., 2019, 141, 18264–18270 CrossRef CAS PubMed.
- V. V. Voronin, M. S. Ledovskaya, A. S. Bogachenkov, K. S. Rodygin and V. P. Ananikov, Molecules, 2018, 23, 2442 CrossRef PubMed.
- D. Chakraborty, C. D. Damsgaard, H. Silva, C. Conradsen, J. L. Olsen, H. W. Carvalho, B. Mutz, T. Bligaard, M. J. Hoffmann and J. D. Grunwaldt, Angew. Chem., 2017, 129, 8837–8841 CrossRef.
- Y. Jiao, Y. Zheng, K. Davey and S.-Z. Qiao, Nat. Energy, 2016, 1, 1–9 Search PubMed.
- J.-Q. Chi, X.-Y. Zhang, X. Ma, B. Dong, J.-Q. Zhang, B.-Y. Guo, M. Yang, L. Wang, Y.-M. Chai and C. Liu, ACS Sustainable Chem. Eng., 2019, 7, 17714–17722 CrossRef CAS.
- J. Wan, Z. Zhao, H. Shang, B. Peng, W. Chen, J. Pei, L. Zheng, J. Dong, R. Cao and R. Sarangi, J. Am. Chem. Soc., 2020, 142, 8431–8439 CrossRef CAS PubMed.
- X. Guo, J. Gu, X. Hu, S. Zhang, Z. Chen and S. Huang, Catal. Today, 2020, 350, 91–99 CrossRef CAS.
- G. Galeotti, F. De Marchi, E. Hamzehpoor, O. MacLean, M. R. Rao, Y. Chen, L. Besteiro, D. Dettmann, L. Ferrari and F. Frezza, Nat. Mater., 2020, 19, 874–880 CrossRef CAS PubMed.
- A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- M. Grewer and R. Birringer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 184108 CrossRef.
- Q. Zhou, S. Lu, Y. Wu and J. Wang, J. Phys. Chem. Lett., 2020, 11, 3920–3927 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. Von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- G. Zheng, Y. Li, X. Qian, G. Yao, Z. Tian, X. Zhang and L. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 16336–16344 CrossRef CAS PubMed.
- M. O. Jäger, E. V. Morooka, F. F. Canova, L. Himanen and A. S. Foster, npj Comput. Mater., 2018, 4, 1–8 CrossRef.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- M. Dwass, Ann. Math. Stat., 1957, 181–187 CrossRef.
- J. Greeley and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5829–5836 CrossRef CAS.
- X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721 CrossRef CAS PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- A. Hajibabaei and K. S. Kim, J. Phys. Chem. Lett., 2021, 12, 8115–8120 CrossRef CAS PubMed.
- A. Hajibabaei, C. W. Myung and K. S. Kim, Phys. Rev. B, 2021, 103, 214102 CrossRef CAS.
- P. Sabatier, Chem. Ber., 1911, 44, 1984–2001 CrossRef CAS.
- M. Park, I. Shin, N. J. Singh and K. S. Kim, J. Phys. Chem., 2007, 111, 10692–10702 CrossRef CAS PubMed.
- G. Di Liberto, L. A. Cipriano and G. Pacchioni, J. Am. Chem. Soc., 2021, 143(48), 20431–20441 CrossRef CAS PubMed.
- X. Wang, S. Ye, W. Hu, E. Sharman, R. Liu, Y. Liu, Y. Luo and J. Jiang, J. Am. Chem. Soc., 2020, 142, 7737–7743 CrossRef CAS PubMed.
- A. Abbas, L. Boithias, Y. Pachepsky, K. Kim, J. A. Chun and K. H. Cho, Geosci. Model Dev. Discuss., 2021, 1–29 Search PubMed.
- S. M. Lundberg, G. Erion, H. Chen, A. DeGrave, J. M. Prutkin, B. Nair, R. Katz, J. Himmelfarb, N. Bansal and S.-I. Lee, Nature Machine Intelligence, 2020, 2, 56–67 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta09878k |
| This journal is © The Royal Society of Chemistry 2022 |