Peculiar anharmonicity of Ruddlesden Popper metal halides: temperature-dependent phonon dephasing†
Esteban
Rojas-Gatjens
 a,
Carlos
Silva-Acuña‡
a,
Carlos
Silva-Acuña‡
 *abc and
Ajay Ram Srimath
Kandada
*abc and
Ajay Ram Srimath
Kandada
 *d
*d
aSchool of Chemistry and Biochemistry, Georgia Institute of Technology, 901 Atlantic Drive, Atlanta, Georgia 30332, USA. E-mail: carlos.silva@gatech.edu
bSchool of Physics, Georgia Institute of Technology, 837 State Street, Atlanta, Georgia 30332, USA
cSchool of Materials Science and Engineering, Georgia Institute of Technology, North Avenue, Atlanta, GA 30332, USA
dDepartment of Physics and Center for Functional Materials, Wake Forest University, 1834 Wake Forest Road, Winston-Salem, NC 27109, USA. E-mail: srimatar@wfu.edu
First published on 9th December 2021
Abstract
The anharmonicity of the Ruddlesden Popper metal-halide lattice, and its consequences for their electronic and optical properties, are paramount in their basic semiconductor physics. It is thus critical to identify specific anharmonic optical phonons that govern their photophysics. Here, we address the nature of phonon–phonon scattering probabilities of the resonantly excited optical phonons that dress the electronic transitions in these materials. Based on the temperature dependence of the coherent phonon lifetimes, we isolate the dominant anharmonic phonon and quantify its phonon–phonon interaction strength. Intriguingly, we also observe that the anharmonicity is distinct for different phonons, with a few select modes exhibiting temperature-independent coherence lifetimes, indicating their predominantly harmonic nature. However, the population and dephasing dynamics of excitons are dominated by the anharmonic phonon.
New conceptsElectron–phonon interactions govern several key characteristics of semiconductors, including the transport parameters, recombination rates and quantum dynamics. It is common to formulate such interactions under the harmonic approximation, especially in crystalline semiconductors, where the lattice displacement is considered to be negligible in the presence of the carrier. Such a weak-coupling treatment of the large polaron, termed as the Fröhlich framework, assumes that the anharmonic component of the vibrational potential has no consequences in the polaron dynamics. Here, we present a quantitative relationship between the temperature dependent phonon dephasing dynamics and polaron coupling mechanisms in a prototypical layered metal halide perovskites and highlight the limitations of such a treatment. Consequently, we establish an experimental basis to go beyond the Fröhlich framework to explain the electron–phonon interactions in Ruddlesden Popper metal halides. Moreover, the consequence of phonon–phonon interactions on excitonic characteristics is often under-explored by existing research. This study in conjunction with our previous works establishes the critical role of lattice anharmonicity in the coherent nonlinear dynamics of excitons. |
1 Introduction
The ionic lattice of metal-halide perovskites is a deterministic component of their photophysical behaviour.1 The lattice dynamics are mostly driven by multiple optical phonons in the 1–10 meV energy range and acoustic phonon modes at energies <2 meV.2 The optical phonons, in particular, have been identified to play a critical role in the electronic dynamics via strong polaronic coupling mechanisms.3 The consequences of the strong phonon interactions in the structural stabilization,4 carrier thermalization,5 carrier recombination,6,7 carrier transport8,9 and dephasing dynamics10,11 are widely reported. The acoustic modes, on the other hand, determine the thermal properties of the material, including thermal conductivity, molar specific heat, and thermal expansion of the lattice. These are clear manifestations of the anharmonicity of the lattice, models for which are available in any basic textbook for solid-state physics such as ref. 12. The distinction of metal-halide perovskites from classical semiconductors lies, however, in the softness of the lattice and rather large anharmonicity induced by substantially high multi-phonon scattering probabilities.1,13 In addition, the non-polar dynamic fluctuations from the independent motion of the organic cation2,14 lead to a rapid escalation of the complexity of the microscopic picture of the carrier-lattice dynamics, where the polaronic nature of the material is described as an interplay between long (Fröhlich-like) and short range (dynamic disorder) carrier-lattice coupling.8A similar photophysical scenario can be identified in other derivatives of metal-halide perovskites, including layered two-dimensional systems such as the Ruddlesden–Popper (RP) metal halides.15,16 However, given the globally neutral character of excitons that are the primary photo-excitation in these systems, one might expect a diminished role for the Coulomb-mediated polaron coupling.17 We have previously highlighted, on the contrary, the critical role played by the phonon interactions in various exciton dynamics using a number of unambiguous experimental observations. We demonstrated that distinct excitonic states are distinctly phonon-dressed,18 elastically scattered19 and coupled non-adiabatically to the lattice phonons.20 We have also suggested that the photoexcitations must, in fact, be treated within the exciton polaron framework.17,18,21 As a corollary to this hypothesis, one may expect to perceive the seemingly independent many-body dynamics of phonons in the dynamics of exciton polarons.
For example, consider the thermal dephasing of excitons, which is primarily driven by the elastic scattering of a coherent exciton population with the thermally populated phonons. If the coherent population is that of exciton polarons, then the thermal dephasing of phonons (in other words, phonon–phonon interactions driven by the anharmonicty of the polaron dressing phonons) will also contribute to the elastic scattering. The models used to fit the temperature dependence of the exciton dephasing rates or the exciton linewidths do not, however, consider phonon–phonon scattering explicitly. Moreover, direct observations of the structural dynamics and lattice anharmonicity in RP metal halides are missing.
In this manuscript, we provide an experimental measurement of the anharmonicity of optical phonons in phenethylammonium lead iodide ((PEA)2PbI4, Fig. 1(a)), a prototypical Ruddlesden–Popper metal halide, by analysing the temperature dependence of the dynamics of impulsively generated coherent phonons. We clearly identify the co-existence of a dominant anharmonic mode with energy of 4.40 meV and various harmonic phonons, the most important one with energy 2.61 meV. We attribute the anharmonic behaviour of the 4.40 meV mode to its decay into two lower-energy acoustic phonons via a three-phonon interaction mechanism, as has been reported in other polar semiconductors.22,23 This mechanism has a direct influence on the exciton dephasing rates, especially at higher temperatures. We compare the strength of the anharmonicity of the dominant phonon with that in other semiconductors, and find that it approaches values found in the most highly anharmonic lattices such as SrTiO3.
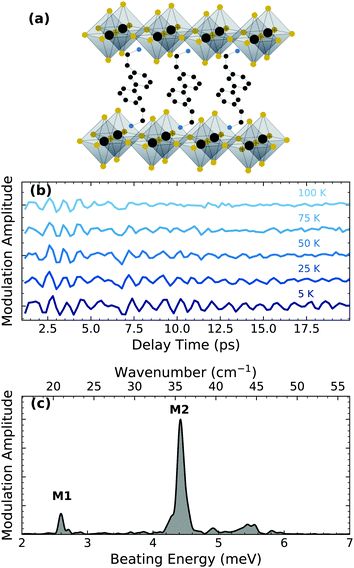 | ||
| Fig. 1 (a) (PEA)2PbI4 structure with Pb (grey), I (yellow), C (black) and N (blue). The hydrogen atoms are omitted for simplicity. (b) Oscillatory component of the ultrafast differential transmission experiment at distinct temperatures. Data extracted from ref. 18. (c) Cumulative RISRS spectrum measured at 5 K. | ||
2 Results and discussion
In this work, we analyze the temperature dependence of the coherent phonon dynamics reported previously in ref. 18. Fig. 1(b) shows the periodic modulations observed in the ultrafast differential transmission experiment (details in ESI†) by photo-exciting the free carriers at 3.06 eV with a train of ultrashort optical pulses at sample temperatures ranging over 5–100 K. Note that no first-order phase transitions are present within this temperature range.24,25 These periodic modulations of the optical absorption of the sample are the signatures of coherent phonons generated by resonant impulsive stimulated Raman scattering (RISRS). Briefly, the ultrashort optical pulse generates a coherent wavepacket – a superposition state of phonon modes that are excited with a common phase – and cause a coherent lattice motion. The coherent motion influence the complex refractive index which modulates the differential transmission. An exhaustive description of the physical processes responsible for the generation of the coherent wavepacket can be found in ref. 26. The intensity of transmission modulation reduces with time due to the dephasing of the coherent phonon population. The dephasing rate becomes faster at higher temperatures, indicating that the scattering with the thermally-generated incoherent phonon population is the primary dephasing mechanism. The RISRS spectrum at 5 K, shown in Fig. 1(c), is obtained by taking the Fourier transform of the time dynamics (the temperature dependence of the RISRS spectrum is shown in the ESI†). Two dominant phonon modes are clearly observed, labelled M1 at 2.61 meV and M2 at 4.40 meV, in addition to a few modes between 5–6 meV. All the observed phonons have been previously assigned to the lattice vibrations predominantly within the lead iodide layer.18 Specifically, M1 and M2 correspond to octahedral twisting along one of pseudocubic axes and octahedral twist and Pb–I–Pb bending, respectively (see ref. 18 for details of the assignment).It is worth noting that M1–M6 (assigned in the ref. 18) correspond to the modes coupled to electronic transitions, identified in the resonant excitation condition. There are several other lattice modes at higher energies, including those involving vibrations of the organic cation, which have been identified previously under non-resonant conditions27,28 and thus are not relevant for the polaronic coupling of charge carriers. Accordingly, we limit ourselves to these low energy modes. Even among M1–M6, only M1 and M2 are dominant dressing modes for the free carriers, evident from their larger spectral intensity.
The temperature dependence of the dephasing rates of M1 and M2 reflects differences in their multi-phonon interactions. While one can fit the experimental dynamics to several damped oscillators to estimate the coherence lifetimes of each of the modes, the large number of fitting parameters and possible energy shifts that cannot be rigorously accounted make the fitting routine unreliable. We instead implement a continuous wavelet transform (CWT) approach based on a complex Morlet wavelet29 (the details are presented in ESI†) to analyze and visualize the coherence evolution in time for each of the individual modes. The wavelet transformation decomposes the impulsive oscillatory signals allowing time-frequency visualization. This was described in detail by Staszewski for simulated examples of multi-component impulsive responses.30 Briefly, the CWT transform of an oscillatory function generates two-dimensional spectra, shown in Fig. 3 for selected temperatures, where the normalized amplitude is plotted as a function of the beating energy and the pump–probe delay. The complete range of temperatures studied can be found in the ESI.† The amplitude of the observed modes represents the modulation depth in the differential transmission experiment and correlates directly with the intensity of the RISRS spectrum of Fig. 1(c). We observe that, for all observed modes, it decays in tens of picoseconds at all temperatures.
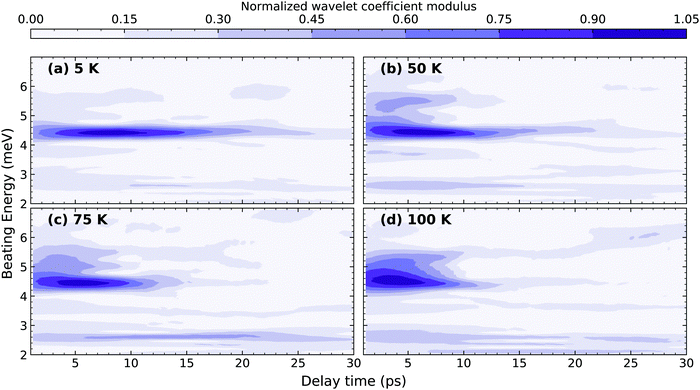 | ||
| Fig. 2 Wavelet transformation (CWT) spectra of the time-domain RISRS data with a complex Morlet wavelet at (a) 5 K, (b) 50 K, (c) 75 K and (d) 100 K. The amplitude axis corresponds to the modulus of the wavelets coefficients, as defined in ESI.† | ||
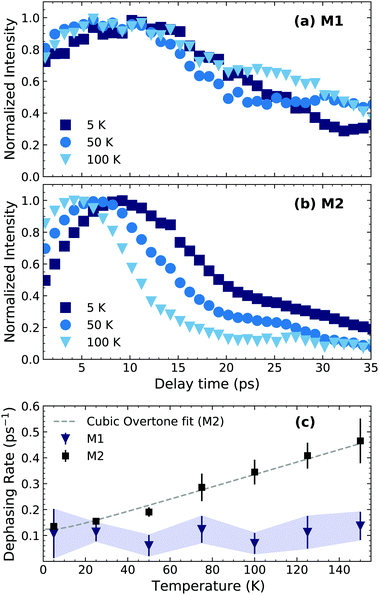 | ||
| Fig. 3 CWT amplitude cut at beating energies (a) 2.61 meV (M1) and (b) 4.40 meV (M2) at different temperatures. (c) Dependence of the dephasing time of M1 and M2 with temperature. The dashed line is a fit to eqn (2) with γ0 = 0.030 ± 0.005 ps−1 and Γ0 = 0.09 ± 0.02 ps−1. The M1 dephasing rate was estimated as the time taken for the signal to reach 1/e of its maximum value and the error bars limits as 1/e ± 0.2. | ||
We first focus on the most prominent feature at a beating energy of 4.40 meV, which corresponds to the mode M2. Qualitatively, it can be noted that as the temperature increases the mode amplitude decays at a faster rate. This can be qualitatively explained by the increased probability of elastic many-body interactions with a thermally generated incoherent phonon population. We also observe that the relative amplitude of M2 decreases at higher temperatures in comparison to the other modes, which can also be observed in the temperature-dependent resonant Raman spectra (Fig. SI1, ESI†). On the other hand, mode M1 (2.61 meV) presents a very different scenario in which its dynamics are not sensitive to the temperature, at least within the temperature range of the measurement. This implies a significantly different anharmonic interaction potential for M1 compared to M2. To further highlight the differences between M1 and M2, kinetic traces at their energies, at selected temperatures, are shown at Fig. 3(a and b). The amplitude of M2 decays exponentially with a clear temperature-dependent dynamics. The effective lifetime of this mode can be estimated via mono-exponential fits; the inverse of the decay time constant is plotted in Fig. 3(c) for all the temperatures. The amplitude of M1, on the contrary, exhibits a non-exponential, temperature-independent decay. An effective lifetime can be estimated, for the sake of comparison, as the time taken for the signal to reach 1/e of its maximum value. The corresponding values of dephasing rate are shown in Fig. 3(c). The difference in the temperature dependence of M1 and M2 is further evidenced here. Additionally, in Fig. SI9 (ESI†), we show the time-integrated spectrum between 5–10 and 10–15 ps. From this data it is clear that M1 dominates at longer times and at higher temperatures.
As noted earlier, the temperature dependence of the phonon dephasing dynamics is interpreted as a consequence of phonon–phonon interactions that are mediated by the anharmonicity of the lattice. The latter was theoretically modelled as a third-order anharmonic Hamiltonian considering three-phonon interactions, which reads as:22,23
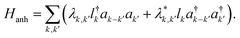 | (1) |
Here λk,k′ is the phonon–phonon coupling, lk and ak′ represent the quantum operators that destroy optical and acoustic phonons respectively. The dispersion relations for optical and acoustic phonons, respectively, are characterised by ωLO(k) and ωLA(k′). This model includes phonon downconversion – decay of the generated longitudinal optical phonon into two lower energy acoustic phonons and upconversion – fusion of two acoustic phonons to generate one optical phonon. Both these processes when conserving both energy and momentum act as plausible pathways for the phonon decoherence. In the case of (PEA)2PbI4, the higher-energy phonons correspond to localized, dispersionless vibrations of the organic moiety25,31 and it is unlikely that such an upconversion process will conserve momentum. Thus, we only consider downconversion processes as the primary dephasing mechanisms. It is worth noting that four-phonon interactions, where the phonon decays into three or more phonons, are also plausible decay pathways; however, these are not significant at low temperatures.32,33 Hence, we consider the simplest case of downconversion of the optical phonon into two acoustic phonons of equal energy, referred to as the cubic overtone model. We disregard any constraints from the wavevector mismatch, but we do note that this mechanism can be expected given the measured phonon dispersion for similar metal-halide derivatives.34 Moreover, the polycrystalline nature of the thin film studied here, with grain sizes of hundreds of nanometers, might compromise the long range lattice order as perceived by phonons, thus relaxing the momentum conservation condition and reducing the relevance of wavevector mismatch. In such a scenario, the anharmonic potential results in a dephasing rate Γ which can be written as:
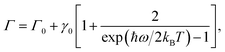 | (2) |
In Table 1 we compare the anharmonicity constants of different materials reported in the literature with that of (PEA)2PbI4 determined in this work. We tabulate the materials going from covalent to strongly ionic systems, thus moving towards strongly anharmonic lattices. However, it is evident that there is no apparent trend in the value of γ0. Given that we are comparing phonons of varying softness, and for our comparison to be independent of the phonon energy, we calculate a dimensionless parameter – ω/2πγ0, which is the ratio of the frequency of the phonon and the anharmonicity constant. We interpret this parameter as the average number of cycles in the phonon oscillation before the phonon encounters a scattering event with another phonon. We clearly observe an increase in the value of this parameter with increasing ionicity of the material. In single-layer MoS2, the optical phonon is fairly immune to thermal dephasing, while in GaAs, which is a slightly polar compound, the phonon scatters in about 80 oscillation cycles. Optical phonons in inorganic lead-halide perovskite nanocrystals appear to have comparable anharmonicity to that of GaAs, although the presence of an organic cation is most likely to reduce ω/2πγ0. We observe much higher anharmonicity in (PEA)2PbI4 with ω/2πγ0 comparable to that of strongly ionic solids such as SrTiO3.
| Material | α F (—) | ħω (meV) | γ 0 × 102 (ps−1) | ω/2πγ0 (—) | Ref. |
|---|---|---|---|---|---|
| a Specific value is not reported, this range reported covers distinct lead-halide perovskites with similar compositions. | |||||
| MoS2 | — | 47.6 | 1.6 | 1000 | 38 |
| GaAs | 0.068 | 36.6 | 11 | 83 | 39,40 |
| CsPbCl3 NCs | ∼1–2a | 4.46 | 1.5 | 71 | 35,41,42 |
| 9.42 | 4.8 | 48 | |||
| 11.78 | 4.2 | 67 | |||
| (PEA)2PbI4 | 2.2 | 4.40 | 3.0 ± 0.5 | 33 | This work |
| 2.61 | — | — | 21 | ||
| SrTiO3 | 4.5 | 5.58 | 8.0 | 12 | 40,43 |
| 1.65 | 1.5 | 27 | |||
As we have already discussed, in Fig. 3 the mode M1 exhibits weak temperature dependence and thus we deduce a very low degree of anharmonicity. One could rationalize this with the cubic overtone model, wherein M1 does not have access to two acoustic modes of exactly half its energy. This claim can be qualitatively substantiated through the density of states for acoustic phonons of low frequency in isotropic media, which can be shown to scale as ω2, where ħω is the energy of the acoustic phonon.12 This suggests that M1 will have access to a lower density of acoustic phonons and thus, will be less likely to undergo downconversion. Similar scenarios have been proposed for CsPbBr3, where a higher density of states, between 1–3 THz, increase the dephasing rate in comparison to lower energy modes.44 Similarly, for (n-butylammonium)2PbI4 the phonon lifetime was calculated to be higher at lower frequencies following an ω−2 trend.34 This interpretation relies on the assumption of M1 decaying into two acoustic phonons of similar energy. However, different pathways including phonons of higher energy with larger density of states might also be plausible. It is imperative here to have detailed knowledge of the entire dispersion of the low-energy acoustic phonons to obtain better insight into the different scattering pathways that are energetically allowed and that obey momentum conservation. Unfortunately, such data is not yet available for Ruddlesden–Popper metal halides.
The disparity in the dynamics of M1 and M2 can also be rationalized by invoking the dipolar nature of the lattice vibrations. Due to the polar character of the lattice, asymmetric phonon modes may be perceived as oscillating dipoles45 and, accordingly, phonon–phonon interactions as dipolar. Based on the assignment of M1 and M2 presented in ref. 18, we recall that M1 primarily involves the motion of the iodide ions while M2 has a substantial additional contribution from the motion of the lead ion around its equilibrium position. This indicates that the M2 mode, with its larger asymmetry, can induce larger lattice dipoles, and accordingly acquires greater anharmonicity. More detailed modelling of the lattice motion combining first-principles calculations and molecular dynamics, albeit being computationally expensive, can offer pertinent insights in this context.
It is worth noting that the anharmonic phonon M2 was observed to play deterministic role in the polaranic interactions of carriers and excitons in these materials. Such interactions are typically treated within the Fröhlich framework, which considers weak coupling of electronic excitations with harmonic lattice vibrations although its applicability in metal-halide perovskites has been questioned.8,17 This approximation can be interpreted as minimal displacement of the atoms from their equilibrium in the presence of a charge, resulting in an effective interaction potential which can be considered to be quadratic close to the zero-point and away from the anharmonic deviations. As one moves progressively from the large polaron limit, which is characterized by coupling constant, αF<1, towards the strong coupling limit of small polarons, the contribution from the anharmonic parts of the vibrational potential become more relevant to the non-adiabatic electron–phonon interactions.
In Table 1, we also show the Fröhlich coupling constants (αF), which relates to the size of the polaron in different materials. We note a clear anti-correlation between αF and the anharmonic parameter (ω/2πγ0). Material systems which host large polarons such as GaAs are composed of comparatively harmonic vibrational potentials, while strongly ionic lattices such as SrTiO3, which are known to host small polarons have substantially larger anharmonicity. Ruddledden Popper metal halides studied here are clearly in the intermediate regime and importantly beyond the weak coupling limit. We invoke again the interpretation of the vibrations in ionic lattices as oscillating dipoles, in which phonon–phonon interactions (anharmonicity) can be thought in terms of dipole–dipole interactions, and its strength will be determined by the asymmetry of the vibration (dipole moment), the ionic character and softness of the lattice. It then becomes clear that the size of the polaron and the anharmonicity of the vibrational mode are both consequences of the same physical problem – Coulomb interactions in an ionic lattice. This train of thought indicates the need to include anharmonicity in the description of polarons as the small polaron limit is approached in highly ionic lattices, where the harmonic potential approximation is compromised by strong phonon–phonon (dipole–dipole) interactions. Recent work has aimed for the inclusion of anharmonicity into the Fröhlich formalism,46 which is a necessary step in the description of polarons even in metal halide perovskites although contributions from dynamic disorder from the short-range fluctuations of the organic cation will add to the complexity.8,17 The anharmonicity of the phonons that dress the electronic transitions is of relevance in the context of exciton polarons, which we consider as the primary photoexcitations in Ruddlesden–Popper metal-halides.17–19,21 Exciton polarons are stationary eigenstates of a system where the Coulomb interactions between the electrons and holes and their respective coupling with phonons are the integral components. Due to the inherent mixing of exciton and phonon eigenstates, the phonon–phonon interactions assume relevance in the exciton dephasing dynamics. Such a consideration was initially put forward by Verzelen et al. in the context of semiconductor quantum dots.47–49
In this context, we recall the spectral fine structure at the exciton energy ubiquitous to Ruddlesden–Popper metal halides with a characteristic energy spacing of 35–40 meV (see numerous references in ref. 17). We had hypothesised, based on a series of experimental observations, that the resonances observed in this fine structure correspond to distinct exciton polaron states with different binding energies and effective masses,18,21 which is different from the more widely used vibronic replica interpretion.17 We concluded that two of the observed excitonic resonances, labelled XA and XB, are dressed by distinct lattice modes.18 Specifically, XA is dressed predominantly by M2, while XB had additional dressing from M4 and M6, which are the higher-energy modes at 5.22 and 5.75 meV. Note that these higher-energy modes exhibit large anharmonicities similar to that of M2, as evident in their comparable dynamics to that of M2 at higher temperatures, Fig. 2. Intriguingly, M1 does not contribute significantly to the exciton polaron while it dresses the carrier polaron. Coincidentally, no evidence was found for the participation of M1 in the exciton polaron dynamics. On the contrary, the strongly anharmonic M2 mode was identified to be the primary phonon participating in the non-adiabatic mixing of XA and XB, eventually driving the population exchange between these two states, see ref. 20. The anharmonic phonons can also be clearly identified to be playing a role in the thermal dephasing of excitons, as reported in ref. 19. The increase in the homogeneous linewidths of excitonic resonances with temperature can be analysed to estimate the energy of the phonons that scatter the exciton. Such an analysis revealed that average energy of the phonon that broadens XA is about 6 meV, clearly indicating the role of the higher energy anharmonic modes, dominated by M2, in the exciton–phonon elastic scatting. The temperature dependence of the XB linewidth, on the other hand, yielded a phonon energy of over 20 meV. However, the vibrational modes at such energies correspond to the motion within the organic layer and thus should not contribute to the scattering of excitons that are confined within the inorganic layer. We consider that this discrepancy is due to inadequacy of the LO phonon scattering model of exciton polarons, which does not explicitly consider the contributions from phonon–phonon interactions to the exciton dephasing.50
3 Conclusions
In conclusion, we quantified the anharmonicity of optical phonons that are impulsively generated via photoexciation of free carriers in polycrystalline thin films of (PEA)2PbI4. We find that each of the observed lattice eigen modes that are associated with the motion of the lead-iodide network exhibit distinct dynamics. The lower energy mode, labelled M1, exhibits temperature independent dephasing dynamics, indicating a low probability of phonon scattering. The higher energy modes, however, exhibit temperature dependence, which we analysed considering downconversion of optical phonons into two acoustic modes. We also extracted the anharmonicity constant, which is a measure of phonon–phonon scattering, and based on the comparison with other material systems, we conclude that the anharmonicity of the Ruddlesden–Popper metal halides is as large as in strongly ionic solids. Based on a critical comaparison of polaron coupling constants and the lattice anharomonicities of different material systems, we conclude that the electron–phonon coupling mechanism goes beyond the weak coupling limit, and the lattice anharmonicity quantified in this work has to be rigorously considered in its description.Many previous works on carrier dephasing10,11 and thermalization5 in three dimensional lead halide perovskites have clearly identified the role of anharmonic lattice interactions in electronic processes. On a very similar note, albeit in the context of electrically neutral excitons, we find that all the phonons that dress the excitons and thus are the integral components of the exciton polaron wavefunction exhibit strong anharmonicity. Based on this observation, we emphasize the need to expand the theoretical model for excitons in these systems, similar to what was proposed by Verzelen et al.,47–49 but also to include phonon anharmonicity in the exciton many-body dynamics. We consider that the coherent phonon dynamics presented in this work, along with the independent observations of phonon dressing of excitons,18 thermal dephasing of excitons,19 and exciton many-body interactions,51 establish a solid experimental ground to build a theoretical framework to comprehend exciton polarons in semiconductor materials beyond the metal halides addressed in this manuscript.
Author contributions
E. R. G. analyzed the data under the supervision of A. R. S. K. and C. S. A. A. R. S. K. participated in the original data collection and analysis reported in ref. 18. The intellectual basis for this work was conceived by A. R. S. K. and C. S. A. All co-authors contributed to the redaction of this manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the National Science Foundation (DMR-1904293). CSA acknowledges support from the School of Chemistry and Biochemistry and the College of Science at the Georgia Institute of Technology. ERG acknowledges support from the Renewable Bioproducts Institute fellowship at the Georgia Institute of Technology.Notes and references
- C. Katan, A. D. Mohite and J. Even, Nat. Mater., 2018, 17, 377–379 CrossRef CAS PubMed.
- A. M. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodrguez-Martnez, O. J. Weber, A. Pallipurath, M. I. Alonso and M. Campoy-Quiles, et al. , Phys. Chem. Chem. Phys., 2016, 18, 27051–27066 RSC.
- M. Z. Mayers, L. Z. Tan, D. A. Egger, A. M. Rappe and D. R. Reichman, Nano Lett., 2018, 18, 8041–8046 CrossRef CAS PubMed.
- C. E. Patrick, K. W. Jacobsen and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 201205 CrossRef.
- P. P. Joshi, S. F. Maehrlein and X. Zhu, Adv. Mater., 2019, 31, 1803054 CrossRef CAS PubMed.
- D. W. deQuilettes, K. Frohna, D. Emin, T. Kirchartz, V. Bulovic, D. S. Ginger and S. D. Stranks, Chem. Rev., 2019, 119, 11007–11019 CrossRef CAS PubMed.
- X.-Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS PubMed.
- M. J. Schilcher, P. J. Robinson, D. J. Abramovitch, L. Z. Tan, A. M. Rappe, D. R. Reichman and D. A. Egger, ACS Energy Lett., 2021, 6, 2162–2173 CrossRef CAS.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X.-Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS PubMed.
- S. A. March, D. B. Riley, C. Clegg, D. Webber, X. Liu, M. Dobrowolska, J. K. Furdyna, I. G. Hill and K. C. Hall, ACS Photonics, 2017, 4, 1515–1521 CrossRef CAS.
- S. A. March, D. B. Riley, C. Clegg, D. Webber, I. G. Hill, Z.-G. Yu and K. C. Hall, J. Chem. Phys., 2019, 151, 144702 CrossRef PubMed.
- D. Snoke, Solid State Physics: Essential Concepts, Addison-Wesley, 2009 Search PubMed.
- R. Sharma, Z. Dai, L. Gao, T. M. Brenner, L. Yadgarov, J. Zhang, Y. Rakita, R. Korobko, A. M. Rappe and O. Yaffe, Phys. Rev. Mater., 2020, 4, 092401 CrossRef CAS.
- F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goni, A. M. Leguy, P. R. Barnes and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144308 CrossRef.
- L. Mao, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 141, 1171–1190 CrossRef PubMed.
- C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192 CrossRef CAS PubMed.
- A. R. Srimath Kandada and C. Silva, J. Phys. Chem. Lett., 2020, 11, 3173–3184 CrossRef CAS PubMed.
- F. Thouin, D. A. Valverde-Chávez, C. Quarti, D. Cortecchia, I. Bargigia, D. Beljonne, A. Petrozza, C. Silva and A. R. Srimath Kandada, Nat. Mater., 2019, 18, 349–356 CrossRef CAS PubMed.
- F. Thouin, D. Cortecchia, A. Petrozza, A. R. S. Kandada and C. Silva, Phys. Rev. Res., 2019, 1, 032032 CrossRef CAS.
- F. Thouin, A. R. Srimath Kandada, D. A. Valverde-Chávez, D. Cortecchia, I. Bargigia, A. Petrozza, X. Yang, E. R. Bittner and C. Silva, Chem. Mater., 2019, 31, 7085–7091 CrossRef CAS.
- S. Neutzner, F. Thouin, D. Cortecchia, A. Petrozza, C. Silva and A. R. Srimath Kandada, Phys. Rev. Mater., 2018, 2, 064605 CrossRef CAS.
- P. G. Klemens, Phys. Rev., 1966, 148, 845–848 CrossRef CAS.
- F. Vallée, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 2460–2468 CrossRef PubMed.
- F. Thouin, S. Neutzner, D. Cortecchia, V. A. Dragomir, C. Soci, T. Salim, Y. M. Lam, R. Leonelli, A. Petrozza, A. R. S. Kandada and C. Silva, Phys. Rev. Mater., 2018, 2, 034001 CrossRef CAS.
- D. B. Straus, N. Iotov, M. R. Gau, Q. Zhao, P. J. Carroll and C. R. Kagan, J. Phys. Chem. Lett., 2019, 10, 1198–1205 CrossRef CAS PubMed.
- L. Dhar, J. A. Rogers and K. A. Nelson, Chem. Rev., 1994, 94, 157–193 CrossRef CAS.
- M. Menahem, Z. Dai, S. Aharon, R. Sharma, M. Asher, Y. Diskin-Posner, R. Korobko, A. M. Rappe and O. Yaffe, ACS Nano, 2021, 15, 10153–10162 CrossRef PubMed.
- B. Dhanabalan, Y.-C. Leng, G. Biffi, M.-L. Lin, P.-H. Tan, I. Infante, L. Manna, M. P. Arciniegas and R. Krahne, ACS Nano, 2020, 14, 4689–4697 CrossRef CAS PubMed.
- G. R. Lee, R. Gommers, F. Waselewski, K. Wohlfahrt and A. O’Leary, J. Open Source Softw., 2019, 4, 1237 CrossRef.
- W. Staszewski, J. Sound Vib., 1997, 203, 283–305 CrossRef.
- V. A. Dragomir, S. Neutzner, C. Quarti, D. Cortecchia, A. Petrozza, S. Roorda, D. Beljonne, R. Leonelli, A. R. S. Kandada and C. Silva, 2018, arXiv:1812.05255 [condmat.mtrl-sci].
- M. Balkanski, R. F. Wallis and E. Haro, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1928–1934 CrossRef CAS.
- C. Ramkumar, K. P. Jain and S. C. Abbi, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 13672–13681 CrossRef CAS PubMed.
- C. Li, H. Ma, T. Li, J. Dai, M. A. J. Rasel, A. Mattoni, A. Alatas, M. G. Thomas, Z. W. Rouse, A. Shragai, S. P. Baker, B. J. Ramshaw, J. P. Feser, D. B. Mitzi and Z. Tian, Nano Lett., 2021, 21, 3708–3714 CrossRef CAS PubMed.
- P. Němec and P. Malý, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 235324 CrossRef.
- M. Hase, K. Ishioka, M. Kitajima, K. Ushida and S. Hishita, Appl. Phys. Lett., 2000, 76, 1258–1260 CrossRef CAS.
- K. K. Tiong, P. M. Amirtharaj, F. H. Pollak and D. E. Aspnes, Appl. Phys. Lett., 1984, 44, 122–124 CrossRef CAS.
- L. Sun, P. Kumar, Z. Liu, J. Choi, B. Fang, S. Roesch, K. Tran, J. Casara, E. Priego, Y.-M. Chang, G. Moody, K. L. Silverman, V. O. Lorenz, M. Scheibner, T. Luo and X. Li, Nano Lett., 2021, 21, 1434–1439 CrossRef CAS PubMed.
- F. Vallée and F. Bogani, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 12049–12052 CrossRef PubMed.
- J. T. Devreese, in Polarons, American Cancer Society, 2003 Search PubMed.
- L. R. V. Buizza and L. M. Herz, Adv. Mater., 2021, 33, 2007057 CrossRef CAS PubMed.
- M. Puppin, S. Polishchuk, N. Colonna, A. Crepaldi, D. N. Dirin, O. Nazarenko, R. De Gennaro, G. Gatti, S. Roth, T. Barillot, L. Poletto, R. P. Xian, L. Rettig, M. Wolf, R. Ernstorfer, M. V. Kovalenko, N. Marzari, M. Grioni and M. Chergui, Phys. Rev. Lett., 2020, 124, 206402 CrossRef CAS PubMed.
- T. Kohmoto, K. Tada, T. Moriyasu and Y. Fukuda, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 064303 CrossRef.
- C. Gehrmann and D. A. Egger, Nat. Commun., 2019, 10, 3141 CrossRef PubMed.
- Y. Wang, S. Shang, Z.-K. Liu and L.-Q. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 224303 CrossRef.
- M. Houtput and J. Tempere, Phys. Rev. B, 2021, 103, 184306 CrossRef CAS.
- O. Verzelen, R. Ferreira and G. Bastard, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R4809–R4812 CrossRef CAS.
- O. Verzelen, R. Ferreira and G. Bastard, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 075315 CrossRef.
- O. Verzelen, R. Ferreira and G. Bastard, Phys. Rev. Lett., 2002, 88, 146803 CrossRef CAS PubMed.
- S. Rudin and T. L. Reinecke, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 3017–3027 CrossRef PubMed.
- A. R. Srimath Kandada, H. Li, F. Thouin, E. R. Bittner and C. Silva, J. Chem. Phys., 2020, 153, 164706 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1mh01010g |
| ‡ Currently visiting as Honorary Professor, Departamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, 97310 Mérida, Yucatán, México |
| This journal is © The Royal Society of Chemistry 2022 |
