Open Access Article
Open Access ArticlePhotoionization of the aqueous phase: clusters, droplets and liquid jets
Ruth
Signorell
 a and
Bernd
Winter
a and
Bernd
Winter
 b
b
aDepartment of Chemistry and Applied Biosciences, ETH Zürich, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: ruth.signorell@phys.chem.ethz.ch
bMolecular Physics Department, Fritz-Haber-Institute der Max-Planck-Gesellschaft, Faradayweg 4-6, 14196 Berlin, Germany. E-mail: winter@fhi-berlin.mpg.de
First published on 27th April 2022
Abstract
This perspective article reviews specific challenges associated with photoemission spectroscopy of bulk liquid water, aqueous solutions, water droplets and water clusters. The main focus lies on retrieving accurate energetics and photoelectron angular information from measured photoemission spectra, and on the question how these quantities differ in different aqueous environments. Measured photoelectron band shapes, vertical binding energies (ionization energies), and photoelectron angular distributions are influenced by various phenomena. We discuss the influences of multiple energy-dependent electron scattering in aqueous environments, and we discuss different energy referencing methods, including the application of a bias voltage to access absolute energetics of solvent and solute. Recommendations how to account for or minimize the influence of electron scattering are provided. The example of the hydrated electron in different aqueous environments illustrates how one can account for electron scattering, while reliable methods addressing parasitic potentials and proper energy referencing are demonstrated for ionization from the outermost valence orbital of neat liquid water.
Introduction
Continued interest in the properties of liquid water mirrors water's ubiquitous presence on Earth, its indispensable role in the chemical and biological processes of life and in the environment, and its involvement in technological processes. Although the structure of a single water molecule is so simple, it is the ability to form hydrogen bonds and the associated polarizability that makes water unique and multifaceted. Water acts as a solvent, electrolyte or reaction catalyst. It naturally exists in very different aqueous-phase environments – neat liquid water, ice, aqueous solutions – and sample dimensions, including microscopic clusters, droplets, or macroscopic liquid jets (LJ). A correspondingly large number of experimental techniques has been developed aiming at the detailed understanding of the properties of these objects on the molecular level. This includes chemical and physical processes, such as hydration, intermolecular/atomic energy and charge transfer between water and solute, encompassing chemical reactivity, with the expectation that properties typically differ between the respective interfaces and the bulk/interior.The present article focusses on the electronic structure of liquid water, also touching upon aqueous solutions in liquid jets, clusters, and aerosols, as accessed by (linear) photoemission spectroscopy. Time-resolved studies will not be explicitly considered. We use the term ‘photoemission’ to distinguish between the emission of a direct photoelectron (this is usually referred to as photoelectron spectroscopy, PES,1 and relates to probing the system's electronic ground-state) and the emission of electrons generated by some second-order relaxation process. Direct PES in the aqueous phase has been extensively reviewed.2–4 Regarding the relaxation channels usually following core-level ionization, we distinguish between (local) Auger decay and non-local autoionization decays, observed for weakly bound systems, such as hydrogen-bonding systems.5–8 While the Auger process leads to a 2+ final state with the charges localized at the initially ionized species, there is also a special type of local decay, proton-transfer-mediated charge separation, involving proton dynamics.5–8 In the case of non-local autoionization the resulting 2-hole state is delocalized over the initially ionized (molecular) species and the solvation shell, stabilized by the Coulomb energy resulting from the separation of the two positive charges. Interatomic/intermolecular Coulombic Decay (ICD) processes in liquid water and clusters, as well as other non-local processes, and their role in determining electronic and even geometric structure details of aqueous solutions have recently been comprehensively reviewed.9
Our particular focus in the present work lies on an aspect not considered in most previous studies, namely the contribution to the photoemission spectrum arising from the multiple energy-dependent electron-scattering processes in solution, mostly electron–water collisions.10–13 Especially low-energy electron scattering can severely distort the true (“genuine”) photoelectron spectrum to the point that energetics (electron binding energies) are only accessible by way of complex modelling of electron scattering in liquid water. We discuss the fate of an electron born upon photoionization within the aqueous phase, until it crosses the aqueous phase–vacuum interface and is eventually detected in vacuum, and we explain where caution must be taken when measuring PES spectra. Retrieving the genuine photoelectron spectrum from measured spectra distorted by electron scattering will be discussed in detail for the smallest solute, the hydrated electron.14,15 At high enough electron kinetic energies (and correspondingly high enough photon energies) the influence of electron scattering is typically less pronounced, whereas processes near the ionization threshold are difficult to detect, posing a great challenge to several novel applications of LJ-PES. Prime examples are post-collision interactions (PCI16,17) and photoelectron circular dichroism (PECD18–21) in aqueous phase, both of which will be discussed here.
Our other main focus in this article is on recent advancements in liquid-jet PES that provide access to accurate energetics of liquid water and aqueous solutions, by applying condensed-matter concepts instead of relying on the usually ill-defined gas-phase energy referencing method.22,23 We discuss major implications for liquid-phase PES, including a potential extension to explicitly access solution interfacial properties, which is conceptually difficult to accomplish within the commonly used purely molecular description of liquid water.
Experiments described in this article use different devices for sample preparation, different ranges of photon energies and hence different light sources, and different electron detectors. Fig. 1a presents a schematic setup of the cluster/particle/droplet photoemission imaging experiment.24–27 Particles/droplets are produced with various particle/droplet generators and size-selected using commercial aerosol instrumentation outside vacuum, prior to the transfer into vacuum by different air–vacuum interfaces. For volatile droplets, size selection can be achieved by special air–vacuum interfaces. Clusters are generated by supersonic expansions into vacuum using various expansion nozzles (not shown in Fig. 1a). The clusters/particles/droplets are excited/ionized using radiation from the infrared (IR) to X-ray range, and detected with a velocity map imaging (VMI) photoelectron spectrometer. VMI allows one to record electron kinetic energies and photoelectron angular distributions with high collection efficiency and angular multiplexing. Fig. 1b sketches a typical LJ-PES experiment,28 equipped with a vacuum liquid microjet, the laminar phase of which is photoionized at a distance of a few millimeters from the entrance of a hemispherical electron analyzer (HEA); see the inset photo for the actual arrangement. Unlike the particle experiment, capable of covering an electron detection angle of 4π, only a very small fraction of all emitted electrons is detected in the present LJ experiment, but HEAs maintain a constant and very high resolution up to high kinetic energies. This detector is typically used in conjunction with soft-X-ray radiation as it is capable of detecting electrons with kinetic energies >1000 eV,29 but may also be used in conjunction with a typical laboratory ultraviolet (UV) source such as a plasma discharge lamp. Other LJ-PES studies often use magnetic-bottle time-of-flight (MB-ToF) detection instead, but typically applying photon energies <100 eV from lab-based laser systems, and usually aiming at time-resolved LJ-PES measurements. MB-ToFs feature a high collection efficiency, but have poorer energy resolution, particularly at higher energies.
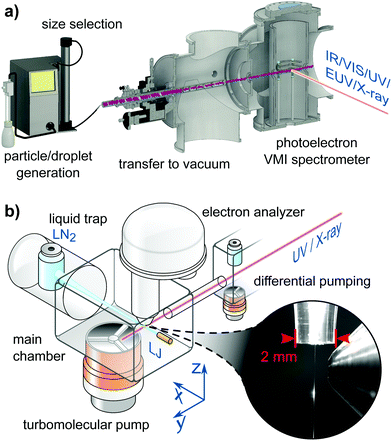 | ||
| Fig. 1 (a) Schematic of a cluster/particle/droplet velocity map imaging (VMI) photoelectron spectrometer.26 Particles/droplets are generated in a particle/droplet generation unit and transferred into the VMI photoelectron spectrometer through an air–vacuum transfer device. The latter usually consists of aerodynamic lenses135 or aerodynamic-mechanical selectors.24 Size selection is performed before transfer into vacuum for non-volatile particles/droplets or in the air–vacuum transfer device for volatile particles/droplets. Clusters are formed by supersonic expansion into vacuum (not shown) using different types of expansion nozzles. The clusters/particles/droplets are excited and ionized with various light sources ranging from the infrared (IR) to the X-ray regime. The generated photoelectrons are projected onto an electron detector with the help of a set of electrostatic lenses operated in the VMI mode.136 (a) is reproduced from Fig. 2 in ref. 26 with permission from the Annual Review of Physical Chemistry, Volume 71 ©2020 by Annual Reviews, https://www.annualreviews.org/. (b) Schematic of a LJ-PES setup used in conjunction with soft-X-ray ionization. In this particular arrangement the jet propagates horizontally, hitting a liquid-nitrogen cold trap at some tens centimeter distance from the jet-forming capillary. Additional cold traps in the main chamber assist with pumping the vapor from the liquid jet (LJ). The laminar part of the LJ is ionized at <1 mm distance from the typically 500–800 μm diameter entrance cone of the analyzer, depicted in the photograph. The LJ is mounted onto a precise XYZ-manipulator to optimize positioning on a micrometer scale. The detection axis of the hemispherical electron analyzer (HEA) is usually perpendicular to the LJ propagation direction. The X-ray or UV light is introduced through a pinhole from a differential pumping stage as last element of a beamline connection or a capillary from a plasma discharge lamp. The angle of the light propagation direction and polarization vector is often variable by means of using different ports or a rotation mechanism to realize different experimental configurations depending on the measurement goal. The main chamber, differential pumping stage and lens elements of the HEA are equipped with multiple high-throughput turbomolecular pumps to effectively reduce the pressure from the evaporating liquid jet. Modern near-ambient pressure HEAs feature three to four differential pumping stages until the detection unit. Together with the short distance to the detector orifice the pressure is quickly reduced, which enables the passthrough of photoelectrons for detection. (b) is adapted from Fig. 2 of ref. 28. | ||
1. Electron scattering in water
1.1 Influence on binding energy spectra and photoelectron angular distributions
Photoemission spectra and images can be pronouncedly influenced by elastic and inelastic electron transport scattering – an important factor that has only recently received the attention it deserves.10,12,14,24–26,30–37 Photoionization of liquid water, water droplets and water clusters, or of solutes in these aqueous environments results in the formation of quasi-free electrons (e− in Fig. 2a), which have different electron kinetic energies (eKEs) depending on the binding energy (eBE) of the bound state of origin and on the photon energy (hν) used for ionization. To be detected, these electrons have to travel from their point of origin to the water–vacuum interface and then escape into vacuum (evac−). On the way, the electrons’ kinetic energies and trajectories (“linear momentum”) are modified by elastic and inelastic scattering of the electrons at the water molecules that lie along their path (thick blue arrow). As a result of these so-called transport scattering processes, the genuine (also referred to as intrinsic or nascent) binding energy spectrum, eBEgen, and the genuine photoelectron angular distribution, PADgen, i.e., the quantities at the point of origin, can differ from the corresponding quantities that are measured at the electron detector after escape of the electrons into vacuum (eBE and PAD, respectively). Often, the true interest lies in eBEgen and PADgen and not in the measured eBE and PAD because the former contains the physically relevant information about the orbital from which the electron arises. In particular for low-kinetic energy electrons scattering can hinder direct experimental access to eBEgen and PADgen since it can falsify the information on these genuine quantities (see later). This is because energy losses will be on the order of <100 meV and thus generating signal right at the base of the initial photoelectron peak with peak widths typically 1.0–1.5 eV in aqueous phase. In these cases, corrections for the influence of scattering are required for the retrieval of eBEgen and PADgen. Yet, electron scattering can also be helpful in applications of PES to condensed matter. For example, in the so-called depth-profiling, the kinetic energy dependence of the electron's escape depth is exploited to probe at different depths from the surface simply by varying the photon energy.38,39 However, the lack of detailed understanding of scattering processes in liquid water still limits the accurate quantification of the depth scale. Another promising future application may be to utilize the scattering (background) signal itself as a probe, e.g., to observe the layered interface structure of surface-active species via changes in the scattering behavior. Such techniques have been successful in solid-state applications to reveal detailed surface structures.40–42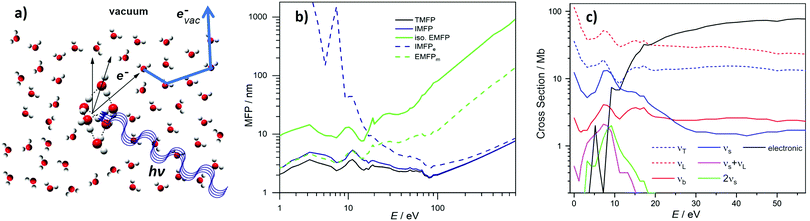 | ||
| Fig. 2 (a) Formation of a quasi-free electron, e−, in liquid water, water droplets or water clusters by photoionization with light of photon energy hν. This photoelectron is formed with a characteristic genuine kinetic energy (eKEgen) and angular distribution (PADgen). On its way from its point of origin into vacuum, where it is detected as evac−, inelastic and elastic scattering at the water molecules (electron transport scattering, blue arrow), have changed both the electron's kinetic energy and its direction of travel. The measured kinetic energy (eKE) and angular distribution (PAD) thus differ from the corresponding genuine quantities. (b) Mean free paths (MFPs) for electrons in liquid bulk water retrieved in ref. 10 (see also ref. 11). TMFP is the total MFP, which contains the contributions from all inelastic and isotropic elastic scattering channels. IMFP is the total inelastic MFP. IMFPe is the electronically inelastic MFP, which contains all inelastic channels associated with electronic scattering. iso. EMFP is the isotropic contribution to the elastic MFP. EMFPm is the quasi-elastic momentum transfer MFP. It describes the propensity of the photoelectron to change its direction in a quasi-elastic scattering event (i.e., with no or only small changes of the eKE). E is the kinetic energy outside the sample (as measured by the detector and as defined by Michaud et al.11). The kinetic energy inside the sample is E + 1 eV (because of the escape barrier of 1 eV). (b) Is reproduced from Fig. S2 in the SM of ref. 10 with permission, Copyright ©2011 by American Physical Society. (c) Scattering cross sections for electrons in liquid bulk water retrieved in ref. 10 (see also ref. 11). T = translational phonons combined, L = librational phonons combined, b = OH-bend, s = OH-stretches combined, electronic = all electronic channels combined (incl. dissociative attachment). The figure illustrates the strongly varying contributions of the various inelastic scattering channels, in particular below kinetic energies of 20 eV. 1 Mb = 10−18 cm2. E is the kinetic energy outside the sample (as measured by the detector and as defined by Michaud et al.11). The kinetic energy inside the sample is E + 1eV (because of the escape barrier of 1eV). | ||
Scattering contributions depend in a non-trivial way on the kinetic energy of the electrons, and thus on hν, and on the type and dimension of the aqueous environment (e.g., liquid bulk water, water clusters). The eKE dependence leads to an explicitly energy-dependent scattering correction term, Esca, that also depends on the sample/detection geometry and needs to be taken into account when relating measured eBE to genuine eBEgen values
| eBEgen = hν − eKE − Esca = eBE − Esca, | (1) |
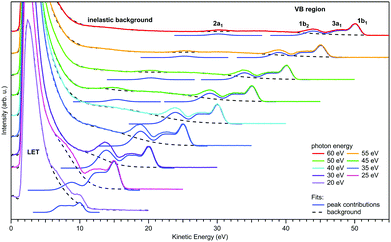 | ||
| Fig. 3 Valence photoemission spectra from a negatively-biased liquid water ionized at photon energies between 20 and 60 eV; the nominally applied voltage of −50 V has been subtracted from the measured eKEs to produce the eKE scale shown here. Photoelectron peaks due to ionization of the water 1b1, 3a1, 1b2, and 2a1 orbitals are labeled. Individual contributions are shown by the respective Gaussians. LET denotes the low-energy spectral tail, with intensity maxima clipped here. The dashed black curves represent the contribution from the background signal and the dark blue curves are fits of Gaussians to the peak features. For more details of the fitting procedure, including the description of the background signal we refer to Malerz et al.34 It is apparent that the peaks are suppressed when the eKE decreases below the critical threshold of ∼10 eV, while at the same time the inelastic background below the peak increases drastically. Figure is reproduced from Fig. 1 of ref. 34 with permission from the PCCP Owner Societies. | ||
Regarding the explicit effect of scattering on peak energy and shape, we see in Fig. 3 that for high enough photon energies the valence spectrum resides on top of a flat background of inelastically scattered electrons. Here, the primary peaks are still largely unaffected by inelastic scattering so that the correction term, Esca, is still relatively small. With decreasing hν, and hence decreasing eKE, the peaks sit atop a larger and larger background of increasing slope. This means that Esca has contributions small enough to keep the scattered electrons approximately within the energy range of the peak, affecting its shape. Eventually, near hν = 20 eV, water's 1b1 emission can only be detected as a small shoulder near 10 eV eKE. This is accompanied by a sudden decline of the primary direct peak intensities, counter-balanced by the relative contribution of the inelastically scattered background signal which rises steeply for eKEs below 10–14 eV.34 In other words, small-energy loss contributions also increase in probability here. In the energy range below 10 eV, electron scattering in liquid water is mostly accompanied by the excitation of inter- and intramolecular vibrations as the kinetic energy hardly suffices to cause (known) electronic excitation. This is reflected in the different contributions to the mean free path (MFP, i.e., the average distance between consecutive scattering events) and scattering cross sections10,11 shown in Fig. 2b and c, respectively. Up to kinetic energies of ∼20 eV vibrational inelastic scattering events dominate the total inelastic MPF (IMFP) because electronically inelastic scattering events are far less likely to occur (IMFPe » IMFP in Fig. 2b) due to the much higher minimal energy requirements for these processes; see below. Fig. 2c illustrates the strong variation of the vibrationally inelastic cross sections and their dominance over the electronically inelastic contributions for kinetic energies below ∼20 eV. We refer to this dominance of vibrational scattering over electronic scattering as “pure vibrational scattering”. For clarity, we have combined the individual scattering cross sections from ref. 10 (see also ref. 11) into seven different classes: T refers to the translational phonons, L to the librational phonons, b to the OH-bend vibration, s to the two OH-stretch vibrations, and “electronic” combines all channels involving electronic excitation including dissociative attachment. Pure vibrational scattering has a pronounced influence on the shape of a photoelectron band because the typical bandwidth of a few eV exceeds the small kinetic energy losses on the order of 0.01–0.9 eV accompanying a vibrational scattering event. Thus, the measured kinetic energy of electrons (eKE) stays relatively close to their initial kinetic energy (eKEgen), so that the scattered electrons are detected within the width of the photoelectron band. But different vibrational scattering channels open up at different energies (roughly corresponding to the typical average energy loss per scattering event of that channel) and the values of their scattering cross section vary pronouncedly with energy10 (Fig. 2c). The resulting uneven redistribution of scattered electrons on the energy scale can significantly distort and broaden the measured band shape compared with the genuine band shape (see Section 2).
The situation changes with increasing eKEgen, i.e., for increasing hν. As the vibrational cross sections gradually decrease, they tend to vary much more slowly with energy so that the distorting effect of vibrational scattering on the genuine band shape gradually fades away. At the same time, electronically inelastic channels start to take over for eKEgen above the lowest ionization energy of water (∼10 eV) as the probability of electronic inelastic excitations increases (IMFPe decreases), shown in Fig. 2b and c. Typical kinetic energy losses per scattering event associated with an electronic excitation of water exceed several eV (except for the total loss of the photoelectron through dissociative attachment in the eKE range around 5eV,11 the smallest energy for electronic excitation is approximately 7 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43). Consequently, electronically scattered electrons appear at eKEs well below the original PE peak and thus barely affect the shape of photoelectron bands. The majority of these electronically scattered electrons appears at kinetic energies outside the considered photoelectron band, on the low kinetic energy side of the band. Lower-lying bands will often sit atop a background of inelastically scattered electrons from the higher ones, which is however mostly flat and featureless, and thus does not affect the peak shape. While electronically inelastic processes do not directly affect the observed band shape, they do have an indirect effect by reducing the escape depth of electrons, as explained before. An electronic scattering event is the more likely to happen the more scattering events an electron has to undergo before reaching the vacuum, i.e., the further away an electron starts from the surface. As cross sections for electronic scattering events rise, only electrons formed closer to the surface have a chance to reach the vacuum with eKE within the range of the photoelectron band (i.e., with only elastic or vibrational scattering). In other words, the so-called escape depth of the electrons detected in a given band decreases. The trajectories of electrons detected in a given band are shorter, so that they undergo fewer (vibrational) scattering events before they escape into vacuum. Fewer vibrational scattering events produce less distortion of the genuine band shape. At even higher eKEs beyond 100–200 eV the cross-sections for electronic processes decrease again, increasing the mean free path (Fig. 2b). Here, the cross section for vibrational excitations is very small, nearly negligible. Thus, distortions of the band shape due to scattering is only of concern for low eKEs.
43). Consequently, electronically scattered electrons appear at eKEs well below the original PE peak and thus barely affect the shape of photoelectron bands. The majority of these electronically scattered electrons appears at kinetic energies outside the considered photoelectron band, on the low kinetic energy side of the band. Lower-lying bands will often sit atop a background of inelastically scattered electrons from the higher ones, which is however mostly flat and featureless, and thus does not affect the peak shape. While electronically inelastic processes do not directly affect the observed band shape, they do have an indirect effect by reducing the escape depth of electrons, as explained before. An electronic scattering event is the more likely to happen the more scattering events an electron has to undergo before reaching the vacuum, i.e., the further away an electron starts from the surface. As cross sections for electronic scattering events rise, only electrons formed closer to the surface have a chance to reach the vacuum with eKE within the range of the photoelectron band (i.e., with only elastic or vibrational scattering). In other words, the so-called escape depth of the electrons detected in a given band decreases. The trajectories of electrons detected in a given band are shorter, so that they undergo fewer (vibrational) scattering events before they escape into vacuum. Fewer vibrational scattering events produce less distortion of the genuine band shape. At even higher eKEs beyond 100–200 eV the cross-sections for electronic processes decrease again, increasing the mean free path (Fig. 2b). Here, the cross section for vibrational excitations is very small, nearly negligible. Thus, distortions of the band shape due to scattering is only of concern for low eKEs.
The above considerations illustrate the complicated interplay of various energy-dependent processes behind the influence of transport scattering on binding energy spectra. Section 2 discusses the resulting energy-dependent trends for the hydrated electron.14,15,44–47 The conclusions to be drawn can be summarized as follows: Binding energy spectra recorded at photon energies less than ∼15–20 eV above the VBE of a given photoelectron band are strongly influenced by electron scattering. The measured binding energy spectrum deviates pronouncedly from the genuine spectrum. The influence of electron scattering on binding energy spectra can be minimized by choosing higher photon energies for ionization, at least ∼20 eV above the VBE of the photoelectron band of interest. Such photon energies yield a measured binding energy spectrum that resembles the genuine spectrum.
This strategy, however, is not successful for the photoelectron angular distribution (PAD) because scattering has a pronounced influence on the angular distribution at all electron kinetic energies in the sub-keV range, necessary for exploring different probing depths into solution. Scattering processes change the propagation direction of the electrons, resulting in a measured PAD that is more isotropic than the genuine one (PADgen).10,14,15,30,33,48 Two main factors contribute to the generally strong influence of scattering on the PAD. At all photon energies, a photoelectron band contains a certain fraction of elastically-scattered electrons (Fig. 2c), in addition to the purely vibrationally-scattered electrons discussed above. Only these two classes (together with electrons that have not been scattered) contribute to a given photoelectron band. Elastic scattering does not change the kinetic energy, but it strongly modifies the PAD. Typically, the change in the propagation direction of an electron is already very pronounced for only a single scattering event. This holds especially at lower kinetic energies, where scattering tends to be isotropic, while it tends to become more forward directed at higher energies.11,24,30,49 The propensity of a scattering event to change the direction of the electron, while keeping its eKE within a given photoelectron band, can be described by the (quasi-elastic) momentum transfer cross-section σm, given by
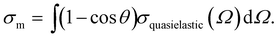 | (2) |
I(φ) ∝ 1 + βP2 (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) = 1 + β/2 (3cos2 φ) = 1 + β/2 (3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ − 1). φ − 1). | (3) |
φ is the angle between the linear polarization vector of the light and the direction of photoelectron emission, and P2 is the second-order Legendre polynomial which provides the non-isotropic part of the overall distribution. I(φ) is the electron signal detected at angle φ. β is constrained to values −1 ≤ β ≤ 2, with β = 0 indicating a completely isotropic distribution. A similar expression holds for circularly polarized light.58,59 Both are special cases of a more general expression (see eqn (4) in Section 3), which also allows one to describe the influence of chiral effects on the PAD, such as photoelectron circular dichroism (PECD) in aqueous solutions briefly discussed in Section 3.
Nowadays, detailed electron scattering simulations allow us to predict measured β parameters when the genuine parameters, βgen, are known. Fig. 4a illustrates this for the ionization from the O 1s orbital and the valence bands (inset) of neat liquid water; for details see ref.10 and for experimental liquid-phase data of O 1s and the valence region refs. 30 and 50. The weak intermolecular interaction in the liquid phase leaves inner-shell atomic orbitals of the molecules involved virtually unaffected. Therefore, the orbital character of O 1s in liquid water is essentially the same as in gas-phase water. Since the genuine PAD largely reflects the orbital character, the genuine anisotropy parameter βgen in the liquid is well approximated by the measured anisotropy parameter for ionization from the O 1s orbital of gas-phase water (values given in ref. 30 note that in the gas phase measured and genuine PADs are the same). These gas-phase values were used as βgen values for the liquid simulations in Fig. 4a. Simulation and experiment for the liquid show almost perfect agreement, demonstrating that for O 1s ionization the decrease of β in the liquid compared to the gas phase (βgen) arises from electron transport scattering. For eKEs above ∼100eV, βgen reaches the maximum value of 2, as expected for ionization from an s-orbital at sufficiently high energies where interference effects can be neglected.30 In the liquid, however, this maximum value is never reached for the measured β because of the influence of electron transport scattering. The inset of Fig. 4a illustrates the analogous approach for the valence bands (1b1, 3a1, 1b2) of liquid water. The measured β values are in excellent agreement with scattering simulations. In the case of the valence orbitals the influence of the solvation shell is no longer negligible. This effect was accounted for by using βgen values retrieved from independent photoelectron studies on small neutral water clusters as described in ref. 32. The small clusters mimic the local solvation motif of the liquid, while essentially retaining the PADgen as electron transport scattering is negligible on the length scale of the cluster dimension. For the eKE range shown in the inset of Fig. 4a, βgen lies between ∼0.5 and ∼1. This again highlights the strong influence of electron-transport scattering, which reduces the genuine values to the measured values between ∼0.1 and 0.3. This effect remains active even at much higher eKE values, as confirmed by a recent valence ionization study of liquid water reporting β parameters over a very broad energy range up to eKEs of 700 eV.33 The comparison of measured and computed anisotropies leads to the conclusion that the reduction in β at high kinetic energies is mostly due to scattering rather than rehybridization due to solvation.33β parameters in the valence region have also been reported for large neutral water clusters as a function of cluster size25 (Fig. 4b). As we discuss below (Section 1.2), electron scattering cross sections in large water clusters exceed those in liquid water.
 | ||
| Fig. 4 (a) Comparison of experimental and calculated anisotropy parameters β in liquid water.10 The black dots show experimental β values for ionization from the O 1s orbital of liquid water from ref. 30. The full black line shows a prediction for the measured β based on electron transport scattering calculations. As explained in ref. 10, these calculations used measured gas phase values from ref. 30 as input for the genuine anisotropy parameters of the liquid phase, βgen, and an electron scattering calculation to account for the influence of electron scattering on measured values. The shaded green area represents the uncertainty of the calculation. The good agreement between experiment and simulation demonstrates how well detailed electron transport scattering calculations can predict experimental liquid phase anisotropies. The same holds for ionization from the valence orbitals (1b2, 3a1, and 1b1) of liquid water. The corresponding comparison between measurements (black dots, from ref. 50) and simulation (full black line10) is shown in the inset of Fig. 4a. The input values βgen used in the simulations were taken from photoelectron studies on small neutral water clusters described in ref. 32. Fig. 4a is reproduced from Fig. 2 of ref. 10 with permission, Copyright ©2011 by American Physical Society. (b) Anisotropy parameters β of water clusters.25 The black dots show measured β values for water clusters as a function of the cluster size 〈n〉 for ionization from the 1b1 orbital of water. High harmonic radiation at a photon energy of 26.5 eV was used for ionization. 〈n〉 is the average number of H2O molecules in the clusters. The red, green and blue lines show predictions for β of water clusters as a function of 〈n〉 from electron transport scattering calculations using gas phase, cluster and liquid phase scattering cross sections, respectively. The comparison with the experimental data clearly reveals that only the simulation using the cluster cross sections (green line) reproduces the cluster experiment, while the simulations with gas phase (red line) and liquid (blue line) cross sections predict too small and too high values, respectively. This visualizes on the level of anisotropy parameters that electron scattering cross section in water clusters differ both from those in the gas and from those in the liquid phase. The blue triangle is a prediction for β in a liquid water microjet (bulk liquid) for ionization at 26.5 eV using the liquid cross sections. The fact that this liquid β is similar to β of the largest clusters is accidental since convergence to infinite cluster size (bulk) is not yet reached for the largest clusters.25Fig. 4b is reproduced from Fig. 4 of ref. 25 with permission from the PCCP Owner Societies. | ||
The two cases reported in Fig. 4a, however, are an exception in terms of the availability of independent information on βgen. In most cases, βgen is not accessible from another independent measurement, but has to be determined from measured β values instead. This requires correcting the measured β values for the contributions of electron-transport scattering. A corresponding procedure is further outlined in Section 2 for the example of the hydrated electron in different aqueous environments. As explained above, such a correction is always required when information about genuine photoelectron distributions (e.g., βgen) is to be retrieved, because scattering strongly modifies the latter at all electron kinetic energies. The same holds for genuine electron binding energies in situations when they are strongly influenced by scattering, i.e., usually when the photon energy used for ionization does not exceed the VBE by more than ∼20 eV, as discussed above.
At this point, one should mention that the concept of genuine quantities is a heuristic approach implying a sequence of separate steps on different time and length scales from the (local) ionization event via the transport through the sample to the final detection. It is not a priori given that such a concept (similar to the subdivision of complex chemical processes into separate elementary reaction steps) is always applicable. It remains the subject of future studies to establish the conditions under which genuine properties can be defined. In this context it is important to keep in mind that the genuine properties themselves depend on the photon energy used for ionization. They can be particularly affected for ionization close to threshold because the final state depends on the energy in terms of the wave function both of the remaining ion core and the outgoing electron. Hence, a genuine photoelectron spectrum close to threshold can differ from the genuine spectrum obtained at high photon energies. For related reasons explicit near-threshold ionization effects exist, such as in the case of PECD (Section 3).
1.2 Scattering cross section for bulk liquid and clusters
The procedure to retrieve genuine binding energies and anisotropies generally requires an explicit model to describe the transport of electrons from their point of origin in the sample to the point of detection. With this model, the genuine spatial and energy distribution of electrons can be fitted to the measured data recorded by the detector (see e.g., procedure described in ref. 14). The fitted genuine spatial and energy distribution provide genuine binding energies and anisotropies. The modelling of the electron transport within the sample requires detailed knowledge of energy- and angle-dependent scattering cross sections (or equivalently MFPs) for all different scattering channels (all vibrationally inelastic, all electronically inelastic and elastic channels). For liquid water, the derivation of accurate scattering cross sections has proven to be extremely challenging in the sub-keV range. This holds for both theory and experiment. Theoretical models are usually based on different treatments of the dielectric response (ref. 60–67 and references therein). The various models differ markedly, in particular in the kinetic energy range below a few 10 eV, where their appropriateness is disputed. In the sub-excitation range (eKEs ≤ 7 eV), models are largely missing. A major reason for the uncertainty of the models in the eKE range below a few 10 eV is their difficulty to describe the complex contribution from vibrational excitations. However, as we have seen above, exactly these vibrational processes are the most important for a proper description of the influence of scattering on photoemission spectra. A further issue is the adequate description of the angular dependence of scattering parameters. For all these reasons, scattering parameters from current theoretical models are not sufficient for the accurate retrieval of genuine quantities from measured ones.For a long time, the major issue with retrieving scattering parameters for liquid bulk water from experiments was the incompatibility of the high vapor pressure of water with the requisite vacuum conditions. To work around this problem, Sanche and coworkers determined detailed scattering cross sections in the kinetic energy range below 100 eV from electron-energy loss experiments using amorphous ice as a proxy for liquid water.11,49 The use of these ice data as a substitute for liquid cross sections has been discussed controversially, even though general physical considerations clearly hint at a very similar scattering behavior in the two phases.10,11,49 Photoelectron studies on liquid water have only become possible in combination with water microjets and more recently with water droplets,2,4,24,26,28,55,68–70 (compare Fig. 1) because these two samples can deal with the issue of the high vapor pressure of water. So far, however, liquid microjet studies have only reported electron attenuation lengths (EALs),30,31,33,38,71 but no detailed scattering parameters. One reason for this is that the information content of many microjet studies is limited, largely because angle-dependent information was often not recorded. The undefined (averaged) surface orientation of a cylindrical liquid jet, with the surface normal having all orientations between 0 and 90° along the curvature with respect to the detection axis, is one issue here. A more defined flat surface (no variation of surface normal relative to detection) may be prepared with a flat jet,29 which would make angle-dependent measurements more consistent. The combination of droplets with photoelectron VMI provides decisive advantages because the retrieval of angle-dependent and droplet size dependent information is straightforward and optical confinement can be exploited.24,26,51 VMI enables angular multiplexing, and the variation of size and related tuning of optical confinement effects maximizes the information content of electron scattering by modifying the point of origin of the electrons with respect to the droplet's surface.24,26 We have used this method to determine detailed scattering cross sections for liquid water in the sub-excitation range,10,14,24i.e., in a region where scattering corrections are very important. These studies showed that the liquid and amorphous ice cross sections are identical within uncertainties.10,11 The same should also apply at higher kinetic energies.11,49 From a comparison of available liquid water photoemission data with amorphous ice simulations using an extension of the model of ref. 11 and 49, we could indeed confirm that liquid water and amorphous ice have very similar scattering properties in the entire sub-keV range, i.e., that the same scattering parameters apply to both phases.10 The scattering cross sections for liquid water over the entire sub-keV range recommended by us are available from the SI of ref. 10, with a selection of different MFPs and cross sections retrieved from these data shown in Fig. 2b and c, respectively. This set of data corresponds to the most detailed scattering data for liquid water available to date. As we demonstrate in Section 2, they allow correcting measured photoelectron spectra and anisotropies for the influence of scattering contributions to retrieve genuine quantities. We would like to point out that currently available experimental data for liquid water do not contain sufficiently reliable information on certain scattering processes (e.g., secondary electron formation). Further refinement of the corresponding scattering parameters thus has to await improved experimental data. It should be emphasized that detailed electron scattering cross sections are not only important for the analysis of photoemission data but are also crucial ingredients for modelling radiation-damage processes in aqueous systems.72,73
Recent photoemission studies on large water clusters have shown that electron-transport scattering cross sections in confined systems can differ from those in the extended condensed phase.25 We found that the cross sections in large water clusters exceed those in liquid water, but are smaller than those in the gas phase. This is illustrated in Fig. 4b, which shows β parameters for ionization from the 1b1 valence orbital of water as a function of the average cluster size 〈n〉. The experimental β values (circles) decrease with increasing cluster size because more scattering events take place with increasing cluster size. This behavior is well reproduced by simulations using cluster cross sections from ref. 25 to describe transport scattering (green line). The blue and red lines, however, show that this is not the case when liquid or gas phase cross sections are used for the simulation, respectively. The liquid-phase cross sections are too small and the gas-phase cross sections are too large to properly describe scattering in clusters. This can be rationalized by the different dielectric screening in the cluster compared with the liquid and the gas phase. The interaction between electron and water is electromagnetic in nature, and thus scales inversely with the dielectric constant. The cross sections scale with the square of the interaction matrix elements and thus with the inverse square of the dielectric constant. Adding the dielectric screening to the gas phase scattering leads to the cluster cross sections of ref. 25.
2. Hydrated electron in water clusters and liquid water
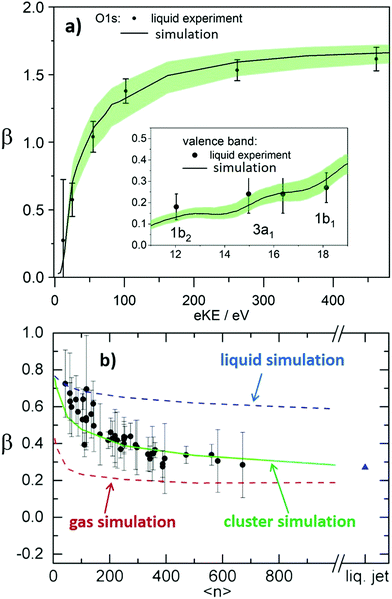
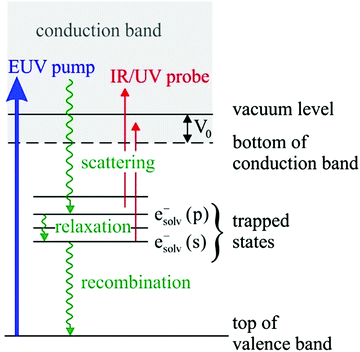
Solvated electrons in molecular liquids, especially in water, have sparked broad interest because of their widespread occurrence and their fundamental properties (ref. 14, 15, 44–47, 51, 54, 74–87 and references therein). The hydrated electron is one of the simplest quantum solutes. Such solvated excess electrons play an important role in chemistry and radiation damage of biological materials, where they appear as intermediates in various charge-induced, charge-transfer and reactive chemical and biological processes. The hydrated electron is one of the very few solutes for which photoemission studies have been performed in different aqueous environments, including liquid water microjets (bulk water), neutral water clusters, anion water clusters and Na-doped water clusters.14,15,44–47,51,54,74,80–86 Furthermore, it has also received broad attention from theory (ref. 75–79 and references therein). It is therefore a unique system to compare the genuine properties of the same solute in different environments, and with results from theory.Hydrated electrons are inter-band, trapped states, which lie energetically between the top of the valence band and the bottom of the conduction band, depicted in Fig. 5. This representation relies on the description of liquid water as a large-band-gap semiconductor, with an associated valence and conduction band.88–90 We will come back to that description in Section 4 when addressing explicit surface properties of liquid water and aqueous solutions. In this section, we focus on the properties of the energetically lowest lying s-state (esolv− in Fig. 5), i.e., on the electronic ground state of the hydrated electron. A generally accepted picture is that the ground-state structure corresponds to a cavity with an s-like orbital character.75,77 There are various possibilities to experimentally produce hydrated electrons in aqueous environments. One consists of light excitation either above or below the vacuum level (e.g., extreme ultraviolet (EUV) pump laser in Fig. 5) and subsequent relaxation into the s-state51,81,91–93 (and references therein). Different mechanisms for solvated electron formation involving hydronium cation formation have been proposed, e.g., “hot H atom mechanism” or “proton-coupled electron transfer”94–97 (and references therein). Other possibilities are the formation via a charge-transfer state,45,71,86,98,99 or an electron attachment process in the case of water anion clusters.46 In Na-doped water clusters, hydrated electrons form spontaneously by charge separation of the Na s-electron and the Na+ ion.47,74 Photoemission spectra or images are then recorded usually after laser ionization in the UV range (e.g., UV probe in Fig. 5), from which measured binding energy spectra and photoelectron anisotropies are deduced. Fig. 6 presents photoemission spectra of the hydrated electron in a liquid microjet as a function of hν (see legend) exhibiting large spectral changes indicative of severe distortions of the genuine photoelectron spectrum.14 The measured VBE (eBE at the band maxima) varies over a broad range from ∼3.3 to 4.5eV.44 In the past, measured values of VBE and β obtained from different measurements of the hydrated electron in the same or in different environments were directly compared with each other. However, this comparison of measured quantities is not meaningful because VBE and β are influenced by electron transport scattering:
 | ||
| Fig. 5 Schematic energy diagram of solvated electrons in water, esolv−. Hydrated electrons are trapped interband states. Two electronic states are indicated in the figure, the electronic ground state, esolv−(s), and the first electronically excited state esolv−(p). Binding energies and photoelectron anisotropies of the former are discussed in the present work (see also Tables 1 and 2). The wiggly lines indicate different relaxation processes that occur after formation of the hydrated electron with a EUV pump laser pulse, which can be probed with a time-delayed IR/UV probe pulse. These processes include deactivation by electron scattering processes, solvent relaxation and geminate recombination (see references in ref. 85). V0 correspond to the escape barrier mentioned in the caption of Fig. 2b and c. | ||
 | ||
| Fig. 6 (B) Electron binding energy (eBE) spectra of esolv−(s) in liquid water at twelve different photon energies, hν, of the ionizing laser indicated in the legend.14 The colored lines correspond to measured spectra, and the eBE values at the maxima of the bands correspond to measured vertical binding energies (VBE), which vary between ∼3.3 and 4.5 eV. The stars represent the genuine binding energy spectrum, eBEgen, with a VBEgen of 3.7 eV. It represents the binding energy spectrum of esolv−(s) that has been corrected for the influence of electron transport scattering. This genuine spectrum was retrieved from a simultaneous fit to the spectra measured at different hν, employing detailed electron scattering simulations based on a Monte Carlo solution of the transport equation.14 Figure reproduced from Fig. 3 of ref. 14 with permission from Science Advances under Creative Commons Attribution-NonCommercial International License (CC BY-NC 4.0; https://creativecommons.org/licenses/by-nc/4.0/). | ||
VBEgen, βgen → electron transport scattering → VBE, β
Because of the different influence of electron scattering depending on the conditions under which VBE and β were measured, a meaningful comparison can only be made at the level of the genuine values, VBEgen and βgen, which are not influenced by transport scattering. As mentioned in Section 1, VBEgen and βgen can in principle be retrieved from VBE and β by correcting the latter for the effects of electron scattering:VBE, β → correction for electron transport scattering → VBEgen, βgen
Such a correction is complicated by the fact that the degree of electron scattering depends not only on the photon energy used for ionization (e.g., Fig. 2b, c, 3 and 6) but also on the type of environment (e.g., clusters versus liquid; see Section 2, Fig. 4b). To account properly for electron scattering therefore requires detailed knowledge of how electron scattering cross sections depend on energy and on the specific solvent environment. While this information is not yet available for most solvents, the situation is more favorable in the case of water. The detailed cross sections recently proposed for electron scattering in the liquid and in clusters10,11 make it possible to retrieve VBEgen and βgen for the ground state of the hydrated electron.14,15,51 This was achieved by fitting a common genuine eBE spectrum to the experimental spectra recorded at different hν, using a probabilistic transport scattering model and the scattering cross sections for water.14 The stars in Fig. 6 indicate the retrieved genuine binding energy spectrum which narrows down the broad range of measured VBE values to a single genuine value, yielding VBEgen = 3.7 ± 0.1eV. Results are summarized in Tables 1 and 2, and briefly discussed in the following.| Environment | VBEgen [eV] |
|---|---|
| a Earliest reported anion value 3.3 eV in ref. 100. Another recent value is 3.9 eV from ref. 83. | |
| Experiment esolv− in (H2O)liquid | 3.70 ± 0.1014 |
| Experiment esolv− in (H2O)n (n ∼ 300) | 3.70 ± 0.1515 |
| Experiment esolv− in Na(H2O)n (for n > 6) | ∼3.747 |
| Extrapolated experiment esolv− in (H2O)n− (internally-solvated electron) | ∼3.646![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| Theory esolv− in (H2O)liquid | 3.38–3.75101–103 |
Table 1 compares VBEgen of the ground-state hydrated electron in the different environments, i.e., liquid water, neutral water clusters, anion–water clusters and neutral Na-doped water clusters. Surprisingly good agreement is found in all four different environments,14,15,46,47,83,100 and also fairly good agreement with the theoretical predictions.101–103 Three points are worth mentioning here: (i) Since the polarization shift between the neutral ground state and the anionic state is cluster-size dependent,46,83,100 vertical binding energies for clusters must first be extrapolated to infinite cluster size so that they can be compared with bulk liquid values. Table 1 thus quotes extrapolated values for anionic water clusters. For neutral and Na-doped clusters, by contrast, such an extrapolation is not required. It has been shown that the VBE of Na(H2O)n clusters already reaches the liquid bulk value at a cluster size of n ∼ 6.47,74 This can be rationalized by assuming that in these systems the charge-separated ground state (esolv−(s) and H+(aq) in (H2O)n clusters, and esolv− and Na+(aq) in Na(H2O)n clusters) experiences the same polarization shift as the cationic final state; i.e., by a cluster-size independent polarization shift. (ii) Several different isomers of the hydrated electron (internally-solvated and surface-solvated electrons46,82,83,100) with distinct binding energies were identified for anion water clusters, while the spectra of the hydrated electron in the neutral water clusters do not contain any signatures that would hint at the coexistence of different isomers (e.g., surface electrons with distinct energetics). The latter also seems to hold for solvated electrons in liquid water.71,76 (iii) The smallest observed neutral cluster that can sustain a solvated electron contains about 14 water molecules.85 How this compares with anion clusters remains unclear since the binding motif of the excess electron in small water clusters also includes dipole-bound states and electrons bound to specific water molecules.100,104,105
The influence of electron scattering on the photoelectron anisotropy is particularly pronounced because even a single scattering event can significantly change the trajectory of the electron. Table 2 lists values of the measured β and the genuine βgen for the hydrated electron in the different environments. For the relatively small anionic (H2O)n− and neutral Na(H2O)n clusters, which contained less than a few tens of water molecules, βgen![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47,54 and β are identical. The influence of transport scattering is negligible in such small clusters.25 This, however, changes completely for systems that contain more than a few hundred molecules, i.e., in the large, neutral (H2O)n clusters15 and in bulk liquid water45 in Table 2. The biggest effect is observed in the latter because the electron undergoes many scattering events before it escapes into vacuum where it is detected. As a result, the measured PAD becomes almost isotropic and β almost vanishes, in spite of a fairly high value of βgen of 0.6. The neutral (H2O)n clusters show a similar behavior, although the difference between β and βgen is less pronounced. At first glance, this seems surprising because the scattering cross sections in clusters are actually larger than those in the bulk liquid25 (see also Section 1.2). But, the trajectories in the cluster are shorter than in the liquid, evidently out-weighing the effects of the larger cluster-scattering cross sections. As for the VBEgen (Table 1), we find surprisingly good agreement for the βgen values in the different environments, which all lie around 0.6. The relatively high βgen value is consistent with the computed s-like cavity structure of the ground-state structure of the hydrated electron. The small measured β of the large neutral (H2O)n clusters, i.e., without correcting for scattering, would not have been consistent with an s-like character of the ground state.
47,54 and β are identical. The influence of transport scattering is negligible in such small clusters.25 This, however, changes completely for systems that contain more than a few hundred molecules, i.e., in the large, neutral (H2O)n clusters15 and in bulk liquid water45 in Table 2. The biggest effect is observed in the latter because the electron undergoes many scattering events before it escapes into vacuum where it is detected. As a result, the measured PAD becomes almost isotropic and β almost vanishes, in spite of a fairly high value of βgen of 0.6. The neutral (H2O)n clusters show a similar behavior, although the difference between β and βgen is less pronounced. At first glance, this seems surprising because the scattering cross sections in clusters are actually larger than those in the bulk liquid25 (see also Section 1.2). But, the trajectories in the cluster are shorter than in the liquid, evidently out-weighing the effects of the larger cluster-scattering cross sections. As for the VBEgen (Table 1), we find surprisingly good agreement for the βgen values in the different environments, which all lie around 0.6. The relatively high βgen value is consistent with the computed s-like cavity structure of the ground-state structure of the hydrated electron. The small measured β of the large neutral (H2O)n clusters, i.e., without correcting for scattering, would not have been consistent with an s-like character of the ground state.
The above examples show how important it is to account for the influence of electron transport scattering (i.e., to retrieve genuine values) when comparing binding energies and anisotropies in different solvent environments or from different experiments. For the hydrated electron, we find very similar values for VBEgen and βgen in the four different aqueous environments, and in addition good agreement with theoretical predictions. Furthermore, we and others51 (and references therein) have recently shown that the relaxation dynamics of excited-state solvated electrons into the s-ground state, for below and above band-gap excitation, is also similar in large neutral clusters and in liquid water. It would be tempting to conclude that the nature of the ground-state solvated electron must be identical in the different aqueous environments. This might be rash, however, since neither binding energies nor anisotropies contain sufficient information to draw an unequivocal conclusion. To give an example, the cavity in which the solvated electron resides could differ in the various aqueous environments, while the photoelectron spectra might still look very similar. A hypothesized long-lived surface electron in liquid water with considerably lower binding energy has not been confirmed.71,76
3. Near-threshold ionization processes in liquid water and aqueous solution
In Sections 1 and 2 we have seen that low eKEs cause distortions of genuine photoelectron band shapes which makes the determination of absolute energies either elusive or requires a complex spectral analysis by taking into account all electron scattering processes to retrieve the original undisturbed spectrum. Note that retrieving the genuine spectrum of a concentrated aqueous solution is even more challenging since electron scattering processes will differ from those in neat liquid water.36 Such problems and the intricate and laborious analysis they necessitate can be effectively circumvented though, when using sufficiently high photon energies, readily available from synchrotron-light facilities, resulting in correspondingly high eKEs (>12–15 eV (compare Fig. 3). This is rather straight-forward for retrieving water eBEs, but detection of esolv from liquid jets is more complicated.93 It requires femtosecond pump-probe schemes, i.e., UV excitation pulses in conjunction with sufficiently large probe photon energies, EUV and higher, e.g., based on high-harmonic generation. In addition, pulse repetition rates need to be on the order of 10 kHz and higher, so as to keep the pulse energies low enough to avoid the formation of space charges on the liquid-jet surface. Surface charging of aqueous jets will be detailed in Section 4. An associated current technical challenge is to extend the photon-energy range into the soft X-ray region, up to 600 eV, while maintaining sufficiently high repetition rates and pulse power to ionize the water oxygen 1s core level (such as currently developed by the Wilkinson group106).On the other hand, several phenomena, other than those considered this far, produce sufficiently large effects only in near-threshold ionization, i.e., they are “intrinsic” near-threshold phenomena, for which the above-mentioned issues in the liquid phase cannot be circumvented by using higher photon energies. Perhaps the most familiar example is post-collision interaction (PCI).16,17 Core-level ionization usually leads to a short-lived, highly excited and positively-charged species (for instance H2O+*) which interacts with the outgoing photoelectron. Depending on the photoelectron's KE, it may have traveled only a short distance when the decay and subsequent emission of a secondary (Auger) electron occurs. Both electrons then interact with each other in the Coulomb field of the then doubly-charged ion. This effect will be strong when the eKE of the photoelectron, adjustable by the photon energy, is much smaller than that of the Auger electron. Within a most simple classical picture, this can be viewed as the Auger electron overtaking the photoelectron, and the latter thus sensing a ‘change of charge state’ (i.e., the ion is screened less after the Auger electron has passed), e.g., H2O+ into H2O2+. Coulomb interaction of the two electrons with the ion then leads to a decrease of the eKE of the photoelectron, associated with a small eBE shift. The opposite is true for the Auger electron, which will speed up and exhibit a positive energy shift from the screening of the ion by the photoelectron. No such measurements have been reported for solutions. Arguably, PCI might provide a tool to directly determine core-level lifetimes in aqueous solution, and even probe (photo)electron scattering in solution. Such routes are explored jointly with the Thürmer107 and Slavíček108 groups.
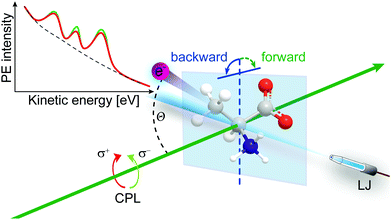
Another ionization-threshold effect that has more recently attracted much attention is chirality-sensitive and large-cross section Photoelectron Circular Dichroism (PECD)21,109 of chiral molecules, uniquely connecting molecular electronic structure to chirality. In addition, it is site-specific and sensitive to chemical environment and especially to the conformation of small (bio-)molecules.110,111 Besides a large chiral asymmetry, core- and valence-shell studies have shown that PECD is a strongly dynamic (final-state) effect showing a rich photon energy dependence and also that it clearly depends on the ionized orbital (initial-state effect).21,112,113 PECD leads to a forward–backward asymmetry in the photoelectron emission intensity relative to the light propagation axis. In such an experiment a chiral molecule is ionized by circularly polarized light (CPL), and the sign of the asymmetry depends on the enantiomer that is probed and on the helicity of the ionizing radiation, left or right-, l-CPL or r-CPL. That is, the asymmetry can be flipped when either replacing a given enantiomer by its other form, or upon changing the light helicity. Liquid-jet PECD studies require to be performed solely in the backward-detection geometry (with respective variation of enantiomer or light polarization) though, depicted in Fig. 7, i.e., the convenient simultaneous detection of the forward-backward asymmetry as for gas-phase samples is not possible since electrons cannot be probed from the far side of the liquid-jet target. This is due to the combination of strong light absorption in the dense liquid and the small electron escape depth,29 the latter making PES distinctively surface sensitive. And most noticeable, the PECD effect exceeds more conventional circular dichroism processes by orders of magnitude as its mechanism is solely based on the larger electric dipole transition amplitudes. However, asymmetries are largest for photon energies within only a few electron volts above ionization threshold. PECD has been intensively explored for isolated chiral molecules, clusters and nanoparticles, including single-photon ionization and multi-photon processes and associated time-resolved ultrafast studies.114–119 But measurements of PECD effects in aqueous solution have not been reported even though chiral complexes are highly relevant to life sciences, where hydration and chiral recognition are fundamental biochemical processes, typically occurring at aqueous interfaces.
The PECD magnitude is expressed via the chiral anisotropy parameter b1. It is given by the more general expression:
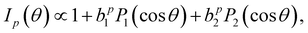 | (4) |
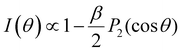 for the case of CPL. Particularly relevant for the present work is that for the specific case of a chiral molecule ionized with CPL, the P1(x) (first-order Legendre polynomial) coefficients no longer vanish for symmetry reasons. Furthermore, they switch signs with respect to a change of light polarization:
for the case of CPL. Particularly relevant for the present work is that for the specific case of a chiral molecule ionized with CPL, the P1(x) (first-order Legendre polynomial) coefficients no longer vanish for symmetry reasons. Furthermore, they switch signs with respect to a change of light polarization: 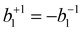 . The same change in sign of the b±1 coefficient is also encountered upon changing the enantiomer. As
. The same change in sign of the b±1 coefficient is also encountered upon changing the enantiomer. As 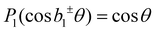 , the largest asymmetry (largest PECD effect) can be observed at θ = 0° (or 180°). In present-day liquid-jet PECD experiments a single detection angle of 50° in the backward direction has been realized.29 This angle is close enough to the magic angle (θ = 54.7°;
, the largest asymmetry (largest PECD effect) can be observed at θ = 0° (or 180°). In present-day liquid-jet PECD experiments a single detection angle of 50° in the backward direction has been realized.29 This angle is close enough to the magic angle (θ = 54.7°; 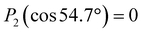 ) largely to suppress the angular dependence of the electron intensity on the dipolar parameter β. Note that the PECD asymmetry vanishes in the dipole plane (at θ = 90°), which is the standard (and only) electron detection arrangement realized in previous LJ-PES setups.29
) largely to suppress the angular dependence of the electron intensity on the dipolar parameter β. Note that the PECD asymmetry vanishes in the dipole plane (at θ = 90°), which is the standard (and only) electron detection arrangement realized in previous LJ-PES setups.29
Aqueous-phase PECD is a yet untouched field of research, with literally no results reported from aqueous solution but a single pioneering study on liquid fenchone has been reported.120 Detection and quantification of PECD in aqueous environment would indeed be a major accomplishment for several reasons. It potentially enables the characterization of the effect of hydrogen-bonding and of the interaction with solvation-shell ions on PECD, by way of comparison with measurements for a suitable reference molecule performed in the gas phase. Another intriguing question is whether a chiral molecule induces a chiral imprint on its solvation shell. In the longer run and within a yet larger context, there is a potential to unravel asymmetric (stereo-selective) chemical reaction mechanisms in the aqueous phase. This encompasses both relatively slow ground-state stereo-selective chemical reactions of chiral species/reactants dissolved in water, and ultrafast asymmetric photochemical reactions, where the chirality of the irradiating light is transformed into chiral molecular structural information in the solution.
From the discussion in Sectionss 1 and 2 we expect that such near-threshold ionization measurements are very challenging. Even the mere extraction and quantification of the associated genuine PES signal arising from the chiral center will be complicated by the large LET overlapping with the photoelectron peaks of interest for eKEs < 12–15 eV. Indeed, electron scattering, which cannot be switched of, prohibits any easy access to liquid-phase PECD. And yet, there is a demand for significant instrumentation developments that would permit the recording of PECD images, using some sophisticated VMI spectrometer compatible with liquid jets. One major obstacle to the realization of such a device is that it cannot image the full photoelectron angular distribution (PAD) from a cylindrical jet since photoelectrons born inside the solution and heading away from the detector will not turn around due to the electron-scattering processes. Moreover, the large background vapor pressure in a liquid-jet experiment (∼10−3 mbar to 10−5 mbar range water pressure, depending on setup and type of liquid jet),29 necessitates some efficient pumping for electron detection but excludes typical differential pumping to be used.
In the meantime, ongoing measurements with liquid jets are restricted to detecting the PECD signal solely into the backward-emission direction. This is realized by a dedicated experimental setup, equipped with a HEA with micron-sized entrance orifice, and very small effective acceptance angle.29 Current studies, exploring liquid-jet core-level PECD from amino acids in solution, indicate that the effect can indeed be detected for not too small eKEs. Although, these measurements are performed under conditions where PECD cross sections are arguably very small, existing experimental instrumentation seems sufficient to make several promising observations. One aspect would be the effect of the charge state of an amino acid, tuned by varying the solution pH, on PECD. Note that unlike in the gas phase, anionic, zwitterionic, and cationic chiral molecules can be readily produced in sufficient quantities. Overall, these studies promise to mark the beginning of a new research area, accompanied by a better understanding of electron scattering processes in aqueous solution.
4. Accurate vertical ionization energy and condensed-matter approach to LJ-PES from liquid water and aqueous solutions
Valence electronic structure, and in particular the lowest vertical ionization energy, VIE (or equivalently vertical binding energy, VBE; compare our comment in Section 1), is intimately connected with chemical reactivity.121 It is the most probable energy associated with the vertical promotion of an electron into vacuum, i.e., without giving it any excess energy, and with no nuclear rearrangement being involved. Experimentally, the value is determined from the energetic position of maximum intensity of the respective photoelectron peaks. Liquid water's lowest VIE1b1(l) is 11.33 eV which corresponds to the ionization of the highest occupied molecular orbital, 1b1, referenced to a yet to be specified vacuum level. With that notation, water is described within the common molecular orbital formalism. The effect of condensation, when going from gas to liquid phase, is then considered as a weak perturbation of the orbital structure upon hydrogen bonding. This has been the description of liquid water adopted since the very first LJ-PES measurements.68,122 A major deficiency, however, is that the simple molecular-physics picture does not explicitly account for the liquid-water and aqueous-solution surface. In fact, water is a large-band-gap semiconductor which calls for a conceptional inclusion of a surface. Associated with that is the question how a condensed-matter concept can help to characterize several previously inaccessible quantities of liquid water and aqueous solutions, the solution's work function being one of them. Before addressing the implementation of these descriptors, we return to above-stated value of liquid water's lowest ionization energy of 11.33 eV. This is useful in order to appreciate the need of an advanced LJ-PES technique, not only for accessing additional solution properties; here we follow the presentation by Thürmer et al.22We begin with a discussion of VIE1b1(l) = 11.33 eV itself. The exact value has been debated for more than a decade since the very first measurements about 20 years ago,68,122 reporting an energy range between 11.16 eV68 and 11.31 eV,123 with one recently reported outlier of 11.67 eV124 which, however, results from improper energy calibration.22,125 Ironically, though, all these measurements have used the same unreliable minimalistic method, in the following simply referred to as ‘Gas-Phase Method’, which is dubious for the determination of an accurate value of VIE1b1(l). Aside from very few exceptions, previous LJ-PES measurements have detected a narrow photoelectron KE range which just includes the leading liquid and gas-phase water signals, 1b1(l) and 1b1(g); the latter arising from ionizing the gaseous water molecules surrounding the liquid jet. Then with VIE1b1(g) accurately known (12.621 ± 0.008 eV126), it has been common practice to determine VIE1b1(l) from the difference of the measured peak positions, ΔEg-l = VIE1b1(g) − VIE1b1(l). Conveniently, a determination of the exact photon energy used is not required. However, ΔEg-l, was found to vary from experiment to experiment, and between different laboratories, which is attributed to multiple sample charging effects and contact-potential differences that occur in liquid-jet spectrometer systems, and causes an electric field gradient between the jet and the electron detector. This is sketched in the inset of Fig. 8a, where electrons experience a different field strength from the parasitic potential depending on their origin of creation. Liquid jet charging can be of different origin, arising from electrokinetic charging by the liquid flow, from uncompensated charges upon ionization of low-conductivity samples, and change or evolution of the solution surface potential due to a molecular dipole layer.127 A quantitative elimination of each individual contribution is illusive and an overall compensation of the sum of all effects is very challenging to accomplish experimentally, as detailed by Thürmer et al.;22 most commonly electrokinetic charging is mitigated by adding a well-determined small amount of salt,123 which, however, is extremely impractical and may be even impossible for an arbitrary aqueous solution. From the inset of Fig. 8a it is inferred that gaseous water molecules ionized at different distance from the liquid jet will take up different energies in the electric field between liquid jet and analyzer which leads to a broadening of the gas-phase water 1b1 peak and to associated energy shifts. Thürmer et al.22 discussed the implications when measuring PES spectra under non-field-free conditions. The main conclusions are that (1) accurate liquid water BEs cannot be determined, and (2) the seemingly unobjectionable procedure to use an inaccurate VIE1b1(l) to find solute BEs is very problematic and not justified. To explain the former point, we consider water valence PES spectra measured under field-free and non-field-free conditions, respectively. Both are shown in column (a) of Fig. 8, with the displayed spectral range covering water 1b1, 3a1, and 1b2 orbitals; see Fig. 3 for peak labels. One clearly sees the broadened gas-phase peak in the case of an electric field (not field-free; right), while at zero field the water gas-phase peak is sharp and occurs at its undisturbed energy position (left). As mentioned, it is possible to achieve conditions where the gas-phase peak becomes sharp by tuning electrokinetic charging through the addition of empirically determined amounts of salt to precisely compensate for other potentials such as the contact potential (see also Fig. 8 below). Hence, the field-free condition is a balance of all acting fields to yield a zero effective potential, which, however, hinges on the precise experimental conditions. This procedure, however, is very time-consuming, as it has to be repeated on a day-to-day basis for each particular experimental condition. Furthermore, it only achieves a net compensation of the sum of all charge contributions. Note that field-free conditions are not achievable though for most aqueous solutions, owed to the different electrokinetic properties and surface propensities of differently charged solute species. With its small (yet experimentally to be determined) surface dipole, water is rather an exception.
 | ||
| Fig. 8 (a) Top: Depiction of potential drop between charged liquid jet (LJ) and grounded electron detector. Horizontal arrows indicates that photoelectrons from water gas-phase ionization gain different energy in the resulting electric field gradient than photoelectrons from the liquid surface, resulting in different measured eKEs depending on the distance of the point of origin from detector/jet. Bottom, right: Valence liquid-water jet photoelectron spectrum measured with the ‘Gas-Phase Method’ (see main text) under non-field-free conditions, i.e., in presence of parasitic potentials, which is usually the case. Under these conditions VIE1b1(g) is not a reliable energy reference. Bottom, left: Valence liquid-water jet photoelectron spectrum measured with the ‘Gas-Phase Method’ under field-free conditions, i.e., where the solution and experimental conditions have been precisely tuned to eliminate all potentials. This leads to a sharp water 1b1 gas-phase peak, and correct peak separation from the liquid-phase 1b1 peak, such that ΔE = VIE1b1(g) – VIE1b1(l) yields the accurate VIE1b1(l) value, and VIE1b1(g) being the known literature value; see main text. (b) Left: A bias voltage applied to the LJ shifts all liquid features under the influence of an accelerating field, Eacc (blue spectrum); the gas-phase PE signal is smeared out and does not appear here. Biasing reveals the full LET curve and cutoff energy of the sample spectrum. Without bias (grey spectrum), the real cutoff is obscured by the work-function difference between the liquid and analyzer, ΔeΦ. Ecut constitutes a low-energy limit for photoelectrons to still overcome the liquid–surface barrier, and is thus connected to the local vacuum level above the LJ surface, Eloc,v. The precisely known photon energy, hν (vertical purple arrow) is used to map Eloc,v onto the measured spectrum and define the VIEvac scale. Thus, with the knowledge of hν and the energetic distance of a peak feature to the cutoff, ΔEw, the accurate VIE of this feature can be determined. (c) As for (b) but for an arbitrary aqueous solution; here, the spectra are arbitrarily aligned to the cutoff, which at the same time aligns Eloc,v. Changes in ΔEw directly translate to changes in the VIE. The lower part of this panel shows the full unbiased spectrum (compare to the spectra shown in panel A and bottom part of panel B). Fig. 8 is adapted from Fig. 1 of ref. 22 | ||
We next discuss the issues arising from inaccurate values of the water 1b1 BE in aqueous solution, VIE1b1(sol), as derived via the Gas-Phase Method. In previous works, this quantity has been determined under the generally erroneous assumption that VIE1b1(sol) = VIE1b1(l), i.e., with reference to the BE of neat liquid water, in the absence of a more suitable value. Only a handful of very recent studies22,23,128 have been in the position to determine accurate VIE1b1(sol) as well as solute values, VIEsolute, by applying the novel strategy which we describe in the following. This also implies that in almost all previous LJ-PES studies it was impossible, by experimental concept, to access solute-induced changes of the water electronic structure, which also prevented the determination of accurate VIEsolute values. Note though that in some cases, exemplified for low and high-concentration aqueous solutions of NaI,127 even the Gas-Phase Method enabled a reasonable estimate of solute-induced binding-energy effects. It is useful to begin by comparing the two different approaches with the help of Fig. 8a. Here, the spectrum shown to the right depicts a valence PES spectrum from an aqueous solution, representative of the many short-range solution spectra that have been previously measured, and based on which inaccurate VIE1b1(sol) as well as inaccurate VIEsolute values were inevitably inferred. Here, VIEsolute corresponds to a fictive (matching iodide) solute PES peak, obtained as the energy difference VIEsolute − VIE1b1(sol), taken as the maxima of the respective liquid-phase photoelectron peaks. In that approach VIEsolute is referenced to VIE1b1(sol), which is unknown. To illustrates the problem further we also consider the short-range PES spectrum from neat liquid water measured under field-free conditions, presented to the left in Fig. 8a. This spectrum exhibits a noticeable sharp gas-phase peak and a considerably smaller ΔEg-l compared with the spectrum on the right. The sharp gas-phase peak is a distinct signature of zero field between jet and analyzer, and hence the associated ΔEg-l will yield a VIE1b1(l) value close to the accurate value of 11.33 eV. By contrast, the broader shifted gas-phase peak in the spectrum on the right is a clear signature of non-field-free conditions, which prevent the determination of meaningful binding energies.
In the following we describe the recent advances in LJ-PES benchmarking which permit to access accurate absolute energetics of liquid water and aqueous solutions. This includes the determination of VIE1b1(l) and the justification of its value of VIE1b1(l) = 11.33 eV. The above discussion has demonstrated the requirement for a novel and robust experimental procedure that relies on an energy reference other than VIE1b1(g). The concept for that, exploiting the low-energy photoelectron signal cutoff, Ecut, introduced along with Fig. 3, has been widely applied in solid-state PES. Although the first measurement of Ecut from a liquid jet was reported as early as 2003129 the approach was only recently re-introduced130 and accurately applied.22,131 With Ecut experimentally determined, a given eBE of liquid water or of an aqueous solution can then be unequivocally assigned, as depicted in Fig. 8b (for neat water) and in c (for an arbitrary aqueous solution). We will explain this figure step-by-step. The spectrum (light grey) at the bottom is an extended version of the bottom spectrum of Fig. 8a, now including the LET and associated Ecut. However, the LET arising from liquid water overlaps with the energy cut-off of the HEA spectrometer (and often enough a diminishing photoelectron transmission at very low measured energies inside the HEA distorts the cutoff shape), making an accurate determination of the solution Ecut impossible. These contributions can be separated though upon applying a negative bias voltage to the liquid jet; the latter requires that the solution is sufficiently electrically conductive to support the applied bias, as discussed in detail in ref. 22; note that the exact value of the applied bias potential, and in fact other (parasitic) potentials present in the experiment are completely irrelevant for this method. The effect of the bias voltage is that photoelectrons from the aqueous phase are accelerated towards the grounded detector which results in a rigid shift of the entire liquid-phase PES spectrum to higher eKEs, and most important, to a separation of the two cutoff energies. This leads to the top (blue) spectrum in Fig. 8b. It is seen that the eKE of the water 1b1(l) peak can be accurately determined via its energy separation from Ecut, i.e., the spectral width, ΔEw. The associated VIE is correspondingly determined as VIE1b1(l) = hν − eKE1b1(l) + Ecut where it is implied that the photon energy is precisely known. The water gas-phase peak is no longer visible as it is massively broadened in the presence of a large enough bias voltage (see the discussion of Fig. 3). Note further that field-free conditions are no longer required with this approach, which will be referred to as the ‘Cutoff Method’ in the following. Thürmer et al.22 have applied this approach to neat liquid water, using a large range of exactly calibrated photon energies, spanning the (vacuum) ionization threshold region up to more than 900 eV above it, to explore if VIE1b1(l) is the same for the very surface region and bulk liquid water. We refer back to Fig. 2b for the expected ranges of probing depths into solution. VIE1b1(l) = 11.33 ± 0.03 eV was found for photon energies between approximately 25–300 eV (yielding 12 eV < eKEs < 290 eV), followed by a slight increase however on the order of the experimental error bars for hν > 300 eV. Until here we have been quite vague about the vacuum level the energies discussed here are referenced to. To address this, we refer to the distinction made in Fig. 8. The molecular approach, assuming ionization of gaseous species, refers to the transfer of a photoelectron to an infinite distance from the jet, which necessarily corresponds to the vacuum level at infinity, E∞v. In the case of a (liquid) surface, ionization energies refer to the local vacuum level, Elocv, but not necessarily to E∞v. This difference, corresponding to the small surface dipole of liquid water, related to the outer (Volta) potential eφouter,132 is shown in Fig. 8a. In simple terms, an electron ‘just outside the surface’ is in general still affected by the surface potential, which originates mostly from present surface dipoles (and possibly surface charges), and thus the experienced ‘local’ vacuum level must differ from the theoretical vacuum level at infinity.133 For this reason, the local vacuum level is somewhat dependent on the surface condition. For example, in an aqueous solution, which poses a strong solute-induced surface potential may have a local vacuum level which differs considerably from the vacuum level at infinity. The transition between both vacuum levels, as the distance from the surface increases, can be understood as the attenuation of the dipole field. Even neat water possesses a small surface dipole and thus non-zero eφouter. Its value for the aqueous–gas interface is expected to be on the millivolt-to-volt scale depending on solution properties. The exact value is yet to be experimentally determined, and should be possible with the new tools available.
As concluded above, the Cutoff Method illustrated in Fig. 8b is readily applicable to aqueous solutions as well as non-aqueous solutions (Fig. 8c). That is, we can now in particular access solute-induced electronic structure changes of the water solvent, and even observe the dependence on solute concentration, as recently demonstrated for sodium-iodide and tetrabutylammonium-iodide (TBAI) aqueous solutions.22,23,134 Equally, concentration-dependent solute–solute interaction effects on solute electronic structure can be measured. A most recent work has demonstrated the potential of the new experimental approach for the determination of solvent and solute BEs of liquid jets from liquid ammonia, benzene in liquid ammonia, and liquid (non-polar) benzene.128
In the remainder of this section, we discuss the novel information on the solution–vacuum interface potentially provided by the Cutoff Method approach. For that it is useful to describe the aforementioned experiment on aqueous TBAI solutions in some greater detail. TBAI is a strong surfactant, expected to form a considerable molecular dipole moment at the solution surface, and is thus an appropriate system to illustrate our new ability to measure this quantity. In ref. 23 LJ-PES spectra of aqueous TBAI solutions were reported as a function of concentration. One result of these measurements is that the water 1b1 energy, VIE1b1(TBAI), exhibits large energy shifts, up to 0.7 eV towards lower BE, with increasing concentration. This result is obtained with the Cutoff Method, fully analogous to the neat-water analysis, i.e., based on a measurement of Ecut and subsequent determination of ΔEw (see Fig. 8c). As discussed in ref. 22 and 23 the observed (large) energy shift could arise from electronic structure changes of the bulk solution, or from interfacial molecular dipoles, or from their combination. Several arguments have been made in favor of a considerable contribution from surface dipoles.23 Qualitatively, the drop of the work function, i.e., increase of the eKE of photoelectrons accelerated by the dipole field, is in line with the negative charge pointing into the solution and positive charge residing at the top surface. This corresponds to the commonly assumed structure of the TBA+I− segregation layer. A quantitative energy analysis would have to take into account the molecular and charge orientation at the interface, particularly the net normal surface dipole moment, and the solute concentration at the solution surface.23 But this does not need to be detailed further here. We rather explain how the surface dipole, which correlates with the work function of the solution, can be experimentally verified. For that we refer to Fig. 9 which is adapted from ref. 22. The figure shows the 1b1 PES spectra of neat liquid water (in blue) and of a 25 mM aqueous TBAI solution (in green; corresponding to one single TBAI monolayer coverage); the latter spectrum also exhibits signal from iodide 5p ionization. Experimental details are described in the figure caption. The important point to note is that these spectra have been measured from grounded liquid jets, under special experimental conditions, where parasitic potentials other than the contact potential between the liquid jet and the detector have been eliminated; this will be referred to as Fermi-aligned condition for reasons explained below. This is a different situation than the one depicted in Fig. 8a, where the contact potential is compensated as well to achieve field-free conditions. Indeed, the gas-phase peak of the neat-water spectrum in Fig. 8 is slightly broadened which indicates the presence of the non-zero contact potential in this case. We note that neither zero-field nor Fermi-aligned conditions are achievable for aqueous solutions in general, though.22 This condition is specifically prepared here to align the Fermi level of the liquid water/aqueous solution to that of the electron analyzer. Using the results of accurate VIE measurements explained above, we can affix VIE energy scales to the water 1b1 peak of each case, i.e., so that VIE1b1(l) = 11.33 eV and VIE1b1,TBAI = 10.7 eV, as extracted from the Cutoff Method; these represent the top-most two energy scales in the figure. Under these circumstances, i.e., when accomplishing conditions free of parasitic potentials (suppression of both the streaming potential and ionization-induced sample charging is given), one can make an attempt to introduce a Fermi energy of the solution which then connects to a (measurable) work function.22 We then have a means to determine the solution work function in order to distinguish bulk solution electronic structure changes. Experimentally, this requires the simultaneous measurement of the system's Fermi energy and the solution spectra. This, however, is just an auxiliary (hypothetical) strategy since large-band-gap semiconductors like liquid water do not exhibit a measurable Fermi edge itself since the electron density at the Fermi level/electrochemical potential is zero. Thus, the Fermi-edge spectrum of an external (metallic) reference electrode in equilibrated electrical contact with the solution has to be measured separately, and yet relating this external (metallic) reference spectrum to the spectrum of the solution is not straight-forward. One associated problem is the fact that the photoelectrons emitted from the metallic sample, a gold wire in the present case mounted next to the liquid jet, even though measured under jet operational condition, do not cross the solution (water) interface, and do not experience the usually present parasitic potentials from the liquid jet. Thus, in general the measured metallic spectrum cannot be directly related to a measured solution spectrum as both spectra experience different energy shifts; only under the condition that parasitic potentials from the liquid jet have been compensated can a direct comparison be attempted. Hence, the described procedure, which we refer to as the “Fermi Method”, arguably enables the measurement of rather accurate work functions of solutions. Coming back to Fig. 9, we see the measured Fermi edge and the respective spectral fit. Noticeably, the Fermi edge, defining the zero point of the VIEFE (EF) energy scale in the spectrum (bottom-most axis scale at the top of the panel), is the same for neat water and the TBAI aqueous solution under the sole assumption that both solutions were measured under conditions which are free of parasitic potentials. With eΦ being the difference between Evac and the solution EF, one finds VIEFE,1b1(l) = 6.60 eV and eΦwater = 4.73 eV for (almost) neat water. The respective values for the TBAI solution are, VIEFE,1b1,TBAI = 6.45 eV and eΦTBAI = 4.25 eV.
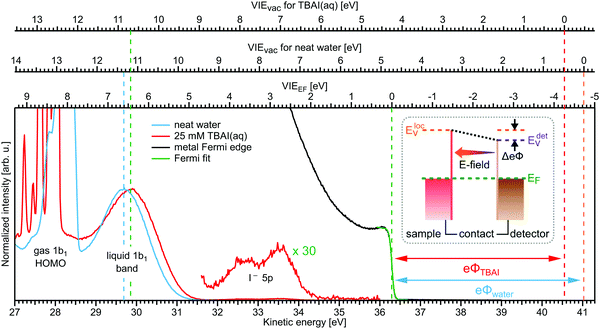 | ||
| Fig. 9 Valence PES spectra from neat liquid water (blue) and 25 mM TBAI aqueous solution (red) from a grounded liquid jets measured at 40.814 eV (He IIα line) photon energy. This measurement is done specifically under conditions free of parasitic potentials other than the contact potential, originating from the difference in work functions between the liquid jet/reference sample and detector. As shown in the inset, this ensures that the Fermi level is aligned for all measurements, including the metallic reference used to determine the position of the Fermi edge. The spectral range covers the 1b1 emission from gas (sharper peaks to the far left), liquid phase and the emission resulting from ionization of the iodide 5p orbitals in case of the TBAI solution. The figure also presents the PES spectrum from gold measured under jet operation conditions, shown in black (only the Fermi edge is visible). The bottom axis shows the as-measured kinetic energy scale (of the detector). The Fermi edge was fitted with a Fermi function (green line), and its position defines the zero point of the VIEEF energy scale in the spectrum (lowest energy scale at the top of the panel). This enables us to determine the VIEEF,1b1(l) value of 6.60 eV for (almost) neat water. For TBAI(aq) we determine VIEEF,1b1(sol) = 6.45 eV, and the solute features are found at VIEEF,5p1/2 = 3.80 eV and VIEEF,5p3/2 = 2.84 eV. Recalling that the VIEs of water's 1b1 orbital referenced to the (local) vacuum-level were VIEvac,1b1(l) = 11.33 eV for neat water and VIEvac,1b1(sol) = 10.70 eV for TBAI(aq), we can add a VIEvac scale for both solutions using the liquid 1b1 peak as fixpoint; these are the center (neat water) and top (TBAI) energy axes at the top of the graph. The difference between VIEEF and VIEvac each then gives, per definition, the solutions work function, eΦwater = 4.73 eV and eΦTBAI = 4.25 eV, respectively. Figure is adapted from Fig. 6 of ref. 22. | ||
Conclusions
We have reported on the current understanding of electron scattering processes in aqueous environments, ranging from bulk liquid water and aqueous solutions to water clusters, and its relevance to photoelectron spectroscopy of these systems in the sub-keV range. An important finding is that at electron kinetic energies lower than ∼15 eV inelastic electron transport scattering (mainly phonon and vibronic scattering) can severely disturb the genuine (intrinsic, nascent, original) photoelectron band shape, and thus hinder the direct measurement of vertical binding energies (ionization energies). Whenever possible, this can largely be circumvented by using photon energies for ionization that lie ∼15–20 eV above the ionization threshold of interest.34 Since electron scattering at these higher kinetic energies is strongly influenced by scattering via electronic channels, genuine band shapes and vertical binding energies are hardly disturbed by electron scattering. Elastic and inelastic electron scattering also render it impossible to directly measure genuine photoelectron angular distributions, which holds over the entire kinetic energy range for the angular distributions in contrast to the situation for the band shapes and binding energies. The reason for this is the high sensitivity of the angular distribution to any single elastic or inelastic scattering event. For cases, where the genuine band shapes, binding energies and angular distributions cannot be measured directly, they can be retrieved from the measured photoelectron spectra by accounting for the influence of electron scattering using suitable electron scattering models. We have demonstrated this method for the example of the solvated electron in different aqueous environments,14,15 including water microjets, neutral water clusters, Na-doped water clusters and anion water clusters. For these retrievals, we recommend using the detailed electron scattering cross sections for bulk liquid water from ref. 10 and for water clusters from ref. 25 and 32. It is worth highlighting that scattering cross sections for water clusters lie in between those of the gas and the liquid phase – mainly an effect of the different dielectric screening.25 We discussed two photoemission mechanisms, Post Collision Interaction (PCI) and Photoelectron Circular Dichroism (PECD), which occur only near the ionization threshold. Hence, the influence of electron scattering on band shapes, binding energies and photoelectron angular distributions are inevitably high. Both processes are expected to be fundamentally important in aqueous solution but currently their detection remains experimentally very challenging, requiring further technical development.However, electron transport scattering is not the only phenomenon that makes the derivation of accurate binding (ionization) energies of neat water or solutes in water challenging. We also discussed how an advanced liquid-jet PES method enables the measurement of accurate absolute energetics of both solvent and solute, including solute-induced changes of solvent electronic structure.22,23 Moreover, the novel method provides a means to access explicit surface properties of liquid water, such as solution surface dipoles and the related solution work function. The latter implies an introduction of the Fermi energy to solutions which for large-band-gap liquid water is not straight-forward. Yet, concepts presented here will help to make a perspective connection between LJ-PES electrochemistry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. W. acknowledges Stephan Thürmer and Iain Wilkinson for their strong involvement and continuous stimulating discussions on almost every aspect presented, and he thanks Stephan Thürmer for critical reading and comments on this manuscript. B. W. furthermore thanks all the Liquid-Jet Team at FHI for making this research possible. B. W. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and investigation programme (grant agreement No. 883759; AQUACHIRAL), from the Deutsche Forschungsgemeinschaft (Wi 1327/5-1), and support by the MaxWater initiative of the Max-Planck-Gesellschaft. R. S. thanks all group members and collaborators for their contributions to the work discussed in this perspective article. R. S. acknowledges funding from the European Union's Horizon 2020 research and innovation program from the European Research Council under the Grant Agreement No. 786636; and from the Swiss National Science Foundation (SNSF) supported by NCCR MUST, ETH-FAST, and SNSF project No. 200020_200306. R. S. is a grateful recipient of a Humboldt Research Prize from the Alexander von Humboldt Foundation and a Mildred Dresselhaus Guestprofessorship from the Centre for Ultrafast Imaging in Hamburg.References
- S. Hüfner, Photoelectron Spectroscopy: Principles and Applications, Springer-Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo, Hong Kong, Barcelona, Budapest, 1995 Search PubMed.
- B. Winter and M. Faubel, Photoemission from Liquid Aqueous Solutions, Chem. Rev., 2006, 106, 1176–1211 CrossRef CAS PubMed.
- R. Seidel, B. Winter and S. E. Bradforth, Valence Electronic Structure of Aqueous Solutions: Insights from Photoelectron Spectroscopy, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, 2016, vol. 67, pp. 283–305 Search PubMed.
- R. Dupuy, C. Richter, B. Winter, G. Meijer, R. Schlögl and H. Bluhm, Core level photoelectron spectroscopy of heterogeneous reactions at liquid–vapor interfaces: Current status, challenges, and prospects, J. Chem. Phys., 2021, 154, 060901 CrossRef CAS PubMed.
- S. Thürmer, M. Ončák, N. Ottosson, R. Seidel, U. Hergenhahn, S. E. Bradforth, P. Slavíček and B. Winter, On the nature and origin of dicationic, charge-separated species formed in liquid water upon X-ray irradiation, Nat. Chem., 2013, 5, 590–596 CrossRef PubMed.
- P. Slavíček, N. Kryzhevoi, E. F. Aziz and B. Winter, Relaxation Processes in Aqueous Systems upon X-ray Ionization: Entanglement of Electronic and Nuclear Dynamics, J. Phys. Chem. Lett., 2016, 7, 234–243 CrossRef PubMed.
- D. Hollas, M. N. Pohl, R. Seidel, E. F. Aziz, P. Slavicek and B. Winter, Aqueous Solution Chemistry of Ammonium Cation in the Auger Time Window, Sci. Rep., 2017, 7, 756 CrossRef PubMed.
- P. Slavíček, B. Winter, L. S. Cederbaum and N. V. Kryzhevoi, Proton-transfer mediated enhancement of nonlocal electronic relaxation processes in X-ray irradiated liquid water, J. Am. Chem. Soc., 2014, 136, 18170–18176 CrossRef PubMed.
- T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P. V. Demekhin, K. Gokhberg, L. S. Cederbaum, A. Ehresmann, A. Knie and A. Dreuw, Interatomic and Intermolecular Coulombic Decay, Chem. Rev., 2020, 120, 11295–11369 CrossRef CAS PubMed.
- R. Signorell, Electron Scattering in Liquid Water and Amorphous Ice: A Striking Resemblance, Phys. Rev. Lett., 2020, 124, 205501 CrossRef CAS PubMed.
- M. Michaud, A. Wen and L. Sanche, Cross sections for low-energy (1–100 eV) electron elastic and inelastic scattering in amorphous ice, Radiat. Res., 2003, 159, 3–22 CrossRef CAS PubMed.
- H. T. Nguyen-Truong, Low-energy electron inelastic mean free paths for liquid water, J. Phys.: Condens. Matter, 2018, 30, 155101 CrossRef PubMed.
- H. Shinotsuka, B. Da, S. Tanuma, H. Yoshikawa, C. J. Powell and D. R. Penn, Calculations of Electron Inelastic Mean Free Paths. XI. Data for Liquid Water for Energies from 50 eV to 30 keV, Surf. Interface Anal., 2017, 49, 238–252 CrossRef CAS PubMed.
- D. Luckhaus, Y. I. Yamamoto, T. Suzuki and R. Signorell, Genuine binding energy of the hydrated electron, Sci. Adv., 2017, 3, e1603224 CrossRef PubMed.
- T. E. Gartmann, L. Ban, B. L. Yoder, S. Hartweg, E. Chasovskikh and R. Signorell, Relaxation Dynamics and Genuine Properties of the Solvated Electron in Neutral Water Clusters, J. Phys. Chem. Lett., 2019, 10, 4777–4782 CrossRef CAS PubMed.
- S. A. Sheinerman and V. Schmidt, PCI and interference effects in the energy and angular correlation between the photoelectron and the Auger electron for equal electron energies, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 1677–1690 CrossRef CAS.
- P. van der Straten, R. Morgenstern and A. Niehaus, Angular Dependent Post-Collision Interaction in Auger Processes, ZPhys-e. D: At., Mol. Clusters, 1988, 8, 35–45 CAS.
- B. Ritchie, Theory of the angular distribution of photoelectrons ejected from optically active molecules and molecular negative ions, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1411–1415 CrossRef.
- B. Ritchie, Theory of the angular distribution for ejection of photoelectrons from optically active molecules and molecular negative ions. II, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 359–362 CrossRef CAS.
- I. Powis, Photoelectron Spectroscopy and Circular Dichroism in Chiral Biomolecules:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l-Alanine, J. Phys. Chem. A, 2000, 104, 878–882 CrossRef CAS.
l-Alanine, J. Phys. Chem. A, 2000, 104, 878–882 CrossRef CAS. - I. Powis, Photoelectron Circular Dichroism in Chiral Molecules, Adv. Chem. Phys., 2008, 267–329, DOI:10.1002/9780470259474.ch5.
- S. Thürmer, S. Malerz, F. Trinter, U. Hergenhahn, C. Lee, D. M. Neumark, G. Meijer, B. Winter and I. Wilkinson, Accurate Vertical Ionization Energy and Work Function Determinations of Liquid Water and Aqueous Solutions, Chem. Sci., 2021, 12, 10558–10582 RSC.
- B. Credidio, M. Pugini, S. Malerz, F. Trinter, U. Hergenhahn, I. Wilkinson, S. Thürmer and B. Winter, Quantitative electronic structure and work-function changes of liquid water induced by solute, Phys. Chem. Chem. Phys., 2022, 24, 1310–1325 RSC.
- R. Signorell, M. Goldmann, B. L. Yoder, A. Bodi, E. Chasovskikh, L. Lang and D. Luckhaus, Nanofocusing, shadowing, and electron mean free path in the photoemission from aerosol droplets, Chem. Phys. Lett., 2016, 658, 1–6 CrossRef CAS.
- T. E. Gartmann, S. Hartweg, L. Ban, E. Chasovskikh, B. L. Yoder and R. Signorell, Electron scattering in large water clusters from photoelectron imaging with high harmonic radiation, Phys. Chem. Chem. Phys., 2018, 20, 16364–16371 RSC.
- L. Ban, B. L. Yoder and R. Signorell, Photoemission from Free Particles and Droplets, Annu. Rev. Phys. Chem., 2020, 71, 315–334 CrossRef CAS PubMed.
- B. L. Yoder, A. H. C. West, B. Schläppi, E. Chasovskikh and R. Signorell, A velocity map imaging photoelectron spectrometer for the study of ultrafine aerosols with a table-top VUV laser and Na-doping for particle sizing applied to dimethyl ether condensation, J. Chem. Phys., 2013, 138, 044202 CrossRef PubMed.
- R. Seidel, S. Thürmer and B. Winter, Photoelectron spectroscopy meets aqueous solution: Studies from a vacuum liquid microjet, Phys. Chem. Lett., 2011, 2, 633–641 CrossRef CAS.
- S. Malerz, H. Haak, F. Trinter, A. Stephansen, C. Kolbeck, M. Pohl, U. Hergenhahn, G. Meijer and B. Winter, A setup to measure photoelectron circular dichroism from chiral molecules in aqueous solution, Rev. Sci. Instrum., 2022, 93, 015101 CrossRef CAS PubMed.
- S. Thürmer, R. Seidel, M. Faubel, W. Eberhardt, J. C. Hemminger, S. E. Bradforth and B. Winter, Photoelectron Angular Distributions from Liquid Water: Effects of Electron Scattering, Phys. Rev. Lett., 2013, 111, 173005 CrossRef PubMed.
- Y.-I. Suzuki, K. Nishizawa, N. Kurahashi and T. Suzuki, Effective attenuation length of an electron in liquid water between 10 and 600 eV, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 010302 CrossRef PubMed.
- S. Hartweg, B. L. Yoder, G. A. Garcia, L. Nahon and R. Signorell, Size-Resolved Photoelectron Anisotropy of Gas Phase Water Clusters and Predictions for Liquid Water, Phys. Rev. Lett., 2017, 118, 103402 CrossRef PubMed.
- S. Gozem, R. Seidel, U. Hergenhahn, E. Lugovoy, B. Abel, B. Winter, A. I. Krylov and S. E. Bradforth, Probing the Electronic Structure of Bulk Water at the Molecular Length Scale with Angle-Resolved Photoelectron Spectroscopy, J. Phys. Chem. Lett., 2020, 11, 5162–5170 CrossRef CAS PubMed.
- S. Malerz, F. Trinter, U. Hergenhahn, A. Ghrist, H. Ali, C. Nicolas, C. M. Saak, C. Richter, S. Hartweg, L. Nahon, C. Lee, C. Goy, D. M. Neumark, G. Meijer, I. Wilkinson, B. Winter and S. Thürmer, Low-energy constraints on photoelectron spectra measured from liquid water and aqueous solutions, Phys. Chem. Chem. Phys., 2021, 23, 8246–8260 RSC.
- A. Jablonski and C. J. Powell, Effective Attenuation Lengths for Different Quantitative Applications of X-ray Photoelectron Spectroscopy, J. Phys. Chem. Ref. Data, 2020, 49, 033102 CrossRef CAS.
- G. Olivieri, K. M. Parry, C. J. Powell, D. J. Tobias and M. A. Brown, Quantitative interpretation of molecular dynamics simulations for X-ray photoelectron spectroscopy of aqueous solutions, J. Chem. Phys., 2016, 144, 154704 CrossRef PubMed.
- L. Ban, T. E. Gartmann, B. L. Yoder and R. Signorell, Low-Energy Electron Escape from Liquid Interfaces: Charge and Quantum Effects, Phys. Rev. Lett., 2020, 124, 013402 CrossRef CAS PubMed.
- N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth and B. Winter, Photoelectron spectroscopy of liquid water and aqueous solution: Electron effective attenuation lengths and emission-angle anisotropy, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 60–70 CrossRef CAS.
- S. Ghosal, J. C. Hemminger, H. Bluhm, B. S. Mun, E. L. D. Hebenstreit, G. Ketteler, D. F. Ogletree, F. G. Requejo and M. Salmeron, Electron Spectroscopy of Aqueous Solution Interfaces Reveals Surface Enhancement of Halides, Science, 2005, 307, 563–566 CrossRef CAS PubMed.
- S. Tougaard, Universality classes of inelastic electron scattering cross-sections, Surf. Interface Anal., 1997, 25, 137–154 CrossRef CAS.
- S. Tougaard, Energy loss in XPS: Fundamental processes and applications for quantification, non-destructive depth profiling and 3D imaging, J. Electron Spectrosc. Relat. Phenom., 2010, 178-179, 128–153 CrossRef CAS.
- M. C. López-Santos, F. Yubero, J. P. Espinós and A. R. González-Elipe, Non-destructive depth compositional profiles by XPS peak-shape analysis, Anal. Bioanal. Chem., 2009, 396, 2757–2768 CrossRef PubMed.
- V. Cobut, Y. Frongillo, J. P. Patau, T. Goulet, M. J. Fraser and J. P. Jay-Gerin, Monte Carlo simulation of fast electron and proton tracks in liquid water- I. Physical and physicochemical aspects, Radiat. Phys. Chem., 1998, 51, 229–243 CrossRef CAS.
- Y.-i Yamamoto, S. Karashima, S. Adachi and T. Suzuki, Wavelength Dependence of UV Photoemission from Solvated Electrons in Bulk Water, Methanol, and Ethanol, J. Phys. Chem. A, 2016, 120, 1153–1159 CrossRef CAS PubMed.
- Y.-I. Yamamoto, Y.-I. Suzuki, G. Tomasello, T. Horio, S. Karashima, R. Mitríc and T. Suzuki, Time- and Angle-Resolved Photoemission Spectroscopy of Hydrated Electrons Near a Liquid Water Surface, Phys. Rev. Lett., 2014, 112, 187603 CrossRef PubMed.
- R. M. Young and D. M. Neumark, Dynamics of Solvated Electrons in Clusters, Chem. Rev., 2012, 112, 5553–5577 CrossRef CAS PubMed.
- A. H. C. West, B. L. Yoder, D. Luckhaus, C.-M. Saak, M. Doppelbauer and R. Signorell, Angle-Resolved Photoemission of Solvated Electrons in Sodium-Doped Clusters, J. Phys. Chem. Lett., 2015, 6, 1487–1492 CrossRef CAS PubMed.
- T. Lewis, B. Winter, S. Thürmer, R. Seidel, A. B. Stephansen, J. A. Freites, D. J. Tobias and J. C. Hemminger, Molecular Arrangement of a Mixture of Organosulfur Surfactants at the Aqueous Solution–Vapor Interface Studied by Photoelectron Intensity and Angular Distribution Measurements and Molecular Dynamics Simulations, J. Phys. Chem. C, 2018, 123, 8160–8170 CrossRef.
- M. Michaud and L. Sanche, Total cross sections for slow-electron (1-20 eV) scattering in solid H2O, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 4672 CrossRef CAS PubMed.
- J. Nishitani, C. W. West and T. Suzuki, Angle-resolved photoemission spectroscopy of liquid water at 29.5 eV, Struct. Dyn., 2017, 4, 044014 CrossRef PubMed.
- L. Ban, C. W. West, E. Chasovskikh, T. E. Gartmann, B. L. Yoder and R. Signorell, Below Band Gap Formation of Solvated Electrons in Neutral Water Clusters?, J. Phys. Chem. A, 2020, 124, 7959–7965 CrossRef CAS PubMed.
- A. H. West, B. L. Yoder, D. Luckhaus and R. Signorell, Solvated Electrons in Clusters: Magic Numbers for the Photoelectron Anisotropy, J. Phys. Chem. A, 2015, 119, 12376–12382 CrossRef CAS PubMed.
- C. Zhang, T. Andersson, M. Foerstel, M. Mucke, T. Arion, M. Tchaplyguine, O. Björneholm and U. Hergenhahn, The photoelectron angular distribution of water clusters, J. Chem. Phys., 2013, 138, 234306 CrossRef PubMed.
- A. E. Bragg, J. R. Verlet, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Electronic relaxation dynamics of water cluster anions, J. Am. Chem. Soc., 2005, 127, 15283–15295 CrossRef CAS PubMed.
- M. Faubel, K. R. Siefermann, Y. Liu and B. Abel, Ultrafast Soft X-ray Photoelectron Spectroscopy at Liquid Water Microjets, Acc. Chem. Res., 2012, 45, 120–130 CrossRef CAS PubMed.
- J. Cooper and R. N. Zare, Angular distribution of photoelectrons, J. Chem. Phys., 1968, 48, 942 CrossRef CAS.
- V. Schmidt, Electron spectrometry of atoms using synchrotron radiation, Electron spectroscopy of atoms using synchrotron radiation, University Press, Cambridge, 1997 Search PubMed.
- G. A. Garcia, L. Nahon, C. J. Harding and I. Powis, Chiral signatures in angle-resolved valence photoelectron spectroscopy of pure glycidol enantiomers, Phys. Chem. Chem. Phys., 2008, 10, 1628–1639 RSC.
- K. L. Reid, Photoelectron angular distributions, Annu. Rev. Phys. Chem., 2003, 54, 397–424 CrossRef CAS PubMed.
- H. Nikjoo, D. Emfietzoglou, T. Liamsuwan, R. Taleei, D. Liljequist and S. Uehara, Radiation track, DNA damage and response-a review, Rep. Prog. Phys., 2016, 79, 116601 CrossRef CAS PubMed.
- D. Emfietzoglou, I. Kyriakou, R. Garcia-Molina and I. Abril, Inelastic mean free path of low-energy electrons in condensed media: beyond the standard models, Surf. Interface Anal., 2017, 49, 4–10 CrossRef CAS.
- J. Meesungnoen, J.-P. Jay-Gerin, A. Filali-Mouhim and S. Mankhetkorn, Low-Energy Electron Penetration Range in Liquid Water, Radiat. Res., 2002, 158, 657–660 CrossRef CAS PubMed.
- D. Emfietzoglou and H. Nikjoo, The effect of model approximations on single-collision distributions of low-energy electrons in liquid water, Radiat. Res., 2005, 163, 98–111 CrossRef CAS PubMed.
- M. Dingfelder, D. Hantke, M. Inokuti and H. G. Paretzke, Electron inelastic-scattering cross sections in liquid water, Radiat. Phys. Chem., 1998, 53, 1–18 CrossRef CAS.
- A. Akkerman and E. Akkerman, Characteristics of electron inelastic interactions in organic compounds and water over the energy range 20-10 000 eV, J. Appl. Phys., 1999, 86, 5809–5816 CrossRef CAS.
- J. C. Ashley, Interaction of low-energy electrons with condensed matter: stopping powers and inelastic mean free paths from optical data, J. Electron Spectrosc. Relat. Phenom., 1988, 46, 199–214 CrossRef CAS.
- H. Shinotsuka, S. Tanuma and C. J. Powell, Calculations of electron inelastic mean free paths. XIII. Data for 14 organic compounds and water over the 50 eV to 200 keV range with the relativistic full Penn algorithm, Surf. Interface Anal., 2022, 54, 534–560 CrossRef.
- B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. V. Hertel, Full valence band photoemission from liquid water using EUV synchrotron radiation, J. Phys. Chem. A, 2004, 108, 2625–2632 CrossRef CAS.
- C. C. Su, Y. Yu, P. C. Chang, Y. W. Chen, I. Y. Chen, Y. Y. Lee and C. C. Wang, VUV Photoelectron Spectroscopy of Cysteine Aqueous Aerosols: A Microscopic View of Its Nucleophilicity at Varying pH Conditions, J. Phys. Chem. Lett., 2015, 6, 817–823 CrossRef CAS PubMed.
- O. Kostko, B. Xu, M. I. Jacobs and M. Ahmed, Soft X-ray spectroscopy of nanoparticles by velocity map imaging, J. Chem. Phys., 2017, 147, 013931 CrossRef CAS PubMed.
- F. Buchner, T. Schultz and A. Lübcke, Solvated electrons at the water-air interface: surface versus bulk signal in low kinetic energy photoelectron spectroscopy, Phys. Chem. Chem. Phys., 2012, 14, 5837–5842 RSC.
- E. Alizadeh and L. Sanche, Precursors of Solvated Electrons in Radiobiological Physics and Chemistry, Chem. Rev., 2012, 112, 5578–5602 CrossRef CAS PubMed.
- E. Alizadeh, T. M. Orlando and L. Sanche, Biomolecular Damage Induced by Ionizing Radiation: The Direct and Indirect Effects of Low-Energy Electrons on DNA, Annu. Rev. Phys. Chem., 2015, 66, 379–398 CrossRef CAS PubMed.
- T. Zeuch and U. Buck, Sodium doped hydrogen bonded clusters: Solvated electrons and size selection, Chem. Phys. Lett., 2013, 579, 1–10 CrossRef CAS.
- J. M. Herbert and M. P. Coons, The Hydrated Electron, Annu. Rev. Phys. Chem., 2017, 68, 447–472 CrossRef CAS PubMed.
- F. Uhlig, O. Marsalek and P. Jungwirth, Electron at the Surface of Water: Dehydrated or Not?, J. Phys. Chem. Lett., 2013, 4, 338–343 CrossRef CAS PubMed.
- J. R. Casey, B. J. Schwartz and W. J. Glover, Free Energies of Cavity and Noncavity Hydrated Electrons Near the Instantaneous Air/Water Interface, J. Phys. Chem. Lett., 2016, 7, 3192–3198 CrossRef CAS PubMed.
- L. Turi and P. J. Rossky, Theoretical Studies of Spectroscopy and Dynamics of Hydrated Electrons, Chem. Rev., 2012, 112, 5641–5674 CrossRef CAS PubMed.
- J. Lan, V. Kapil, P. Gasparotto, M. Ceriotti, M. Iannuzzi and V. V. Rybkin, Simulating the ghost: quantum dynamics of the solvated electron, Nat. Commun., 2021, 12, 766 CrossRef CAS PubMed.
- T. Horio, H. Shen, S. Adachi and T. Suzuki, Photoelectron spectra of solvated electrons in bulk water, methanol, and ethanol, Chem. Phys. Lett., 2012, 535, 12–16 CrossRef CAS.
- Y. I. Yamamoto and T. Suzuki, Ultrafast Dynamics of Water Radiolysis: Hydrated Electron Formation, Solvation, Recombination, and Scavenging, J. Phys. Chem. Lett., 2020, 11, 5510–5516 CrossRef CAS PubMed.
- J. V. Coe, S. T. Arnold, J. G. Eaton, G. H. Lee and K. H. Bowen, Photoelectron spectra of hydrated electron clusters: Fitting line shapes and grouping isomers, J. Chem. Phys., 2006, 125, 014315 CrossRef PubMed.
- L. Ma, K. Majer, F. Chirot and B. von Issendorff, Low temperature photoelectron spectra of water cluster anions, J. Chem. Phys., 2009, 131, 144303 CrossRef PubMed.
- P. Kambhampati, D. H. Son, T. W. Kee and P. F. Barbara, Solvation Dynamics of the Hydrated Electron Depends on Its Initial Degree of Electron Delocalization, J. Phys. Chem. A, 2002, 106, 2374–2378 CrossRef CAS.
- L. Ban, B. L. Yoder and R. Signorell, Size-Resolved Electron Solvation in Neutral Water Clusters, J. Phys. Chem. A, 2021, 125, 5326–5334 CrossRef CAS PubMed.
- K. R. Siefermann, Y. X. Liu, E. Lugovoy, O. Link, M. Faubel, U. Buck, B. Winter and B. Abel, Binding energies, lifetimes and implications of bulk and interface solvated electrons in water, Nat. Chem., 2010, 2, 274–279 CrossRef CAS PubMed.
- R. A. Crowell and D. M. Bartels, Multiphoton Ionization of Liquid Water with 3.0-5.0 eV Photons, J. Phys. Chem., 1996, 100, 17940–17949 CrossRef CAS.
- A. Bernas, C. Ferradini and J. P. JayGerin, On the electronic structure of liquid water: Facts and reflections, Chem. Phys., 1997, 222, 151–160 CrossRef CAS.
- C. Adriaanse, J. Cheng, V. Chau, M. Sulpizi, J. VandeVondele and M. Sprik, Aqueous Redox Chemistry and the Electronic Band Structure of Liquid Water, J. Phys. Chem. Lett., 2012, 3, 3411–3415 CrossRef CAS PubMed.
- A. P. Gaiduk, T. A. Pham, M. Govoni, F. Paesani and G. Galli, Electron affinity of liquid water, Nat. Commun., 2018, 9, 247 CrossRef PubMed.
- M. H. Elkins, H. L. Williams, A. T. Shreve and D. M. Neumark, Relaxation Mechanism of the Hydrated Electron, Science, 2013, 342, 1496–1499 CrossRef CAS PubMed.
- C. G. Elles, A. E. Jailaubekov, R. A. Crowell and S. E. Bradforth, Excitation-energy dependence of the mechanism for two-photon ionization of liquid H2O and D2O from 8.3 to 12.4 eV, J. Chem. Phys., 2006, 125, 044515 CrossRef PubMed.
- J. Nishitani, Y. I. Yamamoto, C. W. West, S. Karashima and T. Suzuki, Binding energy of solvated electrons and retrieval of true UV photoelectron spectra of liquids, Sci. Adv., 2019, 5, eaaw6896 CrossRef CAS PubMed.
- D. M. Bartels and R. A. Crowell, Photoionization Yield vs Energy in H2O and D2O, J. Phys. Chem. A, 2000, 104, 3349–3355 CrossRef CAS.
- D. Madsen, C. L. Thomsen, J. Thøgersen and S. R. Keiding, Temperature dependent relaxation and recombination dynamics of the hydrated electron, J. Chem. Phys., 2000, 113, 1126–1134 CrossRef CAS.
- H. T. Liu, J. P. Muller, M. Beutler, M. Ghotbi, F. Noack, W. Radloff, N. Zhavoronkov, C. P. Schulz and I. V. Hertel, Ultrafast photo-excitation dynamics in isolated, neutral water clusters, J. Chem. Phys., 2011, 134, 094305 CrossRef CAS PubMed.
- V. Svoboda, R. Michiels, A. C. LaForge, J. Med, F. Stienkemeier, P. Slavicek and H. J. Worner, Real-time observation of water radiolysis and hydrated electron formation induced by extreme-ultraviolet pulses, Sci. Adv., 2020, 6, eaaz0385 CrossRef CAS PubMed.
- A. Lübcke, F. Buchner, N. Heine, I. V. Hertel and T. Schultz, Time-resolved photoelectron spectroscopy of solvated electrons in aqueous NaI solution, Phys. Chem. Chem. Phys., 2010, 12, 14629–14634 RSC.
- X. Chen and S. E. Bradforth, The ultrafast dynamics of photodetachment, Annu. Rev. Phys. Chem., 2008, 59, 203–231 CrossRef CAS PubMed.
- J. V. Coe, G. H. Lee, J. G. Eaton, S. T. Arnold, H. W. Sarkas, K. H. Bowen, C. Ludewigt, H. Haberland and D. R. Worsnop, Photoelectron spectroscopy of hydrated electron cluster anions, (H2O)n=2–69−, J. Chem. Phys., 1990, 92, 3980–3982 CrossRef CAS.
- M. P. Coons, Z. Q. You and J. M. Herbert, The Hydrated Electron at the Surface of Neat Liquid Water Appears To Be Indistinguishable from the Bulk Species, J. Am. Chem. Soc., 2016, 138, 10879–10886 CrossRef CAS PubMed.
- M. P. Coons and J. M. Herbert, Quantum chemistry in arbitrary dielectric environments: Theory and implementation of nonequilibrium Poisson boundary conditions and application to compute vertical ionization energies at the air/water interface, J. Chem. Phys., 2018, 148, 222834 CrossRef PubMed.
- S. K. Paul, M. P. Coons and J. M. Herbert, Erratum: “Quantum chemistry in arbitrary dielectric environments: Theory and implementation of nonequilibrium Poisson boundary conditions and application to compute vertical ionization energies at the air/water interface, J. Chem. Phys., 2018, 148, 222834 CrossRef PubMed , J. Chem. Phys., 2019, 151, 189901.
- N. I. Hammer, J. W. Shin, J. M. Headrick, E. G. Diken, J. R. Roscioli, G. H. Weddle and M. A. Johnson, How do small water clusters bind an excess electron?, Science, 2004, 306, 675–679 CrossRef CAS PubMed.
- K. R. Asmis, G. Santambrogio, J. Zhou, E. Garand, J. Headrick, D. Goebbert, M. A. Johnson and D. M. Neumark, Vibrational spectroscopy of hydrated electron clusters (H2O)15–50−via infrared multiple photon dissociation, J. Chem. Phys., 2007, 126, 191105 CrossRef PubMed.
- Locally-Sensitive & Time-Resolved Spectroscopy Lab, Helmholtz Zentrum Berlin, Head: Dr Iain Wilkinson, https://www.helmholtz-berlin.de/forschung/oe/ps/spectroscopy/index_en.html.
- Stephan Thürmer, Kyoto University, https://kyouindb.iimc.kyoto-u.ac.jp/e/sC7qA.
- P. Slavíček, Theoretical Photodynamics Reseach Group, University of Chemistry and Technology Prague, http://photox.vscht.cz/.
- M. H. Janssen and I. Powis, Detecting chirality in molecules by imaging photoelectron circular dichroism, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- L. Nahon, G. A. Garcia, H. Soldi-Lose, S. Daly and I. Powis, Effects of dimerization on the photoelectron angular distribution parameters from chiral camphor enantiomers obtained with circularly polarized vacuum-ultraviolet radiation, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 032514 CrossRef.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Geneaux and I. Powis, Determination of accurate electron chiral asymmetries in fenchone and camphor in the VUV range: sensitivity to isomerism and enantiomeric purity, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706 RSC.
- S. Turchini, D. Catone, G. Contini, N. Zema, S. Irrera, M. Stener, D. Di Tommaso, P. Decleva and T. Prosperi, Conformational effects in photoelectron circular dichroism of alaninol, ChemPhysChem, 2009, 10, 1839–1846 CrossRef CAS PubMed.
- A. F. Ordonez and O. Smirnova, Propensity rules in photoelectron circular dichroism in chiral molecules. II. General picture, Phys. Rev. A: At., Mol., Opt. Phys., 2019, 99, 043417 CrossRef CAS.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Kohler, C. Sarpe and T. Baumert, Circular dichroism in the photoelectron angular distributions of camphor and fenchone from multiphoton ionization with femtosecond laser pulses, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- M. M. Fanood, N. B. Ram, C. S. Lehmann, I. Powis and M. H. Janssen, Enantiomer-specific analysis of multi-component mixtures by correlated electron imaging-ion mass spectrometry, Nat. Commun., 2015, 6, 7511 CrossRef CAS PubMed.
- P. V. Demekhin, Photoelectron circular dichroism with Lissajous-type bichromatic fields: One-photon versus two-photon ionization of chiral molecules, Phys. Rev. A: At., Mol., Opt. Phys., 2019, 99, 063406 CrossRef CAS.
- S. Beaulieu, A. Comby, A. Clergerie, J. Caillat, D. Descamps, N. Dudovich, B. Fabre, R. Geneaux, F. Legare, S. Petit, B. Pons, G. Porat, T. Ruchon, R. Taieb, V. Blanchet and Y. Mairesse, Attosecond-resolved photoionization of chiral molecules, Science, 2017, 358, 1288–1294 CrossRef CAS PubMed.
- M. Tia, M. Pitzer, G. Kastirke, J. Gatzke, H. K. Kim, F. Trinter, J. Rist, A. Hartung, D. Trabert, J. Siebert, K. Henrichs, J. Becht, S. Zeller, H. Gassert, F. Wiegandt, R. Wallauer, A. Kuhlins, C. Schober, T. Bauer, N. Wechselberger, P. Burzynski, J. Neff, M. Weller, D. Metz, M. Kircher, M. Waitz, J. B. Williams, L. P. H. Schmidt, A. D. Muller, A. Knie, A. Hans, L. Ben Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, R. Dörner, T. Jahnke, P. V. Demekhin and M. Schoffler, Observation of Enhanced Chiral Asymmetries in the Inner-Shell Photoionization of Uniaxially Oriented Methyloxirane Enantiomers, J. Phys. Chem. Lett., 2017, 8, 2780–2786 CrossRef CAS PubMed.
- S. Hartweg, G. A. Garcia, D. K. Bozanic and L. Nahon, Condensation Effects on Electron Chiral Asymmetries in the Photoionization of Serine: From Free Molecules to Nanoparticles, J. Phys. Chem. Lett., 2021, 12, 2385–2393 CrossRef CAS PubMed.
- M. Pohl, S. Malerz, F. Trinter, C. Lee, C. Kolbeck, I. Wilkinson, S. Thürmer, D. M. Neumark, L. Nahon, I. Powis, G. Meijer, B. Winter and U. Hergenhahn, Photoelectron circular dichroism in angle-resolved photoemission from liquid fenchone, Phys. Chem. Chem. Phys., 2022, 24, 8081–8092 RSC.
- P. Atkins and L. Jones, Chemical Principles: the Quest for Insight, Freeman, W. H. and Co., New York, 5th edn, 2010 Search PubMed.
- M. Faubel, B. Steiner and J. P. Toennies, Photoelectron spectroscopy of liquid water, some alcohols, and pure nonane in free micro jets, J. Chem. Phys., 1997, 106, 9013–9031 CrossRef CAS.
- N. Kurahashi, S. Karashima, Y. Tang, T. Horio, B. Abulimiti, Y.-I. Suzuki, Y. Ogi, M. Oura and T. Suzuki, Photoelectron spectroscopy of aqueous solutions: Streaming potentials of NaX (X = Cl, Br, and I) solutions and electron binding energies of liquid water and X, J. Chem. Phys., 2014, 140, 174506 CrossRef PubMed.
- C. F. Perry, P. Zhang, F. B. Nunes, I. Jordan, A. von Conta and H. J. Wörner, Ionization Energy of Liquid Water Revisited, J. Phys. Chem. Lett., 2020, 11(5), 1789–1794 CrossRef CAS PubMed.
- J. Nishitani, S. Karashima, C. W. West and T. Suzuki, Surface potential of liquid microjet investigated using extreme ultraviolet photoelectron spectroscopy, J. Chem. Phys., 2020, 152, 144503 CrossRef CAS PubMed.
- S. Y. Truong, A. J. Yencha, A. M. Juarez, S. J. Cavanagh, P. Bolognesi and G. C. King, Threshold photoelectron spectroscopy of H2O and D2O over the photon energy range 12-40 eV, Chem. Phys., 2009, 355, 183–193 CrossRef CAS.
- M. N. Pohl, E. Muchová, R. Seidel, H. Ali, S. Sršeň, I. Wilkinson, B. Winter and P. Slavíček, Do water's electrons care about electrolytes?, Chem. Sci., 2019, 10, 848–865 RSC.
- H. C. Schewe, K. Brezina, V. Kostal, P. E. Mason, T. Buttersack, D. M. Stemer, R. Seidel, W. Quevedo, F. Trinter, B. Winter and P. Jungwirth, Photoelectron Spectroscopy of Benzene in the Liquid Phase and Dissolved in Liquid Ammonia, J. Phys. Chem. B, 2022, 126, 229–238 CrossRef CAS PubMed.
- R. Weber, Doctoral thesis, Freie Universität Berlin, 2003.
- G. Olivieri, A. Goel, A. Kleibert, D. Cvetko and M. A. Brown, Quantitative ionization energies and work functions of aqueous solutions, Phys. Chem. Chem. Phys., 2016, 18, 29506–29515 RSC.
- L. Perez Ramirez, A. Boucly, F. Saudrais, F. Bournel, J. J. Gallet, E. Maisonhaute, A. R. Milosavljevic, C. Nicolas and F. Rochet, The Fermi level as an energy reference in liquid jet X-ray photoelectron spectroscopy studies of aqueous solutions, Phys. Chem. Chem. Phys., 2021, 23, 16224–16233 RSC.
- W. F. Egelhoff, Core-level binding-energy shifts at surfaces and in solids, Surf. Sci. Rep., 1987, 6, 253–415 CrossRef.
- D. Cahen and A. Kahn, Electron Energetics at Surfaces and Interfaces: Concepts and Experiments, Adv. Mater., 2003, 15, 271–277 CrossRef CAS.
- Y. I. Yamamoto, T. Ishiyama, A. Morita and T. Suzuki, Exploration of Gas-Liquid Interfaces for Liquid Water and Methanol Using Extreme Ultraviolet Laser Photoemission Spectroscopy, J. Phys. Chem. B, 2021, 125, 10514–10526 CrossRef CAS PubMed.
- P. Liu, P. J. Ziemann, D. B. Kittelson and P. H. McMurry, Generating Particle Beams of Controlled Dimensions and Divergence: II. Experimental Evaluation of Particle Motion in Aerodynamic Lenses and Nozzle Expansions, Aerosol Sci. Technol., 1995, 22, 314–324 CrossRef CAS.
- A. T. J. B. Eppink and D. H. Parker, Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
| This journal is © the Owner Societies 2022 |