Aperiodic metal–organic frameworks

Abstract

Metal–organic frameworks (MOFs) represent one of the most diverse structural classes among solid state materials, yet few of them exhibit aperiodicity, or the existence of long-range order in the absence of translational symmetry. From this apparent conflict, a paradox has emerged: even though aperiodicity frequently arises in materials that contain the same bonding motifs as MOFs, aperiodic structures and MOFs appear to be nearly disjoint classes. In this perspective, we highlight a subset of the known aperiodic coordination polymers, including both incommensurate and quasicrystalline structures. We further comment upon possible reasons for the absence of such structures and propose routes to potentially access aperiodic MOFs.

---

Introduction

Long-range order is the defining characteristic of a crystal. Until the end of the 20th century, it was synonymous with translational periodicity, that any crystalline material is built of a unit cell repeated infinitely and identically in up to three Cartesian dimensions. This principle changed when two materials that lack such periodicity yet still possess long-range order were discovered. The first was made upon interpretation of the crystal structure of γ-Na₂CO₃ whose diffraction peaks were accompanied by satellite peaks: this phase is now known as an incommensurately modulated structure.^1,2 Another was the discovery of a quasicrystalline phase in an Al–Mn solid solution that exhibited non-crystallographic symmetry in its diffraction patterns.³ These two works laid down the foundation for a new field of crystallography, the study of ordered materials with no translational periodicity: aperiodic crystallography. Since then, a plethora of other systems, both molecular⁴ and polymeric,⁵ including such key systems such as cuprate superconductors⁶ and lead halide perovskites,⁷ have been found to form aperiodic phases.

Concurrently with this explosive growth in aperiodic research, significant effort has been devoted to studying metal–organic frameworks (MOFs), a subclass of coordination polymers (CPs), due to their intrinsic porosity and chemical tunability. Despite the Cambridge Structural Database containing over 90 000 published MOF structures,^8,9 reports of coordination polymers and MOFs with aperiodicity are in the single digits.^10–14 This is particularly notable as the types of crystal-packing forces commonly found within MOFs are similar to those that typically lead to many aperiodic systems: weak interactions such as hydrogen bonding, dipole–dipole interactions, and π-stacking.¹⁵ As an emerging field of research, there are still many unknowns, but aperiodic MOFs are potentially of broad interest due to their phonon, electric, molecular transport, and photonic properties that likely diverge from those found with periodic MOFs.^16–19 Herein, we discuss a selection of the known aperiodic MOFs and coordination polymers, and comment on the general design principles that may lead to aperiodicity.

General concepts of periodic and aperiodic crystals

As it is now known that crystallinity does not imply periodicity, the International Union of Crystallography has modified the definition of a crystal to be “any solid having an essentially discrete diffraction diagram”.²⁰ This general description includes, among others, the diffraction diagrams of periodic crystals and the several classes of aperiodic crystals,²¹ which all diffract discretely due to the preservation of long-range order (Fig. 1). Aperiodic crystals is a broad class of solids that encompasses two subcategories: solids that possess crystallographic point-group symmetries (such as N-fold rotational symmetries where N = 2, 3, 4, 6) and those that possess non-crystallographic (or quasicrystallographic) point-group symmetries (such as N-fold rotational symmetries with N = 5, >6).²² The solids in the first class can be further subdivided into incommensurately modulated structures and incommensurately modified composites, whereas the latter class includes quasicrystals. Sometimes, the former class is further subdivided into orientation, displacement, interface, composition, and intergrowth types, but we find the more common subdivision into modulations and composites/intergrowth to be more descriptive and useful.²³ Although aperiodic structures lack translational periodicity in at least one of the three Cartesian dimensions, they can be described as periodic in a higher-dimensional space (n > 3). This superspace approach to aperiodic crystals allows for significantly simplified mathematical treatment of aperiodic crystals, with much of the typical crystallographic methods transferrable to this relatively new class of materials.¹⁶ The purpose of this work is not to offer a comprehensive review of all types of aperiodic crystals and their intricacies (including structures whose magnetic interactions are incommensurate), for which we will refer to ref. 8, 9 and 15–18. Instead, in this perspective we will focus on key points that apply to MOFs and CPs in particular.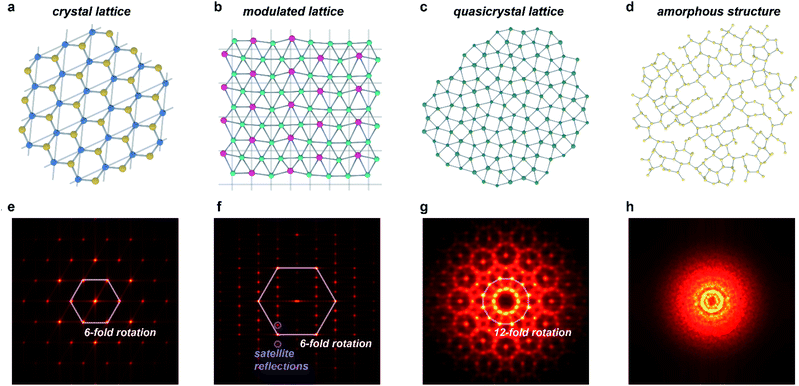

Fig. 1 Order in aperiodic crystallography and its manifestation in diffraction. (a–d) Structures of periodic and aperiodic crystallography: (a) periodic crystal lattice (illustrated with a structure of boron nitride);⁵⁸ (b) incommensurately modulated crystal lattice, where strict translational symmetry is broken by a periodic modulation (illustrated with a structure of Li_xZn_4−x;⁵⁹ the modulation amplitudes are scaled by a factor of 3). (c) Quasicrystal lattice, lacking any translational symmetry (illustration based on the dodecagonal square-triangle quasicrystal).⁶⁰ (d) Amorphous structure, lacking not only translational symmetry, but also any long-range order (illustrated with a calculated structure of amorphous silicon).⁶¹ (e–h) Simulated diffraction patterns of structures in (a–d): (e) periodic crystals show isolated spots related by crystallographic symmetry operations, and indexable in a single three-dimensional space group. (f) Incommensurately modulated crystals show patterns similar, but not identical to periodic crystals: they necessarily also include sets of satellite peaks incompatible with any three-dimensional space group. (g) Quasicrystals show isolated spots related by non-crystallographic symmetry operations, such as 5 or 7+ fold rotation. (h) Amorphous structures show only diffuse scattering arising from short-range order. Patterns in (e–h) were produced via a fast Fourier transform of atomic positions shown in (a–d).

A solid is said to possess a modulated structure when the parent translational symmetry is broken by the introduction of at least one periodic modulation. The direction and the period of the modulation is described by the modulation wavevector(s). When this vector can be expressed as a linear combination of the reciprocal lattice vectors with simple fractional coefficients, the structure is said to be commensurately modulated. If irrational coefficients are required to define the wavevector, such a structure is incommensurately modulated.²⁴ Importantly, this definition implies that a periodic supercell with translational symmetry can always be defined for commensurate structures, but never for incommensurate ones – giving rise to aperiodicity (Fig. 2). Incommensurately modulated structures are typically described in (3 + n)-dimensional superspace groups, where n is the dimensionality of modulation(s). These superspace groups can be thought of as extensions of the 230 three-dimensional space groups; if averaged over the modulation, the structure would have the symmetry of the parent three-dimensional space group.

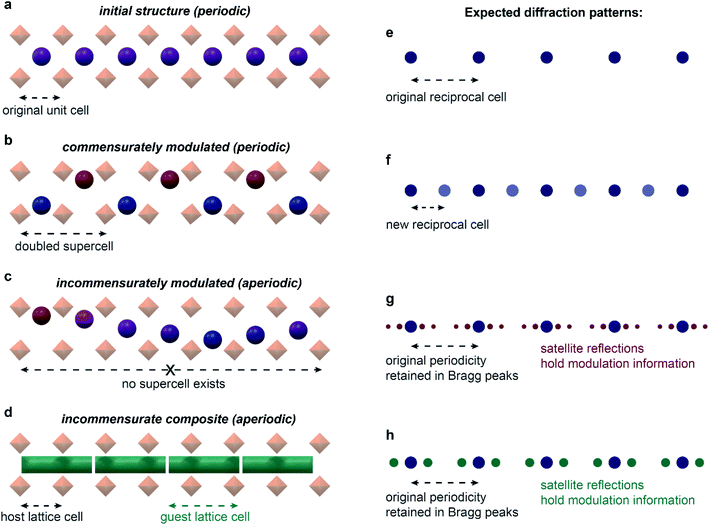Fig. 2 Modulated structures and their diffraction. Initial, periodic one-dimensional channel structure (a) shows a regular set of diffraction maxima (e). When commensurately modulated (b), the structure can be represented with a doubled supercell, and a new set of diffraction maxima appears (f), with the new reciprocal cell half as large as the initial reciprocal cell. No supercell exists in the incommensurately modulated case (c), and additional satellite reflections appear surrounding the initial set of diffraction maxima (g). Incommensurate composite structures (d) lead to similar diffraction as in regular incommensurately modulated structures (h). In certain cases, structures may be interpreted with similar quality as either incommensurate composites or incommensurately modulated.⁶²

An important subset of incommensurately modulated structures resides in composite crystals – phases that can be represented as several intergrown sublattices. As with other modulated structures, the interaction of the length scales of the component lattices can give rise to a commensurate or incommensurate structure. A common type of composite material that is most relevant to MOF systems is the host–guest system. For example, in a one-dimensional channel host–guest system, such as the nonadecane and urea composite, the host urea honeycomb lattice allows for the inclusion of guest nonadecane molecules. However, as the ratio of the length scale of the urea lattice down the channel to the length scale of the nonadecane lattice cannot be expressed as a simple fraction, the system forms an incommensurate composite crystal.^25,26 Not every host–guest system is capable of giving rise to an incommensurate structure: if the guest molecules are too small, the host may accommodate them into the lattice; the interaction must also be ordered enough to not give rise to a completely disordered phase. It is also important to distinguish incommensurate ordering of the guest molecules from incommensurate adsorption – a term commonly used in the field of gas sorption in microporous materials.²⁷ Whereas incommensurate ordering implies a well-defined periodic ordering of the molecules, incommensurate adsorption simply means that the dimensions of the guest are incompatible with the host framework. Although this incompatibility can and does sometimes lead to incommensurate ordering, incompatibility does not always lead to ordering.

Like the previously discussed structures, quasicrystals are also aperiodic structures as they can be constructed as irrational three-dimensional cuts in a superspace periodic structure.²⁸ Quasicrystals can be divided into two classes based on their compositions (and not on their symmetry): those made from hard matter and those from soft matter. Hard matter quasicrystals are typically composed of intermetallics, such as in the Al–Fe–Cu and Al–Mn systems. On the other hand, soft matter quasicrystals can be composed of a wide variety of soft materials, including polymers, colloids, liquid crystals, and nanoparticles.²⁹

Aperiodic systems can be difficult to study, and even more so to model: although electronic and vibrational states of aperiodic crystals satisfy Bloch's theorem, the complexity of these states and the high number of degrees of freedom preclude or significantly complicate theoretical investigation by most ab initio methods such as density functional theory.¹⁶ Instead, computations largely focus on molecular clusters or periodic analogs of both quasicrystals and modulated structures. For quasicrystals, their approximants are large unit cell periodic structures that mimic the non-crystallographic symmetries of their parent structures. The atomic compositions of these approximants are typically also close to their parent structures.²⁸ On the other hand, incommensurately modulated structures can often be approximated by their related commensurate phases, which are often formed in very similar conditions.¹⁶

Due to their uncommon electronic and phononic properties, aperiodic materials boast many potential applications^28,30 in fields ranging from photovoltaics³¹ to optics,³² thermoelectrics,³³ gas storage,³⁴ and catalysis.³⁵ Due to difficulties of growing these crystals at scale, few of these directions have to date prompt commercial interest. Most prominent in that regard are quasicrystalline metal alloys that show exceptional anti-friction properties while maintaining high hardness, making the materials competitive with polytetrafluoroethylene coatings.³⁰

Identification of aperiodic structures is relatively straightforward and uses techniques readily accessible to a modern chemist, such as single-crystal X-ray and electron diffraction. For modulated structures, analysis generally starts with powder or single-crystal X-ray diffraction, looking for the key identifier of such structures: satellite reflections. Satellite reflections surround the main Bragg reflections at regular d-space intervals, generally with each subsequent satellite shell at lower intensity (Fig. 2); these reflections cannot be indexed in any three-dimensional space group. The lower intensities of satellites can make them difficult to see and fit or integrate if the diffraction facilities are inadequately equipped. In such cases, synchrotron facilities offer an excellent alternative to in-house data collection. Access to single-crystal diffraction is key to structure determination of incommensurately modulated crystals: although powder refinement is a powerful tool in crystallography of incommensurate structures, it is applied either to known structure types or alongside a single-crystal method such as electron diffraction. Most modern single-crystal diffractometers include tools for working with modulated datasets which assist with finding the modulation wavevector and integration. Structure solution of incommensurate phases is usually done with charge flipping, using Superflip,³⁶ which allows solution directly in superspace. Refinement of single-crystal and powder data is generally done using JANA2006,³⁷ which also incorporates Superflip for efficient workflow. Structural data for incommensurate crystals, similarly to normal crystals, is written to a CIF file, which can be opened by most current crystal structure visualization tools, although most cannot plot the modulation (the authors are aware of such functionality only in Jmol),³⁸ and instead display only the average structure.

Identification of quasicrystals also generally starts with diffraction-based analysis. A versatile starting tool is electron backscatter diffraction in scanning electron microscopy: Kikuchi patterns with non-crystallographic symmetries allow rapid identification of quasicrystallinity in small grains. Analysis is then most commonly continued with single-crystal electron or X-ray diffraction, where the non-crystallographic symmetry is evident in the reciprocal space. Although in an ideal quasicrystal the reciprocal space would be densely filled with Bragg peaks, in practice, these delta function-like Bragg peaks are smoothed out and only a finite number of peaks are measured.³⁹ Quasicrystallinity can also be determined by directly imaging atoms using transmission electron microscopy. Structure analysis for quasicrystals often ends after confirming the quasicrystal symmetry, however some examples of structure solution in high-dimensional space are provided in the literature.⁴⁰

Twinning can complicate identification and refinement of aperiodic structures. Complex twinning can produce diffraction patterns possessing the non-crystallographic symmetry operators characteristic of quasicrystalline lattices.⁴¹ Although merohedral twinning can generally be fully accounted for during refinement of incommensurately modulated crystals, non-merohedral twinning can potentially obscure the satellite reflections and preclude structural analysis.

Examples of aperiodic structures in MOFs and CPs

Exceedingly few examples of aperiodic MOFs and coordination polymers exist in the literature despite the heavy focus on structural studies in the field. In this section, we will draw upon these unique materials as case studies to better appreciate the design principles behind their formation, as well as the possible reasons for their scarcity.

Incommensurate composites represent perhaps the more obvious aperiodic structure to be realized in MOFs: as in the case of the alkane–urea systems,²⁶ one might imagine guest molecules ordering incommensurately with the framework lattice. However, despite the breadth of crystallographic work performed on numerous MOF–guest systems, and the wide variety of guest molecules sampled, we were able to find few reports of incommensurate modulation in the literature, and none of those examples reports a complete crystallographic investigation. However, these isolated examples still provide valuable insights into the crystal chemistry of aperiodic MOFs.

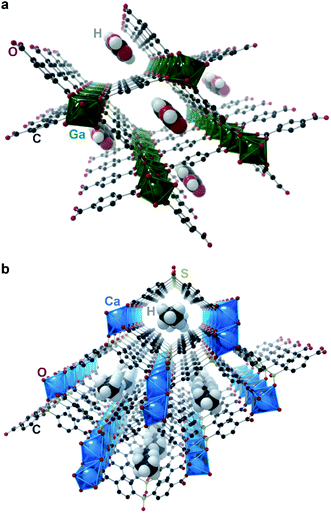
Chaplais et al. reported in 2009 the only case of crystallographically proven incommensurate modulation in MOFs that we are aware of.¹⁰ Ga(OH)(BDC)·0.75H₂BDC (IM-19 ps; BDC²⁻ = benzene dicarboxylate; Fig. 3a) shows clear satellite peaks up to the fourth order. The authors were able to index the reflections in an orthorhombic cell with a = 17.4370(2) Å, b = 6.7475(4) Å, c = 12.1541(4) Å, and modulation vector q = (0, 0.104, 0). Although no additional crystallographic work was performed, the authors note that the satellite reflections disappeared upon washing the material with N,N-dimethylformamide, which led to removal of the guest H₂BDC molecules. The authors thus believe the guest linker molecules to be responsible for the modulation, and this material to be an incommensurate composite crystal. Without knowing the actual modulated structure of the material, it is difficult to guess the origin of the incommensurate structure. Regardless, this work demonstrated first evidence of incommensurate modulation in MOFs, and as such, IM-19 ps is a prime candidate for future studies in aperiodic crystallography of MOFs and CPs.

Fig. 3 Incommensurate metal–organic frameworks. Representations of (a) IM-19 ps and (b) Ca(sbd). Guest H₂BDC molecules for IM-19 ps and guest n-pentane molecules for Ca(sbd) were added by the artist to illustrate a possible pore filling configuration.

Banerjee et al. reported in 2015 a change from commensurate to incommensurate adsorption in the microporous Ca(sbd) (sbd = sulfonyldibenzoate; Fig. 3b) system upon adsorption of small hydrocarbons (C_n, n = 2–7) moving from butane to pentane: the larger hydrocarbons can no longer pack into the unit cell in a commensurate fashion due to geometrical constraints.⁴² Although, as discussed above, incommensurate adsorption does not imply incommensurate ordering, this case is unique in providing a detailed crystallographic investigation of the adsorption. Importantly, single crystal diffraction studies of the materials showed a clear commensurate ordering for the smaller (C₂–C₄) hydrocarbons, while the larger hydrocarbons (C₄–C₇) are unable to order inside the pores in a commensurate fashion, and instead lead to a completely disordered pore filling. This example highlights that a mismatch in lattice parameters between the host and guest lattices are often not sufficient to produce an incommensurate composite.

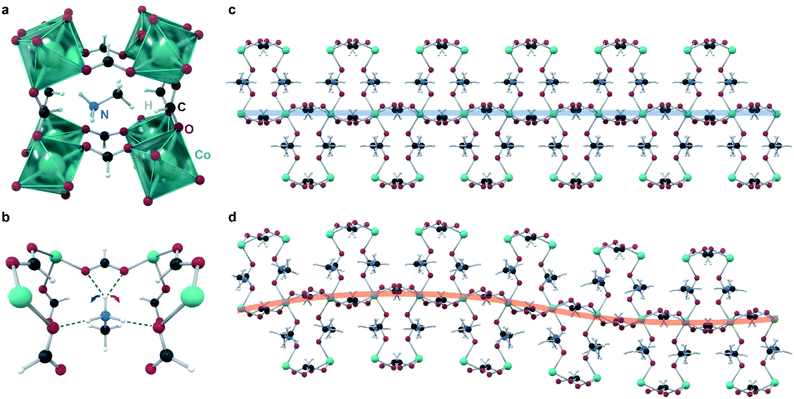
Canadillas-Delgado reported¹¹ in 2019 the first and only example to date of a fully crystallographically characterized incommensurate structure in a coordination polymer, with the formula [CH₃NH₃][Co(COOH)₃] (Fig. 4). At room temperature, this material crystallizes in the space group Pnma with the general perovskite structure type ABX₃, where A is methylammonium, B is Co(II), and X is formate. Cooling below approximately 128 K leads to a phase transition into an incommensurately modulated phase, which transitions into another incommensurate phase at 96 K, with a significantly larger modulation vector; and then into a commensurate monoclinic phase below 78 K. The modulation is complex, and involves all atoms of the unit cell. The key feature of the modulation appears to be the orientation of the methylammonium cation, and its hydrogen bonds to the cobalt formate framework: competition between different formate oxygens acting as proton acceptors leads to many possible bonding structures that are close in energy. Different hydrogen bonds lead to different structural distortions in the framework, and ultimately lead to an incommensurate structure. Specifically, at room temperature, one of the ammonium protons (Fig. 4) does not form hydrogen bonds (distances to closest acceptor oxygen atoms); in the incommensurate phases, this proton flips between forming bonds with either acceptor oxygen (closing the contact distance to ∼2.00 Å), with the different orientations ordered incommensurately. Below the third phase transition, the crystal splits into two domains, with the proton hydrogen-bonded exclusively to a different oxygen acceptor in each domain. Although this material is completely non-porous, this study provides a valuable example of incommensurate modulation achieved in a material with same bonding interactions and overall structural features as in a MOF, illustrating that the inherent flexibility of such frameworks does not necessarily impede the ordering.

Fig. 4 Structure of the incommensurate modulation in the perovskitic cobalt formate. (a) Each unit cell of the average structure contains one methylammonium cation in a perovskitic cage of cobalt formate. (b) The methylammonium cation has close contacts with four formate oxygens, with mirror symmetry; in the modulated structure this symmetry is broken. (c) Structure of the commensurate phase, given for comparison. (d) A supercell depicting the modulation vector (amplitude of modulation scaled up six times for clarity).

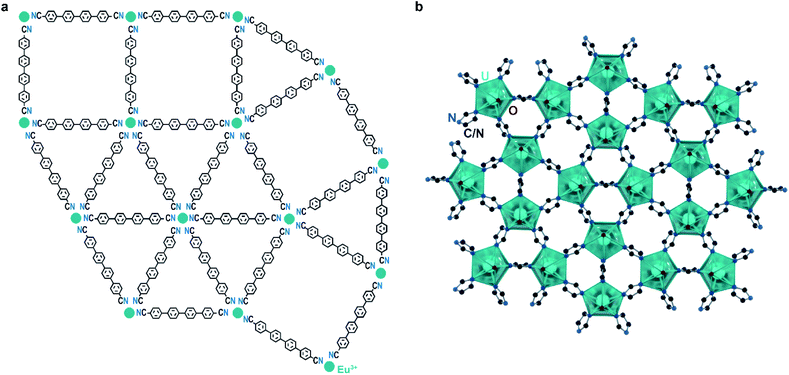
Examples of quasicrystallinity in MOFs and coordination polymers are even more scarce than those of incommensurate modulation. This is unsurprising given the relative difficulty in identifying quasicrystallinity, as well as the overall novelty of the field. To our knowledge, there is only a single system of coordination networks that expresses quasicrystallinity, the Ln–qdc (Ln = Eu, Ce, Gd and qdc = para-quaterphenyldicarbonitrile; Fig. 5a) system. These materials are produced by self-assembly of organic linkers and rare earth metal atoms on noble metal surfaces under high vacuum conditions and heating. Importantly, with certain metal-to-linker ratios, Eu–qdc displays clear quasicrystalline tiling, while Ce–qdc and Gd–qdc show tiling schemes highly resemblant of dodecagonal quasicrystals.^12–14 Although it is difficult to say with certainty what leads to the quasicrystalline order, a feature that plays a crucial role is the coordinational flexibility of the rare earths: the metals in these two-dimensional nets must be able to accommodate four-, five-, and six-fold coordination.

Fig. 5 Quasicrystalline coordination polymers. (a) Representation of a fragment of the Eu–qdc quasicrystal with dodecagonal tiling. (b) Crystal structure of the uranyl triazolate quasicrystal approximant shows a similar triangle-square connectivity with five-coordinate uranyl nodes.

One possible reason that quasicrystalline MOFs remain elusive is that many SBUs are not capable of simultaneously supporting the required numbers of linkages, especially the rarely seen planar five-coordinate geometry. To this point, Smetana et al. recently reported that uranyl moieties form a dodecagonal quasicrystalline approximant network when allowed to react with 1,2,4-triazole. The structure, [Hmim][(UO₂)₂(1,2,4-triazolate)₅]·3mim (mim = methylimidazole; Fig. 5b),⁴³ leverages the ability of the uranyl ion to coordinate to five equatorial ligands. As quasicrystal approximants are typically found at similar compositions to their parent quasicrystals, it is possible that a quasicrystal phase lies in this system, warranting further studies.

Although the metal–organic systems we discussed are dense, porosity is not necessarily a detriment to quasicrystalline order. Indeed, several reports in the last decade demonstrated formation of quasicrystalline phases in mesoporous silica. By taking advantage of accessible quasicrystalline phases in soft-matter systems (surfactant micelles in particular), it is possible to template the formation of mesoporous silica with similar order.^44–46 These methods offer an accessible approach to porous quasicrystals, on the one hand enabling studies of the interactions of guest molecules with porous quasicrystalline hosts, on the other hand providing, perhaps, an alternative pathway towards quasicrystalline MOFs.

Design insights and criteria for aperiodic structures

In this section, we discuss some key concepts derived from both theoretical models and chemical intuition, in an attempt to better understand why aperiodicity is so scarce in MOFs and CPs, as well as to find approaches most applicable to the deliberate design of new materials in this class. Although we will not discuss in detail theoretical models used for aperiodic structures, we note that they are paramount for the understanding of these materials, as commonly used first principles calculations such as density functional theory cannot be applied directly to them, but only to molecular clusters or crystalline approximants. For a comprehensive overview of such models we direct the reader to ref. 23.

A key design concept of soft quasicrystal chemistry is the idea of frustration by multiple length scales. This concept can be analyzed through the Lifshitz–Petrich equation, which is a modification of the Swift–Hohenberg model, for the description of two-dimensional pattern formations. To produce quasicrystalline patterns, the Lifshitz–Petrich equation introduces a second length scale,⁴⁷ which allows it to produce crystalline or decagonal and dodecagonal quasicrystalline solutions. Importantly, this model reveals that quasicrystalline structures can be stabilized by having multiple length scales. Although it is true that multiple length scales are not always needed for the emergence of quasicrystallinity,⁴⁸ frustration by multiple length scales can be a useful characteristic for the design of materials.

The cluster line rule⁴⁹ for hard quasicrystals further builds upon the concept of multiple length scales. It has been empirically demonstrated in ternary systems (A_xB_yC_z), that the stability region of quasicrystalline phases consistently coincides at compositions where binary atomic clusters can form (A_xB_y and A_xC_z). This suggests that at the composition A_xB_yC_z, where both clusters A_xB_y and A_xC_z can form, the clusters are unable to form a close packed structure, and instead form a ‘frustrated’ quasicrystalline structure. For 2D quasicrystals, such as the Ln–qdc system, this frustration is the result of an incompatibility between the triangle and square building units. Frustration can also likely be induced by having a SBU that can only accommodate one geometry and is surrounded by multiple linkers with similar binding affinities but different lengths.

For many types of quasicrystal structures, it is additionally necessary to have subunits that possess particular non-crystallographic symmetries (e.g. a center with 5-fold symmetry). In molecular and mononuclear SBU systems, there are only a limited number of such building blocks (including the f-block element examples with Eu and U). Further work should focus on the incorporation of non-f-block building units to induce these non-crystallographic symmetries. Such building blocks could include SBUs such as the icosahedral unit in MOF-812,⁵⁰ polyoxovanadates,⁵¹ and hypothetical organic linkers based on the 10,5-coronene family.⁵² Although such building blocks can promote quasicrystal formation, they are not always sufficient because their local high order point symmetry need not translate to higher-order space symmetry. This has been demonstrated recently with the pseudo-five-fold symmetric penta(4-(benzoic acid))pyrrole organic linker,⁵³ which consists of linkers with local pseudo-five-fold symmetry whose higher symmetry is broken upon coordination to metal nodes.

Incommensurate structures also often originate from a competition of several different types of interactions with different acting length scales: for example, in the solid-state structure of biphenyl (C₁₂H₁₀), intramolecular steric repulsions causing a dihedral twist in molecular biphenyl counteract intermolecular interactions forcing a planar shape, leading to a frustrated incommensurate structure.⁴ The types of competing interactions vary over different materials and structures, and can be broadly categorized into those which preserve covalent bonds, and those which can break and create covalent bonds over the modulation. Whereas the former are most commonly responsible for modulation in molecular crystals, the latter feature mostly in polymeric inorganic structures.¹⁵

The key interactions that are most common in molecular crystals (Fig. 6a–c) are both inter- and intramolecular steric repulsion; various non-covalent bonds, such as hydrogen or halogen bonds; dipole–dipole interactions, π–π stacking and other van der Waals interactions. In polymeric inorganic structures, however, Jahn–Teller distortions, defect ordering, substoichiometry, and coordination mismatch all influence the modulation (Fig. 6d and e). Importantly, all of these interactions, along with the multiple length scales important for quasicrystal formation, feature in some role in most MOF and CP structures, provoking the question: why are aperiodic structures so rare in MOFs and CPs?

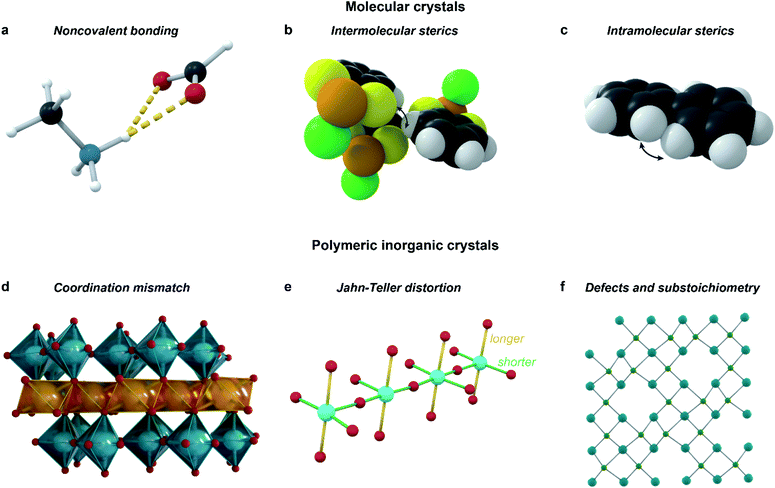Fig. 6 Types of interactions that should be considered when designing incommensurate materials. Examples include: hydrogen-bonding interactions in the perovskitic cobalt formate (a);¹¹ steric repulsion, both intermolecular as in C₆H₄S₂AsCl (b),⁶³ and intramolecular as in biphenyl (c);⁴ mismatch of coordination environments between the larger In³⁺ and the smaller Ti⁴⁺ in InAl_0.289Ti_0.701O_3.355 (d);⁶² Jahn–Teller distortion along with intermediate valence inducing modulation in LaSrCuO_3.52 (e);⁶⁴ ordering of defects in the substoichiometric AlB₂-type ErGe_2−x (f).⁶⁵

Approaches for aperiodic MOFs and outlook

We see several possibilities that can elucidate this scarcity. In many cases, it may be that aperiodicity is simply dismissed by an untrained eye as “bad diffraction” or a problematic crystal. Less casually, aperiodicity may be technically too difficult to experimentally measure due to a lack of necessary facilities, as we discussed above. That said, synchrotron facilities, including mail-in services, are becoming increasingly available to chemists around the world. It is also possible that some intrinsic reasons exist why aperiodicity is less common in MOFs and coordination polymers, such as the intrinsic flexibility of porous hybrid frameworks, although it is difficult to even speculate on this account as of yet. However, there are several potential design elements researchers may target in searching for aperiodic structures within CPs and MOFs. For quasicrystalline materials and approximants, such strategies may include using linkers and SBUs with non-crystallographic symmetries. Examples may be chosen from rare earth and actinide elements, known for their coordinational flexibility as in the case of the aforementioned uranyl triazolate; linkers based on pentagonal and decagonal, e.g., on cyclopentadiene or [10,5]-coronene, or perhaps even fullerenes; or larger SBUs with non-crystallographic symmetries; the multiple length scale approach is easy to adhere by in MOFs due to the disparity in SBU and linker size – still, it should be taken into account. For incommensurate materials, linkers and SBUs that support more noncovalent interactions should be used – the most approachable are likely π–π stacking and hydrogen bonding; rigid linkers should be prioritized to prevent the structure from easily relaxing into a commensurate phase; sufficiently large guest molecules should be used in order to observe host–guest incommensurate composites.

The most crucial reason for the lack of reported aperiodic MOF and quasicrystal structures, however, in our opinion is twofold. Firstly, the general lack of awareness of aperiodic structures largely prohibits their discovery. The concept of aperiodicity, especially that of incommensurately modulated and composite structures is not commonly discussed by the molecular chemistry community, and, as a young and relatively exotic field, aperiodic crystallography requires fairly specialized and uncommon knowledge to even recognize and identify incommensurate structures. Secondly, it is possible that even when aperiodic MOF structures are recognized as such from an initial diffraction pattern, detailed crystallographic or structural characterization is often not pursued because of its laborious and purely fundamental nature that is eclipsed by the more lucrative pursuit of tangible performance metrics in various applications. The MOF field benefits from the considerable interest elicited by its potential practical applications, but fundamental structural advances have been foundational to the field, from its very beginnings to the more recent developments such as multivariate MOFs.^54,55 These types of structures are not discussed here and have been recently reviewed elsewhere,^56,57 but we note that many of these multivariate MOFs exhibit a disordered distribution of the organic ligands comprising them, with likely important consequences for their properties – and perhaps may prove to be a pathway towards aperiodic MOF structures. Likewise, we hope that this perspective has broadened the general knowledge of and interest in these structure types and has kindled a more vigorous search for new materials in this class.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge financial support from the National Science Foundation through the Alan T. Waterman award to M. D. (DMR-1645232).

Notes and references

1. W. van Aalst, J. den Holander, W. J. A. M. Peterse and P. M. de Wolff, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 47–58.
2. E. Brouns, J. W. Visser and P. M. de Wolff, Acta Crystallogr., 1964, 17, 614.
3. D. Shechtman and I. A. Blech, Metall. Trans. A, 1985, 16, 1005–1012.
4. C. Benkert and V. Heine, J. Phys. C: Solid State Phys., 1987, 20, 3355–3367.
5. R. T. Fredrickson and D. C. Fredrickson, Inorg. Chem., 2013, 52, 3178–3189.
6. Y. Gao, P. Lee, P. Coppens, M. A. Subramanian and A. W. Sleight, Science, 1988, 241, 954–956.
7. Y. Guo, O. Yaffe, D. W. Paley, A. N. Beecher, T. D. Hull, G. Szpak, J. S. Owen, L. E. Brus and M. A. Pimenta, Phys. Rev. Mater., 2017, 1, 042401.
8. C. R. Groom, I. J. Bruno, M. P. Lightfoot, S. C. Ward and IUCr, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
9. P. Z. Moghadam, A. Li, X.-W. Liu, R. Bueno-Perez, S.-D. Wang, S. B. Wiggin, P. A. Wood and D. Fairen-Jimenez, Chem. Sci., 2020, 11, 8327–8628.
10. G. Chaplais, A. Simon-Masseron, F. Porcher, C. Lecomte, D. Bazer-Bachi, N. Bats and J. Patarin, Phys. Chem. Chem. Phys., 2009, 11, 5241.
11. L. Canadillas-Delgado, L. Mazzuca, O. Fabelo, J. A. Rodriguez-Velamazan and J. Rodriguez-Carvajal, IUCrJ, 2019, 6, 105–115.
12. J. I. Urgel, D. Ecija, W. Auwärter, A. C. Papageorgiou, A. P. Seitsonen, S. Vijayaraghavan, S. Joshi, S. Fischer, J. Reichert and J. V. Barth, J. Phys. Chem. C, 2014, 118, 12908–12915.
13. D. Écija, J. I. Urgel, A. C. Papageorgiou, S. Joshi, W. Auwärter, A. P. Seitsonen, S. Klyatskaya, M. Ruben, S. Fischer, S. Vijayaraghavan, J. Reichert and J. V. Barth, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6678–6681.
14. J. I. Urgel, D. Écija, G. Lyu, R. Zhang, C. A. Palma, W. Auwärter, N. Lin and J. V. Barth, Nat. Chem., 2016, 8, 657–662.
15. C. B. Pinheiro and A. M. Abakumov, IUCrJ, 2015, 2, 137–154.
16. T. Janssen and A. Janner, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 617–651.
17. A. N. Poddubny and E. L. Ivchenko, Phys. E, 2010, 42, 1871–1895.
18. J. M. de Regt, J. van Dijk, J. A. M. van Mullen and D. Schram, J. Phys. D: Appl. Phys., 1995, 28, 40–46.
19. Z. V. Vardeny, A. Nahata and A. Agrawal, Nat. Photonics, 2013, 7, 177–184.
20. IUCr, Acta Crystallogr., Sect. A: Found. Crystallogr., 1992, 48, 922–946.
21. U. Grimm, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 258–274.
22. R. Lifshitz, Found. Phys., 2003, 33, 1703–1711.
23. H. Z. Cummins, Phys. Rep., 1990, 185, 211–409.
24. T. Wagner and A. Schönleber, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 249–268.
25. A. E. Smith, Acta Crystallogr., 1952, 5, 224–235.
26. K. D. M. Harris and J. M. Thomas, J. Chem. Soc., Faraday Trans., 1990, 86, 2985–2996.
27. R. Krishna and J. M. Van Baten, Phys. Chem. Chem. Phys., 2017, 19, 20320–20337.
28. C. Janot, Quasicrystals. A primer, Clarendon Press, Oxford, 2nd edn, 1995.
29. T. Dotera, Isr. J. Chem., 2011, 51, 1197–1205.
30. E. M. Barber, Aperiodic structures in condensed matter: fundamentals and applications, CRC Press, Boca Raton, 2009.
31. C. Bauer and H. Giessen, Opt. Express, 2013, 21, A363.
32. C. Jin, B. Cheng, B. Man, Z. Li, D. Zhang, S. Ban and B. Sun, Appl. Phys. Lett., 1999, 75, 1848–1850.
33. E. Maciá, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 100201.
34. A. Takasaki and K. F. Kelton, International Journal of Hydrogen Energy, Pergamon, 2006, vol. 31, pp. 183–190.
35. M. Yoshimura and A. P. Tsai, J. Alloys Compd., 2002, 342, 451–454.
36. L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790.
37. V. Petrícek, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352.
38. Jmol: an open-source Java viewer for chemical structures in 3D, http://jmol.sourceforge.net/, accessed 19 July 2020.
39. D. Levine and P. J. Steinhardt, Phys. Rev. Lett., 1984, 53, 2477–2480.
40. H. Takakura, C. P. Gómez, A. Yamamoto, M. De Boissieu and A. P. Tsai, Nat. Mater., 2007, 6, 58–63.
41. L. Pauling, Nature, 1985, 317, 512–514.
42. D. Banerjee, H. Wang, Q. Gong, A. M. Plonka, J. Jagiello, H. Wu, W. R. Woerner, T. J. Emge, D. H. Olson, J. B. Parise and J. Li, Chem. Sci., 2016, 7, 759–765.
43. V. Smetana, S. P. Kelley, A. V. Mudring and R. D. Rogers, Sci. Adv., 2020, 6, eaay7685.
44. C. Xiao, N. Fujita, K. Miyasaka, Y. Sakamoto and O. Terasaki, Nature, 2012, 487, 349–353.
45. Y. Sun, K. Ma, T. Kao, K. A. Spoth, H. Sai, D. Zhang, L. F. Kourkoutis, V. Elser and U. Wiesner, Nat. Commun., 2017, 8, 1–10.
46. S. H. Tolbert, Nat. Mater., 2012, 11, 749–751.
47. S. Savitz, M. Babadi and R. Lifshitz, IUCrJ, 2018, 5, 247–268.
48. P. Bak, Phys. Rev. Lett., 1985, 54, 1517–1519.
49. C. Dong, Q. Wang, J. B. Qiang, Y. M. Wang, N. Jiang, G. Han, Y. H. Li, J. Wu and J. H. Xia, J. Phys. D: Appl. Phys., 2007, 40, R273–R291.
50. H. Furukawa, F. Gándara, Y. B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381.
51. N. Xu, H. Gan, C. Qin, X. Wang and Z. Su, Angew. Chem., Int. Ed., 2019, 58, 4649–4653.
52. Z. Zhou and K. D. M. Harris, ChemPhysChem, 2006, 7, 1649–1653.
53. F. Haase, G. A. Craig, M. Bonneau, K. Sugimoto and S. Furukawa, J. Am. Chem. Soc., 2020, 142, 13839–13845.
54. H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, 2010, 846–851.
55. Z. Ji, T. Li and O. M. Yaghi, Science, 2020, 369, 674–680.
56. A. Helal, Z. H. Yamani, K. E. Cordova and O. M. Yaghi, Natl. Sci. Rev., 2017, 4, 296–298.
57. W. Xu, C. S. Diercks, O. M. Yaghi, Y.-B. Zhang and H. Deng, Nat. Rev. Mater., 2020, 1–16.
58. O. O. Kurakevych and V. L. Solozhenko, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2007, 63, i80–i82.
59. V. Pavlyuk, I. Chumak, L. Akselrud, S. Lidin and H. Ehrenberg, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 212–217.
60. T. Ishimasa, Isr. J. Chem., 2011, 51, 1216–1225.
61. V. L. Deringer, N. Bernstein, A. P. Bartók, M. J. Cliffe, R. N. Kerber, L. E. Marbella, C. P. Grey, S. R. Elliott and G. Csányi, J. Phys. Chem. Lett., 2018, 9, 2879–2885.
62. P. J. Bereciartua, F. J. Zũiga and T. Breczewski, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 405–416.
63. R. C. Bakus, D. A. Atwood, S. Parkin, C. P. Brock and V. Petricek, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 496–508.
64. J. Hadermann, O. Pérez, N. Créon, C. Michel and M. Hervieu, J. Mater. Chem., 2007, 17, 2344–2350.
65. J. Christensen, S. Lidin, B. Malaman and G. Venturini, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 272–280.

---

Footnote

† These authors contributed equally to this work.

---