Open Access Article
Open Access ArticleRare “Janus”-faced  single-molecule magnet exhibiting intramolecular ferromagnetic interactions†
single-molecule magnet exhibiting intramolecular ferromagnetic interactions†
Dimitris I.
Alexandropoulos
a,
Kuduva R.
Vignesh
 a,
Theocharis C.
Stamatatos
a,
Theocharis C.
Stamatatos
 *b and
Kim R.
Dunbar
*b and
Kim R.
Dunbar
 *a
*a
aDepartment of Chemistry, Texas A&M University, College Station, Texas 77843, USA. E-mail: dunbar@chem.tamu.edu
bDepartment of Chemistry, Brock University, 1812 Sir Isaac Brock Way, L2S 3A1 St. Catharines, Ontario, Canada. E-mail: tstamatatos@brocku.ca
First published on 5th November 2018
Abstract
A rare 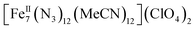 disk-like single-molecule magnet (SMM) exclusively bridged by end-on azides with a spin ground state of S = 14 was prepared by the reaction of a divalent FeII precursor with Me3SiN3 under basic conditions. AC magnetic susceptibility studies revealed unusual, “Janus”-faced SMM behavior for the dried and pristine forms of the
disk-like single-molecule magnet (SMM) exclusively bridged by end-on azides with a spin ground state of S = 14 was prepared by the reaction of a divalent FeII precursor with Me3SiN3 under basic conditions. AC magnetic susceptibility studies revealed unusual, “Janus”-faced SMM behavior for the dried and pristine forms of the 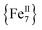 compound attributed to solvation/de-solvation effects of the coordinated MeCN ligands which leads to alterations in the crystal field and symmetry of the metal ions. DFT calculations confirmed the ferromagnetic nature of the interactions between the FeII spin carriers with the zero-field splitting parameters D = −0.2323 cm−1 and E/D = 0.027. The results have important implications for the future study of single-molecule magnets incorporating volatile solvent molecules in the first coordination sphere of the metal ions and their effect on the relaxation dynamics.
compound attributed to solvation/de-solvation effects of the coordinated MeCN ligands which leads to alterations in the crystal field and symmetry of the metal ions. DFT calculations confirmed the ferromagnetic nature of the interactions between the FeII spin carriers with the zero-field splitting parameters D = −0.2323 cm−1 and E/D = 0.027. The results have important implications for the future study of single-molecule magnets incorporating volatile solvent molecules in the first coordination sphere of the metal ions and their effect on the relaxation dynamics.
Introduction
Single-molecule magnets (SMMs) are coordination compounds that exhibit slow relaxation of their magnetization at the molecular level,1 a property that renders them suitable candidates for emerging technologies including high density data storage,2 molecular electronic devices,3 and quantum computation.4 In the quest for strongly-coupled polynuclear SMMs with enhanced properties, one of the most difficult challenges to overcome is the combination of a large spin ground state (S) with a large and negative zero-field splitting parameter, as defined by the axial parameter, D.1 To this end, bridging ligands have played a special role in not only fostering ferromagnetic exchange interactions between the metal ions they bridge, through either a superexchange5 or direct mechanism,6 but also in controlling the orientation of the magnetic anisotropy axes7 and stabilizing microstates with the largest spin and orbital angular momenta.8In recent years 4f metal containing molecules have attracted considerable interest in the SMM field vis-à-vis enhancing the magnetization dynamics (i.e., large energy barriers and blocking temperatures).9 The progress in this area notwithstanding, there are limitations including effective quantum tunneling of the magnetization at zero field and weak-to-negligible magnetic exchange interactions due to the efficient shielding of the 4f orbitals by the outer 5s and 5p-orbitals.10 Given these issues, 3d metal based SMMs of oligo- and polynuclear complexes are still worth pursuing.11
The syntheses of transition metal molecules with interesting magnetic properties often relies on self-assembly reactions between 3d-metal precursors and organic chelating/bridging ligands.11b This strategy has afforded a plethora of SMMs with modest barriers but also some of the most spectacular and well-known SMMs to date including the ubiquitous {Mn12}-carboxylate12 and {Mn6}-oximate complexes,13 and, recently, a nanosized {Mn31} cluster14 and a low-coordinate {Co4} compound,15 all with high energy barriers and blocking temperatures. Unlike Mn compounds, Fe-based SMMs are scarce in the literature. Only a few trivalent FeIII SMMs16 have been reported to date and divalent FeII examples are limited to three examples, viz., an 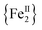 ,17 a family of
,17 a family of 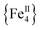 cubanes,18 and a nonanuclear
cubanes,18 and a nonanuclear 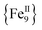 compound.19 Although organic bridging ligands assist in the thermodynamic stability, solubility, and crystallinity of 0-D compounds, their presence as neutral linkers often limits the magnetic properties and dynamics of SMMs, leading to competing magnetic interactions, moderate-to-weak magnetic couplings, and low-lying excited states, among others.11–14,16–19 A potential solution to these obstacles in preparing molecules with large S values and enhanced SMM properties is the discovery of new synthetic avenues to 3d compounds with exclusively ferromagnetic couplers.
compound.19 Although organic bridging ligands assist in the thermodynamic stability, solubility, and crystallinity of 0-D compounds, their presence as neutral linkers often limits the magnetic properties and dynamics of SMMs, leading to competing magnetic interactions, moderate-to-weak magnetic couplings, and low-lying excited states, among others.11–14,16–19 A potential solution to these obstacles in preparing molecules with large S values and enhanced SMM properties is the discovery of new synthetic avenues to 3d compounds with exclusively ferromagnetic couplers.
Apart from their coordination versatility and multifunctional binding affinity to 3d metal ions, end-on (EO) bridging azides (N3−) are also known for their ability to promote ferromagnetic exchange interactions for a wide range of M–N–M angles.20 We recently demonstrated that Me3SiN3 can be used for the synthesis of azido-bridged metal complexes without requiring the presence of any chelating or bridging organic ligand. Isoskeletal and ferromagnetically coupled 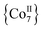 and
and 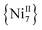 complexes with appreciable S values were obtained albeit with modest or negligible SMM properties.21 Initial attempts to prepare the
complexes with appreciable S values were obtained albeit with modest or negligible SMM properties.21 Initial attempts to prepare the 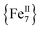 analogue of this family of complexes were hampered by the prompt oxidation of FeII to FeIII which led to a mixed-valence {FeII/III} 2-D polymer that exhibited long-range ferromagnetic ordering below 80 K.21
analogue of this family of complexes were hampered by the prompt oxidation of FeII to FeIII which led to a mixed-valence {FeII/III} 2-D polymer that exhibited long-range ferromagnetic ordering below 80 K.21
Herein we report the anaerobic reaction between divalent Fe(ClO4)2·xH2O, Me3SiN3 and NEt3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in dry MeCN to yield yellow crystals of the heptanuclear complex
1 ratio in dry MeCN to yield yellow crystals of the heptanuclear complex 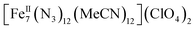 ·4MeCN (1) in 45% yield. Complex 1, along with the isoskeletal
·4MeCN (1) in 45% yield. Complex 1, along with the isoskeletal 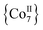 and
and 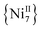 analogues,21 are the first metal complexes in moderate oxidation states that are exclusively bridged by N3− groups without organic bridging or chelating ligands.
analogues,21 are the first metal complexes in moderate oxidation states that are exclusively bridged by N3− groups without organic bridging or chelating ligands.
Experimental section
Synthesis
All manipulations were carried out under an inert atmosphere of N2 using standard Schlenk and glovebox techniques unless otherwise noted. The starting materials Fe(ClO4)2·xH2O and Me3SiN3 were purchased from Sigma Aldrich and used as received. The solvents MeCN and Et2O were purchased from Sigma Aldrich, purified using an MBRAUN solvent purification system, and stored over fresh molecular sieves in an inert atmosphere prior to use. Caution! Azide and perchlorate salts and their corresponding metal complexes are potentially explosive; such compounds should be synthesized and used in small quantities and treated with the utmost of care at all times. Complex 1, both in its dried (1-d) and as-prepared wet (1-w) forms, has been found to be safe when used in small quantities and under the reported conditions.[Fe7(N3)12(MeCN)12](ClO4)2 (1)
To a stirred, colorless solution of Me3SiN3 (0.56 mL, 0.40 mmol) and NEt3 (14 μL, 0.10 mmol) in MeCN (10 mL) was added a solution of Fe(ClO4)2·xH2O (0.10 mmol, 0.04 g for x ∼ 6) in the same solvent (10 mL). The resulting purple solution was stirred for 10 min during which time a color change to dark red was observed. The solution was filtered and the filtrate was layered with Et2O (20 mL). Orange crystals of 1·4MeCN were obtained after 24 h. The yield was ∼55%.Single-crystal X-ray crystallography
A single crystal of 1·4MeCN (0.73 × 0.33 × 0.26 mm) was placed in Paratone® oil and selected under ambient conditions using a MiTeGen microloop. The crystal was placed under a stream of cold N2 at 100(1) K on a Bruker D8-QUEST diffractometer equipped with a IμS Mo microsource (λ = 0.71073 Å). An initial unit cell was determined using SAINT from a set of three ω-scans consisting of thirty 0.5° frames and a sweep width of 15°. From this unit cell, a data collection strategy to collect all independent reflections to a resolution of at least 0.82 Å was implemented using APEX3.22The data for 1·4MeCN were corrected for absorption using SADABS-2014/5.23 The space group was determined from analysis of the systematic absences and E-statistics using XPREP. The structure was solved using the intrinsic phasing routine in SHELXT.24 Non-hydrogen atoms were located from the Fourier difference map and refined using a least-squares refinement algorithm in SHELXL-2014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 and were refined anisotropically. All hydrogen atoms were placed in calculated positions and refined with thermal parameters constrained to their parent atoms. The programs used for molecular graphics were Mercury and Diamond.26 Unit cell parameters, structure solution and refinement details for 1·4MeCN are summarized in Table S1.† Further crystallographic details can be found in the corresponding CIF file provided in the ESI.†
25 and were refined anisotropically. All hydrogen atoms were placed in calculated positions and refined with thermal parameters constrained to their parent atoms. The programs used for molecular graphics were Mercury and Diamond.26 Unit cell parameters, structure solution and refinement details for 1·4MeCN are summarized in Table S1.† Further crystallographic details can be found in the corresponding CIF file provided in the ESI.†
Compound [Fe7(N3)12(MeCN)12](ClO4)2·4MeCN (1) crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one-half of the heptanuclear cation, one perchlorate anion and two MeCN molecules of crystallization in the asymmetric unit. The perchlorate anion atoms O1, O2, O3, O4 are positionally disordered over two nearly equal positions (major component occupancy: 50.6(1)%). Bond distance and thermal parameter restraints were used to model the disorder to ensure a chemically reasonable and computationally stable refinement.
with one-half of the heptanuclear cation, one perchlorate anion and two MeCN molecules of crystallization in the asymmetric unit. The perchlorate anion atoms O1, O2, O3, O4 are positionally disordered over two nearly equal positions (major component occupancy: 50.6(1)%). Bond distance and thermal parameter restraints were used to model the disorder to ensure a chemically reasonable and computationally stable refinement.
Results and discussion
Synthesis
Crystals of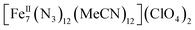 ·4MeCN were treated in two ways for the performance of magnetic and spectroscopic studies. A portion of the crystalline material was collected by filtration and dried under N2 for a maximum of 3 h (1-d), while the other portion of the crystalline material was immediately transferred (as-prepared) and sealed in an NMR tube (1-w). Selected IR data for 1-w (Nujol mull, cm−1): 2308 (s), 2279 (s), 2103 (vs), 1459 (m), 1376 (s), 1349 (m), 1294 (m), 1260 (w), 1227 (m), 1100 (s), 1035 (w), 935 (w), 722 (m), 667 (m), 625 (s), 597 (w). For 1-d, we were not able to perform single crystal or powder X-ray diffraction studies due to the poor crystallinity and extreme air and moisture sensitivity of the sample. Elemental analysis data of 1-d, however, are consistent with the formula {Fe7(N3)12(MeCN)2(ClO4)2} that accounts for the presence of the {Fe7(N3)12}2+ core, two ClO4− anions and only two MeCN molecules, instead of the sixteen that appear in the crystal structure of 1 (including the interstitial MeCN molecules). Elemental analysis data for 1-d (after drying for 3 h under N2), calculated for C4H6N38O8Cl2Fe7: C, 4.08; H, 0.51; N, 45.25%. Found: C, 3.95; H, 0.32; N, 45.38%. Selected IR data for 1-d (Nujol mull, cm−1): 2104 (vs), 1635 (w), 1461 (m), 1377 (s), 1292 (m), 1225 (w), 1100 (s), 1031 (m), 914 (w), 722 (m), 666 (w), 622 (m).
·4MeCN were treated in two ways for the performance of magnetic and spectroscopic studies. A portion of the crystalline material was collected by filtration and dried under N2 for a maximum of 3 h (1-d), while the other portion of the crystalline material was immediately transferred (as-prepared) and sealed in an NMR tube (1-w). Selected IR data for 1-w (Nujol mull, cm−1): 2308 (s), 2279 (s), 2103 (vs), 1459 (m), 1376 (s), 1349 (m), 1294 (m), 1260 (w), 1227 (m), 1100 (s), 1035 (w), 935 (w), 722 (m), 667 (m), 625 (s), 597 (w). For 1-d, we were not able to perform single crystal or powder X-ray diffraction studies due to the poor crystallinity and extreme air and moisture sensitivity of the sample. Elemental analysis data of 1-d, however, are consistent with the formula {Fe7(N3)12(MeCN)2(ClO4)2} that accounts for the presence of the {Fe7(N3)12}2+ core, two ClO4− anions and only two MeCN molecules, instead of the sixteen that appear in the crystal structure of 1 (including the interstitial MeCN molecules). Elemental analysis data for 1-d (after drying for 3 h under N2), calculated for C4H6N38O8Cl2Fe7: C, 4.08; H, 0.51; N, 45.25%. Found: C, 3.95; H, 0.32; N, 45.38%. Selected IR data for 1-d (Nujol mull, cm−1): 2104 (vs), 1635 (w), 1461 (m), 1377 (s), 1292 (m), 1225 (w), 1100 (s), 1031 (m), 914 (w), 722 (m), 666 (w), 622 (m).
The IR spectra of both 1-w and 1-d are depicted in Fig. S1† as a single superimposed image illustrating: (i) the presence of end-on bridging N3− groups (IR bands ∼2100 cm−1),27 and (ii) the de-solvation of 1 as evidenced by the disappearance of the IR bands attributed to MeCN molecules of the wet-sample (2280–2310 cm−1).28 Unfortunately, the potentially explosive nature of 1 owing to the presence of a large number of azido groups as well as ClO4− anions, renders the use of the TGA technique impossible as an additional tool for the study of the solvation/de-solvation effects of 1.
Structural determination
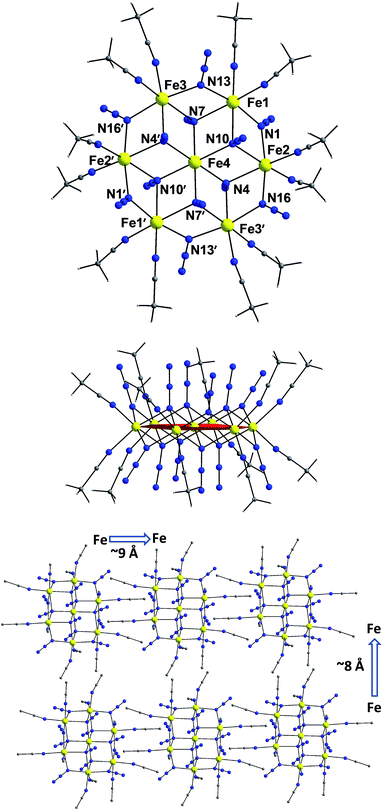
The centrosymmetric heptanuclear cation in compound 1 (Fig. 1, top) consists of a nearly ideal planar hexagon of alternating FeII ions surrounding a central FeII atom, reminiscent of the known Anderson-type structure.29 The oxidation states of the metal ions and the formula of 1 were determined by inspection of the metrical parameters (Table S2†), bond valence sum (BVS) calculations (Table S3†), and charge balance considerations. The {Fe7} disk-like unit possesses virtual S6 symmetry and is stitched together by twelve nitrogen atoms of six μ3-1,1,1 and six μ-1,1 end-on bridging azido ligands. The μ3-1,1,1 azides bridge the {Fe6} hexagon with the central FeII ion, while the μ-1,1 azides link the Fe centers in the outer ring to form the hexagon. Peripheral ligation is completed by twelve terminal MeCN molecules, two on each of the external FeII ions. All FeII ions are six-coordinate with nearly octahedral geometries. All of the Fe–N bond distances fall into the expected range for compounds of high-spin FeII ions with N-donor atoms.30The [Fe7(μ3-N3)6(μ-N3)6]2+ inorganic core of 1 (Fig. S2†) can also be described as consisting of six {Fe3(N3)4} partial-cubane units, each double face-sharing and which share six vertices with the central FeII ion. Complex 1 exhibits a layered structure, with layers of N atoms from azide and MeCN ligands situated above and below the {Fe7} plane (Fig. 1, middle). The intramolecular Fe⋯Fe separations and Fe–(μ-N3)–Fe angles span the range 3.336–3.354 Å and 95.6–104.9°, respectively. Several magnetostructural correlations for azido-bridged systems, especially for CuII, NiII and MnII complexes, have been developed and discussed in terms of the exchange interactions between non-orthogonal magnetic orbitals.20,21 Importantly, the MII–N3(EO)–MII angles affect the nature and strength of the superexchange interactions. For divalent 3d metal complexes with EO bridging N3− ligands, the angle for switching from ferro- to antiferromagnetic coupling is typically >104°. Exchange interactions between the FeII ions in 1 (av. Fe–N–Fe angle = 99.2°) are therefore expected to be ferromagnetic on the basis of the structural parameters.19–21 The packing of the {Fe7} cations in the crystal (Fig. 1, bottom) lead to large separations between FeII ions of neighboring molecules, with the closest intermolecular Fe⋯Fe contact being ∼8 Å owing to the coordinated MeCN molecules.
Magnetic susceptibility data for 1-d
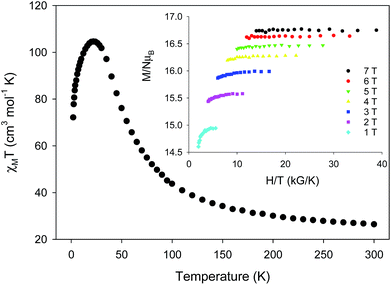
Variable-temperature direct-current (DC) magnetic susceptibility measurements were initially performed on a sample of 1-d in the temperature range 2–300 K under an applied field of 1 kG (0.1 T). The χMT versus T plot is depicted in Fig. 2. The value of χMT at 300 K is 26.43 cm3 mol−1 K, higher than the value of 21 cm3 mol−1 K (calculated with g = 2) expected for seven high-spin FeII (S = 2) non-interacting ions. The χMT value rapidly increases in the 300–22 K region, reaching a maximum of 104.61 cm3 mol−1 K, and then decreases to a value of 72.16 cm3 mol−1 K at 2 K. The shape of the curve suggests an overall ferromagnetic system; the low-T decrease is attributed to the presence of significant zero-field splitting in the ground state and/or antiferromagnetic intermolecular exchange interactions between neighboring cations. The χMT maximum value of 104.61 cm3 mol−1 K at 22 K indicates an S = 14 ground state, the maximum possible value for a ferromagnetically-coupled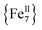 complex; the spin-only (g = 2) value for a state with S = 14 is 105 cm3 mol−1 K. Reduced magnetization studies performed on 1-d at different fields and low temperatures (Fig. 2, inset) clearly indicate the presence of magnetic anisotropy as the various isofield lines do not superimpose onto a master curve expected for a system with a well-isolated spin ground state and negligible anisotropy. The magnetization curves fall substantially short of reaching the magnetization saturation of 28 μB expected for an S = 14 ground state with g = 2, also an indication of magnetic anisotropy.
complex; the spin-only (g = 2) value for a state with S = 14 is 105 cm3 mol−1 K. Reduced magnetization studies performed on 1-d at different fields and low temperatures (Fig. 2, inset) clearly indicate the presence of magnetic anisotropy as the various isofield lines do not superimpose onto a master curve expected for a system with a well-isolated spin ground state and negligible anisotropy. The magnetization curves fall substantially short of reaching the magnetization saturation of 28 μB expected for an S = 14 ground state with g = 2, also an indication of magnetic anisotropy.
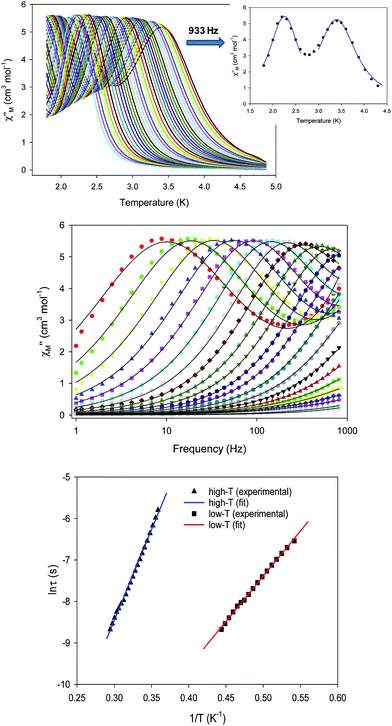
To probe the magnetization dynamics of 1-d, alternating-current (AC) magnetic susceptibility measurements, as a function of both temperature (Fig. 3, top) and frequency (Fig. 3, middle and S3†), were performed under a zero applied dc field. Interestingly, the dried form of the 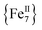 compound displays frequency dependent in-phase (χ′Μ) and out-of-phase (χ′′Μ) signals, which are entirely resolved, at two different temperature regions. The peak maxima for 1-d in the low-T (1.8–2.6 K) and high-T (2.7–5 K) regimes exhibit similar intensities (Fig. 3, inset) and they do not overlap with each other. This is indicative of two individual relaxation processes, which both appear to be thermally assisted. The data were fit to obtain relaxation times (τ) for the respective ac frequencies (1–933 Hz; 37 frequencies in total) and the Tmax of the peaks (Fig. 3, inset). The data were then fit to the Arrhenius law [ln
compound displays frequency dependent in-phase (χ′Μ) and out-of-phase (χ′′Μ) signals, which are entirely resolved, at two different temperature regions. The peak maxima for 1-d in the low-T (1.8–2.6 K) and high-T (2.7–5 K) regimes exhibit similar intensities (Fig. 3, inset) and they do not overlap with each other. This is indicative of two individual relaxation processes, which both appear to be thermally assisted. The data were fit to obtain relaxation times (τ) for the respective ac frequencies (1–933 Hz; 37 frequencies in total) and the Tmax of the peaks (Fig. 3, inset). The data were then fit to the Arrhenius law [ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ = ln
τ = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ0 + Ueff/kBT], where Ueff is the effective energy barrier for the magnetization reversal and kB is the Boltzmann constant, resulting in the parameters Ueff = 43.7(1) K and τ0 = 4.2(1) × 10−10 s, and Ueff = 21.9(2) K and τ0 = 1.1(2) × 10−8 s for the high- and low temperature regimes, respectively (Fig. 3, bottom). The pre-exponential factor, τ0, is usually within the 10−6 to 10−10 s range for SMMs and it provides a quantitative measure of the attempt time of relaxation from the thermal phonon bath.
τ0 + Ueff/kBT], where Ueff is the effective energy barrier for the magnetization reversal and kB is the Boltzmann constant, resulting in the parameters Ueff = 43.7(1) K and τ0 = 4.2(1) × 10−10 s, and Ueff = 21.9(2) K and τ0 = 1.1(2) × 10−8 s for the high- and low temperature regimes, respectively (Fig. 3, bottom). The pre-exponential factor, τ0, is usually within the 10−6 to 10−10 s range for SMMs and it provides a quantitative measure of the attempt time of relaxation from the thermal phonon bath.
The Cole–Cole plots (Fig. S4†) of 1-d exhibit two sets of semicircular shapes at different temperatures; the data were fit using a generalized Debye model.31 The α-values for each set of low- and high-temperature data are in the range 0.26–0.38 and 0.13–0.39, respectively, suggesting the presence of multiple relaxation processes. The same magnetic results were reproduced three times from independent samples of 1 that were dried under the same conditions. The presence of two thermally-assisted relaxation processes is a rare phenomenon in polynuclear 3d-metal SMMs and, to the best of our knowledge, has only been previously observed for a few members of the {Mn12} family of SMMs as a result of the ‘Jahn–Teller isomerism’ effect.32
Magnetic susceptibility data for 1-w
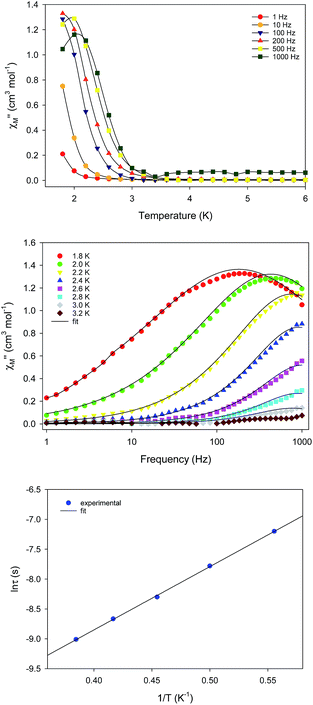
The unusual emergence of two distinct relaxation processes in 1-d prompted us to investigate the magnetic properties of the wet (as-prepared) crystalline form of 1-w to measure a sample in which the coordinated and interstitial MeCN molecules are intact. The freshly prepared crystalline sample of 1-w was immediately transferred and sealed in an NMR tube which was immediately used for the acquisition of the reported magnetic data. DC magnetic susceptibility studies for 1-w, including χMT versus T (Fig. S5†) and reduced magnetization (Fig. S6†) studies, revealed a response similar to 1-d and an S = 14 ground state. The only noticeable difference is the decrease of the χMT product at a lower temperature of 10 K as compared to 1-d.AC magnetic susceptibility studies as a function of both temperature (Fig. 4, top) and frequency (Fig. 4, middle) carried out for 1-w led to the observation of a single slow relaxation of the magnetization below ∼3 K. The χM′′ versus frequency data were fit to a generalized Debye model to extract the corresponding relaxation times. The data were then fit to the Arrhenius law (Fig. 4, bottom), yielding the parameters: Ueff = 14.1(2) K and τ0 = 3.3(2) × 10−7 s. Cole–Cole plots of 1-w exhibit semicircular shapes at different temperatures below 3 K and the fit of the data gave α-values in the 0.12–0.37 range, indicating a wide distribution of relaxation times (Fig. S7†). The magnetic results of 1-w are also reproducible, and the measurements were performed with two different wet samples of 1. In addition, the AC magnetic dynamics of both 1-d and 1-w were also studied under an applied DC field of 0.1 T, but no noticeable differences were observed regarding the number of relaxation processes and magnitude of energy barriers.
Computational studies
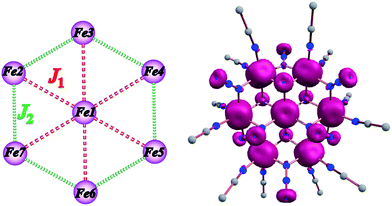
The experimental magnetic susceptibility data for 1 were not fit due to the large size and low symmetry of the complex. Thus, the exchange interactions and magnetic anisotropy of 1 were determined using DFT calculations in order to evaluate the observed magnetic behavior. This strategy has been previously employed in a family of {Mn7} disk-like complexes, where the metal ions were bridged by organic groups, and it was able to reproduce very accurately the experimental findings.35c The exchange topology used for the computational calculations for 1 is shown in Fig. 5 (left). The following exchange Hamiltonian was employed to evaluate the magnetic exchange interactions (J) in 1.| Ĥ = −[2J1(SFe1SFe2 + SFe1SFe3 + SFe1SFe4 + SFe1SFe5 + SFe1SFe6 + SFe1SFe7) + 2J2(SFe2SFe3 + SFe3SFe4 + SFe4SFe5 + SFe5SFe6 + SFe6SFe7 + SFe2SFe7)] | (1) |
To extract the exchange interactions on the full structure of 1, the energies of three different spin configurations were used (Table S4†).33 The exchange coupling constants were calculated using the broken symmetry (BS) approach developed by Noodleman.34 This method has been employed extensively to compute good numerical estimates of exchange interactions in numerous polynuclear complexes.35 DFT calculations were performed using the B3LYP basis functional36 and Aldrich's triple-ζ-quality basis set37 with the Gaussian 09 program.38
Apart from the magnetic coupling, the ZFS (D) has also been computed for complex 1 using the Orca 3.0 programme suite.39 In our DFT calculations, the spin–orbit coupling operators are represented by an effective one electron, using the spin–orbit mean field (SOMF) method as implemented in Orca.39 We have used the coupled perturbed (CP) SOC approach to evaluate the spin–orbit contribution to D (DSOC). The spin–spin contribution (DSS) was estimated by using the unrestricted natural orbital40 approach. Furthermore, to improve the accuracy of the estimated D values, relativistic corrections are performed using the DKH method.39
The coupling between the central and the outer FeII ions is designated as the J1 interaction and the coupling between the two outer ring FeII ions is described as J2 interaction. The DFT computed values predict that both the J1 and J2 interactions are ferromagnetic with values of +3.0 and +3.3 cm−1, respectively. Ferromagnetic coupling is consistent with the observation of ferromagnetic interactions in dinuclear Ni(II), Fe(III) and Mn(II) complexes with one or more μ-bridging azido ligands41 and in the azido-bridged {Ni7} and {Co7} disk-like complexes.21 Given that both J1 and J2 interactions are ferromagnetic, the ground state is S = 14. The computed spin density plots (Fig. 5, right) reveal a dominant spin delocalization mechanism. Calculations were performed also by using the diamagnetic substitution method (DSM), where, except for the desired pair of FeII centres, the remaining ions are substituted by diamagnetic ZnII ions.35c,42 Such calculations are essential for validating the J values computed from the full structure and to realize the influence of other paramagnetic centres on a particular J value. This method also yields ferromagnetic coupling constants for both interactions (J1 = +3.1 and J2 = +4.5 cm−1) which are in excellent agreement with the full cluster coupling values.
Given the large ground state spin value and the observed slow relaxation of the magnetization for 1 at zero DC field, one would expect a negative D value for the molecule, thus the value of D was computed to further probe the SMM behavior. Although ab initio CASSCF/NEVPT2 calculations have proven to yield accurate estimates of D values,43 this method cannot be employed for such large molecules.44 The full cluster anisotropy was therefore computed using DFT methods which yielded the parameters D = −0.2323 cm−1 and E/D = 0.027, where E is the rhombic zero-field splitting parameter. The Dsoc plays a key role with a value of −0.191 cm−1. The major contributions to Dsoc arise from DOMO (doubly-occupied molecular orbital) to SOMO (singly-occupied MO) β→β excitations (−0.127 cm−1) and SOMO to SOMO α→β excitations (−0.072 cm−1). The SOMO to VMO (Virtual Molecular Orbital) α→α excitations and DOMO to VMO β→α excitations contribute to a small extent with values of 0.003 and 0.005 cm−1, respectively.45 Comparable behavior is observed for DSS contributions of −0.04 cm−1.
Magnetic properties of 1-dversus1-w
The differences in the magnetic properties of 1-dversus1-w, as indicated by the low temperature regimes of the χMT versus T plots and the AC magnetic susceptibility data, are due, in part, to the changes in intermolecular interactions between the individual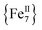 molecules. The intermolecular distances in 1-w are expected to be larger due to the presence of all of the MeCN ligands (Fig. 1, bottom). In the case of 1-d, the drying process results in the removal of MeCN molecules and the
molecules. The intermolecular distances in 1-w are expected to be larger due to the presence of all of the MeCN ligands (Fig. 1, bottom). In the case of 1-d, the drying process results in the removal of MeCN molecules and the 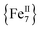 cations are expected to be less well separated in the solid state. Moreover, the molecular magnetic anisotropy of 1 is expected to deviate from 1-w to 1-d due to the dissimilar coordination environment of the six peripheral FeII ions. In 1-w, all of the FeII ions are six-coordinate with a distorted octahedral geometry. In 1-d, however, drying leads to loss of coordinated MeCN molecules and the peripheral FeII ions will be primarily four-coordinate. These low-coordinate FeII ions are expected to exhibit larger single-ion magnetic anisotropies which, in turn, effects the global molecular anisotropy.46 For example, complete removal of all twelve bound MeCN molecules in 1 would render the six external FeII ions four-coordinate with slightly distorted see-saw geometries (CShM values = 0.82–0.85, C2v point group; Fig. S8 and Table S5†). In support of this contention is the fact that large uniaxial magnetic anisotropy and slow magnetization relaxation with high energy barriers have been reported for a family of four-coordinate, trigonal pyramidal FeII–pyrrolide complexes with C3v point group symmetry.47 Therefore, the crystal field around four-coordinate FeII ions in 1-d would induce increased molecular magnetic anisotropy for this system and consequently a larger energy barrier than for 1-w. It is also possible that the two ClO4− anions found in the elemental analyses of 1-d are bound to the FeII centers. Although rare,48a–c terminally coordinated ClO4− ions are of precedence in FeII chemistry, and this is also expected to affect the crystal field and coordination geometries of some of the outer FeII ions in 1-d. On a final note, the shift (ΔTmax) in the χ′′M peak maximum temperature (Tmax) with AC frequency (f) was measured by a parameter φ = (ΔTmax/Tmax)/Δ(log
cations are expected to be less well separated in the solid state. Moreover, the molecular magnetic anisotropy of 1 is expected to deviate from 1-w to 1-d due to the dissimilar coordination environment of the six peripheral FeII ions. In 1-w, all of the FeII ions are six-coordinate with a distorted octahedral geometry. In 1-d, however, drying leads to loss of coordinated MeCN molecules and the peripheral FeII ions will be primarily four-coordinate. These low-coordinate FeII ions are expected to exhibit larger single-ion magnetic anisotropies which, in turn, effects the global molecular anisotropy.46 For example, complete removal of all twelve bound MeCN molecules in 1 would render the six external FeII ions four-coordinate with slightly distorted see-saw geometries (CShM values = 0.82–0.85, C2v point group; Fig. S8 and Table S5†). In support of this contention is the fact that large uniaxial magnetic anisotropy and slow magnetization relaxation with high energy barriers have been reported for a family of four-coordinate, trigonal pyramidal FeII–pyrrolide complexes with C3v point group symmetry.47 Therefore, the crystal field around four-coordinate FeII ions in 1-d would induce increased molecular magnetic anisotropy for this system and consequently a larger energy barrier than for 1-w. It is also possible that the two ClO4− anions found in the elemental analyses of 1-d are bound to the FeII centers. Although rare,48a–c terminally coordinated ClO4− ions are of precedence in FeII chemistry, and this is also expected to affect the crystal field and coordination geometries of some of the outer FeII ions in 1-d. On a final note, the shift (ΔTmax) in the χ′′M peak maximum temperature (Tmax) with AC frequency (f) was measured by a parameter φ = (ΔTmax/Tmax)/Δ(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f). For the dried sample, 1-d, we obtained φ = 0.11–0.19 and 0.17–0.22 for the high- and low-T regions, which are both within the range of normal superparamagnets, thereby excluding the possibility of a spin glass state.48d
f). For the dried sample, 1-d, we obtained φ = 0.11–0.19 and 0.17–0.22 for the high- and low-T regions, which are both within the range of normal superparamagnets, thereby excluding the possibility of a spin glass state.48d
Conclusions and outlook
In summary, the synthesis of a rare, ferromagnetically-coupled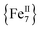 (1) disk-like cluster with an S = 14 ground state and unusual “Janus”-faced SMM behavior has been found to exhibit different AC magnetic dynamics in the dried (1-d) versus wet (1-w) forms of the crystals. Such a rare phenomenon in 3d-cluster SMMs is primarily rationalized in terms of the loss or presence of coordinated/interstitial MeCN molecules in 1-d or 1-w, respectively. The [Fe7(N3)12]2+ core is present in both forms of 1, as confirmed by X-ray diffraction studies (for 1-w), elemental analyses (for 1-d) and DC magnetic studies (S = 14 for both forms). The different number of relaxation processes (two for 1-d and one for 1-w) and values of energy barriers for the magnetization reversal are attributed to differences in intermolecular interactions49 and the dissimilar molecular anisotropies emanating from different crystal fields around the peripheral FeII ions.
(1) disk-like cluster with an S = 14 ground state and unusual “Janus”-faced SMM behavior has been found to exhibit different AC magnetic dynamics in the dried (1-d) versus wet (1-w) forms of the crystals. Such a rare phenomenon in 3d-cluster SMMs is primarily rationalized in terms of the loss or presence of coordinated/interstitial MeCN molecules in 1-d or 1-w, respectively. The [Fe7(N3)12]2+ core is present in both forms of 1, as confirmed by X-ray diffraction studies (for 1-w), elemental analyses (for 1-d) and DC magnetic studies (S = 14 for both forms). The different number of relaxation processes (two for 1-d and one for 1-w) and values of energy barriers for the magnetization reversal are attributed to differences in intermolecular interactions49 and the dissimilar molecular anisotropies emanating from different crystal fields around the peripheral FeII ions.
These results underscore the importance of solvation/de-solvation effects on the structural and magnetic properties of polynuclear metal complexes and the sensitivity of magnetic dynamics upon altering the first coordination sphere of 3d-metal ions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. R. D. gratefully acknowledges support for this work by the National Science Foundation (CHE-1808779) and the Robert A. Welch Foundation (Grant A-1449). The SQUID magnetometer was purchased with funds provided by the Texas A&M University Vice President of Research. We are grateful to the HPRC at Texas A&M for the computing resources. Th. C. S. thanks NSERC-DG, ERA and Brock Chancellor's Chair for Research Excellence.Notes and references
- R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011–1026 RSC.
- M. del Carmen Giménez-López, F. Moro, A. La Torre, C. J. Gómez-García, P. D. Brown, J. van Slageren and A. N. Khlobystov, Nat. Commun., 2011, 2, 407 CrossRef PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357 CrossRef CAS PubMed.
- G. Aromi, D. Aguila, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC.
- P. W. Anderson, Phys. Rev., 1950, 79, 350–356 CrossRef.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- D. Gatteschi and L. Sorace, J. Sol. State Chem., 2001, 159, 253–261 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- K. Binnemans, Chem. Rev., 2009, 109, 4283–4374 CrossRef CAS PubMed.
- (a) J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC; (b) C. Papatriantafyllopoulou, E. E. Moushi, G. Christou and A. J. Tasiopoulos, Chem. Soc. Rev., 2016, 45, 1597–1628 RSC.
- N. E. Chakov, S.-C. Lee, A. G. Harter, P. L. Kuhns, A. P. Reyes, S. O. Hill, N. S. Dalal, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2006, 128, 6975–6989 CrossRef CAS PubMed.
- C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 2754–2755 CrossRef CAS PubMed.
- P. Abbasi, K. Quinn, D. I. Alexandropoulos, M. Damjanović, W. Wernsdorfer, A. Escuer, J. Mayans, M. Pilkington and T. C. Stamatatos, J. Am. Chem. Soc., 2017, 139, 15644–15647 CrossRef CAS PubMed.
- K. Chakarawet, P. C. Bunting and J. R. Long, J. Am. Chem. Soc., 2018, 140, 2058–2061 CrossRef CAS PubMed.
- C. J. Milios and R. E. P. Winpenny, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, pp. 1–109 Search PubMed.
- A. K. Boudalis, Y. Sanakis, J. M. Clemente-Juan, A. Mari and J. P. Tuchagues, Eur. J. Inorg. Chem., 2007, 2409–2415 CrossRef CAS.
- H. Oshio, N. Hoshino, T. Ito and M. Nakano, J. Am. Chem. Soc., 2004, 126, 8805–8812 CrossRef CAS PubMed.
- A. K. Boudalis, Y. Sanakis, J. M. Clemente-Juan, B. Donnadieu, V. Nastopoulos, A. Mari, Y. Coppel, J. P. Tuchagues and S. P. Perlepes, Chem.–Eur. J., 2008, 14, 2514–2526 CrossRef CAS PubMed.
- A. Escuer, J. Esteban, S. P. Perlepes and T. C. Stamatatos, Coord. Chem. Rev., 2014, 275, 87–129 CrossRef CAS.
- D. I. Alexandropoulos, L. Cunha-Silva, A. Escuer and T. C. Stamatatos, Chem.–Eur. J., 2014, 20, 13860–13864 CrossRef CAS PubMed.
- APEX-III, Bruker AXS Inc, Data Collection Software, Bruker AXS, Delft, USA, 2016 Search PubMed.
- G. M. Sheldrick, SADABS v.2.01, Bruker/Siemens Area Detector Absorption Correction Program, Bruker AXS, Madison, WI, 1998 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr. Sect. A, Found. and Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- (a) C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453–457 CrossRef CAS; (b) W. Pennington, J. Appl. Crystallogr., 1999, 32, 1028–1029 CrossRef CAS.
- T. C. Stamatatos, G. S. Papaefstathiou, L. R. MacGillivray, A. E. Escuer, R. Vicente, E. Ruiz and S. P. Perlepes, Inorg. Chem., 2007, 46, 8843 CrossRef CAS PubMed.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, 4th edn, Wiley, New York, 1986 Search PubMed.
- N. Hoshino, A. M. Ako, A. K. Powell and H. Oshio, Inorg. Chem., 2009, 48, 3396–3407 CrossRef CAS PubMed.
- H. Phan, J. J. Hrudka, D. Igimbayeva, L. M. Lawson Daku and M. Shatruk, J. Am. Chem. Soc., 2017, 139, 6437–6447 CrossRef CAS PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- S. M. J. Aubin, Z. Sun, H. J. Eppley, E. M. Rumberger, I. A. Guzei, K. Folting, P. K. Gantzel, A. L. Rheingold, G. Christou and D. N. Hendrickson, Inorg. Chem., 2001, 40, 2127–2146 CrossRef CAS PubMed.
- A. Bencini and F. Totti, Int. J. Quantum Chem., 2005, 101, 819–825 CrossRef CAS.
- L. Noodleman, J. Am. Chem. Soc., 1981, 74, 5737–5743 CAS.
- (a) P. Christian, G. Rajaraman, A. Harrison, J. J. W. McDouall, J. T. Raftery and R. E. P. Winpenny, Dalton Trans., 2004, 1511–1512 RSC; (b) G. Rajaraman, E. Ruiz, J. Cano and S. Alvarez, Chem. Phys. Lett., 2005, 415, 6–9 CrossRef CAS; (c) K. R. Vignesh, S. K. Langley, K. S. Murray and G. Rajaraman, Chem.–Eur. J., 2015, 21, 2881–2892 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. P. Jr, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, a. J. Cioslowski, D. J. Fox and I. Gaussian, Revision A.02 ed., Gaussian 09, Wallingford CT, 2009 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- K. Koizumi, M. Shoji, Y. Kitagawa, T. Taniguchi, T. Kawakami, M. Okumura and K. Yamaguchi, Polyhedron, 2005, 24, 2720–2725 CrossRef CAS.
- (a) R. Cortes, J. L. Pizarro, L. Lezama, M. I. Arriortua and T. Rojo, Inorg. Chem., 1994, 33, 2697–2700 CrossRef CAS; (b) G. De Munno, T. Poerio, G. Viau, M. Julve and F. Lloret, Angew. Chem., Int. Ed., 1997, 36, 1459–1461 CrossRef CAS; (c) J. Ribas, M. Monfort, C. Diaz, C. Bastos and X. Solans, Inorg. Chem., 1994, 33, 484–489 CrossRef CAS.
- E. Ruiz, J. Cano, S. Alvarez, A. Caneschi and D. Gatteschi, J. Am. Chem. Soc., 2003, 125, 6791–6794 CrossRef CAS PubMed.
- (a) S. Sinnecker, F. Neese, L. Noodleman and W. Lubitz, J. Am. Chem. Soc., 2004, 126, 2613–2622 CrossRef CAS PubMed; (b) S. K. Singh and G. Rajaraman, Chem.–Eur. J., 2014, 20, 113–123 CrossRef CAS PubMed.
- K. R. Vignesh, S. K. Langley, C. J. Gartshore, B. Moubaraki, K. S. Murray and G. Rajaraman, Inorg. Chem., 2017, 56, 1932–1949 CrossRef CAS PubMed.
- M. Schmidt, D. Wiedemann, B. Moubaraki, N. F. Chilton, K. S. Murray, K. R. Vignesh, G. Rajaraman and A. Grohmann, Eur. J. Inorg. Chem., 2013, 958–967 CrossRef CAS.
- (a) R. Maurice, P. Verma, J. M. Zadrozny, S. Luo, J. Borycz, J. R. Long, D. G. Truhlar and L. Gagliardi, Inorg. Chem., 2013, 52, 9379–9389 CrossRef CAS PubMed; (b) M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC; (c) J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577 CrossRef CAS PubMed; (d) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126 CrossRef CAS PubMed.
- (a) O. Singh, N. Tyagi, M. M. Olmstead and K. Ghosh, Dalton Trans., 2017, 46, 14186–14191 RSC; (b) S. K. Ghosh, R. Patra and S. P. Rath, Inorg. Chem., 2010, 49, 3449–3460 CrossRef CAS PubMed; (c) K. Chen and L. Que Jr, J. Am. Chem. Soc., 2001, 123, 6327–6337 CrossRef CAS PubMed; (d) J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, 1993 Search PubMed.
- For mononuclear 3d-SMMs exhibiting two relaxation processes, see: (a) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734 CrossRef CAS PubMed; (b) F. Habib, O. R. Luca, V. Vieru, M. Shiddiq, I. Korobkov, S. I. Gorelsky, M. K. Takase, L. F. Chibotaru, S. Hill, R. H. Crabtree and M. Murugesu, Angew. Chem., Int. Ed., 2013, 52, 11290–11293 CrossRef CAS PubMed; (c) F. Habib, I. Korobkov and M. Murugesu, Dalton Trans., 2015, 44, 6368–6373 RSC; (d) J. Miklovič, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484–12487 RSC; (e) J. Li, Y. Han, F. Cao, R.-M. Wei, Y.-Q. Zhang and Y. Song, Dalton Trans., 2016, 45, 9279–9284 RSC; (f) L. T. A. Ho and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 104422 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Spectroscopy data, crystallographic data and tables, and magnetism details. CCDC 1850963. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc04384a |
| This journal is © The Royal Society of Chemistry 2019 |