Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How 2-periodic coordination networks are interweaved: entanglement isomerism and polymorphism†
Eugeny V.
Alexandrov
 *a,
Vladislav A.
Blatov
*a,
Vladislav A.
Blatov
 *a and
Davide M.
Proserpio
*a and
Davide M.
Proserpio
 *ab
*ab
aSamara Center for Theoretical Materials Science (SCTMS), Samara University, Ac. Pavlov Street 1, Samara 443011, Russia. E-mail: aleksandrov_ev1@mail.ru; blatov@samsu.ru; davide.proserpio@unimi.it
bDipartimento di Chimica, Università degli Studi di Milano, Via C. Golgi 19, 20133, Milano, Italy
First published on 15th March 2017
Abstract
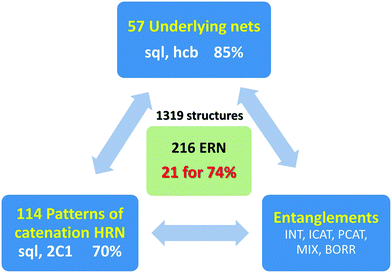
The entanglements of 1319 2-periodic coordination polymers are examined and fully classified using the extended ring nets (ERNs) approach. The ERNs characterize the entanglement to the greatest detail ever achieved: all possible classes/types/modes of entanglements observed and reported in the literature so far result in 216 ERN topologically distinct modes of entanglements with 74% of all the structures falling into only 21 of them. We also introduce the notion of entanglement isomerism to designate the coordination polymers that have the same chemical composition, local and overall topology, but differ by their catenation patterns as mapped into their ERNs.
1. Introduction
The importance of catenation in chemistry has a long history as shown in a recent tutorial review entitled “Knot theory in modern chemistry” where one paragraph (4.1) is dedicated to the more recent findings in coordination and supramolecular networks.1 The entanglement of coordination polymers has been a phenomenon described in great detail since the seminal work of Batten & Robson in 1998, using a heuristic approach based on visual analysis, then extended by some of us in 2003 to include all possible achievable entanglements of periodic nets of any dimension (some of which were observed in later years).2–6 Since 2004, we have developed some computational tools (now implemented in the program package ToposPro) that allowed us to classify the entanglements in a more quantitative way, see e.g. interpenetration of 3-periodic coordination networks, interpenetration of supramolecular networks based on hydrogen bonds, introducing classes of interpenetration that helped the analysis and description of complex structures.7–10 But the true topological description of entanglement should be free of crystallographic symmetry relationships which may be affected by non-topological factors such as molecular geometries, the presence and placement of guest species, etc. This was achieved by introducing the Hopf ring net, a topological method for classification of entanglements that extracts the pattern of catenation mapping the Hopf-links (the simplest two-ring link).11 With this approach, it is now possible to prove when two or more entanglements of the same underlying nets are topologically equivalent, i.e. they can be superimposed by distorting them without ripping or gluing any edges.12 Other recent works analyze the entanglement searching for group-theoretical relations searching for the maximum symmetry embedding with the help of Hopf ring nets.13,14 In this paper, we apply this topological analysis to examine 2-periodic entanglements that we have recently reviewed, update the results, and show that most of the structures fall into a few patterns.15 All the results are also collected in the ToposPro electronic databases that will allow future researchers to easily compare their findings and classify their motif as known or new; furthermore, analysis of the chemical composition vs. entanglement will help in the design of new structures with special properties.7,16,17 Preliminary results of this work, presented at a meeting, helped a recent analysis of 2-fold interpenetrated coordination networks of pto topology that suggests a simple enumeration scheme for generating MOF entanglements via two-dimensional surfaces.18,192. Experimental
2.1. Topological descriptors of entangled coordination networks
In our review on single 2-periodic coordination polymers, we announced an idea of developing an expert system that could be able to predict the overall topology of the polymers resting upon correlations between various chemical, geometrical, and topological descriptors.17 The correlations compose the knowledge database of the expert system; this database should be created in an automatic way by checking for significant combinations of the descriptors. The key task is to define as many robust descriptors as possible.In ref. 17, we looked for correlations between chemical composition (metal complexing center and molecular ligands), local topological descriptors (coordination number of metal atoms and coordination modes of ligands) and overall topology of the same polymeric group.
Here, we extend the list of descriptors to create a knowledge database for ensembles of entangled coordination polymers. We use four descriptors, which were proposed earlier: (i) entanglement type (interpenetration, inclined or parallel polycatenation, Borromean or Brunnian entanglement); (ii) number of entangled nets in the interpenetrated array (Z); (iii) degree of catenation (Doc) for inclined or parallel polycatenation, implying evaluation of the number of links (Hopf or multilink) a particular ring of one net forms with rings of other nets in the array; (iv) index of separation (Is) of 2D motifs in the case of parallel polycatenation, that is, the number of motifs which have to be removed to disjoin the array into two separate parts.4 We also take into account if the entangled nets have 2-loops, that is, rings in which all nodes, but two, have a coordination number of 2.
In addition to these four descriptors, we introduce new ones derived from the so-called Hopf ring net (HRN), a tool proposed recently to classify in detail the entanglements in coordination polymers.11 The method of topological analysis based on the HRN concept is described below.
2.2. The method for classification of entanglements with extended ring nets
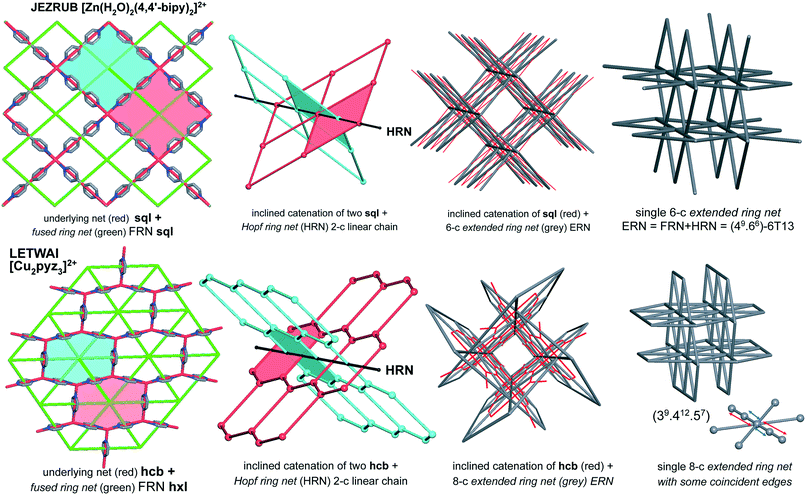
The idea of detailed classification of entanglements consists of representing each ring in the initial net by its centroid (geometrical center) and constructing the so-called extended ring net (ERN). The nodes of this net correspond to the ring centroids, while the edges connect the nodes if the corresponding rings are adjacent to each other in the initial net. There are two kinds of such adjacency: the rings can have common edges in the initial net (fused rings), or they can catenate each other (catenated rings, Fig. 1). Accordingly, there are two kinds of edges in the extended ring net (ERN) corresponding to pairs of fused and catenated rings. With these edges, the extended ring net can be split into two subnets: the fused ring net (FRN) and the Hopf ring net (HRN), each of which contains only one kind of edge (Fig. 1).11,20 The former net (FRN) reflects the topology of the initial net or a set of nets if the crystal structure contains several separated groups; the latter one (HRN) characterizes the topology of the entanglement. Thus, the HRN can be treated as the net of catenated rings characterizing the method of interweaving the rings. The name ‘Hopf’ means that the net is supported only by 2-ring links with the simplest 2-ring 2-crossing link called the Hopf link.1,11,15 More crossing 2-ring links are included, such as the 4-crossing Solomon links. This feature limits the types of entanglements that can be expressed only in terms of pairwise links; more complicated links, for example, Borromean or Brunnian, require another approach.21 It should be noted, however, that such complicated links are very rare in coordination polymers.15The extended ring net ERN is a very powerful tool to explore and classify the topology of entangled ensembles of coordination polymers. In particular, the periodicity n of the extended ring net coincides with the periodicity of the whole ensemble, while the periodicity mi of an ith connected constituent of the fused ring net characterizes the periodicity of an ith polymeric group in the ensemble. Obviously, mi ≤ n; there are two possible cases: (i) all mi = n and (ii) at least one mi < n corresponding to interpenetration and polycatenation phenomena, respectively.4,6,17 The topology of the ring nets can be determined in the same way as that for underlying nets of crystal structures,22 however, one should take into account that ring nets can have collisions if the centroids of different rings coincide with each other (Fig. 1); if such rings are in addition symmetry-equivalent, then the ring net has a lower symmetry compared to the initial net. Once the topology of the HRN is determined, the overall catenation motif can be referred to a particular topological type that is independent of the ring size and the topology of the initial net, so it may occur that different entanglements of different nets present the same HRN.11 The information about the nature of the net that gives the entanglement is stored in the topology of the ERN. In the present analysis, we observed that the ERN characterizes the entanglement to the greatest detail ever achieved: all possible classes/types/modes of entanglements observed and reported in the literature (see in particular the work of Batten & Robson3,23) are classified in separated sets, resulting in a total of 216 ERN topologically distinct modes of entanglements (see below) from 114 HRNs.
We have implemented the method of topological analysis of entanglements with ERN/HRNs into the program package ToposPro (http://www.topospro.com).7 ToposPro performs the topological analysis in an automatic way through the stages of recognizing interatomic bonds in the coordination polymer, separating all rings, determining the ring catenation, constructing the Hopf, fused, and extended ring nets, and assigning to each net its topological types.
2.3. Objects
We applied the method described above to entangled 2-periodic coordination polymers, which we have recently collected and overviewed.15 We have updated the sample with the structures published in the last 5.37 release of the Cambridge Structural Database (CSD, November 2015). In total, we have considered 1319 crystal structures, where 2-periodic polymeric motifs form 2- or 3-periodic entangled ensembles. This sample contains information about 38 structures with Borromean entangled systems and 1281 entangled structures constructed with Hopf links. We found seven new examples of Borromean entanglements similar to the ones already reported,15 so we will not discuss this class further. For the 1281 structures, the ring nets of all kinds were constructed and the corresponding HRNs and ERNs were tabulated and classified. All the data and classifications are available in the ESI† in a spreadsheet format. It should be noted that the sample increased by 68% in two years (1319 vs. 783) showing the constantly growing interest in the synthesis of coordination networks.3. Results and discussion
3.1. Topological classification of 2-periodic coordination networks
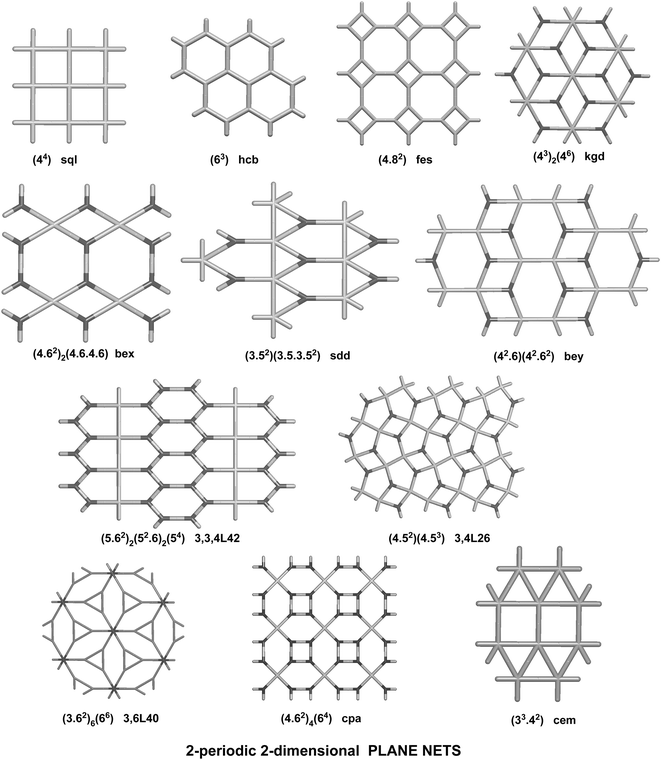
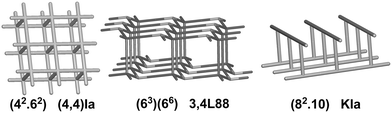
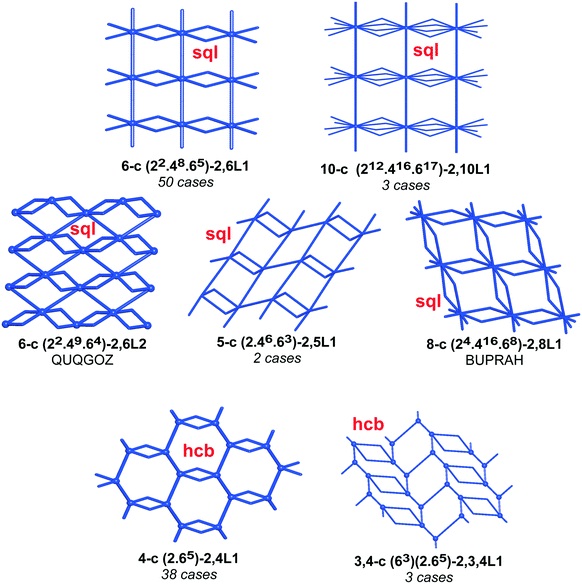
We have already explored in detail the topological features of individual entangled networks;15 the extension of the sample with 536 new structures published in 2014–2015 does not essentially influence the main conclusions. Here, we update our previous results now with full classification of the topology of the entanglement.The distribution of the networks on 57 types of underlying topologies is very uneven (Fig. 2), again the two most frequent topological types, sql and hcb, include 85% of the structures. These nets are intrinsically planar (or 2D), i.e. can be embedded into the Euclidean plane without collisions or edge crossings. There are a total of 12 planar nets observed in 1170 structures (89%), illustrated in Fig. 3, with three new ones: 3,6L40 for KEQCAM,24cpa for JUHTIR25 and cem for XOVXOW.26 The three most frequent thick layers (representing 76 structures, 6%) are shown in Fig. 4, and two of them are related to sql and hcb: a double layer of sql called (4,4)Ia and a double layer of hcb called 3,4L88. The remaining 42 nets are 2-periodic but 3D and represent thick layers (observed in 73 structures, 5%). 98 structures belong to the entanglements of layers containing 2-membered loops15,27 and in particular three new topologies have been observed: 2,3,4L1 and 2,8L1 in the 2-fold interpenetrated hcb and sql; 2,5L1 in the parallel catenation of sql (see Fig. 5).
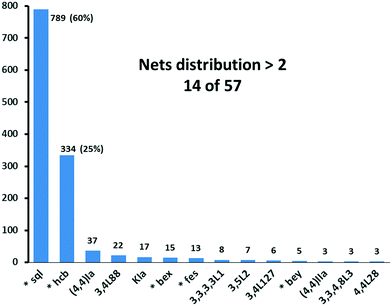 | ||
| Fig. 2 Net distribution of the 1319 2D entangled motifs. Since our review,15 new names have been given to bex = 3,4L13 and bey = 3,4L83. Nets with (*) are intrinsically planar. | ||
3.2. Topological classification of entanglements in 2-periodic coordination networks
The scheme used in our review15 can now be updated and extended using the ring net approach. As was shown in part 2.1, analysis of periodicity of the extended ring nets allows the distinction between the two main groups of 2-periodic entangled motifs: the interpenetrated array is described by a 2-periodic ERN, while the polycatenated ensemble produces a 3-periodic ERN. These two groups are almost equal; the latter group is further divided into parallel (PCAT) and inclined (ICAT) catenated motifs depending on the mutual orientation of the catenated networks (Fig. 6). Also, the distribution of planar and thick layers (89% vs. 11%) is unchanged with respect to our review, as shown in Fig. 6, with the thick layers predominant in parallel polycatenation.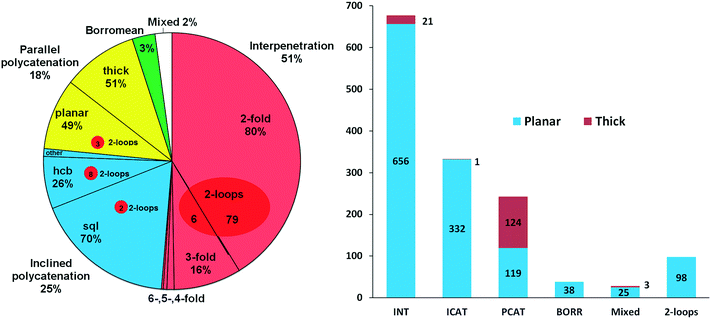 | ||
| Fig. 6 (left) Distribution of interpenetration vs. polycatenation in 1319 2D entangled structures and (right) distribution of planar and thick layers among the six types of entangled structures. | ||
In total, we have found 114 topological types of HRNs, i.e. motifs of catenated rings. Two are dominant as they are observed in 70% of the structures: a 1-periodic simple chain (2C1) with rings catenated with the two adjacent in a row and a 2-periodic square lattice (sql) where rings catenate with four adjacent as illustrated in Fig. 1 and 7. This should not be surprising because these topological types are the simplest possible extension of periodicity for links: from the isolated two-component Hopf link, we get infinite chains (1-periodic 2C1 HRN) adding more components along one direction or a chain mail (2-periodic sql HRN) adding components along two directions. Both HRNs occur in all groups of entanglements (Fig. 7), though 2C1 is rare for parallel polycatenation.
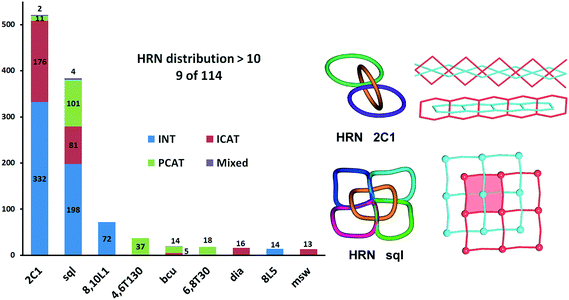 | ||
| Fig. 7 Distribution of types of entangled structures among the most frequently observed patterns of catenation expressed by the Hopf-ring nets HRN. | ||
Many other HRNs are specific for a particular group, like the third most frequent HRN, the 2-periodic 8,10L1 type, which is realized only for 2-fold interpenetrating networks; 71 of them have sql or hcb topology and contain 2-loops, with the only exception of Ag4(CN)4[1,4-bis(1-imidazolylmethyl)benzene]2 (PEVBEY).28 Also, the fourth most frequent HRN, the 3-periodic 4,6T130 type, was found only in parallel polycatenation with 35 of 37 having the “double square” (4,4)Ia topology.
HRNs can have any periodicity, but zero-periodic (finite) ensembles of catenated rings are very rare; we have revealed only 4 such cases: two for 2-fold interpenetration and two in parallel polycatenation (see the ESI† for all the references). A 3-periodic catenated ring motif could exist only in the polycatenated ensemble of networks, and it appears for 191 structures. Among them, four structures, WUJDIO,29 ZEFLON,30 GOQMIK31 and YEGJAX,32 possess even 2-fold interpenetrated 3-periodic systems of catenated rings. This peculiarity is reflected in the unique pattern observed for WUJDIO/ZEFLON/GOQMIK which have the same parallel polycatenation of KIa nets (see our ChemRev and Fig. 39 therein). Also, the entanglement of undulated sql observed for YEGJAX is unique.32
Are these 114 HRN patterns of catenation enough to fully characterize the whole variety of observed entanglements described over the years? For example, can we separate the two kinds of inclined polycatenation of sql observed and classified differently by Zaworotko and coworkers as p/p and d/d,33 or find all the kinds of interpenetration of sql listed by Batten and Robson?3 Not with HRNs, since they do not bear information about links between fused rings (rings of the initial net), but with ERNs yes. Obviously, this more detailed classification generates more patterns up to 216 ERNs.
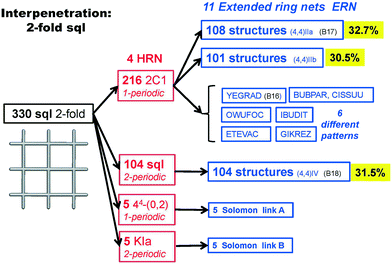
We illustrate the finer resolution of the ERN analysis on the 2-fold interpenetrated layers with hcb and sql topologies that are observed in 499 structures including 79 with 2-loops. In the seminal work of Batten and Robson,3 two paragraphs were devoted to the possible different (parallel) entanglements of two interpenetrating nets: 63-hcb [called (6,3) by them in §3.1.1] and 44-sql [called (4,4) in §3.1.2], also considering the case with 2-loops. We are now able to retrieve all the patterns found by them and even more. Scheme 1 shows how 94% of the 330 2-fold sql entangled arrays are sorted in three most abundant patterns (ERN (4,4)IIa, (4,4)IIb, and (4,4)IV) with almost equal distribution. The three undulated modes are shown in Fig. 8, and two of them [ERN (4,4)IIb and (4,4)IV] need bent ligands to be formed. The remaining eight patterns are unique, two of them contain Solomon links (four-crossing 2-ring link), and they are illustrated in Fig. S1.† Two of the most frequent patterns ERN (4,4)IIa and (4,4)IV were described by Batten & Robson3 in their Fig. 17 and 18, the third one (4,4)IIb was missed by them because the first example was published only in 1998, instead the unique example YEGRAD34 was reported in Fig. 16 (see Fig. S1†). The 48 cases with 2-loops are also detected and classified in four different patterns, with the predominant (90%) one reported by Batten & Robson in their Fig. 20 (see our Fig. S2†). A systematic enumeration of sql 2-fold interpretation patterns has been proposed recently by Hyde and coworkers.19
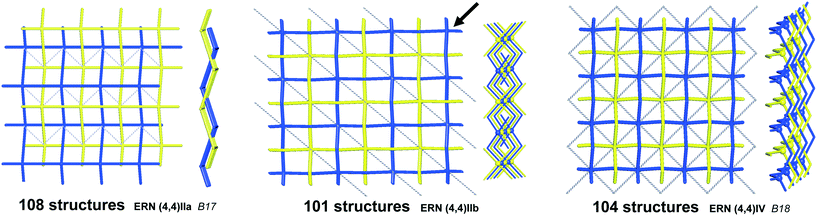 | ||
| Fig. 8 The three most common patterns of entanglement observed in 2-fold interpenetrated sql. The HRNs are represented by dotted lines. The undulation and bending of ligands is visible from the lateral views. B17 and B18 refer to the corresponding figures in ref. 3. See also Scheme 1. | ||
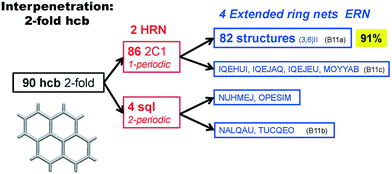
Scheme 2 shows that 90 2-fold interpenetrated layers with hcb topology are distributed over four patterns, shown in Fig. 9, with most (91%) of them having ERN-(3,6)II. Batten & Robson3 also illustrated four possible patterns, three of which (B11a–c) correspond to the patterns in Scheme 2 and Fig. 9, while one still remains unseen in real structures. The 31 cases having 2-fold hcb topology with 2-loops show three different patterns, with the predominant (84%) one reported by Batten & Robson in their Fig. 15b (see our Fig. S3†).
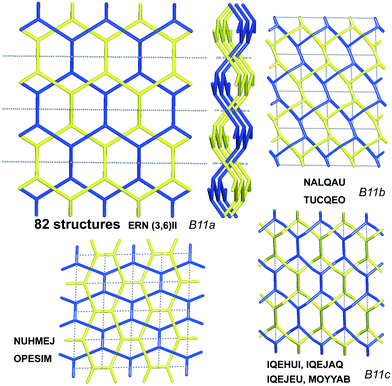 | ||
| Fig. 9 The four patterns of entanglement observed in 2-fold interpenetrated hcb. The HRNs are represented by dotted lines. The undulation of the layers for the most common pattern ERN (3,6)II is shown from the lateral views. B11a–c refer to the corresponding figures in ref. 3. See also Scheme 2. | ||
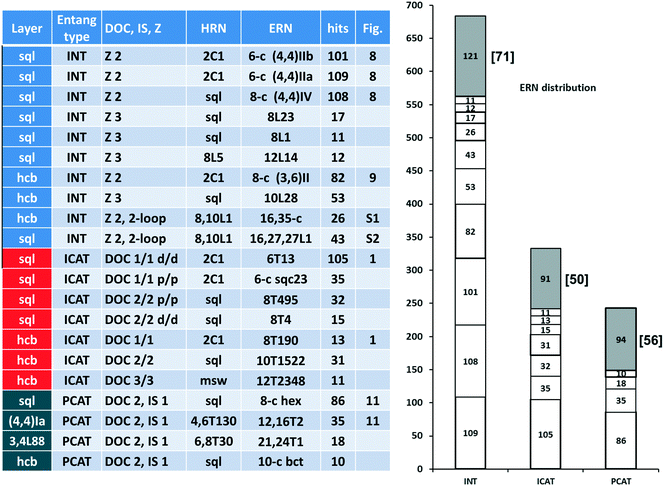
In Fig. 10 (left part), we collect descriptors for the most frequent 21 catenation patterns, namely the 21 ERNs, observed at least in 10 structures: they explain the entanglements for 953 structures. In other words, 74% of the entangled arrays fall into 21 patterns, which are only 10% of the 216 observed. Obviously, the four underlying nets (layer topologies sql, hcb, (4,4)Ia, and 3,4L88) and the seven patterns of catenation (HRNs) listed in the table are the most frequent ones (compared with those in Fig. 2 and 7). The distribution of ERNs over types of entanglements (interpenetration INT, inclined polycatenation ICAT and parallel polycatenation PCAT) is shown in the right part of Fig. 10. From the plot, it can be seen that for every type of entanglement only a few catenation patterns are characteristic. The major part, 82%, of the interpenetrated layers fall into ten patterns from 81 ERNs. Moreover, the occurrence of catenation patterns dramatically drops with increasing complexity of catenation (number of Hopf ring links). Thus, the coordination number of HRNs is the smallest, 2, for the most abundant patterns of 2-fold interpenetrating nets sql [ERN (4,4)IIa and (4,4)IIb], but it rises to 4 and 8 for the less abundant 3-fold sql, and becomes 8 and 10 for the rare case of catenation involving 2-loops.
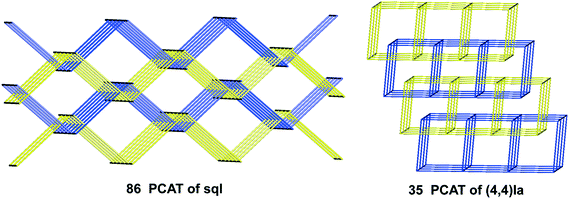
For the inclined polycatenation, the seven abundant modes account for 73% of the structures that distribute on 57 ERNs. Zaworotko33 in his analysis of inclined polycatenation of sql observed three possible arrangements depending on the relative orientation of the frames: parallel–parallel (p/p), parallel–diagonal (p/d), and diagonal–diagonal (d/d); ERNs fully classify all observed structures showing that the d/d mode is preferred and that there are only three cases of p/d, SARFOH,35 VIRVIF,36 and MOVSEW.37 One new case of inclined polycatenation with more than two crossing sets of parallel layers has been found for the sql in FARJEP38 with doc 2/3/3. Parallel polycatenation shows 60 ERNs with half of the structures (121/243) having the simplest possible polycatenation for undulated sql and (4,4)Ia (double sql) illustrated in Fig. 11.
Some patterns of inclined polycatenation have been analyzed by O'Keeffe and coworkers13 and named in the RCSR22 (see Table S1†).
3.3. Entanglement isomerism and polymorphism
Discrimination of catenation motifs within the HRN & ERN concept allows one to predict the existence of new types of coordination isomerism. The IUPAC rules embrace many types of isomerism of coordination compounds but all of them take into account only the local topology of the complex group (it concerns, for example, the cis/trans-isomerism). If one considers the overall topology of the coordination network, the term network isomerism can be introduced, when two coordination polymers have the same chemical composition and methods of connecting metal atoms and ligands, i.e. the same local topology, but their overall topologies are different (cf.ref. 39–46, where the term supramolecular isomerism was used). Similarly, we introduce the notion of entanglement isomerism to designate the coordination polymers that have the same chemical composition, local and overall topology, but differ by their catenation patterns, i.e. by their HRNs and/or ERNs.Out of our sample of 1319 entangled structures, 416 have analogs with the same ligand composition; in total, there are 145 combinations of ligands, and they form 295 unique metal–ligand combinations. Expectedly, almost all these structures present clathrates (supramolecular systems) with different guest molecules and/or ions. Among them, we have detected 10 isomeric pairs of entangled networks that can be considered as entanglement isomers. These 20 network arrays are realized in 32 crystal structures, which contain different guest species. Below, we consider the entanglement isomers grouped in accordance with their entanglement modes.
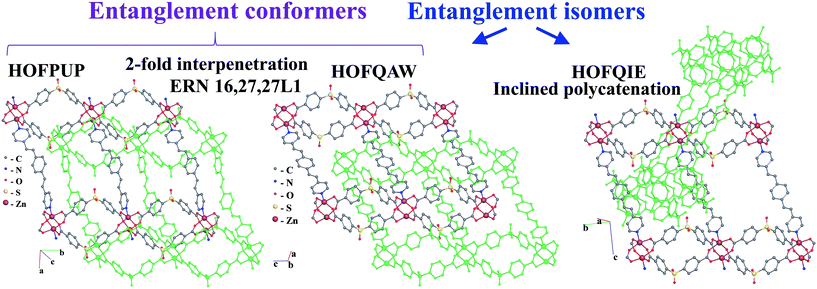
Further, the inclined polycatenation of [CuII(bpp)2]2+ (bpp = 1,3-bis(4-pyridyl)propane) networks with the sql topology (VOJPIU) is directed by the large polyoxometallate anion {W12O36(SiO4)}4−,49 while 2-fold interpenetrating arrays adopt small anions: NO3− (CUHZIO),50 ClO4− (CUHZOU),50 and SCN− (EFAFUN, YOMKUH).51,52 The origin of the guest-dependent entanglement isomerism is the flexibility of the abp and bpp ligands, which allows the networks to adopt the undulating or planar conformation depending on the guest species, which leads to interpenetration or inclined polycatenation, respectively. Similarly, the solvent, as well as the temperature of solvothermal synthesis, determines the mode of entanglement for the [Zn2(pdedp)(sdb)2] networks (pdedp = 4,4′-(1,4-phenylenediethene-2,1-diyl)dipyridine, H2sdb = sulfonyldibenzoic acid) of the sql topology.53 The rigid geometry of the pdedp ligands and 2-loop pairs of sdb ligands provides a planar conformation of the network. However, the presence of in-plain rectangular rings and 2-loops orthogonal to these rings gives choice for catenation of two types: with and without threading of 2-loops (Fig. 13). Threading of 2-loops by pdedp links predetermines the in-plane interpenetration of two 2-periodic networks (HOFQAW, HOFPUP)53 and complex catenation of rings (8,10-c HRN), while catenation without participation of 2-loops gives a rather simple (2-c HRN) d/d inclined polycatenation mode of entanglement (HOFQIE).53 Due to its large porosity (up to 34%), the 2-fold interpenetrating arrays [Zn2(pdedp)(sdb)2]·G (HOFQAW, HOFPUP) allow solvent-induced flexibility of the entangled system.53 Therefore, the two 2-fold interpenetrating structures (HOFQAW and HOFPUP) with different solvent guests were called ‘distortional supramolecular isomers of polyrotaxane coordination polymers’. In our approach, the network arrays, which can be transformed to each other without breaking bonds, are not entanglement isomers, instead we can call them entanglement conformers. Thus, in our approach, HOFQAW and HOFPUP are two different conformers of the same entanglement isomer (Fig. 13), which is described by the 16,27,27-c ERN.
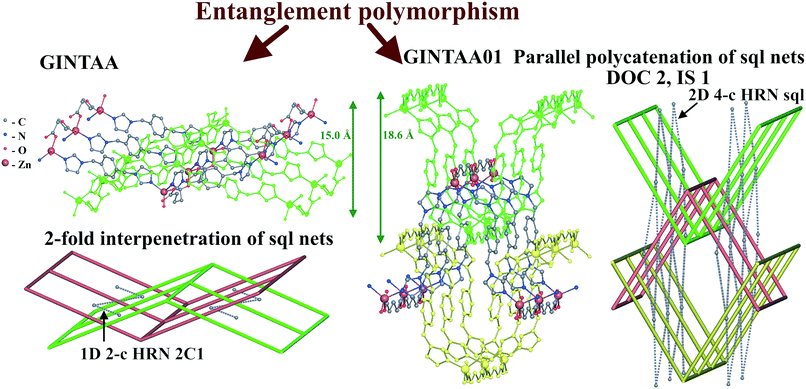 | ||
| Fig. 14 Networks and entanglement modes of underlying sql nets of interpenetrating (GINTAA) and parallel polycatenated (GINTAA01) polymorphs of [Zn(glut)(bix)]·2H2O. | ||
It should be noted that the [Zn(glut)(bix)]·2H2O complexes present a rare example of entanglement polymorphism of coordination polymers, which has not been described by the authors.56,57 In contrast to entanglement isomerism, this kind of polymorphism relates to substances, not molecules or complex groups.40,44 Such polymorphic crystalline forms have the same composition and set of structural groups including guest molecules, but differ by entanglement type.
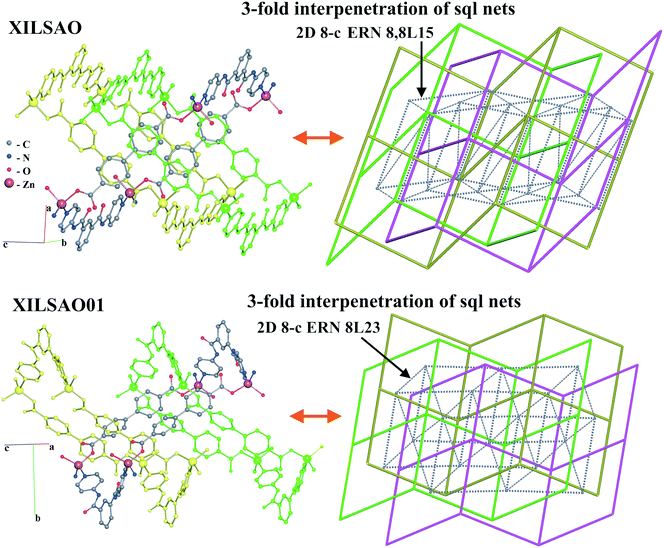
In the last example, the 3-fold interpenetrating isomeric arrays of [Zn(bpdc)(dpipa)] (dpipa = di(pyridin-4-yl)isophthalamide, H2bpdc = biphenyl-4,4′-dicarboxylic acid) (XILSAO, XILSAO01), the sql-type networks are also highly undulated (Fig. 17).44 A decrease of temperature of hydrothermal synthesis leads to an increase of the undulation degree of layers, but the degree of interpenetration remains the same. The authors described the substances as “framework isomers”, while the difference concerns only the type of entanglement, not the network topology. These entanglement isomers have the same catenation mode of rings (the same HRN of the sql topology). However, such isomers can be easily distinguished with ERNs, which are both 8-coordinated but have different point symbols (36·417·54·6)(36·420·5·6) and (36·419·52·6). This latter example cannot be called entangled polymorphism because there are different guest molecules not determined by crystallography.
4. Concluding remarks
We have applied a novel method of classification of entanglements in coordination polymers with ring nets. This method allowed us to discriminate and classify catenation patterns in all known 2-periodic coordination networks. A new type of isomerism, entanglement isomerism, can be introduced which is used for coordination polymers to be distinguished by their Hopf and extended ring nets. Parameters of the Hopf and extended ring nets extend the list of topological descriptors of interweaved architectures and can be used to find correlations with other chemical, geometrical and topological descriptors as well as to create a knowledge database for predicting possible catenation motifs. The power of this approach is reflected in the last Scheme 3 that summarizes the results: 3/4 of the 1319 observed entangled arrays fall into only 21 few well-known patterns which are only 10% of all ERNs observed: like an Ockham's razor, nature prefers few more probable patterns, but we provide a tool to distinguish all the more subtle ones.Acknowledgements
The authors are grateful to the Russian Science Foundation for financial support (Grant No. 16-13-10158). EVA thanks the Russian Foundation for Basic Research (Grant No. 16-37-00147).References
- K. E. Horner, M. A. Miller, J. W. Steed and P. M. Sutcliffe, Chem. Soc. Rev., 2016, 45, 6432 RSC
.
- S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk, Pure Appl. Chem., 2013, 85, 1715 CrossRef CAS
.
- S. R. Batten and R. Robson, Angew. Chem., Int. Ed., 1998, 37, 1460 CrossRef
.
- L. Carlucci, G. Ciani and D. M. Proserpio, Coord. Chem. Rev., 2003, 246, 247 CrossRef CAS
.
- X. Kuang, X. Wu, R. Yu, J. P. Donahue, J. Huang and C.-Z. Lu, Nat. Chem., 2010, 2, 461 CrossRef CAS PubMed
.
- D. M. Proserpio, Nat. Chem., 2010, 2, 435 CrossRef CAS PubMed
.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576 CAS
, http://topospro.com.
- V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2004, 6, 377 RSC
.
- I. A. Baburin, V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2008, 10, 1822 RSC
.
- I. A. Baburin, V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, Cryst. Growth Des., 2008, 8, 519 CAS
.
- E. V. Alexandrov, V. A. Blatov and D. M. Proserpio, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 484 CAS
.
- E. V. Alexandrov, V. A. Blatov, A. V. Kochetkov and D. M. Proserpio, CrystEngComm, 2011, 13, 3947 RSC
.
- C. Bonneau and M. O'Keeffe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 82 CAS
.
- I. A. Baburin, Acta Crystallogr., Sect. A: Found. Crystallogr., 2016, 72, 366 CAS
.
- L. Carlucci, G. Ciani, D. M. Proserpio, T. G. Mitina and V. A. Blatov, Chem. Rev., 2014, 114, 7557 CrossRef CAS PubMed
.
- E. V. Alexandrov, A. P. Shevchenko, A. A. Asiri and V. A. Blatov, CrystEngComm, 2015, 17, 2913 RSC
.
- T. G. Mitina and V. A. Blatov, Cryst. Growth Des., 2013, 13, 1655 CAS
.
- D. M. Proserpio, 2014, lecture delivered at conference ‘150 Years of Beautiful Structures and Defects’, Ho Chi Minh City, November 2014.
- S. T. Hyde, B. Chen and M. O'Keeffe, CrystEngComm, 2016, 18, 7607 RSC
.
- This term corresponds to the term ‘ring net’ introduced in I. A. Baburin and V. A. Blatov, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 791 CrossRef CAS PubMed
.
- L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2003, 5, 269 RSC
.
- M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782 CrossRef PubMed
.
- S. R. Batten, CrystEngComm, 2001, 3, 67–72 RSC
.
- S. Sen, N. N. Nair, T. Yamada, H. Kitagawa and P. K. Bharadwaj, J. Am. Chem. Soc., 2012, 134, 19432 CrossRef CAS PubMed
.
- X.-L. He, Y.-P. Liu, K.-N. Gong, Z.-G. Han and X.-L. Zhai, Inorg. Chem., 2015, 54, 1215 CrossRef CAS PubMed
.
- L.-L. Wen, Z.-D. Lu, X.-M. Ren, C.-Y. Duan, Q.-J. Meng and S. Gao, Cryst. Growth Des., 2009, 9, 227 CAS
.
- J. Yang, J.-F. Ma and S. R. Batten, Chem. Commun., 2012, 48, 7899 RSC
.
- J.-D. Lin, Z.-H. Li, J.-R. Li and S.-W. Du, Polyhedron, 2007, 26, 107 CrossRef CAS
.
- Z.-Y. Fu, X.-T. Wu, J.-C. Dai, S.-M. Hu and W.-X. Du, New J. Chem., 2002, 26, 978 RSC
.
- F.-H. Zhao, Y.-X. Che and J.-M. Zheng, CrystEngComm, 2012, 14, 6397 RSC
.
- C.-Q. Wan, X.-L. Sun, A.-M. Li, X.-Z. Sun, H. K. Lee, H.-L. Han and G.-B. Che, CrystEngComm, 2015, 17, 797 RSC
.
- F. Guo, F. Wang, H. Yang, X. Zhang and J. Zhang, Inorg. Chem., 2012, 51, 9677 CrossRef CAS PubMed
.
- M. J. Zaworotko, Chem. Commun., 2001, 1 RSC
.
- T. Soma and T. Iwamoto, Chem. Lett., 1994, 821 CrossRef CAS
.
- M.-H. Zeng, W.-X. Zhang, X.-Z. Sun and X.-M. Chen, Angew. Chem., Int. Ed., 2005, 44, 3079 CrossRef CAS PubMed
.
- Y.-F. Qi, D. Xiao, E. Wang, Z. Zhang and X. Wang, Aust. J. Chem., 2007, 70, 871 CrossRef
.
- X.-Y. Cao, Q.-P. Lin, Y.-Y. Qin, J. Zhang, Z.-J. Li, J.-K. Cheng and Y.-G. Yao, Cryst. Growth Des., 2009, 9, 20 CAS
.
- G.-Z. Liu, J.-G. Wang and L.-Y. Wang, CrystEngComm, 2012, 14, 951 RSC
.
- T. L. Hennigar, D. C. MacQuarrie, P. Losier, R. D. Rogers and M. J. Zaworotko, Angew. Chem., Int. Ed. Engl., 1997, 36, 972 CrossRef CAS
.
- B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629 CrossRef CAS PubMed
.
- H. Abourahma, B. Moulton, V. Kravtsov and M. J. Zaworotko, J. Am. Chem. Soc., 2002, 124, 9990 CrossRef CAS PubMed
.
- J. P. Zhang, X. C. Huang and X. M. Chen, Chem. Soc. Rev., 2009, 38, 2385 RSC
.
- D. Zhao, D. J. Timmons, D. Yuan and H.-C. Zhou, Acc. Chem. Res., 2011, 44, 123 CrossRef CAS PubMed
.
- X.-L. Wu, F. Luo, G.-M. Sun, A.-M. Zheng, J. Zhang, M.-B. Luo, W.-Y. Xu, Y. Zhu, X.-M. Zhang and S.-Y. Huang, ChemPhysChem, 2013, 14, 3594 CrossRef CAS PubMed
.
- J.-S. Hu, L. Qin, M.-D. Zhang, X.-Q. Yao, Y.-Z. Li, Z.-J. Guo, H.-G. Zheng and Z.-L. Xue, Chem. Commun., 2012, 48, 681 RSC
.
- L. Carlucci, G. Ciani, D. M. Proserpio and L. Spadacini, CrystEngComm, 2004, 6, 96 RSC
.
- M. A. Withersby, A. J. Blake, N. R. Champness, P. A. Cooke, P. Hubberstey and M. Schroder, New J. Chem., 1999, 23, 573 RSC
.
- M. Kondo, M. Shimamura, S. Noro, S. Minakoshi, A. Asami, K. Seki and S. Kitagawa, Chem. Mater., 2000, 12, 1288 CrossRef CAS
.
- X. Wang, H. Lin, Y. Bi, B. Chen and G. Liu, J. Solid State Chem., 2008, 181, 556 CrossRef CAS
.
- M. J. Plater, M. R. St. J. Foreman and A. M. Z. Slawin, J. Chem. Res., 1999, 74, 728 Search PubMed
.
- R. De, A. Farani, W. M. Teles, C. B. Pinheiro, K. J. Guedes, K. Krambrock, M. I. Yoshida, L. F. C. De Oliveira and F. C. Machado, Inorg. Chim. Acta, 2008, 361, 2045 CrossRef
.
- Yu.-Y. Niu, B.-L. Wu, Q.-L. Wang, X.-L. Guo, H.-Yu. Zhang, H.-W. Hou, Y. Han and L.-F. Wang, Inorg. Chim. Acta, 2009, 362, 556 CrossRef CAS
.
- I.-H. Park, R. Medishetty, J.-Y. Kim, S. S. Lee and J. J. Vittal, Angew. Chem., Int. Ed., 2014, 53, 5591 CrossRef CAS PubMed
.
- F. Zhao, S. Jing, Y. Che and J. Zheng, CrystEngComm, 2012, 14, 4478 RSC
.
- X. Li, X. Sun, X. Li and X. Xu, New J. Chem., 2015, 39, 6844 RSC
.
- G. X. Liu and Z. Q. Liu, Coord. Chem., 2013, 39, 292 Search PubMed
.
- J.-X. Yang, Y.-Y. Qin, J.-K. Cheng, X. Zhang and Y.-G. Yao, Cryst. Growth Des., 2015, 15, 2223 CAS
.
- G.-X. Liu, K. Zhu, H. Chen, R.-Y. Huang and X.-M. Ren, CrystEngComm, 2008, 10, 1527 RSC
.
- M.-H. Hu, G.-L. Shen, J.-X. Zhang, Y.-G. Yin and D. Li, Cryst. Growth Des., 2009, 9, 4533 CAS
.
- Q. Wang, J. Zhang, C.-F. Zhuang, Y. Tang and C.-Y. Su, Inorg. Chem., 2009, 48, 287 CrossRef CAS PubMed
.
- C.-F. Zhuang, J. Zhang, Q. Wang, Z.-H. Chu, D. Fenske and C.-Y. Su, Chem. – Eur. J., 2009, 15, 7578 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: A spreadsheet file with all the 1319 structures described here, three figures and a table. See DOI: 10.1039/c7ce00313g |
| ‡ The thickness is calculated as the maximal sum of deviations of van der Waals radii of atoms from opposite sides of the middle plane. |
| This journal is © The Royal Society of Chemistry 2017 |