Open Access Article
Open Access ArticleConformations of cyclopentasilane stereoisomers control molecular junction conductance†
Haixing
Li‡
a,
Marc H.
Garner‡
b,
Zhichun
Shangguan‡
c,
Qianwen
Zheng
c,
Timothy A.
Su
d,
Madhav
Neupane
d,
Panpan
Li§
c,
Alexandra
Velian
 d,
Michael L.
Steigerwald
d,
Shengxiong
Xiao
d,
Michael L.
Steigerwald
d,
Shengxiong
Xiao
 *c,
Colin
Nuckolls
*cd,
Gemma C.
Solomon
*b and
Latha
Venkataraman
*ad
*c,
Colin
Nuckolls
*cd,
Gemma C.
Solomon
*b and
Latha
Venkataraman
*ad
aDepartment of Applied Physics and Applied Mathematics, Columbia University, New York 10027, USA. E-mail: lv2117@columbia.edu
bNano-Science Center and Department of Chemistry, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark. E-mail: gsolomon@chem.ku.dk
cThe Education Ministry Key Lab of Resource Chemistry, Shanghai Key Laboratory of Rare Earth Functional Materials, Optoelectronic Nano Materials and Devices Institute, Department of Chemistry, Shanghai Normal University, Shanghai 200234, China. E-mail: senksong@msn.com
dDepartment of Chemistry, Columbia University, New York 10027, USA. E-mail: cn37@columbia.edu
First published on 30th May 2016
Abstract
Here we examine the impact of ring conformation on the charge transport characteristics of cyclic pentasilane structures bound to gold electrodes in single molecule junctions. We investigate the conductance properties of alkylated cyclopentasilane cis and trans stereoisomers substituted in the 1,3-position with methylthiomethyl electrode binding groups using both the scanning tunneling microscope-based break junction technique and density functional theory based ab initio calculations. In contrast with the linear ones, these cyclic silanes yield lower conductance values; calculations reveal that the constrained dihedral geometries occurring within the ring are suboptimal for σ-orbital delocalization, and therefore, conductance. Theoretical calculations reproduce the measured conductance trends for both cis and trans isomers and find several distinct conformations that are likely to form stable molecular junctions at room temperature. Due to the weakened σ-conjugation in the molecule, through-space interactions are found to contribute significantly to the conductance. This manuscript details the vast conformational flexibility in cyclopentasilanes and the tremendous impact it has on controlling conductance.
Introduction
Though silicon is the most prevalent semiconductor material in integrated circuits, its conductance has been scarcely studied at the molecular scale. With the dramatic scaling of silicon devices to the sub-20 nm length scale, it is becoming critical to probe transport properties of complex silicon-based nanoscale structures, such as silicon clusters, nanowires and silicene 2D layers.1–4 Efforts in molecular electronics have demonstrated the use of silicon surfaces as electrodes5–9 and amino-silanes as chemical binding groups to the electrodes.10,11 Moreover, investigation on cyclohexasilane12 has shown that conformations affect the molecule's electronic structure and another study on [2,2,2]bicyclic carbosilane systems13 has suggested that different disilanylene bridges in the cage compounds do not act as parallel resistors. Recently we synthesized linear chains of molecular silicon that demonstrated conductance decay properties comparable to those of π-conjugated hydrocarbons.14–16 While Si–Si σ-bonds are strongly conjugated, similar to C–C π-bonds, a fundamental difference between them is that the Si–Si σ-bond network is tetrahedral and not planar. This tetrahedrality enables oligosilane-based wires to access many more conformations, which opens up the possibility to harness σ-bond stereoelectronics to design functional molecular electronic components.16Cyclic sp3 σ-based structures can adopt many possible ring conformations as demonstrated by many years of synthetic17–20 and theoretical studies,21–24 however, charge transport measurements at a single molecule level on such systems are heretofore unexplored. Here we synthesize the cis and trans isomers of a cyclic pentasilane di-functionalized with aurophilic methyl sulfide groups (chemical structures shown in Fig. 1) and measure their single-molecule junction conductance using scanning tunneling microscope-based break junction technique (STM-BJ).25,26 We find that the cis and trans isomers are distinctly different in their conductance behavior. The cis isomer shows a double-peaked conductance histogram indicative of the formation of two structures. In contrast, the trans isomer shows a single-peaked conductance histogram at a conductance value lower than that of the cis. Through density functional theory (DFT) based ab initio calculations, we model junctions for a large number of conformers of both the cis and trans isomers. Our calculations indicate that the constraint imposed on the internal ring dihedrals hinders σ-conjugation across the molecule, which contributes to the lower conductance value that we observe in these cyclic structures compared with linear oligosilanes of similar oligomer order. We find that the unique conductance profile of each isomer we observe experimentally relates to the different junction conformations accessible to each isomer and the structural differences between the two isomers.
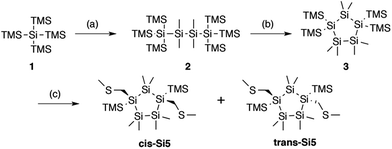 | ||
| Fig. 1 Synthesis of trans and cis cyclopentasilane terminated with methylthiomethyl end groups. (a) (i) KOtBu, THF, r.t. (ii) ClSiMe2SiMe2Cl, toluene, −70 °C to r.t., 85% yield. (b) (i) KOtBu, 18-crown-6, toluene, r.t. (ii) SiMe2Cl2, toluene, r.t., 81% yield. (c) (i) KOtBu, 18-crown-6, toluene, r.t. (ii) ClCH2SMe, toluene, −78 °C to r.t. 15% yield for cis-Si5, 10% yield for trans-Si5. Additional details on the synthetic methods are in the ESI Section I.† | ||
Results and discussion
We prepare the cis and trans isomers following the synthetic procedure shown in Fig. 1. We quench the combination of tetrakis(trimethylsilyl)silane 1 and potassium tertbutoxide (KOtBu),19 with 1,2-dichlorotetramethyldisilane to yield oligosilane 2. Next, we cleave two TMS groups from 2 with KOtBu and 18-crown-6 and quench the dianion with dichlorodimethylsilane to produce cyclopentasilane 3.17,18 We then functionalize cyclopentasilane 3 with electrode linking methylthiomethyl (CH2SMe) groups at the 1,3-positions by cleaving the terminal TMS groups with KOtBu/18-C-6 and adding the chloromethyl methyl sulfide electrophile. We separate the two isomers by silica gel chromatography to yield the cis-Si5 and trans-Si5 molecules for this study. We were able to grow single crystals suitable for single crystal X-ray diffraction for cis-Si5 from diethyl ether at −30 °C (the .cif file and details are contained in the ESI†).The five-membered rings have two predominant conformations, envelope (Cs) and twist (C2), with the nomenclature defined by the number of Si-atoms that lie in and out of the plane of the ring. The envelope conformer has four Si-atoms in plane and one above or below the plane of the ring. The twist conformer has three Si-atoms in plane, one above the plane, and one below the plane. As the cyclopentasilane is di-substituted, six unique conformations appear by rotating the position of the substituents relative to the ring conformation as illustrated in Fig. 2a. Five of these conformations are further divided in two classes as the linkers can be on either side of the plane of the ring, the exceptions being cis-2-twist and trans-2-envelope as the linker positions are symmetric.
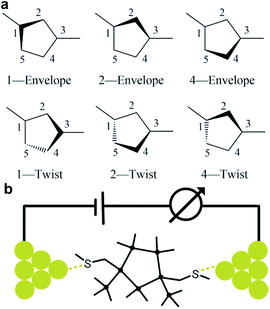 | ||
| Fig. 2 (a) Six generic conformer types of a di-substituted five membered ring. (b) A schematic of the scanning tunneling microscope break-junction (STM-BJ). | ||
We measure the single molecule junction conductance (current/voltage) of cis-Si5 and trans-Si5 using STM-BJ technique (schematic shown in Fig. 2b) under ambient conditions (see ESI† Section II for more details).25,26 We repeatedly form and break Au point contacts between an Au tip and an Au-on-mica substrate and measure conductance as a function of displacement. A single molecule junction is formed when the atomic contact is broken in a 1 mM solution of the target molecule in 1,2,4-trichlorobenzene. Each conductance-displacement measurement shows plateaus at a conductance close to integer multiples of the conductance quantum, G0 = 2e2/h and additional molecular plateaus below 1 G0. These plateaus below 1 G0 signify that an Au-molecule-Au junction is formed after the metal contact breaks.
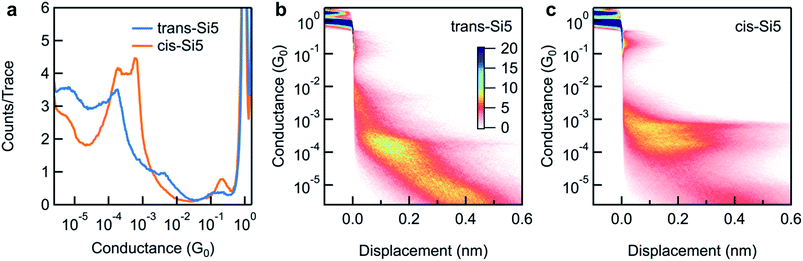
We repeat the measurements and collect thousands of traces to determine the most frequently measured conductance value for each molecule. We compile all measured conductance traces into logarithmically binned one-dimensional histograms27 in Fig. 3a. We find that the trans-Si5 histogram shows a single conductance peak at ∼1.6 × 10−4G0 while that of cis-Si5 shows a higher conducting peak at 6 × 10−4G0 and a lower conducting peak at 2 × 10−4G0. In Fig. 3b and c, we overlay all measured conductance traces, aligning them along the displacement axis at 0.5 G0 and generate two-dimensional conductance-displacement histograms to show the evolution of conductance as we elongate the junction.27 We see that both cis-Si5 and trans-Si5 can form junctions that extend to roughly 6 Å beyond the rupture of the Au point-contact, although a majority of the junctions rupture after a ∼2–3 Å elongation.
Our past work has shown that the displacement extent of the molecular plateau in a 2D histogram is related to the molecular backbone length.28 Since both the cis-Si5 and trans-Si5 show similar plateau lengths in their 2D histograms, we can conclude that the lower intensity observed for trans-Si5 in the 1D histogram is a result of fewer junctions formed with this isomer. It has been shown computationally29–31 and experimentally16 that linear oligosilanes attain maximum elongation and conductance as they are near all-anti conformations where all backbone dihedral angles are 180°. Such anti conformations are not accessible in the cyclopentasilane molecules here because of the intrinsic dihedral constraints of tetrahedral bonding geometries in the rings. We would therefore expect that conductance is lower in cyclic oligosilane pathways in contrast to their equivalent linear counterparts considering one of the two pathways can be completely suppressed due to unfavorable dihedrals. Two possible through-bond conduction pathways occur in the cyclopentasilane from one anchor group to the other: a trisilane and tetrasilane pathway. We compare the conductance properties of the cyclopentasilane molecules with the linear Si3 and Si4 oligosilane (see ESI Fig. S1 and S2†).16 In contrast, we find that the higher conductance peak value of cis-Si5 is between that of Si3 and Si4 while the lower conductance peak value is lower than that of the Si4. This distinct double-peak conductance feature we observed for cis-Si5 indicates that cyclopentasilanes are significantly different from linear silanes. To understand these phenomena further, we turn to ab initio calculations carried out using DFT to investigate both the conformers of each isomer that are likely to form junctions at room temperature and their computed conductance values.
We examine the conductance behavior of a large number of conformers of cis-Si5 and trans-Si5 by calculating the transmission with a combined DFT and non-equilibrium Green's functions approach.32 Our aim is to understand the impact of the molecular conformation on conductance; we do not intend to quantitatively compare DFT results with experiment due to errors inherent to DFT.33,34 We create the full set of conformers for both cis-Si5 and trans-Si5 by varying the Si(CH3)2–Si–CH2–S dihedrals around their threefold torsional axis while keeping the terminal Si–CH2–S–CH3 dihedrals in anti-configuration (180°). This procedure yields 93 conformers each. We optimize the structures to a force threshold of 0.02 eV Å−1 using DFT with the PBE exchange–correlation functional35 and double-ζ plus polarization basis sets as implemented in ASE36 and GPAW.37,38 After this process, we are left with 84 cis-Si5 and 86 trans-Si5 conformers in their local energy minima. Details on the conformer nomenclature and the Boltzmann distribution at room temperature are included in ESI Section IV.1 and IV.2.† We have not calculated the energy barriers between these conformers, but a previous report shows the energy barriers are quite low for a simpler unsubstituted cyclopentasilane.21
Next, we attach gold electrodes onto the calculated vacuum conformers. In principle, each conformer can bind to the electrodes in 16 different idealized configurations, as the Si–CH2–S–Au dihedral of each linker can be in either the ortho (±90°) or transoid (±170°) conformation. However, the majority of these structures are unrealistic, as parts of the molecule will block the electrodes from binding to the linker group. After applying an algorithm to exclude the sterically unfeasible junction structures, we generate a complete set of junction geometries for all vacuum conformers. We place the molecule between two 4-atom Au-pyramids on 4 × 4 fcc Au(111) surfaces and relax the molecule to 0.05 eV with the Au-atoms fixed using DFT with the PBE exchange–correlation functional. A single-ζ basis set is used for the Au-surface and double-ζ plus polarization basis sets are used for the Au-pyramids and molecule. Finally the transmission is calculated using double-ζ plus polarization basis sets for all atoms. Descriptions of the junction construction algorithm and the computational details are included in ESI Section IV.3.†
We optimize and calculate the transmissions for a total of 279 trans-Si5 junctions and 211 cis-Si5 junctions. Previous studies for linear systems indicate that the geometry with the terminal methyl group in ortho-configuration (equivalent to Au–S–CH2–Si dihedrals in anti) is dominant as the junction is fully elongated. However, the cyclic pentasilane is structurally very different from the equivalent linear systems. In vacuum the most stable configuration for cyclic pentasilane is CH3–S–CH2–Si dihedrals in the anti-configuration. Therefore, we hypothesize that the initial junction structure binds to the electrodes with Au–S–CH2–Si dihedrals in ortho-configuration and proceed to analyze the results for junctions with this geometry alone in the manuscript. A detailed discussion of binding geometries and the transmissions for other electrode configurations (ortho/anti and anti/anti) are included and discussed in ESI Section IV.5 and IV.6.†
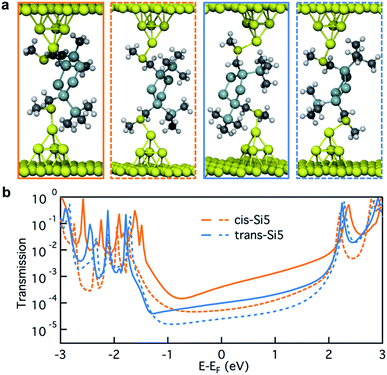
In Fig. 4a, we illustrate the optimized junction structures for sample cis-Si5 and trans-Si5 conformers and plot their transmissions in Fig. 4b. Due to the structural variation in these junction geometries, the transmission close to the Fermi energy varies considerably. Considering the vast conformational flexibility of the molecule, we do not think that each of the experimental conductance peaks in Fig. 3a can originate from a single dominant conformer. Instead we hypothesize that a number of conformations can be accessed at different junction lengths during the junction elongation. To test this hypothesis we analyze the structural information for 74 cis-Si5 and 91 trans-Si5 junction conformations optimized with Au–S–CH2–Si dihedrals in ortho-configuration (the full set of junctions with ortho/ortho contact geometry).
In Fig. 5a we compare the calculated conductance for cis-Si5 and trans-Si5 by generating the histogram of the transmissions at the Fermi energy with the contribution from each conformer weighted by its vacuum population at 300 K. The calculated histograms do not fully represent the experimental data as we do not pull the system or allow it to switch from one conformation to another. The shapes of these calculated histograms are sensitive to the bin-size and the method used to calculate the vacuum energies (see ESI Section IV.2†) therefore should not be over-interpreted. We see that in agreement with the experiment, the transmissions for cis-Si5 are distributed at higher values than the transmissions for trans-Si5. Although the exact values are underestimated, we note that this is the analysis for ortho/ortho contact geometry only. Further discussion is included in ESI Section IV.4 and IV.6.†
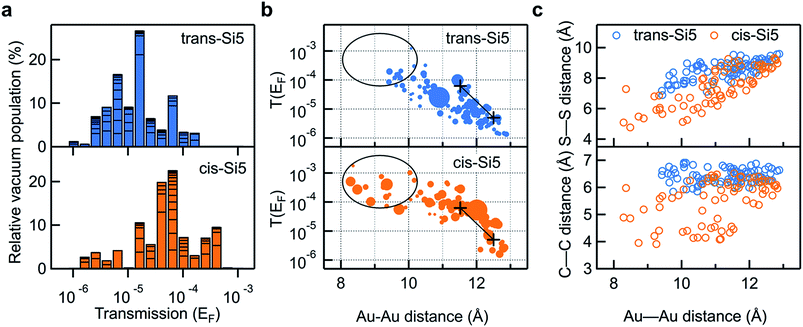 | ||
| Fig. 5 (a) Logarithmically binned histogram of transmission at Fermi energy of the 91 trans-Si5 and 74 cis-Si5 conformers. The horizontal stack lines in the bars indicate the vacuum population of each conformer. The histogram is normalized to sum up to 100%. (b) Transmission at Fermi energy plotted against the Au–Au junction distance for each trans-Si5 and cis-Si5 conformer bridged between four-atom Au pyramids. For easier visualization, the size of each dot has been scaled by 1/(1 + E), where E is the relative vacuum energy of each conformer in units of kT at 300 K, see Tables S1 and S2 in ESI.† Black+ are the calculated transmissions for the two configurations of the linear Si3 with both terminal Au–S–CH2–Si dihedrals in ortho conformations. Black circles and lines highlight the difference between the two isomers. (c) S–S (upper panel) and C–C junction distance (lower panel) plotted against the Au–Au junction distance for each trans-Si5 and cis-Si5 conformer. S refers to sulfur; C refers to the CH2-group that bridges the silicon ring and the methylsulfide group. All three plots share the same color scheme: orange for cis-Si5 and blue for trans-Si5. | ||
To compare the experimental data of conductance as a function of junction elongation, we plot the transmission of each conformer at the Fermi energy against the Au–Au distance of the junction in Fig. 5b. The size of each dot scales with the energy of the conformer (in units of kT) in vacuum by 1/(1 + E). Therefore a larger dot corresponds to a conformer with higher vacuum population. First, we note that more cis-Si5 conformers are populated at short Au–Au lengths (highlighted in black circles) and obtain higher transmission compared with trans-Si5, which agrees with what we observe in the experiment (Fig. 3). Both plots indicate that the junction length can reach an Au–Au separation of 8–13 Å, which would yield a step length of around 1–6 Å in the 2-dimensional histograms considering the distance that the Au electrodes snap back (6–8 Å) after the Au point contact ruptures.28,39–41 We note that the snap back of the Au electrodes is not considered in other cases, such as the STM current-distance technique where the Au tip is positioned above the Au substrate (no Au–Au contact) before forming a molecular junction.42 The transmissions for both cis-Si5 and trans-Si5 conformers decay with an increasing Au–Au distance, however, cis-Si5 conformers have higher transmissions than trans-Si5 conformers at the same junction length. The transmission data suggests that the different conductivity for cis-Si5 and trans-Si5 may be due to intrinsic structural differences beyond the junction length.
The transmission of the silanes is very sensitive to the dihedrals of the backbone,29,43 however, we do not find any significant difference in backbone dihedrals between cis-Si5 and trans-Si5, as detailed in ESI Section IV.5 and IV.6.† Next, apart from the backbone σ-conjugation, we also consider the transmission originating from through-space interactions in the molecule, i.e., non-nearest neighbor interactions that might contribute to the different conductance in cis-Si5 and trans-Si5. As the molecule is spatially crowded, intramolecular distances between atoms are relatively small, so that through-space interactions may give rise to a significant contribution to the total transmission. This contribution to the transmission has recently been thoroughly studied in π-conjugated helicenes,44–46 and have also been demonstrated to be significant in cyclic and linear silanes.12,13,43 We note the distinction between through-bond and through-space interactions is a bit arbitrary and no difference was found between the physical mechanisms of these two processes.43,47 In Fig. 5c we plot two decisive through-space distances of the molecule, the S–S and CH2–CH2 linker-to-linker distances, against the Au–Au distance of the junction. For junctions of the same Au–Au length, the S–S and CH2–CH2 distances are consistently shorter for cis-Si5 than for trans-Si5. This is a geometrical consequence of cis–trans isomerism: while the absolute values of backbone dihedrals are similar, the intramolecular distances in the trans-isomer are longer. The systematically higher transmission for cis-Si5 in junction with the same Au–Au length is a direct consequence of this structural difference of the two isomers.
Finally, we re-examine the conductance measurements with the theoretical conformational analysis. As discussed above, when considering the experimental conductance peak obtained for cis-Si5, trans-Si5 and linear Si3, we see that the cyclic isomers exhibit lower conductance. However, for the linear Si3, junctions with one or both terminal Au–S–CH2–Si dihedrals in ortho conformation have a lower conductance than the peak conductance measured for junctions with both dihedrals in the anti conformation. Thus, the low conductance measured for the cyclic systems could result from some of their dihedrals never achieving a 180° anti-configuration, which maximizes the conductance.16,29 The Si–SiMe2–Si–CH2 dihedrals range from gauche (60°) to deviant orientation (∼140°)48 (see ESI Fig. S8†). In contrast, a linear silane achieves an anti conformation with dihedral angles close to 180° along its entire backbone in its energetically favorable conformation, giving the linear Si3 and Si4 the best orbital delocalization and a higher conductance than is achievable for the cyclic structures. Calculations also support the finding that the tetrasilane path within the cyclic pentasilane has a Si–SiMe2–SiMe2–Si dihedral smaller than 50° (see ESI Fig. S8†) and therefore does not contribute significantly to the cis-Si5 or trans-Si5 conductance when compared with the trisilane path (see ESI Fig. S7†).
Conclusions
To conclude, in this study, we synthesize cis and trans isomers of cyclic pentasilane with aurophilic methylsulfide anchor groups, measure their conductance using the STM-BJ technique and compare these results with DFT calculations. We show that the large conformational freedom in these systems controls both the probability of junction formation and the measured conductance. We attribute the reduced conductance of the studied cyclic structures compared with linear chains to the diminished conjugation in Si–Si σ-bond together with through-space coupling effect when an all-anti conformation cannot be achieved. Our results illustrate the importance of bond orientation in σ-coupled silicon systems that is comparable to the impact of dihedral angles in π-conjugated carbon structures.49Acknowledgements
H. L. is supported by the Semiconductor Research Corporation and New York CAIST program. We thank the NSF for the support of experimental studies under grant no. CHE-1404922. G. C. S. and M. H. G. received funding from the Danish Council for Independent Research|Natural Sciences. Z. S., P. L., and S. X. are sponsored by National Natural Science Foundation of China (No. 21473113), Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning (No. 2013-57), “Shuguang Program” supported by Shanghai Education Development Foundation and Shanghai Municipal Education Commission (14SG40), Program for Changjiang Scholars, Innovative Research Team in University (IRT1269), and International Joint Laboratory on Resource Chemistry (IJLRC). T. A. S. is supported by the NSF Graduate Research Fellowship under grant no. 11-44155. Single crystal X-ray diffraction was performed at the Shared Materials Characterization Laboratory supported by Columbia University.Notes and references
- M. Schulz, Nature, 1999, 399, 729–730 CrossRef CAS
.
- Y. Cui and C. M. Lieber, Science, 2001, 291, 851–853 CrossRef CAS PubMed
.
- J. Lu and S. Nagase, Phys. Rev. Lett., 2003, 90, 115506 CrossRef PubMed
.
- L. Tao, E. Cinquanta, D. Chiappe, C. Grazianetti, M. Fanciulli, M. Dubey, A. Molle and D. Akinwande, Nat. Nanotechnol., 2015, 10, 227–231 CrossRef CAS PubMed
.
- N. P. Guisinger, M. E. Greene, R. Basu, A. S. Baluch and M. C. Hersam, Nano Lett., 2004, 4, 55–59 CrossRef CAS
.
- S. Lenfant, C. Krzeminski, C. Delerue, G. Allan and D. Vuillaume, Nano Lett., 2003, 3, 741–746 CrossRef CAS
.
- M. C. Hersam, N. P. Guisinger and J. W. Lyding, Nanotechnology, 2000, 11, 70 CrossRef CAS
.
- T. Rakshit, G.-C. Liang, A. W. Ghosh and S. Datta, Nano Lett., 2004, 4, 1803–1807 CrossRef CAS
.
- S. Sergani, Y. Furmansky and I. Visoly-Fisher, Nanotechnology, 2013, 24, 455204 CrossRef CAS PubMed
.
- M. Nakamura, S. Yoshida, T. Katayama, A. Taninaka, Y. Mera, S. Okada, O. Takeuchi and H. Shigekawa, Nat. Commun., 2015, 6, 8465 CrossRef CAS PubMed
.
- W. Hong, H. Li, S. X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431 CrossRef CAS PubMed
.
- R. Emanuelsson, H. Löfås, A. Wallner, D. Nauroozi, J. Baumgartner, C. Marschner, R. Ahuja, S. Ott, A. Grigoriev and H. Ottosson, Chem. –Eur. J., 2014, 20, 9304–9311 CrossRef CAS PubMed
.
- H. Löfås, R. Emanuelsson, R. Ahuja, A. Grigoriev and H. Ottosson, J. Phys. Chem. C, 2013, 117, 21692–21699 Search PubMed
.
- R. S. Klausen, J. R. Widawsky, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, J. Am. Chem. Soc., 2012, 134, 4541–4544 CrossRef CAS PubMed
.
- W. Chen, J. R. Widawsky, H. Vazquez, S. T. Schneebeli, M. S. Hybertsen, R. Breslow and L. Venkataraman, J. Am. Chem. Soc., 2011, 133, 17160–17163 CrossRef CAS PubMed
.
- T. A. Su, H. Li, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Chem., 2015, 7, 215–220 CrossRef CAS PubMed
.
- S. M. Whittaker, M. Brun, F. Cervantes-Lee and K. H. Pannell, J. Organomet. Chem., 1995, 499, 247–252 CrossRef CAS
.
- R. Fischer, D. Frank, W. Gaderbauer, C. Kayser, C. Mechtler, J. Baumgartner and C. Marschner, Organometallics, 2003, 22, 3723–3731 CrossRef CAS
.
- C. Marschner, Eur. J. Inorg. Chem., 1998, 221–226 CrossRef CAS
.
- A. Wallner, J. Hlina, T. Konopa, H. Wagner, J. Baumgartner, C. Marschner and U. Flörke, Organometallics, 2010, 29, 2660–2675 CrossRef CAS
.
- V. S. Mastryukov, M. Hofmann and H. F. Schaefer, J. Phys. Chem. A, 1999, 103, 5581–5584 CrossRef CAS
.
- Y. Naruse, J. Ma, K. Takeuchi, T. Nohara and S. Inagaki, Tetrahedron, 2006, 62, 4491–4497 CrossRef CAS
.
- M. Zhao and B. M. Gimarc, Inorg. Chem., 1996, 35, 5378–5386 CrossRef CAS
.
- C. L. Wadsworth and R. West, Organometallics, 1985, 4, 1664–1668 CrossRef CAS
.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed
.
- L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2006, 6, 458–462 CrossRef CAS PubMed
.
- M. T. González, S. Wu, R. Huber, S. J. van der Molen, C. Schönenberger and M. Calame, Nano Lett., 2006, 6, 2238–2242 CrossRef PubMed
.
- M. Kamenetska, M. Koentopp, A. C. Whalley, Y. S. Park, M. L. Steigerwald, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Phys. Rev. Lett., 2009, 102, 126803 CrossRef CAS PubMed
.
- C. B. George, M. A. Ratner and J. B. Lambert, J. Phys. Chem. A, 2009, 113, 3876–3880 CrossRef CAS PubMed
.
- A. Bande and J. Michl, Chem. –Eur. J., 2009, 15, 8504–8517 CrossRef CAS PubMed
.
- H. A. Fogarty, C.-H. Ottosson and J. Michl, J. Mol. Struct., 2000, 556, 105–121 CrossRef CAS
.
- J. Chen, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155140 CrossRef
.
- S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482 CrossRef CAS PubMed
.
- M. Koentopp, K. Burke and F. Evers, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 121403 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS
.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef
.
- A. H. Larsen, M. Vanin, J. J. Mortensen, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195112 CrossRef
.
- A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agrait and J. M. van Ruitenbeek, Nature, 1998, 395, 783–785 CrossRef CAS
.
- M. T. González, E. Leary, R. García, P. Verma, M. Á. Herranz, G. Rubio-Bollinger, N. Martín and N. Agraït, J. Phys. Chem. C, 2011, 115, 17973–17978 Search PubMed
.
- A. M. Christian, D. Dapeng, S. J. v. d. Z. Herre and M. v. R. Jan, New J. Phys., 2008, 10, 065008 CrossRef
.
- M. S. Inkpen, M. Lemmer, N. Fitzpatrick, D. C. Milan, R. J. Nichols, N. J. Long and T. Albrecht, J. Am. Chem. Soc., 2015, 137, 9971–9981 CrossRef CAS PubMed
.
- G. C. Solomon, C. Herrmann, T. Hansen, V. Mujica and M. A. Ratner, Nat. Chem., 2010, 2, 223–228 CrossRef CAS PubMed
.
- J. Vacek, J. V. Chocholousova, I. G. Stara, I. Stary and Y. Dubi, Nanoscale, 2015, 7, 8793–8802 RSC
.
- Y.-D. Guo, X.-H. Yan, Y. Xiao and C.-S. Liu, Sci. Rep., 2015, 5, 16731 CrossRef CAS PubMed
.
- Y. Tsuji and R. Hoffmann, Chem. –Eur. J., 2016, 22, 4878–4888 CrossRef CAS PubMed
.
- R. Hoffmann, Acc. Chem. Res., 1971, 4, 1–9 CrossRef CAS
.
- J. Michl and R. West, Acc. Chem. Res., 2000, 33, 821–823 CrossRef CAS PubMed
.
- L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic procedures, STM-BJ measurement details, supplemental figures, computational details, characterization data and xyz files for calculated structures. CCDC 1470541. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc01360k |
| ‡ H. L., M. H. G. and Z. S. contributed equally to this work. |
| § Present address: Rm 204, Chong Yuet Ming Chemistry Building, The University of Hong Kong, Pokfulam Road, Hong Kong, China. |
| This journal is © The Royal Society of Chemistry 2016 |