 Open Access Article
Open Access ArticleTheoretical design of highly active SrTiO3-based photocatalysts by a codoping scheme towards solar energy utilization for hydrogen production†
Pakpoom
Reunchan
ae,
Shuxin
Ouyang
a,
Naoto
Umezawa
*abd,
Hua
Xu
a,
Yuanjian
Zhang
cf and
Jinhua
Ye
acd
aEnvironmental Remediation Materials Unit, National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan. E-mail: Umezawa.Naoto@nims.go.jp
bPRESTO, Japan Science and Technology Agency (JST), 4-1-8 Honcho, Kawaguchi, Saitama 332-0012, Japan
cInternational Center for Materials Nanoarchitectonics (MANA), National Institute for Materials Sciences, Ibaraki 305-0047, Japan
dTU-NIMS Joint Research Center, School of Materials Science and Engineering, Tianjin University, 92 Weijin Road, Nankai District, Tianjin, P. R. China
eDepartment of Physics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand. E-mail: pakpoom.r@ku.ac.th
fSchool of Chemistry and Chemical Engineering, Southeast University, Nanjing 211189, China
First published on 21st December 2012
Abstract
SrTiO3 is a promising photocatalyst for the production of hydrogen from water splitting under solar light. Cr doping is an effective treatment for adjusting its absorption edge to the visible-light range, although the performance of Cr-doped SrTiO3 is strongly affected by the oxidation number of the Cr ions. In this study, we theoretically predict that elevating the Fermi level, i.e., n-type carrier doping in SrTiO3, can stabilize the desirable oxidation number of chromium (Cr3+), contributing to a higher activity for H2 evolution. Our computational results, based on hybrid density-functional calculations, reveal that such an n-type condition is realized by substituting group-V metals (Ta, Sb, and Nb), group-III metals (La and Y), and fluorine atoms for the Ti, Sr, and O sites in SrTiO3, respectively. From our systematic study of the capability of each dopant, we conclude that La is the most effective donor for stabilizing Cr3+. This prediction is successfully evidenced by experiments showing that the La and Cr codoped SrTiO3 dramatically increases the amount of H2 gas evolved from water under visible-light irradiation, which demonstrates that our guiding principle based on Fermi level tuning by the codoping scheme is valid for the design of advanced photocatalysts.
Introduction
There has recently been much interest in the potential use of photocatalytic materials in the production of clean-energy fuels and the reduction of environmental pollutants.1 Since the discovery of the Honda–Fujishima effect,2 TiO2 has been extensively studied and applied to various commercial products, mainly for decomposing harmful chemicals or antifouling coatings. However, its application to fuel production is still limited due to the insufficient efficiency of overall water splitting for H2 evolution.2,3 It is therefore a challenge to find a highly active photocatalyst to meet today's demands for alternative energy resources. The perovskite strontium titanate (SrTiO3 or STO) is a promising photocatalyst because of several advantages, such as high chemical stability and abundance of the constituent elements. The valence-band and conduction-band edges of STO are favorably situated for overall water splitting:4–7 the valence-band maximum (VBM) is much lower than the oxidation potential of water, and the conduction band minimum (CBM) is ∼0.8 eV (at pH = 0) higher than the standard hydrogen electrode potential (SHE).7 The sufficiently large band offset of the CBM with respect to SHE, which is much larger than that of anatase TiO2 (0.1–0.2 eV), is a great benefit for the chemical reactions of photoexcited electrons with protons on the surface: 2H+ + 2e− → H2. Nevertheless, the photoabsorption range of STO is restricted to ultra-violet light because of its relatively wide band gap (3.25 eV), and the majority of sunlight, i.e. visible light is hardly utilized in photocatalytic reactions on pristine STO. One approach to overcome this problem is to induce a red-shift of the absorption edge while keeping the position of the CBM unchanged, in order to maintain its potential for proton reduction. Chromium (Cr) is of particular interest as an effective dopant for activating visible-light absorption in wide-gap semiconductor oxides.8–14 In fact, Cr-doped STO can work continuously and stably under visible light for more than 500 hours, and therefore possesses great potential for future solar hydrogen production.10,12 Importantly, Cr-doped STO is active only when the Cr ions possess a lower oxidation number (Cr3+), while it is inactive for higher oxidation states of Cr.11,12 Thus, the stabilization of Cr3+ is a key strategy for enhancing the photocatalytic performance of Cr-doped photocatalysts.Recently, we have theoretically shown that the desirable oxidation state Cr3+ predominates in n-type STO,15 namely the condition at which the Fermi level (εF) is located near the CBM. The negatively charged substitutional Cr at the titanium site (Cr−Ti), which was identified as the source of Cr3+ in Cr-doped STO, gives rise to fully occupied states above the VBM. Fig. 1(a) shows schematically the electronic structures associated with substitutional Cr at a Ti site with two different charge states (Cr0Ti and Cr−Ti). In a low εF condition, the neutral charge state Cr0Ti, which corresponds to a high oxidation state of the Cr ion, is stabilized and photo-exited electrons are likely to be trapped in unoccupied gap states, degrading photocatalytic reactions. By contrast, shifting εF towards the conduction band eliminates the trapping centers due to the realization of the desirable charge state Cr−Ti. Our computational results revealed that the occupied gap states associated with Cr−Ti play an important role both in the photoresponse under visible light and in the elimination of electron trapping centers.15
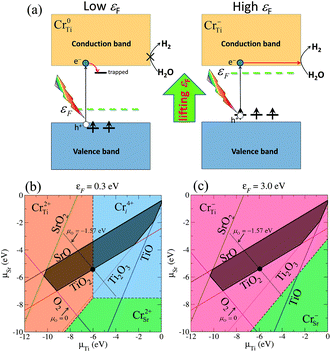 | ||
| Fig. 1 (a) Schematic illustration of the effect of shifting εF towards the conduction band on the stabilization of a low oxidation state of the Cr ion associated with Cr−Ti in Cr-doped STO. The energy levels of the in-gap Cr d states are shown. The arrows indicate the electron occupation corresponding to the associated charge state. (b) and (c) Illustrations of the conditions under which various Cr-related defects are stable, derived from the formation energy, with respect to the chemical potentials of Sr and Ti for (b) εF = 0.3 eV (p-type STO) and (c) εF = 3.0 eV (n-type STO). For the growth of STO under thermal equilibrium, μSr, μTi, and μO must lie in the dark-shaded region. | ||
Previously, some experimental reports showed that the photocatalytic performance of Cr-doped STO is improved by codoping with antimony (Sb),10 tantalum (Ta),11 or niobium (Nb),11 or by pretreatment in a reducing H2 atmosphere.11 In all of these treatments, the concentration of Cr3+ is expected to increase because of the electron carrier doping upon incorporation of these elements into STO. Although the effect of Cr3+ has been clearly addressed in our previous work,15 knowledge of the role played by codopants is still lacking. Since STO is also a promising semiconductor for oxide electronics,16,17 carrier doping of this technologically important material is of great interest to a wide range of researchers. In particular, n-type doping of this wide band-gap semiconductor is a key target in many different fields of research,18–21 and the most suitable donor for STO remains to be identified.
Here, we systematically investigate the effects of doping STO with the group-V metals Ta, Sb, Nb, and vanadium (V), the group-III metals lanthanum (La) and yttrium (Y), and the halogen fluorine (F), in order to theoretically identify the most effective donor in STO and the best candidate codopant for stabilizing Cr3+ in Cr-doped STO.
The above-mentioned metal dopants can be readily incorporated into the STO lattice thanks to the similarity of their ionic radii to those of the host elements. For instance, the ionic radii of La3+ (1.16 Å) and Nb5+ (0.64 Å) are very close to those of Sr2+ (1.26 Å) and Ti4+ (0.61 Å), respectively, that is, the group-V metals preferentially occupy the Ti site rather than the Sr site, while the group-III metals tend to occupy the Sr sites. Our theory, based on hybrid density-functional calculations, predicts that La is the best donor among the candidate elements in terms of electron doping ability and the ability to stabilize Cr3+. The prediction is successfully validated by our experiments, which clearly show that La and Cr codoped STO exhibits the best performance for hydrogen evolution from water splitting under visible-light irradiation among the candidate materials examined in this work.
Methods of calculation
Our calculations were based on density-functional theory with the hybrid-functional of Heyd, Scuseria, and Ernzerhof (HSE),22 which was implemented in the Vienna Ab initio Simulation Package (VASP) code.23 In the HSE approach, the Coulomb potential in the exchange energy of the Perdew, Burke, and Ernzerhof (PBE)24 functional is divided into short-range and long-range parts with a screening length of 10 Å. The long-range part and correlation potential are represented by the PBE functional, while the short-range part is mixed with the non-local Hartree–Fock (HF) exchange. We reproduced the experimental band gap of STO (3.25 eV) by using the HF mixing parameter of 28%. The HSE functional has been shown to improve the band gap of semiconductors and give a good description of the electronic structure and formation energies of defects and impurities.25,26 The cutoff energy of 400 eV was used for the plane-wave basis set. The defect calculations were performed using a (3 × 3 × 2) 90-atom supercell and a 2 × 2 × 2 grid of Monkhorst-Pack special k points for the Brillouin zone integration. The effects of spin polarization were included in all calculations involving unpaired electrons.The solubility of a donor-type impurity must be sufficiently high under a given sample growth condition. The formation energy is the key quantity that must be calculated to investigate the stability of a dopant, and is given by the following equation:
| Ef(XqTi) = Etot(XqTi) − Etot(STO) + μTi − μX + qεF | (1) |
Results and discussion
Here we initially examine the effect of an upward shift of εF on the stabilization of Cr−Ti. Fig. 1(b) and 1(c) illustrate the Cr impurities that give the lowest formation energy at each chemical potential condition of (μSr, μTi):CrTi, Cr substituted for Sr (CrSr), and Cr at an interstitial site (Cri). These are shown in Fig. 1(b) for εF = 0.3 eV (p-type STO) and in Fig. 1(c) for εF = 3.0 eV (n-type STO). Here, μO is uniquely determined at each point (μSr, μTi) through the above-mentioned equilibrium condition. For p-type STO, Cr2+Ti and Cr4+i are the dominant species under the stable growth condition, as illustrated by the dark-shaded domain in Fig. 1(b). By contrast, for n-type STO where εF is located near the CBM, the dark-shaded domain is associated only with Cr−Ti (Fig. 1(c)). This suggests that a higher concentration of Cr−Ti, which is advantageous for photocatalytic activity, can be obtained under n-type conditions. However, such an n-type condition is not achieved without external doping, as addressed in the following. In order to determine realistic values of the chemical potentials, μO was estimated by including contributions from enthalpy and entropy.28μO is expressed as| μO(T, P0) = {(H0 + ΔH(T)) + T(S0 + ΔS(T))}/2 | (2) |
Here, we address how to estimate the chemical potential of the dopants μX, which is an important factor in determining the impurity solubility. Fig. 2 illustrates the thermodynamically stable phases for the relevant transition metal (TM) compounds over the range of possible growth conditions between the O-poor limit (μO = −5.27 eV) and the extreme O-rich limit (μO = 0). μx can be derived from the formation enthalpy of its limiting phase which is subject to an upper bound. For instance, for the realistic growth condition μO = −1.57 eV (dashed-dotted line in Fig. 2), μCr is determined by the formation enthalpy of Cr2O3, that is, 2μCr + 3μO ≤ ΔHf(Cr2O3), where the upper bound of μCr = (μCr2O3 − 3μO)/2: if μCr is pushed higher than the upper bound, Cr2O3 will form in addition to the Cr incorporated in the STO lattice. Using a similar procedure, the upper bound for μX where X = Ta, Sb, Nb, V, La, and Y can be determined.
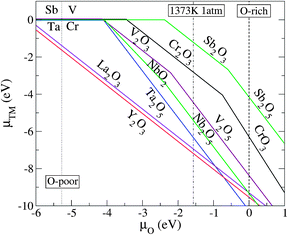 | ||
| Fig. 2 The relationship between the transition metal (TM) chemical potentials μTM and the O chemical potential μO, as derived from the equilibrium growth of the host: xμTM + yμO = ΔHf(TMxOy). Only the μTM that gives the upper bound (the lowest μTM) for the respective μO are shown. The dotted-, dashed-, and dashed-dotted vertical lines denote the O-poor (μO = −5.42 eV), O-rich (μO = 0), and realistic O-rich conditions (μO = −1.57 eV), respectively. | ||
Fig. 3 shows the calculated formation energies of the Cr-related defects for these realistic chemical potentials, indicating that CrTi is a more stable form of chromium than the other forms (CrSr or Cri) for a wide Fermi level range, as we discussed in our previous paper.15 Under a thermodynamic equilibrium condition, the charge neutrality must be satisfied when the concentrations of the positively charged Cr+Ti and the negatively charged Cr−Ti are balanced. This determines the pinning level of εF, shown as an arrow in Fig. 3. Here, the neutral Cr0Ti, which is likely to act as an electron trapping center,15 is the predominant charge state at the pinned εF. To stabilize the favorable charge state, Cr−Ti, the pinning level must be elevated. This motivated us to seek donor dopants that can effectively shift εF upwards and stabilize Cr−Ti without the formation of electron-trapping centers.
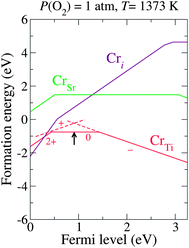 | ||
| Fig. 3 Calculated formation energy as a function of εF for Cr-related defects under a realistic growth condition (μO = −1.57 eV). The arrow indicates the estimated pinned εF. The slope of each line indicates the charge state. The transition levels between different charge states are denoted as kinks in each plot. | ||
First, we explore the group-V elements (V, Nb, and Ta) and another pentavalent element Sb (we include Sb in “group-V” in the following discussion). As the ionic radii of all four dopants are closer to that of Ti than that of Sr, preferential substitution at the Ti site is expected. This is supported, for example, by the fact that the calculated formation energy of TaSr is ∼7 eV higher than that of TaTi. We found that SbTi, TaTi, and NbTi do not introduce in-gap states when positively charged (Sb+Ti, Ta+Ti, and Nb+Ti). For the neutral charge state (Sb0Ti, Ta0Ti, and Nb0Ti), an extra electron occupies the bottom of the conduction band, which consists of an extended state resulting from the perturbation of the Ti-d states of the host band induced by the impurity. Fig. 4(a) shows the formation energies of the substitutional group-V impurities, along with that of CrTi. We found that the positive charge state is energetically stable for SbTi, TaTi, and NbTi over the entire range of εF positions in the band gap. The transition levels at which the stable charge state changes from 1+ to 0, ε(+/0), were found to be located just above the CBM for SbTi, TaTi, and NbTi (not shown in Fig. 4), indicating that they act as shallow donors in STO. By contrast, VTi creates deep levels in the band gap as characterized by the transition levels ε(+/0), ε(0/−), and ε(−/2−). The in-gap states originate from the vanadium t2g orbitals and are likely to give rise to carrier-trapping centers.
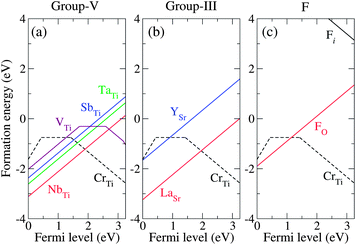 | ||
| Fig. 4 Calculated formation energies as a function of εF for (a) group-V codopants (Nb, Ta, Sb, and V), (b) group-III codopants (La and Y), and (c) F, as well as CrTi in each case. All formation energies were calculated for μO = −1.57 eV. | ||
For the group-III codopants, we focused on the Sr site for the substitution, because the calculated formation energies showed that La preferably substitutes Sr rather than Ti. The formation energies of LaSr and YSr shown in Fig. 4(b) indicate that they act as shallow donors. Without forming any impurity states in the band gap, LaSr and YSr are unlikely to act as trapping centers for photoexcited electrons. Fig. 4(c) also shows that FO is a shallow donor in STO. The ionic radius of F− (1.33 Å) is slightly smaller than that of O2− (1.40 Å), suggesting that O2− is readily substituted by F−. In a similar fashion to the other shallow donors, the extra electron of F0O was found to occupy the extended state located at the bottom of the conduction band, whereas F+O does not form any in-gap states. We note that interstitial F (Fi) is energetically unstable, having a much higher formation energy than FO. The density of states (DOS) for SbTi, TaTi, NbTi, LaSr, YSr, and FO in the positive charge state, showing that they do not introduce in-gap states, are shown in the ESI.†
We now discuss the capability of the codopants to stabilize Cr3+ and enhance the photocatalytic activity of STO. The first factor to consider is that the codopants should not cause trapping centers for photoexcited electrons. This is true for the Ta, Nb, Sb, Y, La, and F impurities that are incorporated into STO (based on the assumption that the dominant forms of the Ta, Nb, Sb, Y, La, and F impurities are TaTi, NbTi, SbTi, YSr, LaSr, and FO, respectively). By contrast, the incorporated V impurity creates deep states in the gap and should therefore be excluded from the candidate codopants. The second factor to consider when choosing suitable codopants is their solubility. The donor impurities are activated only when their solubility in the host material is sufficiently high. From Fig. 4, it is clear that LaSr has the lowest formation energy (highest solubility) among the examined donors under the realistic growth condition corresponding to μO = −1.57 eV, which determines the upper bound of the chemical potential of each dopant as discussed before; TaTi, NbTi, VTi, SbTi, YSr, and LaSr are limited by the formation of the binary metal oxides Ta2O5, Nb2O5, V2O5, Sb2O3, Y2O3, and La2O3, respectively (see Fig. 2). The solubility of FO is limited by the formation of SrF2. In other words, the chemical potential of a dopant must be carefully estimated from the limiting phase, since it significantly affects the solubility of the dopant.
In Cr-doped STO, the pinned Fermi level (εF = 0.92 eV) is relatively low, and the majority of the CrTi is present in the neutral charge state (Cr0Ti), as mentioned above. Under this condition, the photocatalytic activity of Cr-doped STO is suppressed.15 Because the photocatalytic activity is triggered when Cr−Ti is stabilized, an upward shift of the pinned εF should improve the performance of the material. This is made feasible by incorporating a shallow donor that has a sufficiently low formation energy in the positive charge state (for example, La+Sr), thus suppressing the formation of Cr0Ti. Here, εF becomes pinned at a higher level (εF = 1.95 eV for LaSr) corresponding to the intersection of the lines for La+Sr (positive slope) and Cr−Ti (negative slope) in Fig. 4(b), as a consequence of the charge balance. The same method was used to determine the pinning levels of εF for STO codoped with Cr−Ti and the other dopants considered here. The donor impurity with a lower formation energy gives a higher position of the pinning level. The position of the pinning level with respect to VBM significantly affects the relative concentrations of Cr0Ti and Cr−Ti, as shown in Fig. 5.
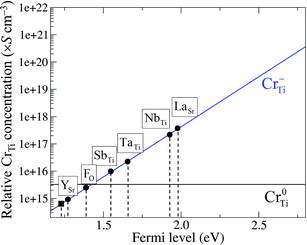 | ||
| Fig. 5 Calculated relative concentration of CrTi defects, derived from hypothetical formation energies, as a function of Fermi level (εF). The pinned εF results from the charge-neutrality condition for codoped (circles) and non-codoped (square) Cr-doped STO. | ||
Under thermal equilibrium, the concentration of CrqTi can be expressed as Nsitesexp(−Ef(CrqTi)/kBT), where Nsites (∼1.67 × 1022 cm−3) is the number of available Ti sites in STO that can be substituted by Cr atoms. The negative formation energy of CrTi, shown in Fig. 3, gives a concentration that is too high for an impurity, indicating that the actual μCr is much lower than the upper bound estimated by our calculations; to obtain a positive value of Ef(CrTi), the actual μCr should be at least 0.9 eV lower than the value of μCr taken from Cr2O3. Therefore, in order to estimate the relative concentrations of Cr0Ti and Cr−Ti for different values of the pinned εF (Fig. 5), we consistently added a constant value to the formation energies of the impurities shown in Fig. 4 such that Ef(CrTi) became positive over the entire range of εF. Without the incorporation of the codopant, Cr0Ti remains the predominant species (solid square in Fig. 5). Codoping successfully shifts the pinning level towards the CBM, and the majority of CrTi is replaced by the favorable charge state Cr−Ti at the εF for SbTi substitution. The concentration of Cr−Ti scales exponentially as a function of the pinned εF; we found the best and worst dopants for increasing the concentration of Cr−Ti to be La and Y, respectively.
We also investigated the possibility of the formation of a neutral defect-complex by coupling Cr−Ti with a codopant, which can be computed from the binding energy,
| Eb = Ef(Cr−Ti) + Ef(D+) − Ef((CrTi–D)0). | (3) |
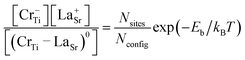 | (4) |
Previous experimental results have shown that codoping Cr-doped STO with Ta,11 Sb,10 or Nb,11 significantly enhances the photocatalytic activity, whereas codoping with V11 decreases the activity, in good agreement with our calculations. It has also been found that Cr3+ is stabilized under O-deficient conditions,30 which enhances the n-type condition. Our results are not only applicable to the stabilization of active Cr ions in the Cr-doped STO photocatalyst, but can also provide a route towards the fabrication of n-type STO. Our study clearly shows that n-type STO can be realized by doping with Nb or La, both of which have high solubility under the realistic growth condition discussed above. Indeed, it has long been realized that doping STO with Nb or La induces a transition from an insulator to an n-type semiconductor.31–33 The dopants Ta, Sb, and Y also act as shallow donors, although their solubility in STO is limited due to their relatively high formation energies compared to those of Nb and La (see Fig. 4). As in other oxides, such as ZnO,34 FO is a shallow donor in STO and is highly soluble under O-deficient conditions. By contrast, Fi is a deep acceptor with a high formation energy, and thus cannot contribute to p-type conductivity in STO. Theoretical studies of electron-doped STO have also been carried out and are consistent with our results.19,35
Now we demonstrate the photocatalytic performance of Cr-doped STO codoped with La, Nb, Sb, and Y, which are theoretically predicted to be the best to the worst codopants for increasing Cr−Ti, in that order. The detail of experiments can be found in the ESI.† We found that all codoped samples can absorb light in the visible region, as shown in Fig. S1.†Fig. 6 shows the photocatalytic activities of Cr-doped STO codoped with La, Nb, Sb, and Y for H2 evolution from water splitting under visible light irradiation. Cr-doped STO codoped with La (La–Cr:STO) showed the highest activity, in excellent agreement with our theoretical prediction. However, the H2 evolution activity of Nb–Cr:STO is the lowest, which is inconsistent with our prediction. This discrepancy might result from the presence of other types of Nb-related defects, such as Nb interstitials or its complexes, and the carrier concentration of doped electrons is not sufficiently high to shift the Fermi level up to the expected position under our growth condition. However, the identification of the most stable Nb-related defect in STO is beyond the scope of this work.
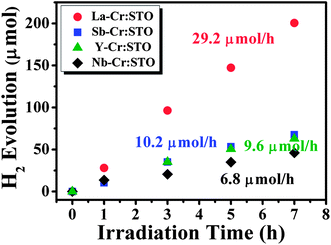 | ||
| Fig. 6 Photocatalytic H2 evolution from water splitting of Cr and D codoped SrTiO3 under visible light irradiation, where D = La, Sb, Y, and Nb. All codoped samples were prepared using 5 mol% of Cr and 5 mol% of D. | ||
In contrast, although the H2 evolution activity of Sb–Cr:STO was much lower than that of La–Cr:STO, it is still higher than that of Nb–Cr:STO. This could be attributed to the fact that Sb does not have partially filled d states, and thus its related defects, if formed, are unlikely to cause carrier recombination. Y–Cr:STO exhibits H2 evolution activity comparable to that of the Sb–Cr:STO sample at the beginning of the photochemical reaction. However, the activity gradually decreases with longer irradiation time (Fig. 6). This is qualitatively consistent with our prediction that the activity of Y–Cr:STO is lower than that of Sb–Cr:STO. As mentioned above, the La–Cr:STO possesses the highest amount of Cr−Ti compared to the other codoped samples and thus is a highly active photocatalyst under visible-light irradiation; recently, via a synthesis improvement and a reaction-environment modulation, La–Cr:STO was found to exhibit a high quantum yield of 25.6% (λ = 425 ± 12 nm) for H2 evolution,36 which lends strong support to the findings of our study herein. Next we discuss the effect of donor impurities on the oxidation state of Cr in the codoped samples.
X-ray photoelectron spectroscopy (XPS) measurements were performed to investigate the oxidation state of doped Cr. Fig. 7 shows the XPS spectra of Cr 2p of the codoped samples. All the codoped samples showed a peak at about 576.4 eV, which is very close to the peak assigned to Cr3+ at 576.7 eV, however, some of our samples showed the peak assigned to Cr6+ at 579.2 eV.10 The relative intensity of XPS allows us to understand the effect of the codopant on the oxidation state of doped Cr as follows. La–Cr:STO and Nb–Cr:STO showed a high peak intensity of Cr3+, while the peaks assigned to Cr6+ are almost negligible, in agreement with our calculations that codoping with either La or Nb should efficiently increase the concentration of Cr3+. However, based on our experimental result, codoping with Nb does not enhance the photocatalytic activity even though the concentration of Cr3+ is high, indicating that codoping with Nb possibly leads to the formation of other types of defects which cause carrier recombination. Sb–Cr:STO showed a relatively low peak intensity of Cr3+, while a small shoulder of the peak assigned to Cr6+ was observed. Y–Cr:STO clearly showed a high peak intensity of Cr6+ compared to that of Cr3+, in agreement with our theory (Fig. 5) and experiment (Fig. 6).
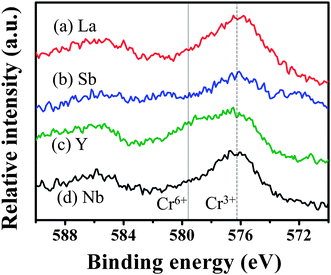 | ||
| Fig. 7 X-ray photoelectron spectra of Cr 2p of (a) La–Cr, (b) Sb–Cr, (c) Y–Cr, and (d) Nb–Cr codoped SrTiO3. The peaks assigned to Cr3+ and Cr6+ are indicated by dashed and dotted lines, respectively. | ||
Conclusions
In summary, we have systematically studied the capability of several dopants (V, Nb, Ta, La, Y, and F) for the enhancement of the photocatalytic performance of Cr-doped SrTiO3. Based on our density-functional calculations for the stability of the donor-type impurities, La substituted for Sr (LaSr) was predicted to be the best donor for shifting the Fermi level towards the conduction band of SrTiO3. The n-type condition is advantageous for increasing the concentration of negatively charged Cr−Ti (Cr3+), which is the key oxidation state for activating photocatalytic reactions. The prediction from theory has been successfully evidenced by our experiments showing that La and Cr codoped SrTiO3 shows markedly high activity for H2 evolution from water splitting under visible-light irradiation compared to the other candidate dopants (Nb–Cr, Sb–Cr, or Y–Cr). Furthermore, our computational results show that the other substitutional defects, SbTi, TaTi, NbTi, YSr, and FO, are also shallow donors, although they are less soluble in SrTiO3 than LaSr is, whereas VTi creates deep states in the band gap and is unable to produce the n-type condition. By combining theoretical and experimental investigations, our guiding principle of Fermi level tuning by a codoping scheme was found to be reliable for the design of Cr-doped SrTiO3, and represents a significant step forward in the development of advanced photocatalysts.Acknowledgements
This work was partially supported by the Japan Science and Technology Agency (JST) Precursory Research for Embryonic Science and Technology (PRESTO) program, and the World Premier International Research Center Initiative on Materials Nanoarchitectonics (MANA), MEXT. P.R. and N.U. thank the High-Performance Computing Center of the California NanoSystems Institute (CNSI, UCSB) and the Synchrotron Light Research Institute (SLRI, Thailand) for their hospitality. P.R. thanks S. Limpijumnong for the advice.Notes and references
- H. Tong, S. Ouyang, Y. Bi, N. Umezawa, M. Oshikiri and J. Ye, Adv. Mater., 2012, 24, 229–251 CrossRef CAS.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS.
- A. L. Linsebigler, G. Lu and J. T. Yates, Chem. Rev., 1995, 95, 735–758 CrossRef CAS.
- M. S. Wrighton, A. B. Ellis, P. T. Wolczanski, D. L. Morse, H. B. Abrahamson and D. S. Ginley, J. Am. Chem. Soc., 1976, 98, 2774–2779 CrossRef CAS.
- A. K. Ghosh and H. P. Maruska, J. Electrochem. Soc., 1977, 124, 1516–1522 CrossRef CAS.
- K. Domen, S. Naito, T. Onishi, K. Tamaru and M. Soma, J. Phys. Chem., 1982, 86, 3657–3661 CrossRef CAS.
- Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543–556 CAS.
- R. U. E. ’t Lam, L. G. J. de Haart, A. W. Wiersma, G. Blasse, A. H. A. Tinnemans and A. Mackor, Mater. Res. Bull., 1981, 16, 1593–1600 CrossRef.
- M. Matsumura, M. Hiramoto and H. Tsubomura, J. Electrochem. Soc., 1983, 130, 326–330 CrossRef CAS.
- H. Kato and A. Kudo, J. Phys. Chem. B, 2002, 106, 5029–5034 CrossRef CAS.
- T. Ishii, H. Kato and A. Kudo, J. Photochem. Photobiol., A, 2004, 163, 181–186 CrossRef CAS.
- D. Wang, J. Ye, T. Kako and T. Kimura, J. Phys. Chem. B, 2006, 110, 15824–15830 CrossRef CAS.
- J. W. Liu, G. Chen, Z. H. Li and Z. G. Zhang, J. Solid State Chem., 2006, 179, 3704–3708 CrossRef CAS.
- W. Wei, Y. Dai, H. Jin and B. Huang, J. Phys. D: Appl. Phys., 2009, 42, 055401 CrossRef.
- P. Reunchan, N. Umezawa, S. Ouyang and J. Ye, Phys. Chem. Chem. Phys., 2012, 14, 1876–1880 RSC.
- A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426 CrossRef CAS.
- D. Kan, T. Terashima, R. Kanda, A. Masuno, K. Tanaka, S. Chu, H. Kan, A. Ishizumi, Y. Kanemitsu, Y. Shimakawa and M. Takano, Nat. Mater., 2005, 4, 816–819 CrossRef CAS.
- R. Astala and P. D. Bristowe, J. Phys.: Condens. Matter, 2002, 14, L149 CrossRef CAS.
- W. Luo, W. Duan, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 214109 CrossRef.
- A. Kinaci, C. Sevik and T. Çağin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155114 CrossRef.
- R. K. Astala and P. D. Bristowe, Modell. Simul. Mater. Sci. Eng., 2004, 12, 79 CrossRef CAS.
- J. Heyd, G. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212 CrossRef.
- A. Stroppa, G. Kresse and A. Continenza, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 085201 CrossRef.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef CAS.
- J. Osorio-Guillén, S. Lany, S. V. Barabash and A. Zunger, Phys. Rev. Lett., 2006, 96, 107203 CrossRef.
- Y. Gai, J. Li, S.-S. Li, J.-B. Xia and S.-H. Wei, Phys. Rev. Lett., 2009, 102, 036402 CrossRef.
- S. F. Alvarado, F. La Mattina and J. G. Bednorz, Appl. Phys. A: Mater. Sci. Process., 2007, 89, 85–89 CrossRef CAS.
- O. N. Tufte and P. W. Chapman, Phys. Rev., 1967, 155, 796 CrossRef CAS.
- T. Tomio, H. Miki, H. Tabata, T. Kawai and S. Kawai, J. Appl. Phys., 1994, 76, 5886–5890 CrossRef CAS.
- R. Moos, A. Gnudi and K. Härdtl, J. Appl. Phys., 1995, 78, 5042 CrossRef CAS.
- A. Janotti, E. Snow and C. G. Van de Walle, Appl. Phys. Lett., 2009, 95, 172109 CrossRef.
- N. Shanthi and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2153 CrossRef CAS.
- S. Ouyang, H. Tong, N. Umezawa, J. Cao, P. Li, Y. Bi, Y. Zhang and J. Ye, J. Am. Chem. Soc., 2012, 134, 1974–1977 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: details of sample synthesis and experimental details for photocatalytic H2 evolution, XPS measurements, and optical absorption spectra for the selected codoped SrTiO3. The calculated density of states for the supercell containing Cr defects and the supercell containing donor-type codopant defects. See DOI: 10.1039/c2ta00450j |
| This journal is © The Royal Society of Chemistry 2013 |
