Interpretable and uncertainty-informed machine learning to accelerate the design and discovery of lead-free piezoceramics with large piezoelectric constant†
Heng
Hu
a,
Bin
Wang
a,
Didi
Zhang
a,
Kang
Yan
 *a,
Tao
Tan
*b and
Dawei
Wu
*a
*a,
Tao
Tan
*b and
Dawei
Wu
*a
aState Key Laboratory of Mechanics and Control of Mechanical Structures, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China. E-mail: yankang@nuaa.edu.cn; dwu@nuaa.edu.cn
bFaculty of Applied Sciences, Macao Polytechnic University, Macao 999078, China. E-mail: taotan@mpu.edu.mo
First published on 16th April 2025
Abstract
Potassium sodium niobate (KNN)-based ceramics are promising alternatives to lead-containing piezoelectric materials. However, the vast design space, characterized by multiple dopant choices and variable content, presents a considerable challenge in the chemical modification of KNN compositions to improve their piezoelectric performance. In recent years, the rapid advance of machine learning (ML) techniques has facilitated expedited materials design and discovery with deeply sought insights into the materials. In this study, we constructed an interpretable and uncertainty-informed ML framework to optimize the piezoelectric coefficient d33 of a KNN-based lead-free system. We identified and analyzed the influential features for the d33 prediction and conducted three experimental iterations based on the uncertainty-informed predictions obtained from the Monte Carlo dropout (MCDropout). Promising KNN compositions exhibiting large d33 values over 300 pC N−1 were located and synthesized. Furthermore, the MCDropout markedly reduced the computational cost by 33% compared to the commonly used bootstrap method for uncertainty assessment. This study exhibits an ML framework with enhanced interpretability and search efficiency for optimizing the crucial piezoelectric properties of piezoceramics. The application scope of the utilized methods can be extended to various materials with tailored properties.
1. Introduction
Chemical modification is one of the most frequently used approaches to enhance the piezoelectricity of lead-free materials, which makes them promising alternatives to the Pb(Zr,Ti)O3-based materials.1 However, the vast chemical design space significantly limits the exploration efficiency for high-performance compositions. In recent years, the machine learning (ML) framework that combines feature engineering, ML modeling, and iterative experimental observations has emerged as a promising tool to accelerate the design and discovery of novel materials.2–6 Previously unobserved piezoelectric compositions with enhanced properties have been effectively located. Typically, Yuan et al.6–8 used ML methods to design the BaTiO3 (BT)-based piezoceramics with large electrostrain and piezoelectric coefficient. Gu et al.9 and Sun et al.10 constructed ML models to accelerate the design of high-performance (K,Na)NbO3 (KNN)-based ceramics. The ML model exhibits excellent ability to establish the hidden patterns between input features and output properties, making it an efficient tool for materials design and discovery.Recently, a critical concern of ML about its interpretability or explainability has received rising attention.11,12 The lack of transparency poses challenges in understanding the rationale behind the ML predictions, thus necessitating the development of an interpretable ML framework that shows exact physical meanings and closely engages with observations from experimentation.13–15 Besides, training robust ML models implicitly assumes the availability of a sufficiently large and diverse database.16 Unfortunately, this rarely occurs in the investigation of piezoelectric materials due to the laborious and lengthy experimental procedures. ML models are prone to generating less reliable predictions when exploring the materials far from the observed domain than when exploiting those near the observed domain in the design space.17 Therefore, it is crucial to seek out rationality and evaluate the reliability of ML predictions when using ML methods to accelerate the search for materials with tailored properties.
This study aims to establish an interpretable and uncertainty-informed ML framework for designing and discovering lead-free piezoceramics. This framework is centered around shapley additive explanations (SHAP),18 Monte Carlo dropout (MCDropout),19 and Bayesian optimization (BO),20 which are integrated to search for promising KNN-based lead-free piezoelectric ceramics with enhanced piezoelectric coefficient d33. Extensive research has been conducted on enhancing the piezoelectric properties of KNN-based ceramics using multicomponent co-dopants, such as Li, Sb, BaZrO3, etc.21–25 The selection of dopants and their stoichiometry is mainly based on expertise-driven empirical observations due to the complex and obscure mechanisms underlying piezoelectricity enhancement in KNN-based ceramics. Therefore, the application of the SHAP method here aims to interpret the influence of material features on d33 prediction in the data-driven materials design, which might give insight into these materials from a statistical learning perspective. Uncertainty quantification (UQ) is essential for studies with limited and unbalanced experimental databases as it provides a rigorous evaluation of the ML predictions.26 We emphasized the role of UQ, which is realized by the MCDropout. This technique extends the traditional dropout employed to prevent overfitting during the training phase of ML and generate uncertainty-informed predictions during the inference phase.27 It has been explored for various applications, such as digital histopathology,28 soil spectroscopy,29 and object detection.30 For the materials research, the potential of MCDropout is valuable to be further validated and developed. In addition, BO has emerged at the forefront of expensive “black box” optimization due to its data efficiency.31 It can guide global optimal search with a small number of experimental observations, which has attracted intense interest in materials research.32,33 Our experimental design strategies based on BO functions, including the exploitation (ET) and expected improvement (EI), leverage predictions and predictive uncertainty captured by the MCDropout to determine the compositions for the experimental observations.
The influential features interpreted by the SHAP show consistency with the conventional understanding of KNN-based ceramics. Simultaneously, additional insights into the previously unfocused features affecting the direction of d33 predictions were revealed. The model implemented with MCDropout effectively generated multiple predictions for compositions in the vast design space. The shape of the predictive distribution can be approximated as the bell curve of normal distribution, which is ideal for the UQ. Furthermore, the computational results reveal that the applied MCDropout made more efficient inferences than the commonly used bootstrap method.7–9,34,35 This benefit can be strengthened when the iteration and model complexity increase. Ultimately, three iterations of the experiment guided by the BO led to the discovery of KNN compositions with enhanced d33 exceeding 300 pC N−1, validating the effectiveness of the utilized method.
2. Methods
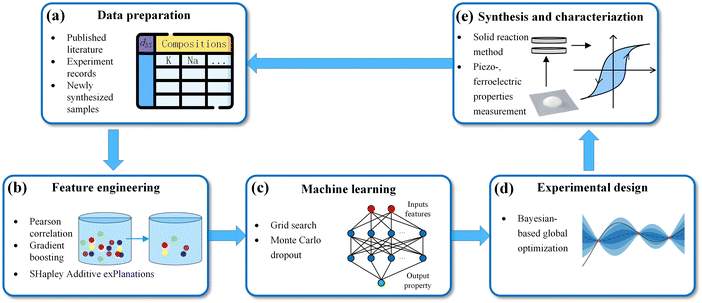
The iterative ML workflow of this study is shown in Fig. 1, which consists of five parts for each iteration: data preparation, feature engineering, machine learning, experimental design, and synthesis and characterization.2.1 Computational details
The design space was defined according to the chemical formulae (1 − x)(Ky1Nay2Li1−y1−y2)(NbzSb1−z)O3-xMZrO3 (xM = aBa, bCa, cBi0.5K0.5, dBi0.5Na0.5, or eBi0.5Li0.5). The mole fraction of each variable was constrained by 0 ≤ x ≤ 0.06, 0.4 ≤ y1 ≤ 0.5, 0.5 ≤ y2 ≤ 0.6, 0.9 ≤ z ≤ 1, 0 ≤ a, b, c, d, e ≤ 0.05 to avoid the possible appearance of relaxor phase, which can be harmful to d33 enhancement. It leads to approximately 331![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible compositions if the mole fraction is controlled to 0.01. The database (shown in Table S1, ESI†) is included in the design space. All ceramic specimens in the database were prepared using the conventional solid-state reaction method and sintered at a sintering temperature around 1120 °C, which ensures data comparability. We took the nominal compositions in literature as actual compositions, excluding the impact of processing variance.36
000 possible compositions if the mole fraction is controlled to 0.01. The database (shown in Table S1, ESI†) is included in the design space. All ceramic specimens in the database were prepared using the conventional solid-state reaction method and sintered at a sintering temperature around 1120 °C, which ensures data comparability. We took the nominal compositions in literature as actual compositions, excluding the impact of processing variance.36
Feature engineering involves a three-step process: feature construction, feature screening, and feature interpretation. Firstly, the KNN compositions were transformed into features that had been defined according to the knowledge of ferroelectrics.6,37 The feature pool covers the size factors (e.g., atomic volume), electrochemical factors (e.g., electronegativity), atomic number factors (e.g., atomic number), etc. of A and B-site dopants (shown in Tables S2 and S3, ESI†). The prepared features are representative, related to target properties, and easily accessible.38 Subsequently, Pearson correlation analysis was used to screen out highly correlated features. The Pearson correlation coefficient r between two features is defined by
 | (1) |
![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) and Ȳ are the mean of Xi and Yi. One of the highly correlated features with r > 0.95 was retained, while others were removed.39 The retained features served as the inputs of the ML model. Lastly, gradient boosting and SHAP methods were used to improve the interpretability of ML models. The gradient boosting method provided relative importance of features to the model prediction, which is calculated based on the contribution of features to the performance of the gradient boosting regressor. The SHAP method explained the direction of the top-ranked features that contributed to the prediction of d33. The important features and their impact on predictions are illustrated by combining these two methods.
and Ȳ are the mean of Xi and Yi. One of the highly correlated features with r > 0.95 was retained, while others were removed.39 The retained features served as the inputs of the ML model. Lastly, gradient boosting and SHAP methods were used to improve the interpretability of ML models. The gradient boosting method provided relative importance of features to the model prediction, which is calculated based on the contribution of features to the performance of the gradient boosting regressor. The SHAP method explained the direction of the top-ranked features that contributed to the prediction of d33. The important features and their impact on predictions are illustrated by combining these two methods.
We used the artificial neural network (ANN) to learn the patterns between input features and output d33. Compared to traditional ML models, it can be more advantageous when dealing with high-dimensional features and non-linear patterns.40 The ANN architecture consists of an input layer, one or more hidden layers, and an output layer that can be flexibly adjusted depending on specific problems. The shape of the input layer corresponds to the dimension of features. The rectified linear unit served as the activation function for the hidden layers, whereas the linear function was employed for the output layer. The grid search method was used to determine hidden layer configurations, including the number of hidden layers and the number of neurons within each hidden layer. The search range for the hidden layer number is defined from 1 to 2. The hidden nodes in each hidden layer range from 2 to 30 with an increment of 2. Leave-one-out cross-validation (LOOCV) method was used to calculate the performance of ANN models with different hidden layer configurations. This method works by training all but one sample and testing the left-out sample. The above procedure was repeated until every sample had been the test sample. The metric to evaluate model performance is the root mean square error (RMSE) across all test samples (RMSELOOCV), which is defined by
 | (2) |
The MCDropout was used to assess model uncertainty. This method works by randomly activating and switching off different subsets of neurons in the hidden layers of ANN with a dropout rate of p. The model architecture has 2n variations during each inference if there are n neurons in the hidden layers as a result of p. Different architectures lead to different predictions for the same input. Consequently, we can uncover uncertainty by inspecting the predictive distributions provided by the MCDropout. In this study, the uncertainty is evaluated through two key parameters: the mean μ and standard deviation σ of the predictions. We implemented MCDropout on all the neurons in the hidden layers with a dropout rate of 0.2. That means 20% of the neurons, together with connected synapses, are randomly set inactive at each epoch during the inference phase. The forward pass frequency was set to 500, resulting in 500 predictions for each composition in the search space.
We used the normal quantile–quantile (Q–Q) plot to test the normality of the predictive distributions. The Q–Q plot illustrates discrepancies between a sample distribution (sample quantiles) and what is expected from a normal distribution of a similar number of values with the same μ and σ (theoretical quantiles). A strong agreement between the theoretical and sample quantiles indicates a satisfactory approximation to normality in the predictive distribution. We used R2 to numerically measure the agreement, which is defined by
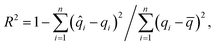 | (3) |
![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) i is the theoretical quantile and
i is the theoretical quantile and ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) is the μ of n sample quantiles. At last, we compared the inference time using the MCDropout method with the widely used bootstrap method. The principle of bootstrapping is to randomly resample with replacement from the initial database to construct multiple datasets. Based on 500 bootstrapped datasets, we trained 500 ANN models with the same layer configurations to infer the design space.
is the μ of n sample quantiles. At last, we compared the inference time using the MCDropout method with the widely used bootstrap method. The principle of bootstrapping is to randomly resample with replacement from the initial database to construct multiple datasets. Based on 500 bootstrapped datasets, we trained 500 ANN models with the same layer configurations to infer the design space.
The search for high-performance compositions is inspired by the BO and surrogate-based optimization.41,42 We used ANN as the surrogate model to approximate the features-d33 relationship. Two typical acquisition functions, ET and EI, based on the predictions obtained from ANN models, were employed to guide the experimental design. The ET function selects the composition with the highest predicted μ at point x, which is defined by
| ET(x) = argmax[μ(x)]. | (4) |
The EI function takes into account both the predicted μ and σ, which is defined by
| EI(x) = argmax[(μ − f(x*))Φ((μ − f(x*))/σ) + σφ((μ − f(x*))/σ)], | (5) |
2.2 Experimental procedures
The KNN-based piezoceramics were prepared using the conventional solid-state method. K2CO3(99.99%), Na2CO3(99.8%), LiCO3(99.9%), Nb2O5(99.9%), Sb2O3(99.9%), ZrO2(99.9%), Bi2O3(99.9%), CaCO3(99.9%), and BaCO3(99.9%) were used as raw materials. These materials were mixed in stoichiometric ratios by ball milling using alcohol as a solvent for 12 hours. The powders were calculated at 950 °C for 6 hours after drying. The calcined powders were milled and dried again before being pressed into pellets using polyvinyl alcohol (PVA) as a binder. The pellets were fired at 600 °C to remove the binder and subsequently sintered at 1070–1170 °C for 6 hours in an ambient atmosphere. Different sintering temperatures were exhaustively tested for the pellets with the same composition to find out the optimal sintering temperature for d33. The sintered ceramic specimens were polished and coated with silver electrodes on the top and bottom surfaces for electrical testing.The ceramic surfaces were polished and thermally etched to expose the microstructure and grain morphologies, which were observed by scanning electron microscopy (SEM) (Vega 3, TESCAN, Czech). The ferroelectric and electromechanical properties were characterized at 10 Hz and room temperature using a precision ferroelectric workstation (Radiant Technologies, Inc., USA) equipped with a photonic sensor (MTI-2100, MEMS Technology, USA). The d33 of the ceramic specimens poled in silicone oil at 4 kV mm−1 was measured by a quasi-static piezo-d33 meter (ZJ-3A, Institute of Acoustics Academia Sinica, China).
3. Results and discussion
3.1 Interpretable feature engineering
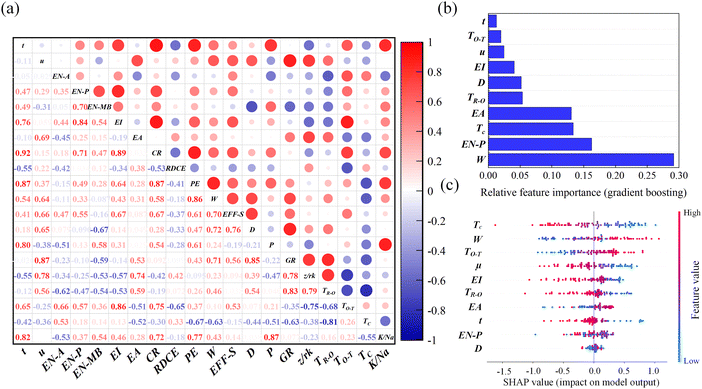
The r is widely used to measure the degree and direction of the linear dependence between two features. We grouped highly correlated features (r > 0.95) and retained one of them as they essentially provided identical information to the model, which led to a reduction of the feature numbers to 20. The groups of highly correlated features and their respective correlations are shown in Table S4 and Fig. S1, ESI.†Fig. 2(a) illustrates the r matrix between the remaining features for model training. The value in the grids indicates the r value between each feature. The red grid indicates a positive correlation, whereas the blue grid indicates a negative correlation. The color intensity is proportional to the absolute value of r.To improve interpretability, we identified the most contributive features to the d33 prediction using the gradient boosting feature importance, as shown in Fig. 2(b). The atomic mass (W), Pauling electronegativity (EN-P), and the effect on the cubic to tetragonal (C–T) ferroelectric transition temperature of the doping cations (Tc) were recognized as the three primary contributory features. Essentially, the W is a crucial atomic number factor to be considered when selecting doping elements. An increase in the EN-P of the metal element results in a higher covalent interaction and hybridization. The addition of high electronegativity elements, e.g., Bi3+, into KNN-based materials would increase the local covalency, leading to a high polarization region or local octahedral titling, which can be important for d33 enhancement.1 Besides, the effect of dopants on Curie temperature acts as a key indicator when constructing a polymorphic phase boundary (PPB) for achieving high piezoelectric performance of KNN-based materials.43
Fig. 2(c) displays an informative SHAP overview of the effects of features on the direction of d33 prediction. For each feature, every sample in the dataset is distributed horizontally along the x-axis according to their SHAP values. The color bar corresponds to the original values of the features for each sample. Examining the color distribution horizontally of all the samples in each feature row provides insights into the directional influence of the features on the model's predictions. For instance, higher W values have positive SHAP values as the points extending towards the right are increasingly red, indicating that increasing the A/B-site ratio can lead to higher predicted d33. This may explain why adding Bi3+ can enhance d33 from the statistical perspective.44 The TO–T and TR–O represent the influence of dopants on the tetragonal to orthorhombic (O–T) and rhombohedral to orthorhombic (R–O) phase transition temperatures, respectively. The Tc and TO–T exhibit negative values, but TR–O has positive values as the dopants generally decrease C–T, O–T and increase the R–O phase transition temperatures.45 Lower Tc values lead to a more positive impact on d33 prediction, reflecting the inverse relationship between Tc and d33. Increasing TR–O and decreasing TO–T to construct PPB is an effective way to improve d33.23,46 The SHAP values of TR–O and TO–T indicate that limited additives capable of shifting R–O and O–T phase transition temperature points lead to the d33 improvement, while an excess of these additives can negatively impact d33. The SHAP analyses show agreement with the reported phase and d33 evolution tendency.47,48 Overall, the demonstrated interpretable ML not only corroborates established knowledge but hopefully provides unexploited insights into the materials of interest.
3.2 Machine learning model configuration
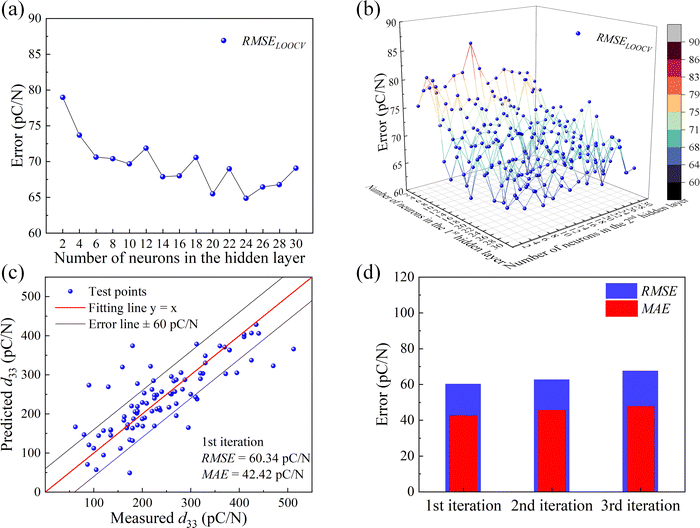
This study used the exhaustive grid search method to calculate the average of cross-validated RMSE on the left-out test points. It is suitable for this small-sized dataset problem, providing highly accurate and consistent results of performance assessment as every sample has been the test point. Fig. 3(a) shows the evolution of RMSELOOCV as the number of neurons in the one-hidden-layer architecture models increases. The global performance tended to improve with increased neurons. However, some fluctuations were captured. The error can increase in the overfitted models due to increased neurons in the hidden layer, eventually reflected in the RMSELOOCV. Adding one more hidden layer can stabilize the feedback in the nonlinear system and lead to better generalization performance.49,50Fig. 3(b) shows the evolution of RMSELOOCV with increasing neurons in the two-hidden-layer architecture models. The optimal performance was achieved by the model with 22 neurons in the first hidden layer and 30 neurons in the second hidden layer. The RMSE and mean absolute error (MAE) were further reduced to 60.34 pC N−1 and 42.42 pC N−1, respectively. The global performance of this model architecture for the first experimental iteration is shown in Fig. 3(c). Approximately 85% of the test points were constrained in the error lines ± 60 pC N−1, indicating a moderate predictive capability of the selected model architecture. The global performance of the model with the same architecture for the second and third experimental iterations is shown in Fig. S2, ESI.†
Fig. 3(d) shows the evolution of global performance with experimental iterations. The predictive errors remain stable after three iterations. Despite the efforts that have been made to improve and maintain model performance, the common challenges in constructing ML models for data-driven materials studies, including the noise in samples, the small sample size, the imperfect features, etc.,6,36 can induce uncertainty and prevent the model from achieving reduced errors. Thus, it is necessary to carefully evaluate the predictive uncertainty for the subsequent deployment of the ML model in the search space.
3.3 Uncertainty-guided experimental design
To obtain uncertainty-informed predictions, we applied the ANN with MCDropout to the entire search space. Fig. 4(a)–(c) show the predictive distributions of the candidates that maximized ET and EI throughout three experimental iterations. Eqn (4) indicates that the ET function is a pure exploitation strategy without considering assessed uncertainty. As seen from the red columns and approximated bell curve, the ET function selects the composition with the highest μ of predictions, illustrated as a narrow distribution centered at a high predicted d33 value. On the contrary, the EI function balances the trade-off between exploitation and exploration. As indicated by eqn (5), the first component of EI is dominated by predicted μ, which stands for exploitation. The second component of EI is dominated by predicted σ, which stands for exploration. The distribution of the composition selected by ET exhibits a broader form, indicating more significant uncertainty. The distribution shapes reflect the exploitative tendency of ET and the explorative tendency of EI.A normal distribution possesses consistent properties, such as its symmetry around μ and asymptote determined by σ. These properties provide a consistent, rigorous and accurate uncertainty estimation based on the predictive distribution, which is ideal for the use of acquisition functions. We used the Q–Q plot to graphically check whether the predictions conformed to a normal distribution. As shown in Fig. 4(d)–(f), the majority of points cluster around the 45-degree reference line, indicating that the predictions calculated by MCDropout show good normality. In summary, the MCDropout provides comprehensive and well-formed uncertainty estimates for compositions in the materials search space.
3.4 MCDropout versus bootstrapping
This study employed MCDropout as a substitute for the commonly used bootstrap method for UQ. Fig. 5 compares the computational time of individual predictions across the entire design space using MCDropout and bootstrap methods. The predictions were executed 500 times. Compared to the average time of 9.98 seconds using the bootstrap method, the average time to make predictions on the design space is 6.71 seconds using MCDropout under the same computation environment. This result reveals that the used MCDropout outperformed the bootstrap method in computational efficiency.To explain the computational advantage of MCDropout over bootstrapping, Fig. 6(a) and (b) demonstrate the schematic workflow of these two methods. The computational time to obtain N predictions using bootstrapping can be represented as N × (tt_b + ti_b), where tt and ti represent training and inference time, respectively. By contrast, it costs tt_m + N × ti_m using the MCDropout method because it does not require resampling data or retraining models. The tt_m becomes insignificant when N is sufficiently large. Besides, as indicated by the red points in Fig. 5, the computational time using the bootstrap method tends to increase with an increase in inference times. The efficiency benefit of MCDropout can be more obvious when the iteration and model complexity increase. The computational results reveal that the MCDropout is a straightforward and time-saving alternative to the commonly used bootstrap method for UQ.
3.5 Experimental validation
The preparation of all ceramic specimens was undertaken at the optimized sintering temperature in order to achieve the respective optimal intrinsic d33.51Table 1 shows their compositions and measured d33. The compositions identified by the pure exploitation ET function exhibit a higher d33 than those identified by the EI function that balances the trade-off between exploration and exploitation. A similar result was reported in the search for high d33 values of BT-based piezoceramics.8 One possible explanation is that the observed points in this study are extremely sparse compared to the unobserved points of the design space. The EI function is inclined to make more risky decisions than the ET function as it extra considers the predictions with larger deviations. As a result, the risk did not result in higher d33 for the initial three iterations. However, from the global optimization perspective, the utilization of EI can mitigate the risk of converging on local optima.52 Incorporating EI samples into the database for the subsequent iterations updates the information on the areas with high uncertainty in the design space.| # | Iteration | Strategy | Composition | Measured d33 (pC N−1) |
|---|---|---|---|---|
| 1 | 1st | ET | (K0.49Na0.51Nb0.96Sb0.04O3)0.96(Bi0.5Na0.5ZrO3)0.02(Bi0.5K0.5ZrO3)0.02 | 330 |
| 2 | 1st | EI | (K0.5Na0.5Nb0.96Sb0.04O3)0.94(BaZrO3)0.02(Bi0.5K0.5ZrO3)0.04 | 150 |
| 3 | 2nd | ET | (K0.45Na0.55Nb0.97Sb0.03O3)0.96(Bi0.5K0.5ZrO3)0.04 | 348 |
| 4 | 2nd | EI | (K0.4Na0.6Nb0.98Sb0.02O3)0.96(Bi0.5Na0.5ZrO3)0.03(BaZrO3)0.01 | 260 |
| 5 | 3rd | ET | (K0.47Na0.53Nb0.96Sb0.04O3)0.96(Bi0.5Na0.5ZrO3)0.01(Bi0.5K0.5ZrO3)0.03 | 335 |
| 6 | 3rd | EI | (K0.45Na0.55Nb0.98Sb0.02O3)0.94(Bi0.5Na0.5ZrO3)0.05(BaZrO3)0.01 | 222 |
Fig. 7 shows the surface morphologies of selected samples. All samples presented relatively dense microstructures and heterogeneous grains. Although alterations in grain size that have occurred due to compositional variation in the ceramics, the SEM results suggest that the ceramics selected by ET and EI functions exhibit no significant differences in microstructure, hence excluding the influence of processing on the different ceramics.
Fig. 8(a)–(c) show the polarization hysteresis loops (P–E), bipolar, and unipolar strain curves (Sb–E and Su–E) of the samples under the external electric field, respectively. All samples have well-defined P–E loops except for composition #5, which appears to have a relatively high leakage current. It is shown that the ET-selected compositions have considerably high Pr exceeding 26 μC cm−2, indicating strong ferroelectricity. The observed enhanced piezoelectric properties in these ceramics are related to their high Pr. In addition, as shown in Fig. 8(b), the multiple ions doping gives rise to defect dipoles in KNN-based ceramics, thereby inducing an asymmetry in bipolar S–E loops.53,54 All samples show slim Su–E loops and the maximum Su was obtained for the ET selected composition #3. It reaches a large electric field – induced strain over 0.18% at 30 kV cm−1, corresponding to large high-field piezoelectric strain coefficients of d33* over 600 pm V−1. This composition shows the maximum d33 of 348 pC N−1, surpassing most compositions in the database. The experimental results confirmed the accelerated search efficiency of the methods utilized for materials design and discovery.
 | ||
| Fig. 8 Ferroelectric test of the newly synthesized ceramic samples. (a) Polarization hysteresis loops. (b) Bipolar strain loops. (c) Unipolar strain loops. | ||
4. Conclusion
This study presents an active learning framework incorporating SHAP feature engineering, MCDropout UQ, and Bayesian-based global optimization to accelerate the design and discovery of high-performance KNN compositions. The crucial features for the d33 prediction were statistically identified and found to show good consistency with the knowledge of d33 enhancement in the KNN-based ceramics based on experimental observations. Our results suggest that interpretable feature engineering can be utilized as a promising tool for deepening and enlightening the complex physics behind the properties of materials. We investigated and demonstrated how to leverage quantified uncertainty to guide experimental observation. The potential and effectiveness of MCDropout for UQ in materials search were illustrated from computational and experimental aspects. The comparative study between the two UQ methods indicates that MCDropout is a compelling alternative to the bootstrap method, enabling a 33% reduction in computational cost. Finally, the experimentally synthesized candidates selected by the ET strategy reached d33 values exceeding 300 pC N−1, demonstrating the efficient and stable performance of the utilized methods. This study is expected to provide insight into the ML-driven investigation of piezoelectric materials and other various materials.Author contributions
Heng Hu: writing – original draft, investigation, formal analysis, data curation. Bin Wang: methodology, investigation. Didi Zhang: investigation, data curation. Tao Tan: writing – review & editing, funding acquisition. Kang Yan: writing – review & editing, supervision, project administration, funding acquisition, formal analysis, conceptualization. Dawei Wu: writing – review & editing, supervision, project administration, funding acquisition.Data availability
The data that support the findings of this study are available within the article and its additional ESI.†Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this manuscript.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 12227808 and 12227802), the National Key Research and Development Program of China (Grant No. 2024YFB4205600), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20221483) and the Macao Polytechnic University Grant (RP/FCA-15/2022).References
- Y. Zhang and J.-F. Li, J. Mater. Chem. C, 2019, 7, 4284–4303 RSC
.
- M. O. Buzzy, D. Montes de Oca Zapiain, A. P. Generale, S. R. Kalidindi and H. Lim, Acta Mater., 2025, 284, 120537 CrossRef CAS
.
- A. K. Srinithi, A. Bolyachkin, X. Tang, H. Sepehri-Amin, S. Dieb, A. T. Saito, T. Ohkubo and K. Hono, Scr. Mater., 2025, 258, 116486 CrossRef CAS
.
- M. Zhang, C. Luo, G. Zhang, H. Xu and G. Li, J. Alloys Compd., 2024, 1006, 176354 CrossRef CAS
.
- M. Wang and J. Jiang, Adv. Funct. Mater., 2024, 34, 2314683 CrossRef CAS
.
- R. Yuan, D. Xue, Y. Xu, D. Xue and J. Li, J. Alloys Compd., 2022, 908, 164468 CrossRef CAS
.
- R. Yuan, Z. Liu, P. V. Balachandran, D. Xue, Y. Zhou, X. Ding, J. Sun, D. Xue and T. Lookman, Adv. Mater., 2018, 30, 1702884 CrossRef PubMed
.
- R. Yuan, D. Xue, D. Xue, Y. Zhou, X. Ding, J. Sun and T. Lookman, IEEE Trans. Ultrason., Ferroelectr., Freq. Control, 2019, 66, 394–401 Search PubMed
.
- W. Gu, B. Yang, D. Li, X. Shang, Z. Zhou and J. Guo, J. Adv. Ceram., 2023, 12(7), 1389–1405 CrossRef CAS
.
- Y. Sun, B. Hu, Y. Zhang, X. Song, J. Feng, Y. Xu, H. Tao and D. Ergu, J. Alloys Compd., 2024, 1003, 175598 CrossRef CAS
.
- L. Scorzato, Minds Mach., 2024, 34, 27 CrossRef
.
- E. Barbierato and A. Gatti, Electronics, 2024, 13, 416 CrossRef
.
- X. Zhong, B. Gallagher, S. Liu, B. Kailkhura, A. Hiszpanski and T. Y.-J. Han, npj Comput. Mater., 2022, 8, 1–19 CrossRef
.
- J. Dean, M. Scheffler, T. A. R. Purcell, S. V. Barabash, R. Bhowmik and T. Bazhirov, J. Mater. Res., 2023, 38, 4477–4496 CrossRef CAS
.
- F. Oviedo, J. L. Ferres, T. Buonassisi and K. T. Butler, Acc. Mater. Res., 2022, 3(6), 597–607 CrossRef CAS
.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal, S. J. L. Billinge, E. Holm, S. P. Ong and C. Wolverton, npj Comput. Mater., 2022, 8, 59 CrossRef
.
- L. Alzubaidi, J. Bai, A. Al-Sabaawi, J. Santamaría, A. S. Albahri, B. S. N. Al-dabbagh, M. A. Fadhel, M. Manoufali, J. Zhang, A. H. Al-Timemy, Y. Duan, A. Abdullah, L. Farhan, Y. Lu, A. Gupta, F. Albu, A. Abbosh and Y. Gu, J. Big Data, 2023, 10, 46 CrossRef
.
- H. Wang, Q. Liang, J. T. Hancock and T. M. Khoshgoftaar, J. Big Data, 2024, 11, 44 CrossRef
.
- Y. Gal and Z. Ghahramani, Proceedings of The 33rd International Conference on Machine Learning, PMLR, 2016, vol. 48, pp. 1050–1059.
- E. Brochu, V. M. Cora and N. de Freitas, arXiv, 2010, preprint, arXiv:1012.2599 DOI:10.48550/arXiv.1012.2599.
- C. Zhou, J. Zhang, W. Yao, X. Wang, D. Liu and X. Sun, J. Appl. Phys., 2018, 124, 164101 CrossRef
.
- B. Zhang, J. Wu, X. Cheng, X. Wang, D. Xiao, J. Zhu, X. Wang and X. Lou, ACS Appl. Mater. Interfaces, 2013, 5, 7718–7725 CrossRef CAS PubMed
.
- L. Tan, Q. Sun and Y. Wang, J. Alloys Compd., 2020, 836, 155419 CrossRef CAS
.
- D. Pan, Y. Guo, X. Fu, R. Guo, H. Duan, Y. Chen, H. Li and H. Liu, Solid State Commun., 2017, 259, 29–33 CrossRef CAS
.
- T. Mei, T. Chen, Y. Liu, J. Zhang, T. Zhang, G. Wang and J. Zhou, J. Mater. Sci.: Mater. Electron., 2017, 28, 4879–4884 CrossRef CAS
.
- T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, npj Comput. Mater., 2019, 5, 21 CrossRef
.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed
.
- J. M. Dolezal, A. Srisuwananukorn, D. Karpeyev, S. Ramesh, S. Kochanny, B. Cody, A. S. Mansfield, S. Rakshit, R. Bansal, M. C. Bois, A. O. Bungum, J. J. Schulte, E. E. Vokes, M. C. Garassino, A. N. Husain and A. T. Pearson, Nat. Commun., 2022, 13, 6572 CrossRef CAS PubMed
.
- J. Padarian, B. Minasny and A. B. McBratney, Geoderma, 2022, 425, 116063 CrossRef
.
- S. H. Yelleni, D. Kumari, P. K. Srijith and C. K. Mohan, Pattern Recognit., 2024, 146, 110003 CrossRef
.
- X. Wang, Y. Jin, S. Schmitt and M. Olhofer, ACM Comput. Surv., 2023, 55, 287:1–287:36 Search PubMed
.
- A. Ishii, S. Kikuchi, A. Yamanaka and A. Yamamoto, J. Alloys Compd., 2023, 966, 171613 CrossRef CAS
.
- R. Yuan, Y. Tian, D. Xue, D. Xue, Y. Zhou, X. Ding, J. Sun and T. Lookman, Adv. Sci., 2019, 6, 1901395 CrossRef CAS PubMed
.
- J. Li, Y. Zhang, X. Cao, Q. Zeng, Y. Zhuang, X. Qian and H. Chen, Commun. Mater., 2020, 1, 1–10 CrossRef
.
- C. Kim, A. Chandrasekaran, A. Jha and R. Ramprasad, MRS Commun., 2019, 9, 860–866 CrossRef CAS
.
- B. Ma, X. Wu, C. Zhao, C. Lin, M. Gao, B. Sa and Z. Sun, npj Comput. Mater., 2023, 9, 1–11 CrossRef
.
- J. He, J. Li, C. Liu, C. Wang, Y. Zhang, C. Wen, D. Xue, J. Cao, Y. Su, L. Qiao and Y. Bai, Acta Mater., 2021, 209, 116815 CrossRef CAS
.
- Q. Tao, P. Xu, M. Li and W. Lu, npj Comput. Mater., 2021, 7, 23 CrossRef
.
- H. Akoglu, Turk. J. Emerg. Med., 2018, 18, 91–93 CrossRef PubMed
.
- S. F. Ahmed, Md. S. B. Alam, M. Hassan, M. R. Rozbu, T. Ishtiak, N. Rafa, M. Mofijur, A. B. M. Shawkat Ali and A. H. Gandomi, Artif. Intell. Rev., 2023, 56, 13521–13617 CrossRef
.
- B. Lei, T. Q. Kirk, A. Bhattacharya, D. Pati, X. Qian, R. Arroyave and B. K. Mallick, npj Comput. Mater., 2021, 7, 194 CrossRef
.
- A. I. J. Forrester and A. J. Keane, Prog. Aerosp. Sci., 2009, 45, 50–79 CrossRef
.
- H. Tao, H. Wu, Y. Liu, Y. Zhang, J. Wu, F. Li, X. Lyu, C. Zhao, D. Xiao, J. Zhu and S. J. Pennycook, J. Am. Chem. Soc., 2019, 141, 13987–13994 CrossRef CAS PubMed
.
- W. Yang, Y. Wang, P. Li, S. Wu, F. Wang, B. Shen and J. Zhai, J. Mater. Chem. C, 2020, 8, 6149–6158 RSC
.
-
J.-F. Li, Lead-free piezoelectric materials, Wiley-VCH, Weinheim, 2021 Search PubMed
.
- X. Lv, J. Zhu, D. Xiao, X. Zhang and J. Wu, Chem. Soc. Rev., 2020, 49, 671–707 RSC
.
- T. Zheng, J. Wu, D. Xiao, J. Zhu, X. Wang and X. Lou, ACS Appl. Mater. Interfaces, 2015, 7, 20332–20341 CrossRef CAS PubMed
.
- L. Tan, Q. Sun and Y. Wang, J. Alloys Compd., 2020, 836, 155363 CrossRef CAS
.
- E. D. Sontag, IEEE Trans. Neural Networks, 1992, 3, 981–990 CrossRef CAS PubMed
.
-
A. J. Thomas, M. Petridis, S. D. Walters, S. M. Gheytassi and R. E. Morgan, in Engineering Applications of Neural Networks, ed. G. Boracchi, L. Iliadis, C. Jayne and A. Likas, Springer International Publishing, Cham, 2017, pp. 279–290 Search PubMed
.
- H. Hu, M. Huang, B. Wang, D. Zhang, T. Tan, K. Yan and D. Wu, Ceram. Int., 2024, 50, 54536–54546 CrossRef CAS
.
- D. Zhan and H. Xing, J. Global Optim., 2020, 78, 507–544 CrossRef
.
- S. Tian, J. Xin, Y. Cheng, L. Lai, B. Li and Y. Dai, Acta Mater., 2024, 280, 120344 CrossRef CAS
.
- G. Huangfu, K. Zeng, B. Wang, J. Wang, Z. Fu, F. Xu, S. Zhang, H. Luo, D. Viehland and Y. Guo, Science, 2022, 378, 1125–1130 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00865d |
| This journal is © The Royal Society of Chemistry 2025 |