 Open Access Article
Open Access ArticlePushing the boundary of the stability and band gap Pareto front by going towards high-entropy perovskites†
Zhendian
Zhang
a,
Victor
Fung
 *b and
Guoxiang
Hu
*b and
Guoxiang
Hu
 *ac
*ac
aSchool of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332, USA. E-mail: emma.hu@mse.gatech.edu
bSchool of Computer Science and Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332, USA. E-mail: victorfung@gatech.edu
cSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332, USA
First published on 4th April 2025
Abstract
Lead-free Cs2BX6 (B = Zr4+, Sn4+, Te4+, Hf4+, Re4+, Os4+, Ir4+, and Pt4+ and X = Cl−, Br−, and I−) vacancy-ordered double perovskites have gained significant attention due to their high performance in solar cell devices. Besides mitigating toxicity concerns associated with the use of lead, the presence of a formally tetravalent B-site in Cs2BX6 has been demonstrated to improve the stability against air and moisture. Recently, experimental studies have shown that high-entropy forms of vacancy-ordered double perovskites can be synthesized and stabilized at room temperature, which opens new opportunities for designing better solar cell absorbers. In this work, we employed high throughput density functional theory (DFT) calculations using the HSE06 hybrid functional to study 546 medium-to-high-entropy vacancy-ordered double perovskites. Our results show that Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6 perovskites can break the existing linear scaling relationships between the bandgap and formation energy observed in the pure Cs2BX6 and Cs2B{XX′}6 perovskites, which enables materials that simultaneously exhibit an optimal band gap of ∼1.3 eV for single-junction solar cells along with a low formation energy. Electronic structure analysis reveals that this can be attributed to the weak coupling between the BX6 octahedra in Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6. Based on these findings, we identified the analytical equations that can be used to efficiently predict the band gap and formation energy of high-entropy perovskites from their constituent pure perovskites. Our study offers simple and practical guidelines for the design and synthesis of novel high-entropy perovskites with improved photovoltaic performance.
Introduction
At present, lead halide perovskites are the best performing solution-processed photovoltaic materials with a power conversion efficiency record of 26.7% in single-junction perovskite solar cells and 34.6% in perovskite/Si 2T tandem solar cells in 2024.1–5 However, the ultimate commercialization of these materials still faces serious practical challenges due to their toxicity from lead and their instability against moisture, air, and temperature.6–10 Alternative compositional and structural derivatives of the perovskite family have consequently been explored to assess their potential in photovoltaic applications.11–16 Among these novel perovskites developed over the past decade, Cs2BX6 (B = Zr4+, Sn4+, Te4+, Hf4+, Re4+, Os4+, Ir4+, and Pt4+ and X = Cl−, Br−, and I−) vacancy-ordered double perovskites have attracted particular attention following the recent demonstrations of their high performance in solar cell devices.17–21 Besides mitigating toxicity concerns associated with the use of lead, the presence of a formally tetravalent B-site in Cs2BX6 can also improve air and moisture stability relative to the divalent B-site in conventional CsBX3 perovskites.22–24High-entropy halide perovskites are an emerging class of materials that combine the intriguing properties of halide perovskites with the concept of high entropy.25,26 Common advantages of high-entropy materials, which contain five or more different elements distributed in a single crystal structure, include entropic stabilization (at high temperature) and a tunable continuum of materials properties.25,27–29 This innovative design strategy has been widely explored in metals and oxides,30–33 but its application to halide perovskites is a relatively new concept and holds great untapped potential. A recent experimental study has demonstrated a viable route to synthesize and stabilize high-entropy vacancy-ordered double perovskites at room temperature such as the five-element Cs2{SnTeReIrPt}1Cl6 and six-element Cs2{SnTeReOsIrPt}1Cl6 compositions.25 This opens up new opportunities for designing novel materials based on high-entropy vacancy-ordered double perovskites for photovoltaic devices beyond the state-of-the-art lead halide perovskites.
In this work, we performed high throughput density functional theory (DFT) calculations using the hybrid functional HSE06 to study over five hundred medium-to-high-entropy vacancy-ordered double perovskites. We calculated the band gap and formation energy of these perovskites and found that high-entropy perovskites exhibit emerging properties that are not present in their pure counterparts. We further analyzed their density of states (DOS) and revealed that this can be attributed to the unique electronic structure of vacancy-ordered double perovskites with weakly coupled octahedra. Finally, we identified the analytical equations that can be used to efficiently predict the band gap and formation energy of high-entropy perovskites using the values of their constituent pure perovskites. Our work demonstrated new opportunities for applications of high-entropy halide perovskites in solar cell devices.
Results and discussion
Vacancy-ordered double perovskites are a specialized class of perovskite materials in which specific atomic sites within the crystal structure are deliberately left vacant, leading to a unique arrangement of atoms. In conventional Cs2BB′X6 (B = Cu+, Ag+, Au+, K+, In+, and Ti+ and B′ = Bi3+, Sb3+, and Tl3+) double perovskites, two different cations B and B′ occupy alternating positions within the lattice. However, in Cs2BX6 vacancy-ordered double perovskites, as shown in Fig. 1, one of the cation sites is left vacant, creating a pattern of missing atoms within the structure. In this work, we considered 8 elements (Zr, Hf, Re, Os, Ir, Pt, Sn and Te) at the B-site, and 3 elements (Cl, Br, and I) at the X-site. Besides the pure Cs2BX6 perovskites, we also investigated three types of mixed perovskites: (1) Cs2B{XX′}6 with the X-site mixed, (2) Cs2{B1B2B3B4}1X6 with the B-site mixed, and (3) Cs2{B1B2B3B4}1{XX′}6 with both B- and X-sites mixed. For X-site mixing, we examined the combinations of Cl4Br2, Cl2Br4, Br4I2, and Br2I4, considering their atomic radii and structural symmetry.25,34 Previous studies have shown that the large difference in atomic radii between the Cl− and I− anions leads to low ionic miscibility, preventing Cl− from substituting into the I− lattice, particularly for relatively high concentration levels.35–37 This in total yields 546 perovskite structures: (1) 24 pure Cs2BX6 perovskites (8 elements at the B-site × 3 elements at the X-site), (2) 32 Cs2B{XX′}6 perovskites (8 elements at the B-site × 4 combinations at the X-site), (3) 210 Cs2{B1B2B3B4}1X6 perovskites (70 combinations at the B-site × 3 elements at the X-site), and (4) 280 Cs2{B1B2B3B4}1{XX′}6 perovskites (70 combinations at the B-site × 4 combinations at the X-site). | ||
| Fig. 1 The chemical space and atomic structures of the pure and mixed vacancy-ordered double perovskites investigated in this work. | ||
Fig. 2 presents the DFT-calculated formation energy and band gap for the 546 vacancy-ordered double perovskites. The computed values for the lattice constant, band gap, formation enthalpy, entropy, and Gibbs free energy at 298 K are provided in Table S1.† A linear scaling relationship between them can be observed for Cs2BX6 and Cs2B{XX′}6 perovskites: the band gap increases as the magnitude of the formation energy increases. This has been widely reported for vacancy-ordered double perovskites and can be roughly explained by molecular orbital theory.38–40 Typically, perovskites with stronger chemical (covalent) bonds have more negative formation energies (i.e. larger magnitude) along with a wider splitting between the bonding and anti-bonding molecular orbitals (i.e. larger band gap). As a result, perovskites with desirable band gaps (1.1–1.5 eV)41 for light absorption normally exhibit relatively poor stability. As highlighted by a grey box in Fig. 2, only very few Cs2BX6 and Cs2B{XX′}6 perovskites are in this band gap range and their formation energy are relatively high, corresponding to low stability. Table 1 lists the chemical composition, band gap, and formation energy of these perovskites. Our computational predictions of the band gaps agree very well with previous computational and experimental studies.22,40,42–44 It is also worth noting that all these perovskites are made of expensive metals (i.e., Pt, Os, or Ir). However, very excitingly, we found that the B-site-mixed Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6 medium-to-high-entropy perovskites can break the linear scaling relationship between the formation energy and band gap, allowing for significantly more candidates exhibiting an optimal band gap and high stability for solar absorbers.
 | ||
| Fig. 2 DFT-calculated formation energy and band gap for 546 vacancy-ordered double perovskites including Cs2BX6, Cs2B{XX′}6, Cs2{B1B2B3B4}1X6, and Cs2{B1B2B3B4}1{XX′}6. | ||
| Cs2PtI6 | Cs2PtBr4I2 | Cs2OsCl2Br4 | Cs2OsBr4I2 | Cs2IrCl4Br2 | |
|---|---|---|---|---|---|
| E g (eV) | 1.13 | 1.49 | 1.12 | 1.22 | 1.33 |
| E f (eV) | −7.72 | −9.15 | −9.55 | −7.91 | −10.55 |
Table S2† presents 99 promising vacancy-ordered double perovskites with band gaps ranging from 1.1 to 1.5 eV. It is important to highlight that, as solar-absorbing materials, these perovskites may exhibit dipole-allowed transition gaps (referred to as “allowed gaps”) that are larger than their direct band gaps.45 For example, the direct band gap of Cs2SnI6 was calculated to be 0.7 eV, while its dipole-allowed transition gap was found to be 1.1 eV. Additionally, these materials may exhibit significant exciton binding energies, which can impede charge separation and reduce open-circuit voltages in solar cells.46 Therefore, in addition to the fundamental band gaps (VBM–CBM) shown in Fig. 2, it is crucial to further investigate the optical band gap and exciton binding energy of these promising candidates in future studies. Moreover, while formation energy provides an initial estimate of the stability of predicted perovskites, phonon calculations and finite-temperature molecular dynamics simulations can be further employed for a more comprehensive evaluation of their dynamic and thermodynamic stability.
We then sought to understand the origin of the breaking of the linear scaling relationship between the formation energy and band gap of the B-site-mixed Cs2{B1B2B3B4}1X6 perovskites. As shown in Fig. 3a, we found that the formation energy of Cs2{B1B2B3B4}1X6 can be predicted very well by the average of the formation energy of the constituent pure perovskites using the following equation:
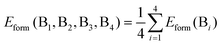 | (1) |
 | (2) |
 | ||
| Fig. 3 The comparison between (a) the predicted formation energy from eqn (1) and the DFT-calculated formation energy and (b) the predicted band gap from eqn (2) and the DFT-calculated band gap. | ||
The dramatically different correlations with the constituent pure perovskites for the formation energy and band gap shown in Fig. 3 explain the breaking of scaling observed in Fig. 2. To gain a better understanding of the correlation of the band gap of Cs2{B1B2B3B4}1X6 with their constituent pure perovskites, we performed a detailed analysis of their electronic structures. We found that for the diamagnetic metal ions (i.e., Hf4+, Pt4+, Sn4+, Te4+, and Zr4+), the projected density of states is very similar in the mixed Cs2{B1B2B3B4}1X6 and pure Cs2BX6 perovskites. This also applies to the paramagnetic metal ion Re4+ with each t2g orbital being singly occupied (Fig. 4a). As for the paramagnetic metal ions Ir4+ and Os4+, we found that the pure perovskites exhibit degenerate t2g orbitals (i.e., dxz, dyz, and dxy orbitals), which agrees with previous reports.47–49 However, as shown in Fig. 4b and c, in the mixed perovskites, the breaking of symmetry leads to splitting of the t2g orbitals. It is noted that while the t2g orbitals are different for the mixed and pure perovskites, the energy range of the projected density of states is not significantly changed.
The highly overlapped energy range of the electronic states in the pure and B-site-mixed perovskites shown in Fig. 4 can be attributed to the relatively weak coupling between the neighboring BX6 octahedra in the vacancy-ordered double perovskites. Consequently, the conduction band minimum (CBM) and valence band maximum (VBM) of the pure perovskites can be used to estimate the band gap of the B-site-mixed perovskites. Fig. 5 shows the alignment of the density of states between the B-site-mixed and the constituent pure perovskites using Cs2{ZrSnTeHf}1Cl6 as an example. As one can see, the band gap of a B-site-mixed perovskite is essentially determined by the highest VBM and the lowest CBM of the constituent pure perovskites, as expressed by the following equation:
 | (3) |
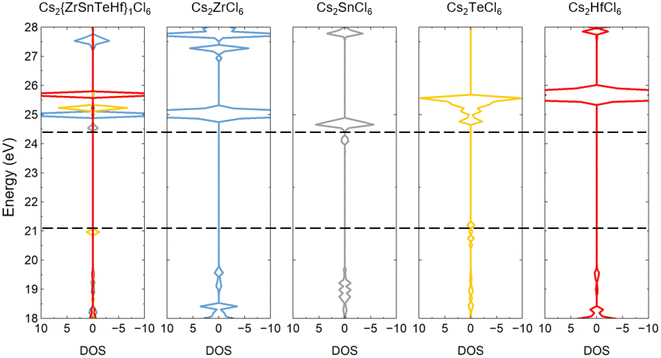 | ||
| Fig. 5 Alignment of the density of states for the B-site-mixed Cs2{ZrSnTeHf}1Cl6 perovskite and its constituent pure perovskites: Cs2ZrCl6, Cs2SnCl6, Cs2TeCl6, and Cs2HfCl6. | ||
We then applied eqn (3) to all B-site-mixed Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6 perovskites, and Fig. 6a shows the comparison between the predicted band gap from eqn (3) and the DFT-calculated band gap. We found that eqn (3) can qualitatively predict the band gap of Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6, especially when there are one or fewer paramagnetic metal ions (e.g., Re4+, Os4+, and Ir4+). The red circles in Fig. 6a correspond to Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6 with multiple paramagnetic metal ions. Excluding these data points, the root-mean-square-error (RMSE) of prediction is reduced from 0.79 eV to 0.67 eV (Fig. 6b). The poor performance of eqn (3) for Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6 with multiple paramagnetic metal ions can be attributed to the complex interactions between the spins of the paramagnetic metal ions, which gives rise to different band edges from the pure perovskites.
One key approximation for eqn (3) is that the positions of projected density of states are identical in the B-site-mixed and pure perovskites. However, realistically, they are not exactly the same, as shown in Fig. 4 and 5. In particular, we found that the VBM of the pure perovskite is ∼0.2 eV higher than that of the B-site-mixed perovskite, while the CBM of the pure perovskite is ∼0.2 eV lower than that of the B-site-mixed perovskite (Fig. 5). Thus, the band gap predicted from eqn (3) using the pure perovskite band edges are on average ∼0.4 eV less than those from DFT calculations. Fig. 6c shows that the RMSE is reduced from 0.67 eV to 0.21 eV, if the VBM and CBM values are obtained from randomly selected B-site-mixed perovskites instead of the pure perovskites. We have further analyzed the standard deviations of the VBM and CBM of the VODPs in various B-site-mixed perovskites and found that they are quite small (less than 0.1 eV). This suggests minimal fluctuations in the band edges of VODPs across various B-site-mixed perovskites and using the average VBM and CBM of the VODPs for eqn (3) will not change the RMSE significantly, as shown in Fig. 6c.
Conclusions
To summarize, we calculated the band gap and formation energy for 546 vacancy-ordered double perovskites and found that the linear scaling relationship observed in Cs2BX6 and Cs2B{XX′}6 perovskites can be broken in medium-to-high-entropy perovskites. As a result, more than 90 Cs2{B1B2B3B4}1X6 and Cs2{B1B2B3B4}1{XX′}6 perovskites were predicted to be promising for solar absorbers with an optimal band gap and high stability. We performed a detailed electronic structure analysis to understand the breaking of the scaling relationship and developed simple analytical equations to predict the band gap of B-site-mixed perovskites using the band gap of their constituent pure perovskites. This will significantly accelerate the design and discovery of novel medium/high-entropy perovskites with desired band gaps for both experimental and computational studies. In addition, the generated data from high throughput DFT calculations using the hybrid functional in this work will be beneficial for the community to further develop machine learning models for materials screening.Computational methods
Spin-polarized DFT calculations were performed as implemented in the Vienna ab initio simulation package (VASP 6.2.1).50,51 The electron exchange–correlation was represented by the Perdew–Burke–Ernzerhof revised functional for solids (PBEsol) of generalized gradient approximation (GGA).52 While the geometry optimizations were performed using the PBEsol functional, the band gap and density of states calculations were performed using the hybrid HSE06 functional.22 The ion–electron interaction was described with the projector augmented wave (PAW) method.53 A cutoff energy of 500 eV was used for the plane-wave basis set. The energies were converged with a 1 × 10−5 eV tolerance and the forces were optimized to within 0.01 eV Å−1. The cubic phase of vacancy-ordered double perovskites was used, with a unit cell consisting of 8 Cs atoms, 4 B-site metals, and 24 halides. A 6 × 6 × 6 Monkhorst–Pack k-point grid was used for the geometry optimizations with the PBEsol functional, while a 3 × 3 × 3 Monkhorst–Pack k-point grid was used for the band gap calculations with the HSE06 hybrid functional. It is important to note that while the HSE06 functional is generally effective in predicting band gaps for many semiconductors, it has been shown to underestimate band gaps, particularly in halide perovskites.54 Table S3† compares our calculated fundamental band gaps (VBM–CBM) from HSE06 with previous computational studies and experimentally measured optical band gaps. Our calculations are in excellent agreement with prior computational work. However, when compared to experimentally measured optical gaps, our results are consistently lower, which can be attributed to the dipole-allowed transition gaps discussed previously. Thus, determining the optical band gap and employing more accurate functionals, such as PBE0 or dielectric-dependent hybrid functionals, to better align with the experimental results are important avenues for future research.The formation energy of the pure perovskite Eform(Cs2BX6) was calculated using the following equation:55
| Eform(Cs2BX6) = Etotal(Cs2BX6) − 2E(Cs) − E(B) − 6E(X) | (4) |
Data availability
All data from this work will be shared, including the data needed to reproduce the results and the raw data from VASP calculations. The data will be shared on the open-source repository Figshare. They will be made available immediately following the publication of the work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This article is based on work supported as part of the Atomic-C2E project by the U.S. Department of Energy, Office of Science under award number DE-SC-0024716. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under contract no. DE-AC02-05CH11231 using NERSC award BES-ERCAP0032102.References
- G. Szabó, N. G. Park, F. De Angelis and P. V. Kamat, Are Perovskite Solar Cells Reaching the Efficiency and Voltage Limits?, ACS Energy Lett., 2023, 3829–3831 CrossRef.
- G. Li, Z. Su, L. Canil, D. Hughes, M. H. Aldamasy, J. Dagar, S. Trofimov, L. Wang, W. Zuo, J. J. Jerónimo-Rendon, M. M. Byranvand, C. Wang, R. Zhu, Z. Zhang, F. Yang, G. Nasti, B. Naydenov, W. C. Tsoi, Z. Li, X. Gao, Z. Wang, Y. Jia, E. Unger, M. Saliba, M. Li and A. Abate, Highly Efficient P-i-n Perovskite Solar Cells That Endure Temperature Variations, Science, 2023, 379, 399–403 CrossRef CAS PubMed.
- M. Li, B. Jiao, Y. Peng, J. Zhou, L. Tan, N. Ren, Y. Ye, Y. Liu, Y. Yang, Y. Chen, L. Ding and C. Yi, High-Efficiency Perovskite Solar Cells with Improved Interfacial Charge Extraction by Bridging Molecules, Adv. Mater., 2024, 36, 2406532 CrossRef CAS PubMed.
- A. S. R. Bati, Y. L. Zhong, P. L. Burn, M. K. Nazeeruddin, P. E. Shaw and M. Batmunkh, Next-Generation Applications for Integrated Perovskite Solar Cells, Commun. Mater., 2023, 4, 2 CrossRef CAS.
- NREL, Best Research-Cell Efficiency Chart. https://www.nrel.gov/pv/cell-efficiency.html (accessed 24 October 2024).
- J. I. Kwak, T. Y. Lee and Y. J. An, Assessing the Potential Toxicity of Hazardous Material Released from Pb-Based Perovskite Solar Cells to Crop Plants, J. Cleaner. Prod., 2023, 423, 138856 CrossRef CAS.
- Z. Yue, H. Guo and Y. Cheng, Toxicity of Perovskite Solar Cells, Energies, 2023, 4007 CrossRef CAS.
- J. P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Promises and Challenges of Perovskite Solar Cells, Science, 2017, 739–744 CrossRef CAS PubMed.
- Y. Rong, Y. Hu, A. Mei, H. Tan, M. I. Saidaminov, S. I. Seok, M. D. McGehee, E. H. Sargent and H. Han, Challenges for Commercializing Perovskite Solar Cells, Science, 2018, 361, eaat8235 CrossRef PubMed.
- D. Wang, M. Wright, N. K. Elumalai and A. Uddin, Stability of Perovskite Solar Cells, Sol. Energy Mater. Sol. Cells, 2016, 255–275 CrossRef CAS.
- G. Y. Kim, K. Kim, H. J. Kim, H. S. Jung, I. Jeon and J. W. Lee, Sustainable and Environmentally Viable Perovskite Solar Cells, EcoMat, 2023, e12319 CrossRef CAS.
- W. Zhang, H. Liu, F. Yan, B. Dong and H. L. Wang, Recent Progress of Low-Toxicity Poor-Lead All-Inorganic Perovskite Solar Cells, Small Methods, 2024, 2300421 CrossRef CAS PubMed.
- C. Wu, Q. Zhang, Y. Liu, W. Luo, X. Guo, Z. Huang, H. Ting, W. Sun, X. Zhong, S. Wei, S. Wang, Z. Chen and L. Xiao, The Dawn of Lead-Free Perovskite Solar Cell: Highly Stable Double Perovskite Cs2AgBiBr6 Film, Adv. Sci., 2018, 5, 1700759 CrossRef PubMed.
- Z. Zhu, X. Jiang, D. Yu, N. Yu, Z. Ning and Q. Mi, Smooth and Compact FASnI3 Films for Lead-Free Perovskite Solar Cells with over 14% Efficiency, ACS Energy Lett., 2022, 7, 2079–2083 CrossRef CAS.
- T. Dureja, A. Garg, S. Bhalla, D. Bhutani and A. Khanna, Double Lead-Free Perovskite Solar Cell for 19.9% Conversion Efficiency: A SCAPS-1D Based Simulation Study, Mater. Today: Proc., 2022, 71, 239–242 CAS.
- J. Yang, P. Manganaris and A. Mannodi-Kanakkithodi, A High-Throughput Computational Dataset of Halide Perovskite Alloys, Digit Discovery, 2023, 2, 856–870 RSC.
- E. E. Morgan, G. T. Kent, A. Zohar, A. O'Dea, G. Wu, A. K. Cheetham and R. Seshadri, Hybrid and Inorganic Vacancy-Ordered Double Perovskites A2WCl6, Chem. Mater., 2023, 35, 7032–7038 CrossRef CAS.
- M. G. Ju, M. Chen, Y. Zhou, H. F. Garces, J. Dai, L. Ma, N. P. Padture and X. C. Zeng, Earth-Abundant Nontoxic Titanium(IV)-Based Vacancy-Ordered Double Perovskite Halides with Tunable 1.0 to 1.8 EV Bandgaps for Photovoltaic Applications, ACS Energy Lett., 2018, 3, 297–304 CrossRef CAS.
- K. Zheng, B. Chen, L. Xie, X. Li, B. Lu, M. Wang, Y. Wu, T. Jiang, F. Zhang, X. Li and Y. Wang, Vacancy-Ordered Double Perovskite Rb2ZrCl6−xBrx: Facile Synthesis and Insight into Efficient Intrinsic Self-Trapped Emission, Adv. Opt. Mater., 2022, 10, 2101661 CrossRef CAS.
- I. Vázquez-Fernández, S. Mariotti, O. S. Hutter, M. Birkett, T. D. Veal, T. D. C. Hobson, L. J. Phillips, L. Danos, P. K. Nayak, H. J. Snaith, W. Xie, M. P. Sherburne, M. Asta and K. Durose, Vacancy-Ordered Double Perovskite Cs2TeI6Thin Films for Optoelectronics, Chem. Mater., 2020, 32, 6676–6684 CrossRef PubMed.
- X. Ye, A. Liu, L. Gao, C. Zhang, L. Yan, S. Wen and T. Ma, Computational Screening of Cs Based Vacancy-Ordered Double Perovskites for Solar Cell and Photocatalysis Applications, EcoMat, 2023, 5, e12295 CrossRef CAS.
- B. Cucco, G. Bouder, L. Pedesseau, C. Katan, J. Even, M. Kepenekian and G. Volonakis, Electronic Structure and Stability of Cs2TiX6and Cs2ZrX6(X = Br, I) Vacancy Ordered Double Perovskites, Appl. Phys. Lett., 2021, 119, 181903 CrossRef CAS.
- A. Liu, H. Zhu, Y. Reo, M. G. Kim, H. Y. Chu, J. H. Lim, H. J. Kim, W. Ning, S. Bai and Y. Y. Noh, Modulation of Vacancy-Ordered Double Perovskite Cs2SnI6 for Air-Stable Thin-Film Transistors, Cell Rep. Phys. Sci., 2022, 3, 100812 CrossRef CAS.
- M. Faizan, X. Wang, S. A. M. Abdelmohsen, K. C. Bhamu, S. Sappati, A. Laref, N. Muhammad, M. Mushtaq, A. M. M. Abdelbacki and R. Khenata, Understanding the Electronic Structure and Optical Properties of Vacancy-Ordered Double Perovskite A2BX6for Optoelectronic Applications, Energy Fuels, 2022, 36, 7065–7074 CrossRef CAS.
- M. C. Folgueras, Y. Jiang, J. Jin and P. Yang, High-Entropy Halide Perovskite Single Crystals Stabilized by Mild Chemistry, Nature, 2023, 621, 282–288 CrossRef CAS PubMed.
- X. Wang, J. Yang, X. Wang, M. Faizan, H. Zou, K. Zhou, B. Xing, Y. Fu and L. Zhang, Entropy-Driven Stabilization of Multielement Halide Double-Perovskite Alloys, J. Phys. Chem. Lett., 2022, 13, 5017–5024 CrossRef CAS PubMed.
- S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin, T. Harrington, K. Vecchio and J. Luo, A New Class of High-Entropy Perovskite Oxides, Scr. Mater., 2018, 142, 116–120 CrossRef CAS.
- T. Wang, H. Chen, Z. Yang, J. Liang and S. Dai, High-Entropy Perovskite Fluorides: A New Platform for Oxygen Evolution Catalysis, J. Am. Chem. Soc., 2020, 142, 4550–4554 CrossRef CAS PubMed.
- A. M. Stratulat, C. Tantardini, M. Azizi, T. Altalhi, S. V. Levchenko and B. I. Yakobson, Electronic Properties of Zn2 V(1-x)NbxN3 Alloys to Model Novel Materials for Light-Emitting Diodes, J. Phys. Chem. Lett., 2023, 14, 9118–9125 CrossRef CAS PubMed.
- Y. Ning, Y. Pu, C. Wu, Z. Chen, X. Zhang, L. Zhang and B. Wang, Design Strategy of High-Entropy Perovskite Energy-Storage Ceramics: A Review, J. Eur. Ceram. Soc., 2024, 4831–4843 CrossRef CAS.
- T. X. Nguyen, Y. C. Liao, C. C. Lin, Y. H. Su and J. M. Ting, Advanced High Entropy Perovskite Oxide Electrocatalyst for Oxygen Evolution Reaction, Adv. Funct. Mater., 2021, 31, 2101632 CrossRef CAS.
- A. Amiri and R. Shahbazian-Yassar, Recent Progress of High-Entropy Materials for Energy Storage and Conversion, J. Mater. Chem. A, 2021, 782–823 RSC.
- D. Wu, K. Kusada, T. Yamamoto, T. Toriyama, S. Matsumura, S. Kawaguchi, Y. Kubota and H. Kitagawa, Platinum-Group-Metal High-Entropy-Alloy Nanoparticles, J. Am. Chem. Soc., 2020, 142, 13833–13838 CrossRef CAS PubMed.
- M. M. S. Karim, A. M. Ganose, L. Pieters, W. W. Winnie Leung, J. Wade, L. Zhang, D. O. Scanlon and R. G. Palgrave, Anion Distribution, Structural Distortion, and Symmetry-Driven Optical Band Gap Bowing in Mixed Halide Cs2SnX6 Vacancy Ordered Double Perovskites, Chem. Mater., 2019, 31, 9430–9444 CrossRef CAS PubMed.
- S. Colella, E. Mosconi, P. Fedeli, A. Listorti, F. Gazza, F. Orlandi, P. Ferro, T. Besagni, A. Rizzo, G. Calestani, G. Gigli, F. De Angelis and R. Mosca, MAPbI3-XClx Mixed Halide Perovskite for Hybrid Solar Cells: The Role of Chloride as Dopant on the Transport and Structural Properties, Chem. Mater., 2013, 25, 4613–4618 CrossRef CAS.
- E. L. Unger, A. R. Bowring, C. J. Tassone, V. L. Pool, A. Gold-Parker, R. Cheacharoen, K. H. Stone, E. T. Hoke, M. F. Toney and M. D. McGehee, Chloride in Lead Chloride-Derived Organo-Metal Halides for Perovskite-Absorber Solar Cells, Chem. Mater., 2014, 26, 7158–7165 CrossRef CAS.
- J. Chae, Q. Dong, J. Huang and A. Centrone, Chloride Incorporation Process in CH3NH3PbI3-XClx Perovskites via Nanoscale Bandgap Maps, Nano Lett., 2015, 15, 8114–8121 CrossRef CAS PubMed.
- H. J. Xiao, H. Li, L. Chang, H. X. Zhang and H. C. Xuan, Theoretical Prediction for the Band Gap of Semiconductor Nanoparticles as Function of Bond Number, Mater. Chem. Phys., 2016, 184, 285–290 CrossRef CAS.
- A. M. Smith and S. Nie, Semiconductor Nanocrystals: Structure, Properties, and Band Gap Engineering, Acc. Chem. Res., 2010, 43, 190–200 CrossRef CAS PubMed.
- A. E. Maughan, A. M. Ganose, D. O. Scanlon and J. R. Neilson, Perspectives and Design Principles of Vacancy-Ordered Double Perovskite Halide Semiconductors, Chem. Mater., 2019, 1184–1195 CrossRef CAS.
- T. Kirchartz and U. Rau, What Makes a Good Solar Cell?, Adv. Energy Mater., 2018, 8, 1703385 CrossRef.
- X. H. Zhao, X. N. Wei, T. Y. Tang, L. K. Gao, Q. Xie, L. M. Lu and Y. L. Tang, First-Principles Study on the Structural, Electronic and Optical Properties of Vacancy-Ordered Double Perovskites Cs2PtI6 and Rb2PtI6, Opt. Mater., 2021, 114, 110952 CrossRef CAS.
- S. Yang, L. Wang, S. Zhao, A. Liu, Y. Zhou, Q. Han, F. Yu, L. Gao, C. Zhang and T. Ma, Novel Lead-Free Material Cs2PtI6with Narrow Bandgap and Ultra-Stability for Its Photovoltaic Application, ACS Appl. Mater. Interfaces, 2020, 12, 44700–44709 CrossRef CAS PubMed.
- A. E. Maughan, A. M. Ganose, M. M. Bordelon, E. M. Miller, D. O. Scanlon and J. R. Neilson, Defect Tolerance to Intolerance in the Vacancy-Ordered Double Perovskite Semiconductors Cs2SnI6 and Cs2TeI6, J. Am. Chem. Soc., 2016, 138, 8453–8464 CrossRef CAS PubMed.
- S. R. Kavanagh, C. N. Savory, S. M. Liga, G. Konstantatos, A. Walsh and D. O. Scanlon, Frenkel Excitons in Vacancy-Ordered Titanium Halide Perovskites (Cs2TiX6), J. Phys. Chem. Lett., 2022, 13, 10965–10975 CrossRef CAS PubMed.
- B. Cucco, C. Katan, J. Even, M. Kepenekian and G. Volonakis, Fine Structure of Excitons in Vacancy-Ordered Halide Double Perovskites, ACS Mater. Lett., 2023, 5, 52–59 CrossRef CAS.
- M. Saura-Múzquiz, M. Avdeev, H. E. A. Brand and B. J. Kennedy, Structural and Magnetic Properties of Some Vacancy-Ordered Osmium Halide Perovskites, Inorg. Chem., 2022, 61, 15961–15972 CrossRef PubMed.
- Y. Zhang, L.-F. Lin, A. Moreo and E. Dagotto, Electronic and, Magnetic Properties of Quasi-One-Dimensional Osmium Halide OsCl4, Appl. Phys. Lett., 2022, 120, 23101 CrossRef CAS.
- Y. Song, J. Pan, Y.-F. Zhang, H. Yang and S. Du, Monolayer Iridium Sulfide Halides with High Mobility Transport Anisotropy and Highly Efficient Light Harvesting, J. Phys. Chem. Lett., 2021, 2021(12), 6007–6013 CrossRef PubMed.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of Ab initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- H. Wang, A. Tal, T. Bischoff, P. Gono and A. Pasquarello, Accurate and Efficient Band-Gap Predictions for Metal Halide Perovskites at Finite Temperature, npj Comput. Mater., 2022, 8, 1–13 CrossRef CAS.
- X. H. Zhao, X. N. Wei, T. Y. Tang, Q. Xie, L. K. Gao, L. M. Lu, D. Y. Hu, L. Li and Y. L. Tang, Theoretical Prediction of the Structural, Electronic and Optical Properties of Vacancy-Ordered Double Perovskites Tl2TiX6 (X = Cl, Br, I), J. Solid State Chem., 2022, 305, 122684 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 11002 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr05013d |
| This journal is © The Royal Society of Chemistry 2025 |



