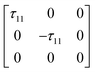DOI:
10.1039/D4NR04378B
(Communication)
Nanoscale, 2025,
17, 9094-9106
Born–Kuhn coupled oscillator model for optical activity in ordered media
Received
23rd October 2024
, Accepted 4th March 2025
First published on 5th March 2025
Abstract
Considering the phenomenological electromagnetic description of optical activity, we establish a unified formal framework, wherein the gyration and permittivity tensors of any ordered medium (a molecule or a crystal) can be derived using the classic Born–Kuhn coupled oscillator model. This model allows for efficient parameterisation of both tensors in terms of configurational and structural parameters (orientations, positions and coupling strengths) of a system of coupled oscillators having the same symmetries as the medium of interest. Thus, Born–Kuhn molecular models of all optically active crystal classes are established.
Introduction
Optical activity (OA), also known as circular birefringence, is most commonly defined as the ability of certain media to rotate the plane of polarisation of linearly polarised light upon transmission.1,2 The presence of OA in a given substance is commonly considered to be due to enantiomorphism (or chirality), i.e., the existence of two non-superimposable forms of a substance that are mirror images of each other. However, detailed analysis shows that enantiomorphism is sufficient but not necessary for OA.1 Similarly, the rotation of the plane of polarisation upon transmission, or rotatory power, is the most common manifestation of OA; however, certain media, despite being optically active, do not exhibit it.2 Although experimentally discovered and phenomenologically explained in the very beginning of the nineteenth century by Biot3 and Fresnel,4 OA was formally described almost a hundred years later. Drude5 and Voigt6 were the first to realise that the common homogeneous constitutive relations (or material equations) complementing Maxwell's equations in matter need to be extended to account for OA, as well as to formulate such extensions. Drude likewise proposed a qualitative microscopic picture to support extended constitutive relations. Some years later, Born7 and Kuhn8 analysed Drude's qualitative picture on a quantitative basis by considering a system of coupled electronic oscillators whose spatial extent is smaller than the wavelength of the probing light. Born considered the general case of a system of coupled oscillators, whereas Kuhn focused on the most elementary structure exhibiting OA, namely, the system of two coupled oscillators in a chiral arrangement. Born was further able to derive Drude's extended constitutive relations using his microscopic model for isotropic optically active media. However, none of them applied the oscillator model (referred to as the Born–Kuhn model from now on) to ordered structures such as crystals. A first step in this yet unexplored direction was taken by Chandrasekhar,9 who successfully used the Born–Kuhn model to describe the OA of quartz at the molecular level. Chandrasekhar's approach was later refined and extended by V. Vyšín10 and, particularly, I. Vyšín and coworkers.11
The advent of nonlinear optics and, more recently, nanoplasmonics and metamaterials has significantly revived interest in the classic Born–Kuhn oscillator model. Svirko and Zheludev12 applied the model in its general (Born's) version to derive the gyration and permittivity tensors of an infinite optically active medium. In recent years, the simplest two-oscillator (Kuhn's) version of the model has been successfully used by several authors13 to phenomenologically describe the optical response of chiral nanostructures.
Developments in nanoplasmonics have been particularly relevant for resurged interest in the Born–Kuhn model. Plasmonic nanostructures, which exhibit strong interactions with light at the nanoscale, are conceptually analogous to plasmonic systems, where metallic nanoparticles act as oscillators coupled through near-field interactions.14 The model provides insights into the tunability of optical activity through geometric parameters, inter-particle coupling, and material composition, facilitating the design of plasmonic metamaterials with tailored chiroptical properties for applications in sensing, polarization control, and photonic devices. However, very few studies15 have explored scenarios beyond the two-oscillator model, particularly in complex three-dimensional arrangements that essentially reproduce crystal structures. These configurations are increasingly relevant owing to advancements in modern design and nanofabrication tools, which allow for precise engineering of intricate geometries. Investigating such multi-oscillator systems could unveil new regimes of optical activity, enabling unprecedented control over light–matter interactions and expanding the functional capabilities of photonic materials.
The purpose of the present paper is twofold. Firstly, it revisits the phenomenological description of OA, creating a formal unified framework within which it derives the gyration and permittivity tensors from the Born–Kuhn coupled oscillator model for finite and infinite ordered media. Secondly, it establishes, as an illustrative application, parametric forms of gyration tensors for all optically active crystal classes. The framework bridges the gap between microscopic descriptions of optical activity based on coupled oscillator models and macroscopic electromagnetic theory of matter based on the gyration and permittivity tensors, both of which can be experimentally probed through polarised light measurements. Since the approach is general, it allows for efficient geometric representation and analytic parameterisation of any natural or artificial optically active structure as a function of its symmetries.
Constitutive relations for optically active media
Herein, we assume plane monochromatic wave dependence, exp(ikr − iωt), for all electromagnetic vectors (k is the wavevector, r is the position and ω is the cyclic frequency of the wave). The usual linear homogeneous constitutive relations for anisotropic nonmagnetic media:16relate the electric (magnetic) induction (D (B)) to the electric (magnetic) field (E (H)) through the vacuum permittivity (permeability) (ε0 (μ0)) and the permittivity tensor (ε) of a generally anisotropic medium. From an optical viewpoint, these relations describe only linear polarisation effects such as linear birefringence and dichroism, i.e., the difference in phase velocities and extinction coefficients for polarised light waves with orthogonal linear (e.g. horizontal and vertical) polarisations. To formally describe circular polarisation effects, namely, circular birefringence (or OA) and dichroism, originating from different phase velocities and extinction coefficients of circularly polarised light waves, respectively, with orthogonal (left-handed and right-handed) polarisations, a more general, inhomogeneous form of linear constitutive relations must be used:where POA and MOA are additional polarisation and magnetization terms arising from OA, respectively. As shown phenomenologically by Drude5 and Voigt,6 as well as formally by Boys17 and Condon,18 the OA polarisation and magnetization terms entering the electric and magnetic constitutive relation, respectively, depend on quantities of an opposite physical (magnetic or electric) nature, i.e.POA = POA(B) and MOA = MOA(E).
By performing Fedorov's transformation,19
leaving invariant Ampère's law,
and not affecting Faraday's law,
the general magnetic constitutive relation
(2b) can be made homogeneous, such as
eqn (1b), but at the cost of redefining electric induction from
D to
D′ and magnetic field from
H to
H′. Indeed, the elimination of
D and
H from
eqn (2) with the help of
eqn (3) transforms the former set of constitutive relations as follows.
| | | D′ = ε0εE + POA − ω−1k × MOA | (5a) |
Contrarily, by expanding the permittivity tensor in powers of the wavevector within the framework of the spatial dispersion picture, Landau and Lifshitz16 obtained the following set of constitutive relations for optically active media:
| | | D′ = ε0εE + iε0cω−1(gk) × E | (6a) |
where
g is the gyration tensor describing OA and
c is the speed of light in vacuum. Comparison of the electric constitutive relations from the two sets
(5) and
(6) gives the following relation.
| | | POA − ω−1k × MOA = iε0cω−1(gk) × E | (7) |
Eqn (7), first established by Pauli20 in the special case of isotropic media, allows the determination of the gyration tensor when OA-induced polarisation and magnetization of the medium are known. As given in the following section, the latter can be derived from the microscopic description of the medium. Thus, Pauli's eqn (7) provides the link between microscopic and macroscopic cases on the formal basis of the Born–Kuhn approach.
Before ending this section, it should be emphasized that the constitutive relations (6) featuring a homogeneous magnetic relation are valid for infinite media only, as noted by Landau and Lifshitz.16 When dealing with layered optically active media instead (as is commonly the case in optical characterisation), the following Fedorov's transformation must be performed,
| | | D′ = D + iε0cω−1k × fTE | (8a) |
bringing
eqn (6) into the inhomogeneous set,
where
f is the OA tensor and is related to the gyration tensor (
g) as follows:
21(the notation ‘
tr’ stands for the trace, whereas
I denotes the identity matrix). Set
(9) was established first by Drude
5 and Boys
17 in the case of isotropic optically active media. It satisfies the common boundary conditions at interfaces (continuity of the tangential components of the fields and the normal components of the inductions), as demonstrated theoretically
22 and experimentally.
23 Note that set
(9) is similar to generic set
(2), its OA-induced polarisation and magnetization terms being dependent on quantities of an opposite physical nature,
i.e.POA =
POA(
B) and
MOA =
MOA(
E).
Coupled oscillator model for optically active media
The Born–Kuhn model for OA, largely inspired by the classic Lorentz microscopic model of electromagnetism,24 considers a system of electrons constrained to oscillate about spatially-separated equilibrium positions under the action of an externally applied electric field. The spatial extent (a) of the system of electrons is sufficiently smaller with respect to the wavelength (λ) of the electric field; therefore, only linear expansions in the a/λ ratio can be considered.
The approach is as follows: First, the “mechanical” part of the model, the oscillation amplitudes of all electrons, is determined from the equations of motion. Electrons are assumed to oscillate along straight lines under the influence of the time-varying electric field of probing light. The second “electromagnetic” part of the model consists of the evaluation of the polarisation and magnetization of the medium to various multipole degrees of approximation, in either finite medium (molecule) or infinite medium (crystal) cases. For simplicity, the induced electric and magnetic multipole densities constituting polarisation and magnetization are evaluated classically; although a quantum-mechanical approach exists,25 it has been shown to yield similar results.26 Finally, eqn (7) is applied to retrieve the gyration tensor from OA-induced contributions to polarisation and magnetization, while the permittivity tensor is obtained with the help of the electric constitutive relation (5a).
Equations of the motion of a system of coupled oscillators
For simplicity and following Kuhn's original derivation,8 we shall start with a system of only two coupled oscillators, whose results are readily generalizable to an arbitrary number. Consider two electrons oscillating along straight lines with respective unit vectors u1 and u2. The equilibrium positions r1 and r2 of the electrons are measured with respect to the centre (r0) of the system. The time evolutions of the displacements a1(t) and a2(t) of the electrons with respect to r1 and r2 are given by the following simultaneous coupled equations of motion:| |  | (10a) |
| |  | (10b) |
where k12 = k21 = k is the coupling between two electrons with charge e and mass me. Physically, the coupling originates from the multipole–multipole (typically, dipole–dipole) electromagnetic interaction between the oscillating electrons.27 In eqn (10), En(t) = E(t, r0 + rn), n = 1, 2, is the probing light electric field acting upon the nth oscillator at the equilibrium position; its projection upon the oscillation direction (un), multiplied by the charge, equals the driving force. Finally, ω1 and ω2 are the frequencies of free oscillations of the two electrons considered uncoupled, i.e. if En(t) = 0 and k = 0.
For a monochromatic electric field (∝exp(−ωt)), eqn (10) can be represented in the matrix form,
| |  | (11) |
which is readily solvable for the two oscillation amplitudes
a1 and
a2,
| |  | (12a) |
where
| | | D(ω) = (ω12 − ω2)(ω22 − ω2) − k2, | (12b) |
Eqn (11) and (12) express the linear relationships existing between the amplitudes of the two oscillating electrons and the magnitude of the electric field driving them out of their respective equilibrium positions. The generalization of these equations in the case of N > 2 oscillators whose oscillation amplitudes are grouped in the vector a is immediate. Eqn (11) then takes the following form:
where
D is the
N ×
N “dynamic” matrix with elements
Dnm =
Dmn =
mekmn/
e for
m ≠
n and
Dnn =
me(
ωn2 −
ω2)/
e, whereas
e′ is the “electric” vector with components

,
n = 1, 2, …,
N. Note that the matrix
D is symmetric by virtue of the reciprocity of the coupling within the pairs of oscillators.
The solution of eqn (13) is obviously:
or, in component form (summation over repeated indices being understood, unless otherwise stated),
| |  | (15) |
(Note that Dmn−1 designates the mnth element of the inverse matrix D−1 rather than the reciprocal of Dmn.)
Born–Kuhn model for a finite structure (molecule)
As mentioned in the previous section, the second step in the Born–Kuhn approach consists of evaluating the polarisation and magnetization of the optically active structure (molecule or crystal) by calculating the microscopic electric and magnetic multipole moments to different orders of approximation using the oscillation amplitudes of the system of electronic oscillators. Raab and De Lange28 showed that the first, electric dipole order of approximation is insufficient to account for OA; for a complete description of the phenomenon, calculations should be performed to the second-order electric quadrupole–magnetic dipole. In our calculations, we shall consider both orders consecutively, the first being an essential intermediate step for the second, and critically compare the results obtained.
Electric dipole approximation.
Within this first-order approximation of multipole theory, the polarisation P of the molecule is identified with the induced electric dipole moment density p of the system of electronic oscillators,| |  | (16) |
where v ∼ a3 is the volume occupied by a molecule of size a. Substituting eqn (15) for the oscillation amplitudes am yields the polarisation.| |  | (17) |
We have put Amn = ε0−1eDmn−1/v and have expressed the electric field En applied on the nth oscillator through the field E = E(0) at the molecular centre r0 = 0 by means of linear expansion, i.e., En = E(rn) ≈ (1 + ikrn)E.
Again, within the first-order approximation, the magnetization M, identified by the induced magnetic dipole moment density m of the system of oscillators, is neglected since it is of a higher order with respect to the electric dipole moment density, i.e., M = m = 0. Next, we evaluate the expression P − ω−1k × M = p with the help of eqn (17).
| |  | (18) |
The above expression contains both OA- and non-OA contributions. Comparison of eqn (18) and (7) allows to isolate the OA contribution as the last term:
| | | POA − ω−1k × MOA = i[½ε0Amn(un × um)rTn]k × E | (19) |
and consequently, to identify the gyration tensor of the molecule:
| | | g′ = ½c−1ωAmn(un × um)rTn | (20) |
(We have used a primed notation for the tensor to emphasize the first order of the approximation.) To give meaning to the first non-OA term in eqn (18), the redefined electric constitutive relation (5a) can be written in the general inhomogeneous form:
where polarisation
P′ is redefined as follows.
| | | P′ = ε0(ε′ − I)E + POA − ω−1k × MOA | (22) |
The last two terms in eqn (22) represent the OA-contribution already identified in eqn (18). Consequently, the first term corresponds to the non-OA contribution; when put in correspondence with the first term from eqn (18), it provides the permittivity tensor of the molecule.
| | | ε′ = I + AmnumuTn + i½Amnkrn(umuTn + unuTm) | (23) |
This result is unphysical since the last term explicitly depends on the wavevector. Furthermore, the presence of the last term breaks the essential symmetry property of the permittivity tensor, εT = ε, following from the conservation of energy.16,20 In fact, the Lorentz classic electron theory of the permittivity in the absence of OA yields only the first two physical terms in eqn (23).12 This points out the deficiency of the first-order electric dipole approximation. To obtain the correct forms of permittivity and gyration tensors, second-order electric quadrupole–magnetic dipole approximation must be considered.
Electric quadrupole–magnetic dipole approximation.
In this order of multipole approximation, polarisation (P) of the molecule comprises the induced electric dipole moment density (p) and the induced electric quadrupole moment density (q) contributions.28,29
Dipole moment density (p) is given by eqn (16), whereas the induced electric quadrupole moment density of the system of electronic oscillators is:
| |  | (25) |
at the first order in the oscillation amplitude (
am), substituted for from
eqn (15). At this order of approximation, magnetization (
M) of the molecule is given by the induced magnetic dipole moment density (
m) of the system of oscillators,
| |  | (26) |
into which expression
(15) for
am has been substituted, as previously mentioned. Note that magnetization depends on the electric field and not on the magnetic field,
i.e.,
M =
M(
E). This observation implies that the magnetization of a molecule is entirely due to OA,
M =
MOA, in accordance with the discussion following the constitutive relations
(5). Generally, the Born–Kuhn model based on electrons oscillating along straight lines can model only non-magnetic media,
i.e. it formally yields
μ =
I for the permeability tensor.
The expression from eqn (18) involving polarisation and magnetization is therefore as follows.
| | | P − ω−1k × M = p − i½kq − ω−1k × m | (27) |
The first term on the right-hand side of eqn (27) is the electric dipole contribution already calculated in eqn (17). The quadrupole contribution due to the last two terms is evaluated using eqn (25) and (26).
| | | −i½kq − ω−1k × m = −iε0AmnkrmumuTnE | (28) |
The addition of eqn (17) and (28) finally yields the right-hand side of eqn (27).
| | 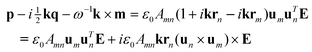 | (29) |
As mentioned in the previous section, identification of the above expression with eqn (19) and (22) yields:
| | | g = c−1ωAmn(un × um)rTn | (30) |
for the gyration tensor and
for the permittivity tensor of the molecule, respectively.
Comparison of the two expressions for the gyration tensor obtained at different degrees of multipole approximations, as given by eqn (20) and (30), shows that the electric quadrupole–magnetic dipole contribution is equal in magnitude and of the same structure as the electric dipole contribution alone since g = 2g′. This observation confirms the general result from multipole theory28 that taking the multipole order next to the electric dipole order into account is essential for the complete quantitative description of the OA phenomenon. Furthermore, addition of the electric quadrupole–magnetic dipole contribution effectively removes the unphysical dependence of the permittivity tensor on the directional derivatives (compare ε′ from eqn (23) with ε from eqn (31)).
It should be noted that the electric quadrupole contribution (q) can be neglected with respect to the magnetic dipole contribution (m) if an ensemble of randomly oriented molecules, representing an isotropic optically active substance, is considered. It can be easily observed from eqn (28) that if q = 0, then the correct expression (30) for the gyration tensor is still obtained; however, the expression for the permittivity tensor contains extra unphysical directional derivative terms, such as those in eqn (23). These spurious terms vanish upon the orientational averaging of the molecule, as shown by Caldwell and Eyring,27 as well as in the original works of Born7 and Kuhn.8 Nevertheless, as already discussed, the electric quadrupole contribution is essential for obtaining the correct results for both tensors in case of an oriented (i.e., an orientationally non-averaged) molecule. In ordered systems, where the molecular orientation is not random, the electric quadrupole–magnetic dipole contribution ensures that the model effectively predicts the optical response of the material in practice, irrespective of the propagation direction of the probing light.
Born–Kuhn model for an infinite structure (crystal)
The case of an infinite structure is computationally simpler since it is sufficient to work to the first-order, electric dipole, of multipole theory. In fact, as shown by Robinson29 and Rosenfeld,30 the consideration of the second-order, electric quadrupole–magnetic dipole, is necessary only when the structure is inhomogeneous or, in particular, discontinuous, such as in the case of finite (molecular) structures.
Following Svirko and Zheludev,12 we modelled the crystal as a three-dimensional regular lattice of N unit cells (N ≫ 1) of volume v. Thus, the induced electric dipole moment density of the unit cell whose centre is located at r0 is as follows.
| | | p(r0) = eumamδ(r − r0 − rm) = eDmn−1umuTnEnδ(r − r0 − rm) | (32) |
In accordance with the electric dipole approximation, polarisation (P) of the crystal equals the induced electric dipole moment density averaged over the lattice:
| |  | (33) |
where
E(
r +
rn −
rm) has been replaced with
En−m to simplify the notations. Since
M = 0 at this order of approximation, the expression
P −
ω−1k ×
M appearing in
eqn (18) is transformed to the following one:
| |  | (34) |
In eqn (34), electric field (En−m) has been linearly expanded about its value E = E(r) at an arbitrary position (r) in the crystal, i.e.En−m = E(r + rn − rm) ≈ (1 + ikrn − ikrm)E.
Identification of eqn (34) with eqn (7) and (22) yields the gyration tensor,
| | | g = c−1ωAmn(un × um)rTn | (35) |
as well as the permittivity tensor,
of the crystal.
The Born–Kuhn model provides identical results for finite and infinite optically active media. Indeed, the expressions for the gyration tensors, as well as those for the permittivity tensors, coincide; compare eqn (30) and (31) with eqn (35) and (36), respectively. In the framework of the Born–Kuhn model, the properties of the crystal are entirely determined by the properties of its unit cell, i.e. the crystal is equivalent to an oriented molecule.
Another prominent feature of the Born–Kuhn model is that it provides not only the gyration tensor of the optically active medium but also the permittivity tensor, both tensors being closely related physically. An important practical consequence of this fact is that the same model should be used to describe both tensors when fitting the simulated optical response of the medium or structure under study to experimental data.
Eventually, it should be noted that both gyration and permittivity tensors depend on the cyclic frequency (ω) of the probing light either explicitly or implicitly through the matrix element Amn. This phenomenon, called time or frequency dispersion,16 which results in the spectral dependence of both tensors, has been addressed in detail by many authors over the years9–11 and is still an active topic;31 thus, it will not be dealt with here. Indeed, spatial and time (or frequency) dispersions are treated independently in theoretical models considering their distinct physical origins.16 Alternatively, spatial dispersion results from the non-local response of the medium, while time dispersion arises from the finite-time response of the medium.
Properties of the gyration tensor
The gyration tensor of the molecule (or the crystal) given by eqn (30) (or by eqn (35)) can be readily represented asby substituting rn = dnvn and cmn = dnc−1ωAmn (no summation over repeated indices being assumed), where dn is the distance of the nth oscillator from the centre of the molecule (or of the unit cell) and vn is the unit vector along rn. It should be noted that while Amn satisfies Amn = Anm, the matrix formed by the coupling coefficients cmn is not symmetric, i.e., cmn ≠ cnm, because dn ≠ dm, in general. Note that eqn (30), (35) and (37) present the gyration tensor in the form of a dyadic, i.e., a linear combination of dyads (or outer products of vectors).
In the case of only two coupled oscillators i and j forming Kuhn's pair, eqn (37) reduces to:
| | | gij = (ui × uj)(cjivTi − cijvTj) | (38) |
(no summation over repeated indices), where
ui and
uj are the oscillation directions of the two oscillators forming the pair, while
vi and
vj are the unit vectors pointing at their positions.
In isotropic disordered optically active media, the gyration tensor must be averaged over all possible orientations. Tensor (37) then becomes a scalar equal to its trace, i.e., g = trgI, where
| | | trg = cmn(un × um)vn = cmn(unumvn) | (39) |
in which (
unumvn) = (
un ×
um)
vn is the scalar triple product of vectors.
Before proceeding with the identification of the properties of gyration tensor g, it should be recalled that strictly speaking, the second-rank tensor g is not a true (or a polar) tensor but rather a pseudo-tensor (or an axial tensor), as shown by Landau and Lifshitz.16 In fact, when written in component form in the general (non-plane-wave) case, the redefined electric constitutive relation (6a) becomes:
| |  | (40) |
where
is the true (or polar) third-rank gyration tensor obeying the anti-symmetry relation
γikn = −
γkin by virtue of Onsager's principle (
eijk is the Levi–Civita symbol,
i.e., the fully antisymmetric third-rank pseudo-tensor). Note that
eqn (40) is the first-order expansion of the redefined electric induction
D′ in the position and
∇ is the gradient operator, in agreement with the spatial dispersion picture of OA.
16Eqn (41) defines
g as a second-rank axial tensor (or pseudo-tensor), unlike the third-rank polar (or true) tensor (
γ). Consequently, gyration tensor
g transforms similar to a pseudo-tensor––it behaves similar to a polar tensor under rotation transformations; however, unlike a polar tensor, it changes its sign upon reflection transformations.
16
We can now draw a list of properties satisfied by the gyration tensor that follow directly from eqn (37).
1. If un → −un, then g → g. Time reversal, i.e., inversion of the oscillation directions of all oscillators, does not alter the tensor.
2. If vn → −vn, then g → −g. Space inversion, i.e., inversion of the system of oscillators to its centrosymmetric image, reverses the sign of the tensor, in agreement with g being a pseudo-tensor. Therefore, if the system itself is centrosymmetric, then g = 0 (centrosymmetric media do not exhibit OA, as is well known).16
3. If un → −un and vn → −vn, then g → −g. Simultaneous time reversal and space inversion reverse the sign of the tensor.
4. If R is a rotation transformation leaving the system of oscillators invariant, i.e., if Rum = un and Rvm = vn, then RgRT = g, i.e., the tensor is unaltered. This property is in agreement with g being a pseudo-tensor behaving as a true (polar) tensor with respect to rotations.
5. If S is an inversion (e.g., mirror reflection) operation leaving the system of oscillators invariant, i.e., if Sum = un and Svm = vn, then SgST = −g, i.e., the tensor reverses its sign. Similar to the previous property, this is in agreement with g being a pseudo-tensor and changing its sign upon inversion.
6. If the system of oscillators decomposes into two subsystems that are uncoupled from one another with respective tensors g1 and g2, then g = g1 + g2. This is an obvious consequence from g being a dyadic, i.e., a sum of dyads. In particular, if every oscillator from the system is coupled to another one only, i.e., if the coupling is pairwise, then gyration tensor g of the whole system is made up of Kuhn's pair contributions of the form given by eqn (38).
7. The gyration tensor vanishes when
(a) cmn = 0 for m ≠ n, i.e., all oscillators are uncoupled. Coupling is essential for OA.
(b) vn = 0: a system of centred oscillators, i.e., oscillators whose equilibrium positions coincide with the centre of the molecule (or of the unit cell) exhibit no OA. Spatial dispersion is essential for OA.16
8. The trace of the gyration tensor given by eqn (39) vanishes when
(a) um, un and cmnvn − cnmvm are coplanar, i.e., all oscillators lie in a plane.
(b) um||vm, i.e., all oscillators are radial, i.e., oscillations take place along the radius vectors joining the oscillators to the centre of the molecule (the unit cell). Note that this condition is equivalent to pairwise coplanar oscillators, i.e., coplanar Kuhn's pairs. Since the gyration tensor of each coplanar Kuhn's pair is traceless, thus, the tensor of the whole system will also be traceless (being a sum of Kuhn's pair contributions by virtue of property 6.)
Consequently, a system of coplanar or radial (i.e., pairwise coplanar) oscillators exhibits no molecular enantiomorphism.
Coupled oscillator models for optically active crystal classes
The formal coincidence of the expressions for the gyration tensor of a molecule and a crystal, given by eqn (30) and eqn (35), respectively, suggests the possibility of constructing molecular models for all optically active crystal classes. The molecular model of a given crystal class consists of a system of coupled oscillators whose spatial configuration obeys the symmetries of the class. While constructing the model, the total number of oscillators and the coupling between them can be minimised. As a result, all optically active crystal classes can be modelled by systems of coupled oscillators containing a certain number of Kuhn's pairs. Consequently, we shall establish the molecular models of all optically active crystal classes. The configurations are shown in figures in which oscillators are represented by red rods. Coupled oscillators are connected by straight lines. Equal symmetric coupling between oscillators within different pairs (i.e. Aij = Amn, cij = cji and cmn = cnm for pairs ij and mn) is represented by connecting lines of the same colour, while distinct colours indicate unequal (Amn ≠ Anm) or asymmetric (cij ≠ cji, cmn ≠ cnm) coupling.
Biaxial crystals
Class 1. This triclinic class exhibits no symmetries, and therefore, all nine tensor elements are generally non-zero. To model it, three arbitrarily oriented oscillators are considered:| | uk = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θkcos θkcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φk sin φk sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θksin θksin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φk cos φk cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk]T, θk]T, | (42) |
which are located along the coordinate axes v1 = [1 0 0]T, v2 = [0 1 0]T and v3 = [0 0 1]T, respectively, as shown in Fig. 1. In eqn (42), φk and θk are the azimuth and the polar angle of the kth oscillator, respectively (k = 1, 2, and 3). The gyration tensor results from the pairwise coupling of the triplet of oscillators:and is obtained using eqn (38) for gij. The model has twelve parameters, nine of which can be considered independent, while the remaining three can be assigned predefined values to match the number of non-zero tensor elements. The nine independent model parameters uniquely determining the non-zero tensor elements are the three polar angles θ1, θ2 and θ3 together with the six coupling coefficients c12, c21, c23, c32, c13 and c31, whereas the remaining three azimuths φ1, φ2 and φ3 may be ascribed (non-uniquely) to φ1 = 0, φ2 = π/4 and φ3 = π/2.
 |
| | Fig. 1 Molecular model for crystal class 1. | |
Class m. This monoclinic class features a single mirror plane coinciding (by convention) with the xy-plane. Its gyration tensor is traceless, does not exhibit any symmetries, and has four non-zero elements.
| |  | (44) |
To model it, an arbitrarily oriented oscillator is considered:
| | u1 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 sin φ1 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 cos φ1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T θ1]T | (45a) |
coupled with a second one that is its mirror image with respect to the
xy-plane.
| | u2 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 sin φ1 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 −cos φ1 −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T θ1]T | (45b) |
Both oscillators are located along the z-axis symmetrically with respect to the origin so that v1 = −v2 = [0 0 1]T and d1 = d2. A third oscillator lies entirely in the xy-plane, i.e.,
| | u3 = [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 sin φ2 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 0]T φ2 0]T | (46a) |
and
| | v3 = [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ3 sin φ3 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ3 0]T φ3 0]T | (46b) |
and is coupled with the first two. This configuration is shown in
Fig. 2. The tensor is given by
eqn (43) and (38), with
c12 =
c21 =
c1,
c13 =
c23 =
c2 and
c32 =
c31 =
c3 (because
d1 =
d2 and
A13 =
A23). The model has seven parameters, four of which can be considered as independent. The four independent parameters are the azimuth
φ3 and the three coupling coefficients
c1,
c2 and
c3, whereas the remaining three parameters may be fixed to
φ1 =
θ1 = π/4 and
φ2 = −
φ1.
 |
| | Fig. 2 Molecular model for crystal class m. | |
Class 2. This monoclinic class has a single 2-fold axis taken (conventionally) along the z-axis. Its gyration tensor does not exhibit any symmetry and has five non-zero elements.
| |  | (47) |
It can be modelled with two Kuhn's pairs. The first pair consists of two arbitrarily oriented oscillators:
| | u1 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 sin φ1 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 cos φ1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T θ1]T | (48a) |
| | u2 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2cos θ2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 sin φ2 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2sin θ2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 cos φ2 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2]T θ2]T | (48b) |
whose position directions are considered symmetric with respect to the
x-axis.
| | v1 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp sin φp sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp cos φp cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T θp]T | (49a) |
| | v2 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −sin φp −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T θp]T | (49b) |
The pair is rotated through π about the z-axis to produce the opposite, z-axis-symmetric second pair,
| | u3 = [−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 −sin φ1 −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 cos φ1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T θ1]T | (50a) |
| | u4 = [−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2cos θ2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 −sin φ2 −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2sin θ2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 cos φ2 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2]T θ2]T | (50b) |
and
| | v3 = [−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −sin φp −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp cos φp cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T θp]T | (51a) |
| | v4 = [−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp sin φp sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T θp]T | (51b) |
The oscillators within each pair and the first and second oscillators from the opposite pairs are coupled so that all oscillators are coupled “peripherally”; see Fig. 3. The tensor is given by the sum of the pairwise contributions,
| | | g12 + g34 + g23 + g41 | (52) |
and
eqn (38) with
c12 =
c34 =
c1,
c21 =
c43 =
c2,
c23 =
c41 =
c3 and
c32 =
c14 =
c4 (because
d1 =
d3 and
d2 =
d4, as well as
A12 =
A34 and
A23 =
A14). The model has ten parameters, five of which can be fixed. The independent model parameters are the polar angle
θ1 and the four coupling coefficients
c1,
c2,
c3 and
c4, whereas the fixed parameters are
φ1 = π/4,
φ2 = −
φ1,
θ2 = −
θ1,
φp = π/4 and
θp = π/2.
 |
| | Fig. 3 Molecular model for crystal class 2. | |
Note that assuming coupling between all oscillators, i.e., adding g13 + g24 with c13 = c31 = c5 and c24 = c42 = c6 to eqn (52), would yield a tensor of the same form as eqn (47), resulting in an over-parameterised model.
Class 222. This orthorhombic class has three mutually orthogonal 2-fold axes coinciding with the three coordinate axes. Its tensor is diagonal and has three non-zero elements.
| |  | (53) |
To obtain it, two Kuhn's pairs, eqn (48)–(51) from the class-2 model, can be used by adding extra symmetries. The second oscillator within each pair is oriented symmetrically to the first with respect to the x-axis, i.e. φ2 = −φ1 and θ2 = π − θ1 are used in eqn (48b) and (50b). Similar to that in the class 2 model, the oscillators within each pair and the first and second oscillators from the opposite pairs are coupled (so that all oscillators are coupled “peripherally”). Fig. 4 exemplifies the configuration. The tensor is represented by eqn (52) and (38) with c12 = c21 = c34 = c43 = c1 and c14 = c41 = c23 = c32 = c2 (because d1 = d2 = d3 = d4, A12 = A34 and A23 = A14). By fixing three of the six model parameters, the number of non-zero tensor elements is matched. The polar angle θ1 and two coupling coefficients c1 and c2 are independent whereas φ1 = φp = θp = π/4 are fixed.
 |
| | Fig. 4 Molecular model for crystal class 222. | |
Class mm2. This orthorhombic class features a single 2-fold axis along the z-axis and two mirror planes coinciding with xz- and yz-planes, respectively. Its tensor is off-diagonal, exhibits no definite symmetry and has only two non-zero elements.
| |  | (54) |
Similar to that in orthorhombic class 222, additional symmetries can be imposed on the two Kuhn's pairs from class 2, given by eqn (48)–(51), to model the tensor. The second oscillator from the pair is the mirror image of the first with respect to the xz-plane, as shown in Fig. 5, i.e. θ2 = θ1 and φ2 = −φ1 are used in eqn (48b) and (50b). Furthermore, the centres of all four oscillators lie in the xy-plane, and therefore, θp = π/2 is substituted into eqn (49) and (51). The tensor is obtained from eqn (52) and (38) when all coupling coefficients equal cc (because the oscillators are equidistant from the origin). Two model parameters can be fixed, θ1 = φp = π/4, while the two independent ones are the azimuth φ1 and the common coupling coefficient cc.
 |
| | Fig. 5 Molecular model for crystal class mm2. | |
Uniaxial crystals
Class ![[4 with combining macron]](https://www.rsc.org/images/entities/b_char_0034_0304.gif) . This tetragonal class has a single inversion 4-fold axis along the z-axis. Its tensor is traceless symmetric:
. This tetragonal class has a single inversion 4-fold axis along the z-axis. Its tensor is traceless symmetric:| |  | (55) |
and depends on two parameters. Similar to that in the two orthorhombic classes 222 and mm2, the above tensor can be modelled by imposing additional symmetries on the two Kuhn's pairs from class 2, described by eqn (48)–(51). The second oscillators from each pair are oriented and located so as to satisfy both π/2-rotation and inversion, as shown in Fig. 6, i.e., φ2 = φ1 − π/2 and θ2 = π − θ1 are substituted into eqn (49b) and (51b). Their position directions are taken to be:| | v2 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −sin φp −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T θp]T | (56a) |
in the first pair and| | v4 = [−sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp sin φp sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T θp]T | (56b) |
in the second one. The tensor is given by eqn (52), with all coupling coefficients, equal to cc as they are equidistant from the origin, substituted in eqn (38). The independent model parameters are the azimuth φ1 and the common coupling coefficient cc, while the fixed ones are θ1 = π/4, φp = 0 and θp = π/2.
 |
| | Fig. 6 Molecular model for crystal class ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) . . | |
Class ![[4 with combining macron]](https://www.rsc.org/images/entities/b_char_0034_0304.gif) 2m. Besides the single inversion 4-fold axis along the z-axis, this class has two orthogonal 2-fold axes perpendicular to the 4-fold axis and two mirror planes containing the 4-fold axis and bisecting the two 2-fold axes. Its tensor is traceless diagonal:
2m. Besides the single inversion 4-fold axis along the z-axis, this class has two orthogonal 2-fold axes perpendicular to the 4-fold axis and two mirror planes containing the 4-fold axis and bisecting the two 2-fold axes. Its tensor is traceless diagonal:
| |  | (57a) |
and depends only on a single parameter. This class can be treated as a higher-symmetry special case of class
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif)
. It is therefore sufficient to use
φ1 = 0,
θ1 = π/4 and
φp =
θp = π/2 in the model equations for class
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif)
from the previous subsection. The configuration is shown in
Fig. 7. The only model parameter is the common coupling coefficient
cc.
 |
| | Fig. 7 Molecular model for crystal class ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m. 2m. | |
It should be noted that one may also use φp = 0 instead of φp = π/2. This would yield the alternative traceless symmetric form of the tensor.16
| |  | (57b) |
It is straightforward to show that the two tensors given by eqn (57a) and (57b) transform into one another via a π/4-angle rotation about the z-axis.
Classes 3, 4 and 6. These classes have a single n-fold axis along the z-axis. Their tensors are of the following form:
| | 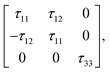 | (58) |
and therefore, they depend on three parameters. These classes can be modelled by sets of
n uncoupled Kuhn's pairs. We shall consider the case
n = 3, with the other two being analogous. Two arbitrarily oriented oscillators forming a Kuhn's pair, given by
eqn (48), with positions directed symmetrically with respect to the
x-axis, given by
eqn (49), are consecutively rotated twice about the
z-axis through 2π/3 by the rotation matrix,
| |  | (59) |
yielding two more pairs,
u3 =
R3u1,
u4 =
R3u2, and
v3 =
R3v1,
v4 =
R3v2 as well as
u5 =
R3u3,
u6 =
R3u4,
v5 =
R3v3, and
v6 =
R3v4. The configuration is represented in
Fig. 8. The tensor is given by the contributions of the initial and rotated pairs,
with
c12 =
c34 =
c56 =
c1 and
c21 =
c43 =
c65 =
c2 (because
d1 =
d3 =
d5,
d2 =
d4 =
d6 and
A23 =
A34 =
A56) substituted into
eqn (38). The independent model parameters are the two polar angles
θ1 and
θ2 together with the coupling coefficient
c1, whereas the fixed ones are
φ1 =
θp = π/4,
φp = π/2,
φ2 = −
φ1 and
c2 =
c1 (because all six oscillators can be assumed to be equidistant from the origin).
 |
| | Fig. 8 Molecular model for crystal class 3. | |
Similar to class 2, assuming additional couplings between oscillators, does not change the form of the tensor but only over-parameterises it.
Classes 32, 422 and 622. Besides the single n-fold axis along the z-axis, these classes have n evenly spaced coplanar 2-fold axes normal to the n-fold axis. Their tensors are diagonal:
| |  | (61) |
and depend on two parameters. They can be modelled as higher-symmetry special cases of the
n-classes by adding extra symmetries. In the case
n = 3, the second oscillator from the initial Kuhn's pair is considered symmetric to the first with respect to the
x-axis (see
Fig. 9) so that
φ2 = −
φ1 and
θ2 = π −
θ1 are put into
eqn (48b) and (50b). The tensor is obtained from
eqn (60) and (38) with all coupling coefficients put equal to
cc (because all oscillators are equidistant from the origin). The independent model parameters are the polar angle
θ1 and the common coupling coefficient
cc, while the fixed ones are
φ1 =
θp = π/4 and
φp = π/2.
 |
| | Fig. 9 Molecular model for crystal class 32. | |
Classes 3m, 4mm and 6mm. Besides the single n-fold axis along the z-axis, these classes have n evenly spaced mirror planes containing the n-fold axis. Their tensors are antisymmetric:
| |  | (62) |
and depend only on a single parameter. In the case
n = 3, an oscillator lying on the
xz-plane:
| | u1 = [sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 0 cos θ1 0 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T θ1]T | (63) |
and located along the
x-axis,
v1 = [1 0 0]
T, is consecutively rotated twice about the
z-axis through 2π/3 by the rotation matrix
R3 given by
eqn (59), yielding two more oscillators,
u2 =
R3u1,
v2 =
R3v1 and
u3 =
R3u2,
v3 =
R3v2, as shown in
Fig. 10. The tensor of the triplet is given by
eqn (43) and (38), all three coupling coefficients being equal to a common value
cc (because
d1 =
d2 =
d3). The only model parameter is the coupling coefficient
cc, and
θ1 = π/4 is fixed.
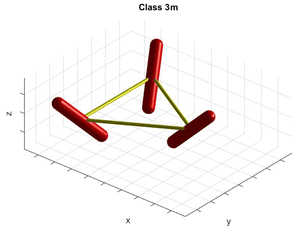 |
| | Fig. 10 Molecular model for crystal class 3m. | |
Isotropic crystals
Class 23. This isotropic class presents tetrahedral symmetry: three 2-fold axes along the three coordinate axes together with four 3-fold axes. Six oscillators are oriented along the edges of a regular tetrahedron, u1 = a[0 1 1]T, u2 = a[0 −1 1]T, u3 = a[−1 0 1]T, u4 = a[1 0 1]T, u5 = a[1 −1 0]T and u6 = a[−1 −1 0]T, where  , and are located at mid-points between the summits so that v1 = [1 0 0]T, v2 = [−1 0 0]T, v3 = [0 1 0]T, v4 = [0 −1 0]T, v5 = [0 0 1]T and v6 = [0 0 −1]T, as shown in Fig. 11. The tensor is given by the contributions of the three Kuhn's pairs consisting of opposite coupled oscillators with equal pairwise coupling coefficients, i.e.eqn (60) is applied with all cij equalling cc (because all oscillators are equidistant from the origin). It reduces to a scalar proportional to the coupling coefficient cc, and only molecular enantiomorphism occurs.1
, and are located at mid-points between the summits so that v1 = [1 0 0]T, v2 = [−1 0 0]T, v3 = [0 1 0]T, v4 = [0 −1 0]T, v5 = [0 0 1]T and v6 = [0 0 −1]T, as shown in Fig. 11. The tensor is given by the contributions of the three Kuhn's pairs consisting of opposite coupled oscillators with equal pairwise coupling coefficients, i.e.eqn (60) is applied with all cij equalling cc (because all oscillators are equidistant from the origin). It reduces to a scalar proportional to the coupling coefficient cc, and only molecular enantiomorphism occurs.1
 |
| | Fig. 11 Molecular model for crystal class 23. | |
Class 432. The octahedral (or cubic) symmetry of this isotropic class presents three 4-fold axes along the three coordinate axes, four 3-fold axes and six 2-fold axes. This class requires three couples of Kuhn's pairs, i.e. a total of twelve oscillators. The couples are located at the centres of the opposite faces of a cube. The respective oscillators from the two pairs in a couple are perpendicular in orientations (“cross” structure); the two triplets of pairs thus formed have 222-symmetry (“2 × 3 tilted crosses”). This configuration is represented in Fig. 12. The tensor, evaluated using eqn (37), reduces to a scalar proportional to the common coupling coefficient cc. Similar to the other optically active class 23, only molecular enantiomorphism occurs.1
 |
| | Fig. 12 Molecular model for crystal class 432. | |
Table 1 summarizes the derived tensors for the molecular models discussed. Note that it coincides with the complete table of optical activity tensors in crystallography.1
Table 1 Optically active crystal classes in international (and in Schönflies) notations and their associated OA tensors
| Crystal system |
Crystal class point symmetry |
OA tensor |
Crystal system |
Crystal class point symmetry |
OA tensor |
| Triclinic (biaxial) |
1 (C1) |

|
Trigonal, tetragonal, hexagonal (uniaxial) |
3, 4, 6 (C3, C4, C6) |

|
| Monoclinic (biaxial) |
2 (C2) |
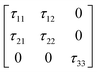
|
32, 422, 622 (D3, D4, D6) |

|
m (Cs![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C1h) C1h) |

|
3m, 4mm, 6mm (C3v, C4v, C6v) |

|
| Orthorhombic (biaxial) |
222 (D2![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) V) V) |

|
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) (S4) (S4) |

|
|
mm2 (C2v) |

|
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m (D2d 2m (D2d![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Vd) Vd) |
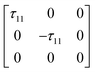
|
| |
Cubic (isotropic) |
23, 432 (T, O) |

|
Conclusions
By combining the phenomenological description of OA with the inhomogeneous forms of electromagnetic constitutive relations, it was possible to construct microscopic models based on systems of coupled oscillators for optically active media and structures. Specifically, the evaluation of the OA-induced polarisation and magnetization of a system of coupled oscillators obeying the symmetries of an ordered medium of interest allowed to derive parameterised forms of the gyration and permittivity tensors of the medium. In particular, the coupled oscillator model of the gyration tensor enabled to establish a convenient list of properties common to all optically active media. The proposed approach is very general: the only condition for its applicability is knowing the symmetries of the ordered medium. To illustrate it, parameterised models of all optically active crystal classes were constructed. We believe that this contribution is of interest to modelling theoreticians as it provides them with microscopic models for arbitrary ordered structures and to experimentalists willing to describe the optical responses of optically active media through their gyration and permittivity tensors in terms of a minimal set of meaningful microscopic parameters.
Author contributions
R. Ossikovski performed the analytical calculations and parameterised the molecular models. O. Arteaga performed the symbolic calculations and designed the figures. The authors jointly established the molecular models for the optically active crystal classes.
Data availability
All the data necessary for the analytical calculations and to parameterize the molecular models are provided in the manuscript. The Mathcad symbolic calculations of the molecular models of the optically active crystal classes and the code for figure plotting are freely available from O. Arteaga upon request.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was funded by projects TED2021-129639B-I00, CNS2022-136051, PID2022-138699OB-I00 (Ministerio de Ciencia e Innovación, Spain) and European Metrology Programme for Innovation and Research Grant No. 20IND04ATMOC (10.13039/100014132).
References
- R. Ossikovski, O. Arteaga and C. Sturm, Adv. Photonics Res., 2021, 2100160 CrossRef.
- J. K. O'Loane, Chem. Rev., 1980, 80, 41–61 CrossRef.
-
J.-B. Biot, Mémoires de l'Académie de Sciences de l'Institut, 1817, vol. 2, pp. 114 Search PubMed.
-
A. Fresnel, in Oeuvres complètes d'Augustin Fresnel, ed. H. de Sénarmont, E. Verdet and L. Fresnel, Imprimerie Impériale, Paris, 1866 Search PubMed.
- P. Drude, Gött. Nachr., 1904, 1, 1–8 Search PubMed;
P. Drude, The Theory of Optics, Longmans, New York, 1902 Search PubMed.
- W. Voigt, Gött. Nachr., 1903, 4, 155–185 Search PubMed.
- M. Born, Ann. Phys., 1918, 55, 177–240 CrossRef CAS;
M. Born, Optik, Springer, Berlin, 1972 Search PubMed.
- W. Kuhn, Z. Phys. Chem., Abt. B, 1929, 4, 14–36 Search PubMed; W. Kuhn, Trans. Faraday Soc., 1930, 26, 293–308 RSC.
- S. Chandrasekhar, Proc. – Indian Acad. Sci., Sect. A, 1953, 37, 468–484 CrossRef CAS; S. Chandrasekhar, Proc. R. Soc. A, 1961, 259, 531–553 Search PubMed.
- V. Vyšín, Proc. Phys. Soc., 1966, 87, 55–60 CrossRef; V. Vyšín, Opt. Commun., 1970, 1, 307–310 CrossRef.
- I. Vyšín, J. Říha and K. Sváčková, J. Opt. A:Pure Appl. Opt., 2006, 8, 584–593 CrossRef; I. Vyšín and J. Říha, Optik, 2012, 123, 1568–1579 CrossRef; I. Vyšín and J. Říha, Optik, 2016, 127, 1335–1344 CrossRef.
-
Yu. P. Svirko and N. I. Zheludev, Polarisation of Light in Non-Linear Optics, J. Wiley, New York, 1998 Search PubMed.
- T. W. H. Oates, T. Shaykhutdinov, T. Wagner, A. Furchner and K. Hinrichs, Adv. Mater., 2014, 26, 7197–7201 CrossRef CAS PubMed; M. S. Davis, W. Zhu, J. Strait, J. K. Lee, H. J. Lezec, S. Blair and A. Agrawal, Nano Lett., 2020, 20, 3656–3662 CrossRef PubMed; X. Yin, M. Schäferling, B. Metzger and H. Giessen, Nano Lett., 2013, 13, 6238–6243 Search PubMed; H. Kurosawa and S. Inoue, Phys. Rev. A, 2018, 98, 053805 CrossRef; W. Wu, W. Liu, Z. Chun, Y. Ling, J. Ding, X. Wang, L. Huang and H. Li, Opt. Express, 2020, 20, 29496–29512 Search PubMed.
- M. A. Kuntman, E. Kuntman, J. Sancho-Parramon and O. Arteaga, Phys. Rev. B, 2018, 98, 045410 CrossRef CAS; M. S. Davis, W. Zhu, J. K. Lee, H. J. Lezec and A. Agrawal, Sci. Adv., 2019, 5, eaav8262 CrossRef PubMed; X. Gui, M. Hentschel, J. Defrance, J. Krauth, T. Weiss and H. Giessen, ACS Photonics, 2019, 6, 3306–3314 CrossRef; L. A. McCarthy, K. W. Smith, S. A. Hosseini, L. Bursi, A. Alabastri, W. S. Chang, P. Nordlander and S. Link, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 16143–16148 CrossRef; N. Karimitari, B. Ai and Y. Zhao, J. Phys. D: Appl. Phys., 2022, 55, 325104 CrossRef.
- Y. Zhao, A. Galiautdinov and J. Tie, Nanomaterials, 2024, 14, 270 CrossRef CAS.
-
L. D. Landau and E. M. Lifshitz, Electrodynamics of Continuous Media, Pergamon Press, Oxford, 1960 Search PubMed.
- S. F. Boys, Proc. R. Soc. London, 1934, 144, 655–675 CAS.
- E. U. Condon, Rev. Mod. Phys., 1937, 9, 432–457 CrossRef CAS.
- F. I. Fedorov, Sov. Phys. Uspekhi, 1973, 15, 849–851 CrossRef.
-
W. Pauli, Pauli's Lectures on Physics. Volume 2. Optics and the Theory of Electrons, Dover, New York, 2000 Search PubMed.
- B. V. Bokut’ and A. N. Serdyukov, Sov. Phys. JETP, 1972, 34, 962–964 Search PubMed.
- R. Ossikovski and O. Arteaga, Opt. Lett., 2017, 42, 3690–3693 CrossRef.
- C. Sturm, V. Zviagin and M. Grundmann, Opt. Lett., 2019, 44, 1351–1354 CrossRef CAS.
-
H. A. Lorentz, The Theory of Electrons, Dover, New York, 2011 Search PubMed.
- L. Rosenfeld, Z. Phys., 1928, 52, 161–174 CrossRef CAS; H. Nakano and H. Kimura, J. Phys. Soc. Jpn., 1969, 27, 519–535 CrossRef.
-
E. B. Graham and R. E. Raab, in Advances in Complex Electromagnetic Materials, ed. A. Priou, et al., Kluwer, 1997 Search PubMed.
-
D. J. Caldwell and H. J. Eyring, Theory of Optical Activity, Wiley, New York, 1971 Search PubMed.
-
R. E. Raab and O. L. De Lange, Multipole Theory in Electromagnetism, Clarendon Press, Oxford, 2005 Search PubMed.
-
F. N. H. Robinson, Macroscopic Electromagnetism, Pergamon Press, Oxford, 1973 Search PubMed.
-
L. Rosenfeld, Theory of Electrons, Dover, New York, 1965 Search PubMed.
- D. Franta, J. Appl. Phys., 2020, 127, 223101 CrossRef CAS; D. Franta and J. Vohánka, J. Opt. Soc. Am. B, 2021, 38, 553–561 CrossRef; D. Franta, J. Vohánka and B. Hroncová, J. Opt. Soc. Am. B, 2023, 40, 2928–2941 CrossRef; B. Hroncová, D. Franta, J. Dvořák and D. Pavliňák, J. Opt. Soc. Am. B, 2023, 40, 3209–3220 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Oriol
Arteaga
*a and
Oriol
Arteaga
 *b
*b




 , n = 1, 2, …, N. Note that the matrix D is symmetric by virtue of the reciprocity of the coupling within the pairs of oscillators.
, n = 1, 2, …, N. Note that the matrix D is symmetric by virtue of the reciprocity of the coupling within the pairs of oscillators.






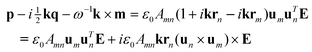



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θkcos
θkcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φk sin
φk sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θksin
θksin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φk cos
φk cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θk]T,
θk]T,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos
θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 sin
φ1 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin
θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 cos
φ1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T
θ1]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos
θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 sin
φ1 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin
θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 −cos
φ1 −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T
θ1]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 sin
φ2 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 0]T
φ2 0]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ3 sin
φ3 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ3 0]T
φ3 0]T
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos
θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 sin
φ1 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin
θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 cos
φ1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T
θ1]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2cos
θ2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 sin
φ2 sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2sin
θ2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 cos
φ2 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2]T
θ2]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos
θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp sin
φp sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin
θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp cos
φp cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T
θp]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos
θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −sin
φp −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin
θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos
φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T
θp]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos
θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 −sin
φ1 −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1sin
θ1sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ1 cos
φ1 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T
θ1]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2cos
θ2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 −sin
φ2 −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2sin
θ2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ2 cos
φ2 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2]T
θ2]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos
θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −sin
φp −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin
θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp cos
φp cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T
θp]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos
θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp sin
φp sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin
θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos
φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T
θp]T

![[4 with combining macron]](https://www.rsc.org/images/entities/b_char_0034_0304.gif) . This tetragonal class has a single inversion 4-fold axis along the z-axis. Its tensor is traceless symmetric:
. This tetragonal class has a single inversion 4-fold axis along the z-axis. Its tensor is traceless symmetric:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin
θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −sin
φp −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos
θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos
φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T
θp]T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpsin
θpsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp sin
φp sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θpcos
θpcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φp −cos
φp −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θp]T
θp]T![[4 with combining macron]](https://www.rsc.org/images/entities/b_char_0034_0304.gif) 2m. Besides the single inversion 4-fold axis along the z-axis, this class has two orthogonal 2-fold axes perpendicular to the 4-fold axis and two mirror planes containing the 4-fold axis and bisecting the two 2-fold axes. Its tensor is traceless diagonal:
2m. Besides the single inversion 4-fold axis along the z-axis, this class has two orthogonal 2-fold axes perpendicular to the 4-fold axis and two mirror planes containing the 4-fold axis and bisecting the two 2-fold axes. Its tensor is traceless diagonal:
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) . It is therefore sufficient to use φ1 = 0, θ1 = π/4 and φp = θp = π/2 in the model equations for class
. It is therefore sufficient to use φ1 = 0, θ1 = π/4 and φp = θp = π/2 in the model equations for class ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) from the previous subsection. The configuration is shown in Fig. 7. The only model parameter is the common coupling coefficient cc.
from the previous subsection. The configuration is shown in Fig. 7. The only model parameter is the common coupling coefficient cc.

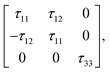



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 0 cos
θ1 0 cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1]T
θ1]T , and are located at mid-points between the summits so that v1 = [1 0 0]T, v2 = [−1 0 0]T, v3 = [0 1 0]T, v4 = [0 −1 0]T, v5 = [0 0 1]T and v6 = [0 0 −1]T, as shown in Fig. 11. The tensor is given by the contributions of the three Kuhn's pairs consisting of opposite coupled oscillators with equal pairwise coupling coefficients, i.e.eqn (60) is applied with all cij equalling cc (because all oscillators are equidistant from the origin). It reduces to a scalar proportional to the coupling coefficient cc, and only molecular enantiomorphism occurs.1
, and are located at mid-points between the summits so that v1 = [1 0 0]T, v2 = [−1 0 0]T, v3 = [0 1 0]T, v4 = [0 −1 0]T, v5 = [0 0 1]T and v6 = [0 0 −1]T, as shown in Fig. 11. The tensor is given by the contributions of the three Kuhn's pairs consisting of opposite coupled oscillators with equal pairwise coupling coefficients, i.e.eqn (60) is applied with all cij equalling cc (because all oscillators are equidistant from the origin). It reduces to a scalar proportional to the coupling coefficient cc, and only molecular enantiomorphism occurs.1















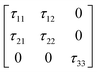

![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)