Trapping a non-cognate nucleotide upon initial binding for replication fidelity control in SARS-CoV-2 RNA dependent RNA polymerase†
Moises E.
Romero‡
a,
Shannon J.
McElhenney‡
 a and
Jin
Yu
a and
Jin
Yu
 *b
*b
aDepartment of Chemistry, University of California, Irvine, CA 92697, USA
bDepartment of Physics and Astronomy, Department of Chemistry, NSF-Simmons Center for Multi-scale Cell Fate Research, University of California, Irvine, CA 92697, USA. E-mail: jin.yu@uci.edu
First published on 11th December 2023
Abstract
The RNA dependent RNA polymerase (RdRp) in SARS-CoV-2 is a highly conserved enzyme responsible for viral genome replication/transcription. To understand how the viral RdRp achieves fidelity control during such processes, here we computationally investigate the natural non-cognate vs. cognate nucleotide addition and selectivity during viral RdRp elongation. We focus on the nucleotide substrate initial binding (RdRp active site open) to the prechemical insertion (active site closed) of the RdRp. The current studies were first carried out using microsecond ensemble equilibrium all-atom molecular dynamics (MD) simulations. Due to the slow conformational changes (from open to closed) during nucleotide insertion and selection, enhanced or umbrella sampling methods have been further employed to calculate the free energy profiles of the nucleotide insertion. Our studies find notable stability of noncognate dATP and GTP upon initial binding in the active-site open state. The results indicate that while natural cognate ATP and Remdesivir drug analogue (RDV-TP) are biased toward stabilization in the closed state to facilitate insertion, the natural non-cognate dATP and GTP can be well trapped in off-path initial binding configurations and prevented from insertion so that to be further rejected. The current work thus presents the intrinsic nucleotide selectivity of SARS-CoV-2 RdRp for natural substrate fidelity control, which should be considered in antiviral drug design.
1 Introduction
The SARS-CoV-2 virus responsible for the COVID-19 pandemic continues to evolve1 and pose a threat to human life.2 While much of the drug development besides successful vaccines has been focused on targeting the viral spike protein3–6 or the main protease,7–10 there are significant challenges remaining. The spike protein is known for its high variability1,11,12 and the protease13 can also mutate, becoming resistant to drugs, e.g., as seen in Hepatitis C virus (HCV).14,15 In contrast, the core replication machinery of SARS-CoV-2, the RNA dependent RNA polymerase (RdRp) or nonstructural protein nsp12, is a highly conserved drug target.16,17 Here we focus on studying SARS-CoV-2 RdRp to understand its elongation and fidelity control mechanism incorporating nucleotide substrates during viral replication for future antiviral drug development. Although nucleotide analogue compounds or inhibitors have been widely implemented for targeting on viral RdRps, the underlying mechanism remains vague.18–22 It is expected that successful nucleotide analogue drugs would overcome the RdRp fidelity control so that they can inhibit the viral replication.Upon the pandemic upheaval in 2020, a few high-resolution cryo-EM structures of SARS-CoV-2 RdRp were released immediately, including an apo form with the RdRp active site open23,24 and a post-catalysis form with the active site closed.24 The post-catalysis structure was bound with a nucleotide drug analogue from remdesivir (RDV).24 These structures were in complex with segments of the nsp7/nsp8 cofactors. Later, additional high-resolution structures were resolved with longer nsp8 being “sliding poles”,25 as well as RdRp in conjunction with the nsp13 helicase enzyme,26 and in both pre- and post-translocation states.27 Further structures also illustrated RdRp back-tracking28 or stalling29 due to the interaction with the drug analogue RDV. Similarly, there were structures obtained with favipiravir, another nucleotide analogue drug.30,31 Overall, these structures adopt the post-catalysis state24 in the nucleotide addition cycle (NAC) of the viral RdRp, leaving the initial nucleotide binding (active site open) and pre-catalytic insertion or substrate (closed) states unresolved. It was only very recently that the insertion state with ATP as a cognate nucleoside triphosphate (NTP) bound in the active site was resolved.32 Currently, the initial binding or open state structure of RdRp remains unresolved, although the corresponding structure has been identified for poliovirus33 (PV) or enterovirus34 (EV) RdRp, which share structural similarities with SARS-CoV-2 RdRp.
Efforts to identify drug inhibitors for SARS-CoV-2 RdRp have been extensively made.18,35,36 Computational docking has often been employed, which predominantly focuses on nucleotide immediate binding to an apo-form RdRp structure,37,38 non-differentiating the active open or closed form, and initially largely overlooking the functional RdRp (nsp12) elongation complex composed additionally of nsp8, nsp7, and RNA strands.39 Moreover, while atomic molecular dynamics (MD) studies have provided insights into interactions of nucleotide analogues with the viral RdRp, they often directly utilize the insertion state,40–42 ignoring the initial nucleotide analogue binding stage that can be essential for nucleotide screening or selectivity upon entry. Meanwhile, single-molecule studies have offered a glimpse into the dynamics of the elongation cycle, revealing that RdRp can adopt fast, slow, or very slow catalytic pathways with variable rates contingent upon the kinetic pathway.43 Additionally, information in regard to the RdRp translocation in the NAC has advanced through the cryo-EM studies, which demonstrated structural re-arrangement in nsp8 to accommodate the exiting RNA duplex.27 Computational work has shown that the incorporation of RDV-TP into the primer strand results in a steric clash at the conserved motif-B of the RdRp leading to an unstable post-translocation state in comparison with pre-translocation, i.e., as a mechanism for antiviral analogue termination of elongation.44 An alternative suggestion based on single-molecule studies43 proposes that RdRp backtracks up to 30 nucleotides (nts) after RDV-TP incorporation, which can be interpreted as elongation termination in standard assays. Despite these efforts on quantitative studies of the RdRp NAC, a critical gap remains in understanding initial nucleotide substrate binding to insertion, which is fundamental for nucleotide selectivity and antiviral drug design, given the substrate screening and pre-chemistry inhibition as essential fidelity checkpoints in stepwise NAC.45–47
Accompanied by the nucleotide substrate binding to insertion, a substantial protein conformational transition or active-site re-arrangement happens, which is likely to be a rate limiting step in the NAC, as demonstrated in structurally similar single-subunit RNA or DNA polymerases (RNAPs or DNAPs).48–50 The rate-limiting pre-chemical step accordingly plays a highly essential role in the nucleotide substrate selectivity.51 To quantify the process with energetics, we calculated the free energy profile or the potential of mean force (PMF) of the nucleotide insertion recently for cognate substrate ATP and the corresponding nucleotide drug analogue RDV-TP,52 and calculated in current studies the insertion PMFs of non-cognate dATP and GTP. We found that both ATP and RDV-TP become significantly more stabilized in the insertion state than upon the initial binding. In comparison with natural substrate ATP, RDV-TP behaves differently in its interaction with the template nt. As ATP forms Watson–Crick (WC) base pairing with template uracil at the +1 position, from the initial binding to insertion, RDV-TP initially forms base stacking with the template nt at +1 upon binding. RDV-TP then inserts into the active site, across an energetic barrier that is comparable to that of cognate ATP.52
Note that the RDV-TP analogue differs from the cognate ATP structurally by only a few atoms: with a 1′ cyano group attached on the sugar C1′ and 3 atomic replacements on the base. Interestingly, we have also noticed that the conserved motif-F essentially facilitates the insertion of cognate ATP via interactions with the ATP-triphosphate tail. While such phosphate interactions could potentially hinder the drug analogue RDV-TP insertion, it was subtly avoided upon sufficient thermal fluctuations from the template nt +1 that forms base stacking with RDV-TP.52
Also note that the intrinsic nucleotide selectivity serves for fidelity control in general for viral RdRp transcription/replication as well as in other RNA/DNA polymerase (RNAP/DNAP) systems.20 The equilibrium free energetic disparity between the WC template-cognate NTP base pairing vs. non-WC pairing (e.g. 2–3 kcal mol−1) cannot explain the error rate down to 10−4 to 10−6 or lower. Indeed, this fidelity control is achieved via a non-equilibrium elongation process dictated by the polymerase enzyme. The fundamental issues were initially addressed via kinetic proofreading mechanisms by Hopfield53 and Ninio.54 A recent kinetic framework addressing the stepwise nucleotide selectivity of RNAP via multiple kinetic checkpoints can be found from our previous works.46,51
In the current work, we focus on characterizing the intrinsic nucleotide polymerase enzyme selectivity of SARS-CoV-2 RdRp, i.e., the selectivity or differentiation between natural cognate NTP (ATP here) and natural non-cognate NTP substrates. To do that, we examined the nucleotide insertion dynamics of non-cognate dATP and GTP, in comparison with cognate ATP and RDV-TP analogue, and calculated the insertion PMFs of dATP and GTP starting from the initial binding stage. Since the polymerase NAC lasts over tens of milliseconds in general,43 the rate-limiting transition accompanying the nucleotide binding to insertion stage (or active site from open to closed) of RdRp is expected to be on the millisecond timescale.48–50 Therefore, this kind of insertion process cannot be sampled directly using equilibrium MD simulation that is limited by the sub-microsecond to microseconds timescale.55,56 To obtain free energetics of this dynamics process, we extended our previous methodology on employing umbrella sampling MD simulations to construct the PMFs of various NTPs from initial binding to insertion.52,57 In this implementation, harmonic forces are added to certain molecular configurations to ensure that high-energy or non-favored configurations are well sampled and the free energy profiles can be obtained after reweighting.58,59 We first constructed atomic structural models of the RdRp–nsp7–nsp8–RNA complexes bound with the noncognate nucleotide (ncNTP) species, in both the initial binding and insertion states. Subsequently, we performed all-atom equilibrium simulations at sub-microseconds in ensembles to characterize the respective initial binding and insertion states of the non-cognate dATP/GTP bound RdRp complexes. Lastly, we obtained the PMFs of the dATP/GTP insertion processes using the umbrella sampling MD simulations, following the initial insertion paths constructed on top of collective reaction coordinates (RCs), according to displacements of atomic coordinates from seven highly conserved structural motifs of RdRp (A to G) and incoming NTP (with and without the associating template nt). Our aim is to elucidate the intrinsic nucleotide selectivity of SARS-CoV-2 RdRp, which turns out to be primarily relying on ‘trapping’ the non-cognate nucleotide species upon entry or initial binding to certain configurations at the active site and preventing them from further insertion. It is expected that newly designed nucleotide drug compounds would be able to avoid this selectivity in order to be incorporated into the viral RNA chain for inhibition.
2 Methods
2.1 Modeling details
Note that recent high-resolution characterizations of post-translocation (active-site open) and insertion state (active-site closed) structures of the SARS-CoV-2 RdRp complex became available (PDB: 6YYT and 7CTT respectively).62,63 We structurally aligned the currently modeled NTP initial binding (active site open) state and insertion (active site closed) states with the above two structures, respectively (shown in the ESI,† Fig. S1), and the aligned structures showed high similarities in the active site. In addition, we also aligned the open and closed structures together in order to show subtle structural differences between the two states (ESI,† Fig. S1). Due to contact between the fingers tip and thumb subdomain of the RdRp, the open–closed conformation transition is indeed quite limited.20,33
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms in size. A cut-off of 10 Å was used to treat short range electrostatics interactions and the Particle–Mesh–Ewald (PME) algorithm to treat long range interactions.70 The LINCS algorithm is used to constrain bonds to hydrogen atoms allowing the use of a 2 fs timestep when integrating the equations of motion.64 The temperature was kept at 310 K using the velocity rescaling thermostat. The pressure was kept at 1 bar using a Berendsen barostat71 during equilibration and Parrinello–Rahman barostat72 for production, targeted MD (TMD), and umbrella simulation runs. Each system was minimized for a maximum of 50
000 atoms in size. A cut-off of 10 Å was used to treat short range electrostatics interactions and the Particle–Mesh–Ewald (PME) algorithm to treat long range interactions.70 The LINCS algorithm is used to constrain bonds to hydrogen atoms allowing the use of a 2 fs timestep when integrating the equations of motion.64 The temperature was kept at 310 K using the velocity rescaling thermostat. The pressure was kept at 1 bar using a Berendsen barostat71 during equilibration and Parrinello–Rahman barostat72 for production, targeted MD (TMD), and umbrella simulation runs. Each system was minimized for a maximum of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps using the steepest-descent algorithm, followed by a slow equilibration with restraints released (every 1 ns) going from the NVT (canonical or constant volume and temperature) ensemble to NTP (constant pressure and temperature) as previously used.52
000 steps using the steepest-descent algorithm, followed by a slow equilibration with restraints released (every 1 ns) going from the NVT (canonical or constant volume and temperature) ensemble to NTP (constant pressure and temperature) as previously used.52
For each NTP initial binding and inserted states ten 100 ns equilibration trajectories were launched, with 10 ns removed from the start, to create 900 ns for each NTP state, totaling ∼7.2 μs of simulation time for RDV-TP/ATP/dATP/GTP in both open and closed conformation states. The choice of running multiple comparatively short trajectories over a long one is to improve the sampling efficiency in the conformation space of the NTP bound structure. The generated equilibrium ensemble was then used for analysis and selection of references for free energy calculations.
2.2 Reaction coordinate (RC), launching NTP insertion path, and construction of the potential of mean force (PMF)
In order to enforce the milliseconds slow conformation transition to happen in all-atom MD simulations at sub-microseconds to measure the corresponding free energetic profile or PMF, one can implement the umbrella sampling method73,74 to enhance sampling, i.e., by imposing harmonic potentials to certain molecular configurations along a selected path or reaction coordinate (RC).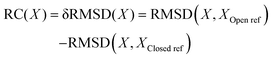 | (1) |
2.3 Structural dynamics analyses
 | ||
| Fig. 1 The constructed structural models of the SARS-CoV-2 RdRp elongation complex in its initial NTP substrate binding (open) and then inserted (closed) states. (A) The simulated elongation complex is depicted with the nsp12 pol domain (purple) and the N-terminal domain (gray), two cofactor nsp8 (blue) and nsp7 (green), RNA (red) and an NTP in the active site (left). The three major subdomains within the pol domain: fingers in blue, palm in pink, and thumb in green. The RNA is shown in red as well as NTP shown in space filling spheres (right). (B) The modeled and simulation equilibrated ATP is shown as bound initially to an open active site, with the seven protein motifs highlighted in color. The boxes to the right show the initially bound RDV-TP, dATP, and GTP that were also modeled and equilibrated from the simulations (left). The modeled and equilibrated ATP is shown in the insertion or the active site closed state, with the seven structures motifs shown as well, and the boxes to the right displaying the modeled and equilibrated insertion configurations of RDV-TP, dATP, and GTP to the closed active site (right). (C) The subdomain root mean squared deviation (RMSD) for simulating initial binding (top) and insertion (bottom) for ATP, see the ESI,† Fig. S2 for the rest of the NTPs. (D) The motif RMSD for initial binding (top) and insertion (bottom) for ATP, see the ESI,† Fig. S3 and Tables S1, S2 for the rest of the NTPs. | ||
Plots were created using python packages seaborn80 and matplotlib.81
3 Results
3.1 Equilibrium ensemble simulations: protein structural variations and distinctive dynamical responses to different NTPs upon initial binding and insertion
3.2 Constructing the PMFs for noncognate GTP/dATP from the initial binding to insertion
Upon conformational samplings from the equilibrium ensemble simulations, we noticed essential variations of protein structural motifs along with diverse NTP dynamics. Accordingly, we included structural motifs and NTP configurations into constructing a collective reaction coordinate, based on RMSD changes with respect to the open and closed state23,24 structures (see the Methods section).52,57 Upon selecting appropriate reference states for each NTP initial binding/insertion system, we then proceeded to calculate the free energy profiles or PMFs of NTP insertion and to quantify the processes for NTP selectivity from the initial binding (active site open) to the insertion (closed). The procedures of the PMF construction via umbrella sampling simulations can be found in the Methods section. The overlaps of umbrella sampling windows are provided in the ESI,† Fig. S10. In the current studies, we constructed the PMFs of the non-cognate GTP and dATP insertion, so that we can compare with the PMFs obtained previously for cognate ATP and RDV-TP.52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) binding ∼ 2 kcal mol−1 (>0). This is in contrast with cognate ATP and RDV-TP analogue insertion, which are more stabilized in the insertion state, demonstrating ΔG (<0) values of −5.2 kcal mol−1 and −2.7 kcal mol−1, respectively (Fig. 3).52 Nevertheless, the initially bound GTP forms no WB base pairing with the template nt +1, whereas approximately 81% WB base pairing between GTP and the template is identified in the insertion state. Hence, there have to be other interactions to stabilize the initial binding GTP (to be addressed in the next subsection). Additionally, the PMF calculations show that the non-cognate GTP is subject to an insertion barrier hins ∼ 7 kcal mol−1 from the initial binding state, much larger than that of ATP and RDV-TP (hins ∼ 2.6 kcal mol−1 and 1.5 kcal mol−1, respectively; see Fig. 3).52 Note that the convergence of the PMF for GTP was reached after 50 ns per window in the umbrella sampling simulation, following the protocol without (or with) enforcing on the uracil template +1 nt (Fig. S4, ESI†), which show similar results.
binding ∼ 2 kcal mol−1 (>0). This is in contrast with cognate ATP and RDV-TP analogue insertion, which are more stabilized in the insertion state, demonstrating ΔG (<0) values of −5.2 kcal mol−1 and −2.7 kcal mol−1, respectively (Fig. 3).52 Nevertheless, the initially bound GTP forms no WB base pairing with the template nt +1, whereas approximately 81% WB base pairing between GTP and the template is identified in the insertion state. Hence, there have to be other interactions to stabilize the initial binding GTP (to be addressed in the next subsection). Additionally, the PMF calculations show that the non-cognate GTP is subject to an insertion barrier hins ∼ 7 kcal mol−1 from the initial binding state, much larger than that of ATP and RDV-TP (hins ∼ 2.6 kcal mol−1 and 1.5 kcal mol−1, respectively; see Fig. 3).52 Note that the convergence of the PMF for GTP was reached after 50 ns per window in the umbrella sampling simulation, following the protocol without (or with) enforcing on the uracil template +1 nt (Fig. S4, ESI†), which show similar results.
 | ||
Fig. 3 The potentials of mean force (PMFs) calculated for NTP from the initial binding (active site open) to the insertion (closed) state via umbrella sampling simulations. The difference of RMSDs with respect to open and closed reference structures RMSD(X,XOpen![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ref) − RMSD(X,XClosed ref) − RMSD(X,XClosed![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ref),52 was used as the reaction coordinate in the PMF construction (see the Methods section, see the umbrella windows in the ESI,† Fig. S10). The top left shows the PMF for GTP (green) and top right that for dATP (magenta), both in comparison with the PMFs obtained for cognate ATP (blue) and analogue RDV-TP (pink).52,82 Smoothing has been applied to each PMF for clarity (see the original PMFs and converging tests in the ESI,† Fig. S4). Note that the placement of the PMF of GTP relative to that of ATP/RDV-TP is according to the alchemical calculation in the closed state,82 while the placement of the PMF of dATP relative to that of ATP/RDV-TP is still uncertain, as the relative binding free energy at the closed state, denoted as δg, is estimated between 2–7 kcal mol−1 (see the text). The bottom left shows schematics of the different PMF profiles for the cognate and ncNTP insertions. The bottom right shows the insertion free energy and barrier heights for the four PMFs shown in the top panel. ref),52 was used as the reaction coordinate in the PMF construction (see the Methods section, see the umbrella windows in the ESI,† Fig. S10). The top left shows the PMF for GTP (green) and top right that for dATP (magenta), both in comparison with the PMFs obtained for cognate ATP (blue) and analogue RDV-TP (pink).52,82 Smoothing has been applied to each PMF for clarity (see the original PMFs and converging tests in the ESI,† Fig. S4). Note that the placement of the PMF of GTP relative to that of ATP/RDV-TP is according to the alchemical calculation in the closed state,82 while the placement of the PMF of dATP relative to that of ATP/RDV-TP is still uncertain, as the relative binding free energy at the closed state, denoted as δg, is estimated between 2–7 kcal mol−1 (see the text). The bottom left shows schematics of the different PMF profiles for the cognate and ncNTP insertions. The bottom right shows the insertion free energy and barrier heights for the four PMFs shown in the top panel. | ||
The placement of the GTP insertion PMF relative to that of ATP/RDV-TP was conducted according to alchemical simulations performed recently.82 Given that the GTP-template WB base pairing geometries are comparatively stable in the insertion state (Fig. 3 lower right), we placed the GTP insertion state ∼3 kcal mol−1 above that of the ATP insertion state, as the alchemical calculations indicate that ΔΔGbinding 2.95 ± 0.66 kcal mol−1 for the relative binding free energy of GTP with respect to ATP in the insertion state.82
The placement of the dATP insertion PMF relative to that of ATP/RDV-TP is, however, less certain. Given a wide range of association configurations between dATP and template even in the insertion state (Fig. 2 upper right), one cannot directly use the alchemical calculation results, which were conducted around local configurational space (for stabilized ATP and slightly destabilized dATP) with limited sampling.82 An estimation is nevertheless made here, based on the relative binding free energy calculated locally between dATP and cognate ATP (∼2 kcal mol−1) along with that from the mmPBSA calculation (∼7 kcal mol−1),82 suggesting a range of free energetic values 2–7 kcal mol−1 in between the inserted dATP and ATP (shown as parameter δg in Fig. 3).
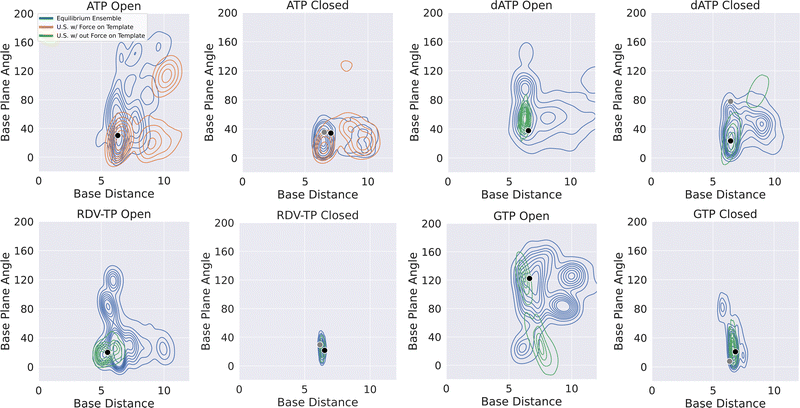 | ||
| Fig. 4 Comparing NTP-template association geometry distributions obtained from the umbrella sampling simulations (for the PMF calculations) and that from the ensemble equilibrium simulations. A kernel density estimate has been used to visualize the data. For each simulation system (open and closed, for ATP, RDV-TP, dATP and GTP as in Fig. 2), the equilibrium ensemble distribution is shown (blue), along with that obtained from the umbrella sampling (w/force on template +1 nt in orange; w/out force on the template +1 nt in green; see the Methods section and the ESI,† for further details). The black dot indicates the reference state used to generate the initial paths (see the Methods section) for the umbrella sampling, and the grey dot the reference state used in the alchemical calculations,82 for the full dataset see the ESI,† Fig. S13. | ||
Since the initially bound non-cognate dATP or GTP could not be well stabilized by association with the template +1 nt (nor the 3′-end primer), it must be interactions from the RdRp protein along with the RNA scaffold around the active site that strongly hold the non-cognate dATP or GTP, which we examine and elaborate below.
3.3 Trapping noncognate dATP/GTP upon initial binding by persistent HB interactions from motif F/G/A, to NTP, template nt +1, or 3′ end primer
Though there were no WC or WB base pairing interactions observed for non-cognate dATP/GTP with the template uracil upon initial binding toward the open active site, some populations of dATP/GTP are strongly stabilized upon the initial binding according to their insertion free energetics or PMFs (shown in Fig. 3). To gain understanding of this phenomena, we analyzed all HB interactions present among protein residues, NTP, and RNA strands (template and primer), around the active site. Given the variations amongst NTPs, we simplified the analyses by summing up the overall HB populations exceeding 10–20% of occupancy (during the umbrella simulation 40 ns per window) amongst the protein (residues within 10 Å of the active site center), template +1 nt, 3′ end of the primer, and the initially bound NTP; those HBs were further grouped according to interactions with the NTP on polyphosphate, sugar, or base (see Fig. 5). The cumulative HB measure is then calibrated over that of the cognate ATP. Accordingly, those HB components showing small deviations from the ATP level are regarded similar in strength with that in the ATP binding system. Those deviating largely from the ATP level are notable HBs that differentiate noncognate GTP/dATP from ATP. | ||
| Fig. 5 Summary of hydrogen bonding (HB) interactions that stabilize non-cognate GTP/dATP or surroundings upon initial binding from umbrella sampling simulations. Four interacting partners are considered: protein, incoming NTP (ATP, RDV-TP, dATP, and GTP), uracil template nucleotide +1, and the 3′-end primer. The HBs with occupancy >10–20% in the simulations were identified among these four interaction partners. The relative HB occupancy levels are shown for the initial binding dATP and GTP (along with RDV-TP) with respect to that of cognate ATP as reference (with bar; see the ESI,† Fig. S14 for full HB statistics for all the simulation systems). | ||
As a result, by reading the HB components shown in Fig. 5, one can see that GTP differs from ATP in the initial binding by protein HBs formed with its phosphates and sugar, and protein HBs with template nt +1, similar to ATP by protein HBs with its base, and almost no HB formed with the 3′-end primer as in ATP binding (ESI,† Fig. S14). In comparison, one sees that dATP differs from ATP mainly by protein HBs with its base and 3′-end primer, and 3′-end primer HB with its sugar; while dATP is similar to ATP on protein HB with its sugar and with template nt.
Notably, one finds that the GTP initial binding is stabilized predominantly by HBs (and salt bridges in the case of positively charged residues LYS/ARG) formed between its polyphosphate group and the protein residues in motifs (mainly motif F and A). In addition, the protein residues (motif F and G) stabilize particularly the template nt +1, due to the absence of WC or WB base pairing between the initially bound GTP and the template nt. Meanwhile, there is a lack of protein HB association with the 3′ end primer around the initially bound GTP. However, this association is present around the initially bound RDV-TP (see the ESI,† Fig. S14), and the association appears even stronger around the initially bound non-cognate dATP.
In the case of dATP initial binding, though it does not form WC base pairing with the template nt +1, the adenine base is nonetheless stabilized via protein HB (again from motif-F). Intriguingly, despite dATP's lack of a 2′ OH group, it still maintains a strong HB via the sugar and the 3′ end primer. As mentioned above, the 3′ end primer around the initially bound dATP displays the strongest HB interactions among all the NTPs with the protein.
Below, we show the individual HB interactions structurally around GTP and dATP and compare them with those in the case of cognate RDV-TP or ATP binding, respectively (Fig. 6 and 7). One can find statistics of HBs formed between NTP (polyphosphate, sugar, or base) and protein residues or template nt +1/3 end primer, and between protein residues and template nt +1 or the 3 end primer (ESI,† Fig. S14).
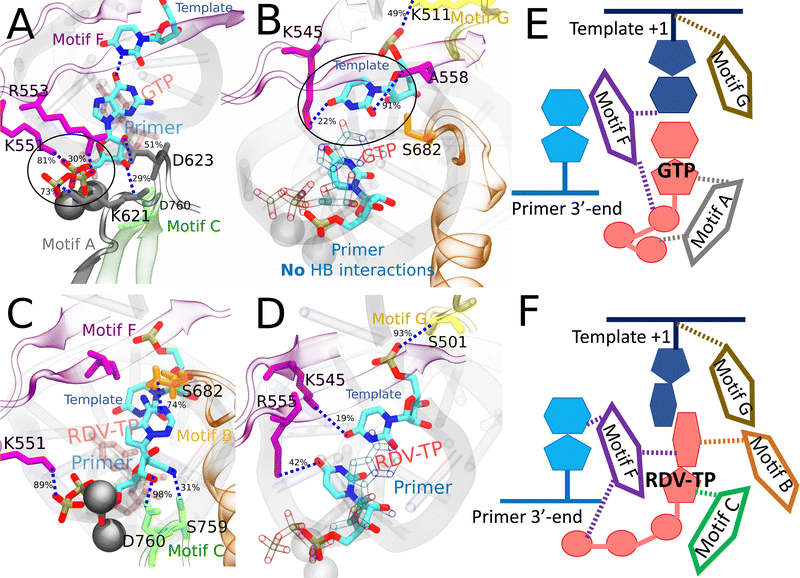 | ||
| Fig. 6 Comparing key interactions that stabilize the non-cognate GTP (and surroundings) and drug analogue RDV-TP in the initial binding system. The conserved protein motifs are shown in cartoon representation while interacting residues from these motifs are shown in licorice using the same color. (A) and (C) Incoming GTP/RDV-TP and template nucleotide are shown in licorice colored by atom name. Hydrogen bonds (HBs) formed between GTP (or RDV-TP) and template nucleotide uracil/protein/3 end RNA primer. The black circle highlights the essential interactions involved in trapping non-cognate GTP phosphate in the initially bound state (A), which are absent for RDV-TP phosphate (C). HBs formed between the protein and template for stabilization, without appropriate WB base pairing for GTP-template (B) and with template base stacking in RDV-TP (D). For detailed HB occupancy plots see the ESI,† Fig. S14. (E) Schematic and cartoon of key motifs stabilizing GTP. (F) Schematic and cartoon of key motifs stabilizing RDV-TP. For stereoscopic views of (A) and (B) see the ESI,† Fig. S15. | ||
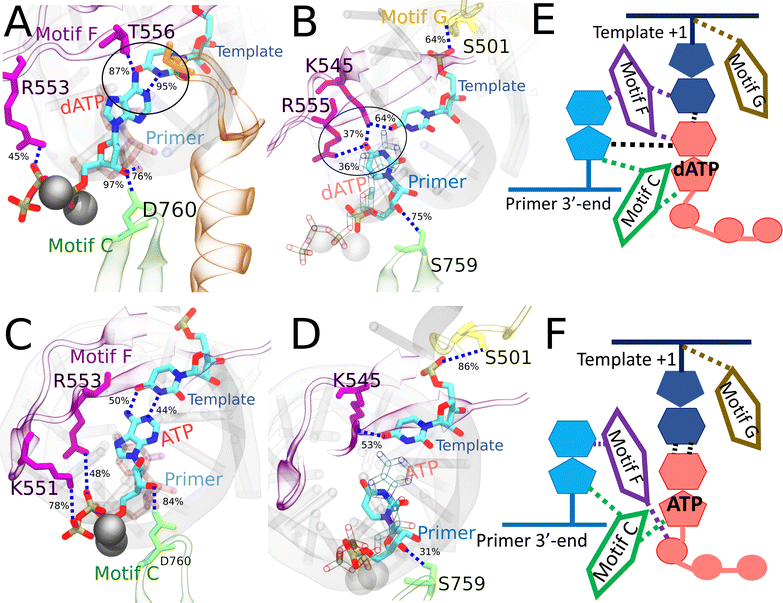 | ||
| Fig. 7 Comparing the key interactions that stabilize the non-cognate dATP (and surroundings) and cognate ATP in the initial binding system. The conserved protein motifs are shown in cartoon representation while interacting residues from these motifs are shown in licorice using the same color. (A) and (C) Incoming dATP/ATP and template nucleotide are shown in licorice colored by atom name. Hydrogen bonds (HBs) formed between dATP (or ATP) and template nucleotide uracil/protein/3′-end RNA primer. The black circle highlights the strongest interactions involved in trapping non-cognate dATP in the initially bound state. (B) and (D) Incoming dATP/ATP is shown in transparent representation for clarity, and the 3′-end primer and template nucleotide are shown in licorice colored by atom name. HBs formed between the protein and template nucleotide uracil/3′-end RNA primer for stabilization, in the absence of appropriate WC base pairing in dATP (B). HBs formed between the protein and template nucleotide uracil/3′-end RNA primer for stabilization, with appropriate WC base pairing in ATP (D). For detailed HB occupancy plots see the ESI,† Fig. S14. (E) Schematic and cartoon of key motifs stabilizing dATP. (F) Schematic and cartoon of key motifs stabilizing ATP. For stereoscopic views of (A) and (B) see the ESI,† Fig. S16. | ||
In the case of RDV-TP initial binding via base stacking with the template nt +1 (in the absence of force on the template nt), however, only one HB is observed on the polyphosphate from motif-F K551 (see Fig. 6C and Table S4, ESI†), so that the RDV-TP won’t be hindered by the phosphate interaction for its insertion.52 In addition, the base stacking configuration of RDV-TP with the template allows for a unique HB to form between motif-B S682 and the RDV-TP base, while the template nt +1 has fewer HBs with motif-F than that upon GTP initial binding (Fig. 6D and Table S4, ESI†).
In the case of ATP initial binding, its base is stabilized by forming occasional WC base pairing. Note that the initially bound ATP formed two HBs with template nt +1, with occupancies of 50% and 44%, respectively. The ATP sugar forms a consistent single HB with motif-C D760. Stable associations also form between motif-F K551/R553/R555 and the ATP polyphosphate (Fig. 7C and Table S4, ESI†). These interactions were suggested to facilitate the cognate ATP insertion instead.52 The template nt +1 forms a stable HB with motif-F K545 and motif-G S501, similar to dATP initial binding. In addition, the 3′ end primer forms only a single transient HB with motif-C S759 (Fig. 7D and Table S4, ESI†), weaker than that present between the 3′ end and motif-C/F upon the dATP initial binding (Fig. 7B and Table S4, ESI†).
4 Discussion
In current work, we have focused on computationally probing from the initial binding to the insertion and selectivity mechanisms of noncognate natural nucleotides to SARS-CoV-2 RdRp. Note that for viral RdRp core structures, the fingers subdomain has its tip touching the top of thumb subdomain to encircle the active site, so that it cannot support large conformational changes upon incoming nucleotide binding and insertion, during which nucleotide selection takes place.20,33,34 The insertion step process involves a subtle conformational change of the RdRp pol domain (Fig. 1), leading to essentially an active site open or nucleotide initial binding state to the active site closed or insertion state, with coordination of seven highly conserved structural motifs. In all NTP incorporation systems simulated, the fingers subdomain displays similar low conformational flexibility as the palm subdomain, which moves closer to the finger's subdomain in the insertion state than in the initial NTP binding state (ESI,† Fig. S2). In the insertion state of cognate ATP or RDV-TP, motif-B and C have similar conformational flexibility (via RMSD) demonstrated in the equilibrium simulation, while this feature is absent in noncognate GTP (ESI,† Fig. S3). Overall, the motifs respond differently for each incoming NTP studied. The equilibrium ensemble simulations showed generically that the insertion state sampled a restricted subspace between the NTP and template nt +1 over that of the initial binding state, which indeed accommodates a wide range of configurations (Fig. 2). Additionally, RNA template/primer nucleotides or protein residues around the active site forms more HBs with the NTP in the insertion state than in the initial binding state (ESI,† Fig. S8).Due to the time scale limit of equilibrium sampling, we probed the NTP insertion dynamics and calculated the corresponding insertion energetics using the umbrella sampling methods. The energetic profile or insertion PMF was constructed along a collective RC according to a difference of RMSDs between the modeled intermediate structure of the RdRp and the open and closed reference states, respectively. The essential atomic coordinates included those of backbone atoms from seven highly conserved structural motifs (A to G), which are crucial for recruiting nucleotide substrates with selectivity and supporting catalysis,83 and heavy atoms on incoming NTP along with (or without) the template nt +1. While this choice on enforcing on the template nt or not played some significant role in the PMF construction of cognate ATP and analogue RDV-TP (see the ESI,† Fig. S4),52 it made little difference in the non-cognate dATP or GTP results, e.g., as observed from the base pairing geometry measured between NTP and template nt +1 (Fig. 4 and Fig. S13, ESI†). The insertion barriers were not affected much by the choices for dATP or GTP either (ESI,† Fig. S4). In contrast with the insertion PMFs of cognate ATP and RDV-TP analogue that bias toward a more stabilized insertion state, we have found intriguingly that the initial binding states for ncNTPs (dATP and GTP currently) can be much more stabilized than their insertion state. In addition, the insertion barrier of ncNTP becomes very high (up to 7–10 kcal mol−1), also in contrast with the marginally low insertion barriers of cognate ATP and RDV-TP (∼2 kcal mol−1) identified previously.52 These free energetic calculations and structural dynamics examinations reveal intrinsic nucleotide selectivity of SARS-CoV-2 RdRp, i.e., to inhibit the insertion of ncNTPs to the active site by trapping the ncNTPs off-path upon initial binding to the peripheral of the RdRp active site.
4.1 Free energetics favor insertion of cognate NTPs but disfavor insertion of non-cognate NTPs
In previous work,52 we calculated the insertion PMFs for ATP and RDV-TP, respectively. While the RDV-TP initial binding could form WC base pairing with the template nt +1, a more stabilized conformation was found for RDV-TP in base stacking with the template nt +1. Besides, the RDV-TP insertion barrier would become high (hins ∼ 5 kcal mol−1) when the enforcing in the umbrella sampling simulation included the template nt +1 (ESI,† Fig. S17A). The striking feature was due to the enhanced HB (or salt-bridge from positively charged LYS/ARG) interactions between the motif-F residues (K551/R553/R555) and the RDV-TP polyphosphate (ESI,† Fig. S17B), upon the enforcing on the template nt. Removing forcing on the template nt +1, i.e., allowing sufficient thermal fluctuations on the template, however, the motif-F interactions with the polyphosphate reduce, and the insertion barrier lowers to a marginal value (hins ∼ 1.5 kcal mol−1).Upon the cognate ATP binding, including the template nt +1 for enforcing in the umbrella sampling simulations nevertheless supports an insertion barrier hins as low as ∼2.6 kcal mol−1 (ESI,† Fig. S17A). The well controlled template nt +1 facilitated WC base pairing and supported enhanced HB interactions between the motif-F K551/R555 and polyphosphate (ESI,† Fig. S17C). Consequently, it was suggested that the motif-F interactions with the phosphate actually facilitate insertion of the cognate ATP, while the motif F-phosphate interactions also appear to be important for NTP insertion in the PV RdRp.84 Regardless of the exact protocol, the insertion state was always more stable than the initial binding state for the cognate ATP and analogue RDV-TP, both of which are actively biased or recruited into the closed active site for catalytic incorporation to the 3′-end of primer, experiencing marginally high barriers of insertion to the active site.52
In contrast, upon the initial binding of ncNTP (dATP or GTP), a large configuration space of the ncNTP with respect to the template +1 nt and 3-end primer was identified, and the PMF tilts toward the initial binding state, i.e., biased or energetically stabilized upon initial binding of certain ncNTP configurations (Fig. 3 and Fig. S4, ESI,†). Additionally, the insertion barriers insertion became very large for noncognate GTP and dATP (hins ∼ 7.0 and 9.6 kcal mol−1, respectively). The stability bias toward the initial binding state and tremendously large barrier of insertion seem to trap the ncNTP upon initial binding at certain configurations (or the off-path), which would likely lead to dissociation of the ncNTPs from the active site or from the RdRp in the end.
Our current discoveries regarding such stabilization of the non-cognate substrate upon initial binding may seem counterintuitive. Commonly, the high binding affinity of a ligand substrate to the receptor protein indicates a preference of the receptor to the substrate.85,86 This idea prevails in the drug design which aims at identifying high-affinity binders. In the current viral RdRp system, however, the NAC proceeds with two pre-chemical steps: substrate initial binding and insertion. As shown in the current study, a high substrate binding affinity at the first step may also contribute to the high insertion barrier for the second step, which slows down the NAC or an enzymatic cycle. Hence, the ncNTP stabilization or trapping upon initial binding becomes an intriguing but effective strategy to deter or inhibit the non-cognate substrate from further incorporation. On the other hand, antiviral drug design targeting on the viral RdRp would develop nucleotide analog drug compounds that are capable of avoiding or escaping from such a trapping mechanism of nucleotide selectivity upon initial binding.
4.2 Key residues from conserved motifs detect and stabilize the non-cognate dATP/GTP and its surroundings at the initial binding off-path state
Current free energy calculations reveal that the noncognate GTP/dATP is more stabilized upon initial binding to the RdRp active site than in the insertion state, in contrast with cognate ATP/RDV-TP which is more stabilized in the insertion state. To explain notable stabilized configurations sampled for the ncNTP initial binding state from the umbrella sampling simulations, we identified a variety of HB interactions around the active binding site formed among NTP (base, sugar and phosphate), RNA strands (template and primer), and the conserved protein motifs (Fig. 5). To well explain the trapping mechanism, we can also compare the current system with a previously studied RdRp from enterovirus or EV,34 which is structurally similar to SARS CoV-2 RdRp. In EV RdRp, NTP insertion to the active site is suggested via several steps: first the base recognition, next the ribose sugar recognition, and then followed by the active site open to closed conformational transition, accompanied by the palm subdomain (motifs A, B, C, D, E) closing. Below we connect current observations of NTP initial binding to those suggested steps.In the case of GTP initial binding, the template nt +1 (uracil) fails to interact with the mismatch GTP in the absence of WC or WB base pairing. The template nt +1 and GTP cannot be mutually stabilized, hence the protein motif-F residues (K545/A558) respond by stabilizing the template base. Additionally, motif-G K511 forms HB with the template RNA backbone, instead of S501 in the ATP/RDV-TP system. Given the non-stabilized GTP base, the sugar is next checked by the protein via motif-A D623, which is prominent upon GTP initial binding (in the umbrella sampling ensemble). The D623 interaction brings motif-A closer to GTP and allows a unique HB (or salt bridge) from K621 to the polyphosphate. Substantial HBs (or salt bridges) with the polyphosphate come additionally from motif-F K551/R553, similarly as seen in RDV-TP (with force on template nt +1). In both cases of initial binding (GTP and RDV-TP with force on the template nt +1), the insertion barriers are high. Such observations support the previously proposed mechanism that the Lys/Arg interactions with phosphates inhibit the ncNTP insertion but facilitate cognate NTP insertion,52 or say, the protein-NTP phosphate interactions play a significant role in nucleotide selectivity or fidelity control. Recent NMR experiments on the structurally similar PV RdRp suggest that interactions from charged residues in motif-F are an important fidelity checkpoint, as they allow the triphosphate to rearrange prior to catalysis.87
In the case of dATP binding, obviously, it fails on the sugar recognition. The sugar is unable to anchor in the active site due to missing the 2′ OH functional groups. Instead, the 3′ OH group forms HB with motif-C D760 (Fig. 7A), similar to ATP and RDV-TP. On the other hand, since dATP has the same base as the cognate ATP, it is capable of forming stable WC base pairing with the template nt, but it does not. Indeed, the dATP base adopts a tilted conformation, which supports only one persistent HB w/template nt +1 (Fig. 7A). The dATP base is then further stabilized by motif-F T556. The missing WC base pairing between dATP and the template nt +1 in it is supplemented by another HB formed between the dATP base and motif-F K545 (Fig. 7B). In addition to the HB formed between the dATP sugar and D760 from motif C, further stabilization of dATP comes from a HB formed between the dATP sugar and 3′-end primer, and another HB formed between the 3′ end primer and motif-C S759 (Fig. 7B). Hence, it appears that the 3′-end primer plays an important role in stabilizing dATP with a network of HB interactions upon initial binding or say, off-path.
Although the non-cognate dATP initial binding stability appears perplexing, prior crystal structure studies on the structurally similar PV RdRp have used dCTP to stall and resolve the RdRp structure in the open state,33 supporting a stable binding configuration of dNTP binding to the viral RdRp. In addition, experimental work on the nsp14 exonuclease enzyme of SARS-CoV-2 has shown that for excision of an incorrect nt, the nt needs to have an appropriate RNA sugar,88 indicating the 2′ OH group of the RNA ribose is a critical component for RdRp template recognition and elongation. Furthermore, recent experimental studies have shown that an elongation complex soaked in solution with dNTPs had no catalytic activity.89 Michaelis–Menten kinetics also showed the SARS-CoV-2 RdRp selectivity of ATP over dATP is ∼1000 ( in dATP and 23 in ATP).90 Similar trends were observed in PV in vitro biochemical studies with ∼117 discrimination factor
in dATP and 23 in ATP).90 Similar trends were observed in PV in vitro biochemical studies with ∼117 discrimination factor  .91 Other computational studies also tested the design of inhibitors with ribose sugar modifications or removal of the OH function groups entirely.40,41
.91 Other computational studies also tested the design of inhibitors with ribose sugar modifications or removal of the OH function groups entirely.40,41
In general, the nucleotide selection can be achieved by initial NTP-template base pairing and then the ribose recognition. A cluster of residues responsible for the ribose hydroxyl recognition have been suggested also for the PV RdRp, in which motif A and D move toward the active site upon closing to assist nucleotide insertion and selection.33 It was also found that mutations inhibiting the open–closed transition likely improve the fidelity control.16,17 In HCV, the RdRp or N5SB has its motif B in addition to motif A for positioning ribose of incoming NTP, using an extensive hydrogen bonding network from motif A and B to recognize 2-hydroxyl of the incoming nucleotide.92 NS5B has been suggested to contain a nucleotide mediated excision mechanism in order to excise the mismatched nucleotide at the 3′-end of the nascent RNA in vitro.93,94 Interestingly, motif B involved in translocation of the HCV RdRp is also linked to fidelity control, as mutations in motif B could not only slow down translocation, but also increase the time of residency of a mismatch in the active site to allow it to be excised.93 Motif G may also affect the NTP recognition and selection as it influences the orientation of the template strand/nucleotide or nt.93 Motif F can be linked to fidelity control as well since it guides the nucleotide into the tunnel as well as directs the pyrophosphate out of the tunnel after catalysis, which can be rate limiting in NS5B to improve the fidelity.95 In the ESI,† Table S5, we provide a summary of motifs A–G and sequence alignments for various RdRps in comparison (from SARS-CoV-2, PV, EV, and HCV).
5 Conclusion
To conclude, we have employed all-atom MD simulations in equilibrium ensembles and umbrella sampling methods to demonstrate the intrinsic nucleotide selectivity of SARSCoV-2 RdRp, comparing non-cognate dATP/GTP with a cognate ATP/RDV-TP analog on structural dynamics and free energetics from binding to insertion to the RdRp active site. Our studies show that the non-cognate dATP/GTP is well stabilized or trapped upon initial binding to certain off-path configurations, as the highly conserved structural motifs F/G/A/C of the viral RdRp form HBs with the ncNTP, RNA template nt, and/or 3′-end RNA primer. Intrinsically, it is not the polymerase enzyme that determines a right/cognate or wrong/non-cognate nucleotide substrate in the template-based polymerization. The cognate or non-cognate NTP species are determined by the RNA template nt primarily via the WC base pairing, and additionally by the 3′-end primer via base stacking etc. With incoming ncNTP that is incapable of stabilizing the template counterpart or the 3′-end primer, the RdRp structural motifs sense such instability, and then take over to select against the ncNTP. Presumably, ncNTP can be rejected in the case of low binding affinity, i.e., upon initial binding to RdRp. However, it appears that in SARS-CoV-2 RdRp, the ncNTP can be particularly stabilized, say off-path, upon initial binding to certain configurations, so that to be prevented or inhibited from further insertion to the active site. This mechanism of nucleotide selection seems to be well supported by the two-step binding and insertion processes, pre-chemically, in the single-subunit viral polymerase enzymes. Partial off-path initial binding and inhibition for insertion of ncNTPs were also suggested computationally for single-subunit T7 RNAP.57,96 These nucleotide substrate selection mechanisms on trapping non-cognate species upon initial binding to prevent further incorporation would particularly draw attention from future antiviral drug design, to develop drug compounds that are capable of escaping from this kind of initial binding and trapping mechanism by the viral RdRp.Technically, we have employed the umbrella sampling simulations to characterize the slow NTP insertion dynamics that is accompanied by the open to closed conformational changes around the RdRp active site. As the slow pre-chemical conformational transition likely takes place over milliseconds, it becomes indispensable to enhance computational sampling while limiting the artifacts to be introduced. In the simulation, we well manipulated collective atomic coordinates from all structural motifs along with key players of NTP/template. Nevertheless, how to identify the most essential coordinates is a continual challenging issue.97,98 Additionally, accelerated simulations99 may be conducted to sample a sufficient number of conformational transitions, i.e., from open to closed. For multiple NTP species incorporation, enhanced computational sampling would become even more demanding, considering that multiple reaction paths exist.100 Further exploration and validation of our current studies would also require substantial experimental studies. Recent high-resolution characterizations of SARS-CoV-2 RdRp complexes have brought about additionally the post translocation and pre-catalytic states for improved modeling.62,63 Resolving high-resolution structures of the SARS-CoV-2 RdRp complexes with the stabilized off-path initial binding configurations of non-cognate dATP or GTP, as being proposed in current computational work, would be highly anticipated.
Data availability
Input files are available. Trajectories are available on request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Part of this work was supported by the National Science Foundation (NSF) Award #2028935. This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725. Additional computational resources were provided by UCI HPC3 – High Performance Community Computing Cluster. JY has also been supported by the CMCF of UCI via NSF DMS 1763272 and the Simons Foundation grant #594598 and start-up funding from UCI.Notes and references
- W. T. Harvey, A. M. Carabelli, B. Jackson, R. K. Gupta, E. C. Thomson, E. M. Harrison, C. Ludden, R. Reeve, A. Rambaut, S. J. Peacock and D. L. Robertson, Nat. Rev. Microbiol., 2021, 19, 409–424 CrossRef CAS.
- Y. Araf, F. Akter, Y. D. Tang, R. Fatemi, M. S. A. Parvez, C. Zheng and M. G. Hossain, J. Med. Virol., 2022, 94, 1825–1832 CrossRef CAS.
- P. Pandey, J. S. Rane, A. Chatterjee, A. Kumar, R. Khan, A. Prakash and S. Ray, J. Biomol. Struct. Dyn., 2020, 39, 1–11 Search PubMed.
- A. C. Papageorgiou and I. Mohsin, Cells, 2020, 9, 2343 CrossRef CAS PubMed.
- A. M. Almehdi, G. Khoder, A. S. Alchakee, A. T. Alsayyid, N. H. Sarg and S. S. Soliman, Infection, 2021, 49, 855–876 CrossRef CAS.
- R. Singh, V. K. Bhardwaj, J. Sharma, D. Kumar and R. Purohit, Comput. Biol. Med., 2021, 136, 104631 CrossRef CAS PubMed.
- S. Ullrich and C. Nitsche, Bioorg. Med. Chem. Lett., 2020, 30, 127377 CrossRef CAS PubMed.
- Z. Jin, H. Wang, Y. Duan and H. Yang, Biochem. Biophys. Res. Commun., 2021, 538, 63–71 CrossRef CAS PubMed.
- H. Tarannum, K. Rashmi and S. Nandi, Curr. Drug Targets, 2021, 23, 802–817 Search PubMed.
- V. K. Bhardwaj, R. Singh, J. Sharma, V. Rajendran, R. Purohit and S. Kumar, J. Biomol. Struct. Dyn., 2020, 1–10 CAS.
- N. Magazine, T. Zhang, Y. Wu, M. C. McGee, G. Veggiani and W. Huang, Viruses, 2022, 14, 640 CrossRef CAS.
- V. Papanikolaou, A. Chrysovergis, V. Ragos, E. Tsiambas, S. Katsinis, A. Manoli, S. Papouliakos, D. Roukas, S. Mastronikolis, D. Peschos, A. Batistatou, E. Kyrodimos and N. Mastronikolis, Gene, 2022, 814, 146134 CrossRef CAS PubMed.
- J. A. Mótyán, M. Mahdi, G. Hoffka and J. Tözsér, Int. J. Mol. Sci., 2022, 23, 3507 CrossRef.
- S. Iketani, H. Mohri, B. Culbertson, S. J. Hong, Y. Duan, M. I. Luck, M. K. Annavajhala, Y. Guo, Z. Sheng, A. C. Uhlemann, S. P. Goff, Y. Sabo, H. Yang, A. Chavez and D. D. Ho, Nature, 2022, 613, 558–564 CrossRef.
- Y. Hu, E. M. Lewandowski, H. Tan, X. Zhang, R. T. Morgan, X. Zhang, L. M. C. Jacobs, S. G. Butler, M. V. Gongora, J. Choy, X. Deng, Y. Chen and J. Wang, bioRxiv, 2022 DOI:10.1101/2022.06.28.497978.
- D. G. Ahn, J. K. Choi, D. R. Taylor and J. W. Oh, Arch. Virol., 2012, 157, 2095–2104 CrossRef CAS PubMed.
- M. Sevajol, L. Subissi, E. Decroly, B. Canard and I. Imbert, Virus Res., 2014, 194, 90–99 CrossRef CAS.
- W. Zhu, C. Z. Chen, K. Gorshkov, M. Xu, D. C. Lo and W. Zheng, SLAS Discovery, 2020, 25, 1141–1151 CrossRef CAS.
- P. Gong, Front. Mol. Biosci., 2022, 8, 822218 CrossRef.
- C. Long, M. E. Romero, D. La Rocco and J. Yu, Comput. Struct. Biotechnol. J., 2021, 19, 3339–3348 CrossRef CAS PubMed.
- L. P. Jordheim, D. Durantel, F. Zoulim and C. Dumontet, Nat. Rev. Drug Discovery, 2013, 12, 447–464 CrossRef CAS.
- M. Gaetani, P. Sabatier, A. A. Saei, C. M. Beusch, Z. Yang, S. L. Lundström and R. A. Zubarev, J. Proteome Res., 2019, 18, 4027–4037 CrossRef CAS PubMed.
- Y. Gao, L. Yan, Y. Huang, F. Liu, Y. Zhao, L. Cao, T. Wang, Q. Sun, Z. Ming, L. Zhang, J. Ge, L. Zheng, Y. Zhang, H. Wang, Y. Zhu, C. Zhu, T. Hu, T. Hua, B. Zhang, X. Yang, J. Li, H. Yang, Z. Liu, W. Xu, L. W. Guddat, Q. Wang, Z. Lou and Z. Rao, Science, 2020, 368, 779–782 CrossRef CAS PubMed.
- W. Yin, C. Mao, X. Luan, D.-D. Shen, Q. Shen, H. Su, X. Wang, F. Zhou, W. Zhao, M. Gao, S. Chang, Y.-C. Xie, G. Tian, H.-W. Jiang, S.-C. Tao, J. Shen, Y. Jiang, H. Jiang, Y. Xu, S. Zhang, Y. Zhang and H. E. Xu, Science, 2020, 368, 1499–1504 CrossRef CAS PubMed.
- H. S. Hillen, G. Kokic, L. Farnung, C. Dienemann, D. Tegunov and P. Cramer, Nature, 2020, 584, 154–156 CrossRef CAS PubMed.
- J. Chen, B. Malone, E. Llewellyn, M. Grasso, P. M. Shelton, P. D. B. Olinares, K. Maruthi, E. T. Eng, H. Vatandaslar, B. T. Chait, T. M. Kapoor, S. A. Darst and E. A. Campbell, Cell, 2020, 182, 1560–1573 CrossRef CAS PubMed.
- Q. Wang, J. Wu, H. Wang, Y. Gao, Q. Liu, A. Mu, W. Ji, L. Yan, Y. Zhu, C. Zhu, X. Fang, X. Yang, Y. Huang, H. Gao, F. Liu, J. Ge, Q. Sun, X. Yang, W. Xu, Z. Liu, H. Yang, Z. Lou, B. Jiang, L. W. Guddat, P. Gong and Z. Rao, Cell, 2020, 182, 417–428 CrossRef CAS.
- B. Malone, J. Chen, Q. Wang, E. Llewellyn, Y. J. Choi, P. D. B. Olinares, X. Cao, C. Hernandez, E. T. Eng, B. T. Chait, D. E. Shaw, R. Landick, S. A. Darst and E. A. Campbell, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 2102516118 CrossRef.
- J. P. Bravo, T. L. Dangerfield, D. W. Taylor and K. A. Johnson, Mol. Cell, 2021, 81, 1548–1552 CrossRef CAS PubMed.
- Q. Peng, R. Peng, B. Yuan, M. Wang, J. Zhao, L. Fu, J. Qi and Y. Shi, Innovation, 2021, 2, 100080 CAS.
- K. Naydenova, K. W. Muir, L. F. Wu, Z. Zhang, F. Coscia, M. J. Peet, P. Castro-Hartmann, P. Qian, K. Sader, K. Dent, D. Kimanius, J. D. Sutherland, J. Löwe, D. Barford and C. J. Russo, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2021946118 CrossRef CAS.
- B. F. Malone, J. K. Perry, P. D. B. Olinares, H. W. Lee, J. Chen, T. C. Appleby, J. Y. Feng, J. P. Bilello, H. Ng, J. Sotiris, M. Ebrahim, E. Y. Chua, J. H. Mendez, E. T. Eng, R. Landick, M. Götte, B. T. Chait, E. A. Campbell and S. A. Darst, Nature, 2023, 614, 781–787 CrossRef CAS PubMed.
- P. Gong and O. B. Peersen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22505–22510 CrossRef CAS PubMed.
- B. Shu and P. Gong, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4005–E4014 CAS.
- J. H. Beigel, K. M. Tomashek, L. E. Dodd, A. K. Mehta, B. S. Zingman, A. C. Kalil, E. Hohmann, H. Y. Chu, A. Luetkemeyer, S. Kline, D. Lopez de Castilla, R. W. Finberg, K. Dierberg, V. Tapson, L. Hsieh, T. F. Patterson, R. Paredes, D. A. Sweeney, W. R. Short, G. Touloumi, D. C. Lye, N. Ohmagari, M.-D. Oh, G. M. Ruiz-Palacios, T. Benfield, G. Fätkenheuer, M. G. Kortepeter, R. L. Atmar, C. B. Creech, J. Lundgren, A. G. Babiker, S. Pett, J. D. Neaton, T. H. Burgess, T. Bonnett, M. Green, M. Makowski, A. Osinusi, S. Nayak and H. C. Lane, N. Engl. J. Med., 2020, 383, 1813–1826 CrossRef CAS PubMed.
- T. K. Warren, R. Jordan, M. K. Lo, A. S. Ray, R. L. Mackman, V. Soloveva, D. Siegel, M. Perron, R. Bannister, H. C. Hui, N. Larson, R. Strickley, J. Wells, K. S. Stuthman, S. A. Van Tongeren, N. L. Garza, G. Donnelly, A. C. Shurtleff, C. J. Retterer, D. Gharaibeh, R. Zamani, T. Kenny, B. P. Eaton, E. Grimes, L. S. Welch, L. Gomba, C. L. Wilhelmsen, D. K. Nichols, J. E. Nuss, E. R. Nagle, J. R. Kugelman, G. Palacios, E. Doerffler, S. Neville, E. Carra, M. O. Clarke, L. Zhang, W. Lew, B. Ross, Q. Wang, K. Chun, L. Wolfe, D. Babusis, Y. Park, K. M. Stray, I. Trancheva, J. Y. Feng, O. Barauskas, Y. Xu, P. Wong, M. R. Braun, M. Flint, L. K. McMullan, S. S. Chen, R. Fearns, S. Swaminathan, D. L. Mayers, C. F. Spiropoulou, W. A. Lee, S. T. Nichol, T. Cihlar and S. Bavari, Nature, 2016, 531, 381–385 CrossRef CAS PubMed.
- S. Ahmed, R. Mahtarin, S. Islam, A. Das, S. Al Mamun, A. Samina, A. Ali, S. Das, A. Al Mamun and S. Ahmed, J. Biomol. Struct. Dyn., 2022, 40, 11111–11124 CrossRef CAS.
- S. Koulgi, V. Jani, V. N. Mallikarjunachari Uppuladinne, U. Sonavane and R. Joshi, J. Biomol. Struct. Dyn., 2022, 40, 7230–7244 CrossRef CAS PubMed.
- R. Singh, V. K. Bhardwaj and R. Purohit, Comput. Biol. Med., 2021, 139, 104965 CrossRef CAS.
- A. Parise, G. Ciardullo, M. Prejanò, A. De La Lande and T. Marino, J. Chem. Inf. Model., 2022, 62, 4916–4927 CrossRef CAS.
- Y. Li, D. Zhang, X. Gao, X. Wang and L. Zhang, J. Phys. Chem. Lett., 2022, 13, 4111–4118 CrossRef CAS.
- M. Giannetti, C. Mazzuca, G. Ripani and A. Palleschi, Molecules, 2023, 28, 191 CrossRef CAS.
- S. C. Bera, M. Seifert, R. N. Kirchdoerfer, P. van Nies, Y. Wubulikasimu, S. Quack, F. S. Papini, J. J. Arnold, B. Canard, C. E. Cameron, M. Depken and D. Dulin, Cell Rep., 2021, 36, 109650 CrossRef CAS PubMed.
- X. Luo, T. Xu, X. Gao and L. Zhang, Chin. J. Chem. Phys., 2022, 35, 407–412 CrossRef CAS.
- Y. Yuzenkova, A. Bochkareva, V. R. Tadigotla, M. Roghanian, S. Zorov, K. Severinov and N. Zenkin, BMC Biol., 2010, 8, 54 CrossRef PubMed.
- J. Yu, Comput. Math. Biophys., 2014, 2, 141–160 CAS.
- K. A. Johnson, Annu. Rev. Biochem., 1993, 62, 685–713 CrossRef CAS PubMed.
- J. Huang, L. G. Brieba and R. Sousa, Biochemistry, 2000, 39, 11571–11580 CrossRef CAS.
- T. Schlick, K. Arora, W. A. Beard and S. H. Wilson, Theor. Chem. Acc., 2012, 131, 1287 Search PubMed.
- V. S. Anand and S. S. Patel, J. Biol. Chem., 2006, 281, 35677–35685 CrossRef CAS PubMed.
- C. Long and J. Yu, Entropy, 2018, 20, 306 CrossRef PubMed.
- M. E. Romero, C. Long, D. La Rocco, A. M. Keerthi, D. Xu and J. Yu, Mol. Syst. Des. Eng., 2021, 6, 888–902 RSC.
- J. J. Hopfield, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 4135–4139 CrossRef CAS.
- J. Ninio, Biochimie, 1975, 57, 587–595 CrossRef CAS PubMed.
- J. L. Klepeis, K. Lindorff-Larsen, R. O. Dror and D. E. Shaw, Curr. Opin. Struct. Biol., 2009, 19, 120–127 CrossRef CAS.
- R. Lazim, D. Suh and S. Choi, Int. J. Mol. Sci., 2020, 21, 1–20 Search PubMed.
- C. Long, E. Chao, L. T. Da and J. Yu, Nucleic Acids Res., 2019, 47, 4721–4735 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- R. Kierzek, M. E. Burkard and D. H. Turner, Biochemistry, 1999, 38, 14214–14223 CrossRef CAS PubMed.
- L. Zhang, D. Zhang, X. Wang, C. Yuan, Y. Li, X. Jia, X. Gao, H. L. Yen, P. P. H. Cheung and X. Huang, Phys. Chem. Chem. Phys., 2021, 23, 5852–5863 RSC.
- Q. Peng, R. Peng, B. Yuan, M. Wang, J. Zhao, L. Fu, J. Qi and Y. Shi, The Innovation, 2021, 2, 100080 CrossRef CAS PubMed.
- B. F. Malone, J. K. Perry, P. D. B. Olinares, H. W. Lee, J. Chen, T. C. Appleby, J. Y. Feng, J. P. Bilello, H. Ng, J. Sotiris, M. Ebrahim, E. Y. D. Chua, J. H. Mendez, E. T. Eng, R. Landick, M. Götte, B. T. Chait, E. A. Campbell and S. A. Darst, Nature, 2023, 614, 781–787 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2015, 13, 55–58 CrossRef PubMed.
- K. L. Meagher, L. T. Redman and H. A. Carlson, J. Comput. Chem., 2003, 24, 1016–1025 CrossRef CAS PubMed.
- M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banáš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro, D. Branduardi, R. Capelli, P. Carloni, M. Ceriotti, A. Cesari, H. Chen, W. Chen, F. Colizzi, S. De, M. De La Pierre, D. Donadio, V. Drobot, B. Ensing, A. L. Ferguson, M. Filizola, J. S. Fraser, H. Fu, P. Gasparotto, F. L. Gervasio, F. Giberti, A. Gil-Ley, T. Giorgino, G. T. Heller, G. M. Hocky, M. Iannuzzi, M. Invernizzi, K. E. Jelfs, A. Jussupow, E. Kirilin, A. Laio, V. Limongelli, K. Lindorff-Larsen, T. Löhr, F. Marinelli, L. Martin-Samos, M. Masetti, R. Meyer, A. Michaelides, C. Molteni, T. Morishita, M. Nava, C. Paissoni, E. Papaleo, M. Parrinello, J. Pfaendtner, P. Piaggi, G. M. Piccini, A. Pietropaolo, F. Pietrucci, S. Pipolo, D. Provasi, D. Quigley, P. Raiteri, S. Raniolo, J. Rydzewski, M. Salvalaglio, G. C. Sosso, V. Spiwok, J. Šponer, D. W. Swenson, P. Tiwary, O. Valsson, M. Vendruscolo, G. A. Voth and A. White, Nat. Methods, 2019, 16, 670–673 CrossRef.
- D. J. Price and C. L. Brooks, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- H. J. Berendsen, J. P. Postma, W. F. Van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- J. Schlitter, M. Engels and P. Krüger, J. Mol. Graphics, 1994, 12, 84–89 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- A. Grossfield, WHAM – Grossfield Lab, https://membrane.urmc.rochester.edu/?page_id=126.
- B. Efron and R. Tibshirani, An Introduction to the Bootstrap, Chapman and Hall/CRC, 1994 Search PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- M. L. Waskom, J. Open Source Software, 2021, 6, 3021 CrossRef.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- C. Long, M. Ernesto Romero, L. Dai and J. Yu, Phys. Chem. Chem. Phys., 2023, 25, 13508–13520 RSC.
- O. Poch, I. Sauvaget, M. Delarue and N. Tordo, EMBO J., 1989, 8, 3867–3874 CrossRef CAS.
- J. Shi, J. M. Perryman, X. Yang, X. Liu, D. M. Musser, A. K. Boehr, I. M. Moustafa, J. J. Arnold, C. E. Cameron and D. D. Boehr, Biochemistry, 2019, 58, 3735–3743 CrossRef CAS.
- H. Alonso, A. A. Bliznyuk and J. E. Gready, Med. Res. Rev., 2006, 26, 531–568 CrossRef CAS.
- J. Schimunek, P. Seidl, K. Elez, T. Hempel, T. Le, F. Noé, S. Olsson, L. Raich, R. Winter, H. Gokcan, F. Gusev, E. M. Gutkin, O. Isayev, M. G. Kurnikova, C. H. Narangoda, R. Zubatyuk, I. P. Bosko, K. V. Furs, A. D. Karpenko, Y. V. Kornoushenko, M. Shuldau, A. Yushkevich, M. B. Benabderrahmane, P. Bousquet-Melou, R. Bureau, B. Charton, B. C. Cirou, G. Gil, W. J. Allen, S. Sirimulla, S. Watowich, N. A. Antonopoulos, N. E. Epitropakis, A. K. Krasoulis, V. P. Pitsikalis, S. T. Theodorakis, I. Kozlovskii, A. Maliutin, A. Medvedev, P. Popov, M. Zaretckii, H. Eghbal-Zadeh, C. Halmich, S. Hochreiter, A. Mayr, P. Ruch, M. Widrich, F. Berenger, A. Kumar, Y. Yamanishi, K. Y. J. Zhang, E. Bengio, Y. Bengio, M. J. Jain, M. Korablyov, C.-H. Liu, G. Marcou, E. Glaab, K. Barnsley, S. M. Iyengar, M. J. Ondrechen, V. J. Haupt, F. Kaiser, M. Schroeder, L. Pugliese, S. Albani, C. Athanasiou, A. Beccari, P. Carloni, G. D’Arrigo, E. Gianquinto, J. Goßen, A. Hanke, B. P. Joseph, D. B. Kokh, S. Kovachka, C. Manelfi, G. Mukherjee, A. Muñiz-Chicharro, F. Musiani, A. Nunes-Alves, G. Paiardi, G. Rossetti, S. K. Sadiq, F. Spyrakis, C. Talarico, A. Tsengenes, R. C. Wade, C. Copeland, J. Gaiser, D. R. Olson, A. Roy, V. Venkatraman, T. J. Wheeler, H. Arthanari, K. Blaschitz, M. Cespugli, V. Durmaz, K. Fackeldey, P. D. Fischer, C. Gorgulla, C. Gruber, K. Gruber, M. Hetmann, J. E. Kinney, K. M. Padmanabha Das, S. Pandita, A. Singh, G. Steinkellner, G. Tesseyre, G. Wagner, Z.-F. Wang, R. J. Yust, D. S. Druzhilovskiy, D. A. Filimonov, P. V. Pogodin, V. Poroikov, A. V. Rudik, L. A. Stolbov, A. V. Veselovsky, M. De Rosa, G. De Simone, M. R. Gulotta, J. Lombino, N. Mekni, U. Perricone, A. Casini, A. Embree, D. B. Gordon, D. Lei, K. Pratt, C. A. Voigt, K.-Y. Chen, Y. Jacob, T. Krischuns, P. Lafaye, A. Zettor, M. L. Rodríguez, K. M. White, D. Fearon, F. Von Delft, M. A. Walsh, D. Horvath, C. L. Brooks III, B. Falsafi, B. Ford, A. García-Sastre, S. Yup Lee, N. Naffakh, A. Varnek, G. Klambauer and T. M. Hermans, Mol. Inf., 2023, e202300262 CrossRef.
- X. Yang, X. Liu, D. M. Musser, I. M. Moustafa, J. J. Arnold, C. E. Cameron and D. D. Boehr, J. Biol. Chem., 2017, 292, 3810–3826 CrossRef CAS PubMed.
- A. N. Jones, A. Mourão, A. Czarna, A. Matsuda, R. Fino, K. Pyrc, M. Sattler and G. M. Popowicz, Sci. Rep., 2022, 12, 9593 CrossRef CAS.
- I. Petushkov, D. Esyunina and A. Kulbachinskiy, FEBS J., 2023, 290, 80–92 CrossRef CAS PubMed.
- C. J. Gordon, E. P. Tchesnokov, E. Woolner, J. K. Perry, J. Y. Feng, D. P. Porter and M. Götte, J. Biol. Chem., 2020, 295, 6785–6797 CrossRef CAS PubMed.
- G. Campagnola, S. McDonald, S. Beaucourt, M. Vignuzzi and O. B. Peersen, J. Virol., 2015, 89, 275–286 CrossRef PubMed.
- T. C. Appleby, J. K. Perry, E. Murakami, O. Barauskas, J. Feng, A. Cho, D. Fox, D. R. Wetmore, M. E. McGrath, A. S. Ray, M. J. Sofia, S. Swaminathan and T. E. Edwards, Science, 2015, 347, 771–775 CrossRef CAS PubMed.
- B. Selisko, N. Papageorgiou, F. Ferron and B. Canard, Viruses, 2018, 10, 59 CrossRef PubMed.
- Z. Jin, V. Leveque, H. Ma, K. A. Johnson and K. Klumpp, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E348–E357 CrossRef CAS.
- B. Villalba and K. A. Johnson, J. Biol. Chem., 2020, 295, 16436–16444 CrossRef CAS PubMed.
- C. Long, E. Chao, L. T. Da and J. Yu, Comput. Struct. Biotechnol. J., 2019, 17, 638–644 CrossRef CAS PubMed.
- S. Bhakat, RSC Adv., 2022, 12, 25010–25024 RSC.
- L. Bonati, E. Trizio, A. Rizzi and M. Parrinello, bioRxiv, 2023.
- J. Wang, P. R. Arantes, A. Bhattarai, R. V. Hsu, S. Pawnikar, Y. M. Huang, G. Palermo and Y. Miao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1521 CAS.
- L. T. Chong, A. S. Saglam and D. M. Zuckerman, Path-sampling strategies for simulating rare events in biomolecular systems, 2017 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary figures and tables are included in the ESI. See DOI: https://doi.org/10.1039/d3cp04410f |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2024 |

