DOI:
10.1039/C5RA06439B
(Paper)
RSC Adv., 2015,
5, 44247-44257
Multiple-pulse spin locking in nanofluids
Received
12th January 2015
, Accepted 14th April 2015
First published on 14th April 2015
Abstract
We study the multiple-pulse spin locking dynamics of the nuclear spins in a liquid or gas entrapped in nanosized cavities. Two cases are considered with the cavities being either in orientational order or isotropically disordered. The spins inside the cavities are coupled by dipole–dipole interactions with the same interaction constant. It is shown that, under the high temperature approximation in a spin system irradiated by a multiple-pulse sequence, the quasi-equilibrium state is established. An analytical expression is obtained describing the dependence of the steady-state magnetization on the structural parameters of a nanocavity and the characteristics of a gas or liquid confined in nanocavities. The relaxation process which follows the establishment of the equilibrium is considered. For the case of the orientationally ordered cavities, the analytical expression for the relaxation time is derived. When the nanocavities are isotropically disordered, the time dependence of the magnetization is numerically calculated. As shown for this case, the relaxation process is characterized by two time constants differing by two orders of magnitude. An advantage of the application of the multiple-pulse spin locking measurement method over the NMR cryoporometry technique is that the measurements of magnetization and its relaxation, along with the information about the cavity size, allow determination of the shape and orientation of the nanocavity.
I Introduction
Nuclear magnetic resonance (NMR) has become a powerful analytical tool in the study of structure and dynamic properties of molecules (both organic and inorganic) in solutions, liquid crystals, solids, and compound environments such as membranes.1–3
Over the past two decades, it became increasingly clear that the NMR technique is a very applicable tool for studying soft matter systems such as nanostructures and nanoporous materials.4–6 Based on a significant difference in magnetic and non-magnetic properties of materials enclosed in nanocavities, several methods for studying the structure of these materials have been proposed.7–14 Molecular geometries can be derived from cross-relaxation rates which depend on the internuclear distances due to spin–spin interactions, such as the dipole–dipole interactions (DDI) between nuclear spins.4–6 In isotropic liquids the secular dipole–dipole coupling essentially vanishes, but it is still possible to use the non-secular dipole–dipole coupling by way of their effect on the relaxation of the spin system.1–3
Various NMR techniques, ranging from the cryoporometry technique,14 spin locking,15 spin dynamics in a local field,16,17 and multiple-quantum NMR18–22 to spin-relaxation experiments,6,23 were used to identify and quantify finite size effects. Nanoporous materials have found wide application, from gas separation in the petrochemical industry to air or water purification, and in medicine such as for controlled drug delivery.
The feature of the NMR spectroscopy which makes it so useful for chemical and structural analysis of liquids and solutions is high resolution allowing one to observe extremely weak interactions such as the interactions of nuclear spins with magnetic fields induced by the orbital motions of electrons which leads to a chemical shift. These weak interactions are sensitive to the local properties of an environment and may be used as a determinative method for characterizing the environment. However, in solids, sufficiently strong DDI “cover” these weaker interactions and do not enable one to use the latter interactions to specify the environment.
The idea of coherent averaging of strong interactions such as DDI, for the purpose of narrowing the NMR spectral lines has spawned various high-resolution NMR techniques for solids. Of particular interest has been the development of methods for suppressing the effects of homonuclear dipolar broadening, thus obtaining high resolution NMR spectra of solids. One of the most effective and promising techniques is the multiple-pulse radio-frequency (RF) irradiation, application which can increase by several orders the sensitivity of the NMR method in studying weak interactions in solids.24,25 Multiple-pulse NMR can provide a much higher data rate because the NMR signal can be sampled between the RF pulses, and the relaxation curve is recorded during one scan. Accordingly, the spin-lock experiment may yield information about slowly fluctuating processes.24,25
However, most studies using multi-pulse RF NMR methods deal with the spin dynamics of a nuclear spin system in a bulk solid. To the best of our knowledge, the multiple-pulse NMR methods were not applied to studying the spin dynamics and spin–spin and spin–lattice relaxations in gases or liquids confined to nanoscale volumes such as nanopores and nanocavities. The motivation for the application of multiple-pulse NMR methods to the study of nanoscale structures can be explained by the fact that in gases or liquids the intermolecular DDI between nuclear spins are not averaged to zero,26 as it usually happens in bulk gases or isotropic liquids.27 Only very weak long-range residual DDI do not vanish in liquids.8 The measurement of residual long-range dipolar coupling can potentially provide unique information on structured media.10 The difference between long-range DDI and DDI in nanoscale materials is that the latter is characterized by a single universal dipolar coupling constant which depends on the volume and shape of the nanocavity and its orientation relative to the external magnetic field.26,28–30 This dependence can be used to obtain useful information on the structure of nanosized objects from NMR experiments.31
In this paper, we consider the multiple-pulse spin locking dynamics and spin lattice relaxation in liquids or gases entrapped in nanosized cavities (Fig. 1). We investigate two cases. In the first case, the material is in orientational order as the cavities are oriented along a common direction, their long axis a (see Fig. 1a). In the second case, the material is isotropically disordered, as schematically illustrated in Fig. 1b.
 |
| | Fig. 1 Oriented (a) and disoriented (b) nanocavities containing water molecules (c). θ is the angle between the external magnetic field (![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0∥ 0∥![[z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_007a_20d1.gif) ) and the principal axis a of the nanocavity. ) and the principal axis a of the nanocavity. | |
This paper is organized as follows: in section II, for the convenience of the reader, we describe the procedure of averaging in the coordinate and spin spaces. In section III, we consider a quasi-equilibrium state and steady-state magnetization. In section IV, the evolution of the spin system during multiple-pulse spin locking is analyzed. The last section is the conclusion.
II Averaging of the dipole–dipole Hamiltonian in the coordinate and spin spaces
The possibility of extracting the structural and dynamic parameters from NMR experiments is largely based on averaging the spin motion in the coordinate and spin spaces. Part of this averaging occurs quite naturally, for example, averaging in the coordinate of the dipole–dipole interactions in liquid samples. An example of averaging in the spin space is the truncation of the internal spin–spin interaction Hamiltonians of spin systems in high magnetic fields.
For an adequate description of a spin system restricted by a cavity and irradiated by a multiple-pulse RF sequence, the Hamiltonian should be averaged in both the coordinate and spin spaces.
A Averaging in the coordinate space
Let us consider a system of N nuclear spins, I = 1/2, enclosed in an elongated cavity with the principal axes a, b, and c = b, and an external field H0 is directed along the z-axis (Fig. 1). The dipole–dipole Hamiltonian of a spin system in the external magnetic field can be separated into the two parts: one of them is the secular part with respect to Iz (Iz is the projection of the spin angular momentum operator ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) on the z-axis) and the second is the non-secular part. The secular part of the DDI Hamiltonian is given by1,32
on the z-axis) and the second is the non-secular part. The secular part of the DDI Hamiltonian is given by1,32| |
 | (1) |
where γ is the gyromagnetic ratio,  ,
,  , Ijμ is the projection of the angular momentum operator of the j-th spin (j = 1, 2,…, N) on the μ-axis (μ = x, y, z), and θij is the angle between the z-axis and the radius-vector
, Ijμ is the projection of the angular momentum operator of the j-th spin (j = 1, 2,…, N) on the μ-axis (μ = x, y, z), and θij is the angle between the z-axis and the radius-vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij from the i-th to the j-th spins.
ij from the i-th to the j-th spins.
For bulk gases or liquids, molecular diffusion1,33 causes practical vanishing of the averaged DDI Hamiltonian.34 Actually, the averaged value of the intensity of interactions depends on the angle θij in P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij). The averaged value of this quantity over the angle θij is zero:
θij). The averaged value of this quantity over the angle θij is zero:  .
.
In contrast to bulk gases or liquids, in nanosized cavities the molecules of a gas or liquid are subjected to restricted diffusion, but still move randomly throughout the whole cavity, from one cavity wall to another, during a time tmov which is much less than the NMR time scale, tmov ≪ tNMR.26,28–30,35 As a result, the averaged value of P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij) can be different to zero. Let us estimate the characteristic size l of a nanocavity containing water at which the condition tmov ≪ tNMR is fulfilled. The diffusion coefficient of water molecules can be estimated using the Einstein–Stokes equation. The diffusion coefficient for spherical particles moving through a liquid is
θij) can be different to zero. Let us estimate the characteristic size l of a nanocavity containing water at which the condition tmov ≪ tNMR is fulfilled. The diffusion coefficient of water molecules can be estimated using the Einstein–Stokes equation. The diffusion coefficient for spherical particles moving through a liquid is  , where kB is the Boltzmann constant, T is the absolute temperature, σ = 8.94 × 10−4 N s m−2 is the dynamic viscosity and λ = 2 × 10−10 m is the molecular van der Waals radius.36 Within the framework of this hydrodynamic model, we estimate D ≈ 2 × 10−9 m2 s−1 which is close to the experimental value D ≈ 2.299 × 10−9 m2 s−1 at 25 °C.37
, where kB is the Boltzmann constant, T is the absolute temperature, σ = 8.94 × 10−4 N s m−2 is the dynamic viscosity and λ = 2 × 10−10 m is the molecular van der Waals radius.36 Within the framework of this hydrodynamic model, we estimate D ≈ 2 × 10−9 m2 s−1 which is close to the experimental value D ≈ 2.299 × 10−9 m2 s−1 at 25 °C.37
The typical NMR time scale which characterizes the flip–flop transition is  . Therefore, the averaged DDI Hamiltonian can be non-zero if the typical length l of the water-confined cavity is much shorter than
. Therefore, the averaged DDI Hamiltonian can be non-zero if the typical length l of the water-confined cavity is much shorter than  . Then, taking into account the ergodic theorem,26,28,29 the spin evolution in a nanosize cavity can be described by the averaged DDI Hamiltonian
. Then, taking into account the ergodic theorem,26,28,29 the spin evolution in a nanosize cavity can be described by the averaged DDI Hamiltonian
| |
 | (2) |
with the space-averaged pair coupling
G for any pair of the
i-th and
j-th spins:
28,29| |
 | (3) |
where
V is the cavity volume,
F(
ε) is the form-factor depending monotonically on the ratio

:

,
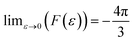
, and lim
ε→1 (
F(
ε)) = 0,
26 and
θ denotes the orientation of the cavity with respect to the external magnetic field
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0
0 (
Fig. 1c). It should be noted that for spherical cavities
ε = 1 and
F(
ε) = 0, and hence, averaging the DDI Hamiltonian gives zero, as in the case of a bulk liquid. The averaged DDI Hamiltonian
(2) can be rewritten in the following form
29| |
 | (4) |
where
![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) 2
2 =
Ix2 +
Iy2 +
Iz2 is the square of the total nuclear spin operator and

is the operator of the projection of the total spin operator onto the
μ-axis (
μ =
x,
y,
z).
B Averaging in the spin space
The evolution of a spin system containing nuclear spins I entrapped in a nanosized cavity and irradiated by a RF pulse train 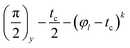 (here, φl denotes the pulse which rotates spins through an angle φ around the l-axis, and tc is the time interval between the pulses) can be described by solving the following equation for the density matrix ρ(t):
(here, φl denotes the pulse which rotates spins through an angle φ around the l-axis, and tc is the time interval between the pulses) can be described by solving the following equation for the density matrix ρ(t):| |
 | (5) |
with the Hamiltonian
Here ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 is the Zeeman energy
0 is the Zeeman energy
| |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = −ω0Iz 0 = −ω0Iz
| (7) |
which represents the interaction of the spin system with an external magnetic field
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0
0 directed along the
z-axis and
ω0 =
γH0.
HRF(
t) gives the action of the RF field on the spin system:
| |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) RF(t) = γH1( RF(t) = γH1(![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) )f(t)cos )f(t)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt ωt
| (8) |
where
H1 and
ω are the amplitude and frequency of a RF field pulse, respectively,
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif)
is the unit vector along the direction of the RF field,
f(
t) is the pulse function that describes the pattern of the RF field pulses:
| |
 | (9) |
and
tw is the duration of the pulse. Without loss of generality, we can assume that
ω =
ω0 and
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif)
= {1, 0, 0}.
To solve eqn (5), we apply the unitary transformation
| |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) = U(t)e−it (t) = U(t)e−it![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0ρ(t)eit 0ρ(t)eit![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0U+(t) 0U+(t)
| (10) |
with the unitary operator
| |
 | (11) |
where

is the magnitude of the effective field.
Eqn (5) for the density matrix after the transformation (10) can be rewritten as
| |
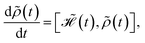 | (12) |
where
| |
 | (13) |
with
ϕm(
t) being the periodic function with the period
tc:
| |
 | (14) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0)dx
(0)dx is the secular part ([
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0)dx
(0)dx,
ωeIx] = 0):
| |
 | (15) |
and
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (m)d
(m)d is the non-secular part ([
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (m)d
(m)d,
ωeIx] =
mωe![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (m)d
(m)d):
| |
 | (16) |
where
I+i and
I−i are the raising and lowering spin angular momentum operators of the
i-th spin.
To account for the time-dependent terms in eqn (13), we expanded the periodic function ϕm(t) (14) in the Fourier series:
| |
 | (17) |
where
| |
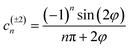 | (18) |
and
In the case where ωe ≃ ωloc (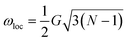 is the local dipolar field19), the Hamiltonian (13) can be divided into two parts:
is the local dipolar field19), the Hamiltonian (13) can be divided into two parts:
| |
 | (19) |
where
| |
 | (20) |
is the sum of the time-independent terms and
| |
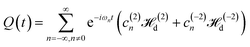 | (21) |
is the time-dependent term.
Similar to considering the multiple-pulse technique for bulk solid NMR,38–40 we apply the perturbation theory which, in the first approximation, takes into account only the time-independent Hamiltonian (20). It should be noted that, when φ approaches zero, the Hamiltonian (20) coincides with the Hamiltonians for the spin systems irradiated by a continuous RF magnetic field, providing spin locking in bulk solids32 and nanocavities.15
The effective Hamiltonian (20) describes a dipolar coupled spin system of a liquid or gas in a cavity under an effective magnetic field with the amplitude ωe ≃ ωloc.
Below, we analyze the characteristics of the considered spin system based on the structure of hydrogenated amorphous silicon a-Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H with nano-cavities of ∼45 nm3 containing H2 at 2 kbar (N ∼ 600).26,41
H with nano-cavities of ∼45 nm3 containing H2 at 2 kbar (N ∼ 600).26,41
Fig. 2 presents the dependences of the local dipolar field ωloc on the angle θ and volume V (Fig. 2a), the angle θ and number of spins N (Fig. 2b), the angle θ and form factor F (Fig. 2c), and the volume V and form factor F (Fig. 2d).
 |
| | Fig. 2 Local dipolar field (ωloc) as a function of: (a) angle θ and volume V (nm3) at N = 500 and F = 2, (b) angle θ and number of spins N in cavity at V = 20 nm3 and F = 2, (c) angle θ and form factor F at V = 20 nm3 and N = 500, (d) volume V and form factor F at θ = 0 and N = 500. | |
In the case of gas, the number of spins and the cavity volume are independent values and the local field decreases with increase in volume as 1/V (Fig. 2a). For a liquid with a constant spin density  , the local field decreases as
, the local field decreases as  . The local dipolar field can be practically regarded as a negligible quantity in experiments with a liquid at ωloc ≤ 100 Hz which corresponds to a volume of about 600 nm3.
. The local dipolar field can be practically regarded as a negligible quantity in experiments with a liquid at ωloc ≤ 100 Hz which corresponds to a volume of about 600 nm3.
The absolute value of the local field reaches its maxima at θ = 0 and θ = π (parallel and antiparallel to the external DC magnetic field) and at 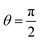 (perpendicular to this field). It should be noted that at
(perpendicular to this field). It should be noted that at
| |
 | (22) |
the local dipolar field vanishes (
Fig. 2).
Eqn (22) has two solutions:
θmag = 54.74° (which is known as “the magic angle”
32 for bulk solids) and
θ = 125.26°. At these angles, the first approximation for the local magnetic field gives zero.
In the range of angles from θ = 0 to θmag = 54.74°, the local field is reduced when the form factor increases from −4 to 2, and between 54.74° and 125.26° the local field increases (Fig. 2c). The strong dependence on the form factor is observed at small volumes, and this dependence decreases with increasing cavity volume (Fig. 2d). From experiments at θ = 0.96, the spin–spin relaxation time T2 was determined to be 1.3 ms.26 The angle θ = 0.96 is very close to the magic angle where the spin–spin relaxation due to DDI is relatively small, and one can observe the contribution of other mechanisms. The local field ωloc is defined as  ,1,32 which gives ωloc ≃ 770 Hz. Our estimation of the DDI contribution gives ωloc ∼ 400 Hz. Therefore, the contribution of non-DDI mechanisms to the local field can be estimated as ∼370 Hz. With increasing deviation from the magic angle, the relative contribution of DDI to the local field increases.
,1,32 which gives ωloc ≃ 770 Hz. Our estimation of the DDI contribution gives ωloc ∼ 400 Hz. Therefore, the contribution of non-DDI mechanisms to the local field can be estimated as ∼370 Hz. With increasing deviation from the magic angle, the relative contribution of DDI to the local field increases.
During the time T2 ∼ ω−1loc, the behavior of the spin system is described by the Hamiltonian Heff, and a quasi-equilibrium state is established. A decrease in magnetization during further evolution of the spin system is described by the time-dependent Hamiltonian part, Q(t) (21).
III Multiple-pulse spin locking state and steady-state magnetization
The spin locking state can be achieved using a technique which provides magnetization parallel to an effective field ωe. A quite simple but convincing experiment to reach the spin locking state consists of the application of the first short RF 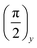 pulse that turns the magnetization along the x-axis. At a high temperature approximation, the density matrix just after the
pulse that turns the magnetization along the x-axis. At a high temperature approximation, the density matrix just after the  pulse is given by the following expression:where α0 is the initial inverse temperature of the Zeeman reservoir. Then, the phase of the RF pulses is suddenly changed to zero, so that the RF field of the multiple-pulse sequence becomes directed along the x-axis, i.e. in the same direction as the magnetization.
pulse is given by the following expression:where α0 is the initial inverse temperature of the Zeeman reservoir. Then, the phase of the RF pulses is suddenly changed to zero, so that the RF field of the multiple-pulse sequence becomes directed along the x-axis, i.e. in the same direction as the magnetization.
The last terms in the effective dipolar Hamiltonian (20) contain flip–flop terms, I+iI−j + I+iI−j,15 which ensure the establishment of a quasi-equilibrium state of the spin system for a time of order of the spin–spin relaxation time T2 ∝ ω−1loc. A spin system in the quasi-equilibrium state can be described by the density matrix which is similar to the matrix considered at the study of processes in bulk solids32
where
αe is the inverse temperature of the spin system in the quasi-equilibrium state. During the establishment of the state (
t ≲
T2), we may also neglect the absorption of energy by the system from external RF fields and apply the law of the energy conservation (similar to bulk solids
32),
i.e. the conservation of energy 〈
Heff〉 =
Tr(
ρeqHeff),
| | |
Tr(ρ(0)Heff) = Tr(ρeqHeff)
| (25) |
from which follows that
| |
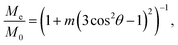 | (26) |
where
| |
 | (27) |
Tr(…) is the sum of the matrix elements on the main diagonal. Me is the projection of the steady-state magnetization at t ≳ T2 on the observation axis, and M0 is the magnetization immediately after the  pulse application.
pulse application.
In multiple-pulse experiments with bulk solid samples the period tc is usually chosen such that φ ≃ ωloctc < 1.24,25 Fig. 3 gives the steady-state magnetization as a function of θ and φ (Fig. 3a), θ and N (Fig. 3b), φ and N (Fig. 3c), V and N (Fig. 3d), φ and V (Fig. 3e), and θ and V (Fig. 3f).
 |
| | Fig. 3 Normalized steady-state magnetization as a function of: (a) the angles θ and φ at V = 50 nm3, N = 500 and F = 2, (b) the angle θ and number of spins N at V = 50 nm3, φ = π/2 and F = 2, (c) φ and N at V = 50 nm3, θ = 0 and F = 2, (d) the volume V and number of spins N at φ = π/2, θ = 0 and F = 2, (e) φ and V at N = 500, θ = π/2 and F = 2, and (f) θ and V at N = 500, φ = π/2 and F = 2. Here and in the figures below ωe = 1000 G. | |
The normalized magnetization Me/M0 is changed from 10% up to 40% by varying the orientation of the nanocavity θ, the pulse duration tc and the number of spins in the cavity N and the volume V, with a constant form factor F (Fig. 3). Variations of θ and φ lead to a change of the normalized magnetization by about 30%, keeping the other parameters constant (Fig. 3a). A change of Me/M0 by about 10% is also obtained when only the number of spins and the pulse duration are varied (Fig. 3b and c). A significant change (up to 50%) in the magnetization is caused by varying the volume, especially when the cavity volume is relatively small, about 10–25 nm3 (Fig. 3d–f). The change in magnetization with the variation of the form factor is shown in Fig. 4: as a function of φ and F (Fig. 4a), θ and F (Fig. 4b), V and F (Fig. 4c), and N and F (Fig. 4d). It can be stated that the change in magnetization varies from 50% (Fig. 4a and c) to 60% (Fig. 4b and d).
 |
| | Fig. 4 Normalized steady-state magnetization as a function of: (a) φ and the form factor F for V = 20 nm3, N = 500 and θ = π/2, (b) θ and F at V = 20 nm3, φ = π/2 and N = 500, (c) V and F at θ = π/2, φ = π/2 and N = 500, and (d) N and F at φ = π/2, θ = π/2 and V = 20 nm3. | |
The results obtained above are valid for the case when all cavities in the sample have the same orientation (Fig. 1a). Such cavernous material, for example, was described in ref. 26 and 42. To compare the experimental data and theoretical results in the case when the cavities are oriented arbitrarily, it is necessary to perform averaging of the steady-state magnetization over θ. At a uniform distribution of directions over angle θ, the averaged normalized magnetization is:
| |
 | (28) |
The integration gives
| |
 | (29) |
Eqn (29) can be converted to an expression containing only real variables, but this expression is too cumbersome and we do not give its explicit form here. Fig. 5 presents the averaged value of the steady-state magnetization as a function of φ and V (Fig. 5a), φ and N (Fig. 5b), and V and N (Fig. 5c).
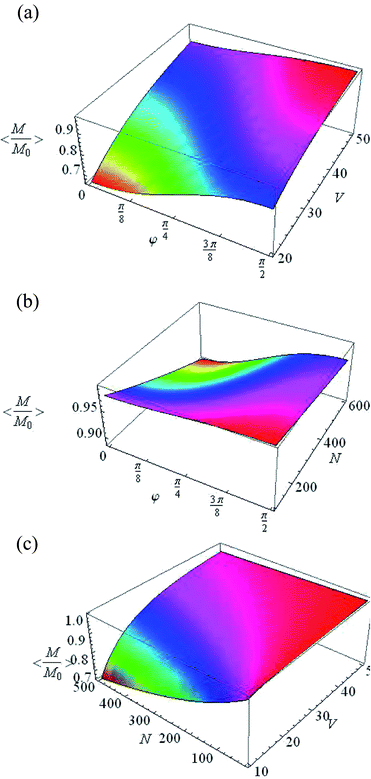 |
| | Fig. 5 Averaged normalized steady-state magnetization as a function of: (a) φ and V at N = 500 and F = 2, (b) φ and N at V = 20 nm3 and F = 2, and (c) V and N at φ = π/2 and F = 2. | |
In the case of disoriented cavities, the averaged normalized steady-state magnetization 〈Me/M0〉 is changed to 60% by varying the pulse duration tc, the number of spins in the cavity N and the volume V, with a constant form factor F (Fig. 5). The largest change in magnetization as a function of the form factor (Fig. 6) is achieved at large number of spins (Fig. 6a), low volume (Fig. 6b) and small φ (Fig. 6c).
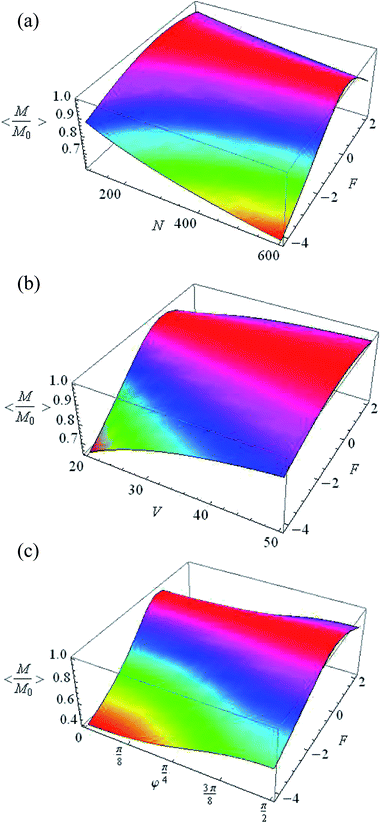 |
| | Fig. 6 Averaged normalized steady-state magnetization as a function of: (a) N and F (φ = π/2, V = 20 nm3), (b) V and F (N = 500, φ = π/2), and (c) φ and F (V = 20 nm3, N = 500). | |
IV Evolution of the spin system during multiple-pulse spin locking
After establishing the quasi-equilibrium state of a spin system, described by eqn (24), further evolution of the spin system at times t ≫ T2 is characterized by a slow change of the effective energy 〈Heff〉. The change of the effective energy is governed by the time-dependent term of the Hamiltonian, eqn (21). In the high temperature approximation, using the results for a bulk solid,46 we can write| |
 | (30) |
The equation for the inverse temperature αe(t) will be derived using the method of the non-equilibrium state operator46 which gives
| |
 | (31) |
where
T1e is the characteristic time of the spin lattice relaxation during the multiple-pulse RF irradiation of the spin system:
| |
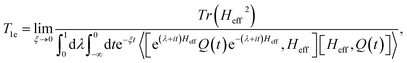 | (32) |
where 〈…〉 denotes the thermodynamic averaging with the quasi-equilibrium operator
(24). Using the relation
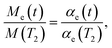
we obtain that the nuclear magnetization relaxes according to the expression
| |
 | (33) |
where
Me(
T2) is the steady-state magnetization just after the establishment of the quasi-equilibrium state, considered as the initial value for the relaxation process.
To calculate the relaxation time T1e, one has to know the correlation function gqq(t, t′) = 〈Q(t)Q(t′)〉. Following ref. 43, we will assume that the function gqq(t, t′) depends on t and t′ only through their difference t − t′. As in the case of a solid,43 we assume an exponential correlation function defined by
| |
 | (34) |
Eqn (32) can be expressed as
| |
 | (35) |
where
| |
 | (36) |
and
The expressions (35) and (36) give the dependence of the spin lattice relaxation time on the correlation time τc, the period of the pulse sequence tc, the local magnetic field ωe, the characteristics of a gas or liquid inside the cavity: the volume V and number of the molecules N, and the parameters of the cavity: the shape F (ε) and orientation θ. Fig. 7 presents the dependencies of T1etc on θ and φ (Fig. 7a), θ and ζ (Fig. 7b), V and N (Fig. 7c), V and ζ (Fig. 7d), obtained from eqn (35). Fig. 7a and b show that the relaxation time increases sharply at orientations of the cavity close to θmag = 54.74° and θ = 125.26°. At θ = 57.74° and 125.26°, in the considered approximation, the averaged Hamiltonian terms (4) are zero and, for correct description of the processes, one should consider new approximations. In the experiments, parameter ζ can vary over a wide range from 0.01 to 100, however, the main peculiarities of the relaxation time on ζ lie near the point ζ = 1 (Fig. 7b and d). At ζ ≫ 1, the relaxation time increases proportionally to this parameter, but does not exceed the value at ζ ≪ 1 The relaxation time T1e decreases as ζ increases and attains its minimum at ζ ∼ 1. For a gas, the relaxation time increases with the cavity volume as V2 and decreases with the spin number as ∼1/N (Fig. 7c and d). It is interesting that for a liquid, when the spin density is constant, the relaxation time is independent of the spin number and linearly increases with the cavity volume. Usually in experiments, tc ≃ 10−5 s (ref. 24 and 25) and from our results T1e is estimated to range from 0.05 up to 30 s (Fig. 7).
 |
| | Fig. 7 T1etc as a function of: (a) θ and φ at V = 50 nm3, N = 500, F = 2 and ζ = 1, (b) θ and ζ at V = 50 nm3, N = 500, F = 2 and φ = π/2, (c) V and N at θ = 0, F = 2, φ = π/2 and ζ = 1, and (d) V and ζ at θ = 0, F = 2, φ = π/2, ζ = 1 and N = 500. | |
At a uniform distribution of directions of the cavity axes over the angle θ (Fig. 1a), to compare the experimental relaxation data and the theoretical results, it is necessary to perform averaging of the magnetization over θ:
| |
 | (37) |
The integral in eqn (37) cannot be solved by quadrature, the results of the numerical calculation are shown in Fig. 8 and 9. Fig. 8 presents the averaged normalized magnetization as a function of N and V at (a) t = 5 s and (b) t = 50 s. Fig. 9 shows the time dependence of the normalized magnetization. This dependence is substantially non-exponential (Fig. 9b). In the initial stage of relaxation at t ≫ T2, the magnetization decays with the characteristic relaxation time 〈T1e〉θ ≃ 5 s (Fig. 9c), while in the last stage the characteristic time is 〈T1e〉θ ≃ 286 s (Fig. 9d). This can be explained as follows: the relaxations in the cavities oriented along and opposite the external magnetic field occur faster than the relaxations in the cavities with the axes oriented near the magic angles: θ = 54.74° and 125.26° (Fig. 7). The values of the spin–lattice relaxation times 〈T1e〉θ are in good agreement with those obtained in the case of continuous spin locking,15 while the time dependence of the magnetization is non-exponential.
 |
| | Fig. 8 Averaged normalized magnetization as a function of N and V: (a) t = 5 s, and (b) t = 50 s (F = 2, φ = π/2, ζ = 1, tc = 10−5 s). | |
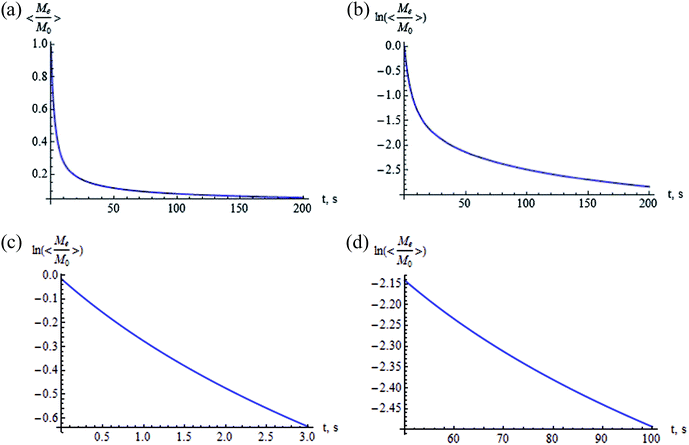 |
| | Fig. 9 Time dependence of the averaged normalized magnetization (a) and of  (b). (c) and (d) demonstrate different time constants of the dependence of (b). (c) and (d) demonstrate different time constants of the dependence of  at different stages of the relaxation: (c) 0 < t < 2 s and (d) 50 s < t < 100 s. Here, N = 500, V = 50 nm3, F = 2, φ = π/2, ζ = 1, and tc = 10−5 s. at different stages of the relaxation: (c) 0 < t < 2 s and (d) 50 s < t < 100 s. Here, N = 500, V = 50 nm3, F = 2, φ = π/2, ζ = 1, and tc = 10−5 s. | |
V Conclusion
Our study has shown that the spin locking state can be realized in gases and fluids confined in nanocavities. We have obtained analytical expressions that describe the dependence of the magnetization on the structural parameters of a nanocavity and the characteristics of a gas or liquid. It was shown that the relaxation measurements can also be used to determine the volume and shape of a nanocavity, for both the ordered and disordered isotropic orientations of nanocavities. The theoretical models we considered in this work touch upon various soft matter and biological systems. This model can be used for the description of the relaxation processes in liquid crystals and other anisotropic liquids under the condition that intramolecular dipole–dipole couplings are not completely averaged. The most obvious connection comes from the physics of molecules dissolved in complex fluids. Our approach can be used to characterize complex fluids confined to the nanoscale. Our results are also relevant in the situation when nanoconfinement is provided by a vesicle, in particular, in biological systems. Finally, we would like to point out an advantage of the proposed multiple-pulse spin locking measurement method of the magnetization and relaxation time over the NMR cryoporometry technique:14,44,45 the measurements of Me (ordered) and 〈Me〉θ (isotropically disordered), along with the information about the cavity size, enable the determination of the shape and orientation of the cavity.
References
- A. Abragam, The Principles of Nuclear Magnetism, Oxford Clarendon Press, 1961 Search PubMed.
- C. P. Slichter, Principles of Magnetic Resonance, Springer Series in Solid-State Sciences, 1996 Search PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford Clarendon Press, 1995 Search PubMed.
- P. T. Callaghan, Principles of Nuclear Magnetic Resonance Microscopy, Oxford Clarendon Press, 1991 Search PubMed.
- E. Breitmaier, Structure Elucidation by NMR in Organic Chemistry: A Practical Guide, John Wiley&Sons Ltd., 2002 Search PubMed.
- C. Alba-Simionesco, B. Coasne, G. Dosseh, G. Dudziak, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, J. Phys.: Condens. Matter, 2006, 18, R15 CrossRef CAS PubMed.
- J. H. Strange and M. Rahman, Phys. Rev. Lett., 1993, 71, 3589 CrossRef CAS.
- W. S. Warren, W. Richter, A. H. Andreotti and B. T. Farmer II, Science, 1993, 262, 2005 CAS.
- W. Richter, S. Lee, W. S. Warren and Q. He, Science, 1995, 267, 654 CrossRef CAS.
- R. Bowtell and P. Robyr, Phys. Rev. Lett., 1996, 76, 497 CrossRef.
- P. Robyr and R. Bowtell, J. Chem. Phys., 1997, 106(8), 467 CrossRef CAS PubMed.
- P. Robyr and R. Bowtell, J. Chem. Phys., 1997, 107, 702 CrossRef CAS PubMed.
- R. Bowtell, S. Gutteridge and C. Ramanathan, J. Magn. Reson., 2001, 150, 147 CrossRef CAS PubMed.
- S.-Y. Ryu, D. S. Kim, J.-D. Jeon and S.-Y. Kwak, J. Phys. Chem. C, 2010, 114, 17440 CAS.
- E. B. Fel’dman, G. B. Furman and S. D. Goren, Soft Matter, 2012, 8, 9200 RSC.
- G. Furman and S. Goren, Z. Naturforsch., A: Phys. Sci., 2011, 66, 779 CrossRef CAS.
- G. Furman and S. Goren, Mater. Sci. Forum, 2012, 721, 47 CrossRef.
- E. B. Fel’dman and A. I. Zenchuk, Chem. Phys., 2011, 390, 20 CrossRef PubMed.
- S. I. Doronin, E. B. Fel’dman and A. I. Zenchuk, JETP Lett., 2011, 113, 495 CrossRef CAS.
- G. B. Furman and S. D. Goren, J. Phys.: Condens. Matter, 2005, 17, 4501 CrossRef CAS.
- S. I. Doronin, E. B. Fel’dman, E. I. Kuznetsova, G. B. Furman and S. D. Goren, JETP Lett., 2007, 86, 24 CrossRef CAS.
- S. I. Doronin, E. B. Fel’dman, E. I. Kuznetsova, G. B. Furman and S. D. Goren, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 144405 CrossRef.
- A. M. Panich and G. B. Furman, Diamond Relat. Mater., 2012, 23, 157 CrossRef CAS PubMed.
- U. Haeberlen, High resolution NMR in solids, Academic Press, New York, 1976 Search PubMed.
- M. Mehring, Principles of High Resolution NMR in Solids, Springer-Verlag, New York, 1983 Search PubMed.
- J. Baugh, A. Kleinhammes, D. Han, Q. Wang and Y. Wu, Confinement Effect on Dipole–Dipole Interactions in Nanofluids, Science, 2001, 294, 1505 CrossRef CAS PubMed.
- W. Richter and W. S. Warren, Concepts Magn. Reson., 2000, 12, 396 CrossRef CAS.
- M. G. Rudavets and E. B. Fel’dman, JETP Lett., 2002, 75, 635–637 CrossRef CAS.
- E. B. Fel’dman and M. G. Rudavets, JETP Lett., 2004, 98, 207 CrossRef.
- S. I. Doronin, A.
V. Fedorova, E. B. Fel’dman and A. I. Zenchuk, J. Chem. Phys., 2009, 131, 104109 CrossRef PubMed.
- T. Tsukahara, W. Mizutani, K. Mawatari and T. Kitamori, J. Phys. Chem. B, 2009, 113, 10808 CrossRef CAS PubMed.
- M. Goldman, Spin Temperature and Nuclear Resonance in Solids, Oxford Clarendon Press, 1970 Search PubMed.
- D. K. Green and J. G. Powlees, Proc. Phys. Soc., 1965, 85, 87 CrossRef CAS.
- J. Jeener, J. Chem. Phys., 2000, 112, 5091 CrossRef CAS PubMed.
- J. Jeener, J. Chem. Phys., 2011, 134, 114519 CrossRef CAS PubMed.
- T. Gabler, A. Paschke and G. Schuurmann, J. Chem. Eng. Data, 1996, 41, 33 CrossRef CAS.
- M. Holz, S. R. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2000, 2, 4740 RSC.
- Y. N. Ivanov, B. N. Provotorov and E. B. Fel’dman, JETP Lett., 1978, 27, 153 Search PubMed.
- E. B. Fel’dman, Phys. Lett., 1984, 104A, 479 CrossRef.
- M. Y. Svetlov and G. B. Furman, Izvestiya VUZOV, Radiophysics, 1987, 30, 557 Search PubMed.
- Y. J. Chabal and C. K. N. Patel, Molecular hydrogen in a-Si
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H, Rev. Mod. Phys., 1987, 59, 835 CrossRef CAS.
H, Rev. Mod. Phys., 1987, 59, 835 CrossRef CAS. - Y. Zhang, A. Faraone, W. A. Kamitakahara, K.-H. Liu, C.-Y. Mou, J. B. Leão, S. Chang and S.-H. Chen, Unusual phase behavior of nano-confined water: new insights, http://arxiv.org/abs/1005.5387.
- D. E. Woessner and H. S. Gutovsky, J. Chem. Phys., 1963, 39, 440 CrossRef CAS PubMed.
- J. H. Strange, M. Rahman and E. C. Smith, Phys. Rev. Lett., 1993, 71, 3589 CrossRef CAS.
- J. Mitchell, J. B. W. Webber and J. H. Strange, Phys. Rep., 2008, 461, 1 CrossRef CAS PubMed.
- D. N. Zubarev, Nonequilibrium Statistical Thermodynamics, Imprint Consultants Bureau, New York, 1974 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0∥
0∥![[z with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_007a_20d1.gif) ) and the principal axis a of the nanocavity.
) and the principal axis a of the nanocavity.![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) on the z-axis) and the second is the non-secular part. The secular part of the DDI Hamiltonian is given by1,32
on the z-axis) and the second is the non-secular part. The secular part of the DDI Hamiltonian is given by1,32
 ,
,  , Ijμ is the projection of the angular momentum operator of the j-th spin (j = 1, 2,…, N) on the μ-axis (μ = x, y, z), and θij is the angle between the z-axis and the radius-vector
, Ijμ is the projection of the angular momentum operator of the j-th spin (j = 1, 2,…, N) on the μ-axis (μ = x, y, z), and θij is the angle between the z-axis and the radius-vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij from the i-th to the j-th spins.
ij from the i-th to the j-th spins.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij). The averaged value of this quantity over the angle θij is zero:
θij). The averaged value of this quantity over the angle θij is zero:  .
.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij) can be different to zero. Let us estimate the characteristic size l of a nanocavity containing water at which the condition tmov ≪ tNMR is fulfilled. The diffusion coefficient of water molecules can be estimated using the Einstein–Stokes equation. The diffusion coefficient for spherical particles moving through a liquid is
θij) can be different to zero. Let us estimate the characteristic size l of a nanocavity containing water at which the condition tmov ≪ tNMR is fulfilled. The diffusion coefficient of water molecules can be estimated using the Einstein–Stokes equation. The diffusion coefficient for spherical particles moving through a liquid is  , where kB is the Boltzmann constant, T is the absolute temperature, σ = 8.94 × 10−4 N s m−2 is the dynamic viscosity and λ = 2 × 10−10 m is the molecular van der Waals radius.36 Within the framework of this hydrodynamic model, we estimate D ≈ 2 × 10−9 m2 s−1 which is close to the experimental value D ≈ 2.299 × 10−9 m2 s−1 at 25 °C.37
, where kB is the Boltzmann constant, T is the absolute temperature, σ = 8.94 × 10−4 N s m−2 is the dynamic viscosity and λ = 2 × 10−10 m is the molecular van der Waals radius.36 Within the framework of this hydrodynamic model, we estimate D ≈ 2 × 10−9 m2 s−1 which is close to the experimental value D ≈ 2.299 × 10−9 m2 s−1 at 25 °C.37 . Therefore, the averaged DDI Hamiltonian can be non-zero if the typical length l of the water-confined cavity is much shorter than
. Therefore, the averaged DDI Hamiltonian can be non-zero if the typical length l of the water-confined cavity is much shorter than  . Then, taking into account the ergodic theorem,26,28,29 the spin evolution in a nanosize cavity can be described by the averaged DDI Hamiltonian
. Then, taking into account the ergodic theorem,26,28,29 the spin evolution in a nanosize cavity can be described by the averaged DDI Hamiltonian

 :
:  ,
, 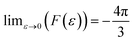 , and limε→1 (F(ε)) = 0,26 and θ denotes the orientation of the cavity with respect to the external magnetic field
, and limε→1 (F(ε)) = 0,26 and θ denotes the orientation of the cavity with respect to the external magnetic field ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 (Fig. 1c). It should be noted that for spherical cavities ε = 1 and F(ε) = 0, and hence, averaging the DDI Hamiltonian gives zero, as in the case of a bulk liquid. The averaged DDI Hamiltonian (2) can be rewritten in the following form29
0 (Fig. 1c). It should be noted that for spherical cavities ε = 1 and F(ε) = 0, and hence, averaging the DDI Hamiltonian gives zero, as in the case of a bulk liquid. The averaged DDI Hamiltonian (2) can be rewritten in the following form29
![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) 2 = Ix2 + Iy2 + Iz2 is the square of the total nuclear spin operator and
2 = Ix2 + Iy2 + Iz2 is the square of the total nuclear spin operator and  is the operator of the projection of the total spin operator onto the μ-axis (μ = x, y, z).
is the operator of the projection of the total spin operator onto the μ-axis (μ = x, y, z).
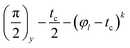 (here, φl denotes the pulse which rotates spins through an angle φ around the l-axis, and tc is the time interval between the pulses) can be described by solving the following equation for the density matrix ρ(t):
(here, φl denotes the pulse which rotates spins through an angle φ around the l-axis, and tc is the time interval between the pulses) can be described by solving the following equation for the density matrix ρ(t):
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t) =
(t) = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 +
0 + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) RF(t) +
RF(t) + ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) d.
d.
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 is the Zeeman energy
0 is the Zeeman energy![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 = −ω0Iz
0 = −ω0Iz
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 directed along the z-axis and ω0 = γH0. HRF(t) gives the action of the RF field on the spin system:
0 directed along the z-axis and ω0 = γH0. HRF(t) gives the action of the RF field on the spin system:![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) RF(t) = γH1(
RF(t) = γH1(![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif)
![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) )f(t)cos
)f(t)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt
ωt
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) is the unit vector along the direction of the RF field, f(t) is the pulse function that describes the pattern of the RF field pulses:
is the unit vector along the direction of the RF field, f(t) is the pulse function that describes the pattern of the RF field pulses:
![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) = {1, 0, 0}.
= {1, 0, 0}.
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (t) = U(t)e−it
(t) = U(t)e−it![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0ρ(t)eit
0ρ(t)eit![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0U+(t)
0U+(t)

 is the magnitude of the effective field.
is the magnitude of the effective field.
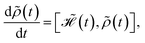


![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0)dx is the secular part ([
(0)dx is the secular part ([![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0)dx, ωeIx] = 0):
(0)dx, ωeIx] = 0):
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (m)d is the non-secular part ([
(m)d is the non-secular part ([![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (m)d, ωeIx] = mωe
(m)d, ωeIx] = mωe![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (m)d):
(m)d):

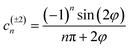
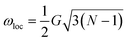 is the local dipolar field19), the Hamiltonian (13) can be divided into two parts:
is the local dipolar field19), the Hamiltonian (13) can be divided into two parts:

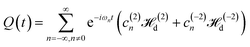
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H with nano-cavities of ∼45 nm3 containing H2 at 2 kbar (N ∼ 600).26,41
H with nano-cavities of ∼45 nm3 containing H2 at 2 kbar (N ∼ 600).26,41 , the local field decreases as
, the local field decreases as  . The local dipolar field can be practically regarded as a negligible quantity in experiments with a liquid at ωloc ≤ 100 Hz which corresponds to a volume of about 600 nm3.
. The local dipolar field can be practically regarded as a negligible quantity in experiments with a liquid at ωloc ≤ 100 Hz which corresponds to a volume of about 600 nm3.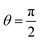 (perpendicular to this field). It should be noted that at
(perpendicular to this field). It should be noted that at
 ,1,32 which gives ωloc ≃ 770 Hz. Our estimation of the DDI contribution gives ωloc ∼ 400 Hz. Therefore, the contribution of non-DDI mechanisms to the local field can be estimated as ∼370 Hz. With increasing deviation from the magic angle, the relative contribution of DDI to the local field increases.
,1,32 which gives ωloc ≃ 770 Hz. Our estimation of the DDI contribution gives ωloc ∼ 400 Hz. Therefore, the contribution of non-DDI mechanisms to the local field can be estimated as ∼370 Hz. With increasing deviation from the magic angle, the relative contribution of DDI to the local field increases. pulse that turns the magnetization along the x-axis. At a high temperature approximation, the density matrix just after the
pulse that turns the magnetization along the x-axis. At a high temperature approximation, the density matrix just after the  pulse is given by the following expression:
pulse is given by the following expression: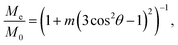

 pulse application.
pulse application.





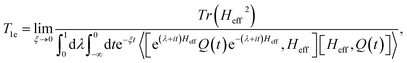
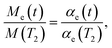 we obtain that the nuclear magnetization relaxes according to the expression
we obtain that the nuclear magnetization relaxes according to the expression





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H, Rev. Mod. Phys., 1987, 59, 835 CrossRef CAS.
H, Rev. Mod. Phys., 1987, 59, 835 CrossRef CAS.







