Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Open circuit voltage of an all-vanadium redox flow battery as a function of the state of charge obtained from UV-Vis spectroscopy†
Jana
Heiß
 and
Maximilian
Kohns
*
and
Maximilian
Kohns
*
Laboratory of Engineering Thermodynamics (LTD), RPTU Kaiserslautern, Erwin-Schrödinger-Straße 44, 67663 Kaiserslautern, Germany. E-mail: maximilian.kohns@rptu.de
First published on 13th September 2024
Abstract
A unique feature of redox flow batteries (RFBs) is that their open circuit voltage (OCV) depends strongly on the state of charge (SOC). In the present work, this relation is investigated experimentally for the all-vanadium RFB (AVRFB), which uses vanadium ions of different oxidation states as redox pairs in both half-cells. In contrast to several literature studies, which use OCV measurements to deduce the SOC via the Nernst equation, we propose a method based on UV-Vis spectroscopy for SOC estimation, thereby enabling completely independent SOC and OCV measurements. Moreover, rather than relying on data at a single wavelength this UV-Vis method uses the entire absorption spectrum to obtain more robust values for the SOC. The obtained SOC-OCV data agree reasonably well with literature values and reveal a significant influence of the thermodynamic non-ideality of the solutions on the OCV as described by the Nernst equation.
1. Introduction
The growing share of sustainable energy generation has led to and is continuing to lead to a significant increase in the importance of efficient energy storage systems, since it is becoming more and more necessary to be capable of compensating for fluctuations in renewable energies in the power grid.1,2 Among the plethora of possible techniques, one promising electrochemical energy storage system is the redox flow battery (RFB), such as the all-vanadium redox flow battery (AVRFB).3,4 In AVRFBs, vanadium species of different oxidation states are used as redox pairs in both half-cells. This represents a significant advantage over RFBs that employ different metal redox pairs in each half-cell, since cross contamination of vanadium species through the membrane does not result in permanent loss of capacity in AVRFBs which would consequently lead to a shorter lifetime of the system.5,6 The principle of an AVRFB is illustrated in Fig. 1. The two half-cells of the battery are separated by a proton exchange membrane (PEM), which facilitates charge balancing through proton transfer, while an electrical conductor ensures the flow of electrons. It should be noted that anion exchange membranes can be employed as well; however, PEMs are the most commonly used membranes.7–9 Consequently, anion exchange membranes will not be addressed in the following. Both half-cells contain vanadium species in aqueous solutions of sulfuric acid. In galvanic operation, i.e. during discharging, in one half-cell VO2+ is reduced to VO2+ while in the other half-cell V2+ is oxidized to V3+.10 These species correspond to vanadium in the oxidation states V, IV, II, and III and undergo the following chemical reactions:11 | (I) |
 | (II) |
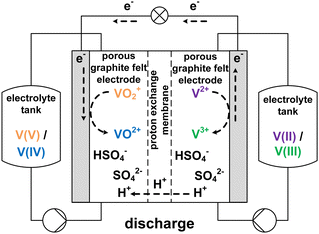 | ||
| Fig. 1 Sketch of an AVRFB with proton exchange membrane in galvanic operation, i.e. while discharging. | ||
The V(V)/V(IV) half-cell has a standard potential of E0V/IV = 1.000 V versus the standard hydrogen electrode (SHE),12 while the V(II)/V(III) half-cell has a potential of E0III/II = −0.256 V versus SHE.13 This results in a standard cell potential of E0cell = 1.256 V for the overall cell reaction:
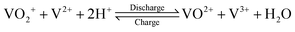 | (III) |
The state of charge (SOC) of the AVRFB can be calculated from the concentrations of the different vanadium species. In continuation of previous work,14 we use molalities to denote concentrations and, hence, to define the SOC. The molality of a vanadium species i is defined as
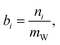 | (1) |
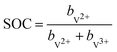 | (2) |
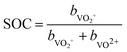 | (3) |
As for any battery type, the availability of an accurate method for SOC estimation is quintessential. In the literature, several approaches to SOC estimation have been discussed, which are briefly discussed in the following, a review on the topic has been presented in ref. 15.
The most basic method is Coulomb counting, which is however prone to uncertainties especially after many charge–discharge cycles.15 Other measurement methods use the SOC-dependence of thermophysical properties of the electrolyte solutions in the half-cells, such as conductivity.16,17 Several research groups have proposed approaches based on the measurement of the open circuit voltage (OCV)15,18,19 or open circuit potentials of the half-cells.19,20 However, there are some inherent uncertainties associated with these approaches as they involve making assumptions in evaluating the Nernst equation, as will be detailed below. Lastly, in aqueous solution, the different vanadium species absorb light at different wavelengths, resulting in the colors chosen in Fig. 1 for those species. Upon undergoing the successive reduction from V(V) to V(II), the solution color changes from yellow to blue to green to purple.3,21 The observed colors are a consequence of the excitation of molecules from the ground state to an excited state, with the required energy being in the UV-Vis range. In transition metals such as vanadium, three types of transitions are observed: d–d transfer as well as charge transfer from metal to ligand and vice versa.22 It has been demonstrated for the different vanadium species that the Beer–Lambert law can be applied in the concentration range of interest for the AVRFB.23,24 Consequently, the color changes can be used to monitor the concentration of the vanadium species via UV-Vis absorption spectroscopy during charging and discharging. A SOC measurement method based on UV-Vis spectroscopy is proposed in the present work and different such approaches have been proposed in the literature.15,16,18,24–28 However, in many of the literature methods, the absorption spectra are typically analyzed at a single wavelength.16 This results in the omission of a significant amount of information of the spectrum. In this context, of special interest for the present work is an approach proposed by Loktinov et al.27 and subsequently extended by Maurice et al.,28 which is based on spectral deconvolution of the wavelength-dependent UV-Vis data. Furthermore, ref. 28 provides a detailed overview on different approaches of SOC estimation from UV-Vis absorption spectra.
As mentioned above, some of the methods for determining the SOC rely on calculations of vanadium concentrations from the measured OCV. The OCV, denoted here with the symbol Erevcell, is the voltage in the currentless equilibrium state. It thus marks the starting point of the voltage–current curves of the system and is therefore an important starting point for modeling and optimization of batteries.29 For an AVRFB with a PEM, the open circuit voltage is described by the Nernst equation:30
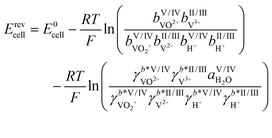 | (4) |
Herein, E0cell is the standard cell potential discussed above, R is the universal gas constant, T is the temperature in K, F is the Faraday constant, 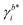 is the activity coefficient of species i on the molality scale (normalized according to Henry's law) and aH2O is the activity of water (normalized according to Raoult's law). For a formal definition of the underlying chemical potentials and activity coefficients, the interested reader is referred to ref. 31. The superscripts to the molalities and activity coefficients denote in which half-cell these properties are to be evaluated.
is the activity coefficient of species i on the molality scale (normalized according to Henry's law) and aH2O is the activity of water (normalized according to Raoult's law). For a formal definition of the underlying chemical potentials and activity coefficients, the interested reader is referred to ref. 31. The superscripts to the molalities and activity coefficients denote in which half-cell these properties are to be evaluated.
In the literature on AVRFBs, the activity coefficients of the species in question are frequently neglected due to a lack of measurement data. However, previous studies by our research group on different RFB systems demonstrated that the activity coefficient term of the Nernst equation plays a significant role and should not be disregarded. Furthermore, the activity term itself exhibits a dependence on the SOC.14 This indicates that precise SOC determinations should not be based on OCV data that do not account for the activity term.
Once reliable experimental data for the determination of the SOC are available, data processing methods come into play. Different algorithms have been proposed that are either applied to equivalent circuit models or to process the noisy data measured with the aforementioned methods.15 Such algorithms include not only statistical algorithms, e.g. the Kalman filter,32–34 but also methods from the field of machine learning such as neural networks and deep reinforcement learning.35–37 While these approaches can be powerful, they typically require large data sets for effective training, and their outcomes are closely tied to the quality of the input data. Consequently, the quality of the results will be limited if the training data sets contain inaccuracies or rely on simplifying assumptions, such as the ones mentioned above for the interpretation of OCV data.38,39 Hence, truly independent and accurate experimental SOC data are key to the further development of machine learning-based approaches for battery monitoring.
In the present work, we investigate the dependence between the SOC and the OCV in AVRFBs. To this end, a test rig for measuring important properties of the AVRFB, including OCV, voltage and current in operation, temperature, and UV-Vis absorption spectra of the two half-cells was set up. Moreover, a method to determine the SOC from UV-Vis absorption spectra using a wide wavelength range of the spectra was developed for allowing independent measurements of SOC and OCV. Hence, this SOC estimation method does not rely on simplifying assumptions about the activity term in the Nernst equation. In subsequent charging/discharging experiments, the relationship between the OCV and the SOC was investigated, and the measured data were compared to the few available literature data and to calculations based on the incomplete Nernst equation that lacks the activity term.
2. Experimental
2.1. Experimental setup
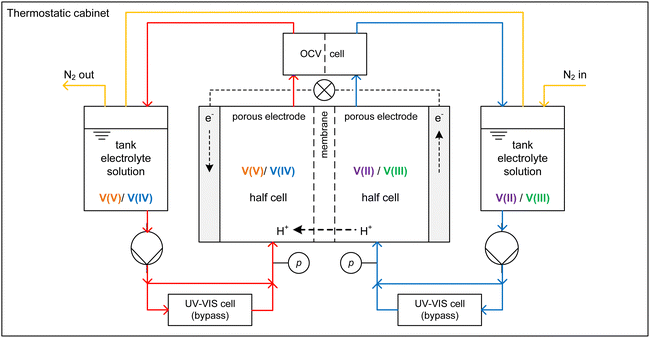
Charging and discharging experiments were conducted using a test rig where the core piece is a redox flow cell with an active area of 20 cm2, carbon felt electrodes (Pinflow Energy Storage s.r.o., Czech Republic) and a PEM (Fumasep F-1850, FUMATECH BWT GmbH, Germany). Fig. 2 shows the AVFRB as well as the periphery of the redox flow cell. The redox flow cell and the equipment in contact with the electrolyte solution are housed in a thermostatic cabinet (POL EKO, Poland) for temperature control. The electrolyte solutions of the two half-cells are stored in a 100 ml tank each and pumped to the redox flow cell with a peristaltic pump (Watson-Marlow Pumps, England). The atmosphere of the two tanks is connected by tubing and has closable outlets to a nitrogen line through which the atmospheric oxygen can be displaced. This is important to prevent the undesired oxidation of V(II) by atmospheric oxygen during the experiment.3 A cell for measuring the OCV (Pinflow Energy Storage s.r.o., Czech Republic) is integrated into the electrolyte solution loop after the redox flow cell. The pressure is measured with two manometers (EM-Technik GmbH, Germany). A potentiostat (PTC-0520 E, kolibrik.net, Czech Republic, not shown in the figure) is used to control and measure current and voltage of the redox flow cell and measure the OCV with the OCV cell. UV-Vis spectroscopic measurements were conducted in situ in a bypass between the tanks and the redox flow cell. The spectrometer consists of the light source HL-2000-FHSA-LL (OceanInsight, USA, not shown in the figure), the flow-through UV-Vis cuvette 584.4-Q-0.2-Z15 (Starna GmbH, Germany) with an optical pathway of 0.2 mm in a cuvette holder (CUV-UV, OceanInsight, USA) and the detector FLAME-T-VIS-NIR-ES (OceanInsight, USA, not in the figure) with a wavelength range of 350 to 1000 nm. The different components of the spectrometer are connected with UV-Visible optical fiber (OceanInsight, USA, not shown in the figure).2.2. Preparation of electrolyte solutions
For the experiments carried out in this work, a commercial 1.6 M vanadium electrolyte solution by GfE (Gesellschaft für Elektrometallurgie mbH, Germany) was used in both electrolyte tanks. The solution is composed of 1.774 mol kg−1 total vanadium, 4.384 mol kg−1 sulfuric acid, ≤ 0.05 mol kg−1 phosphoric acid and water. This solution is equimolar in V(III) and V(IV), which is sometimes referred to as an oxidation state of +3.5 in the literature.20 Starting from this solution, the battery was precharged by oxidizing V(III) to V(IV) in the V(V)/V(IV) half-cell and reducing V(IV) to V(III) in the V(II)/V(III) half-cell. After precharging to an extent such that only V(IV) was present in the V(V)/V(IV) half-cell and only V(III) was present in the V(II)/V(III) cell, the solution was ready for use in charging/discharging experiments.19Vanadium electrolyte solutions containing solely the V(V) oxidation state were obtained by filling electrolyte solution in excess into the V(II)/V(III) half-cell and charging while monitoring the UV-Vis absorption spectra. The reverse procedure was applied to obtain vanadium electrolyte solutions containing solely V(II) species. Vanadium electrolyte solutions containing solely V(IV) or V(III), respectively, were obtained by discharging slowly and carefully monitoring the UV-Vis absorption spectra. Special care was taken to not overshoot the reduction of V(IV) towards V(III) and the oxidation of V(III) towards V(IV) by monitoring all parameters closely.
2.3. Overview on experiments
All experimental data shown in this work are available in a spreadsheet file in the ESI.† All experiments were carried out at a constant temperature of 298.15 K, at a volumetric flow rate of 40 cm3 min−1, and with 50 ml electrolyte solution in each tank. The OCV, current, voltage, and UV-Vis absorption spectra for SOC determination were measured in increments of 1 s. For charging experiments, the precharged AVRFB with 50 ml electrolyte solution in each tank was charged by applying a constant voltage of 1.64 V. During this process, the current decreased from 1.1 to 0.01 A. The duration of a charging experiment in this setup was about 2 h. For discharging experiments, the voltage was set to 0.80 V. During this process, the current decreased from 4 to 0.01 A (in the opposite direction of the charging experiment, of course). The duration of a discharging experiment in this setup was about 50 min.In order to investigate UV-Vis absorption spectra in general and to determine the SOC from UV-Vis absorption spectra, vanadium electrolyte solutions were prepared ex situ: vanadium electrolyte solution containing solely vanadium species in the V(II) oxidation state and vanadium electrolyte solution with solely V(III) were combined to obtain mixtures with SOCs between 0 and 1 in increments of 0.1. Subsequently, the absorption spectra of these mixtures were measured with time steps of 1 s and an integration time of 100 ms for 120 s and averaged. The same approach was applied to solutions containing solely vanadium species of the oxidation state V(V) and V(IV).
2.4. Processing of the UV-Vis spectra
During the experiments, UV-Vis spectra were obtained as a function of time (with time steps of 1 s and an integration time of 100 ms) and of wavelength (in the range of 350–1000 nm in steps of about 0.2 nm). To smooth the raw data, a Hann window with a size of 101 data points (corresponding to a width of ± 10.1 nm) was applied along the wavelength axis. Subsequently, a second smoothing step was performed using a Hann window with a size of 51 data points (corresponding to a width of ± 25 s) along the time axis. A Hann window w is defined by:40,41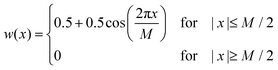 | (5) |
Therein, M + 1 is the size of the window and in our case x denotes either wavelength or time. In a third processing step for the spectra of the V(II)/V(III) half-cell, the absorbance at the isosbestic point at a wavelength of 725 nm was set to zero in order to perform a baseline correction. This method allows for the observation and correction of faulty shifts of the baseline, which may arise between different experiments. In the following, the UV-Vis spectra are shown in a wavelength range between 400 and 900 nm. Outside this range, the data are too noisy, primarily due to the limits of the detector.
3. Results and discussion
3.1. Single vanadium species and isosbestic points
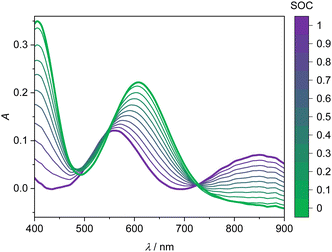
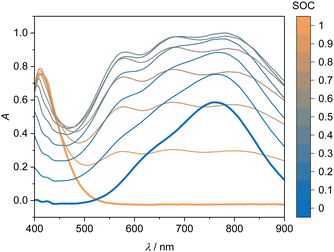
Fig. 3 shows the four UV-Vis absorption spectra of electrolyte solutions that contain solely vanadium species in one oxidation state. Smooth spectra are obtained from applying the Hann window on the raw data as outlined in Section 2.4, indicating that this easy-to-implement filter is an adequate tool for the initial processing of the UV-Vis absorption data. The UV-Vis absorption spectrum of V(II) exhibits two peaks in the considered wavelength range, one at about 560 nm and a smaller one at about 850 nm, leading to a purple color. V(III) exhibits a peak at 608 nm and the flank of a peak can be seen at about 400 nm, which is equivalent to a greenish color of the solution. For V(IV), one large absorption peak exists at about 760 nm in the yellow to red range, which results in a blue color, while V(V) exhibits a peak at about 413 nm, close to the periphery of the considered wavelength range in the range of violet and blue, leading to a yellow color.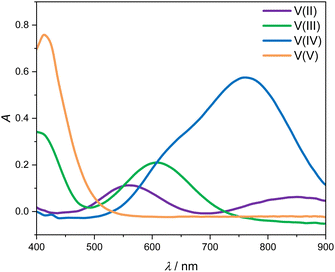 | ||
| Fig. 3 UV-Vis absorption spectra for wavelengths between 400 and 900 nm of 1.774 mol kg−1 vanadium in different oxidation states in aqueous solution with 4.384 mol kg−1 sulfuric acid at 298.15 K. | ||
All peak positions and shapes are in good agreement with data from the literature.3,24–28 For a direct comparison of the entire absorption spectra from this work to the recent and comprehensive data from Maurice et al.,28 two steps have to be taken: first, the baseline of the spectra has to be aligned since in this work, we correct the baseline using the isosbestic point at 725 nm, while in the work of Maurice et al., the baseline is set in a manner that ensures that there are only positive values. Second, it must be taken into account that the cuvettes used by Maurice et al. and in this work differ in pathlength. This can be accounted for by simply scaling the respective spectra with the pathlength. When carrying out those two alignment steps, the spectra for the individual vanadium oxidation states are in excellent agreement between the work of Maurice et al. and this work.
The spectra of V(II) and V(III) exhibit isosbestic points at wavelengths of 488 nm, 550 nm as well as the isosbestic point at 725 nm used for the baseline correction. Even though the spectra of V(V) and V(IV) exhibit the same absorption at 530 nm, there is no isosbestic point, as will become evident in the following.
3.2. State of charge
The UV-Vis spectra of the V(II) and V(III) mixtures prepared ex situ (as detailed in Section 2.3) are presented in Fig. 4. The UV-Vis spectra of the V(II)/V(III) electrolyte solutions exhibit a linear dependence between SOC and absorption. This dependence can be used for the determination of the SOC. A spectrum of a mixture of V(II)/V(III) can be described by weighting both spectra of the solutions containing solely vanadium of either species (cf.Fig. 3) with the mole fraction of the respective species relative to the whole vanadium concentration.42 For V(II), this mole fraction equals the SOC (cf.eqn (2)) while it is 1-SOC for V(III). This summation condition can be applied to the absorption spectrum of a mixture A at a given wavelength λ:| A(λ) = SOC AV(II)(λ) + (1 − SOC) AV(III)(λ) | (6) |
Here, Ai is the absorption of vanadium of the species i. For a known spectrum and thus known absorption at the given wavelength A(λ), the SOC for the mixture can be calculated:
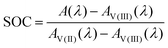 | (7) |
This equation can be applied to every wavelength data point of a spectrum and the SOC can then be averaged over broad ranges of the spectrum. Since at isosbestic points, the denominator of the fraction in eqn (7) becomes zero, areas close to the isosbestic points should not be taken into account. Consequently, the data are averaged from 600 to 700 nm and 750 to 900 nm to obtain the values for the SOC.
The UV-Vis spectra for the V(V) and V(IV) solutions are shown in Fig. 5. The UV-Vis spectra of the V(V)/V(IV) electrolyte solutions demonstrate no simple correlation between SOC and absorption over the entire wavelength range. This phenomenon is attributed to the formation of a mixed valence V(V)/V(IV) complex, which absorbs light over a broad wavelength spectrum.21,23 Due to the strong absorption of this complex, the spectra of the reaction from V(V) to V(IV) do not show an isosbestic point. In summary, the spectra in the V(V)/V(IV) half-cell are not suitable for a straightforward linear evaluation with an equation similar to eqn (7). Nevertheless, it would be desirable to investigate this more closely in future work, i.e. for identifying potential ion crossover, charge imbalances or other degradation processes.20,43 In the following, we use the evaluation of the V(II)/V(III) half-cell viaeqn (7) for describing the SOC of the system.
3.3. Open circuit voltage
In the charging/discharging experiments, as detailed in Section 2.3, we measured the OCV together with the SOC. Fig. 6 shows the measured data from this work (red line), measured data from the literature18,30,44,45 (dots), and the calculated OCV, in which the activity term of the Nernst equation is disregarded (black line). The measured data from this work show good overall agreement with experimental data from the literature, particularly with the more recent data sets.18,30 A comparison between the measured data and the calculated data from the Nernst equation without the activity term demonstrates the necessity to account for the activities of the species. Hence, concentrations of vanadium species and, consequently, the SOC should not be calculated from measured OCV data using the incomplete Nernst equation. In future work, we plan to obtain experimental data on osmotic coefficients of the electrolyte solutions, from which thermodynamic models for the activity coefficients can be developed. These models offer a thermodynamically sound and predictive route to the Nernst equation of AVRFBs. By this, also SOC determination from OCV measurement might become possible, potentially also allowing for detecting battery faults or monitoring degradation by a comparison to the expected UV-Vis spectra at the current SOC.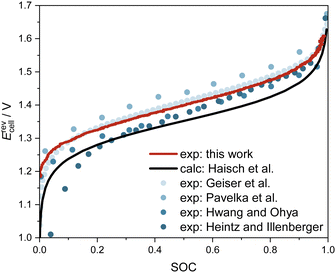 | ||
| Fig. 6 OCV of the AVRFB as a function of SOC at 298.15 K. Measured data from this work and the literature18,30,44,45 as well as data calculated by the Nernst equation, disregarding the activity term.19 Note that the experimental conditions differ: only in ref. 18, the temperature and concentrations were identical to this work; in ref. 30 and 44, the concentrations of vanadium and sulfuric acid were higher and at standard temperature, respectively 308 K; while in ref. 45, an electrolyte solution with lower concentrations of vanadium and sulfuric acid was investigated at 298 K. | ||
4. Conclusions
A laboratory-scale test rig for studying the AVRFB was set up and used for investigating the dependence of the OCV on the SOC. To this end, a method for determining the SOC of the AVRFB was established using UV-Vis spectroscopy: the absorption in the half-cell containing V(II) and V(III) species is directly proportional to the SOC. However, the presence of a mixed-valence complex prevents the straightforward evaluation of spectra gathered in the half-cell containing V(V) and V(IV).Having established the SOC determination, measurements of the OCV as a function of the SOC were carried out. Overall, the results are in agreement with the available literature data. Discrepancies mainly arise from the fact that many literature studies determine the SOC from voltage measurements, which is inherently flawed since this requires assuming ideal thermodynamic behavior of the solutions when evaluating the Nernst equation. These findings confirm the importance of activity coefficients in the highly concentrated electrolyte solutions used in AVRFBs.
A next step will be to combine SOC determination from UV-Vis absorption spectra in both half-cells. Together with additional, independent measurements of osmotic coefficients, the OCV data from the present work will be used in future work for developing a thermodynamic model for the vanadium-containing electrolyte solutions. This model can then be employed to bridge the gap between the measured OCV and the calculated OCV, potentially also enabling a sound SOC determination from OCV measurements.
Author contributions
Jana Heiß: conceptualization, data curation, formal analysis, investigation, methodology, validation, writing – original draft. Maximilian Kohns: conceptualization, funding acquisition, methodology, project administration, supervision, writing – review & editing.Data availability
All experimental data shown in this work are available in a spreadsheet file in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the German Research Foundation (DFG) under grant KO 5844/3-1 (project number 464239829).Notes and references
- C. S. Lai, Y. Jia, L. L. Lai, Z. Xu, M. D. McCulloch and K. P. Wong, Renewable Sustainable Energy Rev., 2017, 78, 439–451 CrossRef.
- P. Alotto, M. Guarnieri and F. Moro, Renewable Sustainable Energy Rev., 2014, 29, 325–335 CrossRef CAS.
- M. Skyllas-Kazacos, L. Cao, M. Kazacos, N. Kausar and A. Mousa, ChemSusChem, 2016, 9, 1521–1543 CrossRef CAS PubMed.
- L. Arenas, C. Ponce de León and F. Walsh, J. Energy Storage, 2017, 11, 119–153 CrossRef.
- C. Lenihan, D. Oboroceanu, N. Quill, D. Ní Eidhin, A. Bourke, R. P. Lynch and D. N. Buckley, ECS Trans., 2018, 85, 175–189 CrossRef CAS.
- E. Sánchez-Díez, E. Ventosa, M. Guarnieri, A. Trovò, C. Flox, R. Marcilla, F. Soavi, P. Mazur, E. Aranzabe and R. Ferret, J. Power Sources, 2021, 481, 228804 CrossRef.
- J. Vrána, J. Charvát, P. Mazúr, P. Bélský, J. Dundálek, J. Pocedič and J. Kosek, J. Membr. Sci., 2018, 552, 202–212 CrossRef.
- J. Charvát, P. Mazúr, M. Paidar, J. Pocedič, J. Vrána, J. Mrlík and J. Kosek, J. Membr. Sci., 2021, 629, 119271 CrossRef.
- T. Lemmermann, M. Becker, M. Stehle, M. Drache, S. Beuermann, U. Gohs, U. E. Fittschen, T. Turek and U. Kunz, J. Power Sources, 2024, 596, 233983 CrossRef CAS.
- M. Skyllas-Kazacos and F. Grossmith, J. Electrochem. Soc., 1987, 134, 2950–2953 CrossRef CAS.
- M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55 CrossRef CAS.
- J. E. Carpenter, J. Am. Chem. Soc., 1934, 56, 1847–1850 CrossRef CAS.
- G. Jones and J. H. Colvin, J. Am. Chem. Soc., 1944, 66, 1573–1579 CrossRef CAS.
- N. Hayer and M. Kohns, J. Electrochem. Soc., 2020, 167, 110516 CrossRef CAS.
- O. Nolte, I. A. Volodin, C. Stolze, M. D. Hager and U. S. Schubert, Mater. Horiz., 2021, 8, 1866–1925 RSC.
- M. Skyllas-Kazacos and M. Kazacos, J. Power Sources, 2011, 196, 8822–8827 CrossRef CAS.
- S. Corcuera and M. Skyllas-Kazacos, Eng. Chem. Mater. Sci., 2012, 511–519 CAS.
- J. Geiser, H. Natter, R. Hempelmann, B. Morgenstern and K. Hegetschweiler, Z. Phys. Chem., 2019, 233, 1695–1711 CrossRef CAS.
- T. Haisch, H. Ji and C. Weidlich, Electrochim. Acta, 2020, 336, 135573 CrossRef CAS.
- S. Ressel, F. Bill, L. Holtz, N. Janshen, A. Chica, T. Flower, C. Weidlich and T. Struckmann, J. Power Sources, 2018, 378, 776–783 CrossRef CAS.
- N. Kausar, R. Howe and M. Skyllas-Kazacos, J. Appl. Electrochem., 2001, 31, 1327–1332 CrossRef CAS.
- B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Applications, Wiley-VCH, New York, 1999 Search PubMed.
- P. Blanc, C. Madic and J. P. Launay, Inorg. Chem., 1982, 21, 2923–2928 CrossRef CAS.
- R. P. Brooker, C. J. Bell, L. J. Bonville, H. R. Kunz and J. M. Fenton, J. Electrochem. Soc., 2015, 162, A608–A613 CrossRef CAS.
- C. Choi, S. Kim, R. Kim, Y. Choi, S. Kim, H.-Y. Jung, J. H. Yang and H.-T. Kim, Renewable Sustainable Energy Rev., 2017, 69, 263–274 CrossRef CAS.
- J. Geiser, H. Natter, R. Hempelmann, B. Morgenstern and K. Hegetschweiler, Z. Phys. Chem., 2019, 233, 1683–1694 CrossRef CAS.
- P. Loktionov, R. Pichugov, D. Konev, M. Petrov, A. Pustovalova and A. Antipov, J. Electroanal. Chem., 2022, 925, 116912 CrossRef CAS.
- A. A. Maurice, A. E. Quintero and M. Vera, Electrochim. Acta, 2024, 482, 144003 CrossRef CAS.
- K. Knehr and E. Kumbur, Electrochem. Commun., 2011, 13, 342–345 CrossRef CAS.
- M. Pavelka, F. Wandschneider and P. Mazur, J. Power Sources, 2015, 293, 400–408 CrossRef CAS.
- M. Kohns, G. Lazarou, S. Kournopoulos, E. Forte, F. A. Perdomo, G. Jackson, C. S. Adjiman and A. Galindo, Phys. Chem. Chem. Phys., 2020, 22, 15248–15269 RSC.
- R. E. Kalman, J. Basic Eng., 1960, 82, 35–45 CrossRef.
- B. Xiong, J. Zhao, Z. Wei and M. Skyllas-Kazacos, J. Power Sources, 2014, 262, 50–61 CrossRef CAS.
- Z. Wei, K. J. Tseng, N. Wai, T. M. Lim and M. Skyllas-Kazacos, J. Power Sources, 2016, 332, 389–398 CrossRef CAS.
- H. Cao, X. Zhu, H. Shen and M. Shao, ASME 2015 13th International Conference on Fuel Cell Science, Engineering and Technology, 2015.
- M. Ben Ahmed and W. Fekih Hassen, Batteries, 2023, 10, 8 CrossRef.
- D. Xiao, B. Li, J. Shan, Z. Yan and J. Huang, ACS Omega, 2023, 8, 45708–45714 CrossRef CAS PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, New York, 1st edn, 2006 Search PubMed.
- M. R. Carbone, MRS Bull., 2022, 47, 968–974 CrossRef.
- F. Harris, Proc. IEEE, 1978, 66, 51–83 Search PubMed.
- R. W. S. Alan and V. Oppenheim, Discrete-Time Signal Processing, Prentice Hall, Upper Saddle River, NJ, 3rd edn, 2010 Search PubMed.
- M. Maeder and Y.-M. Neuhold, Practical Data Analysis in Chemistry, Elsevier, 1st edn, 2007, vol. 26 Search PubMed.
- T. Haisch, H. Ji, L. Holtz, T. Struckmann and C. Weidlich, Membranes, 2021, 11, 232 CrossRef CAS PubMed.
- G. Hwang and H. Ohya, J. Membr. Sci., 1997, 132, 55–61 CrossRef CAS.
- A. Heintz and C. Illenberger, Ber. Bunsengesellschaft Phys. Chem., 1998, 102, 1401–1409 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00360h |
| This journal is © The Royal Society of Chemistry 2024 |