Open Access Article
Open Access ArticleShort-range disorder mediated stability of Zn in rock-salt MgO beyond configurational entropy†
Shengnan
Sun‡
 *a,
Jun
Zhou‡
*a,
Jun
Zhou‡
 a,
Shibo
Xi‡
b,
Hui Ru
Tan
a,
Fengxia
Wei
a,
Shibo
Xi‡
b,
Hui Ru
Tan
a,
Fengxia
Wei
 a,
Debbie Hwee Leng
Seng
a,
Wei Ying
Lieu
a,
Debbie Hwee Leng
Seng
a,
Wei Ying
Lieu
 ac,
Yi
Ren
a,
Shijie
Wang
ac,
Yi
Ren
a,
Shijie
Wang
 *a and
Zhi Wei
Seh
*a and
Zhi Wei
Seh
 *a
*a
aInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Innovis #08-03, Singapore 138634, Republic of Singapore. E-mail: sun_shengnan@imre.a-star.edu.sg; sj-wang@imre.a-star.edu.sg; sehzw@imre.a-star.edu.sg
bInstitute of Sustainability for Chemicals, Energy and Environment (ISCE2), Agency for Science, Technology and Research (A*STAR), 1 Pesek Road, Jurong Island, Singapore 627833, Republic of Singapore
cPillar of Engineering Product Development, Singapore University of Technology and Design, 8 Somapah Road, Singapore 487372, Republic of Singapore
First published on 4th July 2024
Abstract
High-entropy rock-salt Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O has been intensively studied in the energy field due to its unique composition–function relationship and synergistic effect. Entropy-stabilization of Cu and Zn in rock-salt Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O is the key characteristic of this material. As a parent binary oxide, ZnO exists as wurtzite in nature. Herein, for the first time we investigated the role of late 3d transition metals Co, Ni and Cu in stabilizing Zn in MgO-based rock-salt oxides under the same configurational entropy condition and their structural stability in alkaline solutions. We found that Co, Ni and Cu can increase the Zn solubility in MgO-based rock-salt oxides, Mg0.50TM0.25Zn0.25O (TM = Co, Ni and Cu, configurational entropy 1.04 R), with Cu being the best. Simulation results show that the formation energy of Zn substitution for Mg is the lowest in Mg0.50Cu0.25Zn0.25O. Moreover, Cu incorporation can create a wide metal–oxygen bond length distribution, which causes short-range disorder and enhances Zn stabilization. Surprisingly, CuO with square-planar Cu–O coordination is more effective in stabilizing rock-salt ZnO in MgO, compared to rock-salt CoO and NiO, as Cu2+ ions undergo splitting of eg orbitals due to strong Jahn–Teller distortion. Mg0.50Cu0.25Zn0.25O with medium entropy 1.04 R can stabilize 25 at% Cu and 25 at% Zn simultaneously. Besides, the Ni substitution is found to be effective in improving the structural stability in alkaline solutions. This work gives insight into understanding the complementation of orbital distribution in high-entropy oxides for metal stabilization, and provides a rational composition design for applications in the energy field.
1. Introduction
High-entropy oxides (HEOs) are single-phase oxide solid solutions that have a configurational entropy greater than 1.5R and contain five or more cations.1,2 Recently, HEOs with various crystal structures have demonstrated great potential and enhanced properties in the energy field,3–5 such as in electrocatalysis and battery areas, due to the synergistic effect and unique composition–function relationship.6,7 For example, enhanced oxygen evolution reaction (OER) on perovskite HEO LaCr0.2Mn0.2Fe0.2Co0.2Ni0.2O3−δ has been reported compared with all its parent compounds LaMO3 (M = Cr, Mn, Fe, Co, Ni), which is ascribed to a synergistic effect in the adsorbate binding on several transition metal surfaces.8 The HEO composition for better OER is also optimized by Nguyen et al. to La(CrMnFeCo2Ni)O3.9 Enhanced OER is also observed on the spinel HEO (Fe0.20Co0.20Ni0.20Cu0.20Zn0.20)Al2O4 by Katzbaer et al., which is attributed to a narrower band gap of the HEO than that of all parent spinel oxides.10 We recently also found surface entropy evolution on spinel HEO Zn(CrMnFeCoNi)2O4 during OER cycling, accompanied by the changed reaction mechanism and promoted OER performance.11 In the battery area, Liu et al. investigated the Co concentration effect in spinel (CrFeMnNiCox)3O4 on Li storage and found that higher Co concentrations contribute to higher Li storage capability.12Besides perovskite and spinel HEOs, the rock-salt HEOs also exhibit excellent performance in catalysis,13 anodes14,15 and cathodes16 in batteries, in particular, Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O, as a single phase stabilizing tenorite CuO and wurtzite ZnO in a single rock-salt structure by configurational entropy.2 In the study by Liu et al., Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O has regulated electronic and geometric structures for superior intrinsic OER activity compared with CoO, NiO, and Co0.5Ni0.5O.17 In our recent study, we found that the ammonia generation from nitrate reduction can be promoted on Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O due to the spin-related Cu–Co pair.13 In battery anodes, the cycling performance of Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O and the synergy of cations have been intensively investigated. Sarkar et al. reported that entropy-stabilization in Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O is beneficial to the Li-ion anode cycling stability, and the removal of any one of Co, Cu and Zn led to severe capacity degradation, especially Co.14 Inactive material MgO and well-mixed cations in HEO are found to be essential to remarkable cycling, rate performance and high capacity by Qiu et al.18 The lithiation–delithiation process of Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O was investigated by Ghigna et al. using X-ray absorption spectroscopy (XAS) and they found that the reduction of cations begins from Cu to Co and Ni, followed by alloying Mg and Zn with Li, and furthermore the reaction is not fully reversible. They also suggest that both ZnO and MgO, especially MgO, are responsible for the high capacity compared with the oxides without Mg and Zn.19 Moreover, in the XAS study by Wang et al., metallic Co, Ni, Cu and Zn were observed and the rock-salt fcc Mg-dominated oxide matrix was left after lithiation, while Cu, Ni and a large fraction of Co were not being oxidized after delithiation.20 Additionally, an improvement in Li-storage was reported in Li-substituted (MgCoNiZn)O21 and (MgCoNiCuZn)O,22 which is ascribed to the generation of oxygen vacancies. These findings imply the significance of the intrinsic composition–function relationship in cubic rock-salt oxides in electrocatalysis and Li-ion batteries.
While Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O is considered as an entropy-stabilized oxide that stabilizes tenorite CuO and wurtzite ZnO in a single rock-salt structure, an investigation by Fracchia et al. demonstrates an important role of solubility in stabilizing Cu2+ (t2g6eg3 in 3d orbitals) in rock-salt oxides beyond configurational entropy.23 Aamlid et al. categorized HEOs based on two characteristics, configurational entropy and entropy stabilization, that is, conventional solid solutions have low configurational entropy and are not entropy-stabilized while HEOs exhibit either configurational entropy (>1.5R) and/or entropy stabilization.24 Brahlek et al. indicated that “entropy-stabilized” as a subset of “high-entropy” does not necessarily restrict the equilibrium entropy stabilization at room temperature.25 Chen et al. experimentally pointed out that the formation of entropy-stabilized oxide does not necessarily need the configurational entropy to reach 1.5R and the critical temperature is significant in the annealing process for obtaining a single-phase state, taking medium configurational entropy (Mg1/3Co1/3Ni1/3)1−xZnxO for example.26 Besides CuO, ZnO is also stabilized in the cubic rock-salt phase Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O. Differing from Cu2+, Zn2+ has fully occupied 3d orbitals that are symmetrical in all directions with an electron configuration of [Ar]3d10. Wurtzite ZnO has a typical sp3 covalent bonding and a substantial ionic character.27 ZnO is identified as a selective electrocatalyst for water oxidation (to generate hydrogen peroxide28 and oxygen29), oxygen reduction reaction,30 and CO2 reduction,31,32 and also as a suitable coating material for carbon anodes33 and LiCoO2 cathodes34 in Li-ion batteries.
Inspired by the phase stabilization studies above and the composition–function relationship in electrocatalysis and batteries, herein for the first time, we unveil the Zn stabilization in the MgO-based rock-salt Mg0.75−xTMxZn0.25O (TM = Co, Ni and Cu) in powder form by focusing on the impact of late 3d transition metals Co, Ni and Cu. We chose MgO as the matrix due to the stable orbital 1s22s22p6 and non-magnetic properties of Mg2+ ions and its wide application in the energy field, for example, as a promoter in oxygen electrochemistry35,36 and alcohol electrooxidation,37,38 and as a coating to improve the electrode stability and capacity retention in batteries.39–42 We found that the substitution of Co, Ni and Cu for Mg can increase the Zn solubility, among which Cu is the most effective, which is contrary to the intuition that CoO and NiO could be more effective because of their rock-salt structure. We also found that the Ni substitution is effective to improve the resistance to alkaline solutions and structural stability. Our results provide a design guideline for increasing the doping amount with the assistance of another transition metal, potentially in tuning Zn fractions and structural stability in solid solutions. We also for the first time indicate that the medium-entropy Mg0.50Cu0.25Zn0.25O (1.04R) suffices for stabilizing 25 at% Cu and 25 at% Zn in the rock-salt structure simultaneously.
2. Experimental
2.1 Materials
The oxides were synthesized by the sol–gel method as our previous report.13 All chemicals were purchased from Sigma-Aldrich, including magnesium nitrate hexahydrate, cobalt nitrate hexahydrate, nickel nitrate hexahydrate, copper nitrate hemi(pentahydrate), zinc nitrate hexahydrate, nitric acid and citric acid, and urea. The metal nitrates, citric acid, and urea were dissolved in de-ionized water with the feeding mole ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 with less nitric acid under stirring. The solution was kept at ∼95 °C until the gel formed and then dried at 170 °C in an oven overnight. This was followed by annealing at 1000 °C for 6 h at a 5 °C min−1 ramping rate and cooling down naturally. The stability of these oxides in alkaline solutions was evaluated by soaking these oxides in 2 M KOH for four weeks at room temperature under constant stirring. The oxides were collected by centrifugation at 8000 rpm and then drying in an oven overnight. The procedure of centrifugation is as follows. First, the alkaline centrifugate was removed by centrifugation. Then, the remaining oxides were washed by centrifugation at least twice in deionised water until the centrifugate was neutral, followed by a single wash in ethanol. X-ray diffraction (XRD, Bruker D8 Advance using Cu-Kα radiation) was used to characterize the crystal structure. Rietveld refinement was conducted using TOPAS v5, using fundamental parameters and the full axial model. A scanning electron microscope (SEM, JEOL JSM7600F equipped with an Oxford Instruments X-Max 50 mm2 detector) and transmission electron microscope (TEM, FEI Titan equipped with an EDAX detector) were used to obtain the morphology and energy-dispersive X-ray spectroscopy (EDX) mapping. SEM-EDX was used to obtain the atomic ratios of metal elements by at least three independent measurements. The extended X-ray absorption fine structure (EXAFS) and X-ray absorption near edge structure (XANES) were studied at the Singapore Synchrotron Light Source, XAFCA beamline. X-ray photoelectron spectroscopy (XPS) was carried out using a Thermo Fisher Scientific Theta Probe and the binding energy was calibrated from carbon contamination (C 1s peak 284.8 eV). The number of XPS scans was adjusted as needed to achieve a high resolution and signal-to-noise ratio, considering the possibly low ratio of some metal elements. The XPS of commercial MgO (Kanto Chemical), CoO (Alfa Aesar), NiO (Sigma-Aldrich), CuO (Sigma-Aldrich) and ZnO (Kanto Chemical) were used as the control and reference.
2 with less nitric acid under stirring. The solution was kept at ∼95 °C until the gel formed and then dried at 170 °C in an oven overnight. This was followed by annealing at 1000 °C for 6 h at a 5 °C min−1 ramping rate and cooling down naturally. The stability of these oxides in alkaline solutions was evaluated by soaking these oxides in 2 M KOH for four weeks at room temperature under constant stirring. The oxides were collected by centrifugation at 8000 rpm and then drying in an oven overnight. The procedure of centrifugation is as follows. First, the alkaline centrifugate was removed by centrifugation. Then, the remaining oxides were washed by centrifugation at least twice in deionised water until the centrifugate was neutral, followed by a single wash in ethanol. X-ray diffraction (XRD, Bruker D8 Advance using Cu-Kα radiation) was used to characterize the crystal structure. Rietveld refinement was conducted using TOPAS v5, using fundamental parameters and the full axial model. A scanning electron microscope (SEM, JEOL JSM7600F equipped with an Oxford Instruments X-Max 50 mm2 detector) and transmission electron microscope (TEM, FEI Titan equipped with an EDAX detector) were used to obtain the morphology and energy-dispersive X-ray spectroscopy (EDX) mapping. SEM-EDX was used to obtain the atomic ratios of metal elements by at least three independent measurements. The extended X-ray absorption fine structure (EXAFS) and X-ray absorption near edge structure (XANES) were studied at the Singapore Synchrotron Light Source, XAFCA beamline. X-ray photoelectron spectroscopy (XPS) was carried out using a Thermo Fisher Scientific Theta Probe and the binding energy was calibrated from carbon contamination (C 1s peak 284.8 eV). The number of XPS scans was adjusted as needed to achieve a high resolution and signal-to-noise ratio, considering the possibly low ratio of some metal elements. The XPS of commercial MgO (Kanto Chemical), CoO (Alfa Aesar), NiO (Sigma-Aldrich), CuO (Sigma-Aldrich) and ZnO (Kanto Chemical) were used as the control and reference.
2.2 Calculation
The solid solution of oxides is effectively modeled using special quasirandom structures (SQSs) generated by the Alloy Theoretic Automatic Toolkit (ATAT).43 These SQSs are designed to minimize pair correlation differences with the ideally random alloy within a radius greater than 7 Å. The size of the SQSs is consistently set to 64 atoms, corresponding to 2 × 2 × 2 supercells of the rock-salt oxides. To perform further density functional theory (DFT) simulations, the generated SQS structures serve as initial configurations and are inputted into the Vienna ab initio Simulation Package (VASP 5.4.4).44,45 The Perdew–Burke–Ernzerhof (PBE) approximation is utilized for the exchange–correlation functional, and the frozen-core all-electron projector augmented wave (PAW) method is employed to describe the electron–ion interaction.46 The cutoff energy for the plane wave expansion is set to 600 eV. For all simulations, a Monkhorst-pack 6 × 6 × 6 k-point grid is applied. Moreover, the generalized gradient approximation (GGA) with Hubbard U is used specifically for the d orbitals of Ni, Cu, and Co.47,48 The Hubbard U parameters for Ni, Cu, and Co are determined based on suggested values from systematic investigations carried out using high-throughput simulations.49 While the lattice vectors of the SQS structures are kept fixed, their scale factors are optimized during the simulations. The atoms within the structure are fully relaxed until both the energy and force converge to 10−5 eV and 0.01 eV Å−1, respectively.3. Results & discussion
3.1 Material structure and morphology
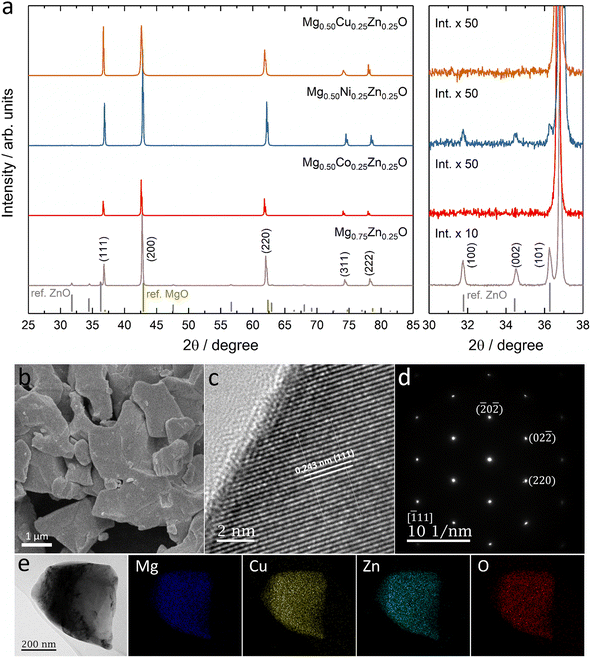
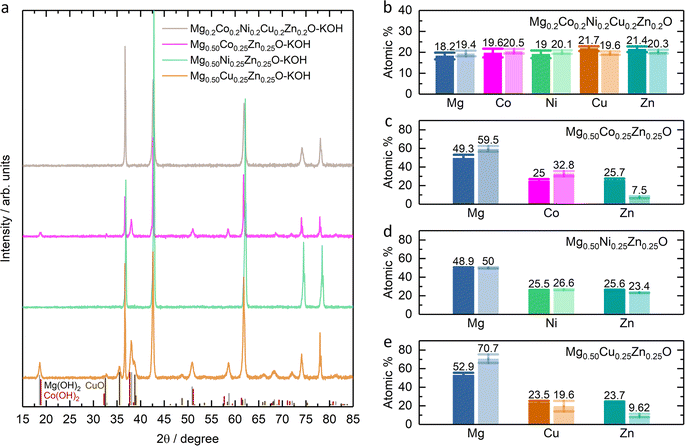
Fig. 1a shows the XRD patterns of Mg0.75Zn0.25O, Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O, and the Rietveld refinements can be found in Fig. S1–S4.† Mg0.75Zn0.25O has an obvious rock-salt structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, lattice parameter a = 4.2278 Å) and contains the second phase wurtzite ZnO (1.52 wt%). The diffraction peaks corresponding to the rock-salt structure shift to a lower angle compared to the standard rock-salt MgO, indicating that Zn introduction increases the lattice constant according to Bragg's law. Such an increase in the lattice constant is consistent with the effective ionic radii order: Zn2+ (0.745 Å) > Mg2+ (0.720 Å).50 When substituting Co, Ni and Cu for Mg, the wurtzite ZnO peaks became weaker and even disappeared. Mg0.50Co0.25Zn0.25O is a single rock-salt phase (lattice parameter a = 4.2428 Å) without the wurtzite ZnO impurity, which indicates that Co is effective in increasing Zn solubility in rock-salt MgO. However, the diffraction peaks of Mg0.50Co0.25Zn0.25O have lower intensities compared with that of Mg0.75Zn0.25O, indicating that Co substitution reduces the crystallization. The Ni substitution for Mg only increases Zn solubility and rock-salt structure crystallization (lattice parameter a = 4.2200 Å), however an impurity-free single rock-salt Mg0.50Ni0.25Zn0.25O could not be obtained (0.088 wt% ZnO). Apart from Co and Ni substitution, substituting Cu for Mg also increases Zn solubility in rock-salt MgO and makes Mg0.50Cu0.25Zn0.25O a single rock-salt phase (lattice parameter a = 4.2394 Å). Different from the XRD profiles of Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, Mg0.50Cu0.25Zn0.25O has a strong (111) diffraction peak, indicating that Cu can increase the order in the [111] direction. It is well known that the (111) planes in rock-salt oxides consist of either metal atoms or oxygen atoms exclusively, and metal atoms contribute more than oxygen atoms in the diffraction peak intensity due to their relatively higher masses. Mg0.50Cu0.25Zn0.25O has a low intensity ratio of I(200)/I(111), indicative of the less ordered (200) planes, which can be explained using the Jahn–Teller effect induced by Cu2+.51 To further compare the enhancement effect between Co and Cu on Zn solubility, we increased the Zn fraction to 30 at% and found that Cu is more effective than Co (Fig. S5†).
m, lattice parameter a = 4.2278 Å) and contains the second phase wurtzite ZnO (1.52 wt%). The diffraction peaks corresponding to the rock-salt structure shift to a lower angle compared to the standard rock-salt MgO, indicating that Zn introduction increases the lattice constant according to Bragg's law. Such an increase in the lattice constant is consistent with the effective ionic radii order: Zn2+ (0.745 Å) > Mg2+ (0.720 Å).50 When substituting Co, Ni and Cu for Mg, the wurtzite ZnO peaks became weaker and even disappeared. Mg0.50Co0.25Zn0.25O is a single rock-salt phase (lattice parameter a = 4.2428 Å) without the wurtzite ZnO impurity, which indicates that Co is effective in increasing Zn solubility in rock-salt MgO. However, the diffraction peaks of Mg0.50Co0.25Zn0.25O have lower intensities compared with that of Mg0.75Zn0.25O, indicating that Co substitution reduces the crystallization. The Ni substitution for Mg only increases Zn solubility and rock-salt structure crystallization (lattice parameter a = 4.2200 Å), however an impurity-free single rock-salt Mg0.50Ni0.25Zn0.25O could not be obtained (0.088 wt% ZnO). Apart from Co and Ni substitution, substituting Cu for Mg also increases Zn solubility in rock-salt MgO and makes Mg0.50Cu0.25Zn0.25O a single rock-salt phase (lattice parameter a = 4.2394 Å). Different from the XRD profiles of Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, Mg0.50Cu0.25Zn0.25O has a strong (111) diffraction peak, indicating that Cu can increase the order in the [111] direction. It is well known that the (111) planes in rock-salt oxides consist of either metal atoms or oxygen atoms exclusively, and metal atoms contribute more than oxygen atoms in the diffraction peak intensity due to their relatively higher masses. Mg0.50Cu0.25Zn0.25O has a low intensity ratio of I(200)/I(111), indicative of the less ordered (200) planes, which can be explained using the Jahn–Teller effect induced by Cu2+.51 To further compare the enhancement effect between Co and Cu on Zn solubility, we increased the Zn fraction to 30 at% and found that Cu is more effective than Co (Fig. S5†).
The SEM images show that Mg0.50TM0.25Zn0.25O (TM = Co, Ni and Cu) exist in the form of particles without regular morphology (Fig. 1b and S6†). The particles have good crystallization. For example, the TEM images show the (111), (200) and (220) lattices of Mg0.50Cu0.25Zn0.25O, corresponding to 0.243 nm, 0.210 nm and 0.151 nm, respectively, consistent with the XRD pattern (Fig. 1c and S7†). The selected area electron diffraction (SAED) pattern (Fig. 1d) shows that the particles exist in the form of single crystals, corresponding to the location in Fig. 1c. The SEM-EDX mapping results indicate that the element distribution is homogeneous in these three oxides (Fig. S8†). Furthermore, the metal element ratios in the oxides are close to the metal precursor feeding ratios (Tables S3–S5†). Within a single particle, the element distribution is also homogeneous as evidenced by the TEM-EDX mapping of Mg, Cu, Zn and O in Fig. 1e.
Fig. 2 shows the k3-weighting Fourier-transformed EXAFS (FT-EXAFS) results of Zn, Co, Ni and Cu in Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O. The experimental EXAFS data can be found in Fig. S9 and S10.† In Fig. 2a, the peaks at around 1.66–1.69 Å and at 2.58 Å are attributed to the first-shell neighbour (Zn–O) and the second-shell neighbour Zn–metal scattering, respectively. Similar attributions can made to Co/Ni/Zn for the peaks in Fig. 2b.52 Considering that the peak position at distances in FT-EXAFS is shifted from the real interatomic distance by 0.2–0.5 Å,53 the EXAFS fitting is performed to obtain the nearest metal–oxygen and metal–metal distances as well as the coordination number. The fitted results for the first and second shells and the parameters can be found in Fig. 2, S11, Tables 1 and S1.† Theoretically, in ideal cubic rock-salt oxides the first-shell coordination number of metal with oxygen is 6 and the second-shell coordination number of metal with metal is 12. From Table 1, in Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, the first-shell distances of Zn–O, Co–O, and Ni–O are close (∼2.12 Å). The first-shell coordination number of Zn with O is around 5.7, which is lower than that of Co/Ni (around 6.3). The first-shell Zn–O distance and the coordination number of Zn in Mg0.50Cu0.25Zn0.25O are close to that in Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, while the Cu–O distance (2.00 Å) and coordination number (3.1) are much smaller compared with Zn, Co and Ni. It could be caused by the Jahn–Teller distortion of Cu2+ ions.51 In Mg0.50Cu0.25Zn0.25O, the second-shell Zn–Mg/Cu/Zn distances are in the range of 2.98 to 3.00 Å. The coordination number of Zn with Mg is 7.9, which is larger than 6 (based on the metal stoichiometric ratio in the oxides), while the coordination number of Zn with Cu/Zn is 2.1, smaller than 6. This suggests that more Mg instead of Cu/Zn occupies the second shell of Zn. Cu has a normal coordination number of 6.1 with Mg and a smaller one of 1.2 with Cu/Zn, which means Cu has a low coordination environment in the second shells, suggesting the less ordered structure around Cu. In Mg0.50Ni0.25Zn0.25O, the same Zn–Mg and Ni–Mg distance 2.96 Å is calculated in the second shell of Zn and Ni with the coordination numbers 7.9 and 8.1, respectively. Zn–Ni/Zn and Ni–Ni/Zn have close distances 2.98 Å and 2.97 Å, and coordination numbers 2.0 and 2.3 with Ni/Zn, respectively. Compared with Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O, Zn in Mg0.50Co0.25Zn0.25O has a close coordination number (8.1) with Mg and a much smaller coordination number (0.2) with Co/Zn, suggesting Zn is less coordinated in the second shell, particularly with Co/Zn. In contrast to Zn, Co has a larger coordination number of 9.6 with Mg and 2.8 with Co/Zn. This indicates that more metals are around Co and less around Zn. Besides, Zn–Mg, Zn–Co/Zn, Co–Mg and Co–Co/Zn in Mg0.50Co0.25Zn0.25O have a very close distance around 2.98 Å.
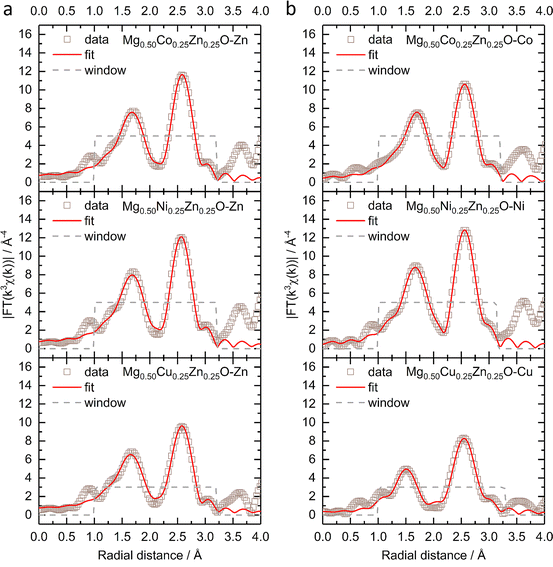 | ||
| Fig. 2 The k3-weighting FT-EXAFS and the fitting of (a) the Zn K-edge and (b) Co, Ni and Cu K-edges of Mg0.50TM0.25Zn0.25O (TM = Co, Ni, Cu) under a Hanning-shaped window. | ||
| Zn–O | TM–O | Zn–Mg | Zn–TM/Zn | TM–Mg | TM–TM/Zn | |
|---|---|---|---|---|---|---|
| Mg0.50Co0.25Zn0.25O | 2.13 Å/5.6 | 2.12 Å/6.4 | 2.99 Å/8.1 | 2.99 Å/0.2 | 2.98 Å/9.6 | 2.98 Å/2.8 |
| Mg0.50Ni0.25Zn0.25O | 2.12 Å/5.7 | 2.10 Å/6.2 | 2.96 Å/7.9 | 2.98 Å/2.0 | 2.96 Å/8.1 | 2.97 Å/2.3 |
| Mg0.50Cu0.25Zn0.25O | 2.12 Å/5.7 | 2.00 Å/3.1 | 2.98 Å/7.9 | 3.00 Å/2.1 | 2.97 Å/6.1 | 2.99 Å/1.2 |
Considering the deviation of the coordination number from ideal values, additional fitting has been performed by fixing the coordination numbers. For Co, Ni and Zn, the first-shell coordination number of the metal with oxygen is fixed to 6, while for Cu, 4 planar and 2 axial coordinating oxygens are considered.54 Because the coordinating metals are randomly distributed and cannot be identified precisely,55 the total second-shell coordination number of metal with metal is fixed to 12. The fitted results and the parameters applied can be found in Fig. S12, S13, Tables 2 and S2.† The fitted Zn–O distances are about 2.14 Å in Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O, which are very close to the fitted values in Table 1. The Co–O and Ni–O distances remain unchanged for the two fittings. For Cu–O, the planar distance is 2.02 Å and the axial distance is 2.28 Å, which are close to reported values in Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O.54–56 For Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, the fitted second-shell metal–metal distances do not change significantly before and after fixing the coordination numbers. In Mg0.50Cu0.25Zn0.25O, the fitted Cu–Mg and Cu–Cu/Zn distances are the same as the values in Table 1, while a dramatic metal–metal distance decrease is observed in Zn–Mg and Zn–Cu/Zn. Though the second-shell coordination numbers for the specific metals still deviate from the ideal coordination numbers after fixing the total coordination number, the trend remains similar to that shown in Table 1.
| Zn–O | TM–O | Zn–Mg | Zn–TM/Zn | TM–Mg | TM–TM/Zn | |
|---|---|---|---|---|---|---|
| Mg0.50Co0.25Zn0.25O | 2.14 Å/6 | 2.12 Å/6 | 3.02 Å/11.5 | 3.01 Å/0.5 | 2.98 Å/9.4 | 2.98 Å/2.6 |
| Mg0.50Ni0.25Zn0.25O | 2.13 Å/6 | 2.10 Å/6 | 2.97 Å/9.0 | 2.97 Å/3.0 | 2.97 Å/8.9 | 2.97 Å/3.1 |
| Mg0.50Cu0.25Zn0.25O | 2.14 Å/6 | 2.02 Å/4 | 2.88 Å/9.7 | 2.75 Å/2.3 | 2.97 Å/8.7 | 2.99 Å/3.3 |
| 2.28 Å/2 |
3.2. Electronic states
The electronic states of Co, Ni, Cu and Zn were further investigated by XANES (Fig. S14†). No obvious change can be observed in the Zn K-edge XANES profile amongst Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O (Fig. S14a†), while their Zn profiles differ from those of ZnO and the reported profile.57 In ZnO (Fig. S14a†), one small shoulder E1 at ∼9663.5 eV, peaks E2 at ∼9669.3 eV and E3 at ∼9680.3 eV, and EXAFS oscillation E4 at ∼9714.9 eV are observed, consistent with the reported ZnO profile by Rodrigues et al.57 Moreover, the E3 peaks for Zn in Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O are shifted by ∼5 eV to higher energy with respect to ZnO, which is also consistent with the report on wurtzite ZnO and cubic ZnO.58 This can be explained by the difference in the Zn chemical environment in these three oxides and wurtzite ZnO. This is in contrast to the Co and Ni XANES profiles of Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, which have no obvious changes and energy shifts compared to commercial CoO and NiO (Fig. S14b and c†), thus suggesting that the Co and Ni valence states are close to +2. Fig. S14d† shows that the Cu XANES profile is different from that of commercial CuO, which can be explained that the environment of Cu in Mg0.50Cu0.25Zn0.25O is different from that in tenorite CuO. Besides XANES, XPS are used to further reveal the surface electronic state of Mg0.50TM0.25Zn0.25O (TM = Co, Ni, Cu) (Fig. 3 and S15†). The XPS results of commercial MgO, CoO, NiO, CuO and ZnO are also provided in Fig. S16 and S17† as references. The Zn 2p profiles have no obvious change among Mg0.50TM0.25Zn0.25O (TM = Co, Ni, Cu) (Fig. 3a, c and e), and the binding energies of Zn 2p3/2 (∼1021.3 eV) and Zn 2p1/2 (∼1044.4 eV) and their difference (∼23.1 eV) are almost the same as that of the commercial ZnO (Fig. S16c†). This indicates a valence state of +2 for Zn. The Co 2p3/2 spectrum in Mg0.50Co0.25Zn0.25O is split into three peaks at 779.8 eV, 781.5 eV and 786.5 eV, respectively (Fig. 3b), which have a similar profile to that of the commercial CoO (Fig. S17a†) and the report by Biesinger et al.59 The binding energies of 779.8 eV and 786.5 eV can be assigned to Co2+ and the satellite, respectively. The attribution to the binding energy of 781.2 eV is still under debate. Some studies assigned it to Co2+,60,61 while others to Co3+.59,62 The early work by McIntyre and Cook indicated that the Co formal oxidation states are hardly differentiated from the binding energy.63 The Ni 2p3/2 profile has a main peak at 854.9 eV and a satellite peak at 860.8 eV (Fig. 3d), which agrees with our reported one in Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O. The main peak has no obvious doublet structure at 853.5 eV (local screening) and 855.4 eV (nonlocal screening)52,64 like commercial NiO (Fig. S17c†). The missing peak can be explained by the negligible nonlocal screening contribution from Ni as the next nearest neighbours as the diluted NiO in the MgO–ZnO matrix,65 which is in agreement with the report by Altieri et al.66 The attribution of the Cu 2p3/2 profile in Fig. 3f is similar to our previous report13 and commercial CuO in Fig. S17e.† The main difference is the relative intensity of Cu+ (932.5 eV) on the surface. Besides, no obvious changes of Mg 1s profiles are observed in Mg0.50TM0.25Zn0.25O (TM = Co, Ni, Cu) (Fig. S15†) and commercial MgO (Fig. S16†), indicating the existence of Mg2+ in the oxides. The O 1s has three distinct peaks at 529.3 eV, 531.0 eV and 533.0 eV (Fig. S15†), take the O 1s profile of Mg0.50Co0.25Zn0.25O as an example, which are assigned to the lattice oxygen, oxygen vacancy and chemically adsorbed oxygen, respectively.21,67 The recent work by Frankcombe and Liu68 pointed out that the binding energy of 531 eV is ascribed to the water molecules strongly bound to the surface as distinct from more loosely bound water at 533 eV.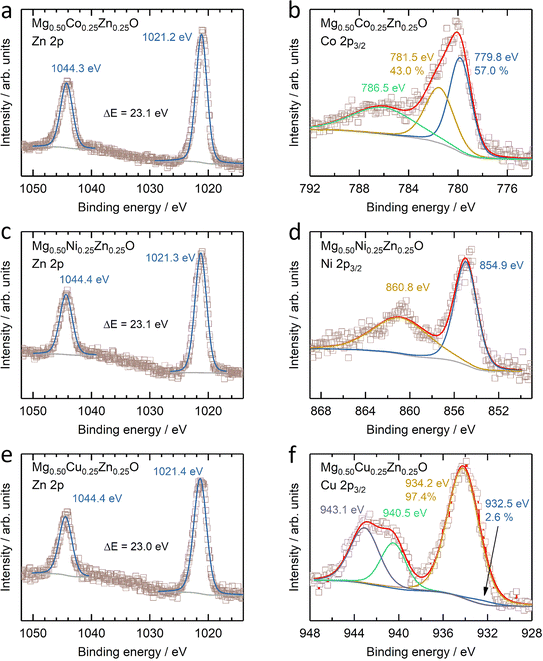 | ||
| Fig. 3 XPS results of (a, c and e) Zn 2p and (b) Co 2p3/2, (d) Ni 2p3/2 and (f) Cu 2p3/2 of (a and b) Mg0.50Co0.25Zn0.25O, (c and d) Mg0.50Ni0.25Zn0.25O and (e and f) Mg0.50Cu0.25Zn0.25O. | ||
3.3. Cu promoted Zn stabilization
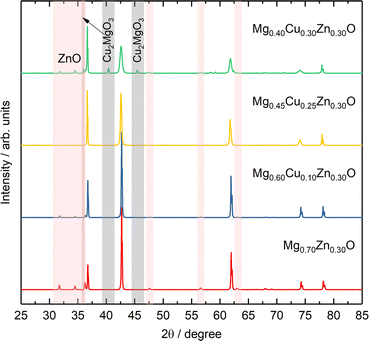
To further investigate the effect of Cu on Zn stabilization in MgO-based rock-salt oxides, we kept the Zn fraction at 30 at% and further tune the relative ratios of Mg and Cu. From the XRD patterns in Fig. 4, Mg0.70Zn0.30O has a more obvious wurtzite ZnO phase than Mg0.75Zn0.25O in Fig. 1a. This suggests that ZnO further evolves when the Zn fraction increases from 25% in the Mg1−xZnxO series. As the Cu fraction increases to 10% and 20%, the ZnO diffraction peaks become increasingly weaker, which means that Cu is effective in stabilizing Zn and inhibiting the ZnO evolution in the rock-salt oxide, even though the amount of phase formation agent Mg decreases and is replaced by Cu. Meanwhile, an increasing (111) peak intensity can be observed, which indicates that the introduction of Cu improves the order in the [111] direction. In addition, the (200) peak becomes weaker gradually, which is caused by the Jahn–Teller distortion of Cu2+ ions.51 The Rietveld refinements of Mg0.70Zn0.30O, Mg0.60Cu0.10Zn0.30O and Mg0.45Cu0.25Zn0.30O can be found in Fig. S18–S20.† There are no obvious attribution changes in the XPS profiles of Mg0.45Cu0.25Zn0.30O (Fig. S21†). When the Cu fraction reaches 30%, an obvious ZnO phase is observed again and a new Cu2MgO3 impurity appears. This means that the introduction of excess Cu does not contribute to Zn stabilization in the rock-salt oxide, and in contrast it causes Cu2MgO3 formation, which lowers Zn solubility in the rock-salt oxides.3.4 Formation energy and bond length distribution
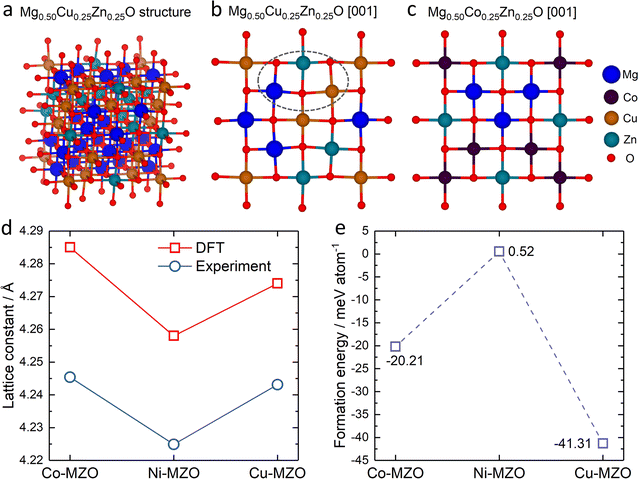
To gain deeper insights into the experimental findings, we further perform density functional theory (DFT) simulations for the three compositions: Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O. Special quasirandom structures (SQSs) are used to model the solid solution state of these rock-salt oxides. As shown in Fig. 5a–c, the relaxed structures demonstrate significant differences. In the case of Mg0.50Cu0.25Zn0.25O (Fig. 5b), the inclusion of Cu atoms results in noticeable lattice distortions. This distortion can be attributed to the Jahn–Teller effect induced by Cu2+. The observed deviation in the oxygen positions of the relaxed structure of Mg0.50Cu0.25Zn0.25O aligns with the low intensity of the metal–oxygen peak in the EXAFS results. Conversely, the lattice distortion is found to be less profound in Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O (Fig. 5c and S22†). The trend of the lattice constants obtained from the relaxed models is also consistent with our experimental observations (Fig. 5d), further strengthening the reliability of our simulations.To investigate the influence of lattice distortions on Zn solubility in MgO, we calculated the formation energies for the substitution of Mg by Zn in the three structures mentioned above. The reference structures to obtain the formation energies are constructed by replacing all the Zn atoms with Mg atoms for Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O, Mg0.50Cu0.25Zn0.25O and Mg0.75Zn0.25O while keeping the atom positions of the gnateater structures fixed. The calculated average formation energies for Zn substitution of Mg for Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O, with respect to Mg0.75Zn0.25O, are −20.21 meV, 0.52 meV, and −41.31 meV, respectively (Fig. 5e). These results indicate that the inclusion of Cu or Co atoms stabilizes the solubility of Zn in MgO, while the presence of Ni has negligible effects. Furthermore, the lowest formation energy is observed for Mg0.50Cu0.25Zn0.25O, suggesting that Zn is most readily stabilized in this composition among the three samples investigated. These findings are consistent with the XRD results obtained for Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O.
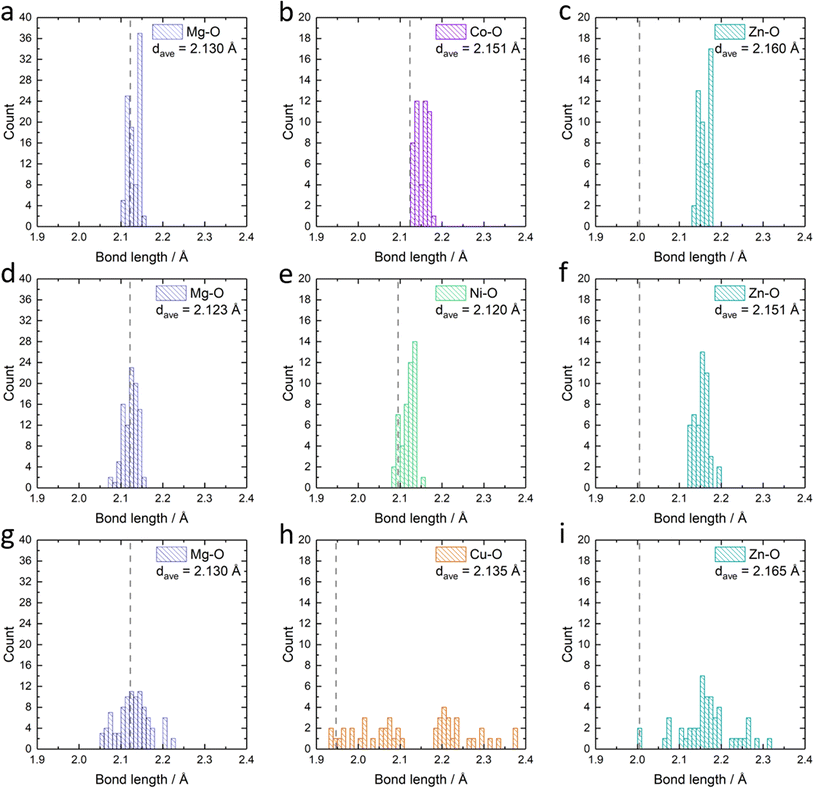
Apart from the different formation energies, we can also observe the change in the metal–oxygen bond length distribution in the relaxed Mg0.50Co0.25Zn0.25O, Mg0.50Ni0.25Zn0.25O and Mg0.50Cu0.25Zn0.25O structures (Fig. 6). In Mg0.50Co0.25Zn0.25O, the Mg–O, Co–O and Zn–O bond lengths are distributed and concentrated in the ranges of 2.10–2.15 Å, 2.13–2.18 Å, and 2.13–2.18 Å, with their average bond lengths being 2.13 Å, 2.15 Å and 2.16 Å, respectively (Fig. 6a–c). This is consistent with the order of the metal ionic radii: 0.720 Å (Mg2+) < 0.735 Å (Co2+, high spin) < 0.745 Å (Zn2+). In Mg0.50Ni0.25Zn0.25O (Fig. 6d–f), the distribution ranges of the Mg–O (2.07–2.16 Å) and Zn–O (2.12–2.19 Å) bond lengths are larger than that of Mg0.50Co0.25Zn0.25O. The Ni–O bond length distributes around 2.09–2.15 Å, which is ascribed to the smaller radius (0.70 Å) of Ni2+. In Mg0.50Ni0.25Zn0.25O, the average bond lengths for Mg–O, Ni–O and Zn–O are 2.12 Å, 2.12 Å and 2.17 Å, respectively. Interestingly, the distributions of Mg–O, Cu–O and Zn–O bond lengths in Mg0.50Cu0.25Zn0.25O (Fig. 6g–i) are much more widespread than that in the other two materials. In particular, the Cu–O bond lengths are distributed across two separate regions, that is, 1.94–2.10 Å and 2.19–2.38 Å, which is attributed to the Jahn–Teller effects of Cu2+ ions. The average bond length value of Cu–O is 2.14 Å, which is smaller than that of Co–O but larger than that of Ni–O. Zn also has a more random Zn–O bond length distribution (2.01–2.31 Å, average bond of 2.17 Å) in Mg0.50Cu0.25Zn0.25O. The larger average Zn–O and Cu–O bond lengths in Mg0.50Cu0.25Zn0.25O may partially result from the large distribution range of Cu–O/Zn–O bonds. The bond lengths for Mg–O are in the range of 2.05–2.22 Å with an average of 2.12 Å. Thus, Cu substitution causes a more random metal–oxygen bond length distribution, potentially improving space flexibility for Zn accommodation. However, this flexible space does not exist in Mg0.50Co0.25Zn0.25O and Mg0.50Ni0.25Zn0.25O, thus leading to a low Zn stabilization in the rock-salt oxide.
Inferring from the XRD, EXAFS and calculation results, creating a structure with long-range order and short-range disorder is crucial in stabilizing Zn2+ ions in the rock-salt oxide. From the perspective of the coordination environment, a properly flexible spatial environment facilitates the Zn stabilization in the rock-salt oxide. When considering the orbitals, such flexible spatial environment is caused by the splitting of eg orbitals due to the Jahn–Teller distortion. Therefore, in our cases, the short-range disorder and flexible spatial environment produce more remarkable results than increasing configurational entropy by employing the isostructural rock-salt CoO and NiO to stabilize Zn.
3.5 Stability of Mg0.50TM0.25Zn0.25O in alkaline solutions
The stability of Mg0.50TM0.25Zn0.25O (TM = Co, Ni and Zn) in alkaline solutions was evaluated by soaking them in 2 M KOH at room temperature for four weeks under constant stirring. The high-entropy oxide Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O was treated by the same method as a control sample. According to the XRD patterns of these soaked oxides as shown in Fig. 7a, no obvious impurity is observed for soaked Mg0.50Ni0.25Zn0.25O and Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O. However, the metal hydroxide (Mg(OH)2/Co(OH)2) phases are observed for soaked Mg0.50Co0.25Zn0.25O; and Mg(OH)2 and CuO phases are observed for soaked Mg0.50Cu0.25Zn0.25O. Fig. 7b–e demonstrate the atomic ratios of these oxides before and after soaking in KOH (Tables S3–S10†). For soaked Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O and Mg0.50Ni0.25Zn0.25O, no obvious change is observed compared to their raw counterparts. For soaked Mg0.50Co0.25Zn0.25O, the Zn atomic ratio decreases from 25.7 to 7.5, indicating that the Zn is preferentially leached from Mg0.50Co0.25Zn0.25O. Accordingly, this leads to the increase of the atomic ratios of Mg and Co. For soaked Mg0.50Cu0.25Zn0.25O, the atomic ratios of Zn and Cu decrease from 23.7 to 9.62 and 23.5 to 19.6, and accordingly, the Mg atomic ratio increases from 52.9 to 70.7, indicating the preferential leaching-out of Zn and Cu. These results suggests that Mg0.50Ni0.25Zn0.25O and Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O, which contain Ni, have stronger resistance to alkaline solutions and maintain high structural stability. It should be noted that our results do not imply that metal elements like Co and Ni are completely retained in raw materials. Instead, they indicate that the Zn and Cu are preferentially leached, reducing the structural stability. We did not test the ratio of metal elements in alkaline centrifugates, because we cannot ensure that the powder does not exist in alkaline centrifugates, which could affect the leached element ratios.From the XPS results (Fig. S23–S26†), one obvious change is the ratio increase at ∼531 eV binding energy in the O 1s profile (Fig. 8) for soaked oxides, and this peak also suggests more hydroxides on the surface,63 which is consistent with the hydroxide appearance from the XRD profile (Fig. 7a). This phenomenon is also expected as more water molecules bound to the surface after soaking, in combination with 531 eV attribution reported by Frankcombe and Liu.68 Another obvious change is the decrease of the signal-to-noise ratios of the Zn 2p profile for the soaked Mg0.50Co0.25Zn0.25O (Fig. S24†) and Mg0.50Cu0.25Zn0.25O (Fig. S26†), indicating the deduced Zn concentration on the surface. It agrees with the atomic ratio shown in Fig. 7c and e. In addition, the signal-to-noise ratio of the Cu 2p3/2 profile for the soaked Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O (Fig. S23†) also decreases, suggesting a decreased Cu ratio on the surface. The SEM images of soaked oxides are provided in Fig. S27.† The optical photographs of Mg0.50TM0.25Zn0.25O (TM = Co, Ni, Cu) and Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O before and after soaking in 2 M KOH for 4 weeks are also provided in Fig. S28.†
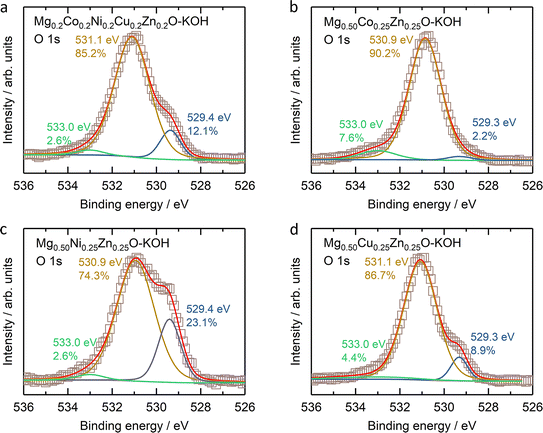 | ||
| Fig. 8 The O 1s XPS results of (a) Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O, (b) Mg0.50Co0.25Zn0.25O, (c) Mg0.50Ni0.25Zn0.25O, and (d) Mg0.50Cu0.25Zn0.25O. | ||
4. Conclusions
In summary, we investigated the roles of Co, Ni and Cu in stabilizing Zn in MgO-based rock-salt oxides. Experimental results demonstrate that incorporation of Co, Ni and Cu increases ZnO solubility in the rock-salt MgO–ZnO system, in which Cu contributes the most to stabilizing Zn despite the absence of rock-salt CuO in nature. Simulation results show that the incorporation of Cu with the Jahn–Teller effect causes a relatively lower formation energy of Zn substitution for Mg and creates a wide metal–oxygen bond length distribution and a flexible space for Zn accommodation, which do not occur in the Co- and Ni-incorporated MgO–ZnO. More importantly, medium-entropy Mg0.50Cu0.25Zn0.25O can also stabilize 25 at% Cu and 25 at% Zn simultaneously like high-entropy Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O. The Ni substitution is found effective to improve the structural stability in alkaline media. This work serves as a guide to enable metal stabilization in HEOs by means of short-range disorder and a flexible space environment for rational composition design, and to enable structural stability in alkaline media by metal element selection for future applications in the energy field.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
S. S., J. Z., and S. X. contributed equally to this work. S. S. and Z. W. S. conceived the original concept and initiated the project. S. S. wrote the manuscript. J. Z., S. X., S. W. and Z. W. S. revised it. S. S. synthesized the materials and performed the characterization with assistance from S. X. (XANES and EXAFS), H. R. T. (TEM), F. W. (XRD), D. H. L. S. (XPS), W. Y. L. (XPS) and Y. R. (XPS). S. X. did the EXAFS fitting. J. Z. carried out the theoretical calculation and results analysis. S. W. supervised the simulation work.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Agency for Science, Technology and Research (Central Research Fund Award). We acknowledge the National Supercomputing Centre Singapore for providing the computing resource.References
- A. Sarkar, B. Breitung and H. Hahn, Scr. Mater., 2020, 187, 43–48 CrossRef CAS.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J. P. Maria, Nat. Commun., 2015, 6, 8485 CrossRef CAS.
- A. Sarkar, Q. Wang, A. Schiele, M. R. Chellali, S. S. Bhattacharya, D. Wang, T. Brezesinski, H. Hahn, L. Velasco and B. Breitung, Adv. Mater., 2019, 31, e1806236 CrossRef PubMed.
- A. Amiri and R. Shahbazian-Yassar, J. Mater. Chem. A, 2021, 9, 782–823 RSC.
- C. Oses, C. Toher and S. Curtarolo, Nat. Rev. Mater., 2020, 5, 295–309 CrossRef CAS.
- S. Schweidler, M. Botros, F. Strauss, Q. Wang, Y. Ma, L. Velasco, G. C. Marques, A. Sarkar, C. Kübel, H. Hahn, J. Aghassi-Hagmann, T. Brezesinski and B. Breitung, Nat. Rev. Mater., 2024, 9, 266–281 CrossRef.
- B. Ouyang and Y. Zeng, Nat. Commun., 2024, 15, 973 CrossRef CAS PubMed.
- M. V. Kante, M. L. Weber, S. Ni, I. C. G. van den Bosch, E. van der Minne, L. Heymann, L. J. Falling, N. Gauquelin, M. Tsvetanova, D. M. Cunha, G. Koster, F. Gunkel, S. Nemsak, H. Hahn, L. Velasco Estrada and C. Baeumer, ACS Nano, 2023, 17, 5329–5339 CrossRef CAS PubMed.
- T. X. Nguyen, Y. C. Liao, C. C. Lin, Y. H. Su and J. M. Ting, Adv. Funct. Mater., 2021, 31, 2101632 CrossRef CAS.
- R. R. Katzbaer, F. M. Dos Santos Vieira, I. Dabo, Z. Mao and R. E. Schaak, J. Am. Chem. Soc., 2023, 145, 6753–6761 CrossRef CAS PubMed.
- J. Wang, S. Sun, S. Xi, Y. Sun, S. J. H. Ong, Z. W. Seh and Z. J. Xu, J. Phys. Chem. C, 2024, 128, 4978–4987 CrossRef CAS.
- C. Liu, J. Bi, L. Xie, X. Gao and J. Rong, J. Energy Storage, 2023, 71, 108211 CrossRef.
- S. Sun, C. Dai, P. Zhao, S. Xi, Y. Ren, H. R. Tan, P. C. Lim, M. Lin, C. Diao, D. Zhang, C. Wu, A. Yu, J. C. J. Koh, W. Y. Lieu, D. H. L. Seng, L. Sun, Y. Li, T. L. Tan, J. Zhang, Z. J. Xu and Z. W. Seh, Nat. Commun., 2024, 15, 260 CrossRef CAS.
- A. Sarkar, L. Velasco, D. Wang, Q. Wang, G. Talasila, L. d. Biasi, C. Kübel, T. Brezesinski, S. S. Bhattacharya, H. Hahn and B. Breitung, Nat. Commun., 2018, 9, 3400 CrossRef PubMed.
- Q. Wang, A. Sarkar, Z. Li, Y. Lu, L. Velasco, S. S. Bhattacharya, T. Brezesinski, H. Hahn and B. Breitung, Electrochem. Commun., 2019, 100, 121–125 CrossRef CAS.
- Z. Lun, B. Ouyang, D. H. Kwon, Y. Ha, E. E. Foley, T. Y. Huang, Z. Cai, H. Kim, M. Balasubramanian, Y. Sun, J. Huang, Y. Tian, H. Kim, B. D. McCloskey, W. Yang, R. J. Clement, H. Ji and G. Ceder, Nat. Mater., 2021, 20, 214–221 CrossRef CAS PubMed.
- F. Liu, M. Yu, X. Chen, J. Li, H. Liu and F. Cheng, Chin. J. Catal., 2022, 43, 122–129 CrossRef CAS.
- N. Qiu, H. Chen, Z. Yang, S. Sun, Y. Wang and Y. Cui, J. Alloys Compd., 2019, 777, 767–774 CrossRef CAS.
- P. Ghigna, L. Airoldi, M. Fracchia, D. Callegari, U. Anselmi-Tamburini, P. D'Angelo, N. Pianta, R. Ruffo, G. Cibin, D. O. de Souza and E. Quartarone, ACS Appl. Mater. Interfaces, 2020, 12, 50344–50354 CrossRef CAS.
- K. Wang, W. Hua, X. Huang, D. Stenzel, J. Wang, Z. Ding, Y. Cui, Q. Wang, H. Ehrenberg, B. Breitung, C. Kubel and X. Mu, Nat. Commun., 2023, 14, 1487 CrossRef CAS.
- E. Lokcu, C. Toparli and M. Anik, ACS Appl. Mater. Interfaces, 2020, 12, 23860–23866 CrossRef CAS.
- X. Liu, Y. Xing, K. Xu, H. Zhang, M. Gong, Q. Jia, S. Zhang and W. Lei, Small, 2022, 18, e2200524 CrossRef.
- M. Fracchia, M. Coduri, M. Manzoli, P. Ghigna and U. A. Tamburini, Nat. Commun., 2022, 13, 2977 CrossRef CAS.
- S. S. Aamlid, M. Oudah, J. Rottler and A. M. Hallas, J. Am. Chem. Soc., 2023, 145, 5991–6006 CrossRef CAS PubMed.
- M. Brahlek, M. Gazda, V. Keppens, A. R. Mazza, S. J. McCormack, A. Mielewczyk-Gryń, B. Musico, K. Page, C. M. Rost, S. B. Sinnott, C. Toher, T. Z. Ward and A. Yamamoto, APL Mater., 2022, 10, 110902 CrossRef CAS.
- K. Chen, J. Ma, H. Wang, C. Li and L. An, Ceram. Int., 2021, 47, 9979–9983 CrossRef CAS.
- J. E. Jaffe, R. Pandey and A. B. Kunz, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 14030–14034 CrossRef CAS PubMed.
- S. R. Kelly, X. Shi, S. Back, L. Vallez, S. Y. Park, S. Siahrostami, X. Zheng and J. K. Nørskov, ACS Catal., 2019, 9, 4593–4599 CrossRef CAS.
- J. Pfrommer, M. Lublow, A. Azarpira, C. Gobel, M. Lucke, A. Steigert, M. Pogrzeba, P. W. Menezes, A. Fischer, T. Schedel-Niedrig and M. Driess, Angew Chem., Int. Ed. Engl., 2014, 53, 5183–5187 CrossRef CAS PubMed.
- M. R. Shakil, A. M. El-Sawy, H. Tasnim, A. G. Meguerdichian, J. Jin, J. P. Dubrosky and S. L. Suib, Inorg. Chem., 2018, 57, 9977–9987 CrossRef CAS.
- R. Subhash Kanase, G. Mulualem Zewdie, M. Arunachalam, J. Badiger, S. Abdelfattah Sayed, K.-S. Ahn, J.-S. Ha, U. Sim, H. Shin and S. Hyung Kang, J. Energy Chem., 2024, 88, 71–81 CrossRef CAS.
- X. Jiang, F. Cai, D. Gao, J. Dong, S. Miao, G. Wang and X. Bao, Electrochem. Commun., 2016, 68, 67–70 CrossRef CAS.
- G. Zhang, S. Hou, H. Zhang, W. Zeng, F. Yan, C. C. Li and H. Duan, Adv. Mater., 2015, 27, 2400–2405 CrossRef CAS.
- W. Chang, J.-W. Choi, J.-C. Im and J. K. Lee, J. Power Sources, 2010, 195, 320–326 CrossRef CAS.
- A. J. Laghari, U. Aftab, A. Tahira, A. A. Shah, A. Gradone, M. Y. Solangi, A. H. Samo, M. kumar, M. I. Abro, M. w. Akhtar, R. Mazzaro, V. Morandi, A. M. Alotaibi, A. Nafady, A. Infantes-Molina and Z. H. Ibupoto, Int. J. Hydrogen Energy, 2023, 48, 12672–12682 CrossRef CAS.
- X. He, J. Tan, J. Wei, F. Yin, B. Chen, X. Liang and G. Li, Appl. Surf. Sci., 2020, 508, 144758 CrossRef CAS.
- Y.-z. Su, Q.-z. Xu, Q.-s. Zhong, C.-j. Zhang, S.-t. Shi and C.-w. Xu, Mater. Res. Bull., 2015, 64, 301–305 CrossRef CAS.
- C. Xu, P. K. Shen, X. Ji, R. Zeng and Y. Liu, Electrochem. Commun., 2005, 7, 1305–1308 CrossRef CAS.
- H. Sclar, O. Haik, T. Menachem, J. Grinblat, N. Leifer, A. Meitav, S. Luski and D. Aurbach, J. Electrochem. Soc., 2012, 159, A228–A237 CrossRef CAS.
- Y. Wang, Y.-F. Zhang, H.-R. Liu, S.-J. Yu and Q.-Z. Qin, Electrochim. Acta, 2003, 48, 4253–4259 CrossRef CAS.
- B. Xu, H. Shen, J. Ge and Q. Tang, Appl. Surf. Sci., 2021, 546, 148814 CrossRef CAS.
- J. S. Gnanaraj, V. G. Pol, A. Gedanken and D. Aurbach, Electrochem. Commun., 2003, 5, 940–945 CrossRef CAS.
- A. van de Walle, P. Tiwary, M. de Jong, D. L. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L. Q. Chen and Z. K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276, 238–257 Search PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- G. C. Moore, M. K. Horton, E. Linscott, A. M. Ganose, M. Siron, D. D. O’Regan and K. A. Persson, Phys. Rev. Mater., 2024, 8, 014409 CrossRef CAS.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., 1969, B25, 925–946 CrossRef.
- D. Berardan, A. K. Meena, S. Franger, C. Herrero and N. Dragoe, J. Alloys Compd., 2017, 704, 693–700 CrossRef CAS.
- M. A. Peck and M. A. Langell, Chem. Mater., 2012, 24, 4483–4490 CrossRef CAS.
- B. K. Teo, Data analysis in practice, in EXAFS: Basic Principles and Data Analysis, Springer, Berlin, Heidelberg, 1986, ch. 6, p. 124 Search PubMed.
- J. Sushil, A. Kumar, A. Gautam and M. I. Ahmad, Mater. Chem. Phys., 2021, 259, 124014 CrossRef CAS.
- O. J. Marques, C. Chen, E. V. Timofeeva and C. U. Segre, J. Power Sources, 2023, 564, 232852 CrossRef CAS.
- C. M. Rost, Z. Rak, D. W. Brenner and J. P. Maria, J. Am. Ceram. Soc., 2017, 100, 2732–2738 CrossRef CAS.
- A. Rodrigues, M. d. C. M. Alves and J. Morais, Mater. Des., 2018, 142, 240–246 CrossRef CAS.
- A. N. Baranov, P. S. Sokolov, V. A. Tafeenko, C. Lathe, Y. V. Zubavichus, A. A. Veligzhanin, M. V. Chukichev and V. L. Solozhenko, Chem. Mater., 2013, 25, 1775–1782 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- J. Yang, H. Liu, W. N. Martens and R. L. Frost, J. Phys. Chem. C, 2010, 114, 111–119 CrossRef CAS.
- Y. Lykhach, S. Piccinin, T. Skala, M. Bertram, N. Tsud, O. Brummel, M. Farnesi Camellone, K. Beranova, A. Neitzel, S. Fabris, K. C. Prince, V. Matolin and J. Libuda, J. Phys. Chem. Lett., 2019, 10, 6129–6136 CrossRef CAS PubMed.
- K. Tanwar, D. S. Gyan, S. Bhattacharya, S. Vitta, A. Dwivedi and T. Maiti, Phys. Rev. B, 2019, 99, 174105 CrossRef CAS.
- N. S. McIntyre and M. G. Cook, Anal. Chem., 1975, 47, 2208–2213 CrossRef CAS.
- K. J. Gaskell, A. Starace and M. A. Langell, J. Phys. Chem. C, 2007, 111, 13912–13921 CrossRef CAS.
- S. Hüfner, Charge-excitation final states: satellites in Photoelectron Spectroscopy Principles and Applications, Springer, Berlin, Heidelberg, 2003, ch. 3, pp. 29–130 Search PubMed.
- S. Altieri, L. H. Tjeng, A. Tanaka and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 13403–13409 CrossRef CAS.
- J. C. C. Fan and J. B. Goodenough, J. Appl. Phys., 1977, 48, 3524–3531 CrossRef CAS.
- T. J. Frankcombe and Y. Liu, Chem. Mater., 2023, 35, 5468–5474 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02175d |
| ‡ S. S., J. Z. and S. X. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |