Theory and simulation of ligand functionalized nanoparticles – a pedagogical overview
Thi
Vo

Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: tvo12@jhu.edu
First published on 15th April 2024
Abstract
Synthesizing reconfigurable nanoscale synthons with predictive control over shape, size, and interparticle interactions is a holy grail of bottom-up self-assembly. Grand challenges in their rational design, however, lie in both the large space of experimental synthetic parameters and proper understanding of the molecular mechanisms governing their formation. As such, computational and theoretical tools for predicting and modeling building block interactions have grown to become integral in modern day self-assembly research. In this review, we provide an in-depth discussion of the current state-of-the-art strategies available for modeling ligand functionalized nanoparticles. We focus on the critical role of how ligand interactions and surface distributions impact the emergent, pre-programmed behaviors between neighboring particles. To help build insights into the underlying physics, we first define an “ideal” limit – the short ligand, “hard” sphere approximation – and discuss all experimental handles through the lens of perturbations about this reference point. Finally, we identify theories that are capable of bridging interparticle interactions to nanoscale self-assembly and conclude by discussing exciting new directions for this field.
Introduction
Materials complexity required to make modern day technologies and devices has grown exponentially, especially in recent years.1–13 For example, wearable electronics necessitate multifunctional soft materials that combine high flexibility, high power density, and efficient energy generation into a small, portable device.14–16 Similarly, membrane and separation technologies require materials with molecular scale resolution in selectivity to be fabricated with low to zero defects at the micron/millimeter length scales.17–24 Lastly, soft robotics require materials that are mechanically stable yet highly malleable so that they can be reconfigured under load/stimuli.25–28 While there are many additional examples related to photonic,29,30 sensing,2,3,31 and catalytic32,33 properties, the feature pervading across every single case is that the core design aspects involve combining multiple components into a single, composite entity. There are barriers, however, that arise from such a requirement. Achieving the level of precision spatial ordering needed to obtain the desired macroscopic properties is often undermined by kinetic traps, as multicomponent systems are more susceptible to fabrication defects. Furthermore, depending on the chemical species, phase segregation can counteract co-assembly to disrupt the emergence of desired properties.Efforts to bypass these constraints have progressively shifted towards self-assembly as an alternative route to top-down approaches for materials fabrication.34–43 Such an approach is of interest due to the ability to pre-program interactions into each individual building block unit, enabling nanoscale control over interparticle spatial/orientation ordering beyond what is achievable via top-down methods. Over the past several decades, research on self-assembly has resulted in a suite of nanoscale building blocks capable of achieving long-range structural ordering at the mesoscale.40,44,45 This toolkit spans a diverse range of techniques that include surface modifications,46–50 emulsion-templating,51 solvent evaporation,52,53 and microphase separation.54,55 Amongst this expansive library, shape anisotropy and nanoparticle (NP) ligand functionalization have emerged as two popular strategies that are now widely used for controlling assembly.40,56 For clarity, shape anisotropy is defined as the usage of NPs whose shapes are aspherical, that is, cubic, octahedral, tetrahedral, etc. With respect to ligands, our definition encompasses a wide range of different chemical species that include short oligomers (i.e. oleic acids, alkanes, and dendrimers), polymers, and DNA oligonucleotides. These two design handles readily synergize with each other to produce a distinct class of building blocks called ligand functionalized nanoparticles (LNPs). To date, there have been excellent reviews that cover both synthesis and experimentally observed assemblies of LNPs.40,44,45,57,58 As such, we refer the reader to those works for current experimental advances.
Our focus in this review is to provide a comprehensive overview of state-of-the-art computational and theoretical modeling approaches developed for predicting LNP self-assembly to complement the experimental literature. We specifically focus on linking ligand conformations and ligand surface distributions about the NP core to emergent LNP interactions to highlight the physical driving forces governing LNP self-assembly. These insights are correlated to key features needed for the construction of interaction potentials to accurately translate experimental parameters to coarse-grained computational models. Due to the expansive nature of LNPs, we organize our review into two broad categories of ligand types employed in NP functionalization – short versus long ligands. For long ligands, we additionally split discussion into three ligand classes: (1) oligomeric, (2) polymeric, and (3) DNA-based. For each of the four ligand types, we discuss their functionalization onto spherical and polyhedral NPs to dissect the interplay between geometry and ligand features in directing LNP interactions and self-assembly (Fig. 1).
 | ||
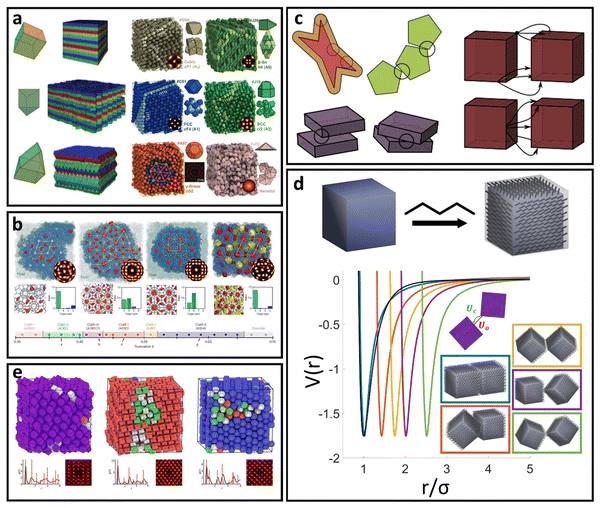
| Fig. 1 Classes of ligand functionalized nanoparticles. We organize LNPs into subcategories to facilitate discussion of theory/simulations. Specifically, we define 4 classes of ligands (short, oligomeric, polymeric, and DNA) and 2 classes of NP cores (spherical and polyhedral), totaling 8 different types of LNPs. Corresponding emergent inter-LNP interaction types (hard, soft, directional, etc.) are also indicated for each classification. The figure contains images reproduced from ref. 42, 43, 48, 72, 79, 109, 142, 182–184; ref. 42, 43, 72, 183 and 48 with permission from Springer Nature (© 2006, 2011, 2020, 2021, and 2022); ref. 182, 109 and 184 with permission from the American Chemical Society (© 2013 and 2021); ref. 79 with permission from the American Association for the Advancement of Science (© 2019); and ref. 142 with permission from Wiley (© 2023). | ||
While such classifications are based on ligand chemistry and/or NP core geometry to provide concrete connections to experimentally synthesizable systems, the selected demarcations directly correlate to the emergent nature of the inter-LNP attraction/repulsion. For example, short ligands give rise to hard particle interactions while oligomers/polymers manifest into softer, deformable, and more complex interaction potentials. In this way, our classifications provide a direct connection between molecular features associated with ligand chemistry and particle geometry and a unique type of inter-LNP interaction. In other words, each defined LNP category can be mapped to a class of effective interactional potentials, providing a roadmap for computational modeling of experimental systems. For all ligand/geometry based classifications discussed, we explicitly highlight the corresponding class of coarse-grained interaction potentials within their respective sections.
To build intuition and physical understanding for each class of LNP, we specifically explain the underlying physics of how the interplay between core–core, ligand–core, and ligand–ligand interactions sculpts the shape of the ligand shell (corona) and how corona morphology can be used to predict LNP interactions. We then provide context on how the predicted interaction potentials are employed in simulations of LNP self-assembly. In particular, we discuss guiding heuristics that can be utilized to approximate potential parameters based on experimental handles. Key takeaways are highlighted at the end of each section to emphasize how each perturbation in design parameters (ligand length, core geometry, ligand architecture, solvent conditions, etc.) influences emergent inter-LNP interactions and hierarchical self-assembly. For our discussions, we first establish the “hydrogen atom” equivalent for LNPs – spherically symmetric particles whose interactions are dominated by steric repulsion (i.e. the hard sphere model). We then iteratively increase LNP complexity as a function of both ligand chemistry and core geometry. Each additional complexity is contrasted against those previously discussed to help establish intuition as to how each additional aspect builds upon each other to sculpt the emergent inter-LNP interactions. As a final note, we discuss theoretical capabilities for a priori prediction of LNP self-assembly for each class of LNPs and conclude by presenting new directions where advances in theory and computational modeling of LNPs are needed to guide experiments.
Short ligand functionalization
We start at one simplifying extreme of LNP designs: high NP surface coverage (grafting density, σ) using short, sterically repulsive ligands. In this limit, traditional approaches assume that ligands are isotropically distributed on the NP surface and the corona shape of the ligand coating is conformal to the underlying NP shape. Our discussion here is split into two subcategories: spherical NP cores and polyhedral NP cores.Spherical NPs with short ligands – hard sphere interaction
For spherical NP cores, the LNP behaves effectively as a larger sphere whose hydrodynamic radius is the NP core radius plus the thickness of the ligand shell. More quantitatively, the boundary for grafting density and ligand lengths is as follows: firstly, ligand grafting density must be at or near the limit of full coverage (σ ≥ 1.0 nm−2). Secondly, the ligand length N must be on the order of N ≤ Rcoreσ1/2, where Rcore is the NP radius.59 This crossover is obtained by determining the radial distance from the surface at which the monomer density is no longer unitary (rs ∼ Rcoreσ1/2b). Due to the high monomer density, the monomers must be organized in a radially linear manner. This means that rs must also scale as rs ∼ Nb. Substituting for r* immediately yields the crossover condition in N. Another way to interpret the length constraint is by requiring that Rg ≪ Rcore, where Rg is the ligand's radius of gyration and Rcore is the NP radius. The physical manifestation of these boundaries in N and σ is that ligand conformations within the corona behave akin to rigid rods anchored at one end to the NP surface. Coupled with the sterically repulsive nature of the functionalized ligands, this means that inter-LNP interactions are completely driven by steric repulsion. The only constraint for LNPs in this limit is that they cannot occupy the same space as other LNPs as there is an infinitely strong repulsive force preventing such overlaps. All other forces that govern how particles should interact with their neighbors are negligible in this limit. For this reason, common approaches employed to model interactions between LNPs with short ligands are the hard sphere (HS) and the Weeks–Chandler–Anderson (WCA) potentials60 (Fig. 2a).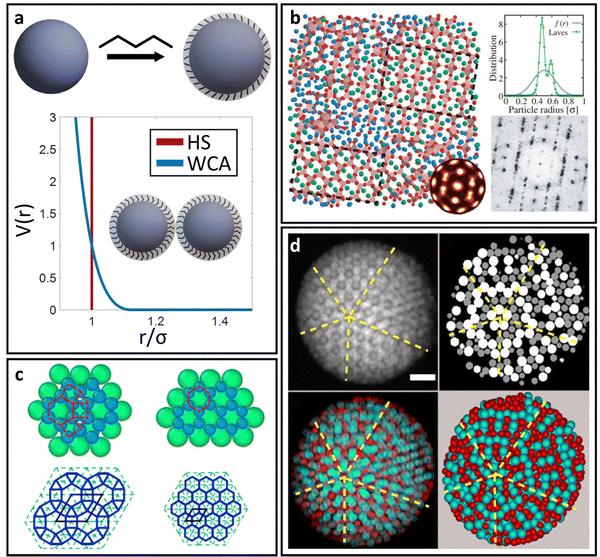 | ||
| Fig. 2 “Hard” spherical LNPs. (a) Emergent interaction between “hard” spherical LNPs: HS or WCA interaction. Binary hard sphere assembly into (b) Laves phases,68 (c) periodically tessellating and honeycomb 2D lattices,69 and (d) spherically confined icosahedral clusters.72 Figures are reproduced from ref. 68 with permission from the American Physical Society (© 2019) and ref. 72 and 69 with permission from Springer Nature (© 2020 and 2022). | ||
The HS potential takes the following form:61
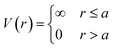 | (1) |
A corollary to eqn (1) is the WCA potential:60
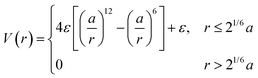 | (2) |
Polyhedral NPs with short ligands – hard shape interaction
A common perturbation about the ideal LNP limit is the usage of polyhedral, as opposed to spherical, NPs. In this section, we again consider the case of high grafting density and short, sterically repulsive ligands. This ensures that NP geometry is the sole difference relative to the ideal HS limit discussed above. Similar to spherical geometry, strong steric repulsion between functionalized ligands results in high ligand extension and a uniform ligand distribution about the NP surface (isotropic grafting). As such, the corona shape is conformal to the underlying geometry of the polyhedral NP core and the LNP can be modelled as a hard polyhedron whose size is the core size plus the thickness of the ligand shell (Fig. 3d). With respect to grafting density, the quantitative boundary is analogous to that of spherical NPs: (σ ≥ 1.0 nm−2). However, the same is not true for the ligand length. Unlike spheres, polyhedral NPs possess surface locations of varying curvatures. High curvature surfaces impose less spatial confinement due to an increase in local free volume available per unit of solid angle. This means that a ligand of identical length can relax away from its rigid, rod-like configuration when anchored to high curvature locations thanks to decreased confinement. As such, the upper limit for ligand length must incorporate the effect of local curvature. Accounting for the relevant geometrical packing constraints, the curvature corrected upper limit for ligand length to enforce the “hard” polyhedron limit is: N ∼ Rcoreσ1/2Ω−3/2, where Rcore here defines the polyhedral NP's insphere radius and Ω defines the distance from the NP surface to its center of mass, normalized by its insphere radius.79 As a clarifying example, in the case of a cubic NP,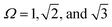 for the face, edge, and corner, respectively. In the limit of a spherical NP core, Ω = 1 and this constraint converges back to the HS limit for ligand length. Note that the curvature effect is inversely related to the maximum ligand length. This reflects the physical picture discussed above where a shorter ligand is necessary at high curvatures to maintain both a high density within the ligand shell and enforce zero ligand interpenetration between LNPs. Within this regime, theoretical modeling of inter-LNP interactions in the dilute limit is a simple extension of the HS (eqn (1)) and WCA (eqn (2)) to account for shape anisotropy.
for the face, edge, and corner, respectively. In the limit of a spherical NP core, Ω = 1 and this constraint converges back to the HS limit for ligand length. Note that the curvature effect is inversely related to the maximum ligand length. This reflects the physical picture discussed above where a shorter ligand is necessary at high curvatures to maintain both a high density within the ligand shell and enforce zero ligand interpenetration between LNPs. Within this regime, theoretical modeling of inter-LNP interactions in the dilute limit is a simple extension of the HS (eqn (1)) and WCA (eqn (2)) to account for shape anisotropy.
 | ||
| Fig. 3 “Hard” polyhedral LNPs. MC self-assembly of hard polyhedra yields a diverse suite of (a) closed-packed, high entropy structures82,83 and (b) host–guest, open lattice structures.90 MD simulation of hard polyhedra is enabled either by (c) DEM96 or (d) a generalized anisotropic version of common isotropic potentials (here WCA).98 (e) MD simulation using the anisotropic WCA potential reproduces known results from MC.98 Figures are reproduced from ref. 82 and 90 with permission from Springer Nature (© 2011 and 2023); ref. 83 with permission from the American Association for the Advancement of Science (© 2012); ref. 96 with permission from Elsevier (© 2017); and ref. 98 with permission from the American Institute of Physics (© 2020). | ||
Analytical generalizations of the HS potential to polyhedral geometry do not exist. However, adapting shape overlap detection protocols such as the Gilbert–Johnson–Keerthi algorithm80 (GJK) or Minkowski Portal Refinement81 (MPR) from the computer graphics literature provides a way to obtain an algorithmic formulation of the HS potential (eqn (1)) for all convex polyhedral shapes. Briefly, both algorithms define support mappings that reduce overlap detection between complex shapes to a series of Minkowski difference calculations between triangles (2D) or tetrahedra (3D). This complexity reduction allows on-the-fly shape overlap checks, making GJK and MPR ideal for simulation based overlap calculations. Similar to the HS model, polyhedral dimensions in MC are proportional to the thickness of the ligand layer. Utilizing a qualitative dependence of a ∼ Nσ1/3b enables a mapping of experimental handles to the coarse-grained particle size. Coupling eqn (1) with shape overlap detection has enabled a diverse range of different MC simulations of hard polyhedral particles82–84 (Fig. 3a). Seminal MC simulations for unary systems of hard polyhedral models for LNPs have reproduced the observed crystallization behaviors for a wide range of different core geometries.43,85–87 Examples include the formation of simple cubic superlattices using cubic NPs,82–84 Minkowski superlattices using octahedral NPs,82–84 dodecagonal quasicrystalline morphologies using tetrahedral NPs,88,89 and clathrate structures using pentagonal bipyramidal NPs90,91 (Fig. 3b). Recent studies have also explored the space of multicomponent systems for hard polyhedra as well, yielding previously unobserved structures such as space-tiling assemblies of complementary polyhedra92 and compartmentalization of non-complementary polyhedra into host–guest superlattices.90 Due to the simplicity of the hard sphere approximation, MC simulations of experimentally unexplored hard polyhedral LNPs have also revealed a diverse suite of crystalline morphologies. These superlattices include open host–guest motifs,90,93 complex layered crystals with 2, 3, or 4 unique Wyckoff sites, and even a Bergman-like superlattice with a 432-particle unit cell.94
To enable MD simulation of “hard” polyhedral LNPs, there are several approaches to capture anisotropic geometries within a pair potential. Here, our focus is on MD potentials that explicitly consider core geometry in their force evaluations. For the alternative case of creating an effective polyhedron via a superposition of WCA spheres, we refer the reader to the rigid body literature.95 One approach takes advantages of discrete element methods (DEMs) commonly employed in finite element modeling (Fig. 3c). DEMs assign a WCA potential to all pairwise combinations of face, edge, and corner contacts between neighboring particles.96 Doing so preserves all relevant facet interactions. A net force on the particle's center of mass is then computed by summing over all contributing WCA potentials between pairs of faces, corners, and edges. Using this approach, DEMs can reproduce assembly behaviors of simple shapes in MD. However, due to rounding artifacts arising from usage of a WCA potential at edge and corner facets, DEMs struggle to capture more complex superlattices like quasicrystal formation using tetrahedral LNPs or orientationally ordered face-centered cubic formation of rhombic dodecahedral LNPs. Efforts to address this “rounding” effect have led to the development of another class of anisotropic HS-like potentials based on computing effective potentials of mean force between shaped particles.97,98 These approaches typically assume a set of particle configurations, which enable symmetry-dependent simplification of the multidimensional integrals used to compute the average force. The caveat, however, is that they are no longer amenable to “on-the-fly” force evaluations needed for MD simulation. One exception is a generalized mean-field approach that was developed to provide analytical functional forms for anisotropic variants of isotropic pair potentials98 (Fig. 3d). In the limit of the WCA potential, the corresponding anisotropic WCA potential applies a contact potential between the closest surface points on two neighboring particles as shown below (eqn (3)):
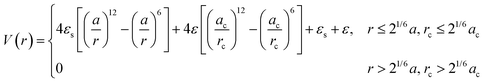 | (3) |
Limitations of the “hard” LNP approximation
There are two caveats, however, that need to be considered for “hard” LNPs. While the above discussion applies to 3D polyhedral/spherical cores, care must be taken in the limit of 2D polygonal nanoplates or nanodiscs. This is because the plate/disc thickness (lt) can often be small enough that Rg ≪ lt no longer holds.99 In fact, Rg ∼ lt for most 2D cases. This indicates that the ligand size is on par with particle thickness. In this regime, entropy plays a major role in driving ligand partition and the ligand corona morphology is no longer conformal to the core geometry. We provide detailed discussion of such phenomena in the ligand functionalized polyhedral NPs section, where this effect dominates. Another important feature to consider is emergent directional interaction due to crowding (high LNP density). Hard polyhedra are known to exhibit preferential orientational orderings along their large facets that arise due to entropy maximization.100–102 This means that inter-LNP interactions no longer follow the HS limit and emergent directional forces start to play a larger role. Care, therefore, must be taken when trying to model “hard” polyhedral LNPs outside of the dilute concentration regime. We provide a discussion of this effect in the “Theoretical prediction of LNP self-assembly” section.Long ligand functionalization on spherical NPs
In this category, we relax the constraint of short ligands for spherical LNPs but keep the high grafting density limit. There are now 3 classes of ligands that are of specific interest: (1) oligomers with the degree of polymerization N > Rcoreσ1/2, (2) polymeric chains, and (3) DNA oligonucleotides. Furthermore, DNA oligonucleotides and polymeric ligands have an additional handle of tunable attraction/repulsion between different ligand species enabled by complementary base-pairing and molecular recognition terminal units,103 respectively. This feature makes DNA/polymeric ligands popular for binary LNP systems as they enable species-specific control over inter-LNP interactions. We consider all the above in our discussion of long ligand functionalization of spherical NPs.Regardless of oligomeric, DNA, or polymeric ligand type, the major change relative to the “hard” spherical LNP limit lies in how ligands are organized within the corona as they are no longer forced to take on a rigid, rod-like morphology due to strong confinement. This transition arises purely from geometry and consideration of the local free volumes available between neighboring functionalized ligands. For a spherical geometry, the volume of a spherical sector (Vss) grows with increasing radial distance rs away from the NP surface for any given solid angle Γ: that is, Vss = 3−1Γrs3. As a result, monomers located near the non-functionalized terminal of the ligand (i.e. those sitting further away from the NP surface) have more space available to them relative to monomers near the ligand's anchored head. The net result is a decrease in local confinement experienced by all monomers located at distances rs > Rcoreσ1/2b, which ultimately enhances ligand flexibility.79 This additional flexibility makes the “hard” LNP approximation invalid for ligand parameters within this regime.
Spherical NPs with oligomeric ligands – soft sphere interaction
For oligomeric ligands, ligand–ligand interactions and corona morphologies are still dominated by steric interactions. However, unlike the hard sphere limit where high confinement creates an impenetrable ligand shell, the increased flexibility associated with longer ligands results in a splaying of their linear conformation when in close contact with a neighboring oligomer functionalized LNP. Depending on the local coordination of particles surrounding a reference LNP, different degrees of splaying can occur.104 The net effect is an increase in local free volume available to each ligand that favors interpenetration between neighboring coronas. This is because ligand intercalation is energetically favored compared to conformational entropy loss and increased bond tension associated with ligand compression. In other words, LNPs are no longer impenetrable and we obtain an effectively “soft” sphere whose corona can deform as needed to minimize its total free energy (Fig. 4a). When considering oligomeric ligands, the extent of ligand splaying, emergent corona shape, and degree of corona overlap can all be predicted using the Orbifold Topological Model.104–106 | ||
| Fig. 4 “Soft” spherical LNPs – oligomeric/polymeric ligands. (a) Emergent interaction between oligomer/polymer functionalized spherical NPs. Soft, compressible ligands can produce a net attraction with a variable range or even multi-well interaction potentials. (b) Net short range attraction can speed up assembly dynamics.112 (c) Multi-well interactions can produce a diverse suite of self-assembled lattices.116 Coarse-grained interaction potential can also reduce complexity to capture assembly of (d) 3D superlattices of polymer functionalized NPs125 or (e) 2D LNP networks.124 Figures are reproduced from ref. 112 with permission from Springer Nature (© 2023); ref. 116 with permission from the National Academy of Sciences (© 2021); and ref. 124 and 125 with permission from the Royal Society of Chemistry (© 2014 and 2023). | ||
The net effect of this complex interplay between ligand splaying, local free volume, and corona interpenetration is the emergence of an attractive potential well between LNPs.105,107–110 It is here that the starkest contrast between “hard” and “soft” LNPs becomes apparent. Unlike the hard sphere limit, there is an optimal center-to-center separation that arises from the presence of an attractive well between two LNPs. For this reason, the Mie potential is commonly used to model the class of oligomeric LNP interactions111 (Fig. 4a):
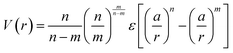 | (4) |
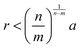 . In the limit of n = 12 and m = 6, both equations are identical. In short, the Mie potential is a more versatile variant of the WCA potential and can be employed to capture both attractive and repulsive interactions between LNPs. Transitioning from eqn (2) to (4) now yields four parameters (a, ε, n and m) that must be mapped correctly to meaningful trends from experimental systems. In general, there are two common approaches. The first involves measuring the second virial coefficient (B2) between LNPs in experiments and then fitting to analytical expression from statistical mechanics:
. In the limit of n = 12 and m = 6, both equations are identical. In short, the Mie potential is a more versatile variant of the WCA potential and can be employed to capture both attractive and repulsive interactions between LNPs. Transitioning from eqn (2) to (4) now yields four parameters (a, ε, n and m) that must be mapped correctly to meaningful trends from experimental systems. In general, there are two common approaches. The first involves measuring the second virial coefficient (B2) between LNPs in experiments and then fitting to analytical expression from statistical mechanics: 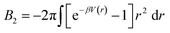 . This approach has recently been employed to model experimentally measured LNP emergent interaction.112 While B2 fitting can yield constants for eqn (4) that accurately captures experimentally observed LNP interactions, measurements of B2 are often not readily available.
. This approach has recently been employed to model experimentally measured LNP emergent interaction.112 While B2 fitting can yield constants for eqn (4) that accurately captures experimentally observed LNP interactions, measurements of B2 are often not readily available.
The alternative approach is similar to the mappings discussed in the short ligand limit, where one can utilize scaling behaviors to qualitatively correlate experimental handles to potential parameters. Due to the increase in the ligand length, the ligand thickness now has the form N1/2σ1/4b. This means that mapping experimental parameters to the particle size a in eqn (4) scales with N1/2σ1/4b. Unlike with hard sphere and hard polyhedra, however, there are now three different parameters that all contribute to the interaction between LNPs: n, m, and ε. Tuning the relative difference between n and m alters the width of the attractive well associated with eqn (4) and provides a handle to tune corona overlaps between LNPs. Since inter-graft separation D scales as σ−1/2, we expect that σ1/2 captures the reduction in space available for corona interpenetration between neighboring LNPs. A counteracting effect, however, lies with increasing ligand lengths. Increasing N enhances ligand flexibility, which favors LNP interpenetration. Here, monomer density for oligomeric graft lengths typically scales113 as N−1/2. Therefore, we expect a composite mapping of n–m scaling as N−1/2σ1/2. Along the same vein, n also scales with N−1/2σ1/2 to capture reduction in corona interpenetration (i.e. increased hardness) of each LNP. Lastly, the slight corona overlap produces an emergent attraction between neighboring LNPs. By inspection, ε controls the well-depth and slope of eqn (4). We expect this to increase with the number of interacting monomers within the overlap region, thus yielding a mapping of ε ∼ N1/2σ1/2. Usage of the Mie potential in MC and MD simulation of oligomer functionalized LNPs can capture the assembly behavior for a diverse range of single-component and multi-component “soft” LNPs made using oligomeric ligand functionalization. Examples include binary superlattices that are isostructural to intermellatic and/or ionic atomic lattices114,115 or metallic coordination lattices116 (Fig. 4c). Simulations also enabled studies that elucidate assembly features such as stoichiometry-driven enhancement of crystallization rates112 (Fig. 4b), superlattice spacing,106 and the effect of confinement on self-assembly112
Spherical NPs with polymeric ligands – ultra-soft sphere interaction
Deviations from the oligomeric limit start to occur when the size of the functionalized ligand is of a similar order of magnitude as the NP core size: Rg ∼ Rcore. Since Rcore is on the nanometer scale, the Rg of a ligand at the transition point is at least an order of magnitude larger than those of traditional oligomeric ligands. By definition, ligands with sizes this large are typically considered to be polymers. Therefore, Rg ∼ Rcore marks the transition from an oligomeric to a polymeric ligand. The key differences in corona behaviors within this limit can be better understood through analysis of the volumetric space available to functionalized ligands. Consider the spherical sector volume Vss ∼ 3−1Γrs3 (from before). A 10× increase in radial distance rs would correspond to a 1000× increase in the volume available to a ligand given the same solid angle. In other words, monomers occupying the regions far away from the NP surface experience drastically lower confinement from neighboring ligands thanks to the increase in space availability. Polymer segments in these regions are free to explore their configurational space and take on more expanded conformations to maximize ligand entropy. There exists a large repository of theoretical works developed over the past several decades that can predict corona morphology arising from such expanded configurations for polymeric ligands functionalized onto flat,117,118 curved,119 dense cores (i.e. star polymers113), or NP surfaces.120,121 Such theories can a priori predict how polymers are organized in concentric radial layers moving outward from the NP surface. The thickness of each layer is determined by balancing energetic contributions from thermal noise, monomer–monomer, monomer–solvent, and exclude volume interactions between neighboring polymeric ligands. The key predictions with respect to corona morphologies in these models are: (1) corona morphologies are spherical, reflecting the underlying NP shape and (2) low monomer density in regions far away from the NP surface. This means that corona interpenetration is highly favorable between neighboring LNPs as steric hinderance/repulsion between interacting polymeric ligands are at a minimum. Due to the high degree of corona overlap between LNPs, NPs functionalized with long polymeric ligands are typically considered to exhibit “ultrasoft” LNP interactions (Fig. 4a). As a result, the physical picture for interacting spherical NPs functionalized with polymeric ligands is that of highly overlapping spherical particles.For polymeric ligands, there exist a diverse library of different effective interaction potentials that can be used to for either MC or MD simulations.122–125 The functional forms of these potentials are either theoretically predicted from analytical theory,122,126–128 adaptation of Mie and/or power law potentials,129 or computationally measured using detailed, atomistic simulations.107,121,124,125,130–132 Analytical potentials rely on geometrical arguments and integration over an averaged monomer density profile along the entire length of the functionalized polymer. Results from this approach often produce a logarithmic like behavior in center-to-center distance between particles: V(r) ∼ −ln(a/r). These potentials typically exhibit both an attractive well and a soft repulsive shoulder to capture both short range attraction and longer range steric hinderances associated with fluctuating polymeric ligands (Fig. 4d and e). Due to the polymeric nature of the corona layer, mapping ligand parameters to particle size a utilized size of the grafted brush, which scales as N3/5σ1/5b for a good solvent. It is assumed that good solvent scaling is typical for LNP self-assembly where particles need to be dispersed in solution to avoid aggregation and/or phase separation. Alternative approaches involve adapting the Mie potential by combining it with either long range repulsive potentials (Yukawa,133eqn (5)) or multi-barrier potentials (oscillating pair potential)116 (eqn (6) or Dzugotov134) to mimic the theoretically predicted multi-well effective inter-LNP interactions. Examples of the functional form for each are shown below:
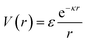 | (5) |
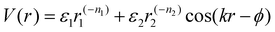 | (6) |
Spherical NPs with DNA ligands – soft, selective sphere interaction
In between the oligomeric and polymeric limits is the special case of DNA (i.e. oligonucleotides) ligands. There are two types of DNA that are commonly used for NP functionalization: single-stranded (ssDNA) and double-stranded (dsDNA). We first discuss the physical picture underlying inter-LNP interactions for both DNA ligand types and then present computational potentials commonly employed for simulating their assembly behaviors.dsDNA ligands are stiff with long persistence length (rod-like behavior) due to the double-helix nature of the hybridized backbone.135 This rod-like nature of dsDNA makes the ligand highly inflexible, prohibiting splaying and/or compression. Furthermore, the negatively charged backbone of the dsDNA ligands creates strong electrostatic repulsions that prevent interpenetration of the ligand shells.136 Through this lens, spherical NPs with dsDNA ligands behave analogous to the hard-sphere limit, where interactions are dominated by steric repulsion between spheres with radii equal to the hydrodynamic radius of the functionalized NP core. The key difference, however, is that dsDNA ligands have unhybridized “sticky-ends” that imbue LNPs with additional attractive/repulsive interactions beyond steric effects. These “sticky-ends” are all positioned at the outermost edge of the ligand corona due to a combination of electrostatic backbone repulsion and rigid nature of the dsDNA double-helix.136 As such, the net LNP interactions for dsDNA functionalized spherical NPs are that of selectively “sticky” hard spheres. More specifically, these LNPs exhibit hard sphere repulsion and uniformly distributed surface-localized attraction between NPs functionalized with non-complementary and complementary dsDNA, respectively (Fig. 5a).
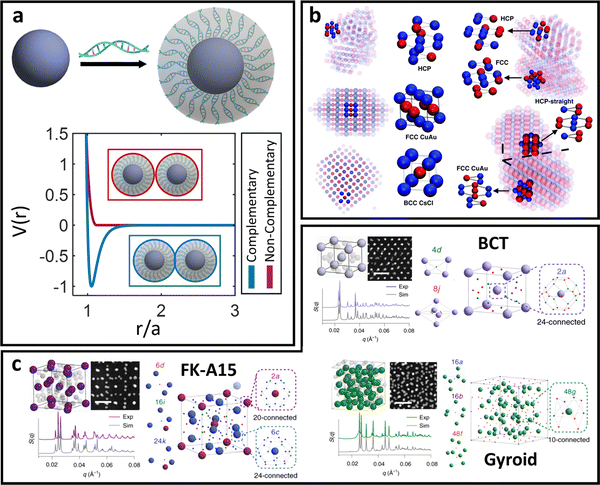 | ||
| Fig. 5 “Soft” spherical LNPs – DNA ligands. (a) Emergent interaction between DNA functionalized spherical NPs. Complementary nature of DNA hybridization can give rise to both attraction and repulsions between particles. (b) Usage of “soft,” partially overlapping potentials in MD can capture assembly of (b) common structures such as HCP, FCC, CuAu, and BCC lattices.138 (c) Soft interaction potentials between DNA functionalized NPs can even drive the formation of low density morphologies such as the FK-A15 and Gyroid lattices.141 Figures are reproduced from ref. 138 with permission from the Royal Society of Chemistry (© 2018) and ref. 141 with permission from Springer Nature (© 2022). | ||
In contrast, ssDNA ligands are more flexible due to the unhybridized nature of the functionalized DNAs. This means that effects related to ligand flexibility and confinement discussed earlier for oligomeric/polymeric ligands also apply to ssDNA. However, ssDNA still possesses a negatively charged backbone. The presence of electrostatic repulsion between neighboring ligands drives ligand extension and prevents excessive interpenetration between ligand shells, albeit not to the same extent as dsDNA. Altogether, this produces two regions of ssDNA organization in the LNP corona: interior and exterior. The interior region sits closer to the NP surface, where electrostatics and ligand extension dominate. The hard-sphere approximation directly applies in this interior regime. The exterior region possesses increased local free volume available to each ligand due to the r3 dependence in Vss, thereby reducing ligand–ligand electrostatic repulsion and providing space for ligand shell interpenetration. This means that “sticky-ends” are no longer forced to localize at the outer edge of the LNP corona but can exist anywhere inside the exterior region. The boundary between these two regimes sits at a distance rB = Rcoreσ1/2ν−1b away from the NP surface, where ν is the excluded volume of a ssDNA Kuhn monomer.79 Note that the boundary is of a similar order of magnitude to Rcore and thus reflects the long ligand requirement for these effects to manifest in the DNA corona. For ssDNA lengths much less than Rcore, the behavior is analogous to dsDNA.
Based on the physical picture discussed, a simple potential that captures inter-LNP interactions for both ssDNA and dsDNA ligands is the square well (SW) potential:137
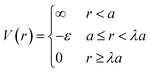 | (7) |
Similar to the HS potential, the SW potential is discontinuous and thus cannot be employed in MD simulations. In the limit of MD, the Mie (eqn (4)) or the Fermi–Jagla (FJ)138 (eqn (8)) potentials are common alternatives to the SW potential. Mie potential features are already discussed above. We note that for dsDNA ligands, n and m are roughly on the order of n = 50 and m = 25 to enforce short-ranged interactions. Conversely, values of n and m are closer to those of the WCA potential (eqn (2)) for ssDNA to allow a longer interaction range and a higher degree of overlap between LNPs. In the ssDNA limit, we expect analogous mapping of experimental handles to potential parameters as those discussed for the Mie potential (eqn (4)). For the FJ potential, its functional form combines the power-law behavior in r with two additional terms designed to capture the interactions specific to DNA:
 | (8) |
Long ligand functionalization on polyhedral NPs
To further increase LNP complexity, we now incorporate the effect of a polyhedral NP core in our discussion of oligomeric, polymer, and DNA ligands. Unlike spherical cores, where separate discussions are used for each ligand type, we combine discussion across ligand lengths using a governing theoretical model capable of predicting a continuous transition from hard to soft to ultrasoft corona morphologies in the limit of polyhedral core geometry.79,99 This theory additionally extends to the limit of low surface coverage48 and branching99 or block copolymeric142 ligand architectures.Ligand functionalized polyhedral NPs – soft/ultrasoft shape interaction
Here, we assume that ligand functionalization falls within the high surface coverage regime. As such, the key feature that influences both corona morphology and emergent inter-LNP interactions lies in the interplay between local curvature and spatial confinement experienced by the functionalized ligands. As suggested by the corona morphologies observed in the spherical NP limit, there are three major regimes with respect to ligand spatial confinement that depend on the distance rs from the NP surface: a rod-like limit at small rs, a splaying/partially compressible limit at intermediate rs, and an ultrasoft limit at large rs. Unlike spherical LNPs, however, we must also consider how NP geometry influences the emergent corona morphology. Quantitatively, the effect of local curvature can be captured by first defining the size (R) of an anchored ligand as a function of relevant experimental parameters and surface position:79 | (9) |
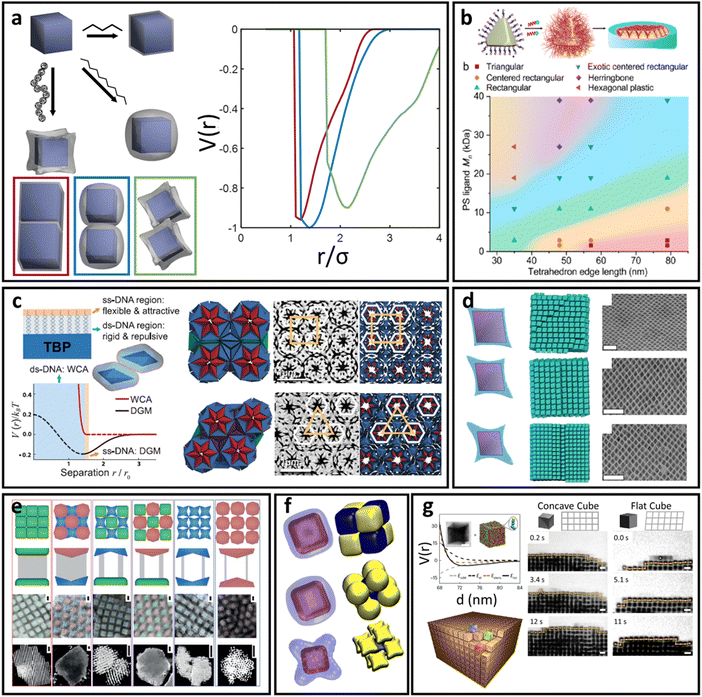 | ||
| Fig. 6 “Soft” polyhedral LNPs. (a) Emergent interaction between ligand functionalized polyhedral NPs. The interplay between ligand confinement and NP surface curvature drives the formation of 3 distinct corona morphologies, each with distinct inter-LNP interactions: conformal (red), convex (blue), and concave (green). (b) Shift in corona morphology (due to the ligand length) can drive lattice transition in 2D assemblies of tetrahedral LNPs.85 (c) DNA-functionalized bipyramids with conformal corona assemble into clathrate-like structures.91 (d) Corona transition drives the formation of an off-set layer-by-layer stacking in nanoplates.99 (e) Engineering corona shape complementarity can drive 3D close packed assembles.146 For cubic NPs, (f) corona transition can drive unusual zig-zag orientational ordering79 or (g) tune their assembly mechanisms.147 Figures are reproduced from ref. 99 and 85 with permission from the American Chemical Society (© 2019 and 2022); ref. 91 and 79 with permission from the American Association for the Advancement of Science (© 2017 and 2019); and ref. 146 and 147 with permission from Springer Nature (© 2015 and 2023). | ||
Conformal coronas occur at short ligand lengths and are identical to the “hard” polyhedral LNPs discussed above. Convex coronas are the polyhedral analogues of “soft” spherical LNPs and occur at intermediate ligand lengths. The transition between these two regimes is identical to that discussed for “hard” polyhedral LNPs: N ∼ Rcoreσ1/2Ω−3/2. Here, the energy difference between ligands at high versus low curvature locations is small enough that the entropic partitioning force is on the order of thermal noise. This means that local chain fluctuations can offset the confinement energetic cost and thus ligands can stretch in place to reduce local confinement rather than undergoing surface partitioning. The net results are protruded spherical cap-like motifs at large faces on the NP surface, where there is a high degree of ligand stretching. Since the ligand stretching energy is on the order of thermal noise, interaction between neighboring convex coronas exhibits a moderate degree of ligand splaying and/or compression, reflective of the same phenomena observed in their “soft” spherical counterparts. Concave coronas are unique to polyhedral LNPs and arise due to a large gain in ligand conformational entropy associated with partitioning to edge/corner surface locations with minimal spatial confinement. This partitioning couples with a concurrent depletion of ligands from NP faces to produce the concave features intrinsic to this regime of corona phase space. The transition between a convex to concave corona happens at N ∼ Rcoreσ1/2Ω−3/2ν−1 or, analogously, when the ligand size is of the same size as the NP core size (Rg ∼ Rcore).
Since conformal coronas are identical to “hard” polyhedral LNPs, we refer the reader to the previous section for their computational modeling, effective inter-LNP interactions, and mapping of experimental handles to potential parameters. Convex and concave coronas, however, have no convenient effective functional forms with respect to inter-LNP potentials. Typically, these LNPs are modeled by first computing a potential of mean force (PMF) from simulation or self-consistent field calculations79,99,143,144 and then fitting to any of the anisotropic variants of the above potentials for spherical LNPs (eqn (4)–(8)). An example set of computed PMF is shown in Fig. 6a for the particle configurations exhibiting the lowest interaction well-depth for each respective corona. The key aspect to note is that the emergent, optimal spatial and orientation ordering between two anisotropic LNPs changes as a function of corona shape. In other words, LNP interactions are highly non-trivial and result from a combination of the interplay between ligand distribution, ligand lengths, and core geometry. This means that corona morphology must be computed before fitting/constructing the coarse-grained computational potential to ensure that the model correctly captures the spatial and orientational behaviors of these LNPs. Incorporating the effect of corona morphology in tuning LNP interactions has yielded a suite of pair potentials capable of capturing a diverse range of ligand functionalized polyhedral NP assemblies in both MC and MD simulations. Example core geometries include tetrahedra assembling into quasicrystalline structures85,86 and closed/opened 2D packings85 (Fig. 6b), bipyramids assembling into host–guest clathrate structures90 (Fig. 6c), rhombuses that assemble into layer-by-layer square tiling99 (Fig. 6d), cubes assembling into simple cubic and brick-wall tiling superlattices,143,145 complementary coronas made using different NP core geometries that mediate close-packed 3D orderings146 (Fig. 6e), octahedra that shift from simple hexagonal to Minkowski assemblies with increasing ligand lengths,92 unusual zig-zag orientational organization of cubic NPs79 (Fig. 6f), and co-assemblies of cubes and triangular nanoplates.144 A recently published work has also expanded the application of this protocol to predict the emergent corona morphology and interaction potentials for a wide range of complementary NP geometries that include truncated octahedra, cuboctahedra, bitetrahedra, and decahedra: all of which self-assemble into space-tiling superlattices.92 Moreover, tuning corona morphology has been shown to provide a handle for control over the assembly mechanism of NP superlattices147 (Fig. 6g).
Ligand surface patterning on NPs – patchy interaction
As a final note, we discuss two LNP design handles that have been much less studied compared to those discussed in the previous sections: low surface coverage and ligand–ligand attraction. These two parameters work synergistically with each other to produce more exotic and orientationally specific LNP interactions. Examples of ligand–ligand attraction can include block copolymers that undergo microphase separation55 or ligand aggregation due to exposure to a poor solvent.148,149 Usage of sparse functionalization is often strategically chosen to allow for a high degree of ligand mobility so that ligand–ligand attraction does not result in kinetically trapped states within the corona. Similar to LNPs with polyhedral cores, there is an entropic driving force that governs ligand partitioning to high curvature locations. Ligand–ligand attractions introduce a counteracting enthalpic force that prevents ligand equipartitioning onto geometrically equivalent edges/corners. It is the interplay between these two opposing interactions that governs how ligands are organized on NP surfaces. In the entropically dominated regime, the emergent corona morphologies fall into one of the cases discussed above. However, in the enthalpically dominated regime, ligand distributions are highly non-ideal and often breaks the underlying NP core symmetry. Corona morphologies in this regime are predicted using modifications of eqn (9) to account for weak attraction between ligands,48 leveraging microphase separation between block copolymeric ligands to produce surface partitioning142 (Fig. 7c), or assuming a complete ligand collapse in the limit of poor solvent.148,149 In general, the predicted coronas are patchy (i.e. localized to specific surface regions) and thus produce LNPs that exhibit directional interactions (Fig. 7a). Experimental realizations of patchy LNPs are still nascent and thus self-assembly of these systems beyond local clusters remains elusive. As such, computational modeling has been the prevalent tool for studying how emergent directionality in interactions drives LNP self-assembly.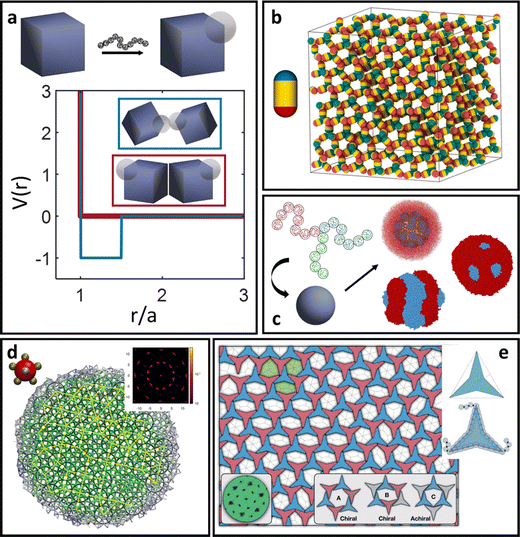 | ||
| Fig. 7 Complex surface patterning of LNPs. (a) Emergent patchy/directional interactions between NPs with surface patterning. Examples of different types of patchy/patterning span a diverse suite of LNPs. (b) Simple diblock patchy ellipsoid self-assembles into a diamond lattice exhibiting a strong photonic band gap.152 (c) Triblock polymer functionalization on NP surface leverages microphase separation to drive complex corona patterning.142 (d) Self-assembly of a dodecagonal quasicrystal obtained from a pentagonal bipyramid patch configuration.157 (e) Vertex patchy 2D concave triangles self-assemble into an open network structure exhibiting tunable, chiral pore structures.158 Figures are reproduced from ref. 152 with permission from the American Chemical Society (© 2021); ref. 142 with permission from Wiley (© 2023); ref. 157 with permission from the American Institute of Physics (© 2021); and ref. 158 with permission from the Royal Society of Chemistry (© 2020). | ||
In MC, an analytical potential developed specifically for patchy interactions is the Kern–Frenkel (KF) potential.150 The KF potential is a generalization of the SW potential (eqn (7)) to account for directionality in interaction and has the form:
 | (10) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i and
i and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) j represent the unit direction of the patch on the ith and jth particle, respectively, and θ defines the opening angle of the patch. Qualitative mappings of experimental handles to potential parameters are: λ ∼ N2/5 defines the interpenetration ratio between interacting patches and ε ∼ N4/5σ2/3 defines the mapping to effective LNP interaction strength. The core size a is simply the bare NP core size due to patchy grafts. Lastly, the opening angle θ depends on the patch size/shape and has been recently shown to scale151 as sin
j represent the unit direction of the patch on the ith and jth particle, respectively, and θ defines the opening angle of the patch. Qualitative mappings of experimental handles to potential parameters are: λ ∼ N2/5 defines the interpenetration ratio between interacting patches and ε ∼ N4/5σ2/3 defines the mapping to effective LNP interaction strength. The core size a is simply the bare NP core size due to patchy grafts. Lastly, the opening angle θ depends on the patch size/shape and has been recently shown to scale151 as sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ∼ N1/2. However, KF is limited to spherical/spheroidal particles. For patchy polyhedral LNPs, creating a polyhedral NP core particle modeled using an anisotropic potential (eqn (3)) that is then decorated with small spherical patches each exhibiting an attractive/repulsive Mie potential (eqn (4)) is the current state-of-the-art approach. Here, mapping the patch size to Mie parameters follows the same qualitative conversion discussed for oligomeric/polymeric ligands on spherical NPs. This approach has the additional benefit of being deployable in MD simulations due to the conservative nature of potentials applied to each subunit making up the entire patchy particle. Applications of such patchy potentials have resulted in a suite of interesting open lattices in simulations. Patchy rod particles are shown to self-assemble into the diamond lattice (Fig. 7b) – a holy grail for photonics applications.152 KF-based patchy NPs can also self-assemble into helices,153 honeycombed morphologies,154 low density liquids,155 clathrate-like structures,156 and quasicrystalline morphologies157 (Fig. 7d). Building upon the idea of breaking particle core symmetry, simulations of vertex-attractive concave triangular PNPs show that a porous, hexagonal lattice with uniform pore sizes can be achieved158 (Fig. 7e). Additional simulations of such concave triangles reveal that the cores can encapsulate guest particles of varying shapes/sizes, making such PNPs ideal for the creation of porous materials with applications in separation or cargo encapsulation/transport.159,160
θ ∼ N1/2. However, KF is limited to spherical/spheroidal particles. For patchy polyhedral LNPs, creating a polyhedral NP core particle modeled using an anisotropic potential (eqn (3)) that is then decorated with small spherical patches each exhibiting an attractive/repulsive Mie potential (eqn (4)) is the current state-of-the-art approach. Here, mapping the patch size to Mie parameters follows the same qualitative conversion discussed for oligomeric/polymeric ligands on spherical NPs. This approach has the additional benefit of being deployable in MD simulations due to the conservative nature of potentials applied to each subunit making up the entire patchy particle. Applications of such patchy potentials have resulted in a suite of interesting open lattices in simulations. Patchy rod particles are shown to self-assemble into the diamond lattice (Fig. 7b) – a holy grail for photonics applications.152 KF-based patchy NPs can also self-assemble into helices,153 honeycombed morphologies,154 low density liquids,155 clathrate-like structures,156 and quasicrystalline morphologies157 (Fig. 7d). Building upon the idea of breaking particle core symmetry, simulations of vertex-attractive concave triangular PNPs show that a porous, hexagonal lattice with uniform pore sizes can be achieved158 (Fig. 7e). Additional simulations of such concave triangles reveal that the cores can encapsulate guest particles of varying shapes/sizes, making such PNPs ideal for the creation of porous materials with applications in separation or cargo encapsulation/transport.159,160
To provide a quick reference for coarse-grain potential parameterization across the LNPs, we summarize the mapping between potential parameters for the various V(r) (eqn (1)–(8) and (10)) discussed and experimental handles in Table 1. We note that these mappings are designed to match trends in interaction strengths, interaction ranges, and particle sizes as a function of experimental variables and are not meant to provide a direct correspondence between simulation and experiments. One-to-one conversions between experiments and coarse-grained potentials will necessitate direct measurements of PMFs or second virial coefficients (B2) in experiments and fitting constants to the various potential parameters.
| Potential | Potential parameter | Experimental parameter | Ligand/NP type | Potential type | Applicability range |
|---|---|---|---|---|---|
| Variable definition: N: ligand degree of polymerization, σ: grafting density, b: ligand Kuhn length, Rcore: NP radius (or insphere radius), Rg: ligand radius of gyration, and Ns: number of DNA “sticky-ends”. | |||||
| HS (eqn (1)) | a | Nσ 1/3 b | Short ligand, spherical NPs | Hard spheres | N ≤ Rcσ1/2 |
| WCA (eqn (2)) | ε | σ 1/2 | |||
| a | Nσ 1/3 b | ||||
| Hard shape (GJK + eqn (1)) | a | Nσ 1/3 b | Short ligand, shaped NPs | Hard polyhedra |

|
| Aniso-WCA (eqn (3)) | ε | σ 1/2 | |||
| a | Nσ 1/3 b | ||||
| Mie (eqn (4)) | ε | N 1/2 σ 1/2 | Oligomeric ligand, polymeric ligand, DNA ligand, spherical/shaped NPs | Soft/ultrasoft spheres/polyhedra | N > Rcσ1/2, Rg < Rc |
| a | N 1/2 σ 1/4 b | ||||
| n − m | N −1/2 σ 1/2 | ||||
| Yukawa (eqn (5)) | ε | N 4/5 σ 2/3 | Polymeric ligand, spherical/shaped NPs | Ultrasoft spheres/polyhedra | R g ∼ Rc |
| κ | N 3/5 σ 1/5 b | ||||
| OPP (eqn (6)) | ε 1, ε2 | N 4/5 σ 2/3 | |||
| k, ϕ | N 3/5 σ 1/5 b | ||||
| Square well (eqn (7)) | ε | N s σ | dsDNA ligand, spherical/shaped NPs | Hard, selective spheres/polyhedra | — |
| a | Nσ 1/3 b | ||||
| λ | 1.25Ns | ||||
| Square well (eqn (7)) | ε | N s σ | ssDNA ligand, spherical/shaped NPs | Soft, selective spheres/polyhedra | N > Rcσ1/2 |
| a | N 3/5s σ 1/5 b | ||||
| λ | N 2/5s | ||||
| Fermi–Jagla (eqn (8)) | ε, Ai, Bi | N s σ | |||
| a | N 3/5s σ 1/5 b | ||||
| n | N −1/2s σ 1/2 | ||||
| Kern–Frenkel (eqn (10)) | ε | N 4/5 σ 2/3 | Polymeric ligand, DNA ligand, spherical/shaped NPs | Patchy spheres/polyhedra | R g ∼ Rc |
| a | R core | ||||
| λ | N 2/3 | ||||
| θ | sin−1(N1/2) | ||||
Theoretical prediction of LNP self-assembly
In addition to MC and MD simulations, the inter-LNP potentials discussed in the previous sections can be merged with theoretical tools designed for a priori prediction of LNP self-assembly. These tools typically quantify the free energy of LNPs when placed in a given spatial and orientational arrangement that corresponds to a candidate superlattice structure. Comparison across a suite of lattice configurations and selecting the one with the lowest free energy then provides a quantitative prediction of LNP self-assembly. Such approaches are extremely powerful in that they only utilize experimentally relevant parameters to characterize mesoscale level morphologies, providing a powerful handle for high throughput design of LNPs. Here, we split our discussion into “hard” vs. “soft” LNP self-assembly.Theoretical prediction of “hard” LNP self-assembly
“Hard” LNPs are characterized by strong steric repulsions between neighboring particles. This means that entropy maximization provides the dominant driving force for LNP self-assembly. Since “hard” LNPs cannot overlap with each other, entropy maximization for these systems seeks configurations that minimize excluded volume between a reference particle and its neighbors.100,101 Minimization of the effective volume that a particle occupies within the lattice increases the space available to other particles, creating a large increase in translational entropy that drives LNP crystallization. For these reasons, seminal works on “hard” spherical LNPs assembly prediction over the past few decades have revolved around utilizing the packing fraction (η) as a proxy for the lattice free energy of formation. Specifically, structures that maximize η correspond to the thermodynamically equilibrium lattices. This approach has shown moderate successes with respect to common lattices such as face-centered cubic, body centered cubic, and Laves structures161,162 (Fig. 8b). However, the packing fraction driven approach fails to capture more complex phases and often over predicts the range of lattice stability. Efforts to address this limitation have resulted in the inclusion of additional features such as emergent directionality/patchy interactions between closely packed LNP lattice prediction (Fig. 8a). Parameters such as nearest neighbor contacts, corona deformation, and corona overlap have all been utilized to define an effective packing fraction ηe. Here, ηe takes into account features such as how ligand splaying can give rise to partial corona overlaps between LNPs or how the coordination shell can produce emergent directional patchiness that slightly alters the LNP's excluded volume163,164 (Fig. 8a). Of note is the recently developed Orbifold Topological Model, which has been shown to capture experimentally observed assembly behaviors across a wide range of “hard” LNP systems.104,106,109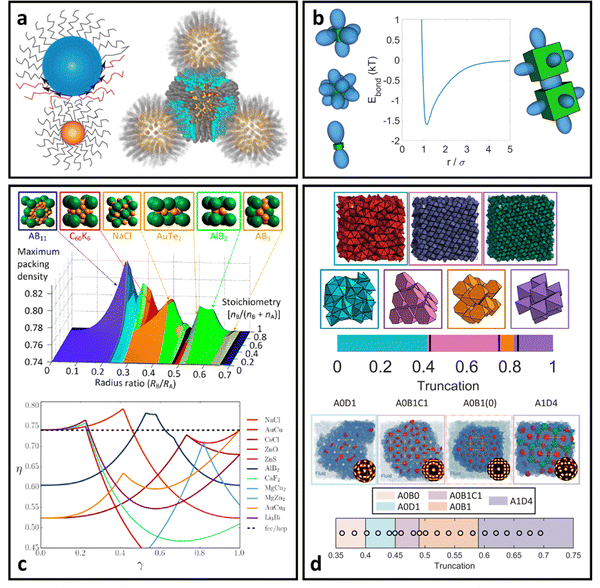 | ||
| Fig. 8 “Hard” LNP self-assembly. (a) Ligand splaying and partial corona deformation between interacting hard spherical LNPs can alter local free volume and packing.105,106 (b) Theoretical prediction of “hard” spherical LNPs relies on analysis of packing density and identifying structures with higher densities than FCC/HCP.40,185 Corona splaying prediction from (a) extends the packing analysis to deformable coronas. (c) Directional interactions between “hard” polyhedral LNPs predicted via EBT.165 (d) Application of EBT to predict a diverse suite of lattices ranging from simple cubic to clathrates to quasicrystals.91,165,186 Figures are reproduced from ref. 186, 40 and 105 with permission from the American Chemical Society (© 2012, 2016, and 2021); ref. 106 with permission from the Royal Society of Chemistry (© 2016); ref. 185 with permission from the American Institute of Physics (© 2016); ref. 165 with permission from the National Academy of Sciences (© 2022); and ref. 91 with permission from the American Association for the Advancement of Science (© 2017). | ||
With respect to “hard” polyhedral LNPs, a recently developed theory called entropic bonding (EBT)165 has shown moderate successes in predicting both emergent directional interactions and the hierarchical self-assembly of hard polyhedra. Recognizing that excluded volume minimization drives entropic crystallization of “hard” polyhedral LNPs, EBT first quantifies the configuration between neighboring particles that minimizes their combined excluded volume. This is mapped to “shape orbitals” around a single polyhedron that indicates the emergent directional interaction between particles at high crowding (Fig. 8c). Through this lens, selecting particle configurations that maximize “shape orbital” overlap across all LNPs immediately results in system states with the lowest excluded volume and therefore the entropically stabilized lattices. Application of EBT to hard polyhedra self-assembly has successfully captured simple lattices such as simple cubic packing of cubes, Minkowski packing of octahedra, and face-centered cubic packing of spheres165 (Fig. 8d). EBT even captures the formation of complex lattices such as clathrates,90 host–guest structures,93 layer-by-layer motifs,94 and ultra-high density packing of bipyramids88 (Fig. 8d). It is important to note that the only required input into EBT is the intrinsic geometry of the particle shape. Emergent direction interactions, optimal particle orientation, and equilibrium spatial positions are all theoretically predicted from this input knowledge of particle geometry. Such simplicity in inputs makes EBT a powerful approach for both a priori prediction and design of “hard” polyhedral LNPs for hierarchical self-assembly.
Theoretical prediction of “soft” LNP self-assembly
“Soft” LNPs are characterized by the interplay between emergent inter-LNP attraction due to favorable corona overlap, steric hinderances arising from stretched ligands or NP core geometry, and species specific attraction/repulsion between ligands. In contrast to “hard” LNPs, assembly here is not governed by entropic maximization (i.e. particle packing) but rather by enthalpic minimization. To date, theories for “soft” LNP self-assembly have been built upon seminal works on Wertheim's thermodynamic perturbation theory (WTPT) for associating liquids.166–170 Briefly, WTPT predicts the excess Helmholtz free energy of formation (Abond) for spherically symmetric patchy particles interacting via the KF potential (eqn (10)), where Abond takes the form: | (11) |
 | (12) |
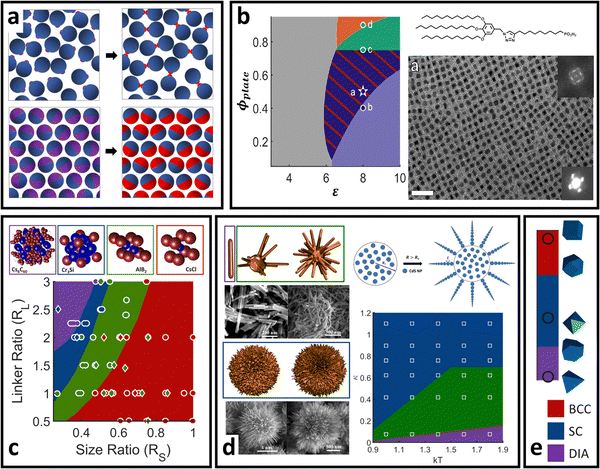 | ||
| Fig. 9 “Soft” LNP self-assembly. (a) Schematic of generalization of WTPT from the hard sphere liquid reference state (top) to the hard sphere/polyhedral crystalline reference state (bottom). Application of this theory for “soft” PNDP is successful across a wide range of different types of nanoscale self-assembly. (b) Co-assembly of ligand functionalized nanocubes and nanoplates as a function of stoichiometry and interaction energy144 (inverse temperature). (c) DNA-mediated spherical AuNP self-assembly.178 (d) Electrostatics driven, self-limiting assembly of CdS supraparticles.179 (e) Patchy DNA nanocage self-assembly showing transition from BCC to SC to a diamond superlattice with the changing core patchy shape.177 All data points on the phase diagrams indicate experimental results and solid phases correspond to WTPT prediction. Figures are reproduced from ref. 144 with permission from the American Association for the Advancement of Science (© 2021); ref. 178 with permission from the National Academy of Sciences (© 2015); ref. 179 with permission from the American Chemical Society (© 2021); and ref. 177 with permission from Springer Nature (© 2020). | ||
 | ||
| Fig. 10 Structural diversity in LNP self-assembly. Schematic of assembly morphologies for LNPs as a function of building block and system complexity phase space. Snapshots indicate classes of structural organizations accessible for each phase space regime and do not reflect the entire space of all accessible assembled morphologies. Abbreviations utilized are: body-centered cubic (BCC), face-centered cubic (FCC), simple cubic (SC), body-centered tetragonal (BCT), zig-zag oriented BCC (zzBCC), tetra-octa honeycomb (toh), gyrated tetra-octa honeycomb (gtoh), rectified cubic honeycomb (rch), Penrose P1 tiling (P1), simple hexagonal (sh), and dodecagonal quasicrystal (DDQC). The figure contains images reproduced from ref. 83, 85, 92, 116, 142, 146, 177, 187–189; ref. 83 and 92 with permission from the American Association for the Advancement of Science (© 2012 and 2024); ref. 116 with permission from the National Academy of Sciences (© 2021); ref. 142 with permission from Wiley (© 2023); ref. 146, 177 and 187 with permission from Springer Nature (© 2015 and 2020); and ref. 188, 85 and 189 with permission from the American Chemical Society (© 2018, 2022, and 2023). | ||
Conclusion and outlook on new directions for LNPs
Despite the unprecedented growth in our ability to synthesize, model, and predict LNP self-assembly, key challenges remain. Firstly, as demands for precision control over inter-LNP interactions increase, more advanced methods are needed to increase surface selectivity in ligand functionalization. Increased precision, however, presents major challenges for synthesis48,181 as LNP surface patterning is constrained by the intrinsic core NP geometry. Development of new theory and computational tools to guide experiments is critical as the number of potential design parameters is too large for a brute force “trial-and-error” approach.Secondly, the advent of patchy LNPs resulting from complex LNP surface patterning has also opened newer avenues for stringing together LNPs into long chains via patch–patch interactions.151 These “colloidal” polymers have been shown to exhibit strong plasmonic responses, making them ideal for applications in creating next-generation sensors. Unlike traditional polymers, however, each monomer here is an entire LNP with well-defined and unique geometry. Little work has been done on looking at how these geometrical effects influence chain conformation and packing, making a priori design of “colloidal” chains to target specific modes of plasmonic responses an on-going challenge.
Thirdly, due to the increased complexity of experimentally accessible LNP building blocks used in self-assembly, the likelihood of kinetic traps during assembly has also dramatically increased. As a result, assembly pathway engineering that explicitly accounts for both LNP softness and directional interactions is also of interest. Questions that will be relevant to answer here are: (1) what is the hierarchy of motifs needed to achieve the final self-assembled structures? (2) how does one assembly pathway reduce the potential for kinetic traps relative to another? and (3) how do rotational and translation dynamics of the highly anisotropic LNPs influence the assembly pathway? Answering these questions not only builds a more fundamental understanding of the complex behaviors underlying LNP assemblies but also provides critical insights into design strategies to develop more novel assembly structures.
In short, the design and synthesis of polymer/DNA functionalized nanoparticles is an exciting field with incredible promise for applications in catalysis, sensing, soft robotics, and energy harvesting. Our review covers the current state-of-the-art computational and theoretical approaches to modeling and predicting how ligand functionalization can imbue complex, emergent interactions between nanoparticles that can sometime break the intrinsic geometry of their constitutive parts. Key developments in fundamental understanding of how ligands are organized when functionalized onto NP surfaces have not only expanded our understanding of assembly physics but also enabled powerful approaches for inverse design of LNPs to develop a wide range of different superlattices with applications spanning across all technologically relevant fields in nanoscience. Altogether, these results suggest that the future of LNP synthesis and self-assembly is bright. Thanks to the chemical diversity of both ligand types and NP core geometry, LNPs present a class of nanoscale synthons capable of realizing complex building blocks for use in creating multifunctional and ordered materials at the mesoscale and beyond.
Author contributions
T. V. led the manuscript development and wrote the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
T. V. thanks the Ralph E. Powe Junior Faculty Enhancement Award for partial financial support of this work.References
- H. A. Nguyen, G. Dixon, F. Y. Dou, S. Gallagher, S. Gibbs, D. M. Ladd, E. Marino, J. C. Ondry, J. P. Shanahan, E. S. Vasileiadou, S. Barlow, D. R. Gamelin, D. S. Ginger, D. M. Jonas, M. G. Kanatzidis, S. R. Marder, D. Morton, C. B. Murray, J. S. Owen, D. V. Talapin, M. F. Toney and B. M. Cossairt, Chem. Rev., 2023, 123, 7890–7952 CrossRef CAS PubMed
.
- N. H. Cho, A. Guerrero-Martínez, J. Ma, S. Bals, N. A. Kotov, L. M. Liz-Marzán and K. T. Nam, Nat. Rev. Bioeng., 2023, 1, 88–106 CrossRef
.
- J. Crassous, M. J. Fuchter, D. E. Freedman, N. A. Kotov, J. Moon, M. C. Beard and S. Feldmann, Nat. Rev. Mater., 2023, 8, 365–371 CrossRef
.
- C. R. Kagan, L. C. Bassett, C. B. Murray and S. M. Thompson, Chem. Rev., 2021, 121, 3186–3233 CrossRef CAS PubMed
.
- Y. Wu, J. Feng, Z. Yang, Y. Liu, S. Liu, Y. Wu, J. Feng, Z. Yang, Y. Liu and S. Liu, Adv. Sci., 2023, 10, 2205536 CrossRef CAS PubMed
.
- P. C. Y. Chow, T. Someya, P. C. Y. Chow and T. Someya, Adv. Mater., 2020, 32, 1902045 CrossRef CAS PubMed
.
- J. Plocher and A. Panesar, Mater. Des., 2019, 183, 108164 CrossRef
.
- R. Kumar, S. Sahoo, E. Joanni, R. K. Singh, W. K. Tan, K. K. Kar and A. Matsuda, Prog. Energy Combust. Sci., 2019, 75, 100786 CrossRef
.
- C. Liu, H. Chen, S. Wang, Q. Liu, Y. G. Jiang, D. W. Zhang, M. Liu and P. Zhou, Nat. Nanotechnol., 2020, 15, 545–557 CrossRef CAS PubMed
.
- J. H. Swisher, L. Jibril, S. H. Petrosko and C. A. Mirkin, Nat. Rev. Mater., 2022, 7, 428–448 CrossRef CAS
.
- K. M. Herbert, S. Schrettl, S. J. Rowan and C. Weder, Macromolecules, 2017, 50, 8845–8870 CrossRef CAS
.
- T. M. Swager, Macromolecules, 2017, 50, 4867–4886 CrossRef CAS
.
- T. P. Russell and Y. Chai, Macromolecules, 2017, 50, 4597–4609 CrossRef CAS
.
- Y. Zhang and S. J. Park, Polymers, 2019, 11, 909 CrossRef CAS PubMed
.
- T. Ray, J. Choi, J. Reeder, S. P. Lee, A. J. Aranyosi, R. Ghaffari and J. A. Rogers, Curr. Opin. Biomed. Eng., 2019, 9, 47–56 CrossRef
.
- G. H. Lee, H. Moon, H. Kim, G. H. Lee, W. Kwon, S. Yoo, D. Myung, S. H. Yun, Z. Bao and S. K. Hahn, Nat. Rev. Mater., 2020, 5, 149–165 CrossRef PubMed
.
- Y. Zhang, D. Kim, R. Dong, X. Feng and C. O. Osuji, Sci. Adv., 2022, 8, 5899 CrossRef PubMed
.
- J. W. Barnett, C. R. Bilchak, Y. Wang, B. C. Benicewicz, L. A. Murdock, T. Bereau and S. K. Kumar, Sci. Adv., 2020, 6, 1–7 Search PubMed
.
- X. Li, G. Jiang, M. Jian, C. Zhao, J. Hou, A. W. Thornton, X. Zhang, J. Z. Liu, B. D. Freeman, H. Wang, L. Jiang and H. Zhang, Nat. Commun., 2023, 14, 1–12 CAS
.
- P. R. Kidambi, P. Chaturvedi and N. K. Moehring, Science, 2021, 374, 1–12 CrossRef PubMed
.
- M. C. Ferrari, Curr. Opin. Chem. Eng., 2023, 40, 100905 CrossRef
.
- M. Galizia, W. S. Chi, Z. P. Smith, T. C. Merkel, R. W. Baker and B. D. Freeman, Macromolecules, 2017, 50, 7809–7843 CrossRef CAS
.
- D. T. Lee, P. Corkery, S. Park, H. K. Jeong and M. Tsapatsis, Ann. Rev. Chem. Biomol. Eng., 2022, 13, 529–555 CrossRef CAS PubMed
.
- Y. Fu, Y. B. Jiang, D. Dunphy, H. Xiong, E. Coker, S. Chou, H. Zhang, J. M. Vanegas, J. G. Croissant, J. L. Cecchi, S. B. Rempe and C. J. Brinker, Nat. Commun., 2018, 9, 1–12 CrossRef PubMed
.
- A. Cangialosi, C. K. Yoon, J. Liu, Q. Huang, J. Guo, T. D. Nguyen, D. H. Gracias and R. Schulman, Science, 2017, 357, 1126–1130 CrossRef CAS PubMed
.
- A. Pantula, B. Datta, Y. Shi, M. Wang, J. Liu, S. Deng, N. J. Cowan, T. D. Nguyen and D. H. Gracias, Sci. Robot., 2022, 7, 1–10 Search PubMed
.
- G. M. Whitesides, Angew. Chem., Int. Ed., 2018, 57, 4258–4273 CrossRef CAS PubMed
.
- S. Lee, H. A. Calcaterra, S. Lee, W. Hadibrata, B. Lee, E. B. Oh, K. Aydin, S. C. Glotzer and C. A. Mirkin, Nature, 2022, 610, 674–679 CrossRef CAS PubMed
.
- M. Annadhasan, S. Basak, N. Chandrasekhar, R. Chandrasekar, M. Annadhasan, S. Basak, N. Chandrasekhar and R. Chandrasekar, Adv. Opt. Mater., 2020, 8, 2000959 CrossRef CAS
.
- G. A. Ermolaev, D. V. Grudinin, Y. V. Stebunov, K. V. Voronin, V. G. Kravets, J. Duan, A. B. Mazitov, G. I. Tselikov, A. Bylinkin, D. I. Yakubovsky, S. M. Novikov, D. G. Baranov, A. Y. Nikitin, I. A. Kruglov, T. Shegai, P. Alonso-González, A. N. Grigorenko, A. V. Arsenin, K. S. Novoselov and V. S. Volkov, Nat. Commun., 2021, 12, 1–8 CrossRef PubMed
.
- M. S. Ergoktas, G. Bakan, E. Kovalska, L. W. Le Fevre, R. P. Fields, P. Steiner, X. Yu, O. Salihoglu, S. Balci, V. I. Fal’ko, K. S. Novoselov, R. A. W. Dryfe and C. Kocabas, Nat. Photonics, 2021, 15, 493–498 CrossRef CAS PubMed
.
- Y. Li and J. Yu, Nat. Rev. Mater., 2021, 6, 1156–1174 CrossRef CAS
.
- E. L. Bell, W. Finnigan, S. P. France, A. P. Green, M. A. Hayes, L. J. Hepworth, S. L. Lovelock, H. Niikura, S. Osuna, E. Romero, K. S. Ryan, N. J. Turner and S. L. Flitsch, Nat. Rev. Methods Primers, 2021, 1, 1–21 CrossRef
.
- R. Verduzco, X. Li, S. L. Pesek and G. E. Stein, Chem. Soc. Rev., 2015, 44, 2405–2420 RSC
.
- E. V. Amadi, A. Venkataraman and C. Papadopoulos, Nanotechnology, 2022, 33, 132001 CrossRef PubMed
.
- L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2014, 14, 2–9 CrossRef PubMed
.
- S. A. Mallory, C. Valeriani and A. Cacciuto, Annu. Rev. Phys. Chem., 2018, 69, 59–79 CrossRef CAS PubMed
.
- Z. Li, Q. Fan and Y. Yin, Chem. Rev., 2022, 122, 4976–5067 CrossRef CAS PubMed
.
- M. Dwivedi, S. L. Singh, A. S. Bharadwaj, V. Kishore and A. V. Singh, Micromachines, 2022, 13, 1–18 CrossRef PubMed
.
- M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed
.
- U. Tritschler, S. Pearce, J. Gwyther, G. R. Whittell and I. Manners, Macromolecules, 2017, 50, 3439–3463 CrossRef CAS
.
- E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O’Brien and C. B. Murray, Nature, 2006, 439, 55–59 CrossRef CAS PubMed
.
- J. Henzie, M. Grünwald, A. Widmer-Cooper, P. L. Geissler and P. Yang, Nat. Mater., 2011, 11, 131–137 CrossRef PubMed
.
- J. S. Kahn and O. Gang, Angew. Chem., Int. Ed., 2022, 61, e202105678 CrossRef CAS PubMed
.
- C. A. Mirkin and S. H. Petrosko, ACS Nano, 2023, 17, 16291–16307 CrossRef CAS PubMed
.
- Y. J. Kim, J. H. Kim, I. S. Jo, D. J. Pine, S. Sacanna and G. R. Yi, J. Am. Chem. Soc., 2021, 143, 13175–13183 CrossRef CAS PubMed
.
- K. H. Ku, Y. J. Kim, G. R. Yi, Y. S. Jung and B. J. Kim, ACS Nano, 2015, 9, 11333–11341 CrossRef CAS PubMed
.
- A. Kim, T. Vo, H. An, P. Banerjee, L. Yao, S. Zhou, C. Kim, D. J. Milliron, S. C. Glotzer and Q. Chen, Nat. Commun., 2022, 13, 1–14 Search PubMed
.
- J. A. A. Diaz, J. S. Oh, G. R. Yi and D. J. Pine, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 10645–10653 CrossRef CAS PubMed
.
- S. Stuij, J. Rouwhorst, H. J. Jonas, N. Ruffino, Z. Gong, S. Sacanna, P. G. Bolhuis and P. Schall, Phys. Rev. Lett., 2021, 127, 108001 CrossRef CAS PubMed
.
- E. Marino, S. W. Van Dongen, S. J. Neuhaus, W. Li, A. W. Keller, C. R. Kagan, T. E. Kodger and C. B. Murray, Chem. Mater., 2022, 34, 2779–2789 CrossRef CAS
.
- H. Joukhdar, A. Seifert, T. Jüngst, J. Groll, M. S. Lord, J. Rnjak-Kovacina, H. Joukhdar, A. M. S. Lord, J. Rnjak-Kovacina, Au. A. Seifert, T. Jüngst and J. Groll, Adv. Mater., 2021, 33, 2100091 CrossRef CAS PubMed
.
- K. C. Elbert, T. Vo, D. Oh, H. Bharti, S. C. Glotzer and C. B. Murray, ACS Nano, 2022, 16, 4508–4516 CrossRef CAS PubMed
.
- C. M. Bates and F. S. Bates, Macromolecules, 2017, 50, 3–22 CrossRef CAS
.
- F. S. Bates and G. H. Fredrickson, Annu. Rev. Phys. Chem., 2003, 41, 525–557 CrossRef PubMed
.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed
.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901 CrossRef PubMed
.
- D. Samanta, W. Zhou, S. B. Ebrahimi, S. H. Petrosko and C. A. Mirkin, Adv. Mater., 2022, 34, 2107875 CrossRef CAS PubMed
.
- Z. G. Wang, Macromolecules, 2017, 50, 9073–9114 CrossRef CAS
.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS
.
- B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1957, 27, 1208–1209 CrossRef CAS
.
- I. Borukhov and L. Leibler, Macromolecules, 2002, 35, 5171–5182 CrossRef CAS
.
- J. J. Erpenbeck and W. W. Wood, J. Stat. Phys., 1984, 35, 321–340 CrossRef
.
- H. N. W. Lekkerkerker and R. Tuinier, Lecture Notes Phys., 2011, 833, 109–129 Search PubMed
.
- W. W. Wood and J. D. Jacobson, J. Chem. Phys., 1957, 27, 1207–1208 CrossRef CAS
.
- J. A. Barker and D. Henderson, Mol. Phys., 1971, 21, 187–191 CrossRef CAS
.
- J. Zhu, M. Li, R. Rogers, W. Meyer, R. H. Ottewill, W. B. Russel and P. M. Chaikin, Nature, 1997, 387, 883–885 CrossRef CAS
.
- P. K. Bommineni, N. R. Varela-Rosales, M. Klement and M. Engel, Phys. Rev. Lett., 2019, 122, 128005 CrossRef CAS PubMed
.
- Y. Zhou and G. Arya, Nat. Commun., 2022, 13, 1–12 Search PubMed
.
- E. Fayen, L. Filion, G. Foffi and F. Smallenburg, Phys. Rev. Lett., 2024, 132, 048202 CrossRef CAS PubMed
.
- S. Jiménez-Millán, C. García-Alcántara, A. Ramírez-Hernández, E. J. Sambriski and S. I. Hernández, J. Mol. Liq., 2021, 335, 116219 CrossRef
.
- D. Wang, T. Dasgupta, E. B. van der Wee, D. Zanaga, T. Altantzis, Y. Wu, G. M. Coli, C. B. Murray, S. Bals, M. Dijkstra and A. van Blaaderen, Nat. Phys., 2020, 17, 128–134 Search PubMed
.
- J. Wang, C. F. Mbah, T. Przybilla, S. Englisch, E. Spiecker, M. Engel and N. Vogel, ACS Nano, 2019, 13, 9005–9015 CrossRef CAS PubMed
.
- M. P. Allen, D. Frenkel and J. Talbot, Comput. Phys. Rep., 1989, 9, 301–353 CrossRef
.
- S. Hess, M. Kröger and H. Voigt, Phys. A, 1998, 250, 58–82 CrossRef CAS
.
- J. Jin, K. S. Schweizer and G. A. Voth, J. Chem. Phys., 2023, 158, 034104 CrossRef CAS PubMed
.
- E. J. Saltzman and K. S. Schweizer, J. Chem. Phys., 2006, 125, 44509 CrossRef PubMed
.
- P. K. Bommineni, M. Klement and M. Engel, Phys. Rev. Lett., 2020, 124, 218003 CrossRef CAS PubMed
.
- F. Lu, T. Vo, Y. Zhang, A. Frenkel, K. G. Yager, S. Kumar and O. Gang, Sci. Adv., 2019, 5, 2399–2416 CrossRef PubMed
.
- E. G. Gilbert, D. W. Johnson and S. S. Keerthi, IEEE J. Rob. Automation, 1988, 4, 193–203 CrossRef
.
- M. Sagardia, T. Stouraitis and J. Lopes e Silva, 11th Conference and Exhibition of the European Association of Virtual Reality and Augmented Reality, EuroVR 2014, 2014, pp. 65–76.
- U. Agarwal and F. A. Escobedo, Nat. Mater., 2011, 10, 230–235 CrossRef CAS PubMed
.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453–457 CrossRef CAS PubMed
.
- A. P. Gantapara, J. De Graaf, R. Van Roij and M. Dijkstra, Phys. Rev. Lett., 2013, 111, 015501 CrossRef PubMed
.
- Y. Wang, J. Chen, Y. Zhong, S. Jeong, R. Li and X. Ye, J. Am. Chem. Soc., 2022, 144, 13538–13546 CrossRef CAS PubMed
.
- Y. Wang, J. Chen, R. Li, A. Götz, D. Drobek, T. Przybilla, S. Hübner, P. Pelz, L. Yang, B. Apeleo Zubiri, E. Spiecker, M. Engel and X. Ye, J. Am. Chem. Soc., 2023, 145, 17902–17911 CrossRef CAS PubMed
.
- X. Ye, J. Chen, M. Engel, J. A. Millan, W. Li, L. Qi, G. Xing, J. E. Collins, C. R. Kagan, J. Li, S. C. Glotzer and C. B. Murray, Nat. Chem., 2013, 5, 466–473 CrossRef CAS PubMed
.
- A. Haji-Akbari, M. Engel and S. C. Glotzer, Phys. Rev. Lett., 2011, 107, 215702 CrossRef PubMed
.
- A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray and S. C. Glotzer, Nature, 2009, 462, 773–777 CrossRef CAS PubMed
.
- S. Lee, T. Vo and S. C. Glotzer, Nat. Chem., 2023, 15, 905–912 CrossRef CAS PubMed
.
- H. Lin, S. Lee, L. Sun, M. Spellings, M. Engel, S. C. Glotzer and C. A. Mirkin, Science, 2017, 355, 931–935 CrossRef CAS PubMed
.
- W. Zhou, Y. Li, K. Je, T. Vo, H. Lin, B. E. Partridge, Z. Huang, S. C. Glotzer and C. A. Mirkin, Science, 2024, 383, 312–319 CrossRef CAS PubMed
.
- T. C. Moore, J. A. Anderson and S. C. Glotzer, Soft Matter, 2021, 17, 2840–2848 RSC
.
- S. Lee, E. G. Teich, M. Engel and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 14843–14851 CrossRef CAS PubMed
.
- M. P. Allen and G. Germano, Mol. Phys., 2006, 104, 3225–3235 CrossRef CAS
.
- M. Spellings, R. L. Marson, J. A. Anderson and S. C. Glotzer, J. Comput. Phys., 2017, 334, 460–467 CrossRef
.
- B. H. J. Lee and G. Arya, Nanoscale Horiz., 2020, 5, 1628–1642 RSC
.
- V. Ramasubramani, T. Vo, J. A. Anderson and S. C. Glotzer, J. Chem. Phys., 2020, 153, 084106 CrossRef CAS PubMed
.
- K. C. Elbert, T. Vo, N. M. Krook, W. Zygmunt, J. Park, K. G. Yager, R. J. Composto, S. C. Glotzer and C. B. Murray, ACS Nano, 2019, 13, 14241–14251 CrossRef CAS PubMed
.
- D. Frenkel, Phys. A, 1999, 263, 26–38 CrossRef CAS
.
- D. Frenkel, Nat. Mater., 2014, 14, 9–12 CrossRef PubMed
.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS
.
- Y. Wang, P. J. Santos, J. M. Kubiak, X. Guo, M. S. Lee and R. J. Macfarlane, J. Am. Chem. Soc., 2019, 141, 13234–13243 CrossRef CAS PubMed
.
- A. Travesset, ACS Nano, 2017, 11, 5375–5382 CrossRef CAS PubMed
.
- X. Zha and A. Travesset, J. Phys. Chem. C, 2021, 125, 18936–18945 CrossRef CAS
.
- A. Travesset, Soft Matter, 2016, 13, 147–157 RSC
.
- D. Meng, S. K. Kumar, J. M. D. Lane and G. S. Grest, Soft Matter, 2012, 8, 5002–5010 RSC
.
- C. Waltmann, N. Horst and A. Travesset, J. Chem. Phys., 2018, 149, 34109 CrossRef PubMed
.
- I. Cherniukh, T. V. Sekh, G. Rainò, O. J. Ashton, M. Burian, A. Travesset, M. Athanasiou, A. Manoli, R. A. John, M. Svyrydenko, V. Morad, Y. Shynkarenko, F. Montanarella, D. Naumenko, H. Amenitsch, G. Itskos, R. F. Mahrt, T. Stöferle, R. Erni, M. V. Kovalenko and M. I. Bodnarchuk, ACS Nano, 2021, 16, 2024 Search PubMed
.
- A. Upah, A. Thomas, J. Hallstrom and A. Travesset, J. Chem. Theory Comput., 2024, 20, 1559–1567 CrossRef CAS PubMed
.
- J. J. Potoff and D. A. Bernard-Brunel, J. Phys. Chem. B, 2009, 113, 14725–14731 CrossRef CAS PubMed
.
- E. Marino, R. A. LaCour, T. C. Moore, S. W. van Dongen, A. W. Keller, D. An, S. Yang, D. J. Rosen, G. Gouget, E. H. R. Tsai, C. R. Kagan, T. E. Kodger, S. C. Glotzer and C. B. Murray, Nat. Synth., 2023, 3, 111–122 CrossRef
.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CrossRef CAS
.
- R. A. Lacour, C. S. Adorf, J. Dshemuchadse and S. C. Glotzer, ACS Nano, 2019, 13, 13829–13842 CrossRef CAS PubMed
.
- R. A. Lacour, T. C. Moore and S. C. Glotzer, Phys. Rev. Lett., 2022, 128, 188001 CrossRef CAS PubMed
.
- J. Dshemuchadse, P. F. Damasceno, C. L. Phillips, M. Engel and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024034118 CrossRef CAS PubMed
.
- W. L. Chen, R. Cordero, H. Tran and C. K. Ober, Macromolecules, 2017, 50, 4089–4113 CrossRef CAS
.
- S. T. Milner, Science, 1991, 251, 905–914 CrossRef CAS PubMed
.
- C. Ligoure and L. Leibler, Macromolecules, 1990, 23, 5044–5046 CrossRef CAS
.
- K. Ohno, T. Morinaga, S. Takeno, Y. Tsujii and T. Fukuda, Macromolecules, 2007, 40, 9143–9150 CrossRef CAS
.
- J. Midya, M. Rubinstein, S. K. Kumar and A. Nikoubashman, ACS Nano, 2020, 14, 15505–15516 CrossRef CAS PubMed
.
- R. Menichetti and A. Pelissetto, J. Chem. Phys., 2013, 138, 124902 CrossRef PubMed
.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450 CrossRef CAS
.
- T. Lafitte, S. K. Kumar and A. Z. Panagiotopoulos, Soft Matter, 2014, 10, 786–794 RSC
.
- Z. Wu, S. Pal and S. Keten, Macromolecules, 2023, 56, 3259–3271 CrossRef CAS
.
- M. Asai, A. Cacciuto and S. K. Kumar, Soft Matter, 2014, 11, 793–797 RSC
.
- J. U. Kim and M. W. Matsen, Macromolecules, 2008, 41, 4435–4443 CrossRef CAS
.
- T. A. Witten, P. A. Pincus and P. A. Pincus, Macromolecules, 1986, 19, 2509–2513 CrossRef CAS
.
- M. M. Marques, T. P. O. Nogueira, R. F. Dillenburg, M. C. Barbosa and J. R. Bordin, J. Appl. Phys., 2020, 127, 54701 CrossRef CAS
.
- K. Binder and A. Milchev, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 1515–1555 CrossRef CAS
.
- K. J. Modica, T. B. Martin and A. Jayaraman, Macromolecules, 2017, 50, 4854–4866 CrossRef CAS
.
- C. Koh, G. S. Grest and S. K. Kumar, ACS Nano, 2020, 14, 13491–13499 CrossRef CAS PubMed
.
- H. Yukawa, Prog. Theor. Phys. Suppl., 1955, 1, 1–10 CrossRef
.
- J. P. K. Doye, D. J. Wales and S. I. Simdyankin, Faraday Discuss., 2001, 118, 159–170 RSC
.
- J. Bednar, P. Furrer, V. Katritch, A. Z. Stasiak, J. Dubochet and A. Stasiak, J. Mol. Biol., 1995, 254, 579–594 CrossRef CAS PubMed
.
- Z. Ovanesyan, B. Medasani, M. O. Fenley, G. I. Guerrero-García, M. O. De La Cruz and M. Marucho, J. Chem. Phys., 2014, 141, 225103 CrossRef PubMed
.
- J. A. Barker and D. Henderson, J. Chem. Phys., 1967, 47, 2856–2861 CrossRef CAS
.
- E. Pretti, H. Zerze, M. Song, Y. Ding, N. A. Mahynski, H. W. Hatch, V. K. Shen and J. Mittal, Soft Matter, 2018, 14, 6303–6312 RSC
.
- R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208 CrossRef CAS PubMed
.
- T. I. N. G. Li, R. Sknepnek, R. J. MacFarlane, C. A. Mirkin and M. Olvera De La Cruz, Nano Lett., 2012, 12, 2509–2514 CrossRef CAS PubMed
.
- S. Wang, S. Lee, J. S. Du, B. E. Partridge, H. F. Cheng, W. Zhou, V. P. Dravid, B. Lee, S. C. Glotzer and C. A. Mirkin, Nat. Mater., 2022, 21, 580–587 CrossRef CAS PubMed
.
- T. Vo, AIChE J., 2023, e18243 CrossRef CAS
.
- X. Chen, T. Vo and P. Clancy, Soft Matter, 2023, 19, 8625–8634 RSC
.
- K. C. Elbert, W. Zygmunt, T. Vo, C. M. Vara, D. J. Rosen, N. M. Krook, S. C. Glotzer and C. B. Murray, Sci. Adv., 2021, 7, eabf9402 CrossRef CAS PubMed
.
- Y. Zhang, G. Giunta, H. Liang and M. Dijkstra, J. Chem. Phys., 2023, 158, 184902 CrossRef CAS PubMed
.
- M. N. O’Brien, M. R. Jones, B. Lee and C. A. Mirkin, Nat. Mater., 2015, 14, 833–839 CrossRef PubMed
.
- B. Luo, Z. Wang, T. Curk, G. Watson, C. Liu, A. Kim, Z. Ou, E. Luijten and Q. Chen, Nat. Nanotechnol., 2023, 18, 589–595 CrossRef CAS PubMed
.
- E. Galati, H. Tao, M. Tebbe, R. Ansari, M. Rubinstein, E. B. Zhulina and E. Kumacheva, Angew. Chem., Int. Ed., 2019, 58, 3123–3127 CrossRef CAS PubMed
.
- R. M. Choueiri, E. Galati, H. Thérien-Aubin, A. Klinkova, E. M. Larin, A. Querejeta-Fernández, L. Han, H. L. Xin, O. Gang, E. B. Zhulina, M. Rubinstein and E. Kumacheva, Nature, 2016, 538, 79–83 CrossRef CAS PubMed
.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS
.
- A. Kim, K. Akkunuri, C. Qian, L. Yao, K. Sun, Z. Chen, T. Vo and Q. Chen, ACS Nano, 2023, 18, 950 Search PubMed
.
- A. Neophytou, V. N. Manoharan and D. Chakrabarti, ACS Nano, 2021, 15, 2668–2678 CrossRef CAS PubMed
.
- R. Guo, J. Mao, X. M. Xie and L. T. Yan, Sci. Rep., 2014, 4, 1–7 Search PubMed
.
- X. Sen Hou, G. L. Zhu, L. J. Ren, Z. H. Huang, R. Bin Zhang, G. Ungar, L. T. Yan and W. Wang, J. Am. Chem. Soc., 2018, 140, 1805–1811 CrossRef PubMed
.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef PubMed
.
- D. F. Tracey, E. G. Noya and J. P. K. Doye, J. Chem. Phys., 2019, 151, 224506 CrossRef PubMed
.
- D. F. Tracey, E. G. Noya and J. P. K. Doye, J. Chem. Phys., 2021, 154, 194505 CrossRef CAS PubMed
.
- N. Pakalidou, J. Mu, A. J. Masters and C. Avendanõ, Mol. Syst. Des. Eng., 2020, 5, 376–384 RSC
.
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 CrossRef PubMed
.
- X. Qian, M. Ostwal, A. Asatekin, G. M. Geise, Z. P. Smith, W. A. Phillip, R. P. Lively and J. R. McCutcheon, J. Membr. Sci., 2022, 645, 120041 CrossRef CAS
.
- M. D. Eldridge, P. A. Madden and D. Frenkel, Nature, 1993, 365, 35–37 CrossRef CAS
.
- N. Hunt, R. Jardine and P. Bartlett, Phys. Rev. E, 2000, 62, 900 CrossRef CAS PubMed
.
- A. Travesset, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9563–9567 CrossRef CAS PubMed
.
- A. V. Tkachenko, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10269–10274 CrossRef CAS PubMed
.
- T. Vo and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116414119 CrossRef PubMed
.
- M. S. Wertheim, J. Stat. Phys., 1984, 35, 19–34 CrossRef
.
- M. S. Wertheim, J. Stat. Phys., 1984, 35, 35–47 CrossRef
.
- M. S. Wertheim, J. Stat. Phys., 1986, 42, 459–476 CrossRef
.
- M. S. Wertheim, J. Stat. Phys., 1986, 42, 477–492 CrossRef
.
- M. S. Wertheim, J. Chem. Phys., 1987, 87, 7323–7331 CrossRef CAS
.
- A. Haghmoradi, L. Wang and W. G. Chapman, J. Phys.: Condens. Matter, 2016, 28, 244009 CrossRef PubMed
.
- F. Smallenburg, L. Filion and F. Sciortino, J. Phys. Chem. B, 2015, 119, 9076–9083 CrossRef CAS PubMed
.
- A. Haghmoradi, B. D. Marshall and W. G. Chapman, J. Chem. Eng. Data, 2020, 65, 5743–5752 CrossRef CAS
.
- L. Rovigatti, J. M. Tavares and F. Sciortino, Phys. Rev. Lett., 2013, 111, 168302 CrossRef PubMed
.
- M. Formanek, L. Rovigatti, E. Zaccarelli, F. Sciortino and A. J. Moreno, Macromolecules, 2021, 54, 6613–6627 CrossRef CAS
.
- B. D. Marshall and W. G. Chapman, Soft Matter, 2014, 10, 5168–5176 RSC
.
- Y. Tian, J. R. Lhermitte, L. Bai, T. Vo, H. L. Xin, H. Li, R. Li, M. Fukuto, K. G. Yager, J. S. Kahn, Y. Xiong, B. Minevich, S. K. Kumar and O. Gang, Nat. Mater., 2020, 19, 789–796 CrossRef CAS PubMed
.
- T. Vo, V. Venkatasubramanian, S. Kumar, B. Srinivasan, S. Pal, Y. Zhang and O. Gang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4982–4987 CrossRef CAS PubMed
.
- L. Tang, T. Vo, X. Fan, D. Vecchio, T. Ma, J. Lu, H. Hou, S. C. Glotzer and N. A. Kotov, J. Am. Chem. Soc., 2021, 143, 19655–19667 CrossRef CAS PubMed
.
- P. Kumar, T. Vo, M. Cha, A. Visheratina, J. Y. Kim, W. Xu, J. Schwartz, A. Simon, D. Katz, V. P. Nicu, E. Marino, W. J. Choi, M. Veksler, S. Chen, C. Murray, R. Hovden, S. Glotzer and N. A. Kotov, Nature, 2023, 615, 418–424 CrossRef CAS PubMed
.
- G. Chen, K. J. Gibson, D. Liu, H. C. Rees, J. H. Lee, W. Xia, R. Lin, H. L. Xin, O. Gang and Y. Weizmann, Nat. Mater., 2018, 18, 169–174 CrossRef PubMed
.
- J. Choi, C. M. Hui, M. Schmitt, J. Pietrasik, S. Margel, K. Matyjazsewski and M. R. Bockstaller, Langmuir, 2013, 29, 6452–6459 CrossRef CAS PubMed
.
- Y. Wang, L. Dai, Z. Ding, M. Ji, J. Liu, H. Xing, X. Liu, Y. Ke, C. Fan, P. Wang and Y. Tian, Nat. Commun., 2021, 12, 1–8 CrossRef PubMed
.
- J. Zhou, M. N. Creyer, A. Chen, W. Yim, R. P. M. Lafleur, T. He, Z. Lin, M. Xu, P. Abbasi, J. Wu, T. A. Pascal, F. Caruso and J. V. Jokerst, J. Am. Chem. Soc., 2021, 143, 12138–12144 CrossRef CAS PubMed
.
- N. Horst and A. Travesset, J. Chem. Phys., 2016, 144, 14502 CrossRef PubMed
.
- P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2012, 6, 609–614 CrossRef CAS PubMed
.
- F. Lu, K. G. Yager, Y. Zhang, H. Xin and O. Gang, Nat. Commun., 2015, 6, 1–10 Search PubMed
.
- D. Morphew, J. Shaw, C. Avins and D. Chakrabarti, ACS Nano, 2018, 12, 2355–2364 CrossRef CAS PubMed
.
- J. Bohlin, A. J. Turberfield, A. A. Louis and P. Šulc, ACS Nano, 2023, 17, 5387–5398 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2024 |

