 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spiers Memorial Lecture: From cold to hot, the structure and structural dynamics of dense ionic fluids†
Matthew S.
Emerson
 ,
Raphael
Ogbodo
,
Raphael
Ogbodo
 and
Claudio J.
Margulis
and
Claudio J.
Margulis
 *
*
Department of Chemistry, The University of Iowa, Iowa City, IA 52242, USA. E-mail: claudio-margulis@uiowa.edu
First published on 4th June 2024
Abstract
The structure of ionic liquids (ILs), which a decade or two ago was the subject of polite but heated debate, is now much better understood. This has opened opportunities to ask more sophisticated questions about the role of structure in transport, the structure of systems with ions that are not prototypical, and the similarity between ILs and other dense ionic fluids such as the high-temperature inorganic molten salts; let alone the fact that new areas of research have emerged that sprung from our collective understanding of the structure of ILs such as the deep eutectic solvents, the polymerized ionic liquids, and the zwitterionic liquids. Yet, our understanding of the structure of prototypical ILs may not be as complete as we think it to be, given that recent experiments appear to show that in some cases there may be more than one liquid phase resulting in liquid–liquid (L–L) phase transitions. This article presents a perspective on what we think are key topics related to the structure and structural dynamics of ILs and to some extent high-temperature molten salts.
1 Introduction
Much of the data discussed in this article is based on scattering or the simulation of scattering in the bulk phase, leaving out important topics such as phenomena at interfaces,1–11 and the relation between ionic liquids and other solvents12 for other presentations in this dense ionic fluids Faraday discussion. Without going into details that have been presented in multiple prior works,13–24 the key observable in bulk scattering is the structure function S(q) obtained from experiments (simulations) via left (right) side formulae in eqn (1). Here, q is the scattering vector magnitude, Icoh(q) is the coherent scattering intensity, and xi, fi(q) are the atomic fraction and X-ray form factor for atomic species i, respectively; gij(r) is the pair distribution function. Similar expressions can be written for neutron scattering by considering neutron scattering lengths instead of X-ray form factors. The right hand side equation can be split into the contributions of cations and anions, that of polar and apolar components, that of charged heads and apolar tails, or that of any other desirable groups that help explain the structure of the liquid at specific q values.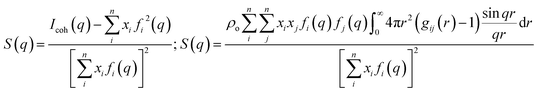 | (1) |
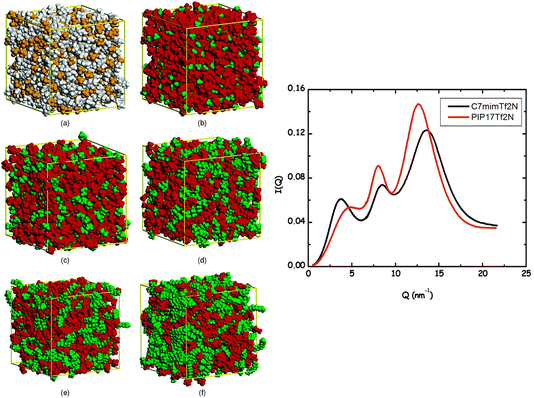 | ||
| Fig. 1 (Left) Simulation snapshots of Cnmim+/PF6− (n = 2, 2, 4, 6, 8, 12). Reprinted (adapted)25 with permission from J. Phys. Chem. B, 2006, 110(7), 3330–3335. Copyright 2006 American Chemical Society. (Right) SWAXS I(q) for 1-heptyl-3-methylimidazolium/NTf2− (C7mim+/NTf2−) and 1-methyl-1-heptylpiperidinium/NTf2− (PIP17+/NTf2−) at ambient temperature. Reprinted (adapted)26 with permission from J. Phys. Chem. Lett., 2012, 3(1), 27–33. Copyright 2012 American Chemical Society. | ||
Our own contribution to this topic began13–17 with the recognition that the lowest two q-peaks on the right side in Fig. 1 are due to liquid phase structural alternations of motifs that are universal for ILs with tails that support the formation of apolar domains, and the third peak at higher q value is generic for all liquids (not just ILs) and it has to do with correlations between intra- and inter-molecular moieties that are adjacent. The lowest q-peak, also called a “prepeak” or a first sharp diffraction peak (FSDP), is related to what is commonly referred to as intermediate range order. It appears because of the alternation between charge-diminished tails spaced by charge networks or between charged subcomponents of the IL when these are separated by tails.17 The second peak (the one between the prepeak and the adjacency peak) is due to positive–negative charge alternation along networks; this peak has to do with the typical distance between anions spaced by a cation head or by cation heads sharing an anionic counterion.17
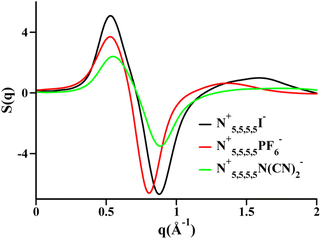
Two very confusing points arise in the literature that we wish to clarify: (1) many ILs do not show a charge alternation peak, and (2) a lowest q-peak is not always a prepeak, at least not in the sense that we are defining the word here or the way we wished the term was used. The first point is demonstrated in Fig. 2 where we see that at around 0.8 Å−1 – where the charge alternation feature is expected to appear in the total S(q) – in all cases it is absent. Notice that this is not because there is no charge alternation in these ILs, but instead because of large cation–cation, anion–anion and cation–anion contributions that when added up fortuitously cancel. In other words, even though charge alternation is present in every ionic liquid and molten salt, it is not always discernible in S(q) due to issues of contrast.
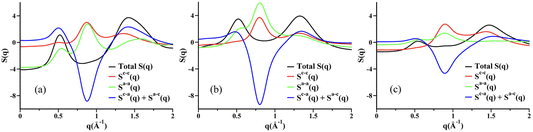 | ||
| Fig. 2 Cation–cation, anion–anion, cation–anion, and total simulated S(q) for (a) N5,5,5,5+/I−, (b) N5,5,5,5+/PF6−, and (c) N5,5,5,5+/N(CN)2− in the liquid state. Reprinted15 (adapted) with permission from J. Phys. Chem. Lett., 2013, 4(1), 105–110. Copyright 2013 American Chemical Society. | ||
As to the second point, this is a matter of definitions and jargon, but it seems to us that calling prepeak or FSDP any peak that appears at lower q value without the peak having a unique physical explanation is not very useful. For example, in some ILs the lowest q-peak may be the charge alternation peak which is unrelated to intermediate range order. The same goes for other common jargon such as “the main peak” which can sometimes be the charge alternation peak or the adjacency peak. For clarity, we prefer to reserve prepeak or FSDP for across-network correlations. This concept extends also to the high-temperature molten salts which are systems that obviously lack apolar domains (or do they? vide infra). Notice that networks need not be charge networks; for example a mixture of DMSO and glycerol will display a prepeak because hydrogen bonding networks of glycerol will be spaced by domains of DMSO.27
An astute reader may ask whether such definitions are only practically applicable when working with simulated data, as it is not simple without resorting to partial deuteration schemes in neutron scattering to know the origin of a low-q peak by simply inspecting the experimental S(q). The answer is no, and the reason is deceptively simple; in most cases we can guess whether a low-q peak is a prepeak based on our definition by inspecting its temperature dependence. If the low q-peak follows an anomalous temperature dependence, it almost always is a prepeak. Prepeaks based on our definition are strange in that their intensity increases (anti-Debye–Waller behavior) with increasing temperature as opposed to other peaks where the intensity decreases. In other words, anomalous temperature behavior for the prepeak is actually normal behavior.17,28–31
2 Results and discussion
Having laid out the basics of IL structure in the Introduction, we will now focus on a set of topics that build on these concepts. First we will explore structural features of high-temperature molten salts that can be understood from what we have learned from ionic liquids, then we will discuss structural dynamics and what one can call the Yamaguchi hypothesis32–36 relating specific features of S(q) with transport. Finally, we will focus on how apolar domains and charge networks move differently in the sub-diffusive regime, particularly at low temperature close to the glass transition.2.1 Inorganic molten salts mixtures and their prepeaks
There has been a renewal of interest in high-temperature molten salt (MS) systems mainly because of their applicability in the energy sector. Particularly relevant applications include novel molten salt nuclear reactors,37 the storage of thermal energy,38 and the recovery and separation of rare earth elements.39 Interestingly, whereas MSs and ILs are both dense ionic fluids, their literature has for the most part grown separate. This section attempts to highlight structural similarities between these. MSs can display the same three structural correlations between ions that we find in ILs, namely adjacency, charge alternation, and intermediate range order leading to a prepeak.19,30,31,40–43 There is a massive historical body of work on molten salts and this article does not attempt to provide a review of what has been done; from a computational perspective, particularly noteworthy are the many studies by Madden, Wilson, Salanne, and others, who introduced the so-called polarizable ion model (PIM).44–54 Whereas the introduction of polarization is also important and a welcome addition in the IL literature,55–59 the PIM model is essential for inorganic molten salts when multivalent cations and highly polarizable anions come into play. A particularly important aspect of it is how interactions get damped when ions are at short distance.44–48 There are excellent articles explaining this and we discuss it no further besides indicating that for the high temperature molten salts intermediate range order is often not correctly captured when using non-polarizable models called rigid-ion models (RIMs).
Fig. 3a–c show simulated S(q) for molten KCl, UCl3, and a 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80% mixture of UCl3 and KCl by mol; Fig. 3d–f show corresponding partial subcomponents of S(q). We focus first on KCl as it is an easy platform to explain two things, (1) what we mean by adjacency correlations and charge alternation in MSs and ILs, and (2) how partial ionic subcomponents of S(q) “cancel” resulting in no charge alternation peak in the overall X-ray S(q). We start by noticing that K+ and Cl− are isoelectronic and their size is similar; this leads to very similar X-ray SK+–K+(q) and SCl−–Cl−(q) functions as can be gleaned from Fig. 3d. Now consider the translucent blue box, which in each graph denotes the region in q space associated with positive–negative charge alternation. In this q-region of Fig. 3d, SK+–K+(q) and SCl−–Cl−(q) contribute almost identical peaks to the overall S(q) in Fig. 3a but SK+–Cl−(q) contributes an antipeak; the sum of the three components results in an overall featureless S(q) in the charge alternation region as can be gleaned from Fig. 3a. Had we not seen the two peaks and the antipeak in the partial subcomponents of S(q), we could not have known there were important liquid features in the q-regime highlighted in blue. These peaks and the antipeak are the hallmark of a liquid phase structural alternation. Now consider the peak starting at q > 2 in Fig. 3a; notice that the feature does not arise from peaks and antipeaks in Fig. 3d but instead from neighboring K+–Cl− correlations (larger q, smaller distance). These are the correlations we refer to as adjacency interactions. Notice that at q values smaller than the charge alternation regime there are no other features in the partial subcomponents of S(q); in other words there is no intermediate range order in neat molten KCl.
80% mixture of UCl3 and KCl by mol; Fig. 3d–f show corresponding partial subcomponents of S(q). We focus first on KCl as it is an easy platform to explain two things, (1) what we mean by adjacency correlations and charge alternation in MSs and ILs, and (2) how partial ionic subcomponents of S(q) “cancel” resulting in no charge alternation peak in the overall X-ray S(q). We start by noticing that K+ and Cl− are isoelectronic and their size is similar; this leads to very similar X-ray SK+–K+(q) and SCl−–Cl−(q) functions as can be gleaned from Fig. 3d. Now consider the translucent blue box, which in each graph denotes the region in q space associated with positive–negative charge alternation. In this q-region of Fig. 3d, SK+–K+(q) and SCl−–Cl−(q) contribute almost identical peaks to the overall S(q) in Fig. 3a but SK+–Cl−(q) contributes an antipeak; the sum of the three components results in an overall featureless S(q) in the charge alternation region as can be gleaned from Fig. 3a. Had we not seen the two peaks and the antipeak in the partial subcomponents of S(q), we could not have known there were important liquid features in the q-regime highlighted in blue. These peaks and the antipeak are the hallmark of a liquid phase structural alternation. Now consider the peak starting at q > 2 in Fig. 3a; notice that the feature does not arise from peaks and antipeaks in Fig. 3d but instead from neighboring K+–Cl− correlations (larger q, smaller distance). These are the correlations we refer to as adjacency interactions. Notice that at q values smaller than the charge alternation regime there are no other features in the partial subcomponents of S(q); in other words there is no intermediate range order in neat molten KCl.
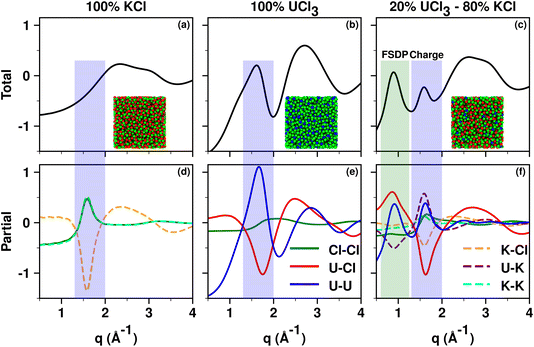 | ||
Fig. 3 From PIM molecular dynamics simulations with methods described in the ESI,† (a)–(c) total X-ray scattering S(q) for molten KCl, UCl3, and UCl3–KCl (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 mol%) respectively all at 900 °C. Panels (d)–(f) show partial ionic contributions. Notice that neither molten KCl nor UCl3 have a prepeak, and intermediate range order arises in the molten state only when the two salts are mixed. Notice also the peaks and antipeaks associated with the charge alternation peak and the prepeak (labeled FSDP) in the partial subcomponents of S(q). 80 mol%) respectively all at 900 °C. Panels (d)–(f) show partial ionic contributions. Notice that neither molten KCl nor UCl3 have a prepeak, and intermediate range order arises in the molten state only when the two salts are mixed. Notice also the peaks and antipeaks associated with the charge alternation peak and the prepeak (labeled FSDP) in the partial subcomponents of S(q). | ||
Now we focus on UCl3, with simulated total X-ray S(q) and partial subcomponents shown in Fig. 3b and e respectively. Notice that just like in the case for KCl, for UCl3 there are no clear structural correlations at q values below charge alternation in Fig. 3e. It turns out that UCl3 is a highly connected networked liquid and it is only when we mix it with a lower valency salt such as KCl that a prepeak or an FSDP appears at low q values as can be gleaned from Fig. 3c. What structural correlations give rise to this prepeak? From Fig. 3f we notice that SU3+–U3+(q) has the shape of a peak in the FSDP region whereas SU3+–K+(q) shows an antipeak. In other words, this is the regime that describes Cl−-decorated U3+ networks spaced by the lower valency KCl salt. As a sidenote, it is less useful or straightforward to focus on the partial subcomponents of S(q) in which Cl− is involved because the anion is counterion to both the high valency and low valency cations, making its contribution difficult to deconvolute. This behavior for mixtures of UCl3 and KCl is the same as we have observed in a recent article42 in the case of LaCl3 in combination with NaCl. We call this “the spacer salt effect” because it is the low valency salt that spaces the higher valency salt networks. Fig. 5 in ref. 42 shows example ion configurations giving rise to the effect in the case of LaCl3–NaCl mixtures.
How does this prepeak in molten salts relate to that in ionic liquids? In one case, cationic heads and anions form networks that are spaced by apolar domains, in the other, high valency cations share Cl− counterions in networks that are spaced by a low valency salt. Put differently, KCl behaves the way apolar tails do in the case of ILs. This phenomenon is recurring for other network-forming liquids which need not be ionic in nature. For example, we have seen the same in mixtures of DMSO and glycerol.27 Glycerol will form hydrogen bonding networks that are separated by pockets of DMSO. In this case, it is DMSO that plays the role of spacer to glycerol networks.
To finish this section, it is important to emphasize that certain molten salts such as MgCl2 have a prepeak without the need of a spacer salt. This has to do with the melt (and also the crystal phase) having two characteristic cation–cation distances; one in which Mg2+ ions share Cl− counterions and the other in which they do not.30,31,41
2.2 IL structural dynamics and a connection to transport
In many applications of ILs such as for batteries, lubrication, and heat transfer, it is their transport properties (viscosity, electrical and heat conductivity, diffusion) that play the most important role.60,61 Obviously, each of these is related to motion of the ions and so is S(q,t) or its real space counterpart the van Hoove function g(r,t). Without getting too technical or comprehensive, we plan to focus on a single transport property, the shear viscosity, and its relation to S(q,t) exploring a hypothesis proposed first by Prof. Tsuyoshi Yamaguchi.32–36 To explain Yamaguchi’s hypothesis, we start with the Green–Kubo expression for the viscosity as an integral over the stress tensor autocorrelation function.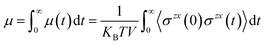 | (2) |
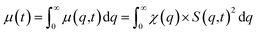 | (3) |
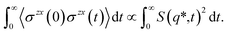 | (4) |
 , the antipeak is the signature of intra-network charge alternation
, the antipeak is the signature of intra-network charge alternation 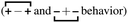 , and because this is the head–anion subcomponent of S(q), the broader peak at higher q values is due to adjacency correlations between opposite charge species
, and because this is the head–anion subcomponent of S(q), the broader peak at higher q values is due to adjacency correlations between opposite charge species 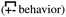 . We add that the q-dependent relaxation of SH–A(q,t) with time is very similar to that of S(q,t), but following the behavior of liquid structural motifs is much more straightforward using the former.
. We add that the q-dependent relaxation of SH–A(q,t) with time is very similar to that of S(q,t), but following the behavior of liquid structural motifs is much more straightforward using the former.
 | ||
| Fig. 4 The cation head–anion subcomponent of S(q), SH–A(q), for different ILs in the liquid state. The cation is always the same in this figure, but peaks and antipeaks in the graph are universal for a multitude of ILs having tails long enough to elicit at least some apolar segregation. Reprinted15 (adapted) with permission from J. Phys. Chem. Lett., 2013, 4(1), 105–110. Copyright 2013 American Chemical Society. | ||
Finally, we introduce two equations that remove issues of units and scale, making the comparison between left and right hand sides of eqn (4) possible. We define the cumulative integral ζ(t) as
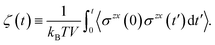 | (5) |
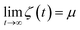 and therefore, ζ(t)/μ is a unitless function that goes from zero to one. Analogously, if we define the structural relaxation function αH–A(q,t) as
and therefore, ζ(t)/μ is a unitless function that goes from zero to one. Analogously, if we define the structural relaxation function αH–A(q,t) as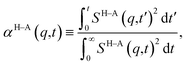 | (6) |
Fig. 5 shows an example of the time behavior of SH–A(q,t) and SH–A(q,t)2 in the relevant charge alternation and adjacency regimes for the prototypical IL Bmim+/NTf2− which does not have a significant prepeak. A vertical line indicates the value q* at which we would evaluate these functions to compute αH–A(q*,t). Of course, one can evaluate αH–A(q,t) at any other q value to also compare against the viscoelastic relaxation ζ(t)/μ. We have used this theoretical framework for several ionic liquids18,20,63,64 and found that the time evolution of ζ(t)/μ tends to fall in between that of the slowest (lowest q) and fastest (highest q) relevant structural motifs as followed by the αH–A(q,t) function; by relevant, we refer to adjacency, charge alternation and polar–apolar alternation. Specifically, if the IL has a prepeak, the relaxation of ζ(t)/μ tends to fall between that of the prepeak (αH–A(qFSDP,t)) and that of the adjacency peak (αH–A(qAdj,t)). Instead, if the IL does not have a prepeak, the relaxation of ζ(t)/μ tends to fall between that of the charge alternation motif (αH–A(q*,t)) and that of the adjacency peak (αH–A(qAdj,t)). For example, we expect that for Bmim+/NTf2− which does not have a significant prepeak, ζ(t)/μ will relax to one somewhat faster than αH–A(q*,t) and a comparison between these two functions is shown in Fig. 5c.
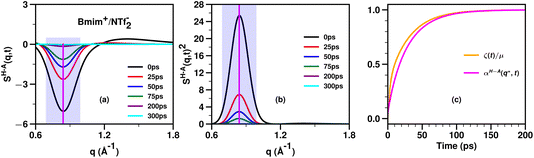 | ||
| Fig. 5 For Bmim+/NTf2− at 400 K and computed from molecular dynamics simulations described in ref. 20, (a) the cation head–anion subcomponent SH–A(q,t), (b) its value squared, SH–A(q,t)2, and (c) a comparison between αH–A(q*,t) and ζ(t)/μ where q* is taken as the wavenumber for charge alternation. The location of q* is denoted with a vertical purple line in subfigures (a) and (b) and the whole charge alternation region with a translucent magenta box. Notice how similar the relaxations of αH–A(q*,t) and ζ(t)/μ are. In our different studies we consistently find that the relaxation of ζ(t)/μ tends to fall somewhere between that of the adjacency feature and that of the slowest (smallest q) relevant intermolecular mode; depending on the length of alkyl tails, this can be the charge alternation feature or the prepeak. | ||
An interesting comparison is for the family Emim+/NTf2−, Bmim+/NTf2−, and Omim+/NTf2−, studied at the same viscosity (different temperatures). In this case one finds that charge alternation contributes about 62–66% of the total viscoelastic relaxation, whereas adjacency correlations contribute between 28–38% to it.64 Notice that the contribution of the prepeak is always quite small (about 6%). In other words, the processes that contribute the most to the viscoelastic relaxation are shorter in range.64 The reader is encouraged to look at Fig. 3 in ref. 18 to see how very close the relaxation of the charge alternation motif αH–A(q*,t) is to the viscoelastic relaxation ζ(t)/μ for an IL with significant apolar tails such as Omim+/NTf2−; in other words, the hypothesis by Yamaguchi works quite well for that system and, as Fig. 5c shows in the current article, it also works reasonably well for Bmim+/NTf2−. In the case of Omim+/NTf2− and other ILs with significant apolar domains we can say that the charge network has three distinct structural dynamic behaviors. The intrachain dynamics associated with adjacency  and charge alternation
and charge alternation  which are most linked to the viscoelastic relaxation, and the across-network
which are most linked to the viscoelastic relaxation, and the across-network  dynamics; whereas each of the three relaxations are coupled, it is common for each of them to be separated by about an order of magnitude in time (adjacency faster than charge alternation and charge alternation faster than the prepeak).
dynamics; whereas each of the three relaxations are coupled, it is common for each of them to be separated by about an order of magnitude in time (adjacency faster than charge alternation and charge alternation faster than the prepeak).
Returning to the hypothesis by Yamaguchi, we can say that the viscoelastic relaxation is mostly related to the loss of memory with time of where positive and negative charges are along a network and less about the much slower across network dynamics. In other words, this is about the random displacement of charged components within networks as well as other faster processes and less about the time scale required for tails to “flood” regions that used to hold charged networks. The relation between within-charge-network structural relaxation and viscoelastic relaxation appears to be quite generic beyond the imidazolium-based ILs even when including atomic substituents in tails such as O and S.20
2.3 Most interesting behavior occurs in the subdiffusive regime
There are some rules on how ions can collectively move in a liquid made purely of cations and anions,65 but beyond this, ion dynamics in the diffusive regime is quite normal. Cationic heads and tails move together as they are tethered, and anions move at their own different rate; cations and anions each have a self diffusion coefficient but these are coupled. By this we mean that the same anion will move faster or slower depending on the identity of the counterion and vice versa. Much more interesting and diverse is the behavior of IL components in the subdiffusive regime. Notice that for many ILs the subdiffusive regime is not short; it can be hundreds of picoseconds or many nanoseconds depending on the viscosity. If we think of it, this time scale encompasses a non-negligible portion of the time for the decay of correlation functions that via Green–Kubo relations give rise to transport properties.In this prediffusive regime, ILs behave like a “liquid inside a liquid”, or a softer material inside a stiffer matrix. By this we mean that on this time scale the whole architecture of charge networks is stiff when compared to softer charge-depleted regions that space them. How do we know this? We have tested this in multiple scenarios and for different ILs. For example, in ref. 66 we studied using the isoconfigurational ensemble Omim+/NTf2−; in this ensemble the key point is that one uses the same exact liquid snapshot from a simulation to launch a swarm of constant energy trajectories each with different initial velocities but all consistent with the same initial temperature. This has been shown67–69 to be useful in teasing out the pure structural origin of motional processes averaging over the different possible dynamics of the multiple trajectories with a common positional origin. What one finds after analyzing the swarm of trajectories is that in the prediffusive regime the parts of the original frame that hardly move are in the charge network, whereas the parts that are highly mobile are in the tails. We called this the “octopus effect” because we saw that on average cationic heads and anions were more or less fixed in space while tails were flailing. This is shown in Fig. 6 where green spheres depict regions of low mobility and red spheres those of high mobility. The green spheres are in the charge network and the red ones in the tail domain.
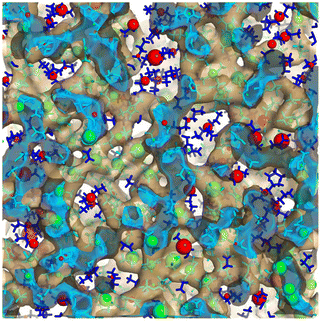 | ||
| Fig. 6 Large green spheres are associated with loci of lowest mobility and large red spheres with loci of highest mobility on a prediffusive time regime; notice that these coincide with the charge network and the apolar domains respectively. In the figure the charge network is enclosed in an isosurface, the inside of which is in cyan and the outside in translucent brown; apolar tails are outside of the isosurface and depicted in blue. Figure reprinted66 from J. Chem. Phys., 2017, 147, 061102, with the permission of AIP Publishing. | ||
Another way to look at this stiff–soft behavior in ILs is from the point of view of a solute. When we study the mobility of small neutral solutes such as gases,70 we see from simulation that mobility of the neutral solute is significantly slower when close to the charge network and faster in charge-depleted regions. This is obviously not because of Coulomb attraction between the solute (taken as charge neutral and non-polarizable) and the ions, but instead because of the stiffness of the environment that results in periods where the gas molecule is caged. We see the same stiff–soft behavior when considering the rotational dynamics of small alcohols in ILs.71
Perhaps the most interesting example of the liquid inside a liquid behavior is as a function of temperature as one goes from the glass regime to the liquid state. In a recent article we posed the question of whether some (all?) ionic liquids slow down or speed up in stages;21 by this we mean that not all subcomponents of an IL become mobile at the same temperature and that at or close to the glass transition one could be in a situation in which apolar domains are dynamically active (liquid-like but tethered to the matrix) whereas the motion of the charge network matrix is much more constrained. The study which involved NMR techniques, dielectric spectroscopy, and simulations looked at the structural dynamics of P666,14+/NTf2− as a function of temperature and found that indeed tails become motionally active on an NMR time scale and on an MD time scale at significantly lower temperatures than the network. Very interesting is the fact that for P666,14+/NTf2−, and for some other ILs with the same cation, there is a new X-ray scattering peak21,72,73 in a q-range that is in between the prepeak and the charge alternation peak close to the glass transition temperature that may be related to the newly discovered L–L phase transition.72–75
3 Conclusions
There are universal organizational rules in ionic liquids, molten salts, and other network forming liquids. In the case of ionic systems, we can often find a shorter and a longer characteristic distance between moieties of the same charge and this gives rise to the charge alternation peak and the prepeak. The shorter length scale (charge alternation) can be that between two anions that are separated by the same positive charge; the longer one (prepeak) can be that between two positive subcomponents that do not share the same anionic counterion. For example, neat molten MgCl2 has a charge alternation peak and a prepeak because there is a typical distance between Mg2+ ions that share Cl− counterions (charge alternation) and a different one for Mg2+ ions that are part of adjacent networks not sharing the same Cl− counterions. Other systems have a prepeak because there is a spacer between charge networks. For example, ionic liquids have apolar domains, and mixtures of molten salts have charge networks separated by spacer salts where the metal ion in the spacer is of lower charge density. We commonly find that prepeaks follow anti-Debye–Waller behavior because as we increase the temperature we break networks; this results in an increase in the across network or across cluster interactions that give rise to the prepeak. We repeatedly find that the structural features most relevant to the viscoelastic relaxation, arguably the most important transport property for ILs, are charge alternation and the shorter-range adjacency correlations; the prepeak appears to be less important because it relaxes more slowly. We have not studied this for the high-temperature molten salts and it may be interesting to do so; however, we speculate that the relaxation of structural features in molten salts may be much less well separated in time than in the case of ILs. For ILs, the behavior of polar and apolar moieties in the pre-diffusive regime, particularly at low temperature, can be quite fascinating with apolar portions having significantly larger mobility than the charge network; let alone the fact that recent articles claim that more than one liquid phase can exist at low temperature for specific ILs involving the P666,14+ cation coupled with different anions. A particularly intriguing finding from scattering is that close to the glass transition region or the L–L phase transition region (for the P666,14+/NTf2− these are only a few degrees apart at ambient pressure) a new scattering peak tends to appear between the prepeak and the charge alternation peak that is still unexplained; our group is making significant inroads in clarifying its origin which will be the subject of a future publication. The possibility of ionic liquids having L–L transitions adds new wrinkles to what we thought we were starting to understand well providing new and established researchers opportunities for stimulating discoveries.Data availability
Data corresponding to Fig. 3a–c are available at the Zenodo repository at https://doi.org/10.5281/zenodo.11505264.Conflicts of interest
There are no conflicts to declare.Acknowledgements
As a perspective article on ionic fluids, this article includes new and already published figures from our own work and that of others. Previously published work discussed here already acknowledged appropriate sources of funding in the original publication. CJM acknowledges support from NSF grant CHE-1954358 for his effort writing this perspective article except that previously unpublished work on high-temperature molten salts presented in Section 2.1 was supported as part of the Molten Salts in Extreme Environments (MSEE) Energy Frontier Research Center, funded by the U.S. Department of Energy Office of Science, Office of Basic Energy Sciences. MSEE work was supported under a subcontract from Brookhaven National Laboratory, which is operated under DOE contract DE-SC0012704. Some of the research presented in Section 2.1 used resources of the National Energy Research Scientific Computing Center (NERSC) at Oak Ridge National Laboratory which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. The authors also acknowledge the University of Iowa High Performance Computing Facility.References
- X. Mao, P. Brown, C. Červinka, G. Hazell, H. Li, Y. Ren, D. Chen, R. Atkin, J. Eastoe, I. Grillo, A. A. H. Padua, M. F. Costa Gomes and T. A. Hatton, Nat. Mater., 2019, 18, 1350–1357 CrossRef CAS PubMed.
- D. Atkins, E. Ayerbe, A. Benayad, F. G. Capone, E. Capria, I. E. Castelli, I. Cekic-Laskovic, R. Ciria, L. Dudy, K. Edström, M. R. Johnson, H. Li, J. M. G. Lastra, M. L. De Souza, V. Meunier, M. Morcrette, H. Reichert, P. Simon, J. Rueff, J. Sottmann, W. Wenzel and A. Grimaud, Adv. Energy Mater., 2022, 12, 2102687 CrossRef CAS.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC.
- H. Li, M. W. Rutland and R. Atkin, Phys. Chem. Chem. Phys., 2013, 15, 14616 RSC.
- S. Perkin, Phys. Chem. Chem. Phys., 2012, 14, 5052 RSC.
- T. Groves and S. Perkin, Faraday Discuss., 2024 10.1039/D4FD00040D.
- W. D. Amith, J. J. Hettige, E. W. Castner, Jr. and C. J. Margulis, J. Phys. Chem. Lett., 2016, 7, 3785–3790 CrossRef CAS PubMed.
- F. Wu, W. V. Karunaratne and C. J. Margulis, J. Phys. Chem. C, 2019, 123, 4914–4925 CrossRef CAS.
- W. V. Karunaratne, S. Sharma, B. M. Ocko and C. J. Margulis, J. Phys. Chem. C, 2021, 125, 25227–25242 CrossRef CAS.
- W. V. Karunaratne, M. Zhao, E. W. Castner and C. J. Margulis, J. Phys. Chem. C, 2022, 126, 13936–13945 CrossRef CAS PubMed.
- W. V. Karunaratne and C. J. Margulis, J. Phys. Chem. C, 2019, 123, 20971–20979 CrossRef CAS.
- A. P. Abbott, K. J. Edler and A. J. Page, J. Chem. Phys., 2021, 155, 150401 CrossRef CAS PubMed.
- H. V. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2010, 114, 16838–16846 CrossRef CAS PubMed.
- H. K. Kashyap, J. J. Hettige, H. V. Annapureddy and C. J. Margulis, Chem. Commun., 2012, 48, 5103–5105 RSC.
- J. J. Hettige, H. K. Kashyap, H. V. Annapureddy and C. J. Margulis, J. Phys. Chem. Lett., 2013, 4, 105–110 CrossRef CAS PubMed.
- H. K. Kashyap and C. J. Margulis, ECS Trans., 2013, 50, 301–307 CrossRef.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Phys. Chem. Lett., 2020, 11, 2062–2066 CrossRef CAS PubMed.
- S. Sharma, A. S. Ivanov and C. J. Margulis, J. Phys. Chem. B, 2021, 125, 6359–6372 CrossRef CAS PubMed.
- R. Ogbodo, W. V. Karunaratne, G. R. Acharya, M. S. Emerson, M. Mughal, H. M. Yuen, N. Zmich, S. Nembhard, F. Wang, H. Shirota, S. I. Lall-Ramnarine, E. W. Castner, J. F. Wishart, A. J. Nieuwkoop and C. J. Margulis, J. Phys. Chem. B, 2023, 127, 6342–6353 CrossRef CAS PubMed.
- B. Borah, G. R. Acharya, D. Grajeda, M. S. Emerson, M. A. Harris, A. Milinda Abeykoon, J. Sangoro, G. A. Baker, A. J. Nieuwkoop and C. J. Margulis, J. Am. Chem. Soc., 2023, 145, 25518–25522 CrossRef CAS PubMed.
- S. Roy, F. Wu, H. Wang, A. S. Ivanov, S. Sharma, P. Halstenberg, S. K. Gill, A. M. Milinda Abeykoon, G. Kwon, M. Topsakal, B. Layne, K. Sasaki, Y. Zhang, S. M. Mahurin, S. Dai, C. J. Margulis, E. J. Maginn and V. S. Bryantsev, Phys. Chem. Chem. Phys., 2020, 22, 22900–22917 RSC.
- F. Lo Celso, G. B. Appetecchi, C. J. Jafta, L. Gontrani, J. N. Canongia Lopes, A. Triolo and O. Russina, J. Chem. Phys., 2018, 148, 193816 CrossRef CAS PubMed.
- A. A. Freitas, K. Shimizu and J. N. Canongia Lopes, J. Chem. Eng. Data, 2014, 59, 3120–3129 CrossRef CAS.
- J. N. Canongia Lopes and A. A. Padua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS PubMed.
- O. Russina, A. Triolo, L. Gontrani and R. Caminiti, J. Phys. Chem. Lett., 2012, 3, 27–33 CrossRef CAS.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Chem. Phys., 2015, 143, 134505 CrossRef PubMed.
- J. J. Hettige, J. C. Araque, H. K. Kashyap and C. J. Margulis, J. Chem. Phys., 2016, 144, 121102 CrossRef PubMed.
- J. J. Hettige, H. K. Kashyap and C. J. Margulis, J. Chem. Phys., 2014, 140, 111102 CrossRef PubMed.
- F. Wu, S. Sharma, S. Roy, P. Halstenberg, L. C. Gallington, S. M. Mahurin, S. Dai, V. S. Bryantsev, A. S. Ivanov and C. J. Margulis, J. Phys. Chem. B, 2020, 124, 2892–2899 CrossRef CAS PubMed.
- S. Sharma, M. S. Emerson, F. Wu, H. Wang, E. J. Maginn and C. J. Margulis, J. Phys. Chem. A, 2020, 124, 7832–7842 CrossRef CAS PubMed.
- T. Yamaguchi, J. Chem. Phys., 2016, 144, 124514 CrossRef PubMed.
- T. Yamaguchi, J. Chem. Phys., 2016, 145, 194505 CrossRef PubMed.
- T. Yamaguchi, Phys. Chem. Chem. Phys., 2018, 20, 17809–17817 RSC.
- T. Yamaguchi and A. Faraone, J. Chem. Phys., 2017, 146, 244506 CrossRef PubMed.
- T. Yamaguchi, K. Mikawa, S. Koda, K. Fujii, H. Endo, M. Shibayama, H. Hamano and Y. Umebayashi, J. Chem. Phys., 2012, 137, 104511 CrossRef PubMed.
- O. Beneš and R. J. M. Konings, in Molten Salt Reactor Fuel and Coolant, 2nd edn, 2020, vol. 5, book section 5.18, pp. 609–644 Search PubMed.
- C. K. Ho, Sol. Energy, 2017, 152, 38–56 CrossRef CAS.
- V. A. Volkovich, D. S. Maltsev, S. Y. Melchakov, L. F. Yamshchikov, A. V. Novoselova and V. V. Smolensky, ECS Trans., 2016, 75, 397–408 CrossRef CAS.
- S. Roy, M. Brehm, S. Sharma, F. Wu, D. S. Maltsev, P. Halstenberg, L. C. Gallington, S. M. Mahurin, S. Dai, A. S. Ivanov, C. J. Margulis and V. S. Bryantsev, J. Phys. Chem. B, 2021, 125, 5971–5982 CrossRef CAS PubMed.
- F. Wu, S. Roy, A. S. Ivanov, S. K. Gill, M. Topsakal, E. Dooryhee, M. Abeykoon, G. Kwon, L. C. Gallington, P. Halstenberg, B. Layne, Y. Ishii, S. M. Mahurin, S. Dai, V. S. Bryantsev and C. J. Margulis, J. Phys. Chem. Lett., 2019, 10, 7603–7610 CrossRef CAS PubMed.
- M. S. Emerson, S. Sharma, S. Roy, V. S. Bryantsev, A. S. Ivanov, R. Gakhar, M. E. Woods, L. C. Gallington, S. Dai, D. S. Maltsev and C. J. Margulis, J. Am. Chem. Soc., 2022, 144, 21751–21762 CrossRef CAS PubMed.
- M. S. Emerson, A. S. Ivanov, L. C. Gallington, D. S. Maltsev, P. Halstenberg, S. Dai, S. Roy, V. S. Bryantsev and C. J. Margulis, J. Phys. Chem. B, 2024, 128(16), 3972–3980 CrossRef CAS PubMed.
- M. Wilson and P. A. Madden, J. Phys.: Condens. Matter, 1993, 5, 6833–6844 CrossRef CAS.
- M. Wilson and P. A. Madden, J. Phys.: Condens. Matter, 1993, 5, 2687–2706 CrossRef.
- M. Wilson and P. A. Madden, J. Phys.: Condens. Matter, 1994, 6, 159–170 CrossRef CAS.
- F. Hutchinson, A. J. Rowley, M. K. Walters, M. Wilson, P. A. Madden, J. C. Wasse and P. S. Salmon, J. Chem. Phys., 1999, 111, 2028–2037 CrossRef CAS.
- F. Hutchinson, M. Wilson and P. A. Madden, Mol. Phys., 2001, 99, 811–824 CrossRef CAS.
- A. Aguado and P. A. Madden, J. Chem. Phys., 2003, 119, 7471–7483 CrossRef CAS.
- M. Salanne, C. Simon, P. Turq and P. A. Madden, J. Phys. Chem. B, 2008, 112, 1177–1183 CrossRef CAS PubMed.
- M. Salanne, B. Rotenberg, S. Jahn, R. Vuilleumier, C. Simon and P. A. Madden, Theor. Chem. Acc., 2012, 131, 1143 Search PubMed.
- N. Ohtori, M. Salanne and P. A. Madden, J. Chem. Phys., 2009, 130, 104507 CrossRef PubMed.
- Y. Ishii, S. Kasai, M. Salanne and N. Ohtori, Mol. Phys., 2015, 113, 2442–2450 CrossRef CAS.
- A. Marin-Laflèche, M. Haefele, L. Scalfi, A. Coretti, T. Dufils, G. Jeanmairet, S. Reed, A. Serva, R. Berthin, C. Bacon, S. Bonella, B. Rotenberg, P. Madden and M. Salanne, J. Open Source Softw., 2020, 5, 2373 CrossRef.
- K. Goloviznina, Z. Gong, M. F. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2021, 17, 1606–1617 CrossRef CAS PubMed.
- K. Goloviznina, J. N. Canongia Lopes, M. Costa Gomes and A. A. H. Padua, J. Chem. Theory Comput., 2019, 15, 5858–5871 CrossRef CAS PubMed.
- K. Goloviznina, Z. Gong and A. A. H. Padua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1572 CAS.
- F. Philippi, K. Goloviznina, Z. Gong, S. Gehrke, B. Kirchner, A. A. H. Pádua and P. A. Hunt, Phys. Chem. Chem. Phys., 2022, 24, 3144–3162 RSC.
- A. Szabadi, A. Doknic, J. Netsch, A. M. Pálvögyi, O. Steinhauser and C. Schröder, Phys. Chem. Chem. Phys., 2023, 25, 19882–19890 RSC.
- H. Li, R. J. Wood, M. W. Rutland and R. Atkin, Chem. Commun., 2014, 50, 4368 RSC.
- S. Cowie, P. K. Cooper, R. Atkin and H. Li, J. Phys. Chem. C, 2017, 121, 28348–28353 CrossRef CAS.
- U. Balucani and M. Zoppi, Dynamics of the Liquid State, Oxford Science Publications, 1994 Search PubMed.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Ionic Liq., 2022, 2, 100012 CrossRef.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Phys. Chem. B, 2021, 125, 6264–6271 CrossRef CAS PubMed.
- H. K. Kashyap, H. V. R. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221 CrossRef CAS PubMed.
- R. P. Daly, J.C. Araque and C. J. Margulis, J. Chem. Phys., 2017, 147, 061102 CrossRef PubMed.
- A. Widmer-Cooper, H. Perry, P. Harrowell and D. R. Reichman, Nat. Phys., 2008, 4, 711–715 Search PubMed.
- A. Widmer-Cooper and P. Harrowell, J. Chem. Phys., 2007, 126, 154503 CrossRef PubMed.
- C. P. Royall and S. R. Williams, Phys. Rep., 2015, 560, 1–75 CrossRef CAS.
- J. C. Araque and C. J. Margulis, J. Chem. Phys., 2018, 149, 144503 CrossRef PubMed.
- J. C. Araque, R. P. Daly and C. J. Margulis, J. Chem. Phys., 2016, 144, 204504 CrossRef PubMed.
- M. A. Harris, PhD Dissertation, University of Tennessee, 2022.
- B. Yao, M. Paluch, J. Paturej, S. McLaughlin, A. McGrogan, M. Swadzba-Kwasny, J. Shen, B. Ruta, M. Rosenthal, J. Liu, D. Kruk and Z. Wojnarowska, ACS Appl. Mater. Interfaces, 2023, 15, 39417–39425 CrossRef CAS PubMed.
- M. A. Harris, T. Kinsey, D. V. Wagle, G. A. Baker and J. Sangoro, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020878118 CrossRef CAS PubMed.
- Z. Wojnarowska, S. Cheng, B. Yao, M. Swadzba-Kwasny, S. McLaughlin, A. McGrogan, Y. Delavoux and M. Paluch, Nat. Commun., 2022, 13, 1342 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00086b |
| This journal is © The Royal Society of Chemistry 2024 |
