Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tiled unitary product states for strongly correlated Hamiltonians
Hugh G. A.
Burton

Yusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. E-mail: hgaburton@gmail.com
First published on 25th July 2024
Abstract
Approximating the electronic wave function for strongly correlated systems remains a major theoretical challenge. Emerging quantum computers can enable new types of wave-function ansatz to be considered, with the potential to overcome the exponential memory storage for strong correlation. I have recently introduced the tiled Unitary Product States (tUPS) ansatz, which successfully combines the preservation of particle-number and spin symmetry with shallow quantum circuits and local qubit connectivity [H. G. A. Burton, Phys. Rev. Res., 2024, 6, 023300]. In this contribution, I investigate the accuracy of this tUPS hierarchy for strongly-correlated Hamiltonians. I consider the picket-fence pairing Hamiltonian and the two-dimensional Hubbard lattice, which collectively describe a range of strong correlation mechanisms found in molecules. Numerical results demonstrate that highly accurate energies can be achieved with a compact approximation for both weak and strong correlation in the Hubbard model, and the repulsive pairing regime. These data provide valuable insights into the applicability of the tUPS hierarchy for strong electron correlation.
1 Introduction
Computing the electronic wave function is fundamental to the ab initio prediction of molecular and materials properties. A single Slater determinant usually provides a sufficient representation for weakly correlated molecules, allowing the remaining correlation energy to be computed with many-body methods such as coupled-cluster theory.1,2 However, for strong electron correlation, we must typically solve the full configuration interaction (FCI) problem within some active space of strongly correlated orbitals,3 for which the memory cost scales exponentially with the number of correlated electrons.Quantum computing offers the ability to design new wave-function approximations that provide high accuracy without an exponentially-scaling memory cost.4–6 A quantum device stores information using an entangled superposition of quantum bits (qubits). Using an encoding such as the Jordan–Wigner transformation,7,8 each qubit can be mapped to the occupation of an individual spin orbital, allowing correlated electronic states to be stored with a linearly scaling number of qubits. Parametrised quantum circuits can then be used to define a wave-function ansatz, which can be optimised using the variational quantum eigensolver (VQE).9
To take advantage of quantum devices, we require new wave-function ansatzes that are suited to the natural operations of quantum computation. Since a quantum circuit corresponds to a unitary transformation Û on the qubit state, these ansatzes must also be represented in the form |Ψ〉 = Û|Φ0〉, where |Φ0〉 is an initial reference state.5 This transformation Û must be easy to implement as a quantum circuit and should ideally conserve the physical symmetries of the Hamiltonian, e.g., particle number and spin quantum numbers. A variety of ansatzes have been proposed, including variants of unitary coupled-cluster theory (UCC),9–11 products of fermionic operators based on disentangled UCC,12–16 qubit coupled cluster,17–19 geminal-based methods,20,21 and the hardware-efficient ansatz.22 However, combining symmetry preservation with efficient quantum circuits has proved challenging. For example, methods based on hardware-efficient Pauli operators can break particle-number and spin symmetry,17 while the fermionic-based UCC ansatz requires a Trotter expansion10 and implementing arbitrary fermionic operators has a relatively high quantum-circuit cost.23,24
In ref. 15, I introduced a new wave-function ansatz, the tiled unitary product state (tUPS), which combines number- and spin-symmetry conservation with efficient quantum circuits. The tUPS approximation encodes electronic states using a layered quantum circuit built from a product of spin-adapted one-body and paired two-body operators that only act between sequential spatial orbitals in a brickwall arrangement (Fig. 1). The restriction to paired two-body operators and nearest-neighbour connectivity enables shallow quantum circuit implementations, while convergence to the exact ground state can be achieved with a sufficient number of layers.15,25 By exploiting orbital optimisation and an initial qubit register with alternating occupied and unoccupied spatial orbitals, the tUPS hierarchy achieves highly accurate energies for strongly correlated molecules with a significantly lower quantum-circuit cost than existing fermionic-based techniques.15
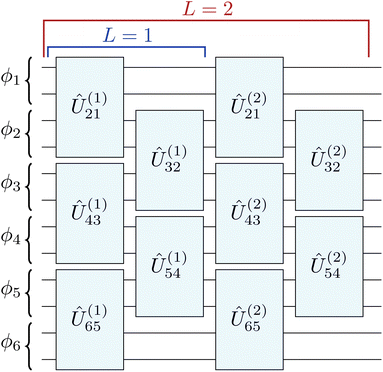 | ||
Fig. 1 Circuit structure of the tUPS ansatz.15 Each qubit encodes the occupation of a spin orbital and the qubits alternate between high- and low-spin orbitals (e.g., ϕ1ϕ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ϕ2ϕ ϕ2ϕ![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) …). …). | ||
As a new approximation, the applicability of the tUPS hierarchy for strongly correlated electronic states has not yet been fully determined. In this work, I aim to characterise the accuracy of tUPS approximations for strongly correlated model Hamiltonians, which can be tuned to control the correlation strength and to introduce different physical interactions. I consider the reduced Bardeen–Cooper–Schrieffer (BCS) picket-fence Hamiltonian for electron pairing interactions,26–29 and the two-dimensional Hubbard Hamiltonian, which models the onset of localised electrons and the metal–insulator transition.30,31 In both cases, varying the interaction strength allows the transition between weak and strong correlation to be probed, creating a challenging test bed for electronic structure techniques. Numerical results indicate that the perfect-pairing tUPS (pp-tUPS) approach is well-suited to describing strongly correlated electron localisation and repulsive pairing interactions, which are the predominant correlation mechanisms in molecular systems.
In Section 2, I review the theoretical structure and properties of the tUPS approximation. In Section 3, I present numerical calculations for the ground state of the pairing Hamiltonian and the two-dimensional Hubbard model. The key conclusions are summarised in Section 4.
2 Theory
2.1 Unitary product states
Since quantum gates correspond to unitary operations, quantum wave-function approximations can be expressed as a unitary product state (UPS) with the form25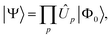 | (1) |
(i) Conserve the physical symmetries of the Hamiltonian Ĥ.
(ii) Enable any exact state to be represented.
(iii) Have a compact quantum circuit implementation.
Any Û can be expressed as the exponential of an anti-Hermitian operator exp(Â), where  = −†. Therefore, from a quantum chemistry perspective, the natural choice for elementary operators are exponential anti-Hermitian fermionic excitation operators exp(trs⋯pq⋯![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) rs⋯pq⋯),10,12 where trs⋯pq⋯ is a continuous real-valued parameter and
rs⋯pq⋯),10,12 where trs⋯pq⋯ is a continuous real-valued parameter and
![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) rs⋯pq⋯ = â†râ†sâqâp − h.c. rs⋯pq⋯ = â†râ†sâqâp − h.c. | (2) |
These operators automatically conserve the particle-number and Pauli antisymmetry. The disentangled unitary coupled-cluster (dUCC) framework shows that any electronic state can be expressed as a UPS containing all possible anti-Hermitian fermionic excitations:12
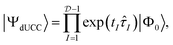 | (3) |
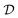 is the Hilbert space dimension, I indexes some set of particle–hole excitations, and |Φ0〉 is a reference HF state. Note that the ordering in eqn (3) is unspecified. However, this representation is impractical since the number of parameters is equal to the FCI dimensionality and higher-order many-body excitations have increasingly expensive circuit representations.4,23,24
is the Hilbert space dimension, I indexes some set of particle–hole excitations, and |Φ0〉 is a reference HF state. Note that the ordering in eqn (3) is unspecified. However, this representation is impractical since the number of parameters is equal to the FCI dimensionality and higher-order many-body excitations have increasingly expensive circuit representations.4,23,24
Eqn (3) provides a guide for new approximations that satisfy the desirable criteria for a practical quantum ansatz. Building on ref. 12, it has been shown in ref. 25 that exact wave functions can be constructed from a unitary product state
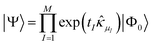 | (4) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)pq = Êpq − Êqp (1)pq = Êpq − Êqp | (5) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (2)pq = Ê2pq − Ê2qp, (2)pq = Ê2pq − Ê2qp, | (6) |
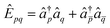 is the singlet excitation operator.32 These operators are not restricted to occupied-virtual orbital pairs, and thus correspond to generalised many-body excitations.11 Here, μI indexes the order of operators (
is the singlet excitation operator.32 These operators are not restricted to occupied-virtual orbital pairs, and thus correspond to generalised many-body excitations.11 Here, μI indexes the order of operators (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)pq or
(1)pq or ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (2)pq), which may appear multiple times in eqn (4) with unique continuous parameters. Since
(2)pq), which may appear multiple times in eqn (4) with unique continuous parameters. Since ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)pq and
(1)pq and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (2)pq are fermionic operators and commute with Ŝz and Ŝ2, any truncation of eqn (4) must conserve the particle-number and fermionic antisymmetry, and spin quantum numbers of the initial state |Φ0〉. Furthermore, any exact state can be represented for M → ∞ since all fermionic excitation operators can be expressed as a nested commutator [[[
(2)pq are fermionic operators and commute with Ŝz and Ŝ2, any truncation of eqn (4) must conserve the particle-number and fermionic antisymmetry, and spin quantum numbers of the initial state |Φ0〉. Furthermore, any exact state can be represented for M → ∞ since all fermionic excitation operators can be expressed as a nested commutator [[[![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) I,
I,![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) J],⋯],⋯] containing only
J],⋯],⋯] containing only ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)pq and
(1)pq and ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (2)pq (see ref. 12 and 25).
(2)pq (see ref. 12 and 25).
2.2 Tiled unitary product states
In practice, the accuracy of ansatzes with the form eqn (4) is highly sensitive to the choice and ordering of the exponential operators.12,13,25,33 The best ordering is system specific and currently must be identified with adaptive ansatz optimisation techniques, such as ADAPT-VQE14 or DISCO-VQE.25 Furthermore, while the quantum-circuit cost of paired two-body operators κ(2)pq is constant and small, the gate count for arbitrary κ(1)pq grows linearly with p − q.23,25To overcome these challenges, I recently introduced the fixed tiled unitary product state (tUPS) ansatz, which has a well-defined ordering of operators and a shallow quantum-circuit implementation, preserves particle-number and spin symmetry, and provides comparable accuracy to adaptive ansatz methods for strongly correlated molecules.15 The tUPS approximation is defined as a layered quantum circuit of fermionic operators that act between sequential spatial orbitals as15
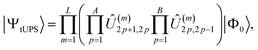 | (7) |
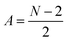 or
or 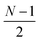 and
and 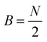 or
or 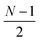 for an even or odd number of spatial orbitals N. The initial state |Φ0〉 corresponds to a single Slater determinant and the circuit structure is shown in Fig. 1. The operators Û(m)pq each contain three parameters for every layer m, defined as
for an even or odd number of spatial orbitals N. The initial state |Φ0〉 corresponds to a single Slater determinant and the circuit structure is shown in Fig. 1. The operators Û(m)pq each contain three parameters for every layer m, defined asÛ(m)pq = exp(θ(m)pq,1![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)pq)exp(θ(m)pq,2 (1)pq)exp(θ(m)pq,2![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (2)pq)exp(θ(m)pq,3 (2)pq)exp(θ(m)pq,3![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)pq) (1)pq) | (8) |
This wave-function structure is closely related to the quantum-number-preserving ansatz.34 However, the definition of Û(m)pq used here contains two one-body operators rather than one, giving more variational flexibility for strongly entangled states.15 The number of layers L provides a systematic hierarchy that converges to the exact ground state for L → ∞. Furthermore, restricting the many-body operators to sequential spatial orbitals means that the circuit cost of ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) (1)p+1,p is constant with local qubit connectivity.15
(1)p+1,p is constant with local qubit connectivity.15
Alongside the standard tUPS approach, ref. 15 also introduced an orbital-optimised variant (oo-tUPS) that significantly increases the accuracy of shallow approximations and removes the dependence on the input orbitals. This orbital optimisation can be implemented with no additional circuit cost by transforming the one- and two-electron integrals used in the energy evaluation.35–38 In ref. 15, and this work, the orbital optimisation is implemented by applying a series of one-body unitary operators after the standard tUPS circuit (see ref. 15).
The accuracy of shallow oo-tUPS approximations can be further improved by modifying the initial qubit register that represents the reference state |Φ0〉. Instead of initialising the first Nelec qubits to |1〉 and the remaining qubits to |0〉, which is analogous to the HF ground state, we can alternate the occupation of spatial orbitals to maximise the correlation captured by the first layer of operators (see Fig. 2).15 This variant is called the “perfect-pairing” tUPS (pp-tUPS) approach since the first half-layer of operators gives a circuit that is analogous to a perfect-pairing wave function.39–43 Since the pp-tUPS approach only changes the set of qubits that are initialised to |1〉, it has no additional circuit cost. The systematic hierarchy of tUPS, oo-tUPS, and pp-tUPS approximations is summarised in Fig. 3.
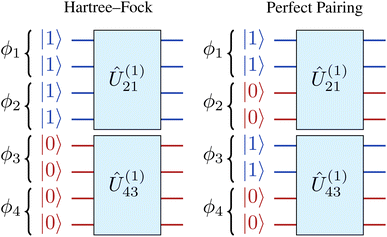 | ||
| Fig. 2 Comparison of the Hartree–Fock and perfect-pairing initial qubit registers. Reproduced from ref. 15. | ||
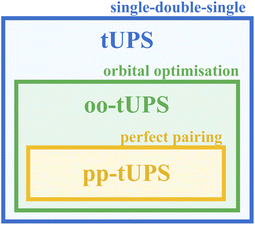 | ||
| Fig. 3 Diagrammatic illustration of the relationship between different variants of the tUPS approximation. | ||
3 Results
The aim of this work is to characterise the best-case performance of the tUPS wave-function hierarchy for strongly correlated model Hamiltonians. In particular, I consider the reduced pairing BCS Hamiltonian and a two-dimensional Hubbard model. While there can be many local minima on the corresponding variational energy landscape, we can systematically search for the global minimum using the basin-hopping global optimisation algorithm.44,45 A detailed analysis into the ease of numerical optimisation and the choice of optimiser is left for future investigations.3.1 Computational details
Classical global optimisation state-vector simulations of the variational quantum eigensolver were performed using a custom basin-hopping algorithm44,45 implemented in a developmental version of the GMIN software,46 following the procedure outlined in ref. 15. Individual energy optimisations for each basin-hopping step were performed using the L-BFGS routine (limited memory Broyden,47 Fletcher,48 Goldfarb,49 Shanno50) with a gradient root-mean-square convergence threshold of 10−5 au (arbitrary units). To maximise the efficiency of this global optimisation, the basin-hopping parallel tempering (BHPT) scheme was used,51 which performs multiple basin-hopping runs using different fictitious temperatures and allows basin-hopping trajectories to transfer between each replica. A total of 250 steps per replica were considered using 8 replicas with fictitious temperatures distributed exponentially between 10−4 au and 10−2 au. Analytic state energies and gradients (see Appendix A) were computed by representing the Hamiltonian and fermionic operators in the number- and 〈Sz〉-preserving Hilbert space using OpenFermion.523.2 Pairing Hamiltonian
I first consider the picket-fence reduced BCS Hamiltonian. Following ref. 53, the Hamiltonian is defined as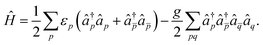 | (9) |
The single particle energies εp are equally spaced as εp = (p − 1)ε, and the separation ε is used to define the units of energy. The ratio g/ε controls the strength of pairing interactions. In this work, I consider a six-site model with six electrons.
For g = 0, the ground state reduces to the Hartree–Fock wave function. The attractive pairing regime (g > 0) leads to a non-degenerate ground state known as an extreme antisymmetrized geminal power, where each spatial orbital is equally occupied.53 This regime represents pairing interactions that arise in nuclear structure or the formation of Cooper pairs in superconductivity. In contrast, the repulsive pairing regime (g < 0) leads to a highly degenerate ground state that corresponds to a product of bonding pairs, equivalent to a generalized valence bond (GVB) state in the dissociated limit.53 While the GVB wave function provides the exact ground state for g → −∞, the intermediate pairing strengths g ∈ [−∞, 0] require a balance between a HF-like and GVB-like approximation. This regime provides a model for covalent bonds at intermediate stretching distances, which are typically the most strongly correlated points on a potential energy surface.54
The ground-state energies obtained using each tUPS variant are shown in Fig. 4. Every tUPS approximation lowers the energy with respect to the HF state, with a greater improvement for the oo- and pp-tUPS approximations. The pp-tUPS and oo-tUPS approaches provide minimal improvement over the standard tUPS approximation in the attractive regime g > 0, with L = 3 required to reach near-exact energies using all variants. In contrast, for the repulsive regime (g < 0), the pp-tUPS state is essentially exact with L = 1, while the oo-tUPS and tUPS approximations require L = 2 and 3, respectively, to provide comparable accuracy.
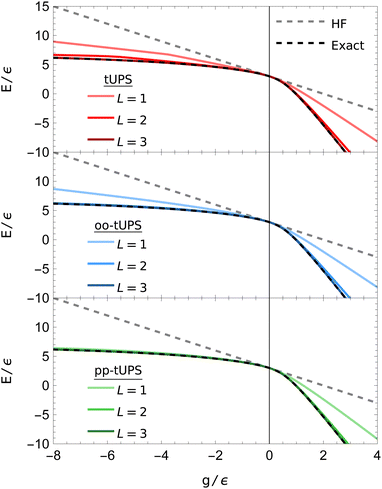 | ||
| Fig. 4 Ground-state tUPS energies for the six-site pairing Hamiltonian [eqn (9)] with six electrons. The pp-tUPS state provides high accuracy with L = 1 for the repulsive regime (g < 0), while all tUPS variants provide comparable accuracy for the attractive regime (g > 0). | ||
The contrasting accuracy for the repulsive and attractive regimes is highlighted in Fig. 5, where the amount of correlation energy captured as the number of layers increases is compared for g = −6ε (solid) and 4ε (dashed). For g = −6ε, the pp-tUPS approach captures a remarkable 96.2% of the correlation energy with L = 1, and 99.5% with L = 2. These data demonstrate the ability of the pp-tUPS approximation to efficiently represent a product of strongly-coupled electron pairs, which is the prevailing correlation mechanism in molecular dissociation.54
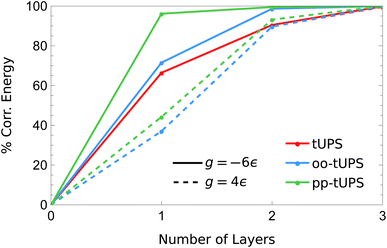 | ||
| Fig. 5 Fraction of the correlation energy for the 6-site pairing Hamiltonian [eqn (9)] captured by each tUPS variant with increasing L in the g < 0 and g > 0 regimes. At g = 4ε, the tUPS and oo-tUPS energies are essentially equivalent. | ||
3.3 Two-dimensional Hubbard model
The Hubbard model is an archetypal example of strong electron correlation and has been extensively used to test the performance of many-body approximations. The Hamiltonian is parametrised in terms of the one-body hopping t between connected sites and the on-site electron repulsion U as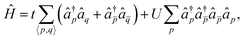 | (10) |
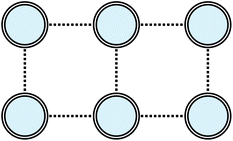
Here, I consider a non-periodic square two-dimensional 3 × 2 Hubbard lattice with six electrons, as illustrated in Fig. 6. Ground-state energies computed with the various tUPS formalisms are shown in Fig. 7, alongside the HF and exact energies. For the standard tUPS approximation, we see that the accuracy progressively improves as the number of layers is increased, but there is still an appreciable error for L = 3. In contrast, incorporating orbital optimisation in the oo-tUPS approach leads to near-exact results for L = 2. Finally, the pp-tUPS approximation with L = 1 provides very accurate energies for all U/t considered here, demonstrating its ability to efficiently capture the strongly correlated antiferromagnetic ground state.
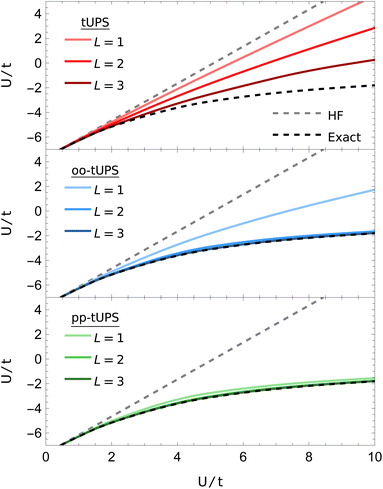 | ||
| Fig. 7 Ground-state tUPS energies for the 3 × 2 Hubbard Hamiltonian [eqn (10)]. The pp-tUPS state provides high accuracy with L = 1 across all correlation strengths U/t. | ||
In Fig. 8, I compare the systematic improvement of tUPS variants with an increasing number of layers for the weakly and strongly correlated regimes with U = 1t and 10t, respectively. Notably, the oo-tUPS and pp-tUPS formalisms become more efficient at capturing the correlation energy for large U/t, while the standard tUPS approximation is less efficient. This feature demonstrates the significant advantage of incorporating orbital optimisation in the wave-function approximation. Remarkably, at U = 10t, the pp-tUPS approach captures 97.3% of the correlation energy with L = 1, which rises to 99.5% with L = 2. These data highlight that the pp-tUPS approximation is well-suited to capturing strong correlation associated with electron localisation, as found in Mott insulators and dissociated hydrogen clusters.
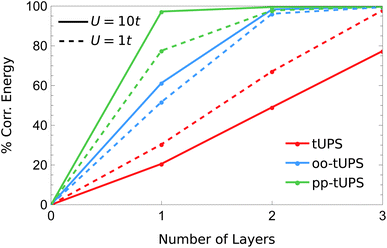 | ||
| Fig. 8 Fraction of the correlation energy for the 3 × 2 Hubbard Hamiltonian [eqn (10)] captured by the different tUPS variants with increasing L in the weakly and strongly correlated regimes. | ||
4 Concluding remarks
In this work, I have investigated the performance of the tUPS ansatz hierarchy for the strongly correlated pairing and Hubbard Hamiltonians. The pp-tUPS approximation provides quantitative accuracy for repulsive pairing interactions and strong electron localisation with remarkably shallow quantum circuits, in agreement with previous results for molecular systems.15 Furthermore, these results reinforce the advantages of orbital optimisation for maximising the accuracy of shallow quantum circuits. On the other hand, the tUPS ansatz hierarchy performs relatively poorly for the attractive pairing Hamiltonian. We can expect geminal-based methods to be more suitable in these scenarios.20,21 This observation indicates that the tUPS hierarchy is not universally accurate for any quantum system, but it is tailored to the dominant electronic interactions in molecular systems.Finally, the two current computational studies on the tUPS ansatz hierarchy (this work and ref. 15) have only considered the best energy that can be achieved. The practical applicability of these high-accuracy wave functions will depend critically on the efficiency of numerical optimisation. It is known that variational quantum algorithms can have many local minima and slow numerical convergence.13,55–58 Assessing the presence or severity of these issues for the tUPS hierarchy is therefore a priority for future investigations.
Conflicts of interest
There are no conflicts to declare.Appendix A
Analytic energy and gradient expressions
Consider a wave function defined with an ordered set of M operators μ and continuous parameters t as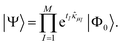 | (11) |
The variational energy is given by the expectation value
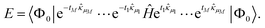 | (12) |
All variants of the tUPS ansatz can be expressed in this form. Since only real-valued operators, Hamiltonians, and coordinates are considered, the analytic energy gradients are given by
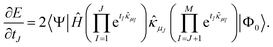 | (13) |
These gradient expressions can be efficiently evaluated using the algorithm described in the ESI of ref. 14.
Acknowledgements
H. G. A. B. gratefully acknowledges financial support from Downing College, Cambridge, through the Kim and Julianna Silverman Research Fellowship. The author thanks Paul Johnson for inspiring discussions on the pairing Hamiltonian.References
- J. Čížek, J. Chem. Phys., 1966, 45, 4256 CrossRef.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157 CrossRef CAS.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Rev. Mod. Phys., 2020, 92, 15003 CrossRef CAS.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth and J. Tennyson, Phys. Rep., 2022, 986, 1 CrossRef.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Chem. Rev., 2019, 119, 10856 CrossRef CAS PubMed.
- P. Jordan and E. Wigner, Z. Phys., 1928, 47, 631 CrossRef CAS.
- E. Wigner, Phys. Rev., 1934, 46, 1002 CrossRef CAS.
- A. Peruzzo, J. McClean, P. Shadbolt, M. H. Yung, X. Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- A. Anand, P. Schleich, S. Alperin-Lea, P. W. K. Jensen, S. Sim, M. Díaz-Tinoco, J. S. Kottmann, M. Degroote, A. F. Izmaylov and A. Aspuru-Guzik, Chem. Soc. Rev., 2022, 51, 1659 RSC.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, J. Chem. Theory Comput., 2019, 15, 311 CrossRef CAS PubMed.
- F. A. Evangelista, G. K.-L. Chan and G. E. Scuseria, J. Chem. Phys., 2019, 151, 244122 CrossRef PubMed.
- H. R. Grimsley, D. Claudino, S. E. Economou, E. Barnes and N. J. Mayhall, J. Chem. Theory Comput., 2020, 16, 1 CrossRef CAS PubMed.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, Nat. Commun., 2019, 10, 3007 CrossRef PubMed.
- H. G. A. Burton, Phys. Rev. Res., 2024, 6, 023300 CrossRef.
- Y. S. Yordanov, V. Armaos, C. H. W. Barnes and D. R. M. Arvidsson-Shukur, Commun. Phys., 2021, 4, 228 CrossRef.
- I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, J. Chem. Phys., 2018, 149, 214105 CrossRef PubMed.
- I. G. Ryabinkin, T.-C. Yen, S. N. Genin and A. F. Izmaylov, J. Chem. Theory Comput., 2018, 14, 6317 CrossRef CAS PubMed.
- R. Xia and S. Kais, Quantum Sci. Technol., 2021, 6, 015001 CrossRef.
- A. Khamoshi, F. A. Evangelista and G. E. Scuseria, Quantum Sci. Technol., 2021, 6, 014004 CrossRef.
- A. Khamoshi, G. P. Chen, F. A. Evangelista and G. E. Scuseria, Quantum Sci. Technol., 2023, 8, 015006 CrossRef.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242 CrossRef CAS PubMed.
- Y. S. Yordanov, D. R. M. Arvidsson-Shukur and C. H. W. Barnes, Phys. Rev. A, 2020, 102, 062612 CrossRef CAS.
- I. Magoulas and F. A. Evangelista, J. Chem. Theory Comput., 2023, 19, 822 CrossRef CAS PubMed.
- H. G. A. Burton, D. Marti-Dafcik, D. P. Tew and D. J. Wales, npj Quantum Inf., 2023, 9, 75 CrossRef.
- R. W. Richardson, Phys. Rev., 1966, 141, 949 CrossRef CAS.
- R. W. Richardson, Phys. Lett., 1963, 3, 277 CrossRef.
- R. W. Richardson and N. Sherman, Nucl. Phys., 1964, 52, 221 CrossRef.
- R. W. Richardson, J. Math. Phys., 1965, 6, 1034 CrossRef.
- J. Hubbard, Proc. R. Soc. London, Ser. A, 1963, 276, 238 Search PubMed.
- J. E. Hirsch, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 4403 CrossRef PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, John Wiley & Sons, 2000 Search PubMed.
- A. F. Izmaylov, M. Díaz-Tinoco and R. A. Lang, Phys. Chem. Chem. Phys., 2020, 22, 12980 RSC.
- G.-L. R. Anselmetti, D. Wierichs, C. Gogolin and R. M. Parrish, New J. Phys., 2021, 23, 113010 CrossRef CAS.
- W. Mizukami, K. Mitarai, Y. O. Nakagawa, T. Yamamoto, T. Yan and Y. Ya Ohnishi, Phys. Rev. Res., 2020, 2, 033421 CrossRef CAS.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, J. Chem. Phys., 2020, 152, 124107 CrossRef CAS PubMed.
- J. Bierman, Y. Li and J. Lu, J. Chem. Theory Comput., 2023, 19, 790 CrossRef CAS PubMed.
- L. Zhao, J. Goings, K. Shin, W. Kyoung, J. I. Fuks, J.-K. K. Rhee, Y. M. Rhee, K. Wright, J. Nguyen, K. Kim and S. Johri, npj Quantum Inf., 2023, 9, 60 CrossRef.
- A. C. Hurley, J. E. Lennard-Jones and J. A. Pople, Proc. R. Soc. London, Ser. A, 1953, 220, 446 CAS.
- W. J. Hunt, P. J. Hay and W. A. Goddard III, J. Chem. Phys., 1972, 57, 738 CrossRef.
- S. Lehtola, J. Parkhill and M. Head-Gordon, Mol. Phys., 2018, 116, 547 CrossRef CAS.
- T. Van Voorhis and M. Head-Gordon, J. Chem. Phys., 2000, 112, 5633 CrossRef CAS.
- G. J. O. Beran, B. Austin, A. Sodt and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 9183 CrossRef CAS PubMed.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U.S.A., 1987, 84, 6611 CrossRef CAS PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111 CrossRef CAS.
- GMIN: A program for finding global minima and calculating thermodynamic properties, http://www-wales.ch.cam.ac.uk/software.html.
- C. G. Broyden, IMA J. Appl. Math., 1970, 6, 76 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647 CrossRef.
- B. Strodel, J. W. L. Lee, C. S. Whittleston and D. J. Wales, J. Am. Chem. Soc., 2010, 132, 13300–13312 CrossRef CAS PubMed.
- J. R. McClean, N. C. Rubin, K. J. Sung, I. D. Kivlichan, X. Bonet-Monroig, Y. Cao, C. Dai, E. S. Fried, C. Gidney, B. Gimby, P. Gokhale, T. Häner, T. Hardikar, V. Havlíček, O. Higgott, C. Huang, J. Izaac, Z. Jiang, X. Liu, S. McArdle, M. Neeley, T. O’Brien, B. O’Gorman, I. Ozfidan, M. D. Radin, J. Romero, N. P. D. Sawaya, B. Senjean, K. Setia, S. Sim, D. S. Steiger, M. Steudtner, Q. Sun, W. Sun, D. Wang, F. Zhang and R. Babbush, Quantum Sci. Technol., 2020, 5, 034014 CrossRef.
- P. A. Johnson, arxiv, 2023, preprint, arxiv:2312.08804 DOI:10.48550/arXiv.2312.08804.
- D. Marti-Dafcik, N. Lee, H. G. A. Burton and D. P. Tew, arxiv, 2024, preprint, arxiv:2402.08858 DOI:10.48550/arXiv.2402.08858.
- B. Choy and D. J. Wales, J. Chem. Theory Comput., 2023, 19, 1197 CrossRef CAS PubMed.
- B. Choy and D. J. Wales, Phys. Rev. A, 2024, 109, 062602 CrossRef.
- M. Cerezo, A. Sone, T. Volkoff, L. Cincio and P. J. Coles, Nat. Commun., 2021, 12, 1791 CrossRef CAS PubMed.
- L. Bittel and M. Kliesch, Phys. Rev. Lett., 2021, 127, 120502 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |