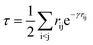Open Access Article
Open Access ArticleStriking the right balance of encoding electron correlation in the Hamiltonian and the wavefunction ansatz
Kalman
Szenes
 ,
Maximilian
Mörchen
,
Maximilian
Mörchen
 ,
Paul
Fischill
and
Markus
Reiher
,
Paul
Fischill
and
Markus
Reiher
 *
*
Department of Chemistry and Applied Biosciences, ETH Zürich, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: mreiher@ethz.ch
First published on 3rd May 2024
Abstract
Multi-configurational electronic structure theory delivers the most versatile approximations to many-electron wavefunctions, flexible enough to deal with all sorts of transformations, ranging from electronic excitations, to open-shell molecules and chemical reactions. Multi-configurational models are therefore essential to establish universally applicable, predictive ab initio methods for chemistry. Here, we present a discussion of explicit correlation approaches which address the nagging problem of dealing with static and dynamic electron correlation in multi-configurational active-space approaches. We review the latest developments and then point to their key obstacles. Our discussion is supported by new data obtained with tensor network methods. We argue in favor of simple electron-only correlator expressions that may allow one to define transcorrelated models in which the correlator does not bear a dependence on molecular structure.
1 Introduction
Closed-shell molecules can be described by a single reference determinant (the Hartree–Fock determinant) and single-reference coupled cluster (CC) theory then yields reliable results which can be systematically improved.1 Standard CC models2,3 are available for reliable calculations of chemical accuracy, and higher accuracy can be achieved by increasing the excitation rank of the cluster operator. Complicated electronic structures, such as those found in open-shell transition metal complexes and clusters, unsaturated molecules, and biradicals, require a different ansatz. In such systems, the Hartree–Fock determinant will not dominate the determinantal expansion of the electronic wavefunction and, hence, single-reference approaches based on it are likely to break down.Multi-configurational wavefunction methods usually start from (complete) active orbital spaces and deliver a qualitatively correct description of the valence shell of electronic states and are, therefore, the standard starting point for tackling challenging electronic structure problems. However, this ansatz introduces by definition an imbalance in the description of electron correlation due to the resulting (somewhat arbitrary) separation of electron correlation into static and dynamic contributions within and outside the active orbital space chosen. Therefore, a holy grail in electronic structure theory has been the accurate calculation of electronic energies in such composite approaches for static and dynamic electron correlation, as they eventually produce unbalanced error contributions.
Active space methods rely on the restriction of the orbital space in which a full configuration interaction (FCI) wavefunction is then constructed (the classic example is the complete active space (CAS)4,5 or full optimized reaction space6 ansatz). However, the orbitals that are ignored in such a CAS-CI ansatz, significantly contribute to the electronic energy, which cannot be ignored.
To include such dynamic correlations,7 CC approaches are the natural choice to turn to. However, multi-reference CC ansätze are plagued by various formal and practical limitations: the multiple-parentage problem, intruder states,8–11 lack of orbital invariance, increased scaling with the active space size,12 or non-truncating cumulant expansion.13–15 Even though most of these drawbacks can be circumvented by the multi-reference formulation of configuration interaction, this approach requires expensive higher-order density matrices and, due to its truncated CI expansion, suffers from size-consistency issues, as does the truncated single-reference CI.16,17 For an in-depth description of multi-reference methods, see ref. 16 and 17.
As a result, various other approaches have been designed to assess dynamic correlation for multi-configurational methods; examples are, multi-reference perturbation theories,18–20 short-range density functional theory,21–26 multi-configurational pair-density functional theory approaches,27,28 and multi-reference-driven single-reference CC models (see for example ref. 29–37). We note also that much work aimed to describe both static and dynamic correlation accurately in the CC framework alone; see, for instance, CC approaches with internal and semi-internal excitations,30,38 method-of-moments CC,39–41 and CC(P;Q).42–46 For further CC-based methods that aim to describe both static and dynamic correlation, see ref. 47 and references therein.
In the end, multi-configurational methods require a combined approach, which treats dynamic correlation on a different footing, compromising the overall accuracy. As a result, no multi-configurational approach is known to achieve a consistent and systematically improvable accuracy as the single-reference CC model does. Therefore, it is highly desirable to establish a formal theory that can address and eventually solve this problem. Here, we consider explicitly correlated ansätze as a possible solution to the problem. Many ideas have already been put forward, and remarkable successes have been achieved (especially when considering developments in explicitly correlated CC models48–51). However, no universal framework has emerged, and various conceptual problems remain open or, at least, require further discussion. Therefore, we first prepare a general formal framework for these approaches. Then, we highlight features of the various proposals made in the context of explicit correlation theory so far, discuss key challenges, and provide new data to substantiate these challenges. After this analysis, we settle on basic principles that could be considered universally valid for explicit correlation approaches.
2 Theory
2.1 General theory
Under the Born–Oppenheimer approximation, the most general expression for the electronic Hamiltonian Ĥel may be written in first quantization for Nel electrons as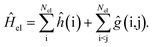 | (1) |
The terms ĥ(i) and ĝ(i, j) correspond to the one- and two-electron operators, respectively. The operator ĥ(i) comprises the electronic kinetic energy operator, which may be chosen according to Dirac or in its non-relativistic limit according to Schrödinger for infinite speed of light,52 and the external potential created by the nuclei. For the sake of simplicity, we omitted the nucleus–nucleus interaction, which contributes a constant term in the Born–Oppenheimer approximation and can be added at any later stage.
The two-electron operator ĝ(i, j) describes the electron–electron interaction. Its leading term is the electrostatic Coulomb interaction of the electrons. In the non-relativistic limit of Schrödinger quantum mechanics, this will be the only contribution. Magnetic and retardation effects contribute to higher order in the inverse speed of light 1/c. They can be taken into account to order 1/c2 by Gaunt and Breit operators, containing the inverse of the particles’ distance (as in the case of the Coulomb interaction) and even up to the inverse distance cubed in the case of the second term of the Breit operator. We note that interactions involving the nuclei are also affected by magnetic and retardation effects, which are usually negligible.
Whichever of these models is chosen for Ĥel, already the Coulomb potential generates singularities in the operator at the coalescence of two or more particles. This property leads to well-known coalescence conditions53–55 in the exact wavefunction which are notoriously challenging to describe by conventional orbital-based wavefunction ansätze. This is due to the need for high angular momentum basis functions in order to capture the linear behavior of the wavefunction in the neighborhood of the point of coalescence of two particles.56 For the purpose of this article, we will restrict ourselves to the standard model, the electrostatic Coulomb interaction.
The central problem in electronic structure theory is obtaining the solutions to the electronic-structure eigenvalue problem for some electronic state ψi
| Ĥelψi = Eiψi. | (2) |
The solutions to the previous equation can be factorized57 as
| ψi = Fϕi | (3) |
2.2 Cusp conditions
In the seminal work by Kato,53 the analytic behavior of the exact electronic wavefunction in the vicinity of particle coalescence was derived, leading to the cusp conditions that bear his name. Subsequently, these results were extended54 by relaxing the fixed-nuclei assumption and deriving coalescence conditions for wavefunctions that contain a node at the point of coalescence. Later, Fournais and collaborators57 introduced three-particle (electron–electron–nuclear) coalescence conditions and proved not only that the universal state independent factor F from eqn (3) exists such that ϕi has continuous first-order derivatives, but also determined its explicit form. Additionally, Tew55 derived higher-order coalescence conditions in the inter-particle distance and showed that these terms introduce system and state-dependent coefficients.The cusp conditions may be classified by the type and number of particles coalescing.
Precisely describing this cusp in the wavefunction is crucial for computing the total energy to high accuracy. However, in the Born–Oppenheimer approximation, errors in the electronic wavefunction at the nuclei are atomically conserved across the potential energy surface as long as one is interested in the valence-shell properties of atoms, molecules, and materials. Therefore, these errors can be expected to cancel when properties, such as energy differences or derivatives, are considered. As an example, we may refer to comparisons of energies obtained for point-like and finite-size nuclei. Both types of nuclear charge distribution models influence the wavefunction in profoundly different ways at electron–nucleus coalescence points,52 which significantly affects, in turn, total energies but leaves relative energies essentially unchanged (see, for example, ref. 58).
We emphasize that the Coulomb singularities arise solely from point particles. By considering finite-size nuclear charge distribution models,59 which is particularly important for large nuclei, the electron–nucleus cusps may be entirely eliminated (although a steep increase of the wavefunction, and hence of the electron density, in the vicinity of atomic nuclei will still be observed).
It is for this reason that we ignore electron–nucleus cusps in this work. This assumption will not hold, however, if we consider properties that probe electron density close to the nucleus, as in the case of the isomer shift of Mössbauer spectroscopy.60 In addition, by assuming the nuclei to be static, the location of these cusps is known a priori, and therefore, atom-centered one-electron basis functions may be employed that explicitly satisfy the cusp condition. This is the case for Slater orbitals,61 and techniques have been devised that also augment existing Gaussian basis sets with this property.62
The electronic coalescence conditions are generally classified into either singlet or triplet, depending on whether the spin function of the considered pair of electrons is symmetric or not with respect to their permutation. For singlet electron pairs, which have antisymmetric spin functions, the cusp condition enforces the following form on the exact wavefunction53
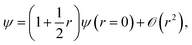 | (4) |
For triplet pairs, the exact wavefunction vanishes at the point of coalescence. Moreover, it possesses continuous first-order derivatives, and the cusp only appears in the second-order derivative.54 The exact wavefunction, therefore, obeys a different condition
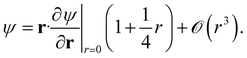 | (5) |
A consequence of this property is that certain states, such as high-spin open-shell systems, do not possess electronic cusps in the wavefunction (only in their derivative).
2.3 Cusp conditions and correlators
Next, it is key to consider how the coalescence conditions affect the choice of the correlator F in general. For this purpose, we revisit in more detail the analytic form of F derived by Fournais et al.57 Assuming an exponential form F = eτ for the ansatz in eqn (6), Fournais and collaborators derived that τ should be composed of three types of terms55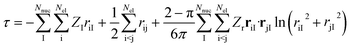 | (6) |
In light of the discussion so far, we argue for omitting the first term, i.e., the one taking care of all electron–nucleus cusps, since we maintain that, although its effect on the total electronic energy may be non-negligible, it introduces an atomically conserved error that drops out for relative electronic energies dominated by changes in the valence region of atoms and molecules. For similar reasons, although the three-particle term has been shown to also have a visible effect on the total electronic energy (see ref. 65 for numerical data and also for a historical perspective on this contribution), we argue that this effect is not likely to be strong for relative properties dominated by valence-shell contributions. Therefore, we contend that its omission will also benefit from systematic error cancellation. We note, however, that correlators that include terms of the first type have been employed recently in the context of transcorrelated multi-reference theories63,64 (see also below).
We highlight that eqn (6) inherently introduces system-dependent quantities into the correlator through the presence of the nuclear positions and charges. However, neglecting the first and third terms removes all system dependence of the correlator and requires the remainder of the wavefunction, that is, ϕi, of eqn (6) to take care of the system- and state-dependence. Note that Tew55 explicitly derived the system- and state-dependence for a spherical model of a particle’s wavefunction around a coalescence point in the form of higher-order expansion coefficients in the partial wave expansion. However, these results are not directly transferable to the product ansatz of eqn (6) that we exploit in this work.
For these reasons, we here advocate for the use of a simple correlation factor, which may be taken to be universal, state- and system-independent, in order to define a comparatively simple yet (for valence-shell dominated relative energies and properties) accurate, explicitly correlated electronic structure method. Hence, the remaining term responsible for the electron–electron cusp is considered the only essential term in eqn (6) for an electronic structure model defined within the Born–Oppenheimer approximation.
2.4 Energy evaluation with correlators
It is well established that the description of the cusp is the dominating cause of the slow convergence of standard ab initio methods with increasing size of one-electron (orbital) basis sets.56 The fact that the wavefunctions may be factorized as in eqn (3), with the function ϕi being smooth and devoid of cusps, lends it to easier treatment by conventional one-particle Gaussian basis sets.By choosing the function F such that the cusp conditions are obeyed, eqn (3) may be employed as an ansatz for the wavefunction. Placing this ansatz into the eigenvalue problem in eqn (2) yields
| ĤelF|ϕ〉 = EF|ϕ〉. | (7) |
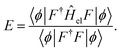 | (8) |
The parameters in |ϕ〉 may be optimized variationally, and the obtained energy will always yield an upper bound on the exact value. Unfortunately, this expression requires the evaluation of Nel-electron integrals,66 which makes it intractable for even the smallest of systems.
An alternative expression for the energy may be obtained through projection onto 〈ϕ|F−1
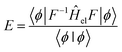 | (9) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = F−1ĤelF corresponds to a similarity transformation of the operator Ĥel by the correlator F. This transformation has the property of preserving the spectrum of the original operator, as it can be interpreted as a change of basis. However, the operator
= F−1ĤelF corresponds to a similarity transformation of the operator Ĥel by the correlator F. This transformation has the property of preserving the spectrum of the original operator, as it can be interpreted as a change of basis. However, the operator ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) is no longer necessarily Hermitian, and thus eqn (9) is not bound from below;67 preventing the use of variational techniques for optimizing |ϕ〉.
is no longer necessarily Hermitian, and thus eqn (9) is not bound from below;67 preventing the use of variational techniques for optimizing |ϕ〉.
The two equations for the energy seem quite similar, and one might ask how they are related. A first observation is that, if the operator F is unitary (i.e., F−1 = F†), the two expressions coincide. Moreover, unitary transformations preserve the norm of vectors, and therefore, by assuming a normalized |ϕ〉, the term in the denominator vanishes
| E = 〈ϕ|F†ĤelF|ϕ〉. | (10) |
As a comment, we recall that certain properties of operators no longer hold once these operators are projected on a finite basis, as done in the second quantization formalism. For instance, projecting two operators into a finite basis and taking their matrix product is not necessarily equal to the product of the two operators projected into the same basis.1 This has the consequence that the similarity transformed operator in eqn (9) is only guaranteed to have the same spectrum as the original operator in the limit of a complete basis.
2.5 Similarity transformation in coupled cluster theory
A similarity transformation of the Hamiltonian is also at the heart of CC theory, which employs an exponential ansatz for the wavefunction|ψ〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |ϕ〉 |ϕ〉 | (11) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) = = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 + 1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 + … 2 + … | (12) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) i are the standard i-fold excitation operators parameterized with unknown amplitudes tia, tijab, …. These amplitudes are determined iteratively by solving the CC equations, which project the Schrödinger equation onto the excited determinants 〈ψμ|
i are the standard i-fold excitation operators parameterized with unknown amplitudes tia, tijab, …. These amplitudes are determined iteratively by solving the CC equations, which project the Schrödinger equation onto the excited determinants 〈ψμ|0 = 〈ψμ|e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥele Ĥele![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |ϕ〉. |ϕ〉. | (13) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = e−
= e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥele
Ĥele![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . Once the amplitudes have converged, the electronic energy may be computed through
. Once the amplitudes have converged, the electronic energy may be computed throughECC = 〈ϕ|![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) |ϕ〉. |ϕ〉. | (14) |
For simplicity, consider a two-electron system for which the CCSD (![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 +
1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2) method delivers the exact solution. Eqn (13) and (14) may be combined into a matrix equation which, for converged amplitudes, has the following structure
2) method delivers the exact solution. Eqn (13) and (14) may be combined into a matrix equation which, for converged amplitudes, has the following structure
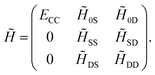 | (15) |
The first column corresponds to the CC energy and amplitude equations, while the other elements correspond to the remaining transformed matrix elements of Ĥel. Note that the structure of the first column guarantees that the reference wavefunction is an eigenfunction of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) . Hence, CC can be interpreted as optimizing the cluster amplitudes such that the reference wavefunction, corresponding to the first column, becomes an eigenvector of the similarity-transformed Hamiltonian
. Hence, CC can be interpreted as optimizing the cluster amplitudes such that the reference wavefunction, corresponding to the first column, becomes an eigenvector of the similarity-transformed Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) . By recalling that |ϕ〉 is usually taken as the Hartree–Fock determinant, which only accounts for mean-field interactions, the similarity transformation has effectively transferred all electronic correlation directly into the operator
. By recalling that |ϕ〉 is usually taken as the Hartree–Fock determinant, which only accounts for mean-field interactions, the similarity transformation has effectively transferred all electronic correlation directly into the operator ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) .
.
In CC theory, the amplitudes may also be obtained variationally68 through the use of a symmetric expectation value
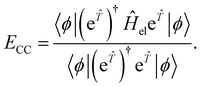 | (16) |
This expression, however, is not used in practice since it does not benefit from the natural truncation of the Taylor expansion of the transformed operator and therefore, the evaluation of eqn (16) requires the computation of matrix elements between determinants of arbitrary excitation rank, making the expression exponentially difficult to evaluate, even for truncated ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . A noteworthy exception is unitary-CC
. A noteworthy exception is unitary-CC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 (UCC) in quantum computing70 since unitary gates may be directly implemented on quantum hardware. In UCC, a similar expression to eqn (16) is used, where the cluster operator
69 (UCC) in quantum computing70 since unitary gates may be directly implemented on quantum hardware. In UCC, a similar expression to eqn (16) is used, where the cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is replaced by an anti-Hermitian operator
is replaced by an anti-Hermitian operator ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −
− ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) † which results in a unitary similarity transformation; preserving the Hermiticity of the original operator.
† which results in a unitary similarity transformation; preserving the Hermiticity of the original operator.
The inadequacies of eqn (16) seem analogous with the ones discussed in Section 2.4 with the correlator F being given by the cluster operator e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . A crucial difference is, however, that in the case of CC theory, the excitation operators
. A crucial difference is, however, that in the case of CC theory, the excitation operators ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) are assumed to be restricted to creating excited determinants in the same Hilbert space as the one spanned by the one-particle basis. Therefore, ECC can, at best, converge to the FCI solution contained in the finite Hilbert space. This restriction is generally not true for an arbitrary correlator F defined in real space. In particular, when the correlator is expressed in real space, the excitations are inevitably produced in orbitals that are not contained in the one-particle basis, and hence, the computed energies may even improve upon the FCI solution in that finite space.
are assumed to be restricted to creating excited determinants in the same Hilbert space as the one spanned by the one-particle basis. Therefore, ECC can, at best, converge to the FCI solution contained in the finite Hilbert space. This restriction is generally not true for an arbitrary correlator F defined in real space. In particular, when the correlator is expressed in real space, the excitations are inevitably produced in orbitals that are not contained in the one-particle basis, and hence, the computed energies may even improve upon the FCI solution in that finite space.
While it is sometimes stated that the non-variational nature of the standard CC energy is due to the similarity transformation only being approximate71 – mirroring the conclusions from the last paragraph of Section 2.4 – in reality the similarity transformation is always exact, in the sense that no matter what amplitudes are inserted into the cluster operator, the spectra of the matrix representation of Ĥel and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) always coincide. The non-variationality of the scheme actually occurs due to the eigenvalue of
always coincide. The non-variationality of the scheme actually occurs due to the eigenvalue of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) only being calculated approximately. For instance, in a four-electron system, if eqn (13) is only solved using CCSDT, the resulting matrix representation would have the form
only being calculated approximately. For instance, in a four-electron system, if eqn (13) is only solved using CCSDT, the resulting matrix representation would have the form
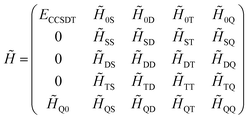 | (17) |
In this case, the reference wavefunction is only an approximate eigenvector of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) , and if the eigenvector was computed exactly by also projecting on the quadruply excited determinants, the energy would be equal to the energy computed from Ĥel.
, and if the eigenvector was computed exactly by also projecting on the quadruply excited determinants, the energy would be equal to the energy computed from Ĥel.
2.6 Choice of the correlator
While the goal is to select the correlator F such that the remaining function ϕ is smooth, there still remains significant freedom in the choice of its explicit form. The remainder of this section is dedicated to an overview of the general class of correlators that have been applied to chemical systems.Subsequently, the class of R12 methods has been extended to accommodate correlators depending non-linearly on rij, which are commonly referred to as F12 methods.75 Examples of correlators used in F12 methods include Gaussian-type Geminals76 e−γrij2 and Slater-type Geminals77 e−γrij. Most of these correlators possess a number of free parameters which must be adjusted for the target system. Some contain a single tunable parameter78 while others are composed of a handful of parameters79 whose optimal values may be deduced based on first principles. In the context of Monte Carlo methods,80–83 flexible correlators are often used, which contain dozens of free parameters that are optimized in a black-box fashion using variance minimization techniques.84 A comparison of the performance of a large set of commonly used correlators can be found in ref. 85 and 86.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88 and FCIQMC.89 Different approaches exist to apply Gutzwiller-like correlators to molecular systems,90,91 as well as approaches based on similarity transformation92–94 of the Hamiltonian with the correlator. However, since this correlator acts in Hilbert space, the correlated and uncorrelated wavefunctions converge to the same FCI energy.
88 and FCIQMC.89 Different approaches exist to apply Gutzwiller-like correlators to molecular systems,90,91 as well as approaches based on similarity transformation92–94 of the Hamiltonian with the correlator. However, since this correlator acts in Hilbert space, the correlated and uncorrelated wavefunctions converge to the same FCI energy.
3 Transcorrelation
In the transcorrelated method,66,96 the conventional electronic Hamiltonian Ĥel is similarity transformed by the correlation factor eτ| Ĥtc = e−τĤeleτ | (18) |
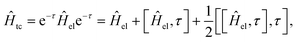 | (19) |
First, while the second nested commutator preserves the Hermiticity of the original operator, the first one introduces a non-Hermitian contribution, which prevents the use of optimization techniques relying on the variational principle. This is because, for non-Hermitian operators, the left and right eigenvectors do not generally coincide, and thus, the conventional Rayleigh quotient for computing eigenvectors no longer applies. This issue may, however, be tackled by employing a biorthogonal approach, which allows for distinct left and right eigenvectors and has successfully been applied to the transcorrelated method.97–101 Moreover, this approach provides a framework for performing orbital optimization within the transcorrelated method.64,102 Efforts have also been made to apply the variational principle directly to the transcorrelated method by disregarding the non-Hermitian terms103,104 in Ĥtc.
Second, the nested commutator introduces a three-body operator, which significantly increases the computational cost of the transcorrelated method compared to the conventional two-body electronic Hamiltonian.
Finally, both additional terms introduce non-standard integrals, which need to be evaluated, as is the case for F12 methods. Approaches for computing these integrals include grid-based methods,63,105 density-fitting techniques106,107 and Monte Carlo approaches.108
The addition of the three-body operator in Ĥtc from the third term in eqn (19), poses a significant challenge for the transcorrelated approach due to the steep increase in required storage for the generated integrals as well as the computational cost of working with them. For instance, in the case of DMRG, the three-body contribution increases the computational cost of the tensor contractions by two orders of magnitude.107 Recently, a promising remedy109–111 for taming the expensive three-body operator has emerged. It is based on the normal-ordering of the operators in Ĥtc with respect to a reference state, usually chosen as the Hartree–Fock solution following the particle-hole formalism. This allows one to include the mean-field, one- and two-body contribution from the three-body operator and leaves a “pure” three-body contribution, which is presumed to be small so that it may be neglected. The validity of this approximation has been demonstrated111 on a set of atoms and small molecules contained in the HEAT112 benchmark dataset.
The transcorrelated method has a number of advantages over other explicitly correlated methods. First, using a projective technique to solve for the energy, the cusp conditions may be satisfied while limiting the required integrals to at most three-electron ones. Second, by directly folding the correlation into the Hamiltonian, through the similarity transformation, and optimizing the wavefunction with this transformed operator, the correlation captured by the determinantal expansion is guaranteed to not overlap with the one already accounted for by the correlator.63 Indeed, to ensure this property for R12/F12 methods, orthogonality conditions113,114 need to be enforced in order to guarantee that the correlator generates excitations outside the Hilbert space spanned by the finite basis. This formalism is quite cumbersome and usually limits the flexibility of correlators to simple functions.63
3.1 Transcorrelated density matrix renormalization group (tcDMRG)
Recently, the transcorrelated method has been adapted to the density matrix renormalization group (DMRG)115 first through the imaginary-time evolution formalism88,107 and subsequently using the time-independent optimization scheme.116 This section reviews key aspects of the imaginary-time evolution variant of tcDMRG developed in our group.88,107In the matrix product operator (MPO) formalism117,118 of DMRG, a matrix product state (MPS) represents the ansatz for the wavefunction
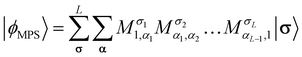 | (20) |
The maximum values of the auxiliary indices αi introduced in the factorization are given by the bond dimension. The bond dimension is the key parameter for determining the accuracy and cost of the DMRG algorithm.119 For the exact FCI solution, the extent of the indices αi must be allowed to grow exponentially along the chain. In practice, the bond dimension is fixed to a maximal value for the duration of the optimization, and the MPS tensors are truncated to this value. However, the validity of a chosen bond dimension can be probed rigorously by inspection of the singular value decompositions inherent to the DMRG algorithm and by systematic extrapolation to infinite bond dimension.120
Similar to the wavefunction, the Hamiltonian is factorized into an MPO
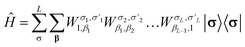 | (21) |
In tcDMRG, due to the non-Hermiticity of Ĥtc, the variational principle no longer holds so that the conventional DMRG optimization of the entries in the MPS is no longer directly applicable. Hence, in order to optimize the MPS, we rely on the imaginary-time tangent-space formulation of DMRG (iTD-DMRG)121–123 in which the imaginary-time evolution of the MPS is performed using the time-dependent Schrödinger equation in the manifold of MPS with fixed bond dimension m
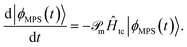 | (22) |
The operator 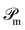 projects the product Ĥtc|ϕMPS(t)〉 onto this manifold. At t → ∞, the solution converges to the optimal approximation of the ground state solution in the manifold. In our implementation, this propagation is performed using a second-order Trotterization scheme.
projects the product Ĥtc|ϕMPS(t)〉 onto this manifold. At t → ∞, the solution converges to the optimal approximation of the ground state solution in the manifold. In our implementation, this propagation is performed using a second-order Trotterization scheme.
Following our original work on tcDMRG,88,107 we employ a correlation factor
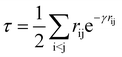 | (23) |
Although the damping function is a necessary ingredient in this ansatz, it introduces the somewhat arbitrary parameter γ that prevents this specific tcDMRG approach from being a well-defined electronic structure model. For this reason, the effect of this parameter on the tcDMRG energy will be investigated in this work.
4 Results
4.1 Lithium hydride
As an example, we chose the lithium hydride molecule for which Ĥtc can be treated with the full three-body operator with our implementation of tcDMRG. These results can be used to validate the normal-ordered approximation of the three-body operator, in which the normal-ordered three-body operator with respect to the Hartree–Fock determinant is neglected. Subsequently, we calculated the potential energy curve for LiH in the normal-ordered approximation and assessed the effect of the value of the γ in the damping function of the correlator.4.2 Computational methodology
The tcDMRG calculations were performed with a development version of our DMRG program QCMaquis.118 First, 10 initial sweeps (back-and-forth) across the orbital lattice were conducted using the time-independent variational DMRG algorithm with the conventional electronic Hamiltonian, assuming that this would lead to a good starting guess for the transcorrelated calculations. Then, the wavefunction was optimized with the transcorrelated Hamiltonian using iTD-DMRG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123 until energy convergence within a threshold of 10−10 Hartree. Unless stated otherwise, a bond dimension of m = 100 was chosen, which we found to be sufficient to converge DMRG to the FCI solution for our model system (see, for instance, Table 1). In all simulations, the two-site optimization variant of DMRG was used. The calculations were performed using the Dunning family of basis sets124 cc-pVXZ (X = D, T, Q, 5), with the corresponding RIFIT basis125 used in the density-fitting of the two-electron integrals, while the uncontracted cc-pV5Z basis set was used for the evaluation of the three-body integrals. These integrals were evaluated analytically with our implementation described in ref. 107.
123 until energy convergence within a threshold of 10−10 Hartree. Unless stated otherwise, a bond dimension of m = 100 was chosen, which we found to be sufficient to converge DMRG to the FCI solution for our model system (see, for instance, Table 1). In all simulations, the two-site optimization variant of DMRG was used. The calculations were performed using the Dunning family of basis sets124 cc-pVXZ (X = D, T, Q, 5), with the corresponding RIFIT basis125 used in the density-fitting of the two-electron integrals, while the uncontracted cc-pV5Z basis set was used for the evaluation of the three-body integrals. These integrals were evaluated analytically with our implementation described in ref. 107.
As a reference, FCI results for LiH were obtained with the CISDTQ module in the Psi4 (ref. 126) program with conventional integrals obtained from the restricted Hartree–Fock routine from Psi4.
4.3 Effect of normal-ordered approximation
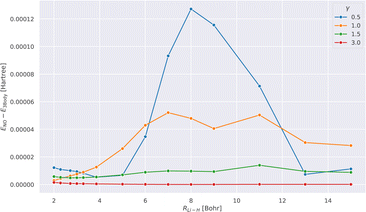
Fig. 1 shows the absolute difference of the energies calculated with tcDMRG using the full treatment of the three-body operator and its normal-ordered approximation for different values of γ along the potential energy curve.We observe that the error resulting from this approximation decreases as the value of γ increases. This can be understood by recalling that as γ → ∞, the effect of the transcorrelated similarity transformation vanishes. Therefore, any approximation that is introduced in the treatment of Ĥtc also disappears. Our results suggest that this approximation is justified, as also shown in ref. 111 since the error is smaller than 0.13 mHartree for all values of γ. Therefore, this approximation is assumed in all our subsequent results.
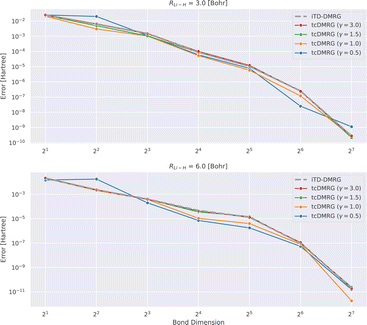
In Fig. 2, we analyze the convergence of the energy with increasing bond dimension in the DMRG calculation.
It appears that for this system, the tcDMRG method leads to either identical or smaller errors for bond dimensions larger than 4, than the conventional DMRG approach, depending on the parameter γ in the correlator. However, in general, the convergence behavior of the two methods remains similar.
4.4 Effects of the damping parameter in the correlator on spectroscopic quantities
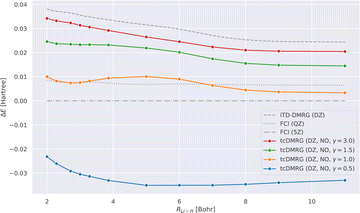
We now study the effect of the damping parameter γ on the potential energy curves; the results are reported in Fig. 3: four tcDMRG curves were calculated with distinct values of γ in the cc-pVDZ basis. For comparison, the energies obtained with DMRG used the conventional electronic Hamiltonian in the cc-pVDZ basis. This calculation was converged to the FCI solution and serves as a baseline on which the transcorrelated method should improve. As a DMRG-independent reference, FCI solutions were calculated in the cc-pVQZ and cc-pV5Z basis sets.124 A single-point explicitly correlated Gaussian (ECG) energy, at a bond length of 3.015 bohr, has been included from the literature,127 which is supposed to be within 10–20 μHartree of the exact Born–Oppenheimer energy, making it a highly accurate estimate of the exact Born–Oppenheimer electronic energy. When considering the FCI energies, even with the large quintuple-ζ basis set, the difference between them and the ECG result is of the order of 20 mHartree. This highlights the accuracy of explicitly correlated methods. However, in practice, relative energies and properties (e.g., energy derivatives) are often desired, for which determinantal expansions can benefit from error cancellation. Systematic error cancellation is key to the success of computational chemistry because the relative energies and properties are then affected by significantly smaller errors than what is observed here in absolute terms.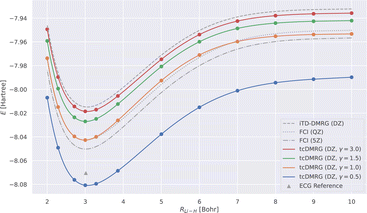 | ||
| Fig. 3 LiH tcDMRG ground-state potential energy curves (cc-pVDZ (DZ) basis set, normal-ordered approximation) obtained with different values of γ. For comparison, imaginary-time time-dependent DMRG (iTD-DMRG) results in the cc-pVDZ basis, and FCI results obtained with the larger cc-pVQZ (QZ) and cc-pV5Z (5Z) basis sets are given. An explicitly correlated Gaussian (ECG) result127 is provided as a highly accurate estimate of the exact Born–Oppenheimer energy. | ||
Turning our attention to the transcorrelated results for increasing values of γ, it is clearly seen that the effect of transcorrelation decreases in such a way that the electronic energies approach the ones obtained by conventional iTD-DMRG in the same one-particle basis (cc-pVDZ). By contrast, we observe for small γ a large effect on the electronic energies leading to solutions that even fall below the exact energy (represented by the ECG reference result of ref. 127), highlighted by the potential energy curve obtained for γ = 0.5. Reducing the value of γ even further to 0.1, we found that the energy at an interatomic distance of 3 bohr even falls to −8.578 hartree, which is ∼0.5 hartree below the exact energy.
For intermediate values of γ, especially for one which corresponds to an omission of this parameter, i.e., for γ = 1.0, we observe that the tcDMRG results coincide with the quadruple-ζ FCI results around the equilibrium distance, resulting in improved accuracy of two cardinal numbers (w.r.t. the zeta parameter of the orbital basis). However, this improvement is not conserved along the entire potential energy curve, and ultimately, the tcDMRG curve undershoots the FCI results.
We monitor the parallelity of the electronic energy obtained with various methods,
| ΔE(RLi-H) = Emethod(RLi-H) − EFCI cc-pV5Z(RLi-H), | (24) |
Table 1 collects the total electronic energy at equilibrium distance, the electronic dissociation energies De, vibrational constants ωe and ωexe and the non-parallelity errors (NPE) obtained by the various methods.
| Method | R eq [bohr] | E(Req) [Ha] | D e [eV] | ω e [cm−1] | ω e x e [cm−1] | NPE [Ha] |
|---|---|---|---|---|---|---|
| Reference | 3.015 (ref. 127) | −8.070538![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ref. 127) (ref. 127) |
2.52 (ref. 128) | 1405 (ref. 128) | 23 (ref. 128) | — |
| FCI (5Z) | 3.005 | −8.050255 | 2.56 | 1369 | 12 | 0 (by definition) |
| FCI (QZ) | 2.995 | −8.042676 | 2.53 | 1409 | 36 | 0.002093 |
| FCI (TZ) | 3.016 | −8.036660 | 2.47 | 1404 | 23 | 0.007405 |
| FCI (DZ) | 3.051 | −8.014803 | 2.26 | 1359 | 22 | 0.013682 |
| iTD-DMRG (DZ) | 3.051 | −8.014803 | 2.26 | 1359 | 22 | 0.013682 |
| tcDMRG (DZ, γ = 3.0) | 3.048 | −8.018552 | 2.25 | 1364 | 22 | 0.013566 |
| tcDMRG (DZ, γ = 1.5) | 3.009 | −8.026977 | 2.32 | 1408 | 25 | 0.009773 |
| tcDMRG (DZ, γ = 1.25) | 2.992 | −8.032831 | 2.37 | 1441 | 26 | 0.008475 |
| tcDMRG (DZ, γ = 1.0) | 2.983 | −8.042693 | 2.44 | 1476 | 26 | 0.006439 |
| tcDMRG (DZ, γ = 0.75) | 3.003 | −8.058122 | 2.53 | 1465 | 24 | 0.005913 |
| tcDMRG (DZ, γ = 0.5) | 3.061 | −8.080827 | 2.50 | 1354 | 22 | 0.011948 |
The NPE is defined as the difference between the maximum and the minimum error of the potential energy curves with respect to FCI/cc-pV5Z taken as reference,
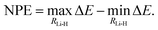 | (25) |
Parallelity of the potential energy curves is a desired property so that the calculation of relative energies can benefit from error cancellation.
Table 1 illustrates that the tcDMRG method with large values of γ converges to the conventional DMRG results in the same basis. By decreasing the parameter γ from 3.0 to 1.0, the downward trend of ΔE (also seen in Fig. 4) is mitigated, but results in the introduction of a hump in the error which becomes more significant with decreasing γ. For γ = 0.5, a relative overestimation of the energy leads to an increase in the NPE.
Concerning the harmonic frequency ωe, we find all approaches are scattered around the experimental result by up to 10%. In fact, we see a strong dependence on the atomic-orbital basis set, where FCI harmonic frequency of the quintuple-ζ basis set significantly deviates from the convergence of FCI results obtained for the smaller basis sets. Inspecting the potential energy curves in these cases does not point toward any serious problem but demonstrates the sensitivity of the harmonic frequency to the local shape of the potential energy curve. Similar observations can be made for the FCI anharmonic constant ωexe in the large basis sets, which deviate significantly from all other anharmonicities obtained, which are in the order of 10% around the experimental value.
Regarding De (see Fig. 4), we see that increasing the parameter γ leads to a decreased slope of ΔE, but also introduces a hump. Overall, the flatter profile results in an improved estimation of De for larger values of γ.
5 Conclusions and current challenges
In this work, we reviewed the contribution of explicit electron correlation in the ansatz for the electronic wavefunction. Different approaches introduce inter-particle distances into correlation factors designed to alleviate the cusp problem of approximations to the electronic wavefunction based on single-particle basis functions (orbitals).Although electron–nucleus and electron–electron–nucleus cusps profoundly impact the electronic wavefunction and, hence, the total electronic energy, we here argued that they may be neglected for an electronic structure model that yields reliable electronic energy differences due to changes in the valence region. The resulting model features a rather simple correlator. We examined the properties of this correlator in comparison with more elaborate correlators that also consider electron–nucleus distances explicitly (and hence, molecular structure in the Born–Oppenheimer approximation). We discussed that our simple electrons-only correlator allows us to define a molecular-structure-independent correlator and, therefore, leaves all structure dependence to be incorporated in the smooth function that is to be multiplied with the correlator.
In our presentation, we highlighted the transcorrelated method’s non-variationality and, hence, the importance of developing reliable variational methods applicable in this context. We also discussed the source of the non-variationality of CC compared to the transcorrelated method.
Our correlator considers the analytic knowledge about the wavefunction near electron–electron cusps. However, this behavior is to be suppressed at large inter-electronic distances, which is the reason for the introduction of an exponential decay that depends on this distance and acts as a damping function. In principle, one may introduce a parameter that can be used to switch off the contributions of the inter-electronic distances so that one recovers results of the orbital basis without introduction of a correlator. We argue that it should be possible to choose the parameter in this (nested) exponential in some simple, maybe even system-independent way. This would guarantee that a well-defined electronic structure model emerges that, for instance, does not rely on structure-dependent correlators that would change along a reaction coordinate or some other trajectory across a Born–Oppenheimer surface.
To highlight our arguments with a specific example, we provided results of the transcorrelated method (with the simple electrons-only correlator and fully analytic integral evaluation techniques) for the LiH diatomic molecule, and related the results to accurate reference calculations. We investigated the effect of the normal-ordering approximation of the three-body operator in the context of the tcDMRG method. Moreover, we demonstrated that while the transcorrelated method has the potential to increase atomic orbital basis convergence, our current choice of correlator leads to non-systematic improvement in the energy along the potential energy curve.
In future work, a systematic analysis of the parameter in the damping function of the correlator should either reveal the best universal choice of this parameter valid for all molecules or provide analytic means to choose this parameter in a system-specific manner without the need for extensive prior optimization. Subsequently, it will be necessary to evaluate the still lacking long-range dynamic correlation that results from the choice of an active orbital space in a multi-configurational ansatz. Those correlations may then be efficiently captured by multi-reference-driven single-reference CC models,29,30,130–133 which might provide higher accuracy results than multi-reference perturbation theory would deliver for a transcorrelated zeroth-order Hamiltonian.
Author contributions
Kalman Szenes: conceptualization, methodology, investigation, software, writing – original draft, validation. Maximilian Mörchen: conceptualization, methodology, investigation, software, writing – original draft, validation. Paul Fischill: software. Markus Reiher: conceptualization, methodology, validation, resource, writing – original draft, writing – review and editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Swiss National Science Foundation (No. 200021_219616) and by ETH Research Grant ETH-43 20-2.Notes and references
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, 2000 Search PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- I. Shavitt and R. J. Bartlett, Many-body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, 1st edn, 2009 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- B. O. Roos, Int. J. Quantum Chem., 1980, 18, 175–189 CrossRef.
- K. Ruedenberg, M. W. Schmidt, M. M. Gilbert and S. T. Elbert, Chem. Phys., 1982, 71, 41–49 CrossRef CAS.
- D. Roca-Sanjuán, F. Aquilante and R. Lindh, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 585–603 CrossRef.
- T. H. Schucan and H. A. Weidenmüller, Ann. Phys., 1972, 73, 108–135 CAS.
- T. H. Schucan and H. A. Weidenmüller, Ann. Phys., 1973, 76, 483–509 Search PubMed.
- K. Jankowski, J. Paldus, I. Grabowski and K. Kowalski, J. Chem. Phys., 1992, 97, 7600–7612 CrossRef CAS.
- J. Paldus, P. Piecuch, L. Pylypow and B. Jeziorski, Phys. Rev. A, 1993, 47, 2738–2782 CrossRef CAS PubMed.
- M. Hanrath, J. Chem. Phys., 2008, 128, 154118 CrossRef PubMed.
- T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2006, 124, 194106 CrossRef PubMed.
- T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 104107 CrossRef PubMed.
- F. A. Evangelista and J. Gauss, Chem. Phys., 2012, 401, 27–35 CrossRef CAS.
- D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Chem. Rev., 2012, 112, 182–243 CrossRef CAS PubMed.
- F. A. Evangelista, J. Chem. Phys., 2018, 149, 030901 CrossRef PubMed.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- R. Lindh and I. F. Galván, Quantum Chemistry and Dynamics of Excited States, John Wiley & Sons, Ltd, Chichester, England, UK, 2020, pp. 299–353 Search PubMed.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151–160 CrossRef CAS.
- E. Fromager, J. Toulouse and H. J. Aa. Jensen, J. Chem. Phys., 2007, 126, 074111 CrossRef PubMed.
- E. D. Hedegård, S. Knecht, J. S. Kielberg, H. J. A. Jensen and M. Reiher, J. Chem. Phys., 2015, 142, 224108 CrossRef PubMed.
- E. D. Hedegård, J. Toulouse and H. J. A. Jensen, J. Chem. Phys., 2018, 148, 214103 CrossRef PubMed.
- J. A. Rodríguez-Jiménez, A. Carreras and D. Casanova, J. Chem. Phys., 2021, 154, 124116 CrossRef PubMed.
- K. Pernal and M. Hapka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1566 CAS.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS PubMed.
- P. Sharma, J. J. Bao, D. G. Truhlar and L. Gagliardi, Annu. Rev. Phys. Chem., 2021, 541–564 CrossRef CAS PubMed.
- N. Oliphant and L. Adamowicz, J. Chem. Phys., 1991, 94, 1229–1235 CrossRef CAS.
- P. Piecuch, N. Oliphant and L. Adamowicz, J. Chem. Phys., 1993, 99, 1875–1900 CrossRef CAS.
- L. Adamowicz, J.-P. Malrieu and V. V. Ivanov, J. Chem. Phys., 2000, 112, 10075–10084 CrossRef CAS.
- V. V. Ivanov and L. Adamowicz, J. Chem. Phys., 2000, 112, 9258–9268 CrossRef CAS.
- T. Kinoshita, O. Hino and R. J. Bartlett, J. Chem. Phys., 2005, 123, 074106 CrossRef PubMed.
- L. Veis, A. Antalík, J. Brabec, F. Neese, Ö. Legeza and J. Pittner, J. Phys. Chem. Lett., 2016, 7, 4072–4078 CrossRef CAS PubMed.
- F. M. Faulstich, A. Laestadius, Ö. Legeza, R. Schneider and S. Kvaal, SIAM J. Numer. Anal., 2019, 57, 2579–2607 CrossRef.
- E. Vitale, A. Alavi and D. Kats, J. Chem. Theory Comput., 2020, 16, 5621–5634 CrossRef CAS PubMed.
- E. Vitale, G. Li Manni, A. Alavi and D. Kats, J. Chem. Theory Comput., 2022, 18, 3427–3437 CrossRef CAS PubMed.
- P. Piecuch, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1999, 110, 6103–6122 CrossRef CAS.
- P. Piecuch, K. Kowalski, I. S. O. Pimienta, P.-D. Fan, M. Lodriguito, M. J. McGuire, S. A. Kucharski, T. Kuś and M. Musiał, Theor. Chem. Acc., 2004, 112, 349–393 Search PubMed.
- K. Kowalski and P. Piecuch, J. Chem. Phys., 2000, 113, 18–35 CrossRef CAS.
- K. Kowalski and P. Piecuch, J. Chem. Phys., 2000, 113, 5644–5652 CrossRef CAS.
- J. Shen and P. Piecuch, Chem. Phys., 2012, 401, 180–202 CrossRef CAS.
- J. Shen and P. Piecuch, J. Chem. Theory Comput., 2012, 8, 4968–4988 CrossRef CAS PubMed.
- J. Shen and P. Piecuch, J. Chem. Phys., 2012, 136, 144104 CrossRef PubMed.
- N. P. Bauman, J. Shen and P. Piecuch, Mol. Phys., 2017, 115, 2860–2891 CrossRef CAS.
- J. E. Deustua, J. Shen and P. Piecuch, Phys. Rev. Lett., 2017, 119, 223003 CrossRef PubMed.
- P. Piecuch, Mol. Phys., 2010, 108, 2987–3015 CrossRef CAS.
- W. Klopper, F. R. Manby, S. Ten-No and E. F. Valeev, Int. Rev. Phys. Chem., 2006, 25, 427–468 Search PubMed.
- S. Ten-no and J. Noga, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 114–125 Search PubMed.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112, 75–107 CrossRef CAS PubMed.
- M. Reiher and A. Wolf, Relativistic Quantum Chemistry, John Wiley & Sons, Ltd, 2014 Search PubMed.
- T. Kato, Commun. Pure Appl. Math., 1957, 10, 151–177 CrossRef.
- R. T. Pack and W. B. Brown, J. Chem. Phys., 1966, 45, 556–559 CrossRef CAS.
- D. P. Tew, J. Chem. Phys., 2008, 129, 014104 CrossRef PubMed.
- C. Schwartz, Phys. Rev., 1962, 126, 1015–1019 CrossRef CAS.
- S. Fournais, M. Hoffmann-Ostenhof, T. Hoffmann-Ostenhof and T. O. Sorensen, Commun. Math. Phys., 2005, 255, 183–227 CrossRef.
- D. Andrae, M. Reiher and J. Hinze, Chem. Phys. Lett., 2000, 320, 457–468 CrossRef CAS.
- D. Andrae, Phys. Rep., 2000, 336, 413–525 CrossRef CAS.
- J. Proppe and M. Reiher, J. Chem. Theory Comput., 2017, 13, 3297–3317 CrossRef CAS PubMed.
- J. C. Slater, Phys. Rev., 1928, 31, 333–343 CrossRef.
- A. Ma, M. D. Towler, N. D. Drummond and R. J. Needs, J. Chem. Phys., 2005, 122, 224322 CrossRef CAS PubMed.
- A. J. Cohen, H. Luo, K. Guther, W. Dobrautz, D. P. Tew and A. Alavi, J. Chem. Phys., 2019, 151, 061101 CrossRef.
- A. Ammar, A. Scemama and E. Giner, J. Chem. Theory Comput., 2023, 19, 4883–4896 CrossRef CAS PubMed.
- C. R. Myers, C. J. Umrigar, J. P. Sethna and J. D. Morgan, Phys. Rev. A, 1991, 44, 5537–5546 CrossRef CAS PubMed.
- S. F. Boys and N. C. Handy, Proc. R. Soc. London, Ser. A, 1969, 310, 43–61 CAS.
- P.-O. Löwdin, Advances in Quantum Chemistry, Academic Press, 1988, vol. 19, pp. 87–138 Search PubMed.
- P. G. Szalay, M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 103, 281–298 CrossRef CAS.
- W. Kutzelnigg, Theor. Chim. Acta, 1991, 80, 349–386 CrossRef CAS.
- J. Romero, R. Babbush, J. R. McClean, C. Hempel, P. J. Love and A. Aspuru-Guzik, Quantum Sci. Technol., 2018, 4, 014008 CrossRef.
- T. D. Crawford and H. F. Schaefer III, Reviews in Computational Chemistry, John Wiley & Sons, Ltd, 2000, pp. 33–136 Search PubMed.
- W. Kutzelnigg, Theor. Chim. Acta, 1985, 68, 445–469 CrossRef CAS.
- W. Klopper and W. Kutzelnigg, Chem. Phys. Lett., 1987, 134, 17–22 CrossRef CAS.
- W. Klopper and H. P. Lüthi, Chem. Phys. Lett., 1996, 262, 546–552 CrossRef CAS.
- A. J. May and F. R. Manby, J. Chem. Phys., 2004, 121, 4479–4485 CrossRef CAS PubMed.
- B. J. Persson and P. R. Taylor, J. Chem. Phys., 1996, 105, 5915–5926 CrossRef CAS.
- S. Ten-no, Chem. Phys. Lett., 2004, 398, 56–61 CrossRef CAS.
- E. Giner, J. Chem. Phys., 2021, 154, 084119 CrossRef CAS PubMed.
- S. Ten-no, Chem. Phys. Lett., 2000, 330, 169–174 CrossRef CAS.
- K. E. Schmidt and J. W. Moskowitz, J. Chem. Phys., 1990, 93, 4172–4178 CrossRef CAS.
- N. Umezawa and S. Tsuneyuki, J. Chem. Phys., 2003, 119, 10015–10031 CrossRef CAS.
- N. D. Drummond and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085124 CrossRef.
- J. P. Haupt, S. M. Hosseini, P. López Ríos, W. Dobrautz, A. Cohen and A. Alavi, J. Chem. Phys., 2023, 158, 224105 CrossRef CAS PubMed.
- N. Handy, Mol. Phys., 1971, 21, 817–828 CrossRef CAS.
- C. M. Johnson, S. Hirata and S. Ten-no, Chem. Phys. Lett., 2017, 683, 247–252 CrossRef CAS.
- D. P. Tew and W. Klopper, J. Chem. Phys., 2005, 123, 074101 CrossRef PubMed.
- M. C. Gutzwiller, Phys. Rev. Lett., 1963, 10, 159–162 CrossRef.
- A. Baiardi and M. Reiher, J. Chem. Phys., 2020, 153, 164115 CrossRef CAS PubMed.
- W. Dobrautz, H. Luo and A. Alavi, Phys. Rev. B, 2019, 99, 075119 CrossRef CAS.
- Y. X. Yao, J. Liu, C. Z. Wang and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 045131 CrossRef.
- Y.-H. Dong, Z. Ye, W.-C. Lu, Y.-X. Yao, C.-Z. Wang and K.-M. Ho, Comput. Theor. Chem., 2020, 1185, 112877 CrossRef CAS.
- S. Tsuneyuki, Prog. Theor. Phys. Suppl., 2008, 176, 134–142 CrossRef CAS.
- E. Neuscamman, H. Changlani, J. Kinder and G. K.-L. Chan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205132 CrossRef.
- J. M. Wahlen-Strothman, C. A. Jiménez-Hoyos, T. M. Henderson and G. E. Scuseria, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 041114 CrossRef.
- R. Jastrow, Phys. Rev., 1955, 98, 1479–1484 CrossRef.
- N. C. Handy, J. Chem. Phys., 1969, 51, 3205–3212 CrossRef CAS.
- N. Lee and A. J. W. Thom, J. Chem. Theory Comput., 2023, 19, 5743–5759 CrossRef CAS PubMed.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- W. R. Fimple and M. J. Unwin, Int. J. Quantum Chem., 1976, 10, 643–658 CrossRef CAS.
- O. Hino, Y. Tanimura and S. Ten-no, J. Chem. Phys., 2001, 115, 7865–7871 CrossRef CAS.
- A. Ammar, A. Scemama and E. Giner, J. Chem. Phys., 2023, 159, 114121 CrossRef CAS PubMed.
- D. Kats, E. M. C. Christlmaier, T. Schraivogel and A. Alavi, Orbital optimisation in xTC transcorrelated methodsarXiv, 2024, preprint, arXiv:2404.07764 DOI:10.48550/arXiv.2404.07764.
- H. Luo, J. Chem. Phys., 2010, 133, 154109 CrossRef PubMed.
- H. Luo, J. Chem. Phys., 2011, 135, 024109 CrossRef PubMed.
- S. Boys and N. Handy, Proc. R. Soc. London, Ser. A, 1969, 311, 309–329 CAS.
- S. Ten-no and F. R. Manby, J. Chem. Phys., 2003, 119, 5358–5363 CrossRef CAS.
- A. Baiardi, M. Lesiuk and M. Reiher, J. Chem. Theory Comput., 2022, 18, 4203–4217 CrossRef CAS PubMed.
- N. Umezawa, S. Tsuneyuki, T. Ohno, K. Shiraishi and T. Chikyow, J. Chem. Phys., 2005, 122, 224101 CrossRef PubMed.
- K. Liao, T. Schraivogel, H. Luo, D. Kats and A. Alavi, Phys. Rev. Res., 2021, 3, 033072 CrossRef CAS.
- T. Schraivogel, A. J. Cohen, A. Alavi and D. Kats, J. Chem. Phys., 2021, 155, 191101 CrossRef CAS PubMed.
- E. M. Christlmaier, T. Schraivogel, P. López Ríos, A. Alavi and D. Kats, J. Chem. Phys., 2023, 159, 014113 CrossRef CAS PubMed.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- K. Szalewicz, B. Jeziorski, H. J. Monkhorst and J. G. Zabolitzky, Chem. Phys. Lett., 1982, 91, 169–172 CrossRef CAS.
- H.-J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126, 164102 CrossRef PubMed.
- S. R. White, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10345–10356 CrossRef CAS PubMed.
- K. Liao, H. Zhai, E. M. Christlmaier, T. Schraivogel, P. L. Ríos, D. Kats and A. Alavi, J. Chem. Theory Comput., 2023, 19, 1734–1743 CrossRef CAS PubMed.
- I. P. McCulloch, J. Stat. Mech.: Theory Exp., 2007, 2007, P10014 CrossRef.
- S. Keller, M. Dolfi, M. Troyer and M. Reiher, J. Chem. Phys., 2015, 143, 244118 CrossRef PubMed.
- S. F. Keller and M. Reiher, Chimia, 2014, 68, 200 CrossRef CAS PubMed.
- C. Hubig, J. Haegeman and U. Schollwöck, Phys. Rev. B, 2018, 97, 045125 CrossRef.
- J. Haegeman, C. Lubich, I. Oseledets, B. Vandereycken and F. Verstraete, Phys. Rev. B, 2016, 94, 165116 CrossRef.
- C. Lubich, I. V. Oseledets and B. Vandereycken, SIAM J. Numer. Anal., 2015, 53, 917–941 CrossRef.
- A. Baiardi and M. Reiher, J. Chem. Theory Comput., 2019, 15, 3481–3498 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O’Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- W. Cencek and J. Rychlewski, Chem. Phys. Lett., 2000, 320, 549–552 CrossRef CAS.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397 CrossRef CAS.
- T. D. Crawford and H. F. Schaefer, J. Chem. Phys., 1996, 104, 6259–6264 CrossRef CAS.
- T. Kinoshita, O. Hino and R. J. Bartlett, J. Chem. Phys., 2005, 123, 074106 CrossRef PubMed.
- L. Veis, A. Antalík, J. Brabec, F. Neese, Ö. Legeza and J. Pittner, J. Phys. Chem. Lett., 2016, 7, 4072–4078 CrossRef CAS PubMed.
- M. Mörchen, L. Freitag and M. Reiher, J. Chem. Phys., 2020, 153, 244113 CrossRef PubMed.
- F. M. Faulstich, M. Máté, A. Laestadius, M. A. Csirik, L. Veis, A. Antalik, J. Brabec, R. Schneider, J. Pittner, S. Kvaal and O. Legeza, J. Chem. Theory Comput., 2019, 15, 2206–2220 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2024 |