Open Access Article
Open Access ArticleElectric field induced associations in the double layer of salt-in-ionic-liquid electrolytes†
Daniel M.
Markiewitz
 a,
Zachary A. H.
Goodwin
a,
Zachary A. H.
Goodwin
 bc,
Michael
McEldrew
bc,
Michael
McEldrew
 a,
J.
Pedro de Souza
a,
J.
Pedro de Souza
 ad,
Xuhui
Zhang
ad,
Xuhui
Zhang
 e,
Rosa M.
Espinosa-Marzal
e,
Rosa M.
Espinosa-Marzal
 ef and
Martin Z.
Bazant
ef and
Martin Z.
Bazant
 *ag
*ag
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. E-mail: bazant@mit.edu
bJohn A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, Massachusetts 02138, USA
cDepartment of Materials, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
dOmenn-Darling Bioengineering Institute, Princeton University, Princeton, New Jersey 08544, USA
eDepartment of Civil and Environmental Engineering, University of Illinois at Urbana – Champaign, Urbana, IL 61801, USA
fDepartment of Materials Science and Engineering, University of Illinois at Urbana – Champaign, Urbana, IL 61801, USA
gDepartment of Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
First published on 22nd March 2024
Abstract
Ionic liquids (ILs) are an extremely exciting class of electrolytes for energy storage applications. Upon dissolving alkali metal salts, such as Li or Na based salts, with the same anion as the IL, an intrinsically asymmetric electrolyte can be created for use in batteries, known as a salt-in-ionic liquid (SiIL). These SiILs have been well studied in the bulk, where negative transference numbers of the alkali metal cation have been observed from the formation of small, negatively charged clusters. The properties of these SiILs at electrified interfaces, however, have received little to no attention. Here, we develop a theory for the electrical double layer (EDL) of SiILs where we consistently account for the thermoreversible association of ions into Cayley tree aggregates. The theory predicts that the IL cations first populate the EDL at negative voltages, as they are not strongly bound to the anions. However, at large negative voltages, which are strong enough to break the alkali metal cation–anion associations, these IL cations are exchanged for the alkali metal cation because of their higher charge density. At positive voltages, we find that the SiIL actually becomes more aggregated while screening the electrode charge from the formation of large, negatively charged aggregates. Therefore, in contrast to conventional intuition of associations in the EDL, SiILs appear to become more associated in certain electric fields. We present these theoretical predictions to be verified by molecular dynamics simulations and experimental measurements.
I. Introduction
Alkali metal salt doped ionic liquids, referred to as salt-in-ionic liquids (SiILs) here, have attracted attention as electrolytes for applications in batteries/energy storage devices,1–17 owing to the combination of the active Li/Na cations coupled with the highly desirable properties of ionic liquids (ILs). ILs have extremely low vapour pressures, are effectively universal solvents, and are non-flammable making them a much safer alternative to carbonate based solvents typically used in conventional battery electrolytes.18–21 Unlike conventional battery electrolytes, SiILs are solely composed of ions, where the anion of the alkali metal salt and IL are often the same, e.g., Li[TFSI] dissolved in [EMIM][TFSI] resulting in there being more anions than either type of the cation. Therefore, these electrolytes are inherently asymmetric, and moreover, strongly correlated because of the super-concentration of salts.22One area where the asymmetry and correlation manifests is in the transport properties of the SiILs.22 In electrophoretic NMR experiments23–27 and MD simulations28–34 of SiILs, it has been revealed that, at low mole fractions of the alkali metal salt, the alkali metal cation has a negative transference number, indicating that it moves in the opposite direction of the electric field. This property has been explained by the alkali metal cation being strongly solvated by anions. Owing to the larger number of anions, these species can form small, but high negatively charged clusters that are transported in a vehicular way.22,28,29
These strong interactions are also evident at higher mole fractions. With increasing mole fraction, the sizes of the clusters increase from only containing 1 cation to containing several cations in an extended cluster connected by anions, as is found to occur in MD simulations.28,29,35 These clusters continue to increase in size with the mole fraction and, eventually, a percolating ionic network of alkali metal cations and anions occurs.28,29 A simple, analytical theory for the ionic clusters of SiILs was developed by McEldrew et al.,22 based on the analogy between polymers and concentrated electrolytes,36 which was able to rationalise the changes to the cluster distribution with mole fraction.22 Drawing from the famous theories of Flory, Stockmayer and Tanaka,37–49 it was predicted that the percolating ionic network of ions should behave like a gel,50–52 and in fact, experimental indications of this gel have been found in water-doped SiILs.53 Therefore, it is clear that ionic aggregation in SiILs is an extremely important phenomena.
One aspect of SiILs that is not well understood at all, however, is the electrical double layer (EDL), i.e. how the ions arrange themselves at an electrified interface. To our knowledge, Haskins et al.54 is one of the only papers investigating this topic in detail, presumably because of the complexity of the electrolyte. It found that the Li+ induces disorder in the EDL and prefers not to reside right at the electrode interface, opting instead to reside within the anion-rich layers. Recently, Goodwin et al.55,56 extended the theories of McEldrew et al.50,51 to make predictions in the EDL finding that the electric field induces cracking of clusters.55,56 However, this work has only been applied to simple symmetric ILs and further development is necessary to extend the theories of McEldrew and Goodwin to the EDL of SiILs.
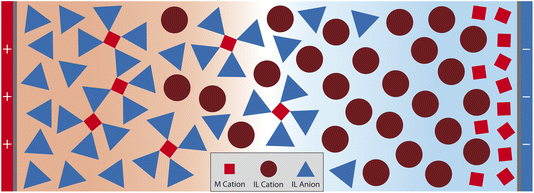
In this paper, we develop a theory for the EDL of SiILs based on the work of McEldrew and Goodwin. Conventional theories for the EDL are not able to correctly capture the associations which occur in the EDL57–60 nor the extended ionic aggregates which occur in SiILs.22,29 Here we present a theory for the EDL of SiILs which accounts for ionic associations in a consistent way and allows us to investigate these associations in the EDL of a strongly correlated and intrinsically asymmetric electrolyte. We find two main observations from this theory. Firstly, a cation exchange occurs at negative potentials, where the IL cation is found to be dominant at small negative potentials but is then replaced by the smaller alkali metal cation at increasingly negative potentials. This exchange occurs because of the competition between different sizes of species and the associations between the alkali metal cations and anions. Secondly, in positive potentials, we find there is some intermediate range of potentials where the SiIL becomes more associated than in the bulk. These results are schematically shown in Fig. 1.
II. Theory
We consider our system to be an incompressible lattice-gas model,50 which is composed of alkali metal cations, denoted by +, and IL cations and anions, denoted by, respectively, ⊕ and −. In the bulk, the total volume fractions, ϕj, of each species are known, where j is +, − or ⊕. The lattice site is assumed to be the size of the alkali metal cation, v+, with the volumes occupied by the other species being determined by v+ξi, where ξi = vi/v+ with i being − or ⊕ here. The dimensionless concentrations of each species are given by cj = ϕj/ξj, with ξ+ = 1 for the alkali metal cations.Similar to previous work, it is assumed that the anions and metal cations may form associations; but, the IL cations only interact with the open association sites of anions through a regular solution term.22 The metal cations can form a maximum of f+ associations and the anions a maximum of f− associations, referred to as the functionality of each species. The number of associations is typically bound by the integer number of coordination of an associating species within the first solvation shell of each species. Typically these associations are determined via a cutoff distance between the key moieties in the molecules, such as the oxygens’ in a TFSI anion and a lithium ion.52 Additionally, they can be determined by studying the spatial distribution functions for the associating species to identify how many “hot-spot” regions exist for the species, which corresponds to the functionality of that species.51 Alternatively, kinetic criteria61 or machine learning methods62 can be used to define associations between ions in electrolytes. As these functionalities are larger than 1, a polydisperse cluster distribution can form clusters of rank lm, where l is the number of cations and m is the number of anions in a cluster with rank lm, with dimensionless concentration clm, but we assume that only Cayley-tree-like clusters can form, i.e. clusters with no loops.50 This Cayley tree assumption of the clusters is required for our approach to remain analytical and physically transparent,50 but the approximation is known to break down sometimes.22,52
For functionalities equal to or larger than 2, a percolating ionic network can emerge.50 This is referred to as the gel here. In the gel regime, we employ Flory’s convention to determine the volume fractions of each species in the sol (ϕsol+/−, which contains the clusters and free species) and gel phase (ϕgel+/−, which only contains the percolating network of ions), where ϕ+/− = ϕsol+/−+ϕgel+/−. The total dimensionless concentration of each species is given by a sum over all possible clusters, 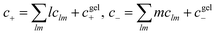 .
.
The free energy functional 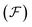 is proposed to take the following form
is proposed to take the following form
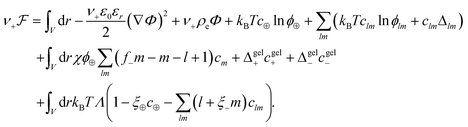 | (1) |
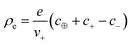 , with e denoting the elementary charge. The third term is the ideal entropy of the IL cations, and the fourth term is the ideal entropy from clusters of rank lm. The fifth term is the free energy of forming clusters, where Δlm is the free energy of forming each cluster of rank lm, with more details following later. The sixth term is the regular solution interaction, with strength χ, between the IL cations and the open association sites, where we find the following identity to be useful
, with e denoting the elementary charge. The third term is the ideal entropy of the IL cations, and the fourth term is the ideal entropy from clusters of rank lm. The fifth term is the free energy of forming clusters, where Δlm is the free energy of forming each cluster of rank lm, with more details following later. The sixth term is the regular solution interaction, with strength χ, between the IL cations and the open association sites, where we find the following identity to be useful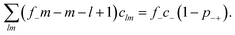 | (2) |
Note that this expression only holds in the pre-gel regime; where the left hand side assumes free anions or anions in clusters can interact with IL cations but the right hand side assumes all anions can interact with IL cations, even those in the gel. The seventh and eighth terms come from the free energy of species associating to the gel, Δgelj, which is a function of ϕ± for thermodynamic consistency. Finally, the last term is a Lagrange multiplier to enforce the incompressibility more explicitly than previously reported.55,56 Note this term introduces another unknown, Λ(r), which needs to be found.63
We consider the free energy of forming a cluster of rank lm to have two contributions
| Δlm = Δcomblm + Δbindlm, | (3) |
Δcomblm = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln{fl+fm−Wlm}, ln{fl+fm−Wlm}, | (4) |
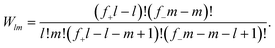 | (5) |
Moreover, the binding free energy is simply given by
| Δbindlm = (l + m − 1)Δf±, | (6) |
We can calculate the chemical potential of the bare ions in the bulk and the EDL, where an overbar will indicate that the variable is the EDL version and Φ is non-zero. For the IL cations, the electrochemical potential, up to arbitrary constants, is given by
β![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) ⊕ = βeΦ + ln ⊕ = βeΦ + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕ + βχξ⊕f− ⊕ + βχξ⊕f−![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) −(1 − −(1 − ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+) − ξ⊕Λ, −+) − ξ⊕Λ, | (7) |
β![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) lm = (l − m)βeΦ + ln lm = (l − m)βeΦ + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) lm + Δlm + βχ lm + Δlm + βχ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕(f−m − m − l + 1) + (l + ξ−m)(d′ − Λ), ⊕(f−m − m − l + 1) + (l + ξ−m)(d′ − Λ), | (8) |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ′ =
′ = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) gel+∂
gel+∂![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) gel+ +
gel+ + ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) gel−∂
gel−∂![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) gel−, with the derivative being with respect to
gel−, with the derivative being with respect to ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) lms.
lms.
In the bulk by asserting that the clusters are in equilibrium with the bare species
| lμ10 + mμ01 = μlm, | (9) |
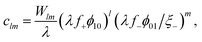 | (10) |
λ = exp{β(−Δf± + χϕ⊕)} = λ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{βχϕ⊕}. exp{βχϕ⊕}. | (11) |
By establishing the chemical equilibrium between free species and clusters within the EDL
l![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 10 + m 10 + m![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 01 = 01 = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) lm, lm, | (12) |
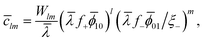 | (13) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) = λ0 = λ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{βχ exp{βχ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕}. ⊕}. | (14) |
Following the work of Goodwin et al.,55 we connect the bulk and EDL cluster distributions to the Poisson equation through closure relations. These closure relations are based on the pre-gel regime and naively extended to the post-gel regime (this assumes the additional chemical potential contribution is not significant, with further research being required to quantify its contribution). Equating the chemical potential of the free ions in bulk and in the EDL allows us to write down 3 additional equations. First, for the alkali metal cations
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 10 = ϕ10 10 = ϕ10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−eβΦ + Λ), exp(−eβΦ + Λ), | (15) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 01 = ϕ01 01 = ϕ01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(eβΦ − βχf−( exp(eβΦ − βχf−(![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕ − ϕ⊕) + ξ−Λ), ⊕ − ϕ⊕) + ξ−Λ), | (16) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕ = ϕ⊕ ⊕ = ϕ⊕![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−eβΦ + βχf−ξ⊕{c−(1 − p−+) − exp(−eβΦ + βχf−ξ⊕{c−(1 − p−+) − ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) −(1 − −(1 − ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+)} + ξ⊕Λ), −+)} + ξ⊕Λ), | (17) |
Lastly to allow us to solve these Boltzmann closure relationships, we need to introduce the idea of association probabilities, conservation of associations and the law of mass action on associations.50 As ϕ10 and ϕ01 are, in principle, experimentally inaccessible. Instead, it is natural to express the cluster distribution in terms of the overall volume fractions of each species, ϕi, which is an experimentally and computationally controllable parameter through the mole fraction of the alkali metal salt.50 This connection is established by introducing ion association probabilities, pij, which is the probability that an association site of species i is bound to species j, where i and j are either the alkali cation (+) or the IL anion (−).22 Therefore, the volume fraction of free alkali cations can be written as ϕ10= ϕ+(1 − p+−)f+ and free anions as ϕ01 = ϕ−(1 − p−+)f−.22
The association probabilities can be determined through the conservation of associations and a mass action law between open and occupied association sites.22,50 The conservation of associations is given by
| p+−ψ+ = p−+ψ−, | (18) |
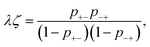 | (19) |
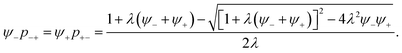 | (20) |
Note, analogous expression for the association probabilities occur in the EDL but where EDL quantities are utilised.
As shown in the works of McEldrew et al.,22,52 the association constants can be found from fitting eqn (19) using association probabilities obtained from MD simulations. For the specific case of SiILs, there are two contributions to the association constant, λ0 and χ, which can be extracted if various salt compositions are studied.22 As the association constant in the EDL only depends on these bulk parameters, and variables in the EDL, we do not need to further determine ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) . In ref. 22, it was found that λ0 ≈ 50 and χ ≈ −2kBT, which shall mainly be used in this study. Therefore, our theory has no free fitting parameters in terms of the associations in the SiILs. This feature is achieved as all the parameters needed to predict the EDL structure can be determined from the bulk SiIL. Explicitly one can extract λ0, χ, and integer bounds on f+ and f− from MD simulations of the SiIL system at various salt compositions and the volume ratios are backed out by molecular data of the species composing the SiIL. Alternatively, one can use integral equations and Wertheim’s formalism to determine the association constants without fitting association constants from MD simulations.65–72 However, this is only accessible for certain cases, such as charged hard spheres with known Mayer f-functions for interacting species, and not for specific chemistries.36
. In ref. 22, it was found that λ0 ≈ 50 and χ ≈ −2kBT, which shall mainly be used in this study. Therefore, our theory has no free fitting parameters in terms of the associations in the SiILs. This feature is achieved as all the parameters needed to predict the EDL structure can be determined from the bulk SiIL. Explicitly one can extract λ0, χ, and integer bounds on f+ and f− from MD simulations of the SiIL system at various salt compositions and the volume ratios are backed out by molecular data of the species composing the SiIL. Alternatively, one can use integral equations and Wertheim’s formalism to determine the association constants without fitting association constants from MD simulations.65–72 However, this is only accessible for certain cases, such as charged hard spheres with known Mayer f-functions for interacting species, and not for specific chemistries.36
Taking the functional derivative of the free energy with respect to the electrostatic potential, we arrive at the Poisson equation,
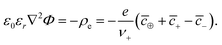 | (21) |
From this equation, we can define the inverse Debye length 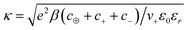 , which will be used to convert distances from the electrode to dimensionless values. The Poisson–Boltzmann (PB) equation follows from a mean-field approximation of Coulomb interactions, which is technically only valid in the dilute limit of point-like ions in a uniform dielectric continuum.73–75 Many modified PB equations are available which involve corrections for finite ion sizes, Coulomb correlations, and non-local dielectric response.63,76–82 In our simple model, such corrections are captured indirectly through their short-range associations, which is to promote the formation of ionic clusters with “spin glass” ordering favoring oppositely charged neighbors.83
, which will be used to convert distances from the electrode to dimensionless values. The Poisson–Boltzmann (PB) equation follows from a mean-field approximation of Coulomb interactions, which is technically only valid in the dilute limit of point-like ions in a uniform dielectric continuum.73–75 Many modified PB equations are available which involve corrections for finite ion sizes, Coulomb correlations, and non-local dielectric response.63,76–82 In our simple model, such corrections are captured indirectly through their short-range associations, which is to promote the formation of ionic clusters with “spin glass” ordering favoring oppositely charged neighbors.83
To solve the system of equations and the Poisson equation, we use the following procedure. First, we calculate bulk properties from eqn (20) using the association constant. Next we solve our closure relations, eqn (15)–(17), with eqn (20) and the incompressibility condition in the EDL (1 = ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + +
+ + ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) − +
− + ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕), as we need 6 equations to solve for our 6 unknowns, to obtain the relationships between
⊕), as we need 6 equations to solve for our 6 unknowns, to obtain the relationships between ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) +,
+,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) −,
−,![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕ and Φ, on a regular grid of Φ. We then use this mapping between Φ and
⊕ and Φ, on a regular grid of Φ. We then use this mapping between Φ and ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) to numerically solve the Poisson equation. Note that this procedure is similar to that of ref. 55, but where we now also solve the Lagrange multiplier, Λ, to account for the different sizes of each species.
to numerically solve the Poisson equation. Note that this procedure is similar to that of ref. 55, but where we now also solve the Lagrange multiplier, Λ, to account for the different sizes of each species.
An informative quantity to understanding the EDL can be the differential capacitance, C, also known as the double layer capacitance,
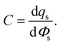 | (22) |
III. Results
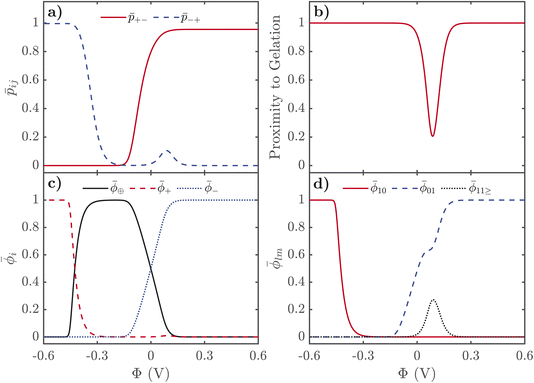
Here we describe the predictions of the model in detail. As the theory heavily relies on previous work for SiILs in the bulk, we suggest the reader is first acquainted with ref. 22. Moreover, reading ref. 55 might help the reader put into context the predictions for the EDL. In all of the results shown in the main text, we choose the following parameters. A mole fraction of alkali metal salt of xs = 0.01 is chosen, which is quite small, and was motivated by ensuring that no gelation occurs for all potentials for the rest of the parameters used. For the functionalities, we choose f+ = 5 and f− = 3, inspired by previous work.22 We have chosen χ = −2kBT and λ0 = 50, which correspond to values previously used for SiILs.22 Finally, we choose ξ+ = 1, ξ− = 7, ξ⊕ = 7. Some predictions of the model highly depend on these parameters. We have included calculations in the ESI† for how the results depend on these parameters.In Fig. 2, we display the solutions to our equations as a function of electrostatic potential. The displayed plot does not correspond to an actual physical situation; but it allows us to first understand the response of SiILs to applied potentials before describing how all of these changes are distributed in space as a function of distance from the electrified interface. First, we focus on the changes in the total volume fractions of each species, i = ⊕, +, −, as a function of potential as seen in Fig. 2c. For positive applied potentials, there is a large increase in ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) −, which plateaus at 1 at 0.2 V, while the IL cations,
−, which plateaus at 1 at 0.2 V, while the IL cations, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕, are monotonically expelled from the EDL. Interestingly, there is an increase in the volume fraction of alkali metal cations,
⊕, are monotonically expelled from the EDL. Interestingly, there is an increase in the volume fraction of alkali metal cations, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) +, at modest applied positive potentials, before the volume fraction decreases to 0 at large applied positive voltages. For negative potentials, the anions are monotonically expelled from the EDL but the response of the cations is more complex. At small to moderate voltages, the IL cation dominates the EDL, and saturates at
+, at modest applied positive potentials, before the volume fraction decreases to 0 at large applied positive voltages. For negative potentials, the anions are monotonically expelled from the EDL but the response of the cations is more complex. At small to moderate voltages, the IL cation dominates the EDL, and saturates at ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕ ≈ 1 at a potential of −0.25 V. At potentials more negative than −0.3 V, a cation exchange occurs, where the IL cations are replaced by metal cations,
⊕ ≈ 1 at a potential of −0.25 V. At potentials more negative than −0.3 V, a cation exchange occurs, where the IL cations are replaced by metal cations, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) ⊕ ≈ 0 and
⊕ ≈ 0 and ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + ≈ 1.
+ ≈ 1.
A cation exchange occurs at negative voltages because of the competition between the different sizes of the cations, and its position is dependent on the strong associations between the metal cations and the anions. At small potentials, the IL cations first populate the EDL because they are not strongly interacting with the anions, which are pushed out of the EDL and take the alkali metal cations with them through the associations. At large negative voltages, it would be expected that the smallest cation populates the EDL, as this maximises the charge density in the EDL and reduces its length. Therefore, it is expected that the smaller alkali metal cation saturates the EDL at large negative voltages instead of the larger IL cation. If both cations are the same size, this cation exchange does not occur as the IL cation remains in the EDL. There is a critical voltage at which this cation exchange occurs, which depends not only on the sizes of the cations but also the association constant between the alkali metal cation and the anion. For larger association constants, the alkali metal cation is more strongly bound to the anions, which means it requires larger fields to break these associations to obtain the cation exchange. In the ESI† we show how the cation exchange depends on these parameters in more detail.
Next we describe the association probabilities as a function of applied voltage, as seen in Fig. 2a. At large negative potentials, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) +− = 0 and
+− = 0 and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+ = 1, which is expected if there is
−+ = 1, which is expected if there is ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + = 1 and
+ = 1 and ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) − = 0 when
− = 0 when ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) is large. This can be understood by considering trace amounts of IL anions in alkali metal cations. In this case, it would expected that the alkali metal picked at random is rarely associated with an IL anion; but, any IL anion picked at random would be associated with alkali metal cations. Similarly, for large positive potentials
is large. This can be understood by considering trace amounts of IL anions in alkali metal cations. In this case, it would expected that the alkali metal picked at random is rarely associated with an IL anion; but, any IL anion picked at random would be associated with alkali metal cations. Similarly, for large positive potentials ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+ = 0 and
−+ = 0 and ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) +− = 1 because of
+− = 1 because of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) − = 1 and
− = 1 and ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + = 0 when
+ = 0 when ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) is large. These limits are also discussed in detail in ref. 55. At a voltage of ∼0.1 V, however, there is also a peak in
is large. These limits are also discussed in detail in ref. 55. At a voltage of ∼0.1 V, however, there is also a peak in ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+, which occurs because there is an increase in the volume fraction of alkali metal cations. These cations are brought to the EDL from the strong associations with the anions, and therefore, results in electric field induced associations in the EDL. This can be further seen in Fig. 2b, which displays the proximity to gelation, 1-
−+, which occurs because there is an increase in the volume fraction of alkali metal cations. These cations are brought to the EDL from the strong associations with the anions, and therefore, results in electric field induced associations in the EDL. This can be further seen in Fig. 2b, which displays the proximity to gelation, 1-![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) +−
+−![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+(f+ − 1)(f− − 1). Here the proximity to gelation measures how close the clusters are to having the capacity to potentially form an infinite cluster, i.e. proximity to percolation. The criterion for percolation for clusters with a cation–anion associated backbone has been previously derived to occur when 1 = (f+ − 1)(f− − 1)
−+(f+ − 1)(f− − 1). Here the proximity to gelation measures how close the clusters are to having the capacity to potentially form an infinite cluster, i.e. proximity to percolation. The criterion for percolation for clusters with a cation–anion associated backbone has been previously derived to occur when 1 = (f+ − 1)(f− − 1) 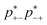 ,50 where
,50 where 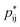 indicates the critical association probability for gelation. From this, we can define the proximity to gelation as 1 −
indicates the critical association probability for gelation. From this, we can define the proximity to gelation as 1 − ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) +−
+−![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+(f+ − 1)(f− − 1) as when it approaches zero the system will approach gelation and as it becomes negative more of the system will be in the gel phase. At most voltages, especially large ones, the system is far from being a gel. At no applied field, the system is not close to the gel point; but as a positive potential is applied, the system gets closer and closer to forming a gel. At an applied potential of ∼0.1 V, the system almost reaches the gel point before the electric field induced associations in the EDL are destroyed in favour of the saturation regime of anions at large potentials. There have been suggestions of similar effects in other electrolyte EDLs.84
−+(f+ − 1)(f− − 1) as when it approaches zero the system will approach gelation and as it becomes negative more of the system will be in the gel phase. At most voltages, especially large ones, the system is far from being a gel. At no applied field, the system is not close to the gel point; but as a positive potential is applied, the system gets closer and closer to forming a gel. At an applied potential of ∼0.1 V, the system almost reaches the gel point before the electric field induced associations in the EDL are destroyed in favour of the saturation regime of anions at large potentials. There have been suggestions of similar effects in other electrolyte EDLs.84
Finally, we describe the response of free ions and aggregates as seen in Fig. 2d. As expected, the volume fraction of free alkali metal cations are practically 0 until the cation exchange has occurred at voltages more negative than −0.3 V. There are still many free anions at no applied voltage owing to the highly asymmetric mixture of the electrolyte. As positive potentials are applied, the volume fraction of free anions increases until 0.1 V, when a plateau occurs. This plateau occurs at the same voltage as the bump in ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+, as the additional anions accumulating in the EDL are not free, but are associating to the additional alkali metal cations in the EDL. For larger potentials, the saturation regime of anions is reached, and the volume fraction of anions reaches 1.
−+, as the additional anions accumulating in the EDL are not free, but are associating to the additional alkali metal cations in the EDL. For larger potentials, the saturation regime of anions is reached, and the volume fraction of anions reaches 1.
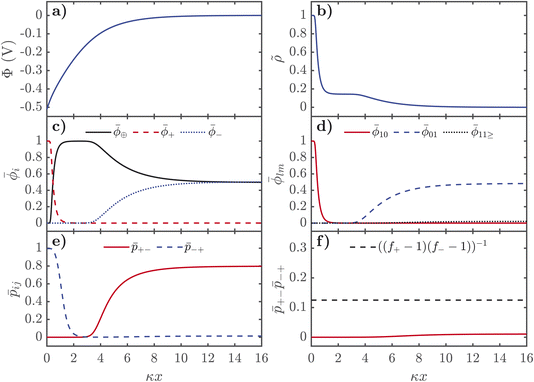
The description of the EDL properties displayed in Fig. 2 allows us to now understand the distributions of ions and association probabilities in the EDL. In Fig. 3, we show the properties of the EDL for negatively charged interfaces. In Fig. 4, we display similar figures but for positively charged interfaces. All plots are shown as a function from the electrified interface, in dimensionless units of distance, normalised by the inverse Debye length, κ, here 1/κ is λD ∼ 0.3 Å for the EDL plots presented here. These plots were produced from numerically solving the grids shown in Fig. 2 in the Poisson equation, shown in eqn (21).
For negative voltages, the electrostatic potential decays in an exponential-like way to 0 in the bulk, as seen in Fig. 3a. The charge density starts from 0 in the bulk, and first reaches a plateau of ∼1/7, in units of the number of lattice sites, which corresponds to the saturation regime of the IL cation, before the cation exchange occurs and the dimensionless charge density saturates at 1, i.e. the alkali metal cation saturates the EDL. As seen in Fig. 3c, the cation exchange is now separated in space. Close to the interface, we find alkali metal cations are saturating the high field. After this dense layer of alkali metal cations, there is an additional saturation layer of the IL cations where the anions are also depleted. Naturally, there is a strong increase of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 10 from the free cations right near the interface and a depletion of free anions
10 from the free cations right near the interface and a depletion of free anions ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 01 occurs further out from the interface. At negative potentials, there is only a monotonic destruction of aggregates, which can also be understood from
01 occurs further out from the interface. At negative potentials, there is only a monotonic destruction of aggregates, which can also be understood from ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) +−
+−![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+, which can be used to quantify the gel transition, which also monotonically decreases.
−+, which can be used to quantify the gel transition, which also monotonically decreases.
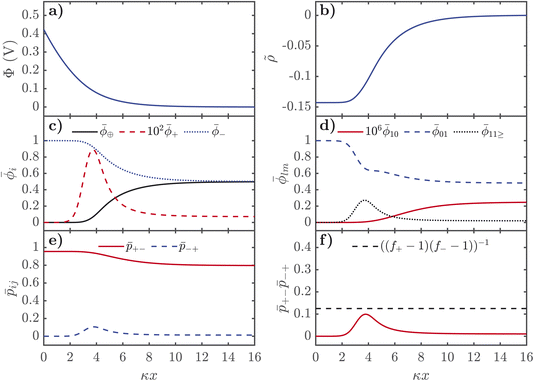
For positive voltages, the behaviour is more complex as seen in Fig. 4. The electrostatic potential decays in a monotonic way from the interface and the charge density has the typical saturation curve of a Fermi-like function.77,85 The structure of the electrolyte is complex despite these relatively simple-appearing electrostatic potential and charge density distributions. As seen in Fig. 4c, the total volume fraction of anions monotonically increases and the IL cation volume fraction monotonically decreases towards the interface. The alkali metal cations, however, have a strongly non-monotonic dependence, as shown in Fig. 4 where the volume fraction has been scaled up by a factor of 100 to make it more visible. Approaching the interface from the bulk, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + dramatically increases, before reaching a peak, to then dramatically decrease in the saturation regime of the anions. Interestingly, as seen in Fig. 4d, this increase in
+ dramatically increases, before reaching a peak, to then dramatically decrease in the saturation regime of the anions. Interestingly, as seen in Fig. 4d, this increase in ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + exclusively corresponds to the formation of large aggregates in the EDL at moderate voltages, as can be seen from
+ exclusively corresponds to the formation of large aggregates in the EDL at moderate voltages, as can be seen from ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 10 monotonically decreasing towards the interface and a large peak in
10 monotonically decreasing towards the interface and a large peak in ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 11>. This large peak in
11>. This large peak in ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) 11> also appears as a peak in
11> also appears as a peak in ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+ in the EDL, as well as
−+ in the EDL, as well as ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) −+
−+![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) +− approaching the critical gel line. Therefore, there are intermediate regions in space of the EDL at positive voltages, where the SiIL becomes more aggregated than in the bulk. This finding is in contrast to previous theories of the EDL with associations, which only predicted the destruction of associations. This finding comes generally from the asymmetry of the interactions, functionality, size and number of species found in the SiIL. However, even with these asymmetries, there are specific compositions of SiIL and parameters such that the electric field induced associations are not present. The system will be most aggregated when the product of the association probabilities is maximized, which is not necessarily guaranteed to occur at zero voltage when asymmetries are present. The observation of electric field induced associations has been seen before in MD simulations of other electrolyte systems;84,86,87 a similar theory to the one presented here may be capable of explaining those observations.
+− approaching the critical gel line. Therefore, there are intermediate regions in space of the EDL at positive voltages, where the SiIL becomes more aggregated than in the bulk. This finding is in contrast to previous theories of the EDL with associations, which only predicted the destruction of associations. This finding comes generally from the asymmetry of the interactions, functionality, size and number of species found in the SiIL. However, even with these asymmetries, there are specific compositions of SiIL and parameters such that the electric field induced associations are not present. The system will be most aggregated when the product of the association probabilities is maximized, which is not necessarily guaranteed to occur at zero voltage when asymmetries are present. The observation of electric field induced associations has been seen before in MD simulations of other electrolyte systems;84,86,87 a similar theory to the one presented here may be capable of explaining those observations.
Overall, the EDL of SiILs is more complex than ILs. At negative voltages, the EDL has three regimes in space: (1) the bulk, where associations occur to create small negative aggregates (note this is for the xs chosen here, see ref. 22 for the more general case); (2) moderate distances in the EDL, where the IL cation dominates; and (3) small distances a saturation layer of alkali metal cations. Similarly for positive voltages, there are three regimes in space: (1) the bulk, where associations occur to create small negative aggregates; (2) moderate distances in the EDL, where the change in composition occurs as large aggregates appear from electric field induced associations; and (3) the saturation regime close to the interface. This is analogous to the overscreening-saturation transition that is known to occur in ILs,78,79,88 and suggests that in SiILs it might be accompanied by dramatic changes in the associations. Moreover, the link between associations and overscreening was established in ref. 81, and further discussed in ref. 55. These associations occur without any visible feature in the charge density, and therefore, must be probed by computing the associations in the EDL through more sophisticated theories81 or through experimental means.
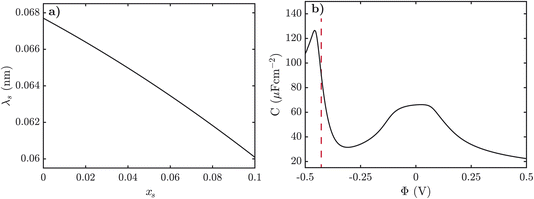
Next we turn to how the screening length, λs, varies with the mole fraction of alkali metal salt, xs, in the pre-gel regime. The screening length was extracted from fitting an exponential function to the electrostatic potential at small potentials for various xs. In Fig. 5a, we observe that as xs increases the screening length decreases. It is typically expected, however, that the screening length increases as the electrolyte becomes more associated, and as xs increases the SiILs becomes more associated. Here we find that the screening length actually decreases with xs because of the formation of small, highly charged aggregates, which is the opposite of conventional intuition.
Lastly, we predict the differential capacitance for SiILs as a function of potential, as shown in Fig. 5b. At low potentials the differential capacitance takes on a slightly asymmetrical bell shape.85 At large positive potentials, we observe the typical decay in differential capacitance.85,89 At negative potentials, however, the differential capacitance initially decays as expected from the saturation of the IL cations.85,89 However, at a critical potential we observe a large peak in differential capacitance which can be attributed to the cation exchange shortening the EDL. This satellite peak can be used to verify the predictions of our theory.
In the ESI,† we display additional plots and discuss the role of changing parameter and variable values from the values chosen in the main text.
IV. Discussion
In ref. 54, Haskins et al. performed molecular dynamics simulations for Li[TFSI] in [pyr14][TFSI] at electrified interfaces. For positive voltages, they found that the anions dominate the first layer of ions with some IL cations. After this layer, there is a sharp peak in alkali metal cations residing between layers of anions.54 The second peak of anions does not have an associated second peak of Li+ ions, which could indicate that the Li+ ions in between these peaks are associating to anions in multiple layers of the overscreening structure.54 Whereas at negative potentials, the IL cation dominates the first layer of the EDL, with no Li+ ions.54 In the second layer of ions, there is pronounced overscreening with an increase in the number density of anions accompanied by a dramatic increase in Li+ ions. In this second layer, large aggregates could be forming. These MD results are promising in confirming the possible electric field induced associations, but further MD simulations must be done to confirm the predictions of our theory. The EDL of SiILs is an extremely understudied problem and we hope our theory will provide a framework in which it can be understood.A few studies have looked at the differential capacitance of SiILs.54,90 In ref. 90, Yamagata et al. experimentally measured the differential capacitance of Li[TFSI] in [EMIM][FSI] and Li[TFSI] in [EMIM][TFSI] at negative potentials. In their experiments, they observe a significant difference between these two SiILs differential capacitance at large negative potentials in comparison to the neat ILs. For Li[TFSI] in [EMIM][FSI], they observe that at low potential the differential capacitance is lower than the neat IL; however for larger negative potentials, the SiILs differential capacitance grows significantly. The sharp rise in differential capacitance seen in the Li[FSI] in [EMIM][FSI] could be coming from a cation exchange occurring in the system. They proposed a schematic of their EDL for this system where the Li+ ion is the cation present at the interface, while still being associated with an FSI anion. In our theory, this peak in the differential capacitance comes from the cation exchange, which is a similar origin to that suggested by Yamagata et al.90 In contrast in the Li[TFSI] in [EMIM][TFSI] system, they do not see this differential capacitance growth at large negative potentials. They consider the EDL for this case to have the interface occupied by the EMIM cations and, therefore, has not undergone the cation exchange yet. This schematic is similar to what is predicted from the MD results in ref. 54, as discussed above. For certain parameters of our theory, we do not obtain this satellite peak from the cation exchange as shown in the ESI.†
Experimentally, it has been found that ILs and other concentrated electrolytes have extremely long force decay lengths as measured from surface force measurements.91–96 The assumption of Gebbie et al.91 was that these forces were electrostatic in origin, owing to a large renormalisation in the concentration of free charge carriers. While this topic remains controversial and unresolved,61,62,97,98 we would like to briefly highlight that the aggregation of the alkali metal cations and anions in SiILs was able to successfully explain the transport properties in these super-concentrated electrolytes.22,28,29 Therefore, aggregates could shed some light onto these measurements of surface force interactions in SiILs and long ranged interactions in other concentrated electrolytes. Recently, experimental evidence for the connection between the cluster-like (soft) structure in a SiIL composed of Na[TFSI] and [EMIM][TFSI], at various mole ratios, and long-range (non-exponentially decaying) surface forces was measured using surface forces apparatus.99 Furthermore, the long-ranged interactions point to the presence of aggregates with a high aspect ratio at the mica interfaces that contribute to the surface force, rather than a purely electrostatic origin. We believe that the theory described here could shed some light not only into these measurements, but also into the long ranged interactions in other concentrated electrolytes.91–96
We have chosen not to include the α-parameter introduced in ref. 57 and adopted in ref. 55. Therefore, the voltages in our curves are smaller than what is expected from MD simulations and experiments which should be kept in mind when interpreting the results. As outlined in ref. 55, there are also some conceptual and technical limitations with our presented theory. Firstly, overscreening, the alternating layers of cations and anions is represented through the thermo-reversible associations between the ions; but, the internal structure of these aggregates is not explicitly defined here. Therefore, we cannot explicitly obtain decaying oscillations in the charge density but need to recognise that overscreening is included through these associations. In SiILs, the electric field induced associations at positive voltages further complicates this problem. If the potential is oscillating, there will be positive potential values at both the cathode and anode. Thus, we might, in fact, predict that there are electric field induced associations at both charged interfaces. This will need to be further studied through MD simulations. In addition, our theory can describe well the diffuse EDL, but not the interfacial layer of ions, where a breakdown of the cluster distribution should occur and specific interactions with the electrode could dominate. This latter point could be predicted by the MD simulations of Haskins et al.54 which found that the IL cation prefers to reside in the first layer of ions, where we expect the alkali metal cations to dominate the saturation regime. However, this could also be a problem with short equilibration times of the simulations as discussed later.
The largest limitation of our theory is that we find the screening length is less than 1 Å. Since λs is smaller than an individual alkali metal cation (∼2.8 Å, as used in this work), and much less than the size of the small clusters predicted to be in the SiIL solution.77 This points to the theory not being self-consistent in terms of its electrostatic predictions, as is generally known to be a problem of mean-field lattice gas models which is discussed in detail in ref. 77. This common failing of mean-field theories can be corrected with more involved modified Poisson–Boltzmann equations that can account for higher-order correlations and/or non-local effects. This issue can be addressed to some extent in local mean field models such as by accounting for higher order local terms such as in BSK theory78 or via modifying the Coulomb interactions.82 However, typically to overcome this inconsistency, one must turn to a non-local model that can capture the entropic effects of excluded volume in a significantly better fashion. The issue from the current inconsistency indicates caution should be used when comparing the model’s predictions of the spatial profile of the ions and clusters near the surface.77 Importantly even with this inconsistency, mean-field models can have valuable predictive power in integrated quantities such as the capacitance of the double layer, the general trends in what accumulates in the EDL, and importantly, the new predictions for how association probabilities change within the EDL.
Finally, we have presented an analysis of the equilibrium properties of SiILs. One of the noteworthy properties of these systems is their transport properties. As outlined in ref. 36, the dynamics of this model can also be investigated, which could yield some interesting effects. Moreover as this system has an active cation for intercalation, developing the theory of coupled ion electron transfer reactions to include microscopic solvation effects could be a promising place to start.100,101
V. Conclusions
Here we have developed a theory for the electrical double layer (EDL) of salt-in-ionic liquids (SiILs). These electrolytes are interesting for applications in energy storage but their behavior at electrified interfaces is not well studied. Here, we found a highly asymmetric response of the SiILs in the EDL. At negative potentials, associations are destroyed in the EDL; but, a cation exchange can occur when the IL cation initially saturates in the EDL but is later replaced by the smaller, associating alkali metal cation. In contrast, the positive potentials predict there to be electric field induced associations, which may lead to gelation. At large positive voltages we obtain the saturation regime for anions. All of these EDL features appear to be captured in the predicted differential capacitance profile for SiILs. Overall, we hope that the predictions made by this theory will inspire further work from molecular dynamics simulations to understand these SiILs, or for experimental measurements to be performed to probe the cation exchange or electric field induced associations.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
D. M. M. & M. Z. B. acknowledge support from the Center for Enhanced Nanofluidic Transport 2 (CENT2), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award #DE-SC0019112. D. M. M. also acknowledges support from the National Science Foundation Graduate Research Fellowship under Grant No. 2141064. We gratefully acknowledge financial support from the National Science Foundation under grants DMR-1904681 and CBET-1916609 to R. M. E. M.References
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190 CrossRef CAS PubMed.
- A. Lewandowski and A. Świderska-Mocek, J. Power Sources, 2009, 194, 601 CrossRef CAS.
- A. Balducci, U. Bardi, S. Caporali, M. Mastragostino and F. Soavi, Electrochem. Commun., 2004, 6, 566 CrossRef CAS.
- K. Dokko, N. Tachikawa, K. Yamauchi, M. Tsuchiya, A. Yamazaki, E. Takashima, J.-W. Park, K. Ueno, S. Seki and N. Serizawa, et al. , J. Electrochem. Soc., 2013, 160, A1304 CrossRef CAS.
- K. Xu, Chem. Rev., 2014, 114, 11503 CrossRef CAS PubMed.
- L. G. Chagas, S. Jeong, I. Hasa and S. Passerini, ACS Appl. Mater. Interfaces, 2019, 11, 22278 CrossRef CAS PubMed.
- Q. Zhou, P. D. Boyle, L. Malpezzi, A. Mele, J.-H. Shin, S. Passerini and W. A. Henderson, Chem. Mater., 2011, 23, 4331 CrossRef CAS.
- D. Monti, E. Jónsson, M. R. Palacin and P. Johansson, J. Power Sources, 2014, 245, 630 CrossRef CAS.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621 CrossRef CAS PubMed.
- K. Matsumoto, J. Hwang, S. Kaushik, C.-Y. Chen and R. Hagiwara, Energy Environ. Sci., 2019, 12, 3247 RSC.
- T. C. Mendes, F. Zhou, A. J. Barlow, M. Forsyth, P. C. Howlett and D. R. MacFarlane, Sustainable Energy Fuels, 2018, 2, 763 RSC.
- J. Zhao, G. Gorbatovski, O. Oll, T. Thomberg and E. Lust, Electrochim. Acta, 2019, 319, 82 CrossRef CAS.
- T. Yamamoto and T. Nohira, Chem. Rec., 2023, 23, e202300169 CrossRef CAS PubMed.
- Q. Guo, P. Fan, Y. Zhang, L. Guan, H. Wang, A. Croft, and G. Z. Chen, RSC Sustainability ( 2024) Search PubMed.
- A. Basile, M. Hilder, F. Makhlooghiazad, C. Pozo-Gonzalo, D. R. MacFarlane, P. C. Howlett and M. Forsyth, Adv. Energy Mater., 2018, 8, 1703491 CrossRef.
- D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232 RSC.
- D. R. MacFarlane, M. Forsyth, P. C. Howlett, M. Kar, S. Passerini, J. M. Pringle, H. Ohno, M. Watanabe, F. Yan and W. Zheng, et al. , Nat. Rev. Mater., 2016, 1, 1 Search PubMed.
- T. Welton, Chem. Rev., 1999, 99, 2071–2084 CrossRef CAS PubMed.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654 CrossRef PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978 CrossRef CAS PubMed.
- M. McEldrew, Z. A. H. Goodwin, N. Molinari, B. Kozinsky, A. A. Kornyshev and M. Z. Bazant, J. Phys. Chem. B, 2021, 125, 13752 CrossRef CAS PubMed.
- B. Qiao, G. M. Leverick, W. Zhao, A. H. Flood, J. A. Johnson and Y. Shao-Horn, J. Am. Chem. Soc., 2018, 140, 10932 CrossRef CAS PubMed.
- M. Gouverneur, J. Kopp, L. van Wüllen and M. Schönhoff, Phys. Chem. Chem. Phys., 2015, 17, 30680 RSC.
- M. Gouverneur, F. Schmidt and M. Schönhoff, Phys. Chem. Chem. Phys., 2018, 20, 7470 RSC.
- M. Brinkkötter, A. Mariani, S. Jeong, S. Passerini and M. Schönhoff, Adv. Energy Sustainability Res., 2021, 2, 2000078 CrossRef.
- F. Ackermann and M. Schönhoff, J. Phys. Chem. C, 2021, 125, 266 CrossRef CAS.
- N. Molinari, J. P. Mailoa, N. Craig, J. Christensen and B. Kozinsky, J. Power Sources, 2019, 428, 27 CrossRef CAS.
- N. Molinari, J. P. Mailoa and B. Kozinsky, J. Phys. Chem. Lett., 2019, 10, 2313 CrossRef CAS PubMed.
- F. Chen and M. Forsyth, Phys. Chem. Chem. Phys., 2016, 18, 19336 RSC.
- P. Kubisiak, P. Wròbel and A. Eilmes, J. Phys. Chem. B, 2020, 124, 413 CrossRef CAS PubMed.
- T. C. Lourenco, L. G. Dias and J. L. Da Silva, ACS Appl. Energy Mater., 2021, 4444–4458 CrossRef CAS.
- N. Molinari and B. Kozinsky, J. Phys. Chem. B, 2020, 124, 2676 CrossRef CAS PubMed.
- J. B. Haskins, W. R. Bennett, J. J. Wu, D. M. Hernaández, O. Borodin, J. D. Monk, J. C. W. Bauschlicher and J. W. Lawson, J. Phys. Chem. B, 2014, 118, 11295 CrossRef CAS PubMed.
- X. Ren and T. Yan, J. Phys. Chem. B, 2023, 10434–10446 CrossRef CAS PubMed.
- Z. A. H. Goodwin, M. McEldrew, B. Kozinsky and M. Z. Bazant, PRX Energy, 2023, 2, 013007 CrossRef.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51 CrossRef CAS.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- W. H. Stockmayer, J. Chem. Phys., 1943, 11, 45 CrossRef CAS.
- W. H. Stockmayer, J. Chem. Phys., 1944, 12, 125 CrossRef CAS.
- W. H. Stockmayer, J. Polym. Sci., 1952, 9, 69 CrossRef CAS.
- F. Tanaka, Macromolecules, 1989, 22, 1988 CrossRef CAS.
- F. Tanaka, Macromolecules, 1990, 23, 3784 CrossRef CAS.
- F. Tanaka and W. H. Stockmayer, Macromolecules, 1994, 27, 3943 CrossRef CAS.
- F. Tanaka and M. Ishida, J. Chem. Soc., Faraday Trans., 1995, 91, 2663 RSC.
- M. Ishida and F. Tanaka, Macromolecules, 1997, 30, 3900 CrossRef CAS.
- F. Tanaka, Phys. A, 1998, 257, 245 CrossRef CAS.
- F. Tanaka and M. Ishida, Macromolecules, 1999, 32, 1271 CrossRef CAS.
- F. Tanaka, Polym. J., 2002, 34, 479 CrossRef CAS.
- M. McEldrew, Z. A. Goodwin, S. Bi, M. Z. Bazant and A. A. Kornyshev, J. Chem. Phys., 2020, 152, 234506 CrossRef CAS PubMed.
- M. McEldrew, Z. A. H. Goodwin, H. Zhao, M. Z. Bazant and A. A. Kornyshev, J. Phys. Chem. B, 2021, 125, 2677–2689 CrossRef CAS PubMed.
- M. McEldrew, Z. A. Goodwin, S. Bi, A. Kornyshev and M. Z. Bazant, J. Electrochem. Soc., 2021, 168, 050514 CrossRef CAS.
- D. Reber, R. Grissa, M. Becker, R.-S. Kühnel and C. Battaglia, Adv. Energy Mater., 2021, 11, 2002913 CrossRef CAS.
- J. B. Haskins, J. J. Wu and J. W. Lawson, J. Phys. Chem. C, 2016, 120, 11993 CrossRef CAS PubMed.
- Z. A. Goodwin, M. McEldrew, J. P. de Souza, M. Z. Bazant and A. A. Kornyshev, J. Chem. Phys., 2022, 157, 094106 CrossRef CAS PubMed.
- Z. A. Goodwin and A. A. Kornyshev, Electrochim. Acta, 2022, 434, 141163 CrossRef CAS.
- Z. A. Goodwin, G. Feng and A. A. Kornyshev, Electrochim. Acta, 2017, 225, 190 CrossRef CAS.
- M. Chen, Z. A. H. Goodwin, G. Feng and A. A. Kornyshev, J. Electroanal. Chem., 2018, 819, 347 CrossRef CAS.
- Z. A. H. Goodwin and A. A. Kornyshev, Electrochem. Commun., 2017, 82, 129 CrossRef CAS.
- Y. Zhang, T. Ye, M. Chen, Z. A. Goodwin, G. Feng, J. Huang and A. A. Kornyshev, Energy Environ. Mater., 2020, 3, 414–420 CrossRef CAS.
- G. Feng, M. Chen, S. Bi, Z. A. Goodwin, E. B. Postnikov, N. Brilliantov, M. Urbakh and A. A. Kornyshev, Phys. Rev. X, 2019, 9, 021024 CAS.
- P. Jones, F. Coupette and A. Härtel, et al. , J. Chem. Phys., 2021, 154, 134902 CrossRef CAS PubMed.
- E. Gongadze, U. van Rienen, V. Kralj-Iglič and A. Iglič, Comput. Methods Biomech. Biomed. Eng., 2013, 16, 463 CrossRef CAS PubMed.
- W. H. Stockmayer, J. Chem. Phys., 1943, 11, 45 CrossRef CAS.
- M. S. Wertheim, J. Stat. Phys., 1984, 35, 19 CrossRef.
- M. S. Wertheim, J. Stat. Phys., 1984, 35, 35 CrossRef.
- M. Wertheim, J. Stat. Phys., 1986, 42, 459 CrossRef.
- M. Wertheim, J. Stat. Phys., 1986, 42, 477 CrossRef.
- D. Laría, H. R. Corti and R. Fernández-Prini, J. Chem. Soc., Faraday Trans., 1990, 86, 1051 RSC.
- L. Blum and O. Bernard, J. Stat. Phys., 1995, 79, 569 CrossRef.
- J.-P. Simonin, O. Bernard and L. Blum, J. Phys. Chem. B, 1999, 103, 699 CrossRef CAS.
- F. Sciortino, E. Bianchi, J. F. Douglas and P. Tartaglia, J. Chem. Phys., 2007, 126, 194903 CrossRef PubMed.
- L. Guldbrand, B. Jönsson, H. Wennerström and P. Linse, J. Chem. Phys., 1984, 80, 2221 CrossRef CAS.
- R. Kjellander and S. Marčelja, Chem. Phys. Lett., 1986, 127, 402 CrossRef CAS.
- P. Grochowski and J. Trylska, Biopolymers, 2008, 89, 93 CrossRef CAS PubMed.
- R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 557 CrossRef CAS.
- M. Z. Bazant, M. S. Kilic, B. D. Storey and A. Ajdari, Adv. Colloid Interface Sci., 2009, 152, 48 CrossRef CAS PubMed.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- J. P. de Souza, Z. A. Goodwin, M. McEldrew, A. A. Kornyshev and M. Z. Bazant, Phys. Rev. Lett., 2020, 125, 116001 CrossRef CAS PubMed.
- J. P. de Souza, A. A. Kornyshev and M. Z. Bazant, J. Chem. Phys., 2022, 156, 244705 CrossRef CAS PubMed.
- Y. Avni, R. M. Adar and D. Andelman, Phys. Rev. E, 2020, 101, 010601 CrossRef CAS PubMed.
- R. M. Adar, S. A. Safran, H. Diamant and D. Andelman, Phys. Rev. E, 2019, 100, 042615 CrossRef CAS PubMed.
- A. Levy, M. McEldrew and M. Z. Bazant, Phys. Rev. Mater., 2019, 3, 055606 CrossRef CAS.
- Z. Yu, N. P. Balsara, O. Borodin, A. A. Gewirth, N. T. Hahn, E. J. Maginn, K. A. Persson, V. Srinivasan, M. F. Toney, K. Xu, K. R. Zavadil, L. A. Curtiss and L. Cheng, ACS Energy Lett., 2022, 7, 461 CrossRef CAS.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545 CrossRef CAS PubMed.
- A. Ahmadiparidari, S. Fuladi, L. Majidi, S. Plunkett, E. Sarnello, H. Gholivand, Z. Hemmat, S. Rastegar, S. N. Misal and N. Jimenez, et al. , J. Power Sources, 2021, 491, 229506 CrossRef CAS.
- P. Robin, N. Kavokine and L. Bocquet, Science, 2021, 373, 687 CrossRef CAS PubMed.
- Z. A. H. Goodwin, J. P. de Souza, M. Z. Bazant, and A. A. Kornyshev, Encyclopedia of Ionic Liquids, 2021, vol. 1 Search PubMed.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021502 CrossRef PubMed.
- M. Yamagata, N. Nishigaki, S. Nishishita, Y. Matsui, T. Sugimoto, M. Kikuta, T. Higashizaki, M. Kono and M. Ishikawa, Electrochim. Acta, 2013, 110, 181 CrossRef CAS.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674 CrossRef CAS PubMed.
- R. M. Espinosa-Marzal, A. Arcifa, A. Rossi and N. D. Spencer, J. Phys. Chem. Lett., 2014, 5, 179 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobes, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157 CrossRef CAS PubMed.
- M. Han, H. Kim, C. Leal, M. Negrito, J. D. Batteas and R. M. Espinosa-Marzal, Adv. Mater. Interfaces, 2020, 7, 2001313 CrossRef CAS.
- M. Han, R. Zhang, A. A. Gewirth and R. M. Espinosa-Marzal, Nano Lett., 2021, 21, 2304 CrossRef CAS PubMed.
- E. Krucker-Velasquez and J. W. Swan, J. Chem. Phys., 2021, 155, 134903 CrossRef CAS PubMed.
- R. M. Espinosa-Marzal, Z. A. H. Goodwin, X. Zhang and Q. Zheng, Am. Chem. Soc., 2023, 123–148 CAS.
- X. Zhang, Z. A. H. Goodwin, A. G. Hoane, A. Deptula, D. M. Markiewitz, N. Molinari, Q. Zheng, H. Li, M. McEldrew, B. Kozinsky, M. Z. Bazant, C. Leal, R. Atkin, A. Gewirth, M. W. Rutland and R. M. Espinosa-Marzal, ChemRxiv, 2024 DOI:10.26434/chemrxiv-2024-hs7sf.
- D. Fraggedakis, M. McEldrew, R. B. Smith, Y. Krishnan, Y. Zhang, P. Bai, W. C. Chueh, Y. S. Horn and M. Z. Bazant, Electrochim. Acta, 2021, 367, 137432 CrossRef CAS.
- M. Z. Bazant, Faraday Discuss., 2023, 246, 60–124 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4fd00021h |
| This journal is © The Royal Society of Chemistry 2024 |