Incorporating solvent effects in DFT: insights from cation exchange in faujasites

Abstract

Zeolites are versatile materials renowned for their extra-framework cation exchange capabilities, with applications spanning diverse fields, including nuclear waste treatment. While detailed experimental characterization offers valuable insight, density functional theory (DFT) proves particularly adept at investigating ion exchange in zeolites, owing to its atomic and electronic resolution. However, the prevalent occurrence of zeolitic ion exchange in aqueous environments poses a challenge to conventional DFT modeling, traditionally conducted in a vacuum. This study seeks to enhance zeolite modeling by systematically evaluating predictive differences across varying degrees of aqueous solvent inclusion. Specifically focusing on monovalent cation exchange in Na-X zeolites, we explore diverse modeling approaches. These range from simple dehydrated systems (representing bare reference states in vacuum) to more sophisticated models that incorporate aqueous solvent effects through explicit water molecules and/or a dielectric medium. Through comparative analysis of DFT and semi-empirical DFT approaches, along with their validation against experimental results, our findings underscore the necessity to concurrently consider explicit and implicit solvent effects for accurate prediction of zeolitic ionic exchange.

---

1. Introduction

Microporous zeolites are recognized as highly effective adsorbent^1–3 and catalytic^4–7 materials. Their diverse utility can encompass water softening in detergent formulations,⁸ various biological and biomedical uses,^9–11 and even nuclear waste treatment.^12–15 With anticipated growth in nuclear power generation,¹⁶ a proven track record in decontaminating radioactive water,^17,18 and the rising significance to safely manage ¹³⁷Cs, zeolites are currently being considered as a key solution^15,19 to address potential hazards^20–23 linked to Cs⁺ radionuclide contamination.

One primary property of zeolites is their ability to participate in extra-framework cation exchange processes. These processes can also markedly impact adsorption behavior and selectivity depending on the cation species. For example, Pirngruber et al. demonstrated that the environmentally friendly capture of CO₂ was stronger in Cs- and K-Y zeolites compared to Na- or Li-Y.²⁴ Regarding the sequestration of highly toxic iodine species, computational²⁵ and experimental²⁶ studies have highlighted the superior adsorption capacity of Cu-FAU and Ag-FAU, while zeolites with H⁺ showed inferior performance. Given the intrinsically diverse behaviors of zeolites, there has been a concerted effort within the scientific community to comprehensively understand the cation distribution within distinct zeolite extra-frameworks.^27–32 Nevertheless, characterizing these systems can be intricate, especially when solvents are present.

Computational modeling offers explicit resolution of individual sites and control in the presence of ions/molecules at each site. This lends itself well to the study of zeolite exchange/adsorption. For instance, density functional theory (DFT) methods have been used to assess the thermodynamics of relative exchanges at distinct sites.^33,34 Moreover, DFT has played a role in deepening our insights into mechanistic adsorption behaviors^35,36 and interactions between the adsorbent and zeolite.^37,38 However, conventional DFT calculations are typically conducted under vacuum conditions, whereas numerous exchange and adsorption processes take place within aqueous environments. The inclusion of solvent effects in computational modeling has been primarily confined to techniques involving molecular dynamics^39–41 or ab initio molecular dynamics,^37,41 although certain studies have implemented the use of semi-empirical potentials.^42,43 The optimal DFT approach for including solvent effects as well as the requisite extent of explicit solvent modeling, remains an open question.

Frising and Leflaive conducted a comprehensive review of previous experimental studies on cation distribution in exchanged samples of X and Y zeolites.²⁹Fig. 1 depicts the distribution of Li⁺, K⁺, and Rb⁺ in exchanged X samples at sites II and III and shows that exchange can take place at both these sites for these cations. Li⁺ exhibits a distinct preference for site II over site III. In the case of K⁺, empirical data shows more variability, with a little over half of the reports indicating a preference for site II. The data for Rb⁺ was limited, with only two reports – one favoring site II and the other site III. To our knowledge, there are no additional reports on Rb⁺ distribution in X zeolite. In our study, we demonstrate that by incorporating high levels of physics and chemistry in the DFT model (via employment of explicitly hydrated models within a dielectric medium), these experimental findings can be reproduced. However, it is essential to note that integrating this additional physics and chemistry into the modeling approach not only improves accuracy but also significantly increases the computational complexity and cost.

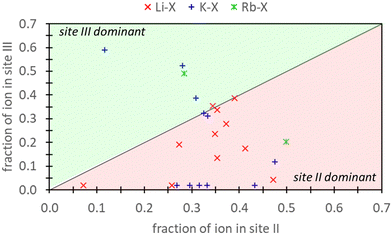Fig. 1 The atomic fraction of Li⁺, K⁺, Rb⁺ ions observed in site III versus site II of X zeolites as reported from experimental work reviewed by Frising and Leflaive.²⁷ Note that atomic fraction should not sum to 1.0 since cations can also be in other sites (e.g., I or I′) which are not depicted here.

Our investigation aims to contribute to zeolite modeling by assessing predictive variances across different degrees of solvation. The objective is to identify optimal DFT methodologies and strategies for treating reference states when modeling solvated exchange processes. Focusing on monovalent cation exchange in Na-X zeolites, we analyze exchange energies ranging from simple dehydrated systems (bare configurations in vacuum) to more elaborate models that incorporate aqueous solvation effects through explicit water molecules and/or a dielectric medium. Our investigation specifically centers on sites II and III within Na-X zeolites, chosen as representative cases due to their heightened propensity for ionic exchange in comparison to site I and I′.²⁹ Despite the omission of inner-cage sites, the modeling of exchange energies at sites II and III can present greater complexity when accounting for solvation effects due to higher ion density within the super cage. Hence, our findings are anticipated to possess broader relevance in understanding implications of diverse modeling approaches in elucidating exchange phenomena within faujasite and, likely, other zeolites.

The remainder of this paper is organized as follows. Section 2 outlines our methodology. Section 3 presents our results, including both quantitative and qualitative assessments, while Section 4 engages in a discussion regarding the comparative analysis and effectiveness of different modeling approaches. Section 5 concludes our work with a summary of key findings and implications for the various exchange models.

2. Computational model and methodology

2.1. Density functional theory calculations

Plane-wave density functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP).^44–46 The Kohn–Sham equations were solved self-consistently until energies reached an accuracy of 10⁻⁶ eV. Atomic positions were fully relaxed until forces were smaller than 0.02 eV Å⁻¹ per atom. Chemical behaviors were modeled using the generalized gradient approximation (GGA), Perdew–Burke–Ernzehof (PBE) exchange correlation functionals⁴⁷ and the projector augmented wave (PAW)^48,49 method. The inner-core s and p electrons were also treated as valence states for Li, Na, K, and Rb atomic species, while standard valence potentials were used for Al, O, and Si atoms. A plane-wave cutoff energy of 700 eV was used and systems were sampled using a 1 × 1 × 1 Monkhorst–Pack k-point grid.⁵⁰ The cutoff energy was chosen as the maximum cutoff for inner-core potentials reached as high as 650 eV. To describe long-range interactions the DFT-D2 Grimme dispersion correction method was also used.⁵¹

2.2. Faujasite structure

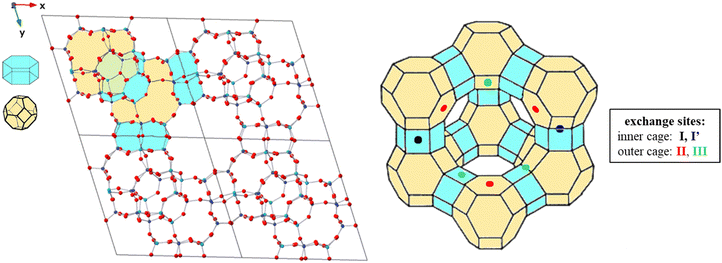
Faujasites are made up of face sharing sodalite cages and d6mr hexagonal prisms that come together to create a crystal in the Fd3̄m symmetry space group (Fig. 2). These cubic cell structures are commonly available in open databases with lattice parameters a = b = c = 24.345 Å and chemical formula Si₁₉₂O₃₈₄.^52,53 To make computational calculations more feasible, a primitive rhombohedral cell of the Na-X zeolite consisting of 144 atoms^25,34 was used, with the chemical formula Na₂₀Al₂₀Si₂₈O₉₆ (Fig. 2). The cationic distribution explored was based on previous experimental/computational works.^29,54 Single site exchange models were created by replacing one Na⁺ ion with a different metal cation at each potential adsorption site.

Fig. 2 Supercell of bare X model used (left) and 2D schematic of the faujasite framework (right) with unique exchange sites shown. The sodalite and d6mr building units are highlighted in yellow and blue, respectively. Green regions on the left depict both sodalite and d6mr from the perspective shown. O atoms are shown in red, H atoms in pink, Al in blue, Si in cyan.

2.3. Reference state models (with and without solvent inclusion)

Fig. 3 illustrates the various reference states used to model the exchange process. In the simplest form, all reference states were dehydrated (labelled D, Fig. 3) such that metal cations were modeled as a bare ion in a 20 Å × 20 Å × 20 Å vacuum box, while zeolite models retained their primitive structure (in vacuum) as described in Section 2.2.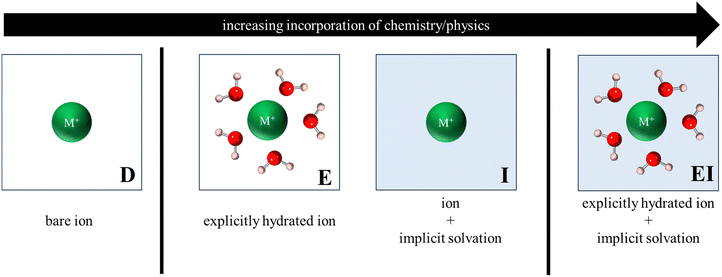

Fig. 3 Depiction of various reference states used to model the exchange process. Only ion reference states are shown for clarity and labels shown are to help denote the type of reference state.

To account for solvation effects, three different approaches were considered, each with varying levels of physical and chemical sophistication. The first approach involved reference states in which atoms/structures were explicitly hydrated (labelled E, Fig. 3), with the hydrated cluster being modeled in vacuum. The second approach incorporated an implicit water environment (labelled I, Fig. 3) in the reference states by applying a polarizable continuum model (PCM) via VASPsol^55–57 and a relative permittivity value of 78.36. Lastly, a hybrid approach was analyzed, wherein explicitly hydrated reference states were modeled within implicit water (labelled EI, Fig. 3). It is noteworthy that this final approach encompasses the most comprehensive representation of physical and chemical interactions and, consequently, carries the highest level of complexity and computational cost.

Calculations of Li⁺ exchange in implicit water led to significant Li⁺ ion mobility within the dielectric medium. We attribute this to the small size of Li⁺; indeed, earlier work on systems involving Li⁺ suggested lowering the explicit cut-off charge density parameter, η_c.^58,59 However, the choice of η_c results in substantial variations in the final optimization results. Consequently, a comprehensive investigation of VASPsol application to Li⁺ systems is warranted but falls beyond the scope of this study. Therefore, we proceed to focus only on K⁺ and Rb⁺ exchange. However, since preliminary calculations on Li⁺ exchange were conducted, for completeness, the results are detailed in the ESI.†

Explicitly solvated ions were hydrated by n water molecules, where n was assigned from experimental characterization. Specifically, for Na⁺ and K⁺, n = 4 waters^60,61 while for the much larger Rb⁺, n = 8 waters.⁶² In the case of zeolite models, ions in the outer cage (i.e., super cage) were hydrated by 2–3 waters, depending on their spatial orientation and involvement in cation exchange. The ramifications of varying hydration numbers within zeolite sites are discussed in Section 3.

2.4. DFT approach for modeling exchange energies

The exchange process with and without explicit water can be respectively represented as,

Na₂₀X + M⁺ → MNa₁₉X + Na⁺ (i)

Na₂₀X·wH₂O + M(H₂O)_n⁺ → MNa₁₉X·wH₂O + Na(H₂O)₄⁺ + (n − 4)H₂O (ii)

where M⁺ is the cation species K⁺ or Rb⁺ and w is the number of water present in zeolite models. Recall that n is the number of waters hydrating K⁺ or Rb⁺ in their respective reference state. Based on these processes, the exchange energies at each site can be determined by taking the sum of total energies of the products minus the sum of total energies of the reactants,

E_exch,DFT = E_Na⁺,Ω + E_MNa19X,Ω − E_M⁺,_Ω − E_Na20X,Ω (1)

where E_Na⁺ is the energy of Na⁺ ion, E_MNa19X is the energy of the exchanged zeolite, E_M⁺ is the energy of K⁺/Rb⁺ ion, E_Na20X is the energy of Na-X, and Ω is either D, I, E, or EI (from Fig. 3) denoting the reference state being modeled.

2.5. Semi-empirical approach for modeling exchange energies

The ion exchange energy can also be calculated by a process in which the ion reference state is represented as its respective chemical potential.^42,43,63 Based on processes (i) and (ii) the exchange energy in vacuum can be defined as,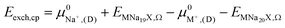where μ_Na⁺,(D)⁰ is the DFT calculated total energy of bare Na⁺ ion in vacuum and μ_M⁺,(D)⁰ is the DFT calculated total energy of a bare K⁺/Rb⁺ ion in vacuum. For systems in water, the chemical potential for ions in eqn (2) is replaced with the solution ion chemical potential, μ_A,(aq)⁰, as proposed by Persson et al.,⁶³

μ⁰_A,(aq) = μ^0,exp_A(aq) + [Δh^0,DFT_(s) − Δh^(0,exp)_s] (3a)

μ⁰_A,(aq) = μ^0,exp_A(aq) + Δμ^0,DFT−exp_(s) (3b)

where μ^0,exp_A(aq) is the experimentally calculated standard chemical potential for a respective aqueous ion,⁶⁴ Δμ^0,DFT−exp_(s) is a correction term based on formation enthalpies, Δh^0,DFT_(s) is the formation energy calculated for Na-, K-, and Rb-chlorides from DFT, and Δh^(0,exp)_s is the experimental formation enthalpies taken from Gunn.⁶⁵ The calculated chemical potentials for ions in vacuum and in water are provided in Table S2 in the ESI.† It is noteworthy that in this case, only the reference states of the zeolites are being modeled directly from DFT.

3. Results

3.1. Hydration number benchmark for explicitly solvated zeolite models

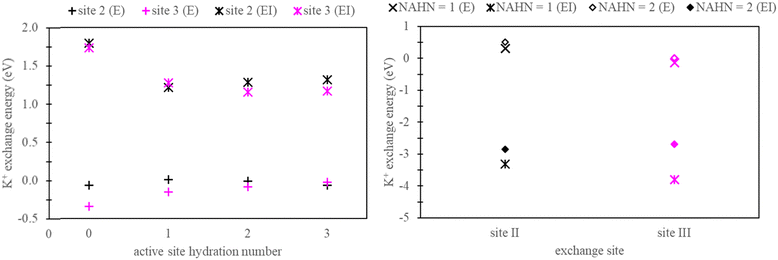
Henceforth, sites facilitating ion exchange will be referred to as “active sites”, while locations devoid of exchange will be referred to as “non-active sites”. In the context of generating explicitly solvated zeolite models, a crucial aspect involves determining the hydration numbers (HNs) of active and non-active sites. To address this, we conducted a series of benchmarks, using K⁺ exchange as a test case.

For active sites, a simplified faujasite model was used with a Si/Al ratio of 47, ensuring the presence of only one active site throughout the model. In this specific instance, the faujasite model has a chemical formula, Na₁A1₁Si₄₇O₉₆. Calculations were conducted to examine exchanges occurring at site II and site III by selectively substituting Si with Al in the zeolite structure at these respective sites. Fig. 4 presents the exchange energy relative to the active site hydration number (AHN) of the ion. Our analysis reveals that convergence is not achieved until AHN reaches 2, a conclusion drawn from assessments conducted in both vacuum and implicit solvation conditions.

Fig. 4 K⁺ exchange energy relative to active site hydration number (left) and calculated K⁺ exchange energy at sites II and site III with zeolite models containing non-active site hydration numbers (NAHN) 1 and 2 (right) in vacuum and implicit water.

In the context of non-active sites in NaX zeolite, explicit hydration is imperative to inhibit the dehydration of the active sites. In this study, our focus is on site II and site III exchange within the super cage. Therefore, explicit hydration was not incorporated within the inner cage of the faujasite model. As a test case, K⁺ exchange was performed in NaX zeolite, as outlined in Section 2.2. These calculations used zeolite models with non-active site hydration numbers (NAHN) set to either 1 or 2, alongside AHN of 3. The results for K⁺ exchange at sites II and III in these models are also depicted in Fig. 4. As expected, minimal differences were observed between systems with NAHN values of 1 and 2 when calculations were done in vacuum. However, in implicit water, discrepancies were observed, especially in the case of site III K⁺ exchange.

Based on the findings presented in Fig. 4, we adopted explicitly solvated zeolite models characterized by an AHN of 3 and NAHN of 2 for the remainder of this study. Two Na-X structures were generated: one where the active site is at site II and the other where the active site is at site III. To obtain the energy associated with ion exchange exclusively, active site Na⁺ ion was replaced with K⁺/Rb⁺ and a selective dynamic relaxation approach was used; this method involved immobilizing water molecules at non-active sites during the relaxation process, ensuring consistency between Na-X and K⁺/Rb⁺ exchanged Na-X zeolites. In particular, only the active sites were allowed to relax in K⁺/Rb⁺ exchanged zeolites. Additional details on the process for generating hydrated zeolite models are given in the ESI.†

3.2. Thermodynamic estimation of exchange energies using various DFT modeling approaches

To evaluate the quantitative accuracy of various DFT modeling approaches, the exchange energies for K⁺ and Rb⁺ exchange in Na-X were computed using each method described in Fig. 3. Additionally, for comprehensive coverage, the exchange energies derived from unconventional method combinations (e.g., bare ion with hydrated zeolite, hydrated ion with bare zeolite, etc.) were also obtained, although these are not recommended. Detailed results from these unconventional approaches are available in the ESI.†

Fig. 5 presents the predicted exchange energies for K⁺, and Rb⁺ ions. Given the superior physical underpinning of the hybrid EI method, which considers both explicit and implicit water, we consider its results as the most reliable. The explicit inclusion of water molecules captures the intricate interactions between water, the zeolite framework, and exchanged ions. Simultaneously, the implicit incorporation of a dielectric medium, based on water, ensures a more encompassing model of electrostatic interactions between the zeolite, cations, and water solvent when immersed in an aqueous environment. This representation is expected to provide a more comprehensive understanding of zeolite ion exchange. Consequently, we designate the EI method as the benchmark for comparative analysis within our study of zeolite ion exchange phenomena. The EI method reveals that both sites II and III demonstrate favorable exchanges for K⁺ and Rb⁺. In contrast, the D and I method yields unfavorable exchange for these cations at both sites. The E method suggests that only Rb⁺ is conducive to exchange in sites II and III and aligns with the EI method solely in predicting favorable exchange for Rb⁺. Notably, none of the other methods replicate the same outcomes as the EI method for K⁺ ion. It is important to note that even though the E method for Rb⁺ is in qualitative agreement with the EI method, it is not in quantitative agreement.

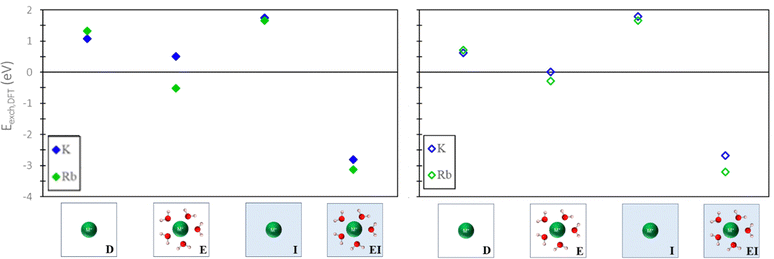Fig. 5 Site II (left) and site III (right) exchange energies predicted from DFT calculations using various reference states to model the exchange process. Labels and images describe the type of reference state used for both zeolite and ions as described in Fig. 3.

3.3. Qualitative prediction of site II versus III exchange using various DFT modeling approaches

The nature of the predictions on relative site exchange can be evaluated by examining the differences in exchange energies between site II and III. For example,

ΔE_exch = E_exch,II − E_exch,III (4)

where E_exch,II is the exchange energy at site II and E_exch,III is the exchange energy at site III. Fig. 6 illustrates the energy differences (ΔE_exch) for systems modeled using the four methods shown in Fig. 3. For detailed results from the unconventional combination of methods, please refer to the ESI.†

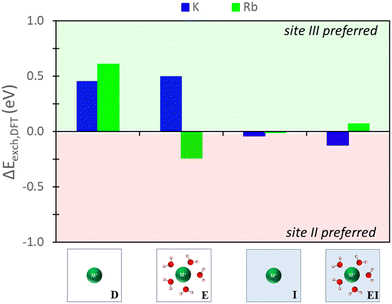Fig. 6 Energy differences between site II and site III ion exchange in Na-X predicted from DFT calculations using various reference states to model the exchange process. Labels and images describe the type of reference state used for zeolite and ions as described in Fig. 3.

The hybrid EI method indicates that K⁺ and Rb⁺ exchange show a slight preference for site II and III, respectively, although the difference is not substantial. The D method suggests significant favorability in site III for K⁺ and Rb⁺. Using the E method results in similar trends for K⁺, but Rb⁺ is now more favorable in site II. Conversely, the I method predicts little favorability towards site II or site III across both cations.

3.4. Predictions from semi-empirical DFT calculations

The exchange energies for sites II and III (Fig. 7) and their energy differences were also calculated using semi-empirical calculations (Section 2.5). For methodological consistency, exchange energies were computed using zeolite reference states in both vacuum (D and E) and implicit water (I and EI). This involved employing chemical potentials of the ions in vacuum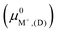 and aqueous solution (μ⁰_A,(aq)), respectively, as defined by eqn (2). Most modeling methods for zeolites reference states yielded unfavorable exchange for K⁺ and Rb⁺. However, favorable exchanges at sites II and III were observed for both ions when the EI method was employed. Exchange energy differences obtained from semi-empirical calculations were nearly identical to that of DFT results. To avoid redundancy, semi-empirical energetic differences are reported in Fig. S5 in the ESI.†

Fig. 7 Site II (left) and site III (right) exchange energies predicted from semi-empirical calculations using various zeolite reference states. Labels denote the specific reference state employed (Fig. 3) and the images denote that only zeolite reference states were modeled with DFT.

4. Discussion

4.1. Impact of water solvation on ion and zeolite reference states

To understand the influence of aqueous solvation on reference states, the relative bond distances between the active site cation, zeolite framework, and water molecules, as applicable, were evaluated. Consistency between our comparative analyses was also ensured by tracking only the minimum bond distance between the cation (M⁺), zeolite oxygen (O_z), and water oxygen (O_w). Fig. 8 illustrates that aqueous solvation effects have minimal impact on M⁺–O_z coordination (<0.3 Å). Additionally, comparisons between the M⁺–O_w in zeolite reference states used in E and EI methods indicated negligible impact between cation and water oxygen from the inclusion of a PCM solvent model. This observation further extends to M⁺–O_w distances in ion reference states (Fig. S11 in ESI†) where changes were also <0.3 Å. Zeolite synthesis typically involves calcination and/or drying treatments post-zeolitic ion exchange in water.^66–68 Our findings (Fig. 8 and Fig. S11, ESI†) indicate minimal differences of M⁺ position under hydrated versus dry conditions. Notably, our analysis primarily focuses on thermodynamic considerations and does not extend to kinetic-driven positional changes. Alternative modeling methods like AIMD may offer additional insight in this regard, but they are beyond the scope of this study.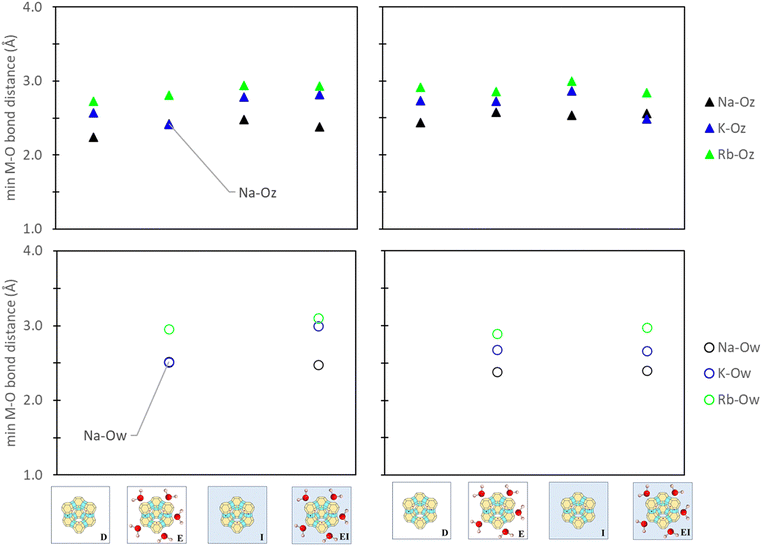

Fig. 8 Minimum cation-to-oxygen bond distances between the cation-zeolite oxygen (M–O_z) and cation-water oxygen (M–O_w) in zeolite site II (left) and site III (right) reference states. Labels denote the specific reference state employed (Fig. 3) and the images denote that only zeolite reference states are being analyzed.

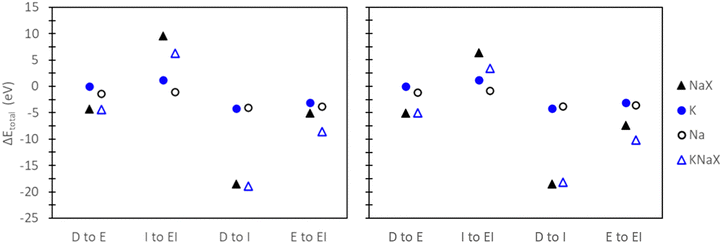
To elucidate the variations in E_exch,DFT predictions across different methods (Fig. 5), a thorough examination of the total energies used in eqn (1) was conducted. Two distinct solvation effects were investigated: (1) the impact of explicit water inclusion, as observed in the comparison of D to E, and I to EI methods and (2) the impact of implicit water inclusion, evident in the comparison of D to I and E to EI methods. Notably, the comparative analyses yielded consistent results for K⁺ and Rb⁺. Therefore, to avoid redundancy, only analysis related to K⁺ reference states will be discussed, though, its implications extend to Rb⁺ exchange. For results on Rb⁺ exchange reference states please refer to Fig. S9 in the ESI.†

In the comparisons of D to I and E to EI, a decreasing trend in E_exch,DFT was observed with the explicit inclusion of water. Examination of the change in total energy observed by each reference state (Fig. 9) reveals that the decrease between D to E can be attributed to the ion reference states, while the decrease between I to EI is influenced by both the ion and zeolite reference states. In the context of employing an implicit water bath to reference states without explicit water, comparing D to I shows an increase in E_exch,DFT. Interestingly, the origin of this increase is contingent on the modeled exchange site. As depicted in Fig. 9, the rise in E_exch,DFT for site II is attributed to the ion reference states, while the increase in E_exch,DFT for site III results from contributions of both ion and zeolite reference states. Comparing E to EI results, where an implicit water bath is applied to reference states already containing explicit water, the decrease in E_exch,DFT is primarily associated with the zeolite reference state (Fig. 9). These analyses show that the origin of the trends observed for E_exch,DFT across different methods are inconsistent and depend on the context in which solvation effects are included.

Fig. 9 Change in total energies of reference states when comparing different modeling approaches used for calculating the exchange energy of K⁺ with Na-X in site II (left) and site III (right). Closed symbols denote total energies of reactants while open symbols denote total energies of products in the exchange process.

4.2. DFT versus semi-empirical modeling on cation exchange

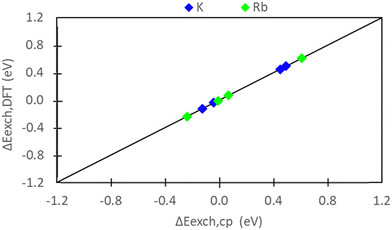
Comparing Fig. 5 and 7, we observe consistent results between pure DFT and semi-empirical calculations. Specifically, the hybrid EI method predicts favorable K⁺ and Rb⁺ exchange at sites II and III, while the D and I methods indicate unfavorable exchange for both ions. The only discrepancy pertains to Rb⁺ exchange predicted by the E method. Semi-empirical calculations suggest unfavorable Rb⁺ exchange at sites II and III, whereas DFT predicts slight favorability at these sites. Fig. 10 systematically evaluates the similarity/differences between DFT and semi-empirical predictions for preferential site exchange by depicting a parity plot of ΔE_exch,DFT (Fig. 6) versus ΔE_exch,cp (Fig. S5, ESI†). In this context, all methods exhibit alignment.

Fig. 10 Parity plot of predicted differences in exchange between sites II and III using pure DFT and semi-empirical calculations. Note that there are four data points, each correlating to exchange energy differences using the D, E, I and EI methods to model zeolite and ion (for pure DFT) reference states.

Given that DFT and semi-empirical predictions largely agree and draw from the same energetic data for zeolite reference states, the effectiveness of DFT in handling ion reference states is evident. It is important to note that there are no significant computational cost differences between semi-empirical and DFT calculations. Both approaches require computationally modeling zeolite reference states, which is the most resource-intensive component in predicting exchange energies. The purely DFT approach does have the advantage of not necessitating experimental input, and thus can be used for systems in which the experimental data required for the semi-empirical approach is not available or not of sufficient accuracy.

4.3. Computational predictions versus experimental results

Ultimately, the relative validity of DFT and semi-empirical calculations necessitates comparison against experimental data. Concerning aqueous ion exchange, the DFT and semi-empirical approaches are equally able to match experiment. Fig. 1 provides experimental evidence that ion exchange in sites II and III are favorable for both K⁺ and Rb⁺. Our analysis reveals that agreement between experimental and computational predictions is attained under specific conditions. For K⁺ exchange, alignment between DFT/semi-empirical and experimental results is exclusively observed when employing the EI method. In contrast, for Rb⁺ exchange, agreement is found when using the E and EI methods for DFT, but only with the EI method for semi-empirical calculations. Notably, the energetic values from the DFT E method are markedly close to 0 eV.

Fig. 1 also illustrates a slight preference for site II K⁺ exchange over site III. In this context, only the EI method within DFT/semi-empirical calculations yield predictions consistent with experimental trends. Due to limited experimental data, definitive conclusions cannot be drawn for Rb⁺ exchange. However, our findings indicate that Rb⁺ exchange is thermodynamically equally favored at both sites II and III.

Given that the semi-empirical approach relies on experimental data to describe ion reference states, the disparity in computational modeling and experimental characterization appears to primarily originate from DFT treatment of zeolite reference states. The EI method stands out in predicting both quantitative and qualitative trends that agree with experimental observations. In contrast, other methods with less sophisticated solvation treatment do not exhibit such consistency. These findings underscore the necessity of employing a hybrid explicit-implicit solvation approach alongside contemporary DFT techniques to effectively model exchange processes in a solvent environment.

5. Conclusion

The evaluation of pure DFT and semi-empirical DFT methodologies as well as strategies for representing reference states was conducted. The ion exchange process of K⁺ in Na-X was chosen as a representative case due its extensive prior research history.²⁹ Additionally, we explored Rb⁺ exchange to provide novel thermodynamic insights. These exchange processes were modeled using reference states represented at varying degrees of aqueous solvation: a bare configuration in vacuum (D method), an explicitly hydrated system in vacuum (E method), a bare configuration in implicit water (I method), and a configuration with both explicit and implicit hydration (EI method).

Previous research has established that K⁺ and Rb⁺ exchange is favorable at sites II and III in X zeolites.²⁹ Our findings demonstrate that the EI method is necessary for accurate thermodynamic predictions of ion exchange in zeolites using DFT modeling. The other methods examined failed to predict favorable K⁺ exchange, with only the E method coinciding with EI in predicting favorable Rb⁺ exchange, although the energetic values were close to 0 eV. K⁺ distribution in X zeolites is also slightly dominant in sites II over III,²⁹ indicating a preference for site II over site III. In this context, the EI method is consistent with previous experimental findings.

A thorough analysis of active site coordination and total energy of reference states yielded additional insights into the influence of aqueous solvation effects. Our examination of active site coordination revealed minimal changes in bond distances between the cation, zeolite, and water, as applicable, across the various methods. Furthermore, the origin of the differences in predicted exchange energies among methods was found to be inconsistent, with variations in the most influential reference states depending on the context in which the solvation effects were incorporated.

Analysis of semi-empirical DFT modeling showed favorable exchange energies only when zeolite reference states were represented using the EI method. Comparative analysis revealed that pure DFT and semi-empirical calculations exhibit similar quantitative and qualitative performance. Since semi-empirical DFT modeling relies on experimental data to represent aqueous ion reference states, the treatment of zeolite reference states (including its degree of solvation) is believed to be a significant determinant in accurately modeling exchange processes within solvent environments. The parity in performance between pure DFT and semi-empirical DFT approaches also highlights the equivalency of both methods for representing ions.

The present study offers a valuable resource for understanding the implications of modeling solvent effects with DFT. By evaluating various methods and approaches for incorporating solvent effects, we provide insights into diverse modeling techniques for ion exchange and established that accurate predictions necessitate the simultaneous explicit and implicit modeling of the solvent. These results are imperative for enhancing our understanding of the utility of DFT predictions and further advanced our understanding of Rb⁺ exchange in Na-X. Given the scarcity of experimental reports on Rb⁺ exchange in Na-X, we were unable to ascertain the relative exchange preference between sites II and III based on prior knowledge. However, our findings using the EI method indicate that Rb⁺ exchange exhibits little preference for either site II or site III.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Center for Hierarchical Waste Form Materials (CHWM), an Energy Frontier Research Center (EFRC) funded by the United States Department of Energy Office of Basic Energy Sciences through Award DESC0016574. We acknowledge University of Florida Research Computing for providing computational resources and support that have contributed to the research results reported in this publication.

References

1. C. Keawkumay, W. Rongchapo, N. Sosa, S. Suthirakun, I. Z. Koleva, H. A. Aleksandrov, G. N. Vayssilov and J. Wittayakun, Paraquat Adsorption on NaY Zeolite at Various Si/Al Ratios: A Combined Experimental and Computational Study, Mater. Chem. Phys., 2019, 238, 121824,  DOI:10.1016/j.matchemphys.2019.121824.
2. S. Komaty, A. Daouli, M. Badawi, C. Anfray, M. Zaarour, S. Valable and S. Mintova, Incorporation of Trivalent Cations in NaX Zeolite Nanocrystals for the Adsorption of O₂ in the Presence of CO₂, Phys. Chem. Chem. Phys., 2020, 22(18), 9934–9942,  10.1039/d0cp00111b.
3. Y. Chai, X. Han, W. Li, S. Liu, S. Yao, C. Wang, W. Shi, I. Da-Silva, P. Manuel, Y. Cheng, L. D. Daemen, A. J. Ramirez-Cuesta, C. C. Tang, L. Jiang, S. Yang, N. Guan, N. Guan and L. Li, Control of Zeolite Pore Interior for Chemoselective Alkyne/Olefin Separations, Science, 2020, 368(6494), 1002–1006,  DOI:10.1126/science.aay8447.
4. C. J. Plank, E. J. Rosinski and W. P. Hawthorne, Acidic Crystalline Aluminosilicates - New Superactive, Superselective Cracking Catalysts, Ind. Eng. Chem. Prod. Res. Dev., 1964, 3(3), 165–169,  DOI:10.1021/i360011a001.
5. M. Boronat and A. Corma, Factors Controlling the Acidity of Zeolites, Catal. Lett., 2015, 145(1), 162–172,  DOI:10.1007/s10562-014-1438-7.
6. C. Liu, I. Tranca, R. A. Van Santen, E. J. M. Hensen and E. A. Pidko, Scaling Relations for Acidity and Reactivity of Zeolites, J. Phys. Chem. C, 2017, 121(42), 23520–23530,  DOI:10.1021/acs.jpcc.7b08176.
7. Y. Chai, B. Qin, B. Li, W. Dai, G. Wu, N. Guan and L. Li, Zeolite-Encaged Mononuclear Copper Centers Catalyze CO₂ selective Hydrogenation to Methanol, Natl. Sci. Rev., 2023, 10(7), nwad04,  DOI:10.1093/nsr/nwad043.
8. D. Bajpai and V. K. Tyagi, Laundry Detergents: An Overview, J. Oleo Sci., 2007, 56(7), 327–340,  DOI:10.5650/jos.56.327.
9. S. Laurent, E. P. Ng, C. Thirifays, L. Lakiss, G. M. Goupil, S. Mintova, C. Burtea, E. Oveisi, C. Hébert, M. De Vries, M. M. Motazacker, F. Rezaee and M. Mahmoudi, Corona Protein Composition and Cytotoxicity Evaluation of Ultra-Small Zeolites Synthesized from Template Free Precursor Suspensions, Toxicol. Res., 2013, 2(4), 270–279,  10.1039/c3tx50023c.
10. S. Komaty, C. Anfray, M. Zaarour, H. Awala, V. Ruaux, S. Valable and S. Mintova, A Facile Route toward the Increase of Oxygen Content in Nanosized Zeolite by Insertion of Cerium and Fluorinated Compounds, Molecules, 2018, 23(2), 37,  DOI:10.3390/molecules23020037.
11. T. Duke, F. Wandi, M. Jonathan, S. Matai, M. Kaupa, M. Saavu, R. Subhi and D. Peel, Improved Oxygen Systems for Childhood Pneumonia: A Multihospital Effectiveness Study in Papua New Guinea, Lancet, 2008, 372(9646), 1328–1333,  DOI:10.1016/S0140-6736(08)61164-2.
12. R. Harjula, J. Lehto, J. H. Pothuis, A. Dyer and R. P. Townsend, Ion Exchange in Zeolites. Part 4. - Hydrolysis and Trace ¹³⁴Cs⁺ Exchange in K- and Na-Mordenite, J. Chem. Soc., Faraday Trans., 1993, 89(11), 1877–1882,  10.1039/FT9938901877.
13. P. K. Sinha, P. K. Panicker, R. V. Amalraj and V. Krishnasamy, Treatment of Radioactive Liquid Waste Containing Caesium by Indigenously Available Synthetic Zeolites: A Comparative Study, Waste Manage., 1995, 15(2), 149–157,  DOI:10.1016/0956-053X(95)00014-Q.
14. A. F. Gualtieri, D. Caputo and C. Colella, Ion Exchange Selectivity of Phillipsite for Cs⁺: A Structural Investigation Using the Rietveld Method, Microporous Mesoporous Mater., 1999, 32(3), 319–329,  DOI:10.1016/S1387-1811(99)00121-3.
15. H. Y. Lee, H. S. Kim, H. K. Jeong, M. Park, D. Y. Chung, K. Y. Lee, E. H. Lee and W. T. Lim, Selective Removal of Radioactive Cesium from Nuclear Waste by Zeolites: On the Origin of Cesium Selectivity Revaealed by Systematic Crystallographic Studies, J. Phys. Chem. C, 2017, 121(19), 10594–10608,  DOI:10.1021/acs.jpcc.7b02432.
16. M. Schneider; A. Froggatt; J. Hazemann; M. Ramana; M. Sailer; T. Suzuki; C. von Hirschhausen; A. J. Wimmers; N. Schneider and F. Meinass, The World Nuclear Industry Status Report 2022, Paris, 2022.
17. G. Brumfiel, Fukushima Set for Epic Clean-Up, Nature, 2011, 472, 146–147.
18. T. Kobayashi, M. Ohshiro, K. Nakamoto and S. Uchida, Decontamination of Extra-Diluted Radioactive Cesium in Fukushima Water Using Zeolite-Polymer Composite Fibers, Ind. Eng. Chem. Res., 2016, 55(25), 6996–7002,  DOI:10.1021/acs.iecr.6b00903.
19. E. Han, Y. G. Kim, H. M. Yang, I. H. Yoon and M. Choi, Synergy between Zeolite Framework and Encapsulated Sulfur for Enhanced Ion-Exchange Selectivity to Radioactive Cesium, Chem. Mater., 2018, 30(16), 5777–5785,  DOI:10.1021/acs.chemmater.8b02782.
20. S. V. Avery, Caesium Accumulation by Microorganisms: Uptake Mechanisms, Cation Competition, Compartmentalization and Toxicity, J. Ind. Microbiol., 1995, 14(2), 76–84,  DOI:10.1007/BF01569888.
21. J. E. Ten Hoeve and M. Z. Jacobson, Worldwide Health Effects of the Fukushima Daiichi Nuclear Accident, Energy Environ. Sci., 2012, 5(9), 8743–8757,  10.1039/c2ee22019a.
22. J. Beyea, E. Lyman and F. N. Von Hippel, Accounting for Long-Term Doses in “Worldwide Health Effects of the Fukushima Daiichi Nuclear Accident.”, Energy Environ. Sci., 2013, 1042–1045,  10.1039/c2ee24183h.
23. B. C. Russell, I. W. Croudace and P. E. Warwick, Determination of ¹³⁵Cs and ¹³⁷Cs in Environmental Samples: A Review, Anal. Chim. Acta, 2015, 7–20,  DOI:10.1016/j.aca.2015.06.037.
24. G. D. Pirngruber, P. Raybaud, Y. Belmabkhout, J. Čejka and A. Zukal, The Role of the Extra-Framework Cations in the Adsorption of CO₂ on Faujasite Y, Phys. Chem. Chem. Phys., 2010, 12(41), 13534–13546,  10.1039/b927476f.
25. M. Chebbi, S. Chibani, J. F. Paul, L. Cantrel and M. Badawi, Evaluation of Volatile Iodine Trapping in Presence of Contaminants: A Periodic DFT Study on Cation Exchanged-Faujasite, Microporous Mesoporous Mater., 2017, 239, 111–122,  DOI:10.1016/j.micromeso.2016.09.047.
26. B. Azambre, M. Chebbi and A. Hijazi, Effects of the Cation and Si/Al Ratio on CH₃I Adsorption by Faujasite Zeolites, Chem. Eng. J., 2020, 379, 122308,  DOI:10.1016/j.cej.2019.122308.
27. W. J. Mortier, Compilation of Extra Framework Sites in Zeolites, Butterworths & Co, Belgium, 1982 DOI:10.1016/0021-9797(82)90223-5.
28. C. Baerlocher; L. B. McCusker and D. H. Olson, Atlas of Zeolite Framework Types, Elsevier, Netherlands, 6th edn, 2007 DOI:10.1016/B978-0-444-53064-6.X5186-X.
29. T. Frising and P. Leflaive, Extraframework Cation Distributions in X and Y Faujasite Zeolites: A Review, Microporous Mesoporous Mater., 2008, 27–63,  DOI:10.1016/j.micromeso.2007.12.024.
30. F. Schüßler, E. A. Pidko, R. Kolvenbach, C. Sievers, E. J. M. Hensen, R. A. Van Santen and J. A. Lercher, Nature and Location of Cationic Lanthanum Species in High Alumina Containing Faujasite Type Zeolites, J. Phys. Chem. C, 2011, 115(44), 21763–21776,  DOI:10.1021/jp205771e.
31. W. Louisfrema, B. Rotenberg, F. Porcher, J. L. Paillaud, P. Massiani and A. Boutin, Cation Redistribution upon Dehydration of Na₅₈Y Faujasite Zeolite: A Joint Neutron Diffraction and Molecular Simulation Study, Mol. Simul., 2015, 41(16–17), 1371–1378,  DOI:10.1080/08927022.2015.1027889.
32. W. Li, Y. Chai, G. Wu and L. Li, Stable and Uniform Extraframework Cations in Faujasite Zeolites, J. Phys. Chem. Lett., 2022, 11419–11429,  DOI:10.1021/acs.jpclett.2c02969.
33. R. E. Fletcher, S. Ling and B. Slater, Violations of Löwenstein's Rule in Zeolites, Chem. Sci., 2017, 8(11), 7483–7491,  10.1039/c7sc02531a.
34. L. Sellaoui, E. P. Hessou, M. Badawi, M. S. Netto, G. L. Dotto, L. F. O. Silva, F. Tielens, J. Ifthikar, A. Bonilla-Petriciolet and Z. Chen, Trapping of Ag⁺, Cu²⁺, and Co²⁺ by Faujasite Zeolite Y: New Interpretations of the Adsorption Mechanism via DFT and Statistical Modeling Investigation, Chem. Eng. J., 2021, 420, 127712,  DOI:10.1016/j.cej.2020.127712.
35. J. Zheng, Y. Qin, Q. Li, L. Zhang, X. Gao and L. Song, A Periodic DFT Study of the Synergistic Mechanisms between Extraframework Aluminum Species and Brønsted Acid Sites in HY Zeolites, Ind. Eng. Chem. Res., 2020, 59(7), 2736–2744,  DOI:10.1021/acs.iecr.9b05277.
36. L. F. Capa-Cobos, X. Jaramillo-Fierro and S. González, Computational Study of the Adsorption of Phosphates as Wastewater Pollutant Molecules on Faujasites, Processes, 2021, 9(10), 1821,  DOI:10.3390/pr9101821.
37. H. Jabraoui, I. Khalil, S. Lebègue and M. Badawi, Ab Initio Screening of Cation-Exchanged Zeolites for Biofuel Purification, Mol. Syst. Des. Eng., 2019, 4(4), 882–892,  10.1039/c9me00015a.
38. H. Petitjean, C. Lepetit, Z. Nour, R. Poteau, I. del Rosal and D. Berthomieu, How CuI and NaI Interact with Faujasite Zeolite? A Theoretical Investigation, J. Phys. Chem. C, 2020, 124(51), 28026–28037,  DOI:10.1021/acs.jpcc.0c06862.
39. S. Chen, M. Zhu, Y. Tang, Y. Fu, W. Li and B. Xiao, Molecular Simulation and Experimental Investigation of CO₂ Capture in a Polymetallic Cation-Exchanged 13X Zeolite, J. Mater. Chem. A, 2018, 6(40), 19570–19583,  10.1039/c8ta05647a.
40. C. Hernandez-Tamargo, B. Kwakye-Awuah, A. J. O’Malley and N. H. de Leeuw, Mercury Exchange in Zeolites Na-A and Na-Y Studied by Classical Molecular Dynamics Simulations and Ion Exchange Experiments, Microporous Mesoporous Mater., 2021, 315, 110903,  DOI:10.1016/j.micromeso.2021.110903.
41. D. E. Resasco, S. P. Crossley, B. Wang and J. L. White, Interaction of Water with Zeolites: A Review, Catal. Rev.: Sci. Eng., 2021, 63(2), 302–362,  DOI:10.1080/01614940.2021.1948301.
42. V. Kocevski, B. D. Zeidman, C. H. Henager and T. M. Besmann, Communication: First-Principles Evaluation of Alkali Ion Adsorption and Ion Exchange in Pure Silica LTA Zeolite, J. Chem. Phys., 2018, 149(13), 131102,  DOI:10.1063/1.5051347.
43. V. Kocevski, S. Y. Hu and T. M. Besmann, Alkaline Earth Ion Exchange Study of Pure Silica LTA Zeolites Using Periodic First-Principles Calculations, New J. Chem., 2019, 43(43), 16835–16840,  10.1039/c9nj04091a.
44. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1016/0022-3093(95)00355-X.
45. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
46. G. Kresse and J. Furthmüller, Efficiency of Ab initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
48. P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
49. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
50. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
51. S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27(15), 1787–1799,  DOI:10.1002/jcc.20495.
52. W. H. Baur, On the Cation and Water Positions in Faujasite, Am. Mineral., 1964, 49, 697–704.
53. F. Porcher, M. Souhassou, Y. Dusausoy and C. Lecomte, The Crystal Structure of a Low-Silica Dehydrated NaX Zeolite, Eur. J. Mineral., 1999, 11(2), 333–344,  DOI:10.1127/ejm/11/2/0333.
54. G. Sastre, N. Katada, K. Suzuki and M. Niwa, Computational Study of Brønsted Acidity of Faujasite. Effect of the Al Content on the Infrared OH Stretching Frequencies, J. Phys. Chem. C, 2008, 112(49), 19293–19301,  DOI:10.1021/jp807623m.
55. M. Fishman, H. L. Zhuang, K. Mathew, W. Dirschka and R. G. Hennig, Accuracy of Exchange-Correlation Functionals and Effect of Solvation on the Surface Energy of Copper, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(24), 245402,  DOI:10.1103/PhysRevB.87.245402.
56. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit Solvation Model for Density-Functional Study of Nanocrystal Surfaces and Reaction Pathways, J. Chem. Phys., 2014, 140(8), 84106,  DOI:10.1063/1.4865107.
57. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory, J. Chem. Phys., 2019, 151(23), 234101,  DOI:10.1063/1.5132354.
58. N. Lespes and J. S. Filhol, Using Implicit Solvent in Ab Initio Electrochemical Modeling: Investigating Li⁺/Li Electrochemistry at a Li/Solvent Interface, J. Chem. Theory Comput., 2015, 11(7), 3375–3382,  DOI:10.1021/acs.jctc.5b00170.
59. A. Hagopian, M. L. Doublet and J. S. Filhol, Thermodynamic Origin of Dendrite Growth in Metal Anode Batteries, Energy Environ. Sci., 2020, 13(12), 5186–5197,  10.1039/d0ee02665d.
60. S. Varma and S. B. Rempe, Coordination Numbers of Alkali Metal Ions in Aqueous Solutions, Biophys. Chem., 2006, 124(3), 192–199,  DOI:10.1016/j.bpc.2006.07.002.
61. P. R. Smirnov and V. N. Trostin, Structure of the Nearest Surrounding of the Na⁺ Ion in Aqueous Solutions of Its Salts, Russ. J. Gen. Chem., 2007, 77(5), 844–850,  DOI:10.1134/S1070363207050052.
62. D. Z. Caralampio, J. M. Martínez, R. R. Pappalardo and E. S. Marcos, The Hydration Structure of the Heavy-Alkalines Rb⁺ and Cs⁺ through Molecular Dynamics and X-Ray Absorption Spectroscopy: Surface Clusters and Eccentricity, Phys. Chem. Chem. Phys., 2017, 19(42), 28993–29004,  10.1039/c7cp05346k.
63. K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Prediction of Solid-Aqueous Equilibria: Scheme to Combine First-Principles Calculations of Solids with Experimental Aqueous States, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(23), 235438,  DOI:10.1103/PhysRevB.85.235438.
64. E. Wiberg, Die Chemische Affinität, Verlag de Gruyter, Berlin, Germany, 2nd edn, 1972 DOI:10.1515/9783110826074.
65. S. R. Gunn, Heats of Formation at 25 Degree of Crystalline Hydrides and Aqueous Hydroxides of Rubidium and Cesium, J. Phys. Chem., 1967, 71(5), 1386–1390.
66. N. Birkner, V. Proust, J. Schaeperkoetter, A. T. Ta, A. Gossard, A. Daouli, M. Badawi, N. Cassell, S. Misture, S. R. Phillpot, H. C. zur Loye, K. S. Brinkman and A. Grandjean, Microstructure, Adsorption Site Energetics, and Formation Enthalpy Control for FAU-Zeolite Cs⁺ Exchange, Microporous Mesoporous Mater., 2024, 373, 113110,  DOI:10.1016/j.micromeso.2024.113110.
67. X. Chen, B. Shen, H. Sun and G. Zhan, Ion-Exchange Modified Zeolites X for Selective Adsorption Desulfurization from Claus Tail Gas: Experimental and Computational Investigations, Microporous Mesoporous Mater., 2018, 261, 227–236,  DOI:10.1016/j.micromeso.2017.11.014.
68. H. Mousavi, J. Towfighi Darian and B. Mokhtarani, Enhanced Nitrogen Adsorption Capacity on Ca²⁺ Ion-Exchanged Hierachical X Zeolite, Sep. Purif. Technol., 2021, 264, 1383–5866,  DOI:10.1016/j.seppur.2021.118442.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00467a

---