Open Access Article
Open Access ArticleExpanding the horizons of porphyrin metal–organic frameworks via catecholate coordination: exploring structural diversity, material stability and redox properties†
Siddhartha
De‡
a,
Georges
Mouchaham§
b,
Fangbing
Liu
a,
Maame
Affram
b,
Brian
Abeykoon
a,
Nathalie
Guillou
b,
Erwann
Jeanneau
a,
Jean-Marc
Grenèche
c,
Lhoussain
Khrouz
d,
Charlotte
Martineau-Corcos
b,
Lotfi
Boudjema
e,
Fabrice
Salles
 e,
Pablo
Salcedo-Abraira
e,
Pablo
Salcedo-Abraira
 f,
Gonçalo
Valente
g,
Manuel
Souto
f,
Gonçalo
Valente
g,
Manuel
Souto
 g,
Alexandra
Fateeva
g,
Alexandra
Fateeva
 *a and
Thomas
Devic
*a and
Thomas
Devic
 *f
*f
aLaboratoire des Multimatériaux et Interfaces, Université Lyon, Université Claude Bernard Lyon 1, UMR CNRS 5615, F-69622 Villeurbanne, France. E-mail: alexandra.fateeva@univ-lyon1.fr
bInstitut Lavoisier de Versailles, UMR 8180 CNRS UVSQ, Université Paris-Saclay, 45 Avenue des Etats-Unis, 78035 Versailles, France
cInstitut des Molécules et Matériaux du Mans, IMMM UMR CNRS 6283, Le Mans Université, Le Mans Cedex 9 F-72085, France
dENS de Lyon, CNRS, Université Claude Bernard Lyon 1, Laboratoire de Chimie UMR 5182, F-69342 Lyon, France
eICGM, Univ. Montpellier, CNRS, ENSCM, Montpellier, France
fNantes Université, CNRS, Institut des Matériaux de Nantes Jean Rouxel, IMN, F-44000 Nantes, France. E-mail: thomas.devic@cnrs-imn.fr
gDepartment of Chemistry, CICECO-Aveiro Institute of Materials, University of Aveiro, Aveiro, 3810-393, Portugal
First published on 3rd November 2023
Abstract
Porphyrin based Metal–Organic Frameworks (MOFs) have generated high interest because of their unique combination of light absorption, electron transfer and guest adsorption/desorption properties. In this study, we expand the range of available MOF materials by focusing on the seldom studied porphyrin ligand H10TcatPP, functionalized with tetracatecholate coordinating groups. A systematic evaluation of its reactivity with M(III) cations (Al, Fe, and In) led to the synthesis and isolation of three novel MOF phases. Through a comprehensive characterization approach involving single crystal and powder synchrotron X-ray diffraction (XRD) in combination with the local information gained from spectroscopic techniques, we elucidated the structural features of the solids, which are all based on different inorganic secondary building units (SBUs). All the synthesized MOFs demonstrate an accessible porosity, with one of them presenting mesopores and the highest reported surface area to date for a porphyrin catecholate MOF (>2000 m2 g−1). Eventually, the redox activity of these solids was investigated in a half-cell vs. Li with the aim of evaluating their potential as electrode positive materials for electrochemical energy storage. One of the solids displayed reversibility during cycling at a rather high potential (∼3.4 V vs. Li+/Li), confirming the interest of redox active phenolate ligands for applications involving electron transfer. Our findings expand the library of porphyrin-based MOFs and highlight the potential of phenolate ligands for advancing the field of MOFs for energy storage materials.
1. Introduction
The ubiquity of carboxylates is prominent in the field of Metal–Organic Frameworks (MOFs); however, alternative complexing groups are also being investigated with increasing interest. While azolates have shown promise when coupled with soft cations of low (typically +2) charge, oxygenated ligands are also appealing for building up new frameworks, especially those based on harder and highly charged (≥+3) cations. Thus, phenolate derivatives, in particular catecholates (cat2−, 1,2-dioxobenzene) and gallates (gal3−, 1,2,3-trioxobenzene), are of particular interest. This is because of their rather high basicity (pKa ≥ 9) and high charge density when fully deprotonated (≤−2), which could drive the formation of MOFs with higher chemical stability,1,2 while their non-innocent character is responsible for their unique electronic conductivity, redox activity and magnetic properties,3–24 leading to potential applications in gas sensing,25–30 electrochemical charge storage31–43 and electrocatalysis.44–47 While molecular and infinite (rod-like) carboxylate-based Secondary Building Units (SBUs) are well documented,48,49 less diversity is found for MOFs built up with pure catecholate and gallate ligands.To our knowledge, considering gallate, most of the porous structures rely on a single inorganic 1-D motif formulated as [Zr2(gal)]n,1,2,50–52 with the exception of a recently reported MOF made of tetrahydroxybenzoquinone (which might be considered as the smallest bis-gallate) and an octameric SBU formulated as FeIII/II8(gal)8.53,54
In contrast, the vast majority of MOFs with catecholate linkers are built up from isolated metal (II, III, and IV) ions surrounded by two (M(cat)2 or M(sq)2) or three (M(cat)3 or M(sq)3) ligands55–68 (with sq−˙ = semiquinolate, the hemi-oxidized form of catecholate). Only very recently (≥2019), examples of 3-D nets based on of polymetallic phenolate SBUs have appeared in the literature. Regarding molecular SBUs, one can mention the dimeric unit ZrIV2(OH)2(sq)6,69 the trimeric units FeIII3(H2O)2(cat)6 (ref. 47) and MIII3O(cat)3(sq)3 (M = Al, Ga, Fe)70,71 and the hexameric unit LnIII6(NO3)(cat)6 (Ln = Y, La, Eu).22,72 Two MOFs based on rod-like SBUs, [BiIII2O(H2O)2(cat)2]n73 and disordered [LnIII(OH)1+x(cat,sq)3]n,74,75 were also reported. All these SBUs have been yet observed in very few structures, and hence their use in designed reticular chemistry is still in its infancy.
For the specific case of functional porphyrin-based MOFs, carboxylate ligands again dominate the field although alternative complexing groups have also attracted interest.76 As part of our general interest in porphyrin-based MOFs, we focused our attention on tetracatechol porphyrins (H10TcatPP and NiH8TcatPP), depicted in Scheme 1 (for the synthesis procedures and NMR spectra see ESI Section 2, Fig. S1–S4†). Metal catecholates are indeed well suited for redox-active materials and enhanced charge transfer compared to carboxylate-based hybrid compounds.11,15,22,77 The free-base H10TcatPP was already reported in the literature to produce few poorly crystallized, moderately porous coordination polymers based on different transition metals (Fe, Co, Ni, Cu, and Ti). Nevertheless, none of these solids was structurally characterized.78–81 We also reported low dimensional supramolecular assemblies (SAs) composed of MIIIH7TcatPP (M = Fe, Mn, In), in which few phenolic oxygen atoms act as terminal ligands to define polymetallic (dimer, tetramer, and chain) entities.82 Eventually, in the course of the present work, a 3-D porous network based on this ligand and FeIII and InIII has been reported,83,84 and the proposed structure will be discussed later in this article.
 | ||
| Scheme 1 Chemical structures of the polyphenolic porphyrins H10TcatPP (left) and NiH8TcatPP (right) used in this work. | ||
We describe here the systematic investigation of the reactivity of both H10TcatPP and NiH8TcatPP with different M(III) (Fe, Al, In) cations. The optimization of synthesis parameters enables the successful isolation and growth of three porous phases as large single crystals. These MOFs are built up from three distinct inorganic SBUs (1D chain, 4-connected dimeric unit and 6-connected trimeric unit), whose formation is closely related to specific experimental parameters. The impact of the key parameters driving the SBU formation is discussed. The crystal structures of the resulting materials have been experimentally determined by both powder and single crystal X-ray diffraction techniques and further corroborated by classical geometry optimization calculations for one of them. Spectroscopic studies (UV-vis, NMR, EPR, and Mössbauer) provided valuable insights into the composition and the redox state of each material. The thermal and chemical stabilities, porosity, electrical conductivity and solid-state redox-activity of the MOFs were also assessed. This significant work not only advances the understanding of reactivity and MOF crystal growth but also broadens the scope of porous coordination network structures accessible for porphyrin-based solids.
2. Results and discussion
2.1. Synthesis
Three trivalent cations, namely Al(III), Fe(III) and In(III), presenting markedly different ionic radii (0.535, 0.645 and 0.80 Å, respectively)85 but known to commonly adopt an octahedral coordination environment when bound to catecholate ligands, were selected. Their reactivity with both free base (H10TcatPP) and Ni(II) metallated (NiH8TcatPP) porphyrins was investigated. It is important to note the diverse possible outcomes depending on the metal and linker used. In particular, when the free base H10TcatPP is combined with Fe(III) and In(III), metal chelation takes place leading to the formation of metalloporphyrin-based compounds that can be either MOFs or supramolecular assemblies (SAs). The latter ones arise from the axial coordination of a metal atom lying in the porphyrinic core to a catechol(ate) from another porphyrinic ligand. The SA formation is precluded in the case of Al(III) as its insertion into the porphyrinic core is incompatible with the synthesis conditions employed here. When combining the nickel porphyrin NiH8TcatPP with any of the investigated metals, SA formation is hindered due to the inherent square planar geometry of nickel.The syntheses were explored in both N,N-dimethylformamide (DMF) or N,N-diethylformamide (DEF), using metal chloride salts, with or without water, initially using the high-throughput solvothermal setup developed by Stock et al.86 The effect of organic (pyrazine (pz) and pyrocatechol (H2cat)) and inorganic (hydrochloric acid and potassium hydroxide) additives, as well as the reactant concentration, was also investigated. Regarding the formation conditions, it was found that rather high temperatures were favorable for the crystallization of MOFs (140 °C and above), that for all metals at least two phases could be isolated, and that the solvent composition was the main parameter controlling this pseudo-polymorphism. Although the associated phase diagram is rather complex, it is possible to qualitatively draw a scheme represented in Fig. 1. Overall, three new MOF phases were identified, initially with NiH8TcatPP and later obtained with a higher crystallinity starting from H10TcatPP, allowing their structure determination (Ga(III) was also used to solve the structure of one phase, see below). These solids are denoted as CatPMOF-1(M) to CatPMOF-3(M) and Ni-CatPMOF-1(M) to Ni-CatPMOF-3(M) depending on the nature of the porphyrin reactant. In addition to the MOF phases, four types of supramolecular assemblies (SA) were isolated in the case of Fe and In, which will not be discussed here in detail.
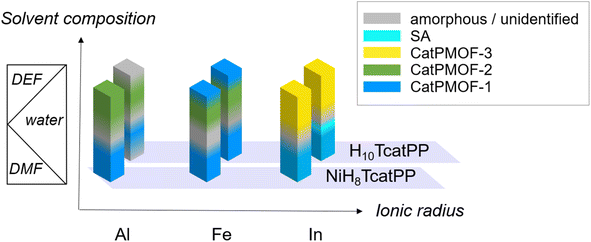 | ||
| Fig. 1 Qualitative phase diagram in the systems NiH8TcatPP-M(III) and H10TcatPP-M(III): influence of the nature of the cation and the solvent mixture (for synthesis at 150–160 °C). | ||
A similar trend is observed for the harder cations Al and Fe: the CatPMOF-1 phase is formed in DMF/H2O mixtures, but a high proportion of either water or formamide results in the formation of amorphous or unidentified solids. More importantly, the choice of the formamide again has a profound effect on the crystallized phase. While DMF leads exclusively to the formation of phase 1 (in agreement with recent reports83,84), its replacement by DEF promotes the formation of phase 2 (CatPMOF-2) based on a very different inorganic SBU and with larger pores (see below). Overall, this difference in reactivity observed for all the metals in DEF is tentatively attributed to a templating effect of the solvent and/or the presence of a small amount of dimethylamine, which can form helicoidal supramolecular assemblies92 promoting the formation of MOFs with larger pores.
2.2. Optimization of the crystal growth
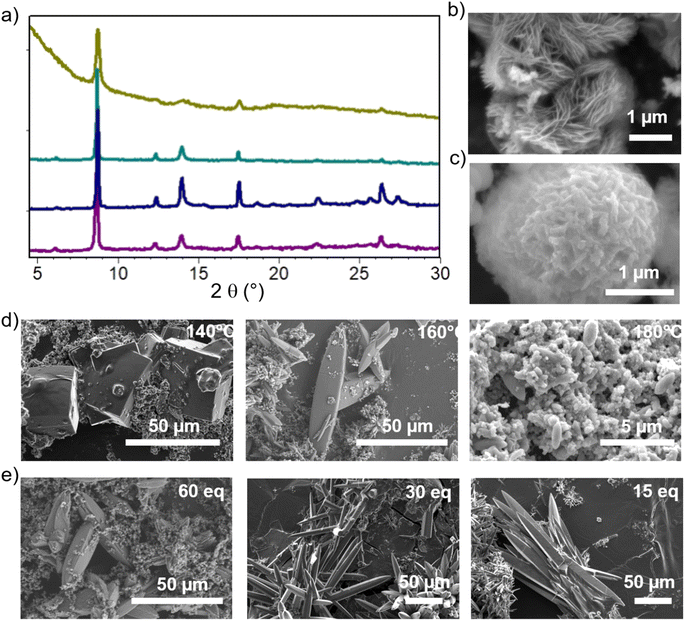
The optimized synthesis conditions for each phase are summarized in the ESI,† together with the corresponding powder X-ray diffraction (PXRD) patterns and the calculated patterns of each phase (Fig. S5†). The subsequent discussion focuses on the optimization of crystallinity for each phase. Notably, the addition of pyrocatechol (H2cat), acting as a modulator (see below), was generally favorable to enhance crystal growth. The discussion is structured in a way to highlight the key synthesis parameters to achieve high crystallinity for each material.For the CatPMOF-1(Fe)-pz phase, single crystal growth could be optimized by further adjusting the reaction temperature and modulator content. Note that as pyrazine easily coordinates to the iron located inside the porphyrin core, it precludes the formation of SA even at lower temperatures, and CatPMOF-1(Fe)-pz with good crystallinity is obtained from 140 °C to 160 °C; however a decrease in the crystal quality is observed at 180 °C (Fig. 2a and d). The reaction conditions were optimized at 150 °C and large crystals (>100 μm) are obtained by adjusting the modulator content (Fig. 2e).
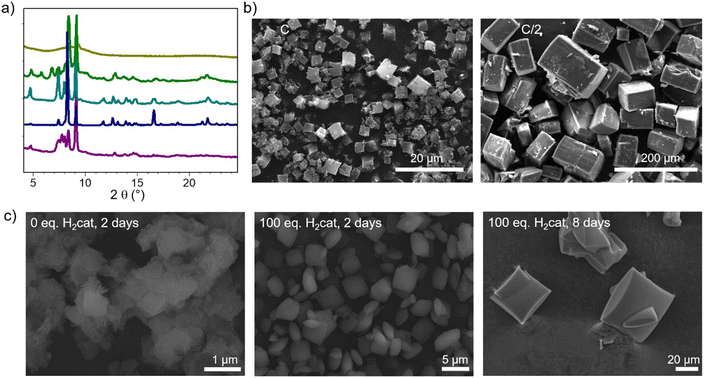
Regarding the formation of Ni-CatPMOF-2(Al), the addition of pyrocatechol (H2cat) was found to significantly enhance the quality of crystals. In the absence of H2cat, thin platelets of submicronic size are recovered, while the addition of 100 eq. of H2cat leads to the formation of 2–5 micrometer sized thicker platelets. We hypothesize that H2cat competes with the tetratopic ligand NiH8TcatPP to bind to the Al and thus acts as a modulator, decreasing the number of nuclei and slowing down the reaction, similar to what is found with monocarboxylic acids in the field of Zr-carboxylate (and to a lesser extent Ti-carboxylate) MOFs.95 This is supported by the fact that increasing the reaction time from 2 to 8 days in the presence of 100 eq. of H2cat produces crystals approximately ten times larger (Fig. 3c). This observation confirms that the H2cat significantly slows down the crystal growth rate. Steinert et al. recently showed that the addition of various monocarboxylic acids has no significant positive effect on the growth of Al-carboxylate MOFs (at least MIL-160) and attributed this to the relative inertness of such a cation.96 Given that catecholate presents a stronger affinity for Al(III) than carboxylate,97 this suggests that in addition to using modulators and ligands with similar binding strength as generally accepted,50 this binding strength must be high enough to achieve a proper control of the crystal growth.
Even larger single crystals can be grown from the free base porphyrin linker. The growth was optimized in the presence of 30 eq. of H2cat and among the parameters tested, the solution concentration has the most significant impact. When the concentration is halved, the resulting crystal size is increased over twenty times, yielding large (>100 μm) crystals of CatPMOF-2(Al) as evidenced in Fig. 3b. The reactant concentration affects both nucleation and crystal growth, but its impact on the former is a few orders of magnitude stronger. Therefore, our results indicate that slowing down the nucleation by reducing the concentration is the most effective pathway to increase the crystal size and quality in this case. This is different from what is observed for the third isolated phase CatPMOF-3(In) (see below) and is consistent with the higher Lewis acidity of Al compared to In, which makes Al centers more reactive.
To conclude, three different crystalline phases are formed and isolated under closely related synthetic conditions. The size of the cation seems to be important: when using DEF-water mixtures as a solvent, the CatPMOF-2 phase is found with the smallest cations (Al, Fe and in the case of Ga, see below), whereas the largest cation (In) gave rise only to the CatPMOF-3 phase under similar experimental conditions. With the DMF–water mixture, the CatPMOF-1 phase is observed for all cations. The pseudo-polymorphism observed here is reminiscent of that described for the Zr(IV)/tetrakis(4-carboxyphenyl)porphyrin (TCPP) system, for which several phases (MOF-525, MOF-545/PCN-222, PCN-225, NU-902, and PCN-224) also exist in a narrow range of experimental conditions.87–91 Nevertheless, they are all based on the same Zr6 unit, although presenting different connectivities (from 12 to 6). In the present study, as described below, the three phases are based on very different SBUs. Although it might be challenging to use the knowledge acquired here to a priori fully design new MOFs from other polycatechol linkers, the formation of one SBU vs. the other seems to be mainly driven by the nature of the solvent mixture. Hence, there is certainly great potential for discovering new compounds based on one of the SBUs identified in this study by using related synthesis conditions. Moreover, all the polyphenolate phases obtained in this work present a remarkably high degree of tunability in terms of crystallite morphology and size. Functional material properties are often related to their morphology and crystallite size and our study contributes to the advancement of crystal growth control strategies, which are highly relevant in materials chemistry.
2.3. Structure and material chemical composition determination
As shown above, crystals of hundreds of microns of phases CatPMOF-1(Fe)-pz, CatPMOF-2(Al) and CatPMOF-3(In) were successfully obtained. Their structures were accessed by using synchrotron radiation (beamline Cristal at Soleil, France) combining high resolution powder and single crystal XRD (PXRD and SCXRD, respectively), with the help of local information gained from solid-state UV-visible absorption spectroscopy, EPR, liquid and solid-state NMR spectroscopy (phases 2 and 3) and Mössbauer spectrometry (phase 1) as detailed below. It should be noted that although the crystals were rather large (for synchrotron radiation), structure determination was not straightforward, and final refinement required several restraints on interatomic distances even during the last stages. For this reason, the following discussion focuses on the nature of the building units and topologies, while accurate analysis of the local geometry (bond distances and angles…) would be irrelevant.More surprisingly, although residual electronic density was detected near the phenyl arms of the ligand, the heavy Fe cations building the SBU could not be located even using synchrotron datasets and lowering the symmetry. This suggests the occurrence of a complex crystal structure with an odd cation environment, as confirmed by Mössbauer and EPR studies (see below). Solids presenting a PXRD pattern similar to that of CatPMOF-1(Fe)-pz were reported in two recent articles. However, in these cases synthesis was carried out without pyrazine, and hence the local environment of the cation embedded in the porphyrin is different. Daliran et al. first suggested a structure isotopic to MOF-1992, a MOF made from the related phthalocyanine (Pc) tetracatecholate ligand.84 This seems very implausible considering that the symmetry of Pc and the related porphyrin are markedly different. Another structural model in a similar tetragonal unit cell, but in the P4mm space group, was recently proposed by Cheng et al. for materials built up from CoTcatPP and M(III) = In, Fe.83 The proposed structure formulated M2(CoTCatPP) was generated by removing 1/3 of the O atoms of the porphyrin tetragallate MOF MIL-173 (ref. 2 and 51) and further refining. This leads to a 3-D structure with channels of ∼6 Å free diameter running parallel to the porphyrin stacks. The position of the porphyrin is consistent with our findings and seems to agree with Fe EXAFS data, while the asymmetry observed on the provided Mössbauer spectrum suggests the occurrence of at least two distinct Fe sites, which is inconsistent with the proposed model. Eventually, the coordination sphere of Fe (or In) is astonishing: although described as octahedral geometry, the 6 coordination environment of the cation is extremely distorted (see Fig. S8†). A systematic analysis of the structure using SHAPE software, which allows a quantitative analysis of the coordination environment,99–101 indicates that the environment of Fe or In proposed in the above model does not match with any of the crystal structures of In and Fe catecholates reported to date, suggesting that the coordination sphere of the cation is not properly described (see ESI, Table S2† for details).
The fact that the SBUs are not detected by XRD suggests that the positions of the Fe atoms poorly correlate with those of the porphyrin core. This could arise from the free rotation of the catechol ring, which gives rise to a number of conformers for the ligand, and thus numerous possible positions for the cation, independently of that of the porphyrin macrocycle. Additional analyses were thus carried out to try to get a better description of the SBU in CatPMOF-1(Fe)-pz. First, the exact amount of Fe was evaluated by TGA analysis and inductively coupled plasma-atomic emission spectroscopy (ICP-AES) after dissolving the solid in an acidic aqueous medium. From the TGA data the amount of Fe per porphyrin was evaluated to give a value of 2.6+/−0.1. Given that 1 Fe is located inside the porphyrin core, this analysis indicates that the SBU is composed of 1.6+/−0.1 Fe per porphyrin (instead of 2 if the SBU was built up of continuous chains). The number of defects was found to be independent of the metal-to-porphyrin ratio used in the synthesis, suggesting that it is truly intrinsic to the structure (see Fig. S13 and Table S3†). Furthermore, ICP analysis of the activated solid shows that it contains 13.4(4) wt% Fe (see Fig. S14†), which is in good agreement with the TGA data as it corresponds to 2.65 Fe per porphyrin. Combining these results, it is possible to propose the formula FeIIIx(DMA)(8−3x)[FeII(Pz)(TcatPP)] (DMA = dimethylammonium), with (x ∼1.6). Hence, when compared to the aforementioned structure model, the SBU holds ∼20% of defects.
Considering that the position of the porphyrin core found by XRD is accurate, classical geometry optimization was used to build up a reasonable model of the inorganic SBU for M = Fe. Whatever the starting point, no chain based on reasonably distorted Fe octahedra could be obtained. The relaxation of various models rather suggests that some defects along the inorganic “chains” are mandatory to achieve a reasonable environment (in terms of geometry) for all Fe cations, and that both 6-fold and 5-fold connected Fe cations are present (Fig. 5c). This model is supported by a deeper analysis of the Mössbauer and EPR data. The Mössbauer spectra of activated CatPMOF-1(Fe)-pz at 77 and 300 K are shown Fig. 7a. The lack of resolution of Mössbauer spectra, which show complex hyperfine structures with broadened and asymmetric lines, leads to a large number of solutions, and fitting requires certain assumptions. Assuming that the porphyrinic core is coordinated to low spin (LS) Fe(II) ions as observed in other MOFs containing the same porphyrin-pyrazine-Fe motif,93,94 the spectrum can be fitted with four main contributions, one LS Fe(II), and three contributions accounting for high spin (HS) Fe(III) species. The LS Fe(II) content represents about 38% of Fe species, which is consistent with the quantitative results from the TGA and ICP-AES analyses (1 LS Fe(II) in the porphyrin core for a total of 2.6+/−0.1 Fe). The HS Fe(III) species need three different components to be fitted correctly (Fig. 7), clearly indicating the presence of several Fe sites in the SBU. The main Fe(III) species is deconvoluted with an isomer shift (δ) of 0.60 mm s−1 at 77 K, compatible with octahedral geometry and at the upper limit δ value for HS Fe(III), suggesting some extent of electron delocalization from the catecholate to the Fe(III) sites. The second Fe(III) site is fitted with a δ of 0.49 mm s−1, consistent with HS Fe(III), and a minor contribution representing 5% of Fe(III) is obtained at δ = 0.41 mm s−1 with a large quadrupole splitting of 2.22 mm s−1 indicating a highly asymmetrical site. The deconvolution of the Mössbauer spectra to these 4 components leads to a good fit at both 77 and 300 K, indicating that the proposed analysis is physically representative of the sample. The complexity of the Fe(III) signals reflects the difficulty to properly disclose the SBU from diffraction data and is attributed to the presence of both terminal Fe (next to the vacant sites), isolated Fe (minor signal) and Fe surrounded by other Fe atoms. Eventually, EPR analysis (Fig. 7b) confirmed the presence of a majority of inorganic unpaired electrons, in agreement with the presence of HS Fe(III) and a negligible number of organic radicals. Again, the deconvolution of the spectrum suggests the presence of 3 different types of Fe(III) at g = 2, 4 and 6.
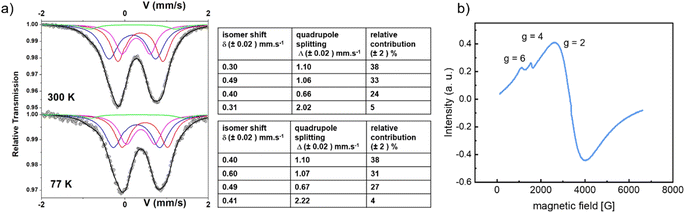 | ||
| Fig. 7 (a) Mössbauer spectra of CatPMOF-1(Fe)-pz at 330 and 77 K and the respective deconvolutions; (b) EPR spectra of CatPMOF-1(Fe)-pz at 120 K. | ||
To conclude, this structural model, made of ordered porphyrin cores and disordered 5- and 6-fold coordinated Fe(III) defining fragments of chains, is in better agreement with the experimental spectroscopic data than the fully ordered model mentioned above, and thus better describes CatPMOF-1(Fe)-pz. Nevertheless, on the Fourier difference map obtained by comparing the synchrotron PXRD pattern with this model, residual electronic density located along the chain axis is still detected, suggesting that the real inorganic motif is even more complex. Eventually, the presence of a poorly defined inorganic SBU might arise from the fact that the whole molecule has a low symmetry, whereas its core is highly symmetrical. Indeed, when switching to the more symmetrical tetragallate porphyrin ligand and the closely related crystal structure of MIL-173, this issue does not occur.2,51
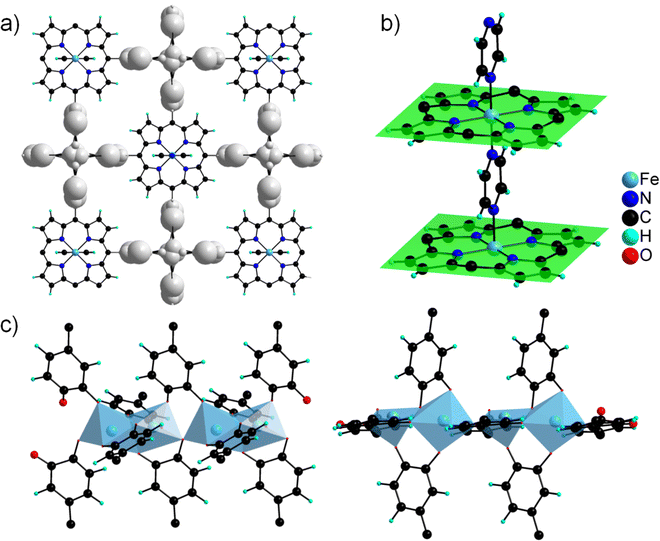
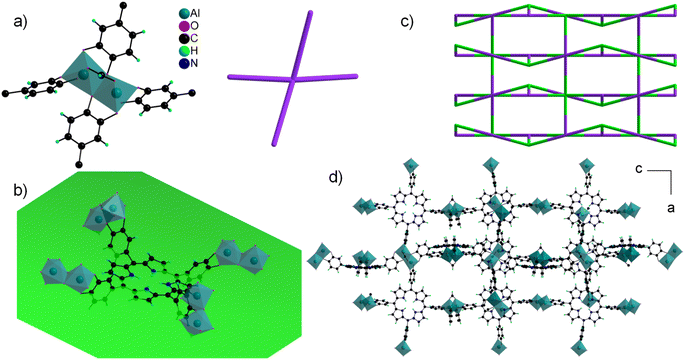
The asymmetric unit contains four independent Al cations and two porphyrin molecules. All the Al cations adopt an oxygenated distorted octahedral environment (SHAPE indices are <2 for an octahedron and >12 for other geometries), with Al–O distances ranging from 1.77(2) to 1.99(2) Å. Specifically, no significantly elongated Al–O distance was detected, suggesting that the catechol moieties are fully deprotonated. Each Al cation is surrounded by two chelating catecholates, and they assemble into edge-sharing dimers through two bridging–chelating catecholates and one bridging formate coming from the degradation of DEF (Fig. 8a). The 27Al solid-state magic-angle spinning (MAS) and 2D multiple quantum MAS (MQMAS) NMR spectra are shown Fig. S15:† two distinct signals of similar intensities with chemical shifts indicative of AlO6 are detected, supporting an SBU composed of two distinct Al octahedra. The quadrupolar coupling constant is 5.6 MHz (asymmetry parameter 0.3) for Al[6] at 25 ppm. The second Al[6] is deconvoluted with a Gaussian line, indicating local disorder around the second type of Al atom. Note that an additional minor signal (∼10%) characteristic of the pentavalent AlO5 unit is detected, which could arise from the partial departure of the formate ion. The SBUs are surrounded by four catecholates and act as distorted square planar motifs (Fig. 8a right). To the best of our knowledge, a single related compound was reported to date, namely a molecular complex based on Fe(III) and pyrocatecholate formulated (pip)3Fe2(cat)2(Ac) (pip = piperidinium, ac = acetate), which was formed under very different synthetic conditions.102,103 Regarding the organic part, the porphyrin is found to be non-metallated, in agreement with the solid-state UV-vis absorption spectrum, which presents typical Q bands of the free-base porphyrin, indicating that the porphyrin core is neither fully protonated (Fig. 6).
The macrocycle is rather flat (mean plane shown in Fig. 8b), with all the catecholate units pointing towards the same face of the plane. The ligand then acts as a second distorted square planar motif, giving rise when combined to the inorganic SBU to a 3-D net presenting the cds topology with the point symbol {65.8} (Fig. 8c). This gives rise to a tortuous 3-D pore network with large apertures (∼6 × 14 Å2) along the a and b directions (Fig. 8d).
In order to evaluate the potential oxidation of the catecholate groups, EPR analysis was carried out on fresh and activated samples. A signal characteristic of an organic radical was detected (Fig. S18†), but accounts for less than 0.1 and 2% of the porphyrin unit for fresh and activated solids, respectively, indicating that the catecholate units are almost exclusively in the reduced dianionic state. The framework is thus negatively charged, with the general formula [Al2(formate)(H2TcatPP)]3−. In an attempt to identify the counterions accounting for the charge balance, a solution NMR study was performed by dissolving a dry activated solid in d6-DMSO containing a small amount of concentrated HCl solution. The 1H NMR spectrum in Fig. S16† clearly displays quartet and triplet signals at 2.86 and 1.13 ppm respectively that are assigned to the ethyl groups of diethylammonium (DEAH) cations originating from the decomposition of DEF solvent during the synthesis course. The integration of these signals gives an approximate number of 3 DEA cations per porphyrin, agreeing well with the MOF molecular formula and charge balance. Moreover, a singlet at 8.1 ppm is assigned to the formate anion originating from the DEF decomposition with its integration giving approximately one formate per porphyrin, here again agreeing well with the molecular formula proposed from single crystal structure resolution. Both the presence of DEAH and formate was further confirmed by 13C NMR (signals at 11.67 (CH3), 42.35 (CH2) and 164 ppm (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), see Fig. S17†). Phase 2(Al) can then be positively formulated [Al2(formate)(H2TcatPP)](DEAH)3.
O), see Fig. S17†). Phase 2(Al) can then be positively formulated [Al2(formate)(H2TcatPP)](DEAH)3.
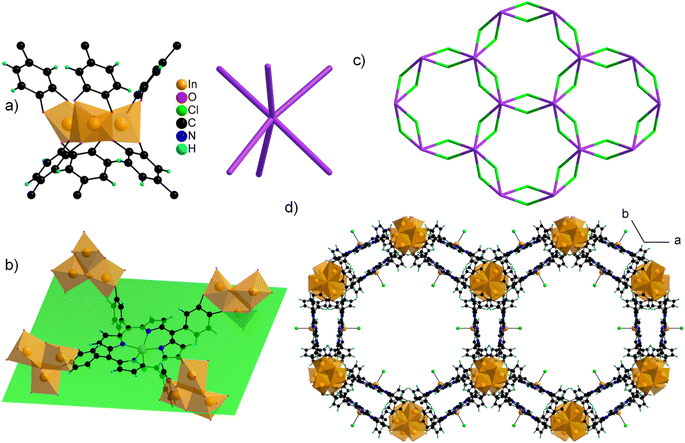
The structure of CatPMOF-3(In) consists of two independent In cations building the inorganic SBU, and one metallated porphyrin. Both In ions defining the inorganic motifs adopt a distorted octahedral coordination sphere (SHAPE indices are <6 for an octahedron and >10 for other geometries) with In–O distances ranging from 1.95 to 2.39 Å, with five O atoms arising from catecholate moieties (one chelating, one bridging–chelating, and one bridging), and one from a μ3-oxo unit. The octahedra share two edges to define a trimeric SBU surrounded by six catecholate groups (Fig. 9a, left) and adopting an octahedral geometry (Fig. 9a, right). This trimer has already been identified in the molecular complex H2Ti3O(cat)6,104 and more recently in the Al and Ga MOFs CAU-42 and the Fe analogue.70,71 It obviously differs from the well-known M(III/II)-carboxylate trimer found in numerous MOFs (MIL-100, -101…), which consists of corner-sharing MO6 octahedra forming a trigonal prismatic SBU. An additional In ion is found in the porphyrin core, lying slightly above the macrocyclic ring. It adopts a square pyramidal coordination environment, with the last position occupied by a chloride ion; as a result, the porphyrin core has a zero net charge. This metalation was again confirmed by solid-state UV-vis absorption spectroscopy (Fig. 6). As found in CatPMOF-2(Al), all catecholate moieties point towards the same face of the mean plan of the porphyrinic core (Fig. 9b). The combination of the organic and inorganic moieties leads to a 3-D network with large channels (up to ∼20 Å) running along the c-axis direction, with the porphyrin ring aligned with the pore axis (Fig. 9d). From a topological point of view, the structure presents an stp net with the point symbol {44.62}3{49.66}2 (Fig. 9c). This net has been reported in the MOF PCN-600 based on porphyrin tetracarboxylate and M(III/II) timers105,106 and is usually built up from square planar 4-fold nodes and trigonal prismatic, rather than octahedral, 6-fold nodes. Nevertheless, the distortion of the square planar motif coming from the loss of the planar symmetry of the porphyrin unit mentioned above accommodates the change of symmetry of the inorganic node to ultimately build up the same network (see Fig. S11†). EPR analysis was again carried out on the fresh and activated samples to quantify the amount of oxidized catecholate (Fig. S21†). Organic radicals were found to account for less than 1 and 2% of the catecholate for the fresh and activated samples respectively, indicating that the ligand is predominantly in a reduced state. To check the bulk sample composition solution NMR analysis was performed by dissolving CatPMOF-3(In) in d6-DMSO containing a small amount of concentrated HCl solution. Similar to the case of CAtPMOF-2(Al), DEA signals are clearly visible on the 1H and 13C NMR spectra (Fig. S19†) that integrate for about 3.5 DEA ions per metalloporphyrin. In this case, no other molecular components such as formic acid are detected by solution NMR in conformity to the proposed structure. Eventually, the absence of carbonyl signals in the 13C NMR spectrum rules out ligand oxidation (Fig. S20†), and the compound can be safely formulated [In3O(InClTcatPP)1.5](DEA)5. This suggests that the catecholate moieties are fully deprotonated, in contrast to the study by Boyle et al. on the molecular compound Ti3(O)(cat)4(Hcat)2,104 and fully reduced in contrast to the case of CAU-42, where the trimers are formulated M3O(cat)3(sq)3 (M = Al, Ga).70
Overall, the structural characterization of the new porphyrinic MOF phases presented significant challenges, demonstrating the necessity of employing a comprehensive approach that integrates both single crystal and powder diffraction techniques complemented by spectroscopic analysis. Specifically, the structure determination of CatPMOF-2(Al) critically relied on PXRD to accurately determine the unit cell parameters and detect the orthorhombic symmetry, without which the single crystal data could never have led to the structural model. Moreover, the major impact of the pore content on PXRD data hindered the achievement of a complete structural model through this technique alone, requiring information gained from single crystal diffraction and spectroscopic analysis (in the case of Ni-CatPMOF-2(Al), Ni-CatPMOF-2(Ga) and Ni-CatPMOF-3(In)). In summary, three MOF structures based on different SBUs were obtained. While molecular SBUs, analogous to those found in molecular compounds were obtained for MOFs in DEF, the solids prepared in DMF exhibited highly disordered, defective chain-like motifs. Furthermore, the larger DEF solvent and the DEA derivative, which is known to form supramolecular assemblies, seem to favor the formation of larger pores, with non-stacked porphyrin units, possibly through a templating effect.
2.4. Porosity, thermal and chemical stability
The thermal stability of the three phases was evaluated by temperature dependent powder XRD, both under air and nitrogen (Fig. S29a and b,† respectively). For CatPMOF-3(In), when the experiment is carried out in air, a first peak broadening is observed between 30 and 40 °C. From 40 to 130 °C, the patterns are almost unchanged, while above this temperature a rapid loss of crystallinity is observed. Both CatPMOF-1(Fe)-pz and CatPMOF-2(Al) do not present any transformation at low temperature, but show a similar thermal stability, with a loss of crystallinity starting at ∼130 °C in air. Hence, the three compounds present a moderate thermal stability in air, significantly lower than that of standard porphyrin carboxylate MOFs. This behavior, which was already observed in other phenolate-based MOFs,50,70,83,107,108 likely relates to the easier oxidation of the ligand. This is supported by the fact that the three solids present a significantly higher thermal stability under nitrogen: as shown Fig. S29b,† all solids remain crystalline up to 170–190 °C, and the transformation observed for CatPMOF-3(In) at 40 °C in air is not present anymore.The chemical stability of the three phases was also evaluated after activation, upon storage in air and suspended in water. As shown Fig. S31–S33,† all the compounds preserve their crystallinity upon activation. Although EPR analysis reveals an increase of radical species (at least for CatPMOF-2(Al) and CatPMOF-3(In)) after activation, the relative number of these radicals remains very low (less than 2% of porphyrinic linkers). When EPR measurement was repeated on fresh and activated CatPMOF-3(In) compounds after 9 weeks, no evolution of the signal was observed, evidencing that the solid is not further oxidized when left in air at room temperature (Fig. S21†), unlike the previously reported behavior for few M3+-catecholate MOFs,22,70 suggesting that the sensitivity of these solids towards air oxidation is ligand dependent. Indeed, when compared to fully conjugated polycatecholate ligands such as hexahydroxytriphenylene (HTTP), the redox potential of H10−nTcatPP−n is expected to be higher, leading to a lower sensitivity to O2 oxidation.
When the solids were exposed to air for several days, no drastic changes of the PXRD patterns were detected for both CatPMOF-1(Fe)-pz and CatPMOF-2(Al) (Fig. S30†). In contrast, the crystallinity of the mesoporous PMOF-3(In) decreased, with a complete amorphization detected after 8 days. The main parameter driving this difference of stability is likely the pore size, as already observed in the field of M(III,IV) carboxylate MOFs.
When suspended in water for 24 hours (2.5 mg mL−1), none of the solids retains its crystallinity (Fig. S31–S33†). This result differs from previous findings from Chen et al., showing Co-CatPMOF-1(Fe) to be stable in water from pH = 4 to 11.83 Hence, at least in our hands and in contrast to the initial expectations, porphyrin based M3+-catecholate MOFs present a moderate stability. The benefit associated with phenolic ligands eventually is far more pronounced when moving to M(IV) and gallate ligands,2,51 likely because of the increased charge of both components leading to stronger metal–ligand connections.
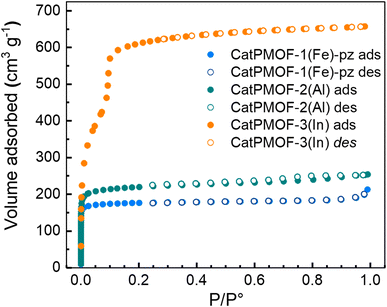
Based on the variable temperature diffraction data, the samples were activated at 150 °C under vacuum after being washed in DMF. Nitrogen adsorption measurements revealed that the three materials are permanently porous compounds (Fig. 10). In agreement with their structures, CatPMOF-3(In) displays a larger accessible BET surface area (2122 m2 g−1) and a type IV isotherm that agrees with the microporous/mesoporous structure of the network. For the compounds CatPMOF-1(Fe)-pz and CatPMOF-2(Al), as expected a type I isotherm is observed, and the corresponding BET surface areas are 710 m2 g−1 and 860 m2 g−1 respectively. This indicates that although being moderately stable, all these solids withstand activation (solvent removal) and present an accessible porosity that could be further exploited.
2.5. Electrical conductivity and redox activity
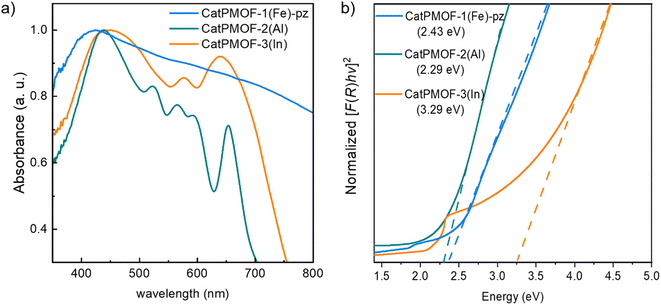
To evaluate the electrical properties of the MOFs, conductivity measurements of the different samples (CatPMOF-1(Fe)-pz, CatPMOF-2(Al) and CatPMOF-3(In)) were performed using four-contact probe pressed pellet devices with three independent samples for each compound (see the ESI† for experimental details). The average room-temperature conductivities were 3.3 (±0.5) × 10−7, 2.2 (±0.6) × 10−7 and 1.03 (±0.03) × 10−8 S cm−1 for CatPMOF-1(Fe)-pz, CatPMOF-2(Al) and CatPMOF-3(In), respectively (Table S4 and Fig. S34–S36†). Note that grain boundaries and anisotropic effects present in bulk pressed pellets may result in larger resistances compared to single-crystal measurements.109 Nevertheless, all MOFs present semiconducting behavior and similar conductivities to other porphyrin-based MOFs.110–113 However, the conductivities are lower than those of other catecholate-based MOFs,14,31,114 which could be related to the almost negligible amount of organic radical species acting as charge carriers (see the EPR section) or to a weaker delocalization between the linker and the metal at least for the 3p cations (Al and In).115 Notably, the conductivity of CatPMOF-3(In) is one order of magnitude lower than that of CatPMOF-1(Fe)-pz and CatPMOF-2(Al), which is consistent with its higher porosity and larger distances between the porphyrin units, as the charge transport mechanism is expected to be redox hopping as observed in other porphyrin-based MOFs.110 Although some mixed-valence FeII/III-based 3D MOFs with high conductivities (1 S cm−1) have been reported,116 this is not the case for CatPMOF-1(Fe)-pz probably due to the predominant presence of Fe(III) species (only the porphyrins contains LS Fe(II) ions). The optical band gaps (Eg) of CatPMOF-1(Fe)-pz, CatPMOF-2(Al) and CatPMOF-3(In) were calculated by linearly fitting the absorption onsets in the Tauc plots of the Kubelka–Munk-transformed data, obtaining values of 2.43, 2.29 and 3.29 eV, respectively (Fig. 6b). The larger optical band gap of CatPMOF-3(In) is consistent with the lower conductivities in comparison to CatPMOF-1(Fe)-pz and CatPMOF-2(Al).Considering the redox activity of the quinone/phenolate couple, the electrochemical properties of the three solids were investigated in the solid state, with the aim to evaluate their interest as positive electrodes for Li-ion batteries. The MOFs were activated prior to assess their electrochemical behavior in a Li half-cell by using 1 M LiPF6 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
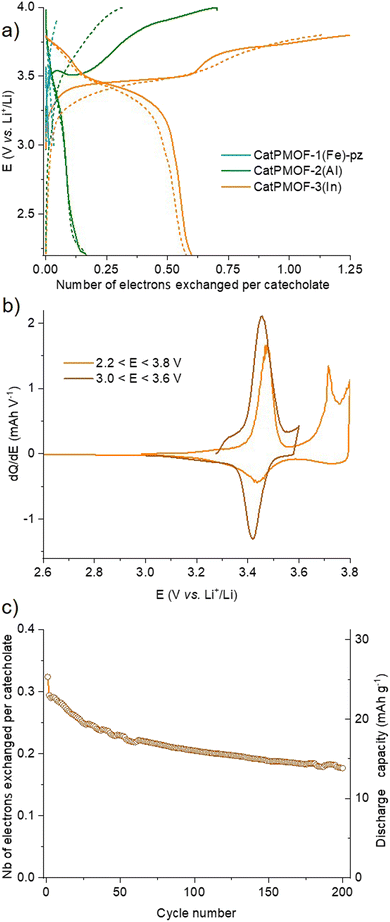
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ethylene carbonate (EC) and dimethylcarbonate (DMC) as the electrolyte (see the ESI† for details). As discussed earlier, all solids contain almost exclusively the reduced catecholate form, and hence tests were carried out starting with oxidation, in a potential range matching with the redox activity of the quinone/phenolate redox couple (∼2 ≤ E ≤ ∼4 V vs. Li+/Li), under galvanostatic conditions. Note that a narrower potential window (3.0 ≤ E ≤ 3.6 V vs. Li+/Li) was first used for CatPMOF-1(Fe)-pz to prevent any interference with the redox activity of the cation. The corresponding potential vs. capacity curves for the first and second cycles are shown in Fig. 11a, where the capacity refers to the number of electrons exchanged per catecholate unit. The redox activity strongly depends on the structure type. For CatPMOF-1(Fe)-pz, almost no redox activity is detected, neither in oxidation nor in reduction. Analysis carried out with another electrolyte (1 M LiClO4 in propylene carbonate (PC)) and a broader potential range (2.0 ≤ E ≤ 4 V vs. Li+/Li) leads to a similar result (Fig. S37†), suggesting that the diffusion of cations is hindered in this solid. For CatPMOF-2(Al), a plateau centered at 3.5 V vs. Li+/Li is detected during the first oxidation, followed by a second event spanning from ∼3.8 to 4.0 V, with a total of ∼0.7 electrons per catecholate unit. These events are likely associated with the stepwise oxidation of catecholate to semiquinone and further to quinone, associated with the release of cations (DEA/Li+) from the pores. It should be mentioned that the first oxidation potential is higher than the reduction potential of O2 (∼3.0 V vs. Li+/Li), explaining why this solid is isolated in its fully reduced form, as deduced from the EPR analysis (see above). Indeed, the redox potential observed for other phenolate-based MOFs, which are typically isolated in a mixed phenolate/semiquinone form in ambient air, is significantly lower (∼2.5–3 V vs. Li+/Li).33–35,37,41,42 The peculiar behavior of CatPMOF-2(Al) (and CatPMOF-3(In), see below) likely arises from the fact that TcatPP presents a lower level of conjugation, and hence a higher redox potential than the ligands used in these examples (such as HHTP). Coordination to a highly charged cation such as Al(III) also further increases the redox potential by inductive effects.117,118 Nevertheless, this redox activity is found to be almost irreversible upon further reduction and cycling, indicating that this solid is not suited for reversible electrochemical energy storage. CatPMOF-3(In) presents a similar behavior during the first oxidation, with two marked plateaus at 3.45 and 3.7 V vs. Li+/Li, accounting each for ∼0.6 electrons per catecholate unit. Interestingly, and in contrast to what is observed for CatPMOF-2(Al), a clear plateau centered at 3.4 V vs. Li+/Li is also detected in reduction. During the second cycle, this plateau remains both in oxidation and reduction, while the one at higher potential tends to disappear. This indicates that the event centered at ∼3.4 V vs. Li+/Li and attributed to the transformation catecholate ↔ semiquinone is reversible, while that at 3.7 V vs. Li+/Li, associated with the reaction semiquinone ↔ quinone is not. This can be clearly seen on the dQ/dE vs. E curve shown in Fig. 11b, where the anodic and cathodic peaks at ∼3.4 V vs. Li+/Li are visible, while only the anodic one is present at 3.7 V vs. Li+/Li. The irreversibility of the second oxidation step towards quinone could be related to the decrease of the cation–ligand bond strength and its dissociation upon the formation of the neutral quinone, ultimately leading to the degradation of the coordination network. Further experiments were then carried out focusing on the reversible redox event only (3.0 ≤ E ≤ 3.6 V vs. Li+/Li) at a ∼x5 faster cycling rate (current = 15.63 vs. 3.92 mA g−1) with the aim to evaluate the capacity retention upon cycling. As shown Fig. 11c and S38,† the capacity slowly decreases upon cycling, but remains around 0.2 electrons per catecholate even after 200 cycles, suggesting that CatPMOF-3(In) can sustain long term cycling, with an average potential close to 3.4 V vs. Li+/Li. This electrochemical stability is associated with the structural stability of the MOF: as shown Fig. S39,† the diffraction peaks characteristic of CatPMOF-3(In) remain visible after cycling, indicating that the structure is stable under these experimental conditions.
1 mixture of ethylene carbonate (EC) and dimethylcarbonate (DMC) as the electrolyte (see the ESI† for details). As discussed earlier, all solids contain almost exclusively the reduced catecholate form, and hence tests were carried out starting with oxidation, in a potential range matching with the redox activity of the quinone/phenolate redox couple (∼2 ≤ E ≤ ∼4 V vs. Li+/Li), under galvanostatic conditions. Note that a narrower potential window (3.0 ≤ E ≤ 3.6 V vs. Li+/Li) was first used for CatPMOF-1(Fe)-pz to prevent any interference with the redox activity of the cation. The corresponding potential vs. capacity curves for the first and second cycles are shown in Fig. 11a, where the capacity refers to the number of electrons exchanged per catecholate unit. The redox activity strongly depends on the structure type. For CatPMOF-1(Fe)-pz, almost no redox activity is detected, neither in oxidation nor in reduction. Analysis carried out with another electrolyte (1 M LiClO4 in propylene carbonate (PC)) and a broader potential range (2.0 ≤ E ≤ 4 V vs. Li+/Li) leads to a similar result (Fig. S37†), suggesting that the diffusion of cations is hindered in this solid. For CatPMOF-2(Al), a plateau centered at 3.5 V vs. Li+/Li is detected during the first oxidation, followed by a second event spanning from ∼3.8 to 4.0 V, with a total of ∼0.7 electrons per catecholate unit. These events are likely associated with the stepwise oxidation of catecholate to semiquinone and further to quinone, associated with the release of cations (DEA/Li+) from the pores. It should be mentioned that the first oxidation potential is higher than the reduction potential of O2 (∼3.0 V vs. Li+/Li), explaining why this solid is isolated in its fully reduced form, as deduced from the EPR analysis (see above). Indeed, the redox potential observed for other phenolate-based MOFs, which are typically isolated in a mixed phenolate/semiquinone form in ambient air, is significantly lower (∼2.5–3 V vs. Li+/Li).33–35,37,41,42 The peculiar behavior of CatPMOF-2(Al) (and CatPMOF-3(In), see below) likely arises from the fact that TcatPP presents a lower level of conjugation, and hence a higher redox potential than the ligands used in these examples (such as HHTP). Coordination to a highly charged cation such as Al(III) also further increases the redox potential by inductive effects.117,118 Nevertheless, this redox activity is found to be almost irreversible upon further reduction and cycling, indicating that this solid is not suited for reversible electrochemical energy storage. CatPMOF-3(In) presents a similar behavior during the first oxidation, with two marked plateaus at 3.45 and 3.7 V vs. Li+/Li, accounting each for ∼0.6 electrons per catecholate unit. Interestingly, and in contrast to what is observed for CatPMOF-2(Al), a clear plateau centered at 3.4 V vs. Li+/Li is also detected in reduction. During the second cycle, this plateau remains both in oxidation and reduction, while the one at higher potential tends to disappear. This indicates that the event centered at ∼3.4 V vs. Li+/Li and attributed to the transformation catecholate ↔ semiquinone is reversible, while that at 3.7 V vs. Li+/Li, associated with the reaction semiquinone ↔ quinone is not. This can be clearly seen on the dQ/dE vs. E curve shown in Fig. 11b, where the anodic and cathodic peaks at ∼3.4 V vs. Li+/Li are visible, while only the anodic one is present at 3.7 V vs. Li+/Li. The irreversibility of the second oxidation step towards quinone could be related to the decrease of the cation–ligand bond strength and its dissociation upon the formation of the neutral quinone, ultimately leading to the degradation of the coordination network. Further experiments were then carried out focusing on the reversible redox event only (3.0 ≤ E ≤ 3.6 V vs. Li+/Li) at a ∼x5 faster cycling rate (current = 15.63 vs. 3.92 mA g−1) with the aim to evaluate the capacity retention upon cycling. As shown Fig. 11c and S38,† the capacity slowly decreases upon cycling, but remains around 0.2 electrons per catecholate even after 200 cycles, suggesting that CatPMOF-3(In) can sustain long term cycling, with an average potential close to 3.4 V vs. Li+/Li. This electrochemical stability is associated with the structural stability of the MOF: as shown Fig. S39,† the diffraction peaks characteristic of CatPMOF-3(In) remain visible after cycling, indicating that the structure is stable under these experimental conditions.
In the field of batteries, there is continuous interest for the development for new materials achieving high energy storage. This energy is the product of the capacity (number of exchanged electrons per mass or volume) by the voltage; for this reason, high potential materials are of particular interest. While potential above 4.0 V vs. Li+/Li is reached by transition metal based inorganic materials, 3.4 V vs. Li+/Li is at the upper limit of what is found in organic materials,119 and appealing for the development of new, more sustainable, positive materials for Li-ion batteries. Although CatPMOF-3(In) is not competitive because of its large molar weight leading to a modest specific gravimetric capacity (∼15 mA h g−1), these results suggest that low molecular weight, non-conjugated polycatecholate ligands are of interest for this purpose.
3. Conclusion
Three novel porphyrinic MOFs of very different topologies have been successfully synthesized both with a free base and the nickel(II) porphyrin ligand. These materials are based on the coordination of trivalent metals (Al, Fe, and In) to catecholate moieties, thus extending the landscape of porphyrin-based coordination networks. Meticulous crystal growth optimization allowed the isolation of single crystals of different sizes and morphologies, reaching sizes exceeding 100 μm. Combining in-depth diffraction studies including single crystal and powder diffraction data along with classical geometry optimization calculations allowed the proposal of reliable structural models for all three phases. Spectroscopic investigations revealed the anionic nature of the three networks. While of strongly different topologies and based on markedly different inorganic SBUs, these MOFs are formed under closely related synthetic conditions, with the solvent playing a pivotal role in driving the phase formation. It is noteworthy that the use of DEF leads to the formation of molecular SBUs, previously identified in the field of molecular or extended coordination chemistry. This finding suggests that a certain level of design might be achieved in these systems, encouraging further exploration with the use of different metals. All the solids exhibit accessible porosity towards nitrogen. Notably, and to the best of our knowledge, among all the catechol porphyrin based porous frameworks, CatPMOF-3(In) displays the highest accessible BET surface area and larger pores. In contrast to the initial expectations, the chemical stability of all three solids is modest. However, the redox properties of the ligand can be exploited in the solid state, confirming the potential of phenolate ligands when compared to redox inert carboxylates or azolates, especially for applications involving electron transfer. In summary, this study introduces three new porphyrinic MOFs with distinct topologies, expanding the scope of porphyrin-based coordination networks. These MOFs exhibit noticeable porosity and original redox properties which opens up opportunities for further material investigations. It is anticipated that tetravalent cation incorporation could improve chemical stability and advance the potential in energy-related fields combining photo- and redox activity offered by these solids.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. S. D., G. M., F. L., M. A., and B. A.: investigation, data curation, and methodology; N. G.: investigation, methodology, visualization, and validation; E. J., J. M. G., L. K., C. M. C, L. B., and F. S.: investigation, methodology, and visualization; P. S. A. and G. V.: investigation; M. S.: visualization and writing – original draft; A. F. and T. D.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization and writing original draft and review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Funding from the region Pays de la Loire (project MatHySE2), from the region Auvergne Rhone Alpes (project SCUSI), the ANR (projects STREAM ANR-17-CE09-0029-01, CONDMOF ANR-06-BLAN-0202-02, ThioMOFs ANR-19-CE08-0029-01 and LABEX CHARMMMAT ANR-11-LABEX-0039) is acknowledged. This work was supported by the LABEX iMUST of the University of Lyon (ANR-10-LABX-0064), created within the program « Investissements d'Avenir » set up by the French government and managed by the French National Research Agency (ANR). The French Ministry of higher education and research is acknowledged for the studentship of B. A. F. L. acknowledges the support of the CSC (China Scholarship Council) scholarship. This work has also received funding from the European Research Council (ERC) under the Horizon Europe Framework Programme (101039748-ELECTROCOFS), FCT (PTDC/QUI-ELT/2593/2021) and CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 & LA/P/0006/2020, financed by national funds through the FCT/MEC (PIDDAC). The authors also thank the synchrotron Soleil for providing access to the beamline Cristal Soleil, and scientific and technical help from Erik Elkaïm and Pierre Fertey. The network RECIPROCS, Lise Marie Chamoreau, and Benoit Baptiste are warmly acknowledged for the data collection. The Centre Technologique des Microstructures of Lyon University is acknowledged for providing electronic microscopy facilities. The authors thank Francois Guillonneau from the University Paris Descatrtes for the MALDI analysis of the ligands. Philippe Poizot is also thanked for fruitful discussion of the electrochemical experiments. A. F. warmly thanks Pr João Rocha for welcoming her at CICECO-Aveiro. We thank Justin Andrews and Mircea Dincă (MIT) for assistance with the electrical measurements.References
- G. Mouchaham, et al., A Robust Infinite Zirconium Phenolate Building Unit to Enhance the Chemical Stability of Zr MOFs, Angew. Chem., Int. Ed., 2015, 54, 13297–13301 CrossRef CAS PubMed.
- G. Mouchaham, et al., Adaptability of the metal(III,IV) 1,2,3-trioxobenzene rod secondary building unit for the production of chemically stable and catalytically active MOFs, Chem. Commun., 2017, 53, 7661–7664 RSC.
- K. Nakabayashi and S. Ohkoshi, Monometallic Lanthanoid Assembly Showing Ferromagnetism with a Curie Temperature of 11 K, Inorg. Chem., 2009, 48, 8647–8649 CrossRef CAS PubMed.
- G. V. Shilov, Z. K. Nikitina, N. S. Ovanesyan, S. M. Aldoshin and V. D. Makhaev, Phenazineoxonium chloranilatomanganate and chloranilatoferrate: synthesis, structure, magnetic properties, and Mössbauer spectra, Russ. Chem. Bull., 2011, 60, 1209–1219 CrossRef CAS.
- M. Atzori, et al., A Family of Layered Chiral Porous Magnets Exhibiting Tunable Ordering Temperatures, Inorg. Chem., 2013, 52, 10031–10040 CrossRef CAS PubMed.
- L. E. Darago, M. L. Aubrey, C. J. Yu, M. I. Gonzalez and J. R. Long, Electronic Conductivity, Ferrimagnetic Ordering, and Reductive Insertion Mediated by Organic Mixed-Valence in a Ferric Semiquinoid Metal-Organic Framework, J. Am. Chem. Soc., 2015, 137, 15703–15711 CrossRef CAS PubMed.
- I.-R. Jeon, B. Negru, R. P. Van Duyne and T. D. Harris, A 2D Semiquinone Radical-Containing Microporous Magnet with Solvent-Induced Switching from Tc = 26 to 80 K, J. Am. Chem. Soc., 2015, 137, 15699–15702 CrossRef CAS PubMed.
- J. A. DeGayner, I.-R. Jeon, L. Sun, M. Dincă and T. D. Harris, 2D Conductive Iron-Quinoid Magnets Ordering up to Tc = 105 K via Heterogenous Redox Chemistry, J. Am. Chem. Soc., 2017, 139, 4175–4184 CrossRef CAS.
- S. Benmansour, A. Abhervé, P. Gómez-Claramunt, C. Vallés-García and C. J. Gómez-García, Nanosheets of Two-Dimensional Magnetic and Conducting Fe(II)/Fe(III) Mixed-Valence Metal–Organic Frameworks, ACS Appl. Mater. Interfaces, 2017, 9, 26210–26218 CrossRef CAS PubMed.
- R. Murase, et al., Mixed Valency in a 3D Semiconducting Iron–Fluoranilate Coordination Polymer, Inorg. Chem., 2017, 56, 9025–9035 CrossRef CAS PubMed.
- M. E. Ziebel, L. E. Darago and J. R. Long, Control of Electronic Structure and Conductivity in Two-Dimensional Metal–Semiquinoid Frameworks of Titanium, Vanadium, and Chromium, J. Am. Chem. Soc., 2018, 140, 3040–3051 CrossRef CAS.
- J. Chen, Y. Sekine, Y. Komatsumaru, S. Hayami and H. Miyasaka, Thermally Induced Valence Tautomeric Transition in a Two-Dimensional Fe-Tetraoxolene Honeycomb Network, Angew. Chem., Int. Ed., 2018, 57, 12043–12047 CrossRef CAS PubMed.
- S. A. Sahadevan, et al., Conducting Anilate-Based Mixed-Valence Fe(II)Fe(III) Coordination Polymer: Small-Polaron Hopping Model for Oxalate-Type Fe(II)Fe(III) 2D Networks, J. Am. Chem. Soc., 2018, 140, 12611–12621 CrossRef CAS PubMed.
- V. Rubio-Giménez, et al., Bottom-Up Fabrication of Semiconductive Metal–Organic Framework Ultrathin Films, Adv. Mater., 2018, 30, 1704291 CrossRef PubMed.
- C. Yang, et al., A semiconducting layered metal-organic framework magnet, Nat. Commun., 2019, 10, 3260 CrossRef PubMed.
- L. Liu, J. A. DeGayner, L. Sun, D. Z. Zee and T. D. Harris, Reversible redox switching of magnetic order and electrical conductivity in a 2D manganese benzoquinoid framework, Chem. Sci., 2019, 10, 4652–4661 RSC.
- Q. Zhao, S.-H. Li, R.-L. Chai, X. Ren and C. Zhang, Two-Dimensional Conductive Metal–Organic Frameworks Based on Truxene, ACS Appl. Mater. Interfaces, 2020, 12, 7504–7509 CrossRef CAS PubMed.
- A. D. Kharitonov, et al., 2D-metal–organic coordination polymers of lanthanides (La(III), Pr(III) and Nd(III)) with redox-active dioxolene bridging ligands, CrystEngComm, 2020, 22, 4675–4679 RSC.
- X. Li, X. Li and J. Yang, Two-Dimensional Multifunctional Metal–Organic Frameworks with Simultaneous Ferro-/Ferrimagnetism and Vertical Ferroelectricity, J. Phys. Chem. Lett., 2020, 11, 4193–4197 CrossRef CAS PubMed.
- Y. Misumi, et al., Quantum Spin Liquid State in a Two-Dimensional Semiconductive Metal–Organic Framework, J. Am. Chem. Soc., 2020, 142, 16513–16517 CrossRef CAS.
- R. Murase, et al., Effects of Mixed Valency in an Fe-Based Framework: Coexistence of Slow Magnetic Relaxation, Semiconductivity, and Redox Activity, Inorg. Chem., 2020, 59, 3619–3630 CrossRef CAS PubMed.
- G. Skorupskii and M. Dincă, Electrical Conductivity in a Porous, Cubic Rare-Earth Catecholate, J. Am. Chem. Soc., 2020, 142, 6920–6924 CrossRef CAS PubMed.
- Y. Sekine, J. Chen, N. Eguchi and H. Miyasaka, Fine tuning of intra-lattice electron transfers through site doping in tetraoxolene-bridged iron honeycomb layers, Chem. Commun., 2020, 56, 10867–10870 RSC.
- S. Benmansour, et al., Slow relaxation of the magnetization, reversible solvent exchange and luminescence in 2D anilato-based frameworks, Chem. Commun., 2020, 56, 9862–9865 RSC.
- M. G. Campbell, S. F. Liu, T. M. Swager and M. Dinca, Chemiresistive Sensor Arrays from Conductive 2D Metal-Organic Frameworks, J. Am. Chem. Soc., 2015, 137, 13780–13783 CrossRef CAS PubMed.
- M. K. Smith, K. E. Jensen, P. A. Pivak and K. A. Mirica, Direct Self-Assembly of Conductive Nanorods of Metal–Organic Frameworks into Chemiresistive Devices on Shrinkable Polymer Films, Chem. Mater., 2016, 28, 5264–5268 CrossRef CAS.
- M.-S. Yao, et al., Layer-by-Layer Assembled Conductive Metal–Organic Framework Nanofilms for Room-Temperature Chemiresistive Sensing, Angew. Chem., Int. Ed., 2017, 56, 16510–16514 CrossRef CAS PubMed.
- L. Mendecki and K. A. Mirica, Conductive Metal–Organic Frameworks as Ion-to-Electron Transducers in Potentiometric Sensors, ACS Appl. Mater. Interfaces, 2018, 10, 19248–19257 CrossRef CAS PubMed.
- M.-S. Yao, et al., A Dual-Ligand Porous Coordination Polymer Chemiresistor with Modulated Conductivity and Porosity, Angew. Chem., Int. Ed., 2020, 59, 172–176 CrossRef CAS PubMed.
- Y. Qiao, et al., High-performance non-enzymatic glucose detection: using a conductive Ni-MOF as an electrocatalyst, J. Mater. Chem. B, 2020, 8, 5411–5415 RSC.
- M. Hmadeh, et al., New Porous Crystals of Extended Metal-Catecholates, Chem. Mater., 2012, 24, 3511–3513 CrossRef CAS.
- W.-H. Li, et al., Conductive Metal–Organic Framework Nanowire Array Electrodes for High-Performance Solid-State Supercapacitors, Adv. Funct. Mater., 2017, 27, 1702067 CrossRef.
- K. Taniguchi, J. Chen, Y. Sekine and H. Miyasaka, Magnetic Phase Switching in a Tetraoxolene-Bridged Honeycomb Ferrimagnet Using a Lithium Ion Battery System, Chem. Mater., 2017, 29, 10053–10059 CrossRef CAS.
- H. Nagatomi, N. Yanai, T. Yamada, K. Shiraishi and N. Kimizuka, Synthesis and Electric Properties of a Two-Dimensional Metal-Organic Framework Based on Phthalocyanine, Chem.–Eur. J., 2018, 24, 1806–1810 CrossRef CAS PubMed.
- C.-H. Chang, et al., Elucidating metal and ligand redox activities of a copper-benzoquinoid coordination polymer as the cathode for lithium-ion batteries, J. Mater. Chem. A, 2019, 7, 23770–23774 RSC.
- K. W. Nam, et al., Conductive 2D metal-organic framework for high-performance cathodes in aqueous rechargeable zinc batteries, Nat. Commun., 2019, 10, 1–10 CrossRef CAS PubMed.
- S. Gu, Z. Bai, S. Majumder, B. Huang and G. Chen, Conductive metal–organic framework with redox metal center as cathode for high rate performance lithium ion battery, J. Power Sources, 2019, 429, 22–29 CrossRef CAS.
- J. Liu, et al., Conjugated Copper–Catecholate Framework Electrodes for Efficient Energy Storage, Angew. Chem., Int. Ed., 2020, 59, 1081–1086 CrossRef CAS PubMed.
- M. Wang, et al., Phthalocyanine-Based 2D Conjugated Metal-Organic Framework Nanosheets for High-Performance Micro-Supercapacitors, Adv. Funct. Mater., 2020, 30, 2002664 CrossRef CAS.
- J. W. Gittins, et al., Insights into the electric double-layer capacitance of two-dimensional electrically conductive metal–organic frameworks, J. Mater. Chem. A, 2021, 9, 16006–16015 RSC.
- H. Dong, et al., Quinone-Based Conducting Three-Dimensional Metal–Organic Framework as a Cathode Material for Lithium-Ion Batteries, J. Phys. Chem. C, 2021, 125, 20814–20820 CrossRef CAS.
- K. Kon, et al., Electron-Conductive Metal–Organic Framework, Fe(dhbq)(dhbq = 2,5-Dihydroxy-1,4-benzoquinone): Coexistence of Microporosity and Solid-State Redox Activity, ACS Appl. Mater. Interfaces, 2021, 13, 38188–38193 CrossRef CAS.
- T. Yu, et al., Catechol-Coordinated Framework Film-based Micro-Supercapacitors with AC Line Filtering Performance, Chem.–Eur. J., 2021, 27, 6340–6347 CrossRef CAS PubMed.
- X.-H. Liu, et al., Well-Defined Metal–O6 in Metal–Catecholates as a Novel Active Site for Oxygen Electroreduction, ACS Appl. Mater. Interfaces, 2017, 9, 28473–28477 CrossRef CAS PubMed.
- E. M. Miner, L. Wang and M. Dincă, Modular O2 electroreduction activity in triphenylene-based metal–organic frameworks, Chem. Sci., 2018, 9, 6286–6291 RSC.
- H. Zhong, et al., A Phthalocyanine-Based Layered Two-Dimensional Conjugated Metal–Organic Framework as a Highly Efficient Electrocatalyst for the Oxygen Reduction Reaction, Angew. Chem., Int. Ed., 2019, 58, 10677–10682 CrossRef CAS PubMed.
- R. Matheu, et al., Three-Dimensional Phthalocyanine Metal-Catecholates for High Electrochemical Carbon Dioxide Reduction, J. Am. Chem. Soc., 2019, 141, 17081–17085 CrossRef CAS PubMed.
- D. J. Tranchemontagne, J. L. Mendoza-Cortes, M. O'Keeffe and O. M. Yaghi, Secondary building units, nets and bonding in the chemistry of metal–organic frameworks, Chem. Soc. Rev., 2009, 38, 1257–1283 RSC.
- A. Schoedel, M. Li, D. Li, M. O'Keeffe and O. M. Yaghi, Structures of Metal–Organic Frameworks with Rod Secondary Building Units, Chem. Rev., 2016, 116, 12466–12535 CrossRef CAS PubMed.
- L. Cooper, et al., ZrIV Coordination Polymers Based on a Naturally Occurring Phenolic Derivative, Eur. J. Inorg. Chem., 2014, 6281–6289 CrossRef CAS.
- E.-X. Chen, et al., Acid and Base Resistant Zirconium Polyphenolate-Metalloporphyrin Scaffolds for Efficient CO2 Photoreduction, Adv. Mater., 2018, 30, 1704388 CrossRef.
- X. Feng, et al., Elucidating J-Aggregation Effect in Boosting Singlet-Oxygen Evolution Using Zirconium–Porphyrin Frameworks: A Comprehensive Structural, Catalytic, and Spectroscopic Study, ACS Appl. Mater. Interfaces, 2019, 11, 45118–45125 CrossRef CAS PubMed.
- G. Chen, et al., Valence-Dependent Electrical Conductivity in a 3D Tetrahydroxyquinone-Based Metal–Organic Framework, J. Am. Chem. Soc., 2020, 142, 21243–21248 CrossRef CAS PubMed.
- X. Wu, et al., Paramagnetic Conducting Metal–Organic Frameworks with Three-Dimensional Structure, Angew. Chem., Int. Ed., 2020, 59, 20873–20878 CrossRef CAS PubMed.
- P. E. Riley, S. F. Haddad and K. N. Raymond, Preparation of praseodymium(III) chloranilate and the crystal structures of Pr2(C6Cl2O4)3.8C2H5OH and Na3[C6H2O(OH)(SO3)2].H2O, Inorg. Chem., 1983, 22, 3090–3096 CrossRef CAS.
- A. Weiss, E. Riegler and C. Robl, Polymerie 2,5-Dihydroxy l,4-benzoquinone Transition Metal Complexes Na2(H20) 24[M2(Q H 20 4)3] (M = Mn2+, Cd2+), Z. Naturforsch., 1986, 41, 1501–1505 CrossRef.
- C. Robl, Complexes with substituted 2,5-dihydroxy-p-benzoquinones: the inclusion compounds [Y(H2O)3]2 (C6Cl2O4)3·6.6H2O and [Y(H2O)3]2 (C6Br2O4)3·6H2O, Mater. Res. Bull., 1987, 22, 1483–1491 CrossRef CAS.
- B. F. Abrahams, J. Coleiro, B. F. Hoskins and R. Robson, Gas hydrate-like pentagonal dodecahedral M2(H2O)18 cages (M = lanthanide or Y) in 2,5-dihydroxybenzoquinone-derived coordination polymers, Chem. Commun., 1996, 603–604 RSC.
- M. K. Kabir, et al., The rational syntheses of manganese–chloranilate compounds: crystal structures and magnetic properties, Polyhedron, 2001, 20, 1417–1422 CrossRef CAS.
- B. F. Abrahams, et al., Dihydroxybenzoquinone and chloranilic acid derivatives of rare earth metals, J. Chem. Soc., Dalton Trans., 2002, 1586–1594 RSC.
- B. F. Abrahams, et al., Synthesis, structure and host-guest properties of (Et4N)2[SnCa(chloranilate)4], a new type of robust microporous coordination polymer with a 2D square grid structure, Dalton Trans., 2011, 40, 12242–12247 RSC.
- B. F. Abrahams, T. A. Hudson, L. J. McCormick and R. Robson, Coordination Polymers of 2,5-Dihydroxybenzoquinone and Chloranilic Acid with the (10,3)-a Topology, Cryst. Growth Des., 2011, 11, 2717–2720 CrossRef CAS.
- S. Halis, et al., Dihydroxybenzoquinone as Linker for the Synthesis of Permanently Porous Aluminum Metal–Organic Frameworks, Inorg. Chem., 2016, 55, 7425–7431 CrossRef CAS PubMed.
- J. Roeser, et al., Anionic silicate organic frameworks constructed from hexacoordinate silicon centres, Nat. Chem., 2017, 9, 977–982 CrossRef CAS PubMed.
- O. Yahiaoui, et al., 3D Anionic Silicate Covalent Organic Framework with srs Topology, J. Am. Chem. Soc., 2018, 140, 5330–5333 CrossRef CAS PubMed.
- K. V. Nielson, L. Zhang, Q. Zhang and T. L. Liu, A Strategic High Yield Synthesis of 2,5-Dihydroxy-1,4-benzoquinone Based MOFs, Inorg. Chem., 2019, 58, 10756–10760 CrossRef CAS PubMed.
- J. Cao, et al., Twist and sliding dynamics between interpenetrated frames in Ti-MOF revealing high proton conductivity, Chem. Sci., 2020, 11, 3978–3985 RSC.
- J.-H. Dou, et al., Atomically precise single-crystal structures of electrically conducting 2D metal–organic frameworks, Nat. Mater., 2021, 20, 222–228 CrossRef CAS PubMed.
- M. P. M. Poschmann, H. Reinsch and N. Stock, [M2(μ-OH)2(DHBQ)3] (M = Zr, Hf) – Two New Isostructural Coordination Polymers based on the Unique M2O14 Inorganic Building Unit and 2,5-Dioxido-p-benzoquinone as Linker Molecule, Z. Anorg. Allg. Chem., 2021, 647, 436–441 CrossRef CAS.
- S. Leubner, et al., Hexahydroxytriphenylene for the synthesis of group 13 MOFs – a new inorganic building unit in a β-cristobalite type structure, Dalton Trans., 2020, 49, 3088–3092 RSC.
- A. Mähringer, et al., An Electrically Conducting Three-Dimensional Iron–Catecholate Porous Framework, Angew. Chem., Int. Ed., 2021, 60, 18065–18072 CrossRef PubMed.
- J. G. Knapp, et al., Electron transitions in a Ce(III)-catecholate metal–organic framework, Chem. Commun., 2022, 58, 525–528 RSC.
- E. S. Grape, et al., A Robust and Biocompatible Bismuth Ellagate MOF Synthesized Under Green Ambient Conditions, J. Am. Chem. Soc., 2020, 142, 16795–16804 CrossRef CAS PubMed.
- G. Skorupskii, et al., Efficient and tunable one-dimensional charge transport in layered lanthanide metal–organic frameworks, Nat. Chem., 2020, 12, 131–136 CrossRef CAS PubMed.
- G. Skorupskii, et al., Porous lanthanide metal–organic frameworks with metallic conductivity, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2205127119 CrossRef CAS PubMed.
- S. De, T. Devic and A. Fateeva, Porphyrin and phthalocyanine-based metal organic frameworks beyond metal-carboxylates, Dalton Trans., 2021, 50, 1166–1188 RSC.
- M. E. Ziebel, J. C. Ondry and J. R. Long, Two-dimensional, conductive niobium and molybdenum metal–organic frameworks, Chem. Sci., 2020, 11, 6690–6700 RSC.
- S. Jin, et al., Simple Fabrication of Titanium Dioxide/N-Doped Carbon Hybrid Material as Non-Precious Metal Electrocatalyst for the Oxygen Reduction Reaction, ACS Appl. Mater. Interfaces, 2017, 9, 18782–18789 CrossRef CAS PubMed.
- S. Jin, J. P. Hill, Q. Ji, L. K. Shrestha and K. Ariga, Supercapacitive hybrid materials from the thermolysis of porous coordination nanorods based on a catechol porphyrin, J. Mater. Chem. A, 2016, 4, 5737–5744 RSC.
- A. Wang, L. Cheng, X. Shen, W. Zhu and L. Li, Mechanistic insight on porphyrin based porous titanium coordination polymer as efficient bifunctional electrocatalyst for hydrogen and oxygen evolution reactions, Dyes Pigm., 2020, 181, 108568 CrossRef CAS.
- A. Wang, et al., Porphyrin coordination polymer/Co1−xS composite electrocatalyst for efficient oxygen evolution reaction, Chem. Eng. J., 2020, 400, 125975 CrossRef CAS.
- G. C. Quan, et al., Supramolecular assemblies of phenolic metalloporphyrins: structures and electrochemical studies, J. Porphyrins Phthalocyanines, 2019, 23, 103–116 CrossRef CAS.
- E.-X. Cheng, et al., Energy Band Alignment and Redox-Active Sites in Metalloporphyrin-Spaced Metal-Catechol Frameworks for Enhanced CO2 Photoreduction, Angew. Chem., Int. Ed., 2022, 61, e202111622 CrossRef PubMed.
- S. Daliran, M. Khajeh, A. R. Oveisi, H. García and R. Luque, Porphyrin Catecholate Iron-Based Metal–Organic Framework for Efficient Visible Light-Promoted One-Pot Tandem C–C Couplings, ACS Sustainable Chem. Eng., 2022, 10, 5315–5322 CrossRef CAS.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- N. Stock, High-throughput investigations employing solvothermal syntheses, Microporous Mesoporous Mater., 2010, 129, 287–295 CrossRef CAS.
- W. Morris, et al., Synthesis, Structure, and Metalation of Two New Highly Porous Zirconium Metal−Organic Frameworks, Inorg. Chem., 2012, 51, 6443–6445 CrossRef CAS PubMed.
- D. Feng, et al., Zirconium-Metalloporphyrin PCN-222: Mesoporous Metal–Organic Frameworks with Ultrahigh Stability as Biomimetic Catalysts, Angew. Chem., Int. Ed., 2012, 51, 10307–10310 CrossRef CAS PubMed.
- H.-L. Jiang, et al., An Exceptionally Stable, Porphyrinic Zr Metal-Organic Framework Exhibiting pH-Dependent Fluorescence, J. Am. Chem. Soc., 2013, 135, 13934–13938 CrossRef CAS PubMed.
- D. Feng, et al., Construction of Ultrastable Porphyrin Zr Metal-Organic Frameworks through Linker Elimination, J. Am. Chem. Soc., 2013, 135, 17105–17110 CrossRef CAS PubMed.
- P. Deria, et al., Framework-Topology-Dependent Catalytic Activity of Zirconium-Based (Porphinato)zinc(II) MOFs, J. Am. Chem. Soc., 2016, 138, 14449–14457 CrossRef CAS PubMed.
- F. Hanke, et al., The simplest supramolecular helix, Chem. Commun., 2018, 54, 6012–6015 RSC.
- A. Fateeva, et al., Iron and Porphyrin Metal-Organic Frameworks: Insight into Structural Diversity, Stability, and Porosity, Cryst. Growth Des., 2015, 15, 1819–1826 CrossRef CAS.
- B. Abeykoon, et al., Tuning the iron redox state inside a microporous porphyrinic metal organic framework, Dalton Trans., 2017, 46, 517–523 RSC.
- A. Schaate, et al., Modulated Synthesis of Zr-Based Metal–Organic Frameworks: From Nano to Single Crystals, Chem.–Eur. J., 2011, 17, 6643–6651 CrossRef CAS PubMed.
- D. M. Steinert, A. Schmitz, M. Fetzer, P. Seiffert and C. Janiak, A caveat on the effect of modulators in the synthesis of the aluminum furandicarboxylate metal-organic framework MIL-160, Z. Anorg. Allg. Chem., 2022, 648, e202100380 CrossRef CAS.
- T. Yokoyama, H. Abe, T. Kurisaki and H. Wakita, 13C and 27Al NMR Study on the Interaction in Acidic Aqueous Solution between Aluminium Ion and Tiron, Salicylic Acid and Phthalic Acid:as Model Compounds with Functional Groups of Fulvic Acid, Anal. Sci., 1997, 13, 425–428 CrossRef CAS.
- K. Muramatsu, et al., Anisotropic Crystal Growth of Layered Nickel Hydroxide along the Stacking Direction Using Amine Ligands, Inorg. Chem., 2022, 61, 8490–8497 CrossRef CAS PubMed.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, Continuous symmetry maps and shape classification. The case of six-coordinated metal compounds, New J. Chem., 2002, 26, 996–1009 RSC.
- S. Alvarez, et al., Shape maps and polyhedral interconversion paths in transition metal chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- S. Alvarez, Distortion Pathways of Transition Metal Coordination Polyhedra Induced by Chelating Topology, Chem. Rev., 2015, 115, 13447–13483 CrossRef CAS PubMed.
- B. F. Anderson, et al., Models for the bacterial iron-transport chelate enterochelin, Nature, 1976, 262, 722–724 CrossRef CAS PubMed.
- B. F. Anderson, J. Web, D. A. Buckingham and G. B. Robertson, Crystal and molecular structure of piperidinium μ-acetato-di-μ-1,2-benzenediolato-bis-1,2-benzenediolatoferrate(III), (C5H12N)3 [(CH3COO){Fe(C6H4O2)2}2]: a compound of relevance to the 2Fe-active site of the respiratory protein hemerythrin, J. Inorg. Biochem., 1982, 16, 21–32 CrossRef CAS.
- T. J. Boyle, L. J. Tribby, T. M. Alam, S. D. Bunge and G. P. Holland, Catechol derivatives of Group 4 and 5 compounds, Polyhedron, 2005, 24, 1143–1152 CrossRef CAS.
- K. Wang, et al., A Series of Highly Stable Mesoporous Metalloporphyrin Fe-MOFs, J. Am. Chem. Soc., 2014, 136, 13983–13986 CrossRef CAS PubMed.
- Q. Liu, H. Cong and H. Deng, Deciphering the Spatial Arrangement of Metals and Correlation to Reactivity in Multivariate Metal–Organic Frameworks, J. Am. Chem. Soc., 2016, 138, 13822–13825 CrossRef CAS PubMed.
- R. K. Feller and A. K. Cheetham, Fe(III), Mn(II), Co(II), and Ni(II) 3,4,5-trihydroxybenzoate (gallate) dihydrates; a new family of hybrid framework materials, Solid State Sci., 2006, 8, 1121–1125 CrossRef CAS.
- N. Heymans, et al., Small-Pore Gallates MOFs for Environmental Applications: Sorption Behaviors and Structural Elucidation of Their High Affinity for CO2, J. Phys. Chem. C, 2020, 124, 3188–3195 CrossRef.
- L. Sun, S. S. Park, D. Sheberla and M. Dincă, Measuring and Reporting Electrical Conductivity in Metal–Organic Frameworks: Cd2(TTFTB) as a Case Study, J. Am. Chem. Soc., 2016, 138, 14772–14782 CrossRef CAS PubMed.
- S. R. Ahrenholtz, C. C. Epley and A. J. Morris, Solvothermal Preparation of an Electrocatalytic Metalloporphyrin MOF Thin Film and its Redox Hopping Charge-Transfer Mechanism, J. Am. Chem. Soc., 2014, 136, 2464–2472 CrossRef CAS PubMed.
- A. Sengupta, et al., Tunable Electrical Conductivity and Magnetic Property of the Two Dimensional Metal Organic Framework [Cu(TPyP)Cu2(O2CCH3)4], ACS Appl. Mater. Interfaces, 2016, 8, 16154–16159 CrossRef CAS PubMed.
- X. Liu, et al., Photoconductivity in Metal–Organic Framework (MOF) Thin Films, Angew. Chem., Int. Ed., 2019, 58, 9590–9595 CrossRef CAS PubMed.
- M. Souto, K. Strutyński, M. Melle-Franco and J. Rocha, Electroactive Organic Building Blocks for the Chemical Design of Functional Porous Frameworks (MOFs and COFs) in Electronics, Chem.–Eur. J., 2020, 26, 10912–10935 CrossRef CAS PubMed.
- A. Mähringer, et al., Oriented Thin Films of Electroactive Triphenylene Catecholate-Based Two-Dimensional Metal?Organic Frameworks, ACS Nano, 2019, 13, 6711–6719 CrossRef PubMed.
- L. S. Xie, G. Skorupskii and M. Dincă, Electrically Conductive Metal–Organic Frameworks, Chem. Rev., 2020, 120, 8536–8580 CrossRef CAS PubMed.
- L. S. Xie, et al., Tunable Mixed-Valence Doping toward Record Electrical Conductivity in a Three-Dimensional Metal–Organic Framework, J. Am. Chem. Soc., 2018, 140, 7411–7414 CrossRef CAS PubMed.
- A. Jouhara, et al., Raising the redox potential in carboxyphenolate-based positive organic materials via cation substitution, Nat. Commun., 2018, 9, 4401 CrossRef PubMed.
- M. Denis, et al., Impact of the metal centre (Al3+, Fe3+) on the post-synthetic lithiation of functionalized MIL-53s and the electrochemical properties of lithiated derivatives, Mol. Syst. Des. Eng., 2023, 8, 1030–1039 RSC.
- P. Poizot, et al., Opportunities and Challenges for Organic Electrodes in Electrochemical Energy Storage, Chem. Rev., 2020, 120, 6490–6557 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The experimental data and additional characterization (PDF). CCDC 2284767–2284771. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ta04490d |
| ‡ Present address: University of Sussex, Department of Chemistry, Falmer, Brighton, BN1 9QJ, UK. |
| § Present address: Institut des Matériaux Poreux de Paris, Ecole Normale Supérieure ESPCI Paris CNRS PSL University, Paris 75005, France. |
| This journal is © The Royal Society of Chemistry 2023 |