Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of calcined clays used in cementitious binders: origin to service life considerations
Theodore
Hanein
 *a,
Hoang
Nguyen
*a,
Hoang
Nguyen
 b,
John L.
Provis
b,
John L.
Provis
 a,
Claire
Utton
a and
Wolfgang
Kunther
a,
Claire
Utton
a and
Wolfgang
Kunther
 c
c
aDepartment of Materials Science & Engineering, University of Sheffield, S1 3JD, Sheffield, UK. E-mail: t.hanein@sheffield.ac.uk
bFibre and Particle Engineering Research Unit, University of Oulu, 90014, Oulu, Finland
cDepartment of Environmental and Resource Engineering, Technical University of Denmark, 2800, Kgs. Lyngby, Denmark
First published on 25th July 2023
Abstract
The use of calcined clays in construction materials has attracted significant attention in the last few years. Based on the continued need for sustainable construction to meet global development challenges, the green transition of the cement industry is an urgent necessity. The use of clay-blended cements will keep increasing to meet the need for mass quantities of materials and the prospect of reducing their embodied CO2, as traditional supplementary cementitious materials are expected to decline in availability. To enable the necessary rapid increase in the fraction of clays that can be used in cements, the use of modeling tools which provide insights into the clays and their reactivity in cementitious systems is of increased interest. The aim is to predict the properties of the calcined clays based on the original rock and calcination conditions, the phase evolution, material properties, and durability of construction materials. This is crucial to reduce the time needed for development and commercialisation, whereas extensive empirical work has been used in the past to achieve material transition in the construction sector, which can be extremely time consuming. This review article therefore aims to provide an overview of available thermodynamic data, issues with database integration, modelling of process parameters, and properties prediction for cementitious materials.
Introduction
The use of calcined clay in cementitious binders is increasing, facilitating the global push towards lower-carbon, sustainable concrete. Global demand for cement exceeds 4 Gt per annum,1 and assuming a technically plausible replacement level of up to 40% or Portland cement by calcined clay,2 there is potential market for >1.5 Gt of calcined clay annually in the cement industry alone. Emerging cementitious systems/technologies using calcined clay, such as the limestone-calcined clay–cement blends known as LC3,2 have already proven to be suitable for wide scale adoption, based on experimental testing of the cement and concrete performance. However, there is little systematic understanding of how the thermodynamic properties of clays (raw and calcined) and their solid solutions or associated minerals (linked to their origin) will affect the production/calcination process (including interaction with process atmosphere) and their reactivity and performance in cementitious binders. Moreover, the lack of consistency in description of important clay minerals across thermodynamic databases is problematic, and it is necessary to assess and document the availability of thermodynamic data as well as the research gaps in the thermodynamics of calcined clays, to enable full exploitation of the potential of this material.In the practical application of concrete technology, materials chemistry must be translated to real-life applications, where workers and engineers with little or no chemical background are tasked with manipulating and optimising the multi-phase, multi-step cement hydration reaction process to produce highly durable engineering materials. This field normally relies heavily on empirical solutions for understanding the reactivity and property development of binders, and many important materials are widely used despite an incomplete understanding of their fundamental chemistry. However, the timeframe that is imposed for the green revolution to reach net-zero targets is more ambitious than can be achieved by this style of development in the field of cement and concrete research. Fortunately, the advancement of computing technology/power makes thermodynamic calculations much more accessible, and potentially also sufficiently user-friendly to enable their direct use in cementitious materials design.3,4
The application of thermodynamic principles to the study of cement chemistry was pioneered by Le Chatelier in the early 20th century,5 and thermodynamic analysis has since been applied to almost all aspects of cement science, particularly in the last two decades.6–8 On the other hand, clays are fine-particulate (<20 μm) weathering products of silicate bearing rocks whose constituents depend on the host rock/deposit and climatic conditions. Weathering can occur locally and produce relatively pure clays, but is often combined with erosion and transport processes, which leads to clay deposits that are then sedimentary in nature and yield combinations of clay minerals, such as kaolinite (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clay) and illite (2
1 clay) and illite (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clay), in addition to other, non-clay, associated minerals. It is therefore timely to collect the available data and approaches used in calcined clays and calcined clay–cement binders, ranging from the raw materials to the calcination process9 and the hydration and durability of the binders: from origin to service life. This will enhance utilisation and understanding of the different models and approaches that will lead to reduced design periods and faster translation to commercial products.
1 clay), in addition to other, non-clay, associated minerals. It is therefore timely to collect the available data and approaches used in calcined clays and calcined clay–cement binders, ranging from the raw materials to the calcination process9 and the hydration and durability of the binders: from origin to service life. This will enhance utilisation and understanding of the different models and approaches that will lead to reduced design periods and faster translation to commercial products.
To be able to predict and understand the behaviour of these complex materials when exposed to certain environments, we will start by discussing the different ideal minerals, to describe their (thermo)chemistry and compositional variability that would represent real-life clays that will be used in blended cement production, which may be either quite pure or relatively impure. It is noted that alkali-activation is another (potentially very attractive) pathway to the production of clay-based cementitious binders,10–12 but is deemed to be beyond the scope of the current review, which is instead focused on blends with Portland cement. The review will include a description of calcination process modeling and the aspects that can be influenced to control and optimise the process. Finally, a review of modeling approaches for the hydration, pozzolanic reactions, and durability of binary and ternary binders, including limestone fines, will be presented.
Survey of related thermodynamic data of raw clays
Due to the varying chemical nature of clays, it is not straightforward to derive and exploit thermodynamic data of clay minerals; nonetheless, some useful data sets do exist. Here, we performed a survey to provide an overview about the consistency and comparability of several of the most common and well-known thermodynamic databases. These datasets are shown in Table 1; for each, we have calculated and compared the solubility constants of various clays (following reaction and species shown in Table 2) as a function of temperature.| Databases | Temperature range (°C) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K calculation K calculation |
References |
|---|---|---|---|
| Minteq | 0–100 | Van't Hoff equation | 13 |
| PHREEQC | 0–100 | Van't Hoff equation | 14 |
| Lawrence Livermore National Laboratory (LLNL) | 0–300 | Van't Hoff equation | 15 |
| Yucca Mountain project | 0–300 | Van't Hoff equation | 16 |
| Thermoddem | 0–300 | Polynomial | 17 and 18 |
| Thermochimie | 0–300 | Polynomial | 19 and 20 |
| NEA | — | Polynomial | 21 |
| JAEA | — | SUPCRT | 22 |
| Holland and Powell | — | — | 23 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K for each clay minerals based on the selected thermodynamic databases
K for each clay minerals based on the selected thermodynamic databases
| Clay mineral | Species |
|---|---|
| Kaolinite | H+; Al3+; SiO2(aq); H2O |
| Halloysite | H+; Al3+; SiO2(aq); H2O |
| Illite | H+; Mg2+; K+; Al3+; Fe2+; SiO2(aq); H2O |
| Pyrophyllite | H+; Al3+; SiO2(aq); H2O |
| Smectite | H+; Mg2+; Na+; K+; Al3+; Fe3+; Fe2+; SiO2(aq); H2O |
Fig. 1 shows the comparison between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K and temperature among the surveyed databases for 1
K and temperature among the surveyed databases for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 1a and b) and 2
1 (Fig. 1a and b) and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays (Fig. 1c–e). Overall, there is a good consistency among databases for kaolinite, halloysite, and pyrophyllite. For illite (Fig. 1c), the Thermoddem17,18 and PHREEQC14 databases exhibit a mismatch with higher log
1 clays (Fig. 1c–e). Overall, there is a good consistency among databases for kaolinite, halloysite, and pyrophyllite. For illite (Fig. 1c), the Thermoddem17,18 and PHREEQC14 databases exhibit a mismatch with higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values in a temperature range of 0–100 °C compared to the other databases. In contrast, smectite shows a high variation in its thermodynamic properties due to the solid solution nature of the clay. The high Fe and Mg content are in a proportional relation with the log
K values in a temperature range of 0–100 °C compared to the other databases. In contrast, smectite shows a high variation in its thermodynamic properties due to the solid solution nature of the clay. The high Fe and Mg content are in a proportional relation with the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K of the clay, while the high content of chemically bound water in the smectite structure correlates with decreasing solubility constants. Therefore, there are several solid solution models established in the literature to predict the thermodynamic properties of these clays.
K of the clay, while the high content of chemically bound water in the smectite structure correlates with decreasing solubility constants. Therefore, there are several solid solution models established in the literature to predict the thermodynamic properties of these clays.
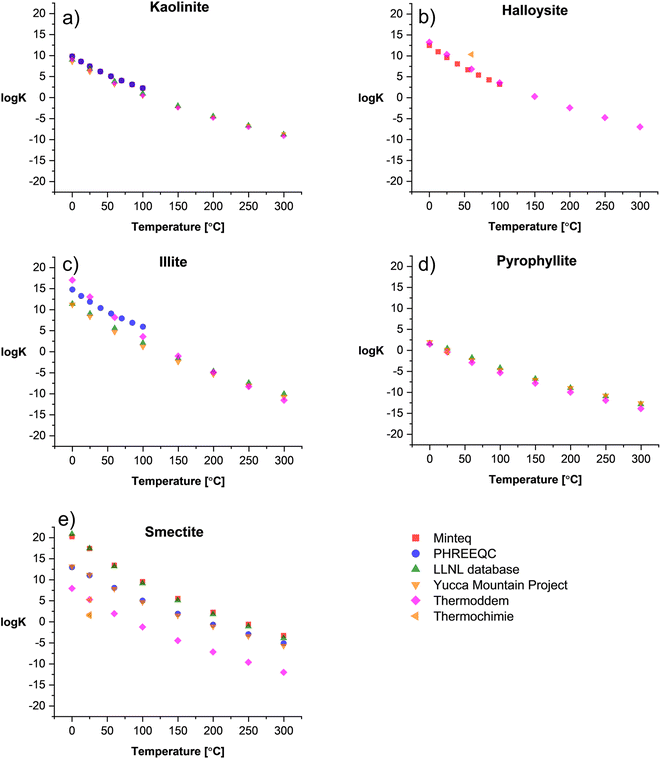 | ||
Fig. 1 log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K vs. temperature of selected (a and b) 1 K vs. temperature of selected (a and b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays and (c–e) 2 1 clays and (c–e) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays summarized from existing TDBs. 1 clays summarized from existing TDBs. | ||
There are two models of solid solutions for clay minerals that are known in the literature. First is the ideal solid solution model proposed by Tardy and Fritz,24 which proposed that the component activities are assumed to be controlled by ideal mixing of end-member components.24,25 This is described viaeqn (1):24
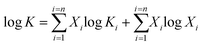 | (1) |
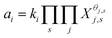 | (2) |
To illustrate this, we take an example from the difference between pyrophyllite and smectite, where pyrophyllite is a pure end-member of aluminosilicate in the smectite group.28 Smectite is a group of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phyllosilicates with a total layer charge between 0.2 and 0.6 (negative) per half unit cell. The group can be classified according to the following criteria (1) dioctahedral or trioctahedral layer, (2) octahedral chemical composition, and (3) density and location of layer charge.28 Hence, a wide range of cations can populate sites in the smectite structure. Like other members in the smectite group, pyrophyllite has a 2
1 phyllosilicates with a total layer charge between 0.2 and 0.6 (negative) per half unit cell. The group can be classified according to the following criteria (1) dioctahedral or trioctahedral layer, (2) octahedral chemical composition, and (3) density and location of layer charge.28 Hence, a wide range of cations can populate sites in the smectite structure. Like other members in the smectite group, pyrophyllite has a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 layered structure with an ideal structural formula of Al2Si4O10(OH)2. The phase is known to have three different layer stacking orders: (1) a two-layer monoclinic (2M), (2) a one-layer triclinic (1Tc), and (3) a disordered form.29 The dehydroxylation of the clay occurs between 500 and 900 °C,9,30 which in turn, gives rise to five-coordinated Al, forming distorted trigonal bipyramidal AlO5 units in the octahedral sheet.31 At 1000 °C, the tetrahedral sheet breaks down and leads to a partial segregation of amorphous SiO2.32
1 layered structure with an ideal structural formula of Al2Si4O10(OH)2. The phase is known to have three different layer stacking orders: (1) a two-layer monoclinic (2M), (2) a one-layer triclinic (1Tc), and (3) a disordered form.29 The dehydroxylation of the clay occurs between 500 and 900 °C,9,30 which in turn, gives rise to five-coordinated Al, forming distorted trigonal bipyramidal AlO5 units in the octahedral sheet.31 At 1000 °C, the tetrahedral sheet breaks down and leads to a partial segregation of amorphous SiO2.32
Fig. 2a shows the formation of trioctahedral and dioctahedral solid-solutions based on their ranges of composition compared to the pure member, while Fig. 2b presents the dehydration model of smectite driven by temperature or water activity. Vidal and Dubacq33 then estimated the V°, S° and Cp(T) of all of the dehydrated end-members defined in Fig. 2 using oxide summation techniques. The formation enthalpy was also calculated to be in-line with the experimental data at 1 bar and 25 °C, to ensure the stability of hydrated smectite instead of mica and aluminosilicate at low temperature, and reproduce the observations of smectite–illite equilibrium, as well as vermiculite or mica segregation observed with increasing temperature in the experiments and in nature.33
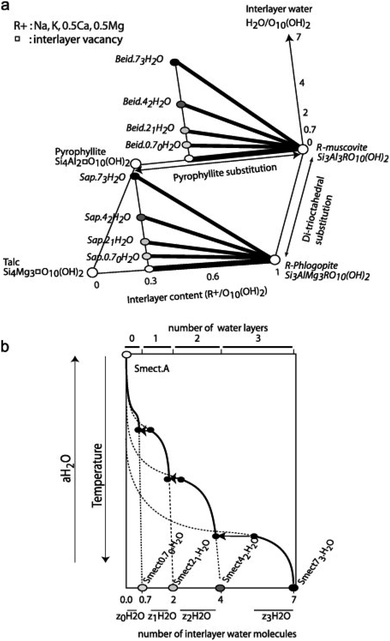 | ||
| Fig. 2 Schematic representation of the solid solution models. (a) The thick lines show the ranges of composition covered by the trioctahedral and dioctahedral solid-solution models and the end-member compositions are in italics in which Beid = beidellite and Sap = saponite. (b) Dehydration model of smectite with temperature or water activity. The water content of the end-members is shown by the circles on the lower horizontal axis. The continuous and dashed lines indicate the stable and metastable parts of the four solid solutions between Smectmn H2O and Smect A. The ranges of interlayer water content for the Smect with 0–3 interlayer water are indicated by z0H2O to z3H2O. The transitions from nw to (n − 1)w occur at discrete values of temperature or aH2O, and are shown by the horizontal arrows. Reproduced from ref. 33 with permission from Elsevier, copyright 2009. | ||
Recently, Blanc et al.34 introduced a computing tool, named ClayTherm (see Fig. 3), to estimate the thermodynamic properties of clay minerals as well as ISTherm dedicated to deriving illite/smectite compositions. The tool uses the thermodynamic properties of ions from Thermochimie19 and Thermoddem17 databases and advances from merging the model of Blanc et al.35 for the anhydrous clays and the Gailhanou et al.36 and Vieillard et al.37 models for the hydration of clays. The model has capability to predict the equilibrium constants of clay minerals and compare the calculated thermodynamic properties to the solubility data selected from the literature.
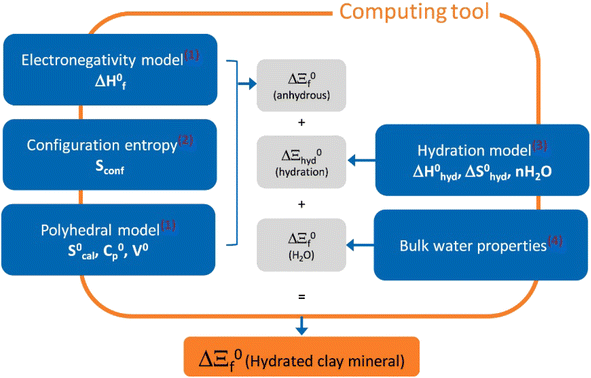 | ||
| Fig. 3 The overall approach of ClayTherm to provide thermodynamic properties for hydrated clay minerals. Reproduced from ref. 34 with permission from Elsevier, copyright 2021. | ||
To further assess the reliability of these databases for the clay minerals, the standard entropies retrieved from these datasets were compared to the estimated standard entropy based on the clay's formula unit volume as proposed by Jenkins and Glasser38 and used for cement minerals by Ghazizadeh et al.8. Those authors identified that the standard molar entropy of inorganic phases not containing discrete water of hydration (i.e., in this context, clay minerals with bound hydroxyl groups but no molecular water) can be correlated with the formula unit volume as follows:
| S0298 = 1262 × Vm + 13 | (3) |
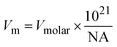 | (4) |
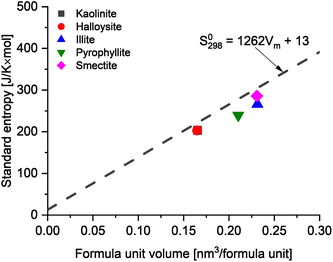 | ||
| Fig. 4 The comparison between data from thermodynamic databases and estimated values of standard molar entropy based on the formula unit volume38 of common clays. | ||
The heat capacity (Cp) of clay minerals is temperature dependent and can often be measured via experiments. Here, we evaluate the empirical Neumann–Kopp (NK) rule to estimate heat capacity of clays. The NK rule39,40 was described as: “Each element (in the solid state) has essentially the same specific or atomic heat in compounds as it has in the free state”. The rule can be expressed as the following equation:
| Cp(AaBbCc(s)) = aCp(A(s)) + bCp(B(s)) + cCp(C(s)) | (5) |
| aA(s) + bB(s) + cC(s) = AaBbCc(s). | (6) |
The estimated Cp from the NK rule is then compared with the Cp = f(T) function:41Cp = A1 + A2 × T + A3 × T−2 + A4 × T−0.5 + A5 × T2. The temperature range and coefficients of kaolinite (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clay), pyrophyllite (2
1 clay), pyrophyllite (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clay), and relevant oxides are shown in Table 3 (extracted from ref. 41).
1 clay), and relevant oxides are shown in Table 3 (extracted from ref. 41).
| Clay | Formula | A 1 | A 2 | A 3 | A 4 | A 5 | Temp. range [K] |
|---|---|---|---|---|---|---|---|
| Kaolinite | Al2Si2O5(OH)4 | 1430.3 | −7.885 × 10−1 | 8.334 × 106 | −1.852 × 104 | 3.034 × 10−4 | 298–800 |
| Pyrophyllite | Al2Si4O10(OH)2 | 746.8 | −5.345 × 10−2 | — | −7.578 × 103 | 1.986 × 10−5 | 298–800 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Oxide | |||||||
| Al2O3 | 161.2 | −1.352 × 10−3 | −1.815 × 106 | −1.059 × 103 | 5.381 × 10−7 | 298–2250 | |
| SiO2 | 81.145 | 1.828 × 10−2 | −1.81 × 105 | −6.985 × 102 | 5.406 × 10−6 | 298–884 | |
| H2O (ideal gas) | 27.057 | 1.7584 × 10−2 | 2.7696 × 105 | −2.766 × 101 | −2.509 × 10−6 | 298–2500 | |
Fig. 5 shows very good agreement between the two approaches to obtain the heat capacity of both 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays. Hence, the NK rule can reliably estimate the Cp value of the clays based on their stoichiometry. Note that the NK rule is applicable in the reported range of temperature (i.e., 298–800 K) for clays; however, there may be a need to adjust the estimated Cp considering the contribution of other factors such as the variation of thermal expansion and compressibility at high temperature, beside the lattice vibrations and dilation.39,42
1 clays. Hence, the NK rule can reliably estimate the Cp value of the clays based on their stoichiometry. Note that the NK rule is applicable in the reported range of temperature (i.e., 298–800 K) for clays; however, there may be a need to adjust the estimated Cp considering the contribution of other factors such as the variation of thermal expansion and compressibility at high temperature, beside the lattice vibrations and dilation.39,42
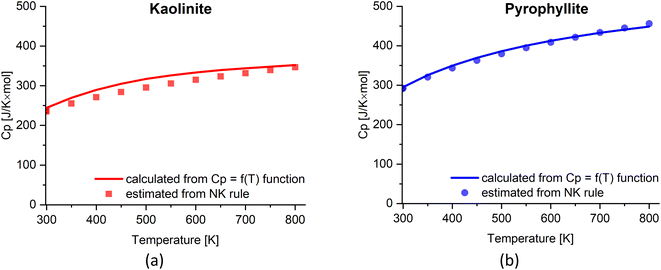 | ||
| Fig. 5 The estimated Cp value of (a) kaolinite and (b) pyrophyllite based on NK rule compared with the Cp = f(T) function.41 | ||
Clay calcination and process atmosphere
The favourable pozzolanic properties of calcined clays can be generated through calcination of the clay under specific conditions to achieve maximum dehydroxylation while avoiding sintering and recrystallisation. Various clay types can be dehydroxylated to produce supplementary cementitious materials (SCMs),† and the most studied is kaolinite, which forms metakaolin when calcined. The ideal calcination temperatures of kaolinite-rich clay reported in the literature vary and are usually reported as a range, depending largely on process conditions (it is a kinetically controlled process43) as well as the degree of disorder (e.g. layer stacking faults) within the clay itself, and associated minerals within the clay.9 For example, calcium carbonate can decompose at clay calcination temperatures and undesirably further react with the aluminosilicate; thus negatively influencing the mineralogy of the final calcined clay product.44 Conversely, the CaO content of calcined marl is sometimes considered to be beneficial to boost its pozzolanic properties45,46The dehydroxylation of clay minerals is the key reaction in clay calcination from a thermodynamic point of view. The dehydroxylation temperature of clays such as kaolinite (Al2Si2O5(OH)4), illite (e.g., K0.65Al2[Al0.65Si3.35O10](OH)2), or montmorillonite (e.g., Ca0.33Al2Si4O10(OH)2·nH2O) will change depending on the H2O partial pressure of the process atmosphere. Atmospheric control has been shown to be a critical aspect in cement clinker calcination7,47,48 and the same phenomenon is at play during the calcination of clays. Considering the reaction Al2Si2O5(OH)4 → Al2Si2O7 + 2H2O↑, applying Le Chatelier's principle, the increase of water vapour pressure in the system will shift the equilibrium to the left (Fig. 7). In a production process, this implies that the formation temperature (and energy demand) of metakaolin will increase with increasing H2O partial pressure. The atmospheric composition and H2O partial pressure can vary greatly depending on the process configuration and fuel used for clay calcination. The H2O partial pressure can vary between 1% and ∼100% depending on the fuel and oxidant (see Appendix).
The thermodynamic data for kaolinite and metakaolin are taken from ref. 49 while the data for H2O are taken from ref. 50. These data are used to calculate the dehydroxylation temperature of kaolinite over a range of H2O partial pressures as shown in Fig. 6. It is shown that the dehydroxylation temperature of kaolinite changes from 525 °C when H2O vapour pressure is 1%, to 605 °C at 10%, and 695 °C at 100%. Calcination under vacuum may also result in dehydroxylation temperatures as low as 300 °C (although this still needs to be tested experimentally). These variations in calcination temperatures will influence the kinetics of calcination as well as the rigidity of microstructure of the produced clay, and thus also the clay reactivity. At higher temperatures, the thermodynamically most stable transformation of metakaolin yields mullite and crystalline SiO2 at 980 °C (ref. 49) with low reactivity in cementitious binders. The influence of H2O partial pressure on the conversion of kaolinite to metakaolin has also recently been assessed through density functional theory51 and the results are in reasonable agreement.
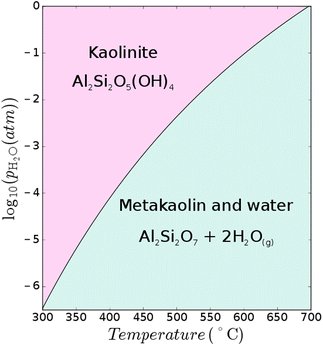 | ||
| Fig. 6 Thermodynamic dehydroxylation temperatures of kaolinite to metakaolin at various H2O partial pressures where the thermodynamic data for kaolinite and metakaolin are taken from ref. 49 while the data for H2O are taken from ref. 50. | ||
Thermodynamic data, up to 1000 K, for kaolinite is taken from ref. 52 and now compared with the data in ref. 49; it is shown that there is a rather large difference in kaolinite enthalpy and Gibbs energy between the two as shown in Fig. 7. Data for andalusite, mullite, and quartz form ref. 52 are also plotted in Fig. 7; it is shown that kaolinite is only thermodynamically stable up to 400 K and 1 bar total pressure. Furthermore, metakaolin is never thermodynamically stable, even if the data are shifted downwards to coincide with the Haas data at known dehydroxylation temperatures. Metakaolin is indeed a metastable phase and more experimental tests are needed to understand the series of reactions that may occur during service life53 (in the context of blended cement/concrete) in the presence of various phases/ions in solution over time which can link to the durability of the binder.
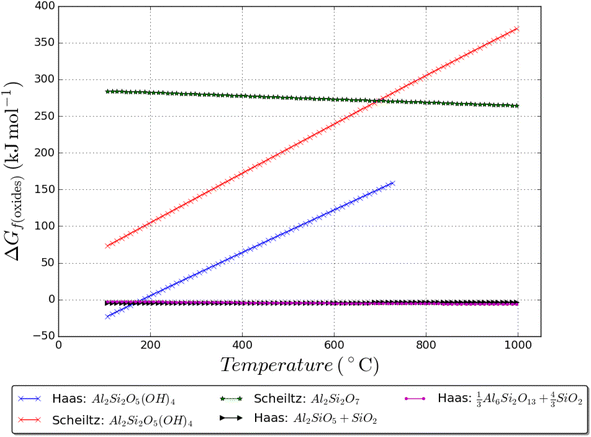 | ||
| Fig. 7 Gibbs energy of formation from the oxides of various sets of phases, showing the thermodynamically stable products. Where H2O gas forms, the pressure is set at 1 bar. Haas = ref. 52 and Schieltz = ref. 49. | ||
Other solid–gas interactions: CO2, O2, SO2, and halogens
The CO2 in the process atmosphere could have a significant role on the calcination of clays. CaCO3 formation as function of CO2 partial pressure is shown in Fig. 8, plotted alongside the kaolinite–metakaolin conversion temperatures previously discussed; both H2O and CO2 are major components of fossil fuel combustion and H2O is the major product of hydrogen combustion. Fig. 8 may be taken as a useful guide, locating a “Goldilocks zone” for manufacturing of calcined clay in various fuels, but kinetic factors will also need to be considered.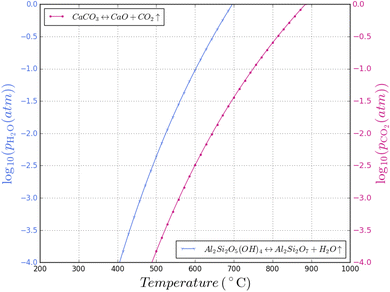 | ||
| Fig. 8 Superimposed plots of kaolinite dehydroxylation and calcium carbonate calcination at various H2O and CO2 partial pressures respectively. | ||
On the other hand, for clay minerals containing calcium, sodium, and potassium (e.g., montmorillonite and muscovite), the CO2 may also play an important role. Under the conditions used for clay calcination, CaCO3, Na2CO3, and K2CO3 are stable; therefore, depending on the CO2 concentration, the clays may interact with the CO2 to form carbonates along with aluminosilicates during calcination. However, this will need to be confirmed via experiments. Any segregation of Ca, Na, and K from the clay minerals may also have a significant effect on the clay reactivity.
Sulfur-containing minerals such as pyrite and alunite are found in clay while sulfur is also usually found in the process atmosphere, originating from the combustion of sour fossil fuels, and depending on the fuel used. SO2 concentration in kilns can range from 100–3000 ppm depending on the fuel properties. The reactions that SO2 can undergo greatly depend on whether the atmosphere is oxidizing (contains O2). Several sulfate compounds may form through the process but they require oxygen gas (SO2 + ½O2 → SO3); furthermore, the breakdown of sulfur containing compounds may also be influenced in the presence/absence of sulfur. Halogen concentrations in calcined clay manufacture may also fluctuate. Depending on fuels used, combustion can introduce halogens into the product through the process atmosphere. Information on the effect of halogens on clay quality is scarce and require further investigation. It is unclear whether these are going to be important at the very low levels that will be found in a practical process; however, in summary, it is important to study the solid gas reactions in clay calcination and thermodynamics can be used here as an important tool.
Clay conversion (forced weathering and diagenesis)
Clay minerals form naturally during the weathering of common rock-forming silicates.54 In nature, clays form as a product of the interaction of silicates and water at ambient or near-ambient conditions in which the minerals slowly accumulate at or near the surface of rocks exposed to atmosphere or in the shallow subsurface. The weathering conditions strongly influence the formation of different clay minerals. A relatively low pH combined with a moderate silica activity and low amounts of (earth)-alkalis are favourable to form kaolinite.55 Therefore, kaolinite is often deposited in tropical soils where the climate (e.g., rainfall and high heat) coupled with organic matter causes extensive leaching of alkali and earth-alkali metals; there are numerous weathering pathways that can lead to the formation of kaolinite.56,57 In contrast, kaolinite is much less abundant in cooler and dry regions. In such climates, other clay minerals such as illite and chlorite are more dominant as weathering products in soils.57 It follows that hydrothermal conversion of clay is also possible, mimicking the weathering process in nature for clay formation. The formation of clay minerals can be also accelerated in hydrothermal conditions by alteration of aluminosilicate parent rocks.It may also theoretically be possible to interconvert between different clay structures. A thermodynamic assessment using data from Haas Jr et al.52 and the model constructed by Hanein et al.7 was used to assess the difference in Gibbs free energy of the reaction Al2(OH)2Si4O10 + H2O → Al2Si2O5(OH)4 + 2SiO2 at varying temperatures and H2O partial pressures as shown in Fig. 9. The possibility to convert 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays to 1
1 clays to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays, by reacting only with water, is thus revealed by our critical assessment of existing data; however, a fully consistent thermodynamic database must be used and validated and further research will be needed to verify and optimize the conditions of accelerating the formation of 1
1 clays, by reacting only with water, is thus revealed by our critical assessment of existing data; however, a fully consistent thermodynamic database must be used and validated and further research will be needed to verify and optimize the conditions of accelerating the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clays of higher cementitious value via low-energy processes.
1 clays of higher cementitious value via low-energy processes.
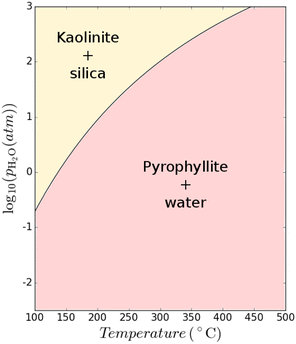 | ||
Fig. 9 Thermodynamic calculations showing the possibility of converting 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clay to 1 1 clay to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clay at various temperature and H2O partial pressure conditions. 1 clay at various temperature and H2O partial pressure conditions. | ||
Transformation of iron oxides for colour control
The aspect/colour of calcined clay is a significant factor that can restrict usage.58 Most low-grade kaolinitic clays contain Fe that is often present in hydrous forms (Fe(OH)3 or FeOOH) in clays that decomposed to form significant amounts of hematite (Fe2O3), greater than a few wt%. Depending on the iron content and oxygen availability, the material is red after calcination, which can be undesirable in the industrial use of cement product. There are four iron oxide minerals as shown in Table 4. There is a change in the oxidation state of iron in reducing atmosphere: hematite (Fe2O3) – magnetite (Fe3O4) – wüstite (FeO) – iron (Fe). The equilibrium stability ranges depend on temperature and partial pressure of oxygen (PO2). The calculated phase diagram (T-PO2) is shown in Fig. 10. Magnetite converts to hematite even in reducing atmospheres at low temperatures.| Mineral name | Chemical formula | Oxidation state of Fe | Crystal structure | Colour |
|---|---|---|---|---|
| Wüstite | FeO | 2+ | Cubic/halite | Black |
| Magnetite | Fe3O4 | 2+, 3+ | Cubic/spinel | Black |
| Maghemite | γ-Fe2O3 | 3+ | Cubic with a tetragonal supercell/spinel | Brown |
| Hematite | α-Fe2O3 | 3+ | Trigonal/corundum/Al2O3 | Red |
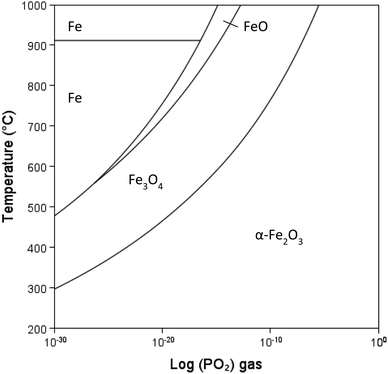 | ||
| Fig. 10 Fe–FeO–Fe3O4–Fe2O3 stability diagram with changing temperature and PO2 gas, calculated using Thermo-Calc software (2022b) and TCOX Metal Slag and Oxides Database version 11.59 | ||
Martirena et al.58 discuss the mechanisms involved in the colour of the final clay product. Stabilisation of magnetite at low temperature is required to avoid the red colour associated with hematite and produce calcined clay with the same gray colour as traditional cement. It is shown that the oxidation states of the final oxides are the key indicator of colour and that the colour can be controlled by maintaining sufficiently reducing conditions upon cooling of the clay, i.e., starving the atmosphere of oxygen by adding oxygen scavengers. However, the transformation to hematite is a naturally occurring process, and whether these reactions will occur in the concrete placed in environments where oxygen is readily available is still not known.
It is not discussed in the cement-related literature, how thermodynamics can play a crucial role in stabilising colour, simply by the introduction of dopants or inorganic modifiers that will enable enhanced thermodynamic stability of magnetite to lower temperatures without the need for an oxygen scavenger. It should be noted that the degree of reducing environment is crucial – systems with an oxygen scavenger (e.g., C or CO) differ from inert atmospheres of nitrogen or argon normally found in laboratory furnaces. Some data of the effects of substitutional elements on magnetite–maghemite and maghemite–hematite transition temperatures are available in the literature.60,61 Thermodynamic data to model iron oxide solid solutions are also available for a number of substitutional elements in e.g., Factsage or Thermo-Calc Software databases.
Using Thermo-Calc software and TCOX Metal Slag and Oxides Database version 11,59 the effect of elements Cr, Mn, Al, Ni and Mg on stability of Fe-oxides was calculated. The database was validated by comparing calculated phases diagram at various PO2 values and temperatures with published literature where available, which showed good agreement for these elements.
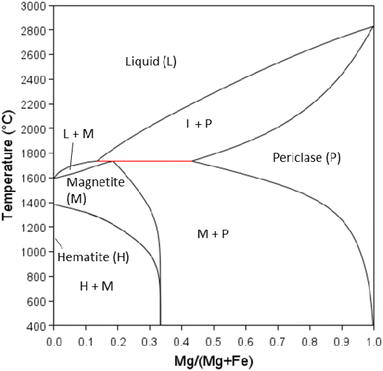
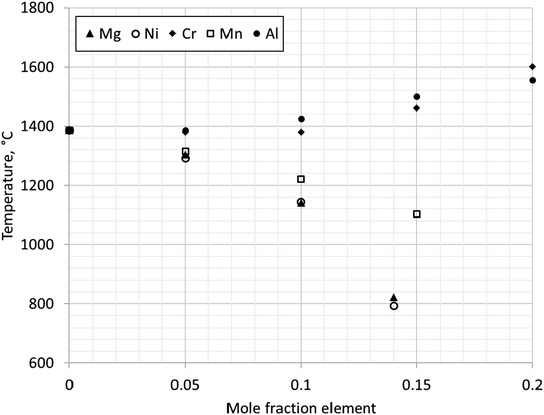
At PO2 = 0.21 (partial pressure of oxygen in earth's atmosphere) undoped magnetite is calculated to be stable between 1384–1594 °C. Adding Mg stabilises magnetite to temperatures below 1384 °C (Fig. 11). The maximum solubility of Mg in magnetite is calculated to be 0.14 mole Mg. The phase diagram predicts the single-phase region of magnetite to be narrow below approximately 750 °C to room temperature. When the mole fraction of Mg is increased above 0.14, both periclase (MgO) and magnetite are stable to low temperatures. Periclase has a relatively high solubility for Fe at high temperatures (max. solubility ∼0.26 mole fraction Fe at 1735 °C) but as temperature decreases the solubility of Fe also decreases significantly. It must be noted however that there is no predicted solubility of Mg in hematite, and therefore a two-phase region of hematite and magnetite exists as soon as Mg is added below 1384 °C. Our calculated phase diagram is in agreement with reported data.62
Fig. 12 shows change in stability of magnetite (single phase region) with additions of elements: Mg, Ni, Cr, Mn or Al. The transition temperature for a given composition was calculated for PO2 = 0.21. Al and Cr stabilise magnetite at higher temperatures, increasing the transformation temperature above 1384 °C. Mn reduces the transformation temperature, but Mn substituted magnetite is not stable below 954 °C. In contrast, Ni and Mg were calculated to stabilise magnetite at room temperature.
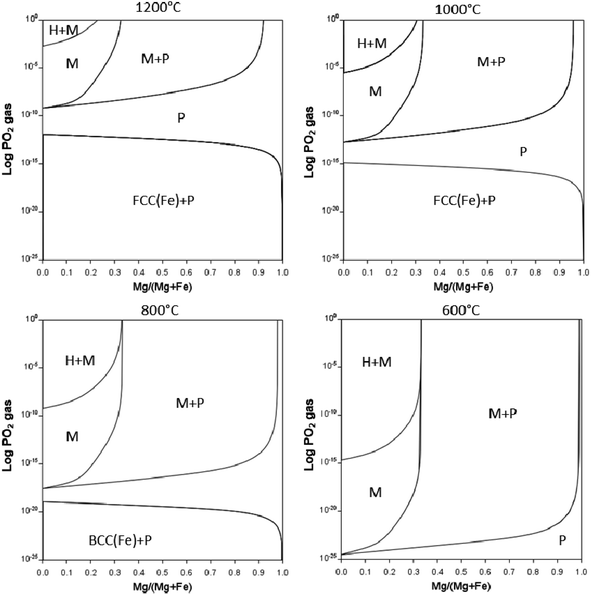
The partial pressure of O2 as well as temperature can aid in stabilising the magnetite to lower temperatures as indicated in Fig. 13. PO2vs. composition plots are calculated for temperatures of 1200, 1000, 800, and 600 °C for Mg substitution. The single-phase magnetite region is stable to lower temperatures when decreasing PO2. Increasing Mg content extends the single-phase magnetite region to higher PO2 values. The two-phase periclase – magnetite region, however, is stable over a wider range of temperature and PO2 range. Although the Mg is calculated to stabilise magnetite to low temperatures, it is still not certain whether these equilibrium phases will form under real-life calcination conditions and further experiments are required.
Using ab initio calculations
Theoretical chemical methods including density functional theory (DFT) can also be a powerful tool for application in understanding the thermochemistry of clay calcination, although also come with some disadvantages when approaching calculations on such complex (often disordered) layered structures. Even the analysis of uncalcined clay minerals by DFT can be controversial, with differences between published studies on fundamental aspects of space groups, bond lengths and orientations for a mineral as well-known as pure, highly-crystalline kaolinite.63,64 More complex structures such as halloysite65 and Fe-substituted kaolinite,66 as well as the role of stacking faults in kaolinite,67 have also been studied with some success by density functional techniques. The importance of correct application of high-level theory including appropriate corrections for dispersion and other physicochemical phenomena has particularly been highlighted.68–70 Much of the literature in this field has been focused on determining surface interactions between kaolinite and other molecules, although exfoliation (which is a process of interest with respect to cementitious reactivity) and small-molecule intercalation have also been considered in a number of studies.70–72Calcination of kaolinite has been described using a stepwise DFT approach,73 progressively removing hydroxyl groups and allowing the structure to relax, in simulations that were intended to describe the thermally induced dehydroxylation process during calcination. Fig. 14 shows the progressive disordering and layer disruption induced by this stepwise process, as simulated by White et al.73. Izadifar et al.51 have also addressed this question for dehydroxylation of both kaolinite and dickite, and provided description of their results in terms of the chemical potential of water accompanying each structure, which is an alternative and potentially very valuable approach to representing data of this type.
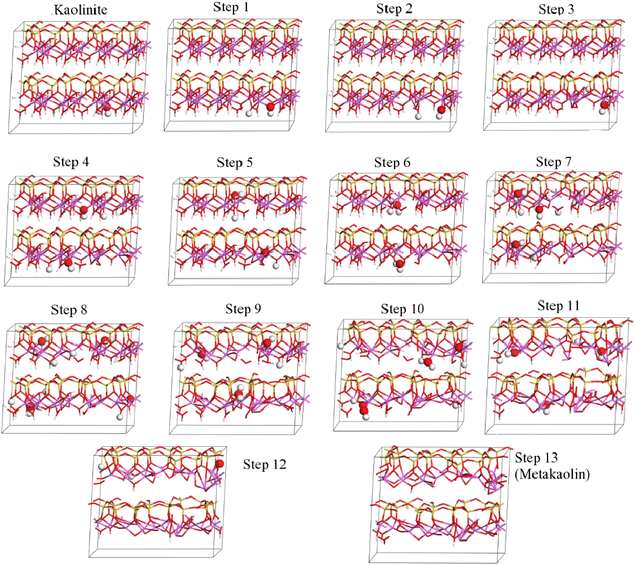 | ||
| Fig. 14 Stepwise dehydroxylation of a kaolinite supercell to metakaolin, as calculated by DFT.73 In that study, the kaolinite model was found to describe the experimentally observed structures (from neutron and X-ray pair distribution functions) for calcination temperatures up to 450 °C; step 9 corresponded to 500 °C, step 12 to 550 °C, and step 13 to 750 °C. The enlarged atoms in each structural model indicate the hydroxyl groups removed in the subsequent step. Reproduced from ref. 73 with permission from American Chemical Society, copyright 2010. | ||
Detailed work has also highlighted the importance of correct relaxation of atom positions in structure determination of disordered structures such as that of metakaolin to ensure chemical plausibility of the structural model,74 and conversely also the importance of incorporation of experimental data into computational approaches to ensure realistic outcomes.74,75 Fundamentally, the structures of dehydroxylated clays are sufficiently complex that application of a pure theoretical approach, or a pure experimental approach without reference to theory, in determination of their structures and thermochemistry is unlikely to succeed in the absence of rigorous validation. Important advances have recently been made in related areas, including simulations of the aqueous dissolution of clay minerals76 and in the application of force-field methods to cement hydrates and hydration.77 It appears likely that future developments in theory and applications will also lead to improvements in how clay calcination processes and products are understood from this fundamental level.
Modeling the reaction of calcined clays in cementitious binders
The understanding of cement hydration is much older than the application of thermodynamic modeling to cementitious binders, which has been gaining major attention in the last few decades.78–82 Several approaches (Table 5) have been developed with different levels of detail and therefore varying modeling input data requirements which can be categorized in the following strategies.| Modeling approach | Input requirements | References | ||||
|---|---|---|---|---|---|---|
| Water/binder ratio | Chemical composition | Mineralogical composition | Hydration degree | Hydration kinetics | ||
| Full hydration | × | × | 83–86 | |||
| Partial cement hydration | × | × | × | 87 and 88 | ||
| Clinker (+SCM) phase separated hydration degrees | × | × | × | × | 89 and 90 | |
| Implementation of hydration kinetics | × | × | × | × | 80 and 83 | |
These modeling approaches can also be combined. For example, one may choose to let fast reacting phases react in an unconstrained manner (full hydration) while reducing the reaction of slowly reacting phases such as belite to approximate the hydration of the binder of interest. Often the hydration kinetics makes the difference between good and poor modeling, based on agreement between the predicted and observed hydrate phases.83
For the hydration of calcined clays, one should distinguish several main binder categories (I) ‘model’ systems activated by lime or alkaline solutions, (II) binary,91 and (III) ternary binders containing Portland cement. The latter binders contain, in most cases, limestone filler, due to the commercial and environmental benefits of these materials92 and standards which allow replacement. Those ternary binders are often, but not necessarily, labelled as LC3-type binders.93 The addition of limestone filler produces stable phase assemblages in which the ettringite is stabilized and the reactive aluminium is incorporated in C–A–S–H and mono- or hemi- carboaluminate AFm phases over a wide range of compositions and clay types.83 Thermodynamically, monocarbonate is often predicted while hemicarbonate may be observed initially, which may be due to kinetics or anion availability. In any case, the solubility of both phases are quite close to each other;6 therefore, small variances may make the difference between the phases observed and predicted. Another feature of these binders for high clay replacement levels is the predicted precipitation of strätlingite in the absence of portlandite, while in experiments often traces of portlandite are still present when strätlingite is observed also, which should not be the case based on thermodynamic modeling and is often explained through either kinetic effects or lack of ionic transport in very fine pore systems.88,94 Binders (III) with low limestone content may display a larger variety of members from the AFm phase family including strätlingite.83 These binders can show phase assemblages closer to binary blends (II), where the calcium sulphate content also plays a crucial role in the resulting phase assemblages.
The challenges that arise for modeling of both binary and ternary binders is to gather the dissolution rates (kinetic) of the calcined clay fraction which may differ due to:
• The chemical and mineralogical composition (including impurities) of the starting material.
• Physical properties of the starting material (particle size, surface areas, etc.).
• The calcination process (temperature, retention time, atmosphere, heating and cooling rates, etc.).
• Type of the cement used for activation.
• Mixture proportion (clay, limestone and gypsum quantities).
Results from such tests have been used for modeling and classification of clays.83,94,95
The binders labelled above as model systems96 (I) represent a range of systems that range from reactivity tests when activated on small scales97,98 and as hydraulic lime-pozzolana mortars based on local alternatives to industrial cementitious binders.99,100 The focus here will be placed on cement-based binders. Interested readers are referred to suitable review papers for alkaline activated binders on this topic.101,102
While the nature of most kinetic models used in thermodynamic modeling has an empirical component, there is the desire in the research community to link these measurable “macro” scale effects to scientific questions on smaller scales, like the dissolution rate which may be complicated by solid solutions of clays utilised in practice. However, while there is no lack of literature on the dissolution of pure clay minerals in the geochemical domain, there are only a few articles tackling this topic for specifically metakaolin in acidic environments or alkali activated binders.103–107
Property and performance prediction
The motivation for the use of thermodynamic modeling is often driven by the attempt to understand underlying material chemistry and link/predict phase development and the durability of binders without decades of testing. Examples of this for calcined clay binders include the comparison of calculated porosity and mechanical properties as shown in Fig. 15. Kunther et al.108 showed that relationships between compressive strength and calculated porosity follow similar trends as described by empirical models such as the Ryshkewitch model.109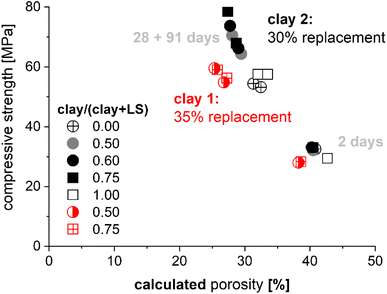 | ||
| Fig. 15 Comparison of the measured compressive strength of mortar bars and the calculated porosity changes during hydration108 based on kinetic inputs.83 The mineralogical compositions were for clay 1: 23% illite, 4% kaolinite, 36% quartz, 1% calcite, 36% amorphous and for clay 2: 48% illite, 5% kaolinite, 8% quartz, 43% amorphous. | ||
These types of calculations provide, especially for similar cement blends, qualitative relationships that appear appropriate. While these relationships may seem intuitive, the comparison between two binders, for example with two different clays and equal replacement rates, can highlight limitations because the same porosity may yield two compressive strengths. Such differences can be explained by changes in mineralogy, reactivity, and replacement of the materials. Other applications could be:
• Estimates for permeable pore spaces or.
• Identification of key minerals relevant for durability assessments.110–112
We do not know all relevant material parameters: the compressive strength of composite materials, where the relevant parameters include the porosity (larger pores are more critical), hydrate phase assemblage including Ca/Si ratio of the C–A–S–H phases, mechanical properties of individual and solid-solutions of hydrate minerals, microstructural features (through homogenization schemes), and impact of other inclusions. It is not a simple task to predict conventional mechanical properties based on the chemistry and kinetics alone. One step forward is therefore to model also the microstructure, as has been proposed by reactive transport models;113 not all the pore space calculated in thermodynamic models is accessible for ionic liquids and thus the permeable volume will be smaller than the predicted volume.
Durability modeling of calcined clay binders is documented in a few studies only,110,112 as a recent review of the durability of binary and ternary binders also supported.114 However, the presented results suggest that the general processes identified. e.g. for carbonation, chloride binding, or sulfate attack will also apply to these binders as long as the phase assemblages are similar in terms of portlandite content, Ca/Si ratio of C–A–S–H phases, and presence of AFm phases, which might be similar to fly ash containing Portland cements (typically 6–35 wt% replacement) and higher replacement slag cements. Hence, one needs to understand the limitations of modeling in context with the expected service environment in order to be able to assess possible durability issues which are affected by the clay reactivity in combination with the chosen cement type and resulting phase assemblage. Additionally, durability issues that are not directly related to the clay properties, such as alkali–silica reaction or frost, may provide additional stressors that may shorten the service life when occurring simultaneously. In summary, a lack of modeling knowledge on durability is apparent.
Concluding remarks
The variety of input data of raw clays, due to solid solutions and physical mixtures of sediment deposits, is large. This requires extensive understanding of the processes to activate and utilize the clays in construction materials. Calcination depends on the minerals present which may impose compromise to achieve maximum reactivity, but relevant thermodynamic data, in particular for metastable/reactive clay phases, is lacking. Several parameters are not yet experimentally verified but modeling attempts have been initiated. There is an apparent lack of models for calcination processes that link the theoretical calculations with process parameters in the publicly available literature, and future work should focus on experimentally assessing the influence of process atmosphere on calcined clay production and quality. The use of inorganic modifiers to stabilise magnetite at low temperature can also be predicted through thermodynamic modeling and the processing of raw clays from one type to another is an unexplored avenue that must be investigated.As highlighted in this article, there are plenty data sources to draw from and information are available when it comes to the hydration of cementitious binders containing calcined clays; other binder types might display similar phase assemblages and synergies such as ternary binders containing fly ash and limestone fillers.115 An aspect that is not well established is the interplay between different cements also within the same cement class in relation to blended binary or ternary cements even though some studies have documented some results already.116 The same will also be valid for alternative activators.
Microstructure differences will arise in new cements. Additionally, the measurement of porosity and permeability has a long-lasting history when it comes to the applicability, sample preparation, and comparison between different measurement methods and sample preparation in concrete technology and cement science.117,118 All these aspects become important when it comes to the estimation of the service life.
Due to the underdeveloped understanding of ab initio prediction of the dissolution of powders of mixtures of minerals with a range of particle sizes, or pyro processing conditions to obtain highly reactive calcined clays as SCMs, this is a topic that requires further exploration. Similarly, the experimental derivation of thermodynamic data that can be achieved using advanced calorimetric and/or dissolution techniques is necessary for co-validation.
Appendix
The combustion of simple fossil fuel (methane) in stoichiometric air (assuming air is 79% V N2 and 21% V O2).| CH4 + 2O2 + 7.5N2 → CO2 + 2H2O + 7.5N2: H2O Pp = 19% |
Oxyfuel combustion of simple fossil fuel (methane):
| CH4 + 2O2 → CO2 + 2H2O: H2O Pp = 67% |
The combustion of hydrogen gas in stoichiometric air (assuming air is 79% V N2 and 21% V O2).
| H2 + ½O2 + 1.9N2 → H2O + 1.9N2: H2O Pp = 35% |
Oxyfuel combustion of hydrogen gas:
| H2 + ½O2 → H2O: H2O Pp = 100% |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. Hanein was funded by UKRI Future Leaders Fellowship (MR/V023829/1). H. Nguyen is grateful for the financial support from the University of Oulu & The Academy of Finland Profi5 326291, as well as the Academy of Finland project 329477. We thank Jasmiini Tornberg for the help with graphical abstract.References
- U.S. Geological Survey, Mineral Commodity Summaries, National Minerals Information Center, 2022, https://www.usgs.gov/centers/national-minerals-information-center/cement-statistics-and-information Search PubMed.
- K. Scrivener, et al., Calcined clay limestone cements (LC3), Cem. Concr. Res., 2018, 114, 49–56 CrossRef CAS.
- D. A. Kulik, et al., CemGEMS–an easy-to-use web application for thermodynamic modelling of cementitious materials, RILEM Tech. Lett., 2021, 6, 36–52 CrossRef.
- G. D. Miron, S. Dmytrieva and D. A. Kulik, ThermoFun: A C++/Python library for computing standard thermodynamic properties of substances and reactions across wide ranges of temperatures and pressures, J. Open Source Softw., 2023, 8(83), 4624 CrossRef.
- H. Le Chatelier, Experimental Researches on the Constitution of Hydraulic Mortars, McGraw Publishing Company, 1905 Search PubMed.
- B. Lothenbach, et al., Cemdata18: A chemical thermodynamic database for hydrated Portland cements and alkali-activated materials, Cem. Concr. Res., 2019, 115, 472–506 CrossRef CAS.
- T. Hanein, F. P. Glasser and M. N. Bannerman, Thermodynamic data for cement clinkering, Cem. Concr. Res., 2020, 132, 106043 CrossRef CAS.
- S. Ghazizadeh, et al., Estimation of standard molar entropy of cement hydrates and clinker minerals, Cem. Concr. Res., 2020, 136, 106188 CrossRef CAS.
- T. Hanein, et al., Clay calcination technology: state-of-the-art review by the RILEM TC 282-CCL, Mater. Struct., 2022, 55(3), 1–29 Search PubMed.
- A. Z. Khalifa, et al., Advances in alkali-activation of clay minerals, Cem. Concr. Res., 2020, 132, 106050 CrossRef CAS.
- J. L. Provis, Alkali-activated materials, Cem. Concr. Res., 2018, 114, 40–48 CrossRef CAS.
- I. H. Shah, et al., Cement substitution with secondary materials can reduce annual global CO2 emissions by up to 1.3 gigatons, Nat. Commun., 2022, 13(1), 5758 CrossRef CAS PubMed.
- minteq.v4.dat: The minteq.v4.dat database. in phreeqc: R Interface to Geochemical Modeling Software, https://rdrr.io/cran/phreeqc/man/minteq.v4.dat.html.
- PHREEQC Version 3, 2021, https://www.usgs.gov/software/phreeqc-version-3 Search PubMed.
- J. Johnson, F. Anderson and D. Parkhurst, Database thermo.com.V8.R6.230, Rev 1.11, Lawrence Livermore National Laboratory, Livermore, California, 2000 Search PubMed.
- C. E. A. Palmer, R. J. Silva and J. J. Bucher, Thermodynamic Data Base Needs for Modeling Studies of the Yucca Mountain Project, Citeseer, 1996 Search PubMed.
- P. Blanc, et al., Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials, Appl. Geochem., 2012, 27(10), 2107–2116 CrossRef CAS.
- Thermoddem, Thermochemical and Mineralogical Tables for Geochemical Modeling: https://thermoddem.brgm.fr/databases/phreeqc.
- L. Duro, M. Grivé and E. Giffaut, ThermoChimie, the ANDRA Thermodynamic Database, MRS Online Proceedings Library (OPL), 2012, vol. 1475 Search PubMed.
- E. Giffaut, et al., Andra thermodynamic database for performance assessment: ThermoChimie, Appl. Geochem., 2014, 49, 225–236 CrossRef CAS.
- NEA, Thermochemical Database (TDB) Project, https://www.oecd-nea.org/jcms/pl_22166/thermochemical-database-tdb-project Search PubMed.
- JAEA, Thermodynamic Database for Nuclear Fuels and Reactor Materials, https://thermodb.jaea.go.jp/en/db/index.html Search PubMed.
- T. J. B. Holland and R. Powell, An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids, J. Metamorph. Geol., 2011, 29(3), 333–383 CrossRef CAS.
- Y. Tardy and B. Fritz, An ideal solid solution model for calculating solubility of clay minerals, Clay Miner., 1981, 16(4), 361–373 CrossRef CAS.
- B. Fritz, Multicomponent solid solutions for clay minerals and computer modeling of weathering processes, in The Chemistry of Weathering, Springer, 1985, pp. 19–34 Search PubMed.
- P. Aagaard and H. C. Helgeson, Activity/composition relations among silicates and aqueous solutions: II. Chemical and thermodynamic consequences of ideal mixing of atoms on homological sites in montmorillonites, illites, and mixed-layer clays, Clays Clay Miner., 1983, 31(3), 207–217 CrossRef CAS.
- W. F. Giggenbach, Construction of thermodynamic stability diagrams involving dioctahedral potassium clay minerals, Chem. Geol., 1985, 49(1–3), 231–242 CrossRef CAS.
- M. F. Brigatti, E. Galan, and B. K. G. Theng, Structure and mineralogy of clay minerals, in Developments in Clay Science, Elsevier, 2013, pp. 21–81 Search PubMed.
- G. W. Brindley and R. Wardle, Monoclinic and triclinic forms of pyrophyllite and pyrophyllite anhydride, Am. Mineral., 1970, 55(7–8), 1259–1272 CAS.
- E. Molina-Montes, et al., DFT research on the dehydroxylation reaction of pyrophyllite 1. First-principle molecular dynamics simulations, J. Phys. Chem. B, 2008, 112(23), 7051–7060 CrossRef CAS PubMed.
- J. J. Fitzgerald, et al., Solid-State 27 Al and 29 Si NMR and H CRAMPS Studies of the Thermal Transformations of the 2: 1 Phyllosilicate Pyrophyllite, J. Phys. Chem., 1996, 100(43), 17351–17360 CrossRef CAS.
- V. A. Drits, A. Derkowski and D. K. McCarty, Kinetics of thermal transformation of partially dehydroxylated pyrophyllite, Am. Mineral., 2011, 96(7), 1054–1069 CrossRef CAS.
- O. Vidal and B. Dubacq, Thermodynamic modelling of clay dehydration, stability and compositional evolution with temperature, pressure and H2O activity, Geochim. Cosmochim. Acta, 2009, 73(21), 6544–6564 CrossRef CAS.
- P. Blanc, et al., Thermodynamics for clay minerals: Calculation tools and application to the case of illite/smectite interstratified minerals, Appl. Geochem., 2021, 130, 104986 CrossRef CAS.
- P. Blanc, et al., A generalized model for predicting the thermodynamic properties of clay minerals, Am. J. Sci., 2015, 315(8), 734–780 CrossRef CAS.
- H. Gailhanou, et al., Methodology for determining the thermodynamic properties of smectite hydration, Appl. Geochem., 2017, 82, 146–163 CrossRef CAS.
- P. Vieillard, et al., A predictive model of thermodynamic entities of hydration for smectites: Application to the formation properties of smectites, Appl. Geochem., 2019, 110, 104423 CrossRef CAS.
- H. D. B. Jenkins and L. Glasser, Standard absolute entropy, values from volume or density. 1. inorganic materials, Inorg. Chem., 2003, 42(26), 8702–8708 CrossRef CAS PubMed.
- J. Leitner, et al., Application of Neumann–Kopp rule for the estimation of heat capacity of mixed oxides, Thermochim. Acta, 2010, 497(1–2), 7–13 CrossRef CAS.
- H. Kopp, XX.—Investigations of the specific heat of solid bodies, J. Chem. Soc., 1866, 19, 154–234 RSC.
- R. A. Robie and B. S. Hemingway, Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 Bar (105 Pascals) Pressure and at Higher Temperatures, 1995 Search PubMed.
- G. Grimvall, Thermophysical Properties of Materials, Elsevier, 1999 Search PubMed.
- C. E. White, et al., Inelastic neutron scattering analysis of the thermal decomposition of kaolinite to metakaolin, Chem. Phys., 2013, 427, 82–86 CrossRef CAS.
- F. Zunino, E. Boehm-Courjault and K. Scrivener, The impact of calcite impurities in clays containing kaolinite on their reactivity in cement after calcination, Mater. Struct., 2020, 53, 44 CrossRef CAS.
- T. Danner, et al., Feasibility of calcined marl as an alternative pozzolanic material, in Calcined Clays for Sustainable Concrete, Springer, 2015, pp. 67–73 Search PubMed.
- T. A. Østnor and H. Justnes, Durability of mortar with calcined marl as supplementary cementing material, Adv. Cem. Res., 2014, 26(6), 344–352 CrossRef.
- T. Hanein, et al., Production of belite calcium sulfoaluminate cement using sulfur as a fuel and as a source of clinker sulfur trioxide: pilot kiln trial, Adv. Cem. Res., 2016, 28(10), 643–653 CrossRef.
- T. Hanein, et al., Stability of ternesite and the production at scale of ternesite-based clinkers, Cem. Concr. Res., 2017, 98(C), 91–100 CrossRef CAS.
- N. C. Schieltz and M. R. Soliman, Thermodynamics of the various high temperature transformations of kaolinite, Clays Clay Miner., 1964, 13(1), 419–428 CrossRef.
- B. J. McBride, M. J. Zehe and S. Gordon, NASA Glenn coefficients for calculating thermodynamic properties of individual species, National Aeronautics and Space Administration, John H. Glenn Research Center at Lewis Field, 2002 Search PubMed.
- M. Izadifar, et al., Comprehensive examination of dehydroxylation of kaolinite, disordered kaolinite, and dickite: Experimental studies and density functional theory, Clays Clay Miner., 2020, 68(4), 319–333 CrossRef CAS.
- J. L. Haas Jr, G. R. Robinson Jr and B. S. Hemingway, Thermodynamic tabulations for selected phases in the system CaO-Al2O3-SiO2-H2 at 101.325 kPa (1 atm) between 273.15 and 1800 K, J. Phys. Chem. Ref. Data, 1981, 10(3), 575–670 CrossRef.
- M. Zajac, et al., Effect of hydration kinetics on properties of compositionally similar binders, Cem. Concr. Res., 2017, 101, 13–24 CrossRef CAS.
- H. Blatt, G. V. Middleton and R. C. Murray, Origin of Sedimentary Rocks. 1972 Search PubMed.
- E. Galán, Genesis of clay minerals, Dev. Clay Sci., 2006, 1, 1129–1162 Search PubMed.
- A. Alujas Diaz, R. S. Almenares Reyes, T. Hanein, E. F. Irassar, M. Juenger, F. Kanavaris, M. Maier, A. T. Marsh, T. Sui, K. C. Thienel and L. Valentini, Properties and occurrence of clay resources for use as supplementary cementitious materials: a paper of RILEM TC 282-CCL, Mater. Struct., 2022, 55(5), 139 CrossRef CAS , under review..
- A. Ito and R. Wagai, Global distribution of clay-size minerals on land surface for biogeochemical and climatological studies, Sci. Data, 2017, 4, 170103 CrossRef CAS PubMed.
- J. F. Martirena Hernandez, et al., Color control in industrial clay calcination, RILEM Tech. Lett., 2020, 5, 1–7 CrossRef.
- Thermo-Calc software TCOX Metal Slag and Oxides Database version 11, https://thermocalc.com/products/databases/metal-oxide-solutions/, accessed 16 November 2022.
- X. Liang, et al., The influence of substituting metals (Ti, V, Cr, Mn, Co and Ni) on the thermal stability of magnetite, J. Therm. Anal. Calorim., 2013, 111(2), 1317–1324 CrossRef CAS.
- A. U. Seybolt, Observations on the Fe-Cr-O System, J. Electrochem. Soc., 1960, 107(3), 147 CrossRef CAS.
- V. Raghavan, Fe-Mg-O (Iron-Magnesium-Oxygen), J. Phase Equilib. Diffus., 2010, 31(4), 368 CrossRef CAS.
- X. L. Hu and A. Michaelides, Water on the hydroxylated (0 0 1) surface of kaolinite: From monomer adsorption to a flat 2D wetting layer, Surf. Sci., 2008, 602(4), 960–974 CrossRef CAS.
- C. E. White, et al., What is the structure of kaolinite? Reconciling theory and experiment, J. Phys. Chem. B, 2009, 113(19), 6756–6765 CrossRef CAS PubMed.
- F. Ferrante, N. Armata and G. Lazzara, Modeling of the halloysite spiral nanotube, J. Phys. Chem. C, 2015, 119(29), 16700–16707 CrossRef CAS.
- D. Richard and N. M. Rendtorff, Local environments in iron-bearing clay minerals by DFT approaches: the case of structural Fe in kaolinite, Appl. Clay Sci., 2021, 213, 106251 CrossRef CAS.
- C. E. White, et al., Structure of kaolinite and influence of stacking faults: reconciling theory and experiment using inelastic neutron scattering analysis, J. Chem. Phys., 2013, 138(19), 194501 CrossRef PubMed.
- D. Tunega, T. Bučko and A. Zaoui, Assessment of ten DFT methods in predicting structures of sheet silicates: Importance of dispersion corrections, J. Chem. Phys., 2012, 137(11), 114105 CrossRef PubMed.
- P. F. Weck, E. Kim and C. F. Jové-Colón, Relationship between crystal structure and thermo-mechanical properties of kaolinite clay: beyond standard density functional theory, Dalton Trans., 2015, 44(28), 12550–12560 RSC.
- M. Cutini, L. Maschio and P. Ugliengo, Exfoliation energy of layered materials by DFT-D: Beware of dispersion!, J. Chem. Theory Comput., 2020, 16(8), 5244–5252 CrossRef CAS PubMed.
- C. E. White, et al., Effect of temperature on the local structure of kaolinite intercalated with potassium acetate, Chem. Mater., 2011, 23(2), 188–199 CrossRef CAS.
- J. Wang, et al., Energetics, interlayer molecular structures, and hydration mechanisms of dimethyl sulfoxide (DMSO)–kaolinite nanoclay guest–host interactions, J. Phys. Chem. Lett., 2021, 12(40), 9973–9981 CrossRef CAS PubMed.
- C. E. White, et al., Density functional modeling of the local structure of kaolinite subjected to thermal dehydroxylation, J. Phys. Chem. A, 2010, 114(14), 4988–4996 CrossRef CAS PubMed.
- C. E. White, et al., Combining density functional theory (DFT) and pair distribution function (PDF) analysis to solve the structure of metastable materials: the case of metakaolin, Phys. Chem. Chem. Phys., 2010, 12(13), 3239–3245 RSC.
- I. G. Richardson, The importance of proper crystal-chemical and geometrical reasoning demonstrated using layered single and double hydroxides, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69(2), 150–162 CrossRef CAS PubMed.
- R. Schliemann and S. V. Churakov, Atomic scale mechanism of clay minerals dissolution revealed by ab initio simulations, Geochim. Cosmochim. Acta, 2021, 293, 438–460 CrossRef CAS.
- R. K. Mishra, et al., cemff: A force field database for cementitious materials including validations, applications and opportunities, Cem. Concr. Res., 2017, 102, 68–89 CrossRef CAS.
- E. M. Gartner and H. M. Jennings, Thermodynamics of calcium silicate hydrates and their solutions, J. Am. Ceram. Soc., 1987, 70(10), 743–749 CrossRef CAS.
- P. Hewlett and M. Liska, Lea's Chemistry of Cement and Concrete, Butterworth-Heinemann, 2019 Search PubMed.
- B. Lothenbach and F. Winnefeld, Thermodynamic modelling of the hydration of Portland cement, Cem. Concr. Res., 2006, 36(2), 209–226 CrossRef CAS.
- D. Damidot, et al., Thermodynamics and cement science, Cem. Concr. Res., 2011, 41(7), 679–695 CrossRef CAS.
- B. Lothenbach and M. Zajac, Application of thermodynamic modelling to hydrated cements, Cem. Concr. Res., 2019, 123, 105779 CrossRef CAS.
- W. Kunther, Z. Dai and J. Skibsted, Thermodynamic modeling of hydrated white Portland cement–metakaolin–limestone blends utilizing hydration kinetics from 29Si MAS NMR spectroscopy, Cem. Concr. Res., 2016, 86, 29–41 CrossRef CAS.
- A. Machner, et al., Portland metakaolin cement containing dolomite or limestone–Similarities and differences in phase assemblage and compressive strength, Constr. Build. Mater., 2017, 157, 214–225 CrossRef CAS.
- G. Puerta-Falla, et al., The influence of metakaolin on limestone reactivity in cementitious materials, in Calcined Clays for Sustainable Concrete, Springer, 2015, pp. 11–19 Search PubMed.
- N. Chitvoranund, et al., Reactivity of Calcined Clay in Alite-Calcium Sulfoaluminate Cement Hydration, in Calcined Clays for Sustainable Concrete, Springer, 2015, pp. 373–379 Search PubMed.
- K. De Weerdt, H. Justnes and M. R. Geiker, Changes in the phase assemblage of concrete exposed to sea water, Cem. Concr. Compos., 2014, 47, 53–63 CrossRef CAS.
- M. Antoni, et al., Cement substitution by a combination of metakaolin and limestone, Cem. Concr. Res., 2012, 42(12), 1579–1589 CrossRef CAS.
- M. Pedersen, et al., Hydrate phase assemblages in calcium sulfoaluminate–metakaolin–limestone blends, in Calcined Clays for Sustainable Concrete, Springer, 2018, pp. 352–357 Search PubMed.
- F. Avet and K. Scrivener, Reaction degree of metakaolin in limestone calcined clay cement (LC 3), in Calcined Clays for Sustainable Concrete, Springer, 2018, pp. 41–45 Search PubMed.
- P. Duan, et al., Influence of metakaolin on pore structure-related properties and thermodynamic stability of hydrate phases of concrete in seawater environment, Constr. Build. Mater., 2012, 36, 947–953 CrossRef.
- K. L. Scrivener, V. M. John and E. M. Gartner, Eco-efficient cements: Potential economically viable solutions for a low-CO2 cement-based materials industry, Cem. Concr. Res., 2018, 114, 2–26 CrossRef CAS.
- F. Zunino, F. Martirena and K. Scrivener, Limestone calcined clay cements (LC3), ACI Mater. J., 2021, 118(3), 49–60 Search PubMed.
- K. E. Rasmussen, et al., Comparison of the pozzolanic reactivity for flash and soak calcined clays in Portland cement blends, in Calcined Clays for Sustainable Concrete, Springer, 2015, pp. 151–157 Search PubMed.
- J. Skibsted and R. Snellings, Reactivity of supplementary cementitious materials (SCMs) in cement blends, Cem. Concr. Res., 2019, 124, 105799 CrossRef CAS.
- N. Garg and J. Skibsted, Dissolution kinetics of calcined kaolinite and montmorillonite in alkaline conditions: Evidence for reactive Al (V) sites, J. Am. Ceram. Soc., 2019, 102(12), 7720–7734 CrossRef CAS.
- J. Ninov, et al., On the kinetics of pozzolanic reaction in metakaolin–lime–water system, J. Therm. Anal. Calorim., 2011, 105(1), 245–250 CrossRef CAS.
- I. Dojkov, et al., On the consumption of lime by metakaolin, fly ash and kaoline in model systems, J. Chem. Technol. Metall., 2013, 48(1), 54–60 CAS.
- C. Shi and R. L. Day, Chemical activation of blended cements made with lime and natural pozzolans, Cem. Concr. Res., 1993, 23(6), 1389–1396 CrossRef CAS.
- J. I. Alvarez, et al., RILEM TC 277-LHS report: A review on the mechanisms of setting and hardening of lime-based binding systems, Mater. Struct., 2021, 54(2), 1–30 CrossRef.
- J. L. Provis, et al., Binder chemistry–Low-calcium alkali-activated materials, in Alkali Activated Materials, Springer, 2014, pp. 93–123 Search PubMed.
- J. J. Jeremiah, et al., Geopolymers as alternative sustainable binders for stabilisation of clays—a review, Geotechnics, 2021, 1(2), 439–459 CrossRef.
- L. Valentini, Modeling dissolution–precipitation kinetics of alkali-activated metakaolin, ACS Omega, 2018, 3(12), 18100–18108 CrossRef CAS PubMed.
- C. E. White, et al., Molecular mechanisms responsible for the structural changes occurring during geopolymerization: multiscale simulation, AIChE J., 2012, 58(7), 2241–2253 CrossRef CAS.
- A. Hajimohammadi and J. S. J. van Deventer, Dissolution behaviour of source materials for synthesis of geopolymer binders: A kinetic approach, Int. J. Miner. Process., 2016, 153, 80–86 CrossRef CAS.
- D. K. Saleh, et al., Dissolution of aluminium from metakaolin with oxalic, citric and lactic acids, Clay Miner., 2019, 54(2), 209–217 CrossRef.
- P. E. A. Lima, R. S. Angélica and R. F. Neves, Dissolution kinetics of metakaolin in sulfuric acid: comparison between heterogeneous and homogeneous reaction methods, Appl. Clay Sci., 2014, 88, 159–162 CrossRef.
- W. Kunther, et al., Evaluation of the compressive strength for Portland cement blends incorporating real calcined clays and limestone by thermodynamic modeling, in 2nd International Conference on the Chemistry of Construction Materials (ICCCM 2016), Munich, Germany, 2016, p. 4 Search PubMed.
- E. Ryshkewitch, Compression strength of porous sintered alumina and zirconia: 9th communication to ceramography, J. Am. Ceram. Soc., 1953, 36(2), 65–68 CrossRef.
- Z. Shi, et al., Friedel's salt profiles from thermogravimetric analysis and thermodynamic modelling of Portland cement-based mortars exposed to sodium chloride solution, Cem. Concr. Compos., 2017, 78, 73–83 CrossRef CAS.
- V. Shah, et al., Changes in microstructure characteristics of cement paste on carbonation, Cem. Concr. Res., 2018, 109, 184–197 CrossRef CAS.
- Z. Shi, et al., Experimental studies and thermodynamic modeling of the carbonation of Portland cement, metakaolin and limestone mortars, Cem. Concr. Res., 2016, 88, 60–72 CrossRef CAS.
- A. Michel, et al., Microstructural changes and mass transport in cement-based materials: A modeling approach, Cem. Concr. Res., 2021, 139, 106285 CrossRef CAS.
- Y. Dhandapani, et al., Durability performance of binary and ternary blended cementitious systems with calcined clay: a RILEM TC 282 CCL review, Mater. Struct., 2022, 55(5), 145 CrossRef CAS.
- K. De Weerdt, et al., Synergy between fly ash and limestone powder in ternary cements, Cem. Concr. Compos., 2011, 33(1), 30–38 CrossRef CAS.
- M. Cyr, et al., Effect of cement type on metakaolin efficiency, Cem. Concr. Res., 2014, 64, 63–72 CrossRef CAS.
- K. Scrivener, R. Snellings and B. Lothenbach, A Practical Guide to Microstructural Analysis of Cementitious Materials, CRC Press, 2018 Search PubMed.
- K. K. Aligizaki, Pore Structure of Cement-Based Materials: Testing, Interpretation and Requirements, CRC Press, 2005 Search PubMed.
Footnote |
| † It must be noted that mechanochemical processes are also possible to dehydroxylate/activate clay, but are beyond the scope of this discussion. |
| This journal is © The Royal Society of Chemistry 2023 |