The cohesive properties and pyrolysis mechanism of an aprotic ionic liquid tetrabutylammonium bis(trifluoromethanesulfonyl)imide†
Shijie
Liu
 a,
Runhong
Wei
b,
Guangjun
Ma
c,
Ailin
Li
a,
Runhong
Wei
b,
Guangjun
Ma
c,
Ailin
Li
 d,
Olaf
Conrad
e and
Jiangshui
Luo
d,
Olaf
Conrad
e and
Jiangshui
Luo
 *a
*a
aLab of Electrolytes and Phase Change Materials, College of Materials Science and Engineering & Engineering Research Center of Alternative Energy Materials & Devices, Ministry of Education, Sichuan University, Chengdu 610065, China. E-mail: Jiangshui.Luo@scu.edu.cn
bFujian Ningde Aishuyuncheng New Materials Technology Co., Ltd., Ningde 355200, China
cChengdu Weilai Engineering Technology Co., Ltd, No. 366 North Section of Hupan Road, Zhengxing Street, Tianfu New District, Chengdu 610299, China
dCollege of Science, Civil Aviation University of China, Tianjin 300300, China
ePajarito Powder LLC, 3600 Osuna Rd, Albuquerque, NM 87109, USA
First published on 25th May 2023
Abstract
As the cohesive properties (such as the enthalpy of sublimation) of solid organic salts (or ionic liquids, ILs) are unmeasurable, a method of their indirect determination is proposed in this paper. For this purpose, the thermogravimetric analysis (TGA) and differential scanning calorimetric analysis (DSC) were carried out over a wide range of temperatures. In this study, the mathematical relationship of the thermodynamic properties between the liquid and solid phases of ILs is established using the Born–Fajans–Haber cycle, in which the sum of the vaporization enthalpy of ILs, melting enthalpy and the enthalpy of solid–solid phase transition is regarded as the sublimation enthalpy of solid organic salts. With this method, the cohesive properties of tetrabutylammonium bis(trifluoromethanesulfonyl)imide ([N4444][NTf2]), which is an aprotic IL, were successfully obtained. Additionally, the difference between the lattice energy and the cohesive energy was employed to quantitatively calculate the charge separation distance of single ion pair (r12) in the gas phase of ionic liquids for the first time, which can serve as a standard methodology to measure the closeness in distance between the anion and the cation in a gas phase ion pair. The pyrolysis mechanism of [N4444][NTf2] was also explored.
Introduction
Ionic liquids (ILs) are generally defined as compounds entirely composed of ions with a melting point below 100 °C. Benefiting from their structural features and unique physical or chemical properties such as low vapor pressure, tuneable polarity and structure, nonflammability, broad solubility, and high thermal stability, multidisciplinary studies of ILs have been emerging, involving chemistry, materials science, chemical engineering, physics, thermal engineering, computational science, and environmental science (such as catalysis,1 gas adsorption/desorption,2 extractants,3 proton conductors,4 electrochemistry,5 thermal energy storage,6 and heat transfer fluids7). Moreover, some fundamental viewpoints are different from the original ones with the understanding of the nature of ILs being deepened. For example, the concept of physicochemical properties of ILs was shifted from non-volatile to principally volatile in the last 15 years.8 The change in the concept about volatility triggered the research on the quantitative analysis of the volatility of the ILs in the condensed phase. A few experimental methods have been modified to measure the enthalpy of vaporization (ΔHvap) and the vapor pressure (Pvap) of both protic and aprotic ILs, such as line-of-sight mass spectrometry (LOSMS),9a isothermogravimetric analysis (IGA),9b ultraviolet spectroscopy (UV),9c quartz crystal microbalance (QCM),9d and the traditional Knudsen method,9e among which IGA is a relatively simple and efficient method.9b,10ΔHvap reflects molecular interactions in the liquid state and can serve as a foundation for calibrating and validating force fields in molecular dynamics simulations9 and as an anchoring parameter in P–V–T equations for neat ILs. Meanwhile, the enthalpy of sublimation (ΔHsub) can be employed to estimate the strength of molecular interactions in the solid organic salts (i.e. crystalline or solidified ILs or ILs in the solid state). The solid organic salts have much lower vapor pressure than the liquid-state ones, while there are few studies on the experimental methods about their ΔHsub. The available few cohesive properties of solid organic salts are calculated by quantum chemical simulation.11 Nonetheless, they are generally scattered data at several temperatures and can hardly reflect their dependence on temperatures because of the massive quantum chemical calculations for a wide temperature range.
Additionally, experimental and computational methods for the volatilization process of ILs have established that the gaseous phase volatilized from aprotic ILs consists of isolated tight neutral ion pairs.12 The gaseous ion pairs are an intermediate state between the gaseous phase ions and condensed matter of aprotic ILs. Consequently, the energy difference between the cohesive energy and lattice energy of solid organic salts can indicate the potential energy of the gaseous ion pairs. However, the quantitative studies on the gaseous ion pairs are insufficient owing to the data scarcity of cohesive properties. Recently, Červinka et al.11 calculated the values of ΔHvap and ΔHsub of condensed ILs using a combination of quantum chemical calculations and thermal analysis. Specifically, ΔHvap and ΔHsub are associated with enthalpy of fusion (ΔHfus): ΔHsub = ΔHfus + ΔHvap. Krossing et al.13 developed a model to predict melting temperatures by using a suitable Born–Fajans–Haber cycle that was closed by the lattice Gibbs energy and the solvation Gibbs energies of the constituent ions in the molten salts.
In this paper, the cohesive properties of solid organic salts are investigated using Born–Fajans–Haber cycles, in which the enthalpy of sublimation is the sum of the enthalpy of solid–solid transitions (if there are), the enthalpy of melting and the enthalpy of vaporization. The basic thermodynamic parameters can be measured by thermogravimetric analyzer (TGA) and differential scanning calorimetry (DSC). In contrast to the complex quantum chemical simulation, the cohesive properties of solid organic salts can be obtained by calculating the sum of the measured data. Thus, the reported method avoids the large time consumed for geometry optimization, thermodynamic equilibria, and energy calculations. The enthalpy of sublimation and the cohesive energy of tetrabutylammonium bis(trifluoromethanesulfonyl)imide ([N4444][NTf2]) as a model solid organic salt were determined for the first time by this method. In addition, the cohesive properties of 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([C2mim][NTf2]) and 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([C4mim][NTf2]) were determined to testify the method's universality for ILs. Moreover, the energy difference between the cohesive energy and lattice energy of solid organic salts is adopted in this study to estimate the average charge separation in the single gaseous ion pair (r12) by the Born–Mayer equation based on the calculated cohesive energy of solid organic salts. The parameter r12 can reflect the degree of contact between the anion and the cation in the gaseous ion pair.
Furthermore, the thermal stability of ILs is a crucial property that allows for long-term and safe applications at high temperatures,14 such as thermal energy storage materials and heat transfer fluids. These properties can provide useful information about the maximum operating temperatures and the pyrolysis half-lives. TGA techniques were thus also employed to examine the pyrolysis kinetics of [N4444][NTf2]. The kinetic parameters during the pyrolysis were calculated with differential and integral methods.
Therefore, the specific objectives of this work are comprised of: (i) an assessment of cohesive properties of [N4444][NTf2] in both the solid and liquid states, and (ii) a systematic investigation of the pyrolysis mechanism of [N4444][NTf2].
Experimental
Materials
Tetrabutylammonium bis(trifluoromethanesulfonyl)imide (abbreviated as [N4444][NTf2]; CAS number: 210230-40-3; molecular weight (MW): 522.61 g mol−1; purity: ≥99%) was purchased from Lanzhou Greenchem ILs, LICP, CAS. Glycerol (Molecular formula: HOCH2CHOHCH2OH; CAS number: 56-81-5; MW: 92.09 g mol−1; purity: ≥98%) was bought from Beijing Solarbio Science & Technology Co., Ltd. The molecular structures of [N4444][NTf2] and glycerol were shown in Scheme 1. All chemicals were used as received.Basic characterizations
The Fourier Transform infrared (FTIR) spectrum of [N4444][NTf2] powders at room temperature was recorded in the spectral range of 400–4000 cm−1 at a resolution of 4 cm−1 using an FTIR spectrometer (INVENIO-R, Bruker) with an attenuated total reflection (ATR) accessory. The NMR spectra were recorded on a Bruker Avance™ II 400 MHz spectrometer at room temperature. Powder XRD measurements of fine powders of [N4444][NTf2] were performed at room temperature under vacuum on a powder X-ray diffractometer (Empyrean, PANalytical) using Cu Kα radiation (λ = 1.5406 Å) to identify the crystalline structure of [N4444][NTf2]. The measurement is composed of θ–2θ scan from 5 to 60° with a step size of 0.026°. The full instrumental specifications and experimental parameters are detailed in the (ESI†).Differential scanning calorimetry (DSC) measurements
DSC measurements were conducted between −150 °C and 335 °C on a DSC3 STARe system (METTLER TOLEDO) at a heating/cooling rate of 10 °C min−1 to identify the melting point (Tm) of [N4444][NTf2] and the liquid temperature range. Additionally, the three-step measurements (isothermal → ramp → isothermal) were carried out over the temperature ranges of −100 to −50, −10 to 25 °C and 95 to 195 °C to determine the heat capacities of the solid and liquid states of [N4444][NTf2]. The experimental results of heat capacities are shown in the ESI.†Thermogravimetric analysis (TGA)
The thermal properties of [N4444][NTf2] and glycerol were recorded on a thermogravimetric analyzer Q5000 (TA Instruments) using the same platinum crucible (volume: 78.5 mL; cross-sectional area (a): 0.785 cm2). Isothermogravimetric analysis (IGA) experiments of [N4444][NTf2] were conducted under a nitrogen atmosphere (60 mL min−1) at 230, 260, 290, 310, 330 and 350 °C successively for 1 h, respectively. Before the IGA measurement, the sample was heated from room temperature to 250 °C at a heating rate of 20 °C min−1 and was held at that temperature for one hour so as to remove possible volatile impurities and water and completely spread the melts in the pan. Afterwards, it was heated or cooled to the target temperatures. The experiments on glycerol were conducted under the same nitrogen atmosphere (60 mL min−1) at 100, 120, 140, and 160 °C for 20 min, respectively. The initial mass of each sample was measured to be between 50.104 and 52.167 mg. Concerning the ramped TGA measurements of [N4444][NTf2], it was guaranteed that each sample possessed an initial mass of around 18 mg and was heated from room temperature to 750 °C at heating rates of 5, 10, and 15 °C min−1, respectively, in a nitrogen atmosphere (60 mL min−1).Density functional theory (DFT) calculations
Density functional theory (DFT) calculations were performed to generate the electrostatic potential maps of the cations and anions through the Dmol3 module in Materials studio software (version 8.0). The structures of ions were optimized to the local minimum, and subsequently, the electrostatic potential maps were generated from the optimized configurations. The BLYP functional was employed with generalized gradient approximation (GGA), and the basis set DNP 4.4 was utilized in the calculation.Theoretical basis
Concept of the thermodynamic cycle of cohesive properties
Under normal experimental conditions, the vapor of aprotic ILs is validated to be ideal gas composed of isolated ion pairs.13 Thus, the cohesive energy (Ecoh) of ILs is the energy required to separate the ions in a condensed state into independent ion pairs.15Ecoh corresponds to the change in internal energy (ΔUvap or ΔUsub) during the transition from condensed matter to the vapor phase, it has relations with ΔHvap or ΔHsub of ILs (eqn (1) and (2)). For liquid state (PV = RT, molar quantities):| Ecoh = ΔUvap = ΔHvap − RT | (1) |
| Ecoh = ΔUsub = ΔHsub − RT | (2) |
In the first Born–Fajans–Haber (Fig. 1(a)), the ΔHsub is regarded as the summation of ΔHvap, fusion enthalpy (ΔHfus) and the enthalpy of a solid–solid phase transition (ΔHCrII → CrI). Moreover, the changes in ΔHsub and ΔHvap induced by the variation of temperature are offset by Kirchhoff's law. Thus, the relation between the parameters is described as:
 | (3) |
 | (4) |
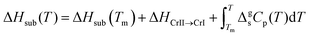 | (5) |
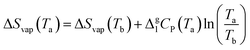 | (6) |
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pvap = A − C/(T + C) Pvap = A − C/(T + C) | (7) |
Specifically, ΔSvap and ΔSsub are derived from ΔSvap(Tb) based on the Born–Fajans–Haber cycle (Fig. 1(b)) and additional integration term representing the contribution of Kirchhoff's law:
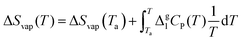 | (8) |
Similarly, ΔSvap(Tm) can be calculated when T = Tm. Regarding the calculated ΔSsub in the temperature range of solid state, the entropy of solid–solid transition (ΔSCrII → CrI) between the melting point and objective temperature, apart from the fusion entropy (ΔSfus), should be added into the equation (eqn (9)).
 | (9) |
The lattice potential energy (UL) of crystalline ionic liquids can be approximated to its electrostatic interaction potential energy (Ees). Then, Ees can be calculated by multiplying the Madelung constant with the electrostatic interaction energy of single ion pair in the crystal (eqn (10)).
 | (10) |
| ΔUsub = ΔUL − ΔUip | (11) |
The approximation of Uip given by the Born–Mayer equation17 is:
 | (12) |
The detailed calculation methods of ΔHvap, Pvap and ΔUL were discussed in the ESI.†
Pyrolysis kinetic method
The pyrolysis kinetic parameters were analyzed by differential and integral methods (ESI†). The differential ones contain Ozawa, Kissinger, and Starink methods, which derive the activation energy (Ea), pre-exponent factor (A), kinetic exponent (n), enthalpy change (ΔH), entropy change (ΔS), and Gibbs free energy change (ΔG) during the formation of transition state through the DTG data from TGA experiments. Meanwhile, the integral ones consist of Flynn–Wall–Ozawa (ASTM E-1641), Kissinger–Akahira–Sunose (KAS), and Starink methods. The Ea at different degradation conversions (α) was calculated using the integral methods.Results and discussions
Cohesive properties
ΔHvap as an essential part of the Born–Fajans–Haber cycle is the first cohesive property to be determined. Hence, the ΔHvap of [N4444][NTf2] was measured using the IGA method at its experimental average temperature (Ta = 295 °C) (ESI†). Except for ΔHvap, the other components of the cycle are the enthalpies of phase change in the condensed state. As expected, [N4444][NTf2] has only a micro solid–solid phase change at −29.4 °C, where the two solid phases were denoted as phases CrI and CrII corresponding to the phase at a higher and lower temperature, respectively (Fig. 2). In the XRD pattern, a similar phenomenon was observed (Fig. S3, ESI†). Moreover, the discontinuous change of heat capacities of [N4444][NTf2] (Fig. 3(a)) can also demonstrate the occurring of phase change at −29.4 °C. The known ΔHvap(Ta), ΔHfus and ΔHCrII → CrI are 144.2, 23.3 and 0.88 kJ mol−1, respectively, forming the Born–Fajans–Haber cycle of enthalpy to derive ΔHsub. The used ΔHvap(Ta), ΔHfus, Ta and Tm of [N4444][NTf2], [C2mim][NTf2]18,19 and [C4mim][NTf2]20,21 are listed in Table 1. However, the calculation of ΔHsub from the thermodynamic cycle involves two parts, which correspond to the phase change (the above-mentioned results) and the temperature variation, respectively. The dependence of molar heat capacities of CrI and CrII (Cp,s), liquid (Cp,l), and gas phase (Cp,g) on the temperature is fitted using polynomial regression to demonstrate the changes in ΔHvap and ΔHsub caused by the temperature variation (Fig. 3(a)). The parameters of polynomials and correlation factor R2 for [N4444][NTf2] were listed in Table 2. Notably, the selected ranges for fitting are the parts of experimental Cp,s and Cp,l, since these experimental results are associated with the temperature far from the phase change point and then reinforce the accuracy of heat capacities. For the ideal gas phase of [N4444][NTf2], Cp,g was assumed as the sum of the contribution of cation and anion.22 The detailed calculations for the molar heat capacities of [N4444]+ and [NTf2]− were presented in ESI.† Additionally, the parameters of the polynomials for Cp,s, Cp,l and Cp,g of [C2mim][NTf2] and [C4mim][NTf2] were listed in Tables S4 and S5 (ESI†). As derived by Kirchhoff's law (eqn (4)), the change in ΔHvap and ΔHsub of [N4444][NTf2] exhibit an increasing tendency with decreasing temperature (Fig. 3(b)). | ||
| Fig. 2 DSC thermogram of [N4444][NTf2] measured at 10 °C min−1 for both the heating and cooling process at −150 °C to 335 °C (a), and its enlarged view at −60 °C to 0 °C (b). | ||
 | ||
| Fig. 3 Heat capacities of CrII, CrI, liquid and ideal gas states of [N4444][NTf2] (a); Change in enthalpy due to the temperature variation (b). | ||
| Parameters | C p,s | C p,l | C p,g | |
|---|---|---|---|---|
| CrII | CrI | |||
| a 0 | −53.13 | 260.02 | −168.23 | 10.21 |
| a 1 | 2.68 | 0.66 | 4.57 | 2.31 |
| a 2 | −1.34 × 10−3 | 2.76 × 10−3 | −3.97 × 10−3 | −1.19 × 10−3 |
| a 3 | — | — | — | 4.16 × 10−7 |
| R 2 | 0.999 | 0.999 | 0.999 | 0.999 |
Therefore, the sum of ΔHvap(Ta), ΔHfus, ΔHCrII → CrI and the change in enthalpy enables the accurate value of ΔHvap or ΔHsub and Ecoh at a given temperature (Fig. 4, 5 and Tables S8–S10, ESI†). It has a negative correlation between Ecoh and temperature in the total liquid temperature range of all the three ILs. As the temperature decreases from 295 to 90.8 °C, Ecoh of [N4444][NTf2] varies from 139.5 to 185.8 kJ mol−1 (Fig. 4), while Ecoh of [C2mim][NTf2] ranges from 118.7 to 137.4 kJ mol−1 in [124.4 °C, −1.7 °C] and Ecoh of [C4mim][NTf2] ranges from 114.3 to 144.8 kJ mol−1 in [204.5 °C, 6.9 °C] (Fig. 5). During the solid-state temperature range, nonetheless, the Ecohversus temperature of the three solid organic salts have diverse tendencies. For the solid phase of [N4444][NTf2], the Ecoh at a temperature slightly lower than 90.8 °C is 209.1 kJ mol−1. Ecoh of solid-state [N4444][NTf2] has monotonical negative correlation with temperature in the total CrI phase and higher-temperature region of the CrII phase range, whereas it reaches its maximum value of 224.7 kJ mol−1 at −110 °C. This can be attributed to that Cp,s is slightly lower than Cp,g below −110 °C for [N4444][NTf2]. As the temperature decreases, the Ecoh of [N4444][NTf2] reaches to 224.1 kJ mol−1 at −173.15 °C. In contrast, Ecoh of solid-state [C2mim][NTf2] and [C4mim][NTf2] show negative correlations with temperature in the total solid temperature (Fig. 5). For [C2mim][NTf2] and [C4mim][NTf2] solid organic salts, the Ecoh at −153.15 °C are 165.4 and 169.6 kJ mol−1, respectively. Moreover, the calculated Ecoh of [C2mim][NTf2] at −273.15 °C is 166.8 kJ mol−1, while the reported values of Ecoh of [C2mim][NTf2] calculated by different quantum chemical methods range from 161.7 to 171.2 kJ mol−1 at −273.15 °C,11 with a deviation lower than 3% from the value in this work, demonstrating the reliability of the method used in this paper. For the three organic salts, the abrupt increase in Ecoh corresponds to a first-order phase change (i.e. solidification). This suggests that the new phase is more stable than the old one in thermodynamics when the temperature is lower than the transition point.
 | ||
| Fig. 4 The cohesive energy (Ecoh), enthalpy of vaporization (ΔHvap) and sublimation (ΔHsub) of [N4444][NTf2] from −173.15 to 295 °C. | ||
 | ||
| Fig. 5 The cohesive energy (Ecoh), enthalpy of vaporization (ΔHvap), and sublimation (ΔHsub) of [C2mim][NTf2] from −273.15 to 124.35 °C (a) and [C4mim][NTf2] from −273.15 to 204.45 °C, respectively. | ||
Additionally, a theoretical boiling point (Tb) of ILs can be defined as the temperature at which the Gibbs energy of vaporization (ΔGvap) equals zero. Therefore, ΔHvap at Tb can be used to calculate the entropy of vaporization (ΔSvap) and sublimation (ΔSsub). Tb of ILs does not exist in the actual conditions because the thermal decomposition would occur prior to the boiling. Nonetheless, the theoretical Tb can be regarded as the extrapolated value of temperature at which Pvap equals the standard pressure (105 Pa) in the function of Pvap about temperature. Besides, the Pvap of [N4444][NTf2] is calculated using the IGA experiments data (Table S11, ESI†) to obtain Tb and ΔHvap(Tb) of [N4444][NTf2], and it ranges from 0.02 to 14.3 Pa between 230 and 350 °C. The data of Pvap at literatures23,24 are adopted for the calculations of ILs [C4mim][NTf2] and [C2mim][NTf2]. Moreover, the function of Pvap is described with the Antoine equation (ESI†). Subsequently, Tb of [N4444][NTf2], [C4mim][NTf2], and [C2mim][NTf2] is determined to be 587.5, 393.6 and 842.1 °C, respectively. However, Δg1Cp between Tb and Ta do not conform to a polynomial function. Thus, Δg1Cp(Ta) was utilized as a rough approximation of the Δg1Cp to calculate ΔHvap(Tb). The determined values of ΔHvap(Tb) and ΔSvap(Tb) of [N4444][NTf2] amount to 105.3 kJ mol−1 and 122.4 J K−1 mol−1, respectively. As the intersections of the cycle, ΔSfus and ΔSCrII → CrI have values of 64.1 and 3.6 J K−1 mol−1, respectively, derived from ΔHfus and ΔHCrII → CrI. Then, ΔSvap and ΔSsub of [N4444][NTf2] were extrapolated to a given temperature (Fig. 6(a)) by the Born−Fajans−Haber cycle of entropy. Similarly, ΔSvap and ΔSsub of [C4mim][NTf2] and [C2mim][NTf2] were also calculated by this approach. The results are employed to calculate ΔGvap and the Gibbs free energy of sublimation (ΔGsub). The detailed results of the three organic salts were listed in Tables S12–S17 (ESI†), respectively. With the purpose of simplifying the marks of the cohesive properties, the terms of ΔHsub and ΔHvap were unified as ΔHvot, ΔSsub and ΔSvap as ΔSvot, and ΔGvap and ΔGsub as ΔGvot in Fig. 6 and 7. The results demonstrate that the phase change in the condensed state of ILs has a negligible effect on ΔGvot and a significant one on ΔHvot and ΔSvot. ΔGvot of [N4444][NTf2] ranges from 43.3 to 186.6 kJ mol−1 in [295 °C, −173.15 °C], and ΔGvot of [C4mim][NTf2] ranges from 29.3 to 164.2 kJ mol−1 in [204.45 °C, −252.85 °C], however, that of [C2mim][NTf2] varies from 60.6 to 166.4 kJ mol−1 in [124.4 °C, −271.7 °C]. Thus, the average rate of ΔGvot variation with temperature of [C2mim][NTf2] is lower than the former tow organic salts. In other words, ΔGvot of [N4444][NTf2] and [C4mim][NTf2] has higher temperature sensitivity than that of [C2mim][NTf2]. This difference may be ascribed to the longer alkyl chains in the cations of the former two salts since more carbon and hydrogen atoms can induce a larger absolute value of Δg1Cp and ΔgsCp.25
Fig. 1(c) depicts the third cycle, which is closed by the ΔUsub, the lattice energy (ΔUL) and the internal energy of gaseous ion pairs (ΔUip). Fig. 8(a) and (b) demonstrate the asymmetric cell and equilibrium geometries of [N4444][NTf2] at 173.15 °C. [N4444][NTf2] is monoclinic with a dipole moment of the unit cell of 29.53 Debye. The electrostatic potential maps (Fig. 8(c) and (d)) imply that the positive charge in cation is concentrated on the nitrogen atom rather than the hydrogen atom, and there are generally no H-bonds regarding C–H. Thus, no possible H-bonds site exits in [N4444]+ and [NTf2]−. Furthermore, the contributions of van der Waals interaction on the UL for simple ionic solids are only about 1%26 revealing that the UL of [N4444][NTf2] approximately equals its pure electrostatic interaction energy in this case (Ees). Similarly, the UL of the other two ILs can be determined based on this approximation. With the crystal structure data of [N4444][NTf2] at −173.15 °C27 and [C2mim][NTf2] and [C4mim][NTf2] at −153.15 °C,28 the ΔUL together with the M and rmin (ESI†) are determined using the EUGEN method. The ΔUL and ΔUsub of [N4444][NTf2] at −173.15 °C are 408.3 and 224.1 kJ mol−1, respectively, while the M of [N4444][NTf2] is 1.205 and rmin is 0.410 nm. Thus, the difference between ΔUL and ΔUsub unveils that ΔUip equals 184.2 kJ mol−1. The detailed results of the other two solid organic salts at −153.15 °C were provided in Table 3. The given ΔUip can estimate r12 of [N4444][NTf2], [C2mim][NTf2] and [C4mim][NTf2] through the Born–Mayer equation (eqn (12)). Meanwhile, r12 is much larger than rmin for the three organic salts, indicating that the charge separation in the ion pair is stronger than the closet counterion in the solid phase for aprotic ILs. The ratios “r12/rmin” of [N4444][NTf2], [C4mim][NTf2], and [C2mim][NTf2] are 1.75, 1.18 and 1.10, respectively. It reflects that r12/rmin may increase with the growing numbers of carbon atoms in alkyl chains since more adjacent but unbonded atoms can result in a larger van der Waals radius in the gas phase. This explanation requires further investigation.
| Features | [N4444][NTf2] | [C2mim][NTf2] | [C4mim][NTf2] |
|---|---|---|---|
| ΔUL (kJ mol−1) | 408.3 | 452.0 | 439.6 |
| ΔUsub (kJ mol−1) | 224.1 | 165.4 | 140.8 |
| ΔUip (kJ mol−1) | 184.2 | 286.6 | 311.2 |
| M | 1.205 | 1.329 | 1.277 |
| r min (nm) | 0.410 | 0.408 | 0.403 |
| r 12 (nm) | 0.718 | 0.447 | 0.477 |
| T (°C) | −173.15 | −153.15 | −153.15 |
Pyrolysis mechanism
The onset temperature (Tonset) of thermal decomposition is determined using the ramped TGA technique to access the thermal stability of [N4444][NTf2] (Table S18, ESI†). The pyrolysis kinetics of [N4444][NTf2] are analyzed using the Ozawa, Kissinger, and Starink methods from the differential thermal gravimetric (DTG) peak temperatures (Table 4). Tonset presents an extremely high linear relation with heating rates, where the correlation R2 exceeds 0.9999. Thus, the heating rate is extrapolated to 0 °C min−1, and the Tonset is obtained as 368.5 °C at that rate. As derived through Ozawa, Kissinger and Starink methods, the average activation energy (Ea) is 242.1 kJ mol−1, highlighting the exceptional thermal stability of [N4444][NTf2]. Moreover, the enthalpy (ΔH) and entropy (ΔS) change during the formation of the transition state are 237.4 kJ mol−1 and 57.1 J K−1 mol−1, respectively. ΔS is minimal compared with ΔH. Therefore, it can be postulated that the transition state of [N4444][NTf2] is far from its initial state, leading to low reactivity. The calculation of the kinetic exponent (n = 0.005) reflects that the pyrolysis of [N4444][NTf2] is a zero-order reaction (ESI†). The half-life (t1/2) of [N4444][NTf2] is derived from the kinetic parameters (Table S19, ESI†).| Method | E a (kJ mol−1) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A (min−1) A (min−1) |
R 2 | ΔH (kJ mol−1) | ΔG (kJ mol−1) | ΔS (J K−1 mol−1) |
|---|---|---|---|---|---|---|
| Ozawa | 244.3 | 42.4 | 0.998 | 238.6 | 198.6 | 58.0 |
| Kissinger | 241.9 | 42.0 | 0.999 | 236.2 | 198.6 | 54.9 |
| Starink | 244.0 | 42.4 | 0.998 | 238.3 | 198.6 | 58.4 |
| Avarage | 242.1 | 42.3 | 237.7 | 198.6 | 57.1 |
In the kinetics analysis at different degradation conversions (α), Flynn–Wall–Ozawa (ASTM E-1641), Kissinger–Akahira–Sunose (KAS), and Starink methods are employed to derive the Ea at the conversion of 5 to 90%. The results demonstrate that Ea of [N4444][NTf2] has reduced dependence with the increasing degradation conversion and becomes a constant value at the conversion of 70% (Fig. 9). The variations of Ea are attributed to the increased temperature during the thermal gravimetric experiments since this degradation process is a zero-order reaction. Thus, the pyrolysis process of [N4444][NTf2] is a multi-step process consisting of an endothermic reversible reaction followed by an irreversible one.29Ea is the sum of the activation enthalpy of the reversible reaction (ΔH0) and the activation energy of the irreversible reaction (E2) (ESI†). The endothermic reversible reaction's equilibrium constant (K1) increases with the increasing temperature, reducing the value of ΔH0. ΔH0 tends to be zero when the condition of K1 ≫ 1 is fulfilled at a high temperature. Hence, the minimum value of Ea approximately equals the activation energy of the irreversible reaction (259.3 kJ mol−1), revealing that the irreversible reaction is a rate-determining step (RDS) in the pyrolysis process of [N4444][NTf2]. Furthermore, the discussions and data associated with cohesive properties and pyrolysis kinetics are available in the ESI.†
Conclusions
In this paper, three Born–Fajans–Haber cycles were adopted to describe the cohesive properties of the condensed state of [N4444][NTf2], [C2mim][NTf2], and [C4mim][NTf2], providing a novel method to detect the cohesive properties of ILs. The internal energy (or cohesive energy), enthalpy, entropy, and Gibbs free energy of the transition from condensed state to gas were successfully derived from the method. Moreover, the internal energy of the gas phase and the charge separation of the single gaseous ion pair were estimated from the cycle. Concerning thermal degradation, [N4444][NTf2] has extremely high thermal stability. The characteristics of condensed matter of the three ILs can be summarized as follows:(1) Longer alkyl chains in cations resulted in higher temperature sensitivity of Gibbs free energy change during the transition from the condensed matter to vapor for aprotic ILs.
(2) The degree of charge separation in the gaseous ion pair was larger than that of the ions in the solid phase.
(3) A longer alkyl chain in cation enlarged the charge separation distance in ion pair and the ratio r12/rmin of aprotic ILs.
(4) The pyrolysis process of [N4444][NTf2] was a multi-step process consisting of an endothermic reversible reaction followed by an irreversible one, where the irreversible one was a rate-determining step.
With the promotion of this method to more types of ILs, these thermodynamic cycle concepts would enlighten research on the nature of the gaseous state of ILs.
Abbreviation
| T | Temperature (K) |
| t | Time (min) |
| m | Weight (mg) |
| a | Cross-sectional area of the crucible (cm2) |
| M W | Molecular weight (g mol−1) |
| N A | Avogadro constant (6.022 × 1023) |
| R | Gas constant (8.314 J K−1 mol−1) |
| ε 0 | Vacuum permittivity (8.854 × 10−12 F m−1) |
| e | Elementary charge (1.602 × 10−19 C) |
| M | Madelung constant |
| P vap | Vapor pressure (Pa) |
| C p | Molar heat capacity (J K−1 mol−1) |
| C p,s | Molar heat capacity of solid state (J K−1 mol−1) |
| C p,l | Molar heat capacity of liquid state (J K−1 mol−1) |
| C p,g | Molar heat capacity of ideal gaseous state (J K−1 mol−1) |
| ΔHvap | Enthalpy of vaporization (kJ mol−1) |
| ΔHsub | Enthalpy of sublimation (kJ mol−1) |
| ΔHfus | Enthalpy of fusion (kJ mol−1) |
| ΔSfus | Entropy of fusion (J K−1 mol−1) |
| ΔHsol | Enthalpy of solidification (kJ mol−1) |
| E coh | Cohesive energy (kJ mol−1) |
| ΔUvap | Internal energy of vaporization (kJ mol−1) |
| ΔUsub | Internal energy of sublimation (kJ mol−1) |
| ΔUL | Lattice energy (kJ mol−1) |
| ΔUip | Internal energy of ion pairs in the gaseous state (kJ mol−1) |
| r min | Minimum distance between the cation and anion (nm) |
| r 12 | The charge separation distance of single ion pair in the gas phase |
| E a | Activation energy (kJ mol−1) |
| A | Pre-exponential factor (min−1) |
| ΔH | Enthalpy change of activated complex formation (kJ mol−1) |
| ΔG | Gibbs energy change of activated complex formation (kJ mol−1) |
| ΔS | Entropy change of activated complex formation (J K−1 mol−1) |
Author contributions
Jiangshui Luo: Conceptualization, supervision, methodology, project administration, data curation, formal analysis, funding acquisition, resources, and writing – review & editing. Shijie Liu: Investigation, formal analysis, methodology, data curation and writing – original draft. Runhong Wei: Writing – review & editing. Guangjun Ma: Writing – review & editing. Ailin Li: Investigation and writing – review & editing. Olaf Conrad: Writing – review & editing.Conflicts of interest
J. Luo and R. Wei have filed four Chinese patent applications (ZL202210151023.7, 202210135274.6, 202210135259.1, and 202210474222.1).Acknowledgements
This work is financially supported by Sichuan Science and Technology Program (project No.: 2022ZYD0016 and 2023JDRC0013), National Natural Science Foundation of China (project No.: 21776120), Hohhot Science and Technology Program (project No.: 2023-JieBangGuaShuai-Gao-3), and Natural Science Foundation of Fujian Province, China (project No.: 2023J01254). We appreciate the Analytical – Testing Center of Sichuan University for providing Materials Studio and we are grateful to Daichuan Ma and Daibing Luo for their help of computational simulation. Finally, we appreciate Samuel Y. S. Tan and Dr. Ekaterina I. Izgorodina (Monash University) for providing the modified version of the EUGEN code.Notes and references
- A. Avid, J. L. Ochoa, Y. Huang, Y. Liu, P. Atanassov and I. V. Zenyuk, Nat. Commun., 2022, 13, 6349 CrossRef CAS PubMed.
- X. Li, D. Wang, Z. He, F. Su, J. Zhang, Y. Wang, Y. Xin, H. Wang, D. Yao, M. Li and Y. Zheng, J. Mater. Chem. A, 2022, 10, 13333–13344 RSC.
- G. Li, Q. Gao, Q. Liu, C. Gui and Z. Lei, AIChE J., 2023, 69, e17914 CrossRef CAS.
- J. Luo, A. H. Jensen, N. R. Brooks, J. Sniekers, M. Knipper, D. Aili, Q. Li, B. Vanroy, M. Wübbenhorst, F. Yan, L. Van Meervelt, Z. Shao, J. Fang, Z.-H. Luo, D. E. De Vos, K. Binnemans and J. Fransaer, Energy Environ. Sci., 2015, 8, 1276–1291 RSC.
- A. Paolella, G. Bertoni, W. Zhu, D. Campanella, A. L. Monaca, G. Girard, H. Demers, A. C. G. Nita, Z. Feng, A. Vijh, A. Guerfi, M. Trudeau, M. Armand and S. A. Krachkovskiy, J. Am. Chem. Soc., 2022, 144, 3442–3448 CrossRef CAS PubMed.
- S. L. Piper, M. Kar, D. R. MacFarlane, K. Matuszek and J. M. Pringle, Green Chem., 2022, 24, 12–117 RSC.
- E. Fabre and S. M. S. Murshed, J. Mater. Chem. A, 2021, 9, 15861–15879 RSC.
- K. R. Seddon, M. A. Gilea, L. P. N. Rebelo, M. J. Earle, J. M. S. S. Esperança, J. A. Widegren, J. N. Canongia Lopes and J. W. Magee, Nature, 2006, 439, 831–834 CrossRef PubMed.
- (a) V. N. Emel’yanenko, S. P. Verevkin, A. Heintz, J.-A. Corfield, A. Deyko, K. R. J. Lovelock, P. Licence and R. G. Jones, J. Phys. Chem. B, 2008, 112, 11734–11742 CrossRef PubMed; (b) G. A. Backer., H. Luo and S. Dai, J. Phys. Chem. B, 2008, 112, 10077–10081 CrossRef PubMed; (c) C. Wang, H. Luo, H. Li and S. Dai, Phys. Chem. Chem. Phys., 2010, 12, 7246–7250 RSC; (d) S. P. Verevkin, D. H. Zaitsau, V. N. Emeĺyanenko and A. Heintz, J. Phys. Chem. B, 2011, 115, 12889–12895 CrossRef CAS PubMed; (e) A. M. Dunaev, V. B. Motalov, L. S. Kudin and M. F. Butman, J. Mol. Liq., 2016, 223, 407–411 CrossRef CAS.
- X. Chen, H. Tang, T. Putzeys, J. Sniekers, M. Wübbenhorst, K. Binnemans, J. Fransaer, D. E. De Vos, Q. Li and J. Luo, J. Mater. Chem. A, 2016, 4, 12241–12252 RSC.
- C. Červinka, M. Klajmon and V. C. Štejfa, J. Chem. Theory Comput., 2019, 15, 5563–5578 CrossRef PubMed.
- J. M. S. S. Esperança, J. N. Canongia Lopes, M. Tariq, L. M. N. B. F. Santos, J. W. Magee and L. P. N. Rebelo, J. Chem. Eng. Data, 2010, 55, 3–12 CrossRef.
- I. Krossing, J. M. Slattery, C. Daguenet, P. J. Dyson, A. Oleinikova and H. Weingärtner, J. Am. Chem. Soc., 2007, 129, 11296 CrossRef CAS.
- B. Wang, L. Qin, T. Mu, Z. Xue and G. Gao, Chem. Rev., 2017, 117, 7113–7131 CrossRef CAS PubMed.
- L. Glasser and D. A. Sheppard, Inorg. Chem., 2016, 55, 7103–7110 CrossRef CAS PubMed.
- E. I. Izgorodina, U. L. Bernard, P. M. Dean, J. M. Pringle and D. R. MacFarlane, Cryst. Growth Des., 2009, 9, 4834–4839 CrossRef CAS.
- J. P. Armstrong, C. Hurst, R. G. Jones, P. Licence, K. R. J. Lovelock, C. J. Satterley and I. J. Villar-Garcia, Phys. Chem. Chem. Phys., 2007, 9, 982–990 RSC.
- K. R. J. Lovelock, A. Deyko, P. Licence and R. G. Jones, Phys. Chem. Chem. Phys., 2010, 12, 8893–8901 RSC.
- Y. U. Paulechka, A. V. Blokhin, G. J. Kabo and A. A. Strechan, J. Chem. Thermodyn., 2007, 39, 866–877 CrossRef CAS.
- J. Troncoso, C. A. Cerdeiriña, Y. A. Sanmamed, L. Romaní and L. P. N. Rebelo, J. Chem. Eng. Data, 2006, 51, 1856–1859 CrossRef CAS.
- D. H. Zaitsau, G. J. Kabo, A. A. Strechan, Y. U. Paulechka, A. Tschersich, S. P. Verevkin and A. Heintz, J. Phys. Chem. A, 2006, 110, 7303–7306 CrossRef CAS PubMed.
- S. P. Verevkin, D. H. Zaitsau, V. N. Emel’yanenko, R. V. Ralys, A. V. Yermalayeu and C. Schick, Thermochim. Acta, 2013, 562, 84–95 CrossRef CAS.
- L. M. N. B. F. Santos, A. I. M. C. L. Ferreira, V. Štejfa, A. S. M. C. Rodrigues, M. A. A. Rocha, M. C. Torres, F. M. S. Tavares and F. S. Carpinteiro, J. Chem. Thermodyn., 2018, 126, 171–186 CrossRef CAS.
- Y. U. Paulechka, D. H. Zaitsau, G. J. Kabo and A. A. Strechan, Thermochim. Acta, 2005, 439, 158 CrossRef CAS.
- D. H. Zaitsau, N. Plechkova and S. P. Verevkin, J. Chem. Thermodyn., 2019, 130, 204–212 CrossRef CAS.
- A. R. West, Solid state chemistry and its applications, Wiley, New York, 1984 Search PubMed.
- X. Han, J. Ke, N. Suleiman, W. Levason, D. Pugh, W. Zhang, G. Reid, P. Licence and M. W. George, Phys. Chem. Chem. Phys., 2016, 18, 14359–14369 RSC.
- Y. U. Paulechka, G. J. Kabo, A. V. Blokhin, A. S. Shaplov, E. I. Lozinskaya, D. G. Golovanov, K. A. Lyssenko, A. A. Korlyukov and Y. S. Vygodskii, J. Phys. Chem. B, 2009, 113, 9538 CrossRef CAS PubMed.
- S. Vyazovkin, Int. J. Chem. Kinet., 1996, 28, 95–101 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00614j |
| This journal is © The Royal Society of Chemistry 2023 |






