Halogen bonding between metal-bound I3− and unbound I2: the trapped I2⋯I3− intermediate in the controlled assembly of copper(I)-based polyiodides†
Mikhail A.
Kinzhalov
 ab,
Daniil M.
Ivanov
ab,
Daniil M.
Ivanov
 ab,
Anastasia V.
Shishkina
ab,
Anastasia V.
Shishkina
 c,
Anna A.
Melekhova
c,
Anna A.
Melekhova
 a,
Vitalii V.
Suslonov
a,
Vitalii V.
Suslonov
 ab,
Antonio
Frontera
ab,
Antonio
Frontera
 d,
Vadim Yu.
Kukushkin
d,
Vadim Yu.
Kukushkin
 *ae and
Nadezhda A.
Bokach
*ae and
Nadezhda A.
Bokach
 *ab
*ab
aSt Petersburg State University, Universitetskaya Nab. 7/9, Saint Petersburg, 199034, Russian Federation. E-mail: n.bokach@spbu.ru; v.kukushkin@spbu.ru
bResearch School of Chemistry and Applied Biomedical Sciences, Tomsk Polytechnic University, 634050 Tomsk, Russian Federation
cDepartment of Physics and Engineering Environmental Protection, Northern (Arctic) Federal University, Arkhangelsk, 163001, Russian Federation
dDepartment of Chemistry, Universitat de les Illes Balears, Crta. de Valldemossa km 7.5, 07122 Palma de Mallorca, Baleares, Spain
eInstitute of Chemistry and Pharmaceutical Technologies, Altai State University, Barnaul, 656049, Russian Federation
First published on 11th January 2023
Abstract
Crystallization of [CuI(CNXyl)3] (1) with I2 (exhibiting strong halogen bond donor properties), at different molar ratios between the reactants, resulted in a series of (XylNC)CuI crystal polyiodides formed along with gradual accumulation of iodine, namely [Cu(I3)(CNXyl)3] (two crystalline polymorphs 2I and 2II), [Cu(I3)(CNXyl)3]·½I2 (2·½I2) and [Cu(CNXyl)3](I5) (3); all these compounds were studied by X-ray diffractometry. Molecular electrostatic potential (MEP) surface plots were also calculated using density functional theory (DFT) for isolated molecules of 2 and I2, showing electrophilic and nucleophilic sites. Halogen bonding in 2·½I2 was additionally elucidated for both crystal and cluster models, including combined quantum theory of atoms-in-molecules (QTAIM) and one-electron potential (OEP) projections. For model clusters, DFT energetic analysis, quantum theory of atoms-in-molecules, combined with the noncovalent interaction index plot (QTAIM/NCIplot), natural bond orbital (NBO) donor–acceptor charge transfer analysis, and Wiberg bond index (WBI) analysis were used. In the structure of 2·½I2, the presence of an I2⋯I3− halogen bonded linkage gives a key toward the understanding of the precise mechanism for the generation of I5− (and then I82−) ligands from I2 and metal-coordinated I3−.
1. Introduction
Polyhalides are a subject of intensive studies,1–3 in view of their broad application as, for instance, electrolytes for batteries and dye sensitized solar cells,1,2 mildly selective oxidants for organic synthesis,2 and synthons for the construction of metal–organic frameworks.4 In particular, polyhalides (especially polyiodides) of various transition metals are utilized for the design of coordination networks4 and fabrication of semiconductive materials;5 halogen–halogen closed-shell bonding interactions have been widely studied theoretically.6–12The ability to generate polyatomic anions, namely polyiodide anions, is a characteristic feature of iodine as an element.1,3,13,14 In the formulation of polyiodides Imn−, there is always a problem whether Imn− can be considered as a single entity or as a composite of the building blocks I2, I−, and I3−, linked by noncovalent interaction(s), including halogen bonding (abbreviated as HaB).
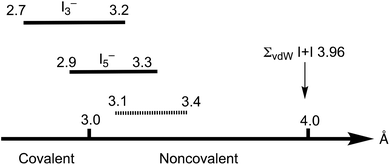
The Cambridge Structural Database (CSD) analysis of the I–I distances in such systems3 revealed a continuum in the distribution of iodine–iodine separations, spanning from approx. 2.7 Å (the distances that are typical of the I2 molecule) to those larger than 4 Å (Bondi van der Waals radii15 sum ∑(I + I) 3.96 Å; Rowland van der Waals radii16,17 sum ∑(I + I) 4.06 Å); values larger than 4 Å exceed the optimistic expectations for noncovalent interactions (Fig. 1). As follows from the recent CSD analysis,13 the iodine–iodine covalent bond for the most widespread and studied polyiodide, I3−, is in the range of 2.7–3.2 Å, while it is 2.9–3.3 Å for the less common I5−.
Starting from approximately 3.2 Å and further, up to ca. 4 Å, lies the region of various noncovalent interactions. Although the interval 3.2–4.0 Å is specific for I⋯I intermolecular bonds, the accurate assignment of contacts in the 3.0–3.6 Å range is often rather ambiguous,3 and the area 3.1–3.4 Å is the so-called “no man's land” with an overlap of covalent and noncovalent contacts.13 This large variability of iodine–iodine interactions hampers a clear assignment of I–I contacts to primary or secondary bonding (in other words HaB) thus blurring, in turn, the accurate difference between covalent and noncovalent contacts.
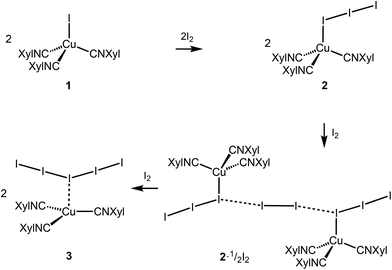
In the framework of our ongoing project focused on noncovalent interactions in organometallics, in particular HaB including iodine and polyiodides,18,19 we studied the [CuI(CNXyl)3] cocrystals with such a strong iodine-based HaB donor (exhibiting two 180°-directing σ-hole donor sites) as I2.20 We obtained a series of (XylNC)CuI polyiodides, whose structural features are outlined in section 2.2. In this series, the change in the composition of the product occurs in accordance with the change in the ratio of the reagents. A transition from a coordinated triiodide to a semicoordinated pentaiodide via an intermediate I82− was observed and studied in detail. In one of these structures (section 2.2.2), we identified a I2⋯I3− entity present between metal-bound I3− and unbound I2. Despite all difficulties in the identification of noncovalent bonding in I2⋯I3− outlined above, our experimental and appropriate theoretical data explicitly confirmed the existence of HaB in the I2⋯I3− linkage and, thus, our results indicate that we trapped the hitherto unreported I2⋯I3− intermediate in the generation of pentaiodide. All our findings are consequently detailed in the sections that follow.
2. Results and discussion
2.1. Cocrystal growth
Copper complexes (first of all, CuII species) demonstrate very rich and versatile polyiodide chemistry, reviewed in ref. 4, while copper(I) polyiodides are far less studied and all these reports are briefly surveyed in the ESI (section S2.1†).The copper(I) iodide complexes [CuI(CNXyl)3] (1) and [Cu(I)3(CNXyl)3] (2) chosen for this study were prepared by known procedures.21 The solvent-dependent crystallization of 2 yielded 2I (from CH2Cl2) and 2II (from CH2Cl2/MeNO2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) polymorphic forms (Scheme 1); the structure of 2II is identical to that obtained previously.21 Crystallization of 2I with I2 (2
1 v/v) polymorphic forms (Scheme 1); the structure of 2II is identical to that obtained previously.21 Crystallization of 2I with I2 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) in CH2Cl2 afforded crystals of the adduct [Cu(I3)(CNXyl)3]·½I2 (2·½I2). The latter was also obtained when 1 was crystallized with a 1.5-fold excess of I2 in CH2Cl2. Crystallization of 1 with a 3-fold excess of I2 from CH2Cl2 furnished [Cu(CNXyl)3](I)5 (3); these crystals were also obtained when 2 was crystallized with I2 (1
1 molar ratio) in CH2Cl2 afforded crystals of the adduct [Cu(I3)(CNXyl)3]·½I2 (2·½I2). The latter was also obtained when 1 was crystallized with a 1.5-fold excess of I2 in CH2Cl2. Crystallization of 1 with a 3-fold excess of I2 from CH2Cl2 furnished [Cu(CNXyl)3](I)5 (3); these crystals were also obtained when 2 was crystallized with I2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio) in CH2Cl2. The indicated crystallizations gave crystals suitable for XRD studies, which were performed for all these species.
2 molar ratio) in CH2Cl2. The indicated crystallizations gave crystals suitable for XRD studies, which were performed for all these species.
2.2. X-ray diffraction studies
The structural parameters of complex 2 in 2·½I2 (τ4 = 0.85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22) are close to those in 2II: ∠(Cu1–I1–I2) 94.399(15)° and ∠(I1–I2–I3) 178.502(17)°. The bond distances within the I3− ligand (I1–I2 2.8204(4), I2–I3 3.0520(5) Å) are normal and agree well with those in the previously reported structures of 2II and 2·CHI3.21 The Cu1–I1 bond length is 2.9015(7) Å, what is somehow longer than those in other structures apparently because of the effect of HaB, which is discussed later.
22) are close to those in 2II: ∠(Cu1–I1–I2) 94.399(15)° and ∠(I1–I2–I3) 178.502(17)°. The bond distances within the I3− ligand (I1–I2 2.8204(4), I2–I3 3.0520(5) Å) are normal and agree well with those in the previously reported structures of 2II and 2·CHI3.21 The Cu1–I1 bond length is 2.9015(7) Å, what is somehow longer than those in other structures apparently because of the effect of HaB, which is discussed later.
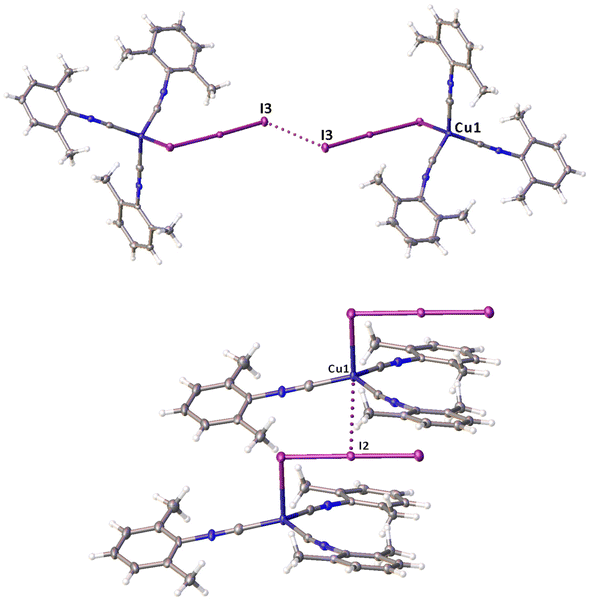
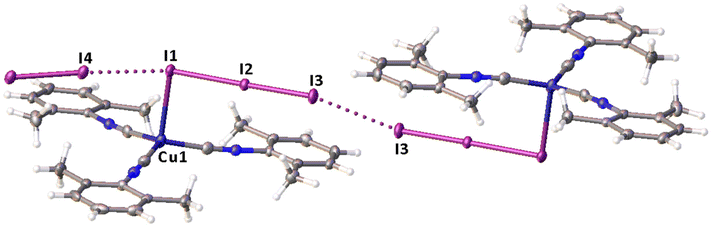
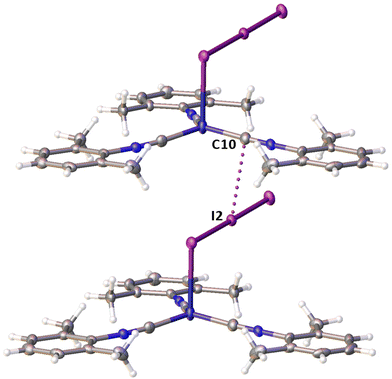
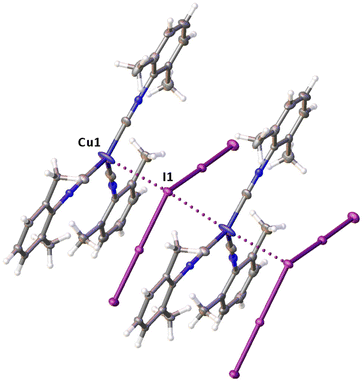
Noncovalent contacts (Table S3†) include Type-I halogen–halogen23 interactions (induced by packing effects) between the I3 atoms from different molecules (Fig. 3), and the lone pair–π-hole interaction between the I2 atom and the π-system (C10) of the isocyano groups (Fig. 4). Intermolecular contact I4⋯I1 between I2 and I3− moieties fulfill the IUPAC criteria for the identification of Type-II halogen–halogen23 interactions (or, in other words, the true HaB) (d(I1–I4) = 3.3658(6) Å vs. Bondi ∑(I + I) = 3.96 Å, ∠(I4–I4–I1) = 174.23(2)°).23 This is the shortest contact between iodine atoms in the structure of 2·½I2. This interatomic separation (3.3658(6) Å) lies on the borderline between the values typical for I5− (2.9–3.3 Å)13 and the area of the “no man's land” range (3.1–3.4 Å;13Fig. 1) with an overlap of covalent and noncovalent contacts.
If we consider only covalent and Type-II noncovalent interactions and put aside packing-driven Type-I contacts, the observed HaB-based adduct I3−⋯I2⋯I3− is relevant to the metal-bound dianion I82−. The Type-I contact I3⋯I3 is longer than the true I1⋯I4 HaB and it is certainly weaker than the HaB; this conclusion was confirmed by the analysis of the computation results (section 2.4). Considering all these, one can formulate the supramolecular organization of 2·½I2 as the 1D-chain built by the copper(I)-ligated I82−; a similar outstretched Z-shaped polyiodide geometry has been previously reported.24
On moving from the structures of 2I–II to that of 2·½I2, the Cu–I bond is further lengthened (by approx. 0.18 and 0.06 Å, correspondingly, for two polymorphs) and the coordination polyhedron is more deviated from the tetrahedral geometry (the Δ∑(∠C–Cu–C) was increased by 13–17 and 1°, respectively). The weak contact Cu⋯I in 2·½I2, as compared to that in 2II, became shorter (by 0.06 Å). As compared to 2I–II, in 2·½I2, an additional I2 molecule appeared and a new HaB contact I4⋯I1 between the I2 and I3− ligand was identified (3.3658(6) Å).
Remarkably, although many examples of different polyiodide sequences, including the I82− moiety, are known, predominantly they belong to the category of metal-free polyiodides. To prove the novelty of our findings, namely the noncovalent nature of the I2⋯I3− linkage, we performed the CSD search of metal-bound polyiodides exhibiting structures similar to 2·½I2, namely those built by I2 and coordinated I3−via relatively short (3.1–3.4 Å) I2⋯I3− contacts. In the nickel(II) triiodide complex (KUGBAS,19Rw 2.20%) the ligated I3− forms a relatively short I⋯I (3.3503(6) Å; Nc = d/(∑vdW Bondi) = 0.85) contact with I2. The other iodine center of I2 forms a slightly longer contact (3.4547(8) Å; Nc 0.87) with another complex via the terminal uncomplexed iodine of the I3− ligand (Fig. 5) and, hence, the supramolecular organization of KUGBAS includes the extended chains {(μ-I1,I3-I3−)·(μ-I1,I2-I2)}n. Notably, the I2 molecule behaves as a bifunctional HaB donor toward two accepting I3− moieties. No detailed discussion of the supramolecular organization of the structure was provided in the corresponding article.19
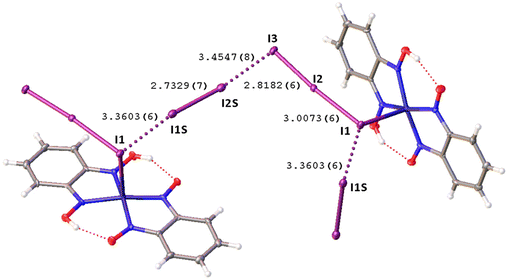 | ||
| Fig. 5 View of the supramolecular organization of KUGBAS bearing coordinated I3−; HaBs are given by dotted lines, interatomic distances (Å) are given for selected iodine–iodine bonds and contacts. | ||
Another structure, [Ru(I3)(ClI2)(CNBu-t)4]·I2 (ZAGTEJ),25 contains both I3− and ClI2− ligands and it includes the {I3−·I2·ClI2−} moieties featuring rather strong I⋯Cl (3.056(9) Å) and I⋯I (3.309(5) Å) noncovalent interactions (Fig. S5†). However, the Rw (13%) value is too high and this prevents an accurate examination of its geometric characteristics and complicates appropriate computational works. The same group studied the structures of cocrystals of RuII–halide species with molecular halogens and identified the polyhalide (X⋯X′2)n and the oligomeric X⋯X′2⋯X linkages involving the halide X ligands.26
We also performed CSD search for the known uncoordinated I5− and I8− systems, although these systems were only relevant but not strictly related to our observations (see the ESI, section S1†). In summary, the analysis of structural parameters of I5− from CSD indicates that I5− demonstrates a noticeable difference in the covalent distances for the terminal (2.7–3.0 Å) and internal (3.0–3.4 Å) I–I bonds. At the same time, the extreme cases of unsymmetric L-shaped I5− can be considered as the supramolecular adducts {I3−·I2}.
The bond length analysis for the I82− CSD structures allowed the formulation of these structures as the associates {I3−⋯I2⋯I3−}, where interatomic distances within the structural units (namely, I2 and I3−) are attributed to covalent bonding (2.74–3.12 Å) and the shortest separations between these units are in the 3.27–3.44 Å range, i.e. lie in the “no man's land” region (3.1–3.4 Å) (see the Introduction section).
A very similar bond length distribution was observed for the fragment {I3−⋯I2⋯I3−} in 2·½I2 (see above), therefore coordinated {I3−·I2·I3−} and uncomplexed (for details of the latter see the ESI†) moieties demonstrate certain structural similarities. However, this work is the first where coordinated polyiodides {I3−⋯I2⋯I3−} were detected in the solid state and structurally characterized.
2.3 Theoretical DFT study of halogen bonding in the structure of 2·½I2
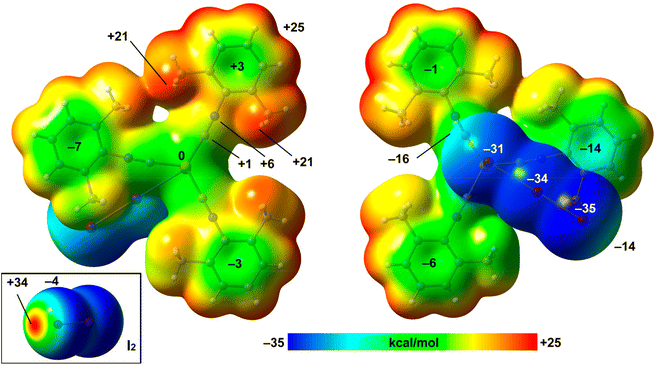
The structure of the 2·½I2 adduct was studied in detail with a particular focus on the HaB.The MEP values over the aromatic rings are in general modest, ranging from slightly positive (+3 kcal mol−1) to slightly negative (−7 kcal mol−1). The MEP value at the Cu-atom is zero and over the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds is slightly positive, thus disclosing that the I⋯C interaction is favored electrostatically. The MEP surface of I2 is also included in Fig. 7 (bottom-left), evidencing a deep σ-hole (+34 kcal mol−1) and a very modest negative belt (−4 kcal mol−1).
N bonds is slightly positive, thus disclosing that the I⋯C interaction is favored electrostatically. The MEP surface of I2 is also included in Fig. 7 (bottom-left), evidencing a deep σ-hole (+34 kcal mol−1) and a very modest negative belt (−4 kcal mol−1).
Thus, to closely interrogate the systems and to verify the nature of the I⋯I interactions, we performed DFT calculations under periodic boundary conditions (the crystal model, PBE30-D331,32 level of theory and DZVP-MOLOPT-SR-GTH33 bases within the Gaussian/plane wave (GPW)34 methodology in CP2K) for the 2·½I2 crystal. In addition, we also performed calculations for the isolated heterotrimeric (2)2·(I2) cluster exhibiting the I⋯I interactions, namely gas-phase DFT calculations (the cluster model, PBE30-D331 level of theory and def2-TZVP35,36 basis) in Gaussian 09, both approaches are based on the experimentally determined coordinates.
The QTAIM analysis for the crystal and cluster models demonstrated the presence of bond critical points (3, −1) (BCP) between the iodine centers of I2 and the iodine atoms of the I3 group (Table 1). Consideration of the negative values of the BCP sign(λ2)ρ(r) values indicates the attractive nature of the I⋯I interaction,37 although with some covalence contribution in view of the negative energy density and the balance of the Lagrangian kinetic energy G(r) and the potential energy density V(r) (−G(r)/V(r) < 1) on the corresponding critical points.38 Remarkably, the sign(λ2)ρ(r), ∇2ρ(r), G(r), and V(r) values are almost the same for the crystal and cluster models.
| Model | sign(λ2)ρ(r) | ∇2ρ(r) | V(r) | G(r) | H b |
|---|---|---|---|---|---|
| Cluster | −0.0216 | 0.0373 | −0.0101 | 0.0097 | −0.0004 |
| Crystal | −0.0205 | 0.0371 | −0.0093 | 0.0091 | −0.0002 |
One-electron potential analysis. Laplacian of electron density ∇2ρ(r),39 and electron localization function (ELF)40 are widely used to locate the electron concentration regions such as, for instance, electron pairs. A quantity, closely related to the Laplacian of the electron density, is the one-electron potential (OEP),41,42 which accurately represents the potential governing the motion of a single electron in an electron system43 and, therefore, OEP serves as a useful tool for the localization of electron pairs. Hamilton44 (for relevant recent work see ref. 45) has revealed topological similarities between ∇2ρ(r) and OEP, as reflected in the valence shell structures of light atoms. Differences arise in heavy atoms (elements beyond the third row) for which the valence shells are generally missing in ∇2ρ(r), but are present in OEP. Notably, the OEP approach is better than the ELF method since the former does not directly depend on wavefunction, and its results can be compared for calculations with and without pseudopotentials using electron density function (EDF) for core electrons.46
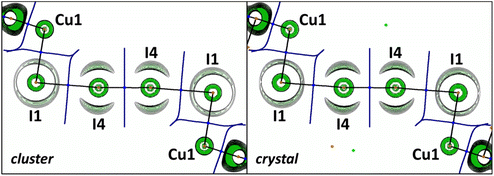
The OEP value can be used, instead of the Laplacian distribution, to reveal noncovalent features of polyiodide chains in the studied crystal. Similar to the previous reports,20,47 we observed a toroidal shape of the OEP around the I4 atom covalently bound to the neighboring (also I4) atoms (Fig. 8). This shape is specific for an anisotropic electron density distribution around the nucleus: the nucleophilic region of the valence shell is localized at the equator, while the electrophilic region is located at the continuation of the covalent σ-bond. For the I1⋯I4 halogen bond the nucleophilic and electrophilic regions of the iodine atoms in the crystal agree well with those obtained in the gas-phase cluster model.
The electrostatic potential features of the observed interactions. Interatomic surfaces in gradient fields of electron density (ρ) and electrostatic potential (φ) allow the identification of the atomic ρ- and φ-basins, respectively. The former defines chemically bonded atoms, while the latter determines electrically neutral atomic fragments within a common electron–nuclear system. The analysis of the superposition of these gradient fields provides useful information about the electrostatic potential features of atomic interactions along the bond paths.
Fig. 9 shows that the ρ- and φ-basin boundaries of atoms coincided completely within the bonds in I2 and I3−. In the case of I1⋯I4 noncovalent interactions, the boundary of the φ-basin of I4 spreads through the region of the ρ-basin of I1. This suggests that some fraction of the electrons belonging to I1 in the triiodide anion is attracted to the I4 nucleus in the I2 molecule. According to ref. 23, this is a conventional case for Type-II HaB. Thus, consideration of mutual arrangement of the zero-flux boundaries of ρ- and φ-basins provides the specific information about the kind of I⋯I interactions in the polyiodide chain in the studied crystal.
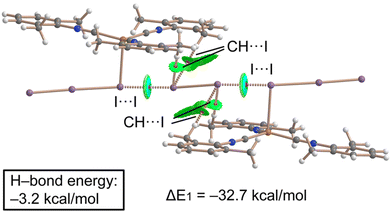
Combined QTAIM/NCIPlot analysis and dimerization energy. In (2)2·(I2), each contact is characterized by a CP bond (red sphere) and bond path (dashed bond) interconnecting both I-atoms (Fig. 10), according to the combined QTAIM and NCIplot analyses. The QTAIM values at the bond CP, as discussed earlier in this section, are typical of a noncovalent interaction. The QTAIM/NCIPlot analysis of the HaB heterotrimer also evidences the formation of secondary CH⋯I interactions involving the methyl groups of the XylNC ligands and the negative belts of the I2 molecule. The dimerization energy is large (ΔE1 = −32.7 kcal mol−1) in line with the strong electrophilicity of the I2 molecule and strong nucleophilicity of the I3− ligand, as demonstrated by the MEP surface analysis. We also estimated the strength of the CH⋯I H-bonds using the Vr predictor,48 which is −3.2 kcal mol−1 for the four contacts altogether, thus confirming the dominant role of the HaB, in line with the blue color of the HaB RDG isosurface compared to the green color of the HBs.
The same calculations were performed for the (2)2 dimers with other interactions extracted from the 2·½I2 adduct, for details see the ESI.†
NBO and WBI analyses in a natural atomic partitioning scheme. To further study the σ-hole nature of the HaB in (2)2·(I2), we performed the natural bond orbital (NBO) analysis in the natural atomic partitioning scheme focusing on the second order perturbation analysis.49 This computational tool is very convenient to study donor–acceptor interactions from an orbital viewpoint.50 Interestingly, we have found two symmetrically equivalent electron transfer from lone pair (LP) orbitals located at the coordinated iodine atoms and to the σ antibonding orbital of the I2 molecule (σ*) with a concomitant stabilization energy of E(2) = 9.04 kcal mol−1 (Fig. 11) for each LP(I) → σ*(I–I) interaction, thus confirming the σ-hole HaB nature of the I3−⋯I2⋯I3− contacts.
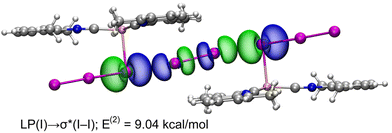 | ||
| Fig. 11 Representation of the NBOs corresponding to the LP → σ* donor–acceptor interactions in (2)2·(I2). The isosurface used for the MOs is 0.006 a.u. | ||
The Wiberg bond index (WBIs)51–53 was also calculated using the natural atomic partitioning scheme for the I⋯I interaction in the cluster model. The WBI is 0.16 and therefore the interaction can be considered as noncovalent but with some covalence.
Therefore, different approaches—QTAIM and OEP analyses in both crystal and cluster modes, combining QTAIM/NCIplot analysis, dimerization energies, NBO charge transfer and Wiberg indexes—clearly demonstrate the noncovalent nature of the I1⋯I4 contact, although with some covalence contribution. The analysis of electrostatic potential features of this contact allowed this attribution to Type-II23 HaB. The I82− units in the structure of 2·½I2 can be interpreted as the associates {I3−·I2·I3−}, where one uncomplexed I2 and two I3− ligands are linked by relatively strong HaBs.
3. Conclusions
The addition of various amounts of molecular iodine to the copper(I) isocyanide complex [CuI(CNXyl)3] provided a series of copper polyiodide complexes and their adducts, namely [Cu(I3)(CNXyl)3], [Cu(I3)(CNXyl)3]·½I2, and [Cu(CNXyl)3](I5) (Scheme 1). In this series, we observed a change in the ligation of (poly)iodide anions to the metal site—a gradual transition from the coordinated iodide, to triiodide, followed by the generation and stabilization of the semicoordinated pentaiodide. In a more general sense, we performed the systematic and controllable creation of metal complexes exhibiting increasing polyiodide content. Polyiodide containing products, like our systems, are often encountered unexpectedly or unreliably and often relegated to the ESI† of other publications. This work, in contrast, demonstrates the controllable design of metal complexes with increasing polyiodide content based on the molar ratio of iodine added during the synthesis. This stepwise addition of iodine to give polyiodides allows the systematic assembly of a HaB network centered on CuI-bound I3−. We consider this as an advancement in the supramolecular assembly of coordination complexes in pursuit of other (e.g., analyzed in recent reviews54,55) higher dimensional networks utilizing HaB. Considering that polyiodide-based materials have been utilized in e.g. photovoltaics,56 the result of this work may be useful for controllable assembly of appropriate polyiodides.In the [Cu(I3)(CNXyl)3]·½I2 cocrystals, we identified the unit I82−, which is built by two coordinated triiodides connected by a bridge of molecular iodine via relatively strong HaBs. The geometric parameters of the HaB indicate its intermediate position between covalent bonds and noncovalent interactions. Theoretical methods within different approaches—QTAIM analysis in both crystal and cluster modes and OEP analysis along with the analysis of Wiberg indexes—allowed the conclusion on the predominantly noncovalent character of HaB, although with small contribution of the covalence. Therefore, the I82− units in the structure of [Cu(I3)(CNXyl)3]·½I2 can be treated as the associates {I3−·I2·I3−}, where I2 molecules and I3− ligands are linked by relatively strong HaBs.
The most significant findings of this study include the trapping of the halogen-bonded compound [Cu(I3)(CNXyl)3]·½I2, and a theoretical confirmation of the noncovalent nature of the I2⋯I3− linkage (as an intermediate between the I3− ligand to I5− or I82− ligands) in this structure. This entity includes Type-II halogen–halogen interactions or, in other words, the true HaB, and it represents a previously unreported intermediate in the generation of metal-bound pentaiodides. In the context of this study, it is noteworthy that although the studies focused on the bonding situation in polyiodides are known,1–3,6–12 no single work is devoted to metal-involving transformation of I82− to I5−. We believe that the identification of HaB in the structure of [Cu(I3)(CNXyl)3]·½I2 is key to understanding the precise mechanism of the generation of I5− (and then I82−) ligands from I2 and metal-coordinated I3−. The HaB-involving mechanism is predictable but has not yet received experimental support; our finding provides the means for its confirmation.
4. Experimental section
4.1. Reagents, instrumentation, and methods
Solvents, CuI, xylylisocyanide, and I2 were obtained from commercial sources and used as received, apart from CH2Cl2, which was purified by the conventional distillation over CaCl2. The complexes [CuI(CNXyl)3] (1) and [Cu(I)3(CNXyl)3] (2) were prepared by the known procedures,21 while the synthesis of 3 is given below in this section.The high-resolution mass spectra were obtained on a Bruker micrOTOF spectrometer equipped with an electrospray ionization (ESI) source and MeOH was used as the solvent. The instrument was operated in the positive ion mode using an m/z range of 50–3000. The most intensive peak in the isotopic pattern is reported. Infrared spectra (4000–400 cm−1) were recorded on a Shimadzu IRAffinity-1 FTIR spectrophotometer in KBr pellets. NMR spectra were recorded on Bruker AVANCE III 400 spectrometers in CDCl3 at ambient temperature (at 400 and 100 MHz for 1H and 13C NMR, respectively). Chemical shifts are given in δ-values [ppm] referenced to the residual signals of the undeuterated solvent (CHCl3): δ 7.27 (1H) and 77.0 (13C).
Method B. A solution of [CuI(CNXyl)3] (190 mg, 0.3 mmol) was mixed with a saturated solution of I2 in CH2Cl2 (2 mL) and the resulting solution was left for slow evaporation at room temperature to 0.5 mL. The formed brown crystals were separated by decantation and dried in air at room temperature. The yield of 3 is 236 mg, 72%.
The obtained compound is rather unstable and it releases molecular iodine on keeping the sample at room temperature. HRESI+, m/z: 325.0774 ([M − I5 − CNXyl]+, calcd 325.0761). FTIR, νmax (KBr)/cm−1: 2162 s ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N). 1H NMR (CDCl3, δ): 2.53 (s, 6H, CH3), 7.17 (d, 3JH,H = 7.5 Hz, 2H, m-H from xylyl), 7.29 (t, 3JH,H = 7.5 Hz, 1H, p-H from xylyl). 13C{1H} NMR (CDCl3, δ): 19.12 (CH3), 125.65 (t, 1JC,N = 10.0 Hz, ipso-C from xylyl), 128.14 (m-C from xylyl), 129.92 (o-C from xylyl), 135.69 (p-C from xylyl), 150.99 (broad, Cisocyanide).
N). 1H NMR (CDCl3, δ): 2.53 (s, 6H, CH3), 7.17 (d, 3JH,H = 7.5 Hz, 2H, m-H from xylyl), 7.29 (t, 3JH,H = 7.5 Hz, 1H, p-H from xylyl). 13C{1H} NMR (CDCl3, δ): 19.12 (CH3), 125.65 (t, 1JC,N = 10.0 Hz, ipso-C from xylyl), 128.14 (m-C from xylyl), 129.92 (o-C from xylyl), 135.69 (p-C from xylyl), 150.99 (broad, Cisocyanide).
4.2. Crystal growth
Crystals of 1 were obtained by slow evaporation of its CH2Cl2 solution at RT. Crystals of 2I were obtained by slow evaporation of a solution of 2 in CH2Cl2 at RT. Crystals of 2·½I2 were grown by the dissolution of a mixture of 2I and I2 (molar ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in CH2Cl2 at RT followed by the slow evaporation of this solution at RT. Crystals of 3 were grown by the dissolution of a mixture of 1 and I2 (1
1) in CH2Cl2 at RT followed by the slow evaporation of this solution at RT. Crystals of 3 were grown by the dissolution of a mixture of 1 and I2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 molar ratio) in CH2Cl2 at RT followed by slow evaporation of this solution at RT. The crystallization of 1 gives colorless crystals, while 2I, 2·½I2, and 3 are brown.
3 molar ratio) in CH2Cl2 at RT followed by slow evaporation of this solution at RT. The crystallization of 1 gives colorless crystals, while 2I, 2·½I2, and 3 are brown.
4.3. X-ray diffraction studies
Single-crystal X-ray diffraction experiments were carried out on “Xcalibur”, Eos (1, 2I, and 3) and “SuperNova” (2·½I2) diffractometers with monochromated MoKα radiation. Crystals were kept at 100(2) K during data collection. Structures have been solved using ShelXT57 (structure solution program using Intrinsic Phasing) and refined by means of the ShelXL58 program incorporated into the OLEX2 program package.59 Crystallographic details are summarized in Table S1.† CCDC numbers 2211053–2211056 contain the supplementary crystallographic data for this paper.†4.4. Computational details
Single-point DFT calculations were performed under periodic boundary conditions using the mixed Gaussian/plane-wave (GPW)34 basis set with a 350 Ry and a 50 Ry relative plane-wave cut-offs for the auxiliary grid and the PBE30-D331,32 functional and the DZVP-MOLOPT-SR-GTH basis for the crystal (1 × 1 × 1 cell) model [Cu(I3)(CNXyl)3]·½I2 was performed using the CP2K-8.1 program.33,60–65 The 1.0 × 10−6 Hartree convergence was achieved for the self-consistent field cycle in the Γ-point approximation. This methodology has been previously used for the study of the related halogen-bonded systems.21 The gas-phase study for the heterotrimeric cluster ([Cu(I3)(CNXyl)3])2·(I2) was performed at the same PBE-D3 level of theory in Gaussian-0966 with the def2-TZVP35,36 basis set. One-electron potential (OEP)67–69 analysis and the quantum theory of atoms in molecules (QTAIM) analysis38,70,71 of the electron density as well as analysis of the electrostatic potential and electron density gradient fields72 were performed and visualized using Multiwfn 3.8.73 The pseudopotential core areas were modelled using the inner code of Multiwfn 3.8 using electron density function (EDF)46 for both OEP and QTAIM analyses. Wiberg bond indexes in the natural atomic partitioning scheme were calculated for cluster models using the GENNBO utility in NBO 7.074 based on 0.47 files generated in Multiwfn 3.8. Other cluster calculations were performed at the PBE36-D337,38/def2-TZVP41,42 level of theory using the Gaussian-16 program75 and the X-ray coordinates. The QTAIM/NCIPlot analysis was performed using the AIMAll program.76 The MEP calculations were performed at the same level of theory and plotted using the 0.001 a.u. isosurface.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Russian Science Foundation projects 22-13-00078 (experimental part and XRD analysis) and 22-73-00021 (theoretical calculations under periodic conditions and for cluster mode). The QTAIM/NCIPlot calculations were funded by the MICIU/AEI of Spain (project PID2020-115637GB-I00 FEDER funds). Measurements were performed at the Center for Magnetic Resonance, the Center for X-ray Diffraction Studies, the Center for Chemical Analysis and Materials Research, and the Computing Center (all belonging to Saint Petersburg State University). This article is in commemoration of the 300th anniversary of St Petersburg State University's founding.References
- P. H. Svensson and L. Kloo, Synthesis, Structure, and Bonding in Polyiodide and Metal Iodide−Iodine Systems, Chem. Rev., 2003, 103, 1649–1684 CrossRef CAS PubMed.
- H. Haller and S. Riedel, Recent Discoveries of Polyhalogen Anions – from Bromine to Fluorine, Z. Anorg. Allg. Chem., 2014, 640, 1281–1291 CrossRef CAS.
- L. Kloo, in Comprehensive Inorganic Chemistry II, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, pp. 233–249. DOI:10.1016/B978-0-08-097774-4.00109-1.
- S. A. Adonin, M. N. Sokolov and V. P. Fedin, Polyhalide-bonded metal complexes: Structural diversity in an eclectic class of compounds, Coord. Chem. Rev., 2018, 367, 1–17 CrossRef CAS.
- J. He, P. Cao, C. Wu, J. Huang, J. Huang, Y. He, L. Yu, M. Zeller, A. D. Hunter and Z. Xu, Highly Polarizable Triiodide Anions (I3−) as Cross-Linkers for Coordination Polymers: Closing the Semiconductive Band Gap, Inorg. Chem., 2015, 54, 6087–6089 CrossRef CAS PubMed.
- G. R. Desiraju and R. Parthasarathy, The nature of halogen.cntdot..cntdot..cntdot.halogen interactions: are short halogen contacts due to specific attractive forces or due to close packing of nonspherical atoms?, J. Am. Chem. Soc., 1989, 111, 8725–8726 CrossRef CAS.
- V. G. Tsirelson, P. F. Zhou, T.-H. Tang and R. F. W. Bader, Topological definition of crystal structure: determination of the bonded interactions in solid molecular chlorine, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 143–153 CrossRef.
- C. F. Matta, N. Castillo and R. J. Boyd, Characterization of a Closed-Shell Fluorine−Fluorine Bonding Interaction in Aromatic Compounds on the Basis of the Electron Density, J. Phys. Chem. A, 2005, 109, 3669–3681 CrossRef CAS PubMed.
- N. Castillo, C. F. Matta and R. J. Boyd, Fluorine−Fluorine Spin−Spin Coupling Constants in Aromatic Compounds: Correlations with the Delocalization Index and with the Internuclear Separation, J. Chem. Inf. Model., 2005, 45, 354–359 CrossRef CAS PubMed.
- T. T. T. Bui, S. Dahaoui, C. Lecomte, G. R. Desiraju and E. Espinosa, The Nature of Halogen⋯Halogen Interactions: A Model Derived from Experimental Charge-Density Analysis, Angew. Chem., Int. Ed., 2009, 48, 3838–3841 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, Halogen bonding and other σ-hole interactions: a perspective, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- E. Aubert, E. Espinosa, I. Nicolas, O. Jeannin and M. Fourmigué, Toward a reverse hierarchy of halogen bonding between bromine and iodine, Faraday Discuss., 2017, 203, 389–406 RSC.
- M. Savastano, Words in supramolecular chemistry: the ineffable advances of polyiodide chemistry, Dalton Trans., 2021, 50, 1142–1165 RSC.
- A. J. Blake, W.-S. Li, V. Lippolis, M. Schröder, F. A. Devillanova, R. O. Gould, S. Parsons and C. Radek, Template self-assembly of polyiodide networks, Chem. Soc. Rev., 1998, 27, 195–206 RSC.
- A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- R. S. Rowland and R. Taylor, Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii, J. Phys. Chem., 1996, 100, 7384–7391 CrossRef CAS.
- S. S. Batsanov, van der Waals Radii of Elements, Inorg. Mater., 2001, 37, 871–885 CrossRef CAS.
- Z. M. Bikbaeva, D. M. Ivanov, A. S. Novikov, I. V. Ananyev, N. A. Bokach and V. Y. Kukushkin, Electrophilic-Nucleophilic Dualism of Nickel(II) toward Ni center dot center dot center dot l Noncovalent Interactions: Semicoordination of Iodine Centers via Electron Belt and Halogen Bonding via sigma-Hole, Inorg. Chem., 2017, 56, 13562–13578 CrossRef CAS PubMed.
- Z. M. Efimenko, A. S. Novikov, D. M. Ivanov, A. V. Piskunov, A. A. Vereshchagin, O. V. Levin, N. A. Bokach and V. Y. Kukushkin, The (Dioximate)NiII/I2 System: Ligand Oxidation and Binding Modes of Triiodide Species, Inorg. Chem., 2020, 59, 2316–2327 CrossRef CAS PubMed.
- F. Bertolotti, A. V. Shishkina, A. Forni, G. Gervasio, A. I. Stash and V. G. Tsirelson, Intermolecular Bonding Features in Solid Iodine, Cryst. Growth Des., 2014, 14, 3587–3595 CrossRef CAS.
- M. A. Kinzhalov, D. M. Ivanov, A. A. Melekhova, N. A. Bokach, R. M. Gomila, A. Frontera and V. Y. Kukushkin, Chameleonic Metal-bound Isocyanides: π-Donating CuI-center Imparts a Nucleophilicity to the Isocyanide Carbon toward Halogen Bonding, Inorg. Chem. Front., 2022, 9, 1655–1665 RSC.
- A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Coordination polymers and molecular structures among complexes of mercury(II) halides with selected 1-benzoylthioureas, Polyhedron, 2015, 90, 47–57 CrossRef CAS.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Definition of the halogen bond (IUPAC Recommendations 2013), Pure Appl. Chem., 2013, 85, 1711 CrossRef CAS.
- P. K. Hon, T. C. W. Mak and J. Trotter, Synthesis and structure of 1-methyl-1,3,5,7-tetraazaadamantan-1-ium octaiodide, [(CH2)6N4CH3]2I8. A new outstretched Z configuration for the polyiodide ion I82, Inorg. Chem., 1979, 18, 2916–2918 CrossRef CAS.
- M. E. G. Mosquera, P. Gomez-Sal, I. Diaz, L. M. Aguirre, A. Ienco, G. Manca and C. Mealli, Intriguing I2 Reduction in the Iodide for Chloride Ligand Substitution at a Ru(II) Complex: Role of Mixed Trihalides in the Redox Mechanism, Inorg. Chem., 2016, 55, 283–291 CrossRef CAS PubMed.
- M. E. G. Mosquera, I. Egido, C. Hortelano, M. López-López and P. Gómez-Sal, Comparison of halogen bonding networks with Ru(ii) complexes and analysis of the influence of the XB interactions on their reactivity, Faraday Discuss., 2017, 203, 257–283 RSC.
- J. Y. Lu and V. Schauss, A Novel Nanostructured Open-Channel Coordination Polymer with an Included Fused-Polyiodide Ring, Eur. J. Inorg. Chem., 2002, 2002, 1945–1947 CrossRef.
- M. C. Aragoni, M. Arca, F. Demartin, F. A. Devillanova, A. Garau, F. Isaia, V. Lippolis, S. Rizzato and G. Verani, [Ni(L)(MeCN)]2+ complex cation as a template for the assembly of extended I3−·I5− and I5−·I7− polyiodide networks {L = 2,5,8-trithia[9](2,9)-1,10-phenanthrolinophane}. Synthesis and structures of [Ni(L)(MeCN)]I8 and [Ni(L)(MeCN)]I12, Inorg. Chim. Acta, 2004, 357, 3803–3809 CrossRef CAS.
- C. A. L. Filgueiras, A. Horn Jr., J. M. S. Skakle and J. L. Wardell, Tetra-methyl-ammonium pentaiodide, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2001, 57, o338–o340 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- B. G. Lippert, J. Hunter and M. Parrinello, A hybrid Gaussian and plane wave density functional scheme, Mol. Phys., 1997, 92, 477–488 CrossRef.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, Properties of atoms in molecules: atomic volumes, J. Am. Chem. Soc., 1987, 109, 7968–7979 CrossRef CAS.
- V. Tsirelson and A. Stash, Determination of the electron localization function from electron density, Chem. Phys. Lett., 2002, 351, 142–148 CrossRef CAS.
- W.-T. Chan and I. P. Hamilton, Correspondence between the one-electron potential and the Laplacian of the electron density as indicators of proton affinity, Chem. Phys. Lett., 1999, 301, 53–58 CrossRef CAS.
- V. Tsirelson and A. Stash, On functions and quantities derived from the experimental electron density, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 418–426 CrossRef PubMed.
- G. Hunter, Conditional probability amplitudes in wave mechanics, Int. J. Quantum Chem., 1975, 9, 237–242 CrossRef CAS.
- I. P. Hamilton, Discussion. Comment on “Are the Bader laplacian and the Bohm quantum potential equivalent?”, Chem. Phys. Lett., 1998, 297, 261–262 CrossRef CAS.
- S. Sadjadi, C. F. Matta and I. P. Hamilton, Bonding and metastability for Group 12 dications, J. Comput. Chem., 2021, 42, 40–49 CrossRef CAS PubMed.
- W. Zou, Z. Cai, J. Wang and K. Xin, An open library of relativistic core electron density function for the QTAIM analysis with pseudopotentials, J. Comput. Chem., 2018, 39, 1697–1706 CrossRef CAS PubMed.
- E. V. Bartashevich, I. D. Yushina, A. I. Stash and V. G. Tsirelson, Halogen Bonding and Other Iodine Interactions in Crystals of Dihydrothiazolo(oxazino)quinolinium Oligoiodides from the Electron-Density Viewpoint, Cryst. Growth Des., 2014, 14, 5674–5684 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: New vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 CAS.
- K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- C. Trindle, Bond index description of delocalization, J. Am. Chem. Soc., 1969, 91, 219–220 CrossRef CAS.
- C. Trindle and O. Sinanoglu, Local orbital and bond index characterization of hybridization, J. Am. Chem. Soc., 1969, 91, 853–858 CrossRef CAS.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Halogen Bonding in Supramolecular Chemistry, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Halogen Bonding in Supramolecular Chemistry, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 CrossRef CAS PubMed.
- A. V. Novikov, A. N. Usoltsev, S. A. Adonin, A. A. Bardin, D. G. Samsonenko, G. V. Shilov, M. N. Sokolov, K. J. Stevenson, S. M. Aldoshin, V. P. Fedin and P. A. Troshin, Tellurium complex polyhalides: narrow bandgap photoactive materials for electronic applications, J. Mater. Chem. A, 2020, 8, 21988–21992 RSC.
- G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. Sheldrick, SADABS-2008/1-Bruker AXS area detector scaling and absorption correction, Bruker AXS, Madison, Wisconsin, USA, 2008 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- M. Frigo and S. G. Johnson, The Design and Implementation of FFTW3, Proc. IEEE, 2005, 93, 216–231 Search PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, cp2k: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- U. Borštnik, J. VandeVondele, V. Weber and J. Hutter, Sparse matrix multiplication: The distributed block-compressed sparse row library, Parallel Comput., 2014, 40, 47–58 CrossRef.
- O. Schütt, P. Messmer, J. Hutter and J. VandeVondele, in Electronic Structure Calculations on Graphics Processing Units, 2016, pp. 173–190. DOI:10.1002/9781118670712.ch8.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- T. D. Kühne, M. Iannuzzi, M. D. Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09W, 2009. https://www.gaussian.com/(accessed on 30 December 2013) Search PubMed.
- A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- B. Silvi and A. Savin, Classification of chemical bonds based on topological analysis of electron localization functions, Nature, 1994, 371, 683–686 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, ELF: The Electron Localization Function, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- R. F. W. Bader and T. T. Nguyen-Dang, in Adv. Quant. Chem, ed. P.-O. Löwdin, Academic Press, 1981, vol. 14, pp. 63–124 Search PubMed.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- I. Mata, E. Molins, I. Alkorta and E. Espinosa, Topological Properties of the Electrostatic Potential in Weak and Moderate N⋯H Hydrogen Bonds, J. Phys. Chem. A, 2007, 111, 6425–6433 CrossRef CAS PubMed.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, 2018 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019. ( https://aim.tkgristmill.com) Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2211053–2211056. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi02634a |
| This journal is © the Partner Organisations 2023 |