Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparison of biokinetic models for non-dissolvable engineered nanomaterials in freshwater aquatic organisms†
Yuanfang
Zheng
and
Bernd
Nowack
 *
*
Empa, Swiss Federal Laboratories for Materials Science and Technologies, Technology and Society Lab, Lerchenfeldstrasse 5, 9014 St. Gallen, Switzerland. E-mail: nowack@empa.ch
First published on 10th March 2023
Abstract
Understanding the uptake and elimination kinetics of engineered nanomaterials (ENMs) in aquatic organisms is essential for their environmental risk assessment. This study offers a comparative mathematical analysis of biokinetic models for non-dissolvable ENMs in freshwater organisms. Five models were applied to 34 datasets covering the following ENMs: titanium dioxide (TiO2), silica (SiO2), fullerene, graphene, gold (Au), carbon nanotubes (CNTs), and graphene oxide. Four of these models are the first-order one-compartment model and its variants considering the storage fraction and growth dilution. The fifth model is the Michaelis–Menten kinetics. The quality of models was evaluated regarding the adjusted R squared and the bias-corrected Akaike information criterion. The results suggest that no general model is able to predict all the experimental data properly. First-order one-compartment models with storage fraction seem to show more flexibility to describe various bioaccumulation patterns, especially when depuration is clearly incomplete. These models can make valid predictions for more than 85% of the experimental data. The uptake rate constants estimated for D. magna (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L kg−1 h−1) are significantly higher than the rate constants for zebrafish (7 L kg−1 h−1). A significant difference in the elimination rate constants between D. magna (0.5 1/h) and zebrafish (0.06 1/h) is only observed in the model with a storage fraction. To better understand the biokinetics of ENMs and reduce the uncertainty in modelling, we suggest to use an appropriate length for the exposure and elimination periods in future experimental designs. Additionally, more information related to particle characterization in the exposure medium should be reported.
000 L kg−1 h−1) are significantly higher than the rate constants for zebrafish (7 L kg−1 h−1). A significant difference in the elimination rate constants between D. magna (0.5 1/h) and zebrafish (0.06 1/h) is only observed in the model with a storage fraction. To better understand the biokinetics of ENMs and reduce the uncertainty in modelling, we suggest to use an appropriate length for the exposure and elimination periods in future experimental designs. Additionally, more information related to particle characterization in the exposure medium should be reported.
Environmental significanceUnderstanding the bioaccumulation and biokinetics of engineered nanomaterials (ENMs) is critical for their environmental risk assessment. To contribute to this subject, this paper investigates the biokinetics of non-dissolvable ENMs in freshwater aquatic biota. ENM uptake and elimination curves were compiled from the published data. A comparative mathematical analysis of biokinetic modeling approaches was performed. The material-specific and organism-specific kinetic parameters obtained from this meta-analysis help us to better predict the internal dose of ENMs in biota. This work also gives suggestions for the experimental design of future bioaccumulation studies and provides guidance on the selection of biokinetic models for curve fitting to different types of experimental data. |
1. Introduction
Due to the rapid development of nanotechnology and the wide application of engineered nanomaterials (ENMs), their ecotoxicity and the potential environmental risks have attracted great attention. After use, ENMs can end up in the aquatic environment through various routes.1 They accumulate in aquatic organisms through the food chain and can result in toxic effects on aquatic organisms. Many studies have reported bioaccumulation of several ENMs by aquatic organisms including algae, Daphnia, and fish.2–4Studies on bioaccumulation are crucial in regulatory decision-making about the potential environmental risks of ENMs.5 Unlike the relatively high concentrations of chemicals that are applied in toxicology studies causing acute toxic effects, bioaccumulation is used to describe the relationship between the environmentally-relevant chemical concentrations in the surrounding media and those in organisms. To account for the limited in situ measurement techniques, model-driven estimations are highly important to enhance experimental studies and deepen our fundamental knowledge of ENM exposure and risks in the environment.6
The bioaccumulation behavior of ENMs in aquatic organisms is different from that of conventional chemicals.7 The methods used to predict bioaccumulation of conventional chemicals may not be applicable to nanomaterials. For instance, the concept of fugacity has been applied to estimate the bioaccumulation of organic compounds.8,9 Fugacity is defined as the partitioning behavior of a chemical between different phases. However, this method is not feasible for ENMs as they are non-volatile. In addition, there have been concerns about the applicability of the bioaccumulation factor (BAF) to ENMs.10 For organic substances, the BAF is independent of the exposure concentration because the mechanism is driven by passive diffusion. However, the BAF of ENMs and their exposure concentrations have been found to be inversely related.11,12 Moreover, unlike dissolved metals, non-dissolvable ENMs ingested by organisms may not be able to cross the epithelial tissues easily.13,14 Making a distinction between ingested ENMs and those internalized after passing through an epithelial tissue is critical. In addition, it is important to note that the full body burden of ENMs in organisms at lower levels of the trophic chain can have ecological significance because it may be transferred to higher levels in the food chain.15,16
Biokinetic models have been applied to describe the relationship between the internal concentration in the aquatic organism and the external concentration in the medium.17 Standard biokinetic models include two phases: uptake and elimination. A number of publications are available about biokinetic modelling of ENMs in aquatic organisms. Garner et al. (2018) developed a model (nanoBio) to predict the long-term bioaccumulation of ENMs across four trophic levels in a freshwater system,18 using a basic first-order single-compartment model. van den Brink et al. (2019) comprehensively reviewed the applicability of several conventional modelling approaches to ENMs.7 The physiologically based pharmacokinetic (PBPK) models were shown to be successful in predicting ENM bioaccumulation. However, only different forms of nano-Ag accumulated in earthworms were investigated in the case study.
A confounding factor in many ENM biouptake studies is the use of ENM that are able to dissolve. Nanomaterials with different dissolution levels behave substantially differently in biokinetic studies. Ions released from nanoparticles can accumulate by a different mechanism than ENM, which is usually faster than particulate uptake and they can be eliminated more rapidly than particles.19–21 The higher uptake of dissolved ions may be explained by passive diffusion and cotransport mechanisms in D. magna. It has been suggested that ions could cross the branchial epithelium of D. magna via Na+ channels.22 The higher uptake rate of ions is caused by the high affinity of ions for membrane transporters. The uptake of non-dissolvable ENM particles needs to proceed through particle-specific uptake mechanisms, dominated by particle-size dependent endocytosis, including pinocytosis and phagocytosis.23 Contradictory findings have emerged from several studies regarding the relative rates of elimination of ionic forms and ENMs. For example, Khan et al. (2015) observed slower elimination of Ag ions (released from Ag NPs) than Ag nanoparticles in Peringia ulvae due to faster internalization of the ions.24 It is still challenging to monitor the conversion between ions and ENM in uptake experiments and distinguish the accumulation of ENM and ions inside organisms. In order to eliminate confounding factors of dissolution, we therefore only focused on studies using non-dissolvable ENM from the literature.
The aim of this study was to perform a comparative mathematical analysis of biokinetic models for non-dissolvable ENMs in freshwater organisms. First, we extracted empirical data from kinetic exposure experiments of non-dissolvable ENMs using freshwater biota. Second, we applied five kinetics models to each dataset to estimate the rate constants. Four of these models are the first-order one-compartment model and its variants considering a storage fraction and growth dilution. The fifth model is the Michaelis–Menten kinetics. Third, we provide an analysis of the observed range of material-specific kinetics parameters. Furthermore, we explored the factors affecting rate constants, including exposure concentration, types of ENMs and feeding scheme during depuration. Lastly, we provide guidance on model selection for curve fitting on different types of experimental data and make suggestions on future experimental design of bioaccumulation studies.
2. Materials and methods
We collected 34 datasets from 10 peer-reviewed articles describing the uptake and depuration process over-time of non-dissolvable ENMs in freshwater organisms. These articles were extracted from Zheng and Nowack (2022),25 where papers published from January 2000 to October 2021 in English were systematically reviewed according to Preferred Reporting Items for Systematic Reviews and Meta-analysis (PRISMA) guidelines.26 We digitized the time series of empirical biokinetics data by using WebPlotDigitizer Ver 4.6.27 Some data were shown as the mean value at each time point, others were in replicates. We only considered the biokinetics data containing both uptake and depuration phases for adult organisms. Due to inconsistencies in many of the reported body burdens and time units, it was necessary to convert the wet weight based body burden found in the literature to dry weight (dw) (mg kg−1 dw), and convert time from days to hours. It is recommended to base on dry mass to reduce the uncertainty arising from differences in water concentration in the organisms.28 The whole body wet-to-dry ratio was taken as 10 for algae,29 12.5 for Daphnia,30 and 5 for fish.312.1. Biokinetic modelling
The following five biokinetics models are commonly applied to estimate ENMs uptake and elimination kinetics parameters for organisms. Model 1 is the classic first-order, one-compartment model.32 The organism is considered as one singular compartment. The model contains two phases: uptake and elimination. During uptake, the organisms are exposed to ENMs via contaminated medium (water or food). During elimination, the organisms are transferred to clean medium or fed with clean food to depurate. Notably, elimination also takes place during the uptake phase. This modelling approach described is included in Organization for Economic Cooperation and Development (OECD) Test Guideline (TG) No. 305.17 The differential equation describing the rate of change in organism body burden is shown as follows: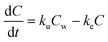 | (1) |
For the depuration phase, Cw (or Cf for dietary exposure) is assumed to be zero. The above equation then becomes:
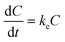 | (2) |
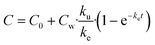 | (3) |
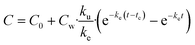 | (4) |
On the basis of model 1, model 2 added a storage fraction during depuration, but not during uptake. The particles enter storage fraction, from which they cannot be eliminated from the organism. This retained fraction inside organism doesn't mean that the particles are internalized. Studies have shown that ENMs are lodged between the gaps of microvilli in the bush boarder of midgut.33,34 This model has been applied to estimate the biokinetics of silver nanoparticles in terrestrial isopod Porcellionides pruinosus and freshwater zooplankton Daphnia magna.19,35 The calculation for the uptake rate is the same as eqn (3) in model 1. The following equation was used for depuration:
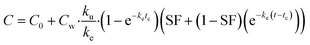 | (5) |
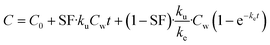 | (6) |
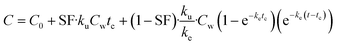 | (7) |
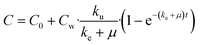 | (8) |
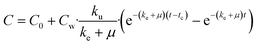 | (9) |
The Michaelis–Menten equation has been commonly used in enzyme kinetic studies.39 Some studies used the combination of the Michaelis–Menten kinetics during uptake and a first-order elimination to model bioaccumulation behavior.40,41 Equations for model 5 can be written as:
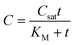 | (10) |
| C = Cd,0·e−ke(t−tc) | (11) |
We first performed the non-linear regression in Excel by using Solver add-in program to find a suitable initial value for the rate constant. By comparing the experimental data with the fitted curves in the graph, we could decide the quality of model's convergence. After that, we introduced the initial values in GraphPad Prism version 9.3.1 by performing the self-defined non-linear regression and constrained the rate constants larger than zero and the storage fraction in the range of zero to one.
2.2. Statistical analysis
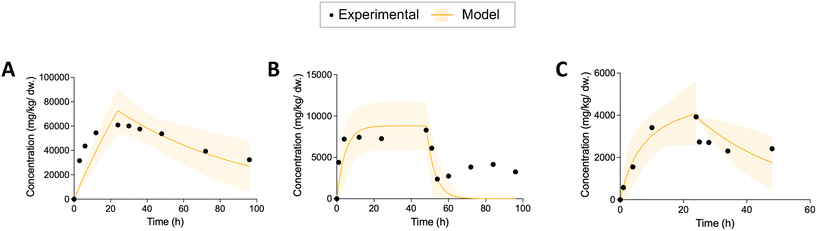
After obtaining the kinetic parameters, we used three statistical metrics to evaluate the prediction of nonlinear models: adjusted R squared (R2), 95% confidence bands and bias-corrected Akaike information criterion (AICc). For each regression, we calculated the adjusted R2 to examine the goodness-of-fit. The adjusted R2 can compensate possible bias resulting from different number of parameters.42 At the same time, we plotted the 95% confidence bands for each regression curve, which show the likely location of the true curve. We visually inspected whether the empirical data were covered by the 95% confidence bands. The regression that could capture all the curve characteristics (rapid uptake, incomplete depuration, or rapid depuration at the beginning of elimination) of the empirical data were considered valid. Examples showing the model results that did not pass the visual inspection were plotted in Fig. 1. Afterwards, the AICc was applied to select the best fitting model. The smaller the AICc is, the better the model is. We also calculated Akaike weight that shows the weight of evidence for each model within a cohort of nonlinear models.42 For a more detailed description and calculation equations see section S1 in ESI.†Kinetic rate constants for different types of ENMs were compared by using one-way analysis of variance (ANOVA) followed by Dunnett's T3 multiple comparisons test in GraphPad Prism. Statistical significance of differences between rate constants and SF for Daphnia and fish was evaluated by using student t-test (GraphPad Prism).
3. Results and discussion
3.1. Database content
Table 1 summarizes the non-linear results from the best model for each dataset, describing the uptake and depuration of non-dissolvable ENMs by freshwater aquatic organisms. We collected one dataset for algae (S. obliquus), 26 datasets for Daphnia (D. magna) and 7 datasets for zebrafish (D. rerio). No datasets for other organisms were found. The following non-dissolvable ENMs are included in our database: titanium dioxide (TiO2), silica dioxide (SiO2), fullerene (C60), graphene, graphene oxide (GO), gold (Au) and carbon nanotubes (CNTs). TiO2 is the most studied material. 31 datasets are for aqueous exposure, three are for dietary exposure. Standard testing guidelines utilized in each study are presented in Table 1. These guidelines primarily focus on the preparation of the stock solution with the standard medium, and do not provide information regarding the uptake and depuration experiments.| Dataset number | Organism | Material | Exposure type | C w | Depuration with feeding | Standard testing guidelines | Best model | k u | k e | SF | C sat | K M | Adjusted R2 | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mg L−1 | L kg−1 h−1 | 1/h | mg kg−1 | h | ||||||||||
| a For dietary exposure, units for food concentration (Cf) are in mg kg−1. b For dietary exposure, units for ku are in mg kg−1 h−1. —: not applicable. | ||||||||||||||
| 1 | S. obliquus | C60 | Aqueous | 2 | No | None | Model 3 | 2300 | 2.7 | 0.0020 | — | — | 0.953 | 29 |
| 2 | D. magna | TiO2 | Aqueous | 1 | Yes | None | Model 1 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.64 | — | — | — | 0.977 | 43 |
| 3 | D. magna | TiO2 | Aqueous | 1 | Yes | None | Model 5 | — | 0.73 | — | 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.9 | 0.932 | 43 |
| 4 | D. magna | TiO2 | Aqueous | 1 | Yes | None | Model 5 | — | 0.48 | — | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4.0 | 0.964 | 43 |
| 5 | D. magna | TiO2 | Aqueous | 1 | Yes | None | Model 1 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.79 | — | — | — | 0.966 | 43 |
| 6 | D. magna | TiO2 | Aqueous | 1 | Yes | None | Model 1 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.74 | — | — | — | 0.978 | 43 |
| 7 | D. magna | TiO2 | Aqueous | 1 | Yes | None | Model 5 | — | 1.0 | — | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3.1 | 0.965 | 43 |
| 8 | D. magna | SiO2 | Aqueous | 1 | Yes | None | Model 5 | — | 0.072 | — | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.0 | 0.915 | 43 |
| 9 | D. magna | SiO2 | Aqueous | 1 | Yes | None | Model 2 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.72 | 0.062 | 0.943 | 43 | ||
| 10 | D. magna | TiO2 | Aqueous | 1 | Yes | OECD 202 | Model 5 | — | 0.02 | — | 1200 | 12 | 0.909 | 44 |
| 11 | D. magna | TiO2 | Aqueous | 1 | No | OECD 202 | Model 2 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.16 | 0.69 | 0.777 | 44 | ||
| 12 | D. magna | TiO2 | Aqueous | 0.1 | No | OECD 202 | Model 5 | — | 0.02 | — | 5300 | 2.6 | 0.930 | 44 |
| 13 | D. magna | C60 | Dietary | 15.02a | No | None | Model 2 | 3308b | 0.64 | 0.46 | — | — | 0.848 | 29 |
| 14 | D. magna | Graphene | Aqueous | 0.25 | Yes | ISO 6341:1996 | Model 3 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.0 | 0.0020 | — | — | 0.762 | 28 |
| 15 | D. magna | Graphene | Aqueous | 0.1 | Yes | ISO 6341:1996 | Model 3 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.89 | 0.0070 | — | — | 0.541 | 28 |
| 16 | D. magna | Graphene | Aqueous | 0.05 | Yes | ISO 6341:1996 | Model 3 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.5 | 0.0070 | — | — | 0.692 | 28 |
| 17 | D. magna | Graphene | Aqueous | 0.25 | No | ISO 6341:1996 | Model 5 | — | 0.042 | — | 8400 | 4.1 | 0.975 | 28 |
| 18 | D. magna | Graphene | Aqueous | 0.1 | No | ISO 6341:1996 | Model 2 | 7000 | 0.2 | 0.62 | — | — | 0.901 | 28 |
| 19 | D. magna | Graphene | Aqueous | 0.05 | No | ISO 6341:1996 | Model 5 | — | 0.004 | — | 2400 | 5.4 | 0.970 | 28 |
| 20 | D. magna | GO | Aqueous | 10 | No | OECD 202 | Model 1 | 1500 | 0.1 | — | — | — | 0.891 | 45 |
| 21 | D. magna | GO | Aqueous | 5 | No | OECD 202 | Model 1 | 2900 | 0.12 | — | — | — | 0.972 | 45 |
| 22 | D. magna | C60 | Aqueous | 2 | No | None | Model 3 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.4 | 0.0010 | — | — | 0.855 | 46 |
| 23 | D. magna | C60 | Aqueous | 0.2 | No | None | Model 3 | 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.1 | 0.0030 | — | — | 0.916 | 46 |
| 24 | D. magna | C60 | Aqueous | 2 | No | OECD 202 | Model 5 | — | 0.033 | — | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6.1 | 0.937 | 30 |
| 25 | D. magna | Au | Aqueous | 0.05 | No | OECD 202 | None | — | — | — | — | — | — | 47 |
| 26 | D. magna | Au | Aqueous | 0.4 | Yes | OECD 202 | Model 5 | — | 3.9 | — | 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
45 | 0.992 | 47 |
| 27 | D. magna | Au | Aqueous | 0.4 | No | OECD 202 | Model 5 | — | 1.3 | — | 290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
110 | 0.999 | 47 |
| 28 | D. rerio | TiO2 | Dietary | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086a 086a |
Yes | OECD 202, OECD 211 | Model 1 | 0.00027b | 0.041 | — | — | — | 0.827 | 40 |
| 29 | D. rerio | TiO2 | Dietary | 4520a | Yes | OECD 202, OECD 211 | Model 1 | 0.0012b | 0.055 | — | — | — | 0.923 | 40 |
| 30 | D. rerio | TiO2 | Aqueous | 0.55 | Yes | OECD 202, OECD 211 | Model 5 | — | 0.013 | — | 230 | 410 | 0.911 | 40 |
| 31 | D. rerio | TiO2 | Aqueous | 0.06 | Yes | OECD 202, OECD 211 | Model 3 | 0.62 | 0.033 | 0.058 | — | — | 0.345 | 40 |
| 32 | D. rerio | CNTs | Aqueous | 0.2 | Yes | None | Model 5 | — | 0.3 | — | 900 | 340 | 0.644 | 48 |
| 33 | D. rerio | C60 | Aqueous | 1 | Yes | None | Model 1 | 130 | 0.082 | — | — | — | 0.306 | 46 |
| 34 | D. rerio | C60 | Aqueous | 2 | Yes | None | Model 1 | 13 | 0.077 | — | — | — | 0.105 | 46 |
3.2. Biokinetics model comparison
76% of the datasets had the best nonlinear regression result with an adjusted R2 above 0.9, as listed in Table 1. The results of the model comparison are summarized in Fig. 2. Overall, the results suggest that first-order one-compartment models with a storage fraction (models 2 and 3) demonstrate the highest degree of flexibility in characterizing the diverse patterns of uptake and elimination observed. As the process of depuration approaches completion, model 5 appears to be more accurate in fitting the experimental data.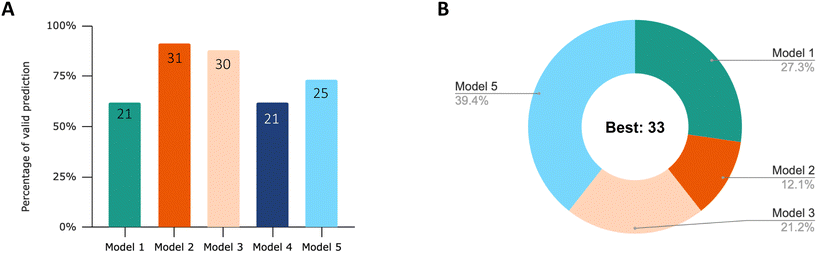 | ||
| Fig. 2 (A) Percentage of valid prediction for each model after visual inspection of the curve fit. The number of valid curves predicted by each model is labeled. The total number of curves is 34. (B) Proportion of the models with the best fit based on the lowest AICc score. This is the result after performing visual screening of the curve fit. When model 1 and model 4 have the same lowest AICc score, model 1 is considered as the best model, since less parameters are used in the modelling equation. The corresponding AICc score, Akaike weight and visual inspection results for each curve are listed in Table S1.† | ||
After visual inspection of the curve fits, the percentage of valid prediction for each model is shown in Fig. 2A. The curve fits of the five models for each dataset can be viewed in the ESI† (Fig. S1). Model 2 and model 3 fit 91% and 88% experimental data, respectively. Only three datasets out of 34 were not fitted successfully by model 2. These three datasets are no. 25, no. 26 and no. 27. They were all extracted from the same article.47 The experimental data from this study are characterized by an uptake phase that is far from steady state and an extremely rapid depuration of ENMs from the body during the first hour of elimination. This behavior clearly does not follow first-order kinetics. Therefore, in the subsequent analysis of the effects of exposure concentration, material, and feeding pattern on the rate constant, we only analyzed those parameters derived from model 2 and partially from model 3 for SF. The basic first-order one-compartment model (model 1) and model 4 with the additional growth dilution fit the least amounts of valid curves (21 out of 34). In all cases, the curves of model 1 and model 4 are almost overlapping. Because we extracted experimental data only from adult organisms, growth dilution during the experimental time has only a very limited influence. These models can be used to capture the curve characteristics of about 60% of the experimental data. The main reason for the failure of the fit is their inability to describe the incomplete depuration.
After identifying the validated curves, we selected the regression curves with the best fit based on the lowest AICc score. Fig. 2B displays the proportions of these best models. When model 1 and model 4 have the same lowest AICc score and the same fit results, model 1 is considered as the best model because fewer parameters are used in the modelling equations. Only one set of experimental data from 34 datasets does not have any model that could be fit. 39% of the dataset was best fitted with model 5, followed by model 1 (27%), model 3 (21%) and model 2 (12.1%).
3.3. Biokinetics model parameters
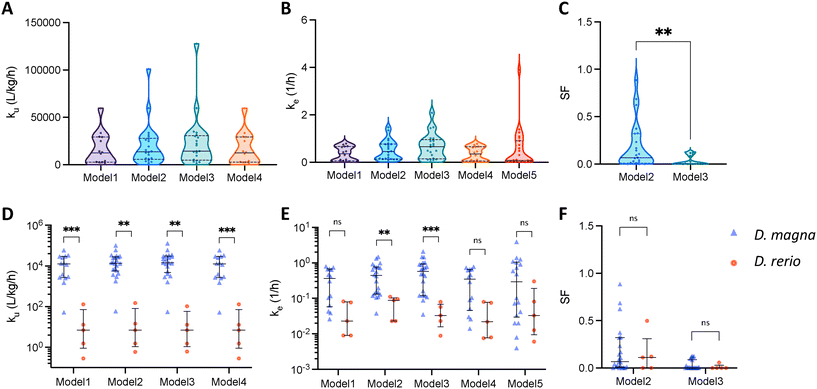
In previous kinetic studies, different models have been used in different studies to predict the patterns of uptake and elimination. By comparing the kinetic parameters derived from different models, we can get a better understanding of the relationships between these parameters. Since we only managed to collect three datasets for dietary exposure, we consider only studies by aqueous exposure in Fig. 3. First, Fig. 3A–C show the kinetic parameters obtained by the different models for the bioaccumulation of ENMs by D. magna. The statistical analysis reveals that there are no significant differences in the uptake and elimination constants among the five models. ku and ke have median values of 2000 L kg−1 h−1 and 2 1/h respectively. The SF values predicted by model 2 are widely distributed between 0 and 1 while model 3 predicts a maximum SF value of 0.13. The discrepancy between the two models may be attributed to the fact that model 2 only accounts for the storage fraction during the elimination phase, which may not adequately capture the physiological mechanisms at play. In contrast, model 3 takes into account the storage fraction during both the uptake and elimination phases, potentially leading to a more reliable estimate of the true storage fraction in the organisms. As mentioned in the previous section, the parameters of model 1 and model 4 almost overlap.Fig. 3D–F depict the differences in kinetic constants between different species. In all models, the uptake rate constant by D. magna is predicted to be faster than the one by zebrafish. The median ku of D. magna is about the forth power of ten, while the median ku of zebrafish is about three orders of magnitude smaller than that of D. magna. In terms of elimination rate constant, only ke estimated by model 2 and model 3 with storage fraction were significantly different. D. magna eliminated more rapidly than zebrafish. Also, we do not observe a significant difference between the two species in terms of SF (Fig. 3F).
Fig. 4 presents eight time profiles of ENM uptake and elimination in freshwater aquatic organisms. We intended to explore the effects of species, exposure pathway (aqueous or dietary), addition of food during depuration, and exposure concentration on the pattern of uptake and elimination of ENMs. To minimize the effects of different experimental designs and experimental conditions, we use pairs of datasets from the same article for this comparison. In Fig. 4A, we selected two datasets with the same exposure concentration of 2 mg L−1 of C60 to compare D. magna and zebrafish (D. rerio) bioaccumulation behavior.46D. magna's uptake is relatively fast and starts to reach a steady state after 24 h whereas the zebrafish uptake starts to stabilize after about 150 h. In addition, the maximum body burden of D. magna (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 dw) was approximately two orders of magnitude greater than that of zebrafish. This can be explained by the relative ratio of gut volume to the total mass of D. magna which is much larger than that of zebrafish. Furthermore, D. magna exhibits relatively rapid and complete elimination. In the first two hours of depuration, the body burden of D. magna rapidly decreased from 39
000 mg kg−1 dw) was approximately two orders of magnitude greater than that of zebrafish. This can be explained by the relative ratio of gut volume to the total mass of D. magna which is much larger than that of zebrafish. Furthermore, D. magna exhibits relatively rapid and complete elimination. In the first two hours of depuration, the body burden of D. magna rapidly decreased from 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 dw to 4400 mg kg−1 dw. The elimination of ENMs from the zebrafish stabilized after about 15 h and a significant portion (60%) could not be depurated.
000 mg kg−1 dw to 4400 mg kg−1 dw. The elimination of ENMs from the zebrafish stabilized after about 15 h and a significant portion (60%) could not be depurated.
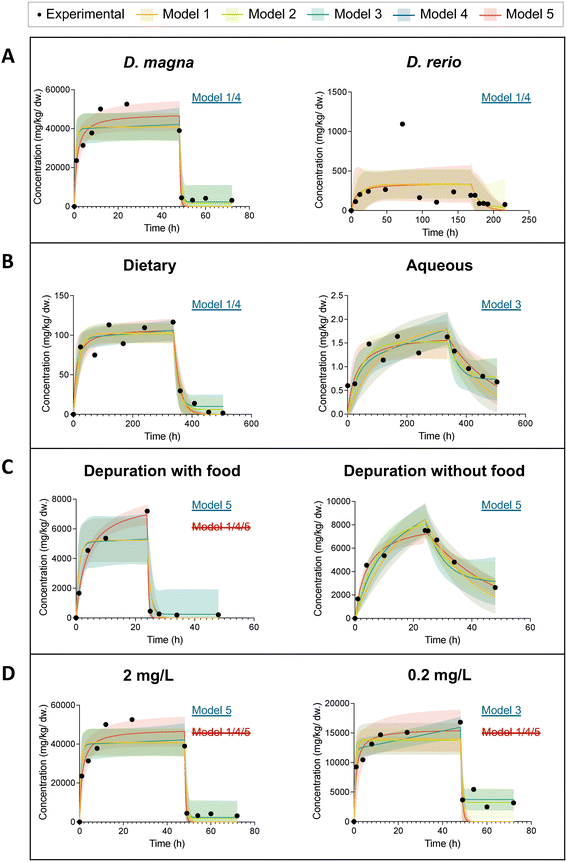 | ||
| Fig. 4 Figures of predicted organism body burden during uptake and elimination of ENMs with 95% confidence bands from five models in comparison with the experimental data for eight datasets. The model with an underline in blue is the model with the lowest AICc score. The model with a strikethrough in red is excluded for further statistical analysis based on a visual inspection with reference to the 95% confidence bands. When a model is marked with both blue underline and red strikethrough, it indicates that although it demonstrates superior curve fit results according to the AICc score, it fails to accurately capture the key characteristics of the curve, and as such, is considered to be invalid. (A) D. magna vs. D. rerio from dataset no. 22 and no. 33; (B) dietary exposure vs. aqueous exposure from dataset no. 29 and no. 31; (C) depuration with feeding vs. depuration without feeding from dataset no. 14 and no. 17; (D) low exposure concentration (2 mg L−1) vs. high exposure concentration (0.2 mg L−1) from dataset no. 22 and no. 23. Detailed curve fitting results are listed Table S1.† | ||
Fig. 4B shows the time profiles of the body burden of a zebrafish under different exposure routes: dietary and aqueous exposure. The two datasets were extracted from the same article.40 Under both exposure routes, steady state is reached after about 14 days. In the zebrafish with dietary exposure, ENMs are eliminated more rapidly (ke = 0.06 1/h) and more completely even though they are both fed with clean food during depuration. This may be due to the fact that zebrafish may accumulate ENMs via different mechanisms for aqueous and dietary exposure. The main uptake pathways in the zebrafish with aqueous exposure are gill uptake and stress-induced drinking.49 Therefore, feeding clean food does not induce significantly the depuration of ENMs from the zebrafish body. In the dietary exposure experiments, ENMs from contaminated food may accumulate in the zebrafish gut and are depurated quickly afterwards.
The difference between the elimination processes with and without feeding in D. magna is shown in Fig. 4C. Under the same concentration of water exposure, food facilitates elimination of graphene from the D. magna to be faster and more complete.28 The ke of the elimination with food is 1 1/h, while the ke without food is only 0.04 1/h. This is consistent with the results from literature that the presence of food improved the depuration efficiency of ENMs from the brine shrimp A. franciscana.50,51 Due to the behavioral traits of filter-feeders, most of the ENM are accumulated within in the body of the D. magna even with water exposure. Food plays a significant role in the elimination of ENMs from D. magna. However, when we compared the results of all the D. magna datasets together, we did not find a significant difference in the elimination process with and without feeding. Although food may have a facilitating effect on the elimination process, in none of the studies ENMs can be completely depurated, given the experimental and analytical uncertainty. Once ENMs enter the intestine, they can be found in two locations. One is the main lumen, where ENMs can be easily pushed out of the gut, and the other is between the brush borders formed by thousands of tightly packed microvilli. This small fraction of ENMs lodged at the gaps between brush borders can hardly be in contact with food.52 ENMs and its agglomerates smaller than 2 μm could be trapped in the gaps. They are likely not pushed out of the intestine like those ENMs in the main lumen. Due to peristalsis, more ENMs would be pushed into the microvilli. This may explain the incomplete elimination.33 Previous studies reported contrary results for two types of ENMs.53,54 Feeding D. magna with algae is necessary for the gut clearance of CNTs.53 Yet even without food, Au nanoparticles can be depurated almost completely.54 This could be due to the fact that the manufacturer's Au nanoparticles suspension contained dissolved organic carbon (tannic acid).54 The digestion of dissolved organic carbon in the gut may facilitate clumping of particles. The large clumps larger than 2 μm are therefore more easily to be depurated.54 An alternative hypothesis is that materials possessing a higher aspect ratio, such as CNTs, have been demonstrated to exhibit slower elimination kinetics compared to ENMs with a smaller aspect ratio, such as spherical nanoparticles.16
Fig. 4D illustrates the effect of exposure concentration. First of all, a rapid increase in C60 concentration in D. magna was observed in both groups during the first two hours of aqueous exposure.46 The higher the exposure concentration, the larger the maximum internal concentration in the organism at steady state. At an exposure concentration of 2 mg L−1, the maximum value of the internal concentration of D. magna reached about 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 dw. The maximum internal concentration in D. magna at 0.2 mg L−1 water exposure was only 17
000 mg kg−1 dw. The maximum internal concentration in D. magna at 0.2 mg L−1 water exposure was only 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg kg−1 dw. When we compare the uptake rate constants of these two datasets in Table 1, we find that ku increases by an order of magnitude with ten times smaller exposure concentration, from 29
000 mg kg−1 dw. When we compare the uptake rate constants of these two datasets in Table 1, we find that ku increases by an order of magnitude with ten times smaller exposure concentration, from 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L kg−1 h−1 to 130
000 L kg−1 h−1 to 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L kg−1 h−1. In addition, a decrease in the body burden during uptake for 2 mg L−1 exposure was recorded. This likely stems from the settling of ENMs in the solution. Furthermore, a more rapid removal (ke = 2.1 1/h) of C60 was observed at lower concentration (0.2 mg L−1). In Table 1, the elimination rate constant of 2 mg L−1 C60 from D. magna was modelled as 1.4 1/h. This is in agreement with other two studies.34,52
000 L kg−1 h−1. In addition, a decrease in the body burden during uptake for 2 mg L−1 exposure was recorded. This likely stems from the settling of ENMs in the solution. Furthermore, a more rapid removal (ke = 2.1 1/h) of C60 was observed at lower concentration (0.2 mg L−1). In Table 1, the elimination rate constant of 2 mg L−1 C60 from D. magna was modelled as 1.4 1/h. This is in agreement with other two studies.34,52
Table 2 lists the material-specific kinetics parameters in D. magna, including ku, ke, and SF. This table provides the possible range of kinetics parameters for each material for future biokinetics modelling. Due to the scarcity of data, we didn't observe a significant difference in rate constants between different ENMs, except for ke of SiO2 and C60 with median values of 0.73 1/h and 1.30 1/h respectively. The p-values for other pairwise comparison of ke were all above 0.24. The largest variation in ku and ke was found for C60. The 25th percentile (Q25) and the 75th percentile (Q75) for the ku of C60 were 3700 L kg−1 h−1 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L kg−1 h−1 respectively. And the Q25 and Q75 for the ke of C60 were 0.11 1/h and 1.5 1/h respectively. Moreover, there was no significant difference in the predicted SF for different types of ENMs from model 2 and model 3. This outcome may be attributed to the possibility that if the ENMs are only transitory in the gastrointestinal tract and partially stored, we would not expect to observe differences in SF between the different types of ENMs.
000 L kg−1 h−1 respectively. And the Q25 and Q75 for the ke of C60 were 0.11 1/h and 1.5 1/h respectively. Moreover, there was no significant difference in the predicted SF for different types of ENMs from model 2 and model 3. This outcome may be attributed to the possibility that if the ENMs are only transitory in the gastrointestinal tract and partially stored, we would not expect to observe differences in SF between the different types of ENMs.
| Number of values | Q25 | Median | Q75 | |
|---|---|---|---|---|
| k u (L kg−1 h−1) from model 2 | ||||
| TiO2 | 9 | 8700 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| SiO2 | 2 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Graphene | 6 | 5600 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Graphene oxide | 2 | 1800 | 2400 | 3000 |
| C60 | 3 | 3700 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| k e (1/h) from model 2 | ||||
| TiO2 | 9 | 0.072 | 0.30 | 0.62 |
| SiO2 | 2 | 0.72 | 0.73a | 0.75 |
| Graphene | 6 | 0.14 | 0.38 | 0.93 |
| Graphene oxide | 2 | 0.12 | 0.13 | 0.13 |
| C60 | 3 | 0.11 | 1.30b | 1.5 |
| SF from model 2 | ||||
| TiO2 | 9 | 0.0015 | 0.01 | 0.25 |
| SiO2 | 2 | 0.06 | 0.08 | 0.09 |
| Graphene | 6 | 0.02 | 0.24 | 0.69 |
| Graphene oxide | 2 | 0.01 | 0.08 | 0.14 |
| C60 | 3 | 0.04 | 0.23 | 0.32 |
| SF from model 3 | ||||
| TiO2 | 8 | 0.00025 | 0.0010 | 0.064 |
| SiO2 | 2 | 0.0030 | 0.0050 | 0.0070 |
| Graphene | 6 | 0.0058 | 0.054 | 0.12 |
| Graphene oxide | 2 | 0.00 | 0.013 | 0.025 |
| C60 | 3 | 0.0010 | 0.0030 | 0.12 |
3.4. Suggestions on model selection
Based on our analysis of all the available bioaccumulation data, we present some suggestions which models should be chosen under certain circumstances when fitting experimental data. Model 5 can better capture the characteristics of the curve when the concentration in the organism during the uptake phase has not stabilized. When the elimination process is clearly incomplete and a certain fraction remains within the body even after long depuration time, only model 2 or model 3 can account for the storage fraction in the organism. When ENMs can be almost completely eliminated from the organism, the basic model 1 is sufficient. Although we have considered only adult organisms, a model that incorporates growth dilution is necessary when simulating organisms in the early stages of development. Sljm et al. (1992)55 reported that due to higher growth dilution and lower uptake typically in the early life stages of fish, juvenile fish typically accumulate less from food than older fish; they also noted that the biomagnification factor (BMF) of growing fish is highly dependent on the growth rate.484. Conclusions and outlook
The assessment of biokinetics is essential to better understand the bioaccumulation potential of ENMs in biota. There are different modelling methods for the determination of uptake and elimination kinetics. This study compared five biokinetic models for non-dissolvable ENMs in freshwater organisms. The comparison suggested that no general model is able to predict all the experimental data properly. First-order one-compartment models with storage fraction (model 2 and model 3) seem to show more flexibility to describe various bioaccumulation patterns, especially when depuration is clearly incomplete. More than 90% of the experimental data predicted by these two models were considered as valid. In addition, for adult organisms, growth dilution has only a very limited impact on the modelling results. The uptake rate constants estimated by first-order one-compartment models and its variants for D. magna (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 L kg−1 h−1) are significantly higher than the rate constants of zebrafish (7 L kg−1 h−1). We provided the possible range of kinetics parameters for each material for that can be used for future biokinetics modelling. Due to the scarcity of data, we cannot yet draw any conclusions about the impact of the material on bioaccumulation. Finally, we provided guidance on the selection of biokinetic models for different patterns of experimental data, which will enhance the environmental risk assessment of ENMs. The lack of specific guidelines for measuring bioaccumulation of ENMs is a significant challenge. Many studies only report basic characteristics of the nanoparticles, such as nominal exposure concentrations, rather than providing a comprehensive understanding of their behavior in different exposure media. This makes it difficult to interpret the results and compare them with other studies. In order to better interpret the experimental data and understand the bioaccumulation of ENMs, we suggest the following points for future experimental designs:
000 L kg−1 h−1) are significantly higher than the rate constants of zebrafish (7 L kg−1 h−1). We provided the possible range of kinetics parameters for each material for that can be used for future biokinetics modelling. Due to the scarcity of data, we cannot yet draw any conclusions about the impact of the material on bioaccumulation. Finally, we provided guidance on the selection of biokinetic models for different patterns of experimental data, which will enhance the environmental risk assessment of ENMs. The lack of specific guidelines for measuring bioaccumulation of ENMs is a significant challenge. Many studies only report basic characteristics of the nanoparticles, such as nominal exposure concentrations, rather than providing a comprehensive understanding of their behavior in different exposure media. This makes it difficult to interpret the results and compare them with other studies. In order to better interpret the experimental data and understand the bioaccumulation of ENMs, we suggest the following points for future experimental designs:
• Only nominal concentrations are reported in many studies. Both the adhesion of ENMs on the test vessels and uptake by filter feeders from the aqueous phase can result in a decrease in the exposure concentration. Thus, the bioaccumulation of ENMs in the organism will be underestimated. We recommend that at least the ENM concentration at the beginning and end of the uptake should be measured and reported. According to the OECD guidelines, it is recommended to ensure that the measured concentration does not differ from the nominal concentration by more than 20%.17 If this range is exceeded a semi-static test system or a flow-through exposure design can be considered.56 An alternative method for incorporating the effects of declining exposure concentrations in the model is through the inclusion of a settling rate constant in the model equations. This has been demonstrated in studies on carbon fullerenes, where the linear regression slope of the natural logarithm of the ENM concentration in the aqueous phase during the uptake period was added to determine the settling rate.30
• To obtain a more precise determination of the uptake rate constant, it is advisable to measure uptake over a duration that is long enough. This is particularly relevant in the case of Daphnia, as it is recommended to extend the measurement period to 48 hours if steady state is not reached after 24 hours.
• The elimination time should also be long enough to determine to what extent ENMs can be depurated.
• It has been observed that the initial stages of the uptake and elimination process tend to be rapid in experimental settings. To obtain a more detailed understanding of this phenomenon, implementing more frequent sampling, such as every 15 minutes, may be beneficial. The initial slope of the uptake curve is generally considered to be a reliable indicator of the bioavailability of compounds, making it particularly important to accurately capture this stage of the process.
• There are still too few kinetic data for algae, fish and other functional groups of zooplankton (e.g., gathering collector, scraper, and shredder) besides filter feeders. We cannot draw relevant conclusions specific to the organism. For example, different species of fish may breathe at different rates, have different metabolic capacities, will grow at different rates, may feed at different rates, and may digest food at different rates.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union's Horizon 2020 research and innovation programme under grant agreement 814426 (NanoInformaTIX).References
- V. Adam, Q. Wu and B. Nowack, Integrated dynamic probabilistic material flow analysis of engineered materials in all European countries, NanoImpact, 2021, 22, 100312 CrossRef CAS PubMed.
- H. Y. Lu, Y. J. Wang and W. C. Hou, Bioaccumulation and depuration of TiO2 nanoparticles by zebrafish through dietary exposure: Size- and number concentration-resolved analysis using single-particle ICP-MS, J. Hazard. Mater., 2022, 426, 127801 CrossRef CAS PubMed.
- H. M. Maes, F. Stibany, S. Giefers, B. Daniels, B. Deutschmann and W. Baumgartner, et al., Accumulation and Distribution of Multiwalled Carbon Nanotubes in Zebrafish (Danio rerio), Environ. Sci. Technol., 2014, 48(20), 12256–12264 CrossRef CAS PubMed.
- S. Rhiem, M. J. Riding, W. Baumgartner, F. L. Martin, K. T. Semple and K. C. Jones, et al., Interactions of multiwalled carbon nanotubes with algal cells: Quantification of association, visualization of uptake, and measurement of alterations in the composition of cells, Environ. Pollut., 2015, 196, 431–439 CrossRef CAS PubMed.
- ECHA, Guidance on information requirements and chemical safety assessment chapter R.11: PBT/vPvB assessment, Eur Chem Agency, 2017, 4, p. 494 Search PubMed.
- M. Baalousha, G. Cornelis, T. A. J. Kuhlbusch, I. Lynch, C. Nickel and W. Peijnenburg, et al., Modeling nanomaterial fate and uptake in the environment: Current knowledge and future trends, Environ. Sci.: Nano, 2016, 3(2), 323–345 RSC.
- N. W. van den Brink, A. Jemec Kokalj, P. V. Silva, E. Lahive, K. Norrfors and M. Baccaro, et al., Tools and rules for modelling uptake and bioaccumulation of nanomaterials in invertebrate organisms, Environ. Sci.: Nano, 2019, 6(7), 1985–2001 RSC.
- J. Campfens and D. Mackay, Fugacity-based model of PCB bioaccumulation in complex aquatic food webs, Environ. Sci. Technol., 1997, 31(2), 577–583 CrossRef CAS.
- J. A. Arnot and F. A. P. C. Gobas, A food web bioaccumulation model for organic chemicals in aquatic ecosystems, Environ. Toxicol. Chem., 2004, 23(10), 2343–2355 CrossRef CAS PubMed.
- E. J. Petersen, M. Mortimer, R. M. Burgess, R. Handy, S. Hanna and K. T. Ho, et al., Strategies for robust and accurate experimental approaches to quantify nanomaterial bioaccumulation across a broad range of organisms, Environ. Sci.: Nano, 2019, 6(6), 1619–1656 RSC.
- J. C. McGeer, K. V. Brix, J. M. Skeaff, D. K. Deforest, S. I. Brigham and W. J. Adams, et al., Inverse relationship between bioconcentration factor and exposure concentration for metals: Implications for hazard assessment of metals in the aquatic environment, Environ. Toxicol. Chem., 2003, 22(5), 1017–1037 CrossRef CAS PubMed.
- D. K. DeForest, K. V. Brix and W. J. Adams, Assessing metal bioaccumulation in aquatic environments: The inverse relationship between bioaccumulation factors, trophic transfer factors and exposure concentration, Aquat. Toxicol., 2007, 84(2), 236–246 CrossRef CAS PubMed.
- A. J. Edgington, E. J. Petersen, A. A. Herzing, R. Podila, A. Rao and S. J. Klaine, Microscopic investigation of single-wall carbon nanotube uptake by Daphnia magna, Nanotoxicology, 2014, 8(1), 2–10 CrossRef CAS PubMed.
- L. Mao, M. Hu, B. Pan, Y. Xie and E. J. Petersen, Biodistribution and toxicity of radio-labeled few layer graphene in mice after intratracheal instillation, Part. Fibre Toxicol., 2016, 13(1), 7 CrossRef PubMed.
- M. Mortimer, E. J. Petersen, B. A. Buchholz, E. Orias and P. A. Holden, Bioaccumulation of Multiwall Carbon Nanotubes in Tetrahymena thermophila by Direct Feeding or Trophic Transfer, Environ. Sci. Technol., 2016, 50(16), 8876–8885 CrossRef CAS PubMed.
- M. Mortimer, T. Kefela, A. Trinh and P. A. Holden, Uptake and depuration of carbon- and boron nitride-based nanomaterials in the protozoa Tetrahymena thermophila, Environ. Sci.: Nano, 2021, 8(12), 3613–3628 RSC , Available from: http://xlink.rsc.org/?DOI=D1EN00750E.
- OECD, Test No. 305: Bioaccumulation in Fish: Aqueous and Dietary Exposure, OECD Guidelines for the Testing of Chemicals, Section 3, 2012.
- K. L. Garner, Y. Qin, S. Cucurachi, S. Suh and A. A. Keller, Linking Exposure and Kinetic Bioaccumulation Models for Metallic Engineered Nanomaterials in Freshwater Ecosystems, ACS Sustainable Chem. Eng., 2018, 6(10), 12684–12694 CrossRef CAS.
- F. Ribeiro, C. A. M. Van Gestel, M. D. Pavlaki, S. Azevedo, A. M. V. M. Soares and S. Loureiro, Bioaccumulation of silver in Daphnia magna: Waterborne and dietary exposure to nanoparticles and dissolved silver, Sci. Total Environ., 2017, 574, 1633–1639 CrossRef CAS PubMed.
- M. Baccaro, A. K. Undas, J. de Vriendt, J. H. J. van den Berg, R. J. B. Peters and N. W. van den Brink, Ageing, dissolution and biogenic formation of nanoparticles: how do these factors affect the uptake kinetics of silver nanoparticles in earthworms?, Environ. Sci.: Nano, 2018, 5(5), 1107–1116 RSC.
- J. Zhao, N. Li, S. Wang, X. Zhao, J. Wang and J. Yan, et al., The mechanism of oxidative damage in the nephrotoxicity of mice caused by nano-anatase TiO2, J. Exp. Nanosci., 2010, 5(5), 447–462 CrossRef CAS.
- A. Bianchini and C. M. Wood, Mechanism of acute silver toxicity in Daphnia magna, Environ. Toxicol. Chem., 2003, 22(6), 1361–1367 CrossRef CAS PubMed.
- J. F. Pan and W. X. Wang, Influences of dissolved and colloidal organic carbon on the uptake of Ag, Cd, and Cr by the marine mussel Perna viridis, Environ. Pollut., 2004, 129(3), 467–477 CrossRef CAS PubMed.
- F. R. Khan, S. K. Misra, N. R. Bury, B. D. Smith, P. S. Rainbow and S. N. Luoma, et al., Inhibition of potential uptake pathways for silver nanoparticles in the estuarine snail Peringia ulvae, Nanotoxicology, 2015, 9(4), 493–501 CrossRef CAS PubMed , Available from: https://www.tandfonline.com/doi/full/10.3109/17435390.2014.948519.
- Y. Zheng and B. Nowack, Meta-analysis of Bioaccumulation Data for Nondissolvable Engineered Nanomaterials in Freshwater Aquatic Organisms, Environ. Toxicol. Chem., 2022, 41(5), 1202–1214 CrossRef CAS PubMed.
- D. Moher, A. Liberati, J. Tetzlaff and D. G. Altman, Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement, Int. J. Surg., 2010, 8(5), 336–341 CrossRef PubMed.
- A. Rohatgi, Webplotdigitizer: Version 4.6, 2022.
- X. Guo, S. Dong, E. J. Petersen, S. Gao, Q. Huang and L. Mao, Biological Uptake and Depuration of Radio-labeled Graphene by Daphnia magna, Environ. Sci. Technol., 2013, 47(21), 12524–12531 CrossRef CAS PubMed.
- Q. Chen, X. Hu, D. Yin and R. Wang, Effect of subcellular distribution on nC60 uptake and transfer efficiency from Scenedesmus obliquus to Daphnia magna, Ecotoxicol. Environ. Saf., 2016, 128, 213–221 CrossRef CAS PubMed.
- K. Tervonen, G. Waissi, E. J. Petersen, J. Akkanen and J. V. K. Kukkonen, Analysis of fullerene-c60 and kinetic measurements for its accumulation and depuration in Daphnia magna, Environ. Toxicol. Chem., 2010, 29(5), 1072–1078 CAS.
- A. Avenant-Oldewage and H. Marx, Manganese, nickel and strontium bioaccumulation in the tissues of the African sharptooth catfish, Clarias gariepinus from the Olifants River, Koedoe: Protected Area Science and Management, 2000, 43(2), 17–33 CrossRef.
- G. L. Atkins, Multicompartment models for biological systems, London: Methuen, 1969, vol. xiii Search PubMed.
- F. Nasser and I. Lynch, Updating traditional regulatory tests for use with novel materials: Nanomaterial toxicity testing with Daphnia magna, Saf. Sci., 2019, 118, 497–504 CrossRef.
- A. T. Wray and S. J. Klaine, Modeling the influence of physicochemical properties on gold nanoparticle uptake and elimination by Daphnia magna, Environ. Toxicol. Chem., 2015, 34(4), 860–872 CrossRef CAS PubMed.
- P. S. Tourinho, C. A. M. van Gestel, A. J. Morgan, P. Kille, C. Svendsen and K. Jurkschat, et al., Toxicokinetics of Ag in the terrestrial isopod Porcellionides pruinosus exposed to Ag NPs and AgNO3 via soil and food, Ecotoxicology, 2016, 25(2), 267–278 CrossRef CAS PubMed.
- J. C. Achar, D. Y. Kim, J. H. Kwon and J. Jung, Toxicokinetic modeling of octylphenol bioconcentration in Chlorella vulgaris and its trophic transfer to Daphnia magna, Ecotoxicol. Environ. Saf., 2020, 194, 110379 CrossRef CAS PubMed.
- T. Bukovinszky, A. M. Verschoor, N. R. Helmsing, T. M. Bezemer, E. S. Bakker and M. Vos, et al., The Good, the Bad and the Plenty: Interactive Effects of Food Quality and Quantity on the Growth of Different Daphnia Species, PLoS One, 2012, 7(9), 1–8 CrossRef PubMed.
- Z. Han, S. Jiao, D. Kong, Z. Shan and X. Zhang, Effects of β-endosulfan on the growth and reproduction of zebrafish (Danio rerio), Environ. Toxicol. Chem., 2011, 30(11), 2525–2531 CrossRef CAS PubMed.
- K. A. Johnson and R. S. Goody, The original Michaelis constant: Translation of the 1913 Michaelis-Menten Paper, Biochemistry, 2011, 50(39), 8264–8269 CrossRef CAS PubMed.
- X. Zhu, J. Wang, X. Zhang, Y. Chang and Y. Chen, Trophic transfer of TiO2 nanoparticles from daphnia to zebrafish in a simplified freshwater food chain, Chemosphere, 2010, 79(9), 928–933 CrossRef CAS PubMed.
- T. C. Hoang, E. C. Rogevich, G. M. Rand and R. A. Frakes, Copper uptake and depuration by juvenile and adult Florida apple snails (Pomacea paludosa), Ecotoxicology, 2008, 17(7), 605–615 CrossRef CAS PubMed.
- A. N. Spiess and N. Neumeyer, An evaluation of R2as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach, BMC Pharmacol., 2010, 10, 1–11 Search PubMed.
- A. R. Arze, N. Manier, A. Chatel and C. Mouneyrac, Characterization of the nano-bio interaction between metallic oxide nanomaterials and freshwater microalgae using flow cytometry, Nanotoxicology, 2020, 14(8), 1082–1095 CrossRef PubMed.
- X. Zhu, Y. Chang and Y. Chen, Toxicity and bioaccumulation of TiO2 nanoparticle aggregates in Daphnia magna, Chemosphere, 2010, 78(3), 209–215 CrossRef CAS PubMed.
- X. Lv, Y. Yang, Y. Tao, Y. Jiang, B. Chen and X. Zhu, et al., A mechanism study on toxicity of graphene oxide to Daphnia magna: Direct link between bioaccumulation and oxidative stress, Environ. Pollut., 2018, 234, 953–959 CrossRef CAS PubMed.
- Q. Chen, D. Yin, J. Li and X. Hu, The effects of humic acid on the uptake and depuration of fullerene aqueous suspensions in two aquatic organisms, Environ. Toxicol. Chem., 2014, 33(5), 1090–1097 CrossRef CAS PubMed.
- d. L. M. Skjolding, K. Kern, R. Hjorth, N. Hartmann, S. Overgaard and G. Ma, et al., Uptake and depuration of gold nanoparticles in Daphnia magna, Ecotoxicology, 2014, 23(7), 1172–1183 CrossRef PubMed.
- H. M. Maes, F. Stibany, S. Giefers, B. Daniels, B. Deutschmann and W. Baumgartner, et al., Accumulation and distribution of multiwalled carbon nanotubes in zebrafish (Danio rerio), Environ. Sci. Technol., 2014, 48(20), 12256–12264 CrossRef CAS PubMed.
- G. Federici, B. J. Shaw and R. D. Handy, Toxicity of titanium dioxide nanoparticles to rainbow trout (Oncorhynchus mykiss): Gill injury, oxidative stress, and other physiological effects, Aquat. Toxicol., 2007, 84(4), 415–430 CrossRef CAS PubMed.
- M. Ates, J. Daniels, Z. Arslan and I. O. Farah, Effects of aqueous suspensions of titanium dioxide nanoparticles on Artemia salina: assessment of nanoparticle aggregation, accumulation, and toxicity, Environ. Monit. Assess., 2013, 185(4), 3339–3348 CrossRef CAS PubMed.
- M. Ates, V. Demir, R. Adiguzel and Z. Arslan, Bioaccumulation, Subacute Toxicity, and Tissue Distribution of Engineered Titanium Dioxide Nanoparticles in Goldfish (Carassius auratus), J. Nanomater., 2013, 2013, 460518 Search PubMed.
- F. R. Khan, G. M. Kennaway, M. N. Croteau, A. Dybowska, B. D. Smith and A. J. A. Nogueira, et al., In vivo retention of ingested au NPs by daphnia magna: No evidence for trans-epithelial alimentary uptake, Chemosphere, 2014, 100, 97–104 CrossRef CAS PubMed.
- E. J. Petersen, J. Akkanen, J. V. K. Kukkonen and W. J. Weber, Biological uptake and depuration of carbon nanotubes by daphnia magna, Environ. Sci. Technol., 2009, 43(8), 2969–2975 CrossRef CAS PubMed.
- S. B. Lovern, H. A. Owen and R. Klaper, Electron microscopy of gold nanoparticle intake in the gut of Daphnia magna, Nanotoxicology, 2008, 2(1), 43–48 CrossRef CAS.
- D. T. H. M. Sljm, S. Willem and O. Antoon, Life-Cycle Biomagnification Study in Fish, Environ. Sci. Technol., 1992, 26(11), 2162–2174 CrossRef.
- S. Kuehr, V. Kosfeld and C. Schlechtriem, Bioaccumulation assessment of nanomaterials using freshwater invertebrate species, Environ. Sci. Eur., 2021, 33, 9 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2en01039a |
| This journal is © The Royal Society of Chemistry 2023 |