Mechanistic model for quantifying the effect of impact force on mechanochemical reactivity

Abstract

Conventional mechanochemical synthetic tools, such as ball mills, offer no methodology to quantitatively link macroscale reaction parameters, such as shaking frequency or milling ball radius, to fundamental drivers of reactivity, namely the force vectors applied to the reactive molecules. As a result, although mechanochemistry has proven to be a valuable method to make a wide variety of products, the results are seldom reproduceable between reactors, difficult to rationally optimize, and hard to ascribe to a specific reaction pathway. Here we have developed a controlled force reactor, which is a mechanochemical ball mill reactor with integrated force measurement and control during each impact. We relate two macroscale reactor parameters—impact force and impact time—to thermodynamic and kinetic transition state theories of mechanochemistry utilizing continuum contact mechanics principles. We demonstrate force controlled particle fracture of NaCl to characterize particle size evolution during reactions, and force controlled reaction between anhydrous copper(II) chloride and (1, 10) phenanthroline. During the fracture of NaCl, we monitor the evolution of particle size as a function of impact force and find that particles quickly reach a particle size of ∼100 μm largely independent of impact force, and reach steady state 10–100× faster than reaction kinetics of typical mechanochemical reactions. We monitor the copper(II) chloride reactivity by measuring color change during reaction. Applying our transition state theory developed here to the reaction curves of copper(II) chloride and (1, 10) phenanthroline at multiple impact forces results in an activation energy barrier of 0.61 ± 0.07 eV, distinctly higher than barriers for hydrated metal salts and organic ligands and distinctly lower than the direct cleavage of the CuCl bond, indicating that the reaction may be mediated by the higher affinity of Fe in the stainless steel vessel to Cl. We further show that the results in the controlled force reactor match rudimentary estimations of impact force within a commercial ball mill reactor Retsch MM400. These results demonstrate the ability to quantitatively link macroscale reactor parameters to reaction properties, motivating further work to make mechanochemical synthesis quantitative, predictable, and fundamentally insightful.

---

Introduction

Mechanochemistry utilizes mechanical force to drive reactions, and has proven to be a versatile method to synthesize a wide range of molecules with similar or better yields than solvothermal chemistry—often without the need for solvent—motivating its use as a less toxic, cheaper, and environmentally friendly synthesis route.^1–8 Previous work has shown the synthesis of complex oxides, nanoparticles, catalytic materials, high porous materials, organic molecules, polymers, and metal complexes.^9–15 A key feature of mechanochemistry is that reactivity depends on both the magnitude and the direction of the applied force vector, unlike in conventional solvothermal chemistry where the reaction depends on scaler quantities such as temperature and hydrostatic pressure. Control over the force vector can thus selectively drive reactions that are difficult or impossible to achieve in solvothermal conditions due to thermodynamic or kinetic limitations, where application of the force vector along the desired reaction pathway favours the reaction over orthogonal undesirable pathways.¹⁶

A number of tools and methodologies exist to experimentally measure the effect of force on bond forming and breaking at the individual molecule level, including the atomic force microscope (AFM), optical tweezers, the surface forces apparatus (SFA), and nano-indenters.^16–25 Many of the techniques originated from the study of tribochemical reactions between solid surfaces in sliding contact and the surrounding environment, but have evolved to include measurement of bond-scission in long chain polymers and biomolecules, as well as reversible bond forming–breaking events between a probe molecule and a surface.^25–27 While these techniques provide detailed measurement and control of the applied force vector on single molecule systems, making them vital tools for studying fundamental mechanochemical phenomena, these techniques are difficult to extend to throughputs relevant for large scale at chemical synthesis. Toward that end, mesoscale instruments heavily used in tribochemistry, such as the pin-on-disc tribometer and the mini-traction-machine, provide force controlled reactive environments within a macroscale solid–solid contact, which can lead to statistically relevant rate mechanics for an ensemble of reacting particles.²⁸ However, these too are not trivially scalable as synthetic techniques.

As mechanochemistry has gained popularity, macroscale reactor designs have improved to provide expanded ranges of applied forces, reaction times, and throughput, evolving from the manual mortar and pestle to automated systems. State-of-the-art mechanochemical tools, such as vibratory and planetary ball mills as well as twin screw extrusion mills, provide energy to reactant solids via compression, shear, or impacts.^29–31 More recently, efforts toward making mechanochemistry quantitative at synthetically relevant scales, incorporating temperature control and in situ spectroscopic measurements to study reaction kinetics have also been advanced.^32–38 However, current state-of-the-art macroscale mechanochemical reactors typically do not provide any measure of or control over the applied forces within the reactor, beyond rudimentary changes in reactor materials. The most common gram scale reactor is the ball mill reactor, where one or more metal or ceramic balls are contained in a vessel with reactant molecules, and mechanical agitation of the vessel results in a large number of solid–solid collisions between the balls and the vessel wall, which imparts mechanical energy to reactants trapped within the contact. Reaction variables are limited to the type of mill, milling speed and time, vibration frequency, milling medium, ball filling ratio and milling atmosphere.³⁹ Significant work has been done to phenomenologically investigate the kinetics of mechanochemical transformation, and explicit connections between the contact mechanics within each impact and the reaction rates can improve predictive power.^40–43 Because there are currently no ways to either measure or control the applied forces in the reactor directly, it is difficult to reliably relate reaction thermodynamics and kinetics observed in mechanochemical synthesis to fundamental rate theories, precluding the ability to purposefully design mechanochemical reactions for any reactors in use today.

Here we investigate the effect of precise force application on the kinetics and energetics of a chemical reaction. In this study, we propose a theoretical framework for quantifying chemical kinetics in a single and multiple impact mechanochemical reaction. Secondly, we developed a force-controlled ball mill reactor that ensures precise force application between 3 N and 30 N on solid reactants. In the synthesis of a metal complex between anhydrous CuCl₂ and 1,10-phenanthroline reactants, results show that the decoupled force component can significantly enhance reaction progression and elucidate quantifiable chemical kinetics. Finally, we demonstrate the effect of applied force on the particle size comminution of NaCl. The effect of quantifiable applied force as it relates to the reaction thermodynamics, kinetics and particle comminution is further discussed.

Theoretical framework

Mechanochemical reactions are modelled using transition state theory, where the mechanical work on the reactants deforms the potential energy surface, modifying the energy barrier between reactant and product states. This complex surface deformation is often approximated as a linear deformation along a one-dimensional (1D) reaction pathway where force in the direction of the reaction pathway linearly reduces the activation energy by an amount equal to the work performed.⁴⁴ The mechanical work is often simplified for the sake of modelling as either a force applied over the distance—or as a stress applied over the change in volume (called activation volume)—between the initial and activated states. While both approximations are not perfect analogies for all chemical reactions, force over a distance is typically used for simple single bond forming/breaking in long-chain molecules, and stress over a volume change is used for more complex molecules and reactions. In our case, because we rely on continuum mechanics to describe the solid–solid contact between a ball and a flat surface under impact, which results in a pressure distribution in the contact, we adopt the stress framework to model reactivity. Transition state theory provides the reaction rate as,where, k₀ is the attempt frequency, E_a is the activation energy, P is the pressure within the impact contact between the ball and counter-surface, ΔV_a is the change in activation volume between reactive and activated states, k_b is Boltzmann's constant, and T is the temperature. The pressure distribution P(r, t) depends both on location r within the impact and time t as the two solid bodies mechanically deform. Here we assume linearly elastic Hertzian contact mechanics within the impact, where in our case the velocity of the ball is constant so the indentation depth can be represented as velocity U multiplied by the impact time t_tot. Note that the impact in our reactor differs from the Hertz theory of impact in that the ball velocity in our reactor is provided continuously by an external motor, and the contact breaks at the point of max loading. As a result, the impact time in our reactor is estimated to be ∼1/4 the impact time of a free moving ball impacting a surface. Further, the assumption of elastic impact is justified by the fact that no noticeable deformation occurs on the vessel walls in experiments, and that Hertz mechanics tends to perform well even with restitution coefficients below 0.7. The impact time can be determined using Hertz contact mechanics, setting the applied load equal to the force setting in the reactor.where R is the radius of the ball and E^* is an effective mechanical modulus given byUsing the elastic modulus E and Poisson ratio v for the ball and vessel materials. The total impact time serves as a limit of integration in future steps. The pressure distribution is given by,where a, is the contact radius given by . Inserting (4) into (1), we can model the rate of change in the reactant concentration within the contact using,where ρ(r, t) is the local reactant concentration (mol m⁻³), and n is the order of the reaction.

Here we solve for the total change in concentration assuming a first order reaction (see ESI† for nth order reaction solution). First, we integrate (5) with respect to time utilizing separation of variables to find the local change in reactant surface concentration over the entire life of the impact, as shown in eqn (6).

Here, ρ(r) is the local change in concentration after impact, ρ₀ is the initial surface concentration of reactants, and A, B, C are constants of integration given in eqn (7)–(9).Fig. 1 shows the local change in concentration within a single ball impact for various applied impact forces, generated using eqn (6). Both the ball and reactor were stainless steel (E = 210 GPa, v = 0.29), and the ball radius was R = 6.35 mm. The reaction has an activation energy of E_a = 0.7 eV, a change in activation volume of ΔV_a = 20 ų, a reaction temperature T = 300 K, and a reaction attempt frequency k₀ = 1 × 10¹³ s⁻¹ is assumed. These values are typical to produce an illustrative form of the curve shown in Fig. 1. At low loads, the reaction proceeds quickly at the centre of the load, and the rate decays out to the edge of the contact. As force increases, the reaction proceeds more fully within a single impact, until at sufficiently large loads the reaction fully progresses in the centre. As the impact force increases, note that the size of the contact also increases, which increases the amount of material reacted in a single impact.

Fig. 1 Normalized local concentration within the impact site after completion of the impact for impact forces between 25–400 N. At low loads, only a partial reaction occurs. At higher loads, the reaction saturates and higher loads result in marginal improvements.

Next, we find the total change in reactant concentration in the contact by integrating over the contact radius. The total change in concentration after a single impact is given by eqn (10) below, for which there is no closed form solution.

where h is the thickness of the reactant layer in the impact area (which we approximate to roughly the diameter of the reactant particles in the reactor). We solve eqn (10) numerically using the parameters described above and plot the quantity ΔN/ρ₀ in Fig. 2 for a wide range of forces. At low loads, the reaction is primarily driven by force, while at high loads the saturation of the reaction within the contact provides limited benefit. In the force activated regime, mechanochemical reactions are highly sensitive to load, and increasing it will dramatically speed up the rate of reaction. In the contact-limited regime, the reactions are governed primarily by the rate of impact within the reactor. Understanding the force-activated and contact-limited regimes is essential for predicting mechanochemical processes and designing reaction conditions for desired outcome. For example, for a reaction with a low activation energy, it might be more beneficial to increase the number of ball bearings within the reactor, and therefore the number of impacts, at the expense of lower impact forces.

Fig. 2 Total change in molar mass normalized to the initial molar concentration. At low loads, the reaction is highly sensitive to the applied force. At higher loads, the force effect saturates, and further gains are primarily gained by an increase in the maximum contact area.

We further attempt to provide a closed form solution to eqn (10) by assuming that the pressure within the contact is constant in both location and time. We then describe the reaction rate using,

where P_eff = F_set/πa² is the constant effective pressure. Inserting (11) into (5), integrating over impact time, and then inserting into (10) and integrating over the impact area leads to the change in local concentration within a single impact as given in eqn (12) and (13).This relatively simple result implies that the total change of reactants within a single impact can be determined by the impact force F_set, the total impact time t_tot, and the concentration density of reactants ρ₀. Fig. 3 shows the change in local concentration over time for different activation energies over applied loads. As can be seen, the approximation reasonably captures the reaction dynamics over a wide range of applied loads and for reactions with widely varying activation energies. Quantitatively comparing (12) and the numerical solution of (10) shows that the maximum error between them is 80%, with an average error of 34%. Although these errors appear large, they are fairly reasonable for a logarithmic process, and it will be shown later that this contributes much less overall error to the quantitative assessment of reaction thermodynamics within the reactor.

Fig. 3 Change in local concentration as a function of reaction activation energy, where in the force activated regime, the reaction proceeds nearly two orders of magnitude slower for each 0.1 eV increase in activation energy.

We next turn our efforts to describing the evolution of the reaction within the vessel over many impacts. We defined the number of moles of reactants, N₀, in the milling vessel as,

where M₀ is the total mass in the milling jar, and M is the mass averaged molar mass of all reactants. First, we assume that reactants are perfectly mixed at all times in the reactor vessel, that is, once material reactions in a single impact, it is perfectly mixed with the unreacted material in the vessel before the next impact. Second, we assume that no reaction is occurring outside of each impact, allowing us to treat the discrete process as a continuous one. Under the assumption of perfect mixing, the instantaneous reactant area concentration is given bywhere N is the molar mass of the reactants. Then using eqn (12) to write the rate of change of N over number of impacts τ results in eqn (16).Finally, applying separation of variables and rearranging results in eqn (17) for a first order reaction.Eqn (17) provides another important insight into ball milling reactions, in that the overall duration of the reaction is proportional to the amount of total reactant mass within the system. The relative error between the approximate and exact activation energy E_a is typically ∼3–5% in the force activated regime and up to 12% in the diffusion activated regime, based on numerical comparison between eqn (17) and the exact numerical solution. In the event that the applied impact force is large enough to lower the thermodynamic energy barrier to zero, it is interesting to note that the rate of product formation still depends on the impact force, as larger impact forces create larger impact areas. Knowledge of the impact force, the geometry and mechanical properties of the vessel and ball bearing, the average molar mass of the reactants, and the impact time of each impact allows one to find the effective kinetic rate of the reaction when monitoring rate of product formation over number of successive impacts.

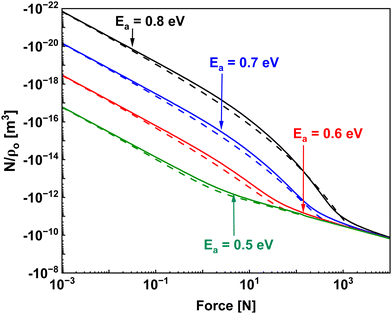
Previous works have suggested the expected dependence of the reaction rate on the milling frequency with power laws between f to f³.⁴¹ For the case where reaction rate varies linearly with frequency, this would require that the reaction is not activated by force (simply a mixing problem) and that the impact area is not a function of force. These conditions could be met for systems with very low energy barriers and very large powder sizes relative to the ball used. For the case where reaction rate varies with the cube of frequency, this would correspond to reactions where the rate only depends on the total energy imparted by an impact and not on the specific time evolution of the applied force. The incorporation of the time evolving mechanics in our model results in a rate that depends on frequency as f^1.8 (at least for first order reactions). Currently, experimental data in the literature does not have enough precision to distinguish between f^1.8 and f³, but future work investigating this relationship could provide clues as to the nature of the reaction under study and the important parameters.

Experimental setup – controlled force reactor (CFR) and Retsch MM400

The controlled force reactor allows for the measurement and control of both the maximum force and impact time of each impact within the reactor.⁴⁵Fig. 4A–D shows diagrams of the primary reactor components, where the actuator assembly reciprocates the ball bearing between the two sample stages of the sample assembly. Each sample stage is held in place by an electromagnetic force applied by the electromagnet assembly. The force applied to the sample stages transmit through to the force sensor assemblies. Once the holding force of the electromagnet is exceeded, the sample stage moves away from the ball bearing, and the opposing stage moves into contact with the opposite electromagnet for the cycle to repeat. Fig. 4B shows a photograph of the reactor. Here, a 1 horsepower Brook Crompton motor connects to a reciprocating arm, which translates the ball bearing within the reactor. The motor is controlled by L510 Teco Westinghouse variable frequency drive. A Cross-slide drill-press vise holds the sample stage sub assembly which consists of the reaction vessel, the electromagnets and force sensors. The Reaction vessel (aluminium, 1 inch ID 1.35 inches OD × 3.5 inches length) is threaded onto two electromagnets (APW Magnets, EM100-12-222). A stainless-steel sample stage attached to an aluminium threaded shaft and hex nut is inserted into the reaction vessel and contacts force sensors (Digi Key, FX1901) positioned on both sides of the reaction vessel.

Fig. 4 Mechanochemical ball mill reactor. (A) Mechanochemical reactor actuator arm and ball. (B) Sample stage assembly. (C) Top view half schematic of subassemblies (D) 3d schematic of mechanochemical ball mill reactor (E) actual picture of all components of the mechanochemical reactor. (F) Close-up view of sample stage subassembly.

Fig. 4(F) shows the schematics of the close-up view of the sample stage subassembly. Polytetrafluoroethylene O-rings are used to seal the sample stage to prevent sample spill and maintain reaction volume. A threaded shaft (6 inches) is welded to ½ inch diameter stainless steel ball and used to contact the sample stage. Power is supplied to the electromagnets using two DC source meters, which sets the holding force of the impacts in the vessel. The effect of the impact is quantified and recorded by force sensors and an NI DAQ is used for data acquisition. Commercially available Retsch MM 400 ball mill reactor is high-performance ball mixer designed for grinding, mixing and homogenizing samples. It uses the principles of friction and impacts to process and mix samples for both dry and wet application. Reactant samples are placed inside the grinding jar along with grinding balls and securely closed before grinding. The Retsch MM400 controls the force applied to the reactants indirectly by adjusting the frequency of the grinding jar oscillations which influences the kinetic energy of the grinding balls. As frequency increases, the balls are subjected to higher centrifugal forces due to the vibratory motion of the grinding jar. These higher centrifugal forces cause the balls to impact the reactants with more energy thus resulting to increased force.

Relating electromagnet voltage to holding force

We first calibrate the force sensors by applying known weights on top of the sensor and measuring the output. Then, we measure the impact force in the CFR as a function of electromagnetic voltage to determine the maximum impact force within the reactor. Fig. 5 shows the force impact profile measured at different electromagnet voltages for both sensors in the reactor. The electromagnets used here can provide consistent force between 3–40 N and provide slightly higher forces with elevated uncertainty.

Fig. 5 Force impact profile. Shaded regions are the 95% confidence intervals of the measurements measured over many impacts. (Inset) Force profile measured on the force sensor over a single impact for forces between 3–57 N.

The force impact profile in the inset of Fig. 2 shows the relationship between the applied force and the time during impact. The shape of the force-impact profile is typically a skewed Gaussian distribution due to the increase to peak force upon impact and decrease back to zero as the sample stage recedes after the holding force is exceeded. This shape is a function of material hardness, impact velocity, and geometry of colliding surfaces. Here the impact profile is negatively skewed and follows a Gaussian distribution. At a constant applied frequency of 10 Hz, the impact time per cycle from low to the peak is ∼2 ms, corresponding to an indentation depth of ∼26 μm during impact which translates to an impact velocity of 0.013 m s⁻¹.

Metal coordination complexes

Here we choose to study the formation of a metal coordination complex, which enables facile in situ reaction progression evaluation owing to its dramatic change in colour. Metal coordination complexes are usually the product of a metal ion and surrounding neutral organic molecules (ligands).⁴⁶ The formation of metal coordination complexes in solution or through mechanical grinding depends on various factors like the oxidation state, size of the metal centre and the nature of the ligand. The Irving–Williams series describes these factors for first-row transition metals. The nature of the ligand impacts stability, with basic ligands tending to donate electrons more easily and the size of the ligand affecting the complex stability due to steric effects. The stability of the complex depends on the arrangement of ligands around the metal centre, which can be modified to promote the reaction.⁴⁷

First-row transition metals tend to form six-coordinate, octahedral complexes due to electrons in their d-orbitals. Ligands like 1,10-phenanthroline and 2,2′-bipyridine can act as chelating agents due to their ability to donate multiple electrons.⁴⁸ Ligand molecules centered on the metal ion prefer an octahedral geometry, especially when the ligand to metal ratio is 3 : 1. Mechanochemical grinding with this ratio is predicted to result in an octahedral complex shape.⁴⁹ The reaction mechanism for complex formation in these systems is believed to be rate limited by the dissociation of solvent (typically H₂O) from the hydrated metal salt, and typically has a small or negligible (<0.2 eV) activation energy of formation. In order to study the effect of force on complex formation, we chose anhydrous forms of the metal salts and conducted all experiments in dry nitrogen, as trace amounts of moisture result in inconsistent reaction rates between experiments.

To study this reaction, the CFR was placed in an inert atmosphere enclosure with a continuous flow of nitrogen to ensure dry conditions during synthesis. 11 mmol (2 g) 1,10-phenanthroline (CAS number: 66-71-7) and 3.7 mmol (0.5 g) copper(II) chloride anhydrous (CAS number: 7447-39-4) with a purity of >99% from Sigma-Aldrich was weighed and placed along with one stainless steel ball in the CFR. The open section of the reaction vessel was sealed with a vinyl-nitrile glove material and fixed to the actuator arm to ensure sample containment during the reaction. Milling parameters such as frequency, impact duration and electromagnet voltage were set for each maximum force level. After the milling process was complete, the reaction product was carefully removed from the CFR onto weighing sheet and images were taken. The same procedures were repeated for the Retsch MM400 ball mill reactor with varied frequency.

Results and discussion

Particle size reduction

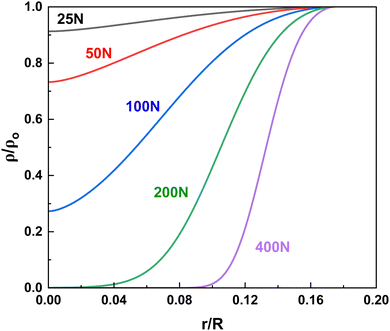
An important parameter in the theoretical framework developed above is the thickness of the particle layer within the impact. We approximate the reactant powder within the impact to be a roughly uniform packed volume with a thickness h equal to the mean diameter of the particles within the vessel. In reality, the particle sizes are typically quite polydisperse, and that distribution evolves over time as impacts within the reactor mechanically fracture the particles. To understand how particle fracture affects particle sizes throughout a milling reaction, we isolate the effect of fracture by milling NaCl particles. Here, we periodically, extracted particles from the sample, imaged them with a microscope, and each particle was sized using custom digital sizing scripts in MATLAB.

Fig. 6 shows the evolution of particle size during the grinding process, where initially the particles were predominantly 250 μm by volume. At low loads, there was an observed delay in the onset of particle fracture, indicating that it took multiple impacts to build up enough defects within the bulk crystal to initiate a complete fracture of the particle. As load was increased from 3 to 50 N, this onset time decreased, as more energy was imparted to the particles per impact at higher loads. After only 2.5 minutes of grinding, the particle size distribution appears to become stable with a maximum volume fraction centered around 100 μm. Interestingly, this mean particle size was relatively insensitive to the amount of force applied. As reactions within ball mills typically take many minutes to hours, we assume in this study that particle fracture occurs much more quickly before the majority of the reaction has occurred, and the particle sizes remain consistent through the majority of the reaction. Based on these preliminary results here, we chose a value of h = 100 μm for our reactant thickness within the impacts. Further study of unique reactant systems would provide further insight into how fracture affects reactivity.

Fig. 6 (A)–(C) Particle diameter distributions of salt particles after grinding in the controlled force reactor. After 2 min of grinding at (A) 3 N, (B) 25 N, and (C) 50 N, each distribution showed a significant size reduction down to 100 microns. The (A–C) insets show microscope images of the salt particles at multiple points during fracture. (D) and (E) 100 μm peak and 250 μm peak volume fractions shown as a function of time. The lines are simply to guide the eye, showing a clear force dependence on the onset of fracture, but a weak dependence on final particle size.

Mechanochemical reaction of anhydrous CuCl₂ and 1,10-phenanthroline

The controlled force reactor and commercial vibratory ball mill Retsch MM400 were used to study the kinetics of the mechanochemical reaction between anhydrous CuCl₂ and 1,10-phenanthroline as a function of applied force. A reaction mixture consisting of anhydrous CuCl₂, and C₁₂H₈N₂ for a total mass of 2.5 g, along with a stainless-steel ball of 12.7 mm diameter, was placed into a stainless-steel reaction jar. Fig. 7 shows the reaction progression via color intensity at different impact time for 3 N and, 30 N in the CFR and 15 Hz and, 30 Hz in the Retsch MM400. The colour evolves from pinkish brown to bright teal as applied force is increased.^50–53 Previous studies on solvent-free synthesis of metal coordination compounds show that when the ligand to metal ratio is changed from 1 : 1 to 2 : 1 and 3 : 1 there is noticeable difference in hue and color intensity.^54,55 The impact duration shown in Fig. 7 is the product of the impact time per cycle as presented earlier (Fig. 5) and the total impacts the solid reactants experience during ball milling. A MATLAB script was written to convert the images taken under natural light at each impact timestamp to the HSV colour scale for accurate colour intensity interpretation.^56,57 Here the reactions proceed from an average of 0.055 to 0.45 on the Hue colour scale. To obtain values for the change in activation volume (ΔV_a), and activation energy (E_a), we fit a non-linear least squares function to the reaction progress curves for all force levels. Reaction rate constants were then estimated from the fit and effective rate constants were calculated from impact time, material properties and the estimated reaction rate constants. To confirm that the reaction proceeded via impacts with the steel ball, we ran two controls. In the first control, we ran the reaction with only anhydrous cupric chloride and the stainless-steel ball. In the second, we ran the reaction with both reactants in the absence of the ball. For both controls, no change in colour was observed, ruling out the possibility that the reaction was driven by moisture or simple mixing.

Fig. 7 Reaction of copper(II) chloride anhydrous and 1,10-phenanthroline with color intensity measured at different force levels and impact cycles using the controlled force reactor and the Retsch MM400 ball mill reactor. Images of products taken after reaction are placed on the right next to the reaction timestamp.

By fitting the data from the CFR using eqn (17) using non-linear least squares fitting, we find that the effective activation energy, i.e., E_eff = E_a− PΔV_a for both curves was 0.61 ± 0.07 eV, where most of the uncertainty arises from uncertainty in the attempt frequency, presumed here to be 1 × 10¹³ s⁻¹. In these force ranges, the quantity PΔV_a is expected to be within the experimental uncertainty, which is unable to resolve changes in activation volume less than 10 ų. Although the small change in activation volume for this chemical system makes it difficult to calculate E_a from the experimental data, it still falls within the experimental uncertainty of E_eff. The absence of atmospheric moisture or oxygen, as well as the magnitude of the activation energy, point to a unique reaction mechanism within the mechanochemical reactor distinct from solution-based thermochemistry. Stainless steel is composed of primarily iron, alloyed with chrome and carbon, and it is known that iron leaches chlorine from cupric chloride in solution, and reports have additionally shown that dry mixtures of cupric chloride with Fe and other metals dramatically reduces the dissociation of cupric chloride in thermochemical reactions.⁵⁸ Thus, we propose a potential mechanism where the application of force between stainless steel and cupric chloride dissociates a chlorine atom, allowing the otherwise labile attachment of the ligands to the Cu centre to proceed. Additional experiments controlling for the surface chemistry could provide a valuable test of this theory under the controlled mechanical conditions within the reactor.

The data is consistent with the Retsch mill results when operated at 15 Hz and 30 Hz, where a doubling of the frequency should roughly double the average impact forces in the reactor, while only providing marginal improvements to the reaction rate, consistent with the finding that the reaction sensitivity to force is small relative to the activation barrier. Although difficult to estimate the forces occurring within the Retsch ball mill reactor, some general observations can provide useful context. First, aggressive milling at the maximum shaking frequency (30 Hz) and input power does not result in any plastic deformation of the reactor vessel when using stainless steel balls and vessel. Previous studies of impact between stainless steel bearings and flat steel walls found that the maximum contact pressure associated with plastic deformation was 1800 MPa.⁵⁹ If we presume that the impact stress must be below this value, and naively presume that the impact force is roughly proportional to the momentum, which is proportional to the frequency of shaking, then we can estimate the pressure at 15 Hz as 900 MPa. This compares surprisingly well with the effective pressure estimated in the CFR at 30 N which is 930 MPa. This provides encouraging indications that, by knowing the impact forces within a reactor, it is possible to predict chemical reaction kinetics, and compare the reactions quantitatively across a range of different reactor systems.

Future work can dramatically improve the quantitative control of individual reactions and allow for repeatability, two much needed capabilities within the chemical synthesis community that are currently lacking for mechanochemical reactions. For example, many reactive systems with multiple reaction pathways could be selectively tuned by modulating the magnitude and/or direction (normal/shear) of the applied force. Current mechanochemical systems offer little to no control over the applied force, making it difficult to explore force selectivity. Additionally, it is still quite difficult to replicate reactions using different commercial mechanochemical mills because there is no established methodology to relate things like mass of reactant, ball and vessel material and geometry, ratio of ball, reactant, and vessel volumes, and milling frequency and sweep length (to name a few!) to reaction thermodynamics and kinetics. This wide variability between experiments potentially veils the importance of other fundamental reaction mechanisms, such as the effect of air or atmospheric moisture on overall reaction rates. The CFR presented here provides evidence that the challenge of relating observed reaction rates to fundamental thermodynamics and kinetics through an understanding of the impact forces in mechanochemical reactors that have been previously believed to be hopelessly chaotic.

Conclusions

The development of a controlled force reactor and theoretical framework matching macroscale continuum contact mechanics to mechanochemical transition state theories provides quantitative, predictable, and insightful information about solid state reactivity. We find during the milling of an inert species, particle fracture occurs much faster than typical reaction rates (minutes vs. hours) and asymptotes to a particle size largely independent of the applied force, greatly simplifying equations that describe mechanochemical reactivity. We measure the activation energy of copper(II) chloride with (1,10) phenanthroline to be 0.61 ± 0.07 eV. The measured activation energy, which is larger than conventional water mediated reactivity, and smaller than direct cleavage of covalent bonds, suggest the solid surfaces during impact might play a role, such as Fe in the stainless-steel surfaces scavenging Cl from the copper chloride. We further provide evidence that the estimated impact force in a commercial ball mill provides similar reaction rates as our controlled force reactor when operated at similar forces. This work provides a novel tool to investigate the force dependence of mechanochemical reactions and provides evidence that such an analysis can be translated to many different commercial mills.

Author contributions

Author contributions to this work according to CRediT standardised contribution descriptions are as follows: EN (conceptualisation, data curation, formal analysis, investigation, methodology, visualisation, writing), SR (conceptualisation, data curation, formal analysis, investigation, methodology, visualisation) MC (conceptualisation, methodology), JF (conceptualisation, project administration, visualisation, supervision, writing), and JB (conceptualisation, funding acquisition, project administration, resources, supervision, writing).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the NSF Center for the Mechanical Control of Chemistry under grant # CHE-2023644.

Notes and references

1. J. J. Gilman, Mechanochemistry, Science, 1996, 274(5284), 65.
2. J.-L. Do and T. Friščić, Mechanochemistry: A Force of Synthesis, ACS Cent. Sci., 2017, 3(1), 13–19.
3. S. L. James and T. Friščić, Mechanochemistry, Chem. Soc. Rev., 2013, 42(18), 7494–7496.
4. J. L. Howard, Q. Cao and D. L. Browne, Mechanochemistry as an emerging tool for molecular synthesis: what can it offer?, Chem. Sci., 2018, 9(12), 3080–3094.
5. E. Boldyreva, Mechanochemistry of inorganic and organic systems: what is similar, what is different?, Chem. Soc. Rev., 2013, 42(18), 7719–7738.
6. P. Baláž, M. Achimovičová, M. Baláž, P. Billik, Z. Cherkezova-Zheleva and J. M. Criado, et al., Hallmarks of mechanochemistry: from nanoparticles to technology, Chem. Soc. Rev., 2013, 42(18), 7571–7637.
7. V. V. Boldyrev, Mechanochemistry and mechanical activation of solids, Russ. Chem. Rev., 2006, 75(3), 177.
8. S. Pagola, Outstanding Advantages, Current Drawbacks, and Significant Recent Developments in Mechanochemistry: A Perspective View, Crystals, 2023, 13(1), 124.
9. A. Krusenbaum, S. Grätz, G. T. Tigineh, L. Borchardt and J. G. Kim, The mechanochemical synthesis of polymers, Chem. Soc. Rev., 2022, 51(7), 2873–2905.
10. T. K. Achar, A. Bose and P. Mal, Mechanochemical synthesis of small organic molecules, Beilstein J. Org. Chem., 2017, 13, 1907–1931.
11. B. Szczęśniak, S. Borysiuk, J. Choma and M. Jaroniec, Mechanochemical synthesis of highly porous materials, Mater. Horiz., 2020, 7(6), 1457–1473.
12. V. V. Zyryanov, Mechanochemical synthesis of complex oxides, Russ. Chem. Rev., 2008, 77(2), 105.
13. T. Tsuzuki and P. G. McCormick, Mechanochemical synthesis of nanoparticles, J. Mater. Sci., 2004, 39(16), 5143–5146.
14. A. P. Amrute, J. De Bellis, M. Felderhoff and F. Schüth, Mechanochemical Synthesis of Catalytic Materials, Chem. – Eur. J., 2021, 27(23), 6819–6847.
15. G. A. Bowmaker, N. Chaichit, C. Pakawatchai, B. W. Skelton and A. H. White, Solvent-assisted mechanochemical synthesis of metal complexes, Dalton Trans., 2008,(22), 2926–2928.
16. S. Garcia-Manyes, J. Liang, R. Szoszkiewicz, T.-L. Kuo and J. M. Fernández, Force-activated reactivity switch in a bimolecular chemical reaction, Nat. Chem., 2009, 1(3), 236–242.
17. S. K. Lower, Atomic force microscopy to study intermolecular forces and bonds associated with bacteria. Bacterial Adhesion: Chemistry, Biol. Phys., 2011, 285–299.
18. H. Zhang and K.-K. Liu, Optical tweezers for single cells, J. R. Soc., Interface, 2008, 5(24), 671–690.
19. C. Arbore, L. Perego, M. Sergides and M. Capitanio, Probing force in living cells with optical tweezers: from single-molecule mechanics to cell mechanotransduction, Biophys. Rev., 2019, 11, 765–782.
20. K. C. Neuman and A. Nagy, Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy, Nat. Methods, 2008, 5(6), 491–505.
21. J. L. Parker, A novel method for measuring the force between two surfaces in a surface force apparatus, Langmuir, 1992, 8(2), 551–556.
22. J. Y. Wong, C. K. Park, M. Seitz and J. Israelachvili, Polymer-cushioned bilayers. II. An investigation of interaction forces and fusion using the surface forces apparatus, Biophys. J., 1999, 77(3), 1458–1468.
23. B. Briscoe, L. Fiori and E. Pelillo, Nano-indentation of polymeric surfaces, J. Phys. D: Appl. Phys., 1998, 31(19), 2395.
24. B. Medeiros, M. Medeiros, J. Fornell, J. Sort, M. Baró and A. J. Junior, Nanoindentation response of Cu–Ti based metallic glasses: Comparison between as-cast, relaxed and devitrified states, J. Non-Cryst. Solids, 2015, 425, 103–109.
25. J. Yeon, X. He, A. Martini and S. H. Kim, Mechanochemistry at solid surfaces: polymerization of adsorbed molecules by mechanical shear at tribological interfaces, ACS Appl. Mater. Interfaces, 2017, 9(3), 3142–3148.
26. S. M. Hsu and R. S. Gates, Effect of materials on tribochemical reactions between hydrocarbons and surfaces, J. Phys. D: Appl. Phys., 2006, 39(15), 3128.
27. S. Huo, P. Zhao, Z. Shi, M. Zou, X. Yang and E. Warszawik, et al., Mechanochemical bond scission for the activation of drugs, Nat. Chem., 2021, 13(2), 131–139.
28. D. Godfrey, Friction oscillations with a pin-on-disc tribometer, Tribol. Int., 1995, 28(2), 119–126.
29. R. Watanabe, H. Hashimoto and G. G. Lee, Computer simulation of milling ball motion in mechanical alloying (overview), Mater. Trans., JIM, 1995, 36(2), 102–109.
30. F. Zhang, M. Zhu and C. Wang, Parameters optimization in the planetary ball milling of nanostructured tungsten carbide/cobalt powder, Int. J. Refract. Met. Hard Mater., 2008, 26(4), 329–333.
31. D. E. Crawford, C. K. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Organic synthesis by Twin Screw Extrusion (TSE): continuous, scalable and solvent-free, Green Chem., 2017, 19(6), 1507–1518.
32. G. Ketteler, D. F. Ogletree, H. Bluhm, H. Liu, E. L. Hebenstreit and M. Salmeron, In situ spectroscopic study of the oxidation and reduction of Pd(111), J. Am. Chem. Soc., 2005, 127(51), 18269–18273.
33. K. Uzarevic, I. Halasz and T. Friscic, Real-time and in situ monitoring of mechanochemical reactions: a new playground for all chemists, J. Phys. Chem. Lett., 2015, 6(20), 4129–4140.
34. N. Cindro, M. Tireli, B. Karadeniz, T. Mrla and K. Užarević, Investigations of thermally controlled mechanochemical milling reactions, ACS Sustainable Chem. Eng., 2019, 7(19), 16301–16309.
35. Y. S. Zholdassov, L. Yuan, S. R. Garcia, R. W. Kwok, A. Boscoboinik and D. J. Valles, et al., Acceleration of Diels-Alder reactions by mechanical distortion, Science, 2023, 380(6649), 1053–1058.
36. R. Rana, R. Bavisotto, K. Hou and W. T. Tysoe, Surface chemistry at the solid–solid interface: mechanically induced reaction pathways of C8 carboxylic acid monolayers on copper, Phys. Chem. Chem. Phys., 2021, 23(33), 17803–17812.
37. J. Guo, C. Xiao, J. Gao, G. Li, H. Wu and L. Chen, et al., Interplay between counter-surface chemistry and mechanical activation in mechanochemical removal of N-faced GaN surface in humid ambient, Tribol. Int., 2021, 159, 107004.
38. R. Rana, N. Hopper, F. Sidoroff and W. T. Tysoe, Critical stresses in mechanochemical reactions, Chem. Sci., 2022, 13(43), 12651–12658.
39. T.-H. Wei, S.-H. Wu, Y.-D. Huang, W.-S. Lo, B. P. Williams and S.-Y. Chen, et al., Rapid mechanochemical encapsulation of biocatalysts into robust metal–organic frameworks, Nat. Commun., 2019, 10(1), 5002.
40. E. Colacino, M. Carta, G. Pia, A. Porcheddu, P. C. Ricci and F. Delogu, Processing and Investigation Methods in Mechanochemical Kinetics, ACS Omega, 2018, 3(8), 9196–9209.
41. M. Carta, E. Colacino, F. Delogu and A. Porcheddu, Kinetics of mechanochemical transformations, Phys. Chem. Chem. Phys., 2020, 22(26), 14489–14502.
42. L. Vugrin, M. Carta, S. Lukin, E. Meštrović, F. Delogu and I. Halasz, Mechanochemical reaction kinetics scales linearly with impact energy, Faraday Discuss., 2023, 241(0), 217–229.
43. M. Carta, F. Delogu and A. Porcheddu, A phenomenological kinetic equation for mechanochemical reactions involving highly deformable molecular solids, Phys. Chem. Chem. Phys., 2021, 23(26), 14178–14194.
44. G. I. Bell, Models for the Specific Adhesion of Cells to Cells, Science, 1978, 200(4342), 618–627.
45. J. R. Felts, J. D. Batteas, S. Raghuraman and T. Reyes, US Pat., US-10894243-B2, Method and device for quantitative control of force in mechanochemical reactions, 2021.
46. M. F. Brown, B. R. Cook and T. E. Sloan, Stereochemical notation in coordination chemistry. Mononuclear complexes, Inorg. Chem., 1975, 14(6), 1273–1278.
47. D. A. Johnson and P. G. Nelson, Factors Determining the Ligand Field Stabilization Energies of the Hexaaqua 2+ Complexes of the First Transition Series and the Irving-Williams Order, Inorg. Chem., 1995, 34(22), 5666–5671.
48. A. Bencini and V. Lippolis, 1,10-Phenanthroline: A versatile building block for the construction of ligands for various purposes, Coord. Chem. Rev., 2010, 254(17), 2096–2180.
49. W. H. Mahmoud, G. G. Mohamed and M. M. El-Dessouky, Synthesis, characterization and in vitro biological activity of mixed transition metal complexes of lornoxicam with 1,10-phenanthroline, Int. J. Electrochem. Sci., 2014, 9, 1415–1438.
50. W. W. Brandt, F. P. Dwyer and E. D. Gyarfas, Chelate complexes of 1,10-phenanthroline and related compounds, Chem. Rev., 1954, 54(6), 959–1017.
51. R. Holyer, C. Hubbard, S. Kettle and R. Wilkins, The kinetics of replacement reactions of complexes of the transition metals with 1,10-phenanthroline and 2,2′-bipyridine, Inorg. Chem., 1965, 4(7), 929–935.
52. H. Nose, Y. Chen and M. Rodgers, Energy-resolved collision-induced dissociation studies of 1,10-phenanthroline complexes of the late first-row divalent transition metal cations: determination of the third sequential binding energies, J. Phys. Chem. A, 2013, 117(20), 4316–4330.
53. D. Hewkin and R. Prince, The mechanism of octahedral complex formation by labile metal ions, Coord. Chem. Rev., 1970, 5(1), 45–73.
54. J. Cantway, Solvent-Free Synthesis of Metal Coordination Compounds Using Ball Mills, MS thesis, Western Kentucky University, 2020.
55. G. Accorsi, A. Listorti, K. Yoosaf and N. Armaroli, 1,10-Phenanthrolines: versatile building blocks for luminescent molecules, materials and metal complexes, Chem. Soc. Rev., 2009, 38(6), 1690–1700.
56. A. Zeileis, J. C. Fisher, K. Hornik, R. Ihaka, C. D. McWhite and P. Murrell, et al., Colorspace: A toolbox for manipulating and assessing colors and palettes, arXiv, 2019, preprint, arXiv:190306490 DOI:10.48550/arXiv.1903.06490.
57. M. W. Schwarz, W. B. Cowan and J. C. Beatty, An experimental comparison of RGB, YIQ, LAB, HSV, and opponent color models, ACM Trans. Graphics, 1987, 6(2), 123–158.
58. T. Fujimori, M. Takaoka, Y. Tanino, K. Oshita and S. Morisawa, A metal mixture lowers the reaction temperature of copper chloride as shown using in situ quick XAFS, J. Phys.: Conf. Ser., 2009, 190, 012183.
59. R. C. Drutowski and E. B. Mikus, The Effect of Ball Bearing Steel Structure on Rolling Friction and Contact Plastic Deformation, J. Basic Eng., 1960, 82(2), 302–306.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02549g

---