Evaluated electron scattering cross section dataset for gaseous benzene in the energy range 0.1–1000 eV†
A.
García-Abenza
 *a,
A. I.
Lozano
*a,
A. I.
Lozano
 *ab,
L.
Álvarez
a,
J. C.
Oller
*ab,
L.
Álvarez
a,
J. C.
Oller
 c,
J.
Rosado
d,
F.
Blanco
d,
P.
Limão-Vieira
c,
J.
Rosado
d,
F.
Blanco
d,
P.
Limão-Vieira
 b and
G.
García
b and
G.
García
 *ae
*ae
aInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, 28006 Madrid, Spain. E-mail: adrian.garcia.abenza@csic.es; g.garcia@csic.es
bLaboratório de Colisões Atómicas e Moleculares, CEFITEC, Departamento de Física, NOVA School of Science and Technology, Universidade NOVA de Lisboa, 2829-516 Caparica, Portugal. E-mail: ai.lozano@fct.unl.pt
cCentro de Investigaciones Energéticas Mediambientales y Tecnológicas – CIEMAT, 28040 Madrid, Spain
dDepartamento de Estructura de la Materia, Física Térmica y Electrónica e IPARCOS, Universidad Complutense de Madrid, 28040 Madrid, Spain
eCentre for Medical Radiation Physics, University of Wollongong, NSW, Australia
First published on 10th July 2023
Abstract
In this study, a complete and self-consistent cross section dataset for electron transport simulations through gaseous benzene in the energy range 0.1–1000 eV has been critically compiled. Its reliability has been evaluated through a joint experimental and computational procedure. To accomplish this, the compiled dataset has been used as input for event-by-event Monte Carlo simulations of the magnetically confined electron transport through gaseous benzene, and the simulated transmitted intensity has been compared with the experimental one for different incident energies and benzene gas pressures.
1. Introduction
Benzene, the simplest aromatic hydrocarbon, is an ideal candidate for further understanding the behaviour of more complex molecules present in living organisms that can be considered derivatives from the C6H6 ring, including heterocyclic compounds such as pyridine and pyrimidine. From a technological perspective, this chemical compound holds significant importance in petroleum industries1 playing a crucial role in various fundamental processes, such as its involvement in alkylation with ethylene to produce ethylbenzene, which serves as the primary feedstock for the production of styrene monomers.2 In addition, benzene has attracted the attention of the astrochemistry research community,3,4 both because of the difficulty in finding its means of formation5,6 and because of its role as a building block for polycyclic aromatic hydrocarbons (PAHs),7 which have been identified in the interstellar medium8,9 and are considered to play a fundamental role in carbon astrochemistry.10 As a consequence electron interactions with gaseous benzene have been extensively studied with both experimental11–19 and theoretical14,20–26 methods (see also references therein). However, to the best of our knowledge, the surveyed literature does not account for a complete cross section dataset for electron scattering from benzene.One of the main reasons for obtaining these datasets is their use as input data for event-by-event Monte Carlo simulations,27 in order to obtain further understanding of the effects induced by radiation as it passes through matter, which is of great interest in a wide range of fields such as astrochemistry, biology and the petrochemical industry. These simulations require a self-consistent data set of cross-sections as input parameters,28–30 making the compilation of these datasets a major area of research as the accuracy of the simulations is directly related to the accuracy of the input data.27 Indeed, the collection of accurate, complete, and self-consistent cross section datasets represents a challenge as there is often a lack of reliable results for some of the physical processes or, even if data are available, significant discrepancies may exist among them. Specifically, a review of the available literature for benzene in the gas-phase reveals the lack of complete vibrational and electronic excitation cross sections, as well as important discrepancies between experimental31–34 and calculated20,22,35,36 ionization cross sections.
In this study, we provide a dataset for electron scattering from benzene in the electron energy range from 0.1 to 1000 eV, to be used for modelling purposes. To achieve this, we have followed the same joint experimental and simulated procedure we successfully used in our recent studies on para-benzoquinone,37 pyridine38 and tetrahydrofuran39 molecules. Additionally, the self-consistency of our integral cross sections (ICSs) is evaluated by comparing the sum of the ICSs assigned to all the scattering channels with our recently measured total cross section (TCS).11 Furthermore, the accuracy of the proposed dataset is assessed through the comparison of the simulated and experimental energy distribution of electrons transmitted through gaseous benzene at different incident energies (15 and 90 eV) and target gas pressures (2.5 and 5.0 mTorr). For this, the present cross section dataset is used to feed our recently developed Monte Carlo code39 in order to simulate the transmitted intensity under the same conditions of the present experiment.
The remaining sections of this paper are organized as follows. The experimental and computational methods are described in Section 2. In Section 3, the compiled cross section dataset is presented. In Section 4, the accuracy of the cross section dataset is evaluated by comparing the Monte Carlo simulations with the present experimental transmitted intensity spectra, ending with a discussion about the level of agreement derived from the comparison. Finally, the attained conclusions are drawn in Section 4.
2. Experimental and computational details
2.1. Magnetically confined electron beam experiment
Transmitted electron intensity spectra through gaseous benzene were measured in a state-of-the-art magnetically confined electron beam experiment,40 including some recent improvements as recently discussed in ref. 39 and 41. The working principle of this setup is based on the axial confinement of the electron beam by applying a magnetic field of about 0.1 T. Briefly, a hairpin filament generates the primary electron beam which is passed through a nitrogen trap where it is cooled, thus reducing its initial energy spread of 500 meV down to about 100–200 meV. Subsequently, it is pulsed at the exit of the nitrogen trap and then transported to the scattering chamber, where gaseous benzene is introduced through a leak valve and maintained at a constant pressure. Before reaching an electron multiplier detector (Micro Channel Plate-MCP), the transmitted electrons traverse a retarding potential analyser (RPA) placed at the exit of the scattering chamber. Integrated transmission curves are obtained by recording the transmission intensity as a function of the retarding voltage which is driven by a voltage ramp. The whole pulsed electron gun control, retarding voltage generation, data acquisition and data analysis are managed by an appropriate custom-designed LabView computer programme. As detailed before,40 due to the magnetically confined conditions of the experiment, any scattering event is translated into momentum, and therefore kinetic energy loss in the forward scattering direction. This feature allows evaluating both the integral and differential cross sections by comparing the measured and simulated spectra.2.2. Simulation procedure
Our specifically designed event-by-event Monte Carlo code was fully built in Python39,41 and has been used to simulate the transmitted intensity of magnetically confined electrons through gaseous benzene. This code has a modular structure that allows easy implementation, revision and modification of each of the physical processes involved in any specific simulation. When simulating the tracks of charged particles, the code considers the different physical processes by sampling the step length between collisions, the interaction type, the energy loss, and the angular deflection of the scattered particles. This sampling is performed from the probability distributions derived from the input dataset comprising the total cross sections, the partial integral cross sections, the energy loss distribution functions (derived from the experimental energy loss spectra) and the angular distribution functions (derived from the differential cross sections). The confinement effect along the axial magnetic field, which is one of the main distinctive characteristics of the experimental setup, is also considered in the simulation by means of the procedure described in a previous study.39 Briefly, the axial magnetic field confines the electron trajectories to a spiral of small radius, allowing them to pass through collimators with a minimum diameter of 1.5 mm. Although the perpendicular component of the momentum rotates, its magnitude remains constant. To simulate the confining effect of the magnetic field, we assume that the electron motion between collisions is restricted to the axial direction and the effect of any scattering event implies a momentum loss in this direction.In the present study, we have generated 104 electrons with the initial energy distribution resulting from the experimental transmission measurements when no gas is introduced (0 mTorr) into the scattering chamber for the considered initial kinetic energies. This number of electrons was enough to assure the reproducibility, within 1%, of the simulated transmission intensity distribution for all the energy and gas pressure conditions considered in this study. It is also important to note that the retarding potential analyser of the present experimental setup affects only the axial component of the electrons momenta. The simulation output consists of a cumulative distribution of the number of electrons reaching the detector with kinetic energy associated with the axial component of the momentum higher than a given energy between 0 and that of the primary electron beam. This energy distribution is directly compared to the experimentally transmitted intensity obtained by varying the retarding potential within that energy range.
3. Results: input data for Monte Carlo simulation of electron transport through gaseous benzene
Our event-by-event Monte Carlo simulation procedure for modelling the transport of electrons through gaseous media requires the following input data groups: (i) a complete set of ICSs for all the relevant processes at each considered energy, (ii) the angular distribution, given by the differential cross sections (DCSs), of the scattered electron after a process occurs, and (iii) the transferred energy by the electron to the target for each collision process, which in this case is obtained from the energy loss spectra. The data selected for each one of these groups are presented in the following subsections.3.1. Total and elastic integral cross section
The proposed integral cross section data for gaseous benzene in the energy range from 0.1 to 1000 eV are shown in Fig. 1 and are also available in the ESI† (Table S1). The TCS represents the sum of all scattering processes occurring at a given incident energy; therefore, following the same criterion as in our previous studies for other polyatomic molecules,37–39,41 we considered the TCS as benchmarking data to address the self-consistency of the complete integral cross section dataset. The TCSs used for this purpose are those presented by Costa et al.11 once corrected by the experimental angular acceptance39 for energies above 2 eV, and those obtained by Gulley et al.15 down to 1 eV. Below 1 eV, as benzene is a non-polar molecule, we simply consider the sum of the elastic and vibrational CSs, as we will discuss later. The absolute uncertainty for the TCS in the whole energy range investigated is estimated to be 10%.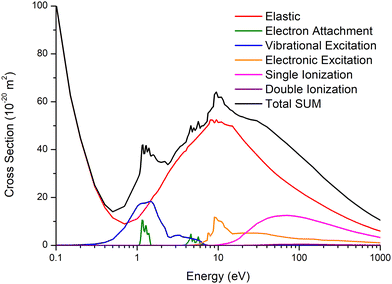 | ||
| Fig. 1 Proposed ICSs together with the TCS for electron scattering from gaseous benzene in the energy range 0.1–1000 eV. See also the legend in the figure. | ||
For the integral elastic cross sections (IECS), we proposed those in ref. 11, which include the calculated Schwinger multichannel method (SMC) with pseudopotentials for energies up to 15 eV, and those from the IAM-SCAR + I calculations for higher energies. Note that for lower energies, we have subtracted the peaks associated with the two shape resonances from the calculated IECS as they are included in the experimental TCS. A detailed discussion of both the experimental TCS and the calculations can be found in ref. 11 and 21.
3.2. Ionization cross section
Regarding the ionization cross section, important discrepancies are observed between the data available in the literature whether they were either derived from experimental31–34 or theoretical20,22,35,36 methods, as depicted in Fig. 2. Apart from considerable differences in magnitude, there is also a reasonable shift in the maximum values of the experimental and theoretical data sets. Considering the ratios between the production yields of benzene dication and parent ion to be around 5–10%,42–44 an overestimation of the experimental CS magnitude can be expected if ion current measurements are not complemented by a mass/charge analysis of the produced cations. Accordingly, the measurements obtained by Bull et al.31 and Zhou et al.34 have been corrected for such contribution (see Fig. 2). However, as the dication contribution to the ion current is within the uncertainties associated with both measurements, this correction is not significant, and these experimentally corrected values are not considered in the following discussion.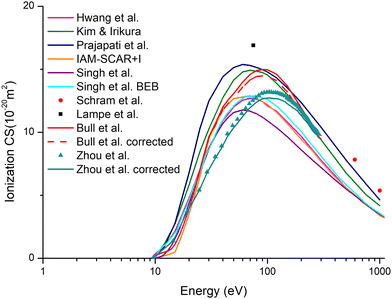 | ||
| Fig. 2 Available ionization cross section for electron scattering with benzene20,22,31–36 together with those obtained through the IAM-SCAR + I method. See also the legend in the figure. | ||
In Fig. 3, we show the available results for the ionization CS together with the TCS once the elastic contribution has been subtracted (TCS-IECS). For energies above 60 eV, the difference between TCS-IECS and the ionization CSs should be attributed to the electronic excitation CS. Based on this, an overestimation of both experimental ionization CSs is anticipated, at least, for energies above 150 eV. Concerning the calculated data, a clear overestimation of the ionization cross section is noticeable for those from Prajapati et al.20 and Kim and Irikura.36 In contrast, we suggest an underestimation of the calculated ionization cross section by Singh et al.22 This suggestion is based on the fact that if we consider their ionization CSs, the electronic excitation would remain almost constant as the energy increases, which is in contradiction with the first Born approximation. From all the above considerations, the most realistic ionization cross sections would be those in the central region, i.e., those calculated by Hwang et al.,35 those obtained through the BEB method by Singh et al.22 and those obtained through the IAM-SCAR + I method.45,46 Nevertheless, and from the impossibility to elucidate which of these data are the most reliable, we adopted as ionization cross section, the average of these with an associated uncertainty of 10%.
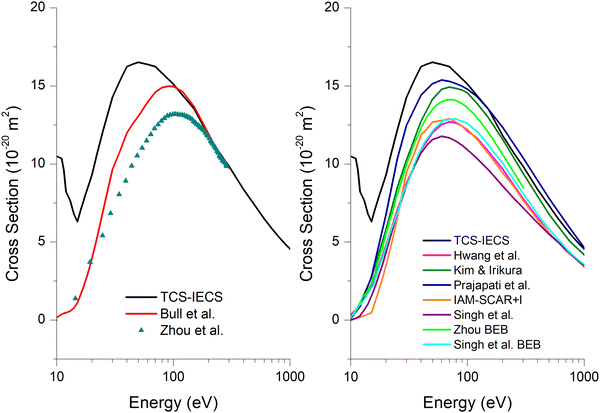 | ||
| Fig. 3 Comparison between the TCS minus elastic CS (TCS-IECS) and (left) experimental ionization cross section from ref. 31 and 34 (right) available calculated ionization cross section20,22,35,36 together with those obtained through the IAM-SCAR + I method. See also the legend in the figure. | ||
In addition, we have estimated the double ionization cross section for benzene by calculating the ratio, 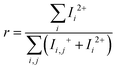 , between the observed double cation (Ii2+ = C6Hi2+) and the total cation intensities (Ii,j+ = CjHi+). For this purpose, we used two different mass spectra recorded at 70 eV.44,47 We first estimated the ratio between the parent ion Ip+ = C6H6+ and the total cation intensities
, between the observed double cation (Ii2+ = C6Hi2+) and the total cation intensities (Ii,j+ = CjHi+). For this purpose, we used two different mass spectra recorded at 70 eV.44,47 We first estimated the ratio between the parent ion Ip+ = C6H6+ and the total cation intensities 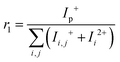 , obtaining the same value for both spectra, as expected. We then assumed that this ratio does not strongly depend on either the electron impact energy or the scattered electron angle.48,49 On the other hand, we estimated the ratio
, obtaining the same value for both spectra, as expected. We then assumed that this ratio does not strongly depend on either the electron impact energy or the scattered electron angle.48,49 On the other hand, we estimated the ratio 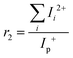 as a function of the electron energy by averaging the data from ref. 43 and 44. Finally, we calculated the ratio r = r1·r2. The estimated uncertainty of the double ionization CSs derived from this procedure is about 30%.
as a function of the electron energy by averaging the data from ref. 43 and 44. Finally, we calculated the ratio r = r1·r2. The estimated uncertainty of the double ionization CSs derived from this procedure is about 30%.
Finally, despite the cross section for the K-shell ionization of the carbon atom50 being several orders of magnitude lower than the total ionization cross section of benzenes (being therefore within the uncertainty limits of the total ionization CSs), for completeness, we have included it in our proposed integral cross section dataset for benzene (see Table S1, ESI†). We have estimated these values by assuming that each carbon atom scatters independently within the benzene molecule, which is a good approximation at such high collision energies (above 277 eV).
3.3. Excitation and attachment cross sections
Vibrational18,19,51–53 and electronic12,20,25,54–62 excitations for benzene have been widely studied. However, comprehensive and sufficiently reliable cross sections of data for these processes are not yet available to serve as valid input for Monte Carlo simulations. We have faced this challenge by using the following procedure.37–39 First, we subtracted the proposed integral elastic cross sections from the TCSs for energies above 1 eV, thus obtaining an inelastic integral cross section from which, once the ionization cross section is removed, the vibrational and electronic excitation cross sections are attained. Subsequently, both were decomposed by setting the electronic excitation threshold at 4 eV. Around this energy, we considered that the available inelastic cross section was progressively transferred between the vibrational and electronic excitation cross sections, resulting in a smooth transition between the two processes. For energies below 1 eV, we propose that the vibrational cross section to decay following the behaviour observed in similar molecules.63,64 According to this procedure, the uncertainty limits for the electronic and vibrational excitation cross section are assumed to be around 25%. Finally, for electron attachment processes, we have simply extracted the resonance peaks found in the TCS profile up to 7 eV, with the uncertainty associated with these values to be around 10%.3.4. Angular distribution functions
The elastic distribution functions have been obtained from normalized elastic DCSs, as a function of the scattering angle. The calculated cross sections were obtained with the SMC with pseudopotentials for energies up to 15 eV21 and with the IAM-SCAR + I method45,46 above that energy (available in the ESI†). Regarding the inelastic processes, despite some data on double and triple differential ionization cross sections,65 as well as for differential electronic excitation cross sections,12,25 are available in the literature, they are restricted to some scarce impact energies or reduced angular ranges. Therefore, we have obtained the angular distribution functions for all inelastic processes using a semi-empirical formula (eqn (1)), which has been proven to be accurate enough to reproduce the inelastic scattering angular distribution dependence for different molecules, including benzene.38,65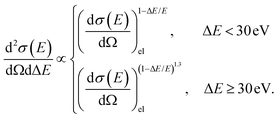 | (1) |
3.5. Energy loss distribution function
The energy loss distribution function for the considered inelastic channels (electronic, vibrational discrete excitations and ionization) has been derived from the normalised energy loss spectrum shown in Fig. 4. The double and K-shell ionization channels are not considered in our simulation due to two major reasons. First, the lack of specific energy loss or angular cross sections data for these processes, and second, both are included in the uncertainty limits of the total ionization CS. Furthermore, note that the ionization of the carbon K-shell is not accessible in the energy range considered in our simulation (up to 90 eV).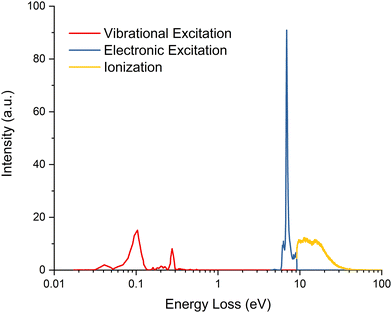 | ||
| Fig. 4 Electron energy loss distribution function associated with different inelastic channels for benzene in the energy range 1–100 eV. See also the legend in the figure. | ||
The energy loss distribution function used in this simulation is shown in Fig. 4. For energies above 4 eV, where ionization and electronic excitation processes are dominant, we used the data obtained from our electron transmission spectrometer at the electron impact energy of 90 eV.46 For lower energy losses, associated with pure vibrational excitations, we have used the data reported by Wong and Schulz.52 In previous investigations,48,49 we have shown that the energy loss spectra do not strongly depend on either the electron impact energy or the scattered electron angle. We have then used in this simulation a single energy loss distribution function, independent of the scattering angle, and whose dependence on the incident energy is restricted to cutting off the distribution at that incident energy. For electron attachment processes, the trapped electron is wiped out from the simulation and its kinetic energy is transferred to the medium. The elastically transferred energy is calculated as a function of the projectile/target mass ratio and the scattering angle. Finally, electrons with energies below 0.1 eV are considered as “thermalized” and hence removed from the simulation.
4. Discussion: evaluation of a benzene dataset for the simulation of electron transport
In this section, we evaluate the consistency and reliability of the proposed dataset through a joint experimental and simulation procedure. For this purpose, the transmitted electron intensity spectra through gaseous benzene have been measured and simulated at different electron incident energies (15 and 90 eV) and target gas pressures (2.5 and 5 mTorr). Note that we focus on energies below 100 eV since in this energy range, the strongest discrepancies are present. A noticeable advantage of this procedure is due to the magnetic confinement of the electron beam, which transforms the expected scattering angle into an energy loss in the axial direction. Hence, as our Monte Carlo code considers this experimental condition (see Section 2.2), the results given by the simulation are very sensitive to the angular distribution functions, derived from the DCSs, used as input data.In Fig. 5–8, we depict the simulated and measured electron intensity distribution of the parallel kinetic energy component for incident electron energies 15 and 90 eV at benzene gas pressures 2.5 and 5.0 mTorr, respectively. The gas pressure fluctuations during the measurements, which have been estimated to be around 10% of the nominal value, have also been considered and shown as a shaded region in all figures.
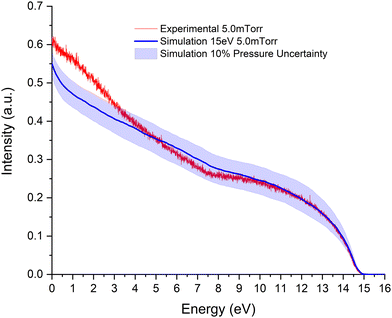 | ||
| Fig. 6 As Fig. 5, for a pressure of 5.0 mTorr. See also the legend in the figure. | ||
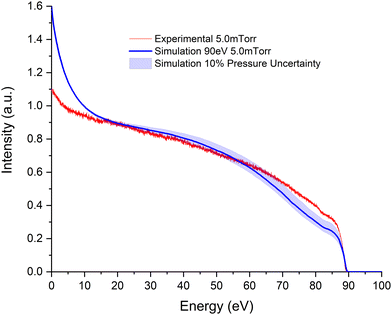 | ||
| Fig. 8 As Fig. 7, for a pressure of 5.0 mTorr. See also the legend in the figure. | ||
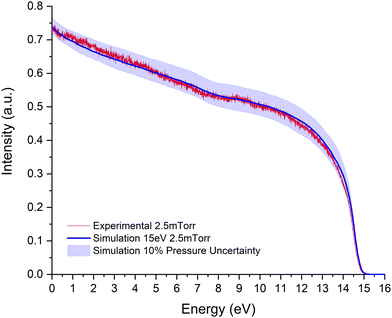
At an impact energy of 15 eV, in general, a good agreement is found between experiment and simulation for both gas pressures considered here (Fig. 5 and 6, respectively). For the lowest pressure (2.5 mTorr), the agreement is excellent, within 5%. However, for the highest pressure (5 mTorr), the experimental electron intensity corresponding to the lower energies (higher energy losses) is higher in magnitude than that given by the simulation. Due to the excellent agreement found at the lower energy losses between simulation and experiment (see Fig. 6), the origin of this discrepancy would be related to the accuracy of the integral inelastic cross sections at the lower collision energies, i.e. below 4 eV, whose effect in the spectra is magnified by the multiple collision processes taking place when the pressure increases. In particular, as this effect is more significant for energies below 4 eV, we can infer that it originated from an overestimation of the vibrational excitation cross section which in turn, within our procedure of extracting the inelastic cross section from the total cross section, means an underestimation of the elastic cross sections at these low energies.
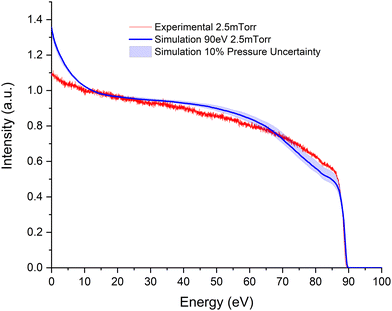
Regarding the highest impact energy (90 eV), ionization processes have significant importance allowing us to discuss the reliability of the averaged ionization CS. A general good agreement between experiment and simulation is found. However, for transmission intensities above 70 eV (see Fig. 7), the simulation does not accurately reproduce the experimental results, being the magnitude of the former lower than the latter. In contrast, below this energy, the simulation remains somewhat above the experiment. Since the electronic excitation cross section has been derived from the consistency of the summed ICSs with our benchmark TCSs, the origin of the observed disagreement in the transmission intensities above 60 eV may be related to the level of accuracy of the ionization and electronic excitation cross sections. As already mentioned, important discrepancies between the available ionization cross sections were found in the first survey of the literature.
As expected from the above discussion, the level of agreement is worse for the highest pressure (see Fig. 8). Apart from the mentioned uncertainties in the ionization cross sections, the increase of multiple scattering processes with pressure (see Table 1) enhances this discrepancy.
| 2.5 mTorr 15 eV | 5.0 mTorr 15 eV | 2.5 mTorr 90 eV | 5.0 mTorr 90 eV | |
|---|---|---|---|---|
| Elastic | 2.478 (88.4%) | 5.309 (87.7%) | 1.777 (70.2%) | 5.948 (75.1%) |
| Ionization | 0.052 (1.9%) | 0.086 (1.4%) | 0.500 (19.8%) | 1.046 (13.2%) |
| Electronic excitation | 0.221 (7.9%) | 0.435 (7.2%) | 0.173 (6.8%) | 0.467 (5.9%) |
| Vibrational excitation | 0.045 (1.6%) | 0.195 (3.2%) | 0.069 (2.7%) | 0.397 (5.0%) |
| Electron attachment | 0.007 (0.2%) | 0.030 (0.5%) | 0.011 (0.4%) | 0.059 (0.8%) |
| Total interactions | 2.729 (100%) | 6.050 (100%) | 2.530 (100%) | 8.900 (100%) |
| Deposited energy | 2.21 eV | 4.86 eV | 5.95 eV | 13.67 eV |
Finally, it can be noted (Fig. 7 and 8) that for both sets of pressures, the simulated spectra remain above the experimental ones for the lower transmitted energies. Since the transmission of the whole magnetically confined apparatus is optimized for the incident energies, for a relatively high incident energy (90 eV in this case) a loss of transmission efficiency for the lower energies can be observed.38,39,41
5. Conclusions
In the present work, we provide, for the first time, a complete and self-consistent cross section dataset for electron scattering from gaseous benzene for impact energies ranging from 0.1 to 1000 eV. These data will be useful for modelling electron transport in different scientific and technological applications. The important discrepancies between the ionization cross sections available in the literature have been critically discussed leading to a reasonable data set based on an average of different theoretical data. In addition, we have estimated the double ionization cross section of benzene by electron impact.We have also applied a joint experimental and simulated procedure to evaluate the accuracy and reliability of our proposed dataset for impact energies of up to around 100 eV. This dataset has been used as input for the simulation of the transmitted electron intensity spectra through gaseous benzene for different incident electron energies (15 and 90 eV) and gas pressures (2.5 and 5.0 mTorr). From the comparison between the experimental and simulated spectra the reliability of the input cross section data has been discussed. Despite the generally good agreement found in this comparison, some discrepancies in the higher energy spectra (90 eV) have been associated with uncertainties in the ionization cross sections and their strong influence on the derivation of other inelastic cross sections. In addition, the results for the lowest incident electron energy (15 eV) indicate an underestimation of the integral elastic cross section for energies below 4 eV.
In summary, this theoretical and experimental study reveals that further investigations to improve the accuracy of electron scattering cross sections from the benzene molecule are still needed. Particularly, there is an urgent need for more accurate electronic excitation, ionization, and elastic cross sections (especially at lower collision energies).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study has been partially supported by the Spanish Ministerio de Ciencia e Innovación (Project PID2019-104727RB-C21), Ministerio de Universidades (Project PRX21/00340), and CSIC (Project LINKA20085). AGA and LA thank MICIU and the local CAM government, respectively, for their corresponding grants within the “Garantía Juvenil” programmes. AIL and PLV acknowledge the Portuguese National Funding Agency (FCT) through research Grants CEFITEC (UIDB/00068/2020). The work is part of COST Action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS).References
- R. Nithyanandam, Y. K. Mun, T. S. Fong, T. C. Siew, O. S. Yee and N. Ismail, J. Eng. Sci. Technol., 2018, 13, 4290–4309 Search PubMed.
- H. You, W. Long and Y. Pan, The Mechanism and Kinetics for the Alkylation of Benzene with Ethylene, Pet. Sci. Technol., 2006, 24, 1079–1088 CrossRef CAS.
- J. Cernicharo, A. M. Heras, A. G. G. M. Tielens, J. R. Pardo, F. Herpin, M. Guélin and L. B. F. M. Waters, Infrared Space Observatory's Discovery of C4H2, C6H2, and Benzene in CRL 618, Astrophys. J., 2001, 546, L123–L126 CrossRef CAS.
- S. A. Sandford, M. Nuevo, P. P. Bera and T. J. Lee, Prebiotic Astrochemistry and the Formation of Molecules of Astrobiological Interest in Interstellar Clouds and Protostellar Disks, Chem. Rev., 2020, 120, 4616–4659 CrossRef CAS PubMed.
- B. M. Jones, F. Zhang, R. I. Kaiser, A. Jamal, A. M. Mebel, M. A. Cordiner and S. B. Charnley, Formation of benzene in the interstellar medium, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 452–457 CrossRef CAS PubMed.
- P. M. Woods, T. J. Millar, A. A. Zijlstra and E. Herbst, The Synthesis of Benzene in the Proto–planetary Nebula CRL 618, Astrophys. J., 2002, 574, L167–L170 CrossRef CAS.
- A. K. Lemmens, D. B. Rap, S. Brünken, W. J. Buma and A. M. Rijs, Polycyclic aromatic hydrocarbon growth in a benzene discharge explored by IR-UV action spectroscopy, Phys. Chem. Chem. Phys., 2022, 24, 14816–14824 RSC.
- B. A. McGuire, R. A. Loomis, A. M. Burkhardt, K. L. K. Lee, C. N. Shingledecker, S. B. Charnley, I. R. Cooke, M. A. Cordiner, E. Herbst, S. Kalenskii, M. A. Siebert, E. R. Willis, C. Xue, A. J. Remijan and M. C. McCarthy, Detection of two interstellar polycyclic aromatic hydrocarbons via spectral matched filtering, Science, 2021, 371, 1265–1269 CrossRef CAS PubMed.
- D. Bradley, Interstellar Polycyclic Aromatic Hydrocarbons, ChemViews, 2021, 27, 5028–5034 Search PubMed.
- C. S. Hansen, E. Peeters, J. Cami and T. W. Schmidt, Open questions on carbon-based molecules in space, Commun. Chem., 2022, 5, 94 CrossRef PubMed.
- F. Costa, L. Álvarez, A. I. Lozano, F. Blanco, J. C. Oller, A. Muñoz, A. S. Barbosa, M. H. F. Bettega, F. Ferreira da Silva, P. Limão-Vieira, R. D. White, M. J. Brunger and G. García, Experimental and theoretical analysis for total electron scattering cross sections of benzene, J. Chem. Phys., 2019, 151, 084310 CrossRef CAS PubMed.
- H. Kato, M. Hoshino, H. Tanaka, P. Limão-Vieira, O. Ingólfsson, L. Campbell and M. J. Brunger, A study of electron scattering from benzene: Excitation of the 1B1u, 3E2g, and 1E1u electronic states, J. Chem. Phys., 2011, 134, 134308 CrossRef PubMed.
- C. Makochekanwa, O. Sueoka and M. Kimura, Comparative study of electron and positron scattering from benzene (C6H6) and hexafluorobenzene (C6F6) molecules, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 032707 CrossRef.
- D. Field, J.-P. Ziesel, S. L. Lunt, R. Parthasarathy, L. Suess, S. B. Hill, F. B. Dunning, R. R. Lucchese and F. A. Gianturco, Very low-energy electron scattering from benzene: experiment and theory, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 4371–4381 CrossRef CAS.
- R. J. Gulley, S. L. Lunt, J. Ziesel and D. Field, Very low energy electron scattering from benzene and deuterated benzenes, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 2735–2751 CrossRef CAS.
- P. Mozejko, G. Kasperski, C. Szmytkowski, G. P. Karwasz, R. S. Brusa and A. Zecca, Absolute total cross section measurements for electron scattering on benzene molecules, Chem. Phys. Lett., 1996, 257, 309–313 CrossRef CAS.
- O. Sueoka, S. Mori and A. Hamada, Total cross section measurements for positrons and electron and electron scattering on benzene molecules, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 1453–1465 CrossRef CAS.
- M. Allan, Forward Electron Scattering in Benzene; Forbidden Transitions and Excitation Functions, Helv. Chim. Acta, 1982, 65, 2008–2023 CrossRef CAS.
- R. Azria and G. J. Schulz, Vibrational and triplet excitation by electron impact in benzene, J. Chem. Phys., 1975, 62, 573 CrossRef CAS.
- D. Prajapati, H. Yadav, P. C. Vinodkumar, C. Limbachiya, A. Dora and M. Vinodkumar, Computation of electron impact scattering studies on benzene, Eur. Phys. J. D, 2018, 72, 210 CrossRef.
- A. S. Barbosa and M. H. F. Bettega, Shape resonances, virtual state, and Ramsauer-Townsend minimum in the low-energy electron collisions with benzene, J. Chem. Phys., 2017, 146, 154302 CrossRef PubMed.
- S. Singh, R. Naghma, J. Kaur and B. Antony, Calculation of total and ionization cross sections for electron scattering by primary benzene compounds, J. Chem. Phys., 2016, 145, 034309 CrossRef PubMed.
- J. Sun, C. Du and Y. Liu, Total cross sections for electron scattering on polyatomic molecules—considering two different shielding effects, Phys. Lett. A, 2003, 314, 150–155 CrossRef CAS.
- F. A. Gianturco and R. R. Lucchese, One-electron resonances and computed cross sections in electron scattering from the benzene molecule, J. Chem. Phys., 1998, 108, 6144–6159 CrossRef CAS.
- A. G. Falkowski, R. F. da Costa, F. Kossoski, M. J. Brunger and M. A. P. Lima, Electronic excitation of benzene by low energy electron impact and the role of higher lying Rydberg states, Eur. Phys. J. D, 2021, 75, 310 CrossRef CAS.
- A. de, A. Cadena, A. G. Falkowski, R. Pocoroba, R. Jones, M. Mathur, J. G. Childers, A. S. Barbosa, M. H. F. Bettega, R. F. da Costa, M. A. P. Lima, F. Kossoski and M. A. Khakoo, Cross sections for elastic electron scattering by benzene at low and intermediate energies, Phys. Rev. A, 2022, 106, 062825 CrossRef.
- R. D. White, D. Cocks, G. Boyle, M. Casey, N. Garland, D. Konovalov, B. Philippa, P. Stokes, J. de Urquijo, O. González-Magaña, R. P. McEachran, S. J. Buckman, M. J. Brunger, G. Garcia, S. Dujko and Z. L. Petrovic, Electron transport in biomolecular gaseous and liquid systems: theory, experiment and self-consistent cross-sections, Plasma Sources Sci. Technol., 2018, 27, 053001 CrossRef.
- A. Verkhovtsev, A. Traore, A. Muñoz, F. Blanco and G. García, Modeling secondary particle tracks generated by intermediate- and low-energy protons in water with the Low-Energy Particle Track Simulation code, Radiat. Phys. Chem., 2017, 130, 371–378 CrossRef CAS.
- S. Incerti, G. Baldacchino, M. Bernal, R. Capra, C. Champion, Z. Francis, P. Guèye, A. Mantero, B. Mascialino, P. Moretto, P. Nieminen, C. Villagrasa and C. Zacharatou, The GEANT4-DNA Project, Int. J. Model. Simul. Sci. Comput., 2010, 01, 157–178 CrossRef.
- M. A. Bernal, M. C. Bordage, J. M. C. Brown, M. Davídková, E. Delage, Z. El Bitar, S. A. Enger, Z. Francis, S. Guatelli, V. N. Ivanchenko, M. Karamitros, I. Kyriakou, L. Maigne, S. Meylan, K. Murakami, S. Okada, H. Payno, Y. Perrot, I. Petrovic, Q. T. Pham, A. Ristic-Fira, T. Sasaki, V. Štěpán, H. N. Tran, C. Villagrasa and S. Incerti, Phys. Med., 2015, 31, 861–874 CrossRef CAS PubMed.
- J. N. Bull, J. W. L. Lee and C. Vallance, Absolute electron total ionization cross-sections: molecular analogues of DNA and RNA nucleobase and sugar constituents, Phys. Chem. Chem. Phys., 2014, 16, 10743–10752 RSC.
- B. L. Schram, M. J. van der Wiel, F. J. de Heer and H. R. Moustafa, Absolute Gross Ionization Cross Sections for Electrons (0.6–12 keV) in Hydrocarbons, J. Chem. Phys., 1966, 44, 49–54 CrossRef CAS.
- F. W. Lampe, J. L. Franklin and F. H. Field, Cross Sections for Ionization by Electrons, J. Am. Chem. Soc., 1957, 79, 6129–6132 CrossRef CAS.
- W. Zhou, L. Wilkinson, J. W. L. Lee, D. Heathcote and C. Vallance, Total electron ionization cross-sections for molecules of astrochemical interest, Mol. Phys., 2019, 117, 3066–3075 CrossRef CAS.
- W. Hwang, Y.-K. Kim and M. E. Rudd, New model for electron-impact ionization cross sections of molecules, J. Chem. Phys., 1996, 104, 2956–2966 CrossRef CAS.
- Y.-K. Kim and K. K. Irikura, Electron-impact ionization cross sections for polyatomic molecules, radicals, and ions, AIP Conf. Proc., 2001, 543, 220 CrossRef.
- A. I. Lozano, J. C. Oller, D. B. Jones, R. F. da Costa, M. T. do, N. Varella, M. H. F. Bettega, F. Ferreira da Silva, P. Limão-Vieira, M. A. P. Lima, R. D. White, M. J. Brunger, F. Blanco, A. Muñoz and G. García, Total electron scattering cross sections from para -benzoquinone in the energy range 1–200 eV, Phys. Chem. Chem. Phys., 2018, 20, 22368–22378 RSC.
- F. Costa, A. Traoré-Dubuis, L. Álvarez, A. I. Lozano, X. Ren, A. Dorn, P. Limão-Vieira, F. Blanco, J. C. Oller, A. Muñoz, A. García-Abenza, J. D. Gorfinkiel, A. S. Barbosa, M. H. F. Bettega, P. Stokes, R. D. White, D. B. Jones, M. J. Brunger and G. García, A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV, Int. J. Mol. Sci., 2020, 21, 6947 CrossRef CAS PubMed.
- A. García-Abenza, A. I. Lozano, L. Álvarez, J. C. Oller, F. Blanco, P. Stokes, R. D. White, J. de Urquijo, P. Limão-Vieira, D. B. Jones, M. J. Brunger and G. García, A complete data set for the simulation of electron transport through gaseous tetrahydrofuran in the energy range 1–100 eV, Eur. Phys. J. D, 2021, 75, 303 CrossRef.
- A. I. Lozano, J. C. Oller, K. Krupa, F. Ferreira da Silva, P. Limão-Vieira, F. Blanco, A. Muñoz, R. Colmenares and G. García, Magnetically confined electron beam system for high resolution electron transmission-beam experiments, Rev. Sci. Instrum., 2018, 89, 063105 CrossRef CAS PubMed.
- A. García-Abenza, A. I. Lozano, J. C. Oller, F. Blanco, J. D. Gorfinkiel, P. Limão-Vieira and G. García, Evaluation of Recommended Cross Sections for the Simulation of Electron Tracks in Water, Atoms, 2021, 9, 98 CrossRef.
- L. Sigaud and E. C. Montenegro, Absolute cross sections for production of molecular dications by electron impact, J. Phys. Conf. Ser., 2020, 1412, 052007 CrossRef CAS.
- W. Wolff, A. Perlin, R. R. Oliveira, F. Fantuzzi, L. H. Coutinho, F. de, A. Ribeiro and G. Hilgers, Production of Long-Lived Benzene Dications from Electron Impact in the 20–2000 eV Energy Range Combined with the Search for Global Minimum Structures, J. Phys. Chem. A, 2020, 124, 9261–9271 CrossRef CAS PubMed.
- L. Sigaud, W. Wolff and E. C. Montenegro, Strong isotopic selectivity on dication formation of benzene, Phys. Rev. A, 2022, 105, 032816 CrossRef CAS.
- F. Blanco and G. García, Screening corrections for calculation of electron scattering differential cross sections from polyatomic molecules, Phys. Lett. A, 2004, 330, 230–237 CrossRef CAS.
- A. T. Dubuis, F. Costa, F. F. da Silva, P. Limão-Vieira, J. C. Oller, F. Blanco and G. García, Total electron scattering cross section from pyridine molecules in the energy range 10–1000 eV, Chem. Phys. Lett., 2018, 699, 182–187 CrossRef CAS.
- NIST Chemistry WebBook, https://webbook.nist.gov/chemistry, available online: https://webbook.nist.gov/chemistry.
- M. C. Fuss, A. G. Sanz, A. Muñoz, T. P. D. Do, K. Nixon, M. J. Brunger, M. J. Hubin-Franskin, J. C. Oller, F. Blanco and G. García, Interaction model for electron scattering from ethylene in the energy range 1-10 000 eV, Chem. Phys. Lett., 2013, 560, 22–28 CrossRef CAS.
- F. Blanco, A. Muñoz, D. Almeida, F. Ferreira da Silva, P. Limão-Vieira, M. C. Fuss, A. G. Sanz and G. García, Modelling low energy electron and positron tracks in biologically relevant media, Eur. Phys. J. D, 2013, 67, 199 CrossRef.
- X. Llovet, C. J. Powell, F. Salvat and A. Jablonski, Cross Sections for Inner-Shell Ionization by Electron Impact, J. Phys. Chem. Ref. Data, 2014, 43, 013102 CrossRef.
- G. A. Gallup, Symmetry selection rules for vibrational excitation by resonant electron impact and a unified treatment of vibronic coupling between resonances and to the continuum: A complete symmetry analysis of vibrational excitation in benzene, J. Chem. Phys., 1993, 99, 827–835 CrossRef CAS.
- S. F. Wong and G. J. Schulz, Vibrational Excitation in Benzene by Electron Impact via Resonances: Selection Rules, Phys. Rev. Lett., 1975, 35, 1429–1432 CrossRef CAS.
- A. Herzenberg and F. Mandl, Vibrational excitation of molecules by resonance scattering of electrons, Proc. R. Soc. London, Ser. A, 1962, 270, 48–71 CAS.
- F. H. Read and G. L. Whiterod, Electron impact spectroscopy III. Calculated cross sections for inelastic scattering from benzene, Proc. Phys. Soc., 1965, 85, 71–77 CrossRef CAS.
- M. Matsuzawa, Excitation of π Electrons in Benzene by Electron Impact, J. Phys. Soc. Jpn., 1963, 18, 1473–1476 CrossRef CAS.
- H. Tanaka, M. J. Brunger, L. Campbell, H. Kato, M. Hoshino and A. R. P. Rau, Scaled plane-wave Born cross sections for atoms and molecules, Rev. Mod. Phys., 2016, 88, 025004 CrossRef.
- J. P. Doering, Electronic energy levels of benzene below 7 eV, J. Chem. Phys., 1999, 67, 4065 CrossRef.
- D. G. Wilden and J. Comer, High resolution electron impact studies of electric dipole-forbidden states of benzene, J. Phys. B: At. Mol. Phys., 1980, 13, 627–640 CrossRef CAS.
- K. C. Smyth, J. A. Schiavone and R. S. Freund, Optical emission spectra produced by electron impact excitation of benzene, J. Chem. Phys., 1974, 61, 4747–4749 CrossRef CAS.
- T. Ogawa, M. Tsuji, M. Toyoda and N. Ishibashi, Emission Spectra of Benzene, Toluene, and Xylenes by Controlled Electron Impact, Bull. Chem. Soc. Jpn., 1973, 46, 2637–2642 CrossRef CAS.
- J. P. Doering, Low-Energy Electron-Impact Study of the First, Second, and Third Triplet States of Benzene, J. Chem. Phys., 1969, 51, 2866–2870 CrossRef CAS.
- E. N. Lassettre, A. Skerbele, M. A. Dillon and K. J. Ross, High-Resolution Study of Electron-Impact Spectra at Kinetic Energies between 33 and 100 eV and Scattering Angles to 16°, J. Chem. Phys., 1968, 48, 5066–5096 CrossRef CAS.
- M. Allan, Absolute angle-differential elastic and vibrational excitation cross sections for electron collisions with tetrahydrofuran, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 3531–3544 CrossRef CAS.
- T. P. T. Do, M. Leung, M. Fuss, G. Garcia, F. Blanco, K. Ratnavelu and M. J. Brunger, Excitation of electronic states in tetrahydrofuran by electron impact, J. Chem. Phys., 2011, 134, 144302 CrossRef CAS PubMed.
- A. I. Lozano, F. Costa, X. Ren, A. Dorn, L. Álvarez, F. Blanco, P. Limão-Vieira and G. García, Double and Triple Differential Cross Sections for Single Ionization of Benzene by Electron Impact, Int. J. Mol. Sci., 2021, 22, 4601 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01908j |
| This journal is © the Owner Societies 2023 |