Effect of variations in manufacturing and material properties on the self-folding behaviors of hydrogel and elastomer bilayer structures†
Jiayu
Zhao
a,
Hesaneh
Kazemi
b,
H. Alicia
Kim
bde and
Jinhye
Bae
 *acde
*acde
aDepartment of NanoEngineering, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA. E-mail: j3bae@ucsd.edu
bStructural Engineering Department University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
cChemical Engineering Program, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
dMaterial Science and Engineering Program, University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
eSustainable Power and Energy Center (SPEC), University of California San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
First published on 2nd November 2022
Abstract
The stimuli-responsive self-folding structure is ubiquitous in nature, for instance, the mimosa folds its leaves in response to external touch or heat, and the Venus flytrap snaps shut to trap the insect inside. Thus, modeling self-folding structures has been of great interest to predict the final configuration and understand the folding mechanism. Here, we apply a simple yet effective method to predict the folding angle of the temperature-responsive nanocomposite hydrogel/elastomer bilayer structure manufactured by 3D printing, which facilitates the study of the effect of the inevitable variations in manufacturing and material properties on folding angles by comparing the simulation results with the experimentally measured folding angles. The defining feature of our method is to use thermal expansion to model the temperature-responsive nanocomposite hydrogel rather than the nonlinear field theory of diffusion model that was previously applied. The resulted difference between the simulation and experimentally measured folding angle (i.e., error) is around 5%. We anticipate that our method could provide insight into the design, control, and prediction of 3D printing of stimuli-responsive shape morphing (i.e., 4D printing) that have potential applications in soft actuators, robots, and biomedical devices.
Introduction
Self-folding structures that are activated in response to external stimuli are of interest for their applications in self-assembly,1 soft actuators,2 biomedical devices,3 and wearable devices.4 Bilayer structure is one of the most commonly used designs to create a self-folding structure.5 However, the entire bulk bilayer structure will undergo large deformation (i.e., bending) when actuated, limiting the ability to form a more complex final configuration. Inspired by the ancient art of origami, hinge-based bilayer structures can greatly simplify the design space by localizing the deformation to hinges.6 In these structures, the strain-mismatch generated between the active component of the hinge and passive component of the substrate in response to environmental cues, including temperature,7 moisture,8 light,9 and electricity,10 will result in folding of the structure.One of the most widely used active materials in self-folding structures is stimuli-responsive hydrogels, which are chemically or physically crosslinked hydrophilic polymers that can have volume expansion when immersed in water due to water absorption. This characteristic makes hydrogels a suitable choice for the active component of the hinge-based bilayer structure. Crosslinked poly(N-isopropylacrylamide) (PNIPAM) is a well-known thermo-responsive hydrogel that exhibits lower critical solution temperature (LCST) at around 32 °C,11 which is close to the physiological temperature, making it a suitable material for biomedical applications. PNIPAM hydrogels can reversibly expand or shrink their volume by controlling the temperature below or above LCST, respectively.11 Recently, we have reported the thermally responsive self-folding structure using the nanocomposite PNIPAM hydrogel as an active hinge and polydimethylsiloxane (PDMS) as a passive substrate.7 Although we experimentally showed that the folding angle can be programmed with prescribed geometric parameters (i.e., PDMS thickness and hinge width), their self-folding behavior has not yet been fully explored, especially in terms of the inevitable variations in manufacturing and measured material properties. Modeling the self-folding structures would allow us to understand and predict the folding process more accurately by providing insight into how the variations raised from material properties and the manufacturing process would influence the folding angles, therefore making it possible to precisely control the folding structure towards the programmed shape, enabling complex final configurations in various applications including soft robotics, biomedical devices, and aerospace. To date, Guo et al. demonstrated modeling of the programmable deformation of origami structures with temperature-sensitive hydrogels,12 where the nonlinear field theory of coupled diffusion and deformation is used to model the hydrogel. However, the accuracy of their model remains unknown because the predicted shape deformation was not directly compared with the experimental results. Tang et al. adopted thermal expansion to model the shape morphing of the thermal responsive magnetic hydrogel/elastomer bilayer structures. Their simulation results exhibited similar final configurations to the experimental results,13 however, they didn’t further examine the results quantitatively. Therefore, the quantitative accuracy of the simulations compared to the experimental results of the hydrogel/elastomer material systems has not been well investigated to our best knowledge.
In recent years, self-folding structures fabricated by additive manufacturing (3D printing) provoke lots of interest, because it allows for fast prototyping of various kinds of materials with spatially programmed compositions and microstructures,14–16 enabling functional materials with new properties that cannot be fabricated using conventional manufacturing techniques. Especially, 3D printing of active materials gives rise to “4D printing”, with the 4th dimension being the time, the 3D printed object can have shape transformation over time in response to external stimuli.17,18 Theoretical models have been developed for different material systems to guide the structural design and predict the final configurations.19,20 However, despite the recent advances, the understanding of 3D printing imperfection, specifically, the dimension difference between the printed and designed structures, on the shape transformation remains limited. Moreover, it has not been investigated how the folding angle would be influenced due to the inevitable variations in material properties of 3D printed samples.
In this work, we study the range of uncertainty observed in both manufacturing (i.e., 3D printing) and sample-to-sample variation in material properties on the folding angle of the nanocomposite PNIPAM hydrogel/PDMS bilayer structures. We characterize the self-folding structures fabricated by extrusion-based 3D printing, quantify their responses by thermal actuation, model their self-folding behavior and quantify the error. We employ a thermal expansion model to predict the folding angle of the hinge-based bilayer structure of nanocomposite PNIPAM hydrogel/PDMS. Compared to the previously reported nonlinear field theory for modeling the thermal responsive hydrogels/PDMS bilayer structures,12 where the energy function depends on the number of chains per polymer volume, the volume of a solvent molecule and the Boltzmann constant, our method is much simpler and computationally efficient while in good agreement with the experimental data (folding angle difference ∼ 5%). As a result, the predicted folding angles using the average Young's modulus (E) of the nanocomposite hydrogel agree reasonably well (i.e., error ∼ 5%) with the experimentally obtained values, given the variabilities associated with the 3D printing process. Furthermore, the possible reasons causing the deviation between the computational and experimental results are discussed from both manufacturing and material aspects. Examining these factors is important in enabling the facilitation of self-folding structure design and providing a deeper insight into their folding mechanism. We anticipate that our work can contribute to the fundamental understanding to support the programming and manufacturing of shape transformations produced by thermal-responsive material systems.
Experiments
Materials
N-Isopropylacrylamide (NIPAM, stabilized with 4-methoxyphenol, MW = 113.16 g mol−1) was purchased from Tokyo Chemical Industry (TCI) America. PDMS (Sylgard 184) was purchased from Dow Corning. N,N′-Methylenebisacrylamide (BIS), Irgacure 2959, and benzophenone were purchased from Sigma-Aldrich (St Louis, MO, USA). Fumed silica nanoparticles (SiNPs, CAB-O-SIL EH-5) were purchased from Cabot Corporation. Nanoclay (NC, LAPONITE®-RD) was obtained by BYK Additives & Instruments. All chemicals were used as received without further purification.Preparation of PDMS precursor inks
The PDMS precursor inks were prepared by a simple one-pot mixing process containing PDMS base/crosslinker (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), benzophenone (1.8 wt% with respect to PDMS base), and SiNPs (15 wt% with respect to PDMS base) in a Thinky planetary mixer (Thinky U. S. A., Inc.) mixing at 2000 rpm for 3 min and followed by degas process at 2000 rpm for 2 min to remove any air bubbles. Since benzophenone is in the solid state at room temperature, to achieve better mixing quality, it was heated in an oven at 70 °C for 10 min to melt before adding to the PDMS precursor. After mixing, the inks were loaded into a 10 mL syringe (Fisher Scientific) and centrifuged at 4000 rpm for 20 min to eliminate any air bubbles.
1), benzophenone (1.8 wt% with respect to PDMS base), and SiNPs (15 wt% with respect to PDMS base) in a Thinky planetary mixer (Thinky U. S. A., Inc.) mixing at 2000 rpm for 3 min and followed by degas process at 2000 rpm for 2 min to remove any air bubbles. Since benzophenone is in the solid state at room temperature, to achieve better mixing quality, it was heated in an oven at 70 °C for 10 min to melt before adding to the PDMS precursor. After mixing, the inks were loaded into a 10 mL syringe (Fisher Scientific) and centrifuged at 4000 rpm for 20 min to eliminate any air bubbles.
Preparation of NC-PNIPAM precursor inks
NIPAM solution (2 M) and BIS solution (0.13 M) were prepared by adding NIPAM and BIS to deionized (DI) water respectively and mixed in a vortex mixer until all chemicals were dissolved at room temperature. Next, NIPAM solution (10 mL, 2 M), BIS solution (120 μL, 0.13 M), Irgacure 2959 (0.04 g), and NC (1 g) were added into a 35 mL container (Thinky U. S. A., Inc.) and mixed at 2000 rpm for 5 min or longer until the solution was mixed well with no visible NC aggregates. Finally, the mixed ink was loaded into a 10 mL syringe (Fisher Scientific) and centrifuged at 2000 rpm for 10 min to eliminate any visible air bubbles.Extrusion-based 3D printing and fabrication
NC-PNIPAM/PDMS bilayer structures were fabricated by extrusion-based 3D printing using a 3D printer (Rokit, Invivo). The 10 mL syringe stored with PDMS precursor ink was placed in the extrusion carriage of the 3D printer and printed on the glass slides (75 mm × 50 mm × 1 mm) using a 20-gauge blunt tip dispensing needle (0.6 mm inner diameter). The printed PDMS substrate with a hinge structure was cured in an oven at 80 °C for 30 min. Subsequently, NC-PNIPAM precursor ink was directly printed on the hinge section of the cured PDMS substrate, the printed bilayer structure was then transferred into a homemade transparent humid box to prevent NC-PNIPAM from drying out while UV irradiation (365 nm) with the intensity of 253 mW cm−2 for 2 min and 22 s (UV source provided by Omnicure).Characterization
The rheological data were obtained using a rheometer (TA Instruments™ Discovery™ HR-30) using a 40 mm plate. The viscosity measurements were conducted using flow sweep mode with the shear rate ranging from 0.1 to 100 s−1. The storage and loss moduli were measured using oscillation mode at a frequency of 1 Hz with strain ranging from 1 to 100%. Stress–strain data was obtained using a universal testing machine (Instron Corp., Instron 5982) with a strain rate of 10 mm s−1. To prepare samples for the tensile test, the NC-PNIPAM were 3D printed to rectangular shapes (35 mm × 10 mm × 0.6 mm), and after photo-crosslinking, they were swelled or de-swelled at 22 °C or 45 °C water bath, respectively. The average values of E for each condition were calculated based on the tensile test results of 5 samples. The PDMS inks (PDMS precursor + 15 wt% SiNPs) were 3D printed to rectangular shapes (35 mm × 10 mm × 0.6 mm) and thermally cured. The average E was obtained by the tensile test of 3 samples.For calculation of the thermal expansion coefficient α of NC-PNIPAM, the NC-PNIPAM hydrogel was fabricated into a rectangular rod-like shape (35 mm × 2 mm × 0.6 mm) using 3D printing. After cross-linking, the NC-PNIPAM was first de-swelled in DI water at 45 °C for at least 48 hours to reach its equilibrium state, and the length was measured. It was then swelled in DI water at temperatures of 40.2, 38.1, 34.7, 28.6, and 22 °C, and the resulting lengths were measured, respectively. Optical micrographs were captured using an optical microscope (Keyence VHX1000).
Simulation
We applied a thermal expansion model to examine the folding angle of the hinge-based bilayer structure of NC-PNIPAM/PDMS due to its similarity with the isotropic swelling/deswelling of the temperature-responsive PNIPAM hydrogel. The thermal strain in the general form can be written as,| εT = αΔT = [(α1α2α3)]ΔT | (1) |
We also assume that the volume change of NC-PNIPAM, which is initially at 45 °C and then placed in water of 22 °C, is the result of thermal expansion only. We obtained the thermal expansion coefficients for NC-PNIPAM at multiple temperatures based on the experiment described in the previous section and by performing a curve fitting. Since NC-PNIPAM expands once cooled, all of these values are negative. Because the PDMS does not elongate once put in cooler water (i.e., 22 °C), we use α = 0 for the PDMS substrate.
We use the neo-Hookean hyperelastic model available in Abaqus,21 where the strain energy function is given by
 | (2) |
In the above expression, μ is the shear modulus, k is the bulk modulus, and Ī1 is the first strain invariant, defined as
Ī1 = trace(![[B with combining macron]](https://www.rsc.org/images/entities/b_i_char_0042_0304.gif) ) ) | (3) |
![[B with combining macron]](https://www.rsc.org/images/entities/b_i_char_0042_0304.gif) =
= ![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) ·
·![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) T denotes the deviatoric stretch matrix,
T denotes the deviatoric stretch matrix,  is the distortional component of the deformation gradient defined as
is the distortional component of the deformation gradient defined as  , and J = det(F) is the determinant of the deformation gradient. The second Piola–Kirchhoff stress S can be computed as
, and J = det(F) is the determinant of the deformation gradient. The second Piola–Kirchhoff stress S can be computed as | (4) |
The static equilibrium of the unit cell under finite deformation is given by
| R = Fext − Fint = 0 | (5) |
| r = fext − fint(u) = 0 | (6) |
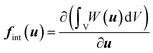 | (7) |
Results and discussion
The fabrication and synthesis of the precursor inks in detail were reported in our previous paper.7 Here, we briefly summarize this process. The hinge-based bilayer structures of the NC-PNIPAM/PDMS are fabricated by extrusion-based 3D printing, which is one of the most commonly used in additive manufacturing.23 Extrusion-based 3D printing greatly enlarges the design space for patterning viscous material (ink) into a 3D structure in a layer-by-layer manner. The printable ink should possess shear-thinning behavior to facilitate the extrusion, and solid-like behavior with storage modulus (G′) > loss modulus (G′′) to maintain the shape retention after deposition.16 We formulated both the PDMS and NC-PNIPAM precursor inks using the compositions from our previous paper,7 so that they not only meet the rheological requirements to allow the extrusion-based 3D printing, but also ensure strong adhesion between the hydrophobic PDMS and hydrophilic NC-PNIPAM with the adhesion strength greater than the fracture strength of the NC-PNIPAM hydrogel, which was 14.8 kPa.7 Specifically, the PDMS precursor ink is composed of PDMS precursor (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 base: crosslinker), benzophenone to create covalent bonding between PDMS and NC-PNIPAM, and SiNPs as the rheological modifier. It is noted that the PDMS precursor without SiNPs possesses liquid-like behavior (G′′ > G′) (Fig. 1A) and low viscosity η = 13 at 0.1 s−1(Fig. 1B). After the addition of SiNPs, the network formed between the silanol groups on the surface of SiNPs24 endows the PDMS ink with solid-like behavior as G′ (16
1 base: crosslinker), benzophenone to create covalent bonding between PDMS and NC-PNIPAM, and SiNPs as the rheological modifier. It is noted that the PDMS precursor without SiNPs possesses liquid-like behavior (G′′ > G′) (Fig. 1A) and low viscosity η = 13 at 0.1 s−1(Fig. 1B). After the addition of SiNPs, the network formed between the silanol groups on the surface of SiNPs24 endows the PDMS ink with solid-like behavior as G′ (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 Pa) > G′′ (8013 Pa) (Fig. 1A) and shear-thinning properties as η = 4052 Pa s at 0.1 s−1 and 6.6 Pa s at 100 s−1 (Fig. 1B). The NC-PNIPAM precursor ink is composed of NIPAM as a monomer, BIS as a crosslinker, Irgacure 2959 as a photoinitiator, and NC as a rheological modifier. NC is known to form a so-called “house-of-cards” structure driven by the electrostatic forces between its positively charged surfaces and negatively charged edges.25 The addition of NC transforms the PNIPAM precursor from a liquid-like fluid with low viscosity to a solid-like paste with shear-thinning properties, where G′ (7263 Pa) > G′′ (158 Pa) (Fig. 1C) and η = 7063 Pa s at 0.1 s−1 and 6.9 Pa s at 100 s−1 (Fig. 1D).
710 Pa) > G′′ (8013 Pa) (Fig. 1A) and shear-thinning properties as η = 4052 Pa s at 0.1 s−1 and 6.6 Pa s at 100 s−1 (Fig. 1B). The NC-PNIPAM precursor ink is composed of NIPAM as a monomer, BIS as a crosslinker, Irgacure 2959 as a photoinitiator, and NC as a rheological modifier. NC is known to form a so-called “house-of-cards” structure driven by the electrostatic forces between its positively charged surfaces and negatively charged edges.25 The addition of NC transforms the PNIPAM precursor from a liquid-like fluid with low viscosity to a solid-like paste with shear-thinning properties, where G′ (7263 Pa) > G′′ (158 Pa) (Fig. 1C) and η = 7063 Pa s at 0.1 s−1 and 6.9 Pa s at 100 s−1 (Fig. 1D).
The PDMS precursor ink was first printed into a cuboid (10 × 20 × 0.8 mm3) with a hinge structure in the middle (Fig. 1E(i)) and cured in an oven heated to 80 °C (Fig. 1E(ii)). In the following text, we denote the cured PDMS precursor ink as PDMS. The NC-PNIPAM precursor ink was then printed onto the hinge structure of the PDMS substrate (Fig. 1E(iii)) and photo-crosslinked by UV light (365 nm, 253 mW cm−2) for 142 s (Fig. 1E(iv)). The resulting NC-PNIPAM is a temperature-responsive nanocomposite hydrogel with reversible expansion and collapse of the PNIPAM network due to swelling and deswelling by water diffusion,26 respectively.
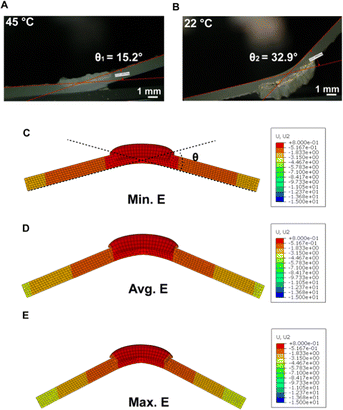
The strain-mismatch generated between active NC-PNIPAM and passive PDMS at high and low temperatures (i.e., 45 and 22 °C, respectively) will result in the folding of the structure. We note that the folding directions at 45 and 22 °C are opposite due to the deswelling and swelling of the NC-PNIPAM hinge. In the as-prepared state, the bilayer structure of NC-PNIPAM/PDMS is flat (Fig. 1F(i)). The bilayer structure was then transferred to a 45 °C water bath for 12 hours, which refers to the initial condition, to release the residual stress generated during the fabrication or curing process, resulting in a negative folding angle −θ1 at the equilibrium state due to the de-swelling of the NC-PNIPAM (Fig. 1F(ii)). After this step, the bilayer structure of NC-PNIPAM/PDMS was transferred to a 22 °C water bath for 12 hours to allow the NC-PNIPAM to reach the equilibrium state by swelling, resulting in a positive folding angle θ2 (Fig. 1F(iii)). The simulated folding angle θ is compared with the experimentally obtained total angle change θ1 + θ2 to evaluate the accuracy of the model (Fig. 1G).
To calculate the thermal expansion coefficient, we measured the length of the rectangular rod-like shape at its equilibrium state in the water of 45, 40.2, 38.1, 34.7, 28.6, and 22 °C and plotted  vs. T, in which ΔL, L0, and T refer to length change, initial length, and temperature, respectively. We performed a cubic curve fitting (norm of residuals = 0.02325, Fig. S1, ESI†) and obtained the thermal expansion coefficient of NC-PNIPAM hydrogel for temperatures of 45, 40, 35, and 30 °C as −0.0213, −0.0192, −0.0251, and −0.0392, respectively.
vs. T, in which ΔL, L0, and T refer to length change, initial length, and temperature, respectively. We performed a cubic curve fitting (norm of residuals = 0.02325, Fig. S1, ESI†) and obtained the thermal expansion coefficient of NC-PNIPAM hydrogel for temperatures of 45, 40, 35, and 30 °C as −0.0213, −0.0192, −0.0251, and −0.0392, respectively.
We performed the tensile tests to obtain E and Poisson's ratios for NC-PNIPAM and PDMS. For the temperature-responsive NC-PNIPAM, the tensile tests were conducted using samples de-swelled at 45 °C and swelled at 22 °C to match with the initial and final conditions set in the simulation, respectively. The E can be calculated from the initial slopes (0–0.1 mm mm−1 strain) of the stress–strain curves (Fig. S2, ESI†), which yield 22 ± 11, 324 ± 94, and 2000 ± 188 kPa for swelled NC-PNIPAM, de-swelled NC-PNIPAM, and PDMS, respectively. The representative plots of NC-PNIPAM and PDMS are shown in Fig. 2A and B, respectively.
 | ||
| Fig. 2 (A) Stress–strain curves of the NC-PNIPAM at swelled state (blue) and de-swelled state (red). (B) Stress–strain curve of PDMS substrate. | ||
The calculated minimum (min.), average (avg.), and maximum (max.) E of NC-PNIPAM was summarized in Table 1, in which the min. and max. E were calculated by subtracting and adding the standard deviation (SD) to the avg. E, respectively. We note that the E of NC-PNIPAM at 45 °C is higher than the one at 22 °C, which can be attributed to the collapsed network of PNIPAM due to de-swelling at a higher temperature. On the other hand, Poisson's ratio ν by definition is the negative ratio of transverse strain (εtrans) to axial strain (εaxial), which can be calculated using the initial and final dimensions of the tensile tested samples (Fig. S3, ESI†),  , in which w0 and wf are the initial and final width, respectively, and εaxial is recorded by the tensile test machine. The Poisson's ratio was calculated based on 3 samples for each condition, yielding the value of 0.14 ± 0.017 and 0.28 ± 0.015 at 45 and 22 °C for NC-PNIPAM, respectively. As for PDMS, we directly adopt Poisson's ratio of 0.49 from the literature since it is a common material.27
, in which w0 and wf are the initial and final width, respectively, and εaxial is recorded by the tensile test machine. The Poisson's ratio was calculated based on 3 samples for each condition, yielding the value of 0.14 ± 0.017 and 0.28 ± 0.015 at 45 and 22 °C for NC-PNIPAM, respectively. As for PDMS, we directly adopt Poisson's ratio of 0.49 from the literature since it is a common material.27
| Temperature | 45 °C | 22 °C |
|---|---|---|
| Avg. E (kPa) | 324 | 22 |
| Min. E (kPa) | 230 | 11 |
| Max. E (kPa) | 418 | 33 |
We performed the Finite Element Analysis (FEA) for five printed bilayer structures of NC-PNIPAM/PDMS with the same programmed dimensions, NC-PNIPAM thickness (h1) of 0.6 mm and PDMS substrate thickness (h2) of 0.4 mm. However, it turns out that each printed sample has a slightly different thickness with h1 = 0.923, 0.779, 0.828, 0.586, and 0.64 mm; h2 = 0.492, 0.473, 0.470, 0.369, and 0.394 mm, respectively (Fig. 3A–C and Fig. S4, ESI†). The differences between the target and actual thickness can be calculated as (actual thickness – target thickness)/actual thickness, yielding values ranging from −2–35%. This thickness variation is caused by the limited printing precision when the nozzle size (0.6 mm) is larger or close to the target dimension.28 To study the effect of 3D printing imperfection (i.e., inaccurate printed thickness) on the folding behavior, we compare the predicted folding angles from the FEA model created using the target thickness (h1 = 0.6 mm, h2 = 0.4 mm, Fig. 4A), defined as θt, with the predicted folding angles from the FEA models created using the actual thickness measured for the printed samples, defined as θa. Fig. 4B shows an example of the simulated sample #2 with θa = 46°. We note that the materials’ properties (i.e., averaged E and Poisson's ratio) were kept the same when running the simulations. The simulation results show that θt = 52° and θa of sample #1, #3, #4, and #5 are 46° 48°, 66°, 60°, and 62°, respectively. We denote the average of θa as ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) a. Therefore, the error caused by the manufacturing process can be calculated as (θt −
a. Therefore, the error caused by the manufacturing process can be calculated as (θt − ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) a)/
a)/![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) a, which is 4.9%. Note that the printing precision can be improved by carefully tuning the ink viscosity as well as printing parameters including printing speed, nozzle size, and layer height.
a, which is 4.9%. Note that the printing precision can be improved by carefully tuning the ink viscosity as well as printing parameters including printing speed, nozzle size, and layer height.
Next, we examine the effect of sample-to-sample variation in E on the folding angle. We created five models for each of these NC-PNIPAM/PDMS bilayer structures based on their actual dimensions after 3D printing and curing (shown in Fig. 3 and Fig. S4, ESI†). For each sample, we run the simulation using the avg., min., and max. E of NC-PNIPAM and compare the predicted folding angles with the experimental results.
The full profiles showing the folding angles of all five samples can be found in Fig. S5 (ESI†). Here, we show sample #2 as one example where the experimental folding angle for the bilayer structure of NC-PNIPAM/PDMS is −15.2° and 32.9° at equilibrium de-swelled state at 45 °C (Fig. 5A) and swelled state at 22 °C (Fig. 5B), respectively. Thus, the experimentally measured folding angle is θe = θ1 + θ2 = 15.2° + 32.9° = 48.1°. A structure with the same geometry was created in Abaqus using the min., avg., and max. E of NC-PNIPAM (Fig. 5C–E), and the predicted folding angles of 30°, 46°, and 56° are obtained, respectively. Therefore, the errors were calculated as the (θs − θe)/θe, where θs is the angle from simulation, which are −37.5%, −4.16%, and 16.67% for these three conditions, respectively. The errors for the folding angles of all five samples are summarized in Table 2, which indicates that the prediction using the average E of NC-PNIPAM gives the most accurate result, with the smallest average error of 5.8%.
| Error | Sample #1 | Sample #2 | Sample #3 | Sample #4 | Sample #5 |
|---|---|---|---|---|---|
| h 1 = 0.923 mm, h2 = 0.492 mm | h 1 = 0.779 mm, h2 = 0.473 mm | h 1 = 0.828 mm, h2 = 0.470 mm | h 1 = 0.586 mm, h2 = 0.369 mm | h 1 = 0.640 mm, h2 = 0.394 mm | |
| Min. E | −38.93% | −37.50% | −38.10% | −28.13% | −31.74% |
| Avg. E | −12.21% | −4.16% | −7.16% | 3.13% | 2.40% |
| Max. E | 6.87% | 16.67% | 12.19% | 21.88% | 19.45% |
In addition to the sample-to-sample variation, another possible reason for the discrepancy between the experimental and computational folding could be inconsistent environmental conditions (i.e., temperature and humidity) while measuring E using the tensile test method. The samples are tested at ambient conditions without temperature and humidity control, thus the temperature and water content of NC-PNIPAM may vary continuously during testing. This can lead to variations in the degree of swelling/deswelling thus mechanical properties. This effect could be more severe for the tensile test of NC-PNIPAM at the de-swelled state of 45 °C, as the temperature will drop from 45 °C to room temperature as soon as the samples are taken out from the hot water bath. We anticipate that the prediction error can be further minimized if the error range in E can be minimized from the measurements by better environmental control.
Conclusions
In summary, we have applied a simple yet effective method by utilizing the thermal expansion model to predict the folding angle of the temperature-responsive hinge-based bilayer structure of NC-PNIPAM/PDMS fabricated by 3D printing. The effect of the accuracy of 3D printed dimensions was investigated on the folding angle. The properties of the materials including thermal expansion coefficients, E, and Poisson's ratios were measured experimentally and assigned to the materials in the simulation. The simulations were conducted using the min., avg., and max. E of NC-PNIPAM, and the errors of the simulations conducted using the avg. E yield around 5%. Given the variations in the printing process and the material properties, we believe our work can lead to new perspectives on modeling shape morphing systems of temperature-responsive material-based structures, and such modeling can facilitate the design, optimization, and manufacturing of these structures that may find applications in soft actuators/robots, biomedical devices, and drug delivery systems.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Science Foundation through the University of California San Diego Materials Research Science and Engineering Center (UCSD MRSEC), grant number DMR-2011924.Notes and references
- W. Zhao, N. Li, L. Liu, J. Leng and Y. Liu, Compos. Struct., 2022, 115669, DOI:10.1016/j.compstruct.2022.115669.
- A. Kotikian, C. McMahan, C. Davidson Emily, M. Muhammad Jalilah, D. Weeks Robert, C. Daraio and A. Lewis Jennifer, Sci. Rob., 2019, 4, eaax7044 CrossRef PubMed.
- C. L. Randall, E. Gultepe and D. H. Gracias, Trends Biotechnol., 2012, 30, 138–146 CrossRef CAS.
- W. Wang, L. Yao, C.-Y. Cheng, T. Zhang, H. Atsumi, L. Wang, G. Wang, O. Anilionyte, H. Steiner, J. Ou, K. Zhou, C. Wawrousek, K. Petrecca, M. Belcher Angela, R. Karnik, X. Zhao, I. C. Wang Daniel and H. Ishii, Sci. Adv., 2017, 3, e1601984 CrossRef.
- Q. Guo, Y. Pan, J. Lin, G. Wan, B. Xu, N. Hua, C. Zheng, Y. Huang, Y. Mei, W. Chen and Z. Chen, Adv Intell. Syst., 2020, 2, 2000101 CrossRef.
- J.-H. Na, A. A. Evans, J. Bae, M. C. Chiappelli, C. D. Santangelo, R. J. Lang, T. C. Hull and R. C. Hayward, Adv. Mater., 2015, 27, 79–85 CrossRef CAS PubMed.
- J. Zhao and J. Bae, Adv. Funct. Mater., 2022, 32, 2200157 CrossRef CAS.
- J. Ryu, M. Mohammadifar, M. Tahernia, H.-I. Chun, Y. Gao and S. Choi, Adv. Mater. Technol., 2020, 5, 1901054 CrossRef CAS.
- E. Ergene, G. Liman, E. Yildiz, P. Yilgor Huri and G. Demirel, ACS Appl. Polym. Mater., 2021, 3, 3272–3277 CrossRef CAS.
- E. Palleau, D. Morales, M. D. Dickey and O. D. Velev, Nat. Commun., 2013, 4, 2257 CrossRef PubMed.
- S. Fujishige, K. Kubota and I. Ando, J. Phys. Chem., 1989, 93, 3311–3313 CrossRef CAS.
- W. Guo, M. Li and J. Zhou, Smart Mater. Struct., 2013, 22, 115028 CrossRef.
- J. Tang, Q. Yin, Y. Qiao and T. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 21194–21200 CrossRef CAS PubMed.
- Q. Chen, J. Zhao, J. Ren, L. Rong, P.-F. Cao and R. C. Advincula, Adv. Funct. Mater., 2019, 29, 1900469 CrossRef.
- M. A. Skylar-Scott, J. Mueller, C. W. Visser and J. A. Lewis, Nature, 2019, 575, 330–335 CrossRef CAS PubMed.
- R. Woo, G. Chen, J. Zhao and J. Bae, ACS Appl. Polym. Mater., 2021, 3, 3496–3503 CrossRef CAS.
- X. Kuang, D. J. Roach, J. Wu, C. M. Hamel, Z. Ding, T. Wang, M. L. Dunn and H. J. Qi, Adv. Funct. Mater., 2019, 29, 1805290 CrossRef.
- F. Momeni, S. M. N. Mehdi Hassani, X. Liu and J. Ni, Mater. Des., 2017, 122, 42–79 CrossRef CAS.
- A. S. Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Nat. Mater., 2016, 15, 413–418 CrossRef PubMed.
- Q. Ge, C. K. Dunn, H. J. Qi and M. L. Dunn, Smart Mater. Struct., 2014, 23, 094007 CrossRef.
- R. W. Ogden and E. Sternberg, J. Appl. Mech., 1985, 52, 740–741 CrossRef.
- E. Süli and D. F. Mayers, An introduction to numerical analysis, Cambridge University Press; 2003 Search PubMed.
- F. D. C. Siacor, Q. Chen, J. Y. Zhao, L. Han, A. D. Valino, E. B. Taboada, E. B. Caldona and R. C. Advincula, Addit. Manuf., 2021, 45, 102043 Search PubMed.
- J.-N. Paquien, J. Galy, J.-F. Gérard and A. Pouchelon, Colloids Surf., A, 2005, 260, 165–172 CrossRef CAS.
- A. Sheikhi, S. Afewerki, R. Oklu, A. K. Gaharwar and A. Khademhosseini, Biomater. Sci., 2018, 6, 2073–2083 RSC.
- Y. Jin, C. Liu, W. Chai, A. Compaan and Y. Huang, ACS Appl. Mater. Interfaces, 2017, 9, 17456–17465 CrossRef CAS.
- A. Müller, M. C. Wapler and U. Wallrabe, Soft Matter, 2019, 15, 779–784 RSC.
- Z. Liu, M. Zhang, B. Bhandari and Y. Wang, Trends Food Sci. Technol., 2017, 69, 83–94 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: See the supplementary material for obtaining the temperature-dependent thermal expansion coefficient of NC-PNIPAM (Fig. S1), the stress-strain curves for calculating E of NC-PNIPAM and PDMS (Fig. S2), the photographs for calculating Poisson's ratios of NC-PNIPAM at swelled and deswelled states, respectively (Fig. S3). The optical microscope images showing the dimension (Fig. S4) and folding angle (Fig. S5). See DOI: https://doi.org/10.1039/d2sm01104b |
| This journal is © The Royal Society of Chemistry 2022 |