Multi-mass velocity map imaging study of the 805 nm strong field ionization of CF₃I

Abstract

Multi-mass velocity map imaging studies of charged fragments formed by near infrared strong field ionization together with covariance map image analysis offer a new window through which to explore the dissociation dynamics of several different highly charged parent cations, simultaneously – as demonstrated here for the case of CF₃I^Z+ cations with charges Z ranging from 1 to at least 5. Previous reports that dissociative ionization of CF₃I⁺ cations yields CF₃⁺, I⁺ and CF₂I⁺ fragment ions are confirmed, and some of the CF₃⁺ fragments are deduced to undergo secondary loss of one or more neutral F atoms. Covariance map imaging confirms the dominance of CF₃⁺ + I⁺ products in the photodissociation of CF₃I²⁺ cations and, again, that some of the primary CF₃⁺ photofragments can shed one or more F atoms. Rival charge symmetric dissociation pathways to CF₂I⁺ + F⁺ and to IF⁺ + CF₂⁺ products and charge asymmetric dissociations to CF₃ + I²⁺ and CF₂I²⁺ + F products are all also identified. The findings for parent cations with Z ≥ 3 are wholly new. In all cases, the fragment recoil velocity distributions imply dissociation dynamics in which coulombic repulsive forces play a dominant role. The major photoproducts following dissociation of CF₃I³⁺ ions are CF₃⁺ and I²⁺, with lesser contributions from the rival CF₂I²⁺ + F⁺ and CF₃²⁺ + I⁺ channels. The CF₃²⁺ fragment ion images measured at higher incident intensities show a faster velocity sub-group consistent with their formation in tandem with I²⁺ fragments, from photodissociation of CF₃I⁴⁺ parent ions. The measured velocity distributions of the I³⁺ fragment ions contain features attributable to CF₃I⁵⁺ photodissociation to CF₃²⁺ + I³⁺ and the images of fragments with mass to charge (m/z) ratio ∼31 show formation of I⁴⁺ products that must originate from parent ions with yet higher Z.

---

1. Introduction

Most studies of gas phase molecular photodissociation processes employ ultraviolet or visible excitation wavelengths, and neutral systems. The dominant process following excitation with higher energy photons in the range 10–25 eV is single ionization. Excitation with yet higher energy photons leads to double ionization (formation of dications) and higher (multiple) ionization. Energy permitting, the multiple ionization will usually be accompanied by fragmentation. Some, at least, of the resulting fragments will be charged and these charged fragments can be detected with unit efficiency. Since all charged fragments arising from the same dissociation event are formed at the same time, it is possible to detect and correlate these various charged particles. Eland was in the vanguard of those developing and using coincidence methods to explore the two- and three-body fragmentation dynamics of small multiply charged cations.^1–3 Early studies of this type generally used atomic resonance lamps, then synchrotrons, as the source of the extreme ultraviolet (XUV) photons required for preparing the multiply charged parent cations,^4,5 but many such studies are now performed using ultrashort (femtosecond (fs)) laser pulses.

Removing multiple electrons from an isolated molecule causes it to undergo a Coulomb explosion (CE)^6–9 and, as noted above, many CEs are now initiated using fs laser pulses at near infrared (NIR, e.g. λ ∼ 805 nm) or short XUV wavelengths. The route to forming multiply charged cations is different in the two cases: strong field ionization (SFI) when using NIR photons, Auger cascade following removal of a core electron when using photons from an X-ray free electron laser.¹⁰ In both cases, the multiply charged cation ‘explodes’ yielding two or more proximal positively charged atomic and/or molecular fragments. Determining the fragment ion velocities and momenta using, for example, coincidence velocity map imaging (VMI) methods or VMI in conjunction with covariance analysis methods offers a route to determine static molecular structures,^10–12 to distinguish isomers^13–18 and enantiomers,¹⁹ to explore the fragmentation dynamics of multiply charged cations²⁰ and, in appropriately-designed ultrashort laser pulse pump–probe experiments, to follow the time-evolving structure and/or the fragmentation of photoexcited small molecules^21–23 and ions.^24–26

The present study explores the fragmentation dynamics of multiply charged CF₃I^Z+ ions formed by non-resonant NIR SFI. Each excitation pulse creates a distribution of multiply-charged parent cations, which display Z-dependent explosion dynamics. The hydrogen analogue, methyl iodide (CH₃I), has been a very popular molecule for testing dynamical understanding of CEs induced both by NIR^27–36 and X-ray^37,38 excitation. Our recent studies of the NIR SFI of CH₃I at three different incident intensities (I)³⁹ revealed a clear transition from ‘diatomic-like’ explosion to CH₃⁺ and I^q+ (q = 1, 2) fragments from parent ions in low Z states (Z = 2, 3), through a complex pattern of fragmentation behaviours involving loss of one or more H atoms or protons from parent ions with intermediate Z, to limiting Coulomb-driven dissociation to the constituent (charged) atoms once Z ≥ 6. Aspects of this behaviour could be rationalised by reference to complementary on-the-fly ab initio trajectory simulations,⁴⁰ but the finding that the observed velocities of the I^q+ (q > 2) fragments were consistently lower than those predicted by such calculations hinted at non-adiabatic coupling effects in the evolution from the photo-prepared parent cation to asymptotic fragments. Thorough investigation of the transition from ‘low’ to ‘high’ Z fragmentation behaviour in the case of CH₃I was hampered by the unfavourable mass ratios: the experimental mass resolution precluded mass-selective imaging of heavier fragments differing by just one mass unit, while the recoil velocities of many of the light H⁺ fragments were too high to permit detection with the available time and position sensitive detector.

Hence the motivation of the present multi-mass imaging study, wherein we present and analyse velocity map images of all major fragment ions arising in the NIR SFI of jet-cooled CF₃I molecules following excitation with ultrashort (40 fs), non-resonant NIR (805 nm) laser pulses at the same three peak intensities as used in the CH₃I studies (I ≈ 2.6 × 10¹⁴–1.3 × 10¹⁵ W cm⁻² (260–1300 TW cm⁻²)). As in the case of CH₃I, many aspects of the CE dynamics of CF₃I^Z+ cations with low Z can be understood using a 1-D picture that recognises the competition between (attractive) bonding and (repulsive) coulombic forces along the C–I bond (R_C–I). In distinction to CH₃I, however, where the loss of one (or more) light H atoms causes only a small (and generally unresolvable) change to the momentum of the CH_n^p+ (and I^q+) fragments formed in any CE and the H⁺ ions can only ever carry a q = 1 charge, F atom (or F⁺ ion) loss during the CE of CF₃I has a discernible effect on the momenta of any CF_n^p+ partner fragments and the F atoms deriving from CE of CF₃I ions in high Z states can carry multiple charges, offering the prospect of richer, further from ‘diatomic-like’ explosion dynamics.

Unravelling these dynamics can be challenging, given that there will generally be more than one route to forming any given fragment ion in a NIR SFI-induced CE experiment. The velocity (and momentum) information encoded in the fragment ion images helps in unravelling this complexity, but the present multi-mass imaging measurements carry time and position of arrival (at the detector) information for all fragments which allows identification of correlated product-pairs (or, at least in principle, even triplets) via analysis of 2-D (and 3-D) covariance-map images.^41,42 Covariance-map imaging methods have already been applied in analysing the CE of CF₃I molecules following electron impact at collision energies in the range 20–100 eV^43,44 and are here used to provide further insights into dominant two-body and some of the more probable three-body SFI-induced fragmentations of CF₃I^Z+ cations.

Analyses of the velocity-map and covariance-map images of the various fragment ions observed at the three NIR field strengths offers a new way of exploring the fragmentation dynamics of multiply-charged CF₃I^Z+ cations. The data reported here complements and extends previous discussions of the dissociative ionization of CF₃I⁺ cations,^45–47 provides additional insights into the more important fragmentation pathways available to the CF₃I²⁺ cations⁴⁸ and provides completely new information about rival fragmentation pathways for CF₃I^Z+ cations with Z ≥ 3. More generally, the present work also illustrates the multiplex advantage afforded by multi-mass imaging coupled with covariance analysis methods; just in the case of CF₃I, this single family of experiments informs on more than 15 fragmentation channels from five different CF₃I^Z+ cations.

2. Experimental

The ultrafast Ti-sapphire laser, the optical set-up, the VMI spectrometer, data collection and sample preparation methods have been described previously.³⁹ CF₃I (Aldrich, 99%) samples, exhaustively degassed by prior freeze–thaw cycling, diluted (1%) in He (Air Liquide, >99.999%), were expanded as a pulsed molecular beam and skimmed en route to the differentially-pumped interaction region, where they were intercepted mid-way between the repeller and extractor plates of a cryo-shielded ion optics assembly by the focussed (f = 30 cm), fundamental output of the Ti-sapphire laser. The resulting ions were accelerated along the time-of-flight (TOF, z) axis and passed through a field-free flight region towards a 40 mm diameter microchannel plate (MCP)/phosphor screen detector. This allowed measurement of the ion TOF spectrum and, using a second-generation Pixel Imaging Mass Spectrometry (PImMS2) sensor,^49,50 2-D (x, y) images of the ions incident at the detector within individual 25 ns time bins. A recognized limitation of the method is that multiple ions hitting the same detector region (most notably the central spot) in a narrow time interval will be under-detected. The data were analysed to provide covariance-map images between different pairs of product ions.⁵¹ Characterisation of the 805 nm laser output returned a pulse duration of 40 fs (full width half maximum) and maximum pulse intensities of ∼1300 TW cm⁻², ∼650 TW cm⁻² and ∼260 TW cm⁻² for the studies reported here.

3. Results and discussion

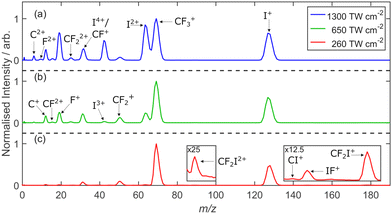
Fig. 1 shows time-of-flight (TOF) mass spectra obtained following 805 nm SFI of CF₃I at I = 260, 650 and 1300 TW cm⁻², with the detector gain gated to preclude detection of the CF₃I⁺ parent ion with mass to charge ratio, m/z 196. The spectrum recorded at lowest I is dominated by peaks with m/z 127 (I⁺) and 69 (CF₃⁺) but other weaker features at m/z 177 (CF₂I⁺), 146 (IF⁺), 139 (CI⁺), 88.5 (CF₂I²⁺), 63.5 (I²⁺), 50 (CF₂⁺), 42 (I³⁺), 34.5 (CF₃²⁺), 31.5 (CF⁺, with varying amounts of contamination from I⁴⁺), 25 (CF₂²⁺), 19 (F⁺), 15.5 (CF²⁺) and 12 (C⁺) are observed in this spectrum and/or in spectra recorded at higher I. The relative yields of the I^q+ (q = 2–4) and F⁺ peaks increase with increasing I, and weak peaks attributable to both F²⁺ and C²⁺ fragment ions also become apparent at the highest I. Clearly, the data allows the opportunity to monitor and image the different CF_n^p+ (n = 0–3, p = 1, 2) fragment ions and, by determining covariance map images, to identify correlations between the various product ions (i.e. products arising via a common fragmentation process).

Fig. 1 TOF mass spectra of the fragment ions observed following SFI of CF₃I with λ = 805 nm photons at I = (a) 1300, (b) 650 and (c) 260 TW cm⁻², displayed with a mass/charge (m/z) scale, with the regions appropriate for CF₂I⁺, IF⁺, CI⁺ and CF₂I²⁺ ions (i.e. m/z 135–185 and 85–100) shown on expanded vertical scales in the insets within panel (c). For ease of comparison, the three spectra are displayed so that the m/z 69 (CF₃⁺) peak appears with the same intensity.

3.1 Fragment velocity map and covariance map images

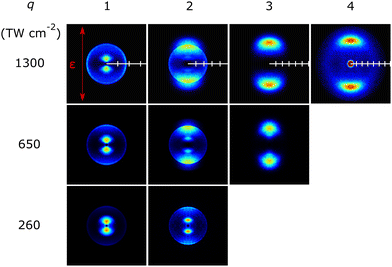
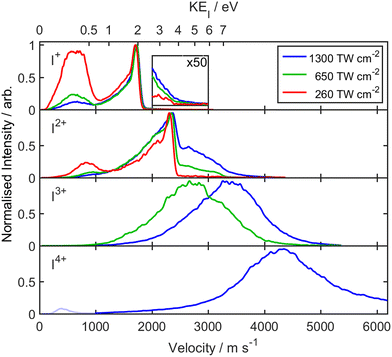
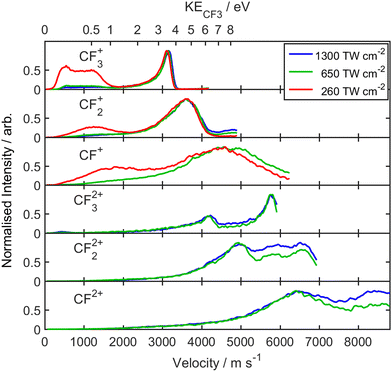
Fig. 2 shows images of the I^q+ (q = 1–4) fragment ions measured at the three different peak intensities. These and all other images presented in this work have been symmetrized prior to display. All were recorded using the highest extraction voltages that satisfied VMI conditions and are displayed on a common radial dispersion. The I⁺ images reveal two distinct product channels. One is ‘slow’ (with a small radius, r), with an anisotropic recoil velocity distribution that is preferentially aligned parallel to the ε vector of the SFI laser radiation. Throughout, an italic θ will be used to define recoil velocities relative to this ε vector. The second is associated with ‘fast’ I⁺ fragments (appearing at larger r). The recoil velocity distribution of this latter component evolves from preferentially parallel (i.e. θ ∼ 0°) to preferentially perpendicular (i.e. θ ∼ 90°) with increasing I. The relative importance of the slow and fast channels also varies with I. The I²⁺ images recorded at lower I also show a slow component but the I^q+ (q > 1) images recorded at higher I are dominated by fast products with an increasing propensity for recoil parallel to ε. Such aligned fragment recoil is typical of SFI processes wherein the interaction is strongest when ε is parallel to a particular molecular axis (here the polar C–I bond) and dissociation then occurs on a timescale much shorter than the parent rotational period.

Fig. 2 Symmetrized images of the different I^q+ fragments observed following SFI of CF₃I with linearly polarized λ = 805 nm photons at I = 1300, 650 and 260 TW cm⁻². The ticks on the white horizontal scale overlaid on each of the 1300 TW cm⁻² images indicate 1000 m s⁻¹ intervals to provide a relative comparison of achievable velocities. The orientation of the ε vector of the SFI laser radiation is shown by the double headed red arrow included in the top left panel. The central feature in the I⁴⁺ image is attributable to O₂⁺ ions from SFI of trace air impurity, and the more isotropic component at large radius in this same image is attributable to CF⁺ fragments.

These data were converted to the corresponding product velocity (v) and kinetic energy (KE) distributions using the r to v scaling determined via two-colour pump (267 nm)–SFI probe (805 nm) measurements of the CH₃ and I fragments (measured via the CH₃⁺ and I⁺ cations) from the well-documented photolysis of CH₃I⁵² at long pump–probe delays using the same ion optics conditions. Fig. 3 shows the velocity distributions P(v) determined for each I^q+ fragment at each incident I with, in each case, the CE-induced feature of most interest scaled to unit peak intensity. The KEs of these I^q+ fragments (KE_I) are shown on the upper abscissa. As before,³⁹ the reported P(v) distributions have been derived by summing signal in three adjacent time bins (i.e., a δt = 75 ns time slice) that span the centre of the TOF peak of interest rather than by Abel inverting the ‘crushed’ image. The three-time-bin analysis approach allows better m/z resolution, but the returned P(v) distributions are somewhat less resolved (though show better signal to noise ratio) – as illustrated in Fig. S1 in ESI.† Key in the present context, the P(v) distributions returned by the two approaches peak at reassuringly similar velocities.

Fig. 3 P(v) distributions for the different I^q+ (q = 1–4) fragments derived from analysis of images obtained from SFI of CF₃I with λ = 805 nm photons at I = 1300, 650 and 260 TW cm⁻² with, in each case, the strongest feature normalised to unit intensity. The corresponding KE_I scale is shown on the top x-axis. The inset in the top panel shows the weak I-dependent yield of fast I⁺ fragments, while the low velocity peak in the I⁴⁺ spectrum (shown in a fainter hue) is attributable to O₂⁺ ions from air impurity.

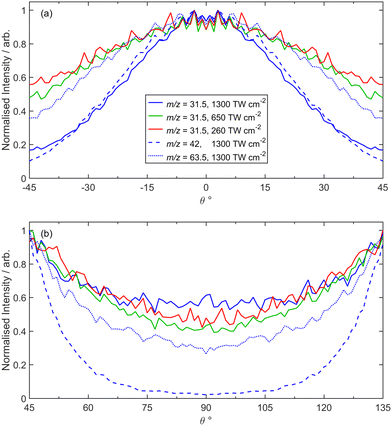
Fig. 4 shows symmetrized images of the various CF_n^p+ (n = 1–3, p = 1, 2) fragment ions measured at these same peak intensities, recorded with the same extraction voltages. The CF_n⁺ (n = 1–3) images also show both ‘slow’ and ‘fast’ components with different recoil anisotropies and I-dependent relative intensities, whereas the CF_n²⁺ (n = 1–3) images all show at least two ‘fast’ components with parallel recoil anisotropy. Note that Fig. 4 shows no image attributed to CF⁺ ions following SFI at I = 1300 TW cm⁻². Given the available TOF mass resolution, CF⁺ and I⁴⁺ (and O₂⁺) ions all appear at the same m/z. The CF⁺ and I⁴⁺ fragment ions appear at similar radius but are deduced to have clearly different angular distributions. Both recoil preferentially along the axis defined by the laser polarization vector but the I⁴⁺ fragments, which only contribute significantly at the highest incident intensity, are much more tightly aligned with ε, as shown in Fig. 5. Hence the decision to display the image of the fragment ions with m/z ∼ 31.5 recorded at I = 1300 TW cm⁻² in Fig. 2 rather than Fig. 4. [Note, the small O₂⁺ contribution (from SFI of O₂ in any trace air impurity) is also readily recognizable as a central dot in the relevant image in Fig. 2.] The P(v) distributions determined from the various CF_n^p+ images are shown in Fig. 6. The images of the F⁺, F²⁺, IF⁺, CF₂I⁺ and CF₂I²⁺ fragment ions all imply that the formation of at least a fraction of each species is also accompanied by some dynamical energy release. These images and the associated P(v) distributions are collected in, respectively, Fig. S2–S4 in the ESI.†

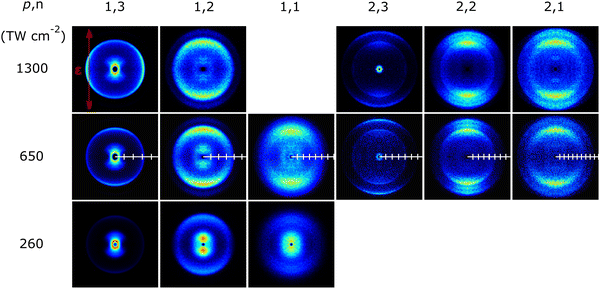Fig. 4 Symmetrized images of the CF_n^p+ (n = 1–3, p = 1, 2) fragments observed following SFI of CF₃I with λ = 805 nm photons at I = 1300, 650 and 260 TW cm⁻². The ticks on the white horizontal scale overlaid on each of the 650 TW cm⁻² images indicate 1000 m s⁻¹ intervals to provide a relative comparison of achievable velocities. The orientation of the ε vector of the SFI laser radiation is shown by the double headed red arrow in the top left panel. The m/z ∼ 31.5 (CF⁺) image recorded at the highest I is omitted as I⁴⁺ fragment ions are adjudged to be the dominant contributor (see Fig. 2).

Fig. 5 Comparisons of P(θ) distributions showing that I⁴⁺ ions make a dominant contribution to the m/z ∼ 31.5 images recorded following SFI of CF₃I with λ = 805 nm photons at the highest I. Panel (a) compares P(θ) distributions for fragments with m/z ∼ 31.5 recorded at I = 260, 650 and 1300 TW cm⁻² and with m/z ∼ 63.5 (I²⁺) and m/z ∼ 42 (I³⁺) recorded at I = 1300 TW cm⁻², plotted over the range −45° ≤ θ ≤ 45°, which highlight the similar P(θ) distributions for the I³⁺ and (assumed) I⁴⁺ fragments at high I. The corresponding P(θ) distributions over the range 45° ≤ θ ≤ 135° shown in panel (b) highlight the relatively much greater ‘perpendicular’ contribution in the m/z ∼ 31.5 (cf. m/z ∼ 42 (I³⁺)) trace, indicating that CF⁺ fragment ions also contribute to the measured recoil velocity distribution in the former case. All P(θ) distributions have been normalised to a peak intensity of unity at the θ value associated with maximum signal intensity.

Fig. 6 P(v) distributions for the CF_n^p+ (n = 1–3, p = 1, 2) fragments derived from analysis of images obtained from SFI of CF₃I with λ = 805 nm photons at I = 1300, 650 and 260 TW cm⁻² with, in each case, the strongest feature normalised to unit intensity. The corresponding KE_CF3 scale is shown on the top x-axis.

Fig. 7 presents covariance map images recorded at I = 260 TW cm⁻² that show clear correlations between the I⁺ and I²⁺ fragments with both the CF₃⁺ and CF₂⁺ fragment ions. These are displayed as (CF_n⁺, I^q+) covariance map images (i.e. where the I^q+ species has been selected as the reference ion and its velocity fixed to be vertically upwards (defined as θ = 0°, with a non-italic θ, by the red arrow in the top left hand panel, and displaying the correlated 2-D velocity distribution of the CF_n⁺ partner in the frame defined by the reference ion). Fig. S5 in the ESI† confirms that the same correlations are revealed in the corresponding (I^q+, CF_n⁺ (n = 1–3)) covariance map images. The correlations between the I^q+ (q = 1, 2) and CF₃⁺ products are tightly focussed along θ = 180°, as required by momentum conservation in the case of a two-body fragmentation, and as demonstrated in Fig. 7(c). The correlations between the CF₂⁺ (and CF⁺) and I^q+ (q = 1, 2) products are also centred along θ = 180°, but the covariance map images are more diffuse, consistent with these ion pairs arising via three- (or more-) body fragmentation processes. The tight correlation between CF₃⁺ and both I⁺ and I²⁺ products is also evident in covariance map images derived from data recorded at the higher laser intensities (Fig. S6 in the ESI†). Fig. S7 and S8 in the ESI† illustrate further detectable covariances between, respectively, CF₃²⁺ and I²⁺ fragment ions in images recorded at I = 650 TW cm⁻², and between IF⁺ and CF₂⁺ and between CF₂I⁺ and F⁺ ions fragment ions in images recorded at I = 260 TW cm⁻².

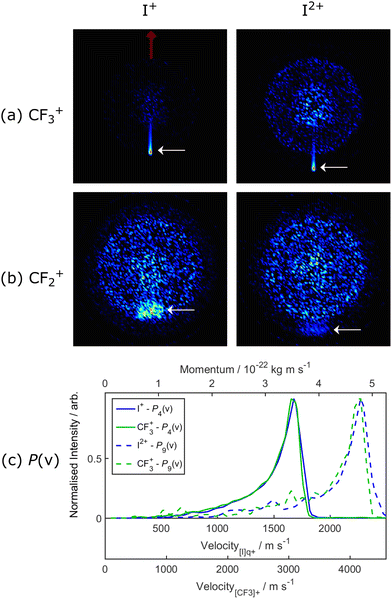Fig. 7 Covariance map images from the I = 260 TW cm⁻² data from SFI of CF₃I, selecting I⁺ (left column) and I²⁺ (right hand column) as the reference ion, and fixing the respective velocity to be vertically upwards (as indicated by the red arrow in the top left hand plot), and displaying the correlated 2-D velocity distributions of the (a) CF₃⁺ and (b) CF₂⁺ counter-fragments in the frame of the reference ion. The covariance signal of interest in each case is bounded by dashed white lines. Panel (c) illustrates the momentum matching between the product pairs from dissociation channels (4) and (11), with each P(v) distribution plotted so that the peak signal is displayed with unit intensity.

3.2 Fragmentation channels

These data are now discussed from the perspective of the CE dynamics of CF₃I^Z+ ions, in order of increasing Z.

Z = 1. The adiabatic first ionization energy (IE_ad) of CF₃I is 10.37 eV⁵³ and the separation between the ground (X²E_3/2) and spin–orbit excited (X²E_1/2) state of the ground state cation is ∼0.64 eV.⁵⁴ Asher and Ruscic⁴⁵ used photoionization mass spectrometry methods to establish the 0 K appearance threshold energy, E, for the dissociative ionization (DI) process

CF₃I + hν → CF₃⁺ + I, E = 11.384 eV (1)

and also reported wavelength dependent yield curves for I⁺ and CF₂I⁺ fragments arising via the rival DI processes

CF₃I + hν → CF₃ + I⁺, E = 12.80 eV (2)

CF₃I + hν → CF₂I⁺ + F, E = 13.40 eV. (3)

The quoted threshold energies for processes (2) and (3) are from, respectively, a Hess law cycle using the best available enthalpies of formation⁵⁵ and from Powis et al.⁴⁶ For convenience, these and other relevant threshold energies for processes are collected in Tables S1 and S2 of the ESI,† while Table S3 (ESI†) provides a summary of all fragmentation channels identified in the present work. One-photon photoelectron–photoion coincidence studies⁴⁶ and VMI studies of the visible photodissociation of state-selected CF₃I⁺(X) ions⁴⁷ have provided further insights into the fragmentation dynamics of electronically excited (A²A₁) state CF₃I⁺ ions via processes (1) and (2).

The present data show signatures of all three of these DI processes, most clearly in the images recorded at low intensity (I = 260 TW cm⁻²). The I⁺ image (Fig. 2) shows a ‘slow’ feature with parallel recoil anisotropy. The breadth of the P(v) distribution of these I⁺ fragments (which spans the range ∼400 < v < 900 m s⁻¹ though, given the previously noted under-detection of on-axis fragments, this distribution may well extend down to zero velocity) may indicate DI from SFI-produced parent ions in a range of vibronic states, and/or a spread of internal energies in the neutral CF₃ partner fragments, and/or that the SFI process yields I⁺ products in all three ³P_J (J = 0–2) spin–orbit states.

The P(v) distribution for the CF₃⁺ fragments (Fig. 6) shows a double humped feature spanning the range ∼300 < v < 1500 m s⁻¹ that is plausibly attributable to branching into ground (²P_3/2) and spin–orbit excited (²P_1/2) I atoms in DI process (1) – as proposed in previous studies of the DI of CF₃I⁺ cations in, respectively, the X and A electronic states.^46,47 Again, we caution that under-detection issues on axis mean that we cannot be certain that this distribution does not extend down to zero velocity. Higher excited states of CF₃I⁺ have been identified in one photon excitation studies⁴⁶ and will likely be populated in the present SFI environment. The fragmentation behaviour of these higher excited states has not been characterised in any detail, but the similarities between the ‘slow’ (small r) features in the CF₃⁺, CF₂⁺ and CF⁺ images suggests that some of the primary CF₃⁺ fragments are formed with sufficient excitation that they decay further, by sequential loss of one (or two) neutral F atoms.

CF₂I⁺ fragments are also observed, with a small relative yield (cf. CF₃⁺, Fig. 1) and a P(v) distribution that peaks at low velocity but also shows a second, more clearly anisotropic component at larger v that grows in relative importance with increasing I (Fig. S3, ESI†). We first focus on the low velocity component, again noting that the ‘hole’ in the centre of the image may reflect known under-detection issues and lead to a somewhat exaggerated mean recoil velocity for this yield of slow CF₂I⁺ fragments. Following Powis et al.,⁴⁶ it is likely that these ions arise via near-threshold autoionization (process (3)). The form of the kinetic energy distribution is also reminiscent of that found for the CF₂I⁺ fragments arising in the dissociative electron ionization of CF₃I using incident electron energies throughout the range 20–80 eV.⁴³ We recognise that secondary decay of internally excited CF₂I⁺ fragments could also contribute to the observed yield of ‘slow’ CF₂⁺ fragments and, conceivably, to the observed yield of IF⁺ products, but note that covariance map image analysis also demonstrates that Z = 2 parent ions contribute to the yields of these fragment ions (see below).

Z = 2. Eland et al.⁴⁸ reported high level electronic structure calculations for the CF₃I²⁺ cation and studies of the fragmentation dynamics of these dications when formed by single photon XUV excitation of CF₃I neutrals at photon energies of 40.81 and 48.37 eV. Consistent with that work, the velocity map images and the P(v) distributions of the I⁺ and CF₃⁺ fragments resulting from SFI (Fig. 2–4 and 6) are dominated by features peaking at, respectively, ∼1700 and ∼3100 m s⁻¹. The momenta of these two fragments match, and their correlation is confirmed by the associated covariance map images (Fig. 7). These fragments are attributable to the dissociation process

CF₃I²⁺ → CF₃⁺ + I⁺, (4)

for which the thermochemical threshold (relative to the ground state neutral) is E = 21.84 eV.⁵⁵

Both fragments display very similar (I-dependent) recoil anisotropies, which evolve from preferential parallel to preferential perpendicular recoil with increasing I (Fig. 4). Such observations serve as reminders that the fragmentation of CF₃I²⁺ cations is still far from the pure Coulomb limit. The valence bonding forces are sufficient to sustain several diabatically bound states of the CF₃I²⁺ cation,⁴⁸ with symmetries that can be accessed by parallel or perpendicular transitions from the ground state. The present data suggest that the latter gain in relative importance at higher I. As also noted in our recent SFI studies of CH₃I,³⁹ the P(v) distributions of the fragments arising from the two-body dissociation process (4) are narrow. Expressed in terms of total kinetic energy release (TKER) derived from the ‘sliced’ image data following Abel inversion (see Fig. S1, ESI†), the CF₃⁺ + I⁺ products display a TKER of ∼5.7 eV with a full width half maximum of only ∼0.6 eV. The earlier double photoionization study at 40.8 eV photon energy identified a similarly narrow TKER distribution for the CF₃⁺ + I⁺ products from dissociation of the CF₃I²⁺ cation.⁴⁸ These energy widths are comparable to the spin–orbit splitting in the I⁺ cation, and less than half that of an 805 nm photon as used in the present study. Both experiments imply that a near-constant amount of the available energy is released as product translation, i.e. that more internally excited CF₃I²⁺ parent cations must dissociate to correspondingly more internally excited CF₃⁺ (and/or I⁺) products.

Weaker CF₂⁺, CF⁺ and even C⁺ fragment ion signals are evident in the TOF mass spectrum (Fig. 1). As Fig. 4 and 6 show, the associated images show an annular ring reminiscent of that seen for the CF₃⁺ fragments but, with decreasing F-content, the peak in the associated P(v) distribution broadens and its centre of gravity shifts to higher velocity. The (CF₂⁺, I⁺) covariance map image shown in Fig. 7 confirms a correlation between the I⁺ and CF₂⁺ ions and, as in the case of the CF₃⁺ products from DI process (1), it is logical to attribute these CF₂⁺ ions to the dissociation of Z = 2 parent ions formed with sufficient internal energy that the resulting CF₃⁺ fragments (formed via process (4)) themselves have sufficient internal energy to dissociate further, by losing one (or more) F atoms to yield eventual CF₂⁺, CF⁺ and even C⁺ fragments, i.e.

CF₃⁺ → CF₂⁺ + F → CF⁺ + 2F → C⁺ + 3F, (5)

as deduced also in covariance analyses of the I⁺, CF₂⁺ and CF⁺ fragments arising in the electron impact induced CE of CF₃I²⁺ cations.⁴⁴ Such a view is further confirmed by the correlations evident in the (I⁺, CF_n⁺ (n = 1–3)) covariance map images shown in Fig. S5 (ESI†). This description envisages successive C–I and C–F bond fissions but, as the excitation energy and the energy transferred upon ionization both increase, the rates of the ‘primary’ (4) and ‘secondary’ (5) processes will also both increase and the distinction between step-wise dissociation and a concerted mechanistic description is likely to blur. Indeed, the finding that the peak of the respective P(v) distributions shifts to higher velocity as the F-content decreases (Fig. 6) would imply that F atom loss in most of the more-than-two-body dissociations occurs whilst the eventual CF_n⁺ and I⁺ fragments are sufficiently proximal that their respective velocities are sensitive to the coulombic repulsion. Such could offer one explanation for the increased parallel recoil anisotropy evident in the CF₂⁺, CF⁺ and C⁺ images recorded at higher I.

Eland et al.⁴⁸ noted the operation of several rival fragmentation pathways for Z = 2 parent ions. One is process (6):

CF₃I²⁺ → CF₂I⁺ + F⁺, (6)

with a calculated thermochemical threshold energy E = 31.8 eV (relative to the ground state neutral).^46,56 As noted previously, the ion TOF mass spectrum (Fig. 1) shows a peak at m/z 177 that confirms CF₂I⁺ fragment ion formation in the present SFI experiments. The major part of the P(v) distribution derived from the CF₂I⁺ images peaks at low v (Fig. S3, ESI†), which we associate with the DI process (3). But the CF₂I⁺ images recorded at higher I show a second, faster component, with an anisotropic recoil distribution, consistent with a contribution from the rival C–F bond fission process (6) at higher SFI intensities. The operation of this channel is confirmed by the (CF₂I⁺, F⁺) covariance map image shown in Fig. S8 (ESI†), which also illustrates the participation of another, hitherto unrecognised, fragmentation pathway for Z = 2 parent cations, namely:

CF₃I²⁺ → IF⁺ + CF₂⁺. (7)

The TOF mass spectrum recorded at I = 260 TW cm⁻² (Fig. 1) shows a clear peak at m/z ∼ 88, attributable to CF₂I²⁺ fragment ions. The associated fragment ion image (Fig. S4, ESI†) is small, with a dominant slow velocity component consistent with the rival charge-asymmetric dissociation process

CF₃I²⁺ → CF₂I²⁺ + F (8)

identified in the earlier one photon, double ionization study.⁴⁸ The I²⁺ fragment ion image and the P(v) distribution derived therefrom (Fig. 2 and 3) show a feature peaking at v ∼ 800 m s⁻¹, with parallel recoil anisotropy, which we attribute to another rival charge-asymmetric fragmentation channel

CF₃I²⁺ → CF₃ + I²⁺. (9)

This process, which was also recognized in the earlier electronic structure calculations but not identified in the accompanying TOF photoelectron–photoelectron–photoion–photoion coincidence studies,⁴⁸ has a thermochemical threshold (again relative to the ground state neutral) of E = 31.94 eV.^55,56

The observation of CF₃²⁺ cations with m/z ∼ 34.5 in the TOF mass spectrum (Fig. 1) and the associated ion images (Fig. 4) confirms the intrinsic stability of this dication,^57,58 but the absence of any slow feature in the CF₃²⁺ (or other CF_n²⁺) images tends to rule out any role in the present experiments for the third possible charge asymmetric dissociation process

CF₃I²⁺ → CF₃²⁺ + I, (10)

the threshold energy for which (relative to the ground state neutral) can be estimated as E ∼ 38 eV given an energy of the CF₃⁺ → CF₃²⁺ ionization process in the range 26.3–26.8 eV.^57,58

Z = 3. The very localised feature in the θ = 180° direction in the (CF₃⁺, I²⁺) covariance map image (Fig. 7) is clear evidence that the

CF₃I³⁺ → CF₃⁺ + I²⁺ (11)

two-body dissociation channel is active, even at I = 260 TW cm⁻². This channel is responsible for the dominant feature in the I²⁺ image (Fig. 2), peaking at v ∼ 2300 m s⁻¹. Momentum matching requires that the CF₃⁺ partner fragments must have v ∼ 4300 m s⁻¹ which, as Fig. 4 and 6 show, fall at the edge of the available detector and are thus likely to be grossly under-detected in the present study. The (CF₂⁺, I²⁺) covariance map images hint at more diffuse correlations between these fragment ion pairs also and, as with CF₃⁺ fragments formed by dissociation of CF₃I²⁺ parents, it is likely that many of the emergent CF₃⁺ fragments in process (11) lose further F atoms via process (5).

Notwithstanding the weakness of the m/z ∼ 34.5 (CF₃²⁺) peak in the TOF mass spectrum (Fig. 1), well-resolved velocity map images of the CF₃²⁺ fragment ions were readily obtainable at I = 650 and 1300 TW cm⁻² (Fig. 4). These show at least two velocity sub-groups, exhibiting parallel recoil anisotropy. The P(v) distribution associated with the weak, slowest sub-group peaks at v ∼ 4200 m s⁻¹ (Fig. 6). As noted above, momentum matching requires that the corresponding I^q+ fragments must have v ∼ 2300 m s⁻¹ and the P(v) distribution of the I⁺ cations shows a weak pedestal (shown in the inset to Fig. 3) stretching out to such velocities. We conclude that CE of Z = 3 parent ions occurs predominantly via process (11), with only a minor contribution from the rival fragmentation

CF₃I³⁺ → CF₃²⁺ + I⁺. (12)

Such a conclusion is consistent with thermodynamic expectations: the threshold energies for forming the products of processes (11) and (12), each defined relative to the ground state neutral, are ∼41 and ∼48.5 eV, respectively.

Fig. S4 (ESI†) shows the m/z 88.5 (CF₂I²⁺) image recorded at all three incident intensities. The image recorded at I = 1300 TW cm⁻² and its analysis must be viewed with some caution. Scrutiny of the image data suggests that the small peak at v ∼ 1050 m s⁻¹ is real, but we cannot exclude the possibility that the more obvious peak centred at v ∼ 2400 m s⁻¹ is associated with fragment ions from SFI of trace bromothiophene contaminant (the immediate prior experiments in the apparatus involved this molecule). Notwithstanding, it is tempting to associate the v ∼ 1050 m s⁻¹ signal (at least) with some contribution from another rival fragmentation channel

CF₃I³⁺ → CF₂I²⁺ + F⁺. (13)

We note that v ∼ 1050 m s⁻¹ for CF₂I²⁺ fragments arising via process (13) is sensibly consistent with the deduced velocity of the CF₂I⁺ fragments formed with F⁺ ions from Z = 2 cations (v ∼ 750 m s⁻¹, Fig. S3, ESI†) if both dissociations are dominated by coulombic repulsion.

Z > 3. The dominant feature in the P(v) distribution derived from the CF₃²⁺ velocity map image, which again displays parallel recoil anisotropy, peaks at v ∼ 5700 m s⁻¹. Momentum matched I^q+ fragments in this case must have velocities v ∼ 3100 m s⁻¹, consistent with the pedestal in the P(v) distributions of the I²⁺ fragments recorded at I = 650 and 1300 TW cm⁻², i.e. with the dissociation process starting with

CF₃I⁴⁺ → CF₃²⁺ + I²⁺, (14)

the threshold energy for which (again defined relative to the ground state neutral) is ∼68 eV. Confirmation of the operation of this process is provided by the (I²⁺, CF₃²⁺) covariance plot shown in Fig. S7 (ESI†). CF₂²⁺ and CF²⁺ (and even C²⁺) fragments are relatively more apparent in the TOF mass spectra measured at higher I, and their respective P(v) distributions also show one (or more) velocity sub-groups with parallel recoil anisotropy. The most probable velocities of the slower sub-groups in the cases of CF₂²⁺ and CF²⁺ are, respectively, ∼5000 m s⁻¹ and ∼6200 m s⁻¹. Such fragments would be consistent with further decay of emerging CF₃²⁺ fragments (from process (14)) by loss of one or more F atoms, i.e.

CF₃²⁺ → CF₂²⁺ + F → CF²⁺ + 2F (15)

(analogues of process (5), but starting from the CF₃²⁺ dication), that occur at sufficiently short C–I separations that the secondary CF_n²⁺ fragments still experience at least some of the available coulombic repulsion. The (CF₃²⁺, I²⁺) covariance map image from the data taken at I = 650 TW cm⁻² (Fig. S7, ESI†) confirms a correlation consistent with the two-body fragmentation process (14), but the (CF₂²⁺, I²⁺) and (CF²⁺, I²⁺) covariance map images are too noisy to reveal the correlations expected from the combined effect of processes (14) and (15). Most CF₂⁺, CF⁺ and even C⁺ fragments from any rival charge separated decay of CF₃²⁺ fragments, i.e.

CF₃²⁺ → CF₂⁺ + F⁺ → CF⁺ + F⁺ + F → C⁺ + F⁺ + 2F (16)

would likely expand beyond the detector edge, but the former might contribute to the I-dependent signal at high velocity in the P(v) distribution of the CF₂⁺ fragments.

The I³⁺ fragment ion images recorded at I = 650 and 1300 TW cm⁻² both show peaked recoil velocity distributions aligned parallel to the ε-vector, but the peaks of the P(v) distributions derived from these images clearly shift to higher velocity with increasing I. The distribution measured at I = 650 TW cm⁻² peaks at v ∼ 2700 m s⁻¹ and is logically assigned to a rival, charge-asymmetric, decay process for Z = 4 parent ions

CF₃I⁴⁺ → CF₃⁺ + I³⁺. (17)

Momentum matching arguments imply that any CF₃⁺ partners from dissociation process (17) would have v ∼ 5000 m s⁻¹, and thus escape detection. But the emerging CF₃⁺ fragments might also decay further via process (5). The final velocities of any CF_n⁺(n = 0–2) fragments formed in this way would be sensitive to the C–I separation at the time of the secondary decay but would converge to ∼5000 m s⁻¹ in the limit that the primary fragment separation was large enough to exclude any further coulombic repulsion. Dissociation processes (17) then (5) might contribute to the yield of CF⁺ fragments with v ∼ 5000 m s⁻¹ ions measured at I = 650 TW cm⁻².

The I³⁺ fragment ion image measured at I = 1300 TW cm⁻² peaks at a larger radius, corresponding to v ∼ 3400 m s⁻¹. Increasing the incident intensity will increase the relative proportion of higher Z parent ions in the interaction region, and the logical source of these ions is the process

CF₃I⁵⁺ → CF₃²⁺ + I³⁺, (18)

for which the energetic threshold would be E ∼ 97 eV. Again, we can expect many of the emerging CF₃²⁺ fragments to shed further F atoms and/or F⁺ ions (processes (15) or (16)). Again, the velocities of any momentum matched CF₃²⁺ fragments (v ∼ 6250 m s⁻¹) would fall outside the detection area, but any that decay by loss of neutral F atoms might contribute to the yield of high velocity CF₂²⁺ and CF²⁺ fragments. Given these assignments, it is tempting to attribute the shoulder evident on the high velocity side of the P(v) distribution of the I³⁺ fragments obtained from the I = 650 TW cm⁻² to products of dissociation process (18).

Given that parent cations with Z = 5 are present in the interaction region at the higher incident intensities, we note that the rival process

CF₃I⁵⁺ → {CF₃³⁺} + I²⁺ (19)

(where the { } signifies that this highly charged 4-atom species is likely to have a very fleeting nature) may contribute to the fast tail in the P(v) distribution of the I²⁺ fragments formed at I = 1300 TW cm⁻² (Fig. 3). We also note that parent cations with Z = 5 are the first that could, in principle, atomize to singly charged atomic products – the threshold energy for which is ∼90.9 eV.

Evidence for CE of CF₃I^Z+ cations with Z > 5 in the present experiments is limited to observations of (i) I³⁺ fragment ions with velocities v > 4500 m s⁻¹ in the data recorded at I = 1300 TW cm⁻² (i.e. much faster than can be accommodated by dissociation process (18)) and (ii) I⁴⁺ fragments. Interpretation of the image of the m/z ∼ 31.5 ions measured at high I (Fig. 2) required rather more thought. The central feature is attributable to O₂⁺ ions from SFI of trace air impurity. The feature centred at v ∼ 4200 m s⁻¹ is plausibly consistent with that expected by extrapolating the CF⁺ data measured at lower I (Fig. 4 and 6) but, as Fig. 5 convincingly shows, I⁴⁺ fragments also contribute to the image recorded at I = 1300 TW cm⁻². No I⁵⁺ fragments are discernible in the TOF mass spectrum measured at this highest incident intensity.

4. Conclusions

This study demonstrates how multi-mass VMI and covariance map imaging studies of the charged fragments formed by near infrared strong field ionization of a neutral gas phase molecule (here CF₃I) can provide many new insights into the dissociation dynamics of the resulting parent cations formed in a range of charge states. The distribution of Z states necessarily varies with the incident intensity and, within any one focussed laser pulse, is both time- and position-dependent. This multiplex aspect is both an asset and a limitation of the approach. The obvious advantage is that one experiment allows the study of multiple fragmentation channels from different parent cations, simultaneously. The most obvious limitation is that a given fragment ion image may contain overlapping contributions from the dissociation of several CF₃I^Z+ ions, but these overlaps can be revealed by probing the image sensitivities to I and, in favourable cases, deconvolved by covariance map imaging methods.

Previous reports that DI of CF₃I⁺ cations can result in CF₃⁺, I⁺ and CF₂I⁺ fragment ions (together with, respectively, I atoms in both spin–orbit states, CF₃ neutrals, and an F atom) are confirmed and some of the CF₃⁺ fragments are deduced to be formed with sufficient internal energy to undergo secondary loss of one or more neutral F atoms.^46,47

The covariance map images confirm the dominance of CF₃⁺ and I⁺ products in the photodissociation of CF₃I²⁺ ions.⁴⁸ The I-dependent recoil anisotropy of these fragments shows that the dissociation of Z = 2 cations is far from Coulomb dominated. Valence bonding forces have an obvious influence on the fragmentation dynamics, and the I-dependent recoil anisotropy is most readily explained by assuming that different incident laser intensities sample different distributions of dissociative parent electronic states of CF₃I²⁺. The measured images reveal that the CF₃⁺ + I⁺ products are formed with a narrow spread of kinetic energies. The data imply a strong propensity for parent internal excitation to map into internal excitation of the products and show that some of the primary CF₃⁺ fragments are formed with sufficient internal energy to decay further by secondary loss of one or more F atoms. Rival dissociations to CF₂I⁺ + F⁺ and to CF₂⁺ + IF⁺ products are revealed by covariance map image analysis. Charge asymmetric dissociations to CF₃ + I²⁺ and CF₂I²⁺ and F are also both identified, but the present study finds no evidence for the alternative (higher energy) CF₃²⁺ + I product channel.

The findings reported here for CF₃I^Z+ ions with Z ≥ 3 are entirely new. In all cases, the coulombic repulsive forces are sufficient to ensure that the photofragments recoil along an axis parallel to ε. The primary products formed in the photodissociation of CF₃I³⁺ ions are mainly CF₃⁺ and I²⁺, with only minor contributions from the rival, more endoergic, CF₂I²⁺ + F⁺ and CF₃²⁺ + I⁺ channels. Again, the covariance map images indicate that the internal energies of some of the CF₃⁺ products are sufficient to allow the subsequent loss of one or more F atoms. The CF₃²⁺ fragment ion images measured at higher I show another faster velocity sub-group consistent with their formation in tandem with I²⁺ fragments from the photodissociation of CF₃I⁴⁺ parent ions. Again, the measured fragment ion yields and ion images suggest that some of the nascent CF₃²⁺ fragments decay further by losing F and/or F⁺ atoms. The P(v) distributions derived from I³⁺ fragment ion images recorded at the highest I show a component attributable to CF₃I⁵⁺ photodissociation to CF₃²⁺ + I³⁺ and the m/z ∼ 31.5 images clearly show I⁴⁺ products from parent ions with Z > 5.

Dissociative pathways from parent ions with CF₃I^Z+ ions where Z ≥ 3 could, in principle, be investigated by application of three-fold covariance methods. Such studies should complement the conclusions in this manuscript, by confirming the kinetic energies of the fragment ions directly. To date, however, successful examples of three-fold covariance analysis generally require the collection of significantly more data (better statistics) than achieved in the present work and/or have been limited to relatively simple molecules with a modest number of dissociative pathways (e.g. the covariance between the D⁺, D⁺, O⁺ fragments arising in the dissociation of D₂O³⁺ parent ions ⁵⁹). Any such experiment on highly charged CF₃I^Z+ ions would surely benefit from pre-alignment of the parent molecules to simplify the data analysis and interpretation, as demonstrated in earlier ground-breaking CEI studies of pre-aligned 3,5-dibromo-3′,5′-difluoro-4′-cyanobiphenyl molecules.⁶⁰

Finally, comparisons with CH₃I are revealing: analogous SFI experiments on CH₃I, at the same incident intensities, yielded measurable images of I⁵⁺ and even I⁶⁺ fragment ions.³⁹ These differences (cf. CF₃I) might be explicable if the cross-sections for SFI of CF₃I at λ ∼ 805 nm are relatively smaller than for CH₃I, or if the SFI-induced charges are less heavily concentrated on the I atom in CF₃I than in CH₃I, i.e. that F atoms (and a CF₃ group) are a better sink for positive charge than H atoms (and a CH₃ group).

Data availability

All underpinning data are available at the University of Bristol data repository, data.bris, at https://doi.org/10.5523/bris.1jmu8pj7rzm6p2td4lwhl569ej.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

The authors are grateful to EPSRC for funding via Programme Grant EP/L005913/1. JWLL acknowledges financial support via the Helmholtz-ERC Recognition Award (ERC-RA-0043) of the Helmholtz Association (HGF).

References

1. D. M. Curtis and J. H. D. Eland, Int. J. Mass Spectrom. Ion Phys., 1985, 63, 241–264.
2. J. H. D. Eland, Mol. Phys., 1989, 61, 725–745.
3. H. Hsieh and J. H. D. Eland, J. Phys. B: At. Mol. Phys., 1997, 30, 4515–4534.
4. D. Mathur, Phys. Rep., 2004, 391, 1–118.
5. K. Ueda and J. H. D. Eland, J. Phys. B: At. Mol. Phys., 2005, 38, S839–S859.
6. Z. Vager, R. Naaman and E. P. Kanter, Science, 1989, 244, 426–431.
7. L. J. Frasinski, K. Codling and P. A. Hatherly, Science, 1989, 246, 1029–1031.
8. K. W. D. Ledingham, R. P. Singhal, D. J. Smith, T. McCanny, P. Graham, H. S. Kilic, W. X. Peng, S. L. Wang, A. J. Langley and P. F. Taday, et al. , J. Phys. Chem. A, 1998, 102, 3002–3005.
9. F. Légaré, K. F. Lee, I. V. Litvinyuk, P. W. Doley, A. D. Bandrauk, D. M. Villeneuve and P. B. Corkum, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 052717.
10. T. Yatsuhashi and N. Nakashima, J. Photochem. Photobiol., C, 2018, 34, 52–84.
11. X. Li, A. Rudenko, M. S. Schöffler, N. Anders, Th. M. Baumann, S. Eckart, B. Erk, A. De Fanis, K. Fehre and R. Dörner, et al. , Phys. Rev. Res., 2022, 4, 013029.
12. R. Boll, J. M. Schäfer, B. Richard, K. Fehre, G. Kastirke, Z. Jurek, M. S. Schöffler, M. M. Abdullah, N. Anders and T. M. Baumann, et al. , Nat. Phys., 2022, 18, 423–428.
13. M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Bocking, R. Dorner and J. Stohner, et al. , Science, 2013, 341, 1096–1100.
14. M. Pitzer, G. Kastirke, M. Kunitski, T. Jahnke, T. Bauer, C. Goihl, F. Trinter, C. Schober, K. Henrichs and J. Becht, et al. , ChemPhysChem, 2016, 17, 2465–2472.
15. U. Ablikim, C. Bomme, H. Xiong, E. Savelyev, R. Obaid, B. Kaderiya, S. Augustin, K. Schnorr, I. Dumitriu and T. Osipov, et al. , Sci. Rep., 2016, 6, 38202.
16. M. Burt, K. Amini, J. W. L. Lee, L. Christiansen, R. R. Johansen, Y. Kobayashi, J. D. Pickering, C. Vallance, M. Brouard and H. Stapelfeldt, J. Chem. Phys., 2018, 148, 091102.
17. U. Ablikim, C. Bomme, T. Osipov, H. Xiong, R. Obaid, R. C. Bilodeau, N. G. Kling, I. Dumitriu, S. Augustin and S. Pathak, et al. , Rev. Sci. Instrum., 2019, 90, 055103.
18. S. Pathak, R. Obaid, S. Bhattacharyya, J. Burger, X. Li, J. Tross, T. Severt, B. Davis, R. C. Bilodeau and C. A. Trallero-Herrero, et al. , J. Phys. Chem. Lett., 2020, 11, 10205–10211.
19. C. Saribal, A. Owens, A. Yachmenev and J. Küpper, J. Chem. Phys., 2021, 154, 071101.
20. J. Yadav, C. P. Safvan, P. Bhatt, P. Kamari, A. Kumar and J. Rajput, J. Chem. Phys., 2022, 156, 141101.
21. M. Burt, R. Boll, J. W. L. Lee, K. Amini, H. Köckert, C. Vallance, A. S. Gentleman, S. R. Mackenzie, S. Bari and C. Bomme, et al. , Phys. Rev. A, 2017, 96, 043415.
22. M. E. Corrales, J. González-Vázquez, R. de Nalda and L. Bañares, J. Phys. Chem. Lett., 2019, 10, 138–143.
23. R. Forbes, F. Allum, S. Bari, R. Boll, K. Borne, M. Brouard, P. H. Bucksbaum, A. J. Howard, P. Johnsson and J. W. L. Lee, et al. , J. Phys. B: At. Mol. Phys., 2020, 53, 224011.
24. M. Li, M. Zhang, O. Vendrell, Z. N. Guo, Q. R. Zhu, X. Gao, L. S. Cao, K. Y. Guo, Q. Q. Su and W. Cao, et al. , Nat. Commun., 2021, 12, 4233.
25. S. T. Alavi, G. A. Cooper and A. G. Suits, Mol. Phys., 2022, 120, e1988170.
26. D. Mishra, J. Reino-González, R. Obaid, A. C. LaForge, S. Diáz-Tendero, F. Martin and N. Berrah, Phys. Chem. Chem. Phys., 2022, 24, 433–443.
27. P. Graham, K. Ledingham, R. Singhai, S. Hankin, T. McCanny, X. Fang, C. Kosmidis, P. Tzallas, P. Taday and A. J. Langley, J. Phys. B: At. Mol. Opt. Phys., 2021, 34, 4015–4026.
28. H. T. Liu, Z. Yang, Z. Gao and Z. C. Tang, J. Chem. Phys., 2017, 126, 044316.
29. Y. M. Wang, S. Zhang, Z. R. Wei and B. Zhang, J. Phys. Chem. A, 2008, 112, 3846–3851.
30. M. E. Corrales, G. Gitzinger, J. Gonzalez-Vazquez, V. Loriot, R. de Nalda and L. Bañares, J. Phys. Chem. A, 2012, 116, 2669–2677.
31. S. G. Walt, N. B. Ram, A. von Conta, O. I. Tolstikhin, L. B. Madsen, F. Jensen and H. J. Wörner, J. Phys. Chem. A, 2015, 119, 11772–11782.
32. D. D. Zhang, S. Z. Luo, H. F. Xu, M. X. Jin, F. C. Liu, B. Yan, Z. G. Wang, H. Liu, D. W. Jiang and A. Eppink, et al. , Eur. Phys. J. D, 2017, 71, 148.
33. Z. R. Wei, J. L. Li, S. T. See and Z.-H. Loh, J. Phys. Chem. Lett., 2017, 8, 6067–6072.
34. Y. Malakar, W. L. Pearson, M. Zohrabi, B. Kaderiya, P. K. Raju, F. Ziaee, S. Xue, A. T. Le, I. Ben-Itzhak and D. Rolles, et al. , Phys. Chem. Chem. Phys., 2019, 21, 14090–14102.
35. A. Sen, S. Mandal, S. Sen, B. Bapat, R. Gopal and V. Sharma, Phys. Rev. A, 2021, 103, 043107.
36. F. Allum, N. Anders, M. Brouard, P. Bucksbaum, M. Burt, B. Downes-Ward, S. Grundmann, J. Harries, Y. Ishimura and H. Iwayama, et al. , Faraday Discuss., 2021, 228, 571–596.
37. R. Boll, B. Erk, R. Coffee, S. Trippel, T. Kierspel, C. Bomme, J. D. Bosek, M. Burkett, S. Carron and K. R. Ferguson, et al. , Struct. Dyn., 2016, 3, 043207.
38. M. Wallner, J. H. D. Eland, R. J. Squibb, J. Andersson, A. Hult Roos, R. Singh, O. Talaee, D. Koulentianos, M. N. Piancastelli and M. Simon, et al. , Sci. Rep., 2020, 10, 1246.
39. S. W. Crane, L. F. Ge, G. A. Cooper, B. P. Carwithen, M. Bain, J. A. Smith, C. S. Hansen and M. N. R. Ashfold, J. Phys. Chem. A, 2021, 125, 9594–9608.
40. W. W. Zhou, L. F. Ge, G. A. Cooper, S. W. Crane, M. H. Evans, M. N. R. Ashfold and C. Vallance, J. Chem. Phys., 2020, 153, 184201.
41. J. W. L. Lee, H. Köckert, D. Heathcote, D. Popat, R. T. Chapman, G. Karras, P. Majchrzak, E. Springate and C. Vallance, Commun. Chem., 2020, 3, 72.
42. L. Minion, J. W. L. Lee and M. Burt, Phys. Chem. Chem. Phys., 2022, 24, 11636–11645.
43. H. Köckert, D. Heathcote, J. W. L. Lee, W. W. Zhou, V. Richardson and C. Vallance, Phys. Chem. Chem. Phys., 2019, 21, 14296–14305.
44. H. Köckert, D. Heathcote, J. W. L. Lee and C. Vallance, Mol. Phys., 2021, 119, e1811909.
45. R. L. Asher and B. Ruscic, J. Chem. Phys., 1997, 106, 210–221.
46. I. Powis, O. Dutuit, M. Richard-Viard and P. M. Guyon, J. Chem. Phys., 1990, 92, 1643–1652.
47. F. Aguirre and S. T. Pratt, J. Chem. Phys., 2003, 119, 9476–9485.
48. J. H. D. Eland, R. Feifel and M. Hochlaf, J. Chem. Phys., 2008, 128, 234303.
49. A. Nomerotski, M. Brouard, E. Campbell, A. Clark, J. Crooks, J. Fopma, J. J. John, A. J. Johnsen, C. Slater and R. Turchetta, et al. , J. Instrum., 2010, 5, C07007.
50. C. Vallance, M. Brouard, A. Lauer, C. Slater, E. Halford, B. Winter, S. J. King, J. W. L. Lee, D. Pooley and I. Sedgwick, et al. , Phys. Chem. Chem. Phys., 2014, 16, 383–395.
51. C. Vallance, D. Heathcote and J. W. L. Lee, J. Phys. Chem. A, 2021, 125, 1117–1133.
52. A. T. J. B. Eppink and D. H. Parker, J. Chem. Phys., 1999, 110, 832–844.
53. N. A. Macleod, S. Wang, J. Hennessy, T. Ridley, K. P. Lawley and R. J. Donovan, J. Chem. Soc., Faraday Trans., 1998, 94, 2689–2694.
54. A. Vredenborg, W. G. Roeterdink, C. A. de Lange and M. H. M. Janssen, Chem. Phys. Lett., 2009, 478, 20–27.
55. B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) Values based on ver. 1.122r of the Thermochemical Network, 2021, available at Active Thermochemical Tables – Thermochemical Data (anl.gov).
56. A. Kramida, Yu Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.9), (Online), 2018, available: https://physics.nist.gov/asd, [2022, January 6], National Institute of Standards and Technology, Gaithersburg, NM DOI:10.18434/T4W30F.
57. C. J. Proctor, C. J. Porter, T. Ast and J. H. Beynon, Int. J. Mass Spectrom. Ion Phys., 1982, 41, 251–263.
58. J. Hrušák, N. Sändik and W. Koch, Int. J. Mass Spectrom., 1999, 185, 701–706.
59. F. Allum, C. Cheng, A. J. Howard, P. H. Bucksbaum, M. Brouard, T. Weinacht and R. Forbes, J. Phys. Chem. Lett., 2021, 34, 8302–8308.
60. J. D. Pickering, K. Amini, M. Brouard, M. Burt, I. J. Bush, L. Christensen, A. Lauer, J. H. Nielsen, C. S. Slater and H. Stapelfeldt, J. Chem. Phys., 2016, 144, 161105.

---

Footnotes

† Electronic supplementary information (ESI) available: A compilation of the thermochemical threshold energies for many of the fragmentation processes relevant to this study and a summary of all fragmentation channels identified; a comparison of the P(v) distributions of the I⁺ and CF₃⁺ fragment ions derived from the symmetrized 3-time bin images shown in Fig. 2 and 4 and by Abel inverting the symmetrized crushed images; symmetrized images (and P(v) distributions derived therefrom) of F⁺, F²⁺, CF₂I⁺, IF⁺ and CF₂I²⁺ fragments obtained following SFI of CF₃I at I = 1300, 650 and 260 TW cm⁻²; the following covariance map images: (I^q+, CF₃⁺), (I^q+, CF₂⁺) and (I^q+, CF⁺) (q = 1, 2) from the I = 260 TW cm⁻² data; (CF₃⁺, I^q+) and (I^q+, CF₃⁺) (q = 1, 2) from the I = 650 and 1300 TW cm⁻² data; (I²⁺, CF₃²⁺) and (CF₃²⁺, I²⁺) from the I = 650 TW cm⁻² data; and (IF⁺, CF₂⁺) and (CF₂I⁺, F⁺) from the I = 260 TW cm⁻² data. See DOI: https://doi.org/10.1039/d2cp02449g

‡ Current address: Department of Chemistry, Brown University, Providence, RI 02912, USA.

---