Expanding the toolbox of the coinage bond: adducts involving new gold(III) derivatives and bioactive molecules

Abstract

X-ray analyses of a small library of adducts between AuX₃ (X = Cl, Br) and several pyridine derivatives indicate the systematic presence of quite short π-hole coinage bonds; computational studies reveal the attractive nature and strength of these short contacts, confirming their prominent role in driving their organization in the solid.

---

Noncovalent interactions¹ have a major role in translating the properties of molecules into the properties of materials. This accounts for their relevance in fields as diverse as supramolecular² and medicinal chemistry.³ In the last decades it has been recognized that the formation of covalent bonds and the subsequent partitioning of the electron density at the outer regions of bonded atoms affects the interactional landscape of a variety of elements. The resulting anisotropic distribution of the electron density determines the presence of regions of depleted electron density opposite to the σ-covalent bonds and above and below the planar regions of molecules. These regions, named σ- and π-holes,⁴ respectively, frequently have a positive electrostatic potential, act as electrophilic sites, and form attractive interactions with regions, in the same or other molecules, where the electrostatic potential is negative. This behaviour is shown by all elements of the p block, and the interactions wherein the electrophilic atom is an element of the 17,⁵ 16,⁶ 15,⁷ and 14 (ref. 8) groups of the periodic table have become valuable tools in supramolecular chemistry.

Recently the same behaviour has been recognized in various elements of the d block. The osme⁹ and matere¹⁰ bonds, the interactions wherein the elements of groups 8 and 7 are the electrophiles, are the last entries in this set of interactions. The electrophilic behaviour of the derivatives of group 11 elements was recognized first as a consequence of the anisotropic distribution of the electron density in Cu, Ag, and Au metal nanoparticles.¹¹ Soon after, the same understanding was extended to derivatives wherein group 11 metals are at +1 and +3 oxidation states^12,13 and the term coinage bond (CiB) was adopted to designate collectively the resulting σ- and π-hole interactions.

CiBs involving gold atoms are particularly important due to their strength and ubiquity and to the roles that they have in the functional properties of a variety of gold derivatives. For instance, these interactions can drive the self-assembly of Au(III) anions,¹⁴ affect the catalytic properties of gold nanoparticles,¹⁵ and be involved in the protein–Au(I) binding.¹⁶ Colloidal gold solutions are frequently employed in nanomedicine, and gold-based drugs are the subject of intense research,¹⁷e.g., for their use in the treatment of rheumatoid arthritis, cancer, or HIV and Sars-Cov-2 infections.¹⁸

Importantly, adducts formed from Au(III) halides and pyridine derivatives are a robust scaffold for most of the aforementioned purposes, e.g., Au(III) adducts of 2-substituted pyridines displayed a very broad and valuable anticancer profile.¹⁹ The relevance of adducts wherein gold is bonded to pyridine nitrogen extends to fields other than medicinal chemistry. Among others, such derivatives have been used in the sensing of chemical weapons like nerve agents (NAs) via surface-enhanced Raman scattering.²⁰

We thus decided to assess the relevance of the CiB in the interactional landscape of a series of adducts from AuX₃ (X = Cl, Br) and several pyridine derivatives (Scheme 1). Single crystal X-ray analyses of these adducts showed that gold atoms invariably formed two quite short contacts with O, Cl, or Br atoms resulting in a distorted octahedral geometry around the metal. Computational studies on some structural motifs extracted from the crystal packings proved the attractive nature of these interactions, revealed their strength, and confirmed their prominent role in determining the adopted crystal packings. Indications from both crystallographic and computational studies are consistent and allow these interactions to be rationalized as π-hole CiBs, where gold acts as the electrophile (CiB donor) and O, Cl, or Br atoms as nucleophiles (CiB acceptors). To the best of our knowledge, this is the first paper acknowledging the ability of AuBr₃ adducts to engage in CiB.

Scheme 1 Molecular structures of adducts from gold trihalides and pyridine derivatives.

Gold trihalides–pyridine adducts 1a–g were obtained by treating chloroauric acid or potassium tetrabromidoaurate with the respective pyridine derivatives in methanol (see the ESI† for details). 1a and 1f were obtained by using cotinine, a tobacco alkaloid and a major nicotine metabolite frequently used as a biomarker for its intake.²¹ Of note, colloidal gold nanoparticles are used in screening devices for the recognition of cotinine in urine samples.²²

The crystallographic analyses of adducts 1a–g (Table 1) showed that all these compounds adopt a square planar arrangement, wherein the Au–N distances fall in the expected range 202–208 pm. Several short²³ C–H⋯O/Cl/Br hydrogen bonds (HBs) are present in all structures and connect single adducts into 3D networks.

Table 1 Summary of crystal data and structure refinement for compounds 1a–g

Identification code	1a	1b	1c	1d	1e	1f	1g
Empirical formula	C10H12AuCl3N2O	C5H4NFCl3AuO	C5H4NCl4Au	C5H4NCl3BrAu	C5H4NCl3IAu	C10H11AuBr3N2O2	C5H4AuBr3FN
Formula weight	479.53	400.41	416.86	461.32	508.31	627.90	533.79
Temperature/K	296	296	296	296	296	296	296
Crystal system	Triclinic	Monoclinic	Monoclinic	Triclinic	Monoclinic	Triclinic	Orthorhombic
Space group	P1	P21/n	P21/n	P1̄	C2/c	P1	P212121
a/Å	7.4947(17)	6.6793(11)	4.0879(5)	7.0468(9)	18.5724(12)	7.3049(4)	4.1948(4)
b/Å	9.945(3)	8.2420(13)	13.4780(19)	7.9600(10)	6.8315(4)	7.9398(4)	13.8237(14)
c/Å	10.000(2)	16.356(3)	17.229(2)	9.2442(12)	16.2536(10)	14.1403(8)	16.8348(18)
α/°	85.660(13)	90	90	80.193(9)	90	91.892(2)	90
β/°	69.881(12)	94.540(8)	90.976(5)	78.165(8)	103.388(2)	101.920(3)	90
γ/°	78.186(12)	90	90	80.695(8)	90	99.075(2)	90
Volume/Å^3	685.0(3)	897.6(3)	949.1(2)	495.75(11)	2006.2(2)	790.57(7)	976.21(17)
Z	2	4	4	2	8	2	4
ρ calc g cm^−3	2.325	2.963	2.917	3.090	3.366	2.638	3.632
μ/mm^−1	11.307	17.230	16.559	19.612	18.480	16.880	27.302
F(000)	448.0	720.0	752.0	412.0	1792.0	570.0	936.0
Crystal size/mm^3	0.08 × 0.06 × 0.04	0.2 0.08 × 0.08	0.2 × 0.08 × 0.08	0.2 × 0.08 × 0.08	0.009 × 0.006 × 0.003	0.08 × 0.04 × 0.02	0.009 × 0.006 × 0.003
Radiation	MoKα (λ = 0.71073)	MoKα (λ = 0.71073)	MoKα (λ = 0.71073)	MoKα (λ = 0.71073)	MoKα (λ = 0.71073)	MoKα (λ = 0.71073)	MoKα (λ = 0.71073)
2θ range for data collection/°	6.046 to 66.954	6.424 to 86.18	7.678 to 61.846	7.402 to 60.27	6.376 to 73.676	5.782 to 67.542	7.628 to 46.362
Index ranges	−11 ≤ h ≤ 10, −14 ≤ k ≤ 14, −13 ≤ l ≤ 15	−10 ≤ h ≤ 12, −15 ≤ k ≤ 14, −31 ≤ l ≤ 30	−5 ≤ h ≤ 5, −18 ≤ k ≤ 19, −24 ≤ l ≤ 24	−9 ≤ h ≤ 9, −11 ≤ k ≤ 11, −13 ≤ l ≤ 13	−29 ≤ h ≤ 27, −10 ≤ k ≤ 11, −26 ≤ l ≤ 24	−10 ≤ h ≤ 11, −12 ≤ k ≤ 11, −18 ≤ l ≤ 20	−4 ≤ h ≤ 4, −15 ≤ k ≤ 15, −18 ≤ l ≤ 18
Reflections collected	12 301	23 205	18 882	9765	22 700	17 402	6125
Independent reflections	7361 [Rint = 0.0434, Rsigma = 0.0910]	6546 [Rint = 0.0781, Rsigma = 0.0791]	2947 [Rint = 0.0333, Rsigma = 0.0241]	2803 [Rint = 0.0561, Rsigma = 0.0689]	4292 [Rint = 0.0347, Rsigma = 0.0276]	8282 [Rint = 0.0252, Rsigma = 0.0456]	1390 [Rint = 0.0884, Rsigma = 0.0625]
Data/restraints/parameters	7361/3/300	6546/0/101	2947/0/100	2803/0/100	4292/0/100	8282/3/318	1390/0/101
Goodness-of-fit on F^2	0.867	1.047	1.062	0.960	1.025	0.958	1.000
Final R indexes [I> = 2σ(I)]	R 1 = 0.0331, wR2 = 0.0578	R 1 = 0.0637, wR2 = 0.1581	R 1 = 0.0200, wR2 = 0.0359	R 1 = 0.0392, wR2 = 0.0647	R 1 = 0.0250, wR2 = 0.0444	R 1 = 0.0250, wR2 = 0.0430	R 1 = 0.0333, wR2 = 0.0697
Final R indexes [all data]	R 1 = 0.0668, wR2 = 0.0665	R 1 = 0.1078, wR2 = 0.1795	R 1 = 0.0325, wR2 = 0.0390	R 1 = 0.0802, wR2 = 0.0747	R 1 = 0.0443, wR2 = 0.0513	R 1 = 0.0391, wR2 = 0.0455	R 1 = 0.0393, wR2 = 0.0719
Largest diff. Peak/hole/e Å^−3	1.46/−1.67	6.88/−5.91	0.81/−0.89	0.95/−1.01	2.05/−1.33	0.97/−0.82	1.41/−1.17
Flack parameter	0.06(2)	—	—	—	—	0.043(10)	0.48(4)
CCDC number	2144993	2144969	2144976	2144963	2144977	214491	2144992

---

Quite short Au⋯O/Cl/Br contacts on either face of the compounds are structure determining features in all adducts of 1. For instance, in the AuCl₃·cotinine adduct 1a, the oxygen of one molecule gets close to the gold of an adjacent molecule.

Consistent with the expected geometry of the π-hole CiBs, this contact is approximately on the perpendicular to the adduct plane (the N/Cl–Au⋯O angles span the range 84.33–96.38°) (Fig. 1). Two different CiBs are present, and the Au⋯O separations are as short as 293.1 and 309.8 pm, corresponding to normalized contacts (N_c)²⁴ as small as 0.80 and 0.85.

Fig. 1 Partial view (Mercury 4.3.1) of the coinage bonded infinite chains in crystalline 1a (top) and 1f (bottom). CiBs and HBs are ocher and black dotted lines. The Au⋯O/Cl/Br separations (pm) and corresponding N_c values are given near the contacts. Color codes: grey, carbon; white, hydrogen; light blue, nitrogen; red, oxygen; green, chloride; brown, bromine; yellow, gold.

Any AuCl₃·cotinine adduct acts as both donor and acceptor of CiB, and infinite supramolecular chains are formed. Two such chains couple into ribbons through the antiparallel pairing of Au–Cl motifs of different units. Au⋯Cl short contacts are formed and can be rationalized as π-hole CiBs. In fact, chlorine sits roughly perpendicular to the adduct plane (the N/Cl–Au⋯Cl angles span the range 84.83–92.77°).

The rectangular and CiB based supramolecular synthon resulting from the antiparallel pairing of Au–Cl/Br motifs of different adducts is recurrent in the crystals of adducts (1). In AuBr₃·cotinine adduct 1f, gold atoms give rise to two Au⋯Br π-hole CiBs thanks to the presence of two such synthons at either face of the square planar arrangement of adducts (Fig. 1). Infinite supramolecular chains are formed in which cotinine ligands are alternating at opposite sides of the chain.

Very similar supramolecular chains with staggered pyridine pendants are present also in the crystals of AuCl₃·m-bromopyridine 1d and its m-iodo analogue 1e. A rectangular and CiB based supramolecular synthon similar to those described above is present at either face of the adducts, and this synthon determines the crystal packings.

The same antiparallel pairing of two Au–Cl/Br motifs of two different units at either face of another unit is responsible for the formation of the infinite chains present in AuCl₃·m-chloropyridine 1c and AuBr₃·m-fluoropyridine 1g. In these chains, the pyridyl pendants are eclipsed on the same side of the chain, rather than alternating on opposite sides as in 1d–f. Gold forms two π-hole CiBs also in AuCl₃·m-fluoropyridine 1b, but a supramolecular synthon different from the rectangular array of other adducts is adopted. Any adduct functions at the bidentate CiB donor (via the gold atom) and bidentate CiB acceptor (via two chlorine atoms) and sits at the nodes of flat (4,4)-networks. Importantly, in all cases Au⋯Cl/Br CiBs are quite short (Fig. 2), suggesting that they play a major role in determining the adopted crystal packings.

Fig. 2 Partial view (Mercury 4.3.1) of the (4,4)-net formed in crystalline 1bvia CiBs (ocher dotted lines). The Au⋯Cl separations (pm) and N_c values are given near the contacts. The color codes are the same as those in Fig. 1.

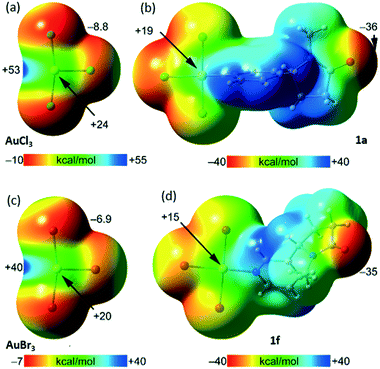
To shed some light into the type of bondings in the systems described above, a DFT study has been carried out (see the ESI† for greater details). First, the molecular electrostatic potential (MEP) surfaces of AuCl₃, AuBr₃, 1a, and 1f have been computed to establish the most nucleophilic and electrophilic parts of the molecules (Fig. 3). The MEP surfaces of the AuX₃ molecules confirm their strong electrophilic nature and show the existence of an intense σ-hole opposite to the Au–X bond (+53 kcal mol⁻¹ for X = Cl and +40 kcal mol⁻¹ for X = Br). Less positive MEP values are also observed above and below the Au-atom (π-holes, +24 kcal mol⁻¹ for X = Cl and +20 kcal mol⁻¹ for X = Br).

Fig. 3 MEP surfaces of AuCl₃ (a), 1a (b), AuBr₃ (c) and 1f (d) at the PBE0-D3/def2-TZVP level of theory. Isovalue 0.001 a.u. The energies at the selected points of the surface are given in kcal mol⁻¹.

The MEP minima in AuX₃ complexes are located at the negative belts of the halogen atoms, being slightly more negative for X = Cl, as expected. In adducts 1a and 1f, where the Au–N coordination bond is present, the MEP values above and below the Au-atom are less positive than in corresponding AuX₃, an expected consequence of the electron donation by the ligand. The MEP maxima are located in both compounds at the aromatic H atoms (+38 kcal mol⁻¹). The MEP minima are located at the amidic O atoms (−36 kcal mol⁻¹ for 1a and −35 kcal mol⁻¹ for 1f). It is worthy to comment that this MEP analysis allows the formation of CiBs and HBs to be anticipated revealed by X-ray analyses. For all complexes, the Au⋯O/Cl/Br contacts were further characterized by using the quantum theory of “atoms-in-molecules” (QTAIM) and the noncovalent interaction index (NCIplot).

Three dimers retrieved from the X-ray structures of 1a and 1f are given in Fig. 4, and the structural fragments, along with dimerization energies, of compounds 1b–e and 1g are given in the ESI† (Fig. S8). The QTAIM analysis evidences the existence of the Au⋯O/Cl/Br CiB interactions, each one characterized by a bond critical point (CP) and a bond path connecting the Au atom to the electron donor atom (Fig. 4). The analysis also discloses the existence of ancillary C–H⋯Cl/Br/O contacts as evidenced by the bond CPs and bond paths connecting the C–H bonds to the electron rich atoms. The presence of these interactions is also confirmed by the NCIplot analysis that shows either green (HBs) or bluish (CiBs) isosurfaces located between the interacting atoms. The blue colour of the isosurfaces characterizing the CiBs compared to the green one of the HBs reveals that the former interactions are stronger.

Fig. 4 QTAIM distribution of the critical points of the intermolecular bond and ring (red and yellow spheres, respectively) and bond paths for the dimeric assemblies of compounds 1a (a and b) and 1f (c). The estimation of the HB dissociation energies (kcal mol⁻¹) are indicated in red next to the bond CPS. The superimposed NCIplot isosurface (RDG isovalue = 0.4 a.u.) is shown. The cut-off ρ = 0.04 a.u. has been used. Color range: −0.025 a.u. ≤ (sign λ₂)ρ ≤ 0.025 a.u. Level of theory: PBE0-D3/def2-TZVP.

The dimerization energies of the assemblies as shown in Fig. 4 indicate that the CiBs are moderately strong, varying from −15.2 kcal mol⁻¹ (Fig. 4a, only one CiB) to −29.5 kcal mol⁻¹ (Fig. 4b, two CiBs). The dissociation energies of the HBs were estimated using the potential energy density (V_r) values measured at the bond CPs that characterize these contacts and using the equation proposed by Espinosa et al.²⁵ It can be observed that they are modest, varying from 0.5 to 1.4 kcal mol⁻¹, thus confirming that the CiBs govern the formation of the dimers. The dimerization energy of the antiparallel dimer of 1f (−20.1 kcal mol⁻¹) is smaller than that of 1a (−29.5 kcal mol⁻¹) in line with the less positive MEP value at the π-hole of Au and the less negative MEP at the belt of X. The strongest CiB in these systems corresponds to the Au⋯O, in line with the more negative MEP (stronger nucleophilicity) of O compared to X.

In order to analyse if orbital contributions are important in the π-hole Au⋯O/Cl/Br interactions, the natural bond orbital (NBO) second-order perturbation analysis²⁶ has been used. This method has been recently used to rationalize donor–acceptor interactions involving AuCl₄⁻ units.¹⁴ Calculations reveal moderate orbital contributions in the antiparallel complexes. These contributions come from electron donations from the lone pair (LP) of electrons on the Cl or Br atoms to the empty the 5d and 6p_z atomic orbitals of Au. The second-order stabilization energies E⁽²⁾ associated with the orbital donor–acceptor interactions are 9.73 kcal mol⁻¹ for 1a and 11.03 kcal mol⁻¹ for 1f. Regarding the dimer of 1a where the Au⋯O CiB is established (Fig. 4a), the orbital contribution is very small (0.9 kcal mol⁻¹), and it is originated from a donation involving the filled π(C=O) bonding orbital and the empty 5d orbital of Au. The LPs at the O atoms are not involved, likely due to the dimer geometry, where the LPs do not point to the π-hole.

Finally, we have compared the nature of the Au–N bond (originated from the interaction of pyridines with the σ-hole of AuX₃ molecules) with the Au⋯O/Cl/Br contacts (π-hole interactions). The values of electron density (ρ_r), total energy densities (H_r) and Wiberg bond index (WBI) are summarized in Table 2. The same parameters for the coordination Au–Cl and Au–Br bonds are also included for comparison purposes.

Table 2 Charge density and total energy density (ρ_r and H_r in a.u.) at the bond CPs and WBI of several Au bonds

Bond (cmpd)	ρ r	H r	WBI
Au–N (1a)	0.1337	−0.0544	0.3409
Au–Cl (1a)	0.1169	−0.0488	0.4725
Au⋯O (1a)	0.0121	+0.0014	0.0075
Au⋯Cl (1a)	0.0096	+0.0011	0.0055
Au–N (2a)	0.1211	−0.0445	0.3044
Au–Br (2a)	0.0987	−0.0361	0.4389
Au⋯Br (2a)	0.0123	+0.0006	0.0134

---

Taking into consideration the large values of ρ(> 0.11 a.u.), negative values of H_r (indicating large covalent character), and WBI values close to 0.4, it can be concluded that the Au–N bonds are coordination bonds. In fact, these values are similar to those obtained for the Au–Cl and Au–Br coordination bonds. In contrast, the small ρ_r (<0.015 a.u.), positive H_r and small WBI values characterizing the Au⋯Cl/Br/O CiBs indicate that they are noncovalent in nature and in the range of previous CiBs involving Au(III) derivatives.¹⁴

In summary, we have recently described how the electrophilic character of gold in anionic gold(III) derivatives results in the formation of CiBs.¹⁴ Experimental and computational studies reported here consistently show that the electrophilic character of gold in neutral gold(III) derivatives can be even greater. It is so pronounced that gold atoms form two quite short, attractive, and moderately strong Au⋯nucleophile contacts in all entries of a small library of AuX₃·pyridine adducts (X = Cl, Br). These interactions can be rationalized as π-hole CiBs and are invariably the most influential interactions in driving the derivatives organization in the solid. The reported results indicate that the distorted octahedral geometry around gold atoms is related to the metal electrophilicity. It is worth mentioning that the entrance of nucleophiles in the region of the most depleted electron density at gold in pure AuX₃, namely the σ-hole located opposite to one of X atoms, results in the formation of coordination bonds (not σ-hole bonds). Differently, the entrance of nucleophiles in the regions of most depleted electron density at gold in the AuX₃·pyridine adducts, namely the π-holes located above and below adducts plane, results in the formation of π-hole CiBs. The systematic presence of π-hole CiBs in 1a–g adducts suggests that these interactions may be a general and impacting feature of most neutral derivatives of gold(III). Indeed, also adducts formed from AuI₃ (ref. 27) and mono-, di-, and triaryl/alkynyl gold(III) compounds^19,28 show the presence of π-hole CiBs. Importantly, these CiBs can be used to rationally design the solid structure of neutral gold(III) derivatives in order to optimize their functional properties, e.g., in sensors,¹⁸ luminescent materials,²⁹ and drugs.¹⁹

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. S. Scheiner, Noncovalent Forces, Springer, 2015.
2. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967.
3. K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17.
4. P. Politzer and J. S. Murray, ChemPhysChem, 2020, 21, 579–588.
5. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimägi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
6. (a) P. Scilabra, G. Terraneo and G. Resnati, Acc. Chem. Res., 2019, 52, 1313–1324; (b) A. Tripathi, A. Daolio, A. Pizzi, Z. Guo, D. R. Turner, A. Baggioli, A. Famulari, G. B. Deacon, G. Resnati and H. B. Singh, Chem. – Asian J., 2021, 16, 2351–2360; (c) A. Pizzi, A. Tripathi, A. Daolio, Z. Guo, D. R. Turner, G. B. Deacon, G. Resnati and H. B. Singh, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C621.
7. K. T. Mahmudov, A. V. Gurbanov, V. A. Aliyeva, G. Resnati and A. J. L. Pombeiro, Coord. Chem. Rev., 2020, 418, 213381.
8. (a) A. Daolio, P. Scilabra, G. Terraneo and G. Resnati, Coord. Chem. Rev., 2020, 413, 213265; (b) M. Calabrese, A. Daolio, A. Pizzi and G. Resnati, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C805.
9. (a) A. Daolio, A. Pizzi, M. Calabrese, G. Terraneo, S. Bordignon, A. Frontera and G. Resnati, Angew. Chem., 2021, 60, 20723–20727; (b) A. Pizzi, A. Daolio, M. Calabrese, G. Terraneo, A. Frontera and G. Resnati, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C800.
10. A. Daolio, A. Pizzi, G. Terraneo, A. Frontera and G. Resnati, ChemPhysChem, 2021, 22, 2281–2285.
11. J. H. Stenlid and T. Brinck, J. Am. Chem. Soc., 2017, 139, 11012–11015.
12. A. C. Legon and N. R. Walker, Phys. Chem. Chem. Phys., 2018, 20, 19332–19338.
13. A. Terrón, J. Buils, T. J. Mooibroek, M. Barceló-Oliver, A. Garcıà-Raso, J. J. Fiol and A. Frontera, Chem. Commun., 2020, 56, 3524–3527.
14. (a) A. Daolio, A. Pizzi, G. Terraneo, M. Ursini, A. Frontera and G. Resnati, Angew. Chem., 2021, 60, 14385–14389; (b) G. Resnati, A. Daolio, A. Pizzi, G. Terraneo, M. Ursini and A. Frontera, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C214.
15. J. Halldin Stenlid, A. J. Johansson and T. Brinck, Phys. Chem. Chem. Phys., 2018, 20, 2676–2692.
16. M. de las Nieves Piña, A. Frontera and A. Bauzá, J. Phys. Chem. Lett., 2020, 11, 8259–8263.
17. I. Ott, Coord. Chem. Rev., 2009, 253, 1670–1681.
18. T. Zou, C. T. Lum, C.-N. Lok, J.-J. Zhang and C.-M. Che, Chem. Soc. Rev., 2015, 44, 8786–8801.
19. R. Rubbiani, T. N. Zehnder, C. Mari, O. Blacque, K. Venkatesan and G. Gasser, ChemMedChem, 2014, 9, 2781–2790.
20. L. Juhlin, T. Mikaelsson, A. Hakonen, M. S. Schmidt, T. Rindzevicius, A. Boisen, M. Käll and P. O. Andersson, Talanta, 2020, 211, 120721.
21. N. L. Benowitz, J. T. Bernert, J. Foulds, S. S. Hecht, P. Jacob, M. J. Jarvis, A. Joseph, C. Oncken and M. E. Piper, Nicotine Tob. Res., 2020, 22, 1086–1097.
22. J. T. Bernert, T. L. Harmon, C. S. Sosnoff and J. E. McGuffey, J. Anal. Toxicol., 2005, 29, 814–818.
23. S. S. Batsanov, Contacts are designated short, or close, when the distance between the involved atoms is smaller than the sum of the van der Waals (vdW) radii of involved atoms. Recommended crystallographic vdW radii proposed by S. S. Batsanov are used, Inorg. Mater., 2001, 37, 871–995.
24. The “normalized contact” Nc for an interaction involving atoms i and j is the ratio D_ij/(r_vdW,i + r_vdW,j), where D_ij is the experimental distance between i and j and r_vdW,i and r_vdW,j are the vdW radii of i and j.
25. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
26. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
27. D. Schneider, A. Schier and H. Schmidbaur, Dalton Trans., 2004, 1995–2005.
28. R. Kumar, A. Linden and C. Nevado, J. Am. Chem. Soc., 2016, 138, 13790–13793.
29. R. Kumar, A. Linden and C. Nevado, Angew. Chem., Int. Ed., 2015, 54, 14287–14290.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis, spectroscopic, and crystallographic data of examined adducts; details on computational analyses. CCDC 2144963, 2144969, 2144976, 2144977 and 2144991–2144993. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00446a

---