Nanoribbons or weakly connected acenes? The influence of pyrene insertion on linearly extended ring systems†
Qianxiang
Ai
 ,
Tanner
Smith
,
A. D. Thilanga
Liyanage
,
Samuel M.
Mazza
,
Sean R.
Parkin
,
Tanner
Smith
,
A. D. Thilanga
Liyanage
,
Samuel M.
Mazza
,
Sean R.
Parkin
 ,
John E.
Anthony
,
John E.
Anthony
 * and
Chad
Risko
* and
Chad
Risko
 *
*
Department of Chemistry & Center for Applied Energy Research, University of Kentucky, Lexington, Kentucky 40506-0055, USA. E-mail: anthony@uky.edu; chad.risko@uky.edu
First published on 18th November 2021
Abstract
Derived from the lateral fusion of benzene rings, acenes are a class of π-conjugated molecules containing a single aromatic sextet, where system size is inversely correlated with chemical stability. In the pursuit of creating graphene nanoribbons/nanowires, several extended-ring structures have been synthesized through linear combinations of azaacenes and pyrene. Importantly, these extended systems demonstrate enhanced chemical stability and allow for the construction of macromolecular-sized structures. Here, we present a combined quantum-chemical and experimental study to reveal the cost of these improved characteristics in fully carbon-based systems. The results clearly show that pyrene moieties inserted among acene units do not result in long acene-like structures, rather the pyrene-inserted acene is, electronically, a series of (nearly) isolated acenes. The origin of pyrene's electronic blocking effect and implications on oxidized and photoexcited states of these extended-ring systems are detailed. The results of this investigation definitively show that coupling pyrene in an orthogonal orientation (through the 4, 5/9, 10 positions or e/l faces) to acenes should be eschewed if nanographene-/nanowire-like structures are desired.
Introduction
It is remarkable how acenes, rather simple molecular structures built from laterally fused benzene rings and studied by Clar and colleagues in the 1930s,1 continue to attract considerable attention. The acene structure can be readily modified to tune the electronic and optical response of the molecule itself and of solid-state materials derived from molecular building blocks that contain acenes. While acene-based organic semiconductors (OSC) used in field-effect transistors2–4 have contributed enormously to the field of organic electronics, there is growing interest in controlling other physicochemical phenomena that stem from the distinctive molecular and material optoelectronic properties, e.g. singlet fission.5–7The syntheses of long, linear acenes (i.e., more than 5 fused rings), which are of interest as graphene nanoribbons (GNR) or carbon nanowires, present considerable challenges due to their notorious air and light instabilities, which pose strict requirements on the reaction environment.8 While the quest to make long acenes led to the successful synthesis of undecacene, albeit only as isolated molecules under cryogenic conditions,9,10 an interesting byproduct of the pathway to long acenes was the development of a wide range of chemical modifications to increase chemical stability, including the attachment of functional groups (e.g., 6,13-bis(triisopropylsilylethynyl)pentacene),11 heteroatom substitution (e.g., azaacenes),12 and the insertion of polycyclic aromatic hydrocarbon (PAH) units of different structure than the acene into the π-conjugated backbone.13 While the last approach, corroborated by Clar's sextet rule, can improve chemical stabilization such that molecules with 15 rings in a row can exist as single crystals at room temperature,14 there are outstanding questions as to whether the resultant molecule can be considered as an acene or graphene nanoribbon, since the molecular backbone has been significantly altered, often containing multiple aromatic sextets (an acene can only have one).15
Among the PAH-inserted acenes and azaacenes,14,16,17 we are intrigued by pyrene-inserted systems.18 Such molecules can be extended to almost macromolecule size without suffering from significant temperature or air instabilities;19,20 these systems are also able to support a stable dianion, whose ground state is believed to be an open-shell singlet.21 There is evidence, however, that these extended-ring systems are not fully coupled electronically, which could result from steric twisting.22 In pyrene-inserted azaacenes, the aromaticity of the molecular backbone has been suggested to be “broken” at the pyrene units, where weak magnetic shielding has been identified.14 Anomalies have also been reported from the UV-vis absorption spectra of pyrene–azaacene systems: The absorption edge scarcely red-shifts as the number of fused rings increases within a homologous series, suggesting minimal electronic communication among the azaacenes across the inserted pyrene segments.14,19,23 Further, density functional theory (DFT) investigations of pyrene-inserted acene polymers reveal dispersionless valence bands, similarly implying minimal electronic couplings among the acene segments.18
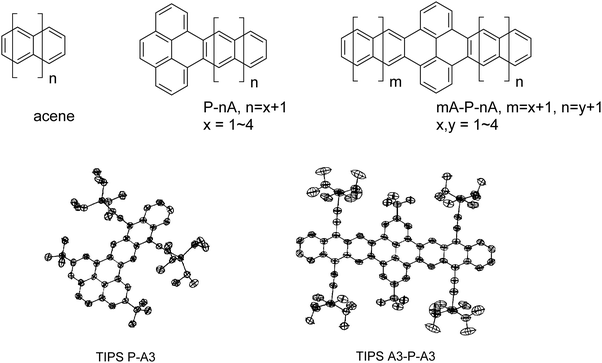
Here we present a joint quantum-chemical and experimental study focused on fully carbon-based pyrene-acene systems to delineate the electronic and optical characteristics of this molecular class. The chemical structures for all molecules under consideration, and their abbreviations, are shown in Fig. 1. These structures are classified as acenes (A), pyrene-acenes (P–A), and acene–pyrene–acenes (A–P–A), where A is n = 2–5 linearly fused rings (from naphthalene to pentacene). Specific molecules are denoted based on the numbers of rings in the acene segments, e.g. P–A3 represents a system comprised of pyrene and anthracene, while A2–P–A3 represents a structure composed of naphthalene, pyrene, and anthracene. Molecules synthesized in this work are labeled by a prefix of “TIPS”, as they contain triisopropylsilylethynyl solubilizing groups. The results of this investigation clearly demonstrate that the seemingly large (aza)acenes – combining the smaller (aza)acene segments and pyrene linkers – are no more than electronically isolated acenes in a chain. We relate this consequence to local structural relaxations, which in turn lead to localized oxidized states and the reported anomalous optical responses, including triplet state localization. Hence, great care needs to be taken when considering reports of extremely long acene and acene-like molecules if they make use of orthogonally coupled pyrene linkers.
Results and discussion
Synthesis and characterization
The overwhelming majority of pyrene–acene hybrid molecules reported to date incorporate nitrogen atoms into the aromatic backbone to simplify synthesis (e.g. pyrene–azaacene systems).13,23–25 Because our interest here is a direct comparison with true acenes, we devised synthetic approaches to the pure carbon chromophores, substituted with t-butyl and triisopropylsilylethynyl (TIPS) groups to enhance stability and solubility. Our approach (Scheme S1, ESI†) begins with methylated pyrenes,26 which are made more scalably from known pyrene dione and pyrene tetraone.27 Benzylic bromination followed by Cava reaction with 1,4-naphthoquinone yielded PA quinone and APA quinone. Unfortunately, the radical bromination of dimethyl pyrene was contaminated with substantial quantities of ring-brominated product, which was addressed following formation of the corresponding acene by debromination with a palladium catalyst in the presence of a mild hydride source. Both products were purified chromatographically and fully characterized including structural analysis by X-ray crystallography, UV-vis absorption spectroscopy and cyclic voltammetry (see ESI,† for details). Thermal ellipsoid plots of TIPS PA (CCDC No. 2097809) and TIPS APA (CCDC No. 2097808) are represented in Fig. 1.Structural, electronic, and redox properties
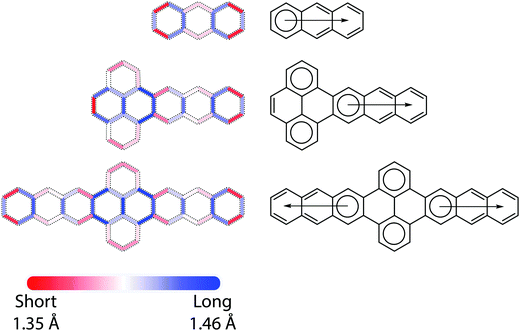
Bond length alternation (BLA) patterns were determined from DFT calculations (see ESI† for more details), as exemplified in Fig. 2. For the trans-polyacetylene-like edges of the acene molecules, the C–C bond length oscillates around the commonly seen aromatic C–C bond length (1.40 Å) from the ends to the middle of molecules with decreasing amplitude. For all P–A and A–P–A molecules, the BLA patterns can be roughly considered as a direct concatenation of those of pyrene and the corresponding acenes, with the exception of the C–C bond shared by these two fragments. In fact, some of the bonds in the pyrene units are so long (1.47–1.48 Å) that P–A (A–P–A) molecules can almost be regarded as a combination of an orthogonal biphenyl unit connected to the acenes by σ bonds. These DFT-determined bond lengths are well supported by crystallographic data, where the bonds connecting the anthracene to the pyrene in TIPS A3–P–A3 are 1.469 Å (and 1.474 Å in TIPS A3–P); we note that in the A–P–A case such a statement remains valid even when acenes with different lengths were appended to each side of the pyrene, e.g. A3–P–A4. Further, results from crystallographic analysis of a TIPS A4–P–A4 derivative show a similar trend (1.474 Å).A chemically intuitive approach to understand such BLA patterns is the Clar formula (Fig. 2), originated from the Clar sextet rule, where the chemical structure with a maximum number of sextets best represents the (localization) behavior of π electrons.1 Within this framework, for acenes of arbitrary length, while degenerate Clar formulae can be drawn based on the number of fused rings, only one sextet, i.e. the migrating sextet,28,29 from their Kekulé formula is allowed without bond breaking (e.g., forming radicals). While the instability of long acenes can be related to the lack of sextets in their Clar formulae, the migrating sextet cannot accurately represent the nature of long acenes: The central rings exhibit higher reactivity and higher aromaticity than the terminal rings. For P–A (A–P–A) molecules, just as with their BLA patterns, the Clar formulae result from merging the Clar formulae of pyrene with the acenes, leading to three (four) isolated sextets. This is also in agreement with the stability of large pyrene–acene systems, e.g., the stability of A3–P–A3 should be comparable to that of an anthracene with a slightly decreased HOMO–LUMO gap, not that of octacene.
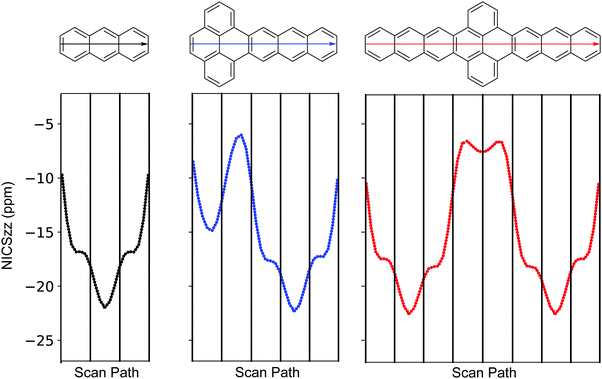
To explore aromaticity in more detail, nucleus-independent chemical shifts (NICS) were calculated using the gauge invariant atomic orbital (GIAO) approach.30,31Fig. 3 shows the NICS-xy scan profile32 of anthracene, P–A3, A3–P–A3, where clear resemblance among the anthracene segments is observed. For A3–P–A3, both rings (two rings on the scan path) at the pyrene segment feature small chemical shifts, while in P–A3 this is true only for the ring next to the anthracene segment (the second ring on the scan path). This observation, along with the BLA patterns and Clar formulae of P–A and A–P–A, suggest that fusing acene to pyrene induces local structural relaxations at the junction, which results in limited orbital interaction among the pyrene and acene segments.
The effect of pyrene insertion can also be seen from the frontier molecular orbitals (FMO) of P–A3 and A3–P–A3 (Fig. S2, ESI†). Both the highest-occupied molecular orbital (HOMO) and lowest-unoccupied molecular orbital (LUMO) of P–A3 localize heavily on the acene segment and the junction ring of pyrene. This localization, along with the resemblance between the HOMO and LUMO of P–A3 and those of tetracene, even that of anthracene to a lesser degree, suggests that the fused pyrene segment, instead of extending the π-conjugation to “five rings in a row”, contributes marginally to the anthracene segment. In the case of A3–P–A3, while the HOMO appears to delocalize along the entire molecular backbone, which was interpreted previously in azaacene–pyrene systems as evidence of extended π-conjugation,14,16 a more appropriate description is that of a tetracene HOMO aligned in a non-interacting tail-to-tail arrangement, just as the LUMO of A3–P–A3 is similar to two isolated tetracene LUMOs. Considering that the HOMO−1 of A3–P–A3 consists of two isolated anthracene HOMO, the small energy splitting (35 meV) between the HOMO and HOMO−1 implies limited interactions among the π orbitals of the pyrene and acene segments, and that the A3–P–A3 system is perhaps representative of a Robin and Day Class II mixed-valence system.33 Such small energy gap between HOMO and HOMO−1 has been reported in pyrene–azaacene systems,19 indicating the generality of the disruptive electronic impact from pyrene insertion. Notably, the effect of pyrene insertion can be understood from MO symmetry: the FMO of pyrene and o-quinodimethane moieties possess mismatched symmetries (Fig. S3, ESI†), which forbids effective MO overlap when they are combined to form P–A2. Thus, fusing a second o-quinodimethane to the other side of the pyrene would lead to limited orbital overlap between the resulting naphthalene segments. The argument of symmetry mismatch implies that other chromophores could have a blocking effect similar to pyrene, e.g., dibenzo(bc,kl)coronene.18
To confirm this assertion, cyclic voltammetry (CV) experiments were performed on both TIPS P–A and TIPS A–P–A (Fig. S5, ESI†). Both derivatives showed a single reduction wave at ≈−1.4 V, with that of the A–P–A derivative showing significant broadening suggesting a two-electron process. Oxidatively, both derivatives underwent oxidation at nearly the same potential (≈1.1 V), with the A–P–A derivative showing evidence of a second oxidation at 1.2 eV. These results suggest that there is minimal-to-no communication between the LUMOs of the anthracenes attached to the pyrene, and only weak interaction among the HOMOs, consistent with the DFT-derived orbital splitting. Further, in the DFT-optimized radical cation state of A3–P–A3, both the structural relaxations and charges are localized at only one of the anthracene segments (Fig. S4, ESI†), lowering the molecular symmetry from D2h to Cs. Such localization gives rise to an intramolecular charge hopping barrier (90 meV, estimated by the energy difference between Cs and D2h conformations of the A3–P–A3 cation), which may limit the potential of A–P–A molecules in transistor applications.34
Optical properties
Excitation energies for low-lying singlet states were determined via linear response time-dependent density functional theory (TDDFT). Fig. 4 shows εS1, the excitation energy of the first singlet excited state, plotted against nxrings, the total number of rings along the long axis for a series of A, P–A, and A–P–A systems. For acenes longer than naphthalene, the first bright excited state (1B2u) is a HOMO→LUMO one-electron transition whose excitation energy decreases with increasing number of fused rings, in agreement with previous studies.35,36 Approximately, εS1P–A(nxrings) can be considered as εS1Acene(nxrings) shifted by one ring along the x-axis, e.g. εS1P–A3 is close to the εs1tetracene. This can be understood by previous MO analyses, as the first excited state of P–A is also dominated by a HOMO→LUMO one-electron transition.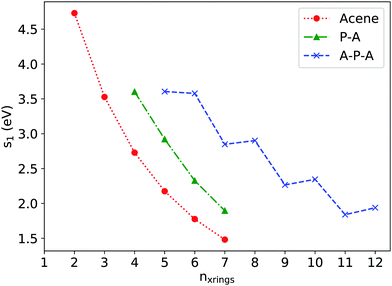 | ||
| Fig. 4 ε S1 as a function of nxrings for acenes, P–A and A–P–A as determined via TDDFT at the (OT)-LC-ωHPBE/Def2TZVP level of theory. | ||
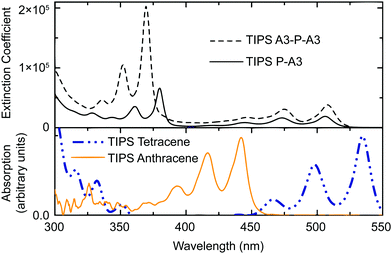
The trend in the TDDFT calculations is confirmed by experimental absorption spectra (Fig. 5), where εS1TIPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P–A3 (2.46 eV) is smaller than εS1TIPS
P–A3 (2.46 eV) is smaller than εS1TIPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anthracene (2.83 eV), but larger than εS1TIPS
anthracene (2.83 eV), but larger than εS1TIPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tetracene (2.32 eV). The 0.14 eV difference between εS1TIPS
tetracene (2.32 eV). The 0.14 eV difference between εS1TIPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tetracene and εS1TIPS
tetracene and εS1TIPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P–A3 is in good agreement with the difference between computed εS1tetracene and εS1P–A3 (0.19 eV). Notably, the absorption cutoffs for both TIPS P–A3 and TIPS A3–P–A3 occur at essentially the same energy, confirming that the pyrene acts as an efficient electronic interruption between the two acene chromophores. Assessment of extinction coefficients shows that while there is no red shift in absorption for the A3–P–A3 compared to the P–A3, the A3–P–A3 absorbs twice as much light in the anthracene regions, again suggesting isolated chromophores.
P–A3 is in good agreement with the difference between computed εS1tetracene and εS1P–A3 (0.19 eV). Notably, the absorption cutoffs for both TIPS P–A3 and TIPS A3–P–A3 occur at essentially the same energy, confirming that the pyrene acts as an efficient electronic interruption between the two acene chromophores. Assessment of extinction coefficients shows that while there is no red shift in absorption for the A3–P–A3 compared to the P–A3, the A3–P–A3 absorbs twice as much light in the anthracene regions, again suggesting isolated chromophores.
Returning to the TDDFT calculations, εS1A–P–A(nxrings) is further shifted along the x-axis when compared with εS1P–A(nxrings) as pyrene insertion breaks the molecular backbone into two shorter acene segments. An odd–even oscillation appears in εS1A–P–A(nxrings), as εS1An–P–An is close to or sometimes even slightly larger than εS1A(n−1)–P–An. Such oscillation can be explained using A2–P–A3 and A3–P–A3 as examples. For A2–P–A3, the first bright excitation can still be described as a HOMO→LUMO transition, with corresponding natural transition orbitals (NTO) shown in Fig. S6 (ESI†), where the electron–hole pair is localized at the side of anthracene segment due to the lowered molecular symmetry (C2v). For A3–P–A3 (D2h), there are two dominant excitation configurations of the first excitation, HOMO(g)→LUMO+1(u) and HOMO−1(u)→LUMO(g) with similar coefficients (0.48 and 0.50, see Fig. S2, ESI† for the MOs), and both resemble the HOMO→LUMO excitation of anthracene. Thus, the excited states for both A2–P–A3 and A3–P–A3 come from anthracene-like excitations, leading to the similar εS1 values. In passing, we note this excitation in A3–P–A3 is always accompanied by an almost degenerate excitation with equally-weighted configurations HOMO(g)→LUMO(g) and HOMO−1(u)→LUMO+1(u), which is dark due to one-photon absorption selection rules (g→u or u→g).
As with the radical-cation state, the first triplet state of A3–P–A3 is localized on one of the acene segments. From the BLA patterns and total spin density (Fig. S7, ESI†), the unpaired electrons are localized at the edges of one anthracene segment, while the other anthracene segment remains in the ground-state-like form. The molecular symmetry is further lowered as the two acene segments deviate from the pyrene plane to form a bent butterfly shape (174° between wings). The adiabatic and vertical triplet energies are estimated to be 1.49 eV and 1.51 eV, respectively. Such triplet state localization in A3–P–A3 is very similar to the case in platinum-acetylide oligomers,37,38 where the optimized triplet state features a distortion around platinum that lowered the symmetry. We hypothesize that such triplet-state localization could be advantageous for singlet fission, as the generated triplets would be spatially separated on a relatively rigid quasi-2D structure (thanks to the pyrene linker).
Conclusion
The structural, electronic, redox, and optical properties of fully carbon-based pyrene-inserted acenes are investigated, along with detailed analyses of their structural relaxation and aromaticity, revealing that pyrene insertion into the backbone effectively blocks electronic communication among acene segments. Newly synthesized pyrene–acene molecules demonstrate nearly zero shift in absorption cutoff after extending the system by three rings, a result that can be traced back to the molecular orbital symmetry of pyrene. The near complete isolation of smaller acene fragments between pyrene units suggests that reported macromolecule-sized ribbons based on this motif, while perhaps interesting from a structural standpoint, are not reasonable models for graphene nanoribbons due to a lack of uninterrupted end-to-end conjugation. While these materials may find use in photophysical applications, their potential as graphene-like systems should be reconsidered.Author contributions
Q. A., J. E. A., and C. R. devised the project. Q. A. carried out all the theoretical investigations, while T. S., A. D. T. L. and S. M. Mazza contributed to molecular synthesis and characterization. S. R. P. solved the X-ray crystal structures. Q. A., J. E. A., and C. R. wrote the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Office of Naval Research (Award No. N00014-18-1-2448 and N00014-16-2390). Portions of this effort were supported by the US. Department of Energy, Office of Basic Energy Sciences (ERW7404). Supercomputing resources were provided by the University of Kentucky Information Technology Department and Center for Computational Sciences (CCS).References
- E. Clar, Ber. Dtsch. Chem. Ges., 1939, 72, 2137–2139 CrossRef.
- Y.-Y. Lin, D. Gundlach, S. F. Nelson and T. N. Jackson, IEEE Trans. Electron Devices, 1997, 44, 1325–1331 CrossRef CAS.
- M. L. Tang, A. D. Reichardt, N. Miyaki, R. M. Stoltenberg and Z. Bao, J. Am. Chem. Soc., 2008, 130, 6064–6065 CrossRef CAS PubMed.
- M. M. Payne, S. R. Parkin, J. E. Anthony, C.-C. Kuo and T. N. Jackson, J. Am. Chem. Soc., 2005, 127, 4986–4987 CrossRef CAS PubMed.
- B. S. Basel, C. Hetzer, J. Zirzlmeier, D. Thiel, R. Guldi, F. Hampel, A. Kahnt, T. Clark, D. M. Guldi and R. R. Tykwinski, Chem. Sci., 2019, 10, 3854–3863 RSC.
- P. M. Zimmerman, Z. Zhang and C. B. Musgrave, Nat. Chem., 2010, 2, 648 CrossRef CAS PubMed.
- T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103 CrossRef PubMed.
- R. Mondal, C. Tonshoff, D. Khon, D. C. Neckers and H. F. Bettinger, J. Am. Chem. Soc., 2009, 131, 14281–14289 CrossRef CAS PubMed.
- R. Zuzak, R. Dorel, M. Kolmer, M. Szymonski, S. Godlewski and A. M. Echavarren, Angew. Chem., Int. Ed., 2018, 57, 10500–10505 CrossRef CAS PubMed.
- B. Shen, J. Tatchen, E. Sanchez-Garcia and H. F. Bettinger, Angew. Chem., Int. Ed., 2018, 57, 10506–10509 CrossRef CAS PubMed.
- J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, J. Am. Chem. Soc., 2001, 123, 9482–9483 CrossRef CAS PubMed.
- B. D. Lindner, J. U. Engelhart, O. Tverskoy, A. L. Appleton, F. Rominger, A. Peters, H. J. Himmel and U. H. Bunz, Angew. Chem., Int. Ed., 2011, 50, 8588–8591 CrossRef CAS PubMed.
- A. H. Endres, M. Schaffroth, F. Paulus, H. Reiss, H. Wadepohl, F. Rominger, R. Kramer and U. H. Bunz, J. Am. Chem. Soc., 2016, 138, 1792–1795 CrossRef CAS PubMed.
- Z. Wang, P. Gu, G. Liu, H. Yao, Y. Wu, Y. Li, G. Rakesh, J. Zhu, H. Fu and Q. Zhang, Chem. Commun., 2017, 53, 7772–7775 RSC.
- M. Müller, L. Ahrens, V. Brosius, J. Freudenberg and U. H. Bunz, J. Mater. Chem. C, 2019, 7, 14011–14034 RSC.
- W. Chen, X. Li, G. Long, Y. Li, R. Ganguly, M. Zhang, N. Aratani, H. Yamada, M. Liu and Q. Zhang, Angew. Chem., Int. Ed., 2018, 57, 13555–13559 CrossRef CAS PubMed.
- M. Feofanov, V. Akhmetov, D. I. Sharapa and K. Amsharov, Org. Lett., 2020, 22, 1698–1702 CrossRef CAS PubMed.
- Q. Ai, K. Jarolimek, S. Mazza, J. E. Anthony and C. Risko, Chem. Mater., 2018, 30, 947–957 CrossRef CAS.
- D. Cortizo-Lacalle, J. P. Mora-Fuentes, K. Strutynski, A. Saeki, M. Melle-Franco and A. Mateo-Alonso, Angew. Chem., Int. Ed., 2018, 57, 703–708 CrossRef CAS.
- B. L. Hu, C. An, M. Wagner, G. Ivanova, A. Ivanova and M. Baumgarten, J. Am. Chem. Soc., 2019, 141, 5130–5134 CrossRef CAS.
- C. Chen, H. Ruan, Z. Feng, Y. Fang, S. Tang, Y. Zhao, G. Tan, Y. Su and X. Wang, Angew. Chem., Int. Ed., 2020, 59, 11794–11799 CrossRef CAS PubMed.
- J. Li, Y. Zhao, J. Lu, G. Li, J. Zhang, Y. Zhao, X. Sun and Q. Zhang, J. Org. Chem., 2015, 80, 109–113 CrossRef CAS PubMed.
- S. More, R. Bhosale, S. Choudhary and A. Mateo-Alonso, Org. Lett., 2012, 14, 4170–4173 CrossRef CAS PubMed.
- B. L. Hu, K. Zhang, C. An, D. Schollmeyer, W. Pisula and M. Baumgarten, Angew. Chem., Int. Ed., 2018, 57, 12375–12379 CrossRef CAS PubMed.
- Z. Wang, J. Miao, G. Long, P. Gu, J. Li, N. Aratani, H. Yamada, B. Liu and Q. Zhang, Asian J. Chem., 2016, 11, 482–485 CrossRef CAS PubMed.
- A. Miyazawa, A. Tsuge, T. Yamato and M. Tashiro, J. Org. Chem., 1991, 56, 4312–4314 CrossRef CAS.
- J. C. Walsh, K.-L. M. Williams, D. Lungerich and G. J. Bodwell, Eur. J. Org. Chem., 2016, 5933–5936 CrossRef CAS.
- D. W. Szczepanik, M. Sola, T. M. Krygowski, H. Szatylowicz, M. Andrzejak, B. Pawelek, J. Dominikowska, M. Kukulka and K. Dyduch, Phys. Chem. Chem. Phys., 2018, 20, 13430–13436 RSC.
- D. Bhattacharya, A. Panda, A. Misra and D. J. Klein, J. Phys. Chem. A, 2014, 118, 4325–4338 CrossRef CAS PubMed.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, J. Chem. Phys., 1996, 104, 5497–5509 CrossRef CAS.
- R. Gershoni-Poranne and A. Stanger, Chemistry, 2014, 20, 5673–5688 CrossRef CAS PubMed.
- M. B. Robin and P. Day, Advances in Inorganic Chemistry and Radiochemistry, Elsevier, 1968, vol. 10, pp. 247–422 Search PubMed.
- Z. Zhang and Q. Zhang, Mater. Chem. Front., 2020, 4, 3419–3432 RSC.
- Y. Yang, E. R. Davidson and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E5098–5107 CrossRef CAS PubMed.
- H. F. Bettinger, C. Tonshoff, M. Doerr and E. Sanchez-Garcia, J. Chem. Theory Comput., 2016, 12, 305–312 CrossRef CAS.
- E. R. Batista and R. L. Martin, J. Phys. Chem. A, 2005, 109, 9856–9859 CrossRef CAS.
- T. M. Cooper, D. M. Krein, A. R. Burke, D. G. McLean, J. E. Rogers, J. E. Slagle and P. A. Fleitz, J. Phys. Chem. A, 2006, 110, 4369–4375 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2097808 and 2097809. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc05193h |
| This journal is © The Royal Society of Chemistry 2021 |