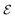Individual particle heating of interacting magnetic nanoparticles at nonzero temperature
Jonathan
Leliaert
 *a,
Javier
Ortega-Julia
*a,
Javier
Ortega-Julia
 b and
Daniel
Ortega
b and
Daniel
Ortega
 bcd
bcd
aDepartment of Solid State Sciences, Ghent University, Ghent, Belgium. E-mail: jonathan.leliaert@ugent.be
bIMDEA Nanoscience, Faraday 9, 28049 Madrid, Spain
cCondensed Matter Physics Department, Faculty of Sciences, Campus Universitario Río San Pedro s/n. 11510 Puerto Real, Cádiz, Spain
dInstitute of Research and Innovation in Biomedical Sciences of the Province of Cádiz (INiBICA), University of Cádiz, 11009 Cádiz, Spain
First published on 26th August 2021
Abstract
Interaction phenomena have become a hot topic in nanotechnology due to their influence on the performance of magnetic nanostructures for biomedical applications. Hysteresis loops give a good account of the particles’ magnetic behaviour, providing valuable clues on subsequent improvements. Nevertheless, the individual hysteresis loops of these systems are also influenced by any potential energy exchanged between the particles, and in contrast to non-interacting particles, are no longer a good measure for the local heat generated by each particle. As of today, there is no method capable of analysing the heat dissipation resulting from the nanoscale magnetisation dynamics in its full generality, i.e. in the presence of interactions and at nonzero temperature (allowing for thermally induced switching), and therefore the means of exploiting these dynamics remain hampered by a lack of understanding. In this work we address this problem by proposing and validating an equation that can be used to resolve the individual heat dissipation of interacting nanoparticles at nonzero temperature. After assessing this equation for different model systems, we have found that the proportion of heat dissipated in each individual particle tends to become more uniformly distributed for larger fields. Our results might have implications for magnetic particle hyperthermia where one of the most long-standing challenges is to achieve a homogeneous therapeutic temperature distribution in the target region during a treatment. Although tackling this issue involves a number of aspects related to the tissues involved, the injected nanoparticles, and the applied magnetic field, we believe that a more homogeneous heating of the particles inside the tumour will help to overcome this challenge.
1 Introduction
Cancer treatment is one of the applications that have been most closely linked to magnetic nanoparticles, perhaps because of the particles’ capability to produce localised heat (hyperthermia) and deliver/release therapeutic agents directly to tumours. Upon applying an ac (or radiofrequency) field, nanoparticles start to dissipate heat due to the generated magnetic losses (reflected in hysteresis loops). For the time being, researchers in the field have been able to make progress towards the clinical implementation of magnetic hyperthermia.1 The two main elements of the therapy, namely magnetic nanoparticles and field applicators, have experienced incremental improvements until clinical trials have started taken place.2 Besides, the availability of new ISO standards around medical applications of magnetic nanocolloids is paving the way towards a more homogeneous deployment of the technique worldwide,3 accelerating a broader adoption in the clinical practice in the short and medium term. However, there is still room for further improvement in some critical aspects, like safety,4–6 given the stringent requirements to be met during the approval of medical devices and drugs.7,8 While this trend towards standardisation has positive connotations for the medical approval process, it also entails increasingly thorough knowledge and control over the physical properties of the chosen magnetic nanoparticles.Concerning the development or improvement of nanoparticles for magnetic hyperthermia, it is difficult to establish a set of general conditions under which magnetic heating effects can be maximised. One of the main reasons is our limited understanding of the physics of single-particle heating, which in turn prevents an adequate consideration of the multi-scale coupling of the magnetic, fluid dynamics and heat exchange processes involved in the therapy. Raikher and Stepanov9 and Muñoz-Menendez et al.10 have proposed both micromagnetic- and Monte Carlo-based models to optimise the single-particle heating effect with respect to different relevant parameters like particle size and polydispersity, as well as the viscosity of the medium. Nevertheless, the corresponding experimental verification is technically challenging, and the other way around: some surprising experimental observations cannot be readily explained from a theoretical point of view. The latter is exemplified by what has been ironically termed by some scientists as “cold hyperthermia”, which is nothing more than achieving cell death without observing an overall heating in the treated culture or tissue. This effect has been observed by Villanueva et al.11 in HeLa cells treated using silica-coated manganese ferrite nanoparticles, Creixell et al.12 in MCF-7 cells treated using EFGR-coated iron oxide nanoparticles and Asín et al.13 in dendritic cells treated using dextran-coated iron oxide nanoparticles. These reports put back under the focus previous theoretical predictions on the feasibility of intracellular hyperthermia, like Rabin's approach neglecting nanoscale heating effects.14
Heat is quickly dissipated from the nanoparticle surface, and this has been verified by dedicated experiments, like the ones by Riedinger et al.15 and Dias et al.16 using thermo-sensitive molecular probes. One of the most recent attempts to measure single particle heating has been carried out by Rodríguez-Rodríguez et al.17 They measured the surface temperature on different magnetic nanoparticle arrangements, namely iron oxide magnetic nanoparticles (IONPs) and SiO2-coated IONPs (SiO2-IONPs) using optical tweezers. It was found that a weakly focused trapping beam in the near infrared induces a temperature rise of ΔT = 14 K with an optical power of 100 mW, whereas a ΔT = 2.4 K increase is deduced from measurements done on SiO2-IONPs. Also Espinosa et al.18 demonstrated the ability to directly determine the local temperature of nanoparticles using an X-ray absorption spectroscopy technique. The combination of accurate theoretical predictions with the nanoscopic experimental validation enabled by these recent advances will be necessary to advance hyperthermia. From a theoretical viewpoint, the main challenge to predict individual nanoparticle heating is that the inter-particle interactions strongly affect each particles’ magnetisation dynamics, and consequently their heating performance. Recently, a method was presented by Muñoz-Menendez et al.19 to estimate the heat generated by each individual particle in an interacting particle ensemble. However, this method is restricted to the field-induced switching of the particles and thus has limited applicability to mirror experimental therapies in which thermal switching of the particles determines the heating rate. In this paper, we extend this approach and propose an equation which allows one to estimate the heat dissipation of individual, interacting, particles that perform thermal switching.
2 Methods
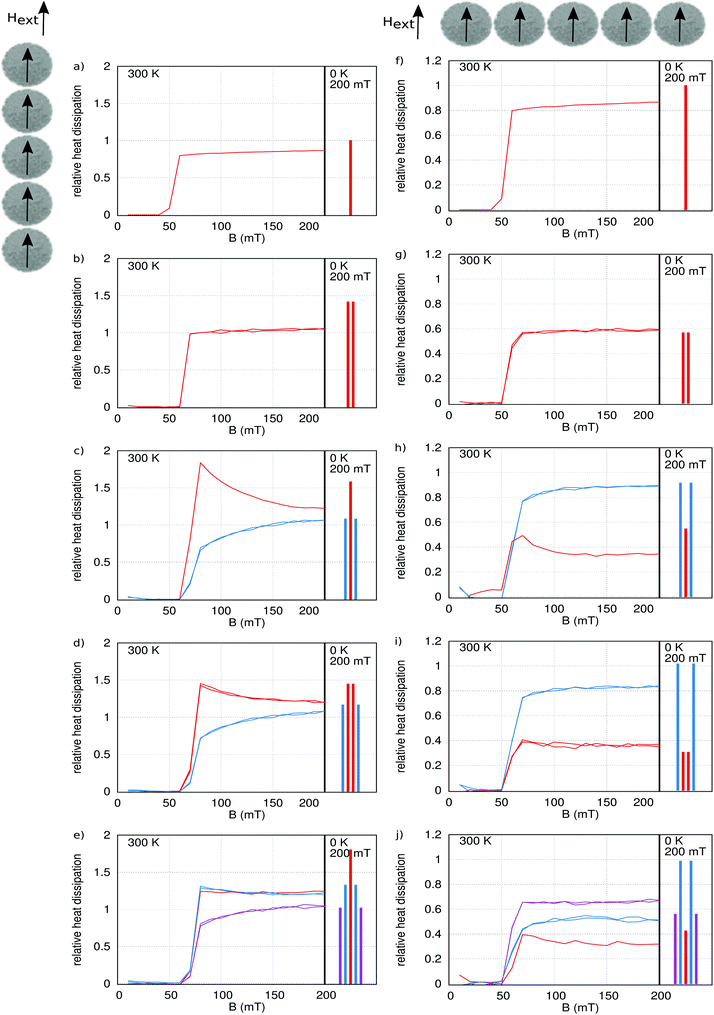
Most magnetic nanoparticles that are used in biomedical applications, like hyperthermia, have a size between a few and a few tens of nanometer.20 This is sufficiently small compared to the exchange length of the materials typically used in these applications (often iron-oxide nanoparticles) to ensure that the particles have a single domain magnetisation state.21 Under this assumption they can be approximated as a macrospin, and their microscopic dynamics can be readily investigated within a micromagnetic framework. In micromagnetism, the magnetisation dynamics of the magnetisation m (with cartesian components mx, my and mz), normalised to the saturation magnetisation Ms, are described by the Landau–Lifshitz–Gilbert equation, eqn (1). | (1) |
Here, γ, α and Ms denote the gyromagnetic ratio, Gilbert damping constant and saturation magnetisation, respectively. Beff is an effective field consisting of the following terms:
| Beff = Bext + Banis + Bth + Bint | (2) |
B
ext denotes an externally applied magnetic field, 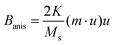 a uniaxial magnetocrystalline anisotropy field with anisotropy constant K and anisotropy axis u. Biint denotes the dipolar field on particle i due to all other particles j ≠ i:
a uniaxial magnetocrystalline anisotropy field with anisotropy constant K and anisotropy axis u. Biint denotes the dipolar field on particle i due to all other particles j ≠ i:
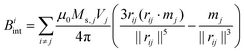 | (3) |
Note that this equation considers the interacting nanoparticles as point dipoles. Additionally, we do not explicitly account for any possible shape anisotropy of non-spherical particles via a demagnetising field, and we will consider only spherical particles in the remainder of this manuscript. The presented methodology can readily be extended to more complex shapes22 by amending eqn (2) with a suitable effective field term, e.g. an additional uniaxial anisotropy term in case of ellipsoidal particles. Finally, Bth is a stochastic thermal field that is uncorrelated in space and time and whose properties are given by eqn (4):23–25
| 〈Bth(t)〉 = 0 | (4a) |
| 〈Bth,i(t)Bth,j(t′)〉 = δijδ(t − t′)q | (4b) |
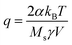 | (4c) |
In the absence of thermal fluctuations, the change in energy density 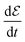 of each individual particle is given by eqn (5)
of each individual particle is given by eqn (5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19,26
19,26
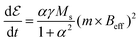 | (5) |
Such changes in 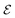 can occur either due to energy dissipation, or through energy exchange with other magnetostatically coupled particles. The former process results in heat generation, whereas in the latter process the total energy of the entire system remains constant.
can occur either due to energy dissipation, or through energy exchange with other magnetostatically coupled particles. The former process results in heat generation, whereas in the latter process the total energy of the entire system remains constant.
At nonzero temperature, i.e., in the presence of thermal fluctuations, the r.h.s. of eqn (5), which accounts for the misalignment of the magnetisation with the stochastic thermal field, is always positive as it is proportional to (m × Beff)2. Using an unaltered form of eqn (5), in which Beff now contains a contribution of the thermal field Bth, would therefore imply that a nanoparticle at nonzero temperature would continuously dissipate energy, thereby heating up. This can't be correct, because in the absence of any externally applied fields, such a particle is in thermodynamic equilibrium with its environment, which implies a constant temperature. This apparent contradiction demonstrates the necessity of an additional term 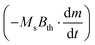 , which accounts for the energy exchange with the heat bath by the random thermal fluctuations.
, which accounts for the energy exchange with the heat bath by the random thermal fluctuations.
The key methodological advance presented in this paper thus is eqn (6).
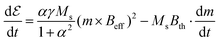 | (6) |
In the following sections, we will validate eqn (6) by numerically integrating the LLG-equation for different systems using the macrospin simulation tool Vinamax.27 The material parameters, specified below, were chosen such that the different examples clearly demonstrate different physical aspects of the systems under study, allowing us to compare the numerical results with their analytical counterparts, without any loss of generality. Because of the universality of eqn (6), our conclusions can readily be extended to other, more complex, systems with material parameters closer to those of other experimentally realisable systems. Furthermore, similar to the approach used to extend the stochastic thermal field derived for uniformly magnetised particles23 to a finite-difference cell-based method,24 our results can be extended to a micromagnetic framework of continuous structures, in which the energy dissipation in each finite-difference cell can be tracked. Such an approach would for instance allow to investigate the heat dissipation of core–shell particles displaying complex non-uniform reversal modes.28
3 Results and discussion
3.1 Non-interacting particles
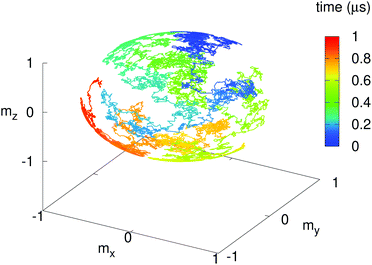
Fig. 1 shows typical magnetisation dynamics for such a system over a timescale of 1 μs. It shows the random walk that the magnetisation performs on the unit sphere as it is driven by the thermal field for a 22 nm diameter nanoparticle with Ms = 400 kA m−1 and α = 0.01 at a temperature of 300 K.
Because the potential energy landscape of the particle is completely flat, the particle has no way available to it to store energy and thus the first and second term in eqn (6) need to cancel each other out identically in order to keep the particle at a constant energy, in thermodynamic equilibrium with its environment.
A bit of algebra shows that this is indeed the case.
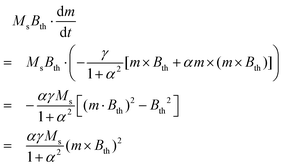 | (7) |
Note the necessity of the factor 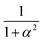 in the first term of eqn (6) to accurately take the dissipated energy into account.26
in the first term of eqn (6) to accurately take the dissipated energy into account.26
Such a particle still is in thermodynamic equilibrium with its environment, but in contrast to the previous example, the anisotropy energy landscape endows the particle with the ability to store energy by misaligning the magnetisation with the anisotropy axis. Therefore we expect the dissipated energy to vanish only when averaged over a sufficiently long time, instead of always being identically zero.
Indeed, in thermodynamic equilibrium, we expect each magnetisation direction θ (with θ = arccos(mz) the azimuthal angle of the magnetisation in a spherical coordinate system) to be occupied by multiplying its density of states with a Boltzmann factor that accounts for the energy of each state, eqn (8).
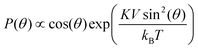 | (8) |
The validity of this equation is confirmed by Fig. 2 for a system identical to the one discussed in section 3.1.1, but with uniaxial anisotropy constant K = 5 kJ m−3.
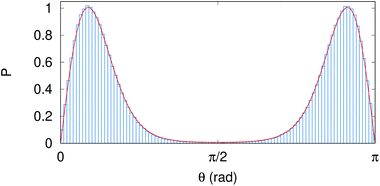 | ||
| Fig. 2 Probability with maximum normalised to 1, P, to find the magnetisation under an angle θ with respect to the anisotropy easy axis, as extracted from simulations (blue bars) and eqn (8) (red line). | ||
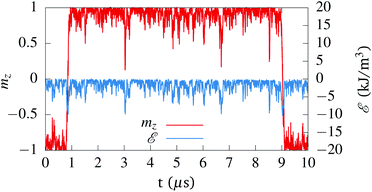
Fig. 3 shows the magnetisation along the z-axis (red line) and the dissipated energy density (blue line). The dissipated energy remains constant on average. However, due to the system's ability to store energy it is not longer identically zero, as was the case in section 3.1.1. In practice it shows noisy peaks in the negative direction, meaning that the system absorbs, and subsequently releases again, a bit of thermal energy from its environment. This makes sense, as the system was initialised in its minimum energy state with the magnetisation aligned with the anisotropy axis, so it does not have any energy available to dissipate, which results in an upper limit of 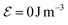 . It is worth noting that the biggest troughs in the energy density are located at switching events (when the magnetisation, shown in the red line, switches from the mz = 1 to mz = −1 direction or vice versa), where the system quickly dissipates all the energy it had accumulated when it overcomes the anisotropy energy barrier.
. It is worth noting that the biggest troughs in the energy density are located at switching events (when the magnetisation, shown in the red line, switches from the mz = 1 to mz = −1 direction or vice versa), where the system quickly dissipates all the energy it had accumulated when it overcomes the anisotropy energy barrier.
3.2 Non-interacting particles in the presence of externally applied fields
Bext = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πft)ez cos(2πft)ez | (9) |
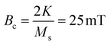 , whose surface thus corresponds to a dissipated energy per particle volume of 4BcMs = 80 kJ m−3.
, whose surface thus corresponds to a dissipated energy per particle volume of 4BcMs = 80 kJ m−3.
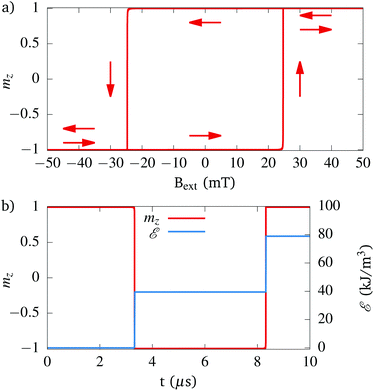
The hysteresis loop shown in Fig. 4a is in perfect agreement with this picture and shows a rectangular loop with two switching events at −25 mT and 25 mT respectively. Fig. 4b shows the magnetisation as function of time (red line), and the energy dissipated as heat in this system (blue line). This result shows that the system only dissipates heat during the irreversible jumps and after one complete loop (2 switches) indeed amounts to 80 kJ m−3, as expected from theory.
Fig. 5a shows the hysteresis loop for an ensemble of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles excited with a time-varying field [see eqn (9)] with amplitudes A = 50 mT and A = 10 mT. The largest amplitude resulted in the rectangular hysteresis loop shown in Fig. 4a in the absence of thermal fluctuations. At nonzero temperature, the loop is no longer rectangular but “lemon-shaped” and shows a smaller coercivity because of the thermal switching that takes place already before the deterministic field-driven switch at 25 mT. Similarly, we observe a small hysteresis loop even for an excitation field of 10 mT, which is driven solely by thermally induced switching. The area of these loops are 59
000 particles excited with a time-varying field [see eqn (9)] with amplitudes A = 50 mT and A = 10 mT. The largest amplitude resulted in the rectangular hysteresis loop shown in Fig. 4a in the absence of thermal fluctuations. At nonzero temperature, the loop is no longer rectangular but “lemon-shaped” and shows a smaller coercivity because of the thermal switching that takes place already before the deterministic field-driven switch at 25 mT. Similarly, we observe a small hysteresis loop even for an excitation field of 10 mT, which is driven solely by thermally induced switching. The area of these loops are 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 kJ m−3 and 6789 kJ m−3, respectively. For non-interacting particles this should agree with the heat dissipation estimated using eqn (6).19 To verify this, the average heat dissipated by a single particle was estimated from an additional simulation, of which the first 10 periods are shown in Fig. 5b. We observe that for A = 50 mT, we see the expected 2 switching events per period, whereas the particle that is excited by the 10 mT field, often does not switch at all for a few periods, resulting in a much smaller heat average dissipation. The dissipated heat per period (averaged over 500 periods) is estimated as 59
214 kJ m−3 and 6789 kJ m−3, respectively. For non-interacting particles this should agree with the heat dissipation estimated using eqn (6).19 To verify this, the average heat dissipated by a single particle was estimated from an additional simulation, of which the first 10 periods are shown in Fig. 5b. We observe that for A = 50 mT, we see the expected 2 switching events per period, whereas the particle that is excited by the 10 mT field, often does not switch at all for a few periods, resulting in a much smaller heat average dissipation. The dissipated heat per period (averaged over 500 periods) is estimated as 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 kJ m−3 and 6778 kJ m−3, respectively, and, as expected, is in excellent agreement with the areas of the corresponding hysteresis loops.
850 kJ m−3 and 6778 kJ m−3, respectively, and, as expected, is in excellent agreement with the areas of the corresponding hysteresis loops.
Together, all previous results confirm the validity of eqn (6) to estimate the dissipated heat of magnetic nanoparticles at nonzero temperatures by comparing the estimates with either analytical counterparts or estimates obtained with other, established, methods. In the next section, a model system will be presented of 2 interacting particles, demonstrating how eqn (6) can be used to gain physical insights in the energetics of the dynamical processes that take place in interacting particles, at nonzero temperatures, as they are driven by an externally applied field, which is the case in any magnetic particle hyperthermia experiment.
3.3 Two interacting particles
This section will demonstrate the main benefit of using equations like eqn (5) and (6), which is that they allow one to estimate the local heat dissipation in a system of interacting nanoparticles. Such an approach is necessary because the hysteresis loops of the individual particles do not account for the potential energy exchanged between the interacting particles, and, in contrast to the case of non-interacting particles, are therefore no longer a correct measured for the heat dissipated by the individual particles.19 Additionally, as argued in the method section, at nonzero temperatures, only eqn (6) yields a correct estimate due to the additional term which accounts for the energy exchange with the heat bath by the random thermal fluctuations.Our model system consists of 2 nanoparticles with diameter equal to 22 nm, placed next to each other along the z-axis with centres spaced 34 nm apart. The particles have a saturation magnetisation Ms of 800 kA m−1, Gilbert damping α = 0.01 and an uniaxial anisotropy axis that is slightly offset from the z-axis (by about 0.25 degrees) to avoid cases where the system numerically gets stuck in an unstable state. The only property in which these particles differ are their anisotropy constant K which equals 20 kJ m−3 for the first particle and 75 kJ m−3 for the second particle. Note that we chose large, well separated values of K to clearly discern the different heating regimes.
We investigate the heat dissipated by each of these particles as function of excitation field strength in 4 distinct cases: at 0 K and at 300 K, and with, and without accounting for the inter-particle interactions. For the simulations at 300 K, the shown results are averaged over 1000 periods of the excitation field. The results of these simulations are shown in Fig. 6.
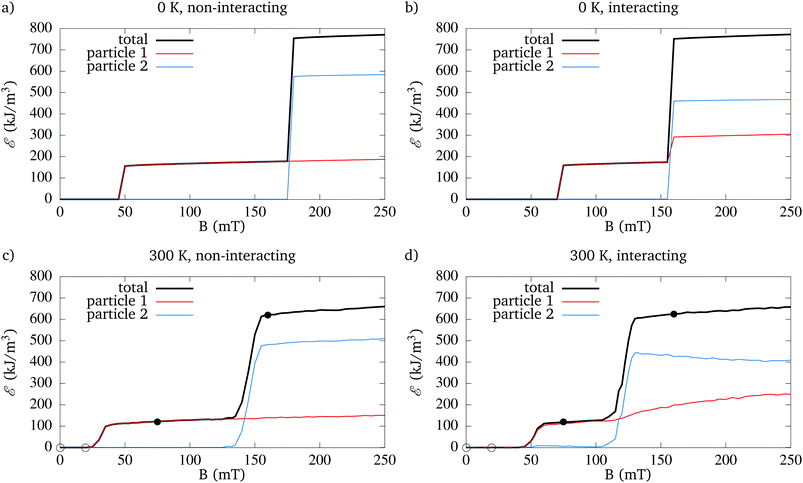 | ||
| Fig. 6 Dissipated heat per excitation field period as function of excitation field strength. The dissipated heat is shown for the two individual particles (red and blue lines) and their sum total (black lines). The different panels show the heat dissipation at 0 K [panels (a) and (b)] and at 300 K [panels (c) and (d)], and in the absence [panels (a) and (c)] and presence [panels (b) and (d)] of magnetostatic inter-particle interactions. The open and filled dots correspond to the cases highlighted in Fig. 7 and 8, respectively. | ||
Fig. 6a depicts the simplest case corresponding to 2 non-interacting particles at 0 K. For this case, we can compare the obtained results with analytical predictions, i.e. that the first particle should start to show switching behaviour from an excitation field of 50 mT onward, in which case it should dissipate 160 kJ m−3 per hysteresis cycle. The second particle is predicted to switch from 187.5 mT onward, and should dissipated 600 kJ m−3 per hysteresis cycle. Generally, Fig. 6a is in agreement with these predictions, except for a few slight deviations (the switching fields and dissipated energy are slightly lower and show a rising trend as function of the excitation field amplitude). This can be explained by the fact that anisotropy axes are slightly offset from the z-axis and the combination of a relatively low damping and large excitation frequency, which cause the system to behave slightly different from its idealised quasistatic analytical prediction.
As compared with the previous case, Fig. 6b, in which interactions are included, shows the following interesting features. First, the interactions cause the switching field for the first particle to increase, and for the second particle to decrease. Next, as already described in Muñoz-Menendez et al.,19 the switching of the second particle causes a non-adiabatic intrawell change in the magnetisation direction of particle 1, causing it to dissipate some of the heat associated with this switching event. This has no impact on the total dissipated heat, but causes particle 1 to dissipate more heat (and particle 2 correspondingly less heat) than the case in which these particles did not interact with each other. Additionally, because the switching field of the second particle is lower than it was in the non-interacting case, high total heat dissipation can be achieved at a lower applied field amplitude.
Panels (c) and (d) show the same systems, now simulated at 300 K. In the case of non-interacting particles, our conclusions are the same as the ones drawn in section 3.2.2, i.e. that thermal switching lowers the switching field, but also results in a slightly lower heat dissipation as compared to the athermal case.
In the final and most realistic case where both interactions and thermal fluctuations are considered, the switching fields are again lower than they were in the absence of thermal fluctuations due to thermal switching events. An intriguing second observation is that the proportion of the heat that is dissipated in each particle (in case the excitation field is sufficiently strong to switch both particles) is no longer constant, but instead becomes a function of the field amplitude. This behaviour has important implications for hyperthermia applications as it might allow to tune the amount of heat generated by different particles. Even though larger fields might not lead to a significant additional total heating, they might help to reach a more uniform heating performance, even when using particles with very different properties.
We continue with a detailed look at a few highlighted cases. Fig. 7 shows the heat dissipation as function of time for both particles in the absence of field (top row) and in an applied field with amplitude of 20 mT (bottom row). Fig. 7a shows the total dissipated heat in the absence of interactions. As we already established in section 3.1.2 and shown in Fig. 3, the dissipated heat fluctuates around 0 for both particles (note that we offset the dissipated heat of particle 2 by −8 kJ m−3 for clarity).
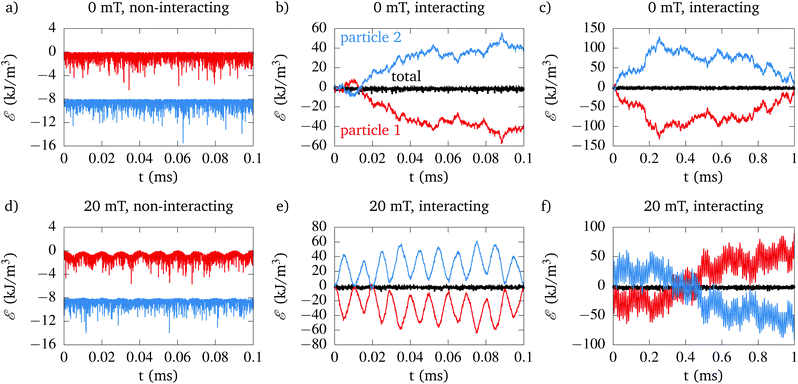 | ||
| Fig. 7 Dissipated heat as function of time for an excitation field strength of 0 mT [panels (a) to (c)] and 20 mT [panels (d) to (f)]. The dissipated heat is shown for the two individual particles (red and blue lines) and their sum total (black lines). Panels (a) and (c) show the heat dissipated for non-interacting particles (where the blue line is offset by −8 kJ m−3 for clarity. Panels (b), (c), (e) and (f) show the heat dissipated in the same system, including magnetostatic inter-particle interactions. Note that panels (c) and (f) show the results of the same simulation as panels (b) and (e), extended to a longer timescale. These figures correspond to the specific cases highlighted with open dots in Fig. 6. | ||
When considering interacting particles, as expected, the total dissipated energy again fluctuates around zero. However, the heat dissipated by the individual particles deviates much further from zero, meaning that it is possible for a particle to extract heat from its environment, exchange this energy with other particles via the magnetostatic field, where it is subsequently dissipated. These fluctuations average out over time, but interestingly there can be a slight imbalance sustained on the timescale of milliseconds, as is the case for the example shown in Fig. 7b and c, where panel (b) zooms in on the first 0.1 ms of the data shown in panel (c).
The specific heat capacity of iron-oxide is 3.48 MJ m−3 K−1,19 so the observed imbalance of 100 kJ m−3 would correspond to a particle temperature difference of about 25 mK, proving that this imbalance is quite small. The simulations we performed also assumed a heat bath with fixed temperature of 300K. In reality the local temperature around the particle would slightly rise as energy is dissipated into it (or fall when energy is extracted from it). This causes a thermal gradient that would counteract the simulated imbalance. Additional simulations (not shown) for this specific case show that two interacting particles at two different temperatures exchange energy at a rate of approximately 15.5–16 MJ m−3 K−1 s−1.
The heat dissipated due to irreversible switching in a single period of the field excitation is also of the order of 100 kJ m−3 (see Fig. 6), meaning that in the theoretical case in which all heat would be retained at the particle it would heat up by a few mK, in line with the figure reported in ref. 19. Such a large temperature increase is clearly impossible and is readily explained by the false assumption that the particle heating does not cause any temperature changes to its environment (i.e. the heat capacity of the heat bath is infinitely large). This assumption is clearly invalid as the entire point of e.g. magnetic nanoparticle hyperthermia is to heat up the particle's surrounding tissues. As modelling the heat flow outside of the particles lies beyond the scope of this work, we abandon this discussion here.
Panels (d)–(f) show the dissipated heat of the same systems in the presence of an applied field with amplitude of 20 mT. This field amplitude is too low to sufficiently lower the switching barrier to see thermal switching, so there is no observed net energy dissipation. What is however visible in panel (d) (for the non-interacting particles) is that the dissipated heat sinusoidally varies with the same frequency as the excitation field (i.e. 100 kHz). This is a physically interesting phenomenon, where the particles periodically extract and dissipate heat from their environment. Microscopically this can be explained as follows: when the field is aligned with the magnetisation direction, the potential energy well that the magnetisation resides in is quite deep and steep. The system will thus dissipate energy as the magnetisation is forced to relax towards this direction. If, half a period later, the applied field is pointing in the opposite direction, it partially counteracts the anisotropy field, which lowers the energy barrier and allows the magnetisation to make much larger excursions from the z-axis using its thermal energy budget corresponding to the environment temperature. As the magnetisation starts off from a “non-thermalised” direction quite closely aligned with the z-axis, it thus extracts energy from the heat bath to perform this motion. Subsequently, as the field changes direction, the magnetisation will dissipate this energy again and the process starts over again. Because the anisotropy constant is much lower for particle 1 than for particle 2, the fluctuations are larger for particle 1. Note that the line depicting the energy dissipation for particle 2 was again shifted by −8 kJ m−3 for clarity.
When also considering inter-particle interactions (panels (e) and (f)), the total energy again displays the same small sinusoidal variations. However, due to their magnetostatic coupling the particles also exchange a lot of energy, thereby amplifying this periodic energy extraction and dissipation. Interestingly, when the field is aligned with the magnetisation direction, particle 1 is extracting energy from particle 2, which it then returns when the field is counter-aligned with the magnetisation. On top of this process, there is a similar longer timescale energy exchange visible, similar to the one observed in the absence of external fields.
Finally, let's have a look at the dynamics at larger field amplitudes, at which the magnetisation does switch. Fig. 8a shows a typical hysteresis loop for an applied field amplitude of 75 mT and 160 mT. In the former case, only particle 1 switches, whereas both particles switch in the latter case. Note that the hysteresis loop for particle 1 becomes wider and the one for particle 2 narrower, resulting in more (or less) heat dissipated in these respective particles as compared to the non-interacting case. This is also corroborated by Fig. 6.
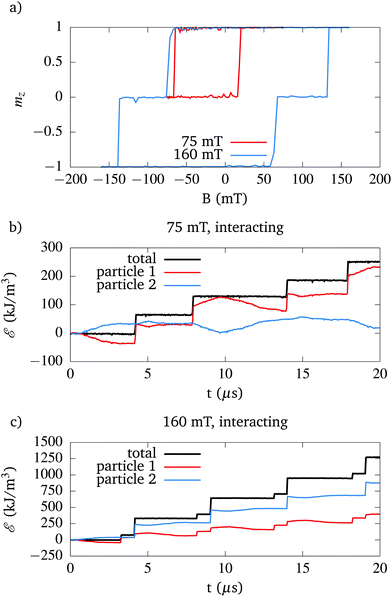 | ||
| Fig. 8 (a) Hysteresis loops for particles, excited with an sinusoidal externally applied magnetic field with amplitudes of 75 mT (red lines) and 160 mT (blue lines). (b) and (c) Dissipated heat by individual particles as function of time for 10 periods of the field excitation with amplitude 75 mT [panel (b)] and 160 mT [panel (c)], respectively. These figures correspond to the cases highlighted with filled dots in Fig. 6. | ||
Fig. 8b shows that the total dissipated energy rises in a stepwise fashion, each time particle 1 switches, and this heat is almost exclusively dissipated in particle 1. Once the field amplitude is sufficiently large to overcome (whether deterministically or by thermal assistance) the switching barrier of the second particle, heat is dissipated in both particles. Interestingly, and as already explained in Muñoz-Menendez et al.,19 the switching of particle 2 causes non-reversible intra-well dynamics in particle 1, which also cause it to dissipate heat. In contrast to the athermal simulations, the simulations at nonzero temperature show a field dependence of which percentage of heat is dissipated in which particles, with a tendency to a more equal heating at larger fields.
3.4 Chains of interacting particles
Finally, we will consider the case of a chain of identical, interacting particles. To this end, we investigate the dissipated heat in particles with material parameters corresponding to iron oxide29 (saturation magnetisation Ms = 360 kA m−1, uniaxial anisotropy constant K = 12.5 kJ m−3, exchange stiffness constant Aex = 26.4 pJ m−1, Gilbert damping α = 0.1). The particles have a diameter of 40 nm, for which we checked with the micromagnetic software package mumax3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 that they have a single domain magnetisation. Chains with a length of 1, 2, 3, 4 and 5 identical particles with their centres spaced 50 nm apart were simulated. The lowest energy configuration is the one in which the magnetisation, the magnetocrystalline anisotropy axes and the chain length axis are all aligned with each other. Next to this configuration, we also simulate the configuration in which the magnetocrystalline anisotropy axis lies perpendicular to the length axis of the chain, similar to the approach presented in Torche et al.31 in which dynamics in both geometries were evaluated using a statistical model. The external magnetic field was applied along the length axis in each case. We simulated these configurations at a temperature of 300 K and of 0 K.
30 that they have a single domain magnetisation. Chains with a length of 1, 2, 3, 4 and 5 identical particles with their centres spaced 50 nm apart were simulated. The lowest energy configuration is the one in which the magnetisation, the magnetocrystalline anisotropy axes and the chain length axis are all aligned with each other. Next to this configuration, we also simulate the configuration in which the magnetocrystalline anisotropy axis lies perpendicular to the length axis of the chain, similar to the approach presented in Torche et al.31 in which dynamics in both geometries were evaluated using a statistical model. The external magnetic field was applied along the length axis in each case. We simulated these configurations at a temperature of 300 K and of 0 K.
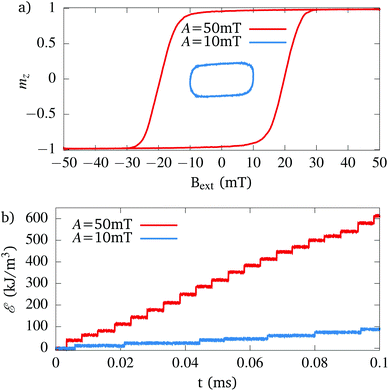
The results are presented in Fig. 9. Similarly to the case shown in Fig. 6b, the lack of thermally induced switching at zero temperature leads the dissipated heat to show a step function from zero to its final value, without any intermediate features as function of applied field strength. Therefore, for the 0 K case, we only show the results obtained at 200 mT. They can easily be compared to the corresponding values at 300 K, which are shown adjacently. Still at 0 K, the heating in the chains is shown using bars to clearly illustrate the contributions of the individual particles. The colour code shown in these bars corresponds to the lines in the field-dependent results obtained at 300 K, again to allow an easy comparison. All heating is relative to the heat dissipated by a single particle at zero temperature.
Panels (a) to (e) show the results of the chains with the anisotropy parallel to the chain axis. In this case, the magnetostatic inter-particle interactions result in an increase of the switching barrier, and correspondingly in a larger heat dissipation. This configuration also corresponds to the one found in magnetosomes, where a similar increase in heat dissipation is observed as compared to individual nanoparticles.32 As expected, both at 0 K and at 300 K the results show that the particles in the centre of the chain dissipate more heat than the outer ones, because they feel the largest magnetostatic field. Interestingly, for the results simulated at 300 K we see that the heat dissipated by the individual particles strongly depends on the applied field strength, with a very strong heat dissipation of the centre ones just above the switching threshold, and a less strong heat dissipation for the outer ones. Similar to what we observed in the previous sections, the homogeneity of the heat dissipation improves for larger fields. For the five-particle chain, we see that the 3 middle particles show a similar heat dissipation, and a smaller contribution from the two outermost ones, which corroborates the results presented in Torche et al.31 and contrasts the result obtained when not explicitly accounting for the thermal switching in which the centre one dissipates much more heat.
Panels (f) to (j) show similar results for chains of particles with their anisotropy axes perpendicular to the chain length axis. In this case, the interparticle interaction results in a lower coercive field, and correspondingly smaller heat dissipation as compared to the non-interacting case. The most interesting result was obtained for the 5-particle chain. In contrast to our expectations, at 0 K, the two outermost particles show less heat dissipation than their neighbours. However, the results obtained at 300 K do corroborate Torche et al.31, and show the expected order. For these configurations, there is a smaller field dependence of the relative dissipated heat of the individual particles, and after a small transient region just above the switching threshold it remains constant as function of applied field.
Although the particle system under study here is quite different from the one in Ref. 31, there is a very good qualitative agreement between both our studies with respect to which particles in the chain dissipated the most heat for all simulated configurations. This agreement further confirms the validity of both our eqn (6) as well as the statistical approach of Torche et al.31 Additionally, these results show that for the case most likely to be found in reality (chains in which the anisotropy axes align with the chain length axis, as encountered e.g. in magnetosomes) the heat dissipation becomes more homogeneous with larger applied fields, whereas the homogeneity remains rather constant in the case of perpendicular anisotropy. This result further confirms our conclusions drawn in section 3.3.
4 Conclusion
In order to deepen the understanding of the underlying magnetisation dynamics that drive magnetic particle hyperthermia, we have presented an equation, eqn (6), which allows to estimate the individual heat dissipation of interacting nanoparticles at nonzero temperature. Because this equation is readily integrated in a numerical micromagnetic framework, it can be used on arbitrarily complex systems. This equation was validated against several simple cases of non-interacting particles for which it could be compared against analytical solutions or other methods (i.e. integrating the area of the resulting hysteresis loop) to estimate the dissipated heat. In sections 3.3 and 3.4, systems of interacting particles at nonzero temperature were investigated. These systems showed very rich dynamics, and allow us to draw the following conclusions. The presence of inter-particle interactions impacts the switching field, and can result in both higher or lower switching fields, and correspondingly higher or lower heat dissipation in the respective particles. Nonzero temperatures invariably lead to lower switching fields, which results in a region where the heat dissipation is higher than it would have been in the absence of thermal fluctuations. Our most interesting observation is that in the presence of both interactions and thermal fluctuations, which is always the case in reality, the total dissipated heat per hysteresis cycle is independent of the excitation field strength to a large extent at sufficiently high fields. Nevertheless, the proportion of heat dissipated in each individual particle tends to become more uniformly distributed for larger fields. Since the equation considers more realistic conditions than other models, we anticipate that it will have direct applications in magnetic hyperthermia treatment planning. More specifically, the use of the proposed equation would simplify the selection process of optimum nanoparticle distributions, or optimal excitation fields, leading to the most homogeneous tumour heating. Its flexibility and simplicity allow it to be included in more complex multi-scale, multi-physics simulations without negatively impacting the overall computational time or calculation stability.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the Fonds Wetenschappelijk Onderzoek (FWO-Vlaanderen) with a postdoctoral fellowship (J. L.). J. L. gratefully acknowledges J. Mulkers for fruitful discussions. This work has been also supported by the NoCanTher project, which has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no 685795. The authors acknowledge support from the COST Association through the COST action “MyWAVE” (CA17115). D. O. and J. O. J. are thankful for funding support from the Spanish Ministry of Science, Innovation under Contract no. PEJ2018-004866-A, grant PID2020-117544RB-I00, the Ramón y Cajal grant RYC2018-025253-I and Research Networks grants RED2018-102626-T. The support from the Ministry of Economy and Competitiveness through the grants MAT2017-85617-R and the “Severo Ochoa” Program for Centers of Excellence in R&D (SEV-2016-0686) is also acknowledged.References
- I. Rubia-Rodríguez, A. Santana-Otero, S. Spassov, E. Tombácz, C. Johansson, P. De La Presa, F. J. Teran, M. Del Puerto, S. Veintemillas-Verdaguer, N. T. K. Thanh, M. O. Besenhard, C. Wilhelm, F. Gazeau, Q. Harmer, E. Mayes, B. B. Manshian, S. J. Soenen, Y. Gu, A. Millán, E. K. Efthimiadou, J. Gaudet, P. Goodwill, J. Mansfield, U. Steinhoff, J. Wells, F. Wiekhorst and D. Ortega, Materials, 2021, 14, 706 CrossRef PubMed.
- D. Cabrera, I. Rubia-Rodríguez, E. Garaio, F. Plazaola, L. Dupré, N. Farrow, F. J. Terán and D. Ortega, Nanomaterials for Magnetic and Optical Hyperthermia Applications, 2019, pp. 111–138 Search PubMed.
- J. Wells, D. Ortega, U. Steinhoff, S. Dutz, E. Garaio, O. Sandre, E. Natividad, M. M. Cruz, F. Brero, P. Southern, Q. A. Pankhurst and S. Spassov, Int. J. Hyperthermia, 2019, 38, 447–460 CrossRef PubMed.
- I. Rubia-Rodríguez, L. Zilberti, A. Arduino, O. Bottauscio, M. Chiampi and D. Ortega, Int. J. Hyperthermia, 2021, 38(1), 846–861 CrossRef PubMed.
- P. Southern and Q. A. Pankhurst, Int. J. Hyperthermia, 2018, 34, 671–686 CrossRef CAS PubMed.
- P. Southern and Q. A. Pankhurst, J. Magn. Magn. Mater., 2019, 473, 74–78 CrossRef CAS.
- European Parliament and the council of the European Union, Regulation (EU) 2017/745 on medical devices, amending Directive 2001/83/EC, Regulation (EC) No 178/2002 and Regulation (EC) No 1223/2009 and repealing Council Directives 90/385/EEC and 93/42/EEC, http://data.europa.eu/eli/reg/2017/745/oj, 2017, accessed on 22/04/2021.
- FDA guidance, Classification of Products as Drugs and Devices and Additional Product Classification Issues: Guidance for Industry and FDA Staff, https://www.fda.gov/regulatory-information/search-fda-guidance-documents/classification-products-drugs-and-devices-and-additional-product-classification-issues, 2018, accessed on 22/04/2021.
- Y. Raikher and V. Stepanov, J. Magn. Magn. Mater., 2014, 368, 421–427 CrossRef.
- C. Muñoz-Menendez, I. Conde-Leboran, D. Baldomir, O. Chubykalo-Fesenko and D. Serantes, Phys. Chem. Chem. Phys., 2015, 17(41), 27812–27820 RSC.
- A. Villanueva, P. de la Presa, J. M. Alonso, T. Rueda, A. Martínez, P. Crespo, M. M. Morales, M. A. Gonzalez-Fernandez, J. Valdés and G. Rivero, J. Phys. Chem. C, 2010, 114, 1976–1981 CrossRef CAS.
- M. Creixell, A. C. Bohórquez, M. Torres-Lugo and C. Rinaldi, ACS Nano, 2011, 5, 7124–7129 CrossRef CAS PubMed.
- L. Asín, M. Ibarra, A. Tres and G. F. Goya, Pharm. Res., 2012, 29, 1319–1327 CrossRef PubMed.
- Y. Rabin, Int. J. Hyperthermia, 2009, 18, 194–202 CrossRef PubMed.
- A. Riedinger, P. Guardia, A. Curcio, M. A. Garcia, R. Cingolani, L. Manna and T. Pellegrino, Nano Lett., 2013, 13, 2399–2406 CrossRef CAS PubMed.
- J. Dias, M. Moros, P. del Pino, S. Rivera, V. Grazú and J. de la Fuente, Angew. Chem., Int. Ed., 2013, 52, 11526–11529 CrossRef CAS PubMed.
- H. Rodríguez-Rodríguez, G. Salas and R. Arias-Gonzalez, J. Phys. Chem. Lett., 2020, 11, 2182–2187 CrossRef PubMed.
- A. Espinosa, G. R. Castro, J. Reguera, C. Castellano, J. Castillo, J. Camarero, C. Wilhelm, M. A. García and A. Muñoz Noval, Nano Lett., 2021, 21(1), 769–777 CrossRef CAS PubMed.
- C. Muñoz-Menendez, D. Serantes, O. Chubykalo-Fesenko, S. Ruta, O. Hovorka, P. Nieves, K. L. Livesey, D. Baldomir and R. Chantrell, Phys. Rev. B, 2020, 102, 214412 CrossRef.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- S. Tong, H. Zhu and G. Bao, Mater. Today, 2019, 31, 86–99 CrossRef CAS PubMed.
- H. Mamiya, H. Fukumoto, J. L. Cuya Huaman, K. Suzuki, H. Miyamura and J. Balachandran, ACS Nano, 2020, 14, 8421–8432 CrossRef CAS PubMed.
- W. F. Brown, Phys. Rev., 1963, 130, 1677–1686 CrossRef.
- A. Lyberatos, D. V. Berkov and R. W. Chantrell, J. Phys.: Condens. Matter, 1993, 5, 8911 CrossRef CAS.
- J. Leliaert, J. Mulkers, J. De Clercq, A. Coene, M. Dvornik and B. Van Waeyenberge, AIP Adv., 2017, 7, 125010 CrossRef.
- There are two differences between eqn (5) and (1b) in Muñoz-Menendez et al.19 First, our equation shows the change in energy density instead of the change in temperature in the l.h.s., which comes down to the omission of the specific heat capacity found in the denominator of eqn (1b) in Muñoz-Menendez et al.19 Secondly, our eqn (6) contains a factor (1 + α2) that is neglected in Muñoz-Menendez et al.19 but which we found to be necessary to accurately account for the dissipated heat in the presence of thermal fluctuations. It's analytical derivation can be found in Mulkers,33 “Using the chain rule for functional derivatives, the definition of the effective field, and the LLG equation, we obtain:”
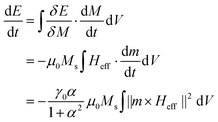 Note that this derivation describes the rate of energy change of the system, meaning that the heat that gets dissipated away carries a minus sign. Conversely, our focus lies on the quantification of this energy, which is why eqn (6) does not carry this minus sign.
Note that this derivation describes the rate of energy change of the system, meaning that the heat that gets dissipated away carries a minus sign. Conversely, our focus lies on the quantification of this energy, which is why eqn (6) does not carry this minus sign. - J. Leliaert, A. Vansteenkiste, A. Coene, L. Dupré and B. Van Waeyenberge, Med. Biol. Eng. Comput., 2015, 53(4), 309–317 CrossRef PubMed.
- K. Simeonidis, C. Martinez-Boubeta, D. Serantes, S. Ruta, O. Chubykalo-Fesenko, R. Chantrell, J. Oró-Solé, L. Balcells, A. S. Kamzin, R. A. Nazipov, A. Makridis and M. Angelakeris, ACS Appl. Nano Mater., 2020, 3, 4465–4476 CrossRef CAS PubMed.
- K. Wu, D. Su, R. Saha, J. Liu and J.-P. Wang, J. Phys. D: Appl. Phys., 2019, 52, 335002 CrossRef CAS.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
- P. Torche, C. Muñoz-Menendez, D. Serantes, D. Baldomir, K. L. Livesey, O. Chubykalo-Fesenko, S. Ruta, R. Chantrell and O. Hovorka, Phys. Rev. B, 2020, 101, 224429 CrossRef CAS.
- E. Alphandéry, S. Faure, L. Raison, E. Duguet, P. A. Howse and D. A. Bazylinski, J. Phys. Chem. C, 2011, 115, 18–22 CrossRef.
- J. Mulkers, PhD thesis, University of Antwerp and Ghent University, 2019.
| This journal is © The Royal Society of Chemistry 2021 |