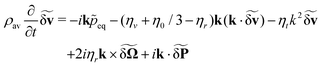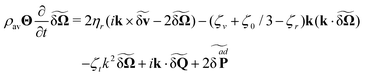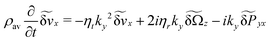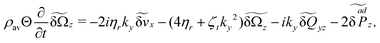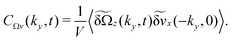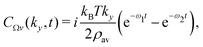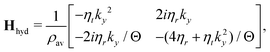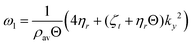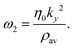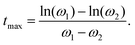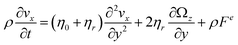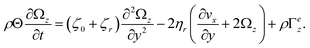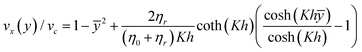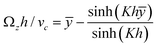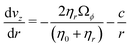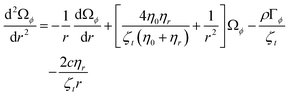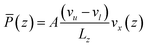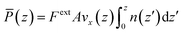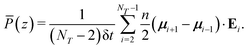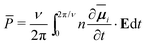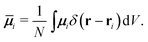DOI:
10.1039/D1CP04139H
(Perspective)
Phys. Chem. Chem. Phys., 2021,
23, 25003-25018
Electropumping of nanofluidic water by linear and angular momentum coupling: theoretical foundations and molecular dynamics simulations
Received
10th September 2021
, Accepted 28th October 2021
First published on 29th October 2021
Abstract
In this article we review the relatively new phenomenon of electropumping in nanofluidic systems, in which nonzero net flow results when polar molecules are rotated by external electric fields. The flow is a consequence of coupling of the spin angular momentum of molecules with their linear streaming momentum. By devising confining surfaces that are asymmetric – specifically one surface is more hydrophobic compared to the other – unidirectional flow results and so pumping can be achieved without the use of pressure gradients. We first cover the historical background to this phenomenon and follow that with a detailed theoretical description of the governing hydrodynamics. Following that we summarise work that has applied this phenomenon to pump water confined to planar nanochannels, semi-functionalised single carbon nanotubes and concentric carbon nanotubes. We also report on the energy efficiency of this pumping technique by comparisons with traditional flows of planar Couette and Poiseuille flow, with the surprising conclusion that electropumping at the nanoscale is some 4 orders of magnitude more efficient than pumping by Poiseuille flow.
1 Introduction
The central idea behind what we term in this review as “electropumping” is the coupling of a molecule's rotational momentum to its translational momentum. This intrinsic coupling was described by Cosserat and Cosserat1 in the late 19th century, and a little later by Max Born in 1920.2 Since then a number of researchers investigated the problem in the contexts of irreversible thermodynamics3–6 or kinetic theory.7 These works showed that rotational motion can be converted into linear motion, and vice versa. These couplings are accomplished via appropriately formulated constitutive equations, in which coupling transport coefficients (the so-called spin and vortex viscosities) are introduced into the governing hydrodynamic conservation equations, as we will discuss in the following section. A further advancement in this field took place in the 1970s and 1980s when the transport coefficients were computable by applications of statistical mechanics and implemented via molecular dynamics computer simulations.8–12 Generally speaking, however, the effects of spin coupling up to this time were limited to homogeneous systems, in which the spin angular velocity of molecules was proven to be directly proportional to the strain rate (velocity gradient) in the linear regime, or when it departs simple linearity, such as the nonlinear Born effect.11 While of theoretical interest, it has little consequence for homogeneous bulk fluids, and due to fortuitous cancellations of terms in the coupled hydrodynamic equations, the classical hydrodynamic predictions for the streaming velocity (ignoring spin-coupling) turn out to be exactly satisfied.
Prior to the year 2000 some limited work had been done in demonstrating the coupling effect for confined fluids,13–15 but it was only in the past two decades that the real potential of spin-coupling has been realised in the context of highly confined, nanofluidic flow. One of the first important consequences was the realisation that spin-coupling reduces the linear streaming velocity of highly confined fluids compared to classical Navier–Stokes predictions. This was demonstrated by us in the context of planar Poiseuille flow,16 oscillatory flow and lid-driven cavity flow.17,18 For Poiseuille flow, it was found through nonequilibrium molecular dynamics (NEMD) simulation that the linear velocity flow rate (and hence overall flow rate) was significantly reduced as the size of the molecule approaches the width of the channel separation.16 Thus, predictions of flow rates in micro/nano cavities or pores were at risk of significant over-prediction by excluding this coupling effect (by as much as around 15% for buta-triene for example). Similarly, the velocity profile and flow rates for highly confined water were also shown to be significantly altered by including spin-coupling into the extended Navier–Stokes equations19 (see section below for a description of including angular momentum conservation into the classical Navier–Stokes equations, leading to the so-called extended Navier–Stokes equations). This has serious consequences in nanofluidic devices, in which the flow of water through nanotubes and nanochannels is becoming a key feature in nanotechnology.20,21 Note that this effect tends to decrease the classically predicted flow velocity. It is not to be confused with the separate issue of flow enhancement due to slip, such as that found in the flow of water through hydrophobic carbon nanotubes or graphene channels.22–24
Up till 2009, studies had been essentially performed to understand how the classical Navier–Stokes predictions for highly confined fluids differed to those predictions when spin-coupling was formally introduced into the governing coupled system of equations. This involved inducing a translational streaming velocity in a molecularly structured fluid by the application of either an external gravity-like field (or pressure gradient) or by shearing a fluid by moving the confining walls. In 2009, Bonthuis et al.25,26 asked the question: what would happen if instead of applying a steady field to drive the flow, instead a mechanism to rotate the molecules directly can then translate into a steady-state translational flow? The mechanism they found was to apply an external rotating electric field to water. The rotating field couples to the dipole moment of water, thus spinning the molecules. This is essentially the same idea that was originally investigated by Condiff and Dahler.4 Due to the intrinsic spin-coupling, some angular momentum is transformed into linear momentum. If water is confined to identical walls on either side of the channel, they found that the solution to the extended Navier–Stokes equations resulted in a streaming velocity profile that was antisymmetric about the channel centre. In other words, flow occurred in equal and opposite measure about the channel centre, but the net flow was zero. However, if the symmetry of the walls was broken, such that one was hydrophobic while the other hydrophilic, then a net flow was induced. These studies were done theoretically, with a number of assumptions made to simplify the coupled differential equations so that they could be solved analytically. Hansen et al.27 solved a similar system numerically and found similar results.
We make a distinction here between what we designate as “electropumping” and what is commonly known as electro-osmotic flow (see for example, the review by Wang et al.28). In the latter, the mechanism relies on the presence of ions and the existence of the electric double layer. When an electric field is applied along the axis of the flow channel, the mobile ions in the diffuse layer move due to the electric field force. These ions in turn drag the uncharged liquid, such as water, along with them, causing flow along the channel. In contrast to this, electropumping does not rely on the existence of an electric double layer, nor the presence of ions at all. In fact, it works on electrically uncharged systems of fluid molecules. The only requirement is that the molecules have a dipole moment, which is the case for most electrically neutral molecular liquids, such as pure water. As a consequence, it is a “clean” pumping mechanism which can be used to pump only single-species polar liquids.
In Sections 3 and 4 we will present a summary of various NEMD simulations performed which demonstrate beyond doubt that the theory of electropumping can be implemented in practice. These studies are confined to water flowing inside planar nanochannels or carbon nanotubes. However, before we consider these specific examples, we also mention some other work performed in recent years to exploit this procedure. Firstly, it is essential to point out that a static electric field applied to an electrically neutral polar fluid like pure water with no free charges can not induce a net flow. While this type of pumping mechanism had been reported in the literature,29,30 it was later demonstrated to be an artifact of MD simulations performed using the GROMACS software package, in which an inappropriate cutoff scheme to truncate the Lennard-Jones forces was used; this situation does not occur when a shifted Lennard-Jones truncation is used, or if the LAMMPS package is implemented.25,26 This was further conclusively demonstrated to be the case in both planar nanochannels and carbon nanotubes by De Luca et al.,31 who implemented the correct Lennard-Jones cutoff conditions for a system of water molecules confined by planar graphene walls under the influence of a rotating electric field. We will therefore not report on other simulations that seem to have implemented the same flawed GROMACS scheme that suggests net flow is possible using either static electric fields or symmetric boundary conditions (as noted above and discussed in what follows).
Li et al.32 used a combination of rotating electric and magnetic fields to induce a flow of water through a carbon nanotube, via molecular dynamics simulation. While in principle they were able to induce streaming velocities up to ∼30 m s−1, these were accomplished under very high electric and magnetic field strengths (0.1–1 V Å−1 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 10–100 T, respectively) and frequencies (∼100 GHz or higher). Whilst being a significant contribution to the literature, it is yet to be seen if such high fields and frequencies are practical to impose under laboratory conditions. A particularly interesting and potentially important application was undertaken by Burnham and English,33 in which they demonstrated that electropumping of water was achieved by applying a circularly polarised electric field axially along channels of human aquaporin (AQP-4). The aquaporin is a naturally occurring porous biological structure with inherent asymmetry in its frictional surface characteristics, one of the key ingredients required for unidirectional electropumping. The significance of their work is that it raises the possibility of enhancing the permeability of water in biological aquaporins or biomimetic channels. Its potential for water treatment technology was particularly emphasised. Zhang et al.34 demonstrated that a rotating electric field applied in a direction normal to a single walled carbon nanotube (SWCNT) filled with water ruptures the hydrogen bond network, enabling a significant flow transmission. When the field is applied axially, the enhancement of this network leads to a reduction in the water transport. It is of course important to note that the electric field applied to an unfunctionalised nanotube can not induce a net flow, as will be discussed in Section 4.
and 10–100 T, respectively) and frequencies (∼100 GHz or higher). Whilst being a significant contribution to the literature, it is yet to be seen if such high fields and frequencies are practical to impose under laboratory conditions. A particularly interesting and potentially important application was undertaken by Burnham and English,33 in which they demonstrated that electropumping of water was achieved by applying a circularly polarised electric field axially along channels of human aquaporin (AQP-4). The aquaporin is a naturally occurring porous biological structure with inherent asymmetry in its frictional surface characteristics, one of the key ingredients required for unidirectional electropumping. The significance of their work is that it raises the possibility of enhancing the permeability of water in biological aquaporins or biomimetic channels. Its potential for water treatment technology was particularly emphasised. Zhang et al.34 demonstrated that a rotating electric field applied in a direction normal to a single walled carbon nanotube (SWCNT) filled with water ruptures the hydrogen bond network, enabling a significant flow transmission. When the field is applied axially, the enhancement of this network leads to a reduction in the water transport. It is of course important to note that the electric field applied to an unfunctionalised nanotube can not induce a net flow, as will be discussed in Section 4.
There are other studies devoted to nanoscale fluid actuation – see for example Arai et al.'s work35 and references therein involving the breaking of symmetry of the confining surfaces to drive flow, or using local heating in nanochannels to drive thermo-osmosis by Wang et al.,36 but we will not focus on these since they do not utilise the application of electric fields.
In what follows, we will first discuss the theory behind the mechanism of spin-coupling, which is fundamental to electropumping. Following that we consider the cases of electropumping in planar nanochannels, semi-functionalised single nanotubes and concentric nanotubes. We then consider the relative efficiency of electropumping compared to the two classical flows, namely boundary-driven Couette flow, and field (or pressure gradient) driven Poiseuille flow. Final remarks and prospects for future work conclude the paper.
2 Theoretical foundation
Before commencing this section we specify at the onset that the theoretical development relies upon two reasonable assumptions. The first is that all flows generated by electropumping can be considered sufficiently weak to moderate such that they remain in the linear, Newtonian flow regime. Shear thinning is thus assumed not to be important and all transport coefficients are assumed to be independent of shear rate. Second, we also assume that despite the high level of confinement in nanofluidic systems, we can approximate all transport coefficients as being “effective”, i.e. they can be represented as constant and independent of the spatial inhomogeneity of the fluid. In previous work,37,38 it has been clearly demonstrated that this is not the case in general, and that non-local effects can become important for highly confined fluids. However, a comprehensive theoretical framework that includes non-locality is far beyond the scope of this review and is a significant theoretical challenge in itself, which has not yet been fully solved.21,39–43 In the papers we review in the following sections, some of the sources of error are indeed attributed to the assumption of constant transport coefficients, and interested readers should refer to them for more detail.
For our purpose we write the local rate of change for a hydrodynamic variable A in terms of three physical mechanisms, namely, (i) a diffusive mechanism that tends to remove system gradients, (ii) an advective mechanism where A is carried along the bulk fluid flow, and (iii) a production mechanism which accounts for all other processes affecting the rate-of-change, e.g., external forces acting on the fluid. The hydrodynamic variable is often written as a product of the mass density, ρ, and an associated field variable ϕ, A = ρϕ. In general, the rate of change can then be expressed as
| | 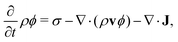 | (1) |
where
σ represents the production, the second term is the advective mechanism,
v being the streaming velocity, and the third term the diffusion mechanism, where
J is the corresponding flux tensor.
Rather than studying the hydrodynamic variable directly it is more convenient to study the corresponding Fourier modes, or specifically, the Fourier coefficients. These coefficients are found by Fourier transforming eqn (1) obtaining
| | 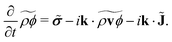 | (2) |
The task at hand is to derive the equation for the Fourier coefficients from the microscopic definitions of the hydrodynamic variables. Doing so reveals both the coupling phenomena and provides a useful microscopic interpretation of the fluxes.
In general, the microscopic (or molecular) definition of a hydrodynamic variable is given by44
| | 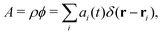 | (3) |
where
i runs over all molecules in the system,
ai is the corresponding molecular variable,
ri is the molecular center of mass, and
δ the Dirac delta function. The Dirac delta function has units of inverse volume and can be thought of as an idealized distribution function. The corresponding Fourier coefficient for wavevector
k reads
| | 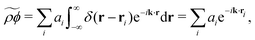 | (4) |
using the linear properties of the Fourier integral. The rate of change is then found directly from the derivative
| | 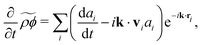 | (5) |
where
vi is the molecular velocity. Notice that
ai is a tensor or pseudo-tensor of any order, however, for this review we have that
ai is of rank one, and
viai is then the standard outer-product, or a tensor of rank two. The molecular velocity is decomposed into a sum of thermal motion (
c) and advective motion (
v) such that
vi(
t) =
ci(
t) +
v(
ri,
t). In terms of the thermal and advective motions
eqn (5) reads
| | 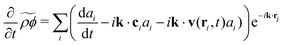 | (6) |
It is informative to explore the small wavevector limit, that is, the classical hydrodynamic limit. To this end, the exponential function is Taylor expanded around zero wavevector
| |  | (7) |
Substitution into
eqn (6) the rate-of-change is to first order in wavevector written as
| | 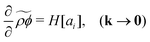 | (8) |
where
| | 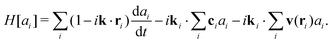 | (9) |
This differential operator (acting on the molecular variable
ai) was first derived by Hansen
et al.,
45 who denoted it the microscopic hydrodynamic operator.
It is important to note that the rate-of-change for the mass density, i.e., the mass balance equation, cannot be derived directly from the H-operator as this gives the wrong microscopic definition of the linear momentum. However, the rate-of-change for the linear and intrinsic angular momenta the operator is applicable.
2.1 The linear momentum balance equation
The microscopic definition of the linear momentum density is44| | 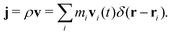 | (10) |
Notice that the associated field variable is ϕ = v and we have that ai = mivi. Using the fact that the sum of outer-products of the thermal and advective velocities is zero46| | 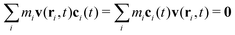 | (11) |
we get| | 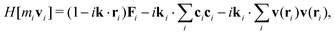 | (12) |
where Fi is the total force acting on molecule i, that is, a sum of conservative forces, Fci, and conservative external forces Fexti, Fi = Fci + Fexti. In terms of these two forces the operator becomes| | 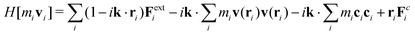 | (13) |
since 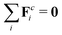 . The first term on the right-hand side of eqn (13) is identified as the production mechanism, to first order in wavevector, the second term is the advection mechanism, and the third term is the first order diffusion mechanism. The rate-of-change for the Fourier coefficients can then be written in the form of eqn (2)
. The first term on the right-hand side of eqn (13) is identified as the production mechanism, to first order in wavevector, the second term is the advection mechanism, and the third term is the first order diffusion mechanism. The rate-of-change for the Fourier coefficients can then be written in the form of eqn (2)| | 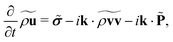 | (14) |
where P is the momentum flux tensor, i.e., the pressure tensor. This is the Fourier transform of| | 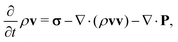 | (15) |
which is the balance equation for the linear momentum.
We will write the momentum balance equation in a different and more informative form. To keep the treatment as simple as possible and still retain the point, we first focus on the zero wavevector pressure tensor, P0; this is given directly from the H-operator
| | 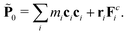 | (16) |
By application of Newton's third law the last term, the configurational part, is written as
| | 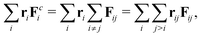 | (17) |
where
Fij is the force on molecule
i due to
j, and
rij =
ri −
rj. In real space we arrive at the Irving–Kirkwood definition
| | 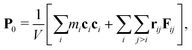 | (18) |
where
V is the system volume. Now, the outer-product
rijFij is not symmetric in general since
rij and
Fij are not parallel for structured molecules. The pressure tensor can then be decomposed into a symmetric part,
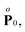
and an anti-symmetric part,
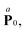
such that
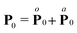
. From the definition of
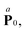
| | 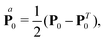 | (19) |
it can be seen by straightforward inspection that there are three independent tensor component. These components can be represented by the cross product
| | 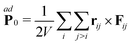 | (20) |
where
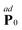
is the vector dual of
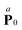
. Thus, the anti-symmetric pressure is due to the torque on
i about
j which results in a change of momentum.
The symmetric part of the pressure tensor is further decomposed into trace and traceless parts
| | 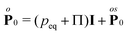 | (21) |
where
peq is the equilibrium normal pressure, and
Π the viscous pressure contribution for compressible fluids. Thus, by this decomposing of the pressure tensor the momentum balance equation,
eqn (14), can be written as
| | 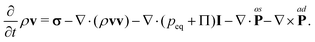 | (22) |
using the vector identity
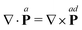
.
2.2 The intrinsic angular momentum balance equation
The microscopic definition of the intrinsic angular momentum density is| | 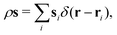 | (23) |
where s is the angular momentum per unit mass and si is the intrinsic angular momentum of molecule i,| |  | (24) |
Here Rα is the position vector of atom α in molecule i with respect to the molecular center of mass, and pα is the atomic momentum.
To clarify an important point below we shall assume that there are no external torques acting on the system and we let 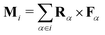 be the total torque on molecule i around its center of mass due to interactions with other molecules. The microscopic hydrodynamic operator then gives
be the total torque on molecule i around its center of mass due to interactions with other molecules. The microscopic hydrodynamic operator then gives
| | 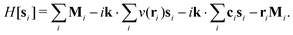 | (25) |
Note that at zero wavevector the
H-operator is non-zero meaning that the intrinsic angular momentum density is not a conserved quantity even in the absence of external torques. Only the total angular momentum is conserved, which is a fact we will use soon. The last term in
eqn (25) is the Irving–Kirkwood definition of the intrinsic angular momentum flux (or couple tensor).
From the H-operator we can write the rate-of-change for the Fourier coefficient directly in the form
| | 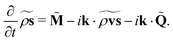 | (26) |
by defining
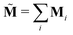
. In real space this gives us the balance equation for the intrinsic angular momentum density
| | 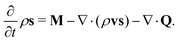 | (27) |
Importantly, for zero wavevector
Q is
| | 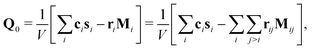 | (28) |
where
Mij is the torque on molecule
i due to
j. Again, note that this is in general not a symmetric tensor, and we again represent the flux as a decomposition of trace, traceless symmetric and anti-symmetric parts, that is, we have
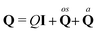
. Moreover, since the total angular momentum is conserved it can be shown
8,9 that
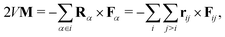
that is,
| | 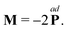 | (29) |
Substitution into
eqn (27) gives
| | 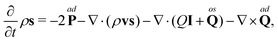 | (30) |
where
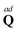
is the vector dual of
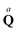
. The angular momentum density can be expressed in terms of the moment of inertia per unit mass,
Θ, and the angular velocity
ΩSpecifically,
Θ is the average molecular inertia at point
r. For single component fluids we then get
Θ =
Θmol where
Θmol is the molecular inertia with respect to the center-of-mass
| | 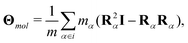 | (32) |
mα being the mass of atom
α in molecule
i. From this definition we see that
Θmol is symmetric and real, thus, there exists an orthogonal matrix
T such that
ΘP =
T−1ΘmolT, where
ΘP is the molecular diagonal (or principal) moment of inertia. From this we have
| Θ·Ω = Θmol·Ω = TΘPT−1·Ω = ΘP·Ω |
using the property that
T·
a =
a·
T−1 for any vector
a.
For rigid molecules the principal moment of inertia is constant, and if we assume inertia homogeneity and isotropy the inertia reduces to a constant scalar, that is,
| | | ρ(r,t)Θ·Ω(r,t) = Θρ(r,t)Ω(r,t) | (33) |
where Θ = trace(
ΘP)/3. Allowing for an external production term
eqn (30) then gives the final form
| | 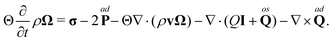 | (34) |
From
eqn (22) and (34) we note that the anti-symmetric stress appears in both the balance equation for the linear momentum and the balance equation for the angular momentum indicating a coupling.
2.3 Evidence of the coupling
We will illustrate the coupling through the relevant hydrodynamic correlation functions in equilibrium. To this end the fluid streaming velocity, the angular velocity and mass density can be written as a sum of the average part and the fluctuating part, i.e.,| | | v = vav + δv, Ω = Ωav + δΩ, and ρ = ρav + δρ. | (35) |
In equilibrium we have that vav = 0 and Ωav = 0. By substitution, the balance equations are to first order in the fluctuations| | 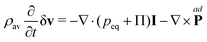 | (36a) |
| | 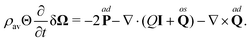 | (36b) |
To proceed we need a set of constitutive equations that relate the fluxes entering the balance equations with the system forces. These are9| | 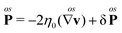 | (37b) |
| | 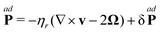 | (37c) |
| | 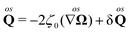 | (37e) |
| | 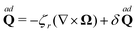 | (37f) |
where η0 and ηr are the shear and rotational viscosities, respectively, and ζ0, ζr and ζv are the shear, rotational, and bulk spin viscosities. The last term in the right hand side of each equation of eqn (37) represents a stochastic force, which has zero mean and is uncorrelated with the hydrodynamic variables v and Ω; this is the stochastic forcing picture.47–49
The coupling between the streaming velocity and angular velocity is evident from the constitutive relation, eqn (37c). The coupling may at first come as a surprise as the two hydrodynamic variables are not of the same tensorial character, however, Curie's principle is fulfilled since both the curl of the streaming velocity and the spin angular velocity are pseudo-vectors as is the vector dual 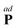 . The difference ∇ × v − 2Ω represents the deviation from a purely rigid body rotation and is also known as the sprain rate.
. The difference ∇ × v − 2Ω represents the deviation from a purely rigid body rotation and is also known as the sprain rate.
Substituting eqn (37) into the balance equations we arrive at the dynamical equations for the fluctuation to first order
| | 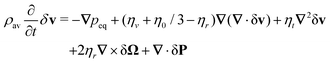 | (38a) |
| | 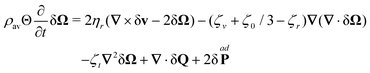 | (38b) |
where
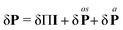
, and
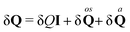
. Furthermore, we have introduced the following short-notation coefficients
| | | ηt = η0 + ηr, and ζt = ζ0 + ζr. | (39) |
In Fourier space we then have for wavevector
k| | 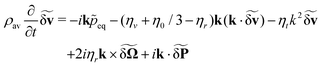 | (40a) |
| | 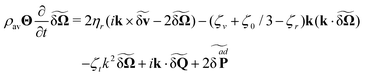 | (40b) |
where
k2 =
k·
k.
If we choose k = (0,ky,0) the velocity x-component and angular velocity z-component become
| | 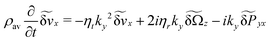 | (41a) |
| | 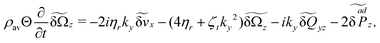 | (41b) |
Hence, only these two transverse components couple for this wavevector. From this we can form four hydrodynamic correlation functions; we will here only explore the cross correlation
| | 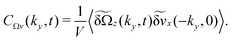 | (42) |
This is formed by multiplying
eqn (41b) by δ
vx(−
ky,0) and ensemble averaging over independent initial conditions. The solution for
CΩv is for sufficiently small wavevectors
| | 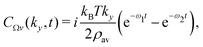 | (43) |
where
ω1 and
ω2 are the eigenvalues for the hydrodynamic matrix
| | 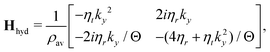 | (44) |
and are up to second order in wavevector
| | 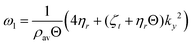 | (45a) |
| | 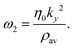 | (45b) |
First, importantly the theory predicts that the cross coupling vanishes as
ky → 0. Secondly, for non-zero wavevector
CΩv is predicted to feature a maximum at
| | 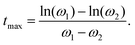 | (46) |
Fig. 1 shows results from molecular dynamics simulations of liquid chlorine. The predictions that the coupling magnitude decreases as the wavevector decreases, and that the correlation function features a maximum, are confirmed.
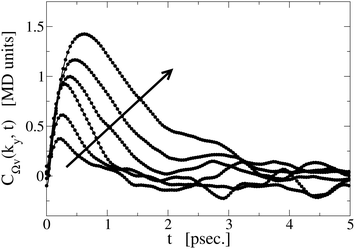 |
| | Fig. 1 The cross correlation function CΩv for molecular liquid chlorine. Arrow indicates increasing wavevector. Data are re-plotted from Hansen et al.45 using molecular dynamics parameters for chlorine. | |
3 Electropumping in planar nanochannels
Eqn (36a) and (36b) show that the linear and angular streaming velocities are coupled via the vector dual of the antisymmetric part of the pressure tensor, so that perturbations of one will affect the other. As early as 1964, Condiff and Dahler4 recognized that the application of a rotating electric field to a polar fluid results in a torque on the molecules that drives rotational molecular motion which, through the coupling described above, can result in translational fluid flow. They also noted the critical role played by the boundary conditions for the translational and angular velocity fields, but they only considered cases where the boundary condition was symmetric, i.e. identical for both confining surfaces. In such circumstances, the coupling, even if it is present, cannot be used to induce a nonzero net flow. The reason for this is that although a flow profile is generated, the flows in the top and bottom halves of the channel are equal in magnitude but opposite in direction, resulting in zero net flow. Bonthuis et al.25 made the crucial observation that asymmetric boundary conditions, along with the injection of torque by a rotating electric field, can induce non zero net flow and hence can be used for electropumping in micro or nanofluidic devices.
To see this more clearly, we consider the coupled set of equations derived previously, known as the extended Navier–Stokes equations, for the specific case of a planar flow, with the velocity in the x-direction and the gradient of the velocity in the y-direction,
| | 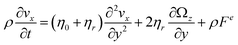 | (47a) |
| | 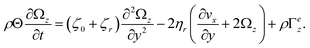 | (47b) |
In these equations, external body forces and torques are accounted for by the last term in each equation. The velocity field and angular velocity field are both assumed to be independent of position in the flow direction (under periodic boundary conditions) for low Reynolds number planar shear flows so the convective terms are absent.
3.1 Evidence of coupling in planar Poiseuille flow
Eqn (47a) and (47b) can be applied to a planar Poiseuille flow driven by the external body force ρFe, which acts like a gravitational field, in the absence of an applied torque. Then a net (spin) angular velocity results, due to the coupling between the translational and angular velocity fields. Analytic solutions for the translational and rotational velocity fields have been obtained for the case of planar Poiseuille flow by Eringen,13| | 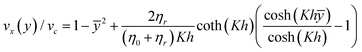 | (48a) |
| | 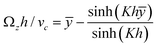 | (48b) |
where vc = ρFeh2/2η is the centre channel fluid velocity in the absence of rotational coupling, h is half the channel width, ȳ is defined as ȳ ≡ y/h and K = [4η0ηr/(η0 + ηr)(ζ0 + ζr)]1/2.
Note that these equations are derived under the assumption that the density and the transport coefficients are all constant, and that the translational and angular velocities both satisfy stick boundary conditions, i.e. they are both equal to zero at the walls.
Eqn (48b) has been verified by molecular dynamics simulations of flows of rigid diatomic molecules in nanochannels by Travis et al.,14,15 although the very rapid variation of the streaming angular velocity near the walls was difficult to obtain to high precision. Hansen et al.27 used eqn (48a) with realistic values for the shear, rotational and spin viscosities of water to show that the flow rate for planar Poiseuille flow in a nanochannel can be significantly reduced (e.g. by 15% at a channel width of 100 nm) by the translational–rotational coupling.
3.2 Electropumping driven by an external torque
Returning to eqn (47a) and (47b), if we remove the external field Fe = 0 and instead apply an external torque Γez ≠ 0 the coupling produces a nonzero translational velocity field. This scenario was investigated theoretically by Bonthuis et al.25 who considered the case where the torque is provided by a rotating electric field acting on water, which is a dipolar molecular fluid. They concluded that an electric field rotating at a frequency of 2.5 GHz and a field strength of 1 × 10−4 V nm−1 could efficiently drive a flow of water in a nanochannel. If we again assume symmetric stick boundary conditions, the net flow is zero, because the velocity profile is then an odd function of the y-coordinate. To achieve a nonzero net flow in one direction, they suggested using one hydrophilic and one hydrophobic wall, resulting in asymmetric boundary conditions. Soon after, Hansen et al.27 calculated the translational and rotational velocity profiles for water driven by a rotating electric field using realistic values of the shear and spin viscosities and verified that a nonzero net flow could be achieved by applying a rotating electric field to water in nonequilibrium molecular dynamics simulations.
The first molecular dynamics simulations to verify these predictions were carried out by De Luca et al.50 In their simulations, a rotating electric field was applied to water confined between two planar surfaces, one hydrophobic and one hydrophilic, separated by 2–3 nm. In a set of simulations on a control system, the water was also placed between identical hydrophilic walls. Fig. 2 shows the system configuration, with the asymmetric boundary condition case on the left and the symmetric case on the right. The velocity profiles shown at the bottom of the figure display the dependence of the flow velocity on the vertical position for different values of the rotation frequency of the electric field. The flow velocity increases with increasing electric field rotation frequency. Note that on the left hand side, a net flow in the negative x-direction is achieved, while the net flow is zero for the symmetric boundary conditions on the right. The flow is in the negative x-direction in the asymmetric case because the molecules slip on the upper surface while they stick or grip on the lower surface. The mechanism for the generation of flow can be simply understood by considering a water molecule in the centre of the channel. The torque applied by the electric field rotates the molecule in the anticlockwise direction. This pushes molecules below to the right and the molecules above to the left. The stick boundary condition at the bottom surface leads to net flow to the left.
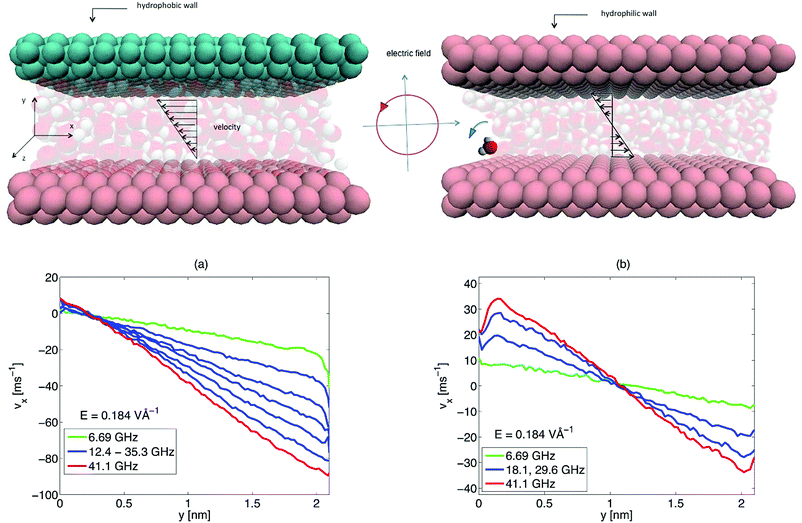 |
| | Fig. 2 System configuration used by De Luca et al.50 and streaming velocity profiles. (a) The lower wall (pink) is hydrophilic wall and the upper wall is hydrophobic. Streaming velocity profiles for different values of the electric field rotation frequency at fixed field amplitude are shown below, where the horizontal axis gives the y-coordinate in the channel. The frequency varies in steps of approximately 6 GHz. (b) Two hydrophilic walls and the associated streaming velocity profiles at fixed field strength and variable frequency. Images generated using VMD.55 Reproduced from De Luca et al.,50 with the permission of AIP publishing. | |
We make the point here that in order to obtain sufficiently good statistics for the velocity flow profiles, electric field strengths of the order of 0.1 V Å−1 or higher needed to be applied. These are high and may in fact result in the dissociation or ionisation of water molecules in an actual laboratory experiment.51,52 However, there is also experimental evidence to suggest that as confinement decreases from millimetre to micrometre dimensions, dissociation occurs at field strengths ranging from 0.001 V Å−1 to 0.01 V Å−1, respectively.53,54 If this trend continued down to nanometre confinement scales then dissociation may occur at electric field strengths at or above the field strengths typically used in MD simulation. However, this has not yet been demonstrated in the laboratory. Nevertheless, if one had the computational power to simulate much larger ensembles of molecules then measurable flow profiles at field strengths safely below the dissociation/ionisation field strengths would be possible because of vastly superior statistics. As such, even though the results of De Luca and colleagues may be somewhat idealistic, they do not invalidate the fundamental physics that ensures flow generation. If dissociation and/or ionisation of water does occur to some extent, it is not yet clear how this would affect the induced flow rates. Further work would be needed to simulate such systems and quantify the flow.
Increasing the amplitude of the electric field from E = 7.89 × 10−2 to 0.237 V Å−1 at fixed rotation frequency of ω/2π = 23.9 GHz increases the flow velocity, as shown in Fig. 3(a) and (b). This is easily understood as the time averaged value of the applied torque is directly proportional to the square of the electric field amplitude. At low values of the field, this results in a quadratic dependence of the maximum flow velocity on the rotating field amplitude,25 which was verified by De Luca et al.50 as shown in Fig. 3(a). However, for larger values of the field, the velocity flattens out and saturates (Fig. 3(b)), which is not predicted by the theory.
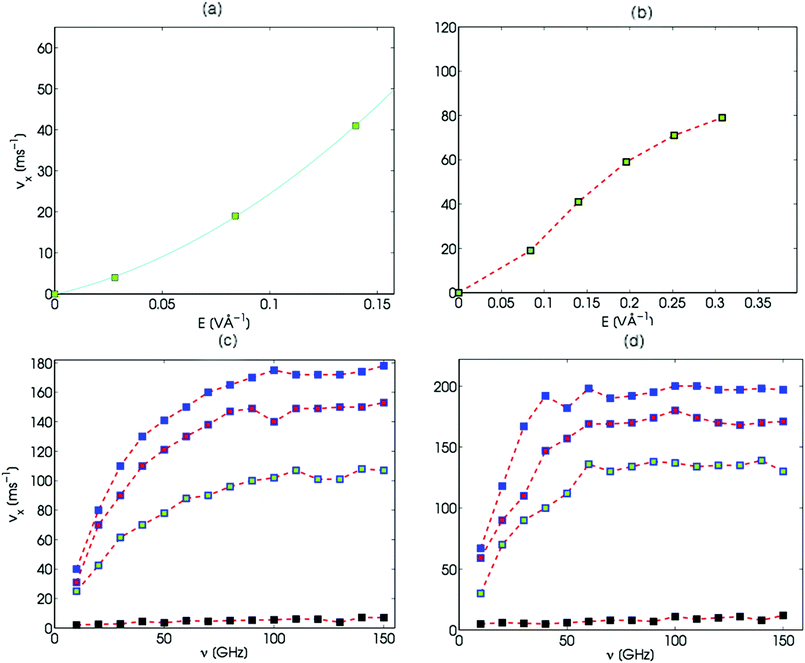 |
| | Fig. 3 Flow driven by a rotating electric field in a planar nanochannel with asymmetric boundary conditions. (a) and (b) Maximum (absolute) streaming velocities adjacent to the hydrophobic wall versus electric field with h = 2.25 nm and frequency 23.9 GHz. (a) 0 ≤ E < 0.15 V Å−1, with a quadratic fit (curve) and (b) 0 ≤ E < 0.35 V Å−1 with points connected to guide the eye. (c) Maximum (absolute) streaming velocities versus electric field frequency for h = 2.25 nm, (d) for h = 2.89 nm. In (c) and (d) E = 0.0289 V Å−1 for the black colored squares, and 0.195, 0.363 and 0.531 V Å−1 for the green, red and blue squares, respectively. The field frequency (x-axis) ranges from 9.5 to 150 GHz. Reproduced from De Luca et al.,50 with the permission of AIP publishing. | |
Likewise, the theory of Bonthuis et al.25 predicts a linear dependence of the maximum flow velocity on the rotation frequency of the electric field at low frequencies, which was confirmed by De Luca et al.50 as shown in Fig. 3(c) and (d) for two different values of the channel width. The full frequency dependence shows saturation at high frequencies, with the maximum flow velocity achieved at around 100 GHz for the narrower channel and 50 GHz for the wider one.
Application of a rotating electric field can result in strong heating of the water. In the simulations described by De Luca et al.,50 the centre channel temperature rose from a marginal increase above the wall temperature of 300 K at ω/2π = 6.69 GHz to around 400 K at ω/2π = 41.1 GHz, both at a field amplitude of E = 0.184 V Å−1. This effect can be managed by keeping the frequency and amplitude of the rotating electric field sufficiently low, but still large enough to generate a useful net flow.
Several assumptions that are made in the theory of Bonthuis et al.25,26 break down under the simulation conditions investigated by De Luca et al.50 They showed that the effective torque applied to the water molecules in a realistic simulation of a nanofluidic flow is spatially non-uniform due to the inhomogeneous density of the confined fluid. The transport coefficients may also be spatially dependent due to density, temperature and deformation rate effects. One crucial property that has received relatively little attention is the slip length of the angular velocity of the fluid. In the absence of better information, the molecular spin angular velocity was assumed to obey a stick boundary condition in the theoretical treatment of Bonthuis et al.,25,26 but the results of De Luca et al.50 show that this assumption is not valid. Good agreement between the solution of the extended Navier–Stokes equations and the simulations could only be obtained by using the boundary conditions for the translational and angular velocities empirically obtained from the molecular dynamics simulation results. While validated molecular dynamics simulation methods for computing the translational velocity slip length are now well known, very little work has been done on the determination of the angular velocity boundary condition. Some guidance on this subject may be found in a discussion in the context of non-equilibrium thermodynamics by Rubi and Casas-Vázquez.56
The 2013 paper by De Luca et al.50 discusses a system with a relatively simple model of the confining walls, consisting of layers of Lennard-Jones type atoms tethered via harmonic spring potentials to lattice points. The hydrophobic wall is designed with a high planar density and truncation at the LJ minimum to remove the attractive component to enhance slip. The hydrophilic wall interacts with the water via a LJ interaction truncated at 2.5σ to include the attractive part, a lower planar density to give a rough surface, and positive and negative charges uniformly distributed over the surface to give stronger stick while maintaining electrical neutrality.
Electropumping in the presence of more realistic walls was later also studied by De Luca et al.31 In this case, the hydrophobic wall consisted of a graphene layer and the hydrophilic wall was constructed to replicate β-cristobalite (silica) with surface silanol group densities chosen to replicate experimental values. These simulations are much more challenging than those performed with simple LJ walls, because the intermolecular forces required to maintain the structure of these materials are large, leading to a relatively rigid structure and poor thermal coupling to the fluid. In real materials, these effects are mitigated by the presence of electronic contributions to the thermal conductivity. To overcome these effects a virtual particle (VP) thermostat was devised.57 In the virtual particle thermostat, additional particles that only interact with the fluid and are tethered to lattice sites and thermostatted separately, are added to the system. These particles conduct heat away from the fluid naturally via the walls, without the need to directly apply a synthetic thermostat via the equations of motion to the fluid. Directly thermostatting the fluid can affect slip and other phenomena and should generally be avoided if possible.58
The electropumping results obtained from the simulations on the more realistic graphene and β-cristobalite planar walled system31 were qualitatively similar to the results previously found by De Luca et al.50 The most effective electropumping for realistic nanochannel materials with only minimal heating effects was found under conditions where the frequency of the rotating electric field was approximately 20 GHz and the field amplitude was 0.03 V Å−1. One of the more striking results found in these simulations was the strong anisotropy of the dielectric relaxation of confined water, which was investigated further by De Luca et al. in a later publication.59 The implications of this for the theoretical analysis of electropumping has not yet been fully explored.
4 Electropumping in nanotubes
In the previous section we showed that electropumping may be achieved in a relatively straightforward manner by functionalising one confining wall such that it is relatively hydrophilic with respect to the other (hydrophobic) wall. The question we now address is, can we somehow induce electropumping in other geometries, in particular can we induce flow in nanotubes of cylindrical geometry? The answer to this, despite its technical challenges, is a resounding yes. There are two ways in which this may be accomplished: first, by functionalising one half of either the inner or outer surface of the nanotube, and second, by a system of concentric nanotubes, in which one nanotube is functionalised. While no experiment has yet been conducted to demonstrate this in the laboratory, NEMD simulations have convincingly demonstrated the viability of both methods, which we now describe.
4.1 Single nanotube functionalisation
The technique of electropumping relies on the breaking of the symmetry of the confining environment, which as we have seen is straightforward for planar nanochannels. In the case of nanotubes, this breaking of symmetry may be accomplished by partial functionalisation of half of the nanotube surface. In principle, this functionalisation could occur on either the outside or inside of the nanotube surface. Functionalisation of outer carbon nanotube surfaces has already been successfully accomplished in the laboratory by various researchers.60–62 Additionally, Kang et al.63 successfully functionalised the inner surface of aluminosilicate nanotubes, although they note the technical difficulties of undertaking this more generally. While functionalisation of the outside of a nanotube is easier to achieve experimentally, for the purposes of computer simulation it results in changes to the intermolecular forces between water and the functionalised walls that are relatively weak. This in turn does not constitute a sufficiently strong symmetry breaking condition to allow unidirectional flow to occur. To date, the only NEMD study to consider electropumping in such an environment was performed by Ostler et al.,64 and in what follows we summarise this work.
In order to achieve a significantly strong symmetry breaking, Ostler et al.64 considered a CNT in which half the inner surface was functionalised with carboxyl groups, COOH. The addition of carboxyl groups increases the hydrophilicity of the affected surface sufficiently well such that a strong unidirectional flow was achieved. The semi-functionalised CNT was filled with water and an external rotating electric field applied with axis of rotation perpendicular to the tube axis, as seen in Fig. 4. In their geometry, the axis of the tube is in the z-direction and the external rotating electric field is in the x–y plane. The semi-functionalisation breaks the symmetry of the tube such that unidirectional flow occurs along the z-direction. Ostler and colleagues then performed NEMD simulations to determine the strength of the flow as a function of tube diameter, percentage functionalisation, external field frequency and amplitude.
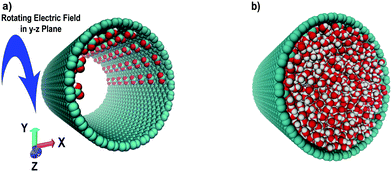 |
| | Fig. 4 (a) Schematic of the semi-functionalised CNT, showing simulation geometry. Direction of electric field rotation is seen to be along the axis of the nanotube, which is also the direction of induced water flow. (b) CNT with water molecules included. Reprinted (adapted) with permission from Ostler et al.64 Copyright 2017 American Chemical Society. | |
In Fig. 5, velocity plots are displayed for a system of water confined to a 3 nm tube, in which the upper half (demarked by the red semi-circle) depicts the functionalised (hydrophilic) half of the nanotube, while the (blue) bottom half is the unfunctionalised hydrophobic carbon nanotube. 2% and 5% functionalisations are shown. Clearly water flows more strongly in the hydrophobic half of the tube and reduces in magnitude closer to the hydrophilic surface. While it might seem reasonable that greater functionalisation would lead to greater net fluid transport, this is not actually the case. The flow is reduced for the 5% functionalised system. Increasing the degree of functionalsation also has the effect of increasing the protrusions of the dangling COOH molecules into the tube interior, which in turn can impede the transport of water molecules.
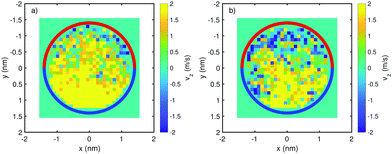 |
| | Fig. 5 (a) Plot of water streaming velocity for 2% functionalisation for external electric field frequency of 20 GHz and amplitude 0.032 V Å−1. (b) As for (a) but with 5% functionalisation. Reprinted (adapted) with permission from Ostler et al.64 Copyright 2017 American Chemical Society. | |
This net flow reduction is also seen in Fig. 6, in which the interior is binned in the y-direction and the time averaged velocity in each bin is plotted.
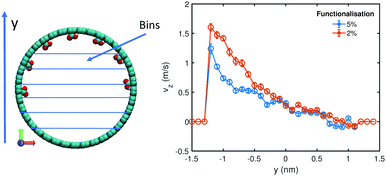 |
| | Fig. 6 Velocity profiles for the systems shown in Fig. 5. | |
The complete effect of tube diameter and percentage functionalisation is displayed in Fig. 7. Optimal flow is a function not only of tube diameter and percentage functionalisation, but also electric field frequency and amplitude, as was shown previously by De Luca et al.31,50 in the case of planar confinement.
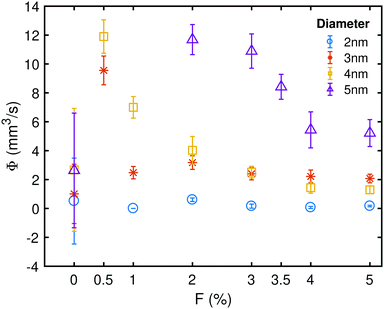 |
| | Fig. 7 Net volume flow rate Φ, defined as the integrated time averaged velocity over the cross-sectional area of the CNT, as a function of nanotube diameter and percentage functionalisation. Electric field frequency and amplitude are as in Fig. 5. Reprinted (adapted) with permission from Ostler et al.64 Copyright 2017 American Chemical Society. | |
4.2 Concentric nanotube functionalisation
While functionalisation of a single nanotube is currently a difficult technological feat to accomplish, it has been accomplished for the outside surface of nanotubes, as we previously noted. Currently, there has not been a successful functionalisation of the inner surface of a carbon nanotube in the laboratory. Easier to accomplish in the laboratory would be a concentric system in which one nanotube is functionalised on the outside surface, and then inserted into another wider unfunctionalised nanotube. Concentric nanotubes have indeed been fabricated in the laboratory and are the subject of considerable research (see for example the article by Pfeiffer et al.65 and references therein). Not only is the practical realisation of such a system possible experimentally, it is also simpler to model theoretically. The previous single functionalised nanotube system is difficult to model by continuum hydrodynamics due to the symmetry breaking of the boundary condition. A system of concentric nanotubes with different boundary conditions is however possible to model, as was demonstrated by Ostler et al.66 The system is depicted in Fig. 8.
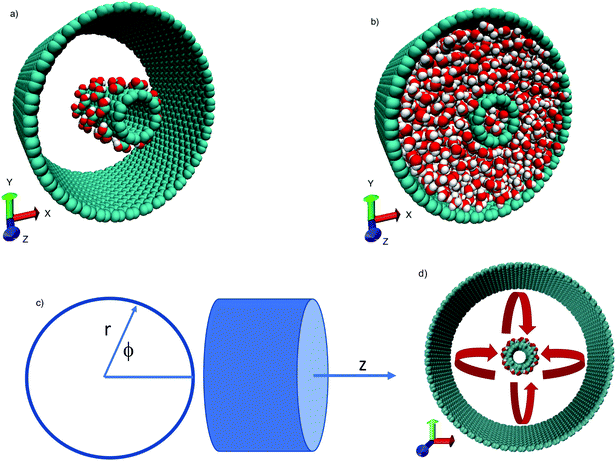 |
| | Fig. 8 (a) Concentric carbon nanotubes, with inner tube functionalised with carboxyl groups. (b) System filled with water molecules. (c) Geometry, where r is the radial coordinate from the common centre of the nanotube system, ϕ is the azimuthal angle and z defines the tube axis. (d) Electric field (red) direction of rotation within the concentric nanotube system. Reprinted (adapted) with permission from Ostler et al.66 Copyright 2019 American Chemical Society. | |
In the steady-state, the coupled hydrodynamic equations in cylindrical geometry reduce to ref. 66
| | 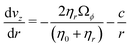 | (49) |
| | 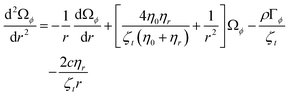 | (50) |
where here
vz is the streaming velocity along the tube axis,
Ωϕ is the spin angular velocity orthogonal to
ϕ (see
Fig. 8 for the system geometry),
Γϕ is the external torque induced by the rotating electric field,
c is a constant of integration, and
ζt is defined as
ζt =
ζ0 +
ζr, as in the previous sections. These two equations can not be solved analytically, but they can be solved numerically as long as the boundary conditions and transport coefficients can be determined from either experiment or simulation. The external electric field is applied in the
r–
z plane as shown in
Fig. 8.
In Fig. 9 the velocity profile for various radii tubes and percentage functionalisations is shown. As was the case of the single functionalised nanotube, the concentric system shows a generally linear increase in flow as a function of radial coordinate. Wider separation tubes (i.e. the space available for water to flow between the inner and outer tubes) generally display higher flow velocities as a function of radial coordinate, as expected. However, again we see that protrusions of carboxyl groups from the inner tube into the accessible flow volume, coupled with their hydrophilic nature, impedes the flow as percentage functionalisation increases, though this not a simple monotonic behaviour and is most noticeable in the 5 nm system. The mass flow rate in turn, obtained by integrating over the velocity profile and multiplying by the mass density of water, is shown in Fig. 10 as a function of radial gap width of the concentric nanotube system and percentage functionalisation, once again confirming this observation.
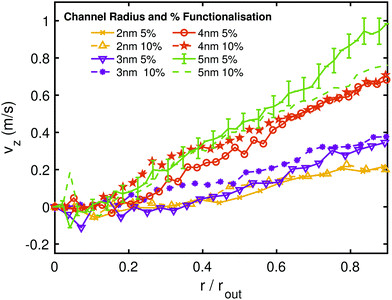 |
| | Fig. 9 Radial velocity profiles for various functionalisations and tube separations for the concentric nanotube system. All simulations were performed at electric field frequency and amplitude of 20 GHz and 0.032 V Å−1, respectively. Radial position between inner and outer tubes is expressed as a fraction of the outer tube radius (rout). Reprinted (adapted) with permission from Ostler et al.66 Copyright 2019 American Chemical Society. | |
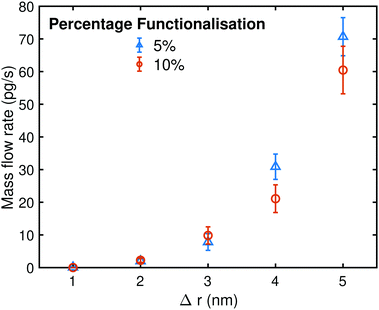 |
| | Fig. 10 Mass flow rate in pg s−1 as a function of nanotube separation radius (Δr) and percentage functionalisation of the inner nanotube. Reprinted (adapted) with permission from Ostler et al.66 Copyright 2019 American Chemical Society. | |
Finally, to demonstrate the accuracy of continuum modelling, Ostler et al.66 compared the numerical solution of eqn (49) and (50) with their NEMD simulation results. While accurate quantitative agreement could not be found – largely due to the various simplifying assumptions made in the continuum modelling input parameters (e.g. constant density, constant local transport coefficients, etc.) and the highly sensitive dependence on initial boundary conditions (streaming and angular slip velocities) – the overall agreement was nevertheless quite impressive. Fig. 11 shows this comparison for a system with a 3 nm tube gap and 5% functionalisation. Interested readers can refer to the original paper to find their sensitivity analysis.
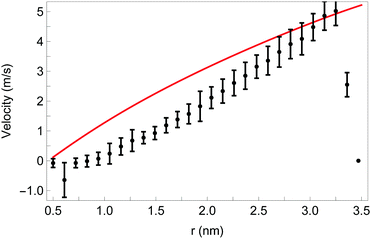 |
| | Fig. 11 Comparison of numerical solution of eqn (49) and (50) (red curve) with NEMD streaming velocity (black points) for a concentric system of 3 nm tube gap and 5% functitonalisation. The external electric field frequency and amplitude were 20 GHz and 0.032 V Å−1, respectively. Reprinted (adapted) with permission from Ostler et al.66 Copyright 2019 American Chemical Society. | |
5 Efficiency of electropumping
Perhaps the main motivation for electropumping is the difficulty of fluid actuation at the nanoscale. Forcing a fluid by application of mechanical pumps is standard at meso or even micro scales, but pressure-driven flows at nanometre length scales becomes more technically challenging. Applications of static electric fields to drive flow is only useful for charged systems, in which charges of one type flow in one direction, whilst opposite charges flow in the opposite direction. But such a technique can not work for uncharged polar liquids, such as water. As demonstrated in this review, electropumping solves these problems by a combination of a rotating electric field and asymmetric slip boundary conditions. However, for the technique to be useful it is important to understand the efficiency of the method, compared with other standard methods of fluid actuation. In order to answer this question, Ostler and colleagues67 performed a comparison of flow of water in planar graphene nanochannels undergoing three types of flow: planar Couette flow (in which fluid is driven by moving boundaries), planar Poiseuille flow (in which a gravity-like field, which is equivalent to a pressure gradient,68 drives the flow), and electropumping. Their calculations were aided by NEMD simulations of each kind of flow. They then calculated the average power dissipation and compared the results. Without going through the detail of their derivations, they found the following expressions for the power dissipation at location z in the channel for each type of flow, where it is assumed that flow is in the x direction and z is the direction of confinement:Planar Couette flow| | 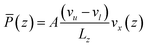 | (51) |
Planar Poiseuille flow| | 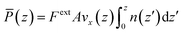 | (52) |
Electropumping| | 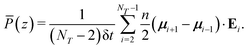 | (53) |
Here A is the wall surface area, vu and vl are the upper and lower wall velocities, respectively for Couette flow, Lz is the effective channel width, vx(z) is the streaming velocity, Fext is the external gravity-like field, n is the number density of water, NT is the total number of simulation time steps of value δt, μ is the dipole moment of water and E is the electric field vector. The summation in eqn (53) is over the total number of simulation time steps. Eqn (53) is in fact the discretized version of the continuum solution given by Bonthuis et al.26| | 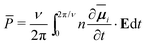 | (54) |
where ν is the frequency of the applied electric field and mi is the average dipole moment per water molecule within volume δV containing N water molecules, given by| | 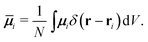 | (55) |
In eqn (54) the integration is over one frequency cycle of the electric field. The discretised equations, eqn (51)–(53), are themselves integrated over the entire channel separation width Lz to obtain the total average power for each system. Details about how these equations were derived and implemented are found in Ostler et al.67 and Bonthuis et al.26
A total of four systems were investgated: two Couette flow systems, in which one system has unfunctionalised graphene walls while the other system has one of the walls functionalised with hydrophilic carboxyl molecules; one unfunctionalised Poiseuille flow system; and one functionalised electropumping system, once again where one wall is pure graphene, while the other is graphene functionalised with COOH molecules. In order to make all efficiencies comparable, they were computed such that the volume flow rates of each flow was within 1% of the value of that obtained by electropumping for each nanochannel width. Thus, the external electric field (electropumping), wall velocity (Couette flow) and external gravity-like field (Poiseuille flow) were all adjusted in order to obtain matching volume flow rates for each channel width.
Flow profiles and comparisons of power dissipation between continuum predictions and simulation calculations can be found in Ostler et al.67 The most significant result of that work is presented in Fig. 12, which shows the average power dissipation for all four systems. While functionalised Couette flow is the most energy efficient, followed by unfunctionalised Couette flow, perhaps surprisingly electropumping is found to be some 4-orders of magnitude more efficient than Poiseuille flow. However, as a means of fluid actuation, Couette flow is impractical and not useful. Thus, of the two practical techniques for pumping nanofluidic water systems (Poiseuille-type or electropumping), electropumping is significantly more efficient for each of the channel widths studied. This is potentially an important result because it suggests that it may actually be easier and more energy efficient to transport water and other polar molecules under high degrees of confinement by a simple use of external rotating electric fields, rather than devise complex mechanical pumping devices. This should be sufficient incentive for experimentalists to attempt such a study in the laboratory to confirm these predictions.
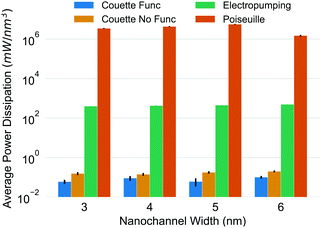 |
| | Fig. 12 Average power dissipation for all flow types as a function of channel width. Reprinted (adapted) from Ostler et al.67 Copyright 2020 American Chemical Society. | |
6 Conclusions and future work
The coupling between the fluid linear flow and local rotation has been known for more than a century now and is included in the dynamical description of liquid crystals, for example.69 However, it is commonly excluded in the hydrodynamic description of fluid flows. We showed in Section 2.3 that the coupling can safely be ignored on large characteristic length scales, but affects the flow dynamics on smaller scales. In particular, on the nanoscale the coupling can lead to a significant flow rate reduction for Poiseuille type flows. Therefore, with the increasing focus on the development of new nanoscale fluid devices, the relevance of the coupling should always be considered.
Pumping fluids in nanoscale channels and tubes is very challenging. For example, if we simply apply a pressure difference, Δp, over channel inlet and outlet, we can expect that the volumetric flow rate is proportional to the pressure difference, Φ = Δp/Rhyd, where Rhyd is the hydraulic resistance. For a slit-pore geometry Rhyd scales as 1/h4,70 hence, for nanoscale channels the extreme resistance leaves this method unusable. Alternatively, electro-osmosis can be used to generate flows, however, this method is invasive in the sense that it requires addition of ions into the fluid leading to possible oxidation processes in the system.
In this review we showed that the coupling between the linear flow and the local rotation can be exploited as a pumping mechanism. The method is based on application of an external rotational electric field that exerts a net torque on the molecular dipoles, and due to conservation of angular momentum this results in a flow. While the method requires a non-symmetric channel design it is non-invasive and, in principle, easy to construct and fabricate. We showed that in terms of power dissipation the electro-pumping method is superior to standard pressure pumping (Poiseuille-type) and wall shear pumping (Couette-type).
There are still unresolved points that should be addressed in the future. The boundary conditions are usually treated on a special case basis, in particular, the Dirichlet no-slip boundary condition is often applied. On the nanoscale, boundary slip phenomena can effect the flow properties considerably, and a more general boundary condition should be applied, for example, the Neumann slip-boundary condition also including for the possibility of coupling between linear flow and local rotation at the boundaries. Only very little attention has been given to this point; Badur et al.71 formulated a generalised boundary condition, however, this study has not been followed by experimental measurements or simulation investigations. Importantly, to our knowledge only preliminary experimental investigations of the electro-pumping mechanism have been carried out,72 hence, the design and practical use of the pumping mechanism is still not clear.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
JSH acknowledges support by the VILLUM Foundation*s Matter-grant (No. 16515).
References
-
E. Cosserat and F. Cosserat, Théorie des corps d'eformables, Hermann, 1909 Search PubMed.
- M. Born, Z. Phys., 1920, 1, 221–249 CrossRef.
- H. Grad, Commun. Pure Appl. Math., 1952, 5, 455–494 CrossRef.
- D. W. Condiff and J. S. Dahler, The Physics of Fluids, 1964, 7, 842–854 CrossRef.
- R. F. Snider and K. S. Lewchuk, J. Chem. Phys., 1967, 46, 3163–3172 CrossRef CAS.
-
S. R. de Groot and P. Mazur, Non-Equilibrium Thermodynamics, Dover, 1984 Search PubMed.
- C. F. Curtiss, J. Chem. Phys., 1956, 24, 225 CrossRef CAS.
- N. K. Ailawadi, B. J. Berne and D. Forster, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 3, 1462 CrossRef.
- D. J. Evans and W. B. Streett, Molec. Phys., 1978, 36, 161–176 CrossRef CAS.
- D. J. Evans and H. J. M. Hanley, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 1771 CrossRef CAS.
- R. Edberg, D. J. Evans and G. P. Morriss, Mol. Phys., 1987, 62, 1357–1369 CrossRef CAS.
- R. J. D. Moore, J. S. Hansen and B. D. Todd, J. Chem. Phys., 2008, 128, 224507 CrossRef CAS PubMed.
-
A. C. Eringen, Proceedings: Contributions to Mechanics, Pergamon, Oxford, 1969 Search PubMed.
- K. P. Travis, B. D. Todd and D. J. Evans, Phys. A, 1997, 240, 315–327 CrossRef CAS.
- K. P. Travis and D. J. Evans, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 1566 CrossRef CAS.
- J. S. Hansen, P. J. Daivis and B. D. Todd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046322 CrossRef CAS PubMed.
- J. S. Hansen, B. D. Todd and P. J. Daivis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 066707 CrossRef CAS PubMed.
- J. S. Hansen, P. J. Daivis and B. D. Todd, Microfluid. Nanofluid., 2009, 6, 785–795 CrossRef CAS.
- J. S. Hansen, J. C. Dyre, P. J. Daivis, B. D. Todd and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 036311 CrossRef CAS PubMed.
- J. C. Eijkel and A. V. D. Berg, Microfluid. Nanofluid., 2005, 1, 249 CrossRef CAS.
- P. J. Daivis and B. D. Todd, Processes, 2018, 6, 144 CrossRef CAS.
- S. K. Kannam, B. D. Todd, J. S. Hansen and P. J. Daivis, J. Chem. Phys., 2012, 136, 024705 CrossRef PubMed.
- S. K. Kannam, B. D. Todd, J. S. Hansen and P. J. Daivis, J. Chem. Phys., 2013, 138, 094701 CrossRef PubMed.
- S. K. Kannam, P. J. Daivis and B. D. Todd, MRS Bull., 2017, 42, 283–288 CrossRef CAS.
- D. J. Bonthuis, D. Horinek, L. Bocquet and R. R. Netz, Phys. Rev. Lett., 2009, 103, 144503–144507 CrossRef PubMed.
- D. J. Bonthuis, D. Horinek, L. Bocquet and R. R. Netz, Langmuir, 2010, 26, 12614–12625 CrossRef CAS PubMed.
- J. S. Hansen, H. Bruus, B. D. Todd and P. J. Daivis, J. Chem. Phys., 2010, 133, 144906–144913 CrossRef CAS PubMed.
- X. Wang, C. Cheng, S. Wang and S. Liu, Microfluid. Nanofluid., 2009, 6, 145–162 CrossRef CAS PubMed.
- S. Joseph and N. R. Aluru, Phys. Rev. Lett., 2008, 101, 064502–064506 CrossRef PubMed.
- X. Gong, J. Li, H. Lu, R. Wan, J. Li, J. Hu and H. Fang, Nat. Nanotechnol., 2007, 2, 709 CrossRef CAS PubMed.
- S. De Luca, B. D. Todd, J. S. Hansen and P. J. Daivis, Langmuir, 2014, 30, 3095–3109 CrossRef CAS PubMed.
- X.-P. Li, G.-P. Kong, X. Zhang and G.-W. He, Appl. Phys. Lett., 2013, 103, 143117 CrossRef.
- C. J. Burnham and N. J. English, J. Phys. Chem. Lett., 2017, 8, 4646–4651 CrossRef CAS PubMed.
- Q.-L. Zhang, R.-Y. Yang, W.-Z. Jiang and Z.-Q. Huang, Nanoscale, 2016, 8, 1886–1891 RSC.
- N. Arai, T. Koishi and T. Ebisuzaki, ACS Nano, 2021, 15, 2481–2489 CrossRef CAS PubMed.
- X. Wang, M. Liu, D. Jing, A. Mohamad and O. Prezhdo, Nano Lett., 2020, 20, 8965–8971 CrossRef CAS PubMed.
- B. D. Todd, J. S. Hansen and P. J. Daivis, Phys. Rev. Lett., 2008, 100, 195901 CrossRef CAS PubMed.
- B. D. Todd and J. S. Hansen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051202 CrossRef CAS PubMed.
- B. A. Dalton, K. Glavatskiy, P. J. Daivis, B. D. Todd and I. K. Snook, J. Chem. Phys., 2013, 138, 044510 CrossRef PubMed.
- B. A. Dalton, P. J. Daivis, J. S. Hansen and B. D. Todd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052143 CrossRef PubMed.
- K. Glavatskiy, B. A. Dalton, P. J. Daivis and B. D. Todd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062132 CrossRef PubMed.
- B. A. Dalton, K. Glavatskiy, P. J. Daivis and B. D. Todd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012108 CrossRef PubMed.
- D. Camargo, J. A. de la Torre, D. Duque-Zumano, P. Espanol, R. Delgando-Buscalioni and F. Chejne, J. Chem. Phys., 2018, 148, 064107 CrossRef PubMed.
-
J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, Amsterdam, 2006 Search PubMed.
- J. S. Hansen, J. C. Dyre, P. J. Daivis, B. D. Todd and H. Bruus, Langmuir, 2015, 31, 13275 CrossRef CAS PubMed.
- B. D. Todd and P. J. Daivis, Mol. Simul., 2007, 33, 189–229 CrossRef CAS.
-
L. Landau and E. Lifshitz, Statistical Physics, Pergmon Press, Oxford, 3rd edn, 1980 Search PubMed.
-
L. Landau and E. Lifshitz, Fluid Mechanics, Elsevier, Amsterdam, 2nd edn, 1987 Search PubMed.
-
J. de Zárate and J. Sengers, Hydrodynamic Fluctuations, Elsevier, Amsterdam, 2006 Search PubMed.
- S. De Luca, B. D. Todd, J. S. Hansen and P. J. Daivis, J. Chem. Phys., 2013, 138, 154712 CrossRef PubMed.
- R. J. Martinez and J. Farrell, Ind. Eng. Chem. Res., 2019, 58, 782 CrossRef CAS.
- G. Cassone, J. Phys. Chem. Lett., 2020, 11, 8983 CrossRef CAS PubMed.
- W. Stygar, T. Wagoner, H. Ives, Z. Wallace, V. Anaya, J. Corley, M. Harjes, J. Lott and G. Mowrer,
et al.
, Phys. Rev. Accel. Beams, 2006, 9, 070401 CrossRef.
- C. Song and P. Wang, Rev. Sci. Instrum., 2010, 81, 054702 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- J. Rub and J. Casas-Vázquez, Phys. A, 1982, 111, 351–363 CrossRef.
- S. De Luca, B. D. Todd, J. S. Hansen and P. J. Daivis, J. Chem. Phys., 2014, 140, 054502 CrossRef PubMed.
- S. Bernardi, B. D. Todd and D. J. Searles, J. Chem. Phys., 2010, 132, 244706 CrossRef PubMed.
- S. De Luca, S. K. Kannam, B. D. Todd, F. Frascoli, J. S. Hansen and P. J. Daivis, Langmuir, 2016, 32, 4765–4773 CrossRef CAS PubMed.
- V. T. Le, C. L. Ngo, Q. T. Le, T. T. Ngo, D. N. Nguyen and M. T. Vu, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2013, 4, 035017 CAS.
- K. Balasubramanian and M. Burghard, Small, 2005, 1, 180–192 CrossRef CAS PubMed.
- M. Abdalla, D. Dean, D. Adibempe, E. Nyairo, P. Robinson and G. Thompson, Polymer, 2007, 48, 5662–5670 CrossRef CAS.
- D. Y. Kang, N. A. Brunelli, C. I. Yucelen, A. Venkatasubramanian, J. Zang, J. Leisen, P. J. Hesketh, C. W. Jones and S. Nair, Nat. Commun., 2014, 5, 3342 CrossRef PubMed.
- D. Ostler, S. K. Kannam, P. J. Daivis, F. Frascoli and B. D. Todd, J. Phys. Chem. C, 2017, 121, 28158–28165 CrossRef CAS.
-
R. Pfeiffer, T. Pichler, Y. A. Kim and H. Kuzmany, Carbon Nanotubes, Springer, Berlin Heidelberg, 2008 Search PubMed.
- D. Ostler, S. K. Kannam, F. Frascoli, P. J. Daivis and B. D. Todd, Langmuir, 2019, 35, 14742–14749 CrossRef CAS PubMed.
- D. Ostler, S. K. Kannam, F. Frascoli, P. J. Daivis and B. D. Todd, Nano Lett., 2020, 20, 3396–3402 CrossRef CAS PubMed.
-
B. D. Todd and P. J. Daivis, Non-Equilibrium Molecular Dynamics: Theory, Algorithms and Applications, Cambridge, 2017 Search PubMed.
-
P. Gennes and J. Prost, The Physics of Liquid Crystals, Claredon Press, 1993 Search PubMed.
-
H. Bruus, Theoretical Microfluidics, Oxford University Press, 2008 Search PubMed.
- J. Badur, P. Ziolkowski and P. Ziolkowski, Microfluid Nanofluid, 2015 Search PubMed.
-
S. Yarden and B. Paul, Electromagnetic Propulsion of Water, Ariel University technical report, 2021 Search PubMed.
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  *c
*c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and 10–100 T, respectively) and frequencies (∼100 GHz or higher). Whilst being a significant contribution to the literature, it is yet to be seen if such high fields and frequencies are practical to impose under laboratory conditions. A particularly interesting and potentially important application was undertaken by Burnham and English,33 in which they demonstrated that electropumping of water was achieved by applying a circularly polarised electric field axially along channels of human aquaporin (AQP-4). The aquaporin is a naturally occurring porous biological structure with inherent asymmetry in its frictional surface characteristics, one of the key ingredients required for unidirectional electropumping. The significance of their work is that it raises the possibility of enhancing the permeability of water in biological aquaporins or biomimetic channels. Its potential for water treatment technology was particularly emphasised. Zhang et al.34 demonstrated that a rotating electric field applied in a direction normal to a single walled carbon nanotube (SWCNT) filled with water ruptures the hydrogen bond network, enabling a significant flow transmission. When the field is applied axially, the enhancement of this network leads to a reduction in the water transport. It is of course important to note that the electric field applied to an unfunctionalised nanotube can not induce a net flow, as will be discussed in Section 4.
and 10–100 T, respectively) and frequencies (∼100 GHz or higher). Whilst being a significant contribution to the literature, it is yet to be seen if such high fields and frequencies are practical to impose under laboratory conditions. A particularly interesting and potentially important application was undertaken by Burnham and English,33 in which they demonstrated that electropumping of water was achieved by applying a circularly polarised electric field axially along channels of human aquaporin (AQP-4). The aquaporin is a naturally occurring porous biological structure with inherent asymmetry in its frictional surface characteristics, one of the key ingredients required for unidirectional electropumping. The significance of their work is that it raises the possibility of enhancing the permeability of water in biological aquaporins or biomimetic channels. Its potential for water treatment technology was particularly emphasised. Zhang et al.34 demonstrated that a rotating electric field applied in a direction normal to a single walled carbon nanotube (SWCNT) filled with water ruptures the hydrogen bond network, enabling a significant flow transmission. When the field is applied axially, the enhancement of this network leads to a reduction in the water transport. It is of course important to note that the electric field applied to an unfunctionalised nanotube can not induce a net flow, as will be discussed in Section 4.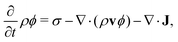
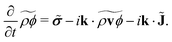
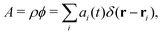
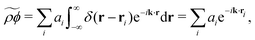
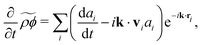
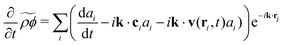

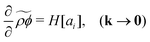
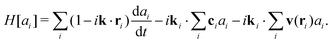
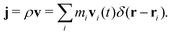
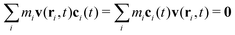
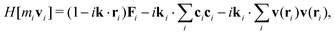
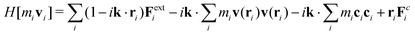
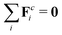 . The first term on the right-hand side of eqn (13) is identified as the production mechanism, to first order in wavevector, the second term is the advection mechanism, and the third term is the first order diffusion mechanism. The rate-of-change for the Fourier coefficients can then be written in the form of eqn (2)
. The first term on the right-hand side of eqn (13) is identified as the production mechanism, to first order in wavevector, the second term is the advection mechanism, and the third term is the first order diffusion mechanism. The rate-of-change for the Fourier coefficients can then be written in the form of eqn (2)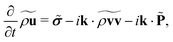
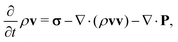
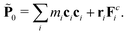
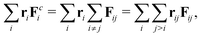
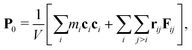
 and an anti-symmetric part,
and an anti-symmetric part, 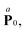 such that
such that 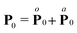 . From the definition of
. From the definition of 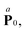
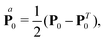
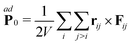
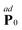 is the vector dual of
is the vector dual of 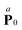 . Thus, the anti-symmetric pressure is due to the torque on i about j which results in a change of momentum.
. Thus, the anti-symmetric pressure is due to the torque on i about j which results in a change of momentum.
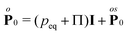
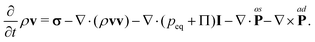
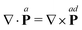 .
.
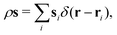

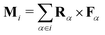 be the total torque on molecule i around its center of mass due to interactions with other molecules. The microscopic hydrodynamic operator then gives
be the total torque on molecule i around its center of mass due to interactions with other molecules. The microscopic hydrodynamic operator then gives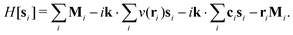
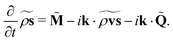
 . In real space this gives us the balance equation for the intrinsic angular momentum density
. In real space this gives us the balance equation for the intrinsic angular momentum density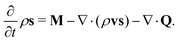
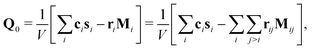
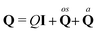 . Moreover, since the total angular momentum is conserved it can be shown8,9 that
. Moreover, since the total angular momentum is conserved it can be shown8,9 that 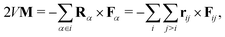 that is,
that is,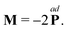
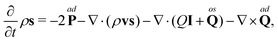
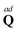 is the vector dual of
is the vector dual of 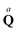 . The angular momentum density can be expressed in terms of the moment of inertia per unit mass, Θ, and the angular velocity Ω
. The angular momentum density can be expressed in terms of the moment of inertia per unit mass, Θ, and the angular velocity Ω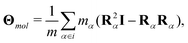
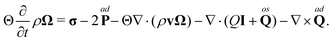
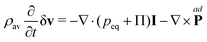
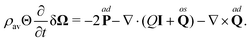
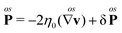
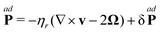
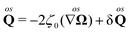
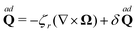
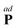 . The difference ∇ × v − 2Ω represents the deviation from a purely rigid body rotation and is also known as the sprain rate.
. The difference ∇ × v − 2Ω represents the deviation from a purely rigid body rotation and is also known as the sprain rate.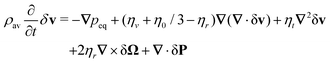
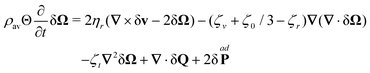
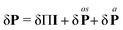 , and
, and 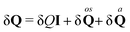 . Furthermore, we have introduced the following short-notation coefficients
. Furthermore, we have introduced the following short-notation coefficients