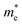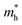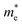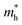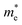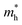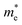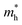Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Emerging piezochromism in lead free alkaline earth chalcogenide perovskite AZrS3 (A = Mg, Ca, Sr and Ba) under pressure
Arnab
Majumdar
 a,
Adebayo A.
Adeleke
a,
Adebayo A.
Adeleke
 b,
Sudip
Chakraborty
b,
Sudip
Chakraborty
 *c and
Rajeev
Ahuja
*c and
Rajeev
Ahuja
 *ad
*ad
aCondensed Matter Theory Group, Department of Physics and Astronomy, Box 516, Uppsala University, Uppsala, SE-75120, Sweden. E-mail: rajeev.ahuja@physics.uu.se
bDepartment of Physics and Engineering Physics, University of Saskatchewan, Saskatoon, Saskatchewan S7N 5E2, Canada
cDiscipline of Physics, Indian Institute of Technology (IIT) Indore, Simrol, Indore-453552, India. E-mail: sudip@iiti.ac.in; sudiphys@gmail.com
dApplied Materials Physics, Department of Materials Science and Engineering, Royal Institute of Technology, Stockholm, SE-10044, Sweden
First published on 27th October 2020
Abstract
Hydrostatic pressure is an effective tool that can give rise to novel crystal structures and physical properties. It has proven to be an alternative to chemical pressure. Therefore new functional materials with intriguing properties can be designed by exerting external pressure. Metal chalcogenide perovskites are a class of perovskites that have several advantages, namely high stability against moisture and light induced degradation along with nontoxic elemental composition. In this letter, we have used first principles methods to study the structural, electronic and optical properties of AZrS3 where A = Mg, Ca, Sr and Ba upon compression. Upon being compressed, the direct band gaps decrease to desired values which can enable this class of zirconium based chalcogenide perovskites to be used in tandem solar cells. The mobility of the charge carriers increases with pressure as the effective masses decrease. Piezochromism is seen to exist upon compression which can be verified from the modifications in the optical absorption spectra. This work elucidates the effects of pressure on the sensitive tuning of properties of zirconium based chalcogenide perovskites, which can have significant photovoltaic applications.
1. Introduction
Although discovered in 2009, in the last decade, organic–inorganic lead halide hybrid perovskites have been one of the most studied classes of materials.1–3 Their potential with respect to enhancing solar cell efficiency has led to the study of a plethora of such materials4–12 with some of their power conversion efficiency (PCE) values overshooting 20%.13–15 Despite having high PCE, the hybrid lead halide perovskites have two major caveats as well. Firstly, they are extremely unstable against moisture and secondly, the presence of toxic lead renders their large-scale usage to be questioned.16,17 In perovskites of the type ABX3, the BX6 octahedron has been found to be the main decisive factor leading to desirable photovoltaic properties.18 Therefore, the quest for ABX3 perovskites with other non-toxic elements took off and oxide perovskites were also studied for photovoltaic applications.19 But recently, the attention has been diverted to chalcogenide perovskites.20–22 Chalcogenide perovskites do not contain lead and have been known for many decades.23 But their electronic and optical properties, although studied recently,21,22,24,25 still need further rigorous scrutiny under different conditions. Besides experiments, several theoretical works have also been performed on these materials.26–31Up to now, a handful of chalcogenide perovskites of the form ABX3 have been realized experimentally.23,32–34 Out of these, only CaZrS3, BaZrS3, CaHfS3, and BaHfS334 exist in the distorted perovskite phase containing corner-shared BX6 octahedrons while the others are made of edge-shared35 or isolated BX6 octahedra.23 The corner-shared octahedrons in CaZrS3, BaZrS3, CaHfS3, and BaHfS3 give rise to less localized band minima and carriers with higher mobility compared to the other phases, thus proving to be more applicable for photovoltaic applications. However, the high electronic band gaps of most of these materials (2.05 eV for SrZrS3 and 1.83 eV for BaZrS325) can prove to be a bottleneck. The applicability of these distorted chalcogenide perovskites can be increased by finding a workaround method to decrease the band gaps that can be attained by applying external pressure. This is what has been addressed in this work. The effect of exerting external pressure on perovskites and studying its effect on optoelectronic properties is a significant area of research.36–38 Generally, within the same phase, upon compression, insulators and semiconductors show band gap decrement. This band gap decrement along with electron–electron correlations and electron–phonon coupling can also lead to metallization and eventually superconductivity.39
Besides the modification of the electronic properties under external pressure, another phenomenon that these materials exhibit on compression is piezochromism.40–45 The external pressure can bring about structural or electronic transitions which can lead to changes in the optical properties as well.46,47 In two-dimensional Cu–Cl perovskites48,49 piezochromism has been attributed to bond compression and octahedral rotation. Thus, from a fundamental perspective, it is interesting to explore the possibility of finding piezochromism even in the three-dimensional perovskites.
In this work, the pressure induced modifications in the electronic and optical properties in the semiconducting alkaline earth chalcogenide perovskite material, AZrS3 (A = Mg, Ca, Sr and Ba) have been studied. The objective is to study the effect of pressure with respect to the changes it may bring about in the structural, electronic and optical properties of the studied materials. Pressure induces modifications of the lattice parameters and atomic arrangements. This in turn introduces changes in the electronic properties. In this work, on compression, the band gaps decrease and possess values ideal for them to be used in tandem solar cells. Along with the band gaps, the effective masses of the carriers are also calculated to decrease with compression. Finally, modification of the characteristics of the optical absorption spectra along with slight red shifts on compression have been reported thus establishing the occurrence of piezochromism. Thus, the electronic properties evolution with pressure seals the applicability of the studied materials in tandem solar cells, but even the piezochromism observed with applied pressure can have significant impact in understanding the optical response of this class of materials from a fundamental perspective.
2. Computational methodology
The geometrical optimizations of AZrS3 (A = Mg, Ca, Sr and Ba) and their total energy computations were performed using the Vienna ab initio simulation package (VASP)50 by solving the Kohn–Sham equations within the density functional theory (DFT) framework.51,52 The projector augmented wave (PAW) method53 was implemented along with the with Perdew–Burke–Ernzerhof parameterization (PBE)54 within the implemented and the generalized gradient approximation (GGA) to describe the electronic exchange–correlation effects. The PAW pseudopotentials of Mg, Ca, Sr, Ba, Zr, and S that have been considered have valence states 2s22p63s2, 3s23p64s2, 4s24p65s2, 5s25p66s2, 4s24p64d25s2 and 3s23p4 respectively. The kinetic energy cut-off values of the employed PAW pseudopotentials for Mg, Ca, Sr, Ba, Zr and S are 495.223 eV, 266.62 eV, 229.35 eV, 187.18 eV, 229.89 eV and 402.43 eV respectively. Overall, a well converged kinetic energy cut-off of 600 eV was used for all the studied systems. All the structures were compressed from 0 to 15 GPa and at every studied pressure point, the structures were relaxed. The initial existing structure was taken at ambient pressure and the volume was reduced subsequently to achieve high pressures. The unit cell of the four compounds consisted of 20 atoms (4 Mg/Ca/Sr/Ba, 4 Zr and 12 S). HSE06 hybrid functional55 was also used for more accurate description of the electronic properties. The Heyd–Scuseria–Ernzerhof (HSE06) functional consisted of 75% of the PBE exchange and 25% of the Fock exchange. For the case of BaZrS3 spin–orbit coupling (SOC) was also included. A gamma-centered k-point mesh (7 × 6 × 7) was used for sampling the mesh. The energy convergence criteria for the self-consistent electronic steps was at 10−6 eV. The ionic forces were relaxed until a residual force of 10−2 eV Å−1 was reached. The optical properties have been determined by considering the independent particle approximation (IP) using the same gamma centered 7 × 6 × 7 k-point mesh.3. Results and discussion
3.1 Crystal structure analysis and equation of state under pressure
Experimentally synthesized CaZrS3, SrZrS3 and BaZrS3 have been found to crystallize in the distorted orthorhombic GdFeO3 structure having space group Pnma at ambient pressure.34 Although, this prototypical structure has not been seen for MgZrS3, previous theoretical works have considered a distorted structure for MgZrS3.56 However, in this work for all the four chalcogenide perovskites studied, AZrS3 (A = Mg, Ca, Sr and Ba), we have considered the distorted Pnma phase for further compression and analysis. The Zr atoms are 6-fold (octahedral) coordinated to the S atoms in a distorted and tilted manner. This gives rise to corner-sharing distorted octahedrons [ZrS6]8− (Fig. 1). The alkaline earth elements are 12-fold coordinated with the S atoms, forming cuboctahedrons. The lattice parameters (a, b and c) of the unit cell (20 atoms) at 0 and 15 GPa can be found in Table 1. Agreeing with earlier results,22,24 for all the four variants of the alkaline earth zirconium chalcogenides studied, the [ZrS6]8− are tilted as can also be seen in Fig. 1. The tilted systems have octahedra tilting around all three pseudo-cubic directions with a tilting pattern of a − b + a-which agrees with the Pnma space group. This means that the tilt angles reported in this work are out of phase along the a and c-axes but in-plane along the b-axis. For MgZrS3 the octahedrons are tilted by an angle of 20.9° and 22.9° at 0 and 15 GPa respectively. Similarly, the corresponding numbers for CaZrS3 are 18.6° and 20.5° at 0 and 15 GPa respectively. For the case of SrZrS3 at 0 and 15 GPa, the tilt angles are 15.0° and 16.0° respectively. Thus, it is clear that for the systems containing Mg, Ca and Sr, the tilt angle increases with pressure. This is in contrast to what happens in BaZrS3 as in this case, the tilt angle decreases slightly from 11.43° to 10.90° when compressed from 0 to 15 GPa.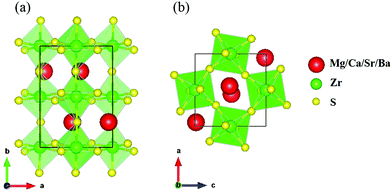 | ||
| Fig. 1 Schematic of the Pnma AZrS3 perovskites (A = Mg, Ca, Sr and Ba) viewed (a) along the c-axis and (b) along the b-axis. | ||
| System | 0 GPa | 15 GPa | ||||
|---|---|---|---|---|---|---|
| a | b | c | a | b | c | |
| MgZrS3 | 6.74 | 9.53 | 6.36 | 6.54 | 9.07 | 5.88 |
| CaZrS3 | 7.07 | 9.63 | 6.57 | 6.87 | 9.16 | 6.01 |
| SrZrS3 | 7.16 | 9.82 | 6.77 | 6.96 | 9.41 | 6.15 |
| BaZrS3 | 7.27 | 10.16 | 7.11 | 6.95 | 9.79 | 6.55 |
The phonon spectra of all the four chalcogenide perovskites has been shown in Fig. 2. They are all dynamically stable. While CaZrS3, SrZrS3 and BaZrS3 are dynamically stable at all pressures between 0 and 15 GPa, however MgZrS3 shows positive phonons only after 8 GPa for the Pnma phase. Therefore, with more tilting of the [ZrS6]8− octahedrons, the phonons harden too for MgZrS3, CaZrS3 and SrZrS3. As expected with higher pressure, the frequencies of the phonon modes at the gamma point are higher due to increased force constant with pressure. For all the four chalcogenide perovskites studied, in the Z → T direction, the four highest optical and three acoustic modes are almost dispersionless. For MgZrS3, between 0 and 8 GPa, the phonon instability is seen in the Γ → X and Γ → Z directions which eventually harden with pressure. In our unit cell, Γ → Z corresponds to the ‘c’ direction (direction along which the octahedral tilting is prevalent). This has been explained later how the compressibility and tilting along the ‘c’ direction are related to the stability. According to the combined experimental and theoretical work of Gross et al.,57 no first order structural phase transition is seen until at least 8.9 GPa in BaZrS3. Therefore, studying the high pressure electronic and optical properties of the chalcogenide perovskites seems imperative to unravel their potential applicability in the realm of photovoltaics.
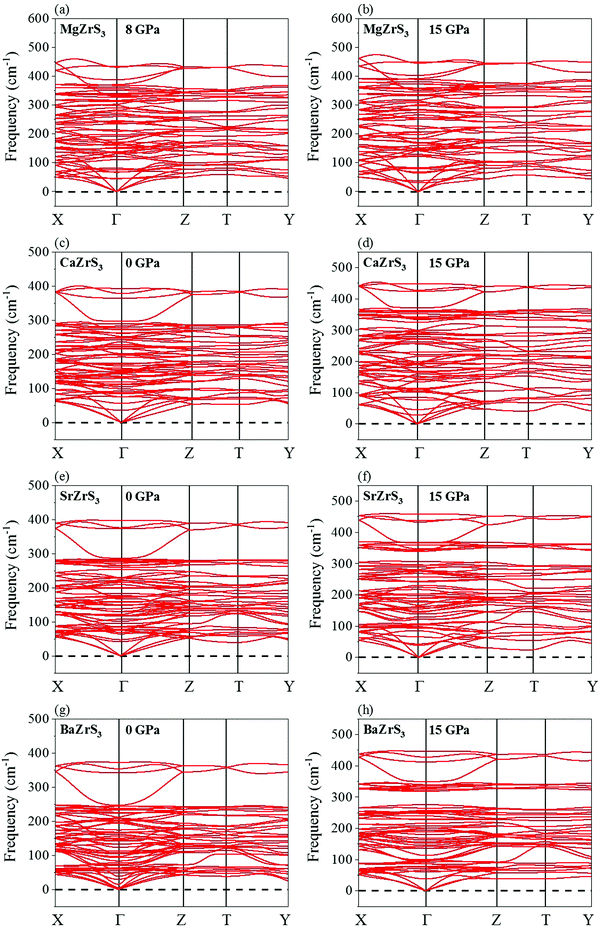 | ||
| Fig. 2 Phonon dispersion curves for MgZrS3 at (a) 8 and (b) 15 GPa, for CaZrS3 at (c) 0 and (d) 15 GPa, for SrZrS3 at (e) 0 and (f) 15 GPa and for BaZrS3 at (g) 0 and (h) 15 GPa. | ||
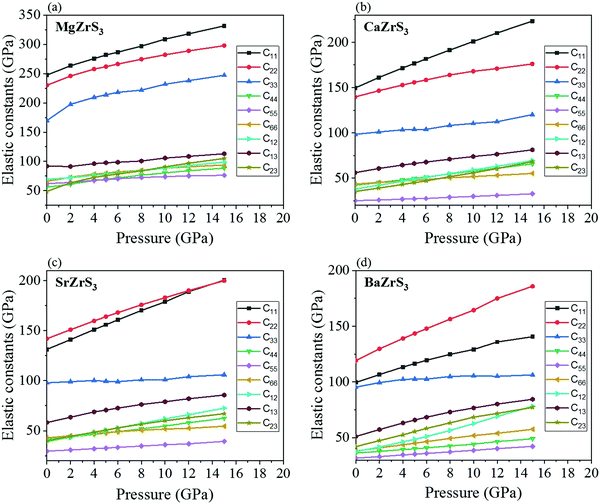
The evolution of the elastic constants with pressure has been shown in Fig. 3. They all satisfy the Born–Huang criteria for orthorhombic systems.58 For MgZrS3 and CaZrS3 the C11 is more than C22 between ambient pressure and 15 GPa. This is different for SrZrS3 and BaZrS3. While for SrZrS3C11 and C22 cross over at 15 GPa, for BaZrS3, the difference between C11 and C22 increases with pressure. The rest of the elastic constants increase with pressure as expected due to the shortening of bond lengths with increasing pressure.
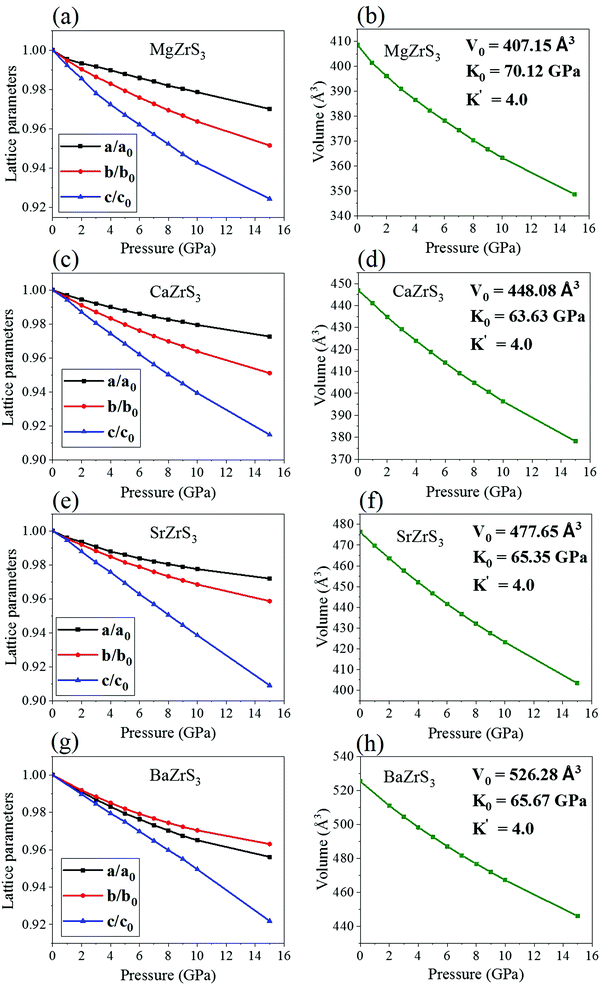
Upon exerting hydrostatic pressure, by reducing the volume of the unit cells, the lattice parameters of all the systems decrease smoothly (Fig. 4). At ambient pressure, the average Zr–S bond lengths are calculated to be 2.53–2.58 Å, 2.55–2.57 Å, 2.54–2.57 Å and 2.59–2.61 Å for MgZrS3, CaZrS3, SrZrS3 and BaZrS3 respectively. The same at 15 GPa are determined to be 2.44–2.48 Å, 2.45–2.48 Å, 2.45–2.48 Å and 2.48–2.49 Å. The range of the bond lengths are given here as the octahedrons are slightly distorted. For both 0 and 15 GPa, from the trends of the bond lengths it can be noted that the distortion decreases with increase in the atomic number of the alkaline earth metal. Therefore, the alkaline earth metal is clearly responsible for determining the amount of distortion that this class of perovskite will undergo. Furthermore, the octahedral distortion goes hand in hand with the octahedral tilting. While the distortion is maximum for MgZrS3, even the tilting is maximum for the same material. Similarly, both the octahedral distortion and tilting are minimum for BaZrS3. This can be attributed to the ionic radii of the Ba atoms which is largest amongst the alkaline earth metals considered in this work. The Ba atoms occupy the voids between the corner-sharing [ZrS6]8− octahedrons hindering the possibility of further tilting and distortion under compression unlike for the cases of Mg, Ca and Sr which having smaller radii provide the space thus enabling further distortion and tilting. The lattice compression, octahedral distortion and tilting all play significant roles in determining the electronic structures. In Fig. 4a, c and e, the trends in the decrement of the lattice parameters (a, b and c) are quite similar thus hinting at similar compressibilities along the three perpendicular directions. But, unprecedentedly, a contrasting trend is noticed for BaZrS3 (Fig. 4g), in which the ‘a’ decreases faster compared to ‘b’ on compression, unlike the other chalcogenide perovskites. Thus, for BaZrS3, the compressibility is higher along the a-axis than that along the b-axis. Possibly, this is one of the reasons why the tilt angle decreases rather than increasing on compression in BaZrS3. The corresponding equations of state (EOS) is shown in Fig. 4b, d, f and h for all the structures. The pressure-volume curves have been fit by employing a 3rd order Birch–Murnaghan EOS fit, fixing the first derivative of the bulk modulus (K′) at a standard value of 4.0. For all the four chalcogenide perovskites, the same Pnma phase up to 15 GPa has been considered. The absence of discontinuities, kinks or sudden changes in trends in the lattice parameters eliminate the chances of second order phase transition too. The ambient pressure bulk modulus (compressibility) are very similar for SrZrS3 and BaZrS3. MgZrS3 has the highest ambient pressure bulk modulus amongst the four variants with a value of 70.12 GPa (Fig. 2b). This implies that the compressibility is the least for this material. On closer inspection of the evolution of the ‘c’ lattice parameter with pressure for the four structures, the lowest compressibility along the c-axis is also seen for MgZrS3 (Fig. 4a) compared to the other three chalcogenide perovskites. In the unit cell that we have considered, the c-axis is the direction along which the octahedral tilting of the [ZrS6]8− is seen. Due to the smaller the compressibility of MgZrS3 along the c-axis compared to the rest, this results in more distortion and tilting. All the four studied systems throughout the pressure range of 0 to 15 GPa, retain the ionic bonding.
3.2 Evolution of electronic properties under external pressure
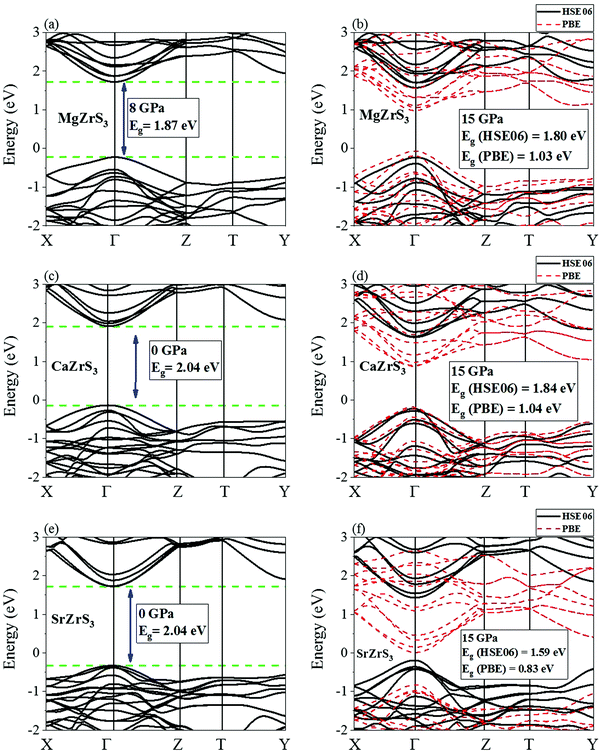
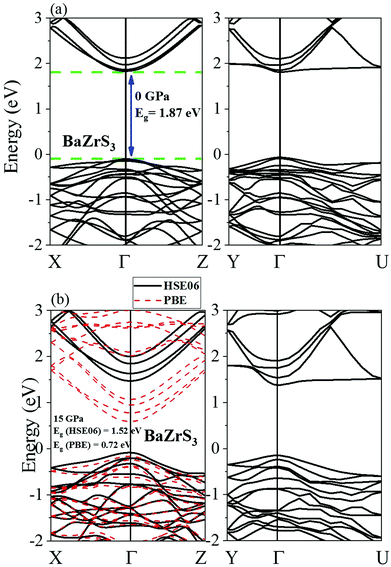
All the four chalcogenide perovskites considered in this work have direct electronic band gaps at the Γ point throughout the pressure range of 0 to 15 GPa. The electronic band structures of MgZrS3, CaZrS3 and SrZrS3 are shown in Fig. 5. At ambient pressure, the direct band gaps are 1.93 eV, 2.04 eV and 2.04 for MgZrS3, CaZrS3 and SrZrS3 respectively. Previously, experimentally the direct band gap of β-SrZrS3 (distorted perovskite) has been reported to be 2.05 eV25 which matches excellently with our obtained value of 2.04 eV. Our calculated value corresponds to the value obtained by using HSE06 functional. On using just PBE approximation, the direct band gap of SrZrS3 turns out to be 1.20 eV, thus significantly lower compared to the experimental value and that obtained from the HSE06 hybrid functional. Therefore, for the rest of the study, we have reported band gaps and discussed the electronic properties as obtained from the hybrid functionals and not PBE. Although, for comparison between PBE and HSE06, in Fig. 5 and 6 for 15 GPa, both the PBE and HSE06 band structures are shown. Experimentally, the direct band gap of Pnma CaZrS3 at 0 GPa was found to be 1.90 eV21 which is slightly less than our calculated value of 2.04 eV. However, the PBE value for the same material at 0 GPa was calculated to be 1.23 eV, thereby once again compelling us to use hybrid functional. Since, MgZrS3 is dynamically stable only from 8 GPa onwards, therefore, we have shown its calculated electronic band structures at 8 and 15 GPa in Fig. 5a and b respectively, although we have still reported the band gaps for the pressures below 8 GPa (see later). At 8 and 15 GPa, the direct band gaps have values of 1.87 and 1.80 eV. The nature of the band structure otherwise remains same at both the pressures. Similarly, for CaZrS3, the direct band gaps at 0 and 15 GPa are 2.04 (Fig. 5c) and 1.84 eV (Fig. 5d) respectively. The same values for SrZrS3 at 0 and 15 GPa are 2.04 (Fig. 5e) and 1.59 eV (Fig. 5f) respectively. Compared to CaZrS3, the electronic band gap of SrZrS3 plummets much more at 15 GPa. As discussed later, this can be attributed to the sudden appearance of a van Hove singularity in the density of states due to the Zr-4d orbitals in the conduction band minimum at 15 GPa. This appearance of the van Hove singularity proves to be beneficial as the band gap reduces to the value which is ideal for photovoltaic applications. This trait is not seen in MgZrS3 and CaZrS3 and can therefore be concluded that it is dependent on the alkaline earth metal.The calculated direct band gap of BaZrS3 (using SOC and HSE06) at 0 GPa has been shown to be 1.87 eV (Fig. 6a). This is in very close agreement with that obtained experimentally (1.83 eV).25 Since barium is a heavy element, we considered spin–orbit coupling in tandem with hybrid functional. On compression to 15 GPa, the gap value decreases to 1.52 eV (Fig. 6b), once again falling into the range of ideal photovoltaic applications. For CaZrS3 and SrZrS3 an interesting feature can be noted in the valence band maximum at 15 GPa. While for all the four chalcogenide perovskites, the direct band gap occurs at the Γ point at all the pressures, but for CaZrS3 and SrZrS3, the original valence band corresponding to the maximum at 0 GPa becomes noticeably anisotropic in the X → Γ and Γ → Z directions. The unprecedented occurrence of this feature which shows significant anisotropy along difference directions of the Brillouin zone will quite obviously also give rise to holes with quite different effective masses.
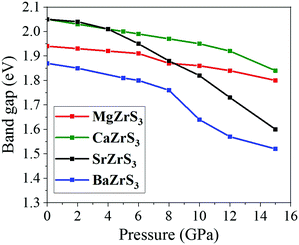
In Fig. 7, the pressure dependence of the direct band gaps of MgZrS3, CaZrS3, SrZrS3 and BaZrS3 have been shown. The rate at which the band gap decreases for MgZrS3 is ∼0.009 eV GPa−1, which is quite sluggish. Between 0 to 12 GPa, for CaZrS3, the band gap decreases at a rate of ∼0.008 eV GPa−1 while this rate increases to ∼0.025 between 12 and 15 GPa. The slope of the band gap vs pressure plot for SrZrS3 can be distinctly divided into two parts. Up to 4 GPa and beyond it, the rates at which the band gap decreases are ∼0.01 and 0.03 eV GPa−1. The faster decrement at higher pressures can perhaps be attributed to the prevalence of the van Hove singularity in the conduction band. Similarly, for BaZrS3, up to 8 GPa the band gap decrement rate is 0.013 eV GPa−1 while it is 0.024 eV GPa−1 between 10 and 15 GPa. The calculated value of 0.013 eV GPa−1 that we obtained between 0 and 8 GPa is in very satisfactory agreement with that obtained from experiment.57 A usual trend is that while lattice compression closes the band gap, octahedral tilting on the other hand opens it up.59 In our case, overall, at every pressure point, the band gap kept on decreasing. The prediction of the band gap tuning of these chalcogenide perovskite materials (∼1.52–2.04 eV) with pressure can help fabricate inexpensive tandem solar cells for large-scale production. In these tandem solar cells, commercial silicon cells are the bottom cells which can be augmented with these chalcogenide perovskites as the top cells.
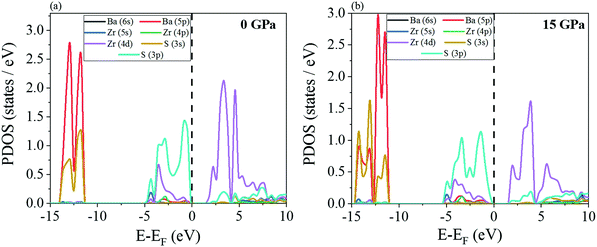
The electronic partial density of states (PDOS) have been shown in Fig. 8 and 9. At 0 GPa, the valence band maximum is contributed primarily by the 3p orbital of S for all the four chalcogenide perovskites while there is a minor contribution from Zr 4d. The opposite happens in the conduction band minimum, i.e. the major contribution comes from Zr 4d while S 3p has a small presence. The exact same trend is noted even at 15 GPa. In the deep valence regions, the contributions of the S 3s and alkaline earth metal p orbitals is present. As indicated earlier, a very interesting feature is noted for both SrZrS3 and BaZrS3, i.e. at high pressure (Fig. 8f and 9b), in the conduction band minimum, a van Hove singularity due to Zr 4d can be seen which is not there at 0 GPa. The sudden finite PDOS brings the conduction band minimum closer to the Fermi level, thus decreasing the band gap and increasing the applicability of these materials in photovoltaics. The high PDOS on either side of the Fermi level increases the probability of these Zr-based chalcogenide perovskites to have high optical absorption coefficients.
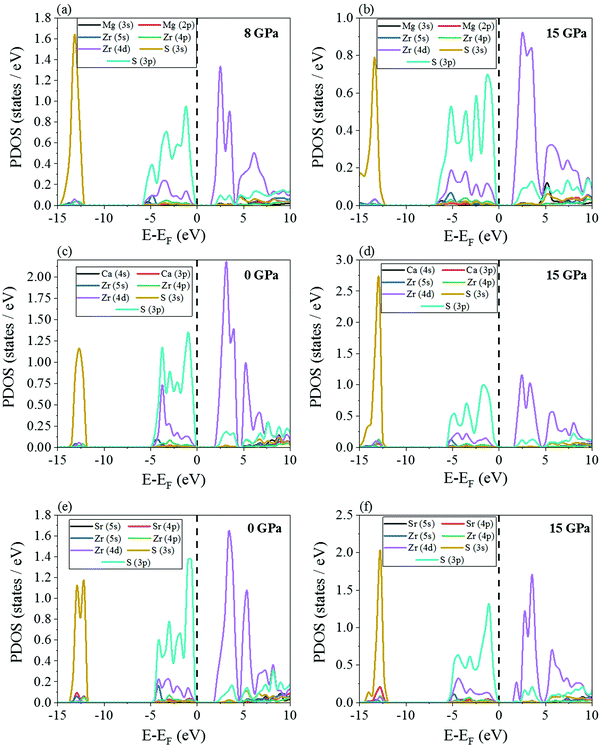 | ||
| Fig. 8 PDOS of MgZrS3 at (a) 8 and (b) 15 GPa, for CaZrS3 at (c) 0 and (d) 15 GPa and for SrZrS3 at (e) 0 and (f) 15 GPa using HSE06 hybrid functional. | ||
To get a qualitative idea of the carrier mobility at the different pressure points, we have reported the effective masses of the electrons and holes in Table 2a–d. They have all been calculated using the HSE06 functional approximation except for BaZrS3 for which the SOC was also taken into account. The effective masses of the carriers were calculated around the conduction band minimum and valence band maximum at the Γ high symmetry point by fitting the refined energy band structure to a parabolic function. The average effective masses were calculated in the x and z-directions of the Brillouin throughout the studied pressure range. For all the four chalcogenide perovskites studied, the effective mass of the electrons are isotropic and identical in the Γ → X and Γ → Z directions. In fact, irrespective of the alkaline earth metal, the electronic effective masses are in the same range and also decrease at similar rates with pressure. The decrement with pressure is not very steep. However, the range ∼0.30–0.38 for all the cases is already quite low and ensures high electron mobility. Unlike the electrons, the effective masses of the holes show anisotropy in the x and z directions. This anisotropy is more visible for CaZrS3 (Table 2b) and SrZrS3 (Table 2c). As expected for all the cases the effective masses of the holes decrease with pressure thus increasing the hole mobility. Significant drops in the hole effective masses are seen in CaZrS3 from 0.83 to 0.36 in the Γ → X, and 0.49 to 0.20 in the Γ → Z directions while being compressed from 0 to 15 GPa. Very similarly in SrZrS3, the hole effective masses plummet from 0.74 to 0.38 in the Γ → X direction and 0.51 to 0.15 from Γ → X on exerting hydrostatic pressure between 0 and 15 GPa. Thus the band gaps in the compressed chalcogenide perovskites along with the low effective masses of the holes and electrons can lead towards satisfactory photovoltaic applications from an electronic perspective.
3.3 Optical absorption spectra under external pressure: piezochromism
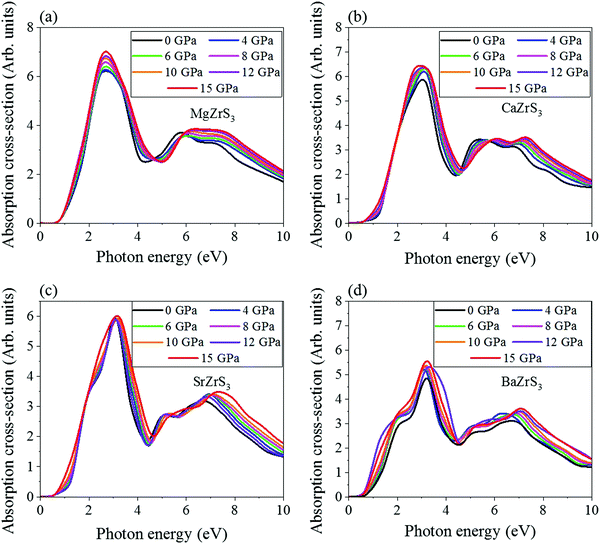
As chalcogenide perovskite materials are promising candidates for photovoltaic applications, exploring the optical absorption spectra under the influence of eternal pressure is an inevitable attempt from the corresponding optoelectronic application perspective. Therefore, in order to have a profound understanding of the pressure induced optical property variation in such materials, it is imperative to study the optical absorption spectra systematically corresponding to each pressure range. The pressure dependence of the absorption cross-section of the chalcogenide perovskites have been depicted in Fig. 10 at selected pressure points from 0 to 15 GPa. We can observe the optical absorption spectra is becoming distinctively finite corresponding to the photon energy value between 0.5 to 0.75 eV, whereas the first prominent absorption peak is occurred at approximately 0.57, 3.05, 3.11 and 3.13 eV e for MgZrS3, CaZrS3, SrZrS3 and BaZrS3 respectively. The absorption spectra become finite between 0.5 and 0.75 eV although the band gaps reported earlier are much higher because the optical properties were determined using PBE approximation, whereas the electronic band gaps were calculated using the HSE06 hybrid functional. In all the four chalcogenide perovskite systems at 0 GPa, between the primary and secondary peaks, intermediate hump like absorption cross sections are observed. These additional absorption peaks insinuate the multivalley characteristic of band structures, which primarily originated due to the allowed optical transition between primary and secondary valence band maxima and conduction band minima of the studied systems. On compression, a slight red shift is seen for all the four perovskite systems, which is attributed to the decrement of bandgap in the optical absorption spectra. Hence, we can certainly infer that in all the chalcogenide perovskite systems considered in this work, the bandgap narrowing can be concluded from the variation of optical absorption spectra in addition to the analysis derived from density of states and band structure calculations. The multivalley optical absorption behavior persists even under the influence of external hydrostatic pressure, while this sensitive tuning of optical absorption spectra manifest the bandgap tuning in chalcogenide perovskite materials, which has been emerged as the exciting field of piezochromism.4. Conclusions
To summarize, we studied the evolution of the structural, electronic and optical properties of AZrS3 (A = Mg, Ca, Sr and Ba) alkaline earth chalcogenide perovskites at selected pressure points between 0 and 15 GPa. This class of Zr-based chalcogenide perovskites were chosen due to some clear advantages they have over halide and oxide based perovskites. Firstly, these Zr-based chalcogenide perovskites are more stable against moisture and light induced degradation compared to lead halide perovskites. Secondly, the reduced electronegativity difference between S and Zr atoms leads to comparatively narrower band gaps and improved charge transport. Finally the lack of toxic lead in this class of materials is huge advantage. We have shown that upon compression, the studied structures retain the distorted tetragonal structure up to at least 15 GPa. Both dynamical and mechanical stability have been established. While CaZrS3, SrZrS3 and BaZrS3 are all dynamically stable at 0 GPa, MgZrS3, shows positive phonons only from 8 GPa onwards. With compression, the octahedral tilting increased in all the materials except for BaZrS3 in which the tilting angle decreased. This can be attributed to the ionic radius of Ba which is much larger than that of the other alkaline earth metals considered in this work. Under hydrostatic compression from 0 to 15 GPa, the electronic band gaps of MgZrS3, CaZrS3 and SrZrS3 decreased from 1.94 to 1.8 eV, 2.04 to 1.84 eV, and 2.04 to 1.59 eV, respectively. Similarly, for BaZrS3 the band gap decreased from 1.87 to 1.52 eV under the same pressure range. For all the structures, the direct nature of the band gaps was retained. The significant narrowing of the band gaps in SrZrS3 and BaZrS3 at 15 GPa compared to the other two is due to the appearance of van Hove singularities. The magnitudes of the band gaps are ideal for them to be used as top cells in tandem solar cells with Si as the bottom cell. Furthermore, on compression, we observed the sensitive variation of optical absorption spectra nature. A slight red shift of the primary absorption peak under the influence of piezochromism has been reported in this work. Thus, the lead-free non-toxicity, environmental stability, direct band gaps in the desired range and low effective masses can render these compressed Zr-based chalcogenide perovskites to be ideal for photovoltaics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. M. and R. A. would like to acknowledge support from Olle Engkvists stiftelse, Sweden; Carl Tryggers Stiftelse for Vetenskaplig Forskning (CTS); and the Swedish Research Council (VR grant no. 2016-06014). SNIC and HPC2N are also acknowledged for providing computing time. S. C. would like to acknowledge IIT Indore. A. A acknowledges the computing resource provided by University of Saskatchewan, Westgrid, and Compute Canada.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS.
- S. Chakraborty, W. Xie, N. Mathews, M. Sherburne, R. Ahuja, M. Asta and S. G. Mhaisalkar, ACS Energy Lett., 2017, 2, 837–845 CrossRef CAS.
- E. R. Dohner, A. Jaffe, L. R. Bradshaw and H. I. Karunadasa, J. Am. Chem. Soc., 2014, 136, 13154–13157 CrossRef CAS.
- D. Giovanni, H. Ma, J. Chua, M. Grätzel, R. Ramesh, S. Mhaisalkar, N. Mathews and T. C. Sum, Nano Lett., 2015, 15, 1553–1558 CrossRef CAS.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. Van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–345 CrossRef CAS.
- D. P. Mcmeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Hörantner, A. Haghighirad, N. Sakai, L. Korte, B. Rech, M. B. Johnston, L. M. Herz and H. J. Snaith, Science, 2016, 351, 151–156 CrossRef CAS.
- P. C. Harikesh, H. K. Mulmudi, B. Ghosh, T. W. Goh, Y. T. Teng, K. Thirumal, M. Lockrey, K. Weber, T. M. Koh, S. Li, S. Mhaisalkar and N. Mathews, Chem. Mater., 2016, 28, 7496–7504 CrossRef CAS.
- C. N. Savory, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2016, 1, 949–955 CrossRef CAS.
- A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, K. Nazeeruddin, M. Gratzel and F. De Angelis, Nano Lett., 2014, 14, 3608–3616 CrossRef CAS.
- J. Even, L. Pedesseau, J. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398 CrossRef CAS.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Graetzel, Nature, 2013, 499, 316–320. CrossRef CAS.
- N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. Il Seok, Nature, 2015, 517, 476–480 CrossRef CAS.
- T. Leijtens, G. E. Eperon, S. Pathak, A. Abate, M. M. Lee and H. J. Snaith, Nat. Commun., 2013, 4, 2885 CrossRef.
- J. A. Christians, P. A. M. Herrera and P. V. Kamat, J. Am. Chem. Soc., 2015, 137, 1530–1538 CrossRef CAS.
- W. Yin, T. Shi and Y. Yan, Adv. Mater., 2014, 26, 4653–4658 CrossRef CAS.
- R. Nechache, C. Harnagea, S. Li, L. Cardenas, W. Huang, J. Chakrabartty and F. Rosei, Nat. Photonics, 2015, 9, 61–67 CrossRef CAS.
- Y. Sun, M. L. Agiorgousis, P. Zhang and S. Zhang, Nano Lett., 2015, 15, 581–585 CrossRef CAS.
- S. Perera, H. Hui, C. Zhao, H. Xue, F. Sun, C. Deng, N. Gross, C. Milleville, X. Xu, D. F. Watson, B. Weinstein, Y.-Y. Sune, S. Zhange and H. Zeng, Nano Energy, 2016, 22, 129–135 CrossRef CAS.
- A. Swarnkar, W. J. Mir, R. Chakraborty, M. Jagadeeswararao, T. Sheikh and A. Nag, Chem. Mater., 2019, 31, 565–575 CrossRef CAS.
- A. Clearfield, Acta Crystallogr., 1963, 16, 134 CrossRef.
- W. Meng, B. Saparov, F. Hong, J. Wang, D. B. Mitzi and Y. Yan, Chem. Mater., 2016, 821–829, 28 Search PubMed.
- S. Niu, H. Huyan, Y. Liu, M. Yeung, K. Ye, L. Blankemeier, T. Orvis, D. Sarkar, D. J. Singh, R. Kapadia and J. Ravichandran, Adv. Mater., 2017, 1604733 CrossRef.
- H. I. Eya, E. Ntsoenzok and N. Y. Dzade, Materials, 2020, 13, 978 Search PubMed.
- J. M. Polfus, T. Norby and R. Bredesen, J. Phys. Chem. C, 2015, 119, 23875–23882 CrossRef CAS.
- H. Zitouni, N. Tahiri, O. El Bounagui and H. Ez-zahraouy, Chem. Phys., 2020, 538, 110923 CrossRef CAS.
- Y. Nishigaki, T. Nagai, M. Nishiwaki, T. Aizawa, M. Kozawa, K. Hanzawa, Y. Kato, H. Sai, H. Hiramatsu, H. Hosono and H. Fujiwara, Sol. RRL, 2020, 4, 1900555 CrossRef CAS.
- P. Zhang, B. Chen, W. Zhu, C. Wang, W. Zhang, Y. Li and W. Liu, Eur. Phys. J. B, 2020, 93, 97 CrossRef CAS.
- S. Filippone, B. Zhao, S. Niu, N. Z. Koocher, D. Silevitch, I. Fina, J. M. Rondinelli, J. Ravichandran and R. Jaramillo, Phys. Rev. Mater., 2020, 4, 091601 CrossRef CAS.
- Y. Wang, N. Sato, K. Yamada and T. Fujino, J. Alloys Compd., 2000, 311, 214–223 CrossRef CAS.
- C. Lee, K. M. Kleinke and H. Kleinke, Solid State Sci., 2005, 7, 1049–1054 CrossRef CAS.
- R. Lelieveld and D. J. W. Ijdo, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2223–2226 CrossRef.
- H. Brasseur and L. Pauling, J. Am. Chem. Soc., 1938, 60, 2886–2890 CrossRef CAS.
- A. Jaffe, Y. Lin, W. L. Mao and H. I. Karunadasa, J. Am. Chem. Soc., 2017, 139, 4330–4333 CrossRef CAS.
- Y. Liang, X. Huang, Y. Huang, X. Wang, F. Li and Y. Wang, Adv. Sci., 2019, 6, 1900399 CrossRef.
- A. Majumdar, S. Chakraborty and R. Ahuja, J. Appl. Phys., 2020, 128, 045102 CrossRef CAS.
- C. Pickard, I. Errea and M. I. Eremets, Annu. Rev. Condens. Matter Phys., 2020, 11, 57–76 CrossRef CAS.
- I. P. Swainson, M. G. Tucker, D. J. Wilson, B. Winkler and V. Milman, Chem. Mater., 2007, 19, 2401–2405 CrossRef CAS.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- M. Trigo, J. Chen, M. P. Jiang, W. L. Mao, S. C. Riggs, M. C. Shapiro, I. R. Fisher and D. A. Reis, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 081102 CrossRef.
- Y. Wang, X. Lu, W. Yang, T. Wen, L. Yang, X. Ren, L. Wang, Z. Lin and Y. Zhao, J. Am. Chem. Soc., 2015, 137, 11144–11149 CrossRef CAS.
- A. Jaffe, Y. Lin, C. M. Beavers, J. Voss, W. L. Mao and H. I. Karunadasa, ACS Cent. Sci., 2016, 2, 201–209 CrossRef CAS.
- A. Jaffe, Y. Lin and H. I. Karunadasa, ACS Energy Lett., 2017, 2, 1549–1555 CrossRef CAS.
- H. Mao, X. Chen, Y. Ding, B. Li and L. Wang, Rev. Mod. Phys., 2018, 90, 15007 CrossRef CAS.
- H. Mao, B. Chen, J. Chen, K. Li, J. Lin, W. Yang and H. Zheng, Matter Radiat. Extremes, 2016, 1, 59–75 CrossRef.
- F. Aguado, F. Rodriguez, R. Valiente, J.-P. Itie and M. Hanfland, Phys. Rev., 2012, 85, 100101(R) CrossRef.
- A. Jaffe, Y. Lin, W. L. Mao and H. I. Karunadasa, J. Am. Chem. Soc., 2015, 137, 1673–1678 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–18979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- K. Kuhar, A. Crovetto, M. Pandey, K. S. Thygesen, B. Seger, P. C. K. Vesborg, O. Hansen, I. Chorkendorf and K. W. Jacobsen, Energy Environ. Sci., 2017, 10, 2579–2593 RSC.
- N. Gross, Y. Sun, S. Perera, H. Hui, X. Wei, S. Zhang, H. Zeng and B. A. Weinstein, Phys. Rev. Appl., 2017, 8, 044014 CrossRef.
- M. Born, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160–172 CrossRef CAS.
- R. Prasanna, A. Gold-parker, T. Leijtens, B. Conings, A. Babayigit, H. Boyen, M. F. Toney and M. D. Mcgehee, J. Am. Chem. Soc., 2017, 139, 11117–11124 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |