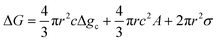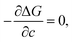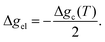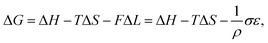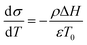Martensitic transition in molecular crystals for dynamic functional materials

Abstract

Molecular martensitic materials are an emerging class of smart materials with enormous tunability in physicochemical properties, attributed to the tailored molecular and crystal structures through molecular design. This class of materials exhibits ultrafast and reversible structural transitions in response to thermal and mechanical stimuli, which underlies fascinating properties such as thermoelasticity, superelasticity, ferroelasticity, and shape memory effect. These dynamic properties are not widely explored in molecular crystals and therefore molecular martensitic materials represent a new frontier in the field of solid-state chemistry. In martensitic transitions, the materials not only exhibit substantial shape changes but also remember the functions in the associated polymorphic phases. This suggests promising applicability towards light-weight actuators, lifts, dampers, sensors, shape-/function-memory and ultraflexible optoelectronic devices. In this article, we review characteristics, detailed transition mechanisms, and potential applications of molecular martensitic materials. In particular, we aim to describe transition characteristics by collecting cases with similar transition principles in order to glean insights into further advancement of molecular martensitic materials. Overall, we believe that molecular martensitic materials are emerging as the next generation smart materials that have shown promise in advancing a wide range of domains of applications.

---

Sang Kyu Park

Sang Kyu Park received his BS degree in the Department of Materials Science and Engineering from Seoul National University in 2010. In 2016, he received his PhD degree from Seoul National University for his thesis on development of a charge-transfer complex with unique optoelectronic functions. In 2017, he joined Dr Ying Diao's research group in University of Illinois at Urbana-Champaign as a Postdoctoral Associate. In Diao's research group, he pursues his research to implement ultraflexible organic electronic devices by harnessing martensitic transition of organic semiconductor materials.

Ying Diao

Professor Diao is a Beckman Fellow, Dow Chemical Company Faculty Scholar, and Lincoln Excellence for Assistant Professor Scholar at University of Illinois at Urbana-Champaign. Her research focuses on molecular assembly and printing innovation with structural control down to the molecular and nanoscale. She was named on the MIT Technology Review's annual list of Innovators Under 35 as a pioneer in nanotechnology and materials. She is also a recipient of th NSF CAREER Award, NASA Early Career Faculty Award and 3M Non-Tenured Faculty Award, and was selected as a Sloan Research Fellow in Chemistry as one of the “very best scientific minds working today”.

---

1. Introduction

Martensite has played a pivotal role in controlling the strength, hardness, and toughness of carbon steel, created by quenching the austenite phase.^1,2 Under the rapid cooling process, carbon atoms have insufficient time for diffusion, and thus transform into the carbon supersaturated ferrite, namely martensite. The transition represents a diffusionless first-order transition, which is accompanied by rapid and cooperative displacement of the atoms. Besides, structural transitions of shape memory alloys and ceramics have manifested corresponding characteristics.^3–6 The representative example is Ni–Ti shape memory alloys (Fig. 1a).⁷ As shown in Fig. 1a, the Ni–Ti alloy is capable of mechanical deformation at the low-temperature martensitic phase, where the shape change is accomplished through lattice reorientation (twinning – detwinning). In addition, by heating the mechanically deformed Ni–Ti alloy above the austenitic phase transition temperature, the shape can be restored to the original state. Such thermo-mechanical transitions underlying the shape memory effect are accomplished by concerted displacement of constituting atoms. Another intriguing example is the contractile tail of bacteriophage T4 (Fig. 1b).^8–10 During the viral genome delivery, the tail sheath of the bacteriophage contracts by 60% and penetrates its non-contractile inner tube through the outer membrane of the target bacteria. Similar to the Ni–Ti alloy case, the significant shape change in the bacteriophage T4 virus is established through cooperative tilting and displacement of the constituting protein, gene product 18 (gp18). The above-described martensitic or cooperative transitions have compelling technological importance and have been regarded as a key element in the development of smart materials and devices that can sense and actuate upon environmental stimulation – for example stent, wrapper, gripper, and memristors to name a few (Fig. 1a).^5,7,11–15 In the recent few years, the realm of martensitic transitions has expanded into the molecular crystals.

Fig. 1 (a) Schematic illustration of the shape memory effect of Ni–Ti alloy and its applications, e.g., superelastic stent and microwrapper. Reprinted with permission from ref. 14 (Copyright 1999 Elsevier Science S. A.) and ref. 12 (Copyright 1999 Elsevier Science B.V.) (b) Schematic illustration of bacteriophage T4 and cooperative movement of gene product (gp) 18 proteins that constitute the contractile tail sheath. The cooperative displacement and tilting of gp 18 proteins accomplish 60% contraction of the length of the tail sheath. Adapted with permission from ref. 9, copyright 2009 European Molecular Biology Organization.

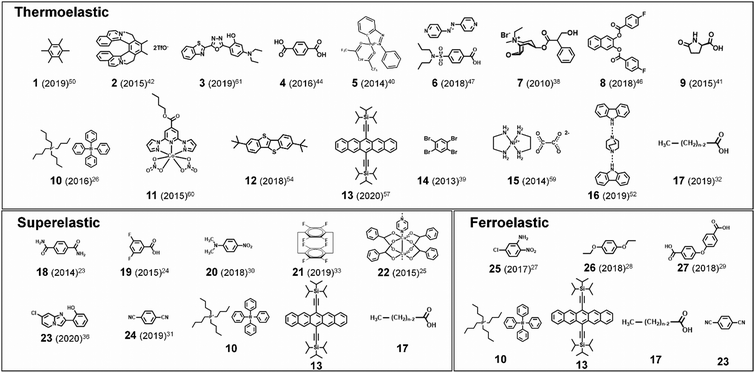
Martensitic transitions are not yet widely known in molecular crystals. Molecular crystals, in comparison to primary bonded metallic alloys or ceramics, are constructed by weak secondary bonding interactions. Their properties – from thermal, mechanical to optoelectronic properties – strongly rely on the molecular packings and molecular structures, which can be tailored by molecular/crystal engineering approaches.^16–21 Although structure–property correlation for organic martensitic transition is elusive to date, this class of materials has tremendous potential towards a new generation of smart devices that can move, bend, or stretch in response to external stimuli, a.k.a. “crystal adaptronics”.²² The molecular crystals exhibiting martensitic transitions with associating thermoelastic, thermosalient, superelastic, and shape memory properties have been reported from the groups of Takamizawa,^23–36 Naumov,^37–52 Diao,^53–58 and others^59–68 (see summarized molecules in Fig. 2). These fascinating properties, which were almost exclusively found from the shape memory alloys and ceramics, have recently been found in molecular crystals (Fig. 2), whose structural transitions are facilitated by the cooperative rearrangements of molecular packing and/or conformation. During the transitions, distinct molecular mechanisms and peculiarities have been discovered, deviating from those found in conventional shape memory materials (i.e., alloys and ceramics). Furthermore, intriguing applications have been demonstrated, such as a sensor, soft actuator,^50,51 lift,²⁶ gas flow controller,²⁵ and ultra-flexible and shape memory optoelectronic device,^54,57 opening avenues for next-generation smart material systems. To spur this emerging research field, we herein summarize the characteristics of the organic martensites published to date, classify them according to molecular mechanisms underlying structural transitions, and provide a bridgehead for material development for the future.

Fig. 2 Representative thermoelastic, superelastic and ferroelastic molecules. Parentheses: reported year of the paper that assigned each molecule as an organic martensite for the first time. The reference number is denoted as the superscript. n equals to 15, 17, 19, and 21 in #17 molecules.

In this review, we introduce molecular martensitic materials, highlight their molecular mechanisms for transitions, and summarize potential applications of this new class of smart materials. In Section 2, we briefly introduce general characteristics of martensitic transitions and associated thermoelastic, superelastic, ferroelastic, and shape memory properties. In Section 3, we introduce case by case molecular mechanisms found in thermoelastic, superelastic, and ferroelastic molecular martensitic materials. Section 4 highlights the potential applications discussed in recent reports. This review is intended to catalyze further advancements in this research field not only by introducing fascinating features of molecular martensitic materials but also by providing insights to devise new materials by summarizing structure–property correlations for cooperative transitions elucidated in recent literature reports. For further readings on related topics, we refer the readers to the following excellent reviews: the review by Ahmed et al. that highlighted various intriguing mechanical responses such as elasticity, plasticity, super-, and ferroelasticity of selected molecular crystals;²² the review by Naumov et al. that comprehensively summarized the mechanical effects of molecular crystals and their mechanisms in response to external stimuli;³⁷ and the review by Reddy et al. on mechanical properties and structure–property correlations of molecular crystals.⁶⁹

2. Characteristics of molecular martensitic materials

2.1. Martensitic transition vs. nucleation and growth transition

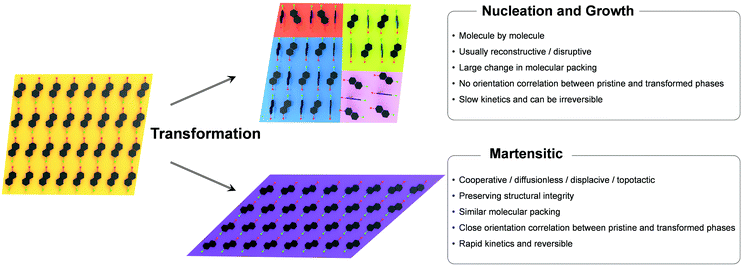
Polymorphism, the ability of a single compound to adopt distinct crystal structures, is a widespread phenomenon in molecular crystals, which can largely modulate physical properties such as mechanical, thermal, optical, electrical, magnetic, and ferroic properties.^70–74 Between the polymorphic phases, solid-state phase transition may occur by controlling the thermodynamic variables (typically temperature and pressure), where the equilibrium structure at given environmental conditions is determined by relative stability between the phases.⁷⁵ Broadly speaking, solid-state phase transitions can be classified into nucleation and growth (reconstructive) and martensitic transition;^76–78 the fundamentals and characteristics of these transitions are comprehensively described in the book by Christian.⁷⁶

The nucleation and growth transitions in the solid state include the nucleation stage that develops small particles of a new phase which is an activated process, followed by the growth stage once the nucleation barrier is overcome. Once nuclei are formed typically at the defective sites, the transition occurs by slow molecular diffusion across the transition interface in a molecule-by-molecule fashion. Such transition is a thermally activated process where the velocity exhibits a clear temperature dependence. Typically, the transformed phase induced by nucleation and growth transition shows a substantial structural dissimilarity compared to its original phase. Therefore, the transition is usually absent from lattice correspondence or orientational relationships, and thus multiple and randomly oriented transformed phase domains may be created in the original matrix. As a result, a crystal that undergoes such nucleation and growth transition may lose structural integrity^56,79–81 but not always. It should be noted that single-crystal-to-single-crystal transitions based on the nucleation and growth mechanism have been reported.^82–88 Attributes of nucleation and growth transitions are summarized in Fig. 3.

Fig. 3 General characteristics found in the nucleation and growth and martensitic transitions.

The martensitic transition is also a two-stage process. The initiation stage of martensitic transition resembles nucleation in that it is an activated process exhibiting 1st order kinetics.^55,89–92 In a typical 1st order martensitic transition, the nucleation/initiation stage is followed by a propagation stage that involves cooperative and displacive atomic/molecular motions, often in a layer-by-layer manner.^{23,24,26,42,44,47,54,55,93,94} This is in stark contrast to the molecule-by-molecule transition in the nucleation and growth mechanism. The transition also features a fast propagation velocity of the phase front, theoretically at the speed of sound in the atomic systems, while it is several orders of magnitude slower in the molecular systems (10³–10⁷ mm s⁻¹).^50,51,54 Since the transition is accomplished by cooperative molecular displacement to an extent that does not require exchanging the nearest neighbors of the molecule, the transition is diffusionless in nature. The original and transformed phases of the martensitic transition present an excellent structural similarity and a specific orientation relationship between the two phases. Specifically, the orientation of the transformed phase is predetermined by the orientation of the original phase, and vice versa. Such transition characteristics enable ultrafast and reversible single-crystal-to-single-crystal transition that preserves structural integrity and exhibits abrupt crystal shape change in most cases, but not always. Due to the first-order nature, changes in the volume, enthalpy, and entropy upon these transitions are discontinuous at the transition point. However, it should be noted that not all the martensitic transitions exhibit 1st order kinetics in the initiation stage. For instance, one of the thermally induced martensitic transitions of #13 in Fig. 2 (I–I(b) transition) features a continuous 2nd order transition absent from the initiation of a phase front.^54,57 In contrast to the 1st order transition, a 2nd order transition is expected to exhibit continuous changes in the volume, enthalpy, and entropy upon transition. As a result, the I–Ib transition is continuous and absent from transition temperature hysteresis. All molecules in the entire crystal displace/rotate continuously and synchronously upon I–Ib transition, not presenting a nucleation stage and phase front sweeping. This is rarely observed among martensitic organic materials. In sum, unique attributes of martensitic transitions are summarized in Fig. 3 in comparison to the nucleation and growth mechanism. Due to such characteristics, martensitic transition is more appealing for stimuli-responsive smart applications, which are dealt with in Section 4.

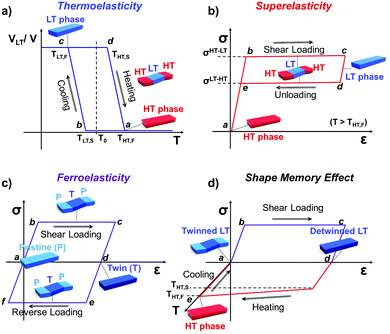
Martensitic transition engenders intriguing thermo-mechanical properties, i.e., thermoelasticity, superelasticity, ferroelasticity, and shape memory effect. Thermoelasticity is referred to as a continuous and reversible martensitic transition between crystal polymorphs driven by thermal energy; it should be distinguished from elasticity which describes the property of a material to resist deformation and thus enables shape restoration upon stress removal. The transition occurs over a narrow temperature range, exhibiting small transition temperature hysteresis. Thermoelasticity is a prerequisite for superelasticity and the shape memory effect, discussed in the next section. Meanwhile, thermoelastic transition between polymorphs can also be accomplished by mechanical work, i.e., superelasticity. By superelasticity a material is capable of substantial deformation through a mechanically induced martensitic polymorph transition, where a mechanical unloading readily leads to a full, spontaneous shape recovery by the reverse polymorph transition. In addition to mechanically induced polymorph transitions, mechanically induced reversible twinning is another type of martensitic transition known as ferroelasticity. Due to the equally stable twin domain formation, this process does not spontaneously reverse until a reverse mechanical loading induces a detwinning process to recover the shape of the deformed crystal. Lastly, the shape memory effect is a combined process of ferroelasticity and thermoelasticity. By ferroelasticity, a crystal can be mechanically deformed through a twinning process; shape recovery of the deformed crystal can then take place by a heating induced polymorph transition (thermoelasticity) that completely de-twins the crystal; subsequent cooling allows the crystal to return to the original polymorph form. Such intriguing phenomena are fascinating sources for devising smart functional applications.^{25,26,43,50,51,54,57} In the following subsections (Sections 2.2–2.5), we introduce fundamentals of thermoelasticity, superelasticity, ferroelasticity, and shape memory effect one by one.

2.2. Thermoelasticity

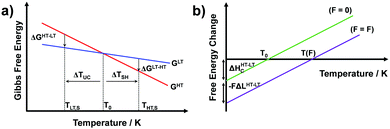
Temperature controlled reversible martensitic transition between enantiotropically related high temperature (HT) and low temperature (LT) polymorphs is referred to as thermoelasticity.^3,4,95–98 Herein, the thermally-induced transition is considered “elastic” as the change in shape is reversible owing to the cooperative nature of the transition. Thermoelasticity is of immense importance and serves as a prerequisite for superelasticity and the shape memory effect.⁴ As schematically described in Fig. 4a, the volume fraction of the LT phase (V_LT/V) increases (decreases) by decreasing (increasing) temperature once a critical transition temperature is surpassed. Such volume fraction change usually occurs as a sharp phase front (i.e. habit plane) that sweeps through the crystal.⁹⁶ The forward HT to LT transition (section a–b–c in Fig. 4a) begins at the LT phase starting temperature (T_LT,S) and completes at the LT phase finishing temperature (T_LT,F). The LT phase starting temperature is usually seen below the equilibrium temperature (T₀), at which the Gibbs free energies (G_c) of the LT and HT phase become identical (thus, ΔG_c = ΔG^HT–LT = G^HT − G^LT in Fig. 5a). Similarly, the reverse LT to HT transition (section c–d–a) begins at the HT phase starting temperature (T_HT,S) and completes at the HT phase finishing temperature (T_HT,F). The HT phase start temperature is usually seen above the equilibrium temperature. Such undercooling (superheating) in the forward (reverse) transition occurs due to the existence of an activation barrier to nucleating the LT (HT) phase. Specifically, the Gibbs free energy change during solid-state thermoelastic transition is expressed as:⁴

ΔG = ΔG_c + ΔG_el + ΔG_s

The activation barrier arises from the elastic energy (ΔG_el) and the surface energy (ΔG_s) terms in this expression that resist forward and reverse martensitic transition, whereas the free energy difference between the LT and HT phase (ΔG_c) serves as the driving force for martensitic transition. In the field of metallurgy, the concept of thermoelastic equilibrium with balanced driving force and resistive forces was illustrated by Olson and Cohen.⁹⁵ Assuming a nucleus of an oblate-ellipsoidal shape for the LT phase (or martensite in metallurgy) – a shape that minimizes the elastic and surface energy terms, the above equation is further expressed as the following:⁹⁵
where Δg_c is the change in the Gibbs free energy per unit volume, r and c are the radius and the thickness of the nucleus (r ≫ c), A is the elastic constant, σ is the interfacial energy per unit area, and Ac/r is the elastic strain energy per unit volume, Δg_el.⁹⁵ The above equation defines a saddle-shaped Gibbs free energy surface, and the lowest free energy is attained at a critical undercooling T_LT,S.^95,98,99 During the growth of the LT phase nucleus, it is assumed that if the radial (r) growth is seized by any existing obstacle, transition proceeds to increase the thickness (c) of the nucleus until it reaches a local equilibrium defined as

Fig. 4 Schematic illustrations of solid-state phase transition in (a) thermoelastic, (b) superelastic, (c) ferroelastic, and (d) shape memory materials. LT: low-temperature, HT: high-temperature, V_LT/V: volume fraction of the LT phase, T₀: equilibrium temperature, T_LT,S: the LT starting temperature upon cooling, T_LT,F: the LT finishing temperature upon cooling, T_HT,S: the HT starting temperature upon heating, T_HT,F: the HT finishing temperature upon heating, σ: stress, ε: strain, σ^HT–LT: critical stress for HT to LT phase transition, σ^LT–HT: critical stress for LT to HT phase transition.

Fig. 5 (a) Schematic free energy curves for high temperature (HT, red) and low temperature phases (LT, blue) of thermoelastic systems, showing the enantiotropic relationship between the LT and HT phases. Low temperature (T_LT,S) and high temperature phase starting temperatures (T_HT,S) as well as required undercooling (ΔT_UC) and superheating (ΔT_SH) for transitions are indicated. (b) Schematic (elastic) Gibbs free energy difference curves before (green) and after (purple) applying external work (FΔL^HT–LT, F: force and ΔL^HT–LT: change in length by the HT-to-LT transition), which leads to an equilibrium temperature shift from T₀ to T(F).

which yields

Therefore, by varying the temperature, the LT phase will grow until its elastic strain energy per unit volume (Δg_el) is equal to half of the change in the Gibbs free energy per unit volume (Δg_c). At this point, half of the Gibbs free energy change incurred in the transition is stored as elastic energy. By the same token, further undercooling will advance the growth of the LT phase until it reaches a new equilibrium at a given temperature. This simple model explains how the driving force is balanced with the resisting terms at a given temperature for a particular nucleus geometry. Besides interfacial energy and stored elastic energy, advancing the phase front requires overcoming additional local energy barriers due to structural defects, which gives rise to avalanche-like dynamics of the phase front. Such frictional work is the source of thermodynamic irreversibility, despite reversible macroscopic shape and crystal structures.⁹⁸

Such thermoelastic transitions are also observed in molecular crystals, which will be detailed in Section 3.2. In many cases, transitions occur in a single-crystal-to-single-crystal fashion displaying a single phase front.⁹⁸ In such a scenario, the transition may show only a small temperature gap between T_LT,S and T_LT,F, or even spontaneous propagation once the temperature reaches T_LT,S.^38–40 This phenomenon can be attributed to minimized morphological defects in single crystals which hinder the growth of the LT phase nucleus.⁹⁹ Interestingly, instantaneous completion of the transition releases accrued elastic stress and thus leads to intriguing crystal motility such as jumping, bending and twisting motions, i.e., thermosalient effects.^{38–41,44,47} Furthermore, thermoelasticity in organic crystals underlies other fascinating properties such as superelasticity and shape-memory effect like in the case of metal and metal alloys.^26,32,57

2.3. Superelasticity

Interestingly, thermoelastic transition can also be induced mechanically under isothermal conditions, which is known as superelasticity.^96–98 As illustrated in Fig. 4b, a superelastic crystal of HT phase deforms upon shear loading, at the temperature typically above the HT phase finishing temperature, T_HT,F when the HT phase is thermodynamically stable in the absence of stress. First, the stable HT phase elastically deforms in section a–b. As the stress surpasses a critical value of σ^HT–LT at point b, HT-to-LT phase transition ensues to accommodate large strain deformation. Beyond point b, slight increase in the shear stress causes abrupt increase in shape strain and extent of transition (the volume fraction of the LT phase) until the transition to LT phase is complete at point c. As the phase transition serves as a stress-releasing mechanism, minimal increase in shear stress occurs during large strain deformation. This phenomenon manifests as a plateau in the stress–strain curve between point b and c. Upon shear unloading, spontaneous shape recovery occurs which is another characteristic of superelasticity. Specifically, LT phase elastically deforms in section c–d until the shear stress decreases to a critical value of σ^LT–HT at point d when the reverse LT-to-HT phase transition begins. As in the forward trace, the phase transition creates a plateau in the stress–strain curve in section d–e, when the progression of LT-to-HT transition relieves stress during shape deformation. Once the transition is complete at point e, the strain recovery is accomplished through linear elastic deformation of the HT phase in section e–a. As depicted in Fig. 4b, superelastic transition typically shows a characteristic stress-hysteresis (σ^HT–LT − σ^LT–HT) arising from the frictional work. Frictional work is a result of structural defects that act as kinetic barriers for phase front motion, like in the thermoelastic process.¹⁰⁰

How can a thermoelastic transition be triggered by mechanical force? Application of mechanical force alters the Gibbs free energy change of the HT-to-LT transition at constant pressure described in Fig. 5b. The Gibbs free energy change shifts by the amount of elastic work done by stress (−FΔL or 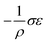) following the relationship

where ΔH is enthalpy change, T is temperature, ΔS is entropy change, F is applied force, ΔL is the length change along the force direction, ρ is density, σ is stress, and ε is strain.^96–98 Simply, the elastic work alters the thermodynamic equilibrium properties and phase stability at a given temperature, thus leading to stress induced HT-to-LT phase transition. Therefore, thermoelastic transition can also be accomplished by application of stress. The Clausius–Clapeyron type equation describes the relationship between interchangeable independent variables, T and σ (or F):
where σ is the stress applied for superelastic transition, T is temperature, ΔH is the enthalpic change of transition, ε is strain, and T₀ is the equilibrium temperature for thermoelastic transition.^101,102 Since the terms in the right-hand side are constant in a given condition, the stress and the temperature are in a linear dependence. Such attributes in molecular crystals are comprehensively studied by Takamizawa et al. using single crystals of #10 and #17 (Fig. 2), which will be detailed in Section 3.^26,32 In addition to typical superelastic transitions based on enantiotropic polymorphic transitions, molecular crystals exhibit other unique superelastic transitions based on shear induced phase formation,²³ deformation twinning,^24,25,30,31 or even monotropic polymorphic transitions,³⁶ which are also detailed in Section 3.

2.4. Ferroelasticity

Besides thermoelasticity and superelasticity, ferroelasticity is also observed in metals, ceramics, and molecular materials.^103–107 The concept of ferroelasticity was established by Aizu,^103,104 which is deduced from the behavior of other ferroic systems showing ferroelectricity and ferromagnetism. A ferroic material exhibits a field-induced directional property that does not return to the original after the field is removed. If the directionality is maintained, the property is said to be spontaneous. Such directional properties arise from the symmetry-breaking process of the phase transition – i.e., from a higher symmetry structure without directional property to a lower symmetry structure with a directional property. The symmetry-breaking process therein gives rise to directional properties of two or more different orientations, the so called orientation states. Another feature of ferroic materials is the switchability between these orientation states, which is accomplished by directional control of the applied field. Such behavior in ferroelectric materials can be explained by the fact that the direction of electric polarization (or orientation states) can be reverted by applying an electric field in the opposite direction. This idea is successfully transferred to the ferroelastic crystal.

By Aizu's definition of ferroelasticity, a crystal can be referred to as ferroelastic, if the stress induced strained state of the crystal is maintained even after the stress is removed, where the crystal has domains of two or more orientations that are mechanically interconvertible by exerting forward/reverse stress onto it.^103,104 Like in other ferroic materials, the formation of these orientation states is a result of a symmetry-breaking process from a structure of higher symmetry to a structure of lower symmetry. The symmetry-breaking process creates two or more ferroelastic orientation states that take the form of twin domains. Since crystal structures are equivalent but differ only in their lattice orientation, these states are equally stable. Therefore, during the stress removal, stress-induced twin domains do not undergo reverse transition. To recover the shape strain, reverse shear stress is required and thus the stress–strain curve manifests a notable mechanical hysteresis. As illustrated in Fig. 4c, the ferroelastic crystals show hysteresis in their stress–strain curve, resembling polarization–electric field (P–E) curves of ferroelectric materials. Like spontaneous polarization in the ferroelectric materials, ferroelastic materials exhibit spontaneous strain since they are capable of forming equally stable orientational states. Specifically, surpassing the elastic deformation region of the pristine state (section a–b), further application of force induces large increase in shape strain (or the volume of orientational states) achieved by twin domain formation in section b–c. Upon removing external force, the structure slightly restores the shape under a linear elastic regime (section c–d). However, ferroelastically induced shape strain remains in place. Such twinned structure and deformed shape can be fully restored to its original state through mechanical detwinning by exerting reverse shear in section d–e–f–a, where d–e and f–a correspond to elastic deformation regimes. The molecular mechanisms of ferroelasticity will be detailed in Section 3.

2.5. Shape memory effect

As previously mentioned, thermoelastic materials generally exhibit superelasticity when the specimen is sheared at T > T_HT,F.⁴ On the other hand, shear loading at T < T_LT,F results in ferroelastic twinning–detwinning, which is the starting point for the shape memory effect. We note that ferroelasticity can occur in non-thermoelastic materials too, therefore we did not specify a temperature requirement in Section 2.4. As schematically illustrated in Fig. 4d, beyond the elastic deformation regime in section a–b, the deformation of a pre-twinned structure is accomplished by ferroelastic detwinning (or further twinning depending on the shear direction) in section b–c. Due to the ferroelastic nature, the deformed shape (or shape strain) does not recover upon unloading (section c–d), but can be restored by thermal treatment (section d–e). It is depicted in Fig. 4d that shape strain starts to decrease from the HT starting temperature (T_HT,S) and becomes zero at the HT finishing temperature (T_HT,F), accomplished by thermoelastic transition. Attaining the shape memory effect requires the HT phase to have a higher symmetry compared to the LT phase and to be non-ferroelastic. These requirements allow the convergence of several different orientation states in the twinned LT structure to a singly oriented state of the HT structure. Interestingly, in the shape memory effect, restored shape at point e is macroscopically maintained upon cooling (section e–a). This is due to the self-accommodating characteristic of HT-to-LT phase transition, meaning that the shape preservation is achieved by the growth of twinned LT domains. In molecular crystals, only a few crystals are reported to exhibit such conventional shape memory behavior (#10 and #17, Fig. 2) which will be detailed in Section 3.5.^26,32

3. Martensitic transitions in organic crystals and their molecular mechanisms

3.1. Classification of molecular mechanisms in martensitic transitions

In Section 2, we discussed the characteristics of martensitic transition by contrasting the characteristics of nucleation and growth transition (Section 2.1), and introduced fundamentals of thermoelasticity, superelasticity, ferroelasticity, and shape memory effect (Sections 2.2–2.5). In the following, we shift our focus to changes in molecular packing and conformation underlying thermo-mechanical martensitic transitions. In the molecular martensitic transitions, several types of molecular motions can occur, such as (i) molecular gliding, (ii) conformational change, (iii) molecular rotation, and their combinations thereof (Fig. 6). Molecular gliding in Fig. 6a, equivalent to cooperative atomic displacement in shape memory alloys, is seen in all thermo-mechanical martensitic transitions. In particular, such molecular motion is prominent during the thermoelastic transition of π-stacking crystals of rigid molecules, exhibiting concerted molecular gliding along the π-plane.^40,44,50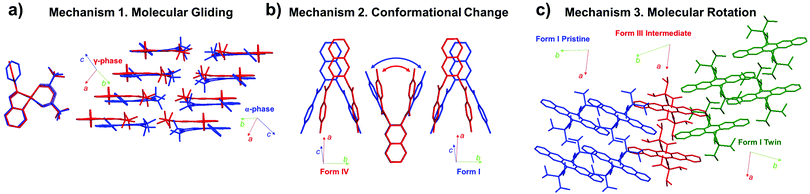

Fig. 6 Molecular mechanisms found in martensitic transitions, showing (a) molecular gliding,⁴⁰ (b) conformational change,⁴⁶ and (c) molecular rotation.⁵⁷ Examples of each mechanism are depicted by structural changes in #5 (CCDC 103651 and 1013657), #8 (CCDC 1583404 and 1583405), and #13 crystals (CCDC 1970910 and 1991343) of Fig. 2, respectively.

In thermoelastic transitions of crystals consisting of (partially) flexible molecules, conformational change can concur with molecular gliding, and may even drive the martensitic transition (Mechanism 2 in Fig. 6b). By this mechanism, the intermolecular distance can be actively regulated by the remarkable conformational change.^38,46 In some cases, dynamic conformational changes take place that can effectively fill the void of the transformed structure, and lead to entropy gain.^54,57,60 Furthermore, in the twinning–detwinning based superelastic molecular crystals bearing hydrogen bonding networks, conformational changes confined at the transition interface have been pointed out as the reason for spontaneous strain recovery.²⁴

In addition to molecular gliding and conformational changes, concerted molecular rotation has been observed in thermo-, super-, and ferroelastic transitions of molecular crystals. For instance, thermoelastic transition of molecular crystals with crisscross packing exhibits intriguing scissoring molecular motion in addition to concerted molecular rotation and displacement.^47,50 Moreover, substantial molecular rotations have been observed in super- and ferroelastic transitions of molecular crystals.^28,33,57 Ferroelastic transition of #13 (Fig. 2), for example, is accomplished through ∼40° rotation of the molecules along the shear direction (Mechanism 3 in Fig. 6c), allowing shape deformation up to ∼60%.⁵⁷ In the following subsections, transition mechanisms of molecular martensitic materials exhibiting thermoelastic, superelastic, and ferroelastic behaviors will be discussed in detail.

3.2. Thermoelasticity

3.2.1. Single crystals consisting of rigid molecules. Single crystals of rigid molecules #1–3 in Fig. 2 have exhibited reversible thermoelastic transitions (Fig. 7).^42,50,61 Thermoelastic transitions between structurally similar enantiotropic polymorphs of #1–3 crystals take place by cooperative interlayer molecular gliding along the molecular plane, which follow Mechanism 1 in Fig. 6a.

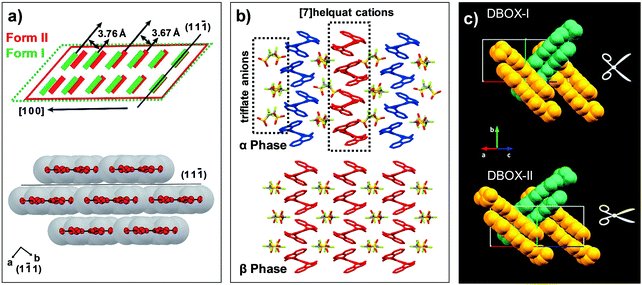Fig. 7 Structural changes in thermoelastic transitions of (a) #1, (b) #2, and (c) #3 crystals of Fig. 2. (a) The crystal of #1 undergoes heating induced Form II (red) to I (green) transition by collective molecular gliding along the (111̄) plane. Adapted with permission from ref. 50, copyright 2019 the Royal Society of Chemistry. (b) The α phase crystal of #2 transform into β phase structure by heating, through molecular gliding of [7]helquat cations and reorientation of triflate anions. Adapted with permission from ref. 42, copyright 2015 John Wiley & Sons, Inc. (c) Crystal of #3, exhibiting a crisscross packing structure, undergoes DBOX-I to DBOX-II transition by molecular gliding as well as pantograph-like molecular rotation. Adapted with permission from ref. 61, copyright 2019 American Chemical Society.

Hexamethylbenzene (#1, Fig. 2) crystal is established by van der Waals interactions such as π–π interaction, showing fascinating mechanical compliance as well as thermoelastic transition capability (Fig. 7a).⁵⁰ As described in Fig. 7a, molecular packing of #1 adopts typical slipped co-facial stacking. Single crystals of #1 undergo Form II to I transition occurring at 382–385 K upon heating, involving changes in the crystal system from triclinic (a = 5.32 Å, b = 6.29 Å, c = 8.10 Å, α = 104.05°, β = 99.08°, γ = 99.34°) to orthorhombic structure (a = 7.52 Å, b = 16.12 Å, c = 9.13 Å, α, β, γ = 90°). The structural change is ascribed to the molecular gliding along the phase front (i.e., transition interface), which is parallel to the molecular π-plane (Fig. 7a). Such molecular gliding results in distance alteration between the adjacent π-stacking layers (3.67 to 3.76 Å) and subtle molecular tilting (1.04°) along the c axis. The structural change leads to 5% elongation of the crystal along the a-axis, with a transition velocity as high as 6.36 mm s⁻¹ at 393 K. The crystals of #1 have been demonstrated as organic actuators and their properties were comprehensively investigated, see Section 4.1.

A helical π-stacking [7]helquat cation and trifuloromethane sulfonate anion (1 : 2 stoichiometry, #2, Fig. 2) molecular salt crystal is a good example of showing both Mechanism 1 and 3 at the same time.⁴² Molecular pairs of #2 co-assemble into segregated columnal stacking in the α phase, where trifuloromethane sulfonate anions are placed in between neighboring columns constructed by [7]helquat cations (Fig. 7b). Within the [7]helquat columns, the molecules stack around a twofold screw axis, while neighboring columns are symmetrically inequivalent (see differently colored stacks in Fig. 7b). Upon α to β thermoelastic transition occurring at ca. 404 K, slight molecular gliding of [7]helquat cations takes place, while the monoclinic P2₁ space group remains unchanged (α phase at 400 K: a = 12.01 Å, b = 12.55 Å, c = 20.91 Å, α = 90°, β = 90.12°, γ = 90°; β phase at 410 K: a = 11.48 Å, b = 12.42 Å, c = 12.49 Å, α = 90°, β = 114.9°, γ = 90°). In the β structure, however, symmetrically independent [7]helquat molecules in the α structure become symmetrical equivalents (Fig. 7b), and columnal stacking becomes more linear. Moreover, triflate anions between the cation columns reorient by 56° rotation, thus exhibiting Mechanism 3 as well upon thermoelastic transition.

Crisscross π-stacking 2-(5-(benzo[d]thiazol-2-yl)-1,3,4-oxadiazol-2-yl)-5-(diethylamino)phenol (DBOX, #3, Fig. 2) crystals not only show fluorescence based on an excited state intramolecular proton transfer (ESIPT) process but also show thermoelastic transition.⁶¹ DBOX-I is the stable phase at room temperature, where DBOX-I to -II transition occurring at around 458 K exhibits martensitic nature. Both DBOX-I and -II have a monoclinic P2₁/c symmetry, and molecules thereof exhibit co-planarity due to intramolecular O–H⋯N hydrogen bonding interaction. In the DBOX-I, co-planar molecules pack into one-dimensional columns driven by π–π interaction, where adjacent stacks show antiparallel arrangement by its inversion symmetry. The layers of π-stacked columns are further arranged into a crisscross pattern (Fig. 7c). In the case of the DBOX-II structure, the overall packing motif of DBOX-I is well preserved, but exhibits dimer slip and tilting in π-stacked columns and pantograph-like molecular action, see Fig. 7c. The structural change results in an anisotropic volume expansion by Δa = +2.1%, Δb = −6.1%, Δc = +5.4%, which underlies a macroscopic ca. 6% contraction of the crystal. In addition, disorder in the diehtylamine units is observed in the reported structures, and thus the transition is apparently an entropy driven process. Although the details of emission changes due to the structural transition have not been studied, the research opens up the potential of molecular martensitic crystals for smart emissive device applications.

Molecules #1, #2 and #3 can be classified as rigid molecules. Single crystals of these molecules are constructed by the common π–π stacking motif, where #1, #2, and #3 molecules arrange in a slipped co-facial stacking, helical stacking, and crisscross stacking, respectively. Regardless of the packing arrangements, upon thermoelastic transitions, they all exhibit molecular gliding along the π-plane, which involves modulation of the intermolecular distance and molecular tilting angle. These attributes are also evident in the single crystals of #4–6 showing thermosalient effects.

Thermosalient crystals can be considered as a special case of thermoelastic crystals that exhibit crystal motility such as hopping, bending, and twisting due to self-actuation during the phase transitions (see Fig. 8a for the hopping case of #9 crystals in Fig. 2).⁴¹ Transduction of heat into the crystal momentum is the result of accumulation and abrupt release of elastic strain and energy during the phase transition. The thermosalient transition typically brings about highly anisotropic structural change (#4–8, and #16, Fig. 2), but not necessarily as revealed in the crystals of #9 and #14 (Fig. 2). Molecular and structural mechanisms in thermosalient crystals are studied in-depth by Naumov and others. Among the reported thermosalient cases, thermoelastic transitions of molecular crystals of #4–6 are best described by Mechanism 1 in Fig. 6a.

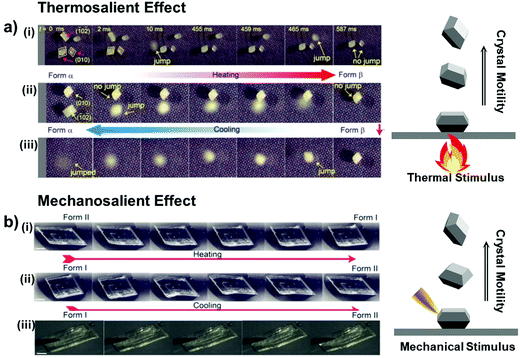Fig. 8 (a) (i and ii) Heating induced thermosalient effect showing crystal hopping (#9 crystals in Fig. 2), relying on the crystals’ facets contacting the temperature-controlled surface. (iii) Cooling-induced thermosalient jump of the remaining crystal which lies on its (010) facet. Reproduced with permission from ref. 41, copyright 2015 American Chemical Society. (b) Thermosalient transitions of #4 crystals in Fig. 2 upon (i) heating and (ii) cooling processes. (iii) Mechanosalient transition of the #4 crystal with supercooled Form I structure. Reproduced with permission from ref. 44, copyright 2016 American Chemical Society.

Terephthalic acid molecules (#4, Fig. 2) form mechanically compliant crystals that exhibit compelling thermally- and mechanically-induced martensitic transitions.⁴⁴ The #4 molecules establish a two-dimensional hydrogen bonding network in the crystals, consisting of the one-dimensional hydrogen bonding tapes of symmetric dimers that are strongly interacting based on O–H⋯O interactions. Adjacent tapes are stitched by C–H⋯O interactions and the neighboring two-dimensional sheets atop each other are held by co-facial π–π interaction (Fig. 9a). Single crystals of #4 undergo Form II-to-I phase transition occurring at 345–358 K upon heating, where the triclinic P1̄ system is preserved upon the polymorphic transition (Form II: a = 5.04 Å, b = 5.36 Å, c = 7.01 Å, α = 71.99°, β = 76.09°, γ = 87.20°; Form I: a = 3.78 Å, b = 6.48 Å, c = 7.41 Å, α = 82.94°, β = 81.01°, γ = 88.98°). The structural transition gives rise to thermosalient/mechanosalient effects (Fig. 8) and also underlies non-destructive plastic deformation based on bimorphic structure formation (detailed below).

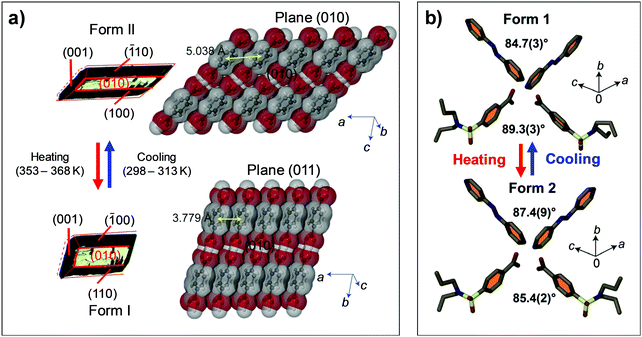Fig. 9 Structural changes found in thermosalient transitions of (a) #4 and (b) #6 crystals in Fig. 2. (a) Changes in the crystal dimension of #4 are accompanied by Form II to I transition. Adapted with permission from ref. 44, copyright 2016 American Chemical Society. (b) The crystal of #6 exhibits heating induced Form 1 to 2 transition which entails molecular gliding along the π-plane and a subtle alteration of the crisscross angle. Reproduced with permission from ref. 47, copyright 2018 John Wiley & Sons, Inc.

Thermosalient effect of #4 crystal is achieved by substantial contraction of the crystal long axis (26%), which is attributed to the Form II to I polymorph transition featuring massive molecular gliding, i.e., Mechanism 1 (Fig. 6a). By undergoing Form II to I polymorph transition, a hydrogen bonded sheet glides cooperatively atop the adjacent sheet (Fig. 9a), thus maintaining overall packing motifs such as O–H⋯O and C–H⋯O interactions within the two-dimensional network. Resultantly, the packing changes in terms of the distance between neighboring two-dimensional sheets (II: 5.038 Å; I: 3.779 Å, measured as the distance between ring centroids, Fig. 9a) as well as the molecular slip angle (II: 134°; I: 106°). Meanwhile, upon cooling, it was reported that some of the crystals did not spontaneously recover their structure and shape, thus undercooled Form I crystals can be obtained under ambient temperature conditions. Interestingly, these undercooled crystals can undergo I–II transition in response to a mechanical trigger (soft poking), which is accompanied by a prominent crystal reshaping and leaping – i.e., mechanosalient effect (Fig. 8b(iii)).

Furthermore, single crystals of #4 represent remarkable plastic deformability without losing their structural integrity.⁴⁹ Upon bending Form II crystals, the mechanically compressed concave part of the crystal transformed into Form I phase, revealed by single crystal X-ray diffraction study. The molecular mechanism is unprecedented, considering that typical plastic deformation of molecular crystals is based on delamination and gliding of the molecular layers rather than polymorph transition.^108–111 In addition to the plastic deformability of #4 crystals, the bent crystals exhibited shape memory properties. Upon heating I/II bimorphic bent crystals, they re-straighten back by a complete transition to the Form I structure. The memorized bent shapes are recovered by cooling, which regains the bimorphic structure of the bent crystal. It should be herein noted that the overall behavior is distinct from the conventional shape memory effect, which is based on ferroelastic deformation and thermoelastic transition induced shape recovery by increasing temperature, where the recovered shape is maintained at a low temperature.

Thermosalient effect of (phenylazophenyl)palladium hexafluoroacetylacetonate (#5, Fig. 2) based on rapid and reversible α–γ transition also exhibits similar interlayer molecular gliding motions (Mechanism 1, Fig. 6a) along with apparent conformation changes at the same time (Mechanism 2, Fig. 6b).^40,51,112 The α–γ transition occurs at 342–355 K upon heating, entailing strongly anisotropic expansion of the unit cell. Although the transition does not lead to alteration in the space group (triclinic, P1̄), the cell constants are substantially changed (α-phase: a = 8.46 Å, b = 13.24 Å, c = 15.76 Å, α = 86.96°, β = 86.45°, γ = 84.67°; γ-phase: a = 4.27 Å, b = 13.56 Å, c = 14.80 Å, α = 83.31°, β = 93.96°, γ = 76.84°). In the α phase, #5 molecules construct a co-facial slipped stack showing weak intermolecular interactions (C–F⋯F–C, C–F⋯C); neighboring stacks (interstack) arrange in a head-to-head fashion. By the γ phase formation, the overall packing motif is maintained yet strained markedly. The structural change is ascribed to shear-like molecular displacement in the stack (3.78 Å and 4.82 Å in the α, and 4.27 Å in the γ structure, measured by intrastack Pd⋯Pd distance), see Fig. 6a. Therefore, the transition gives rise to slip angle alteration from ca. 61.8° to ca. 52.5°, and increased intermolecular distance between head-to-head arranged interstack molecules (11.82 Å in the α, and 12.81 Å in the γ structure, measured by interstack Pd⋯Pd distance). Moreover, the phenyl ring exhibits torsional angle change from 36.7° and 41.4° in the symmetrically inequivalent molecules of the α structure to 87.8° of the γ structure, and thus occupies the space resulting from the molecular gliding process, see overlaid molecular structure in Fig. 6a. Such cooperative molecular displacement renders unusually large positive thermal expansion of the α phase along the a-axis, which is in part compensated by negative thermal expansion along the c-axis.

A single crystal of 2 : 1 cocrystal of probenecid and 4,4′-azopyridine (#6, Fig. 2) is another example of the thermosalient crystal exhibiting impressive crystal twisting, accompanied by interlayer molecular gliding during Form I to II transition (at 332–338 K upon heating).⁴⁷ In the Form I structure, the 2 : 1 complex of probenecid and 4,4′-azopyridine establishes a co-facial hydrogen-bonded (O–H⋯N and C–H⋯O) trimer as a basic building block. These trimers construct one-dimensional columns based on co-facial slipped π-stack, where the parallel neighboring columns are closely packed and form a two-dimensional layer. The layers are further stacked via C–H⋯O interaction in a crisscrossed manner (Fig. 9b). The Form II structure basically retains all packing motifs that appeared in the Form I structure, while slight changes in crisscross angles from 89.3° to 85.4° and 84.7° to 87.4° are found, measured between interplanar angles of benzene rings of probenecid and interplanar angles of azopyridine, respectively. Such packing rearrangement resulted from the molecular gliding of hydrogen-bonded trimers like in the case of #3 crystal which also exhibit crisscross packing. The transition accompanies changes in the space group from monoclinic P2₁/c to triclinic P1̄, with an anisotropic volume expansion by Δa = +5.2%, Δb = +1.6%, Δc = −2.8%. The authors attributed reversible twisting of the crystal to the non-uniform strain generated upon phase transition. In addition to Mechanism 1 type structural changes, conformational changes in the n-propyl chains of probenecid molecules are found, thus exhibiting Mechanism 2 as well upon I to II transition.

Molecules #4, #5 and #6 in Fig. 2 can be classified as (partially) rigid molecules. Like in the cases of #1–3, single crystals of these molecules exhibited π–π stacking motifs, where #4 and #5 show a typical co-facial arrangement while #6 shows a crisscross arrangement. In these cases, the capability of cooperative interlayer molecular gliding can be attributed to the formation of π-stacking layers that serve as easy gliding planes. Upon gliding, crystals exhibit molecular tilting (#4 and #5) and relative molecular orientation change in the crisscross packing (#6), thus manifesting Mechanism 3 as well during the transition.

3.2.2. Single crystals consisting of conformationally flexible molecules. While Section 3.2.1 discusses displacive motions (Mechanism 1) in crystals of rigid molecules (#1–6, Fig. 2), in this section we shift our focus to crystals of flexible molecules (#7–13, Fig. 2). Flexible molecules can also realize thermosalient effects due to significant changes in molecular conformations and intermolecular distances, i.e., Mechanism 2 in Fig. 6b. In the crystals of #7–10 (Fig. 2), drastic conformational changes of molecules and simultaneous packing rearrangements are pointed out as the molecular mechanism for their thermosalient effects.

The single crystal of oxitropium bromide (#7, OXTB, Fig. 2) exhibits thermosalient effect during its OXTB-A to OXTB-B phase transition occurring at ca. 318 K upon heating.³⁸ Both phases are based on the orthorhombic P2₁2₁2₁ space group, with significant alterations in the cell constants during transition (Δa = 0.8%, Δb = 10.9%, Δc = −7.5%). From the resolved crystal structures of OXTB-A and OXTB-B, it was shown that the transition is accompanied by conformational changes in oxitropium cations (depicted in Fig. 10a by overlaying molecules of OXTB-A and -B polymorph) and by a rigid-body wagging motion of the phenyl substituent attributed to flexible ester linkage in the molecular structure (Fig. 10a).

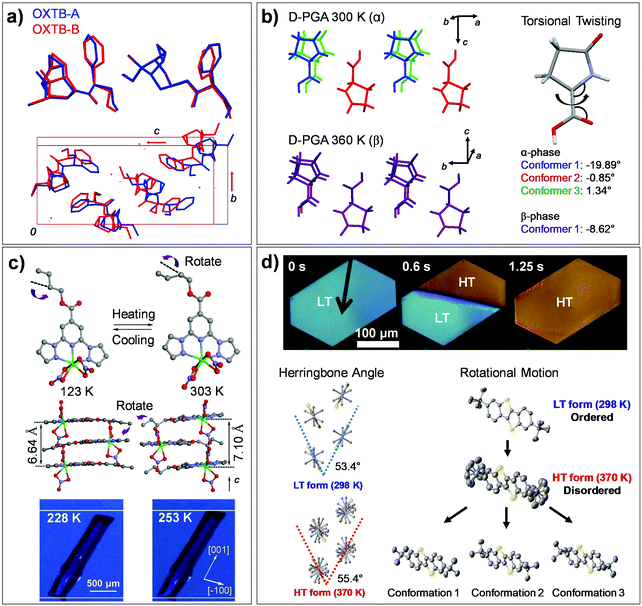Fig. 10 Structural and molecular conformation changes found in thermoelastic/thermosalient transitions of (a) #7, (b) #9, (c) #11, and (d) #12 crystals involving flexible molecules (Fig. 2). (a) The structural changes during thermally induced martensitic transition between OXTB-A and -B of #7. Adapted with permission from ref. 38, copyright 2010 American Chemical Society. (b) The structural changes during α-to-β thermosalient transition of #9. Adapted with permission from ref. 41, copyright 2015 American Chemical Society. (c) The crystal of #11 undergoes thermoelastic polymorph transition, exhibiting cooperative molecular gliding triggered by alkyl chain rotation. Adapted with permission from ref. 60, Copyright 2015 Springer Nature. (d) Thermoelastic transition of the #12 crystal between low temperature (LT) and high temperature (HT) polymorphs. Adapted with permission from ref. 54, copyright 2018 Springer Nature.

A single crystal of naphthalene-2,3-diyl bis(4-fluorobenzoate) (#8, Fig. 2) is another case of thermosalient effect, where the pincer-like molecular motion is pinpointed as the primary molecular basis for its thermosalient structural transition.⁴⁶ Thermosalient effect of this material is accompanied by Form I to IV occurring at 441–443 K upon heating, where both phases are based on a monoclinic C2/c structure. In both Form I and IV phases, #8 molecules establish columnar stacks along the twofold screw axis, where the p-fluorobenzoyl groups of molecules stacked in a zigzag fashion, see Fig. 6b. The structures are stabilized by weak intermolecular interactions such as C–H⋯O, C–H⋯F, C–H⋯π, and π–π interactions. Interestingly, the molecular conformation and the distance between p-fulorobenzoyl arms largely vary depending on the polymorphic phases, see Fig. 6b. This attribute is evident in Form I and IV; for instance, intramolecular arm-to-arm distance between fluorine atoms changes from 7.68 Å (Form I) to 4.95 Å (Form IV). Moreover, the centroid-to-centroid distance between π–π interacting 4-fluorobenzene rings is altered from 4.01 Å to 4.31 Å, giving rise to significant anisotropic volume reduction (Form I: a = 15.82 Å, b = 13.17 Å, c = 9.69 Å, α = 90°, β = 101.81°, γ = 90°; Form IV: a = 13.85 Å, b = 14.99 Å, c = 9.87 Å, α = 90°, β = 105.90°, γ = 90°). Such significant structural transition is mainly driven by conformational change (Mechanism 2, Fig. 6b) giving rise to thermosalient jumping of the crystals.

Single crystals composed of hydrogen-bonded chiral L- or D-pyroglutamic acid molecules (#9, Fig. 2) are capable of thermosalient effects based on the α-to-β structural transition (at 338–340 K and 336–338 K, for the L- and D-pyroglutamic acid crystals, respectively). Significant torsional motion of the molecules occurs during the process (Fig. 10b), and thus we assign this transition to Mechanism 2.⁴¹ Structural analysis based on variable-temperature in situ SC-XRD revealed high extent of structural similarity of α and β polymorphs, preserving both the hydrogen bonding network and the orthorhombic P2₁2₁2₁ space group upon transition. Only minor changes in the cell constants are observed, e.g., Δa = +1.58%, Δb = −1.57%, Δc = 0.55%, ΔV = +0.53% in the L-pyroglutamic acid crystal. On the other hand, significant changes were observed in molecular conformation with subtle adjustments in molecular positions. In addition to the conformational changes of the pyrrolidine rings, the torsional angles of carboxylic acids in three conformers in the α polymorph (−19.89°, −0.85° and 1.34°) converged to that in a single molecular conformer (−8.62°) in the β polymorph (Fig. 10b). The thermosalient effect in the crystals of #9 was reported to be perpetually repeatable without structural degradation, which is attributed to the small structural changes as well as fully elastic nature of strain accumulation and dissipation behavior engendered by a low-dimensional hydrogen bonding network.

Molecules #7–10 in Fig. 2 can be classified as flexible molecules, particularly in their linkage or substituents. The transitions of #7–10 crystals are promoted by noticeable conformation changes (the transition of #10 crystal will be detailed in Section 3.5). Such changes in molecular conformation modulate the volume exclusion interactions and the centroid-to-centroid distance; thus these systems exhibit Mechanism 1 and 2 simultaneously.

In the crystals of #11–13 (Fig. 2), dynamic rotational motions of the molecular substituents are pinpointed as the molecular mechanism for their thermoelastic transitions.^54,57,60 In these cases, ordered molecular substituents become dynamically disordered and trigger thermoelastic transitions, which can be assigned as Mechanism 2 with intriguing dynamicity. However, polymorphic transitions in these crystals did not give rise to thermosalient effects. This is most likely due to slow transition kinetics and insufficient power generated to move the crystals.

The crystals of #11 (Fig. 2) present order–disorder transition of an n-butyl unit, causing cooperative polymorphic transitions.⁶⁰ Within the structure, #11 molecules stack to form one-dimensional columns along the c-axis, where the structure is stabilized by π–π, shape-complementary van der Waals, and C–H⋯O hydrogen bonding interactions. Both low- and high-temperature polymorphs showed a monoclinic space group P2₁/c. Their unit cells differ by Δa = 0.059 Å, Δb = −1.480 Å, Δc = 0.630 Å, Δβ = 0.308°, resulting in ca. 6–7% elongation along the long-axis of the crystal (c-axis) upon low-temperature to high-temperature phase transition occurring at ca. 243 K. Overall, structural similarity between these polymorphs is found, where the structural change is mainly ascribed to interlayer molecular gliding triggered by conformational change (anti to gauche) of the n-butyl unit (Fig. 10c, about 100°, depicted by purple arrows) and its dynamic disorder. Therefore, the transition can be assigned as Mechanism 2 with dynamic nature. Such rotational isomerization (occupying more space) results in repulsive interaction between neighboring molecules and is suggestive of the driving force for the observed structural changes, such as increase in the stacking distance from 3.32 Å to 3.55 Å and decrease in the slip angle from 61.65° to 60.25°.

Single crystals of high performance p-channel semiconductor, di-tert-butyl[1]benzothieno[3,2-b][1]benzothiophene (#12, Fig. 2), are a representative case of thermoelastic transition triggered by order–disorder transition of rotational side-chains.⁵⁴ #12 molecules pack into a layered herringbone structure with a monoclinic P2₁/c space group in its LT form, which undergoes reversible LT to HT phase transition, showing sharp phase boundaries upon transition (see polarized microscope images in Fig. 10d). The variable temperature single crystal X-ray diffraction result revealed that the HT form adopts the same space group with slight changes in the cell constants, Δa: 3.2%, Δb: 2.8%, Δc: −2.2%. The transition entails cooperative interlayer gliding of the molecules, which results in increased herringbone angle from 53.4° to 55.4° (Fig. 10d) and increased molecular tilting angle (LT: 51.2°, HT: 54.8°). In-depth studies of single crystal X-ray diffraction, nuclear magnetic resonance and molecular dynamics simulations revealed the occurrence of order–disorder transition in the tert-butyl side chains during the transition; intermolecularly correlated dynamic rotation of the side chain triggers cooperative displacement of an entire molecular plane during the transition, see multiple conformational states in the HT form in Fig. 10d. Like in the case of #11, the transition is entropy driven and is assigned as Mechanism 2 with dynamic nature. A detailed mechanism of molecular cooperativity has been further addressed, where careful optical microscope experiments showed that the creation and propagation of the transition interface occurs by the cooperative structural transition in a stepwise manner, i.e., breaking the weakest intermolecular interaction during the initiation step followed by breaking the intermediate and the strongest intermolecular interaction in the second and third propagation step.⁵⁵

The significance of order–disorder transition of rotational side-chains for cooperative transition is further corroborated by comparing #12 and its molecular analogue, bis(trimethylsilyl)[1]benzothieno[3,2-b][1]benzothiophene (diTMS-BTBT).⁵⁶ In the diTMS-BTBT molecule, the carbon atom is replaced by silicon and thus has bulkier side-chains than #12. Although diTMS-BTBT molecules pack into a similar layered herringbone structure (triclinic, P1̄ space group), stronger intra- and interlayer interactions associated with the side-chains restricted their rotational motions. This resulted in irreversible nucleation and growth type structural transition, losing structural integrity upon the polymorph transition.

Molecules #11–13 in Fig. 2 consist of rigid molecular backbone and rotator substituents. Upon surpassing the transition temperature, entropy gain due to dynamic rotational motions of rotators drives structural changes such as cooperative molecular displacement or tilting (transition of #13 will be discussed in Section 3.5). Significant conformational disorder in the substituent is also observed in the #3 crystal, which is suggestive of a similar molecular mechanism as in the cases of #11–13. Given that not only bulky rotator side chains of #12 and #13 but also a typical alkyl side chain of #11 and #3 can engender such transitions, the molecular structures of this class of molecules sheds light on molecular design rules for developing organic martensitic materials featuring rigid π-conjugated backbones. Meanwhile, as the literature revealed, even a single atom substitution can fundamentally alter the polymorph transition mechanism,⁵⁶ and it will require precise molecular/crystal engineering as well as further structure–property correlations to rationalize the design of martensitic crystals.

3.2.3. Single crystals consisting of rotating molecules. Displacive motions (Section 3.2.1) and (dynamic) conformational changes (Section 3.2.2) are prominent mechanisms of thermoelastic transitions for molecules discussed above. For crystals of #14–16 (Fig. 2) discussed in this section, remarkable (dynamic) rotation of the entire molecule serves as the molecular mechanism of their thermoelastic transitions. Thermosalient transition of 1,2,4,5-tetrabromobenzene (#14, Fig. 2) crystal represents Mechanism 3 in Fig. 6c, which shows evident rotational motions of the entire molecule. The reversible thermosalient effects of π–π stacking crystals of #14 are accomplished through the β to γ phase transition occurring at ca. 46 °C upon heating.^39,113 Variable temperature single crystal X-ray diffraction revealed that the transition induces only minuscule changes in the molecular packing – both structures are based on the space group of P2₁/a with slight but anisotropic changes of cell constants (Δa = −0.323 Å, Δb = 0.475 Å, Δc = 0.052 Å, Δβ = 1.44°). The structural change of #14 is mainly ascribed to the twisting-like rotation of the molecules (Fig. 11a), where the angle between the π-planes of two distinctly oriented molecules changed from 22.6° to 13.7°. However, concurrent molecular gliding is minute in this case, giving rise to centroid-to-centroid distance changes from 4.02 Å to 4.07 Å. Because the molecule #14 is rigid, the molecule does not exhibit conformational change, while the structural change is mostly accommodated by the elastically modifiable Br⋯Br and Br⋯H interactions.^113–115 The correlation between its polymorphic transition and lattice vibrational modes was examined as well, which revealed a specific rotational vibration mode corresponding to the gateway for the transition.⁴⁸ Moreover, intriguing observations were reported that lattice vibrational mode softening followed by their rigidification upon transition is responsible for the thermosalient effects of #14.¹¹⁶ These vibrational spectroscopy studies elucidate not only the molecular/structural mechanisms but also the origin for stress accumulation in the long-term studied thermosalient crystal of #14.

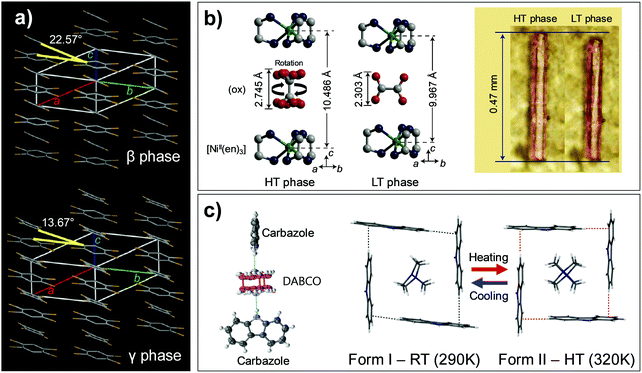Fig. 11 Thermoelastic transition involving rotation of molecules. (a) Thermosalient transition of #14 crystal in Fig. 2 results from cooperative molecular rotation. Adapted with permission from ref. 39, copyright 2013 American Chemical Society. (b) Structural changes and crystal length alteration found in thermally induced HT–LT phase cooperative transition of #15 crystal (Fig. 2). Adapted with permission from ref. 59, copyright 2014 Springer Nature. (c) Trimeric building block of #16 amphidynamic supramolecular crystal and structural changes upon thermosalient transition (Fig. 2). Adapted with permission from ref. 52, Copyright 2019, Elsevier Inc.

On the other hand, the co-assembled crystals based on the #15 and #16 pairs (Fig. 2) exhibited dynamic rotations of one of the molecular entities (i.e., rotator). Upon warming the crystals of [Ni^II(en)₃](ox) complex (#15) (en: ethylenediamine; ox²⁻: oxalate anion), a fast and reversible structural transition is observable at about 270 K, resulting in a 5% elongation of the crystal (see images of the crystal in Fig. 11b).⁵⁹ Upon transition, the crystal symmetry changes from monoclinic P2₁/n of the LT phase to trigonal P3̄1c of the HT phase. Variable temperature single crystal X-ray diffraction also revealed that in addition to the gliding motion of the molecules, an intriguing 90°-rotation of the entire oxalate anions and their dynamic rotational motions around the C–C bond (order–disorder) are concurrent (Mechanism 3 with dynamicity, Fig. 6c), suggesting that the transition is an entropy driven process (Fig. 11b). Despite the unusual 90°-rotations of the oxalate anions, the structure preserves N–H⋯O hydrogen bonds, which is indicative of the molecular origin for a strong cooperative effect – i.e., synchronous oxalate anion rotations.

A multi-scale dynamic supramolecular crystal composed of carbazole and 1,4-diazabicyclo[2.2.2]octane (DABCO) with 2 : 1 stoichiometry (#16, Fig. 2) was reported by Colin-Molina et al. The crystal exhibited (i) a thermally-activated dynamic rotation of DABCO units, (ii) a reversible thermosalient effect accompanied by a phase transition, and (iii) an anomalous change in the dynamic DABCO rotation upon phase transition.⁵² Amphidynamic crystals are an exotic class of materials that represent the long-range molecular ordering of single crystals; however, at the same time, they contain dynamic elements that rotate within their structures.^117,118 In general, they are designed to have rigid frameworks and sufficient free volume to allow the rotational motion of the rotator. Therefore, it is difficult for amphidynamic crystals to achieve a thermosalient effect, requiring a distortion of its rigid frameworks (stators). This issue is resolved in the #16 crystal by utilizing a supramolecular stator based on the carbazole unit. The thermosalient effect of #16 is engendered by Form I to II transition mediated crystal reshaping, occurring at 332–338 K upon heating, where overall molecular packing motifs are well maintained during the transition. As a basic building block, the N–H⋯N interaction induced 2 : 1 carbazole : DABCO trimer is produced (Fig. 11c), showing an interplanar angle of 82.5° and 90° between two carbazole units in the trimer for Form I and II structures, respectively. Between the neighboring building blocks, a T-shape arrangement of the carbazole units based on the C–H⋯π interaction is created, and it encases the DABCO unit in the cavity produced by four neighboring carbazole molecules (Fig. 11c). The Form I to II transition, leading to a symmetry alteration from a P2₁/c to a I4₁/a space group by molecular displacement, also results in a realignment of the rotator and a reshaping of the cavity, causing changes in the dynamics of the DABCO rotation.

Although the thermosalient transition of the #14 crystal is assigned as a Mechanism 3 induced case, the pantograph-like motion in the crisscross packing crystals (#3 and #6, Fig. 2) also exhibits corresponding attributes. In these crystals, thermoelastic transitions clearly entail change in the interplanar angle between molecules of different orientations. Upon the reorientation of the molecules, subtle or large adjustments in intermolecular distance occur, accomplishing an anisotropic volume change. Meanwhile, transitions in the crystals of #15 and #16 represent similar attributes found in #11–13 crystals, while the rotation of the whole molecular entity or changes in the dynamics occurred in these cases. The crystals of #15 and #16 are comprised of stator and rotator entities resembling a supramolecular design of amphidynamic crystals. To achieve a corresponding phase transition behavior, the crystal should be engineered to involve a certain amount of free volume, which promotes the entropy driven rotational motion of the rotator at the transition temperature.

In this subsection, the molecular mechanisms of thermoelastic and thermosalient transitions in the representative molecular crystals are summarized. In all cases, structural changes exhibited subtle or even substantial cooperative molecular displacements, without losing structural integrity. The capability of cooperative interlayer molecular gliding in the crystals of rigid molecules (#1–6, Fig. 2) can be attributed to the formation of π-stacking layers that serve as easy gliding planes. Crystals consisting of partially or entirely soft and flexible molecules (#7–17, Fig. 2) presented much richer molecular motions in their structural transitions. In the crystals of #7–9, the structural transitions can be accompanied by remarkable conformation changes, while the transitions of #11–16 are promoted by dynamic rotational motions of rotator substituents or whole molecules. The thermoelastic crystals comprising the #10, #13 and #17, all exhibiting thermo-, super- and ferroelasticity, will be discussed in Section 3.5.

3.3. Superelasticity

As we discussed in Section 2.3, superelasticity is known as a mechanical analogue to thermoelasticity, i.e., high temperature (HT) to low temperature (LT) phase transition by mechanical loading. However, superelasticity in organic crystals can be attained through multiple structural pathways. For instance, the single crystals of #10, #13 and #17 in Fig. 2 are cases of manifesting superelasticity based on a shear-induced polymorph transition between enantiotropic phases. Because these crystals exhibit rich (thermo-)mechanical transition capabilities based on thermoelasticity, superelasticity and ferroelasticity, the molecular mechanisms thereof are detailed in Section 3.5. In addition to superelasticity between enantiotropic phases, novel shear induced phase formation (#18, Fig. 2), twinning transitions (#19–22 and 24, Fig. 2), or even a transition between monotropic phases (#23, Fig. 2) are pointed out as the structural pathways for superelastic processes.

A single crystal of terephthalamide (#18, Fig. 2) is an interesting example of a superelastic organic crystal, transition of which is not based on enantiotropic polymorphism but is realized through the emergence of a novel shear-induced phase.²³ #18 molecules bear two symmetric amide units, which establish a two-dimensional hydrogen bonding network. In the thermodynamically stable α phase, N–H⋯O=C hydrogen bonding interactions are presented along both molecular long- and short-axis directions, rendering N⋯O distances of 2.932 Å (long-axis) and 2.912 Å (short-axis), forming a unit two-dimensional sheet. Along this unit sheet normal, slipped co-facial molecular stacking is presented, likely by a direct substituent interaction.¹¹⁹ The α crystal presents a triclinic system with a P1̄ symmetry based on symmetrically equivalent molecules. In the metastable β phase, which is obtained through shear loading exerted on the (010) plane of the α phase, the two-dimensional N–H⋯O=C hydrogen bonding network is maintained but with subtle changes in the N⋯O distances (long-axis: 2.943 Å and 2.918 Å; short-axis: 2.965 Å and 3.007 Å). The β crystal exhibits the same crystallographic system (triclinic, P1̄ space group); however, it consists of two asymmetric molecules. In the β structure, the arrangement of phenyl rings becomes largely altered, giving rise to a herringbone type arrangement in the β phase, which is accompanied by a significant torsional twisting of amide substituents (from 24.07° in the α phase to 17.46° and 30.25° in the β phase), as shown in Fig. 12a. This is a representative case of Mechanism 2 (Fig. 6b), which adopts a new conformational state through a phase transition, while the contribution of molecular displacement and rotational motions is non-negligible. Through this mechanism, the #18 crystal can endure 11.34% of shear strain. The transition interface was analyzed to be (100)_α//(001̄)_β, giving rise to an areal ratio of 0.989, thus rendering interfacial stress by a lattice mismatch, which underlies the spontaneous recovery of a shape strain under the superelastic process.

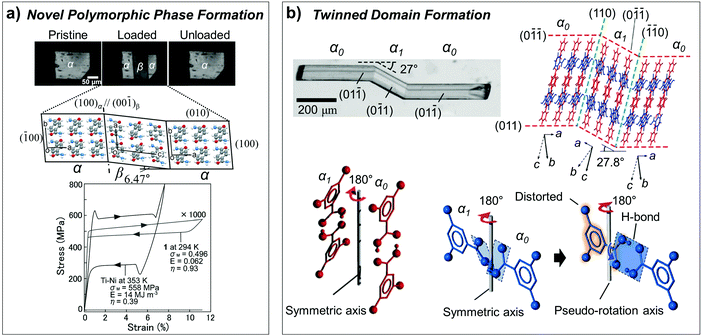Fig. 12 (a) Superelasticity of #18 crystal (Fig. 2) based on shear-induced reversible α–β transition. The measured stress–strain curve is compared to that of the Ni–Ti shape memory alloy, showing about three orders of magnitude lower stress value for transition. Adapted with permission from ref. 23, copyright 2014 John Wiley & Sons, Inc. (b) Superelasticity of #19 crystal (Fig. 2) based on reversible twinning–detwinning. Adapted with permission from ref. 24, copyright 2015 John Wiley & Sons, Inc.

Aside from the novel shear-induced phase formation (#18), the majority of superelastic transitions in molecular crystals is based on deformation twinning (#19–22 and 24, Fig. 2). In the structural transition, molecules present significant torsional twisting and/or rotation, thus exhibiting Mechanisms 2 and/or 3. A single crystal of 3,5-difluorobenzoic acid (#19) is the first discovered example presenting a deformation twinning mediated superelasticity. At first glance, the twin-induced superelasticity is expected to be difficult to achieve due to the insufficient interfacial stress for a spontaneous shape recovery by the absence of an areal difference at the interface.²⁴ In the crystal of #19, molecules dimerize through strong O–H⋯O=C interactions. These dimers further interact based on weak C–H⋯O=C interactions and establish a 2D hydrogen bonding network. Between the adjacent layers, the dimers are stacked by π–π interaction. The structure is monoclinic with a P2₁/c space group, which is composed of four asymmetric molecules. Upon applying shear stress onto the (01̄1̄) surface, the crystal largely deforms, presenting a maximum shear strain of 52.7%. In addition to molecular displacement, it was revealed that twinning occurs based on a 180° rotation around [1̄11] that is parallel to the (110) twinning interface (i.e., type II twinning), the equivalent structure of which is in fact achieved mainly by conformational and slight orientational changes of the molecules. Therefore, the lattice reorientation exhibits Mechanisms 1–3 simultaneously. It should be noted that there are two differently aligned dimers – one oriented along [1̄11] (red molecules in Fig. 12b) and the other along [111̄] (blue molecules in Fig. 12b) – the 180° rotation of the former dimer about the [1̄11] axis will readily retain the hydrogen bonding interaction, while the 180° rotation of the latter dimer will lead to a cleavage of this bond. The authors raised a plausible speculation that the preservation of hydrogen bonds in the latter dimer through conformational changes would result in a sufficient driving energy for the shape recovery process despite the fact that there is no surface area difference between the pristine and twinned domain, as shown in Fig. 12b. To preserve the O–H⋯O=C interactions at the interface, the dihedral angle between the carboxylic acid and the phenyl ring is adjusted (the torsional angle of ca. 16–17° is estimated in the reported structure), causing a distortion energy of about 1.7 × 10⁻⁴ J m⁻² (estimated from the analogue benzoic acid case). This distortion energy surpasses the energy required for the detwinning process (6.5 × 10⁻⁴ J m⁻²); therefore, the superelasticity of #19 based on twin-detwinning is facilitated.

The crystal of N,N-dimethyl-4-nitroaniline (#20, Fig. 2) is another superelastic crystal based on deformation twinning.³⁰ #20 molecules construct monoclinic crystals with a P2₁ space group. Within the ab plane, a co-facial herringbone packing motif is observed – π–π interaction along [100], while a molecule interacts with four other neighboring molecules by C–H⋯π. Along the [101] direction, the layers stack in a head-to-tail fashion based on N=O⋯H–C hydrogen bonding interaction. In the (001) planes, head-to-tail joint molecules establish 1D nanogrooves parallel to [100]. The single crystal of #20 exhibits not only superelasticity but also superplasticity. The superelasticity of #20 single crystals originates from a 180°-rotation of the lattice along the normal vector of the twin interface, (2̄01)_M//(201̄), achieved by exerting shear stress on the (001) face (thus, type I twinning). The twinned structure is achieved by ca. 10° tilting of the molecule and molecular displacements, thus exhibiting both Mechanism 1 and 3, exhibiting a theoretical shear strain of ca. 37%. More interestingly, the superplasticity of #20 – i.e., extremely large plastic deformation (strain over 500% in the case of #20) accomplished through a multi-layer slip in the crystalline materials, is the first example observed in organic crystals. Attributed to a nanogroove created in the molecular assembly, a well-regulated concerted molecular slip is facilitated along [100] and [1̄00], where the [100] slip (with respect to the pristine crystal) is accompanied by a twinning transition at the beginning. This exotic feature suggests an extreme workability of functional molecular crystals without losing structural integrity.

4,5,7,8,12,13,15,16-Octafluoro[2.2]paracyclophane (#21, Fig. 2) forms a superelastic crystal, whose reversible mechanical deformability is attained by a twinning–detwinning process.³³ Upon exerting shear on the (1̄01̄) face of the crystal, a twin domain formation is observed, resulting in a maximum shear strain of 29.2%. The twinned lattice is reoriented from the pristine lattice by a 180° rotation around the normal vector of the twin plane, (010)_M//(01̄0)_D, thus exhibiting type I twinning. The single crystal structure of #21 shows a triclinic system with a P1̄ space group, involving two symmetrically inequivalent molecules (Z′ = 0.5 + 0.5), called Z1 and Z2 molecules, respectively. Molecular packing inside exhibits a two-dimensional brickwork-like motif with C–F⋯H–C interactions between four neighboring molecules. Upon shear-induced twin formation, which results in crystal bending of ca. 16.3°, the Z1 and Z2 molecules are converted into the Z2 and Z1 across the twin interface by a ca. 26° molecular rotation, respectively. Such interconversion between symmetrically inequivalent molecules resembles the case of #13 (Section 3.5), which exchanges the primary and secondary π-stacking axis of the two-dimensional brickwork packing upon deformation twinning.

The single crystal of [Cu(II)₂(bza)₄(pyz)]_n (bza: benzoate; pyz: pyrazine) (#22, Fig. 2) also accomplishes superelasticity by deformation twinning.²⁵ The mechanical twinning of #22 is observed when applying shear onto the (001̄) surface of the crystals, forming a twinned domain based on (1̄00)_P//(001̄)_T interfaces, giving rise to an interfacial area ratio of 0.953. The maximum strain achievable through twinning was evaluated to be ca. 26%. Such a large reorientation of the lattice is in fact accomplished by the systematic conformational changes of the ligands as well as a slight displacement of the one-dimensional chains of #22, thus manifesting the molecular motions of both Mechanisms 1 and 2. In the pristine structure of #22, 1D complex chains are stacked side-by-side and uniaxially aligned along the b-axis of the structure. Upon twinning, benzene rings undergo about 32° rotation, and a slight rearrangement of the columns is anticipated to accommodate the rotated unit cell that exchanges the habit plane between (100) and (001). More interestingly, this lattice reorientation converts the direction of the 1D nanoporous channels that develop along the [001], which are harnessed to realize a microfluidic channel for a mechanically controlled gas flow system (see Section 4 for details).

The single crystals of 7-chloro-2-(2′-hydroxyphenyl)imidazo[1,2-a]pyridine (#23, Fig. 2) are a special case of a molecular superelastic crystal.³⁶ The single crystals of #23 not only manifest photoluminescence changes upon phase transition (yellow-green to orange) but also accomplish superelasticity based on the structural transition between monotropic phases. The YG-phase of #23 is based on a herringbone packing structure with a monoclinic P2₁/n system, while the structure of the shear-induced YO-phase is based on co-facial herringbone packing with a monoclinic P2₁/n system. Both polymorphic crystals are achievable through recrystallization from an ethanol solution; however, they are not interconvertible by thermal energy before the melting point (i.e., monotropic). Upon the shearing of YG-phase crystals, molecules are rotated by 68° and displaced about 1.9–2.0 Å to establish the YO-phase structure, thus exhibiting both Mechanisms 1 and 3. Interestingly, the authors provided varying-temperature stress–strain curves that did not change the forward and the reverse shear stress due to temperature. This result does not support the Clausius–Clapeyron relationship, which is attributed to the monotropic character of the shear-induced structure.

Superelasticity is based on a structural transition upon the shear loading and a spontaneous recovery of shape strain upon the unloading process. Unlike the single crystals of #10, #13 and #17, which represent mechanically-induced polymorphic transitions between enantiotropic phases, other structural origins can also engender the spontaneous shape recoverability of molecular crystals. Such recoverability is granted for the #18 crystal, which creates the unstable mechanically induced structure formation, while the spontaneous recoverability of the #22 crystal is engendered by interfacial stress in the twinning plane predictable by the surface area difference. Although the spontaneous shape recoverability of #19–21 crystals is still elusive, it is likely due to interfacial stress attributed to torsional twisting of the strong hydrogen bonding synthons at the twinning plane (#19), or to unstable structure formation induced by molecular misorientation at the twinning interface (#20 and #21). Moreover, superelasticity based on monotropic polymorphs, as found in #23 crystal, which is unprecedented in shape memory alloys, opens up a new horizon to devise superelastic (or martensitic) molecular crystals.

3.4. Ferroelasticity

Besides superelasticity, ferroelasticity also imparts reversible deformability to single-crystalline materials, albeit not spontaneous and requiring reverse mechanical loading. As described in Section 2.4, the structural foundations of organo-ferroelasticity are deformation twinning, except for #17 in Fig. 2. Upon twinning, in addition to layer-by-layer molecular displacement, concerted molecular rotations and/or conformational changes are concurrent that replicate the molecular arrangement of the type I/II transformed twinned lattice (i.e., 180° rotation of the lattice around twin plane normal and shear direction, respectively). Such rich molecular motions are attributed to a less symmetrical shape of the molecules compared to the atoms in shape memory alloys. Specifically, in the case of the twin operation of alloys, the 180° rotation of the lattice has no effect on the atomic orientation due to their spherical shape, and hence a structural change can be expressed simply by atomic displacements. However, in the case of molecular crystals, such a lattice reorientation can lead to massive molecular reorientation as well. Therein, the 180° rotation of whole molecules in the close packed structure is not valid, while a corresponding molecular orientation can be realized through a systematic conformational change and a rotation of the molecules. Below, we detail molecular and structural mechanisms found in the representative cases of ferroelastic molecular crystals.

In the pristine single crystal of 5-chloro-2-nitroaniline (#25, Fig. 2), the molecules primarily interact through N–H⋯O=N hydrogen bonding, establishing an infinite one-dimensional supramolecular tape.²⁷ In addition, adjacent tapes are weakly bound by a halogen bonding interaction (Cl⋯Cl) thus forming two-dimensional unit layers, which are stacked together based on interlayer π–π interactions. By exerting shear stress onto the (101) facet of the crystal, deformation twinning occurs by a 180° rotation of the lattice along the (101̄) plane normal (type I twinning). The twinned domain is interfaced with a pristine domain through (101̄)_M//(1̄01)_T. As shown in Fig. 13a, this twinning transition is accomplished by a substantial 58.7°-rotation and a displacement of the molecules, therefore clearly exhibiting Mechanisms 1 and 3, as shown in Fig. 6. The theoretical recoverable strain was evaluated to be 115.9%, which is much higher than the maximum strain of ca. 41% afforded in the deformation twinning of FCC-structured metallic crystals.¹²⁰

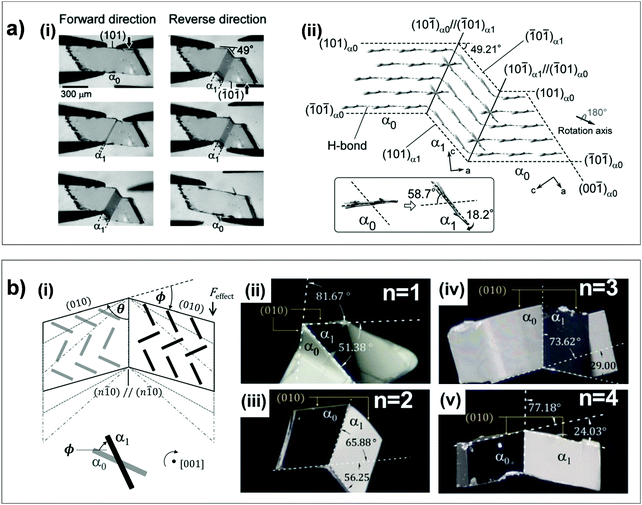Fig. 13 (a) Ferroelasticity found in a #25 crystal (Fig. 2). (i) Shear induced twinning and reverse shear induced detwinning is shown, which is resulted by (ii) substantial molecular rotation upon the twinning–detwinning process. Adapted with permission from ref. 27, copyright 2017 John Wiley & Sons, Inc. (b) Ferroelasticity found in #26 crystals (Fig. 2). (i) The crystals are capable of undergoing multiple different modes of deformation twinning with (n1̄0) twin plane, where molecular rotation by 180 – 2θ degrees about the [1n0] axis is anticipated upon transition. (ii–v) Optical micrographs of twinned crystals based on different twinning modes, i.e., n = 1, 2, 3, and 4, respectively. Adapted with permission from ref. 28, copyright 2018 John Wiley & Sons, Inc.

A herringbone packing single crystal of 1,4-diethoxybenzene (#26, Fig. 2) is a fascinating example of a ferroelastic material that deforms almost freely, enabled by multiple twinning planes/modes.²⁸ In the crystal structure of #26, no hydrogen bonding interaction is observed, but relatively strong electrostatic intermolecular interactions are presented together with C–H⋯π interactions from the herringbone configuration. When shear stress is applied on the (010) or (01̄0) planes, the crystal is deformed by deformation twinning across the twinning interfaces of (n1̄0), where the reorientation of the twinned lattice is explained by a 180°-rotation along the [1n0] shear direction with n = 1, 2, 3…. Thus, type II twinning occurrs in this material, as shown in Fig. 13b. Upon deformation twinning, the crystals bend by θ (i.e., angle between (010)_P and (010)_T) and twinned structures can be achieved by a 180 – 2θ degree rotation of the molecules (Mechanism 3 in Fig. 6c). In addition to showing different twinning modes with n of 1–5, the study demonstrated that several different modes of twinning can occur at the same time, allowing the crystal to be freely deformed like an accordion. Theoretical shear strains are intriguingly large, i.e., 144%, 83%, 57%, 43%, and 35% for n = 1–5, respectively.

A single crystal of 4,4′-dicarboxydiphenyl ether (#27, Fig. 2) is a ferroelastic material, whose lattice reorientation in the twinning–detwinning is accomplished by intriguing conformational changes resulting from the innate flexibility of #27.²⁹ Attributed to two carboxylic acid units at the para-position of the benzene rings, the #27 molecules establish a 1D hydrogen bonding supramolecular network, where C–O⋯H–O hydrogen bonding interactions penetrate the twinning plane, (1̄1̄1̄). By applying shear loading onto the (01̄1̄) face, deformation twinning takes place based on the 180° rotation along the (1̄1̄1̄) habit plane normal (i.e., type I twinning). This orientational relationship between the lattices does not essentially require a 180° rotation of the entire molecule, but the corresponding molecular geometry can be achieved by conformational changes due to the flexibility of #27 (i.e., flipping of the phenyl rings by ca. 30.2°, thus Mechanism 2 in Fig. 6b). Meanwhile, as mentioned, C–O⋯H–O hydrogen bonding interactions across the twin plane are expected to show a 20.1° distortion. Thus, a ca. 0–20° rotation of the carboxylic acid unit is proposed, which would preserve hydrogen bond planarity and relieve interfacial stress, thus causing a spontaneous strain in this case. The ferroelastic transition of the #27 crystal rendered a theoretical shear strain of 15%, which is relatively small compared to the #25 and #26 cases but still noticeable.

Except for the case found in the #17 crystals detailed in Section 3.5, ferroelasticity in molecular crystals is all based on deformation twinning. Drastic crystal deformations are accompanied by cooperative displacements (Mechanism 1) as well as concurrent conformational changes and/or molecular rotations, i.e., Mechanisms 2 and 3, respectively. Remarkable recoverable shear strains even beyond 100% are achievable in these crystals, which implies a myriad of potential applications, such as single crystalline flexible optoelectronics. To establish such an intriguing property in a target crystal, unlike superelastic cases, a twinning interface with negligible stress is required. However, it is elusive still which packing motifs or supramolecular synthons would promote super- or ferroelasticity. To further advance this promising research field, it is required to establish molecular/crystal engineering perspectives and in-depth structure–property correlations supported by theoretical studies based on molecular dynamics simulation for example.

3.5. Molecular crystals demonstrating versatile (thermo)mechanical transitions

As pointed out in Section 3, there are fascinating molecular martensitic materials that exhibit multiple (thermo-)mechanical transition capabilities (#10, #13 and #17 in Fig. 2) as well as an interconvertibility of mechanical deformation phenomena (#24, Fig. 2). An organoionic salt crystal composed of tetrabutyl-n-phosphonium tetraphenylborate (#10) is the first organic system that exhibits shape memory alloy-like behaviors, as reported by Takamizawa et al.²⁶ Since the shapes of both ionic components are spherical to some extent, like atoms in alloys, the thermomechanical properties of #10 are expected to provide thermo-mechanical transition capabilities resembling shape memory alloys. Unlike plastic crystals, which are also made up of spherical molecules, the single crystal of #10 presents diffusionless transitions in response to thermal and mechanical stimulation. First, it is demonstrated that shear loading on the (101̄) face of the α phase crystal results in ferroelastic twinned domain formation (Fig. 14a) with the (103)_α+//(103̄)_α− transition interface (α+ and α− denote the α phase with different lattice orientations). The maximum strain achievable through the ferroelasticity of the #10 crystal is 21.6%. Upon heating, it was discovered that the mechanically deformed twinned crystals recover to a straight shape through the thermoelastic α (triclinic P1̄) to β (triclinic P2₁/n) transition. In this step, the twin interfaces (103)_α+//(103̄)_α− all disappeared, forming a singly-oriented β structure across the (205)_α//(3̄1̄3)_β phase transition boundary. The subsequent cooling of the β crystal produces the α crystal with a single orientation via a reverse thermoelastic transition, as shown in Fig. 14a, indicating the shape memory effect of #10 crystals. The transitions are accompanied by slight molecular displacements and orientational changes but with apparent conformational changes. Furthermore, it was demonstrated that shear loading in the temperature range at which the β phase stabilizes showed superelasticity based on the reversible β to α phase transition. The observed behaviors are essentially identical to the shape memory effect of alloys (see Section 2).

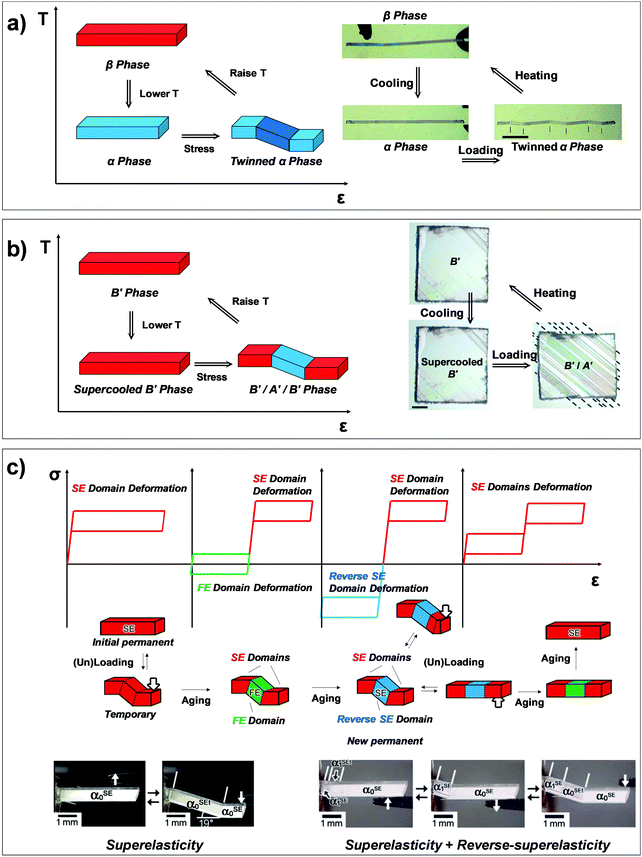Fig. 14 Shape memory effects with different structural origins observed from (a) #10 crystals, (b) #17 crystals, and (c) #24 crystals in Fig. 2. (a) #10 crystals exhibit shape memory effect based on stress induced twinning and heating induced α to β thermoelastic transition. Adapted with permission from ref. 26, copyright 2016 the Royal Society of Chemistry. (b) Shape memory effect of supercooled B′ phase of #17 crystals (n = 15) are presented, based on shear induced B′ to A′ and heating induced A′ to B′ transition. Adapted with permission from ref. 32, copyright 2019 American Chemical Society. (c) Interconversion between superelasticity (SE), ferroelasticity (FE), and reverse-superelasticity (Reverse SE) were found in #24 crystals. Adapted with permission from ref. 31, copyright 2019 John Wiley & Sons, Inc.

Intriguing (thermo-)mechanical transitions of high-performance p-channel semiconductor material, 6,13-bis(triisopropylsilylethynyl)pentacene (#13, Fig. 2), were revealed by us.⁵⁷ The #13 molecules establish a two-dimensional brickwork packing structure in the Form I polymorph (triclinic, P1̄ space group) at a temperature below ca. 121.5 °C. A single crystal of #13 undergoes three reversible thermally induced phase transitions based on four polymorphic phases, namely I–Ib, Ib–II, and II–III transitions, where I–Ib exhibits a second-order nature, while Ib–II and II–III are first-order thermoelastic transitions. Upon thermoelastic transitions, molecules glide along the (210) plane, which is parallel to the direction of the conjugated core, resulting in a remarkable extension of the crystal length (I–II: Δa = −2.1%, Δb = +10.8%, Δc = +1.7%; II–III: Δa = 0%, Δb = +4.8%, Δc = +0.2%). The transitions can also be mechanically-induced by exerting [1̄00] shear onto the (100) facet of Form II and III crystals, leading to superelastic II–I and III–II transitions (Fig. 15a), which are accompanied by a concerted molecular rotation of 12° and 8°, respectively. The theoretical recoverable shear strains of superelastic II–I and III–II transitions were evaluated to be 17.3 and 13.1%, respectively.

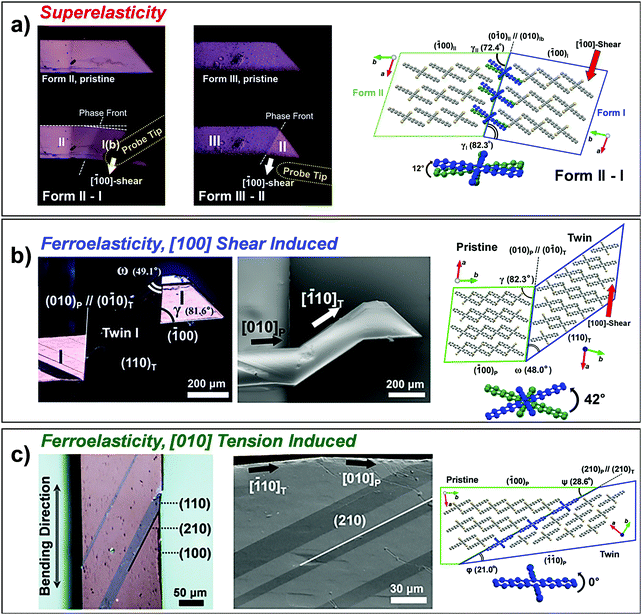Fig. 15 (a) Superelasticity of #13 crystal in Fig. 2 based on [1̄00] shear induced Form II–I and Form III–II transition. (b) Ferroelasticity of #13 crystal based on [100] shear and (c) [010] tension. Adapted with permission from ref. 57, copyright 2020 John Wiley & Sons, Inc.

In addition to the thermo- and superelastic transitions, the crystals of #13 can undergo two different modes of deformation twinning with ferroelastic natures. By applying [100] shear loading onto the crystals, they are significantly deformed by twin domain formation (type I, 180°-rotation along the (010) plane normal with the (010)_P//(01̄0)_T interface). The mechanical transition occurs in all polymorphic structures, giving rise to a recoverable strain of 59.9%, 25.5% and 0.3% in Form I, II and III structures, respectively. As the polarized Raman study revealed, in addition to the molecular displacements, the transition entails a substantial 42°-rotation of the molecules in the Form I structure (Fig. 15b). Moreover, it was concluded that a substantial strain is resulted from the π-stacking axes switching in the two-dimensional brickwork packing – i.e., a reversible exchange of the main π-stacking axis and the secondary π-stacking axis, which forms along the [010] and [1̄10] vectors, respectively. Furthermore, the molecular dynamics simulation results not only verified the structural details observed in the experiments but also suggest an intermediate Form III structure formation at the transition interface. The latter was pinpointed as the mechanism for alleviating interfacial stress incurred from the colossal molecular rotation upon twinning. It is schematically summarized in Fig. 6c that between the pristine (blue) and the twinned domain (green), the intermediate Form III structure (red) is established.

In addition to [100] shear induced deformation twinning, [010] tension engenders type II twinning, which reorients the lattice by a 180°-rotation along [1̄20], which is parallel to the (210) twinning plane (Fig. 15c). This type of transition also occurs in all polymorphic structures with π-stacking axes switching behaviors, giving rise to a recoverable strain of 59.9%, 25.5% and 0.3% in Form I, II and III structures, respectively. Similarly, the molecular dynamics simulation result indicated intermediate Form III structure formation at the twinning boundary. However, unlike the [100] shear induced twinning case, the molecular mechanism in this case is mainly ascribed to the concerted molecular displacement along the [1̄20] direction.

Thermo-mechanical transition behaviors of soft, super- and ferroelastic shape memory materials composed of saturated fatty acids were also investigated.³² Saturated fatty acids with long alkyl chains (#17 in Fig. 2; n: 15–21) establish hydrogen bonded dimers, which construct a lamellar 2D stacking structure, lacking strong intermolecular interactions between hydrogen bonded dimers. Previous research on polymorphism of the fatty acids identified three major structures, A, B, and C (even-numbered fatty acids) and A′, B′, and C′ (odd-numbered fatty acids).¹²¹ The tilt angle of the dimer increases in the order of A–C, where the tilt angle between the same category is nearly identical (e.g., A and A′) regardless of the chain length. The authors corroborated that the B′ crystals of odd-numbered fatty acids transform into A′ by compression, while an inverse transition spontaneously occurs by removing applied stress (i.e., superelasticity). A structural analysis on the pentadecanoic acid (C15) crystal revealed that the transition boundary is (127)_B′//(21̄7)_A′. It also revealed that the transition is accomplished through molecular gliding along the molecular long axis (which lies parallel to the interface) and molecular reorientation. Meanwhile, even-numbered fatty acid crystals are absent from martensitic transition induced deformability. This is attributed to the significant conformational difference at the dimerizing junction of A and B phases, which inhibits the facile molecular conformation and packing alteration required for transition.

In addition to the martensitic phase transition induced superelasticity (B′–A′, T higher than 306–307 K for C15), ferroelasticity on the same structural basis is achievable at a lower temperature condition (284 K < T < 306 K). Undercooled B′ crystals at this temperature range can undergo a B′–A′ transition through mechanical loading. However, the inverse transition (A′–B′) through the unloading process is precluded since B′ is metastable under these temperature conditions. Furthermore, such ferroelastically deformed crystals can recover their shape through the subsequent heating procedure (A′–B′ transition). See Fig. 14b for schematic drawings and optical micrographs illustrating the process. As the authors suggested, martensitic transition-induced deformation and temperature-controlled shape recovery is mechanistically new, given that the shape memory effect of alloys is based on the combination of deformation twinning and thermally-induced phase transition.

A single crystal of 1,4-dicyanobenzene (#24, Fig. 2) is a peculiar case of a superelastic material that can interconvert between superelasticity and ferroelasticity through a cold aging process (Fig. 14c).³¹ A single crystal of #24 belongs to the triclinic P1̄ space group. Along the a-axis direction, the molecules are stacked based on the π–π interaction, where neighboring columns are bound based on C–N⋯H–C interactions. Upon loading shear stress onto the (001̄) facet of the crystal, it deforms by 18.6° (i.e., recoverable strain of 33.7%) accompanied by twin domain formation (type II twinning with the twin plane of (2̄01)_P//(2̄01)_T). The structural change is ascribed to the slight reorientation and small displacement of molecules, and it is expected that molecules in the interface would adopt the orientation of either a pristine or a twinned structure. If the crystal has not undergone the aging process, upon unloading, the twinned domain spontaneously restores the lattice orientation of the pristine structure (i.e., superelasticity, red domain in Fig. 14c). On the other hand, if the deformed state is held for several tens of hours (i.e., cold aging), the twinned crystal does not recover its shape by simply unloading shear stress. Depending on the aging time, this domain can be detwinned by exerting opposite shear stress (green domain in Fig. 14c) or can act as a reverse superelastic domain (blue domain in Fig. 14c). Finally, the crystal with reverse superelastic domain can be retransformed to have an entirely pristine lattice orientation, by holding the crystal straight with an opposite shear stress. Although the molecular mechanism for the time-dependent interconversion between superelasticity and ferroelasticity is yet to be elucidated, the shape-rememorization capability found in the molecular crystal via the cold aging method will extend the mechanical workability of molecular crystals in a single-crystal-to-single-crystal fashion.

4. Potential applications

In the previous sections, we discussed characteristics of molecular martensitic materials (Section 2) and summarized structural and molecular mechanisms for thermoelastic, superelastic, and ferroelastic transitions found in various types of molecular crystals (Section 3). These non-destructive, fast and reversible structural transitions show promise for stimuli responsive materials and smart devices. In this section, several potential applications of molecular martensitic materials are highlighted.

4.1. Light-weight actuators

Recently, the Naumov group demonstrated actuators by harnessing the crystals of #1 and #5 in Fig. 2 and thoroughly investigated their mechanical properties. The #1 crystal, upon thermoelastic transition, elongates ∼5% in its total length with an expansion rate of ∼6.36 mm s⁻¹.⁵⁰ Actuator stress was evaluated to be ∼10² kPa with an actuator strain of 5%. Such performance is comparable to those from nanomuscles, electrostatic actuators and voice coils. More interestingly, due to the light weight and the density of molecular crystals, the force-to-weight ratio was measured to be on the order of 10⁴ which outperforms that of an ant (10³). As shown in Fig. 16a, #1 crystal was strong enough to push a stainless-steel ball (110 mg).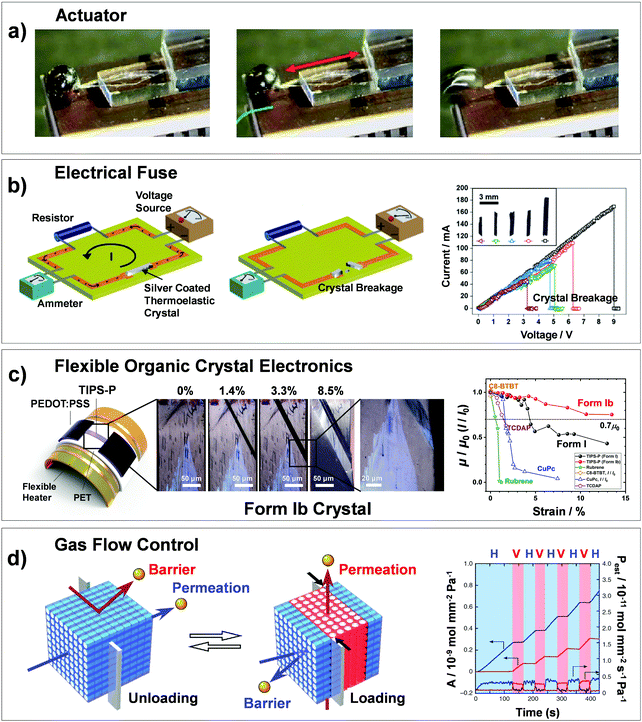

Fig. 16 Applications of molecular martensites. (a) Thermoelastic actuator demonstration based on a #1 crystal (Fig. 2) that pushes a 110 mg stainless steel ball. Adapted with permission from ref. 50, copyright 2019 the Royal Society of Chemistry. (b) Electrical fuse composed of a silver coated #14 crystal (Fig. 2). Adapted with permission from ref. 43, copyright 2017 the Royal Society of Chemistry. (c) Flexible single crystal electronic device utilizing a ferroelastic #13 crystal (Fig. 2). Adapted with permission from ref. 57, copyright 2020 John Wiley & Sons, Inc. (d) Mechanically controlled gas flow using a microporous superelastic crystal of #22 (Fig. 2). Adapted with permission from ref. 25, copyright 2015 Springer Nature.

Naumov and colleagues also utilized thermosalient crystals of #5 as actuators and closely explored their properties depending on the size and shape of the crystals. The crystals were classified into type 1 and 2 by their shapes, where the average length-to-thickness ratio was 2.67 and 5.48, respectively.⁵¹ These crystals exhibited linear dependence of the exerting force on the crystal mass or length, with a measured 6.5 ± 1.5 mN along the length and 1.8 ± 0.4 mN along the thickness direction for type 1 and 80 ± 6 mN along the length and 17 ± 2.5 mN along the thickness direction for type 2 crystals. When the actuator performances are expressed by volumetric power density (VPD), #5 crystals exhibited VPD of 1.3–2.7 MW m⁻³. Given strain values of 0.3–1.6 × 10⁻² by thermosalient transition of #5, the actuator performance was evaluated to be comparable to shape memory actuators which are applied in the industry. Further advantages of organic martensite include light weight of molecular materials as well as high reversibility; due to the latter it does not require a mechanically coupled system to reset to their original state.

4.2. Thermosalient electrical fuse

In addition, Naumov et al. utilized silver nanoparticle coated thermosalient crystals of #14 in Fig. 2 to demonstrate electrical fuses that can find applicability in low-voltage driven circuits (Fig. 16b).⁴³ Upon supplying voltage onto the electrical circuits composed of silver coated crystals, current flows due to the metallic conductivity afforded by silver nanoparticles. However, at the voltage condition that resistive heating of the silver nanoparticle layer surpasses the temperature condition for thermosalient transition (39–46 °C), the circuits readily break by the rapid motion of the crystals (i.e., movement, fracture, or explosion). The maximum current that can be endured by silver coated crystals differs by the size and heat capability of the crystals. Therefore, the response time and the maximum current can be fine-tuned by controlling the crystal sizes.

4.3. Thermo-mechanically driven lift

By utilizing the shape memory effect of #10 crystals in Fig. 2, Takamizawa and collaborator demonstrated a shape-memory lift that can raise the weight more than 10² times heavier than the crystal itself.²⁶ When SUS weights (1 g, 10 g and 100 g) are applied at temperatures below the HT phase starting temperature (T_HT,S), mechanical deformation due to ferroelastic transition occurs. Heating above the HT phase finishing temperature (T_HT,F), ferroelastically deformed crystals straighten back, thereby lifting much heavier weights than the crystals themselves. In particular, it was clearly shown that higher temperature is necessary to lift heavier weight, owing to linear dependence of T vs. σ for superelastic transition (see Section 2.3).

4.4. Shape and function memory electronics

Molecular martensitic crystals with semiconducting characteristics have been mostly discovered by our group. One of their intriguing demonstrations was shape- and function-memory behaviors of this class of materials. Crystalline thin films of #12 and #13 (Fig. 2) fabricated by a meniscus guided coating method were harnessed for organic field-effect transistor (OFET) applications. Intrinsic charge carrier mobility of OFETs is regulated by thermoelastic transitions.⁵⁴ For instance, OFETs of #12 exhibited hole mobility ∼1.9 cm² V⁻¹ s⁻¹ in the saturation regime at low temperature, which decreased by 217% upon thermoelastic transition. The mobility change was attributed to the alteration in its charge transfer integral – 44 and 51 meV of the low temperature polymorph to 35 and 49 meV of the high temperature polymorph for the herringbone and π–π pairs, respectively. The thermoelastic transition and accompanied electronic property changes were highly reversible, without damaging the crystalline thin films or metal-semiconductor contact. This example demonstrates the potential utility of martensitic organic semiconductors as shape- and function-memory devices.

4.5. Ultraflexible single crystal electronics

Our group and collaborators further demonstrated ultraflexible devices composed of ferroelastic single crystals of #13 (Fig. 2).⁵⁷ Upon bending the devices beyond the elastic limit, the crystals exhibited formation and evolution of the twinned domain without fracturing the devices. As shown in Fig. 16c, the devices could tolerate more than 13% tensile strain, which reduces mobility by ∼50% and 30% in single crystal devices of Form I and Form Ib polymorphs, respectively. Furthermore, we demonstrated reversibility of conductivity in the strain range of 1.3–2.5%; beyond 2.5% strain, flexible substrates supporting the devices underwent plastic deformation. We attributed strain-resilient conductivity to π-stacking axes switching during ferroelastic transitions. As we discussed in Section 3.5, ferroelastic transition of #13 entails axes switching behavior – i.e., exchange between the main π-stacking pair and the secondary π-stacking pair (Fig. 16c). Furthermore, due to the 2D carrier transport nature of the 2D brickwork system, the conductivity change with strain is gradual.

4.6. Crystal membrane for spatiotemporally controlled gas flow

Takamizawa et al. devised a crystal membrane capable of controlling gas flow in a spatiotemporal manner by using superelastic microporous crystals of #22 (Fig. 2).²⁵ As discussed in Section 3.3, this material exhibits superelasticity based on deformation twinning, which leads to substantial lattice reorientation. This observation is corroborated by alteration of the habit plane from (001̄) to (100). Such orientational change gives rise to mechanical reorientation of 1D microporous channel direction. As shown in Fig. 16d, the amount and permeability of CO₂ gas flow could be mechanically controlled by changing the microchannel direction via superelastic transitions. Specifically, gas flow is only allowed along the horizontal (vertical) direction before (after) shear loading; see blue (red) schematic drawings and curves.

5. Summary

In this review, we introduce molecular martensitic materials covering recent progress in molecular discoveries, molecular mechanisms, and potential applications. Distinct from the conventional metallic martensites, cooperative transitions in organic crystals exhibit rich molecular motions to accommodate structures of the transformed phase. Moreover, novel phenomena have been frequently observed in molecular martensites, such as thermosalient effects due to abrupt, large change in the crystal structures,^38,40 superelasticity based on transition between monotropic polymorphs or twins,^24,36 and interconvertibility between super- and ferroelasticity.³¹ Molecular martensitic materials show promise for realizing smart functional materials thanks to their (i) rapid/reversible shape and function switching behaviors, (ii) excellent mechanical deformability while maintaining structural integrity, (iii) light weight, (iv) solution processability, and (v) facile tunability of the material chemistry and functions by a judicial molecular design. Molecular mechanisms of martensitic transitions summarized in this review offer perspectives for designing molecular martensites, which remains elusive to date. Specifically, martensitic transitions in molecular crystals can be enabled by molecular features such as (i) existence of easy gliding plane by forming slipped π–π stacking or herringbone structure, (ii) triggerable dynamic motions of a substituent or the entire molecule, (iii) adaptability of supramolecular synthons to molecular motions by introducing torsionally flexible functional units, and (iv) presence of a shared rotation axis for directional cooperative molecular rotation, enabled by uniaxial alignment of molecules either along the short or long-axis of the molecule. The advancement of molecular martensitic materials has just begun. Molecular martensitic materials have ample room for further innovations, from molecular/crystal engineering perspectives to practical applications.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

We acknowledge the Sloan Foundation for the Sloan Research Fellowship in Chemistry and 3M Nontenured Faculty Award that supported this work.

References

1. D. Kalish and M. Cohen, Structural changes and strengthening in the strain tempering of martensite, Mater. Sci. Eng., 1970, 6, 156–166.
2. G. Krauss, Martensite in steel: Strength and structure, Mater. Sci. Eng., A, 1999, 273–275, 40–57.
3. K. Otsuka and X. Ren, Physical metallurgy of ti–ni-based shape memory alloys, Prog. Mater. Sci., 2005, 50, 511–678.
4. K. Otsuka and C. M. Wayman, Shape memory materials, Cambridge University Press, Cambridge, 1999.
5. J. Mohd Jani, M. Leary, A. Subic and M. A. Gibson, A review of shape memory alloy research, applications and opportunities, Mater. Des., 2014, 56, 1078–1113.
6. Z. Wei, R. Sandström and S. Mlyazaki, Review shape-memory materials and hybrid composites for smart systems, J. Mater. Sci., 1998, 33, 743.
7. W. J. Buehler and F. E. Wang, A summary of recent research on the nitinol alloys and their potential application in ocean engineering, Ocean Eng., 1968, 1, 105–120.
8. G. Olson and H. Hartman, Martensite and life: Displacive transformations as biological processes, J. Phys., 1982, 43, C4–C855.
9. A. A. Aksyuk, P. G. Leiman, L. P. Kurochkina, M. M. Shneider, V. A. Kostyuchenko, V. V. Mesyanzhinov and M. G. Rossmann, The tail sheath structure of bacteriophage t4: A molecular machine for infecting bacteria, EMBO J., 2009, 28, 821–829.
10. M. L. Yap, T. Klose, F. Arisaka, J. A. Speir, D. Veesler, A. Fokine and M. G. Rossmann, Role of bacteriophage t4 baseplate in regulating assembly and infection, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2654–2659.
11. K. Bhattacharya and R. D. James, The material is the machine, Science, 2005, 307, 53–54.
12. J. J. Gill, D. T. Chang, L. A. Momoda and G. P. Carman, Manufacturing issues of thin film niti microwrapper, Sens. Actuators, A, 2001, 93, 148–156.
13. N. B. Morgan, Medical shape memory alloy applications—the market and its products, Mater. Sci. Eng., A, 2004, 378, 16–23.
14. T. Duerig, A. Pelton and D. J. M. S. Stöckel, An overview of nitinol medical applications, Mater. Sci. Eng., A, 1999, 273, 149–160.
15. Y. Fu, H. Du, W. Huang, S. Zhang and M. J. S. Hu, Tini-based thin films in mems applications: A review, Sens. Actuators, A, 2004, 112, 395–408.
16. G. R. Desiraju, Supramolecular synthons in crystal engineering—a new organic synthesis, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327.
17. C. B. Aakeröy and K. R. Seddon, The hydrogen bond and crystal engineering, Chem. Soc. Rev., 1993, 22, 397–407.
18. C. Sutton, C. Risko and J.-L. Brédas, Noncovalent intermolecular interactions in organic electronic materials: Implications for the molecular packing vs electronic properties of acenes, Chem. Mater., 2016, 28, 3–16.
19. K. Biradha and R. Santra, Crystal engineering of topochemical solid state reactions, Chem. Soc. Rev., 2013, 42, 950–967.
20. S. K. Park, J. H. Kim and S. Y. Park, Organic 2d optoelectronic crystals: Charge transport, emerging functions, and their design perspective, Adv. Mater., 2018, 30, 1704759.
21. R. Li, W. Hu, Y. Liu and D. Zhu, Micro- and nanocrystals of organic semiconductors, Acc. Chem. Res., 2010, 43, 529–540.
22. E. Ahmed, D. P. Karothu and P. Naumov, Crystal adaptronics: Mechanically reconfigurable elastic and superelastic molecular crystals, Angew. Chem., Int. Ed., 2018, 57, 8837–8846.
23. S. Takamizawa and Y. Miyamoto, Superelastic organic crystals, Angew. Chem., Int. Ed., 2014, 53, 6970–6973.
24. S. Takamizawa and Y. Takasaki, Superelastic shape recovery of mechanically twinned 3,5-difluorobenzoic acid crystals, Angew. Chem., Int. Ed., 2015, 54, 4815–4817.
25. Y. Takasaki and S. Takamizawa, Active porous transition towards spatiotemporal control of molecular flow in a crystal membrane, Nat. Commun., 2015, 6, 8934.
26. S. Takamizawa and Y. Takasaki, Shape-memory effect in an organosuperelastic crystal, Chem. Sci., 2016, 7, 1527–1534.
27. S. H. Mir, Y. Takasaki, E. R. Engel and S. Takamizawa, Ferroelasticity in an organic crystal: A macroscopic and molecular level study, Angew. Chem., Int. Ed., 2017, 56, 15882–15885.
28. E. R. Engel and S. Takamizawa, Versatile ferroelastic deformability in an organic single crystal by twinning about a molecular zone axis, Angew. Chem., Int. Ed., 2018, 57, 11888–11892.
29. E. R. Engel, Y. Takasaki, S. H. Mir and S. Takamizawa, Twinning ferroelasticity facilitated by the partial flipping of phenyl rings in single crystals of 4,4'-dicarboxydiphenyl ether, R. Soc. Open Sci., 2018, 5, 171146.
30. S. Takamizawa, Y. Takasaki, T. Sasaki and N. Ozaki, Superplasticity in an organic crystal, Nat. Commun., 2018, 9, 3984.
31. S. Sakamoto, T. Sasaki, A. Sato-Tomita and S. Takamizawa, Shape rememorization of an organosuperelastic crystal through superelasticity-ferroelasticity interconversion, Angew. Chem., Int. Ed., 2019, 58, 13722–13726.
32. S. Takamizawa and Y. Takasaki, Versatile shape recoverability of odd-numbered saturated long-chain fatty acid crystals, Cryst. Growth Des., 2019, 19, 1912–1920.
33. T. Sasaki, S. Sakamoto and S. Takamizawa, Twinning organosuperelasticity of a fluorinated cyclophane single crystal, Cryst. Growth Des., 2019, 19, 5491–5493.
34. S. H. Mir, Y. Takasaki, E. R. Engel and S. Takamizawa, Enhancement of dissipated energy by large bending of an organic single crystal undergoing twinning deformation, RSC Adv., 2018, 8, 21933–21936.
35. S. H. Mir, Y. Takasaki, E. R. Engel and S. Takamizawa, Controllability of coercive stress in organoferroelasticity by the incorporation of a bulky flipping moiety in molecular crystals, CrystEngComm, 2018, 20, 3807–3811.
36. T. Mutai, T. Sasaki, S. Sakamoto, I. Yoshikawa, H. Houjou and S. Takamizawa, A superelastochromic crystal, Nat. Commun., 2020, 11, 1824.
37. P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Mechanically responsive molecular crystals, Chem. Rev., 2015, 115, 12440–12490.
38. Ž. Skoko, S. Zamir, P. Naumov and J. Bernstein, The thermosalient phenomenon. “Jumping crystals” and crystal chemistry of the anticholinergic agent oxitropium bromide, J. Am. Chem. Soc., 2010, 132, 14191–14202.
39. S. C. Sahoo, S. B. Sinha, M. S. Kiran, U. Ramamurty, A. F. Dericioglu, C. M. Reddy and P. Naumov, Kinematic and mechanical profile of the self-actuation of thermosalient crystal twins of 1,2,4,5-tetrabromobenzene: A molecular crystalline analogue of a bimetallic strip, J. Am. Chem. Soc., 2013, 135, 13843–13850.
40. M. K. Panda, T. Runcevski, S. C. Sahoo, A. A. Belik, N. K. Nath, R. E. Dinnebier and P. Naumov, Colossal positive and negative thermal expansion and thermosalient effect in a pentamorphic organometallic martensite, Nat. Commun., 2014, 5, 4811.
41. M. K. Panda, T. Runcevski, A. Husain, R. E. Dinnebier and P. Naumov, Perpetually self-propelling chiral single crystals, J. Am. Chem. Soc., 2015, 137, 1895–1902.
42. N. K. Nath, L. Severa, R. A. Kunetskiy, I. Cisarova, M. Fulem, K. Ruzicka, D. Koval, V. Kasicka, F. Teply and P. Naumov, Single-crystal-to-single-crystal transition in an enantiopure [7]helquat salt: The first observation of a reversible phase transition in a helicene-like compound, Chem. – Eur. J., 2015, 21, 13508–13512.
43. A. Khalil, E. Ahmed and P. Naumov, Metal-coated thermosalient crystals as electrical fuses, Chem. Commun., 2017, 53, 8470–8473.
44. D. P. Karothu, J. Weston, I. T. Desta and P. Naumov, Shape-memory and self-healing effects in mechanosalient molecular crystals, J. Am. Chem. Soc., 2016, 138, 13298–13306.
45. M. K. Panda, M. Etter, R. E. Dinnebier and P. Naumov, Acoustic emission from organic martensites, Angew. Chem., Int. Ed., 2017, 56, 8104–8109.
46. M. I. Tamboli, D. P. Karothu, M. S. Shashidhar, R. G. Gonnade and P. Naumov, Effect of crystal packing on the thermosalient effect of the pincer-type diester naphthalene-2,3-diyl-bis(4-fluorobenzoate): A new class ii thermosalient solid, Chem. – Eur. J., 2018, 24, 4133–4139.
47. P. Gupta, D. P. Karothu, E. Ahmed, P. Naumov and N. K. Nath, Thermally twistable, photobendable, elastically deformable, and self-healable soft crystals, Angew. Chem., Int. Ed., 2018, 57, 8498–8502.
48. A. J. Zaczek, L. Catalano, P. Naumov and T. M. Korter, Mapping the polymorphic transformation gateway vibration in crystalline 1,2,4,5-tetrabromobenzene, Chem. Sci., 2019, 10, 1332–1341.
49. E. Ahmed, D. P. Karothu, M. Warren and P. Naumov, Shape-memory effects in molecular crystals, Nat. Commun., 2019, 10, 3723.
50. L. Li, P. Commins, M. B. Al-Handawi, D. P. Karothu, J. M. Halabi, S. Schramm, J. Weston, R. Rezgui and P. Naumov, Martensitic organic crystals as soft actuators, Chem. Sci., 2019, 10, 7327–7332.
51. A. Khalil, D. P. Karothu and P. Naumov, Direct quantification of rapid and efficient single-stroke actuation by a martensitic transition in a thermosalient crystal, J. Am. Chem. Soc., 2019, 141, 3371–3375.
52. A. Colin-Molina, D. P. Karothu, M. J. Jellen, R. A. Toscano, M. A. Garcia-Garibay, P. Naumov and B. Rodríguez-Molina, Thermosalient amphidynamic molecular machines: Motion at the molecular and macroscopic scales, Matter, 2019, 1, 1033–1046.
53. Y. Diao, K. M. Lenn, W.-Y. Lee, M. A. Blood-Forsythe, J. Xu, Y. Mao, Y. Kim, J. A. Reinspach, S. Park, A. Aspuru-Guzik, G. Xue, P. Clancy, Z. Bao and S. C. B. Mannsfeld, Understanding polymorphism in organic semiconductor thin films through nanoconfinement, J. Am. Chem. Soc., 2014, 136, 17046–17057.
54. H. Chung, D. Dudenko, F. Zhang, G. D’Avino, C. Ruzié, A. Richard, G. Schweicher, J. Cornil, D. Beljonne, Y. Geerts and Y. Diao, Rotator side chains trigger cooperative transition for shape and function memory effect in organic semiconductors, Nat. Commun., 2018, 9, 278.
55. H. Chung, C. Ruzié, Y. Geerts and Y. Diao, Hybrid mechanism of nucleation and cooperative propagation in a single-crystal-to-single-crystal transition of a molecular crystal, Cryst. Growth Des., 2018, 18, 4245–4251.
56. H. Chung, S. Chen, N. Sengar, D. W. Davies, G. Garbay, Y. H. Geerts, P. Clancy and Y. Diao, Single atom substitution alters the polymorphic transition mechanism in organic electronic crystals, Chem. Mater., 2019, 31, 9115–9126.
57. S. K. Park, H. Sun, H. Chung, B. B. Patel, F. Zhang, D. W. Davies, T. J. Woods, K. Zhao and Y. Diao, Super- and ferroelastic organic semiconductors for ultraflexible single-crystal electronics, Angew. Chem., Int. Ed., 2020, 59, 13004–13012.
58. H. Chung, S. Chen, B. Patel, G. Garbay, Y. H. Geerts and Y. Diao, Understanding the role of bulky side chains on polymorphism of btbt-based organic semiconductors, Cryst. Growth Des., 2020, 20, 1646–1654.
59. Z. S. Yao, M. Mito, T. Kamachi, Y. Shiota, K. Yoshizawa, N. Azuma, Y. Miyazaki, K. Takahashi, K. Zhang, T. Nakanishi, S. Kang, S. Kanegawa and O. Sato, Molecular motor-driven abrupt anisotropic shape change in a single crystal of a ni complex, Nat. Chem., 2014, 6, 1079–1083.
60. S. Q. Su, T. Kamachi, Z. S. Yao, Y. G. Huang, Y. Shiota, K. Yoshizawa, N. Azuma, Y. Miyazaki, M. Nakano, G. Maruta, S. Takeda, S. Kang, S. Kanegawa and O. Sato, Assembling an alkyl rotor to access abrupt and reversible crystalline deformation of a cobalt(ii) complex, Nat. Commun., 2015, 6, 8810.
61. F. Borbone, A. Tuzi, A. Carella, D. Marabello, S. L. Oscurato, S. Lettieri, P. Maddalena and R. Centore, High-temperature reversible martensitic transition in an excited-state intramolecular proton transfer fluorophore, Cryst. Growth Des., 2019, 19, 6519–6526.
62. C. Brandel, Y. Cartigny, N. Couvrat, M. E. S. Eusébio, J. Canotilho, S. Petit and G. Coquerel, Mechanisms of reversible phase transitions in molecular crystals: Case of ciclopirox, Chem. Mater., 2015, 27, 6360–6373.
63. J. Ding, R. Herbst, K. Praefcke, B. Kohne and W. Saenger, A crystal that hops in phase transition, the structure of trans,trans,anti,trans,trans-perhydropyrene, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 739–742.
64. R. Centore, M. Jazbinsek, A. Tuzi, A. Roviello, A. Capobianco and A. Peluso, A series of compounds forming polar crystals and showing single-crystal-to-single-crystal transitions between polar phases, CrystEngComm, 2012, 14, 2645–2653.
65. D. Das, E. Engel and L. J. Barbour, Reversible single-crystal to single-crystal polymorphic phase transformation of an organic crystal, Chem. Commun., 2010, 46, 1676–1678.
66. R. G. Simoes, C. E. S. Bernardes, A. Joseph, M. F. M. Piedade, W. Kraus, F. Emmerling, H. P. Diogo and M. E. Minas da Piedade, Polymorphism in simvastatin: Twinning, disorder, and enantiotropic phase transitions, Mol. Pharmaceutics, 2018, 15, 5349–5360.
67. M. M. H. Smets, M. B. Pitak, J. Cadden, V. R. Kip, G. A. de Wijs, E. R. H. van Eck, P. Tinnemans, H. Meekes, E. Vlieg, S. J. Coles and H. M. Cuppen, The rich solid-state phase behavior of dl-aminoheptanoic acid: Five polymorphic forms and their phase transitions, Cryst. Growth Des., 2018, 18, 242–252.
68. R. Centore and M. Causà, Translating microscopic molecular motion into macroscopic body motion: Reversible self-reshaping in the solid state transition of an organic crystal, Cryst. Growth Des., 2018, 18, 3535–3543.
69. C. M. Reddy, G. Rama Krishna and S. Ghosh, Mechanical properties of molecular crystals—applications to crystal engineering, CrystEngComm, 2010, 12, 2296–2314.
70. J. Bernstein, Polymorphism in molecular crystals, Oxford University Press Inc., New York, 2002.
71. D. Gentili, M. Gazzano, M. Melucci, D. Jones and M. Cavallini, Polymorphism as an additional functionality of materials for technological applications at surfaces and interfaces, Chem. Soc. Rev., 2019, 48, 2502–2517.
72. H. Chung and Y. Diao, Polymorphism as an emerging design strategy for high performance organic electronics, J. Mater. Chem. C, 2016, 4, 3915–3933.
73. T. L. Threlfall, Analysis of organic polymorphs. A review, Analyst, 1995, 120, 2435–2460.
74. W. C. McCrone, “Polymorphism,” chapter 8 in physics and chemistry of the organic solid state, Wiley-Interscience, New York, 1965.
75. F. H. Herbstein, On the mechanism of some first-order enantiotropic solid-state phase transitions: From simon through ubbelohde to mnyukh, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 341–383.
76. J. W. Christian, The theory of transformations in metals and alloys part i, Pergamon, Oxford, 3rd edn, 2002.
77. J. Christian, G. Olson and M. Cohen, Classification of displacive transformations: What is a martensitic transformation?, J. Phys. IV, 1995, 5, C8-3–C8-10.
78. J. D. Dunitz, Phase transitions in molecular crystals from a chemical viewpoint, Pure Appl. Chem., 1991, 63, 177.
79. Q. Jiang, A. G. Shtukenberg, M. D. Ward and C. Hu, Non-topotactic phase transformations in single crystals of β-glycine, Cryst. Growth Des., 2015, 15, 2568–2573.
80. S. Clevers, F. Simon, M. Sanselme, V. Dupray and G. Coquerel, Monotropic transition mechanism of m-hydroxybenzoic acid investigated by temperature-resolved second harmonic generation, Cryst. Growth Des., 2013, 13, 3697–3704.
81. Y. V. Mnyukh, Molecular mechanism of polymorphic transitions, Mol. Cryst. Liq. Cryst., 1979, 52, 163–199.
82. H. Ito, M. Muromoto, S. Kurenuma, S. Ishizaka, N. Kitamura, H. Sato and T. Seki, Mechanical stimulation and solid seeding trigger single-crystal-to-single-crystal molecular domino transformations, Nat. Commun., 2013, 4, 2009.
83. B. P. Krishnan and K. M. Sureshan, A spontaneous single-crystal-to-single-crystal polymorphic transition involving major packing changes, J. Am. Chem. Soc., 2015, 137, 1692–1696.
84. N. Harada, Y. Abe, S. Karasawa and N. Koga, Polymorphic equilibrium responsive thermal and mechanical stimuli in light-emitting crystals of n-methylaminonaphthyridine, Org. Lett., 2012, 14, 6282–6285.
85. M. Dharmarwardana, R. P. Welch, S. Kwon, V. K. Nguyen, G. T. McCandless, M. A. Omary and J. J. Gassensmith, Thermo-mechanically responsive crystalline organic cantilever, Chem. Commun., 2017, 53, 9890–9893.
86. Y. Abe, S. Karasawa and N. Koga, Crystal structures and emitting properties of trifluoromethylaminoquinoline derivatives: Thermal single-crystal-to-single-crystal transformation of polymorphic crystals that emit different colors, Chem. – Eur. J., 2012, 18, 15038–15048.
87. Z. Zhang, X. Song, S. Wang, F. Li, H. Zhang, K. Ye and Y. Wang, Two-dimensional organic single crystals with scale regulated, phase-switchable, polymorphism-dependent, and amplified spontaneous emission properties, J. Phys. Chem. Lett., 2016, 7, 1697–1702.
88. G. Liu, J. Liu, Y. Liu and X. Tao, Oriented single-crystal-to-single-crystal phase transition with dramatic changes in the dimensions of crystals, J. Am. Chem. Soc., 2014, 136, 590–593.
89. R. J. Davey, S. J. Maginn, S. J. Andrews, A. M. Buckley, D. Cottier, P. Dempsay, J. E. Rout, D. R. Stanley and A. Taylor, Stabilization of a metastable crystalline phase by twinning, Nature, 1993, 366, 248–250.
90. G. T. Beckham, B. Peters, C. Starbuck, N. Variankaval and B. L. Trout, Surface-mediated nucleation in the solid-state polymorph transformation of terephthalic acid, J. Am. Chem. Soc., 2007, 129, 4714–4723.
91. Y. Peng, F. Wang, Z. Wang, A. M. Alsayed, Z. Zhang, A. G. Yodh and Y. Han, Two-step nucleation mechanism in solid-solid phase transitions, Nat. Mater., 2015, 14, 101–108.
92. Y. Peng, W. Li, F. Wang, T. Still, A. G. Yodh and Y. Han, Diffusive and martensitic nucleation kinetics in solid-solid transitions of colloidal crystals, Nat. Commun., 2017, 8, 14978.
93. D. Zahn and J. Anwar, Collective displacements in a molecular crystal polymorphic transformation, RSC Adv., 2013, 3, 12810–12815.
94. J. Anwar, S. C. Tuble and J. Kendrick, Concerted molecular displacements in a thermally-induced solid-state transformation in crystals of dl-norleucine, J. Am. Chem. Soc., 2007, 129, 2542–2547.
95. G. B. Olson and M. Cohen, Thermoelastic behavior in martensitic transformations, Scr. Metall., 1975, 9, 1247–1254.
96. L. Delaey, R. V. Krishnan, H. Tas and H. Warlimont, Thermoelasticity, pseudoelasticity and the memory effects associated with martensitic transformations, J. Mater. Sci., 1974, 9, 1521–1535.
97. H. Warlimont, L. Delaey, R. V. Krishnan and H. Tas, Thermoelasticity, pseudoelasticity and the memory effects associated with martensitic transformations, J. Mater. Sci., 1974, 9, 1545–1555.
98. P. Wollants, J. R. Roos and L. Delaey, Thermally- and stress-induced thermoelastic martensitic transformations in the reference frame of equilibrium thermodynamics, Prog. Mater. Sci., 1993, 37, 227–288.
99. O. U. Salman, A. Finel, R. Delville and D. Schryvers, The role of phase compatibility in martensite, J. Appl. Phys., 2012, 111, 103517.
100. A. Roytburd, Intrinsic hysteresis of superelastic deformation, Mater. Sci. Forum, 2000, 327, 389–392.
101. M. W. Burkart and T. Read, Diffusionless phase change in the indium-thallium system, J. Metals, 1953, 5, 1516–1524.
102. P. Wollants, M. De Bonte and J. R. Roos, Thermodynamic analysis of the stress-induced martensitic-transformation in a single-crystal, Z. Metallkd., 1979, 70, 113–117.
103. K. Aizu, Possible species of “ferroelastic” crystals and of simultaneously ferroelectric and ferroelastic crystals, J. Phys. Soc. Jpn., 1969, 27, 387–396.
104. K. Aizu, Possible species of ferromagnetic, ferroelectric, and ferroelastic crystals, Phys. Rev. B: Solid State, 1970, 2, 754–772.
105. E. K. H. Salje, Ferroelastic materials, Annu. Rev. Mater. Res., 2012, 42, 265–283.
106. V. K. Wadhawan, Ferroelasticity and related properties of crystals, Phase Transitions, 1982, 3, 3–103.
107. V. K. Wadhawan, Ferroelasticity, Bull. Mater. Sci., 1984, 6, 733–753.
108. M. K. Panda, S. Ghosh, N. Yasuda, T. Moriwaki, G. D. Mukherjee, C. M. Reddy and P. Naumov, Spatially resolved analysis of short-range structure perturbations in a plastically bent molecular crystal, Nat. Chem., 2015, 7, 65–72.
109. S. P. Thomas, M. W. Shi, G. A. Koutsantonis, D. Jayatilaka, A. J. Edwards and M. A. Spackman, The elusive structural origin of plastic bending in dimethyl sulfone crystals with quasi-isotropic crystal packing, Angew. Chem., Int. Ed., 2017, 56, 8468–8472.
110. U. B. Rao Khandavilli, B. R. Bhogala, A. R. Maguire and S. E. Lawrence, Symmetry assisted tuning of bending and brittle multi-component forms of probenecid, Chem. Commun., 2017, 53, 3381–3384.
111. G. R. Krishna, R. Devarapalli, G. Lal and C. M. Reddy, Mechanically flexible organic crystals achieved by introducing weak interactions in structure: Supramolecular shape synthons, J. Am. Chem. Soc., 2016, 138, 13561–13567.
112. M. C. Etter and A. R. Siedle, Solid-state rearrangement of (phenylazophenyl)palladium hexafluoroacetylacetonate, J. Am. Chem. Soc., 1983, 105, 641–643.
113. H. F. Lieberman, R. J. Davey and D. M. T. Newsham, Br···br and br···h interactions in action:  Polymorphism, hopping, and twinning in 1,2,4,5-tetrabromobenzene, Chem. Mater., 2000, 12, 490–494.
114. A. Mukherjee and G. R. Desiraju, Halogen bonds in some dihalogenated phenols: Applications to crystal engineering, IUCrJ, 2013, 1, 49–60.
115. A. Mukherjee, S. Tothadi and G. R. Desiraju, Halogen bonds in crystal engineering: Like hydrogen bonds yet different, Acc. Chem. Res., 2014, 47, 2514–2524.
116. B. A. Zakharov, A. A. L. Michalchuk, C. A. Morrison and E. V. Boldyreva, Anisotropic lattice softening near the structural phase transition in the thermosalient crystal 1,2,4,5-tetrabromobenzene, Phys. Chem. Chem. Phys., 2018, 20, 8523–8532.
117. M. A. Garcia-Garibay, Crystalline molecular machines: Encoding supramolecular dynamics into molecular structure, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10771–10776.
118. C. S. Vogelsberg and M. A. Garcia-Garibay, Crystalline molecular machines: Function, phase order, dimensionality, and composition, Chem. Soc. Rev., 2012, 41, 1892–1910.
119. S. E. Wheeler and K. N. Houk, Substituent effects in the benzene dimer are due to direct interactions of the substituents with the unsubstituted benzene, J. Am. Chem. Soc., 2008, 130, 10854–10855.
120. J. H. Seo, Y. Yoo, N. Y. Park, S. W. Yoon, H. Lee, S. Han, S. W. Lee, T. Y. Seong, S. C. Lee, K. B. Lee, P. R. Cha, H. S. Park, B. Kim and J. P. Ahn, Superplastic deformation of defect-free au nanowires via coherent twin propagation, Nano Lett., 2011, 11, 3499–3502.
121. E. Moreno, R. Cordobilla, T. Calvet, M. A. Cuevas-Diarte, G. Gbabode, P. Negrier, D. Mondieig and H. A. J. Oonk, Polymorphism of even saturated carboxylic acids from n-decanoic to n-eicosanoic acid, New J. Chem., 2007, 31, 947–957.

---