Polymorphism of CsGaS₂ – structural characterization of a new two-dimensional polymorph and study of the phase-transition kinetics

Abstract

CsGaS₂-mC64 was obtained by reaction of CsN₃ with stoichiometric amounts of Ga₂S₃ and S at elevated temperatures. The crystal structure of the air- and moisture stable compound was determined from single-crystal X-ray diffraction data. The colourless solid crystallizes in the monoclinic space group C2/c (no. 15) with the lattice parameters a = 10.5718(6) Å, b = 10.5708(6) Å, c = 16.0847(8) Å, β = 99.445(4)°, V = 1773.1(2) ų, and Z = 16. The compound crystallizes in the TlGaSe₂ structure type and features anionic layers ²_∞[Ga₄S₈⁴⁻] consisting of corner-sharing Ga₄S₁₀ supertetrahedra. At temperatures above 600 °C an irreversible phase-transition to CsGaS₂-mC16 occurs. The phase-transition kinetics were studied using in situ high-temperature X-ray powder diffraction techniques. This transition can only be reversed by using high pressures (>5 GPa at 500 °C). The compound was further characterized using Raman- and diffuse reflectance spectroscopy. Chemical bonding was analysed by DFT calculations.

---

Introduction

Chalcogenometallates of Group 13 metals containing alkali metal cations M_xT_yQ_z (M = alkali metal, T = triel, Q = chalcogen) crystallize in a large variety of different structure types.¹ Due to their semiconducting properties, these solids are interesting materials for technical applications, e.g. in gas sensors.² The polymeric anions in these compounds are formed by TQ₄ tetrahedra. Condensation of these building blocks leads to the formation of more complex oligomeric or polymeric anionic structures. The crystal structures of the resulting compounds contain these anionic chains, layers or networks embedded in a cationic surrounding of the alkali metal cations.¹ Recently, we reported on the polymorphism of CsGaSe₂.³ During the high-temperature phase-transition of this compound, a complete structural reconstruction of the anionic substructure from two-dimensional layers to one-dimensional chains takes place. Herein, we report on the discovery of CsGaS₂-mC64, a new low-temperature polymorph of CsGaS₂. Prior studies of this compound by Bronger et al.⁴ revealed CsGaS₂-mC16 as the only polymorph of CsGaS₂. At high temperatures CsGaS₂-mC64 undergoes an irreversible phase-transition to CsGaS₂-mC16. The low-temperature polymorph, however, can be restored by a high-pressure treatment. This behaviour is in contrast to the reversible phase-transition of CsGaSe₂.³ The kinetics of the high-temperature phase-transition of CsGaS₂-mC64 were studied by in situ high-temperature X-ray diffraction using the JMAK theory.⁵ We decided to redetermine the crystal structure of CsGaS₂-mC16 to obtain state-of-the-art data for both modifications. Furthermore, both polymorphs were characterized by Raman- and UV/Vis-diffuse reflectance spectroscopy and quantum chemical calculations.

Results and discussion

Crystal structures of both CsGaS₂ polymorphs

Both polymorphs of CsGaS₂ form air and moisture stable colourless crystals. The crystal structures were solved from single-crystal X-ray diffraction data collected at 20 °C. Both polymorphs crystallize in the monoclinic space group C2/c (no. 15) with a = 10.5718(6) Å, b = 10.5708(6) Å, c = 16.0847(8) Å, β = 99.445(4)°, V = 1773.1(2) ų, and Z = 16 for CsGaS₂-mC64 (single-crystal, 20 °C), and a = 7.3875(2) Å, b = 12.1282(4) Å, c = 5.8994(2) Å, β = 113.210(3)°, V = 485.79(3) ų, and Z = 4 for CsGaS₂-mC16 (single-crystal, 20 °C). The structures were solved by charge flipping methods using SUPERFLIP,⁶ implemented in Jana2006,⁷ and refined to R₁ = 0.0397 and wR₂ = 0.0578 (all data) for CsGaS₂-mC64, and R₁ = 0.0122 and wR₂ = 0.0401 (all data) for CsGaS₂-mC16 by full-matrix least squares methods using Jana2006.⁷ Details on the final crystallographic data are listed in Table 1. The atomic coordinates and isotropic displacement parameters are listed in Tables 2 and 3. Anisotropic displacement parameters, interatomic distances, and angles can be found in the ESI (Tables S1–S4‡).

Table 1 Crystallographic data for both polymorphs of CsGaS₂ ^a

	CsGaS2-mC64	CsGaS2-mC16
a Details of the crystal structure investigations may also be obtained from the Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (E-mail: crysDATA@fiz-karlsruhe.de), on quoting the depository numbers CSD 432322 (CsGaS2-mC64) and CSD 432321 (CsGaS2-mC16). Cif-files are included to the ESI.
Formula weight/g mol^−1	266.76
Colour/shape	Colourless plate	Colourless rod
Crystal size/mm^3	0.12 × 0.04 × 0.02	0.29 × 0.04 × 0.02
Crystal system, space group	Monoclinic, C2/c
Lattice constants from single crystals
a/Å	10.5718(6)	7.3875(2)
b/Å	10.5708(6)	12.1284(4)
c/Å	16.0847(8)	5.8994(2)
β/°	99.445(4)	113.210(3)
Volume V/Å^3	1773.1(2)	458.79(3)
Number of formula units Z	16	4
Calculated density ρcalc./g cm^−3	3.997	3.647
Temperature T/°C	20
Diffractometer	Rigaku Supernova
Wavelength λ/Å	0.71073
Absorption coeff. μ(Mo-Kα)/mm^−1	14.892	13.705
θ range of data collection/°	3.16–28.9	3.36–32.35
Index range	−14 ≤ h ≤ 14	−5 ≤ h ≤ 5
	−14 ≤ k ≤ 14	−10 ≤ k ≤ 10
	−21 ≤ l ≤ 20	−14 ≤ l ≤ 14
Absorption correction	Analytical, CrysAlisPro^11
No. of reflections collected	10 492	9633
Independent reflections	2137	844
R int	0.0328	0.0235
Completeness to θ = 25°	99.9%	99.9%
Structure solution	Charge flipping, Superflip^6
Structure refinement	Jana2006^7
Extinction coefficient Giso	0.007(2)	0.007(2)
No. of refined parameters	75	21
No. of constraints	0	0
GooF	1.20	1.56
R 1, wR2 [I > 3σ(I)]	0.0223, 0.0482	0.0116, 0.0399
R 1, wR2 [all data]	0.0397, 0.0578	0.0122, 0.0401
Largest diff. peak & hole/e Å^−3	1.17, −0.75	0.45, −0.29

---

Table 2 Atomic coordinates and equivalent isotropic displacement parameters U_eq (in Ų) for CsGaS₂-mC64

Atom	Wyck.	x	y	z	U eq ^a
a U eq is defined as one third of the trace of the orthogonalized Uij tensor.
Cs1	8f	0.2871(1)	0.0621(1)	0.3997(1)	0.0198(1)
Cs2	8f	0.4629(1)	0.3126(1)	0.1026(1)	0.0197(1)
Ga2	8f	0.1039(1)	0.1892(1)	0.1719(1)	0.0111(1)
Ga2	8f	0.1427(1)	0.4357(1)	0.3283(1)	0.0111(1)
S1	8f	0.0407(1)	0.3123(1)	0.4151(1)	0.0129(1)
S2	8f	0.2097(1)	0.0628(1)	0.0890(1)	0.0118(1)
S3	8f	0.2527(1)	0.3123(1)	0.2503(1)	0.0124(1)
S4	4e	0	0.0598(1)	1/4	0.0129(5)
S5	4e	0	0.5649(1)	1/4	0.0132(5)

---

Table 3 Atomic coordinates and equivalent isotropic displacement parameters U_eq (in Ų) for CsGaS₂-mC16

Atom	Wyck.	x	y	z	U eq ^a
a U eq is defined as one third of the trace of the orthogonalized Uij tensor.
Cs	4e	0	0.14471(1)	1/4	0.0142(1)
Ga	4e	0	0.50357(2)	1/4	0.0089(1)
S	8f	0.18234(6)	0.39873(4)	0.09549(7)	0.0114(1)

---

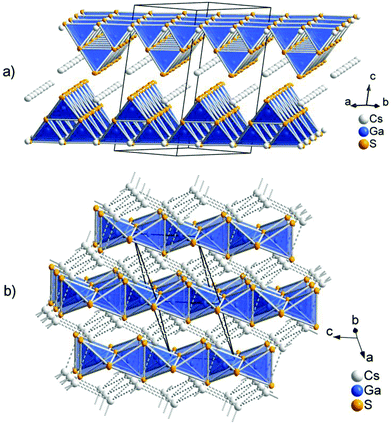
The low-temperature polymorph CsGaS₂-mC64 crystallizes in the TlGaSe₂ structure type⁸ like many related compounds MTQ₂ (M = Na, K, Rb, Cs, Tl; T = Al, Ga, In; Q = S, Se, Te). The crystal structure of the layered compound features anionic layers ²_∞[Ga₄S₈⁴⁻], composed of corner-sharing Ga₄S₁₀ supertetrahedra. These layers are separated by Cs atoms (Fig. 1). The two independent trivalent gallium sites are tetrahedrally coordinated by the S atoms. The interatomic distances in these tetrahedra range from d(Ga–S) = 2.260(1) Å to d(Ga–S) = 2.308(1) Å. The angles ∠(S–Ga–S) range from 107.17(4)° to 113.35(4)°. These values are in good agreement with comparable compounds, like Cs₂Ga₂S₅, CsGa₃S₅, CsGaS₂-mC16, CsGaSe₂, or CsGaTe₂.^3,4,9 The GaS₄ tetrahedra are connected by common corners, forming so-called Ga₄S₁₀ supertetrahedra. These corner-sharing supertetrahedra are condensed to anionic layers ²_∞[Ga₄S₈⁴⁻], which are stacked along [001]. The layers are penetrated by a cationic caesium substructure, formed by two independent Cs sites. The Cs atoms are 6 + 2 coordinated by sulphur, resulting in bicapped trigonal prisms. The interatomic distances within the trigonal prisms range from d(Cs–S) = 3.488(1) Å to d(Cs–S) = 3.583(1) Å. The distances to the capping atoms in the range from d(Cs–S) = 3.741(1) Å to d(Cs–S) = 3.749(1) Å are significantly longer. The CsS₈ polyhedra are connected by common edges (S3, S4; S3, S5) and the capping atoms (S1, S2). The caesium atoms form an irregular cationic substructure with distances d(Cs–Cs) below 5 Å in one layer and in the range between d(Cs–Cs) = 5.256(1) Å to d(Cs–Cs) = 5.297(1) Å between two adjacent layers.

Fig. 1 (a) Anionic layers in CsGaS₂-mC64. (b) Crystal structure of CsGaS₂-mC16, showing the arrangement of the anionic chains in the diamond-like topological arrangement of the Cs⁺ cations (dashed lines).

The high-temperature polymorph CsGaS₂-mC16 crystallizes in the KFeS₂ ¹⁰ structure type like the isotypic compound CsGaSe₂-mC16. The crystal structure was already described by Bronger et al. in 1975.⁴ In order to obtain state-of-the-art data, we decided to redetermine the crystal structure. The compound features anionic SiS₂ analogous chains ¹_∞[GaS₂⁻] embedded in a cationic Cs substructure (Fig. 1). Gallium has a tetrahedral coordination, formed by four sulphur atoms, with interatomic distances of d(Ga–S) = 2.2823(4) Å and d(Ga–S) = 2.2869(5) Å. These tetrahedra are connected by common edges, thus forming infinite chains along [001]. In the crystal structure, these chains are arranged in a hexagonal rod packing. Caesium is eightfold coordinated by sulphur with distances in the range of d(Cs–S) = 3.6200(5) and d(Cs–S) = 3.7025(4) Å. The Cs⁺ cations form a topological network similar to the cubic diamond. The interatomic distances range from d(Cs–Cs) = 4.5023(3) Å to d(Cs–Cs) = 4.5850(3) Å.

Thermal analysis

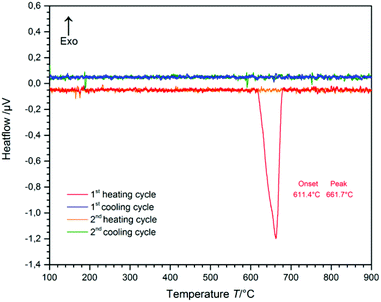
The temperature range of the phase-transition from CsGaS₂-mC64 to the high-temperature phase CsGaS₂-mC16 was determined by differential thermal analysis (DTA) (Fig. 2). The measurement (heating-/cooling rate 10 °C min⁻¹, 2 cycles) revealed an irreversible transition starting at about 610 °C. After the measurement, the sample was identified as CsGaS₂-mC16 by X-ray powder diffraction. The high-temperature phase CsGaS₂-mC16 exhibits a melting point of about 1100 °C as shown in Fig. S1 of the ESI.‡

Fig. 2 Differential thermal analysis (DTA) of CsGaS₂-mC64 (the baseline was manually subtracted). Two heating- and cooling cycles (heating-/cooling rate 10 °C min⁻¹) reveal an irreversible phase-transition.

Pressure-induced phase-transition

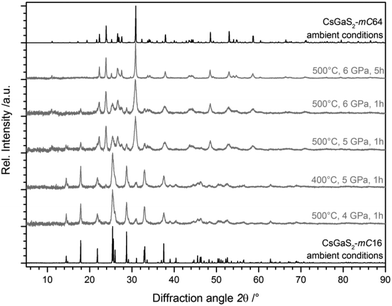
Due to the significant difference (∼10%) of the calculated densities of both polymorphs with ρ(CsGaS₂-mC64) ≫ ρ(CsGaS₂-mC16), the possibility of a pressure-induced phase-transition of CsGaS₂-mC16 was investigated. High-pressure experiments were performed in a belt apparatus as described by Range et al.¹² in the pressure region from 1–6 GPa. For the high pressure synthesis, a small pellet of the sample was placed in a graphite crucible. This crucible was placed in a pressure chamber made of pyrophyllite, surrounded by steel cuffs. High pressure was then applied by axial steel stamps. Heating of the samples is achieved by application of appropriate electric current to the graphite crucible. Pressure and temperature were determined by external calibration.

The experiments revealed a pressure-induced phase-transition to the low-temperature phase CsGaS₂-mC64 at pressures >5 GPa and a temperature of at least 500 °C (Fig. 3). The isotypic compound CsGaSe₂ ³ shows a similar difference of the calculated densities of both polymorphs (∼8%). However, the temperature-induced phase-transition to CsGaSe₂-mC16 can be reverted by annealing below the transition temperature (∼520 °C). High-pressure treatments of CsGaSe₂-mC16 at 6 GPa and temperatures up to 500 °C did not induce a phase-transition. At 6 GPa and temperatures above 500 °C, a phase-transition to CsGaSe₂-mC64 occurs. However, this change is most likely caused by the elevated temperature, rather than the high-pressure. No hints for a phase transition are known for the heavier homologous compound CsGaTe₂,^9f which crystallizes isotypic to CsGaQ₂-mC64 (Q = S, Se). We cannot explain the different behaviour of CsGaQ₂ (Q = S, Se, Te) at elevated temperatures in detail. However, we suppose that the high-pressure phase transition of CsGaS₂-mC16 results from the differences of the crystallographic densities. The densities of the selenide polymorphs differ by 8.2%, whereas the sulphide polymorphs show a difference of 9.6%. Therefore, high pressure supports the formation of the high-density polymorph CsGaS₂-mC64. In case of CsGaSe₂-mC64 and CsGaSe₂-mC16 pressure has a smaller influence and therefore the polymorphs can transform into each another without additional pressure.

Fig. 3 X-ray diffraction patterns of CsGaS₂-mC16 after quenching from elevated pressures (grey lines), revealing a pressure-induced phase-transition starting at 5 GPa and 500 °C. The pure polymorphs without pressure treatment are also shown (black lines). Peak broadening is typically observed for samples treated at high-pressure.

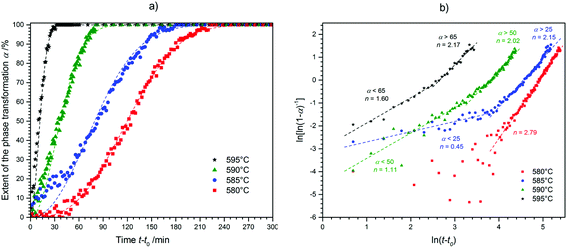
Study of the high-temperature phase-transition kinetics

As the different polymorphs of CsGaS₂ and CsGaSe₂ are isotypic we decided to analyse the phase-transition kinetics similar to CsGaSe₂.³ Due to the irreversibility of the thermally induced phase-transition, only the transformation from CsGaS₂-mC64 to CsGaS₂-mC16 was studied.

Experimental setup. The measurements were carried out in the same manner as described for CsGaSe₂ ³ on a STOE Stadi P diffractometer (monochromatic Mo-Kα₁ radiation, λ = 0.70926 Å) equipped with a Dectris Mythen 1K detector and a high-temperature capillary furnace. The powdered samples were sieved using analytical sieves prior to the experiments. The smallest fraction (0.02–0.04 mm) was used for all measurements. The samples were loaded in quartz capillaries (diameter 0.3 mm). The 2θ-range of 4.55–23.420° (exposure time 60 s per pattern) was detected for all experiments. The powder patterns were analysed using the STOE WinX^POW software package.¹³ After fitting of the reflection profiles using a pseudo-Voigt peak shape, the phase fractions α were determined from the integrated intensities of the strongest reflections of both polymorphs (CsGaS₂-mC64: 223, 14.5°, CsGas₂-mC16: 130, 11.6°).

Non-isothermal analysis. To determine a suitable temperature region for the analysis of the phase-transition kinetics, the temperature region near the thermal effect in the DTA was studied by high-temperature X-ray powder diffraction. The samples were first heated to 550 °C (heating rate 50 °C min⁻¹). Then diffraction patterns were collected until the samples reached 650 °C (step: 1 °C min⁻¹, holding time: 3 min, heating rate 1 °C min⁻¹). A plot of the phase fractions α of both polymorphs (Fig. 4) showed a sigmoidal shape for the phase-transition beginning at 578 °C. The slightly lower temperature region compared to the thermal analysis can be explained by the differing heating rates.

Fig. 4 Change of the phase fractions of CsGaS₂ during the phase-transition investigated by in situ X-ray powder diffraction in the region of the phase-transition.

Isothermal kinetic analysis. The analysis of the phase-transition kinetics was performed as previously described for CsGaSe₂. The obtained data for the progression of the phase fraction of the crystallizing compound as a function of time (Fig. 5a) was fitted to a theoretical expression. The modified Josephson–Mehl–Avrami–Kolmogorov (JMAK) eqn (1) ⁵ with the Avrami exponent n and the kinetic rate constant K was used for all experiments as this equation is widely accepted for the study of crystallization kinetics.¹⁴ The kinetic parameters n and K were determined by plotting ln[ln(1 − α)⁻¹] against ln(t) as seen in Fig. 5b, the Sharp–Hancock plot (2).¹⁵

α(t) = 1 − exp[−(Kt)ⁿ] (1)

ln[ln(1 − α)⁻¹] = n·ln(t) + n·ln(K) (2)

Fig. 5 (a) Progression of the phase fraction of CsGaS₂-mC16 during the isothermal measurements (dashed lines indicate a fit based on the Avrami equation using the determined kinetic parameters n and K). (b) Sharp–Hancock plots for the different experiments (dashed lines indicate a linear fit for the determination of n and K).

Prior to the determination of the kinetic parameters, the individual incubation times t₀ were subtracted. The incubation time was defined as the time until a reflection of the growing phase was observed for the first time. The Avrami exponent n is obtained as the slope of this linear plot whereas K is determined by the intercept of the y-axis. A change in the crystallization mechanism is indicated by a changing slope in the Sharp–Hancock plot. The crystallization mechanisms were determined by comparing a plot of t/t_0.5 against α with theoretical curves (Fig. 6).¹⁶

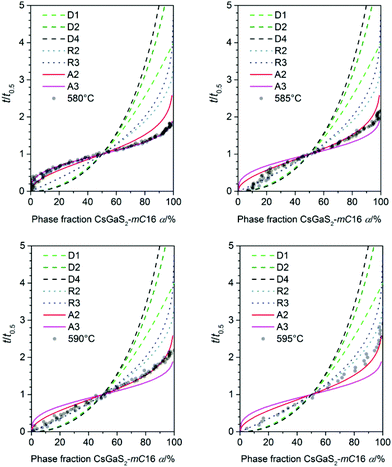Fig. 6 Plot of α against t/t_0.5 for all measured temperatures (transparent dots) used for the determination of the crystallisation mechanism (lines) according to literature.¹⁶

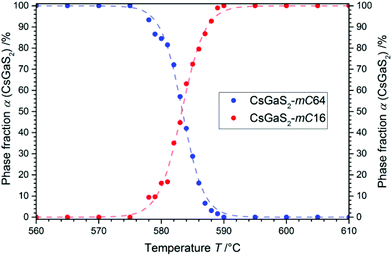
The phase-transition to the high temperature phase CsGaS₂-mC16 was studied in the temperature region from 580–595 °C with an irradiation time of 60 s (per pattern) for all temperatures. The obtained kinetic parameters and characteristic times are listed in Table 4. A trend of a decreasing time t − t₀ for a complete phase-transition can be observed (Fig. 5) with increasing temperatures. This behaviour is in accordance with an increased crystal growth rate. The incubation time t₀ decreases also significantly from 34(1) to 1(1) min.

Table 4 Avrami exponents n, reaction rate constants K, and characteristic times of the phase transition kinetics of CsGaS₂-mC64 for different temperatures T

T/°C	t 0/min	t 0.5/min	Mechanism	Avrami exponent n	Rate constant K/min^−1
580	34(1)	109	A3	2.79(3)	1.1(1) × 10^−6
585 (α < 25)	20(1)	84	R2/R3	0.45(5)	4.3(6) × 10^−3
585 (α > 25)			A2	2.15(4)	0.6(1) × 10^−5
590 (α < 50)	7(1)	37	R2/R3	1.11(7)	1.1(2) × 10^−2
590 (α > 50)			A2	2.02(5)	4.8(9) × 10^−4
595 (α < 65)	1(1)	17	R2/R3	1.60(9)	1.1(3) × 10^−3
595 (α > 65)			A2	2.17(8)	0.7(1) × 10^−3

---

For all experiments in the temperature range from 595 to 585 °C, a dominating one dimensional growth mechanism (A2) with Avrami exponents in the range of 2.17(8) to 2.02(5) can be observed. This observation is in good agreement with the rod-shaped crystallites of CsGaS₂-mC16. The initial stages of crystallization, however, are dominated by a phase-boundary controlled mechanism (R2/R3) with significantly smaller n. The extent of this region is subsequently decreasing from α < 65% at 595 °C to α < 25% at 585 °C. This change from a phase-boundary controlled mechanism towards a growth mechanism according to the JMAK theory was also observed for the phase-transition from CsGaSe₂-mC64 to CsGaSe₂-mC16. The slightly higher Avrami exponents n can probably be attributed to the longer transition times for CsGaS₂ and the corresponding higher resolution of the obtained data. A further change in the crystallization mechanism can be observed at 580 °C. Thus, a two-dimensional growth mechanism (A3) with decreasing nucleation rate can be concluded with an Avrami exponent n of 2.79(3) at this temperature. We did not observe a similar change for CsGaSe₂.³ The decreasing influence of the phase-boundary controlled growth could possibly result from the higher activation energy E_A(R2/R3) for this process (see next paragraph, Fig. 7). At lower temperatures, the thermal energy does not suffice to induce a phase-boundary controlled growth, and only the slower growth mechanism according to the JMAK theory with a smaller activation energy progresses. Even though the experiments revealed the growth of rod-shaped crystallites of CsGaS₂-mC16, no significant macroscopic change of the plate-shaped starting material CsGaS₂-mC64 is observed. At the initial stage of crystallization, the surface of the plates is covered by a thin layer of the high-temperature polymorph (R2/R3). In the course of the phase-transition, the bulk phase is slowly transformed by growing nuclei. Due to the relatively low temperatures and short transformation times, no macroscopic rod-shaped crystals can grow, and the basic shape of the starting material remains unchanged.

Fig. 7 Arrhenius plot used to determine the activation energy of the phase-transition. The dashed line indicates a fit of the data obtained for a phase-boundary controlled process (hollow circles), whereas the solid line indicates a fit based on the data for the JMAK kinetics (black circles).

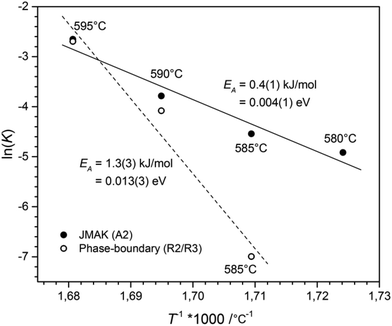
The activation energy for the phase-transition was determined by the Arrhenius equation.¹⁷ The plot of T⁻¹ against the logarithm of the rate constant ln(K), see Fig. 7, revealed an activation energy for the phase-boundary controlled process of E_A = 1.3(3) kJ mol⁻¹ and E_A = 0.4(1) kJ mol⁻¹ for nucleation and growth according to the JMAK theory. These values are in good agreement with the value of E_A = 1.0(6) kJ mol⁻¹, obtained for the transition from CsGaSe₂-mC64 to CsGaSe₂-mC16.³

Vibrational spectroscopy

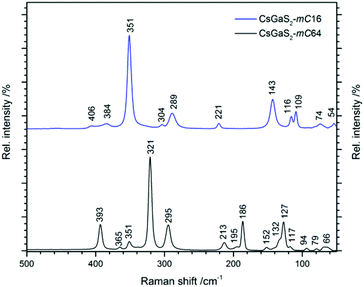
The Raman spectra of CsGaS₂-mC64 and -mC16 are shown in Fig. 8. Vibrations in the range 400–290 cm⁻¹ can be attributed to Ga–S stretching modes.⁹ The Ga–S deformation modes are observed in the region from 290–100 cm⁻¹, whereas all lower vibrations are tentatively assigned to lattice vibrations.⁹

Fig. 8 Raman spectra of the CsGaS₂ polymorphs (black line: mC64, blue line: mC16).

Electronic properties

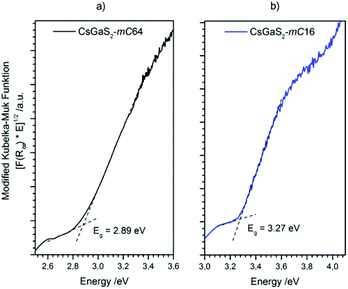
The optical band gaps of both CsGaS₂ polymorphs were determined by using UV/Vis diffuse reflectance spectroscopy. A modified Kubelka–Munk function^18,19 was used to calculate the absorption data. The extrapolation of the linear parts onto the baseline revealed wide band gaps of 2.89 eV and 3.27 eV for CsGaS₂-mC64 and CsGaS₂-mC16, respectively (Fig. 9).

Fig. 9 Diffuse reflectance spectrum of (a) CsGaS₂-mC64 and (b) CsGaS₂-mC16. Optical band gaps were determined by extrapolation of the linear part of the modified Kubelka–Munk function onto the baseline, as indicated by the dashed lines.

The electronic band structure of CsGaS₂ was further analysed by relativistic DFT calculations using the generalized gradient approximation (GGA) according to Perdew–Burke–Enzerhof (PBE).²⁰ The all electron full-potential local-orbital code FPLO¹⁴ was applied for total energy and band structure calculations using the experimentally obtained structures. The calculated direct band gaps of 2.72 eV and 3.34 eV are in good agreement with experimental data and the white powdered samples.

The bonding behaviour of Cs, Ga, and S in the title compound is revealed from the orbital projected density of states (PDOS, Fig. 10). The DOS panels refer to the atomic sites in mC64 (a) and mC16 (b) structures. Despite the fact that there is only one Cs, one Ga and one S site in the modification mC16, but 2 Cs, 2 Ga, and 5 S sites in the modification mC64, similar DOS features are found for equivalent atom types. Due to the similar chemical environment of equivalent atom types, chemical bonding can be discussed in general for the different elements in both structures. Accordingly, Ga–S interactions within the tetrahedra in both polymorphs cause a splitting into Ga-4s and -4p valence- and conduction band contributions. Valence band DOS maxima of Ga-4s are found in the energy range from −4 to −6 eV, and those of Ga-4p between 0 and −4 eV. In the antibonding region (conduction band) again 4s DOS maxima are found at lower energy than the 4p states. As a consequence, the conduction band minimum has to be attributed mainly to Ga-4s states. The DOS maxima for S-3s orbitals are situated around −15 eV (not shown in Fig. 10). Strong contributions of S-3p orbitals below the Fermi energy (0 to −2 eV) form the valence band maximum. They are estimated as non-bonding states. Smaller S-3p DOS peaks below −2 eV and above +3 eV are attributed to covalent gallium sulphur interactions. This observation is in line with the mainly covalent bonding between gallium and the chalcogen atoms as observed for Cs₂Ga₂S₅.^9a The larger band gap of CsGaS₂-mC16 as compared to Cs₂Ga₂S₅ and CsGaS₃ ^9b further confirms the assumption of a significant influence of S₂²⁻ dumbbells on the band gaps of these compounds.^9a The bonding character of Cs is mainly ionic, as concluded from unoccupied Cs-6s states.

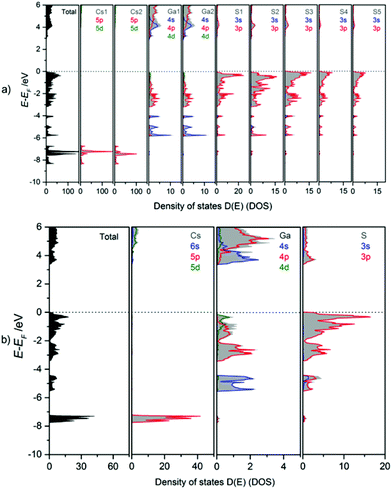Fig. 10 Calculated total (TDOS) and partial density of states (PDOS) for (a) CsGaS₂-mC64 and (b) CsGaS₂-mC16.

Experimental

Synthesis of the starting materials

Gallium sulphide Ga₂S₃ was prepared by annealing of a stoichiometric mixture of Ga (Chempur 99.99%) and S (Chempur 99.999%) at 1000 °C for several days. CsN₃ was obtained by passing hydrazoic acid (prepared by acidifying an aqueous solution of NaN₃) (Sigma-Aldrich 99.0%) into an aqueous solution of Cs₂CO₃ (Rockwood Lithium 99.9%). Attention: Condensed HN₃ is highly explosive. Tools made from transition metals must be avoided.

Synthesis of CsGaS₂

The title compound was obtained by slow thermal decomposition of CsN₃ combined with a stoichiometric mixture of Ga₂S₃ and sulphur in a silica ampoule under dynamic vacuum conditions. The ampoule was flame sealed after complete decomposition of the azide, and the raw product was annealed at elevated temperatures to yield CsGaS₂. Phase pure samples of white CsGaS₂-mC64 were obtained after annealing at 500 °C. Phase pure white CsGaS₂-mC16 was obtained by annealing at 700 °C. Quenching of the samples was not necessary. It should be noted that some samples of CsGaS₂-mC16 had pink colour, like also reported in literature.⁴ This colour remained even after treatment of the air- and moisture stable samples with water or DMF.

Single-crystal X-ray diffraction

Diffraction data of suitable single-crystals were collected on a Rigaku Supernova at ambient temperature using monochromatic Mo-Kα radiation (λ = 0.71073 Å). The obtained diffraction data were corrected for Lorentz- and polarization effects. Absorption was corrected by an analytical absorption correction using the CrysAlisPro software package.¹¹ The resulting data sets had a completeness of 99.9% within 50° 2θ for both modifications. The crystal structures were solved by charge flipping methods using SUPERFLIP⁶ (implemented in Jana2006⁷) and refined on F² with Jana2006⁷ using full-matrix least squares methods. The experimental parameters and details of the structure solution and refinement are summarized in Table 1.

X-ray powder diffraction

The X-ray powder diffraction experiments were performed on a STOE STADI P diffractometer equipped with a Dectris Mythen 1K detector and a high-temperature capillary furnace. Monochromatic Mo-Kα₁ radiation (λ = 0.70926 Å) was used for all experiments. The samples were flame sealed in a 0.3 mm quartz glass capillary and then placed in another 0.5 mm quartz glass capillary due to the furnace architecture. To ensure reproducible results all fine powdered samples were sieved under inert atmosphere using analytical sieves (Retsch GmbH) prior to the experiments (fraction 0.02–0.04 mm grain size). The WinX^POW software package from STOE & Cie¹³ was used for data collection and processing. The furnace temperature was controlled by a Eurotherm 24.16 controller (ΔT = ±1 °C).

Differential thermal analysis

Differential thermal analysis of the compound was performed on a SETARAM TG-DTA 92 16.18 in an evacuated quartz glass ampoule using Al₂O₃ as reference material. The measurements were performed in the range of 25–1000 °C with a heating- and cooling rate of 10 °C min⁻¹.

Vibrational spectroscopy

Raman spectra were recorded on a DXR™ SmartRaman Spectrometer from Thermoscientific (excitation wavelength λ = 532 nm) in the range of 50–1000 cm⁻¹ with a resolution of 0.5 cm⁻¹.

UV/Vis spectroscopy

Diffuse reflectance measurements were performed with a Bruins Omega 20 UV/Vis spectrometer using BaSO₄ as a reference (100% reflectance). Absorption spectra were calculated thereof by using a modified Kubelka–Munk function.^18,19

DFT calculations

The first-principles calculations were carried out within the framework of density functional theory (DFT) with exchange–correlation functionals in the generalized gradient approximation (GGA) according to Perdew–Burke–Enzerhof (PBE).²⁰ The full potential local orbital code FPLO14²¹ was applied for total energy and band structure calculations based on the experimentally obtained structures. FPLO14 applies all electron local basis sets that are described by core and valence functions as implemented in the code. It treats Cs (Z = 55) 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶4d¹⁰ as core and 5s²5p⁶6s¹5d⁰6p⁰6d⁰7s⁰ as valence states, Ga (Z = 31) 1s²2s²2p⁶ as core and 3s²3p⁶3d¹⁰4s²4p¹4d⁰5s⁰5p⁰ as valence, S (Z = 16) 1s² as core and 2s²2p⁶3s²3p⁴3d⁰4s⁰4p⁰ as valence states. Outer shells are automatically optimized for each SCF cycle by the code. A k-grid mesh of 12 × 12 × 12 was used. The calculations converged with a maximum divergence of <10⁻⁷ Hartree.

Conclusions

A new low-temperature polymorph of CsGaS₂ was characterized by single-crystal X-ray diffraction. The compound CsGaS₂-mC64 shows an irreversible phase-transition to CsGaS₂-mC16 at temperatures above 580 °C. Both modifications contain covalently bonded polymeric anions [GaS₂⁻] consisting of condensed GaS₄ tetrahedra. Kinetics of the reconstructive phase-transition were studied by in situ high-temperature X-ray diffraction experiments on powder samples. By means of these studies a dominating one-dimensional growth mechanism for the high-temperature modification is found. This is in good agreement with the results obtained for the parent compound CsGaSe₂.³ Interestingly, the irreversible temperature-induced phase-transition to the high-temperature polymorph can be reverted by a high-pressure treatment (>5 GPa at 500 °C). The band gaps of both modifications are around 3 eV, which is in good accord with the colourless samples.

Acknowledgements

The authors would like to thank Prof. Dr Manfred Scheer (University of Regensburg) for the Raman measurements. We would further like to thank Rockwood-Lithium GmbH for a generous gift of cesium carbonate.

Notes and references

1. B. Krebs, Angew. Chem., 1983, 95, 113–134.
2. (a) J.-J. Zony, F. Bielsa, A. Douillet, L. Hilico, O. Acef, V. Petrov, A. Yelisseyev, L. Isaenko and P. Krinitsin, Opt. Lett., 2007, 32, 1722–1724; (b) V. Pettrov, A. Yelisseyev, L. Isaenko, S. Lobanov, A. Titov and J.-J. Zondy, Appl. Phys. B: Lasers Opt., 2004, 78, 543–546.
3. D. Friedrich, M. Schlosser and A. Pfitzner, Cryst. Growth Des., 2016, 16, 3983–3992.
4. D. Schmitz and W. Bronger, Z. Naturforsch., B: Anorg. Chem. Org. Chem., 1975, 30, 491–493.
5. (a) M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112; (b) M. Avrami, J. Chem. Phys., 1940, 8, 212–224; (c) M. Avrami, J. Chem. Phys., 1941, 9, 177–184.
6. L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790.
7. V. Petricek, M. Dusek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352.
8. D. Müller, F. E. Poltmann and H. Hahn, Z. Naturforsch., B: Anorg. Chem. Org. Chem., 1974, 29, 117–118.
9. (a) D. Friedrich, F. Pielnhofer, M. Schlosser, R. Weihrich and A. Pfitzner, Chem. – Eur. J., 2015, 21, 1911–1817; (b) M. Suseela Devi and K. Vidyasagar, J. Chem. Soc., Dalton Trans., 2002, 4751–4754; (c) M. Schlosser, V. Frettlöh and H.-J. Deiseroth, Z. Anorg. Allg. Chem., 2009, 635, 94–98; (d) D. Friedrich, M. Schlosser and A. Pfitzner, Z. Anorg. Allg. Chem., 2014, 640, 826–829; (e) V. Winkler, M. Schlosser and A. Pfitzner, Z. Anorg. Allg. Chem., 2015, 641, 549–556; (f) E. J. Wu, M. A. Pell, T. M. Fuelberth and J. A. Ibers, Z. Kristallogr. – New Cryst. Struct., 1997, 212, 91.
10. J. W. Boon and C. H. MacGillary, Recl. Trav. Chim. Pays-Bas, 1942, 61, 910–920.
11. Rigaku Oxford Diffraction, CrysAlisPro, Version 1.171.38.37b, 2015.
12. K.-J. Range and R. Leeb, Z. Naturforsch., B: Anorg. Chem. Org. Chem., 1975, 30, 889–895.
13. Stoe & Cie GmbH, WinXPOW, Version 3, Darmstadt, 2014.
14. (a) L. Engelke, M. Schäfer, M. Schur and W. Bensch, Chem. Mater., 2001, 13, 1383–1390; (b) R. Kiebach, M. Schäfer, F. Porsch and W. Bensch, Z. Anorg. Allg. Chem., 2005, 631, 369–374; (c) Y. Zhou, E. Antonova, W. Bensch and G. R. Patzke, Nanoscale, 2010, 2, 2412–2417.
15. J. D. Hancock and J. H. Sharp, J. Am. Ceram. Soc., 1972, 55, 74–77.
16. J. H. Sharp, G. W. Brindley and N. N. Achar, J. Am. Ceram. Soc., 1966, 49, 379–382.
17. A. T. Kempen, F. Sommer and E. J. Mittemeijer, J. Mater. Sci., 2002, 37, 1321–1332.
18. P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 593–603.
19. H. Kisch, Angew. Chem., Int. Ed., 2013, 52, 812–847.
20. J. P. Perdew, K. Burke and M. Enzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
21. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter, 1999, 59, 1743–1757.

---

Footnotes

† Dedicated to Professor Mercouri G. Kanatzidis.

‡ Electronic supplementary information (ESI) available: Anisotropic displacement parameters and interatomic distances and angles of both polymorphs, DTA, and electronic band structures of both polymorphs. See DOI: 10.1039/c6qi00462h

---