Highly efficient rutile TiO₂ photocatalysts with single Cu(II) and Fe(III) surface catalytic sites

Abstract

Highly active photocatalysts were obtained by impregnation of nanocrystalline rutile TiO₂ powders with small amounts of Cu(II) and Fe(III) ions, resulting in the enhancement of initial rates of photocatalytic degradation of 4-chlorophenol in water by factors of 7 and 4, compared to pristine rutile, respectively. Detailed structural analysis by EPR and X-ray absorption spectroscopy (EXAFS) revealed that Cu(II) and Fe(III) are present as single species on the rutile surface. The mechanism of the photoactivity enhancement was elucidated by a combination of DFT calculations and detailed experimental mechanistic studies including photoluminescence measurements, photocatalytic experiments using scavengers, OH radical detection, and photopotential transient measurements. The results demonstrate that the single Cu(II) and Fe(III) ions act as effective cocatalytic sites, enhancing the charge separation, catalyzing “dark” redox reactions at the interface, thus improving the normally very low quantum yields of UV light-activated TiO₂ photocatalysts. The exact mechanism of the photoactivity enhancement differs depending on the nature of the cocatalyst. Cu(II)-decorated samples exhibit fast transfer of photogenerated electrons to Cu(II/I) sites, followed by enhanced catalysis of dioxygen reduction, resulting in improved charge separation and higher photocatalytic degradation rates. At Fe(III)-modified rutile the rate of dioxygen reduction is not improved and the photocatalytic enhancement is attributed to higher production of highly oxidizing hydroxyl radicals produced by alternative oxygen reduction pathways opened by the presence of catalytic Fe(III/II) sites. Importantly, it was demonstrated that excessive heat treatment (at 450 °C) of photocatalysts leads to loss of activity due to migration of Cu(II) and Fe(III) ions from TiO₂ surface to the bulk, accompanied by formation of oxygen vacancies. The demonstrated variety of mechanisms of photoactivity enhancement at single site catalyst-modified photocatalysts holds promise for developing further tailored photocatalysts for various applications.

---

Introduction

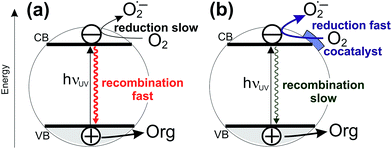
Sunlight-driven heterogeneous photocatalysis utilizing low-cost materials is potentially one of the most attractive methods for decontamination of water or air from toxic organic pollutants.^1–8 However, real-life commercially viable applications of photocatalytic depollution are still rather scarce, due to insufficient performance stability and typically very low photocatalytic reaction rates. In terms of performance stability, the typical material of choice is titanium dioxide due to its excellent stability against photocorrosion, non-toxicity, low cost, and possibility for further functionalization.^3,5,7,9,10 Efforts to improve the photoactivity of TiO₂ have mainly focused on shifting the light absorption edge of pristine TiO₂ (3.2 eV for anatase, 3.0 eV for rutile; ∼390–410 nm) into the visible range by doping TiO₂ with metals or main group elements.⁴ However, this approach has only rarely led to activity enhancements under solar irradiation, mainly because of diminished oxidizing power of photogenerated holes and due to enhanced recombination via intra-bandgap states introduced by doping.^4,11–17 In this context, it is important to realize that even under UV light irradiation the quantum yields of organic pollutant degradation reactions at pristine TiO₂ are very low, typically only a few per cent.¹⁸ This means that majority of charges photogenerated by UV light in TiO₂ are lost via recombination before they can induce redox reactions. Notably, it has long been suggested by Gerischer and Heller that the rate-limiting reaction in environmental photocatalysis is the reduction of oxygen by photogenerated electrons.^1,19 Indeed, this has been recently confirmed by kinetic studies using transient absorption spectroscopy which have shown that the reduction of dioxygen by photogenerated electrons is much slower (∼μs timescale) than, for example, the oxidation of alcohols by photogenerated holes (∼ns timescale).^20,21 This suggests that a very promising strategy for enhancing photodegradation rates at TiO₂ is to improve the kinetics of oxygen reduction at the photocatalyst surface by depositing a cocatalyst which would catalyze the transfer of photogenerated electrons to oxygen molecules. Faster channeling of photogenerated electrons from TiO₂ to oxygen molecules would diminish recombination and enhance charge separation (see Fig. 1).²²

Fig. 1 Simplified scheme showing the concept of enhancing the photocatalytic degradation rates by deposition of cocatalysts for oxygen reduction: without cocatalyst the oxygen reduction is slow and the recombination of photogenerated electrons is fast (a); deposition of a cocatalyst enhances the rate of oxygen reduction, rendering the charge separation more efficient and the recombination slower (b).

The feasibility of this approach is well documented in the literature. For example, it is known that deposition of small amounts of platinum cocatalyst nanoparticles onto TiO₂ leads to enhanced photocatalytic efficiencies for pollutant degradation.^1,23–27 Obviously, for large-scale applications cocatalysts based on abundant, non-noble materials are needed. Notably, Ohno et al. observed enhancement of photocatalytic degradation rates of gaseous acetaldehyde under both UV and visible light on rutile TiO₂ impregnated with Fe(III), Cu(II), Ni(II), and Cr(III) ions.²⁸ Based on double-beam photoacoustic spectroscopy measurements, the authors concluded that the transition metal ions improved the efficiency by acting as electron acceptors and as electron donors under UV and visible light, respectively. Later, Hashimoto et al. reported enhanced visible light activity in photocatalytic decomposition of isopropanol in the gas phase at rutile TiO₂ powders modified with small CuO_x and FeO_x clusters.^29–32 The enhanced photoactivity in the gas phase was ascribed to visible light-mediated direct optical charge transfer from the valence band of TiO₂ to energy levels in the co-catalyst clusters lying below the conduction band edge of TiO₂, whereby the lower reducing power of visible-light photogenerated electrons towards oxygen was compensated by the ability of the cocatalyst to catalyze two-electron transfer to oxygen that occurs at more positive potentials (E⁰ = −0.16 V vs. NHE and +0.69 V vs. NHE for one-electron and two-electron reduction of oxygen, respectively).^{29–31,33–35} Similarly, improved degradation rate of gaseous acetaldehyde under visible light irradiation was reported for N-doped TiO₂ loaded with copper ions by Morikawa et al. who suggested that the presence of Cu leads to prolonged lifetime of photogenerated charge carriers,³⁶ and for WO₃ photocatalysts impregnated with CuO by Sayama et al. who ascribed the activity enhancement to improved catalysis of oxygen reduction reaction.³⁷

In the present work, we focus on the deposition of redox cocatalysts for oxygen reduction onto TiO₂ in order to enhance the intrinsic UV light activity of TiO₂ in degradation of aqueous organic pollutants. We assume that already boosting the reaction rates under UV light irradiation alone due to improved catalysis of the rate-limiting oxygen reaction would yield photocatalysts for commercially viable applications in solar water decontamination. In a similar vein to the work of Ohno et al.²⁸ and Hashimoto et al.,^29–32 we have recently impregnated rutile TiO₂ powders with small amounts of copper(II) or iron(III) nitrate.³⁸ After a mild heat treatment, such surface-modified rutile photocatalysts exhibited highly enhanced activity, as compared to pristine rutile TiO₂, in photocatalytic degradation of 4-chlorophenol (4-CP) in aqueous phase under simulated solar light irradiation (λ > 320 nm). We tentatively suggested that small CuO_x and FeO_x clusters were formed on the TiO₂ surface after impregnation and drying, and that these small clusters allowed for improved catalysis of dioxygen reduction by photogenerated electrons, leading to enhanced photoactivity.³⁸ Herein we report our further detailed structural, spectroscopic, and theoretical investigations of these surface-modified rutile materials, and compare their photoactivity with rutile TiO₂ modified by conventional deposition of platinum nanoparticles. Most importantly, we provide conclusive experimental evidence for the presence of single Cu(II) and Fe(III) cocatalytic sites in our highly active photocatalysts, which differentiates them from conventional composites of TiO₂ with metal or metal oxide particles.^{29–32,36,37,39–43} The mechanistic aspects of the photoactivity enhancement at single ion-modified photocatalysts are discussed based on both theoretical DFT calculations and experimental (spectroscopic and photoelectrochemical) methods.

Results and discussion

Photocatalytic activity

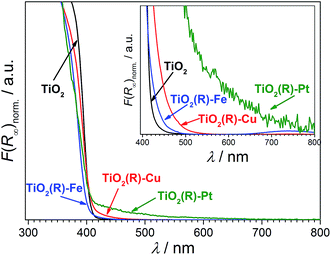
Highly active photocatalysts were prepared by simple impregnation of nanocrystalline rutile TiO₂ powders with very small amounts of copper(II) and iron(III) nitrate. The optimum amount (actual loading) of Cu and Fe leading to maximum photocatalytic degradation rates of a test organic pollutant (4-chlorophenol, 4-CP) was found to be very low: 0.12 wt% for Cu and 0.13 wt% for Fe.³⁸ For comparison, rutile TiO₂ decorated with Pt nanoparticles (optimum Pt loading of 0.34 wt%) was prepared by conventional photoreduction method^44–46 and served as a benchmark. After 3 hours of simulated solar irradiation (λ > 320 nm) the TiO₂(R)–Cu and TiO₂(R)–Fe induced 4-CP degradation of 80% and 54%, respectively (Fig. 2a), a significant enhancement as compared to the photoactivity of pristine rutile TiO₂ (25%). The benchmark platinized TiO₂(R)–Pt material showed degradation of 73%. The highest initial degradation rate of 2.8 × 10⁻⁸ mol L⁻¹ s⁻¹ was observed for TiO₂(R)–Cu (Fig. 2c), a value higher by a factor of 7 than the pristine rutile TiO₂, and is even higher than for TiO₂(R)–Pt (by a factor of 5.5 vs. pristine TiO₂). Furthermore, TiO₂(R)–Fe also demonstrates an enhancement in degradation rate (by a factor of 4 vs. pristine TiO₂), although this is less enhancement than for TiO₂(R)–Cu. After purging the suspension with argon, the initial degradation rates decreased drastically, confirming the crucial role of dissolved oxygen as an electron acceptor in photocatalytic degradation. Complete mineralization of 4-CP molecules to carbon dioxide, water and chloride ions was confirmed by monitoring the TOC (Total Organic Carbon) values during the photocatalytic reaction (Fig. 2b). Interestingly, the platinized TiO₂(R)–Pt sample seems to be more effective in inducing complete mineralization than TiO₂(R)–Cu, which can be ascribed to the well-known high activity of platinized TiO₂ in complete decarboxylation of carboxylic acids^44–46 which are important intermediates in the mineralization process of 4-CP. It should be noted that the photoactivity enhancement of modified samples is not the result of enhanced activity in the visible range. Though TiO₂(R)–Cu and TiO₂(R)–Fe show a very slightly yellowish tint to the naked eye, their fundamental optical absorption edge is the same as in case of pristine TiO₂ (Fig. 3). Accordingly, the photocatalytic degradation under visible light only (λ > 455 nm) was found to be negligible for all samples.³⁸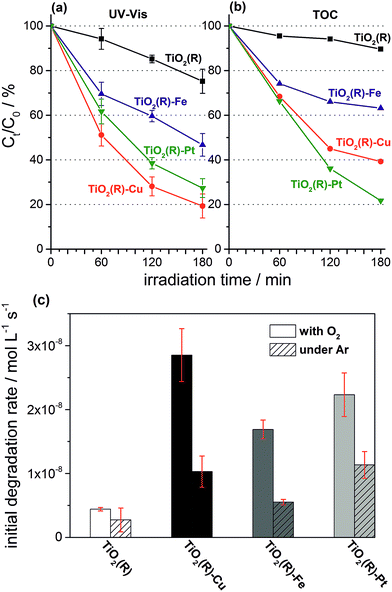

Fig. 2 Comparison of 4-CP degradation monitored by UV-Vis spectroscopy (a) (for UV-Vis absorption spectra see ESI, Fig. S5†), complete mineralization followed by changes of TOC (b), and initial degradation rates (c) during photocatalytic degradation experiments using suspensions of TiO₂(R), TiO₂(R)–Cu, TiO₂(R)–Fe and TiO₂(R)–Pt under ambient and oxygen-free conditions.

Fig. 3 Normalized diffuse reflectance spectra (Kubelka–Munk function vs. wavelength) of TiO₂(R), TiO₂(R)–Cu, TiO₂(R)–Fe, and TiO₂(R)–Pt the inset shows a zoom of the visible light region. The very weak preabsorption bands are probably due to O²⁻ → Cu²⁺ and O²⁻ → Fe³⁺ charge–transfer transitions at TiO₂(R)–Cu, TiO₂(R)–Fe and due to Pt nanoparticle absorption in case of TiO₂(R)–Pt. TiO₂(R)–Fe exhibits also a weak and broad shoulder at 730 nm which corresponds to d–d transitions in Fe(III).

Two things are noteworthy. Firstly, simple physical mixtures of rutile TiO₂ with CuO or Fe₂O₃ (in amounts corresponding to the optimum loading) prepared by grinding do not induce any photoactivity enhancement (see ESI, Fig. S6†). Secondly, while highly active TiO₂(R)–Cu and TiO₂(R)–Fe samples are obtained after a mild drying at 120–150 °C, after calcination at high temperatures (450 °C) the photoactivity is diminished drastically, though the Cu and Fe content is practically the same as in active samples. These results suggest that the chemical nature of Cu and Fe species at the surface of rutile TiO₂ is of crucial significance for high photoactivity.

Structural characterization

Due to the low concentration of Cu and Fe species, both Raman spectra and X-ray diffractograms have shown only the typical pattern of rutile TiO₂ (ESI, Fig. S7 and S8†). The primary crystallite sizes calculated using Scherrer's formula are 12–13 nm for all samples. High temperature treatment results in increase of rutile crystallite size to 20 nm and 15 nm for TiO₂(R)–Cu (450 °C) and TiO₂(R)–Fe (450 °C), respectively, which alone cannot explain the decrease of activity after calcination. We assumed that this is rather related to changes of the chemical nature of Cu and Fe species at the rutile surface.

In this context, it is intriguing to realize that the optimum loading (0.12 wt% Cu and 0.13 wt% Fe) in TiO₂(R)–Cu and TiO₂(R)–Fe is very low, indeed. Given the BET specific surface area of rutile TiO₂ (111 m² g⁻¹), such loading corresponds to the surface density of 0.10 Cu atoms per nm² and 0.13 Fe atoms per nm². This very low surface coverage let us to hypothesize that it could be single Cu(II) or Fe(III) sites which are present at the surface of rutile TiO₂ and are responsible for the enhanced photoactivity of the novel materials. This suspicion was further deepened by the fact that electron energy loss spectroscopy (EELS), which in the setup we used has sensitivity at the single atom level, could only show a very weak signal for Cu, while no signal for Fe could be detected (ESI, Fig. S9†).

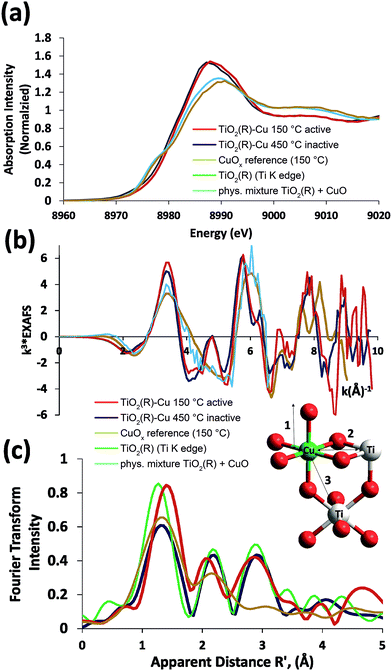
In order to gain further insight into the local chemical environment of Fe and Cu species and their oxidation states, we performed an X-ray absorption study. Fig. 4 presents the Cu K-edge XAS data (for the Fe data see ESI, Fig. S2†). The beamline did not have sufficient energy resolution to resolve pre-edge data, but the lack of intensity indicates that there is not too much deviation from centrosymmetry.^47,48 The major peaks in the Fourier transform are labelled “1” to represent the 6 Cu–O distances @ 1.9–2.1 Å, “2” to represent the Cu–Ti distances @ 2.8–3.00 Å and “3” to represent the Cu–Ti distances at 3.4–3.6 Å. As the data was only suitable for interpretation to k = 10 Å⁻¹ no attempt was made to split the coordination spheres further. A fit of the EXAFS data is given in the ESI (Fig. S1†). The peaks in the Fourier transform of TiO₂(R)–Cu both before and after heating at 450 °C are consistent overall with Cu(II) sitting “on” or “in” the rutile structure. There are, however, minor differences in the structure of the materials before and after heating. Before heating there is a slight splitting of the coordination sphere, consistent with what one expects if the Cu(II) was decorating the surface of TiO₂ in a well distributed form. After heating the material becomes more integrated into the TiO₂ lattice, consistent with the slight shifts of R values of the Fourier transform peaks. Similar effects, though less pronounced, are noted at the Fe edge (ESI, Fig. S3†). Notably, the XAS data of bulk CuO_x and a physical mixture of TiO₂(R) with CuO show only two distinct peaks in the Fourier transform, and are thus clearly different from TiO₂(R)–Cu. The XANES data of Cu are consistent with copper in oxidation state (II), the XANES data of Fe are consistent with Fe(III) with a high spin configuration.

Fig. 4 XAS spectra of photocatalytically active TiO₂(R)–Cu (dried at 150 °C) and inactive TiO₂(R)–Cu (calcined at 450 °C) are compared to the reference data of CuO_x (prepared by heating), rutile TiO₂(R) (Ti K edge), and a physical mixture of TiO₂(R) and CuO. Data are presented as XANES (a), EXAFS (b) and Fourier transform of the EXAFS (c). The inset shows a structural model used for fitting.

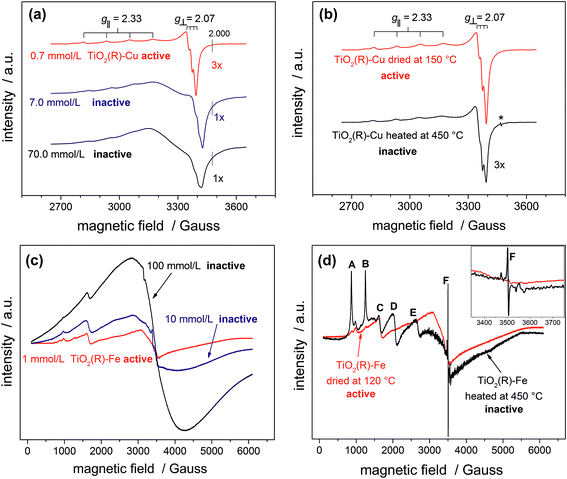
In order to provide conclusive evidence for the presence of single surface Cu(II) and Fe(III) sites in our photocatalysts, an EPR study was performed. EPR is a highly sensitive spectroscopic technique which can give valuable information about the nature of d⁹ Cu(II) and d⁵ Fe(III) paramagnetic species in our materials. The most active TiO₂(R)–Cu sample exhibits an anisotropic signal with hyperfine structure due to I = 3/2 of Cu(II) typical for isolated mononuclear slightly axially distorted octahedral Cu(II) complexes,⁴⁹ with resonance parameters A_‖ = 11.9 mT, g_‖ = 2.33 and g_⊥ = 2.07 (Fig. 5a). This feature is a fingerprint of surface-bound single Cu(II) ions at rutile⁵⁰ or anatase TiO₂,⁴⁹ or Cu(II) substituting lattice Ti(IV),^51,52 both assumed to be spectroscopically equivalent. The increase of Cu(II) concentration during impregnation yields photocatalytically inactive powders containing small CuO_x clusters and nanoparticles. This is apparent from broadening of spectral lines due to long-range dipolar interactions between Cu(II) ions which results in gradual disappearance of the anisotropic hyperfine structure (Fig. 5a). Following this trend, bulk CuO reference and the physical mixture of TiO₂ and CuO show only a very broad EPR signal (ESI, Fig. S10†). The above results provide clear evidence for the presence of single isolated Cu(II) surface sites in highly active TiO₂(R)–Cu.

Fig. 5 EPR spectra of photocatalytically active and inactive TiO₂(R)–Cu (a) and TiO₂(R)–Fe (c) powders prepared using different concentrations of metal ion precursors; change of EPR spectra of TiO₂(R)–Cu (b) and TiO₂(R)–Fe (d) upon heat treatment at 450 °C.

After calcination of TiO₂(R)–Cu at 450 °C the EPR resonance parameters stay the same, but the hyperfine structure is slightly less resolved (Fig. 5b). Importantly, an additional sharp signal with g = 2.005 (denoted by an asterisk in Fig. 5b) appears, which is associated with formation of oxygen vacancies upon migration of Cu(II) ions from the surface to the sub-surface layer where it substitutes Ti(IV).⁵¹ The same feature is observed upon heat treatment of copper complexes in the matrix of silicate glasses or on the surfaces of SnO₂.^53,54 Further evidence for migration of Cu(II) from surface to the bulk after heat treatment at 450 °C comes from a simple experiment using an aqueous ammonia solution. Before the heat treatment the Cu(II) ions in TiO₂(R)–Cu are easily accessible for reaction with ammonia to form a typical blue tetraamminecopper(II) complex, while after the heat treatment at 450 °C the sample does not show blue coloration upon addition of ammonia. In this context it is important to recall that the high-temperature treated sample is not photoactive. Based on our results, we conclude that this loss of activity is both because of migration of catalytically active surface Cu(II) ions to the subsurface layer and concomitant formation of oxygen vacancies, which both give rise to recombination centers.

A similar broadening of EPR spectra upon increasing the amount of Fe(III) is observed for TiO₂(R)–Fe (Fig. 5c). Transition at g = 4.31 (C) can be ascribed to the Fe(III) ions in orthorhombic sites at the surface of rutile TiO₂.⁵⁵ After calcination at 450 °C, the peaks A, B, D and E increased dramatically, suggesting that the Fe(III) ions migrated into the bulk. Indeed, the new EPR resonance transitions at g = 8.02 (A), 5.54 (B), 3.47 (D) and 2.26 (E) have been unambiguously assigned to Fe(III) ions located in substitutional tetragonal sites of distorted axial symmetry where the Fe(III) have substituted Ti(IV) in the TiO₂ bulk lattice.^55,56 And, similar to the case of TiO₂(R)–Cu, the most prominent new EPR signal arising after the heat treatment at 450 °C (g ≈ 2.006, F) is related to substitutional Fe(III) ions accompanied by oxygen vacancies,⁵⁷ which render the sample photocatalytically inactive.

Theoretical calculations

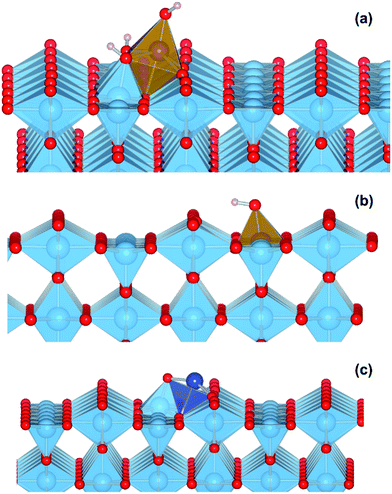
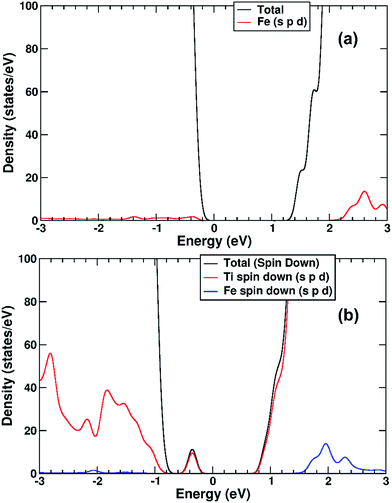
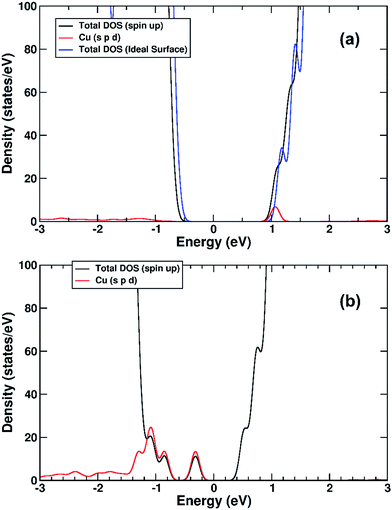
We performed a set of DFT calculations to understand the influence of single Cu(II) and Fe(III) ions on the electronic structure of the rutile TiO₂ surface in order to estimate the effects on photogenerated charge separation. The (110) surface of rutile was used in calculations as it is the most commonly observed surface facet.⁵⁸ First of all, we present the results for the effects of Fe-decoration. As for our previous work on Fe₂O₃ decoration of anatase TiO₂,³⁹ we investigated several different low energy adsorption sites on ideal rutile TiO₂, the lowest of which is shown in Fig. 6a. The Fe(OH)₃ cluster binds to the twofold oxygen row of the rutile surface in such a way that the Fe(III) cation becomes octahedral. This is a very stable structure, with an exothermic binding energy of 3.64 eV. The Fe(OH)₃ cluster binds to two twofold oxygen atoms of the protruding row, and a surface threefold oxygen atom, resulting in a notable tilt. Furthermore, the Fe atom is not centrally located in the resultant FeO₆ octahedra, with one short Fe–O bond of 1.82 Å pointing away from the surface, one long Fe–O bond of 2.46 Å pointing into the surface, and four equatorial Fe–O bonds of 2.03 to 2.11 Å.

Fig. 6 (a) Final atomic structure of model TiO₂(R)–Fe system, red spheres are oxygen atoms, blue spheres are titanium atoms, and brown spheres are iron atoms. (b) Final atomic structure of model TiO₂(R)–Fe(V_Ti) system. (c) Final atomic structure of model TiO₂(R)–Cu system, dark blue spheres are copper atoms. Prominent in all structures are the protruding twofold coordinating oxygen atoms of the ideal rutile surface.

The electronic structure of TiO₂(R)–Fe is shown in Fig. 7a. We focus on the spin-down DOS, as this is where the totality of the Fe contribution to the DOS resides. As can be seen, the Fe atom, and indeed the cluster as a whole does not strongly modify the electronic structure at the band edges, implying that the primary charge separation properties of rutile are not affected. The bandgap of this composite system is at 1.80 eV the same as the ideal surface, this value is slightly smaller than our calculated bulk theoretical bandgap of 2.00 eV. The band edge character is the same as the ideal rutile surface. To further investigate the effects of Fe(III) decoration on charge separation we determined the atomic and electronic structure of the charged system. We relaxed the charged system to observe whether the electron localizes onto a specific site, resulting in the formation of an electron polaron. This will occur in an absorber-cocatalyst system when the conduction band (or LUMO) of the cocatalyst is lower than that of the light absorber.⁴³ Based on our analysis of the DOS of TiO₂(R)–Fe we do not expect the extra electron to reside upon the Fe atom. There is a relaxation energy of 0.47 eV associated with the electron polaron, however upon inspection there is no strong structural rearrangement. Furthermore, from analysis of the DOS (see Fig. 7b), a state that does split off from the conduction band edge is not related to the Fe atom. Rather, this polaron state is associated with the Ti atoms that predominate at the conduction band edge (CBE). From analysis of the charge density difference, we observe that the excess electron localizes on a single Ti site in the middle of the slab, away from the surface. Specifically, this is an octahedral sixfold coordinated Ti directly below a surface fivefold coordinated Ti site, and exactly the same polaron localization as is observed for the ideal rutile TiO₂-(110) surface.⁵⁹ This suggests that single Fe(III) decoration, as depicted in Fig. 6a, does not improve the thermodynamics of charge separation in ideal rutile TiO₂.

Fig. 7 (a) Spin-down DOS of TiO₂(R)–Fe. (b) Spin-down DOS of electron polaron structure of TiO₂(R)–Fe. The red line represents projection of Fe states, blue line projection of Ti states. For both figures, the zero of the x-axis is fitted to the top of the VBM.

In order to account for possible different modes of Fe(III) incorporation into the rutile surface, we further considered the effects of Fe cation addition to defective surfaces of rutile TiO₂-(110), specifically those where a single titanium surface vacancy is present. This defect was chosen as this provides a natural site for Fe(III) cations to reside, in comparison to other native point defects such as oxygen vacancies and titanium interstitials. Furthermore, under oxygen-rich conditions titanium vacancies (V_Ti) have a relatively low defect formation energy of 2.32 eV.⁶⁰ We denote this system TiO₂(R)–Fe(V_Ti). We modelled the adsorption of a FeOH unit on the vacancy; the single OH functional group is required to obtain Fe(III). The structure of the final relaxed geometry is shown in Fig. 6b. As can be seen, the titanium vacancy can easily accommodate the Fe atom, with the hydroxyl functional group pointing out of the surface. The Fe atom is displaced out of the centre of the vacancy, with Fe–O bond lengths of 1.94, 1.96, 2.05, and 2.10 Å with the rutile lattice oxygen atoms. There is bond length extension compared to the rutile Ti–O bonds lengths of 1.96 to 1.97 Å.

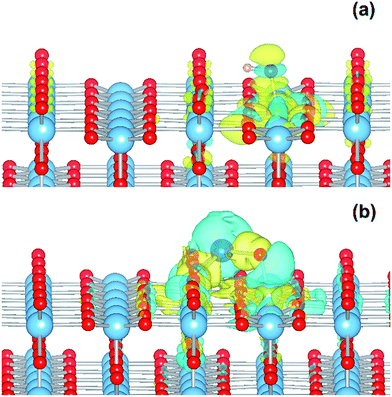
The electronic structure is shown as a DOS plot in Fig. 8. From inspection, it can be clearly seen that there is a significant iron presence in the spin-down channel near the CBE. More interesting, however, is that there is an acceptor state in the gap located above the Fermi level, specifically 0.26 eV above the VBE and 1.54 eV below the CBE. Upon photoexcitation this implies that there would be a thermodynamic driving force for the photoelectron to transfer from the rutile crystal to the Fe(III) cation, improving charge separation. In order to investigate whether this is the case, we determined the geometry and thus the electronic structure of the electron polaron (Fig. 8b). The main difference in the DOS with respect to the uncharged system is that the unoccupied state above the Fermi level is now shifted below the Fermi level, becoming occupied. The relaxation energy involved with this polaron formation is relatively tiny, at 0.022 eV, implying that at room temperature it will be easy for the electron to delocalize into the rutile lattice. Furthermore, although the charge density difference of the electron polaron shows that there is a concentration of electron density on the Fe(OH) site (see Fig. 9a), with closer examination we observe that there is a significant minority of charge on the oxygen twofold coordinated rows, providing further evidence that the electron polaron is not strongly localized on the Fe(OH) site.

Fig. 8 (a) DOS of TiO₂(R)–Fe(V_Ti). (b) DOS of the electronic polaron structure of TiO₂(R)–Fe(V_Ti). The red line represents projection of Fe states in spin up channel, green line projection of Fe states in spin down channel. The zero of the x-axis is set to the top of the VBM.

Fig. 9 (a) Charge density difference for the TiO₂(R)–Fe(V_Ti) system upon electron injection and polaron relaxation. (b) Charge density difference for the TiO₂(R)–Cu system upon electron injection and polaron relaxation. Blue represents charge density accumulation, yellow charge density depletion.

In contrast to the TiO₂(R)–Fe system, the charge separation properties of TiO₂(R)–Cu are much simpler to analyze. We present results for a single CuO cluster adsorbed on the rutile TiO₂–(110) surface, with the geometry shown in Fig. 6c. There is a strong binding between the CuO cluster and the rutile TiO₂-(110) surface, with an exothermic binding energy of 2.82 eV. The Cu(II) cation is fourfold coordinated, with Cu–O bonds of length 1.89 Å, 1.93 Å, 1.98 Å, and 2.39 Å. We were unable to stabilize octahedral species on the surface. We ascribe the missing atoms that enable octahedral coordination to the solvent, which is missing in our calculations where the surface is exposed to vacuum. Furthermore, the oxygen atom of the cluster forms a short bond of 1.79 Å with a fivefold coordinated titanium atom of the surface, closing a TiO₆ octahedra.

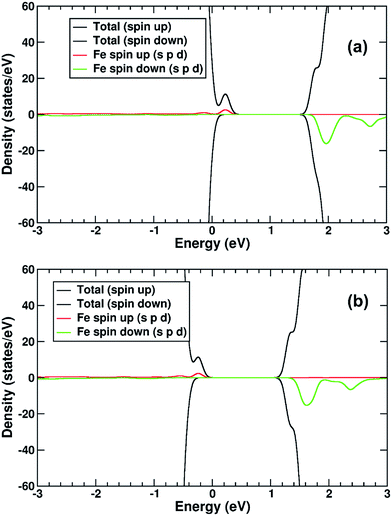
The electronic structure of TiO₂(R)–Cu is shown in Fig. 10a. The Cu atom has a significant presence on the CBE. This is primarily due to the Cu d-states. Further, we compare the position of the decorated rutile TiO₂ surface to the bare rutile surface, by comparison and alignment of the electrostatic potential in the vacuum region.⁶¹ When the alignment is taken into account, the Cu-state is marginally (∼0.1 eV) below the CBE of the ideal rutile surface. This would imply that any photoelectrons would transfer to the Cu(II), rather than stay in the rutile itself, although the thermodynamic driving force is quite weak.

Fig. 10 (a) DOS of the TiO₂(R)–Cu system, spin-up channel only, aligned to the DOS of the ideal TiO₂(R) surface. (b) The spin up channel DOS of the final relaxed electron polaron system for the TiO₂(R)–Cu system. Cu contribution shown. The zero of the x-axis is fitted to the VBM for both plots.

As for the Fe(III)-decorated systems discussed above, we also determine the effects of the Cu(II) decorant on the photoelectron charge separation properties by investigating the thermodynamics for electron polaron formation. The addition of a single electron results in a substantial amount of reconstruction, with a reconstruction energy of 0.48 eV, very similar to the polaron in ideal rutile. As can be readily observed from inspection of the DOS, see Fig. 10b, the Cu-derived state is strongly stabilized by injection of the additional electron, with the state dropping by 1.0 eV and becoming occupied. This is related to the closure of the electronic state that is half-filled by the spare d-electron of the Cu atom. Furthermore, from calculation of the charge density difference we can directly determine where the excess electron, e.g. the photoelectron, resides. This photoelectron is strongly localized on the Cu atom, see Fig. 9b. In other words, Cu(II) decorants do aid charge separation by providing a thermodynamic trap, with a strong localization energy, for photoelectrons.

To summarize, we have shown that both Fe(III) and Cu(II) might improve the primary (thermodynamic) charge separation properties of rutile TiO₂. However, the mechanism for charge separation is different for the two cations. For TiO₂(R)–Fe, separation of the photoelectron from the rutile crystal does not occur for decoration by Fe(III), but for surface implantation. This therefore requires the presence of titanium vacancies, which are going to be a minority presence in any rutile sample. Additionally, the relaxation energy for electron polaron formation is very low at ∼0.02 eV, which may be overcome due to thermal fluctuations. In contrast, for TiO₂(R)–Cu, separation of the photoelectron from the rutile crystal does occur for decoration by Cu(II). These decorated systems also strongly localize the photoelectron at the surface site with a high relaxation energy, potentially improving the kinetics of subsequent oxygen reduction reaction. From our calculations there are clearly different charge separation mechanisms for the two metal cations.

Mechanistic investigations

Notably, the DFT calculations corroborate the experimental results showing that the optical absorption of TiO₂(R)–Cu and TiO₂(R)–Fe is practically the same as for pristine TiO₂, ∼3.0 eV (see Fig. 3). This is important since the redox cocatalysts at the surface of composite photocatalysts (see Fig. 1b) should not parasitically absorb light and diminish thus the light harvesting by the TiO₂ light absorber. Clearly, single metal ion sites are sufficient to positively influence the charge separation, whereby blocking of the light by cocatalyst is avoided since an extended lattice structure such as in metal oxide particles, does not develop. The positive effect of decoration of TiO₂ with single Cu(II) and Fe(III) sites on electron–hole separation is evidenced also by photoluminescence (PL) measurements (see ESI; Fig. S11†). The PL intensity of both TiO₂(R)–Cu and TiO₂(R)–Fe is significantly quenched as compared to pristine rutile TiO₂, suggesting diminished radiative recombination both in the band-to-band mode (2.7–3.0 eV) and in the range typically attributed to surface state-mediated recombination (2.1–2.7 eV).⁶²

Though both Cu(II) and Fe(III) improve the photocatalytic performance (Fig. 2), the DFT results indicate that the reason for the improvement might be different for TiO₂(R)–Cu and TiO₂(R)–Fe. In order to shed light on the detailed mechanism of the photocatalytic degradation of 4-CP the reaction was conducted under different conditions. The 4-CP degradation is completely suppressed for all materials in the presence of EDTA acting as a strongly adsorbing hole scavenger (Fig. 11a). This underlines the substantial role of the oxidative pathway (holes and/or hydroxyl radicals) in the degradation reaction. In argon-purged suspension (see Fig. 2c) the photoactivity of all materials decreases. This finding confirms the essential role of oxygen as a primary electron acceptor. Residual photoactivity under argon can arise from the hole oxidation while electrons reduce residual traces of oxygen, lattice Ti(IV) ions in a rutile lattice, or Cu(II) and Fe(III) in TiO₂(R)–Cu and TiO₂(R)–Fe.

Fig. 11 Comparison of 4-CP degradation yields during photocatalytic degradation experiments using suspensions of TiO₂(R), TiO₂(R)–Cu and TiO₂(R)–Fe under different conditions: in the presence or absence of oxygen and in the presence of scavengers: (a) EDTA (holes), (b) tetranitromethane (electrons), (c) and tert-butanol (OH radicals). Note that the experiments in (b) have been performed in a reactor setup different from (a) and (c).

Degradation curves in the presence of oxygen or an alternative electron acceptor, namely tetranitromethane under argon, are shown in Fig. 11b. Pristine TiO₂(R) degrades 4-CP much more efficiently in the presence of tetranitromethane as an electron scavenger than with oxygen. This means that, at pristine rutile, tetranitromethane scavenges the photogenerated electrons much faster as compared to dissolved oxygen, enabling the holes to oxidize efficiently the 4-CP molecules. This is in line with the reported reduction potential of tetranitromethane (+0.4 V vs. NHE)⁶³ which is more positive than in case of O₂ (−0.16 V vs. NHE).³⁵ In contrast, the degradation rates for TiO₂(R)–Cu are practically the same in the presence of tetranitromethane and oxygen. This finding is very significant. It confirms that the nature of reacting electrons in TiO₂(R)–Cu is different from TiO₂(R). The photogenerated electrons are apparently very efficiently trapped by Cu(II) sites, whereby the reactivity of Cu(II/I)-trapped electrons towards oxygen is enhanced, compensating kinetically the lower thermodynamic driving force for the reduction of oxygen as compared to the reduction of tetranitromethane. Moreover, the electron trapping at Cu(II) sites is clearly very fast, at least much faster than the reduction of tetranitromethane or oxygen by photoelectrons trapped by surface Ti(IV). Exactly as suggested by the DFT calculations, the charge separation in TiO₂(R)–Cu will be dominated by the transfer of photogenerated electrons to surface Cu(II) ions. Rather different results were obtained for TiO₂(R)–Fe which behaves quite similar to pristine TiO₂(R), though the enhancement after addition of tetranitromethane is not so pronounced. This suggests that either a significant portion of reactive electrons in TiO₂(R)–Fe might have a similar chemical nature (i.e., electrons trapped at Ti(IV/III) sites) to those in pristine TiO₂(R), or the reactivity of electrons trapped at Fe(III/II) surface sites towards tetranitromethane is much higher than for Cu(II/I)-trapped electrons. In line with our DFT calculations, the primary charge separation due to electron transfer to Fe(III) in TiO₂(R)–Fe is less effective than in case of TiO₂(R)–Cu. The degradation rates for TiO₂(R)–Fe in the presence of oxygen are lower than for TiO₂(R)–Cu, yet still higher than for pristine rutile TiO₂. However, the mechanism of the enhancement at TiO₂(R)–Fe seems to be different than in case of TiO₂(R)–Cu.

In this context it is important to realize that dissolved oxygen not only serves as an electron acceptor, but can also become a source of various reactive species, like superoxide anion, hydrogen peroxide or hydroxyl radical, which can take an active part in the degradation process. After addition of tert-butanol, which is typically taken as a preferential scavenger of hydroxyl radicals, the photoactivity of TiO₂(R)–Fe hardly changed and that of TiO₂(R)–Cu dropped only slightly (Fig. 11c). It should be noted that tert-butanol does not adsorb strongly onto TiO₂ and therefore efficiently scavenges free hydroxyl radicals (˙OH_f) but not surface-bound hydroxyl radicals (˙OH_s).⁶⁴ Moreover, it has been reported that, in contrast to anatase where ˙OH_f forms efficiently, at rutile TiO₂ mainly ˙OH_s is produced.⁶⁴ Our results therefore indicate that free ˙OH_f radicals do not play any significant role in the enhancement of photocatalytic degradation rates of 4-CP molecules. However, the possibility that, apart from holes, also surface-bound ˙OH_s radicals play some role cannot be completely ruled out. As a next step, we investigated the formation of hydroxyl radicals quantitatively. Fig. S12 (ESI†) shows fluorescence spectra of hydroxyterephthalic acid formed upon irradiation of the material suspensions in a terephthalic acid solution under the ambient conditions. The production of hydroxyl radicals for each sample is proportional to the formation of hydroxyterephthalic acid, and is linear with time (see ESI; Fig. S13†).⁶⁵ No correlation between hydroxyl radical production and photoactivity was found. The most active material, TiO₂(R)–Cu, exhibits the lowest hydroxyl radical production, even lower than pristine TiO₂(R) by a factor of 2. This points to a minor role of the hydroxyl radicals in the photooxidation mechanism at TiO₂(R)–Cu. In contrast, TiO₂(R)–Fe shows the highest rate of hydroxyl radical formation, which is higher by a factor of 2 than in the case of pristine rutile. Since the chemical nature of holes in all samples should be the same, we assume that this enhanced formation of hydroxyl radicals at TiO₂(R)–Fe has its origin in the reductive pathway (initiated by reduction of oxygen). H₂O₂ can be formed by a two-electron reduction of dioxygen catalyzed by Fe(III) sites. The H₂O₂ molecules formed can be converted to hydroxyl radicals by further reduction by photogenerated electrons. Furthermore, Fenton-type reactions might be at play, which would involve reaction of Fe(II) and/or Fe(III) with H₂O₂ under formation of highly oxidizing hydroxyl radicals (˙OH) or hydroperoxyl radicals (HOO˙), respectively. At any rate, apart from the quenching of PL mentioned above, the enhanced formation of (surface-bound) hydroxyl radicals is at present the only prominent feature of TiO₂(R)–Fe which helps us to understand its enhanced photoactivity as compared to pristine rutile.

As it is known that the solubility of first-row transition metal cations increases upon reduction, we investigated also the operational stability of our materials during four successive photocatalytic degradation experiments (ESI, Fig. S14†). The activity of all modified samples, including TiO₂(R)–Pt, decreased by ∼50% during four cycles, however still remaining higher than in case of pristine TiO₂(R). As platinum clusters are not expected to undergo reductive photocorrosion, we attribute the decrease in activity of all samples to accumulation of decomposition intermediates at the surface of photocatalysts or to partial loss of photocatalyst during filtration after each cycle. These problems can be overcome by optimization of operational parameters and reactor design.

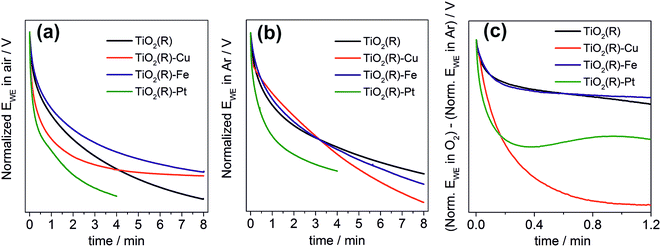
Finally, we performed a set of photopotential decay measurements which are a powerful tool for directly probing the dynamics of photogenerated electrons, including the kinetics of their reaction with dioxygen.^66,67 During prolonged illumination under open-circuit conditions, the photoelectrons accumulate in the TiO₂ and shift the quasi-Fermi level of the electrode to negative potentials, until a steady state is achieved. After switching off the light, the open-circuit potential starts to decay. Under our experimental conditions, the rate of the decay depends on the concentration of accumulated charges and on the rate constants for two processes: the electron–hole recombination, and the reaction of electrons with dioxygen dissolved in the solution. In the presence of oxygen both processes are at work (Fig. 12a), whereas in the absence of oxygen the recombination process is predominant and is chiefly responsible for the potential decay (Fig. 12b). A decay curve obtained by subtracting these two curves can serve as an indicator for the kinetics of dioxygen reduction (Fig. 12c). Our measurements clearly confirm the importance of fast dioxygen reduction for achieving high photocatalytic degradation rates. In the presence of oxygen the fastest potential decays are observed for the most photoactive materials, TiO₂(R)–Cu and TiO₂(R)–Pt. The fast decay is clearly due to enhanced rate of dioxygen reduction at TiO₂(R)–Cu and TiO₂(R)–Pt, as exemplified in Fig. 12c. In other words, Cu(II) sites act as efficient catalyst for O₂ reduction in a similar way as Pt particles. For TiO₂(R)–Fe the situation is very different, the decay curves are similar to TiO₂(R). This again confirms that the mechanism of the photocatalytic rate enhancement at TiO₂(R)–Fe is distinct from TiO₂(R)–Cu. Since the kinetics of primary O₂ reduction at TiO₂(R)–Fe is apparently not improved as compared to TiO₂(R), the enhancement is most probably due to new catalytic pathways to H₂O₂ and hydroxyl radicals, opened by the presence of Fe(III) catalytic sites, as we discussed above.

Fig. 12 Photopotential decay transients under open-circuit conditions for TiO₂(R), TiO₂(R)–Cu, TiO₂(R)–Fe and TiO₂(R)–Pt after switching off the light: (a) under O₂; (b) under argon; (c) subtracted curves. Photoelectrodes (photocatalyst powders on FTO substrates) are in contact with a 0.1 M phosphate buffer (pH 7) purged with oxygen or argon. Electrode area is 0.5 cm²; irradiation wavelength 350 nm. For the sake of clarity, negative potentials are shown as positive. Note that potentials are normalized with respect to the steady-state open-circuit photopotential in each case in order to account for different concentrations of accumulated photogenerated electrons at the beginning of the decay.

Conclusions

Our experimental results combined with theoretical calculations demonstrate that single ion catalytic sites at the surface of TiO₂ photocatalysts are sufficient to considerably enhance the rate of photocatalytic decomposition of organic pollutants in water. The exact mechanism of the photoactivity enhancement can differ depending on the nature of the cocatalyst. For example, Cu(II)-decorated rutile photocatalysts exhibit fast transfer of photogenerated electrons to Cu(II/I) sites, followed by enhanced catalysis of dioxygen reduction, resulting in improved charge separation and higher photocatalytic degradation rates. On the other hand, at Fe(III)-modified rutile the rate of dioxygen reduction is not improved, and the photocatalytic enhancement is attributed to higher production of highly oxidizing hydroxyl radicals produced by alternative oxygen reduction pathways opened by the presence of catalytic Fe(III/II) sites. Importantly, we have shown that excessive heating (at 450 °C) of initially highly active photocatalysts leads to their deactivation due to migration of catalytically active Cu(II) and Fe(III) ions from TiO₂ surface to the bulk, which is accompanied by formation of oxygen vacancies. In terms of light harvesting, single-site-modified photocatalysts capitalize on the intrinsic UV light absorption by TiO₂, whereby the isolated nature of surface cocatalytic sites guarantees negligible losses due to parasitic light absorption by the cocatalyst. The improved photocatalytic performance is chiefly due to the electronic and redox properties of single ion sites, enhancing the charge separation, catalyzing “dark” redox reactions at the interface, and thus improving the typically very low quantum yields which represent the major bottleneck in environmental photocatalysis. These features make this type of materials distinct from more conventional visible light-active modified TiO₂ (ref. 29, 30 and 36) or TiO₂ composites with heterojunction structure,^39–43 and also from “single site photocatalysts” based on light-absorbing metal ion species dispersed on the surface of zeolites or silica.^68–70 As the photocatalytic activity of most photocatalysts is known to be highly substrate-specific^6,71 and depending also on a complex interplay of many material properties (crystallinity, porosity, surface area, relative amounts of specific crystal facets, etc.),⁶ the demonstrated variety of mechanisms of photoactivity enhancement at single site catalyst-modified photocatalysts holds promise for developing many novel, tailored photocatalysts for various applications. Such efforts may also go beyond using TiO₂ as light absorber and include photocatalytic transformations other than aerobic degradation of organic pollutants.

Acknowledgements

Financial support by the EU-FP7 Grant “4G-PHOTOCAT” (Grant No. 309636) and by the MIWFT-NRW within the project “Anorganische Nanomaterialien für Anwendungen in der Photokatalyse: Wasseraufbereitung und Wasserstoffgewinnung“ is gratefully acknowledged. We thank the Sachtleben company for providing rutile TiO₂ material. The support of the Center for Electrochemical Sciences (CES) is gratefully acknowledged. The authors also acknowledge the use of the UCL Legion High Performance Computing Facility (Legion@UCL), the IRIDIS High Performance Computing Facility and associated support services, and the ARCHER National Computing Service as facilitated by a Research Allocation Proposal (project e352), in the completion of this work. S. T. gratefully acknowledges the FWO Flanders for a post-doctoral scholarship under contract number G004413N. M. P. is indebted to the Foundation for Polish Science within the TEAM/2012-9/4 programme.

References

1. H. Gerischer and A. Heller, J. Phys. Chem., 1991, 95, 5261–5267.
2. M. R. Hoffmann, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96.
3. O. Carp, C. L. Huisman and A. Reller, Prog. Solid State Chem., 2004, 32, 33–177.
4. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
5. A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582.
6. B. Ohtani, J. Photochem. Photobiol., C, 2010, 11, 157–178.
7. C. McCullagh, J. M. C. Robertson, D. W. Bahnemann and P. K. J. Robertson, Res. Chem. Intermed., 2007, 33, 359–375.
8. D. Friedmann, C. Mendive and D. Bahnemann, Appl. Catal., B, 2010, 99, 398–406.
9. A. Fujishima, T. N. Rao and D. A. Tryk, J. Photochem. Photobiol., C, 2000, 1, 1–21.
10. A. L. Linsebigler, G. Lu and J. T. Yates Jr, Chem. Rev., 1995, 95, 735–758.
11. B. Ohtani, Recent Pat. Eng., 2010, 4, 149–154.
12. D. Mitoraj and H. Kisch, Angew. Chem., Int. Ed., 2008, 47, 9975–9978.
13. D. Mitoraj, R. Beranek and H. Kisch, Photochem. Photobiol. Sci., 2010, 9, 31–38.
14. J.-M. Herrmann, J. Disdier and P. Pichat, Chem. Phys. Lett., 1984, 108, 618–622.
15. W. Mu, J.-M. Herrmann and P. Pichat, Catal. Lett., 1989, 3, 73–84.
16. J. M. Herrmann, Sci. China: Chem., 2010, 53, 1831–1843.
17. M. D'Arienzo, N. Siedl, A. Sternig, R. Scotti, F. Morazzoni, J. Bernardi and O. Diwald, J. Phys. Chem. C, 2010, 114, 18067–18072.
18. A. Emeline, A. Salinaro and N. Serpone, J. Phys. Chem. B, 2000, 104, 11202–11210.
19. H. Gerischer and A. Heller, J. Electrochem. Soc., 1992, 139, 113–118.
20. Y. Tamaki, A. Furube, M. Murai, K. Hara, R. Katoh and M. Tachiya, J. Am. Chem. Soc., 2006, 128, 416–417.
21. L. Jing, Y. Cao, H. Cui, J. R. Durrant, J. Tang, D. Liu and H. Fu, Chem. Commun., 2012, 48, 10775–10777.
22. P. V. Kamat, J. Phys. Chem. Lett., 2012, 3, 663–672.
23. D. W. Bahnemann, J. Mönig and R. Chapman, J. Phys. Chem., 1987, 91, 3782–3788.
24. D. Hufschmidt, D. Bahnemann, J. J. Testa, C. A. Emilio and M. I. Litter, J. Photochem. Photobiol., A, 2002, 148, 223–231.
25. J. Lee and W. Choi, J. Phys. Chem. B, 2005, 109, 7399–7406.
26. A. A. Ismail and D. W. Bahnemann, Green Chem., 2011, 13, 428–435.
27. A. A. Ismail and D. W. Bahnemann, J. Phys. Chem. C, 2011, 115, 5784–5791.
28. N. Murakami, T. Chiyoya, T. Tsubota and T. Ohno, Appl. Catal., A, 2008, 348, 148–152.
29. H. Irie, K. Kamiya, T. Shibanuma, S. Miura, D. A. Tryk, T. Yokoyama and K. Hashimoto, J. Phys. Chem. C, 2009, 113, 10761–10766.
30. H. Yu, H. Irie, Y. Shimodaira, Y. Hosogi, Y. Kuroda, M. Miyauchi and K. Hashimoto, J. Phys. Chem. C, 2010, 114, 16481–16487.
31. X. Qiu, M. Miyauchi, K. Sunada, M. Minoshima, M. Liu, Y. Lu, D. Li, Y. Shimodaira, Y. Hosogi, Y. Kuroda and K. Hashimoto, ACS Nano, 2011, 6, 1609–1618.
32. M. Liu, R. Inde, M. Nishikawa, X. Qiu, D. Atarashi, E. Sakai, Y. Nosaka, K. Hashimoto and M. Miyauchi, ACS Nano, 2014, 8, 7229–7238.
33. Y. Nosaka, S. Takahashi, H. Sakamoto and A. Y. Nosaka, J. Phys. Chem. C, 2011, 115, 21283–21290.
34. M. Nishikawa, Y. Mitani and Y. Nosaka, J. Phys. Chem. C, 2012, 116, 14900–14907.
35. P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755.
36. T. Morikawa, Y. Irokawa and T. Ohwaki, Appl. Catal., A, 2006, 314, 123–127.
37. T. Arai, M. Horiguchi, M. Yanagida, T. Gunji, H. Sugihara and K. Sayama, J. Phys. Chem. C, 2009, 113, 6602–6609.
38. S. Neubert, P. Pulisova, C. Wiktor, P. Weide, B. Mei, D. A. Guschin, R. A. Fischer, M. Muhler and R. Beranek, Catal. Today, 2014, 230, 97–103.
39. S. J. A. Moniz, S. A. Shevlin, X. An, Z.-X. Guo and J. Tang, Chem.–Eur. J., 2014, 20, 15571–15579.
40. X. An, H. Liu, J. Qu, S. J. A. Moniz and J. Tang, New J. Chem., 2015, 39, 314–320.
41. S. J. A. Moniz and J. Tang, ChemCatChem, 2015, 7, 1659–1667.
42. R. Marschall, Adv. Funct. Mater., 2014, 24, 2421–2440.
43. S. J. A. Moniz, S. A. Shevlin, D. J. Martin, Z.-X. Guo and J. Tang, Energy Environ. Sci., 2015, 8, 731–759.
44. B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 5985–5992.
45. B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 4317–4318.
46. B. Kraeutler and A. J. Bard, J. Am. Chem. Soc., 1978, 100, 2239–2240.
47. T. E. Westre, P. Kennepohl, J. G. deWitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314.
48. R. Hocking and E. Solomon, in Molecular Electronic Structures of Transition Metal Complexes I, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer, Berlin Heidelberg, 2012, pp. 155–184.
49. S. K. Poznyak, V. I. Pergushov, A. I. Kokorin, A. I. Kulak and C. W. Schläpfer, J. Phys. Chem. B, 1999, 103, 1308–1315.
50. A. Amorelli, J. C. Evans and C. C. Rowlands, J. Chem. Soc., Faraday Trans., 1989, 85, 4111–4118.
51. G. Li, N. M. Dimitrijevic, L. Chen, T. Rajh and K. A. Gray, J. Phys. Chem. C, 2008, 112, 19040–19044.
52. H. J. Gerritsen and E. S. Sabisky, Phys. Rev., 1962, 125, 1853–1859.
53. J. G. Darab and R. K. MacCrone, Phys. Chem. Glasses, 1991, 32, 91.
54. P. G. Harrison, C. Bailey, W. Daniell, D. Zhao, I. K. Ball, D. Goldfarb, N. C. Lloyd and W. Azelee, Chem. Mater., 1999, 11, 3643–3654.
55. T. A. Egerton, E. Harris, E. John Lawson, B. Mile and C. C. Rowlands, Phys. Chem. Chem. Phys., 2001, 3, 497–504.
56. A. Amorelli, J. C. Evans, C. C. Rowlands and T. A. Egerton, J. Chem. Soc., Faraday Trans., 1987, 83, 3541–3548.
57. P.-O. Andersson, E. L. Kollberg and A. Jelenski, Phys. Rev. B: Solid State, 1973, 8, 4956–4965.
58. H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Theor. Chem. Acc., 2007, 117, 565–574.
59. N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2011, 115, 7562–7572.
60. F. M. Hossain, G. E. Murch, L. Sheppard and J. Nowotny, Defect Diffus. Forum, 2006, 251–252, 1–12.
61. A. Walsh and C. R. A. Catlow, J. Mater. Chem., 2010, 20, 10438–10444.
62. L. Kernazhitsky, V. Shymanovska, T. Gavrilko, V. Naumov, L. Fedorenko, V. Kshnyakin and J. Baran, J. Lumin., 2014, 146, 199–204.
63. L. Eberson and F. Radner, J. Am. Chem. Soc., 1991, 113, 5825–5834.
64. W. Kim, T. Tachikawa, G.-H. Moon, T. Majima and W. Choi, Angew. Chem., Int. Ed., 2014, 53, 14036–14041.
65. T. Hirakawa and Y. Nosaka, Langmuir, 2002, 18, 3247–3254.
66. T. Berger, D. Monllor-Satoca, M. Jankulovska, T. Lana-Villarreal and R. Gómez, ChemPhysChem, 2012, 13, 2824–2875.
67. D. Monllor-Satoca and R. Gomez, J. Phys. Chem. C, 2008, 112, 139–147.
68. M. Matsuoka and M. Anpo, J. Photochem. Photobiol., C, 2003, 3, 225–252.
69. H. Yamashita and M. Anpo, Curr. Opin. Solid State Mater. Sci., 2003, 7, 471–481.
70. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986.
71. J. Ryu and W. Choi, Environ. Sci. Technol., 2007, 42, 294–300.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and theoretical methods; XAS data; photocatalytic degradations with physical mixtures; UV-Vis spectra during 4-CP degradation; Raman spectra; XRD; HAADF-STEM images and EELS spectra; PL spectra; OH radical measurements; stability measurements. See DOI: 10.1039/c5ta07036h

---